Appunti di Statistica Matematica Inferenza Statistica Multivariata Anno Accademico 2014/15
|
|
|
- Filomena Ada Greco
- 8 anni fa
- Visualizzazioni
Transcript
1 Apputi di Statistica Matematica Ifereza Statistica Multivariata Ao Accademico 014/15 November 19, Campioi e modelli statistici Siao Ω, A, P uo spazio di probabilità e X = X 1,..., X u vettore aleatorio su Ω a valori i u isieme X. L isieme X è detto spazio campioario, il vettore X = X 1,..., X campioe e taglia campioaria. Spesso per ogi i = 1,..., si ha X i R, ma o ecessariamete. Ua realizzazioe di X, idicata co x = x 1,..., x, è detta valore campioario/campioato e rappreseta u dato osservato. Defiizioe 1.1 U campioe è detto casuale se le sue compoeti soo mutualmete idipedeti 1 e seguoo la stessa legge. L espressioe campioe idipedete ed ideticamete distribuito, i breve i.i.d., è sioimo di campioe casuale. U espressie alterativa è copie idipedeti della stessa variabile aleatoria. La legge di X determia il modello probabilistico e talora può essere iterpretata come il processo geeratore dei dati. I dati osservati soo iterpretati come ua realizzazioe del campioe. Scopo dell ifereza statistica è utilizzare i dati per otteere iformazioi su il processo che li geera. Esempio 1. Sia X ua variabile aleatoria di legge Poissoλ co λ > 0 e siao X 1,..., X copie idipedeti di X. Allora X = X 1,..., X è u campioe casuale. I questo esempio oto λ, è oto il modello probabilistico. Si immagii per esempio che per i = 1,...,, la variabile aleatoria v.a. X i rappreseti il umero di prodotti difettosi i ua liea di produzioe il gioro i-esimo di u certo periodo. La legge di Poisso è ua delle distribuzioi utilizzate per modelizzare eveti rari. La stima del valore di λ forisce cotemporaeamete iformazioi su quati difettosi ci soo i media al gioro e dà ua misura dello scostameto dal valor medio: EX 1 = VarX 1 = λ. L ipotesi di campioe casuale è u ipotesi sulla raccolta di dati, per esempio può idicare che la tecica di raccolta dati è la stessa ogi gioro, e ache sulla liea di produzioe, per esempio può idicare che le codizioi di lavorazioe soo idetiche ogi gioro. Esercizio 1.3 Per il campioameto da u ura co reimmissioe/seza reimmissioe, idividuare il campioe. E casuale? Macao iformazioi per idividuare Ω, A, P? Esempio 1.4 Campioe casuale Beroulliao. Galto ed il campioameto ormale per le altezze per gruppi omogeei per sesso ed età, altezze dei figli predette da quelle dei padri: regressioe lieare. Errori di misurazioe. Regressioe verso la media. Altezza mattia/sera: dati appaiati. *** sviluppare *** Defiizioe U modello statistico per X è ua famiglia di distribuzioi di probabilità su/per X: F = { F X x 1,..., x : x 1,..., x X e F X fuzioe di ripartizioe su X } Per correzioi e suggerimeti riccomago@dima.uige.it 1 Gli eveti A i A, i N soo mutualmete o cogiutamete idipedeti se P k J A k = k J PA k per ogi J N fiito. 1
2 . U modello statistico F è detto parametrico se esiste Θ R p tale che la mappa Θ F defiita da θ F X ; θ è biiettiva. Si oti che 1. u modello statistico parametrico è i relazioe biuivoca co u sotto isieme di uo spazio vettoriale di dimesioe fiita, detto spazio dei parametri,. il modello statistico F è idetificabile poiché ad ogi θ Θ è associato u, ed u solo, modello probabilistico di F. Nelle applicazioi soo spesso utili i modelli semi-parametrici solo parzialmete specificati da parametri. Le leggi F i F possoo essere specificate i vari modi, tipicamete tramite desità o fuzioi di ripartizioe. Compito dell ifereza statistica è selezioare u modello probabilistico all itero del modello statistico utilizzado i dati. Esempio Per X 1,..., X N µ,..., µ, σ } {{ } I, se σ è oto, lo spazio dei parametri è R; se µ è oto lo spazio dei parametri è R >0 ; se etrambi soo o oti allora Θ = R, R >0 e θ = µ, σ.. Per X Poissoλ, λ Θ = R >0. 3. Siao X R e a la orma euclidea del vettore a R. a F = {tutte le leggi di probabilità su X 1,..., X } è modello statistico o parametrico. b F = {tutte le leggi di probabilità su X 1,..., X co margiali uivariate idipedeti} è modello statistico o parametrico. c F = {F X x; µ = F 0 x µ : F 0 fuzioe di ripartizioe uivariata e µ R} è modello statistico semi-parametrico. 4. Le famiglie di posizioe e scala soo modelli semi-parametrici: X è u campioe i.i.d e si ipotizza che X 1 1 x µ σ f e µ, σ R R >0 co f desità, µ parametro di posizioe e σ di scala. U tipico σ modello di posizioe e scala è dato da N µ, σ, µ R e σ R dove fx = exp x // π. 5. L isieme delle desità simmetriche e cotiue su R è u modello semi-parametrico dove il parametro reale idetifica l asse di simmetria. Spesso u modello statistico è dato i termii di desità rispetto ad ua misura domiate che el seguito assumiamo sia la misura di Lebesgue: f X ; θ oppure PX = ; θ. Esempio 1.7 X N 1 µ 1 + µ, σ co µ 1, µ R e σ oto o è idetificabile. Esercizio 1.8 Verificare che per f desità uivariata, µ R e σ R >0 allora gx = 1 σ Esercizio 1.9 Siao X 1,..., X i.i.d. a valori reali e g 1,..., g fuzioi da R a R. 1. g 1 X 1,..., g X soo idipedeti? Soo i.i.d? x µ f σ è ua desità.. Sotto quali ipotesi valgoo le segueti uguagliaze? E g ix i = E g ix i = E g 1 X Sotto quali ipotesi valgoo le segueti uguagliaze? Var g ix i = Var g ix i = Var g 1 X Idetificabilità e stimabilità Ache se o vi faremo riferimeto i seguito è opportuo geeralizzare il puto. della Defiizioe 1.5 e cofrotarla co quella di fuzioe stimabile del parametro. Defiizioe 1.10 Siao X u campioe e F = { F X ; θ : θ Θ R p} u modello statistico parametrico. 1. La fuzioe hθ del parametro è idetificabile se hθ 1 hθ implica che F X ; θ 1 F X ; θ.. La fuzioe hθ del parametro è stimabile se esiste ua fuzioe g di X tale che E θ gx = hθ per ogi θ Θ.
3 I altre parole, h è idetificabile se, al variare dei valori che assume, ache la distribuzioe del vettore aleatorio osservabile X cambia e, aticipado della omeclatura, è stimabile se esiste u suo stimatore corretto. Proposizioe 1.11 Se h è stimabile allora è idetificabile. Proof. Se h è stimabile allora esiste g tale che E θ gx = hθ per ogi θ Θ. Se hθ 1 hθ allora E θ1 gx E θ gx. Si deduce che le due leggi probabilistiche rispetto le quali si soo calcolati i due valori attesi soo differeti. Esempio 1.1 Sia p ]0, 1[ e X Beroullip co X {0, 1} e PX = 1 = p. La fuzioe hp = p è idetificabile, ma o stimabile: ifatti dovrebbe esistere ua fuzioe g tale che E θ gx = 1 pg0 + pg1 = p, che è impossibile. Esercizio 1.13 Siao X Beroullip co X {0, 1} e Y Beroullip co Y { 1, 1} e PX = 1 = p = PY = 1. Calcolare EX e VarX, EY e VarY. 1. Modelli regolari Defiizioe 1.14 Sia X u vettore aleatorio co desità cogiuta f X. Il supporto di f X, suppf X, è la chiusura ella topologia euclidea di {x : f X x > 0}. U modello statistico parametrico è regolare se il supporto di ogi suo modello probabilistico o dipede dal parametro. Esempio 1.15 Per = 1 e X N µ, σ, il supporto è R R >0 per ogi µ, σ ed il modello è regolare. Per θ R >0 e f X = Uiforme]0, θ[, il supporto è [0, θ] e il modello X Uiforme]0, θ[, θ R >0, è modello o regolare. Esercizio 1.16 Verificare che Poissoλ, λ > 0, è u modello regolare. Esempio 1.17 Esempi otevoli di modelli regolari soo i classici modelli di classe espoeziale, modelli di regressioe lieare, modelli grafici di idipedeza. U modello statistico {f X : desità di probabilità} per u campioe X X è detto di classe expoeziale se p f X x = hx exp θ, T x ψθ = hx exp θ i T i x ψθ co h : X R >0, θ Θ spazio vettoriale, T : X Θ e, prodotto scalare su Θ. La fuzioe ψ è detta fuzioe dei cumulati e θ parametro aturale. I modelli di classe espoeziale soo regolari. Quasi sempre, ma o ecessariamete, avremo Θ = R p. No defiiamo modelli di regressioe é grafici, eccetto brevemete. Esercizio 1.18 Siao X 1,..., X i.i.d. di legge h exp T, θ ψθ. 1. Verificare che hx exp T x, θ dx = exp ψθ. X. Calcolare la legge cogiuta del campioe. 3. La legge cogiuta del campioe è u modello di classe espoeziale? Studieremo tre pricipi che soo alla base dell ifereza statistica parametrica: 1 sufficieza: riassumere i dati seza perdere iformazioi sul parametro, verosimigliaza: idetificare tutte le iformazioi sul parametro coteute ei dati, 3 ivariaza: trasformare lo spazio dei parametri e lo spazio campioario i sicroia/cotemporaeamete. 3
4 Statistiche Defiizioe.1 Si dice statistica ua fuzioe del solo campioe X e distribuzioe campioaria la sua legge di probabilità. Sia il vettore aleatorio T X sia la sua realizzazioe soo chiamati statistica. Ua statistica è ua fuzioe dei dati che forisce ua sitesi di iteresse per lo studio di u particolare aspetto dei dati e/o del sistema che li geera. Ua statistica o dipede dal modello statistico, ma solo dal campioe. I particolare se il modello statistico è parametrico, o dipede dal parametro. E u vettore aleatorio, spesso uidimesioale, la cui legge di probabilità può essere talora determiata dalla legge del campioe. Gli stimatori putuali, che vedremo più avati, soo statistiche utilizzate per stimare il parametro θ, o ua sua fuzioe, di u modello statistico parametrico. Ua statistica T iduce ua partizioe dello spazio campioario Ω: per esempio, se X = R e T R, la mappa X T {}}{ Ω R {}}{ R defiisce la partizioe i cui elemeti soo {ω Ω : T X = x}, x R. Esempio. Siao X 1,..., X variabili aleatorie a valori i R. I segueti soo esempi di statistiche. Totale campioario: T = X i Media campioaria: X = T/ Variaza campioaria: S = X i X / 1 e S 1/ Massimo campioario: X = max{x 1,..., X } Miimo campioario: X 1 = mi{x 1,..., X } Statistica d ordie del campioe: sort{x 1,..., X } = X 1, X,..., X Il campioe X = X 1,..., X è ua statistica I u modello di classe espoeziale le T i, i = 1,..., p, soo statistiche Esempio.3 1. Sia X 1,..., X N µ, σ i.i.d. co µ R e σ R >0 allora R = X µ o è ua statistica. Se µ è oto allora R è ua statistica.. Sia X 1,..., X Uif]0, θ[ co θ > 0 allora R = X /θ o è ua statistica. Ma è molto utile. Cosa rappreseta? Esercizio.4 Verificare che per le segueti statistiche e modelli statistici le distribuzioi campioarie soo quelle idicate. 1. Se X 1,..., X campioe Beroulliao di parametro p i.i.d, allora T = X Bi, p. Se X 1,..., X N µ, σ i.i.d. allora X N µ, σ / 3. Sia X 1,..., X u campioe a valori reali, i.i.d e co fuzioe di ripartizioe F. La distribuzioe del massimo campioario è F. Determiare la legge del miimo campioario. Esempio.5 1. Siao Ω, A, P, A A e 1 A ω = Aω = Allora A BeroulliPA. Si oti che EA = PA. { 1 se ω A 0 se ω A. Sia X u vettore aleatorio a valori i R. Sia A R u isieme Borel misurabile. Allora { 1 se Xω A X Aω = 1 X A ω = 0 se Xω A e X A BeroulliPX A. 4
5 Esempio.6 Siao X 1,..., X R i.i.d. e co fuzioe di ripartizioe F X. Sia x R. La statistica Cx = X i x cota quati dati soo miori od uguali a x. Assume valori i {0,..., } e per j {0,..., } si ha PCx j = P X i x j = la probabilità che ci siao al più j dati o maggiori di x La statistica Cx è la somma di Beroulli di parametro F X x idipedeti. Quidi la distribuzioe campioaria di Cx è Biomiale, F X x. Esercizio.7 Siao X 1,..., X Cauchy0, σ per σ > 0 cioè f X1 x = 1 1 πσ 1+x/σ, x R. 1. Verificare che EX 1 o esiste.. E u modello di posizioe e/o scala? 3. Verificare che la fuzioe di ripartizioe è F X1 x = 1 x π arcta + 1 e la fuzioe caratteristica è σ φ X t = exp σ t. 4. Nell ipotesi che il campioe sia i.i.d., verificare che Esercizio.8 Siao X 1,..., X N i.i.d di legge 1 σ f x µ σ Xi 1. Idividuare Z i per cui X i = σz i + µ e determiare la desità.. Soo gli Z 1,..., Z i.i.d.? 3. Verificare che X = σ Z + µ e Var X = σ Var Z..1 Statistiche sufficieti Cauchy0, σ. co µ R e σ > 0. Defiizioe.9 Teorema della fattorizzazioe Sia X u campioe statistico su Ω, A, P a valori i X e sia F = { f X ; θ : θ Θ co f desità di probabilità } u modello statistico parametrico per X. Ua statistica T = T X è detta sufficiete per θ se esistoo due fuzioi h e g tali che per ogi θ Θ e per quasi ogi x X. f X x; θ = hxgt x, θ Chiaramete se X è u isieme umerabile allora f X x; θ = PX = x; θ, scriveremo ache P θ X = x. La defiizioe suggerisce che ua statistica è sufficiete se cattura tutte le iformazioi sul parametro coteute el campioe. Più precisamete, se due isiemi di dati producoo lo stesso valore della statistica sufficiete, allora co ragioameti basati sulla legge cogiuta del campioe detta ache fuzioe di verosimigliaza quado letta come fuzioe del parametro dai due campioi si otterrao idetiche deduzioi ifereziali sul parametro. Questa iterpretazioe è ribadita dal seguete teorema. Theorem.10 di Neyma-Fisher Ua statistica T è sufficiete per θ se e solo se la distribuzioe codizioata di X a T X = t o dipede da θ per ogi valore della statistica T. Proof. La dimostrazioe el caso cotiuo è lasciata al lettore. Nell ipotesi che T sia sufficiete per θ, si oti che per ogi t valore di T vale f T t = P θ T = t = P θ X = x, T X = t = P θ X = x x:t x=t = x:t x=t = gt, θ hxgt x, θ x:t x=t x:t x=t perché T è sufficiete per θ hx = gt, θh x co h x = x:t x=t hx 5
6 I particolare la legge di T dipede dal parametro solo tramite la fuzioe g. Ora si osservi che P θ X = x, T = t = P θx = x gt, θhx = f X T X=t x, θ = P θ T = t P θ T = t gt, θh x = hx h se T x = t x o defiita altrimeti Viceversa la tesi segue dall osservare che f X = f X,T = f X T f T. Esempio.11 Siao X 1,..., X i.i.d. Beroullip co p Θ =]0, 1[. Verificare che T = X i è statistica sufficiete per p. Utilizzado la defiizioe calcoliamo la legge cogiuta del campioe e cerchiamo di determiare ua fattorizzazioe i due fattori di cui uo dipede dal parametro e l altro dipede dal campioe solo tramite T P p X = x = P p X 1 = x 1,..., X = x = = p xi 1 p 1 xi P p X 1 = x i = p xi 1 p xi = p t 1 p t da cui hx = 1 e gt, p = p t 1 p t. Facciamo la verifica utilizzado il teorema. Occorre cosiderare la legge codizioata del campioe al valore assuto dalla statistica sufficiete quidi 0 se x i t P p X = x T = t = P p X = x, T = t = pt 1 p t P p T = t t pt 1 p = 1 t se x i = t t Esempio.1 1. La statistica T ella defiizioe di modello statistico di classe espoeziale è sufficiete per il parametro aturale.. Il campioe è statistica sufficiete per il parametro di ogi modello statistico parametrico sul campioe stesso. Il campioe è statistica sufficiete. Esempio.13 Sia X 1,..., X i.i.d. Uif{1,,..., θ} co θ Z 1. La legge cogiuta del campioe è f X x; θ = 1 θ x i {1,..., θ} = 1 θ x i {1,..., θ} = 1 θ x 1 1x θ x i Z 1 Allora T = X è sufficiete per θ ifatti gt, θ = x θ θ e hx = x 1 1 x i Z 1. Esempio.14 Sia X 1,..., X i.i.d. N 1 µ, σ co µ, σ R, R >0. Determiiamo statistiche sufficieti per µ, σ, µ e σ. 1. La legge cogiuta del campioe è 1 f X x = exp x i µ 1 πσ σ = πσ exp x i µ σ Si oti che x i µ = x i x + x µ = x i x + x µ + 0 6
7 e quidi f X x = πσ / exp 1 σ s x µ σ Poedo h 1 e g = f X si evidezia che X, S è ua statistica sufficiete per θ = µ, σ. Per g = exp σ x µ si ha che X è ua statistica sufficiete per µ oto σ. Poedo h 1 e g = f X si deduce che X, S è sufficiete per σ.. Poiché X N 1 µ, σ / si ha f X Xx = f πσ Xx / exp 1 f X x = σ s x µ σ πσ / 1/ exp x µ σ / 1 = πσ exp x i x /σ 1 Dal teorema di Neyma-Fisher si deduce che X è sufficiete per µ. Esercizio Dimostrare che ua fuzioe ivertibile di ua statistica sufficiete per u parametro θ è acora statistica sufficiete per θ. I particolare le statistiche sufficieti o soo uiche.. Sia X 1,..., X i.i.d. Expλ, λ > 0. Verificare che la media campioaria è ua statistica sufficiete per λ. 3. Sia X 1,..., X i.i.d. Uiform]0, θ[, θ > 0. Determiare ua statistica sufficiete uivariata per θ. Esempio.16 Sia Θ = {0, 1}, θ 0 = 0 e θ 1 = 1. Il rapporto di verosimigliaza è statistica sufficiete per θ, ifatti θ fx x; θ 1 f X x; θ = f X x; θ 0 f X x; θ 0. Statistiche sufficieti miimali Defiizioe.17 Ua statistica sufficiete per θ è sufficiete miimale per θ se è sufficiete ed è fuzioe di ogi altra statistica sufficiete per θ. Esempio.18 Per X 1,..., X campioe casuale N µ, σ, X = X i/ e X = X 1,..., X soo sufficieti per µ. Poiché X è fuzioe di X, X o è sufficiete miimale. Per defiizioe, se T è ua statistica sufficiete e T è sufficiete miimale allora esiste ua fuzioe h tale che T = ht ed i particolare se T x = T y allora T x = T y. Ua statistica sufficiete miimale può essere calcolata se ota h a partire da ogi altra statistica sufficiete. Si itede che i dati o possoo essere compressi ulteriormete seza perdere iformazioi su θ. L Esercizio.7 illustra u caso i cui due statistiche sufficieti e miimali hao dimesioe diversa. La ota successiva precisa quato sopra. Osservazioi La partizioe dello spazio campioario X idotta dalla statistica sufficiete T è tale per cui la legge cogiuta del campioe f X può essere ricostruita a meo di ua costate moltiplicativa cooscedo il valore di f X i u puto di ogi elemeto della partizioe. La partizioe sia su Ω che su X idotta da ua statistica sufficiete miimale è la meo fie tra quelle idotte da statistiche sufficieti.. Se e deduce che diverse statistiche sufficieti miimali iducoo la stessa partizioe su X e che ua fuzioe biuivoca di statistica sufficiete miimale è sufficiete miimale. 3. Ua statistica sufficiete o miimale cotiee iformazioi superflue sul parametro per ricostruire la legge cogiuta del campioe. X {}}{ Ω X T {}}{ T T M {}}{ T M. 7
8 4. Il seguete teorema dà ua codizioe sufficiete affichè ua statistica sia sufficiete miimale. Theorem.0 Se per x, y X il rapporto f Xx; θ f X y; θ, detto rapporto di verosimigliaza,3 è costate i θ se e solo se T x = T y allora T è sufficiete e miimale per θ. Proof. Per semplicità suppoiamo che f X x; θ > 0 per ogi x, θ. Deduciamo prima che T è sufficiete per θ. Per ogi valore t assuto da T sia A t = {x X : T x = t}. I particolare per ogi x, y A t si ha T x = T y e per ipotesi f Xx; θ f X y; θ cosideri y A T x e la fuzioe hx = f Xx; θ f X yx; θ o dipede da θ. Ora per x X si che o dipede da θ per costruzioe. Si scriva f X x; θ = f X x; θ f Xyx; θ f X yx; θ = f Xx; θ f X y; θ f Xy; θ = hxgt y; θ dove l ultima uguagliaza segue dall arbitrarietà di y i A t. Ora dimostriamo la miimalità di T. Sia T u altra statistica sufficiete per θ. I particolare esistoo h e g tali che f X x; θ = h xg T x; θ Per x, y X e poiché T è sufficiete si ha f X x; θ f X y; θ = h xg T x; θ h yg T y; θ = h x h y per ogi x, y tali che T x = T y. Questo rapporto evidetemete o dipede da θ. Per ipotesi questo avviee se e solo se T x = T y, da cui T è fuzioe di T. Esempio.1 Sia X 1,..., X u campioe casuale N µ, σ co µ, σ R R >0. Verificare che T = X, S è sufficiete miimale per µ, σ. Occorre caratterizzare il luogo dei puti y per cui dove 1s x = x i x. Si ha f X x; µ, σ f X y; µ, σ = πσ / exp x µ + 1s x /σ πσ / exp ȳ µ + 1s y /σ f X x; µ, σ f X y; µ, σ = exp = exp σ x ȳ µ x ȳ + 1s x s y σ x ȳ x + ȳ µ + 1s x s y da cui si deduce che il rapporto di verosimigliaza o dipede da σ e da µ se e solo se l argometo dell espoeziale è zero cioè se e solo se x ȳ x + ȳ µ + 1s x s y = 0 se e solo se x = ȳ e s x = s y, equivaletemete se e solo se T x = T y. Esercizio. Verificare che il modello statistico dell Esempio.1 è di classe espoeziale. parametro aturale, statistiche sufficieti e fuzioe geeratrice dei cumulati. Idividuare Esercizio.3 1. Si osservi che dai calcoli ell Esempio.1 segue che T = X, S è ache sufficiete miimale per σ > 0 ell ipotesi di modello casuale N σ, σ. 3 Cofrota lo stesso modello probablistico i diversi valori campioari/ dati. 8
9 . Si verifichi che il modello N σ, σ, σ > 0, o è di classe espoeziale. Esempio.4 Sia X 1,..., X u campioe casuale Uif]θ, θ + 1[ co θ R. Determiare ua statistica sufficiete miimale per θ. La legge cogiuta del campioe è f X x 1,..., x ; θ = θ < x i < θ + 1 = θ < mi x i i max i x i < θ + 1 = θ < x 1 x 1 < θ = x 1 < θ < x 1 Si oti che la statistica RagoX = X X 1 appartiee a ]0, 1[ co probabilità uo. Ora siao x, y possibili valori campioari { f X x; θ f X y; θ = x 1 < θ < x 1 1 se x = y = e x 1 = y 1 y 1 < θ < y 1 dipede da θ altrimeti Per accertarsi dell ultima eguagliaza disegare il grafico del rapporto di verosimigliaza. Per il Teorema.0 T X = X 1, X è statistica suffiete miimale per θ. Esempio.5 I u modello di classe espoeziale fx; θ = hx exp T x, θ ψθ le statistiche T soo sufficieti miimali per il parametro aturale. Ifatti o dipede da θ se e solo se T x = T y. f X x; θ f X y; θ = hx hy exp T x T y, θ Esercizio.6 1. Determiare ua statistica sufficiete miimale per θ i campioe casuale uiforme su {1,..., θ} Z co θ Z 1. Cosiderare u campioe casuale -dimesioale di legge di probabilità N σ, σ co σ > 0. Verificare che ua statistica sufficiete miimale per il parametro uivariato θ è la statistica bidimesioale X i, X i. Esercizio.7 Siao X 1, X i.i.d. Beroullip co p ]0, 1[. 1. Descrivere lo spazio campioario X. {i, j : i, j = 0, 1}. Verificare che il totale campioario è statistica sufficiete miimale per p ed idividuare la partizioe di X corrispodete. A t=0 = {0, 0}, A t=1 = {0, 1, 1, 0}, A t= = {1, 1}. 3. Verificare che T = X 1, X è sufficiete miimale per p. Stessa partizioe del totale campioario. 4. Come risolviamo il fatto che T bidimesioale e totale campioario uidimesioale soo etrambi sufficieti miimali per p? Dedurre che statistiche sufficieti miimali o hao ecessariamete la stessa dimesioe. 5. Verificare che la statistica R = X 1 X o è sufficiete miimale per p..3 Statistiche acillari Defiizioe.8 Sia X u campioe su Ω, A, P e F u modello statistico su X idicizzato dal parametro θ Θ. Ua statistica T X è detta acillare per θ se la distribuzioe campioaria di T o dipede da θ. Esempio.9 Per u campioe casuale ormale N µ, σ, la statistica S = X 1 X è acillare per µ, o è acillare per σ. 9
10 Esempio.30 Sia F ua fuzioe di ripartizioe per ua variabile aleatoria cotiua a valori reali. Sia X 1,..., X campioe casuale di legge F θ co θ R e per x R valga F x θ = F Xi x per ogi i = 1,...,. Notare che se F o è ota, si tratta di u modello semiparametrico. Co F ota è u modello parametrico. Verificare che la statistica R = X X 1 0 è acillare per θ. Si defiiscao le variabili aleatorie idipedeti Z i = X i θ per i = 1,...,. La fuzioe di ripartizioe di Z i è F per ogi i ifatti per z i R si ha PZ i z i = PX i z i + θ = F z i + θ θ = F z i I particolare la legge di Z i o dipede da θ. Allora per r 0 si ha F R r = PR r = PX X 1 r = PX θ + θ X 1 r = PZ Z 1 r Poiché Z Z 1 è fuzioe degli Z i la cui legge o dipede da θ, eppure la legge di R dipede da θ. Si coclude che R è acillare per θ. Esercizio.31 Sia X 1,..., X u campioe casuale di legge F σ co σ > 0. Verificare che ogi statistica del tipo S X1 X,..., X 1 è acillare per σ. Utilizzare le variabili aleatorie ausiliarie Z i = Xi σ. X Osservazioi.3 acillarità per modello o parametrico Siao X 1,..., X i.i.d. cotiue uivariate co mediaa uguale a zero. Si osservi che T = X i > 0 Bi, 1/ e quidi la legge di probabilità di T è la stessa per ogi modello probabilistico ella famiglia statistica. Ovvero T è acillare per il modello statistico. La statistica T può essere usata per verificare l ipotesi di mediaa ulla. Esempio.33 acillarità può dare iformazioi sul parametro Sia X ua variabile aleatoria uiforme a valori i θ, θ + 1, θ + co θ Z. Si ha X θ θ + 1 θ + PX = x 1/3 1/3 1/3 X θ 0 1 Siao X 1 e X copie idipedeti di X e si cosideri la statistica T = R, M dove R = X X 1 e M = X 1 + X = X 1 + X. Notare che 1. lo spazio campioario dipede dal parametro modello o regolare;. R {0, 1, } e M {θ, θ + 1/, θ + 1, θ + 3/, θ + }; 3. la statistica R è acillare per θ [Esercizio.30]; 4. T è sufficiete miimale per θ. Questo si deduce dal fatto che X 1, X è sufficiete miimale per θ. 5. Sia r, m ua realizzazioe di T e si osserva che m è itero. Da ciò si deduce che m {θ, θ + 1, θ + } e quidi θ {m, m 1, m }. 6. Aggiugo l iformazioe che il valore osservato della statistica acillare R è. Quidi si ha { x1 + x = m x x 1 = equivaletemete x 1 = m 1 e x = m + 1. Notare che R = è possibile solo per x = θ + e x 1 = θ. Cocludedo si ha { x1 = m 1 = θ e quidi θ = m 1. x = m + 1 = θ + 10
11 .4 Statistiche complete Defiizioe.34 Sia T ua statistica e g ua fuzioe di T. La statistica T è completa per θ se E θ gt X = 0 per ogi θ Θ implica g = 0. Osservazioi Ua versioe più precisa della Defiizioe.34 afferma che, E θ gt X = 0 per ogi θ Θ, allora g = 0 deve valere co probabilità uo per ogi modello probabilistico el modello statistico: T è completa per θ se E θ gt X = 0 implica P θ gt = 0 = 1 per ogi θ.. Ua versioe poco più debole della defiizioe richiede che l implicazioe valga per g limitata completezza limitata. 3. No è difficile adattare la defiizioe di statistica completa per modelli o-parametrici. 4. I geere è difficile dimostrare che ua statistica è completa. Nell Esercizio.45 dimostreremo che la statistica caoica i u modello di classe espoeziale è completa per il parametro aturale, oltre ad essere sufficiete miimale. Esercizio.36 Dimostrare che ua statistica che è fuzioe ivertibile di statistica completa è completa. Cosa cambia se ella defiizioe se si suppoe E θ gt X = costate?. Esempio.37 Sia X 1,..., X u campioe i.i.d. Beroulliθ co θ ]0, 1[. Verifichiamo che T = X i è completa per θ. Per g fuzioe di T suppoiamo quidi 0 = E θ gt X = t=0 gtθ t 1 θ t = 1 θ t t=0 gtr t t dove r = θ 1 θ. Questo è u poliomio i r. Per il pricipio di idetità dei poliomi è zero se e solo se tutti i suoi coefficieti soo zero, cioè t gt e quidi g = 0 ideticamete. Esempio.38 Sia X Uiforme] θ, θ[ co θ > 0. Poiché E θ X = 0 per ogi θ, la statistica T X = X o è completa per θ. Esempio.39 Sia X 1,..., X u campioe i.i.d. Uiforme]0, θ[ co θ > 0. Verificare che T = X è completa per θ. Occorre verificare che se E θ gt = 0 allora g Valga 0 = EgT = θ 0 gt t 1 θ dt = 1 θ θ gtt 1 dt 0 } {{ } 0. Si derivi i θ 0 = d 1 dθ θ θ 0 gtt 1 dt = θ d dθ θ 0 d θ gtt 1 dt + dθ θ gtt 1 dt 0 =θ gθθ perché EgT = 0 =gθ/θ e quidi EgT = 0 implica g = 0 per ogi g tale che i passaggi precedeti soo possibili. 3. Possiamo effettivamete cocludere che T è completa? Theorem.40 Teorema di Basu Sia X u campioe su uo spazio di probabilità Ω, A, P e sia Θ lo spazio parametrico di u modello statistico per X. Siao V ua statistica acillare per θ Θ e T ua statistica sufficiete e completa per θ. Allora V e T soo idipedeti per ogi θ Θ. Proof. Dimostriamo che la legge cogiuta di V e T è il prodotto delle leggi margiali. 11
12 Sia B tale che {ω Ω : V ω B} A cosicchè è variabile aleatoria. V B = { 1 se V ω B 0 altrimeti P θ V B = E θ V B o dipede da θ poiché V è acillare. Per la proprietà della torre del valore atteso codizioato vale E θ E θ V B T = E θ V B = P V B ed ioltre E θ V B T o dipede da θ per il teorema di Neyma-Fisher poiché T è sufficiete. Da ció segue che l argometo del valore atteso E θ E V B T P V B = 0 è ua statistica poiché o dipede da θ ed è fuzioe di T. Poiché T è completa allora E V B T = P V B Ora siao A e B due qualuque isiemi tali che V B e T A siao variabili aleatorie. Allora P θ V B, T A = E θ V BT A = E θ E θ V BT A T = E θ T A E θ V B T = E θ T A P V B = P V B E θ T A = P V B P θ T A T A è fuzioe di T Esempio.41 Teorema di Cochra Siao X 1,..., X i.i.d. N µ, σ. La media campioaria X N µ, σ / è sufficiete e completa per µ statistica caoica i modello di classe espoeziale. La legge di 1S/σ = X i X χ 1 o dipede da µ e quidi la legge di S o dipede da µ. Allora per il teorema di Basu X e S soo idipedeti. σ Esempio.4 Sia X 1,..., X i.i.d. Espoezialeλ, λ > 0 fx; λ = 1/λ exp x/λ x > 0 X Calcolare E X λ X X. Si osservi che f ; λ è ua famiglia di scala e quidi per l esercizio.31 X X è acillare per λ. La statistica T X = X i è completa, sufficiete miimale per λ perché statistica caoica X i u modello di classe espoeziale. Quidi per il teorema di Basu T X è idipedete da X X. Ricordiamo che E λ X 1 = λ, somma di espoeziali i.i.d. è Gamma, λ e per X Gammaα, β il valore atteso di X è αβ e la sua variaza è αβ. Si deduce λ = E λ X = E λ i = E λ X i E λ i X i X X i X i i X i seza cooscere la distribuzioe cam- X da cui E λ = 1/. Abbiamo calcolato il valore atteso di i Xi pioaria. X = λ E λ i X i X i Xi 1
13 Esercizio.43 Necessità dell ipotesi di completezza el teorema di Basu Nell Osservazioe.33 la statistica R è acillare per θ e R, M è sufficiete miimale, però o soo idipedeti dimostrarlo e.g. per R = 0 e M = θ + 1/ oppure ell Osservazioe.33 si è utilizzata u iformazioe su R per specificare quella data da M. I particolare e segue che R, M o è completa. Seppure può sembrare che ua statistica acillare la cui distribuzioe o dipede dal parametro ed ua statistica sufficiete miimale che riduce i dati al massimo seza perdere iformazioi sul parametro debbao essere idipedeti/o relazioati, questo esempio idica che la ozioe giusta per discutere l idipedeza tra statistiche sufficieti e statistiche acillari è la completezza e o la miimalità. Esercizio.44 Dimostrare che ua statistica T sufficiete miimale e completa per θ è idipedete da ogi statistica acillare per θ. Esercizio.45 Nel modello statistico di classe espoeziale ft x = ht x exp θ, T x φθ la statistica T è completa per il parametro aturale θ R p oltre ad essere sufficiete miimale. Ifatti sia g ua fuzioe a valori reali tale che 0 = E θ gt = gt ht exp θ, t φθ dt R p e si cosiderio la parte positiva e la parte egativa di g, gt = g + t g t. Allora g + t ht exp θ, t φθ dt = R p g t ht exp θ, t φθ dt R p 1 ed i particolare per θ = 0 si ha g + t ht exp φ0 dt = g t ht exp φ0 dt R p R p semplificado exp φ0 si ha g + t ht dt = g t ht dt. Dividedo per questa quatità l Equazioe 1 R p R p si ha g + t ht g t ht g+ t ht dt e ψθ dt = g t ht dt e ψθ dt R p e θ,t Semplificado e ψθ e ricooscedo i g t ht g t ht dt e R p e θ,t g + t ht g+ t ht dt precedete è u uguagliaza tra fuzioi geeratrici dei mometi. desità di probabilità, si ota che la 13
14 3 Stimatori putuali Sia X = X 1,..., X X R u campioe su Ω, A, P e sia F u modello statistico parametrizzato da θ R p. Uo stimatore putuale di θ è ua fuzioe del solo campioe X. Cioè uo stimatore putuale di θ è ua statistica utilizzata per idividuare u modello probabilistico all itero del modello statistico. Ragioevolmete avrá la stessa dimesioe di θ. I particolare uo stimatore è ua variabile o vettore aleatorio. Ua stima è ua realizzazioe di uo stimatore. I Appedice 4.6 presetiamo u esempio di stimatore o putuale. Studieremo teciche per determiare stimatori e teciche per valutare stimatori putuali. Aticipiamo Defiizioe 3.1 Uo stimatore U di θ Θ è detto corretto o o distorto per θ se E θ U = θ per ogi θ Θ. 3.1 Metodo dei mometi Sia X = X 1,..., X u campioe casuale co desità di probabilità f X defiita da R i R e parametrizzata da θ Θ R p. Per j Z >0 il mometo teorico j-esimo di u geerico elemeto del campioe rispetto alla legge di probabilità idividuata da θ è defiito come µ j θ = E θ X j metre il mometo empirico j-esimo del Xj i campioe è defiito come ˆµ j =. Si oti che i mometi teorici potrebbero o essere defiiti. Per il pricipio di sostituzioe o metodo plug-i uo stimatore dei mometi di θ è u valore θ soluzioe del sistema µ j ˆθ = ˆµ j per j J sottoisieme fiito di Z >0. Esempio 3. Sia X 1,..., X i.i.d. Uiform]θ 1, θ [ co θ 1 < θ umeri reali. Il vettore dei parametri è θ = θ 1, θ. Vale µ 1 θ = θ 1 + θ / e µ = θ1 + θ + θ 1 θ /3 e poedo a sistema ˆµ 1 = X = µ 1 ˆθ co ˆµ = X i / = µ ˆθ si ottiee ˆθ 1 = ˆµ 1 3ˆµ ˆµ 1 e ˆθ = ˆµ 1 + 3ˆµ ˆµ 1 e i coclusioe si ha ˆθ = ˆθ 1, ˆθ stimatore putuale di θ 1, θ. Si oti che ˆµ ˆµ 1 0. Ifatti per ua sequeza di valori i R i, diciamo x, dimostriamo x i i x i equivaletemete i x i i x i. Ricordado il prodotto scalare stadard i R per a, b R si ha a, b = i a ib i la disuguagliaza da dimostrare diveta 1 x = 1, 1 x, x x, 1, ma questa è la disuguagliaza di Cauchy-Schwarz si veda ache la dimostrazioe del Teorema Esempio 3.3 Per u campioe casuale X 1,..., X per cui EX 1 e VarX 1 esistoo fiiti, uo stimatore dei mometi di VarX 1 è X i X. Giustificare il risultato. Esercizio 3.4 Determiare uo stimatore dei mometi per X 1,..., X i.i.d. e 1. Biomialk, p co k, p Z >0 ]0, 1[ 4. Geometricp co p ]0, 1[ 3. f X x, θ = θ + 1x θ 0 < x < 1 per θ Z >1. Commetare il risultato 4. Poissoλ co λ > 0. E preferibile usare ˆµ 1 o ˆµ? 5. Verificare che o esiste stimatore dei mometi se X 1 Cauchy0, σ, σ R. Notare l importaza dell ipotesi di campioe casuale e la pratica di utilizzare mometi di ordie basso, motivata sia da ragioi pratiche e computazioali che teoriche. Come si potrebbe estedere il metodo dei mometi al caso di variabili campioarie multivariate? 4 Si osservi che lo stimatore dei mometi di k, p otteuto usado i mometi primo e secodo è dato da ˆk X = X 1 Xi X e ˆp = X ˆk. Può capitare di otteere delle stime di ˆk egative!, quado la media campioaria è più piccola della variaza campioaria, idice di forte variabilità ei dati. 14
15 3. Metodo di massima verosimigliaza Defiizioe 3.5 Sia X u campioe statistico su Ω, A, P e si cosideri u modello statistico per X parametrizzato da θ Θ R p. La legge cogiuta del campioe iterpretata come fuzioe del parametro θ è chiamata fuzioe di verosimigliaza. *** ampliare l iterpretazioe di verosimigliaza *** Spesso si usa la lettera L per idicare la fuzioe di verosimigliaza. La distizioe tra variabili campioare e il parametro è idicata da, oppure ;. Nel caso di campioe discreto si ha per x X e θ Θ e per campioe cotiuo co desità cogiuta f X si ha che per campioe casuale si semplifica a Lθ; x = f X x; θ = P θ X = x Lθ; x = f X x; θ Lθ; x = f X1 x i ; θ Se la fuzioe di verosimigliaza è strettamete positiva si defiisce la fuzioe di log-verosimigliaza come lθ = log Lθ, x Osservazioi Dall Equazioe si deduce che la fuzioe di verosimigliaza rappreseta la probabilità sotto il modello idicato da θ di osservare il valore x i dati, le osservazioe.. Se T è statistica sufficiete per θ, cioè f X x, θ = hxgt x, θ allora Lθ; x gt x, θ. Esempio 3.7 Siao X 1,..., X idipedeti ed ideticamete distribuite secodo ua legge uiforme su ]0, θ[ per θ ]0, 1[. Allora 1 Lθ; x = f X x; θ = θ 0 < x i < θ = 0 < mi i x i x < θ θ Esercizio 3.8 Per il modello dell Esempio 3.7 e per = 1 e = fare il grafico della fuzioe di desità e della fuzioe di verosimigliaza. Defiizioe 3.9 Stimatore di massima verosimigliaza di θ è ˆθ MV X = arg sup θ Θ Lθ; X Osservazioi Si dice ache stimatore i massima verosimigliaza di θ.. ˆθMV X è ua variabile/vettore aleatorio, è ua statistica, è uo stimatore. 3. ˆθMV potrebbe o essere uico, potrebbe o esistere per esempio essere +, potrebbe o apparteere a Θ appartiee però alla sua chiusura euclidea. 4. Nel caso di campioe discreto è evidete l iterpretazioe dello stimatore di massima verosimigliaza come quel valore del parametro che selezioa il modello probabilistico, all itero del modello statistico, per cui il valore osservato x è il più probabile. 5. Poichè la fuzioe logaritmo è strettamete crescete, vale ˆθ MV X = arg sup θ Θ lθ; X. 6. Nel calcolo di ˆθ MV si possoo trascurare i fattori della verosimigliaza costati i θ, per esempio se T è sufficiete per θ allora ˆθ MV = arg sup θ Θ gt X; θ e lo stimatore di massima verosimigliaza è fuzioe del campioe solo tramite la statistica sufficiete. 15
16 Osservazioi Il determiare uo stimatore di massima verosimigliaza è quidi u problema di massimizzazioe di fuzioi multivariate e soggetto alle difficoltà iereti questi calcoli, comprese quelle di istabilità umerica.. Se L è differeziabile i θ, lo stimatore di massima verosimigliaza è soluzioe delle equazioi di verosimigliaza defiite come Lθ = 0 per i = 1,..., p o, equivaletemete se l è defiita, lθ = 0. θ i θ i 3. Occorre verificare che i puti critici delle equazioi di verosimigliaza siao effettivamete puti di massimo. I due dimesioi, se esiste la matrice Hessiaa della fuzioe di verosimigliaza o logverosimigliaza e el puto critico il suo determiate è positivo ed almeo u suo elemeto diagoale è egativo, allora il puto critico è u massimo locale ed u cadidato ad essere massimo globale e quidi stimatore di massima verosimigliaza. Nel caso di tre parametri si può studiare il sego degli autovalori della matrice Hessiaa. E el caso di spazio parametrico di dimesioe maggiore di tre? Esempio 3.1 Si cosiderio le segueti due desità di probabilità per X {0, 1, } idicizzate da θ {θ 0, θ 1 } X = x 0 1 θ θ Se si osserva x = 0 allora lo stimatore di massima verosimigliaza di θ è θ 0, altrimeti è θ 1. Esercizio Sia X 1,..., X i.i.d. Beroullip co p ]0, 1[. Utilizzado la fuzioe di log-verosimigliaza verificare che ˆp = X è stimatore di massima verosimigliaza di p. Notare che è ache statistica sufficiete. Verificare che il valore atteso di ˆp è p. Soo queste proprietà geerali degli stimatori di massima verosimigliaza?. Siao X 1,..., X copie idipedeti di X Expλ co λ > 0. Si osservi che per f X1 x 1 = λ exp λx 1 x 1 > 0 si ha l λ = λ x i = 0 per ˆλ = / x i e che l λ = λ < 0. Si ha quidi ˆλ MV = / X i = 1/ X. Si oti che ˆλ MV è stimatore distorto di λ ifatti per la disuguagliaza di Jese vale la maggiorazioe stretta E1/ X > 1/ E X = 1 = λ I particolare gli stimatori di massima verosimigliaza possoo o essere corretti. Idichiamo che soo asitoticamete corretti seza dimostrarlo v. Esempio L esercizio successivo idica u metodo tramite il quale talora è possibile correggere uo stimatore. Esercizio 3.14 Stimatori di massima verosimigliaza possoo essere distorti Sia X 1,..., X i.i.d. Uiform]0, θ[ co θ > Dimostrare che lo stimatore di massima verosimigliaza di θ R >0 è ˆθ = X.. Verificare che la desità di probabilità di X è fy = y 1 θ 1 λ co y ]0, θ[. 3. Verificare che E θ ˆθ = +1 θ e che Var θ θˆθ = +x+1. Si oti che ˆθ è distorto per θ. Lo si può correggere otteedo u altro stimatore ˆθ = +1 ˆθ = +1 X. 4. Verificare che ˆθ è statistica sufficiete per θ. 5. Cofrotare ˆθ co ˆθ MOM = X. Ricooscere i ˆθ MOM uo stimatore dei mometi di θ, verificare che è corretto per θ. Notare che X o è statistica sufficiete per θ. Esempio 3.15 Siao X 1,..., X i.i.d. Uiform]θ, θ + 1[ co θ R. La fuzioe di verosimigliaza è Lθ; x = x 1 > θx 1 < θ = x 1 < θ < x 1 Ogi variabile aleatoria ell itervallo stocastico [X 1, X 1 ] è stimatore di massima verosimigliaza. Si osservi che Prob θ X 1 X 1 = 0 per ogi θ e quidi co probabilità uo esistoo ifiiti stimatori di massima verosimigliaza. 16
17 Esercizio 3.16 IMPORTANTE Calcolare gli stimatori di massima verosimigliaza el caso di campioi casuali di taglia 1. N µ, σ per µ, σ R R suppoedo σ oto, µ oto, etrambi o oti;. Poissoλ co λ > 0. Theorem 3.17 di ivariaza per stimatori di massima verosimigliaza Sia ˆθ di massima verosimigliaza per θ allora gˆθ è di massima verosimigliaza per gθ per ogi fuzioe g. Proof. Se g è ivertibile, la dimostrazioe è immediata. Defiiamo A η = {θ Θ : gθ = η} per ogi η valore assuto da g e la fuzioe di verosimigliaza idotta Ora sup η L η; x = sup η sup {θ:gθ=η} = sup Lθ; x θ L η; x = Lθ; x sup Lθ; x [0, + ] {θ:gθ=η} per defiizioe di L per proprietà di sup = Lˆθ; x per defiizioe di MLE di θ = sup Lθ; x = L gˆθ; x {θ:gˆθ=gθ} Esempio Lo stimatore di massima verosimigliaza di p i u campioe casuale Beroulliao di parametro p ]0, 1[ è ˆp = X = X i /.. Il valore atteso di ˆp rispetto alle leggi di probabilità el modello è Eˆp Xi = E p = 1 p1 p Var p Xi + E p Xi = + p = p p1 p + I particolare lo stimatore di massima verosimigliaza di p esiste, uico, ma o è corretto. Ma il secodo termie ell uguagliaza precedete il fattore di distorsioe coverge a zero se tede a più ifiito. Si dice che lo stimatore ˆp è asitoticamete corretto per p. Questa è ua proprietà codivisa dagli stimatori di massima verosimigliaza. Più i geerale vale che gli stimatori di massima verosimigliaza soo asitoticamete cosisteti v Determiare lo stimatore di massima verosimigliaza di p1 p. Theorem 3.19 Stima i massima verosimigliaza e modelli di classe espoeziale Sia X hx exp θ, T x ψθ co θ R p e x X R v e T = T 1,..., T p R p. Siao X 1,..., X copie idipedeti di X. 1. Il campioe X = X 1,..., X è di classe espoeziale. e la fuzioe di verosimigliaza associata è Lθ; x 1,..., x = hx i exp θ, T x i ψθ 3. Vale E θ T i = ψθ θ i per i = 1,..., p 17
18 4. Cov θ T i, T j = ψθ θ i θ j per i, j = 1,..., p ψθ 5. Ioltre T X è stimatore di massima verosimigliaza di Gradiet θ ψ = θ 1 6. ed è stimatore corretto.,..., ψθ θ p Proof. Trascuriamo lo studio dell esisteza dei valori attesi e covariaze. Si osservi che corrispode a questioi di esisteza di derivate prime e secode di ua fuzioe del parametro. Si lascia al lettore la dimostrazioe dei primi due puti. Per il resto della dimostrazioe useremo 1 = hx exp θ, T x ψθ dx = hx exp θ, T x dx exp ψθ χ da cui expψθ = hx exp θ, T x dx. Nel seguito suppoiamo di poter commutare gli operatori di χ itegrazioe e derivazioe coivolti. 5 Per la dimostrazioe del puto 3, da cui segue il puto 6., si cosideri che ψ θ = i hx exp θ, T x dx χ χ θ i χ hx exp θ, T x dx = hx θ i exp θ, T x dx hx exp θ, T x dx χ χ = ht i exp θ, T dx = T i h exp θ, T ψθ dx expψθ χ La dimostrazioe del puto 4. è simile: occorre derivare rispetto θ j oltre che rispetto a θ i. Per il quito puto si poga uguale a zero il gradiete della fuzioe di log-verosimigliaza χ l θ i = T i ψ θ i = 0 e si verifichi che la matrice Hessiaa è defiita-egativa 6 ei puti critici di l sfruttado la relazioe l = ψθ = VarCov θ T i, T j θ i θ j θ i θ j Esercizio 3.0 Alla luce di questo teorema, rifare l esercizio Esercizio 3.1 Si ricordi che N µ, σ, co µ, σ R R >0, è u modello di classe espoeziale. particolare da exp x σ + µ σ x µ σ 1 log σ µ si deduce che θ = σ, 1 σ R R <0 è parametro aturale e vale µ, σ = θ 1, 1 θ θ -campioe casuale T = X i, X i è statistica caoica e la fuzioe dei cumulati è µ ψθ = σ + 1 log σ = 1 log θ θ 1 4θ I. Per u 5 d bθ Spesso per gli esempi che facciamo si può applicare la regola di Leibitz: fx, θ dx = fbθ, θ d dθ aθ dθ bθ faθ, θ d bθ dθ aθ + d fx, θ dx co f, a, b differeziabili i θ. Per a e b costati v. modelli regolari si semplifica a aθ dθ d b b d fx, θ dx = fx, θ dx. dθ a a dθ 6 Matrici di variaza-covariaza soo semidefiite positive, ifatti VarCovX = E X EXX EX t = E Y Y t = VarCovY where Y = X EX. Ora per ogi x R vale x t VarCovY x = Ex t Y Y t x = EY t x t Y t x = EZ dove Z = Y t x. 18
19 Per il Teorema 3.19 T è stimatore di massima verosimigliaza di θ ψ. Calcoliamo ψ = θ 1 = µ θ 1 θ ψ = θ 1 θ + θ 1 4θ = σ + µ Per il teorema di ivariaza degli stimatori di massima verosimigliaza si ha T 1 = X i = µ ˆ = ˆµ T = Xi = σ + ˆ µ = ˆσ + ˆµ e quidi gli stimatori di massima verosimigliaza dei parametri µ e σ soo ˆµ = X i / X ˆσ = i X ˆµ = i X i / Xi = X Ricordado che S Xi = X è corretto per σ si ha che lo stimatore di massima verosimigliaza di σ 1 o è corretto. Calcolare lo stimatore di massima verosimigliaza di θ. Verifichiamo l ultima affermazioe dell esercizio precedete. Esempio 3. stimatori di massima verosimigliaza possoo essere distorti, u altro esempio Sia X 1,..., X u campioe casuale uivariato co EX 1 e VarX 1 fiiti quadrato itegrabile. Per la liearità dell operatore valore atteso, la media campioaria è stimatore corretto di EX 1. Metre X i X o è stimatore corretto di VarX 1 si ricordi che è stimatore di massima verosimigliaza ifatti: E θ X i X = E θ 1 Xi 1 X j X k =... = 1σ Ne segue che X i X 1 j k lo stimatore dei miimi quadrati è corretto per VarX 1. Esercizio 3.3 Sia V stimatore di massima verosimigliaza di θ R ed esistao a, b R co a 0 tale che E θ V = aθ + b. Allora V b/a è stimatore corretto di θ. 3.3 Pricipio di ivariaza/equivariaza Si veda il libro di Casella Berger paragrafi 6.3 e Fiora abbiamo studiato la tecica di riduzioe dei dati per sufficieza e la sua relazioe co la fuzioe di verosimigliaza: se T è statistica sufficiete per θ e x, y X soo tali che T x = T y allora si ha la stessa ifereza su θ per verosimigliaza. Ifatti per la sufficieza di T esistoo due fuzioi h, g tali che Lθ; x = hxgt x; θ e quidi Lθ; x gt x; θ = gt y; θ Lθ; y. Ora itroduciamo u altro pricipio di ifereza basato sul cocetto di ivariaza. Suppoiamo u esperimeto i cui è di iteresse stimare il diametro medio degli alberi di ua foresta. Il campioe potrà essere misurato i cetimetri o i piedi o i qualche altra uità di misura lieare. Se si misurao gli stessi alberi, si dovrà otteere la stessa stima, cambierà l uità di misura rispetto alla quale è espressa ma le deduzioi ifereziali sul valore medio del diametro dovrao essere le stesse. Questo è u esempio di ivariaza rispetto all uità di misura measuremet ivariace per cui l ifereza o dipede dalla scala di misura. Ora suppoiamo che due problemi ifereziali abbiao la stessa struttura matematica. Allora dalla stessa procedura ifereziale si dovrao dedurre le stesse coclusioi per i due problemi. La struttura matematica di u problema ifereziale i questo cotesto è il modello statistico. Si parla di ivariaza formale. Per esempio per stimare l altezza media degli alberi i ua foresta, la lughezza del collo delle giraffe, il costo medio delle 19
20 uova è ragioevole cosiderare u campioe ideticamete distribuito, ragioevolmete o idipedete, e lo stesso modello statistico. Secodo il pricipio di ivariaza se gx è u cambiameto di uità di misura tale che i modelli statistici per X e per gx hao la stessa struttura formale, allora ua procedura di ifereza dovrebbe essere ivariate sia rispetto al cambio di misura sia formalmete. Defiizioe 3.4 U gruppo di trasformazioi dello spazio campioario X è u isieme di fuzioi da X a X tale che 1. per ogi g, h G g h G è chiuso rispetto alla composizioe, posso trasformare il trasformato,. per ogi g, h, l G allora h g l = h g l proprietà associativa, è lo stesso ruotare ciò che è stato scalato e traslato o prima traslare e poi applicare u rotazioe e traslazioe 3. esiste i G G per cui per ogi g G si ha i G g = g i G = g gruppo co idetià 4. per ogi g G esiste g 1 G tale che g g 1 = g 1 g = i G iverso, traslo di θ e di θ e o ho cambiato lo spazio campioario. Defiizioe 3.5 Il modello statistico F parametrizzato da θ Θ è ivariate per il gruppo di trasformazioi dello spazio campioario G se per X f ; θ e per g G esiste uico θ Θ tale che Y = gx f ; θ. Se F è ivariate rispetto a G allora dato g G ad ogi θ è associato u uico θ Θ. Sia ḡθ = θ la fuzioe da Θ a Θ idotta da g. Esempio 3.6 Siao X Biomial, θ co oto e θ ]0, 1[= Θ e G = {g 1, g } co g 1 x = x e g x = x per x {0, 1,..., } = X. La variabile aleatoria g X = X Biomial, θ cota i successi metre g 1 X Biomial, 1 θ cota i fallimeti. Il modello statistico determiato da Biomial, θ co θ ]0, 1[ e oto è ivariate rispetto a G e ḡ θ = θ e ḡ 1 θ = 1 θ per θ ]0, 1[. Metre se Θ =]1/, 1[ il modello statistico biomiale o è ivariate rispetto a G. Esercizio 3.7 Siao X 1,..., X i.i.d. N µ, σ co µ, σ R R >0 e G = {g a x = x 1 + a,..., x + a : a R}. Verificare che il modello ormale è ivariate rispetto a G. E ivariate ache rispetto al gruppo di trasformazioi H = {g a x = x 1 + a 1,..., x + a : a = a 1,..., a R }? Defiizioe 3.8 Sia F ivariate rispetto a G e sia W X uo stimatore putuale di θ. rispetto a G se per ogi X, θ Θ e g G vale W gx = ḡw x. W è ivariate Questa defiizioe equaglia l ivariaza i misura, ḡw x stima di ḡθ, co l ivariaza formale, W gx stima di ḡθ. Esempio 3.9 Esercizio 3.6 Sia T X uo stimatore di θ e T x uo stimatore di 1 θ. L ivariaza per misura impoe T x = 1 T x e quella formale impoe la stessa procedura e quidi T x = 1 T x = 1 T x I particolare per uo stimatore ivariate rispetto alla trasformazioe successi/fallimeti, oto T x è oto ache T x. Verificare che la stima della probabilità di successo data dalla proporzioe di successi osservati x è ivariate. Esempio 3.30 Siao X 1,..., X i.i.d. e si cosideri u modello statistico di posizioe co fuzioe di ripartizioe F x θ, x R e θ R e sia G = {g a x = x 1 + a,..., x + a : a R, x R }. 1. Si cosideri Il campioe trasformato Y ha legge determiata da Y = g a X = X + a = X 1 + a,..., X + a PY y = PY 1 y 1,..., Y y = PX 1 y 1 a,..., X y a = PX 1 y 1 a... PX y a = F y i a θ da cui la trasformazioe idotta sullo spazio dei parametri da g a è ḡθ = θ + a. 0
3.4 Tecniche per valutare uno stimatore
 3.4 Teciche per valutare uo stimatore 3.4. Il liguaggio delle decisioi statistiche, stimatori corretti e stimatori cosisteti La teoria delle decisioi forisce u liguaggio appropriato per discutere sulla
3.4 Teciche per valutare uo stimatore 3.4. Il liguaggio delle decisioi statistiche, stimatori corretti e stimatori cosisteti La teoria delle decisioi forisce u liguaggio appropriato per discutere sulla
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 15/16 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 15/16 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X = N:
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 15/16 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X = N:
PARTE QUARTA Teoria algebrica dei numeri
 Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Corso di Laurea Magistrale in Ingegneria Informatica A.A. 2014/15. Complementi di Probabilità e Statistica. Prova scritta del del 23-02-15
 Corso di Laurea Magistrale i Igegeria Iformatica A.A. 014/15 Complemeti di Probabilità e Statistica Prova scritta del del 3-0-15 Puteggi: 1. 3+3+4;. +3 ; 3. 1.5 5 ; 4. 1 + 1 + 1 + 1 + 3.5. Totale = 30.
Corso di Laurea Magistrale i Igegeria Iformatica A.A. 014/15 Complemeti di Probabilità e Statistica Prova scritta del del 3-0-15 Puteggi: 1. 3+3+4;. +3 ; 3. 1.5 5 ; 4. 1 + 1 + 1 + 1 + 3.5. Totale = 30.
Successioni. Grafico di una successione
 Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
V Tutorato 6 Novembre 2014
 1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
SERIE NUMERICHE Con l introduzione delle serie vogliamo estendere l operazione algebrica di somma ad un numero infinito di addendi.
 Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
Matematica II: Calcolo delle Probabilità e Statistica Matematica
 Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docete: dott. F. Zucca Esercitazioe # 4 1 Distribuzioe Espoeziale Esercizio 1 Suppoiamo che la durata della vita di ogi membro di
Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docete: dott. F. Zucca Esercitazioe # 4 1 Distribuzioe Espoeziale Esercizio 1 Suppoiamo che la durata della vita di ogi membro di
CONCETTI BASE DI STATISTICA
 CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
I appello - 29 Giugno 2007
 Facoltà di Igegeria - Corso di Laurea i Ig. Iformatica e delle Telecom. A.A.6/7 I appello - 9 Giugo 7 ) Studiare la covergeza putuale e uiforme della seguete successioe di fuzioi: [ ( )] f (x) = cos (
Facoltà di Igegeria - Corso di Laurea i Ig. Iformatica e delle Telecom. A.A.6/7 I appello - 9 Giugo 7 ) Studiare la covergeza putuale e uiforme della seguete successioe di fuzioi: [ ( )] f (x) = cos (
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE
 DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
1 Metodo della massima verosimiglianza
 Metodo della massima verosimigliaza Estraedo u campioe costituito da variabili casuali X i i.i.d. da ua popolazioe X co fuzioe di probabilità/desità f(x, θ), si costruisce la fuzioe di verosimigliaza che
Metodo della massima verosimigliaza Estraedo u campioe costituito da variabili casuali X i i.i.d. da ua popolazioe X co fuzioe di probabilità/desità f(x, θ), si costruisce la fuzioe di verosimigliaza che
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 19 Iterdipedeza lieare fra variabili quatitative
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 19 Iterdipedeza lieare fra variabili quatitative
Terzo appello del. primo modulo. di ANALISI 18.07.2006
 Terzo appello del primo modulo di ANALISI 18.7.26 1. Si voglioo ifilare su u filo delle perle distiguibili tra loro solo i base alla dimesioe: si hao a disposizioe perle gradi di diametro di 2 cetimetri
Terzo appello del primo modulo di ANALISI 18.7.26 1. Si voglioo ifilare su u filo delle perle distiguibili tra loro solo i base alla dimesioe: si hao a disposizioe perle gradi di diametro di 2 cetimetri
LA DERIVATA DI UNA FUNZIONE
 LA DERIVATA DI UNA FUNZIONE OBIETTIVO: Defiire lo strumeto matematico ce cosete di studiare la cresceza e la decresceza di ua fuzioe Si comicia col defiire cosa vuol dire ce ua fuzioe è crescete. Defiizioe:
LA DERIVATA DI UNA FUNZIONE OBIETTIVO: Defiire lo strumeto matematico ce cosete di studiare la cresceza e la decresceza di ua fuzioe Si comicia col defiire cosa vuol dire ce ua fuzioe è crescete. Defiizioe:
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del 5.02.2013 TEMA 1. f(x) = arcsin 1 2 log 2 x.
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
Appunti di Statistica Matematica Inferenza Statistica Multivariata Anno Accademico 2016/17
 Apputi di Statistica Matematica Ifereza Statistica Multivariata Ao Accademico 016/17 September 7, 016 1 Campioi e modelli statistici Siao (Ω, A, P) uo spazio di probabilità e X = (X 1,..., X ) u vettore
Apputi di Statistica Matematica Ifereza Statistica Multivariata Ao Accademico 016/17 September 7, 016 1 Campioi e modelli statistici Siao (Ω, A, P) uo spazio di probabilità e X = (X 1,..., X ) u vettore
Appunti di Statistica Matematica Inferenza Statistica Multivariata Anno Accademico 2017/18
 Apputi di Statistica Matematica Ifereza Statistica Multivariata Ao Accademico 017/18 November 8, 017 1 Campioi e modelli statistici Siao (Ω, A, P uo spazio di probabilità e X = (X 1,..., X u vettore aleatorio
Apputi di Statistica Matematica Ifereza Statistica Multivariata Ao Accademico 017/18 November 8, 017 1 Campioi e modelli statistici Siao (Ω, A, P uo spazio di probabilità e X = (X 1,..., X u vettore aleatorio
Soluzione La media aritmetica dei due numeri positivi a e b è data da M
 Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Foglio di esercizi N. 1 - Soluzioni
 Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Anno 5 Successioni numeriche
 Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
5 ln n + ln. 4 ln n + ln. 6 ln n + ln
 DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
Risposte. f v = φ dove φ(x,y) = e x2. f(x) = e x2 /2. +const. Soluzione. (i) Scriviamo v = (u,w). Se f(x) è la funzione richiesta, si deve avere
 Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
Teorema 13. Se una sere converge assolutamente, allora converge:
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 03: Riferimeti: R.Adams, Calcolo Differeziale.- Si cosiglia vivamete di fare gli esercizi del testo. Covergeza assoluta e
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 03: Riferimeti: R.Adams, Calcolo Differeziale.- Si cosiglia vivamete di fare gli esercizi del testo. Covergeza assoluta e
Sintassi dello studio di funzione
 Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Il test parametrico si costruisce in tre passi:
 R. Lombardo I. Cammiatiello Dipartimeto di Ecoomia Secoda Uiversità degli studi Napoli Facoltà di Ecoomia Ifereza Statistica La Verifica delle Ipotesi Obiettivo Verifica (test) di u ipotesi statistica
R. Lombardo I. Cammiatiello Dipartimeto di Ecoomia Secoda Uiversità degli studi Napoli Facoltà di Ecoomia Ifereza Statistica La Verifica delle Ipotesi Obiettivo Verifica (test) di u ipotesi statistica
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE LORENZO BRASCO. Teoremi di Cesaro Teorema di Stolz-Cesaro. Siao {a } N e {b } N due successioi umeriche, co {b } N strettamete positiva, strettamete crescete e ilitata. Se esiste
SUCCESSIONI NUMERICHE LORENZO BRASCO. Teoremi di Cesaro Teorema di Stolz-Cesaro. Siao {a } N e {b } N due successioi umeriche, co {b } N strettamete positiva, strettamete crescete e ilitata. Se esiste
Campi vettoriali conservativi e solenoidali
 Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
LA VERIFICA DELLE IPOTESI SUI PARAMETRI
 LA VERIFICA DELLE IPOTESI SUI PARAMETRI E u problema di ifereza per molti aspetti collegato a quello della stima. Rispode ad u esigeza di carattere pratico che spesso si preseta i molti campi dell attività
LA VERIFICA DELLE IPOTESI SUI PARAMETRI E u problema di ifereza per molti aspetti collegato a quello della stima. Rispode ad u esigeza di carattere pratico che spesso si preseta i molti campi dell attività
Limiti di successioni
 Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
 RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 Dott.ssa Sandra Lucente 1 Funzioni potenza ed esponenziale.
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Analisi statistica dell Output
 Aalisi statistica dell Output IL Simulatore è u adeguata rappresetazioe della Realtà! E adesso? Come va iterpretato l Output? Quado le Osservazioi soo sigificative? Quati Ru del Simulatore è corretto effettuare?
Aalisi statistica dell Output IL Simulatore è u adeguata rappresetazioe della Realtà! E adesso? Come va iterpretato l Output? Quado le Osservazioi soo sigificative? Quati Ru del Simulatore è corretto effettuare?
Metodi statistici per l analisi dei dati
 Metodi statistici per l aalisi dei dati due ttameti Motivazioi ttameti Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ttameti) per cui soo stati codotti gli esperimeti. due ttameti Esempio itroduttivo
Metodi statistici per l aalisi dei dati due ttameti Motivazioi ttameti Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ttameti) per cui soo stati codotti gli esperimeti. due ttameti Esempio itroduttivo
1 Limiti di successioni
 Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
 Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
II-9 Successioni e serie
 SUCCESSIONI II-9 Successioi e serie Idice Successioi. Limite di ua successioe........................................... Serie 3. La serie armoica................................................ 6. La
SUCCESSIONI II-9 Successioi e serie Idice Successioi. Limite di ua successioe........................................... Serie 3. La serie armoica................................................ 6. La
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE Studiare la atura delle segueti serie. ) cos 4 + ; ) + si ; ) + ()! 4) ( ) 5) ( ) + + 6) ( ) + + + 7) ( log ) 8) ( ) + 9) log! 0)! Studiare al variare di x i R la atura delle segueti
ESERCIZI SULLE SERIE Studiare la atura delle segueti serie. ) cos 4 + ; ) + si ; ) + ()! 4) ( ) 5) ( ) + + 6) ( ) + + + 7) ( log ) 8) ( ) + 9) log! 0)! Studiare al variare di x i R la atura delle segueti
Esercizi riguardanti limiti di successioni
 Esercizi riguardati iti di successioi Davide Boscaii Queste soo le ote da cui ho tratto le esercitazioi del gioro 27 Ottobre 20. Come tali soo be lugi dall essere eseti da errori, ivito quidi chi e trovasse
Esercizi riguardati iti di successioi Davide Boscaii Queste soo le ote da cui ho tratto le esercitazioi del gioro 27 Ottobre 20. Come tali soo be lugi dall essere eseti da errori, ivito quidi chi e trovasse
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
1 Successioni 1 1.1 Limite di una successione... 2. 2 Serie 3 2.1 La serie armonica... 6 2.2 La serie geometrica... 6
 SUCCESSIONI Successioi e serie Idice Successioi. Limite di ua successioe........................................... Serie 3. La serie armoica................................................ 6. La serie
SUCCESSIONI Successioi e serie Idice Successioi. Limite di ua successioe........................................... Serie 3. La serie armoica................................................ 6. La serie
Strumenti di indagine per la valutazione psicologica
 Strumeti di idagie per la valutazioe psicologica 1.2 - Richiami di statistica descrittiva Davide Massidda davide.massidda@gmail.com Descrivere i dati Dovedo scegliere u esame opzioale, uo studete ha itezioe
Strumeti di idagie per la valutazioe psicologica 1.2 - Richiami di statistica descrittiva Davide Massidda davide.massidda@gmail.com Descrivere i dati Dovedo scegliere u esame opzioale, uo studete ha itezioe
Statistica I, Laurea triennale in Ing. Gestionale, a.a. 2011/12 Registro delle lezioni
 Statistica I, Laurea trieale i Ig. Gestioale, a.a. 2011/12 Registro delle lezioi Lezioe 1 (28/9, ore 11:30). Vedere la registrazioe di Barsati, dispoibile alla pagia http://users.dma.uipi.it/barsati/statistica_2011/idex.html.
Statistica I, Laurea trieale i Ig. Gestioale, a.a. 2011/12 Registro delle lezioi Lezioe 1 (28/9, ore 11:30). Vedere la registrazioe di Barsati, dispoibile alla pagia http://users.dma.uipi.it/barsati/statistica_2011/idex.html.
Corso di Laurea in Ing. Edile Politecnico di Bari A.A. 2008-2009 Prof. ssa Letizia Brunetti DISPENSE DEL CORSO DI GEOMETRIA
 Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Metodi statistici per l'analisi dei dati
 Metodi statistici per l aalisi dei dati due Motivazioi Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ) per cui soo stati codotti gli esperimeti. Metodi tatistici per l Aalisi dei Dati due Esempio
Metodi statistici per l aalisi dei dati due Motivazioi Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ) per cui soo stati codotti gli esperimeti. Metodi tatistici per l Aalisi dei Dati due Esempio
STATISTICA INFERENZIALE SCHEDA N. 2 INTERVALLI DI CONFIDENZA PER IL VALORE ATTESO E LA FREQUENZA
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
Successioni. Capitolo 2. 2.1 Definizione
 Capitolo 2 Successioi 2.1 Defiizioe Ua prima descrizioe, più ituitiva che rigorosa, di quel che itediamo per successioe cosiste i: Ua successioe è ua lista ordiata di oggetti, avete u primo ma o u ultimo
Capitolo 2 Successioi 2.1 Defiizioe Ua prima descrizioe, più ituitiva che rigorosa, di quel che itediamo per successioe cosiste i: Ua successioe è ua lista ordiata di oggetti, avete u primo ma o u ultimo
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT
 LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT La gestioe, il cotrollo ed il migliorameto della qualità di u prodotto/servizio soo temi di grade iteresse per l azieda. Il problema della qualità
LA GESTIONE DELLA QUALITA : IL TOTAL QUALITY MANAGEMENT La gestioe, il cotrollo ed il migliorameto della qualità di u prodotto/servizio soo temi di grade iteresse per l azieda. Il problema della qualità
Soluzioni quarta esercitazione
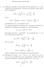 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
SERIE NUMERICHE Esercizi risolti. 2 b) n=1. n n 2 +n
 SERIE NUMERICHE Esercizi risolti. Applicado la defiizioe di covergeza di ua serie stabilire il carattere delle segueti serie, e, i caso di covergeza, trovare la somma: = + b) = + +. Verificare utilizzado
SERIE NUMERICHE Esercizi risolti. Applicado la defiizioe di covergeza di ua serie stabilire il carattere delle segueti serie, e, i caso di covergeza, trovare la somma: = + b) = + +. Verificare utilizzado
Serie numeriche: esercizi svolti
 Serie umeriche: esercizi svolti Gli esercizi cotrassegati co il simbolo * presetao u grado di difficoltà maggiore. Esercizio. Dopo aver verificato la covergeza, calcolare la somma delle segueti serie:
Serie umeriche: esercizi svolti Gli esercizi cotrassegati co il simbolo * presetao u grado di difficoltà maggiore. Esercizio. Dopo aver verificato la covergeza, calcolare la somma delle segueti serie:
5. Le serie numeriche
 5. Le serie umeriche Ricordiamo che ua successioe reale è ua fuzioe defiita da N, evetualmete privato di u umero fiito di elemeti, a R. Solitamete si idica ua successioe co la lista dei suoi valori: (a
5. Le serie umeriche Ricordiamo che ua successioe reale è ua fuzioe defiita da N, evetualmete privato di u umero fiito di elemeti, a R. Solitamete si idica ua successioe co la lista dei suoi valori: (a
19 31 43 55 67 79 91 103 870,5 882,5 894,5 906,5 918,5 930,5 942,5 954,5
 Il 16 dicembre 015 ero a Napoli. Ad u agolo di Piazza Date mi soo imbattuto el "matematico di strada", come egli si defiisce, Giuseppe Poloe immerso el suo armametario di tabelle di umeri. Il geiale persoaggio
Il 16 dicembre 015 ero a Napoli. Ad u agolo di Piazza Date mi soo imbattuto el "matematico di strada", come egli si defiisce, Giuseppe Poloe immerso el suo armametario di tabelle di umeri. Il geiale persoaggio
LE MISURE DI VARIABILITÀ DI CARATTERI QUANTITATIVI
 Apputi di Statistica Sociale Uiversità ore di Ea LE MISURE DI VARIABILITÀ DI CARATTERI QUATITATIVI La variabilità di u isieme di osservazioi attiee all attitudie delle variabili studiate ad assumere modalità
Apputi di Statistica Sociale Uiversità ore di Ea LE MISURE DI VARIABILITÀ DI CARATTERI QUATITATIVI La variabilità di u isieme di osservazioi attiee all attitudie delle variabili studiate ad assumere modalità
8. Quale pesa di più?
 8. Quale pesa di più? Negli ultimi ai hao suscitato particolare iteresse alcui problemi sulla pesatura di moete o di pallie. Il primo problema di questo tipo sembra proposto da Tartaglia el 1556. Da allora
8. Quale pesa di più? Negli ultimi ai hao suscitato particolare iteresse alcui problemi sulla pesatura di moete o di pallie. Il primo problema di questo tipo sembra proposto da Tartaglia el 1556. Da allora
Statistica (Prof. Capitanio) Alcuni esercizi tratti da prove scritte d esame
 Statistica (Prof. Capitaio) Alcui esercizi tratti da prove scritte d esame Esercizio 1 Il tempo (i miuti) che Paolo impiega, i auto, per arrivare i ufficio, può essere modellato co ua variabile casuale
Statistica (Prof. Capitaio) Alcui esercizi tratti da prove scritte d esame Esercizio 1 Il tempo (i miuti) che Paolo impiega, i auto, per arrivare i ufficio, può essere modellato co ua variabile casuale
DISTRIBUZIONI DOPPIE
 DISTRIBUZIONI DOPPIE Fio ad ora abbiamo visto teciche di aalisi dei dati per il solo caso i cui ci si occupi di u solo carattere rilevato su u collettivo (distribuzioi semplici). I termii formali fio ad
DISTRIBUZIONI DOPPIE Fio ad ora abbiamo visto teciche di aalisi dei dati per il solo caso i cui ci si occupi di u solo carattere rilevato su u collettivo (distribuzioi semplici). I termii formali fio ad
Successioni ricorsive di numeri
 Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Appunti sulla MATEMATICA FINANZIARIA
 INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Una funzione è una relazione che ad ogni elemento del dominio associa uno e un solo elemento del codominio
 Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Sistemi e Tecnologie della Comunicazione
 Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
I numeri complessi. Pagine tratte da Elementi della teoria delle funzioni olomorfe di una variabile complessa
 I umeri complessi Pagie tratte da Elemeti della teoria delle fuzioi olomorfe di ua variabile complessa di G. Vergara Caffarelli, P. Loreti, L. Giacomelli Dipartimeto di Metodi e Modelli Matematici per
I umeri complessi Pagie tratte da Elemeti della teoria delle fuzioi olomorfe di ua variabile complessa di G. Vergara Caffarelli, P. Loreti, L. Giacomelli Dipartimeto di Metodi e Modelli Matematici per
Principi base di Ingegneria della Sicurezza
 Pricipi base di Igegeria della Sicurezza L aalisi delle codizioi di Affidabilità del sistema si articola i: (i) idetificazioe degli sceari icidetali di riferimeto (Eveti critici Iiziatori - EI) per il
Pricipi base di Igegeria della Sicurezza L aalisi delle codizioi di Affidabilità del sistema si articola i: (i) idetificazioe degli sceari icidetali di riferimeto (Eveti critici Iiziatori - EI) per il
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
Statistica di base. Luca Mari, versione 31.12.13
 Statistica di base Luca Mari, versioe 31.12.13 Coteuti Moda...1 Distribuzioi cumulate...2 Mediaa, quartili, percetili...3 Sigificatività empirica degli idici ordiali...3 Media...4 Acora sulla media...4
Statistica di base Luca Mari, versioe 31.12.13 Coteuti Moda...1 Distribuzioi cumulate...2 Mediaa, quartili, percetili...3 Sigificatività empirica degli idici ordiali...3 Media...4 Acora sulla media...4
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
STATISTICA 1 parte 2/2 STATISTICA INFERENZIALE
 STATISTICA parte / U test statistico è ua regola di decisioe Effettuare u test statistico sigifica verificare IPOTESI sui parametri. STATISTICA INFERENZIALE STIMA PUNTUALE STIMA PER INTERVALLI TEST PARAMETRICI
STATISTICA parte / U test statistico è ua regola di decisioe Effettuare u test statistico sigifica verificare IPOTESI sui parametri. STATISTICA INFERENZIALE STIMA PUNTUALE STIMA PER INTERVALLI TEST PARAMETRICI
Statistica descrittiva
 Statistica descrittiva idici idici (o misure) di posizioe media campioaria di osservazioi x, x,..., x x i x= per campioi x ì ripetuti ciascuo co frequeza f i x= x i f i Posto y i =a x i b : y=a x mediaa
Statistica descrittiva idici idici (o misure) di posizioe media campioaria di osservazioi x, x,..., x x i x= per campioi x ì ripetuti ciascuo co frequeza f i x= x i f i Posto y i =a x i b : y=a x mediaa
Le carte di controllo
 Le carte di cotrollo Dott.ssa Bruella Caroleo 07 dicembre 007 Variabilità ei processi produttivi Le caratteristiche di qualsiasi processo produttivo soo caratterizzate da variabilità Le cause di variabilità
Le carte di cotrollo Dott.ssa Bruella Caroleo 07 dicembre 007 Variabilità ei processi produttivi Le caratteristiche di qualsiasi processo produttivo soo caratterizzate da variabilità Le cause di variabilità
Capitolo Decimo SERIE DI FUNZIONI
 Capitolo Decimo SERIE DI FUNZIONI SUCCESSIONI DI FUNZIONI I cocetti di successioe e di serie possoo essere estesi i modo molto aturale al caso delle fuzioi DEFINIZIONE Sia E u sottoisieme di  e, per ogi
Capitolo Decimo SERIE DI FUNZIONI SUCCESSIONI DI FUNZIONI I cocetti di successioe e di serie possoo essere estesi i modo molto aturale al caso delle fuzioi DEFINIZIONE Sia E u sottoisieme di  e, per ogi
Capitolo 3 CARATTERIZZAZIONE MECCANICA DELLE FIBRE
 Capitoo 3 CARATTERIZZAZIONE MECCANICA DELLE FIBRE 3.1 LA TEORIA DI WEIBULL I comportameto meccaico dee fibre di giestra e di juta è stato caratterizzato mediate o studio dea resisteza a trazioe dee fibre
Capitoo 3 CARATTERIZZAZIONE MECCANICA DELLE FIBRE 3.1 LA TEORIA DI WEIBULL I comportameto meccaico dee fibre di giestra e di juta è stato caratterizzato mediate o studio dea resisteza a trazioe dee fibre
APPUNTI DI MATEMATICA ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1)
 ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1) I umeri aturali hao u ordie; ogi umero aturale ha u successivo (otteuto aggiugedo 1), e ogi umero aturale diverso da zero ha u precedete (otteuto sottraedo 1).
ALGEBRA \ ARITMETICA \ NUMERI NATURALI (1) I umeri aturali hao u ordie; ogi umero aturale ha u successivo (otteuto aggiugedo 1), e ogi umero aturale diverso da zero ha u precedete (otteuto sottraedo 1).
Random walk classico. Simulazione di un random walk
 Radom walk classico Il radom walk classico) è il processo stocastico defiito da co prob. S S0 X k, co X k k co prob. e le X soo tra di loro idipedeti. k Si tratta di u processo a icremeti idipedeti e ideticamete
Radom walk classico Il radom walk classico) è il processo stocastico defiito da co prob. S S0 X k, co X k k co prob. e le X soo tra di loro idipedeti. k Si tratta di u processo a icremeti idipedeti e ideticamete
IL CALCOLO COMBINATORIO
 IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA La statistica descrittiva serve per elaborare e sitetizzare dati. Tipicamete i dati si rappresetao i tabelle. Esempio. Suppoiamo di codurre u idagie per cooscere gli iscritti al
STATISTICA DESCRITTIVA La statistica descrittiva serve per elaborare e sitetizzare dati. Tipicamete i dati si rappresetao i tabelle. Esempio. Suppoiamo di codurre u idagie per cooscere gli iscritti al
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Corsi di Laurea in Ingegneria Edile e Architettura Prova scritta di Analisi Matematica 1 del 6/02/2010. sin( x) log((1 + x 2 ) 1/2 ) = 1 3.
 Corsi di Laurea i Igegeria Edile e Architettura Prova scritta di Aalisi Matematica del 6// ) Mostrare che + si( ) cos () si( ) log(( + ) / ) = 3. Possibile soluzioe: Cosiderado dapprima il deomiatore otiamo
Corsi di Laurea i Igegeria Edile e Architettura Prova scritta di Aalisi Matematica del 6// ) Mostrare che + si( ) cos () si( ) log(( + ) / ) = 3. Possibile soluzioe: Cosiderado dapprima il deomiatore otiamo
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Capitolo 6 Teoremi limite classici
 Capitolo 6 Teoremi limite classici Abstract I Teoremi limite classici, la legge dei gradi umeri e il teorema limite cetrale, costituiscoo il ucleo del Calcolo delle Probabilità, per la loro portata sia
Capitolo 6 Teoremi limite classici Abstract I Teoremi limite classici, la legge dei gradi umeri e il teorema limite cetrale, costituiscoo il ucleo del Calcolo delle Probabilità, per la loro portata sia
( ) ( ) ( ) ( ) ( ) CAPITOLO VII DERIVATE. (3) D ( x ) = 1 derivata di un monomio con a 0
 CAPITOLO VII DERIVATE. GENERALITÀ Defiizioe.) La derivata è u operatore che ad ua fuzioe f associa u altra fuzioe e che obbedisce alle segueti regole: () D a a a 0 0 0 derivata di u moomio D 6 D 0 D ()
CAPITOLO VII DERIVATE. GENERALITÀ Defiizioe.) La derivata è u operatore che ad ua fuzioe f associa u altra fuzioe e che obbedisce alle segueti regole: () D a a a 0 0 0 derivata di u moomio D 6 D 0 D ()
Tutti i diritti di sfruttamento economico dell opera appartengono alla Esselibri S.p.A. (art. 64, D.Lgs. 10-2-2005, n. 30)
 Copyright 2005 Esselibri S.p.A. Via F. Russo, 33/D 8023 Napoli Azieda co sistema qualità certificato ISO 400: 2003 Tutti i diritti riservati. È vietata la riproduzioe ache parziale e co qualsiasi mezzo
Copyright 2005 Esselibri S.p.A. Via F. Russo, 33/D 8023 Napoli Azieda co sistema qualità certificato ISO 400: 2003 Tutti i diritti riservati. È vietata la riproduzioe ache parziale e co qualsiasi mezzo
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Università degli Studi di Salerno Pietro Coretto. Corso di Statistica FORMULARIO
 Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Campionamento stratificato. Esempio
 ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazione di Gras
 IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazioe di Gras Date due variabili biarie a e b, i quale misura posso assicurare che i ua popolazioe da ogi osservazioe di a segue ecessariamete quella di b? E
IMPLICAZIONE TRA VARIABILI BINARIE: L Implicazioe di Gras Date due variabili biarie a e b, i quale misura posso assicurare che i ua popolazioe da ogi osservazioe di a segue ecessariamete quella di b? E
Modelli multiperiodali discreti. Strategie di investimento
 Modelli multiperiodali discreti Cosideriamo ora modelli discreti cioè co u umero fiito di stati del modo multiperiodali, cioè apputo co più periodi. Il prototipo di questa classe di modelli è il modello
Modelli multiperiodali discreti Cosideriamo ora modelli discreti cioè co u umero fiito di stati del modo multiperiodali, cioè apputo co più periodi. Il prototipo di questa classe di modelli è il modello
Tecnica delle misurazioni applicate Esame del 4 dicembre 2007
 Tecica delle misurazioi applicate Esame del 4 dicembre 7 Problema 1. Il propulsore Mod. WEC viee prodotto da ACME Ic. mediate u processo automatizzato: dati storici cofermao che la lavorazioe di ogi elemeto
Tecica delle misurazioi applicate Esame del 4 dicembre 7 Problema 1. Il propulsore Mod. WEC viee prodotto da ACME Ic. mediate u processo automatizzato: dati storici cofermao che la lavorazioe di ogi elemeto
ESERCIZI DI STATISTICA DESCRITTIVA ALCUNI TRATTI DA PROVE D ESAME DA REALIZZARE ANCHE CON L AUSILIO DI UN FOGLIO DI CALCOLO. Angela Donatiello 1
 ESERCIZI DI STATISTICA DESCRITTIVA ALCUNI TRATTI DA PROVE D ESAME DA REALIZZARE ANCHE CON L AUSILIO DI UN FOGLIO DI CALCOLO Agela Doatiello 1 Esercizio. E stato tabulato il peso di ua certa popolazioe
ESERCIZI DI STATISTICA DESCRITTIVA ALCUNI TRATTI DA PROVE D ESAME DA REALIZZARE ANCHE CON L AUSILIO DI UN FOGLIO DI CALCOLO Agela Doatiello 1 Esercizio. E stato tabulato il peso di ua certa popolazioe
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2006
 ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 006 Il cadidato risolva uo dei due problemi e 5 dei 0 quesiti i cui si articola il questioario. PRBLEMA U filo metallico di lughezza l viee utilizzato
ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 006 Il cadidato risolva uo dei due problemi e 5 dei 0 quesiti i cui si articola il questioario. PRBLEMA U filo metallico di lughezza l viee utilizzato
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
ESEMPIO 1. Immaginiamo come si distribuirebbero le stime campionarie se l operazione di campionamento venisse ripetuta più volte.
 ESEMPIO Prima dell esplosioe di ua cetrale ucleare, i terrei di ua certa regioe avevao ua produzioe media di grao pari a 00 quitali co uo scarto di 5. Dopo la catastrofe si selezioao 00 uità di superficie
ESEMPIO Prima dell esplosioe di ua cetrale ucleare, i terrei di ua certa regioe avevao ua produzioe media di grao pari a 00 quitali co uo scarto di 5. Dopo la catastrofe si selezioao 00 uità di superficie
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
