ELEMENTI DI STATISTICA INFERENZIALE (versione preliminare) Barbara Torti, Mario Abundo
|
|
|
- Camillo Baldi
- 7 anni fa
- Visualizzazioni
Transcript
1 ELEMENTI DI STATISTICA INFERENZIALE (versioe prelimiare) Barbara Torti, Mario Abudo
2 Idice 1 Richiami di Probabilità e Statistica Spazi di Probabilità e variabili aleatorie Teoremi limite Leggi gamma, ormale, chi-quadrato, t di studet, Fischer Legge gamma Legge ormale Legge Chi-quadro co gradi di libertà Legge t di Studet co gradi di libertà Legge F di Fischer co ed m gradi di libertà Modelli statistici e statistiche campioarie Campioameto da ua distribuzioe ormale: proprietà di X e di S Stima putuale e per itervalli 13.1 Stima putuale Stimatori e proprietà di ottimalità Il metodo della massima verosimigliaza Proprietà degli stimatori di massima verosimigliaza Il metodo dei mometi Itervalli di cofideza Costruzioe di itervalli di cofideza: il metodo della quatità pivotale Costruzioe di itervalli di cofideza: il metodo della trasformazioe itegrale Itervalli di cofideza per campioi ormali Itervalli di cofideza asitotici Test d ipotesi Test parametrici Descrizioe e defiizioi Ipotesi semplici i alterativa ad ipotesi semplici Ipotesi composte: test del rapporto di verosimigliaza geeralizzato Test uiformemete più potete per ipotesi uilaterali p-value Verifica di ipotesi per campioameto da popolazioi ormali Test sulla media Test per la variaza
3 3.3.3 Test per la differeza tra medie Test del chi quadrato Test asitotici basati sul rapporto di verosimigliaza geeralizzato Test di adattameto Test di idipedeza Test o parametrici La fuzioe di ripartizioe empirica Il test di adattameto di Kolmogorov e Smirov Aalisi della variaza Aalisi della variaza ad u fattore Aalisi della variaza a due fattori seza iterazioi
4 Capitolo 1 Richiami di Probabilità e Statistica 1.1 Spazi di Probabilità e variabili aleatorie Uo spazio di probabilità è ua tera (Ω, F, P ), dove Ω è u isieme, F è ua σ-algebra di parti di Ω, e P è ua misura di probabilità su (Ω, F). Ua variabile aleatoria reale è u applicazioe X : Ω R tale che ω : X(ω) t} = X 1 (, t] F per ogi t R Osserviamo che questa relazioe esprime il fatto che, per poter calcolare le probabilità di isiemi espressi come fuzioi di u esperimeto aleatorio, tali isiemi devoo essere i F, ovvero devoo essere degli eveti (ad esempio, il umero di teste su laci di moeta...). Le variabili aleatorie, quado utilizzabili, hao la otevole proprietà di trasferire il calcolo delle misure di probabilità di iteresse da (Ω, F, P ) a R. Questo i geerale rappreseta u vataggio, poiché lo spazio (Ω, F, P ) potrebbe essere molto più complicato e, ella stragrade maggioraza dei casi, di dimesioe strettamete maggiore di 1. Idichiamo co B la σ-algebra su R geerata dagli itervalli. Ua variabile aleatoria X iduce quidi ua misura di probabilità P X su (R, B) tramite l applicazioe P X : B [0, 1] tale che P X ((a, b]) = P (ω : X(ω) (a, b]) per ogi a, b R. Chiamiamo tale applicazioe legge della variabile aleatoria X. Acora, la legge è ua fuzioe di isieme, e duque u oggetto o facile da trattare, essedo il suo domiio ua σ-algebra. È tuttavia possibile caratterizzare uivocamete la legge di ua variabile aleatoria X tramite la sua fuzioe di ripartizioe F X defiita come l applicazioe F X : R [0, 1] tale che F X (t) = P (ω : X(ω) t) per ogi t R. La fuzioe di ripartizioe di ua variabile aleatoria gode delle segueti proprietà 1 lim t F X (t) = 0, lim t + F X (t) = 1; 3
5 mootoia: F X (s) F X (t) per ogi s t; 3 cotiuità da destra: lim h + F X (t + 1 h ) = F X(t). Le variabili aleatorie che icotreremo possoo essere classificate i due tipi, a secoda della cardialità dell isieme di valori che possoo assumere. Ua variabile aleatoria X è discreta se ha u codomiio Im(X) fiito o umerabile. È ivece cotiua se il suo codomiio è u sottoisieme cotiuo di R. 1. Teoremi limite LEGGE DEI GRANDI NUMERI TEOREMA DEL LIMITE CENTRALE 1.3 Leggi gamma, ormale, chi-quadrato, t di studet, Fischer Legge gamma Defiizioe 1.1. Si dice fuzioe gamma, l applicazioe Γ : R + R + defiita come segue Proprietà della fuzioe Γ: 1 Γ(1) = 0 e x dx = 1 Γ(α) = 0 x α 1 e x dx 1 Γ(α + 1) = 0 x α e x dx = α 0 x α 1 e x dx = αγ(α) 3 Se N, dalle proprietà precedeti segue facilmete Γ() = ( 1)! 4 Γ ( 1 ) = π Ua v.a. X segue ua legge gamma di parametri α e λ co α, λ R + (X Γ(α, λ)) se ha desità pari a λ α Γ(α) f X (x) = xα 1 e λx se x 0 0 altrove Utilizzado le proprietà della fuzioe Γ determiiamo media e variaza di X E[X] = = x λα Γ(α) xα 1 e λx = 0 λ α Γ(α) xα e λx 1 = y=λx λγ(α) λ α Γ(α) xα e λx = + 0 y α e y dy = Γ(α + 1) λγ(α) = α λ 1 Trae i alcui casi, come ad esempio quado α N, questo itegrale o ha ua primitiva semplice. Pertato la fuzioe gamma resta espressa i questo modo. 4
6 E[X ] = + x 0 λα = = y=λx 1 λ Γ(α) Γ(α) xα 1 e λx = y α+1 e y dy = λ α Γ(α) xα+1 e λx = Γ(α + ) λ Γ(α) = α(α + 1) λ V ar(x) = E[X ] E[X] α(α + 1) = α λ λ = α λ Importate elle applicazioi che faremo è il seguete risultato: Teorema 1.. Siao date v.a. X 1,..., X idipedeti, X i Γ(α i, λ), α i > 0. Allora X i Γ( α i, λ). Ua variabile X Γ(1, λ) è ache detta espoeziale di parametro λ e si idica solitamete co Exp(λ) Legge ormale Ua v.a. X segue ua legge ormale o gaussiaa stadard (X N(0, 1)) se ha desità pari a Proprietà: 1 Simmetria: X X. Ifatti e derivado f X : R R t.c. f X (x) = 1 π e x. F X (t) = P ( X t) = P (X t) = 1 F X ( t) f X (t) = f X ( t)( 1) = f X ( t) = f X (t) dove l ultima uguagliaza deriva dalla parità della desità ormale stadard. Si traduce ella formula operativa Φ(x) = 1 Φ( x), avedo idicato, come cosuetudie, co Φ la fuzioe di ripartizioe di ua variabile aleatoria gaussiaa stadard. Quatili: la proprietà precedete implica φ α = φ 1 α, dove, per ogi α (0, 1) co φ α si idica il quatile di ordie α della legge ormale, ovvero la soluzioe dell equazioe P (X φ α ) = α 3 media e variaza: coicidoo co i parametri (0, 1). 4 Y = σx + µ, co σ R + è ua trasformazioe lieare di X che geera ua v.a. ormale o gaussiaa di parametri µ, σ (Y N(µ, σ )) di desità pari a f Y : R R + t.c. f Y (x) = 1 (x µ) e σ. πσ I alcui libri (ad esempio i [8]) co φ α si idica la soluzioe dell equazioe P (X > φ α ) = α, e quidi il quatile di ordie 1 α. 5
7 Esempio 1.3. Sia Y N(µ, σ ). Mostrare che Y µ σ N(µ, σ ) 3. 5 Date v.a. X 1,..., X idipedeti, X i N(µ i, σ i ) allora X i N( µ i, σ i ). Esempio 1.4. [] p. 154 Es. 3.7 Siao X ed Y due variabili aleatorie idipedeti e gaussiae stadard. Calcolare P (X > Y ) e P (X > Y + 1 ). Esempio 1.5. [8] p (INTRODUCE AI TEST D IPOTESI) U messaggio biario ( 0 oppure 1 ) viee trasmesso da ua sorgete A ad u ricevete B tramite u caale elettrico, iviado u segale di volt se il messaggio era 1, - volt se il messaggio era 0. A causa di disturbi sul caale, il ricevete B riceve u segale pari a R = x + N, dove x può assumere il valore o - ed N N(0, 1). Il ricevete decodifica il segale co 1 se R 0.5, 0 se R < 0.5. Calcolare le probabilità di decodificare erroeamete il segale Legge Chi-quadro co gradi di libertà Siao X 1,..., X v.a. ormali stadard e idipedeti. La variabile aleatoria X = X X è ota come v.a. chi-quadrato co gradi di libertà (X χ ) e la sua desità ha l espressioe f X : R R t.c. f X (x) = 1 Γ( 1 e x 1(x 0). )x 1 Legame co le leggi Γ (, 1 ) : La legge Chi-quadro co gradi di libertà è u caso particolare di legge Gamma, corrispodete alla scelta dei parametri idicata. Date m v.a. X 1,..., X m idipedeti, X i χ i allora m X i χ m i. (Dim: caso particolare di leggi Gamma) 3 Quatili: co χ α, si idica il quatile di ordie α della legge Chi-quadro co gradi di libertà, ovvero la soluzioe dell equazioe P (X χ α,) = α Esempio 1.6. [8] p (OSSERVA CHE BISOGNA SCRIVERE L EVENTO IN TERMINI DI DIS. DI V.A. TABULATE) Per localizzare u oggetto ello spazio tridimesioale si effettua ua misurazioe che porta u errore sperimetale i ciascua delle tre direzioi che segue ua legge N(0, 4). Suppoedo i tre errori lugo le tre diverse direzioi idipedeti tra loro, calcolare la probabilità che la distaza tra la posizioe reale e quella misurata sia maggiore di 3. 3 I geerale, applicado ad ua qualuque variabile aleatoria la trasformazioe lieare otteuta sottraedo la media e dividedo per la deviazioe stadard si ottiee ua variabile aleatoria co media ulla e variaza pari ad 1. Questa operazioe viee chiamata stadardizzazioe. 6
8 1.3.4 Legge t di Studet co gradi di libertà Siao date le v.a. idipedeti Z N(0, 1), C χ. Defiiamo la v.a. T tramite l equazioe T = Z C La variabile aleatoria T prede il ome di v.a. t di Studet co gradi di libertà (T t ) e la sua desità ha l espressioe f T : R R t.c. f T (x) = Γ( +1 ) πγ( ) ] (+1) [1 + x. 1 Simmetria: T T. Si dimostra attraverso i segueti passaggi: (a) (Z, C ) ( Z, C )(idipedeza + simmetria della ormale stadard) (b) g : R R allora g(z, C ) g( Z, C ) (c) posto g(z, c) = z c P (T x) = P l osservazioe precedete implica Z C x = P Z C x = P ( T x) Quatili: la proprietà precedete implica t α, = t 1 α,, dove, per ogi α (0, 1) co t α, si idicao le quatità defiite tramite l equazioe P (T t α, ) = α C 3 P (T x) Φ(x) - Spiegazioe euristica: = X X co X 1,..., X v.a. ormali stadard e idipedeti. Quidi, per la legge dei gradi umeri C 1 e quidi, quado diveta molto grade, T avrà circa lo stesso comportameto di Z Legge F di Fischer co ed m gradi di libertà Siao date le v.a. idipedeti C χ, C m χ m. Defiiamo la v.a. F tramite l equazioe F = La variabile aleatoria F prede il ome di v.a. F di Fischer co ed m gradi di libertà (F F,m ) e la sua desità ha l espressioe f F : R R t.c. f F (x) = C C mm ( m) Γ( +m ) x Γ( )Γ( m) ( m +m x) 1(x 0). Questa legge rivelerà la sua utilità quado affroteremo l aalisi della variaza. 7
9 1 Quatili: co F α,,m si idicao le quatità defiite tramite l equazioe ovvero i quatili di ordie α. P (F F α,,m ) = α, Calcolo dei quatili di ordie α 0.5: le tavole della F Fischer, per vari valori di ed m, soo tabulati solo per α 0.5. Quado α 0.5 si usa la relazioe derivate dalle segueti trasformazioi: P (F F α,,m ) =P ( C C mm =1 P ( Cmm F α,,m ) ) C 1 F α,,m = P ( Cmm = α ) C 1 F α,,m ( ) Cmm ovvero P C 1 = 1 α da cui si evice la relazioe operativa F α,,m F 1 α,m, = 1 F α,,m 1.4 Modelli statistici e statistiche campioarie Fissiamo ua volta per tutte uo spazio di probabilità (Ω, F, P ) su cui, di volta i volta, peseremo realizzate le variabili aleatorie di iteresse 4. Itroduciamo il cocetto di campioe aleatorio. Suppoiamo di voler studiare u particolare carattere (i geere umerico) di u isieme di elemeti (popolazioe). Lo scopo della statistica è quello di produrre iformazioi circa il carattere i esame a partire dalla osservazioe di u sottoisieme di elemeti della popolazioe (campioe). Nell ambito della Statistica Matematica il carattere è descritto da ua variabile aleatoria X la cui legge F o è completamete ota. Produrre iformazioi circa il carattere sigifica, i questo cotesto, descrivere la legge F attraverso l osservazioe di tale carattere su u campioe di ampiezza, ovvero attraverso l osservazioe di u vettore di variabili aleatorie (X 1,..., X ), essedo X i la variabile aleatoria che descrive il carattere i esame dell i-simo elemeto del campioe. Formalmete: Defiizioe 1.7. U campioe aleatorio di ampiezza è ua sequeza di variabili aleatorie (X 1,..., X ) idipedet aveti legge comue F. Il problema i esame è quello di usare le osservazioi per descrivere la legge icogita F. Soo possibili casi: Caso 1 La forma fuzioale della legge F è ota, dipede da u vettore θ di parametri reali icogiti. 4 Nei casi che aalizzeremo i questo corso, l esisteza di uo spazio di probabilità su cui realizzare le variabili aleatorie i esame sarà sempre verificata. = 8
10 Caso La forma fuzioale della legge F o è ota. Nel primo caso produrre iformazioi su F equivale a produrre iformazioi sul vettore dei parametri icogiti θ, e questo è u problema di ifereza parametrica. Nel secodo caso si ha ivece u problema (di più difficile gestioe) di ifereza o parametrica. I questo corso studieremo pricipalmete problemi di ifereza parametrica. Diamo qualche defiizioe di carattere geerale; Defiizioe 1.8. U modello statistico parametrico è ua famiglia di leggi f X (x; θ), θ Θ} dove θ è u parametro o u vettore di parametri che assumoo valore i u itervallo (evetualmete ifiito) di R o R d Diamo qualche esempio di modelli statistici parametrici. idicatrice di u isieme A è defiita come 1 ifx A; 1 A} (x) = 0 ifx A Ricordiamo che la fuzioe Modello di Beroulli: f X (x; θ) = θ x (1 θ) 1 x x 0, 1}, Θ = [0, 1] Modello espoeziale: f X (x; θ) = θe θx 1 [0, ) (x) x R Θ = [0, ) Modello ormale: f X (x; θ 1, θ ) = [0, ) 1 πθ e (x θ 1 ) θ x R Θ = (, ) La modellizzazioe corretta del modello statistico è il primo fodametale passo per affrotare il problema del computo della legge vera della caratteristica di iteresse. Il passo successivo è l estrazioe del campioe casuale. Ua volta oto il modello ed estratto il campioe, il problema della stima dei parametri può essere affrotato. Geeralmete la stima di θ è ua opportua fuzioe delle osservazioi che o dipede dal parametro da stimare. Precisamete Defiizioe 1.9. Ua statistica T è ua variabile aleatoria della forma T = f(x 1,..., X ) co f : R Θ. Le statistiche rappresetao ua opportua sitesi delle osservazioi (i geere la dimesioe di Θ è molto più piccola della dimesioe del campioe). Due statistiche che useremo molto, soo la media campioaria e la variaza campioaria. Defiiamole ed aalizziamo le loro proprietà. Sia X 1,..., X u campioe i esame estratto da ua legge F di media µ e variaza σ. Defiiamo Media campioaria: X = 1 X i Variaza campioaria: S = 1 1 (X i X ) 9
11 La media e la variaza campioaria hao la peculiarità di avere lo stesso valore atteso della media teorica e della variaza teorica della distribuzioe da cui il campioe è estratto. I formule E [ X ] = µ E [ S ] = σ Ioltre applicado la legge dei gradi umeri si verifica che X µ i probabilità + S σ i probabilità + La prima covergeza è proprio la tesi della LGN. Per la secoda basta riscrivere la variaza campioaria come segue ed osservare che 1 S = [ 1 1 1, 1 + X i S ] Xi X + E[X], X E[X] µ = σ + µ così che Campioameto da ua distribuzioe ormale: proprietà di X e di S Aalizziamo il caso i cui F = N(µ, σ ). Lo studio di questo caso particolare è molto importate, perché molte volte sarà possibile fare ifereza sui parametri icogiti di ua distribuzioe qualuque utilizzado l approssimazioe ormale stabilita dal TLC ([8] esempio pag 4). Allora X N ) (µ, σ o, equivaletemete X µ σ N(0, 1). Osserviamo che il valore medio di X è la media µ della legge F, metre la sua variaza si riduce al crescere della dimesioe del campioe. Quidi, se i u problema di stima il parametro icogito è µ, sarà aturale assumere come suo valore approssimato la media campioaria. Esempio vedi [8] esempio pag 16 Ua popolazioe formata da operai maschi, preseta pesi corporei i libbre di media 167 e deviazioe stadard 7. 1 Se si selezioa u campioe di 36 elemeti, quato vale la probabilità che la media campioaria dei loro pesi stia tra 163 e 171? E se si selezioao 144 operai? Cosideriamo ora la Variaza Campioaria. Allora ( 1) S σ X 1 (1.1) La dimostrazioe di questo risultato passa attraverso le segueti tappe 10
12 X e S soo variabili aleatorie idipedeti (seza dim). Se ua variabile aleatoria co distribuzioe X è somma di due variabili aleatorie idipedeti, di cui ua co distribuzioe X 1, allora l altro addedo è ua variabile aleatoria co distribuzioe X 1 (seza dim comuque sul [7] pag 3). Vale la seguete decomposizioe ( ) ( ) Xi µ X µ = + ( 1) S σ σ σ Ifatti ( ) Xi µ = σ ( Xi µ σ ( Xi X + X ) ( µ = ( 1) S X σ σ + µ σ ) X e ( X µ σ ) X 1 Esempio Vedi [8] esempio pag 1 Il tempo impiegato da u microprocessore ad eseguire alcui processi è ua variabile aleatoria N(30, 9). Se si osserva l esecuzioe di u campioe di 15 processi, qual è la probabilità che la variaza campioaria risultate sia maggiore di 1? Da questi risultati se e deducoo altri molto utilizzati. ( X µ) Corollario 1.1. t( 1) S Dimostrazioe. Poichè ( X µ) σ ( X µ) S = N(0, 1) e ( 1) S σ ( X µ) σ t( 1) ( 1) S σ 1 ) X 1 si ottiee facilmete che Corollario Sia X 1,..., X u campioe estratto da ua N(µ 1, σ 1) e Y 1,..., Y m u campioe estratto da ua N(µ, σ ) e siao tali campioi idipedeti tra loro. Allora S 1, σ 1 S,m σ F ( 1, m 1) (La dimostrazioe è immediata dalla defiizioe di F) Esempio [8], esercizio 0 pag 8 Cosideriamo due campioi idipedeti. Il primo ha ampiezza 10 e proviee da ua popolazioe ormale di variaza 4, il secodo ha ampiezza 5 e proviee da ua popolazioe ormale di variaza. Calcolare la probabilità che la variaza campioaria del secodo campioe sia maggiore di quella del primo. 11
13 Corollario Sotto le stesse ipotesi del precedete corollario, allora X Ȳm (µ 1 µ ) ( 1) S 1, σ 1 + (m 1) S, σ + m σ1 + σ m t( + m ) Dimostrazioe. Dall idipedeza e gaussiaità dei campioi si ha ( ) X Ȳm N µ 1 µ, σ 1 + σ m e ( 1) S 1, + (m 1) S, X σ1 σ (+m ) La defiizioe della t di Studet permette di cocludere. 1
14 Capitolo Stima putuale e per itervalli.1 Stima putuale Defiizioe.1. Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe f X (x; θ), θ Θ}. Ua statistica d = d(x 1,..., X ) utilizzata per stimare il parametro icogito θ (o ua sua fuzioe h(θ)) è detta stimatore di θ (di h(θ)). È evidete che tra tutti gli stimatori possibili di θ (di h(θ)) ce e sarao alcui migliori di altri rispetto ad u qualche criterio di ottimalità prescelto. Il criterio che oi scegliamo è che sia piccolo l errore quadratico medio che si commette quado si utilizza lo stimatore d come valore approssimato di θ (di h(θ)), ovvero che sia piccola la quatità E [ (d(x 1,..., X ) θ) ] ( E [ (d(x 1,..., X ) h(θ)) ]).1.1 Stimatori e proprietà di ottimalità Determiare stimatori che miimizzio l errore quadratico medio è quasi impossibile (vedi, ad esempio [4]), a meo che o si restriga la classe degli stimatori. Cosidereremo quidi ua classe di stimatori che ha come pecularietà il fatto di avere come valore medio il parametro da stimare: Defiizioe.. Uo stimatore d = d(x 1,..., X ) di θ (o di h(θ)) è detto stimatore o distorto o stimatore corretto di θ (di h(θ)) se E[d(X 1,..., X )] = θ [E[d(X 1,..., X )] = h(θ)] Se uo stimatore è o distorto allora l errore quadratico medio coicide co la sua variaza. I tal caso, se ci si restrige alla classe degli stimatori o distorti, lo stimatore ottimale è, se esiste, quello di variaza miima: Defiizioe.3. Uo stimatore o distorto d = d (X 1,..., X ) di θ (o di h(θ)) di variaza miima uiformemete rispetto al parametro θ ella la classe degli stimatori o distorti è detto ottimale (UMVUE). Vediamo el seguete esempio che o sempre esistoo stimatori ottimali: 13
15 Esempio.4. [1] esempio. pag 30 Sia X Exp(θ), θ > 0. Allora o esiste uo stimatore o distorto di θ basato su u campioe di ampiezza 1. Ifatti, qualora esista, avrebbe la forma h(x 1 ), co h o egativa e tale che E θ (h(x 1 )) = θ θ > 0, ovvero θ = 0 h(x)θe θx dx θ > 0 1 = 0 h(x)e θx dx θ > 0. Quidi, se cosideriamo due valori θ 1 > θ > 0 otteiamo le uguagliaze 0 = 0 h(x)e θ x dx 0 h(x)e θ 1x dx = 0 h(x)(e θ x e θ 1x )dx. ma (e θ x e θ 1x ) > 0, quidi, affiché l uguagliaza sia vera, deve essere h(x) = 0 per ogi x > 0 ovvero E θ (h(x 1 )) = 0 cotro l ipotesi. Quado gli stimatori ottimali o esistoo, diveta importate poter misurare il grado di botà (efficieza) di uo stimatore corretto. Questa misura viee fatta adado a cofrotare la variaza dello stimatore i esame co u cofie iferiore per la variaza che può essere calcolato grazie al seguete risultato Teorema.5. (Cramer-Rao) Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe f X (x; θ), θ Θ}. Sotto alcue proprietà di regolarità (vedi [7] pag 361 o [5] pag 31) che riguardao proprietà di differeziabilità della desità f X (x; θ) ed il fatto che il suo supporto x R tale che f X (x; θ) = 0} o dipeda da θ, allora la variaza di u qualuque stimatore o distorto d di ua fuzioe derivabile del parametro h(θ) soddisfa la disuguagliaza V ar (d(x 1,..., X )) [h (θ)] ( ) (.1) log fx (x; θ) E θ La quatità a secodo membro è ota come limite iferiore di Cramer Rao, metre la quatità I X (θ) defiita come è ota come iformazioe di Fischer. ( ) log fx (x; θ) I X (θ) = E (.) θ 1 Poiamo B (θ) =. A questo puto se uo stimatore o distorto ha variaza pari I X (θ) al limite iferiore di Cramer Rao, è sicuramete ottimale, altrimeti è possibile utilizzare come misura di efficieza e(d) di uo stimatore o distorto d la quatità e(d) = B (θ) V ar(d) 1 (.3) Defiizioe.6. Uo stimatore corretto d = d(x 1,..., X ) è detto efficiete se la sua variaza coicide co il limite iferiore di Cramer Rao, o, equivaletemete, se e(d) = 1 14
16 Osservazioe.7. Il limite iferiore di Cramer Rao o è l estremo iferiore della variaza degli stimatori o distorti, quidi è possibile che uo stimatore sia il migliore possibile, el seso che abbiamo itrodotto, ache quado la sua variaza è maggiore di tale limite. Facciamo degli esempi di stimatori efficieti: 1 Stimatore efficiete per la media di ua beroulliaa ([1] pag 35) Stimatore efficiete per il parametro θ di ua legge Γ(α, 1 ), co α oto ([1] pag 38) θ Accato alle proprietà di ottimalità per campioi fiiti, ci soo ache delle proprietà asitotiche che elechiamo di seguito. Defiizioe.8. Uo stimatore d = d(x 1,..., X ) di θ è detto asitoticamete corretto se gode della proprietà lim E[d(X 1,..., X )] = θ Defiizioe.9. Uo stimatore d = d(x 1,..., X ) di θ è detto cosistete lim d(x 1,..., X ) = θ dove il limite precedete è da itedersi i probabilità. Due stimatori cosisteti della media e della variaza soo la media campioaria e la variaza campioaria. Ovviamete la cosisteza di uo stimatore implica la sua correttezza asitotica. Defiizioe.10. Uo stimatore d = d(x 1,..., X ) di θ è detto asitoticamete efficiete se lim e[d(x 1,..., X )] = 1 ovvero se dimesioi gradi del campioe V ar[d(x 1,..., X )] B (θ). U ultima proprietà molto importate per gradi campioi è Defiizioe.11. Uo stimatore d = d(x 1,..., X ) di θ è detto asitoticamete ormale se ( ) lim P d(x 1,..., X ) E[d(X 1,..., X )] t = Φ(t) V ar[d(x1,..., X )].1. Il metodo della massima verosimigliaza Comiciamo co i metodi di costruzioe di stimatori. I questo paragrafo aalizziamo u metodo che produce stimatori asitoticamete efficieti e cosisteti, motivo per cui soo tra i più utilizzati i statistica. Comiciamo co qualche defiizioe: 15
17 Defiizioe.1. Sia (X 1 = x 1,..., X = x ) ua realizzazioe di u campioe aleatorio (X 1,..., X ) estratto dalla distribuzioe f X (x; θ), θ Θ}. Sia L : Θ R la desità cogiuta del campioe (X 1,..., X ) calcolata el puto (x 1,..., x ), ovvero L(θ) = Π f X (x i ; θ) Tale desità vista come fuzioe del parametro icogito θ è ota co il ome di fuzioe di verosimigliaza. Defiizioe.13. Sia θ(x 1,..., x ) ua statistica che massimizza la fuzioe di verosimigliaza L(θ) (se esiste!!!). Si chiama stimatore di massima verosimigliaza di θ la statistica θ(x 1,..., X ). Il pricipio euristico che motiva la scelta di tali stimatori è il seguete ([6], pag 587): tra i possibili valori del parametro θ si preferisce quello che corrispode alla massima probabilità di geerare i dati osservati Operativamete la costruzioe di tali stimatori corrispode alla ricerca del massimo di ua fuzioe. Se il parametro è multidimesioale si utilizzao metodi di calcolo relativi alle fuzioi di più variabili. Osservare che il puto che rede massima ua fuzioe o egativa (come ua desità) è lo stesso che rede massimo il logaritmo di tale fuzioe (il logaritmo è ua fuzioe mootoa) semplifica otevolmete i calcoli. Itroduciamo quidi la fuzioe di logverosimigliaza, cioè la fuzioe log(l(θ)). Illustreremo il metodo di calcolo per la ricerca di tali stimatori ei segueti casi: 1 (X 1,..., X ) campioe estratto dalla distribuzioe N(θ, 1), θ R} ([6], pag 588) (X 1,..., X ) campioe estratto dalla distribuzioe N(θ, σ ), (θ, σ ) R R + } ([6], pag 589) 3 (X 1,..., X ) campioe estratto dalla distribuzioe N(0, θ), θ R + } 4 (X 1,..., X ) campioe estratto dalla distribuzioe U(0, θ), θ R + } (Da cofrotare co quello trovato co il metodo dei mometi)([6], pag 590) 5 (X 1,..., X ) campioe estratto dalla distribuzioe Exp(θ), θ R + } 6 (X 1,..., X ) campioe estratto dalla distribuzioe P (θ), θ R + } ([8] pag. 38) Esempio.14. [8] pag Nel 1998 a Berkeley i Califoria, il umero di icideti stradali i 10 giorate seza pioggia scelte a caso è stato di Si usio questi dati per stimare per quell ao la frazioe di giorate seza pioggia co o più di icideti. 16
18 7 (X 1,..., X ) campioe estratto dalla distribuzioe B(θ), θ (0, 1)} 8 (X 1,..., X ) campioe estratto dalla distribuzioe U[θ 1, θ + 1 ], θ R} ([1], pag 54 - sulla o uicità dello stimatore di max verosimigliaza ) Tati esercizi iteressati ed ua sitesi delle proprietà teoriche si trovao su [1]..1.3 Proprietà degli stimatori di massima verosimigliaza Gli stimatori di massima verosimigliaza hao iteressati proprietà di ottimalità sia per campioameto fiito che asitotiche. Suppoiamo che il modello statistico di riferimeto verifichi le codizioi di regolarità acceate ell euciato del Teorema.5. Valgoo allora le segueti proprietà: Proprietà.1. Se esiste uo stimatore o distorto ed efficiete, tale stimatore è quello di massima verosimigliaza. Proprietà.. Gli stimatori di massima verosimigliaza soo asitoticamete efficieti e cosisteti. Proprietà.3. Gli stimatori di massima verosimigliaza soo asitoticamete ormali, ovvero: IX (θ)( θ(x 1,..., X ) θ) N(0, 1), dove I X (θ) è l iformazioe di Fischer defiita ell Eq... La proprietà precedete vale ache quado l iformazioe di Fischer I X (θ) è approssimata per mezzo dello stimatore di massima verosimigliaza I X ( θ), ovvero: Proprietà.4. I X ( θ)( θ(x 1,..., X ) θ) N(0, 1). SERVE UN RIFERIMENTO BIBLIOGRAFICO PER LE DIM DELLE UL- TIME PROPRIETÀ ELENCATE. Queste proprietà possoo essere riassute come segue (cfr. [6] pag. 601) Se esiste uo stimatore efficiete per θ, lo stimatore di max. ver. coicide co esso e quidi è efficiete per per ogi fiito. D altra parte, ache se o esiste uo stimatore efficiete per θ, lo stimatore di max. ver. è comuque asitoticamete efficiete Ua ulteriore proprietà molto utile quado si voglia stimare ua fuzioe del parametro icogito è la seguete: Proprietà.5. Proprietà di ivariaza - Sia g : Θ R ua fuzioe ivertibile. Allora se θ(x 1,..., X ) è uo stimatore di massima verosimigliaza per θ, g( θ) è uo stimatore di massima verosimigliaza per g(θ). Come applicazioe della proprietà precedete facciamo il seguete esempio: 17
19 Esempio.15. [6] 16.1 pag 598 Da u campioe casuale (X 1,..., X ) geerato da misurazioi sulle durate del fuzioameto di compoeti elettroiche, che si suppogoo avere ua legge Exp(θ), θ > 0, si vuole stimare la probabilità che esse sopravvivao almeo 3 ore i più della durata media, ovvero si vuole stimare la quatità ( P X > ) ( = 1 F X ) ) = 1 (1 e θ(3+ 1 θ ) = e (3θ+1) θ θ Si dimostra che lo stimatore di max verosimigliaza di θ è 1 X (CONTROLLARE!!!!) e quidi, per la proprietà di ivariaza, lo stimatore di max verosimigliaza di P ( ) X > θ è e ( 3 X +1 )..1.4 Il metodo dei mometi Ricordiamo la seguete defiizioe Defiizioe.16. Data ua sequeza di variabili aleatorie (X 1,..., X ) idipedeti ed ideticamete distribuite, si chiama mometo campioario di ordie r N la quatità M r così defiita M r = Xr i L applicabilità del metodo dei mometi è basato essezialmete su due codizioi: (.4) 1 Il umero r dei parametri da stimare sia o maggiore del umero dei mometi teorici che possiede la distribuzioe i esame; i parametri da stimare siao delle fuzioi ote di tali mometi. I tal caso, degli stimatori aturali dei mometi teorici soo i relativi mometi campioari (grazie alla legge dei gradi umeri). Si imposta quidi u sistema di r equazioi i r icogite (i parametri da stimare) e si risolve. Le soluzioi otteute i questo modo (se esistoo- approfodire) soo ote come stimatori dei mometi dei parametri. Il metodo dei mometi per il calcolo degli stimatori è uo dei più semplici da implemetare e richiede ipotesi meo strigeti rispetto al metodo della max verosimigliaza. Ad esempio, o richiede la coosceza della forma fuzioale della distribuzioe i esame. Ma, proprio perché ha meo vicoli, le stime che forisce soo i geerale meo buoe. Per le proprietà di tale metodo parafrasiamo dal [6], pag. 584: Poiché soo fuzioi cotiue dei mometi campioari, gli stimatori derivati co il metodo dei mometi soo cosisteti, asitoticamete o distorti ed asitoticamete ormali. D altra parte, o sempre soo efficieti, eppure asitoticamete......ne deriva che le proprietà di tali stimatori soo di atura asitotica...ioltre tali stimatori o garatiscoo sempre stime coereti. Calcoliamo tali stimatori ei casi: 18
20 1 (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = (θ + 1)x θ 1 [0,1] (x), θ R + } [6], pag. 58 esempio 16.3) da osservare che per alcue realizzazioi del campioe forisce stime o coereti(corrispodeti a valori di θ egativi (X 1,..., X ) campioe estratto dalla distribuzioe B(N; θ), (N, θ) N (0, 1)} ( [6], pag. 583) ache qui potrebbero esserci stime o coereti 3 (X 1,..., X ) campioe estratto dalla distribuzioe N(θ, σ ), (θ, σ ) R R + } ( [6], pag. 583) 4 (X 1,..., X ) campioe estratto dalla distribuzioe U(0, θ), θ R + } (Da cofrotare co quello trovato co il metodo della max verosimigliaza)( [6], pag. 584) produce stimatori o efficieti co efficieza asitotica tedete a zero. Come esempio, se = 3 e si osserva (1, 4, ), allora la stima è pari a 18, ma 4 > 18!. Itervalli di cofideza Nel capitolo precedete abbiamo forito metodi per la costruzioe di stimatori di parametri icogiti di ua distribuzioe la cui forma è ota. Però o sappiamo quatificare, eppure el caso i cui gli stimatori godao di proprietà di ottimalità, quato buoe siao le stime otteute. La stima itervallare, a differeza di quella putuale, si preoccupa di forire o u sigolo valore umerico per i parametri icogiti ma u itervallo che, co u grado di fiducia (approfodire il cocetto) fissato a priori, cotega il parametro icogito. Studieremo itervalli di cofideza per parametri scalari, ma segaliamo che ache il caso vettoriale può essere affrotato. Defiizioe.17. Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe f X (x; θ), θ Θ}. Sia 1 α (0, 1) e siao T 1 = t 1 (X 1,..., X ) e T = t (X 1,..., X ) due statistiche tali che: T 1 T ; P (T 1 < θ < T ) = 1 α allora l itervallo casuale (T 1, T ) si chiama itervallo di cofideza al livello 1 α per il parametro icogito θ, metre 1 α è il livello di cofideza. Gli itervalli di cofideza possoo essere ache uilaterali: Defiizioe.18. Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe f X (x; θ), θ Θ}. Sia 1 α (0, 1) e siao T 1 = t 1 (X 1,..., X ) e T = t (X 1,..., X ) due statistiche tali che: P (θ > T 1 ) = 1 α P (θ < T ) = 1 α 19
21 allora la statistica T 1 è l estremo di cofideza iferiore al livello 1 α per θ, metre la statistica T è l estremo di cofideza superiore al livello 1 α per θ 1 Osservazioe.19. Le precedete defiizioi si estedoo i modo aturale ad itervalli di cofideza per fuzioi h(θ) del parametro θ. È evidete che, a parità di livello di cofideza, possoo esistere ifiiti itervalli, metre, el caso di campioameti da distribuzioi cotiue, gli estremi di cofideza soo uivocamete determiati. Vedremo el prossimo paragrafo i criteri più utilizzati per costruire itervalli di cofideza ottimali...1 Costruzioe di itervalli di cofideza: il metodo della quatità pivotale Defiizioe.0. Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe f X (x; θ), θ Θ}. Sia Q ua fuzioe del campioe (X 1,..., X ) e del parametro icogito θ, cioè della forma Q = q(x 1,..., X ; θ) la cui distribuzioe sia ota. Allora Q è detta quatità pivotale. Esempio.1. Sia (X 1,..., X ) campioe aleatorio estratto dalla distribuzioe N(θ, 4), θ R}. Allora X θ N(0, 4 ) e X θ N(0, 1) soo quatità pivotali, perchè dipedoo fuzioalmete dal campioe e dal parametro ma la loro legge è ota. Come si determiao le quatità pivotali? E come si utilizzao ella ricerca di itervalli di cofideza? Espoiamo la procedura ei segueti passaggi: 1 Si cosidera u campioe casuale (X 1,..., X ) oppure ua sua statistica T (X 1,..., X ) (i geere uo stimatore del parametro); si cerca ua trasformazioe Q = q(t (X 1,..., X ); θ) la cui legge sia ota; 3 per ogi fissato livello di cofideza 1 α (0, 1) si determia ua coppia di puti z 1, z tali per cui P (z 1 Q z ) = 1 α; 4 si esprime l eveto z 1 Q z } = T 1 (X 1,..., X ) θ T (X 1,..., X )} laddove possibile. I questo modo si è otteuto u itervallo di cofideza [T 1 (X 1,..., X ), T (X 1,..., X )] al livello 1 α per il parametro icogito θ. La procedura appea descritta lascia aperto il problema della scelta della coppia z 1, z, che, come già osservato, o è uica. I geerale si sceglie la coppia che produce itervalli di cofideza co ua delle due segueti proprietà: 1 Itervalli co code equiprobabili: si sceglie la coppia z 1, z tale per cui P (Q z 1 ) = P (Q z ) = α; ovvero, se 1 α è l ampiezza dell itervallo, z 1 = q α e z = q 1 α. 1 [6], pag. 73 per esempi el caso uilaterale Quest ultimo passaggio è ua procedura di iversioe rispetto al parametro icogito θ ed è molto agevole se la variabile aleatoria pivot Q è ivertibile o meglio acora mootoa come fuzioe del parametro. 0
22 Itervalli di miima lughezza (evetualmete media): si sceglie la coppia z 1, z che, a parità di livello, reda miima la lughezza T (X 1,..., X ) T 1 (X 1,..., X ). U cotrollo sulla forma della desità dalla quale si campioa aiuta a determiare le quatità pivotali. Defiizioe.. Sia dato il modello statistico f(x, θ), θ Θ R}. Il parametro θ è u parametro di posizioe se e solo se la desità f(x, θ) può essere scritta come fuzioe di (x θ), ovvero se per ua opportua fuzioe h, si ha f(x, θ) = h(x θ). Il parametro θ R + è ivece u parametro di scala se e solo se per ua opportua fuzioe h, la desità f(x, θ) può essere scritta come f(x, θ) = 1h ( ) x θ θ. Ora se θ è u parametro di posizioe, allora X θ è ua quatità pivotale, metre se θ è u parametro di scala X θ è ua quatità pivotale. 3 Applichiamo questo metodo per la ricerca di itervalli ei segueti casi: 1 (X 1,..., X ) campioe estratto dalla distribuzioe U(0, θ), θ R + } ([6] pag , oppure [7] (meglio) Es.4 pag 484) Sappiamo che T (X 1,..., X ) = max(x 1,..., X ) := X () è lo stimatore di max verosimigliaza di θ. La desità di tale stimatore è t 1 se t (0, θ) θ f X() (t) = 0 altrimeti Ioltre la variabile aleatoria q(t (X 1,..., X ); θ) = X () ha desità pari a θ t 1 se t (0, 1) f q (t) = 0 altrimeti Possiamo quidi utilizzare X () come quatità pivotale. A questo puto, per otteere θ u itervallo di cofideza a livello 1 α basta determiare z 1, z } tali per cui ( P z 1 X ) () z = 1 α θ z 1 X () X() Poiché l espressioe θ z } = z θ X () z 1 } l itervallo di cofideza cercato ha [ X() z, X ] () z 1 Per avere u itervallo ottimale, bisoga determiare la coppia z 1, z } i modo tale che sia miima la lughezza ( ) dell itervallo, ovvero dobbiamo miimizzare la 1 fuzioe L(z 1, z ) = X () z 1 1 z soggetta al vicolo ( P z 1 X ) z () z = t 1 dt = z z 1 = 1 α θ z 1 3 I realtà quado il modello è di uo dei due tipi descritti, possoo essere costruite molte altre quatità pivotali. 1
23 Da questa uguagliaza si deduce che z 1 = z 1 + α e che (1 α) 1 < z 1. I particolare si ottiee ua espressioe della lughezza dell itervallo come fuzioe della sola z. Applicado le regole stadard per il calcolo dei miimi ed osservado che dz 1 dz si ottiee: = z 1 z 1 1 ( dl = X () 1 dz z1 z 1 z ) z +1 = X z () 1 z +1 z1 +1 z < 0. Quidi L è ua fuzioe decrescete e duque assume il suo miimo assoluto per z = 1. Di cosegueza z 1 = α 1 e quidi l itervallo di cofideza ottimale è [ X (), X ] () α 1 Determiare l itervallo di cofideza a code equiprobabili per u campioe di dimesioe 1 estratto dalla distribuzioe f θ (x) = (θ x), θ 0 < x < θ} [7] pag (X 1,..., X ) campioe estratto dalla distribuzioe Exp(θ), θ R + } [8], esempio pag 69 Suggerimeto: utilizza il fatto che, quado Y Γ(, θ), allora θy χ ()) 4 (X 1,..., X ) campioe estratto dalla distribuzioe f θ (x) = e (x θ) se x > θ 0 altrimeti.. Costruzioe di itervalli di cofideza: il metodo della trasformazioe itegrale La scelta di ua quatità pivotale per la costruzioe di itervalli di cofideza dipede pricipalmete dal modello parametrico i esame. Le difficoltà maggiori si icotrao co i modelli discreti, poiché i tal caso il calcolo dei quatili può risultare difficoltoso. Per i modelli cotiui ivece esiste u metodo sempre perseguibile, basato sulla trasformazioe itegrale di probabilità: Teorema.3. Sia X ua variabile aleatoria cotiua co fuzioe di ripartizioe F X (x). Allora la variabile aleatoria U = F X (X) è distribuita uiformemete ell itervallo (0, 1). La dimostrazioe del precedete risultato è lasciata per esercizio. Sia ora (X 1,..., X ) u campioe estratto dal modello parametrico cotiuo f(x, θ), θ Θ}. Detta F X (x, θ) la fuzioe di ripartizioe comue degli elemeti del campioe, il Teorema.3 garatisce che F X (X i, θ) U(0, 1) per i = 1,...,.
24 Ioltre Y i l F X (X i, θ) exp(1) per i = 1,...,. Ifatti 0 se t < 0; F Yi (t) = P ( l F X (X i, θ) t) = P (F X (X i, θ) e t ) = 1 e t se t 0. È duque possibile cosiderare come quatità pivotale Q 1 (X 1,..., X ; θ) = l F X(X i, θ) Γ(, 1), oppure, alterativamete, Q (X 1,..., X ; θ) = l F X(X i, θ) Γ(, 1) χ (). Abbiamo appea visto u metodo stadard per la determiazioe di ua quatità pivotale ogi qual volta il modello parametrico i esame sia cotiuo. La possibilità poi di utilizzare questa quatità pivotale per la determiazioe di itervalli di cofideza va valutata caso per caso ed è come oto legata alla possibilità di ivertirla rispetto al parametro icogito. Questo è peraltro sempre possibile quado sia mootoa i θ. Esempio.4. ([5] pag 391, esempio 8.4). Sia (X 1,..., X ) u campioe estratto dal modello parametrico θx θ 1 I (0,1) (x), θ > 0}. Calcolare u itervallo di cofideza a code equiprobabili di livello 1 α per θ. Esempio.5. Sia (X 1,..., X ) u campioe estratto dal modello parametrico U[0, θ], θ > 0}. Calcolare u itervallo di cofideza a code equiprobabili di livello 1 α per theta basato sul metodo della trasformazioe itegrale e cofrotarlo co quello otteuto attraverso lo stimatore di massima verosimigliaza...3 Itervalli di cofideza per campioi ormali Sia (X 1,..., X ) u campioe estratto da ua distribuzioe N(µ, σ ). Ricaveremo di seguito itervalli di cofideza per ciascuo dei parametri che caratterizza tale legge. Itervallo di cofideza per la media Notiamo che soo possibili casi 1 σ è u valore oto. Sappiamo che lo stimatore di massima verosimigliaza per la media µ è la media campioaria X e che X ( ) N µ, σ. Di cosegueza stadardizzado si ottiee X µ N(0, 1). Poiché σ è oto σ la variabile aleatoria X µ è ua quatità pivotale. La utilizziamo qui- σ di per determiare u itervallo di cofideza per la media a livello 1 α. Cerchiamo l itervallo di cofideza a code equiprobabili, cioé quello otteuto ivertedo rispetto a µ le segueti disuguagliaze 4 φ α X µ σ φ 1 α Ua semplice procedura di iversioe e la proprietà dei quatili della ormale stadard permettoo di ricavare il seguete itervallo di cofideza per µ X σ φ 1 α µ X + σ } φ 1 α 4 Quado la legge della quatità pivotale i esame è simmetrica, l itervallo di cofideza a code equiprobabili coicide co quello di lughezza miima ([5] per approfodimeti). 3 }
25 o, equivaletemete [ X σ φ 1 α, X + σ φ 1 α ] Esempio.6. [8], esempio pag. 46 È oto che quado u segale elettrico di valore µ viee trasmesso da ua sorgete A, il ricevete B registri effettivamete u valore X distribuito come ua N(µ, 4). Per ridurre l errore, lo stesso segale viee iviato 9 volte e si registra la media campioaria dei segali ricevuti, ovvero X 9. Sapedo che X 9 = 9, determiare u itervallo di cofideza di livello 0.95 per µ. Esempio.7. [8], esempio pag. 49 Il peso dei salmoi cresciuti u u certo allevameto segue ua legge ormale co media µ, che varia di ao i ao, e deviazioe stadard σ = 0.3 libbre. Quato grade occorre predere il campioe, per essere sicuri al 95% che la ostra stima del peso medio dei salmoi di quest ao sia precisa etro ±0.1 libbre? σ è u valore icogito. I tal caso la quatità X µ o è più ua σ quatità pivotale, perché dipede dal parametro icogito σ. Sappiamo però che la variaza campioaria S è idipedete da X e che ( 1) S X 1. Ne deduciamo che X µ σ ( 1) S σ 1 t 1. Facedo le opportue semplificazioi si ricava X µ S t 1 che è quidi ua quatità pivotale. Ache i questo caso procededo i modo aalogo al puto precedete, determiiamo l itervallo di cofideza a code equiprobabili t α, 1 X } µ t 1 α S, 1 da cui o, equivaletemete X S t 1 α, 1 µ X + S t 1 α, 1 } [ X S t 1 α, 1, X + S t 1 α, 1 ] σ Itervallo di cofideza per la variaza Ache i questa situazioe è possibile distiguere casi 1 µ è u valore oto. I tal caso ( Xi ) µ, σ i quato somma di quadrati di ormali stadard idipedeti, è distribuita come ua chi-quadrato co gradi di libertà ed è quidi ua quatità pivotale. La utilizziamo quidi per 4
26 determiare u itervallo di cofideza a code equiprobabili 5 di livello 1 α } χ α, 1 (X σ i µ) χ 1 α, da cui, ivertedo rispetto a σ (X i µ) χ 1 α, σ } (X i µ) χ α, o, equivaletemete [ (X i µ) χ 1 α,, ] (X i µ) χ α, µ è u valore icogito La quatità pivotale che si utilizza i questo caso è ( 1)S = 1 ( σ σ Xi X ) χ 1. Si ottiee l itervallo di cofideza a code equiprobabili di livello 1 α attraverso gli stessi passaggi utilizzati el caso precedete: } χ α, 1 1 ( Xi σ X ) χ 1 α, 1 da cui, ivertedo rispetto a σ ( Xi X ) χ 1 α, 1 σ ( Xi X ) } χ α, 1 o, equivaletemete [ ( Xi X ) ( Xi, X ) ] χ 1 α, 1 χ α, 1 Esempio.8. [8], esempio pag. 56 Ua procedura automatizzata deve produrre rodelle co ua variabilità di spessore molto ridotta. Per testare questa variabilità si scelgoo 10 rodelle dalla produzioe e se e misura lo spessore, che risulta, i pollici Calcolare l itervallo di cofideza di livello 0.9 per la deviazioe stadard dello spessore delle rodelle. 5 Osserviamo che la legge chi-quadrato o è simmetrica e quidi l itervallo di cofideza a code equiprobabili o è il migliore possibile. U metodo per determiare l itervallo di miima lughezza è descritto i [5], pag
27 Itervallo di cofideza per la differeza tra medie Cosideriamo due campioi idipedeti (X 1,..., X ) estratto da ua distribuzioe N(µ 1, σ1) e (Y 1,..., Y m ) estratto da ua ( distribuzioe N(µ, σ). Dalle proprietà della ormale si evice che X Ȳm N µ 1 µ, σ 1 + σ ),e, stadardizzado X Ȳm (µ 1 µ ) σ1 + σ m N(0, 1) (.5) Per determiare u itervallo di cofideza a livello 1 α per la differeza tra medie distiguiamo come al solito casi 1 σ 1, σ soo oti. I tal caso la quatità ell eq..5 è evidetemete ua quatità pivotale e di cosegueza i soliti passaggi permettoo di derivare l itervallo [ X Ȳm σ 1 + σ m φ 1 α, X Ȳm + σ 1 + σ m φ 1 α ] σ1, σ soo icogiti. I questo caso la variabile aleatoria.5 o è più ua quatità pivotale poiché dipede dai parametri icogiti. D altra parte, quado si possa assumere σ1 = σ = σ si riesce a costruire ua quatità pivotale osservado che ( 1)S 1 = 1 ( σ σ Xi X ) χ 1 e che (m 1)Sm = 1 σ m ( σ Yi Ȳm) χ m 1 ; di cosegueza, dalle proprietà della legge chi-quadro si ottiee ( 1)S 1 σ + (m 1)S m σ χ +m Ifie, utilizzado l idipedeza tra questa variabile aleatoria e la.5, si ottiee = ( 1)S 1 +(m 1)S m X Ȳm (µ 1 µ ) σ + σ m ( 1)S 1 σ + (m 1)S m σ +m t +m Posto Sp e semplificado la precedete espressioe, si +m ricava fialmete la quatità pivotale X Ȳm (µ 1 µ ) ( t +m Sp m) La quatità Sp è uo stimatore o distorto di σ ed è ota come variaza campioaria coglobata (perché calcolata sull iformazioe otteuta da due diversi campioi). Siamo fialmete i grado di ricavare l itervallo di cofideza per la differeza tra le medie 6
28 da cui X Ȳm ovvero [ X Ȳm t α,+m X Ȳm (µ 1 µ ) ( Sp 1 + ) t 1 α 1 m S p S p,+m ( ) ( t 1 α m,+m µ 1 µ X 1 Ȳm + Sp + 1 ) t 1 α m,+m ( ) ( t 1 α m,+m, X 1 Ȳm + Sp + 1 ) ] t 1 α m,+m Esempio.9. [8], esercizio 44 pag. 88 Quelli che seguoo soo i tempi di combustioe i secodi di due diversi tipi di cadelotti fumogei: Tipo I Tipo II Assumedo che le popolazioi siao ormali co stessa variaza, calcolare l itervallo di cofideza di livello 0.99 per la differeza media dei tempi di combustioe...4 Itervalli di cofideza asitotici Sia (X 1,..., X ) u campioe estratto dalla distribuzioe f(x, θ), θ Θ}. Suppoiamo che esista uo stimatore di massima verosimigliaza θ = θ(x 1,..., X ) per il parametro θ. Ricordiamo che sotto opportue ipotesi dei regolarità, le proprietà.3 e.4 assicurao la ormalità asitotica degli stimatori di max verosimigliaza, ovvero dove I X (θ) è l iformazioe di Fischer. IX (θ)( θ θ) N(0, 1), I X ( θ)( θ θ) N(0, 1), Duque, se la umerosità del campioe lo permette, le quatità I X (θ)( θ θ) e I X ( θ)( θ θ) possoo essere usate come quatità pivotali asitotiche per la determiazioe di itervalli di cofideza per gradi campioi. Determiiamo itervalli di cofideza asitotici a livello 1 α per le segueti distribuzioi: 1 (X 1,..., X ) campioe estratto dalla distribuzioe B(θ), θ (0, 1)} Lo stimatore di max verosimigliaza di θ è la media campioaria X. Ricordiamo l 7
29 espressioe della desità di Beroulli ella forma f X (x, θ) = θ x (1 θ) 1 x e calcoliamo l iformazioe di Fischer: ( [ ( I X (θ) =E log θ X (1 θ) 1 X)]) ( ) = E [Xθ + (1 X)(1 θ)] = θ θ 1 = θ (1 θ) E (X 1 θ) = θ(1 θ) Osservazioe.30. Se uo stimatore è efficiete, e molti stimatori di max verosimigliaza lo soo, la sua variaza coicide co, ed i calcoli precedeti divetao 1 I X (θ) superflui. Allora utilizzado la quatità I X (θ)( θ θ), dalla relazioe ( P φ 1 α < ) ( θ θ) < φ 1 α = 1 α θ(1 θ) si ricava, risolvedo le disuguagliaze rispetto a θ, P θ + φ 1 φ α 1 α 4 θ + φ 1 4 θ α < θ < ( φ 1 ) α θ + φ 1 α + φ 1 α 4 θ + φ 1 α ( φ 1 α ) 4 θ = Utilizzado ivece la quatità si ricava, molto più agevolmete, θ(1 P θ θ) φ1 α I X ( θ)( θ θ), dalla relazioe P φ 1 α < ( θ θ) θ(1 θ) < φ 1 α = 1 α < θ < θ + φ 1 α θ(1 θ) = 1 α. Esempio.31. [8], esempio 7.5. pag. 66 Il 14 ottobre del 1997 il New York Times riportò u sodaggio che idicava che il 5% della popolazioe, co u margie d errore di ±4% era soddisfatta dell operato del presidete Clito. Cosa sigifica? È possibile stabilire quate persoe furoo itervistate? (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = θe θx 1(x > 0), θ R + } ([5], esempio 8.7 pag 396) 3 (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = θxe θx 1(x > 0), θ R + } ([1], esempio 3.7 pag 106) 8
30 4 (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = θx (θ 1) 1(0 < x < 1), θ R + } ([1], esercizio 3.11 pag 17) 5 (X 1,..., X ) campioe estratto dalla distribuzioe N(0, θ), θ > 0} ([6], esempio 19.6 pag 743) 6 (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = θ(1 θ) (x 1) x N, θ R + } ([1], esercizio 3.9 pag 13) 7 (X 1,..., X ) campioe estratto dalla distribuzioe f(x, θ) = θx x! e( θ), x N θ R + } ([1], esercizio 3.7 pag 11) 8 Sia (X 1,..., X ) u campioe estratto dalla distribuzioe f(x, θ) = 1 θ 1(0 < x < θ), θ R + } Posto Z = (θ max 1 i X i ), si dimostri che Z coverge i legge ad ua variabile aleatoria espoeziale di parametro θ; utilizzado questo risultato, determiare u itervallo di cofideza asitotico per θ. ([1], esercizio 3.1 pag 18) Osservazioe.3. I È evidete che ivertire la quatità X ( θ)( θ θ) è estremamete semplice, perché il fattore I X ( θ) o cotiee il parametro icogito, ma è ua statistica; ifatti usado questa quatità si ottiee sempre u itervallo di cofideza asitotico della forma φ 1 α θ I X ( θ), θ + φ 1 α I X ( θ). Altra cosa è l iversioe di I X (θ)( θ θ). Per cotro, a parità di campioe e di livello, quest ultima quatità pivotale produce itervalli migliori, perché utilizza l esatta iformazioe di Fischer e o ua sua approssimazioe. 9
31 Capitolo 3 Test d ipotesi 3.1 Test parametrici Descrizioe e defiizioi Sia f X (x; θ), θ Θ} u modello statistico parametrico. Ua ipotesi statistica è ua asserzioe circa il valore assuto dal parametro icogito θ della distribuzioe f X (x; θ). Ua ipotesi statistica può specificare completamete la legge f X (x; θ), ed i tal caso viee detta ipotesi statistica semplice; i caso cotrario si parla di ipotesi statistica composta. Per deotare ua ipotesi statistica si usa solitamete il carattere H, seguito dai puti e dalla specificazioe della ipotesi. Esempio 3.1. Sia f X (x; θ) = Bi(θ), potremmo formulare l ipotesi H : p = 1 (ipotesi semplice) oppure H : p < 1 (ipotesi composta). U test (che idicheremo co la lettera Y ) è ua regola costruita sulla base dell osservazioe di u campioe estratto dalla distribuzioe i esame, per decidere se rifiutare o meo u ipotesi. Facciamo u esempio per chiarire: Esempio 3.. Sia f X (x; θ) = N(θ, 16). Formuliamo l ipotesi H : θ = 3. Si suppoga di osservare il campioe (X 1,..., X ). U possibile test Y per decidere se rifiutare o meo l ipotesi H è : si rifiuti H se e solo se X 3 > 4. Sia l ampiezza del campioe osservato. Idichiamo co X () lo spazio di tutte le possibili realizzazioi del campioe (spazio campioario), ovvero: X () = (x 1,..., x ) R tale che (X 1,..., X )(ω) = (x 1,..., x ), ω Ω}. U test idividua ua partizioe dello spazio campioario i isiemi disgiuti C, C c } tale per cui la regola di decisioe per il rifiuto di ua ipotesi H puo essere espressa come: Si rifiuti H se e solo se (x 1,..., x ) C Il sottoisieme C è detto regioe critica del test. La regioe critica di u test si esprime sempre tramite ua relazioe fuzioale che coivolge ua statistica, detta statistica test. Per chiarire facciamo il seguete 30
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Soluzioni quarta esercitazione
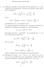 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Appunti per l Orale di Statistica
 Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Apputi per l Orale di Statistica Matteo Giaello 6 ottobre 2011 1 Idice 1 Media e variaza campioaria 3 1.1 Media campioaria............................... 3 1.2 Variaza campioaria.............................
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Sommario. Facoltà di Economia. Campionamento e inferenza statistica
 Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
4. L ipotesi è falsa e la rifiuto bene. H 0 ) p = 0.5. Facciamo dunque n lanci. Otteniamo k teste ed n k croci:
 7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Appunti di Probabilità e Statistica. a.a. 2014/2015 C.d.L. Informatica Bioinformatica I. Oliva. 1 Statistica Inferenziale.
 Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Convergenza di variabili aleatorie
 Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
Covergeza di variabili aleatorie 1 Covergeza quasi certa Ua successioe (X ) 1 di v.a. coverge quasi certamete alla v.a. X se: X X (P-q.c.), cioè P(X X) = 1, ove {X X} = {ω : X (ω) X(ω)} è l issieme di
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Cosa vogliamo imparare?
 Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Università degli Studi di Salerno Pietro Coretto. Corso di Statistica FORMULARIO
 Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
