Ricerca Operativa. Claudio Arbib Universitàdi L Aquila. Alcuni problemi combinatorici (Gennaio 2006)
|
|
|
- Graziano Pepe
- 7 anni fa
- Visualizzazioni
Transcript
1 Claudio Arbib Universitàdi L Aquila Ricerca Operativa Alcuni problemi combinatorici (Gennaio 2006)
2 Alcuni problemi interessanti Problema 1: Le torri Problema 2: A una festa di laurea Problema 3: La rete telematica Problema 4: Il Grande Fratello Problema 5: Produzione del vetro Problema 6: Arredamento
3 Problema 1 (Le torri) Qual èil massimo numero di torri che èpossibile disporre su una scacchiera senza che esse si diano scacco reciproco?
4 Formulazione Due torri si danno scacco se si trovano sulla medesima riga o colonna. A B A B C D C 3 Grafo intersezione righe-colonne D 4
5 Formulazione U = insieme degli archi del grafo G I = famiglia degli insiemi di archi che toccano ogni vertice del grafo G non più di una volta (matching) c = funzione che associa a ogni arco del grafo G un costo pari a 1 Il problema, della forma max c(x) X I consiste nel trovare all interno di G un matchingdi peso massimo.
6 Problema 2 (A una festa di laurea) n ragazzi e m ragazze si incontrano a una festa di laurea. Ciascuno di loro dàmentalmente un punteggio p da 0 a 10 alle persone di sesso diverso dal proprio in base all attrazione provata (0 = attrazione minima, 10 = attrazione massima). Supponiamo di definire l attrazione reciproca di una coppia come il prodotto dei punteggi che ciascun membro della coppia assegna al partner. Qual èl abbinamento ideale che massimizza l attrazione reciproca totale?
7 Voti dei ragazzi alle ragazze Anna Bianca Cecilia Daniela Anna 10 Alberto Alberto Boris Carlo Davide Bianca Cecilia Boris Carlo Voti delle ragazze ai ragazzi Alberto Boris Carlo Davide Daniela 49 Davide Anna Bianca Cecilia Daniela
8 Formulazione U = insieme degli archi del grafo G I = famiglia degli insiemi di archi che toccano ogni vertice del grafo G esattamente una volta (matchingperfetti) c = funzione che associa a ogni arco del grafo G un costo pari al prodotto dei punteggi dei vertici corrispondenti Il problema, della forma max c(x) X I consiste nel trovare all interno di G un matchingperfetto di peso massimo.
9 Problema 3 (La rete telematica) Per monitorare una rete telematica si vuole individuare un insieme di nodi che tocchino tutti i link della rete. Qual èil più piccolo insieme che verifica questa proprietà?
10 Formulazione Si può associare in modo naturale un vertice di un grafo a ogni nodo della rete. Vertici adiacenti = nodi collegati da un link. c d un insieme di vertici che copre tutti gli spigoli b e f i h g = un insieme di nodi che copre tutti i link
11 Formulazione U = insieme degli vertici del grafo G I = famiglia degli insiemi di vertici che toccano ogni arco del grafo G almeno una volta (node-cover, U I) c = funzione che associa a ogni nodo del grafo G un peso pari a 1 Il problema, della forma min c(x) X I consiste nel trovare all interno di G un node-cover di peso minimo.
12 Problema 4 (Il Grande Fratello) Si vuole dotare un museo di un sistema di televisione a circuito chiuso che consenta la sorveglianza in assenza di personale. Sapendo che una telecamera posta all incrocio di due corridoi è in grado, con opportune rotazioni, di sorvegliarli entrambi, qual èil minimo numero di telecamere necessarie?
13 Formulazione Si può associare ogni corridoio rettilineo a un vertice di un grafo. Vertici adiacenti = corridoi che si intersecano. a c d b e f i g h
14 Formulazione Si può associare ogni corridoio rettilineo a un vertice di un grafo. Vertici adiacenti = corridoi che si intersecano. a c c d b e f f i h g g
15 Formulazione Si può associare ogni corridoio rettilineo a un vertice di un grafo. Vertici adiacenti = corridoi che si intersecano. a c d un insieme di spigoli che copre tutti i vertici b e Se non vi sono incroci tra più di due corridoi, ogni incrocio corrisponde a uno spigolo. h g f i = un insieme di telecamere che copre tutti i corridoi
16 Formulazione U = insieme degli archi del grafo G I = famiglia degli insiemi di archi che coprono tutti i vertici del grafo G (edge-cover) c = funzione che associa costo pari a 1 a ogni arco del grafo G Il problema, della forma min c(x) X I consiste nel trovare all interno di G un edge-cover di peso minimo. Si osservi che siccome i corridoi orizzontali (verticali) non si intersecano tra di loro, i vertici sono partizionati in due insiemi stabili, e quindi G è bipartito. In astratto il problema può essere definito su un grafo qualsiasi.
17 Problema 5 (Produzione del vetro) forno float forno float lastra lastra lastra taglio fuori linea (un (un solo solo part part size sizeper per lastra) lastra) pezzo 1 pezzo 1 pezzo 1 pezzo 1 curvatura e finitura sfrido di lavorazione
18 Problema 5 (Produzione del vetro) Obiettivo: Ipotesi: produrre i pezzi nei quantitativi richiesti minimizzando l area totale delle lastre utilizzate per semplicità, tutti i pezzi dello stesso tipo vengono tagliati da lastre di una medesima dimensione domanda d d 2 d i d m lastra 1 lastra 2. lastra k. lastra n pz. 1 pz. 2 pz. i pz. m area totale necessaria per produrre d i pezzi di tipo i con lastre di tipo k 5 m 3 m 4 m
19 Problema 5 (Produzione del vetro) Obiettivo: Ipotesi: produrre i pezzi nei quantitativi richiesti minimizzando l area totale delle lastre utilizzate per semplicità, tutti i pezzi dello stesso tipo vengono tagliati da lastre di una medesima dimensione domanda d d 2 d i d m lastra 1 lastra 2. lastra k. lastra n pz. 1 pz. 2 pz. i pz. m m 3 m 4 m
20 Formulazione Obiettivo: Ipotesi: produrre i pezzi nei quantitativi richiesti minimizzando l area totale delle lastre utilizzate per semplicità, tutti i pezzi dello stesso tipo vengono tagliati da lastre di una medesima dimensione domanda d d 2 d i d m P 1 L 1 lastra 1 lastra 2. lastra k. lastra n pz. 1 pz. 2 pz. i pz. m i m k n Problema: in un grafo bipartito completo G = (P L, P L), trovare un assegnamento di P a L avente peso minimo
21 Problema 6 (Arredamento)
22 Formulazione Possiamo associare a ogni scomparto della libreria un nodo di un grafo simmetrico. Due vertici del grafo saranno adiacenti se e solo se gli scomparti ad essi corrispondenti 1) si trovano sulla stessa riga, o 2) si trovano sulla stessa colonna, oppure 3) hanno la medesima posizione A questo punto diciamo che un nodo di colore rosso corrisponde a una statua, uno giallo a un soprammobile e uno blu a una cornice
Ricerca Operativa. Claudio Arbib Universitàdi L Aquila. Esercizi di ottimizzazione combinatoria
 Claudio Arbib Universitàdi L Aquila Ricerca Operativa Esercizi di ottimizzazione combinatoria 00-006 Grafi 9 Esercizio. Un grafo simmetrico G = (V, E) si dice cubico se tutti i suoi vertici hanno grado
Claudio Arbib Universitàdi L Aquila Ricerca Operativa Esercizi di ottimizzazione combinatoria 00-006 Grafi 9 Esercizio. Un grafo simmetrico G = (V, E) si dice cubico se tutti i suoi vertici hanno grado
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari
 Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
min det det Allora è unimodulare se e solo se det 1, 1, 0 per ogni sottomatrice quadrata di di qualsiasi dimensione.
 Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Matrici unimodulari e totalmente unimodulari
 Matrici unimodulari e totalmente unimodulari Sia una matrice intera di dimensione con, si dice unimodulare se presa una qualsiasi sottomatrice di ordine massimo (di dimensione ) vale det = 1, +1, 0. Una
Matrici unimodulari e totalmente unimodulari Sia una matrice intera di dimensione con, si dice unimodulare se presa una qualsiasi sottomatrice di ordine massimo (di dimensione ) vale det = 1, +1, 0. Una
Ricerca Operativa. Claudio Arbib Universitàdi L Aquila. Layout ottimo di dispositivi elettronici ad altissima scala di integrazione
 Claudio Arbib Universitàdi L Aquila Ricerca Operativa Layout ottimo di dispositivi elettronici ad altissima scala di integrazione Problema Realizzare una funzione booleana f: {0, 1} n {0, 1} m tramite
Claudio Arbib Universitàdi L Aquila Ricerca Operativa Layout ottimo di dispositivi elettronici ad altissima scala di integrazione Problema Realizzare una funzione booleana f: {0, 1} n {0, 1} m tramite
Problemi di localizzazione
 Problemi di localizzazione Claudio Arbib Università di L Aquila Prima Parte (marzo 200): problemi con singolo decisore . Introduzione Un problema di localizzazione consiste in generale nel decidere dove
Problemi di localizzazione Claudio Arbib Università di L Aquila Prima Parte (marzo 200): problemi con singolo decisore . Introduzione Un problema di localizzazione consiste in generale nel decidere dove
a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn mentre le variabili decisionali sono rappresentate dal vettore colonna n-dimensionale x,
 Università degli Studi di Roma Tor Vergata Facoltà di Ingegneria Appunti dal corso di Metodi e Modelli di Ottimizzazione Discreta 1 A.A. 2018-2019 Prof. Sara Nicoloso A seconda del tipo di variabili che
Università degli Studi di Roma Tor Vergata Facoltà di Ingegneria Appunti dal corso di Metodi e Modelli di Ottimizzazione Discreta 1 A.A. 2018-2019 Prof. Sara Nicoloso A seconda del tipo di variabili che
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa 2. Esercizi sul problema dell assegnamento
 UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
Definizione 1.3 (Arco accoppiato) Un arco è accoppiato se è appartenente al matching M.
 Matching. Definizioni Definizione. (Matching di un grafo G = (N, A)) Il matching di un grafo è un sottoinsieme M di archi tali per cui nessuna coppia di essi condivida lo stesso nodo. Definizione.2 (Matching
Matching. Definizioni Definizione. (Matching di un grafo G = (N, A)) Il matching di un grafo è un sottoinsieme M di archi tali per cui nessuna coppia di essi condivida lo stesso nodo. Definizione.2 (Matching
Claudio Arbib Università di L Aquila. Ricerca Operativa. Reti di flusso
 Claudio Arbib Università di L Aquila Ricerca Operativa Reti di flusso Sommario Definizioni di base Flusso di un campo vettoriale Divergenza Integrale di Gauss-Greene Flusso in una rete Sorgenti, pozzi
Claudio Arbib Università di L Aquila Ricerca Operativa Reti di flusso Sommario Definizioni di base Flusso di un campo vettoriale Divergenza Integrale di Gauss-Greene Flusso in una rete Sorgenti, pozzi
Soluzioni degli esercizi di formulazione di PL{0, 1}
 Soluzioni degli esercizi di formulazione di PL{0, 1} Salvatore Nocella 12 febbraio 2007 1 Al lavoro Due operai devono eseguire un certo numero di lavori J = {1,..., n}, ciascuno della durata di un ora.
Soluzioni degli esercizi di formulazione di PL{0, 1} Salvatore Nocella 12 febbraio 2007 1 Al lavoro Due operai devono eseguire un certo numero di lavori J = {1,..., n}, ciascuno della durata di un ora.
Ricerca Operativa. G. Liuzzi. Lunedí 20 Aprile 2015
 1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
1 Lunedí 20 Aprile 2015 1 Istituto di Analisi dei Sistemi ed Informatica IASI - CNR Rilassamento di un problema Rilassare un problema di Programmazione Matematica vuol dire trascurare alcuni (tutti i)
Ottimizzazione Combinatoria A. A
 Ottimizzazione Combinatoria Docente: Mara Servilio A. A. 2007-2008 Orario delle lezioni: Mercoledì 11:30-13:30; Giovedì 11:30-13:30 Orario di ricevimento: giovedì 15:00-17:00 E-mail: servilio@di.univaq.it
Ottimizzazione Combinatoria Docente: Mara Servilio A. A. 2007-2008 Orario delle lezioni: Mercoledì 11:30-13:30; Giovedì 11:30-13:30 Orario di ricevimento: giovedì 15:00-17:00 E-mail: servilio@di.univaq.it
Ottimizzazione Combinatoria A. A
 Ottimizzazione Combinatoria Docente: Mara Servilio A. A. 2008-2009 Orario delle lezioni: Mercoledì 11:30-13:30; Giovedì 11:30-13:30 Orario di ricevimento: Mercoledì 15:00-17:00 E-mail: servilio@di.univaq.it
Ottimizzazione Combinatoria Docente: Mara Servilio A. A. 2008-2009 Orario delle lezioni: Mercoledì 11:30-13:30; Giovedì 11:30-13:30 Orario di ricevimento: Mercoledì 15:00-17:00 E-mail: servilio@di.univaq.it
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
3.2 Rilassamenti lineari/combinatori e bounds
 3.2 Rilassamenti lineari/combinatori e bounds Consideriamo un problema di Ottimizzazione Discreta min{f(x) : x X} e sia z il valore di una soluzione ottima x X. Metodi di risoluzione spesso generano una
3.2 Rilassamenti lineari/combinatori e bounds Consideriamo un problema di Ottimizzazione Discreta min{f(x) : x X} e sia z il valore di una soluzione ottima x X. Metodi di risoluzione spesso generano una
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
INFORMATICA AA Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali»
 Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 2010-2011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 2010-2011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
ALBERI ORIENTATI. Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r);
 ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
Grafi Stessa distanza
 Grafi Stessa distanza In un grafo orientato G, dati due nodi s e v, si dice che: v è raggiungibile da s se esiste un cammino da s a v; la distanza di v da s è la lunghezza del più breve cammino da s a
Grafi Stessa distanza In un grafo orientato G, dati due nodi s e v, si dice che: v è raggiungibile da s se esiste un cammino da s a v; la distanza di v da s è la lunghezza del più breve cammino da s a
Esercizio 2. Domanda 3
 A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione 2; 0; 2. Facendo
A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione 2; 0; 2. Facendo
Teorema 1. Il problema AP è N P-complete.
 (Dalla prova scritta d esame del 18/12/2006.) Si consideri il seguente problema AssegnazioneProgetto (AP). Input: un insieme, P, di n persone, ed un insieme V di m vincoli. Ogni vincolo ha la forma k#(l
(Dalla prova scritta d esame del 18/12/2006.) Si consideri il seguente problema AssegnazioneProgetto (AP). Input: un insieme, P, di n persone, ed un insieme V di m vincoli. Ogni vincolo ha la forma k#(l
Esercizi: Formulare in termini di programmazione lineare (intera) i seguenti problemi
 Esercizi: Formulare in termini di programmazione lineare (intera) i seguenti problemi A1. Presso un Ente per la protezione civile stanno organizzando dei soccorsi da portare a 8 diverse zone, siano 1,
Esercizi: Formulare in termini di programmazione lineare (intera) i seguenti problemi A1. Presso un Ente per la protezione civile stanno organizzando dei soccorsi da portare a 8 diverse zone, siano 1,
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica
 Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I
 ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
G è 2-colorabile se ogni nodo può essere colorato di bianco o di nero in modo che nodi connessi da archi siano colorati con colori distinti.
 Grafi Grafi bipartiti Un grafo non orientato G è bipartito se l insieme dei nodi può essere partizionato in due sottoinsiemi disgiunti tali che nessun arco del grafo connette due nodi appartenenti allo
Grafi Grafi bipartiti Un grafo non orientato G è bipartito se l insieme dei nodi può essere partizionato in due sottoinsiemi disgiunti tali che nessun arco del grafo connette due nodi appartenenti allo
Se il grafo è bipartito, un accoppiamento viene anche detto assegnamento.
 1. Accoppiamento Definizione. Dato un grafo (non orientato) G =(N,E), un sottoinsieme M di archi, tale che ogni nodo del grafo è incidente in al più unarcodim, viene detto accoppiamento, (matching). I
1. Accoppiamento Definizione. Dato un grafo (non orientato) G =(N,E), un sottoinsieme M di archi, tale che ogni nodo del grafo è incidente in al più unarcodim, viene detto accoppiamento, (matching). I
A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa 1 Seconda prova intermedia 17 giugno 2010
 A Ricerca Operativa Seconda prova intermedia La produzione del pane su scala industriale segue un processo in cinque fasi: () preparazione ingredienti, () impasto in gradienti, (3) prima cottura, (4) trattamento
A Ricerca Operativa Seconda prova intermedia La produzione del pane su scala industriale segue un processo in cinque fasi: () preparazione ingredienti, () impasto in gradienti, (3) prima cottura, (4) trattamento
Programmazione Lineare Intera: Piani di Taglio
 Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Problema del trasporto
 p. 1/1 Problema del trasporto Supponiamo di avere m depositi in cui è immagazzinato un prodotto e n negozi che richiedono tale prodotto. p. 1/1 Problema del trasporto Supponiamo di avere m depositi in
p. 1/1 Problema del trasporto Supponiamo di avere m depositi in cui è immagazzinato un prodotto e n negozi che richiedono tale prodotto. p. 1/1 Problema del trasporto Supponiamo di avere m depositi in
I Appello Ricerca Operativa 2 bis Compito A
 I Appello Ricerca Operativa 2 bis Compito A Cognome e nome:. Esercizio 1. Si consideri il problema del matching di cardinalità massima in un grafo G ed il suo problema di decisione associato: esiste un
I Appello Ricerca Operativa 2 bis Compito A Cognome e nome:. Esercizio 1. Si consideri il problema del matching di cardinalità massima in un grafo G ed il suo problema di decisione associato: esiste un
Esercitazione 5 Network Flow
 Esercitazione 5 Network Flow Diamo innanzitutto una definizione informale del concetto di riduzione polinomiale tra problemi: Si dice che un problema A è riducibile polinomialmente ad un problema B, se
Esercitazione 5 Network Flow Diamo innanzitutto una definizione informale del concetto di riduzione polinomiale tra problemi: Si dice che un problema A è riducibile polinomialmente ad un problema B, se
Parte II: Ottimalità, rilassamenti e bound
 Parte II: Ottimalità, rilassamenti e bound Ottimalità, rilassamenti e bound Consideriamo il seguente problema z * = max {c T x : x X, X {0,1} n } dove z* è il valore della soluzione ottima x*. Domanda:
Parte II: Ottimalità, rilassamenti e bound Ottimalità, rilassamenti e bound Consideriamo il seguente problema z * = max {c T x : x X, X {0,1} n } dove z* è il valore della soluzione ottima x*. Domanda:
A-2 a PI. Esercizio 2. Domanda 3
 A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione x = 1; x =
A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione x = 1; x =
Algoritmi e Strutture Dati II: Parte B Anno Accademico Lezione 1
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 004-005 Docente: Ugo Vaccaro Lezione 1 Dalla Teoria della NP-Completezza abbiamo appreso che esiste una classe di problemi (NPhard) per cui non è
Algoritmi e Strutture Dati II: Parte B Anno Accademico 004-005 Docente: Ugo Vaccaro Lezione 1 Dalla Teoria della NP-Completezza abbiamo appreso che esiste una classe di problemi (NPhard) per cui non è
Prof. Giorgio Poletti
 Prof. Giorgio Poletti giorgio.poletti@unife.it «I computer danno esattamente quello che gli è stato immesso; se futilità immettiamo, futilità otterremo, ma gli uomini non sono molto diversi.» Richard Bandlerer
Prof. Giorgio Poletti giorgio.poletti@unife.it «I computer danno esattamente quello che gli è stato immesso; se futilità immettiamo, futilità otterremo, ma gli uomini non sono molto diversi.» Richard Bandlerer
Gioco 10x10. Prova con una matita, che punteggio ottieni?
 Gioco 10x10 Il gioco consiste nel cercare di riempire una tabella quadrata 10x10 con i numeri progressivi da 1 a 100 partendo da una qualunque casella con il numero 1 e passando alla successiva casella
Gioco 10x10 Il gioco consiste nel cercare di riempire una tabella quadrata 10x10 con i numeri progressivi da 1 a 100 partendo da una qualunque casella con il numero 1 e passando alla successiva casella
Progettazione di Algoritmi - lezione 1
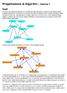 Progettazione di Algoritmi - lezione 1 Grafi Un grafo è una collezione di elementi con una relazione binaria tra di essi. Le situazioni che possono essere modellate dai grafi sono innumerevoli e provengono
Progettazione di Algoritmi - lezione 1 Grafi Un grafo è una collezione di elementi con una relazione binaria tra di essi. Le situazioni che possono essere modellate dai grafi sono innumerevoli e provengono
Certificati dei problemi in NP
 Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
12.1 IL PROBLEMA DEL CAMMINO MINIMO: L ALGORITMO DI DIJKSTRA
 Problemi strutturati. IL PROBLEMA DEL CAMMINO MINIMO: L ALGORITMO DI DIJKSTRA Esercizio.. Dato il grafo di Figura.., trovare il peso dei cammini minimi dal nodo a tutti gli altri nodi del grafo (il peso
Problemi strutturati. IL PROBLEMA DEL CAMMINO MINIMO: L ALGORITMO DI DIJKSTRA Esercizio.. Dato il grafo di Figura.., trovare il peso dei cammini minimi dal nodo a tutti gli altri nodi del grafo (il peso
Esercizi Capitolo 15 - Ricerca locale
 Esercizi Capitolo 5 - Ricerca locale Alberto ontresor 9 Agosto, 04 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare
Esercizi Capitolo 5 - Ricerca locale Alberto ontresor 9 Agosto, 04 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare
Coverage. Visto che il coverage si basa su aree dell ambiente che vengono monitorate non è
 L. Pallottino, Sistemi Robotici Distribuiti - Versione del 10 Dicembre 2015 393 Coverage Si consideri ora il problema di coordinare una squadra di robot con dei sensori omnidirezionali in modo da garantire
L. Pallottino, Sistemi Robotici Distribuiti - Versione del 10 Dicembre 2015 393 Coverage Si consideri ora il problema di coordinare una squadra di robot con dei sensori omnidirezionali in modo da garantire
Massimo flusso e matching
 Capitolo Massimo flusso e matching. Problema del massimo matching. Nel problema del massimo matching è dato un grafo non orientato G(V, A); un matching in G è un insieme di archi M A tale che nessuna coppia
Capitolo Massimo flusso e matching. Problema del massimo matching. Nel problema del massimo matching è dato un grafo non orientato G(V, A); un matching in G è un insieme di archi M A tale che nessuna coppia
ALFABETIZZAZIONE INFORMATICA
 Laurea in ilosofia a.a. 2008-2009 LTIZZZION INORMTI Ogni problema che ho risolto è diventato una regola che in seguito è servita a risolvere altri problemi. (René escartes, artesio iscorso sul metodo )
Laurea in ilosofia a.a. 2008-2009 LTIZZZION INORMTI Ogni problema che ho risolto è diventato una regola che in seguito è servita a risolvere altri problemi. (René escartes, artesio iscorso sul metodo )
GEOMETRIA. Elementi geometrici
 GEOMETRIA Elementi geometrici Ripasso dei principali elementi geometrici e relative definizioni A)Una scatola di gessetti, un barattolo, una palla sono corpi Ogni cosa che occupa uno spazio è, quindi un
GEOMETRIA Elementi geometrici Ripasso dei principali elementi geometrici e relative definizioni A)Una scatola di gessetti, un barattolo, una palla sono corpi Ogni cosa che occupa uno spazio è, quindi un
RICERCA OPERATIVA GRUPPO A prova scritta del 21 luglio 2010
 RICERCA OPERATIVA GRUPPO A prova scritta del luglio 00. Dato il problema di programmazione lineare P) min z = x + x + x max y + y x + x + x = y + y < x + x x y + y < x, x, x 0 y y < y > 0 a) costruirne
RICERCA OPERATIVA GRUPPO A prova scritta del luglio 00. Dato il problema di programmazione lineare P) min z = x + x + x max y + y x + x + x = y + y < x + x x y + y < x, x, x 0 y y < y > 0 a) costruirne
DIFFUSIONE SU GRAFO (rete) E RIPOSIZIONAMENTO DI FARMACI SULLA BASE DELLA SIMILARITA DI STRUTTURA MOLECOLARE
 0 DIFFUSIONE SU GRAFO (rete) E RIPOSIZIONAMENTO DI FARMACI SULLA BASE DELLA SIMILARITA DI STRUTTURA MOLECOLARE Cammini aleatori su grafo (Random walk) 0 «processo di esplorazione casuale di un grafo mediante
0 DIFFUSIONE SU GRAFO (rete) E RIPOSIZIONAMENTO DI FARMACI SULLA BASE DELLA SIMILARITA DI STRUTTURA MOLECOLARE Cammini aleatori su grafo (Random walk) 0 «processo di esplorazione casuale di un grafo mediante
Prova Scritta di Ricerca Operativa Prof. Facchinei 02/07/2002
 Cognome: Nome: Prova Scritta di Ricerca Operativa Prof. Facchinei 02/07/2002 1. (Punti 7) Enunciare e dimostrare il teorema dell adualità debole (Scrivere esplicitamente a quale coppia primale/duale si
Cognome: Nome: Prova Scritta di Ricerca Operativa Prof. Facchinei 02/07/2002 1. (Punti 7) Enunciare e dimostrare il teorema dell adualità debole (Scrivere esplicitamente a quale coppia primale/duale si
1 TEORIA DELLE RETI 1. 1 Teoria delle reti. 1.1 Grafi
 1 TEORIA DELLE RETI 1 1 Teoria delle reti 1.1 Grafi Intuitivamente un grafo è un insieme finito di punti (nodi o vertici) ed un insieme di frecce (archi) che uniscono coppie di punti Il verso della freccia
1 TEORIA DELLE RETI 1 1 Teoria delle reti 1.1 Grafi Intuitivamente un grafo è un insieme finito di punti (nodi o vertici) ed un insieme di frecce (archi) che uniscono coppie di punti Il verso della freccia
Esercizio 1. Esercizio 2
 Esercizio 1 Si scriva un programma C che realizza l'assegnazione ottima di un insieme di persone ad un insieme di città avente la stessa cardinalità. Ogni persona ha espresso una serie di preferenze, elencando
Esercizio 1 Si scriva un programma C che realizza l'assegnazione ottima di un insieme di persone ad un insieme di città avente la stessa cardinalità. Ogni persona ha espresso una serie di preferenze, elencando
Ottimizzazione Combinatoria Proprietà dei Grafi. Ottimizzazione Combinatoria
 Ottimizzazione Combinatoria Ottimizzazione Combinatoria Proprietà dei Grafi ANTONIO SASSANO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Corso di Laurea in Ingegneria Gestionale
Ottimizzazione Combinatoria Ottimizzazione Combinatoria Proprietà dei Grafi ANTONIO SASSANO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Corso di Laurea in Ingegneria Gestionale
Analisi e implementazione dell algoritmo di Dijkstra (Parte 1)
 Analisi e implementazione dell algoritmo di Dijkstra (Parte 1) Algoritmicamente August 1, 2009 http://algoritmicamente.wordpress.com/ 1 Concetti fondamentali Definizione 1 Un grafo è un insieme di vertici
Analisi e implementazione dell algoritmo di Dijkstra (Parte 1) Algoritmicamente August 1, 2009 http://algoritmicamente.wordpress.com/ 1 Concetti fondamentali Definizione 1 Un grafo è un insieme di vertici
ESERCIZIO 1. Ricordiamo il teorema di Gallai: Per ogni grafo G con n nodi si ha: μ(g)+ ρ(g) = n (2) Se inoltre G non ha nodi isolati
 ESERCIZIO 1 Disegnare un grafo G = (V, E) che abbia le seguenti caratteristiche: a) G è connesso, b) G soddisfa il teorema di König, e c) α(g) + τ(g) =. ESERCIZIO 1 Ricordiamo il teorema di Gallai: er
ESERCIZIO 1 Disegnare un grafo G = (V, E) che abbia le seguenti caratteristiche: a) G è connesso, b) G soddisfa il teorema di König, e c) α(g) + τ(g) =. ESERCIZIO 1 Ricordiamo il teorema di Gallai: er
Una breve introduzione all implementazione in C di algoritmi su grafo
 Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
Una breve introduzione all implementazione in C di algoritmi su grafo A cura di Gianmaria Leo Introduzione La lezione è un introduzione a concetti e strumenti che permettono l implementazione di algoritmi
Makespan con set-up dipendenti dalla sequenza. 1/s jk /C max
 Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Esercitazione 2. Progettare un algoritmo che risolva tale problema in tempo O( E + V log V ).
 Esercitazione 2 Problema 4: Dato un grafo G = (V, E) con pesi positivi sugli archi ed un insieme di k centri C = {c 1, c 2, c k } V, si richiede di partizionare l insieme V in k insiemi V 1, V 2, V k in
Esercitazione 2 Problema 4: Dato un grafo G = (V, E) con pesi positivi sugli archi ed un insieme di k centri C = {c 1, c 2, c k } V, si richiede di partizionare l insieme V in k insiemi V 1, V 2, V k in
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi
 Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Esercizi di PLI. a cura di A. Agnetis. Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory:
 Esercizi di PLI a cura di A. Agnetis Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory: max z = 40x + 24x 2 + 5x + 8x 4 8x + 6x 2 + 5x + 4x 4 22 x i 0 x i intero Si tratta di un
Esercizi di PLI a cura di A. Agnetis Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory: max z = 40x + 24x 2 + 5x + 8x 4 8x + 6x 2 + 5x + 4x 4 22 x i 0 x i intero Si tratta di un
Sommario della lezione
 Sommario della lezione Analisi dell Algoritmo di Ford e Fulkerson per il calcolo del massimo flusso Applicazioni del massimo flusso: Matching in Grafi Bipartiti Cammini disgiunti tra vertici Università
Sommario della lezione Analisi dell Algoritmo di Ford e Fulkerson per il calcolo del massimo flusso Applicazioni del massimo flusso: Matching in Grafi Bipartiti Cammini disgiunti tra vertici Università
Appunti del corso di Informatica 1 (IN110 Fondamenti) 7 Grafi e alberi: introduzione
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Matematica Lezione 5
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 5 Sonia Cannas 23/10/2018 Relazioni Dati due insiemi A e B molto spesso capita di definire una relazione (o legge) fra essi. Sia A
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 5 Sonia Cannas 23/10/2018 Relazioni Dati due insiemi A e B molto spesso capita di definire una relazione (o legge) fra essi. Sia A
STRUMENTI MATEMATICI
 1. TABELLA A DOPPIA ENTRATA 1 STRUMENTI MATEMATICI E' un riquadro formato da righe orizzontali e colonne verticali. I dati sulla prima colonna sono i dati in entrata di ciascuna riga; i dati sulla prima
1. TABELLA A DOPPIA ENTRATA 1 STRUMENTI MATEMATICI E' un riquadro formato da righe orizzontali e colonne verticali. I dati sulla prima colonna sono i dati in entrata di ciascuna riga; i dati sulla prima
Parte II: Ottimalità, rilassamenti e bound
 Parte II: Ottimalità, rilassamenti e bound Sommario Definizioni di bound primali e duali. Rilassamento di un problema di OC. Esempi di rilassamenti per il problema del TSP: Il rilassamento albero. Il rilassamento
Parte II: Ottimalità, rilassamenti e bound Sommario Definizioni di bound primali e duali. Rilassamento di un problema di OC. Esempi di rilassamenti per il problema del TSP: Il rilassamento albero. Il rilassamento
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) trovare una assegnazione di valori alle variabili che soddisfa i vincoli.
 PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n i cui valori appartengono a domini D, D,, D n e un insieme di vincoli c(x i, X i,, X ik ) che specificano
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n i cui valori appartengono a domini D, D,, D n e un insieme di vincoli c(x i, X i,, X ik ) che specificano
Algoritmi Avanzati Soluzioni dello scritto del 2 febbraio 2004 (appello straordinario)
 Algoritmi Avanzati Soluzioni dello scritto del febbraio 004 (appello straordinario) 1. Tengo nascosto nel taschino della giacca un grafo misterioso di 7 nodi. Vi dico solo che listando le valenze (= numero
Algoritmi Avanzati Soluzioni dello scritto del febbraio 004 (appello straordinario) 1. Tengo nascosto nel taschino della giacca un grafo misterioso di 7 nodi. Vi dico solo che listando le valenze (= numero
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44;
 1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
3.3 Problemi di PLI facili
 3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn mentre le variabili decisionali sono rappresentate dal vettore colonna n-dimensionale x,
 Università degli Studi di Roma Tor Vergata Facoltà di Ingegneria Appunti dal corso di Metodi e Modelli di Ottimizzazione Discreta A.A. 206-207 Prof. Sara Nicoloso A seconda del tipo di variabili che compaiono
Università degli Studi di Roma Tor Vergata Facoltà di Ingegneria Appunti dal corso di Metodi e Modelli di Ottimizzazione Discreta A.A. 206-207 Prof. Sara Nicoloso A seconda del tipo di variabili che compaiono
Algoritmi Euristici. Corso di Laurea in Informatica e Corso di Laurea in Matematica. Roberto Cordone DI - Università degli Studi di Milano
 Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici. Corso di Laurea in Informatica e Corso di Laurea in Matematica. Roberto Cordone DI - Università degli Studi di Milano
 Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Il valore di flusso che si ottiene è
 1) Si consideri un insieme di piste da sci e di impianti di risalita. Lo si modelli con un grafo orientato che abbia archi di due tipi: tipo D (discesa e orientato nel senso della discesa) e tipo R (risalita
1) Si consideri un insieme di piste da sci e di impianti di risalita. Lo si modelli con un grafo orientato che abbia archi di due tipi: tipo D (discesa e orientato nel senso della discesa) e tipo R (risalita
ALFABETIZZAZIONE INFORMATICA
 Laurea in Filosofia a.a. 2008-2009 ALFABETIZZAZIONE INFORMATICA Tutto dovrebbe essere reso il più semplice possibile, ma non più semplice. (Albert Einstein) Giorgio Poletti giorgio.poletti@unife.it http://docente.unife.it/giorgio.poletti
Laurea in Filosofia a.a. 2008-2009 ALFABETIZZAZIONE INFORMATICA Tutto dovrebbe essere reso il più semplice possibile, ma non più semplice. (Albert Einstein) Giorgio Poletti giorgio.poletti@unife.it http://docente.unife.it/giorgio.poletti
Richiami di Teoria dei Grafi. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone
 Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone Il problema dell assegnamento degli stati versione del 9/1/03 Sintesi: Assegnamento degli stati La riduzione del numero
Sintesi Sequenziale Sincrona Sintesi Comportamentale di reti Sequenziali Sincrone Il problema dell assegnamento degli stati versione del 9/1/03 Sintesi: Assegnamento degli stati La riduzione del numero
GRAFI. Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi!
 G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
Formulazioni. Consideriamo il seguente problema di Knapsack 0-1. max (5x x 2. ) st 3x x 2. < 6 x {0,1} 2
 Formulazioni Consideriamo il seguente problema di Knapsack 0-1 max (5x 1 + 2x 2 ) st 3x 1 + 4x 2 < 6 x {0,1} 2 Insiemi ammissibili F = {(0, 0), (0, 1), (1, 0)} Rappresentiamo sul piano gli insiemi ammissibili.
Formulazioni Consideriamo il seguente problema di Knapsack 0-1 max (5x 1 + 2x 2 ) st 3x 1 + 4x 2 < 6 x {0,1} 2 Insiemi ammissibili F = {(0, 0), (0, 1), (1, 0)} Rappresentiamo sul piano gli insiemi ammissibili.
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A Esercizio 1 (7 punti): LIFO
 Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
Grafi diretti. Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove. V è u n i n s i e m e d i nodi (o vertici);
 Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
Algoritmo per A. !(x) Istanza di B
 Riduzioni polinomiali Una funzione f: T*!T* è detta computabile in tempo polinomiale se esiste una macchina di Turing limitata polinomialmente che la computi. Siano L 1 e L 2 " T* due linguaggi. Una funzione
Riduzioni polinomiali Una funzione f: T*!T* è detta computabile in tempo polinomiale se esiste una macchina di Turing limitata polinomialmente che la computi. Siano L 1 e L 2 " T* due linguaggi. Una funzione
Minimo albero di copertura
 apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
Calcolo delle Probabilità e Statistica Matematica Fisciano, 10/1/2012
 Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
PROBLEMA DEL COMMESSO VIAGGIATORE
 PROBLEMA DEL COMMESSO VIAGGIATORE INTRODUZIONE Il problema del commesso viaggiatore (traveling salesman problem :TSP) è un classico problema di ottimizzazione che si pone ogni qual volta, dati un numero
PROBLEMA DEL COMMESSO VIAGGIATORE INTRODUZIONE Il problema del commesso viaggiatore (traveling salesman problem :TSP) è un classico problema di ottimizzazione che si pone ogni qual volta, dati un numero
Problemi. sbj. x 0, x intero
 Problemi Spiegare e dimostrare in quali intervalli di R la funzione arctan x è concava, convessa o nessuno dei due casi. Si ricordi che la derivata prima di arctan x è +x 2. Si codifichi in una formula
Problemi Spiegare e dimostrare in quali intervalli di R la funzione arctan x è concava, convessa o nessuno dei due casi. Si ricordi che la derivata prima di arctan x è +x 2. Si codifichi in una formula
Triangoli rettangoli. Problema
 Triangoli rettangoli 1. a) Sposta il vertice C 1, fino a quando stimi che l angolo nel vertice C 1 sia 90. b) Allo stesso modo sposta i vertici da C 2 fino a C 9 fino a quando stimi che l angolo sia 90.
Triangoli rettangoli 1. a) Sposta il vertice C 1, fino a quando stimi che l angolo nel vertice C 1 sia 90. b) Allo stesso modo sposta i vertici da C 2 fino a C 9 fino a quando stimi che l angolo sia 90.
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems),, X ik. ) che specificano quali valori delle variabili sono compatibili tra loro,
 PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n D, D,, D n i cui valori appartengono a domini e un insieme di vincoli c(x i, X i,, X ik ) che specificano
PROBLEMI DI VINCOLI CSP (Constraint satisfaction problems) Dato un insieme finito di variabili X, X,, X n D, D,, D n i cui valori appartengono a domini e un insieme di vincoli c(x i, X i,, X ik ) che specificano
Parte IV: Matrici totalmente unimodulari
 Parte IV: Matrici totalmente unimodulari Formulazioni Consideriamo il seguente problema di Knapsack 0-1 max (5x 1 + 2x 2 ) st 3x 1 + 4x 2 < 6 x {0,1} 2 Insiemi ammissibili F = {(0, 0), (0, 1), (1, 0)}
Parte IV: Matrici totalmente unimodulari Formulazioni Consideriamo il seguente problema di Knapsack 0-1 max (5x 1 + 2x 2 ) st 3x 1 + 4x 2 < 6 x {0,1} 2 Insiemi ammissibili F = {(0, 0), (0, 1), (1, 0)}
Esame di Ricerca Operativa del 07/09/2016
 Esame di Ricerca Operativa del 0/09/201 (Cognome) (Nome) (Matricola) Esercizio 1. Un industria chimica produce due tipi di fertilizzanti (A e B) la cui lavorazione è affidata ai reparti di produzione e
Esame di Ricerca Operativa del 0/09/201 (Cognome) (Nome) (Matricola) Esercizio 1. Un industria chimica produce due tipi di fertilizzanti (A e B) la cui lavorazione è affidata ai reparti di produzione e
Sintesi di Reti sequenziali Sincrone
 Sintesi di Reti sequenziali Sincrone Sintesi di Reti Sequenziali Sincrone Una macchina sequenziale è definita dalla quintupla I è l insieme finito dei simboli d ingresso U è l insieme finito dei simboli
Sintesi di Reti sequenziali Sincrone Sintesi di Reti Sequenziali Sincrone Una macchina sequenziale è definita dalla quintupla I è l insieme finito dei simboli d ingresso U è l insieme finito dei simboli
Algebra. Problemi dimostrativi (lavoro singolo) 1. Determinare tutte le funzioni iniettive f : N N tali che. f(f(n)) n + f(n) 2. per ogni n N.
 Algebra Problemi dimostrativi (lavoro singolo) 1. Determinare tutte le funzioni iniettive f : N N tali che per ogni n N. f(f(n)) n + f(n) 2 2. Trovare tutti i polinomi p(x) a coefficienti reali tali che
Algebra Problemi dimostrativi (lavoro singolo) 1. Determinare tutte le funzioni iniettive f : N N tali che per ogni n N. f(f(n)) n + f(n) 2 2. Trovare tutti i polinomi p(x) a coefficienti reali tali che
Triangolazione di Delaunay
 Duccio Mugnaini 1 - duccio.mugnaini@uninsubria.it 1 Dipartimento di Scienza e Alta Tecnologia (DiSTA) Università degli Studi dell Insubria Metodi numerici per la grafica :: Geometria computazionale Approssimazione
Duccio Mugnaini 1 - duccio.mugnaini@uninsubria.it 1 Dipartimento di Scienza e Alta Tecnologia (DiSTA) Università degli Studi dell Insubria Metodi numerici per la grafica :: Geometria computazionale Approssimazione
1 Prodotto cartesiano di due insiemi 1. 5 Soluzioni degli esercizi 6
 1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
ALMA MATER STUDIORUM UNIVERSITA' DI BOLOGNA DIPARTIMENTO DI MATEMATICA PROGETTO LAUREE SCIENTIFICHE A.A GRAFI ED APPLICAZIONI
 ALMA MATER STUDIORUM UNIVERSITA' DI BOLOGNA DIPARTIMENTO DI MATEMATICA PROGETTO LAUREE SCIENTIFICHE A.A. 2015-2016 GRAFI ED APPLICAZIONI DOCENTE: Prof.ssa Laura Faggioli TUTOR: Dott.ssa Loredana Melcarne
ALMA MATER STUDIORUM UNIVERSITA' DI BOLOGNA DIPARTIMENTO DI MATEMATICA PROGETTO LAUREE SCIENTIFICHE A.A. 2015-2016 GRAFI ED APPLICAZIONI DOCENTE: Prof.ssa Laura Faggioli TUTOR: Dott.ssa Loredana Melcarne
Scuole italiane all estero - Bilingue italo-albanesi 2005
 www.matefilia.it Scuole italiane all estero - Bilingue italo-albanesi 25 1) Studiare e rappresentare graficamente in un piano cartesiano ortogonale XOY la funzione F(x) = x2 +1 4 x2. Verificare che le
www.matefilia.it Scuole italiane all estero - Bilingue italo-albanesi 25 1) Studiare e rappresentare graficamente in un piano cartesiano ortogonale XOY la funzione F(x) = x2 +1 4 x2. Verificare che le
