1 Funzioni di variabile reale
|
|
|
- Arianna Cosentino
- 7 anni fa
- Visualizzazioni
Transcript
1 Funzioni di vriile rele. Definizione di funzione Si definise funzione (funtion) d un insieme X un insieme Y un legge, he indiheremo on f, he ssoi isun elemento di X un elemento di Y; tle elemento viene detto immgine di ttrverso f e viene indito on f () (si legg: «f di»). L insieme X viene detto insieme di definizione (set of definition) o dominio (domin) di f, l insieme Y viene detto odominio (odomin) di f. Un lsse notevole di funzioni è quell in ui gli insiemi X e Y sono numerii. In questo so è dett vriile indipendente (independent vrile), e vriile dipendente (dependent vrile). Se e sono numeri reli si h un funzione rele di vriile rele (rel funtion of rel vrile). In molti si è possiile rppresentre un funzione numeri on un espressione nliti, ome d es. =. Nello studio di un funzione è opportuno differenzire le vriili di loro vlori prtiolri, utilizzndo per quest ultimi pedii identifitivi. Se d es. si misur l tempertur in un miente intervlli di un or, indindo on t l vriile tempo, i vri istnti di misur possono essere espressi ome t = 8., t = 9., e. Se già l espressione dell vriile ontiene un pedie, si potrà sempre ggiungere tle pedie un simolo he indihi i vlori prtiolri; d es. un vlore prtiolre di un vriile indit on v, potrà essere indito ome v o v.. Prmetri Nell espressione nliti di un funzione sono in generle presenti i seguenti elementi: vriile indipendente; vlori numerii; grndezze ostnti definite prmetri (prmeters), indite on espressioni letterrie (,, k, e.). I prmetri sono quntità he possono ssumere diversi vlori seond del prolem speifio ui si ppli l funzione in esme, m he devono essere onsiderte ostnti un volt fissto il loro vlore. Considerimo titolo di esempio un utomoile he si muove on moto rettilineo veloità ostnte; se nell istnte t = l utomoile si trov nell origine dell oordint spzile s, il moto dell utomoile è desritto dll funzione (.) s = v t In tle espressione il tempo trsorso t rppresent l vriile indipendente, lo spzio perorso s rppresent l vriile dipendente, mentre l veloità v h le proprietà di un prmetro: può ssumere vlori diversi d so so (5 km/h, 8 km/h, m/s, e.), m nell mito di un so speifio vrà un vlore ssegnto ostnte. Se d es. l veloità dell mhin è v = 8 km/h, si esprime lo spzio perorso s in kilometri in funzione del tempo t trsorso in ore medinte l relzione (.) s = 8 t.3 Proporzionlità dirett e invers Due grndezze e si diono direttmente proporzionli (diretl proportionl) qundo tr esse sussiste un relzione del tipo (.3) = k in ui k è un ostnte. Questo signifi he il rpporto k = è ostnte: dti due vlori di riferimento e, se rddoppi rispetto nhe rddoppi rispetto, se tripli nhe tripli, e. 5
2 Due grndezze e si diono inversmente proporzionli (inversel proportionl) qundo tr esse sussiste un relzione del tipo (.4) k = in ui k è un ostnte. Questo signifi he il prodotto = k è ostnte: dti due vlori di riferimento e, se rddoppi rispetto, si ridue ll metà rispetto, se tripli si ridue un terzo, e..4 Legge di vrizione linere Si die he un grndezz vri linermente (linerl) on, o he è funzione linere (liner funtion) di, qundo tr le due grndezze sussiste un relzione del tipo (.5) = k+ in ui k e sono ostnti. L funzione linere.5 è osì definit perhé il orrispondente grfio è un line rett, in ui è l ordint del punto di intersezione on l sse, e di ui k esprime l pendenz. Per vlori positivi di k, un resit di orrisponde un resit di, per ui l rett h l orientmento di fig., in ui si evidenzi nhe he un vlore mggiore di k orrisponde un pendenz più mrt; per vlori negtivi di k, un resit di orrisponde un diminuzione di, per ui l rett h l orientmento di fig., dove si vede he un vlore più sso (m mggiore in modulo) di k orrisponde un pendenz più mrt. k' + k' > k k' + k' < k () k + k > () k + k < Fig. Rppresentzione grfi di funzioni lineri, on pendenz () positiv e () negtiv..5 Grfii lineri per punti L ostruzione di un grfio è un metodo molto omune di rppresentre in mnier immedit e unifit le informzioni reltive ll dipendenz tr due o più grndezze. Nel so in ui il fenomeno si desritto d un espressione nliti, l urv he ostituise il digrmm dell funzione può essere studit, e quindi trit, on metodi propri dell nlisi mtemti. È possiile, lterntivmente, individure un serie di punti ssegnndo un vlore ll vriile indipendente e lolndo il orrispondente vlore dell vriile dipendente; tli punti srnno poi riportti in un sistem di oordinte, e uniti d un urv he srà più o meno pprossimt in relzione ll viinnz tr punti suessivi (quest operzione può essere eseguit più effiemente e rpidmente medinte strumenti informtii). Nel so in ui non si i un espressione nliti, m un serie di misure in form tellre, si riportno sul grfio i punti orrispondenti lle misure effettute, unendoli suessivmente on un urv ontinu. Un grfio linere è un grfio in ui uguli intervlli sugli ssi orrisponde sempre il medesimo vlore. Il punto di prtenz dell ostruzione di un grfio linere onsiste nell selt delle sle, e ioè dei vlori d ssegnre isun divisione (d es. ogni m), per isun sse. Assegnte le sle, è suffiiente osservre lune regole, dipendenti in ert misur dlle preferenze personli o di si prtiolri, tendenti d ssiurre l leggiilità del grfio. I vlori d ssegnre lle due sle devono essere dettti d lune onsiderzioni:. Il grfio deve essere filmente eseguiile e deifrile, per ui è onsigliile utilizzre sle in ui si hnno, o 5 unità di misur per m, moltiplite eventulmente per un potenz di (, /, /,5 / / / 5 / / / 5 / / e.).. Le sle devono essere tli d ontenere tutti i punti dell tell, sfruttndo ontempornemente l mssimo lo spzio disponiile sul foglio. Per individure i vlori dtti è suffiiente dividere il rnge di vlori ssoito isun vriile per il reltivo numero di entimetri disposizione, ottenendo un vlore he, se fosse dottto ome sl, onsentiree di ontenere esttmente nell sse il rnge speifito. Si seglie quindi ome sl il vlore immeditmente più grnde he rispond lle esigenze evidenzite nel punto. 6
3 Esempio Si suppong di dover ostruire un grfio on i dti dell t., risultnte dll rilevzione dello spzio s perorso d un utomoile l pssre del tempo t. Si immgini inoltre di vere disposizione un foglio di rt millimetrt rettngolre di dimensioni 4 8 m e di voler eseguire il grfio posizionndo l sse del tempo sul lto mggiore. Per l sse orizzontle si dispone di 4 m; il rnge di vriilità di t è pri t m t min = 5 = 5 h. Dto he 5 : 4 =,8 h/m, si seglie ome sl orizzontle,5 h/m. Per l sse vertile si dispone di 8 m; il rnge di vriilità di s è pri s m s min = 5 ( 5) = 3 km. Dto he 3 : 8 = 6,7 km/m, si seglie ome sl vertile km/m. T. Esempio. t (h) s (km) CAP. In luni si, qundo sono presenti punti isolti in ui un grndezz h un vlore osì elevto d determinre un eessivo rvviinmento degli ltri punti, è possiile eliminre un intervllo di vlori dl reltivo sse, segnlndo l interruzione on l simologi di fig.. Un volt determinte le sle d utilizzre si ostruise il grfio medinte i seguenti elementi (si ved l fig. 3, in ui è rppresentto il grfio reltivo ll esempio ): interruzione dell sse 3 Fig. Interruzione dell sse rtesino. Assi. Vnno orientti e posti sulle righe mrte presenti ogni m oppure ogni 5 m. Vriile indipendente (sse orizzontle) e vriile dipendente (sse vertile). Devono essere riportte ll fine dei due ssi. Unità di misur. Devono essere indite tr prentesi dopo le rispettive grndezze fisihe. Vlori ssegnti lle sle. Vnno riportti in orrispondenz del primo entimetro di isun sse. Vlori di riferimento sugli ssi. Si possono riportre,5,5 5 7,5 t (h) i vlori orrispondenti pssi di 5 m prtendo dll origine. Fig. 3 Grfio reltivo ll tell. Punti visiili reltivi i vlori in tell e urv di rordo dei punti inseriti. Eventuli linee trtteggite in orrispondenz di punti prtiolri del grfio he si vogliono evidenzire rispetto gli ltri. s (km) Di seguito sono riportti luni errori in ui si inorre omunemente nell ostruzione di un grfio: Posizionmento degli ssi su linee intermedie rispetto quelle mrte. Riporto sugli ssi dei vlori reltivi ll tell. A tle proposito si riord he il grfio h il fine di mostrte in mnier immedit e unifit le informzioni ontenute nell tell. Se si è interessti un punto prtiolre del grfio si potrnno sempre rivrne le reltive oordinte medinte il retiolo. Disegno di linee trtteggite he unisono tutti i punti gli ssi. Unione dei punti medinte segmenti. L rppresentzione on un urv priv di spigoli desrive on mggior ttendiilità l reltà di un funzione o di un fenomeno fisio. Eserizio Costruire un grfio prtire dll tell in un riqudro di dimensioni 5 8 m. Eserizio Costruire tell e grfio delle seguenti funzioni: ) = 4 per. 4 ) = per..6 Vlore medio Si onsideri un funzione f() di ndmento qulsisi, ome d es. quello di fig. 4. È possiile definire ome vlore medio f del segnle (men vlue), in un erto intervllo (), il livello he si otterree immgi- Si riord he on l notzione si rppresent un intervllo ssegnto dell vriile ; indindo on e gli estremi dell intervllo, può indire si l intervllo stesso [ ; ], si l su estensione. 7
4 nndo di «spinre» il segnle (ome se rppresentsse l onformzione di un terreno) nell mito dell intervllo onsiderto; pertnto, le ree individute d f () superiormente l livello f devono vere un estensione pri quell delle ree individute inferiormente (vd. fig. 4). Nel so in ui si not l espressione nliti del segnle in esme, è possiile, on metodi mtemtii vnzti, lolrne l estto vlore medio nell intervllo Δ; lterntivmente, si può ottenere un vlore medio pprossimto onsiderndo nell intervllo n vlori,,..., n equmente distnziti, ed eseguendo l medi dei orrispondenti vlori f, f,..., f n dell funzione: (.6) f = f + f + + f n n Il risultto dell.6 è pprossimto, perhé lolto su un numero limitto di vlori, m si vviin tnto più l vlore estto qunto più è lto il numero n dei vlori onsiderti in Δ; in prtiolre, utilizzndo un softwre speifio, è possiile lolre l medi su un numero elevtissimo di vlori, ottenendo un risultto prtimente identio l vlore estto. Eserizio 3 Determinre, per punti, il vlore medio dell funzione f() = nell intervllo. Rispost: f =,333 (il risultto ottenuto per punti può disostrsi d tle vlore) Funzione esponenzile Dll lger elementre si onose ome elevre un numero rele un potenz on esponente intero nturle n: (.7) n = n volte f () Are totle = re totle f Fig. 4 Vlore medio di un segnle in un intervllo. p Definendo n q q = e = p è possiile estendere l nozione di potenz esponenti prim negtivi e n quindi rzionli, per rrivre definire, più in generle, il signifito di elevzione di un numero rele > un potenz on esponente rele. Se è un vriile rele, è definit l funzione esponenzile (eponentil funtion) di se (.8) = Si ssum dto he per = l funzione si ridue l vlore ostnte. Il grfio dell funzione esponenzile, on >, è rppresentto in fig. 5. Si noti he = per qulsisi vlore di. Con < il grfio dell funzione esponenzile si modifi ome in fig. 5; lo stesso tipo di grfio si può ttriuire ll funzione (.9) = on >, he orrisponde un esponenzile di se <. Un proprietà notevole delle funzioni esponenzili onsiste nell progressività reltiv ostnte, he srà spiegt on riferimento ll funzione deresente =, on >. Si onsideri un intervllo [ ; + ] sull sse orizzontle; il orrispondente intervllo [ ; + ] sull sse vertile h un estensione pri () = = > < () (.) = ( ) + Fig. 5 Grfii dell funzione esponenzile. 8
5 5% di = log > 5% di Fig. 6 Crtteristihe di vrizione di. Fig. 7 Grfio dell funzione logritmi. L vrizione reltiv, e ioè il rpporto tr e il vlore inizile, è pri (.) ( ) ( + ) ( + ) + = = = = + Come si vede, tle rpporto dipende solo d e non dl vlore inizile ; iò signifi he, prità di vrizione, l vrizione reltiv, o nhe l vrizione perentule %, è sempre ugule (fig. 6). Eserizio 4 Verifire l vlidità di qunto rppresentto in fig. 6, lolndo le vrizioni dell funzione = e orrispondenti vrizioni di pri, prtire di seguenti vlori:,, 4. 3 Funzione logritmi Dti e reli, on >,, >, si definise logritmo (logrithm) di in se, indito on log, quel numero rele tle he si i =. Se è un vriile rele >, è definit l funzione logritmi (logrithmi funtion) in se (.) = log Il grfio dell funzione logritmi, per >, è rppresentto in fig. 7. Si noti he log = ( = per qulsisi vlore di ). I sistemi di logritmi più usti sono quelli in se e (numero di Nepero pri,78...), detti logritmi nturli o neperini e inditi nel seguito on ln, e quelli in se, detti logritmi deimli e inditi nel seguito on log. Eserizio 5 Determinre il vlore dei seguenti logritmi deimli: log; log,; log; log. Le funzioni logritmihe hnno lune proprietà notevoli, he le rendono prtiolrmente utili nei mpi dell elettroni e delle teleomunizioni. Un di esse onsiste nel ftto he il logritmo di un prodotto è pri ll somm dei logritmi dei fttori. Per l definizione di logritmo, e dlle proprietà degli esponenzili, si h (.3) (log + log ) = log log = = log ( ) d ui (.4) log ( ) = log + log Vlgono inoltre le seguenti relzioni, qui per revità solo rihimte: log log log (.5) log m = mlog (d ui in prtiolre log = log) log' = log log' (mimento di se) ( ) 9
6 L funzione logritmi, in qunto funzione invers di quell esponenzile, gode di un proprietà omplementre rispetto quest ultim. Si onsideri un intervllo [ ; + ] sull sse orizzontle; il orrispondente intervllo [ ; + ] sull sse vertile h un estensione pri + (.6) = log ( + ) log = log = log + Poihé rppresent l vrizione reltiv dell vriile indipendente, l relzione.6 indi he un ert vrizione reltiv di, espress nhe in termini di vrizioni per- entuli %, orrisponde un vrizio ne ssolut Δ indipendente dl vlore di prtenz (fig. 8). Eserizio 6 Verifire l vlidità di qunto rppresentto in fig. 8, lolndo le vrizioni dell funzione = log orrispondenti vrizioni perentuli di del 5%, prtire di seguenti vlori:,,. % di % di Fig. 8 Crtteristihe di vrizione di log. 4 Funzioni trigonometrihe 4. Misur degli ngoli L unità di misur degli ngoli utilizzt nell vit di tutti i giorni è il grdo sessgesimle (segesiml degree), definito fendo orrispondere l ngolo giro 36 grdi (si srive 36 ). Anhe se spesso esprimeremo gli ngoli in grdi per prtiità, in mito sientifio è unnimemente dottto, ome unità di misur degli ngoli, il rdinte (rdin), quntità dimensionle definit fendo orrispondere l ngolo giro rdinti. L misur degli ngoli in rdinti filit l trttzione mtemti, poihé permette di esprimere l lunghezz di un ro di ironferenz ome il prodotto tr il rggio e l ngolo he sottende l ro stesso (fig. 9). L nozione di ngolo ome porzione di pino, e quindi positivo e ompreso tr e, può essere estes fendo riferimento ll ide di ro orientto (fig. 9); in questo so un ngolo h segno positivo o negtivo, e non è limitto nei possiili vlori dto he l rotzione tr le semirette he lo delimitno può ontinure oltre il giro ompleto. () A r = r in rdinti () Angolo positivo Angolo negtivo Fig. 9 () Misur di un ngolo in rdinti; () rhi orientti. 4. Funzioni seno e oseno Si immgini di posizionre un stiell lung un metro ome in fig., illuminndol dll lto sinistr. L lunghezz dell omr dell stiell sul muro, misurt in metri (m privt poi dell unità di misur), è per definizione il seno (sine) dell ngolo on ui l stiell stess è inlint; l lunghezz dell omr sul pvimento, in metri (nh ess privt dell unità di misur), è per definizione il oseno (osine) di. In linguggio più strettmente mtemtio: dti un sistem di ssi rtesini, un ironferenz di entro nell origine e rggio, e un ngolo (fig. ), le funzioni seno e oseno sono definite rispettivmente ome le proiezioni vertile e orizzontle del segmento unitrio OP. Dl teorem di Pitgor, pplito l tringolo OPQ di fig., si evine l identità fondmentle dell trigonometri sen + os =.
7 P () m sen () O os sen Q sen + os = os Fig. Definizione di seno e oseno. Al vrire dell ngolo, le proiezioni si llungno e si orino, nei limiti dei vlori (proiezione più estes positiv) e (proiezione più estes negtiv). Poihé non è nessun vlore he un ngolo non poss ssumere, le funzioni seno e oseno sono definite nel dominio dei numeri reli; dto he ngoli he differisono di un ngolo giro sono equivlenti dl punto di vist delle proiezioni, le due funzioni hnno un ndmento ilio (fig. ). Come evidente di grfii, le funzioni seno e oseno hnno lo stesso ndmento, e possono trsformrsi l un nell ltr trslndo l origine degli ngoli del vlore. Si noti inoltre he l funzione seno present vlori opposti per ngoli opposti (si die he l funzione è dispri, odd), mentre l fun- zione oseno present identii vlori per ngoli opposti (si die he l funzione è pri, even). Ulteriori definizioni sono riportte shemtimente in t.. sen( ) = sen sen () os( ) = os os sen = os os= sen + () Fig. Grfii delle funzioni () seno e () oseno. T. Funzioni trigonometrihe funzione notzione funzione invers notzione Seno sen Aroseno rsen, sen Coseno os Arooseno ros, os Tngente Cotngente sen tg = os Arotngente rtg, tg os tg = sen Arootngente rtg, tg
8 5 Numeri omplessi 5. Definizioni Si definise numero omplesso (omple numer) un oppi ordint di numeri reli (, ), dove tr due e- lementi X = (, ) e Y = (, d) dell insieme di tli oppie sono definite le seguenti operzioni: (.7) ddizione: X + Y = ( +, + d) (.8) moltiplizione: X Y = ( d, d + ) Sono ltresì definite le seguenti operzioni inverse: = ( ) (.9) sottrzione: X Y (, d) X Y + Y = X X + d d (.) divisione: =, d d Y + + X Y = X, on Y = (, ) Y Eserizio 7 Eseguire l somm e l moltiplizione dei numeri omplessi X = (, 3) e Y = (, 4). Definite le operzioni di se medinte le relzioni preedenti, è possiile or esprimere i numeri omplessi medinte l somm di un prte rele (rel prt) e di un prte immginri (imginr prt) j, e ioè nell form rele-immginri (rel-imginr form) (.) X = + j Si potrnno desso eseguire le quttro operzioni ome se si trttsse di normli inomi, on l regol he ove si trovi un prodotto j j lo si deve sostituire on. Il termine j dell prte immginri è definito unità immginri (imginr unit), mentre il termine è definito oeffiiente dell immginrio (imginr oeffiient). Nel so in ui si i = il numero omplesso è rele; nel so in ui si i = il numero omplesso è detto immginrio puro (pure imginr). L quntità (.) X = + è definit modulo (modulus) del numero omplesso X (si noti, nell., l ssenz dell line superiore, he distingue il modulo dl numero omplesso). Dto un numero omplesso X = + j, è definito omplesso oniugto (omple onjugte) di X il numero Y = j, indito on X *. Eserizio 8 Rivre le espressioni equivlenti lle.7 e.8 utilizzndo l notzione X = + j ed eseguendo le operzioni on le regole dei inomi. Eserizio 9 Eseguire l somm e l moltiplizione dei numeri omplessi X = + j3 e Y = + j4. Verifire l orrispondenz on i risultti ottenuti nell eserizio Corrispondenz tr numeri omplessi, punti di un pino rtesino e vettori idimensionli Dto he un numero omplesso, osì ome un punto di un pino rtesino, è identifito dl vlore di due numeri reli e, è possiile ssoire ogni numero omplesso X = + j il punto del pino rtesino di oordinte (, ): un dto numero omplesso orrisponderà un punto e vievers. Per rendere più evidente l orrispondenz è possiile identifire i due ssi on Re (prte rele) e Im (oeffiiente dell immginrio), ome in fig.. L orrispondenz individut può essere estes i vettori di oordinte (, ), rppresentti grfimente d un segmento orientto he unise l origine on il punto di oordinte (, ) (fig. ). Nel seguito indiheremo vettori e numeri omplessi orrispondenti on lo stesso simolo. Per il teorem di Pitgor, pplito l tringolo rettngolo he h per teti e e per ipotenus l distnz dll origine, il modulo di X orrisponde ll distnz del punto (, ) dll origine oppure, he è l stess os, ll lunghezz del vettore di oordinte (, ).
9 Im Im () Punto orrispondente l numero omplesso X = + j () X Vettore orrispondente l numero omplesso X = + j Re Re Fig. Corrispondenz tr numeri omplessi, () punti di un pino rtesino e () vettori idimensionli. 5.3 Form trigonometri Con riferimento ll fig., essendo (.3) = X os = Xsen dove è l ngolo orientto formto dl vettore e dll sse orizzontle, si può srivere (.4) X = X os+ jxsen = X(os+ jsen ) L espressione.4 è denomint form trigonometri (trigonometri form) del numero omplesso. L ngolo orientto, he in mito vettorile è denominto fse, nel mpo nei numeri omplessi è definito rgomento (rgument). Al fine di determinre onosendo e, in luni testi viene indit l divisione memro memro delle.3: (.5) X sen = = tg X os e il onseguente risultto (.6) = rtg In reltà, l espressione.6 non è orrett. A titolo di esempio, si pong X = + j e quindi = e = ; dll.6 si ottiene = rtg( ) = 4, mentre evidentemente l'rgomento di X è 3 4. Il prolem è il seguente: il vlore orretto di non può essere restituito dll.6, in qunto l funzione rotngente vri nell intervllo ;. In ltre prole, l funzione rtg non interpret orrettmente i segni di e poihé questi sono in rpporto tr loro, e restituise sempre un ngolo del o qudrnte. In definitiv l.6 deve essere osì modifit: (.7) = rtg + k k = per k = per < Im Eserizio Determinre l form trigonometri, on rgomento in rdinti, dei numeri omplessi X = 3 j4 e Y = + j5. Eserizio Determinre l form rele-immginri del numero omplesso orrispondente l vettore rppresentto in fig. 3. X = 3 =,6 Re Fig. 3 Eserizio. 5.4 Form esponenzile Un funzione di vriile ompless (funtion of omple vrile) è un legge Y = f( X) he ssoi isun vlore dell vriile indipendente X un vlore dell vriile dipendente Y. Nel mpo omplesso, per ogni vlore di X = + j, è definit l seguente funzione esponenzile: (.8) e X = e(os+ jsen ) È possiile dimostrre he l esponenzile omplesso osì definito gode di proprietà nloghe quelle dell esponenzile rele (he ssimil per vlori reli di X ), tr ui, in prtiolre: 3
10 (.9) e e = e e = X X X + X Ponendo nell.8 vlori di X pri j e j, si ottengono le formule di Eulero (Euler formuls), qui riportte on le reltive formule inverse: (.3) ej = os+ jsen e j = os + jsen = os jsen ( ) ( ) e os = e sen = Dll prim delle.3, per onfronto on l.4, risult he un numero omplesso può essere espresso nell form esponenzile j j + e e j j j (.3) X = Xej he risult di più omod pplizione nei si in ui si i he fre on moltiplizioni tr numeri omplessi. 5.5 Moltiplizioni tr numeri omplessi Si vuole esminre or qule effetto i l moltiplizione di un numero omplesso X per un seondo numero omplesso Y, ovvero quli proprietà i il risultto P del prodotto rispetto l numero X. Esprimendo i due fttori in form esponenzile, e ioè ome X = Xe e Y = Ye, si ottiene: (.3) P = X Y = Xe Ye = XYe + Il numero omplesso P h pertnto modulo pri XY e rgomento pri +. Nell rppresentzione vettorile (fig. 4), il vettore P h modulo diverso d quello di X di un fttore Y, e, vendo fse pri +, risult ruotto rispetto X dell quntità (in verso ntiorrio se è positivo, in verso orrio se è negtivo). Im P X Re Fig. 4 Moltiplizione di un numero omplesso per Y = Ye. Srnno or onsiderti luni si prtiolri di moltiplizione per un numero omplesso, l ui sempliità onsente di utilizzre senz prolemi l più fmilire rppresentzione rele-immginri. Moltiplizione per un numero rele k > Moltiplindo un generio numero omplesso X = + j per un numero rele k > si ottiene il numero omplesso P = ( + j) k = k+ jk. Il orrispondente vettore, rppresentto in fig. 5, h un lunghezz pri quell del vettore orrispondente X moltiplit per k (verifire he P = kx), stess direzione di quest ultimo (pplire l.7) e stesso verso, dto he k >. Moltiplizione per j Moltiplindo un generio numero omplesso X = + j per l unità immginri j si ottiene il numero omplesso P = ( + j) j = j + j j = + j. Il orrispondente vettore, rppresentto in fig. 5, h l stess lunghezz del vettore orrispondente X (verifire he P = X ), ed è ruotto di in verso ntiorrio rispetto quest ultimo (si verifi filmente onsiderndo he l somm dei due ngoli non retti di un tringolo rettngolo è pri ). Moltiplizione per j Moltiplindo un generio numero omplesso X = + j per j si ottiene il numero omplesso P = ( + j) j = j ( j j) = j. Il orrispondente vettore, rppresentto in fig. 5, h l stess lunghezz del vettore orrispondente X, m in questo so è ruotto di in verso orrio rispetto quest ultimo. Im Im Im k P X P () () X X () k Re Re P Fig. 5 Moltiplizione di un numero omplesso () per un numero rele k >, () per j, () per j. Re 4
11 6 Aspetti omputzionli CAP. 6. Cifre signifitive In generle, si definise ifr signifitiv (signifint digit) un ifr vente vlore diverso d zero. Considerndo d es. il numero,3, diremo he le prime due ifre non sono signifitive; mindo l notzione on l qule rppresentre il numero, queste ifre possono non omprire:,3 = 3 3. In mtemti sono onsiderti non signifitivi nhe gli zeri he terminno un numero, he non devono essere riportti se si trovno destr dell virgol; d es. i numeri,3 e,3 indino lo stesso punto sull sse dei numeri reli, he quindi deve essere espresso nell form più reve. In modo equivlente se gli zeri finli si trovno sinistr dell virgol possono essere omessi mindo notzione: 35 4 = 354. Si noti he gli zeri intermedi, pur rppresentndo per definizione ifre non signifitive, sono nell prssi omune inlusi nel numero di ifre signifitive ssoito un numero. Diremo pertnto he il numero di ifre signifitive dei numeri,3 / 35 4 / 6,37 è rispettivmente due, tre e quttro. Eserizio Indire il numero di ifre signifitive dei seguenti vlori:,6 5; 76 8; 49,3. Se un erto numero rppresent il risultto pprossimto di un lolo, o è l espressione di un misur, gli zeri finli devono essere onsiderti in modo diverso. In questo so inftti il numero in questione non rppresent un punto, m un intervllo sull sse dei numeri reli, nell espressione del qule risult determinnte l eventule presenz di zeri finli. Prim di proseguire on un esempio è opportuno riordre il proedimento di pprossimzione di un numero l fine di ottenere un espressione on meno ifre. Si onsideri il numero =,38673 e si suppong di volerne esprimerne il vlore on quttro ifre, ossi on il numero quttro ifre più viino. In questo so il numero he si ottiene per tronmento (,386) differise d dell quntità,73, mentre il numero ottenuto inrementndo di uno l qurt ifr (,387) ne differise dell quntità,7. Il vlore di pprossimto quttro ifre srà dunque,387. In generle, dett l ultim ifr d mntenere e d l ifr seguente, si h il seguente prospetto, on i reltivi esempi di pprossimzione tre ifre: d < 5 rimne inltert pprossimzione per difetto 4,36 3 4,36 d = 5 e seguono ltre ifre d > 5 deve essere inrementt di uno pprossimzione per eesso 84,357 84,4 6, ,4 d = 5 e non seguono ltre ifre le due soluzioni si equivlgono pprossimzione per difetto o per eesso 4,835 4,83 o 4,84 Il risultto di un pprossimzione rppresent quindi tutti i numeri he pprossimti dnno quel dto vlore. Ad es. il vlore,47 rppresent i numeri,465,475. Il vlore,4 rppresent llor i numeri,395,45, mentre il vlore,4 rppresent i numeri,35,45; lo zero finle desso «signifi» qulos e v mntenuto nell notzione. Eserizio 3 Approssimre tre ifre i seguenti vlori: 4,37 8; 567,8; 345,556; 3,45; 3, Qundo il vlore onsiderto è il risultto di un misur vlgono gli stessi prinipi: l ultim ifr è determint dll pprossimzione dell misur. Misurndo d es. un lunghezz on il metro d srto (he non riport i millimetri vist l su elstiità) si potree vere l =4 m; eseguendo l stess misur on il metro d flegnme si potree invee vere l' = 4, m, he esprime qunto segue: è stto misurto il numero di millimetri dopo 4 m, e il risultto ottenuto è. Ci si potree or hiedere qunte ifre signifitive si opportuno mntenere nell pprossimre il risultto di un lolo; l rispost dipende dll preisione dei dti e dgli sopi. Per i nostri fini possimo dire he pprossimre tre ifre rppresent un rgionevole selt. Attenzione però: l pprossimzione v eseguit solo sui risultti finli; pprossimndo eessivmente i risultti dei pssggi intermedi l vlidità delle ultime ifre dei risultti finli non è più ssiurt. Se si desider d es. he il risultto finle si pprossimto tre ifre signifitive, è neessrio mntenere nei pssggi intermedi lmeno inque ifre signifitive. 6. Notzione esponenzile L notzione esponenzile (eponentil nottion) onsiste nell esprimere un vlore ome prodotto di un numero, vente l prim ifr signifitiv l posto delle unità, per un potenz di diei. Per esprimere un nume- 5
12 ro in notzione esponenzile è suffiiente spostre l virgol fino he l prim ifr signifitiv non rggiunge le unità; se sono stti ftti n pssi sinistr, equivlenti un divisione del numero per n, si moltipliherà per n, se sono stti ftti n pssi destr, equivlenti un divisione del numero per n, si moltipliherà per n. Per pssre dll notzione esponenzile quell deimle si esegue l operzione invers: n pssi destr se l esponente è positivo, n pssi sinistr se è negtivo. Eserizio 4 Esprimere in notzione esponenzile i seguenti vlori: 3; ;, 45; 3 5,458. Eserizio 5 Esprimere in notzione deimle i seguenti vlori:,37 5 ; 4,567 9 ; 8, ; 7,3. L notzione esponenzile, indit nelle loltrii ome notzione sientifi (sientifi nottion), permette di esprimere quntità molto grndi o molto piole senz dover onteggire gli zeri. Risolve inoltre il prolem delle ifre signifitive di vlori interi on uno o più zeri finli (srivendo 3 non si s qunti zeri sino signifitivi, srivendo,3 5 non i sono miguità). Nelle sienze tenihe risult più prtio un ltro tipo di notzione, indit ome ingegneristi (engineering) nelle loltrii, in ui il modulo dell esponente di diei può essere pri solo multipli di tre, in modo d esprimere multipli o sottomultipli delle unità di misur utilizzte (t. 3). I metodi di onversione sono gli stessi dell notzione sientifi. fttore moltiplitivo prefisso T. 3 Multipli e sottomultipli delle unità di misur. simolo fttore moltiplitivo prefisso ter T 3 milli m 9 gig G 6 miro µ 6 meg M 9 nno n 3 kilo k pio p simolo Eserizio 6 Esprimere i seguenti vlori in notzione ingegneristi e poi medinte multipli o sottomultipli delle unità di misur: m;, 54 g; 4 Hz;,8 s. 6.3 Ordine di grndezz L ordine di grndezz (order of mgnitude) di un vriile o di un prmetro è quell potenz inter di he più si vviin i suoi possiili vlori. Ad es. diremo he l ordine di grndezz dell ltezz h di un edifiio è di m (sriveremo h m); nei si prtii tle prmetro potrà essere pri m, o 8 m, o ltro. L ordine di grndezz è quindi un quntità he serve d vere un ide grossoln dei vlori he un ert grndezz può ssumere. Eserizio 8 Sull se dell esperienz omune, elenre gli ordini di grndezz delle seguenti quntità: peso di un person, ltezz di un tvolo, durt di un interrogzione. 6.4 Quntità trsurili Spesso nelle sienze fisihe è possiile semplifire le espressioni mtemtihe o i modelli fisii diendo he un ert quntità «risult trsurile». È opportuno fr notre he un vlore può diventre trsurile solo in onfronto un quntità esso omogene (misurile on l stess unità di misur), rispetto ll qule deve essere inferiore di lmeno due ordini di grndezz. 6.5 Frzioni L mggior prte degli errori he si ommettono mneggindo frzioni omplesse deriv dl non interpretre orrettmente l ordine in ui vnno eseguite le diverse operzioni di divisione. Se onsiderimo l operzione di ddizione, l vlidità dell proprietà ssoitiv, per ui ( + ) + = + ( + ), onsente di effetture le operzioni di somm nell ordine desiderto, e quindi viene meno l esigenz di indire, d es. on prentesi, un ordine di eseuzione delle operzioni. Dto he, ome è file verifire, per l operzione di divisione tle proprietà non è verifit, è neessrio speifire sempre, on prentesi o medinte i simoli di 6
13 frzione, l ordine delle operzioni he deve essere rispettto per ottenere il risultto orretto. Seguono luni esempi, per l omprensione dei quli si riord he =. CAP. Esempio Si onsideri l seguente espressione: (.33) A = Il segno più mpio dell line di frzione superiore st indire he l quntità risult divis per l frzione. Se si devono eseguire loli numerii si proederà lolre k = e quindi A =. Se si vuole esprimere in form k semplifit l.3, l si può rppresentre ome prodotto tr e, ottenendo (.34) A= = Esempio 3 Si onsideri l seguente espressione: (.35) A = e d Il segno più mpio dell line di frzione entrle st indire he l quntità risult divis per l quntità k e. Se si devono eseguire loli numerii si proederà lolre k =, l = e e quindi A =. Se si vuole e- d d l sprimere in form semplifit l.34, l si può rppresentre ome prodotto tr e e d, ottenendo (.36) e d d A = d = = e e Eserizio 8 Semplifire in un uni frzione le seguenti espressioni: ) V Z V Z ; ) g Eeff R 8 ; 3) d f e g A onlusione del pitolo, si riport per omodità del lettore l lfeto greo. minusol miusol nome minusol miusol nome minusol miusol nome α Α lf ι Ι iot ρ Ρ rho β Β et κ Κ kpp σ Σ sigm γ Γ gmm λ Λ lmd τ Τ tu δ Δ delt μ Μ mi υ Υ upsilon ε Ε epsilon ν Ν ni ϕ Φ phi ζ Ζ zet ξ Ξ i χ Χ hi η Η et ο Ο omiron ψ Ψ psi θ Θ thet π Π pi ω Ω omeg 7
14 Funtion (mthemtis) In mthemtis, funtion is reltion etween set of inputs nd set of potentil outputs with the propert tht eh input is relted to etl one output. An emple of suh reltion is defined the rule f () =, whih reltes n input to its squre, whih re oth rel numers. The output of the funtion f orresponding to n input is denoted f () (red f of ). If the input is 3, then the output is 9, nd we m write f ( 3) = 9. Eponentil funtion In mthemtis, the eponentil funtion is the funtion e, where e is the numer (pproimtel.78888) suh tht the funtion e is its own derivtive. The eponentil funtion is used to model reltionship in whih onstnt hnge in the independent vrile gives the sme proportionl hnge (i.e. perentge inrese or derese) in the dependent vrile. The funtion is often written s ep(), espeill when it is imprtil to write the independent vrile s supersript. Logrithm The logrithm of numer is the eponent whih nother fied vlue, the se, hs to e rised to produe tht numer. For emple, the logrithm of to se is 3, euse is to the power 3: = 3 =. More generll, if =, then is the logrithm of to se, nd is written = log (), so log () = 3. The logrithm to se = is lled the ommon logrithm nd hs mn pplitions in siene nd engineering. The nturl logrithm hs the onstnt e (.78) s its se; its use is widespred in pure mthemtis, espeill lulus. The inr logrithm uses se = nd is prominent in omputer siene. Trigonometri funtions In mthemtis, the trigonometri funtions (lso lled irulr funtions) re funtions of n ngle. The re used to relte the ngles of tringle to the lengths of the sides of tringle. Trigonometri funtions re importnt in the stud of tringles nd modeling periodi phenomen, mong mn other pplitions. The most fmilir trigonometri funtions re the sine, osine, nd tngent. In the ontet of the stndrd unit irle with rdius, where tringle is formed r originting t the origin nd mking some ngle with the -is, the sine of the ngle gives the length of the -omponent (rise) of the tringle, the osine gives the length of the -omponent (run), nd the tngent funtion gives the slope (-omponent divided the -omponent). Comple numer A omple numer is numer whih n e put in the form + i, where nd re rel numers nd i is lled the imginr unit, where i =. In this epression, is lled the rel prt nd the imginr prt of the omple numer. 8
operazioni con vettori
 omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
Vettori - Definizione
 Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
MATRICI E DETERMINANTI
 MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
APPUNTI DI GEOMETRIA ANALITICA
 Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
Ellisse ed iperbole. Osservazione. Considereremo sempre ellissi della forma + = 1 le quali hanno tutte centro nell origine degli
 Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
Relazioni e funzioni. Relazioni
 Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
1) Si ha quindi Un cateto è uguale al prodotto dell ipotenusa per il seno dell angolo opposto.
 Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
Verifica di matematica
 Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Geometria Analitica Domande, Risposte & Esercizi
 Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
Unità Didattica N 08 I sistemi di primo grado a due incognite U.D. N 08 I sistemi di primo grado a due incognite
 66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
Ciro Baratto GONIOMETRIA TRIGONOMETRIA 799 ESERCIZI SVOLTI
 Ciro Brtto GONIOMETRIA TRIGONOMETRIA 99 ESERCIZI SVOLTI INTRODUZIONE Gli eserizi (n. 99) he seguono sono stti svolti per un migliore omprensione dell goniometri e dell trigonometri, erndo, in lrg misur,
Ciro Brtto GONIOMETRIA TRIGONOMETRIA 99 ESERCIZI SVOLTI INTRODUZIONE Gli eserizi (n. 99) he seguono sono stti svolti per un migliore omprensione dell goniometri e dell trigonometri, erndo, in lrg misur,
c β Figura F2.1 Angoli e lati in un triangolo rettangolo.
 F. Trigonometri F. Risoluzione dei tringoli rettngoli Risolvere un tringolo rettngolo signifi trovre tutti i suoi lti e tutti i suoi ngoli. Un ngolo lo si onose già ed è l ngolo retto. Le inognite sono
F. Trigonometri F. Risoluzione dei tringoli rettngoli Risolvere un tringolo rettngolo signifi trovre tutti i suoi lti e tutti i suoi ngoli. Un ngolo lo si onose già ed è l ngolo retto. Le inognite sono
01 Matematica Liceo \ Unità Didattica N 6 La retta 1
 Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
ISTITUTO TECNICO INDUSTRIALE "E. Fermi" LUCCA Anno Scolastico 2017/2018 Programma di MATEMATICA classe prima Sez. G Insegnante: MUSUMECI LUCIANA
 ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
Le equazioni di secondo grado
 Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on 0,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on 0,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Strumenti Matematici per la Fisica
 Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
j Verso la scuola superiore +l calcolo letterale Monomi Polinomi e prodotti notevoli Equazioni
 j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
Geometria. Domande introduttive
 PT, 695 noio Geometri si di mtemti per l MPT 3 Tringoli L pdronnz delle rtteristihe e delle proprietà dei tringoli è fondmentle per pire il pitolo dell trigonometri, uno dei pitoli di geometri non trttto
PT, 695 noio Geometri si di mtemti per l MPT 3 Tringoli L pdronnz delle rtteristihe e delle proprietà dei tringoli è fondmentle per pire il pitolo dell trigonometri, uno dei pitoli di geometri non trttto
TOPOGRAFIA. Prima parte. Prof. Roma Carmelo
 TOPOGRFI Prim prte TOPOGRFI Sommrio onversione tr sistemi di misur ngolri Funzioni goniometrihe tngente e otngente Teorem dei seni (o di Eulero) Teorem di rnot onversione tr sistemi di misur ngolri Sistemi
TOPOGRFI Prim prte TOPOGRFI Sommrio onversione tr sistemi di misur ngolri Funzioni goniometrihe tngente e otngente Teorem dei seni (o di Eulero) Teorem di rnot onversione tr sistemi di misur ngolri Sistemi
L ELLISSE 1. L'ellisse come luogo geometrico ellisse fuochi. centro
 L ELLISSE 1. L ellisse ome luogo geometrio.. Equzione dell ellisse on i fuohi sull sse. 3. Le proprietà dell ellisse.. Clolo dei semissi, dei vertii, dei fuohi e rppresentzione grfi. 5. Equzione dell ellisse
L ELLISSE 1. L ellisse ome luogo geometrio.. Equzione dell ellisse on i fuohi sull sse. 3. Le proprietà dell ellisse.. Clolo dei semissi, dei vertii, dei fuohi e rppresentzione grfi. 5. Equzione dell ellisse
Anno 2. Triangoli rettangoli e teorema delle corde
 Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
1 Integrali doppi di funzioni a scala su rettangoli
 INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
Numeri nello spazio n dimensionale
 Numeri nello spzio n dimensionle Niol D Alfonso Riertore indipendente niol.dlfonso@hotmil.om Sommrio Questo pper introdue i numeri nello spzio n dimensionle. Vle dire, se nell prim dimensione bbimo i numeri
Numeri nello spzio n dimensionle Niol D Alfonso Riertore indipendente niol.dlfonso@hotmil.om Sommrio Questo pper introdue i numeri nello spzio n dimensionle. Vle dire, se nell prim dimensione bbimo i numeri
Test di autovalutazione
 UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
8 Equazioni parametriche di II grado
 Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Appunti di Matematica Computazionale Lezione 1. Equazioni non lineari. Consideriamo il problema della determinazione delle radici dell equazione
 Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
Es1 Es2 Es3 Es4 Es5 tot
 Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
FUNZIONI MATEMATICHE. Una funzione lineare è del tipo:
 FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
+ numeri reali Numeri decimali e periodici Estrazione di radice
 numeri reli Numeri deimli e periodii Estrzione di rdie Numeri deimli e periodii SEZ. G Clol il vlore delle seguenti espressioni. 0 (, ), Trsformimo i numeri deimli nell orrispondente frzione genertrie
numeri reli Numeri deimli e periodii Estrzione di rdie Numeri deimli e periodii SEZ. G Clol il vlore delle seguenti espressioni. 0 (, ), Trsformimo i numeri deimli nell orrispondente frzione genertrie
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
Misura degli archi e degli angoli
 Misur degli rhi e degli ngoli. Si definise ome positivo il verso ntiorrio di perorrenz di un ironferenz; ome negtivo il verso orrio.. Fissto su un ironferenz un punto A ome origine e un punto B ome estremo
Misur degli rhi e degli ngoli. Si definise ome positivo il verso ntiorrio di perorrenz di un ironferenz; ome negtivo il verso orrio.. Fissto su un ironferenz un punto A ome origine e un punto B ome estremo
Algebra lineare ... Per indicare la relazione tra vettore riga e vettore colonna si usa il simbolo T (operazione di trasposizione)
 Alger linere. Vettori: definizioni Un ettore x n dimensioni è un insieme ordinto di n numeri x ( x x...x n ) I numeri x x...xn sono detti omponenti del ettore x. I ettori possono essere sritti sotto form
Alger linere. Vettori: definizioni Un ettore x n dimensioni è un insieme ordinto di n numeri x ( x x...x n ) I numeri x x...xn sono detti omponenti del ettore x. I ettori possono essere sritti sotto form
Elementi di matematica
 Moltiplizione L moltiplizione è un proedimento he onsiste nel sommre sé stesso un numero (o un grndezz) per un erto numero di volte. Per esempio, «4 per 2» orrisponde «4 sommto due volte» o «2 sommto quttro
Moltiplizione L moltiplizione è un proedimento he onsiste nel sommre sé stesso un numero (o un grndezz) per un erto numero di volte. Per esempio, «4 per 2» orrisponde «4 sommto due volte» o «2 sommto quttro
a è detta PARTE LETTERALE
 I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
Algebra Condizioni di Esistenza Equazioni di secondo grado Scomposizione di un trinomio di secondo grado Definizione di valore assoluto
 Alger Condizioni di Esistenz n N x D x A(x) on n pri D x 0 A x 0 tn f(x) f x + k se f(x) f x + k log A x B(x) A x > 0 A x B x > 0 f x α f x 0 on α > 0 irrz. f x α f x > 0 on α < 0 irrz. f x g x f x > 0
Alger Condizioni di Esistenz n N x D x A(x) on n pri D x 0 A x 0 tn f(x) f x + k se f(x) f x + k log A x B(x) A x > 0 A x B x > 0 f x α f x 0 on α > 0 irrz. f x α f x > 0 on α < 0 irrz. f x g x f x > 0
KIT ESTIVO MATEMATICA A.S. 2015/16 CLASSI SECONDE IeFP OPERATORE GRAFICO
 ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
8. Calcolo integrale.
 Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
Grafici elementari 1 - geometria analitica
 Grfii elementri - geometri nliti Un equzione rppresent un funzione se è possiile metterl in form espliit (rivre l y) ottenendo un sol espressione. Un urv rppresent un funzione se, preso un qulsisi punto
Grfii elementri - geometri nliti Un equzione rppresent un funzione se è possiile metterl in form espliit (rivre l y) ottenendo un sol espressione. Un urv rppresent un funzione se, preso un qulsisi punto
FUNZIONI SENO & COSENO TANGENTE & COTANGENTE
 FUNZINI SEN & SEN TNGENTE & TNGENTE DEFINIZINE DI SEN E SEN onsiderndo l ngolo =, trimo un erhio di rggio qulunque R = = e on entro sul vertie dell ngolo. Le intersezioni del erhio on le semirette dell
FUNZINI SEN & SEN TNGENTE & TNGENTE DEFINIZINE DI SEN E SEN onsiderndo l ngolo =, trimo un erhio di rggio qulunque R = = e on entro sul vertie dell ngolo. Le intersezioni del erhio on le semirette dell
Disequazioni di primo grado
 Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
a b c Triangolo rettangolo In un triangolo rettangolo : un cateto è uguale al prodotto dell ipotenusa per il seno dell angolo opposto al cateto.
 Tringolo rettngolo In un tringolo rettngolo : un teto è ugule l prodotto dell ipotenus per il seno dell ngolo opposto l teto. = sen = sen un teto è ugule l prodotto dell ipotenus per il oseno dell ngolo
Tringolo rettngolo In un tringolo rettngolo : un teto è ugule l prodotto dell ipotenus per il seno dell ngolo opposto l teto. = sen = sen un teto è ugule l prodotto dell ipotenus per il oseno dell ngolo
Argomento 10 Integrali impropri
 Premess Argomento Integrli impropri Nell Arg. 9 è stt introdott l nozione di integrle definito f() d per funzioni ontinue f : [, b] R. Un derog ll ontinuità di f è nhe stt introdott, m solo per onsiderre
Premess Argomento Integrli impropri Nell Arg. 9 è stt introdott l nozione di integrle definito f() d per funzioni ontinue f : [, b] R. Un derog ll ontinuità di f è nhe stt introdott, m solo per onsiderre
Ing. Alessandro Pochì
 Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
] + [ ] [ ] def. ] e [ ], si ha subito:
![] + [ ] [ ] def. ] e [ ], si ha subito: ] + [ ] [ ] def. ] e [ ], si ha subito:](/thumbs/24/3548090.jpg) OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit 0) L definizione di equzione di seondo grdo d un inognit 0) L risoluzione delle equzioni di
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit 0) L definizione di equzione di seondo grdo d un inognit 0) L risoluzione delle equzioni di
EQUAZIONI DI SECONDO GRADO
 Autore: Enrio Mnfui - 30/04/0 EQUAZIONI DI SECONDO GRADO Le equzioni di seondo grdo in un inognit sono uguglinze di due polinomi di ui lmeno uno è di seondo grdo e l ltro è di grdo minore o ugule due.
Autore: Enrio Mnfui - 30/04/0 EQUAZIONI DI SECONDO GRADO Le equzioni di seondo grdo in un inognit sono uguglinze di due polinomi di ui lmeno uno è di seondo grdo e l ltro è di grdo minore o ugule due.
La risoluzione di una disequazione di secondo grado
 L risoluzione di un disequzione di seondo grdo Quest nno le disequzioni srnno importntissime. Non si prlerà però proprimente di disequzioni m di studire il segno di un funzione. In effetti un numero può
L risoluzione di un disequzione di seondo grdo Quest nno le disequzioni srnno importntissime. Non si prlerà però proprimente di disequzioni m di studire il segno di un funzione. In effetti un numero può
2 Numeri reali. M. Simonetta Bernabei & Horst Thaler
 2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
Il calcolo letterale
 Appunti di Mtemtic Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre
Appunti di Mtemtic Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre
Il calcolo letterale
 Progetto Mtemtic in Rete Il clcolo letterle Finor imo studito gli insiemi numerici (espressioni numeriche). Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere
Progetto Mtemtic in Rete Il clcolo letterle Finor imo studito gli insiemi numerici (espressioni numeriche). Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE
 VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
Angoli e funzioni goniometriche
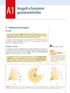 ngoli e funzioni goniometrihe. Definizioni di ngolo ngolo L geometri definise ngolo isun delle prti del pino in ui esso è diviso d due semirette usenti d uno stesso punto ; il punto si die vertie dell
ngoli e funzioni goniometrihe. Definizioni di ngolo ngolo L geometri definise ngolo isun delle prti del pino in ui esso è diviso d due semirette usenti d uno stesso punto ; il punto si die vertie dell
POTENZA 2 5 =2*2*2*2*2 PROPRIETA PRODOTTO DI POTENZE DI UGUALE BASE 3 2 *3 7 =3 2+7 =3 9 ANGOLO ANGOLI CLASSIFICAZIONI. 2 è la BASE 5 è l ESPONENTE
 POTENZ 2 5 =2*2*2*2*2 2 è la SE 5 è l ESPONENTE PROPRIET PRODOTTO DI POTENZE DI UGULE SE 3 2 *3 7 =3 2+7 =3 9 QUOZIENTE DI POTENZE DI UGULE SE 3 12 :3 7 =3 12-7 =3 5 POTENZ DI POTENZ (3 2 ) 7 =3 2*7 =3
POTENZ 2 5 =2*2*2*2*2 2 è la SE 5 è l ESPONENTE PROPRIET PRODOTTO DI POTENZE DI UGULE SE 3 2 *3 7 =3 2+7 =3 9 QUOZIENTE DI POTENZE DI UGULE SE 3 12 :3 7 =3 12-7 =3 5 POTENZ DI POTENZ (3 2 ) 7 =3 2*7 =3
Analisi Matematica I per Ingegneria Gestionale, a.a Primo compitino, 18 novembre 2017 Testi 1
 Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
5. Funzioni elementari trascendenti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
] a; b [, esiste almeno un punto x 0
![] a; b [, esiste almeno un punto x 0 ] a; b [, esiste almeno un punto x 0](/thumbs/88/115232227.jpg) Anlisi Limiti notevoli sen lim = ( lim + = e Un funzione si die ontinu in qundo, + lim f( = lim f(. + sintoti vertili: se lim f ( = ± oppure lim f ( = ± sintoti orizzontli: se sintoti oliqui: l'equzione
Anlisi Limiti notevoli sen lim = ( lim + = e Un funzione si die ontinu in qundo, + lim f( = lim f(. + sintoti vertili: se lim f ( = ± oppure lim f ( = ± sintoti orizzontli: se sintoti oliqui: l'equzione
Δlessio abelli. Studente di Matematica Sapienza - Università di Roma. Dipartimento di Matematica Guido Castelnuovo
 Δlessio elli Studente di Mtemti Spienz - Università di Rom Diprtimento di Mtemti Guido Cstelnuovo we-site: www.selli87.ltervist.org EQUAZIONI DI II GRADO. DEFINIZIONI Si die equzione di seondo grdo nell
Δlessio elli Studente di Mtemti Spienz - Università di Rom Diprtimento di Mtemti Guido Cstelnuovo we-site: www.selli87.ltervist.org EQUAZIONI DI II GRADO. DEFINIZIONI Si die equzione di seondo grdo nell
L IPERBOLE. L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi.
 prof.ss Cterin Vespi 1 Appunti di geometri nliti L IPERBOLE L iperole è il luogo geometrio dei punti del pino per i quli è ostnte l differenz delle distnze d due punti fissi detti fuohi. Sino F1 e F i
prof.ss Cterin Vespi 1 Appunti di geometri nliti L IPERBOLE L iperole è il luogo geometrio dei punti del pino per i quli è ostnte l differenz delle distnze d due punti fissi detti fuohi. Sino F1 e F i
Calcolo integrale per funzioni di una variabile
 Clolo integrle per unzioni di un vriile Clolo integrle Integrle deinito Si :[,] R, limitt ξ ξ ξ ξ 4 ξ 5 = 4 5 = Costruimo l somm di Cuhy-Riemnn n n S n j j j j j n j Dove l suddivisione dell intervllo
Clolo integrle per unzioni di un vriile Clolo integrle Integrle deinito Si :[,] R, limitt ξ ξ ξ ξ 4 ξ 5 = 4 5 = Costruimo l somm di Cuhy-Riemnn n n S n j j j j j n j Dove l suddivisione dell intervllo
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
Appendice. Test per l ammissione all università per i corsi di laurea delle aree architettura e design. Griglie
 T07_PPNII_UNIO 21-01-2009 17:0 Pgin 1 ppendie Test per l mmissione ll università per i orsi di lure delle ree rhitettur e design Griglie onosenze sientifio-tenihe e dell rppresentzione 1 Qule dei seguenti
T07_PPNII_UNIO 21-01-2009 17:0 Pgin 1 ppendie Test per l mmissione ll università per i orsi di lure delle ree rhitettur e design Griglie onosenze sientifio-tenihe e dell rppresentzione 1 Qule dei seguenti
Le equazioni di secondo grado
 Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Formule di Gauss Green
 Formule di Guss Green In queste lezioni voglimo studire il legme esistente tr integrli in domini bidimensionli ed integrli urvilinei sull frontier di questi. In seguito i ouperemo del problem nlogo nello
Formule di Guss Green In queste lezioni voglimo studire il legme esistente tr integrli in domini bidimensionli ed integrli urvilinei sull frontier di questi. In seguito i ouperemo del problem nlogo nello
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
I. S. I. E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I. S. I. E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Ghilrdui Pol Gli insiemi numerii I numeri nturli i numeri interi reltivi i numeri rzionli. ddizione
I. S. I. E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Ghilrdui Pol Gli insiemi numerii I numeri nturli i numeri interi reltivi i numeri rzionli. ddizione
Analisi di stabilità
 Anlisi di stilità Stilità intern modi propri degli stti utovlori di A Stilità estern modi propri dell usit poli dell fdt.-. Stilità : se tutti i modi propri rimngono limitti per ogni t. Stilità : se tutti
Anlisi di stilità Stilità intern modi propri degli stti utovlori di A Stilità estern modi propri dell usit poli dell fdt.-. Stilità : se tutti i modi propri rimngono limitti per ogni t. Stilità : se tutti
quattro trasformazioni
 ilo di rnot e un ilo termio ostituito d quttro trsformzioni p() reversibili di un gs perfetto : un espnsione isoterm d tempertur un espnsione dibti d un ompressione isoterm d tempertur un ompressione dibti
ilo di rnot e un ilo termio ostituito d quttro trsformzioni p() reversibili di un gs perfetto : un espnsione isoterm d tempertur un espnsione dibti d un ompressione isoterm d tempertur un ompressione dibti
Anno 5. Applicazione del calcolo degli integrali definiti
 Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
13. EQUAZIONI ALGEBRICHE
 G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
Unità Didattica N 02. I concetti fondamentali dell aritmetica
 1 Unità Didttic N 0 I concetti fondmentli dell ritmetic 01) Il concetto di potenz 0) Proprietà delle potenze 0) L nozione di rdice ritmetic 0) Multipli e divisori di un numero 05) Criteri di divisibilità
1 Unità Didttic N 0 I concetti fondmentli dell ritmetic 01) Il concetto di potenz 0) Proprietà delle potenze 0) L nozione di rdice ritmetic 0) Multipli e divisori di un numero 05) Criteri di divisibilità
U.D. N 15 Funzioni e loro rappresentazione grafica
 54 Unità Didttic N 5 Funzioni e loro rppresentzione grfic U.D. N 5 Funzioni e loro rppresentzione grfic ) Le coordinte crtesine ) L distnz tr due punti 3) Coordinte del punto medio di un segmento 4) Le
54 Unità Didttic N 5 Funzioni e loro rppresentzione grfic U.D. N 5 Funzioni e loro rppresentzione grfic ) Le coordinte crtesine ) L distnz tr due punti 3) Coordinte del punto medio di un segmento 4) Le
Prof. Roberto Milizia, presso Liceo Scientifico E. Ferdinando Mesagne (BR) 1
 Prof. Roerto Milizi, presso Lieo Sientifio E. Ferdinndo Mesgne (BR) UNITA 7. ESPONENZIALI E LOGARITMI.. L potenz on esponente rele.. Le proprietà delle potenze.. Equzioni esponenzili he si rionduono ll
Prof. Roerto Milizi, presso Lieo Sientifio E. Ferdinndo Mesgne (BR) UNITA 7. ESPONENZIALI E LOGARITMI.. L potenz on esponente rele.. Le proprietà delle potenze.. Equzioni esponenzili he si rionduono ll
I PRODOTTI NOTEVOLI. Nel calcolo letterale capita spesso di incontrare moltiplicazioni tra particolari polinomi.
 I PRODOTTI NOTEVOLI Nel lolo letterle pit spesso di inontrre moltiplizioni tr prtiolri polinomi. I reltivi sviluppi si ottengono pplindo le regole fin qui viste, m i risultti, opportunmente semplifiti,
I PRODOTTI NOTEVOLI Nel lolo letterle pit spesso di inontrre moltiplizioni tr prtiolri polinomi. I reltivi sviluppi si ottengono pplindo le regole fin qui viste, m i risultti, opportunmente semplifiti,
Problema: Calcolo dell'area di una superficie piana
 Corso di Lure in Disegno Industrile Corso di Metodi Numerii per il Design Lezione 7 Novemre 00 Integrle definito F. Cliò Prolem: Clolo dell're di un superfiie pin Metodi Numerii per il Design - Lezione
Corso di Lure in Disegno Industrile Corso di Metodi Numerii per il Design Lezione 7 Novemre 00 Integrle definito F. Cliò Prolem: Clolo dell're di un superfiie pin Metodi Numerii per il Design - Lezione
Il Teorema della media media integrale di una funzione
 FRONTESPIZIO http://www.sitowe.om Interntionl Review of Sientifi Synthesis ISSN 2282-2119 Quderni di Mtemti 2015 Mtemti Open Soure http://www.extryte.info Il Teorem dell medi medi integrle di un funzione
FRONTESPIZIO http://www.sitowe.om Interntionl Review of Sientifi Synthesis ISSN 2282-2119 Quderni di Mtemti 2015 Mtemti Open Soure http://www.extryte.info Il Teorem dell medi medi integrle di un funzione
Le equazioni di secondo grado. Appunti delle lezioni di Armando Pisani A.S Liceo Classico Dante Alighieri (GO)
 Le equzioni di seondo grdo Appunti delle lezioni di Armndo Pisni A.S. 3- Lieo Clssio Dnte Alighieri (GO) Not Questi ppunti sono d intendere ome guid llo studio e ome rissunto di qunto illustrto durnte
Le equzioni di seondo grdo Appunti delle lezioni di Armndo Pisni A.S. 3- Lieo Clssio Dnte Alighieri (GO) Not Questi ppunti sono d intendere ome guid llo studio e ome rissunto di qunto illustrto durnte
Soluzione. Studiamo la funzione. Dominio: la funzione è definita in tutto R; Intersezione asse ascisse: ( x)
 Sessione ordinri LS_ORD Soluzione di De Ros Niol Soluzione Studimo l unzione Dominio: l unzione è deinit in tutto R; ; Intersezione sse sisse: Intersezioni sse delle ordinte: y ; Prità o disprità: l unzione
Sessione ordinri LS_ORD Soluzione di De Ros Niol Soluzione Studimo l unzione Dominio: l unzione è deinit in tutto R; ; Intersezione sse sisse: Intersezioni sse delle ordinte: y ; Prità o disprità: l unzione
Corso di ELETTRONICA INDUSTRIALE
 0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
{ 1, 2,3, 4,5,6,7,8,9,10,11,12, }
 Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
1. In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione: y ax x b = + +
 . In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
. In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
Meccanica dei Solidi. Vettori
 Meccnic dei Solidi Prof. Ing. Stefno Avers Università di Npoli Prthenope.. 2005-06 Lezione 2 Vettori Definizione: Un grndezz vettorile (o un vettore) è un grndezz fisic crtterizzt oltre che d un numero
Meccnic dei Solidi Prof. Ing. Stefno Avers Università di Npoli Prthenope.. 2005-06 Lezione 2 Vettori Definizione: Un grndezz vettorile (o un vettore) è un grndezz fisic crtterizzt oltre che d un numero
Monomi e polinomi. Verifica per la classe prima COGNOME... NOME... Classe... Data...
 Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
ENS: Esame e seconda prova in itinere del 1 Luglio 2008 Per la discussione dello scritto si contatti il docente via
 ENS: Esme e seond prov in itinere del Luglio 8 Per l disussione dello sritto si onttti il doente vi e-mil: ro@elet.polimi.it Eserizio (foglio ino) Esme primo ppello: punti : Filtri FIR e IIR Si onsideri
ENS: Esme e seond prov in itinere del Luglio 8 Per l disussione dello sritto si onttti il doente vi e-mil: ro@elet.polimi.it Eserizio (foglio ino) Esme primo ppello: punti : Filtri FIR e IIR Si onsideri
Programma di matematica Prof.ssa Tacchi Lucia Anno scolastico 2017/2018 classe I A
 Isi E. Fermi Lucc Progrmm di mtemtic Prof.ss Tcchi Luci nno scolstico 7/8 clsse I Gli insiemi numerici i numeri nturli i numeri interi i numeri rzionli ssoluti i reltivi. Potenze nche con esponente intero
Isi E. Fermi Lucc Progrmm di mtemtic Prof.ss Tcchi Luci nno scolstico 7/8 clsse I Gli insiemi numerici i numeri nturli i numeri interi i numeri rzionli ssoluti i reltivi. Potenze nche con esponente intero
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
61 LE EQUAZIONI DI 2 GRADO - SECONDA PARTE. a) RELAZIONI FRA SOLUZIONI E COEFFICIENTI IN UN EQUAZIONE DI 2 GRADO
 6 LE EQUAZIONI DI GRADO - SECONDA PARTE NOTA - Preliminre questi rgomenti, è l onosenz dei numeri omplessi (pitolo preedente) ) RELAZIONI FRA SOLUZIONI E COEFFICIENTI IN UN EQUAZIONE DI GRADO In ogni equzione
6 LE EQUAZIONI DI GRADO - SECONDA PARTE NOTA - Preliminre questi rgomenti, è l onosenz dei numeri omplessi (pitolo preedente) ) RELAZIONI FRA SOLUZIONI E COEFFICIENTI IN UN EQUAZIONE DI GRADO In ogni equzione
RAPPRESENTAZIONE GRAFICA DELLA PARABOLA a ( ) { } f con, è la parabola di equazione y = ax + bx + c. Vogliamo disegnarla. 2
 APPENDICE 1 AL CAPITOLO 3: RAPPRESENTAZIONE GRAFICA DELLA PARABOLA Per 0 l insieme,y / y = + + c, grfico dell funzione f = + + c { } f con, è l prol di equzione y = + + c Voglimo disegnrl non è difficile
APPENDICE 1 AL CAPITOLO 3: RAPPRESENTAZIONE GRAFICA DELLA PARABOLA Per 0 l insieme,y / y = + + c, grfico dell funzione f = + + c { } f con, è l prol di equzione y = + + c Voglimo disegnrl non è difficile
Geometria analitica +l piano cartesiano Le funzioni retta, parabola, iperbole Le trasformazioni sul piano cartesiano
 Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
a > 1 y = 1 x = 1 La funzione esponenziale La funzione y = a x è chiamata funzione esponenziale di x dove a è la base della funzione.
 L funzione esponenzile L funzione = è chimt funzione esponenzile di dove è l bse dell funzione. > 0; Condizioni di vlidità: < < ; > 0 Se > l funzione è monoton crescente > = = = o L funzione esponenzile
L funzione esponenzile L funzione = è chimt funzione esponenzile di dove è l bse dell funzione. > 0; Condizioni di vlidità: < < ; > 0 Se > l funzione è monoton crescente > = = = o L funzione esponenzile
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
Nomogrammi logaritmici
 Prinipi e etodi di relizzzione Prinipi e etodi di relizzzione Versione 1.1 del31/12/99 Distriuzione 31/12/99 Prinipi e etodi di relizzzione Prinipi - 2 1. PRINIPI Un noogr è ostituito d un gruppo di tre
Prinipi e etodi di relizzzione Prinipi e etodi di relizzzione Versione 1.1 del31/12/99 Distriuzione 31/12/99 Prinipi e etodi di relizzzione Prinipi - 2 1. PRINIPI Un noogr è ostituito d un gruppo di tre
MATEMATICA Classe Prima
 Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
