TRASFORMATA DI HILBERT
|
|
|
- Carla Cecilia Manzo
- 7 anni fa
- Visualizzazioni
Transcript
1 TRASFORMATA DI ILBERT La Trasformata di ilbert è una partiolare rappresentazione he, ontrariamente ad altre trasformate (Fourier, Laplae, Z, ) non realizza un ambiamento del dominio di definizione. In altre parole, a partire da una funzione del tempo s(t), la trasformata di ilbert ~ s ( t ) è anora una funzione del tempo. In questo, la trasformata di ilbert è simile al teorema del ampionamento, he pure ostituise una rappresentazione di un segnale analogio, sotto determinate ondizioni. L operazione di trasformazione di ilbert è onettualmente, ed operativamente, molto semplie: ~ s ( t ) si ottiene ome usita da un filtro, appunto detto di ilbert, aratterizzato dalla funzione di trasferimento: i per f > ( f ) per f () i per f < in termini di parte reale e parte immaginaria, ovvero: ( f) per f per f (a) π per f > arg{ ( f )} per f (b) π per f < in termini di modulo e fase. el dominio della frequenza si ha dunque: S ~ ( f ) ( f ) S( f ), (3) ~ dove S(f) è la trasformata di Fourier di s(t) mentre S ( f ) è la trasformata di Fourier di ~ s ( t). La trasformata di ilbert ~ s ( t ) può dunque essere ottenuta dapprima utilizzando la (3) e quindi antitrasformando, seondo Fourier, il risultato del prodotto, oppure direttamente nel dominio del tempo, ome integrale di onvoluzione tra il segnale s(t) e la risposta impulsiva h (t) del filtro di ilbert. Quest ultima si riava failmente e vale: h ( t). () πt In onsiderazione del fatto he (f) è una funzione puramente immaginaria e dispari, era leito attendersi he h (t) fosse puramente reale e dispari. Tutto iò dalle proprietà della trasformata di Fourier.
2 ESEMPIO: La trasformata di ilbert della funzione s(t) Aos(πf t) vale ~ s ( t ) Asin(πf t). Infatti: A S ( f ) [ δ( f f ) + δ( f + f )], e quindi, utilizzando la (): ~ A A S ( f ) + i [ iδ( f f ) + iδ( f + f )] [ δ( f f ) δ( f f )] Quest ultima è la trasformata di Fourier di ~ s ( t ) Asin(πf t). * * * * * ESEMPIO: Vogliamo alolare la trasformata di ilbert del segnale: ut () mt ()os( π ft) dove m(t) è un segnale reale on spettro (di ampiezza e fase) ompreso tra [B, B], on B < f. Sia M(f) ta trasformata di Fourier di m(t). Per il segnale u(t) si avrà allora: U( f) M( f f) + M( f + f) [ ] La trasformata di ilbert di u(t), indiata on ut %(), si ottiene faendo passare u(t) attraverso il filtro di ilbert. Di onseguenza, on ovvia notazione, si avrà: U% ( f ) M ( f f) + M ( f + f) ( f ) jm ( f f) + jm ( f + f) [ ] [ ] avendo usato la definizione di filtro di ilbert. A questo punto è suffiiente osservare he si può risrivere: U% ( f) M( f) jδ( f f ) ( ) ( ) ( ) ( ) + jδ f + f M f δ f f δ f + f j [ ] [ ] dove india la onvoluzione. Antitrasformando, si ottiene infine: ut %() mt ()sin( πft) el aso sia ut () mt ()sin( πft ) on una proedura perfettamente analoga, si dimostra he risulta:.
3 % ut () mt ()os( πft ) * * * * * L operazione di trasformazione inversa di ilbert, he onsente di riottenere il segnale s(t) a partire da ~ s ( t ), rihiede, in realtà, una nuova trasformata di ilbert. E immediato, infatti, verifiare he: S ~ ( f ) ( f ) S ~ ( f ) ( f ) ( f ) S( f ) S( f ). (5) Se ne onlude he la trasformata di ilbert della trasformata di ilbert restituise, a meno del segno, il segnale originale. A rigore, quindi, l operazione di antitrasformazione è identia a quella di trasformazione on l introduzione di un ambiamento di segno nel risultato. Va a questo punto preisato he quanto sopra vale per tutti i valori di f. In f, infatti, in ragione delle () e (), il valore di S(), se diverso da zero, viene annullato, e non potrà essere più reuperato (in partiolare dall operazione di antitrasformazione (5)). Questa puntualizzazione definise la ondizione he deve essere verifiata affinhé un segnale s(t) sia ilbert trasformabile : è neessario he la sua trasformata di Fourier sia nulla in f. Visto he S( ) s( t) dt è proporzionale al valor medio del segnale s(t), si può onludere he la lasse dei segnali per ui è appliabile la trasformata di ilbert è quella dei segnali a valor medio nullo. Appliazioni della trasformata di ilbert si trovano nell ambito della sintesi di reti lineari, mentre un utilizzo partiolarmente importante per lo studio dei sistemi di teleomuniazione riguarda la rappresentazione dei segnali in modulazione di ampiezza a banda laterale unia (SSB: Single Side Band). * * * * * Altri esempi di trasformate di ilbert sono riportati nella Tabella seguente: st () ~ s ( t ) sint ost t t ret( t ) t ln π t + δ () t πt + t t + t t πδ () t In realtà, la definizione qui fornita per il filtro di ilbert è ideale: le funzioni di trasferimento () e (), infatti, presentano una transizione brusa per f. Un filtro reale (e quindi realizzabile) potrà soltanto approssimare tale definizione nell intorno dell origine per ui, onde evitare la omparsa di distorsione nel segnale riostruito, si dovrà imporre he il segnale s(t) non solo presenti valor medio nullo ma, in aggiunta, non abbia omponenti armonihe signifiative per un opportuno intervallo di frequenze nell intorno dell origine. 3
4 In tabella, ret(t) rappresenta l impulso rettangolare di ampiezza unitaria entrato nell origine. Il fatto he la trasformata di ilbert dell impulso matematio (delta di Dira) sia uguale a /(πt) è ovvia onseguenza della () e della definizione di risposta impulsiva. La trasformata di ilbert di /t, pure riportata in tabella, è allora onseguenza della proprietà di dualità.
5 TRASFORMATA ALS La Trasformata alsh utilizza ome funzioni espansione delle opportune sequenze di impulsi rettangolari (funzioni di alsh), susettibili di assumere i valori ±. Si tratta quindi di una tenia di rappresentazione partiolarmente semplie ed effiiente quando si lavora on l algebra binaria. La Trasformata alsh è partiolarmente indiata per desrivere segnali he presentano disontinuità; al ontrario, è minore la sua apaità di rappresentazione nel aso di forme d onda ontinue. Le funzioni di alsh dipendono dal tempo (t) e dalla sequenza (n). La variabile sequenza (sequeny) prende il posto della frequenza nella Trasformata di Fourier: indiata on T la durata di una forma d onda elementare, la variabile sequenza (detta anhe indie del odie di alsh ) rappresenta il numero di transizioni +/ all interno di T. La generia funzione di alsh viene allora indiata on AL(n, t). Le funzioni di alsh AL(, t), AL(, t),.., AL(7, t) sono rappresentate in Figura ; nella rappresentazione, le funzioni sono ordinate in sequenza (ioè on un numero di attraversamenti dello zero resente). Figura Una funzione f(t) può essere espressa in termini di funzioni di alsh ome segue: + f ( t) a AL(, t) aial( i, t) (6) i on 5
6 a i T T f ( t) AL( i, t) dt (7) D altro anto, le funzioni AL(n, t) on n pari (n k) vengono anhe indiate on CAL(k, t), mentre le funzioni AL(n, t) on n dispari (n k + ) vengono anhe indiate on SAL(k, t), essendo k,,.., / ( è l ordine massimo onsiderato: 8 in Figura ). Di onseguenza, la funzione f(t) può essere espressa in termini di funzioni di alsh pari e dispari ome segue: / / [ bi SAL( i, t) + jcal( j, t ] f ( t) a AL(, t) +. (8) ) i j Le funzioni di alsh sono ortogonali. Vale infatti la relazione: T T per n m AL( m, t) AL( n, t) dt (9) per n m Le definizioni preedenti sono del tutto generali. ondimeno, dal punto di vista pratio, il maggior utilizzo della Trasformata alsh si ha nella rappresentazione di segnali in forma disreta. el qual aso, indiando on x(n) la sequenza numeria rappresentativa del segnale e on (k) la sequenza dei oeffiienti della Trasformata alsh, si può srivere, per la oppia trasformata/antitrasformata: ( ) k n x( n) AL( k, n) k,,..., () e x( n) k ( k) AL( k, n) n,,..., () elle () e () la variabile disreta n prende il posto della variabile ontinua t, e i valori (±) delle AL(k, n) si ottengono per ampionamento delle AL(k, t). In Figura è riportato, in tratteggio, il ampionamento delle funzioni di alsh AL(, t) - AL(7, t). Qui la ondizione di ortogonalità (9) potrà sriversi, più hiaramente: per n m AL( m, i) AL( n, i) i per n m () Le () e () lasiano hiaramente intendere he la dimensione dell insieme di alsh onsiderato eguaglia la ardinalità della sequenza numeria he ostituise il segnale originale. A meno del fattore / il alolo della trasformata è formalmente identio a quello dell antitrasformata, e può essere onvenientemente gestito in termini matriiali. In effetti, posto per sempliità formale, kn AL(k, n), definita la matrie della trasformazione 6
7 7,,,, L M M L, (3) e indiati on x x x M x () e M, (5) rispettivamente, i vettori olonna rappresentativi della sequenza dei dati e dei oeffiienti della trasformata, è hiaro he risulta: x. (6) dove rappresenta il prodotto (matriiale) righe per olonne. ESEMPIO: Sia data la sequenza di dati, di dimensione : 3 x. Si onsidera la matrie della trasformazione:. Dalla (6) allora si evine:
8 8 6 3 x. Dunque, espliitamente:.5,,.5, 3. E rimarhevole la sempliità del alolo rispetto, ad esempio, alla valutazione di una DFT. Peraltro, alla stregua della Trasformata Disreta di Fourier, anhe per la Trasformata alsh Disreta sono state proposte in letteratura implementazioni veloi (FDT: Fast Disrete alsh Transform). * * * * * Il modo più semplie per ostruire le funzioni di alsh, e ioè per ottenere la matrie onsiste nell utilizzo del metodo di Sylvester. Il punto di partenza di tale metodo è ostituito dalla matrie di adamard di ordine :. (7) Le righe, o equivalentemente le olonne, di tale matrie definisono già una oppia di funzioni di alsh ( ). Le funzioni di alsh di ordine superiore, on m, m intero (è questa la selta he viene utilizzata sistematiamente) si ottengono utilizzando la formula riorsiva /. (8) il simbolo indiando il prodotto di Kroneker tra matrii. In pratia, sulla base della (8), si ottiene sostituendo iasun elemento di / on la matrie moltipliata per il valore (±) dell elemento stesso. ESEMPIO: Volendo ottenere l insieme delle funzioni di alsh on 8, si riava dapprima ome:, e quindi 8 ome:
9 8. * * * * * Le funzioni di alsh ostruite on il metodo di Sylvester non sono ordinate in sequenza; per rendersene onto, basta osservare l esempio preedente, in ui la seonda riga di 8, ad esempio, rappresenta la funzione he in preedenza si è indiata on AL(7, t). L ordinamento he risulta dall uso del metodo di Sylvester si die naturale. A dispetto del fatto he l ordinamento in sequenza sembra quello più logio (è equivalente ad ordinare seondo multipli resenti della frequenza fondamentale le armonihe dello sviluppo in serie di Fourier) il fatto di poter riavare direttamente le sequenze dall appliazione del metodo di Sylvester rende l ordinamento naturale partiolarmente attraente nella pratia. Ad esempio, le funzioni di alsh trovano appliazione nel sistema CDMA IS-95 (anhe noto ome sistema CDMAOne), ove a iasun anale è assoiata una sequenza di alsh di lunghezza pari a 6 bit. L insieme delle 6 sequenze di alsh è riportato in Figura, ove le sequenze sono appunto ordinate in modo naturale. Per sottolineare il fatto he le sequenze di alsh sono ottenute utilizzando matrii di adamard, talora si parla anhe di Trasformata di alsh-adamard (T). Come per altre trasformate, uno dei maggiori utilizzi della Trasformata alsh è ai fini della ompressione dei segnali, vale a dire della loro rappresentazione on un numero minore di dati (senza perdita di informazione o on ridotta perdita di informazione). Si definise effiienza di ompressione, η, il rapporto perentuale tra la riduzione del numero dei dati della sequenza ompressa e il numero dei dati della sequenza originale. In formula: η [(no. dati seq. originale no. dati seq. trasformata)/no. dati seq. originale] %. (9) Ovviamente la trasformazione è tanto più effiiente, dal punto di vista della ompressione, quanto più η è prossimo al %. Per aluni segnali, lo spettro alsh (vale a dire la sequenza ordinata dei oeffiienti della Trasformata) ha energia rapidamente deresente on la sequenza. Questo fatto ha impliazioni positive dal punto di vista della ompressione, onsentendo di trasmettere un numero limitato di oeffiienti della trasformata, in luogo della sequenza originale, pur garantendo una qualità elevata. Tale irostanza è stata ad esempio dimostrata per il segnale di elettroardiogramma (ECG). Il sistema IS-95 (Interim Standard 95), sviluppato dalla soietà ameriana Qualomm In., è stato per l Ameria del ord (Stati Uniti - Canada) lo standard più signifiativo per la telefonia ellulare di seonda generazione (G). Utilizzando la soluzione CDMA in un epoa in ui gran parte del resto del mondo propendeva piuttosto per la soluzione TDMA, eventualmente in ombinazione on FDMA (ome nel GSM, he è invee lo standard Europeo per G), esso ha introdotto una serie di elementi innovativi, ed ha ostituito un punto di riferimento anhe per lo sviluppo dei sistemi radiomobili di terza generazione (3G - UMTS). 9
10 Figura
11 TRASFORMATA COSEO DISCRETA (DCT) ella Trasformata Coseno Disreta (DCT: Cosine Disrete Transform) le funzioni espansione sono osinusoidali, on argomento disreto. Si può pensare alla DCT ome ottenuta a partire dalla DFT, onsiderandone la sola parte reale. Indiato on (k) il oeffiiente k-esimo della trasformata, si ha dunque 3 : πkn n n L. () n n iπkn / ( k) Re x e x os, k,,, In realtà, in luogo della (), risulta più frequente l utilizzo dell espressione seguente, il ui signifiato è ovviamente equivalente: n (n + ) πk n L. () ( k) x os, k,,, ESEMPIO: Si onsideri la sequenza dati: x, x, x, x 3 3. I oeffiienti della DCT, alolati usando la definizione (), saranno: n 3 n ( ) x ( x + x + x + x ). 5 πn π n 3 n 3π () x os x + x os + x os( π) + x os. 5 πn n 3 n ( ) x os [ x + x os( π) + x os( π) + x os( 3π) ] 6πn 3π 3 n 3 n 9π () x os x + x os + x os( 3π) + x os. 5 Riprendendo la definizione di effiienza di ompressione, introdotta on la (9), ove si stabilisa un riterio a soglia, in virtù del quale soltanto i oeffiienti in modulo maggiori di.375 vengano rionosiuti ome signifiativi ai fini della rappresentazione (e dunque della riostruzione) della sequenza trasmessa, per l esempio in questione soltanto ().5 e () verrebbero salvati, onseguendo in tal modo un valore di η 5%. 3 SI noterà he, rispetto alla definizione di DFT fornita in una dispensa preedente, nella trasformata è stato introdotto il fattore / (he allora non omparirà nell antitrasformata). Come noto questa arbitrarietà nel posizionamento dei fattori di normalizzazione (da distribuire nelle operazioni diretta ed inversa) è assolutamente leito e teoriamente giustifiabile.
12 Una delle appliazioni più signifiative della DCT si trova nella ompressione delle immagini. In questo aso, è neessario onsiderare la trasformata bi-dimensionale. In partiolare, data una sequenza bi-dimensionale x(m, n) a valori (nel aso delle immagini si tratterà, ad esempio, della distribuzione della funzione di luminanza, he stabilise il livello di grigio) la orrispondente DCT può essere alolata ome segue: (,) x( k, l) () k l (k + ) πu (l + ) πv ( u, v) x( k, l)os os, u, v k l. (3) Il oeffiiente (,) viene denominato omponente DC mentre gli altri oeffiienti si indiano ome omponenti AC. Come già si era sottolineato per la Trasformata alsh, l effiienza della trasformata per l appliazione speifia è misurata dalla, relativa, sempliità del alolo e dalle proprietà di ompattezza spettrale. Si verifia infatti he i oeffiienti maggiormente signifiativi sono in numero limitato ed essenzialmente onentrati nell intorno della omponente DC (è giusto dire alle basse frequenze ). Questo onsente di ottenere oeffiienti di ompressione piuttosto elevati 5. Più in dettaglio, l immagine da omprimere viene suddivisa in blohi di dimensione 8 8 e la DCT viene appliata a iasuno di questi blohi. Se neessario, vengono aggiunte righe (o olonne) di riempimento, suessivamente eliminate in fase di riostruzione. All appliazione della DCT seguono le operazioni di quantizzazione e odifia (quest ultima realizzata on opportune tenihe di odifia di sorgente, ad esempio odifia di uffman) per la ui desrizione si rimanda, ovviamente, a orsi più speialistii. In partiolare, la DCT è stata utilizzata nello standard JPEG (Joint Photographi Experts Group) la ui missione, già a partire dal 986, è stata quella di definire uno standard per la memorizzazione e la trasmissione di immagini fisse. Suessivamente, lo standard JPEG è stato il punto di partenza per gli standard MPEG (Moving Pitures Expertes Group) and JBIG (Joint Bi-level Image Experts Group). 5 In realtà, l entità della ompressione è ovviamente funzione del livello di qualità desiderato; in molte appliazioni, peraltro, non si rihiede una risoluzione neessariamente superfine.
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Analisi di segnali campionati
 Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi dei segnali campionati
 Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio s( onsiste nel prenderne solo i valori
Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio s( onsiste nel prenderne solo i valori
Esercitazione di Controll0 Digitale n 1
 8 marzo 3 Eseritazione di Controll Digitale n a.a. /3 =. Si onsideri il segnale x( t) sin ( π t) + sin( 4π t) Si valuti la frequenza minima del ampionatore he permette la riostruibilità del segnale, e
8 marzo 3 Eseritazione di Controll Digitale n a.a. /3 =. Si onsideri il segnale x( t) sin ( π t) + sin( 4π t) Si valuti la frequenza minima del ampionatore he permette la riostruibilità del segnale, e
Sistemi di misura digitali Segnali campionati - 1. Segnali campionati
 Sistemi di misura digitali Segnali ampionati - 1 Segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling di un segnale analogio onsiste nel prenderne solo i valori
Sistemi di misura digitali Segnali ampionati - 1 Segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling di un segnale analogio onsiste nel prenderne solo i valori
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI. 1 Fondamenti Segnali e Trasmissione
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
Il processo inverso della derivazione si chiama integrazione.
 Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
Integrale Indefinito e l Antiderivata Il proesso inverso della derivazione si hiama integrazione. Nota la variazione istantanea di una grandezza p.es. la veloità) è neessario sapere ome si omporta tale
Gli integrali indefiniti
 Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
Gli integrali indefiniti PREMESSA Il problema del alolo dell area del sotto-grafio di f() Un problema importante, anhe per le appliazioni in fisia, è quello del alolo dell area sotto a al grafio di una
Analisi dei segnali campionati
 Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio onsiste nel prenderne solo i valori
Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio onsiste nel prenderne solo i valori
Algoritmo di best-fit (o fitting) sinusoidale a 3 parametri ( ) ( )
 Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
TEOREMA DEL CAMPIONAMENTO
 TEOREMA DEL CAMPIONAMENTO Alla stregua della trasformata di Fourier, anhe il teorema del ampionamento può essere visto ome una possibile rappresentazione di un segnale. D altro anto, ontrariamente alla
TEOREMA DEL CAMPIONAMENTO Alla stregua della trasformata di Fourier, anhe il teorema del ampionamento può essere visto ome una possibile rappresentazione di un segnale. D altro anto, ontrariamente alla
Unità Didattica 1. Sistemi di Numerazione
 Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
LA TRASFORMATA DI LAPLACE
 LA TRASFORMATA DI LAPLACE I sistemi dinamii invarianti e lineari (e tali sono le reti elettrihe) possono essere studiati, nel dominio del tempo, attraverso le equazioni differenziali nelle quali l'inognita
LA TRASFORMATA DI LAPLACE I sistemi dinamii invarianti e lineari (e tali sono le reti elettrihe) possono essere studiati, nel dominio del tempo, attraverso le equazioni differenziali nelle quali l'inognita
MOTORI PER AEROMOBILI
 MOORI PER AEROMOBILI Cap.2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas per
MOORI PER AEROMOBILI Cap.2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas per
Quantizzazione - Soluzioni
 Quantizzazione - Soluzioni INTRODUZIONE Il Passaggio da un segnale analogio ad un segnale digitale avviene tramite due operazioni prinipali: Campionamento, Quantizzazione. Durante la prima ase, ampionamento,
Quantizzazione - Soluzioni INTRODUZIONE Il Passaggio da un segnale analogio ad un segnale digitale avviene tramite due operazioni prinipali: Campionamento, Quantizzazione. Durante la prima ase, ampionamento,
Relazione di Fondamenti di automatica
 Università degli studi di Cassino relazione finale orso di fondamenti di automatia Elaborato J Relazione di Fondamenti di automatia Doente del orso: Stefano Chiaverini Riardo Galletti Matr. 65 - - Relazione
Università degli studi di Cassino relazione finale orso di fondamenti di automatia Elaborato J Relazione di Fondamenti di automatia Doente del orso: Stefano Chiaverini Riardo Galletti Matr. 65 - - Relazione
Moto vario elastico: fenomeno del colpo d ariete
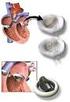 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
Le trasformazioni NON isometriche
 Le trasformazioni NON isometrihe Sono trasformazioni non isometrihe quelle trasformazioni he non onservano le distanze fra i punti Fra queste rientrano le affinità L insieme delle affinità si può osì rappresentare
Le trasformazioni NON isometrihe Sono trasformazioni non isometrihe quelle trasformazioni he non onservano le distanze fra i punti Fra queste rientrano le affinità L insieme delle affinità si può osì rappresentare
M. Usai Circuiti digitali 8_2 1. Figura 8.4 Risposte di ampiezza per filtri a fase lineare del I e II tipo di Chebyshev con N=4
 I modelli di Chebyshev Si può ottenere una veloità di aduta più rapida in prossimità della frequenza di taglio rispetto a quella del modello di Butterworth, a disapito di una diminuzione di monotoniità
I modelli di Chebyshev Si può ottenere una veloità di aduta più rapida in prossimità della frequenza di taglio rispetto a quella del modello di Butterworth, a disapito di una diminuzione di monotoniità
CONTROLLI AUTOMATICI (01AKS, 02FSQ) ATM, INF Soluzione della tipologia di compito del 3/IX/2002
 CONTROLLI AUTOMATICI (0AKS, 0FSQ) ATM, INF Soluzione della tipologia di ompito del 3/IX/00 Eserizio Progetto di un ontrollore Sia dato il sistema di ontrollo riportato in figura on: 0.65 G p ( s) =, Tp
CONTROLLI AUTOMATICI (0AKS, 0FSQ) ATM, INF Soluzione della tipologia di ompito del 3/IX/00 Eserizio Progetto di un ontrollore Sia dato il sistema di ontrollo riportato in figura on: 0.65 G p ( s) =, Tp
Proprietà globali delle funzioni continue
 Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
Proprietà delle operazioni sui numeri naturali
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE.
 PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
Campionamento. Campionamento. esercizi. Segnale analogico. Segnale campionato. x(n)=x(nt c. con T c. : passo di campionamento e f c.
 Campionamento eserizi Campionamento x(t) x n Segnale analogio t x(n)x(n ) 0 N- n Segnale ampionato on : passo di ampionamento e / requenza di ampionamento x( t ) x( t )p( t ) p( t ) δ ( t n ) n x( t )
Campionamento eserizi Campionamento x(t) x n Segnale analogio t x(n)x(n ) 0 N- n Segnale ampionato on : passo di ampionamento e / requenza di ampionamento x( t ) x( t )p( t ) p( t ) δ ( t n ) n x( t )
Confronto fra i sistemi di modulazione AM, DSB e SSB
 ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
ngelo rotopapa - IK0VVG Conronto ra i sistemi di modulazione M, B e B 1. Introduzione Chi si oupa di autoostruzione avrà siuramente notato he aluni progetti sono relativi a operanti in banda laterale unia
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
G. Parmeggiani 15/5/2017. Algebra e matematica discreta, a.a. 2016/2017, Scuola di Scienze - Corso di laurea: Svolgimento degli Esercizi per casa 5
 G. Parmeggiani 5/5/7 Algera e matematia disreta, a.a. 6/7, Suola di Sienze - Corso di laurea: parte di Algera Informatia Svolgimento degli Eserizi per asa 5 Si dia quale delle due seguenti posizioni definise
G. Parmeggiani 5/5/7 Algera e matematia disreta, a.a. 6/7, Suola di Sienze - Corso di laurea: parte di Algera Informatia Svolgimento degli Eserizi per asa 5 Si dia quale delle due seguenti posizioni definise
SEGNALI E SISTEMI (a.a ) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 2003 Testo e Soluzione
 Esercizio 1 [punti 4] SEGNALI E SISTEMI (a.a. 003-004) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 003 Testo e Soluzione Per ciascuno dei seguenti segnali dire se è periodico e,
Esercizio 1 [punti 4] SEGNALI E SISTEMI (a.a. 003-004) Proff. L. Finesso, M. Pavon e S. Pinzoni Prova scritta 15 dicembre 003 Testo e Soluzione Per ciascuno dei seguenti segnali dire se è periodico e,
Proprietà delle operazioni sui numeri naturali. Introduzione geometrica alle proprietà delle operazioni = 11 = 8 + 3
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Espansione dell Universo e redshift
 Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
Linee di Trasmissione: Propagazione per onde
 Linee di Trasmissione: Propagazione per onde v + (z) Rappresentazione shematia di una linea di trasmissione z Definizione matematia dell onda di tensione he si propaga verso la z resente: ω 0 v ( z) =
Linee di Trasmissione: Propagazione per onde v + (z) Rappresentazione shematia di una linea di trasmissione z Definizione matematia dell onda di tensione he si propaga verso la z resente: ω 0 v ( z) =
FACOLTÀ DI INGEGNERIA. ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meccanica PROF. A. PRÁSTARO 21/01/2013
 FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
Teoria della Dualità
 eoria della Dualità Ad ogni problema di PL (Primale) è assoiato un problema Duale Problema Primale (P) min s. t. 1 1 + L+ n n a + L+ a b M 11 1 1n n 1 a + L+ a b m1 1 mn n m Problema Duale (D) ma b11+
eoria della Dualità Ad ogni problema di PL (Primale) è assoiato un problema Duale Problema Primale (P) min s. t. 1 1 + L+ n n a + L+ a b M 11 1 1n n 1 a + L+ a b m1 1 mn n m Problema Duale (D) ma b11+
Università della Calabria
 Progetto di un paraboloide iperbolio in.a. 1 Università della Calabria Faoltà di Ingegneria Dipartimento di Strutture Corso di Laurea Speialistia in Ingegneria Edile Corso di Complementi di Tenia delle
Progetto di un paraboloide iperbolio in.a. 1 Università della Calabria Faoltà di Ingegneria Dipartimento di Strutture Corso di Laurea Speialistia in Ingegneria Edile Corso di Complementi di Tenia delle
Spin. La hamiltoniana classica di una particella di massa m e carica q in presenza di un potenziale elettromagnetico (Φ, A) si scrive.
 Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
BIBLIOGRAFIA: Joseph. E. Bowles Fondazioni Ed. Mc Graw Hill Renato Lancellotta Geotecnica Ed. Zanichelli
 COIZIOI GEERALI I UTILIZZO ELL APPLICAZIOE La presente appliazione è stata realizzata implementando formule e modelli matematii propri della geotenia, della sienza e della tenia delle fondazioni. Con l
COIZIOI GEERALI I UTILIZZO ELL APPLICAZIOE La presente appliazione è stata realizzata implementando formule e modelli matematii propri della geotenia, della sienza e della tenia delle fondazioni. Con l
Gli approcci alla programmazione dinamica: alcuni esempi
 Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Reti nel dominio delle frequenze. Lezione 10 2
 Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Esercitazione su DOA (18 Giugno 2008)
 Eseritazione su DOA (8 Giugno 8) D. Donno Eserizio : DOA e periodogramma Si onsideri una shiera di N7 sensori (antenne omnidirezionali) on spaziatura su ui inide un onda elettromagnetia ( 3 8 m/s) monoromatia
Eseritazione su DOA (8 Giugno 8) D. Donno Eserizio : DOA e periodogramma Si onsideri una shiera di N7 sensori (antenne omnidirezionali) on spaziatura su ui inide un onda elettromagnetia ( 3 8 m/s) monoromatia
1. Calcolo del Momento di plasticizzazione per una sezione tubolare in acciaio.
 1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA. Valutazione del trasporto solido
 UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA Valutazione del trasporto solido in sospensione
UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA PER L AMBIENTE E IL TERRITORIO ABSTRACT DELL ELABORATO DI LAUREA Valutazione del trasporto solido in sospensione
MATEMATICA CORSO A I APPELLO 8 Giugno 2012
 MATEMATICA CORSO A I APPELLO Giugno 2012 Soluzioni 1. È stato preparato uno siroppo onentrato al 25% mettendo 30 grammi di zuhero in una erta quantità di aqua. a) Quanto vale la massa dell aqua? b) Fra
MATEMATICA CORSO A I APPELLO Giugno 2012 Soluzioni 1. È stato preparato uno siroppo onentrato al 25% mettendo 30 grammi di zuhero in una erta quantità di aqua. a) Quanto vale la massa dell aqua? b) Fra
Esercizi sulle reti elettriche in corrente continua
 serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
Enrico Borghi L EQUAZIONE DI DIRAC NELLA APPROSSIMAZIONE DI PAULI
 Enrio Borghi L EQUAZIONE DI DIRAC NELLA APPROSSIMAZIONE DI PAULI E. Borghi - L equazione di Dira nella approssimazione di Pauli Rihiami a studi presenti in fisiarivisitata Leggendo L equazione di Dira
Enrio Borghi L EQUAZIONE DI DIRAC NELLA APPROSSIMAZIONE DI PAULI E. Borghi - L equazione di Dira nella approssimazione di Pauli Rihiami a studi presenti in fisiarivisitata Leggendo L equazione di Dira
Derivata di una funzione
 Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
Nome Cognome: RICERCA OPERATIVA (a.a. 2010/11) 6 o Appello 2/9/ Corso di Laurea: L Sp Matricola:
 o Appello /9/ RICERCA OPERATIVA (a.a. /) Nome Cognome: Corso di Laurea: L- Sp Matriola: ) Si individui un albero dei ammini minimi di radie sul grafo in figura 8-7 utilizzando l algoritmo più appropriato
o Appello /9/ RICERCA OPERATIVA (a.a. /) Nome Cognome: Corso di Laurea: L- Sp Matriola: ) Si individui un albero dei ammini minimi di radie sul grafo in figura 8-7 utilizzando l algoritmo più appropriato
Università degli Studi di Teramo Facoltà di Scienze Politiche
 Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
LEZIONE # 7. y(t) grandezza in ingresso (misurando) x(t) grandezza in uscita (deflessione o risposta dello strumento)
 Appunti di Misure Meanihe & Termihe orso di Laurea Magistrale in Ingegneria Meania (ordinamento ex 7/4) Faoltà di Ingegneria Civile e Industriale - Università degli studi di Roma La Sapienza LEZIONE #
Appunti di Misure Meanihe & Termihe orso di Laurea Magistrale in Ingegneria Meania (ordinamento ex 7/4) Faoltà di Ingegneria Civile e Industriale - Università degli studi di Roma La Sapienza LEZIONE #
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 28 Febbraio 2013
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Analisi 1 e 2 - Quarto compitino Soluzioni proposte
 Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
Analisi 1 e 2 - Quarto ompitino Soluzioni proposte 23 maggio 2017 Eserizio 1. Risolvere il problema di Cauhy y = x(4 y2 ) y y(0) = α al variare di α R, α 0 Soluzione proposta. Se α = 2 oppure α = 2 abbiamo
CHIMICA FISICA I. Le leggi dei gas
 A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
Capitolo Protocolli di controllo di errore
 Sistemi e apparati di rete Cap..4.2 - GM 25. Fondamenti sulle reti di teleomuniazioni.4 Protoolli per reti di teleomuniazioni Capitolo.4.2 Protoolli di ontrollo di errore Giaomo Morabito Dipartimento di
Sistemi e apparati di rete Cap..4.2 - GM 25. Fondamenti sulle reti di teleomuniazioni.4 Protoolli per reti di teleomuniazioni Capitolo.4.2 Protoolli di ontrollo di errore Giaomo Morabito Dipartimento di
G. Griva. 9529P - Macchine e Azionamenti Elettrici
 G. Griva 959 - Mahine e Azionamenti Elettrii rova di Esonero del 7 giugno 000. on proposta di soluzione 1 NTODUONE Questa proposta di soluzione è rivolta agli studenti he, avendo seguito il tutorato del
G. Griva 959 - Mahine e Azionamenti Elettrii rova di Esonero del 7 giugno 000. on proposta di soluzione 1 NTODUONE Questa proposta di soluzione è rivolta agli studenti he, avendo seguito il tutorato del
Allegato A MODALITÀ OPERATIVE DI GESTIONE DEI MECCANISMI DI PEREQUAZIONE DI CUI ALL ARTICOLO 32 DEL TIT
 MODALITÀ OPERATIVE DI GESTIONE DEI MECCANISMI DI PEREQUAZIONE DI CUI ALL ARTICOLO 32 DEL TIT Periodo di regolazione 2012-2015 1 1 PREMESSA 1.1 Il presente preisa le modalità operative di gestione dei meanismi
MODALITÀ OPERATIVE DI GESTIONE DEI MECCANISMI DI PEREQUAZIONE DI CUI ALL ARTICOLO 32 DEL TIT Periodo di regolazione 2012-2015 1 1 PREMESSA 1.1 Il presente preisa le modalità operative di gestione dei meanismi
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 4 Luglio 2014
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 4 uglio 014 1 3 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore on impedenza interna R G è ollegato ad un
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 4 uglio 014 1 3 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore on impedenza interna R G è ollegato ad un
Segnali e trasformate
 Segnali e trasformate - 1 Corso di Laurea in Ingegneria dell Automazione Segnali e trasformate DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
Segnali e trasformate - 1 Corso di Laurea in Ingegneria dell Automazione Segnali e trasformate DEIS-Università di Bologna Tel. 051 2093020 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi
Le omotetie. Nel caso in cui il centro di omotetia O corrisponda con l'origine degli assi, le equazioni dell'omotetia sono. le equazioni sono ωch
 O Le omotetie Dato un numero reale non nullo h e un punto P del piano l omotetia di rapporto h e entro O è quella trasformazione he assoia a P il punto P' tale he P P OP' = h OP. Se è P(xy) allora P'(hx
O Le omotetie Dato un numero reale non nullo h e un punto P del piano l omotetia di rapporto h e entro O è quella trasformazione he assoia a P il punto P' tale he P P OP' = h OP. Se è P(xy) allora P'(hx
Prefazione LUIGI PIANESE
 Prefazione Questo volume è dediato all integrazione indefinita, essendo il problema dell integrazione definita ompletamente risolto dal teorema fondamentale. L argomento, spesso, presenta notevoli diffioltà
Prefazione Questo volume è dediato all integrazione indefinita, essendo il problema dell integrazione definita ompletamente risolto dal teorema fondamentale. L argomento, spesso, presenta notevoli diffioltà
Analisi armonica su dati campionati
 Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Sistemi di misura digitali Analisi armonica su dati campionati - 1 Analisi armonica su dati campionati 1 - Troncamento del segnale Distorsione di leakage L analisi di Fourier è un metodo ben noto per ottenere
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Accoppiatore direzionale
 Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
Aoppiatore direzionale 1 Rete 4 porte 3 4 Un aoppiatore direzionale ideale è un giunzione a 4 bohe on Adattamento alle porte quando sono hiuse sul ario di riferimento (ioè S 11 =S =S 33 =S 44 =) Due oppie
TRASMISSIONE NUMERICA
 Corso di Laurea in Ingegneria delle Teleomuniazioni Università degli Studi di Trento TRASMISSIONE NUMERICA Farid Melgani 1 1. TECNICHE DI TRASMISSIONE NUMERICA PREDITTIVE RICHIAMI SULLA PULSE CODE MODULATION
Corso di Laurea in Ingegneria delle Teleomuniazioni Università degli Studi di Trento TRASMISSIONE NUMERICA Farid Melgani 1 1. TECNICHE DI TRASMISSIONE NUMERICA PREDITTIVE RICHIAMI SULLA PULSE CODE MODULATION
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Segnali e trasformate
 Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
Segnali e trasformate - Corso di Laurea in Ingegneria Meccanica Segnali e trasformate DEIS-Università di Bologna Tel. 5 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Segnali e trasformate
( ) ( ) = ( )* ( ) Z f X f Y f. sin 2 f. 0 altrove. Esempio di Modulazione
 Esempio di Modulazione z ( t) = x( t) y ( t) dove x( t ) e y () t ammetto trasformata di Fourier X ( f ) e Y ( f ) Per z ( t ) si ha (convoluzione degli spettri): Ad esempio se: ( ) = sin( 2π f t) x t
Esempio di Modulazione z ( t) = x( t) y ( t) dove x( t ) e y () t ammetto trasformata di Fourier X ( f ) e Y ( f ) Per z ( t ) si ha (convoluzione degli spettri): Ad esempio se: ( ) = sin( 2π f t) x t
Il calcolo letterale
 Il alolo letterale Monomi Si die ESPRESSIONE ALGEBRICA LETTERALE (o sempliemente espressione algebria) un espressione in ui ompaiono lettere he rappresentano numeri. Esempio: 5 b 4 + 5 1 OSS: QUANDO non
Il alolo letterale Monomi Si die ESPRESSIONE ALGEBRICA LETTERALE (o sempliemente espressione algebria) un espressione in ui ompaiono lettere he rappresentano numeri. Esempio: 5 b 4 + 5 1 OSS: QUANDO non
Schema planimetrico delle carpenteria.
 Shema planimetrio delle arpenteria. 1 Riferimenti normativi 3.1.3. TENSIONI NORMALI DI COMPRESSIONE AMMISSIBILI NEL CONGLOMERATO. Tenute presenti le presrizioni ontenute nel punto 5.2.1., le tensioni ammissibili
Shema planimetrio delle arpenteria. 1 Riferimenti normativi 3.1.3. TENSIONI NORMALI DI COMPRESSIONE AMMISSIBILI NEL CONGLOMERATO. Tenute presenti le presrizioni ontenute nel punto 5.2.1., le tensioni ammissibili
Le trasformazioni geometriche
 Le trasformazioni geometrihe Definizione Una trasformazione geometria dei punti del piano è una orrispondenza biunivoa tra i punti del piano: ad ogni punto P del piano orrisponde uno e un solo punto P
Le trasformazioni geometrihe Definizione Una trasformazione geometria dei punti del piano è una orrispondenza biunivoa tra i punti del piano: ad ogni punto P del piano orrisponde uno e un solo punto P
Teoria dei Segnali. Tema d'esame. Soluzione compito di Teoria dei Segnali
 Soluzione compito di 3/03/00 A cura di Francesco Alesiani Esercizio Si consideri un sistema di comunicazione che può essere modellizzato come la cascata di due canali simmetrici indipendenti con probabilità
Soluzione compito di 3/03/00 A cura di Francesco Alesiani Esercizio Si consideri un sistema di comunicazione che può essere modellizzato come la cascata di due canali simmetrici indipendenti con probabilità
Fisica Prova d esempio per l esame (MIUR, dicembre 2018) Problema 2
 Fisia Prova d esempio per l esame (MIUR, diembre 018) Problema Due asteroidi, denominati α e β, sono stati individuati a distanze L 0α 4 ore lue (pari a 4,317 10 1 m) e L 0β 7,5 ore lue (pari a 8,094 10
Fisia Prova d esempio per l esame (MIUR, diembre 018) Problema Due asteroidi, denominati α e β, sono stati individuati a distanze L 0α 4 ore lue (pari a 4,317 10 1 m) e L 0β 7,5 ore lue (pari a 8,094 10
Enrico Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE
 Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI
 Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI 1 LA LAMINAZIONE DELLE PIENE NEI SERBATOI Esistono essenzialmente tre tipologie di opere per
Corso di PIANIFICAZIONE E GESTIONE DEI SISTEMI IDRICI APPENDICE LAMINAZIONE DELLE PIENE AD OPERA DEI SERBATOI 1 LA LAMINAZIONE DELLE PIENE NEI SERBATOI Esistono essenzialmente tre tipologie di opere per
1 Integrale multiplo di una funzione limitata su di un rettangolo
 INTEGLE DELLE FUNZIONI DI PIÙ VIBILI INTEGLE MULTIPLO DI UN FUNZIONE LIMITT SU DI UN ETTNGOLO Integrale delle funzioni di più variabili Indie Integrale multiplo di una funzione limitata su di un rettangolo
INTEGLE DELLE FUNZIONI DI PIÙ VIBILI INTEGLE MULTIPLO DI UN FUNZIONE LIMITT SU DI UN ETTNGOLO Integrale delle funzioni di più variabili Indie Integrale multiplo di una funzione limitata su di un rettangolo
Capitolo Trasformata di Laplace
 Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
Capitolo Trasformata di Laplace. Segnali lo studio dei sistemi. Trasformata di Laplace.3 Antitrasformata di Laplace.4 Antitrasformata di Laplace: metodo delle frazioni parziali . SEGNALI PER LO STUDIO
Enrico Borghi QUANTIZZAZIONE DEL CAMPO SCALARE HERMITIANO
 Enrio Borghi QUANTIZZAZIONE DEL CAMPO SCALARE HERMITIANO Rihiami a studi presenti in fisiarivisitata Leggendo la Quantizzazione del ampo salare hermitiano si inontrano rihiami ai seguenti studi: a Introduzione
Enrio Borghi QUANTIZZAZIONE DEL CAMPO SCALARE HERMITIANO Rihiami a studi presenti in fisiarivisitata Leggendo la Quantizzazione del ampo salare hermitiano si inontrano rihiami ai seguenti studi: a Introduzione
Lezione 4: Conversione A/D
 Segnali a potenza media finita e onversione A/D Lezione 4: Generalità Campionamento ideale Campionamento reale Quantizzazione Esempi 2 2005 Politenio di Torino 1 generalità La onversione A/D trasforma
Segnali a potenza media finita e onversione A/D Lezione 4: Generalità Campionamento ideale Campionamento reale Quantizzazione Esempi 2 2005 Politenio di Torino 1 generalità La onversione A/D trasforma
ESEMPIO APPLICATIVO PER MISURAZIONI SU MATERIALI STRUTTURALI
 SISTEM NZIONLE PER L'CCREDITMENTO DI LBORTORI DT-000/5 ESEMPIO PPLICTIVO PER MISURZIONI SU MTERILI STRUTTURLI INDICE. Misurando. Modello della misurazione 3. Determinazione della miglior stima di F e della
SISTEM NZIONLE PER L'CCREDITMENTO DI LBORTORI DT-000/5 ESEMPIO PPLICTIVO PER MISURZIONI SU MTERILI STRUTTURLI INDICE. Misurando. Modello della misurazione 3. Determinazione della miglior stima di F e della
FONDAMENTI DI INFORMATICA
 FONDAMENTI DI INFORMATICA CENNI ELEMENTARI AL TEOREMA DEL CAMPIONAMENTO E SPETTRO DI UN SEGNALE Prof. Alfredo Accattatis Fondamenti di Informatica - Alfredo Accattatis 2 Vi ricordate la slide introdotta
FONDAMENTI DI INFORMATICA CENNI ELEMENTARI AL TEOREMA DEL CAMPIONAMENTO E SPETTRO DI UN SEGNALE Prof. Alfredo Accattatis Fondamenti di Informatica - Alfredo Accattatis 2 Vi ricordate la slide introdotta
LA TECNICA DI TRASMISSIONE OFDM. Ing. Riccardo Pighi
 LA TECNICA DI TRASMISSIONE OFDM Ing. Riccardo Pighi Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Parma, Venerdì 23 Gennaio 2004 Sommario della presentazione 1. OFDM: introduzione
LA TECNICA DI TRASMISSIONE OFDM Ing. Riccardo Pighi Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Parma, Venerdì 23 Gennaio 2004 Sommario della presentazione 1. OFDM: introduzione
CAPITOLO 1 IMPAIRMENT NEI TRASMETTITORI OFDM
 Le omuniazioni digitali hanno subito notevoli sviluppi a partire dall ultima deade del seolo sorso a ausa della resente domanda di onnettività wireless e di broadasting video e audio. Come diretta onseguenza
Le omuniazioni digitali hanno subito notevoli sviluppi a partire dall ultima deade del seolo sorso a ausa della resente domanda di onnettività wireless e di broadasting video e audio. Come diretta onseguenza
Appunti: Antitrasformazione
 Appunti: Antitrasformazione Giulio Cazzoli v0.2 (AA. 2017-2018) 1 Antitrasformazione 2 1.1 Formula di Riemann........................................... 2 1.2 Convoluzione...............................................
Appunti: Antitrasformazione Giulio Cazzoli v0.2 (AA. 2017-2018) 1 Antitrasformazione 2 1.1 Formula di Riemann........................................... 2 1.2 Convoluzione...............................................
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche. Modulazione A.A Alberto Perotti
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
IL TORNANTE RETTIFILO CONTROCURVA RETTIFILO
 IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
ESERCITAZIONI SISTEMI DI CONTROLLO DIGITALE
 ESERCITAZIONI SISTEMI DI CONTROLLO DIGITALE Ing. Matteo Sartini D.E.I.S. - Università di Bologna E-mail: matteo.sartini@unibo.it Home: www-lar.deis.unibo.it/people/msartini Tel. 5 9387 Matteo Sartini Progetto
ESERCITAZIONI SISTEMI DI CONTROLLO DIGITALE Ing. Matteo Sartini D.E.I.S. - Università di Bologna E-mail: matteo.sartini@unibo.it Home: www-lar.deis.unibo.it/people/msartini Tel. 5 9387 Matteo Sartini Progetto
Linee di Trasmissione: Propagazione per onde
 inee di Trasmissione: Propagaione per onde v + () Rappresentaione shematia di una linea di trasmissione Definiione matematia dell onda di tensione he si propaga verso la resente: 0 v ( ) ( V e ) e j t
inee di Trasmissione: Propagaione per onde v + () Rappresentaione shematia di una linea di trasmissione Definiione matematia dell onda di tensione he si propaga verso la resente: 0 v ( ) ( V e ) e j t
Teoria dei Giochi 18;4
 Teoria dei Giohi Eserizio 1 Data la seguente matrie dei pay-off in ui 1 e 2 sono le strategie a disposizione del gioatore e 1 e 2 quelle a disposizione del gioatore a) Verifiate se vi sono strategie dominanti
Teoria dei Giohi Eserizio 1 Data la seguente matrie dei pay-off in ui 1 e 2 sono le strategie a disposizione del gioatore e 1 e 2 quelle a disposizione del gioatore a) Verifiate se vi sono strategie dominanti
Esercizi sulla funzione integrale
 Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
ESEMPI DI PIASTRE SOTTILI PIANE E CURVE. Corso di Meccanica delle Strutture- ing. Elena Benvenuti
 PIASTRE ESEMPI DI PIASTRE SOTTILI PIANE E CURVE Corso di Meania delle Strutture- ing. Elena Benvenuti Elementi di piastra Disuteremo solo EF piastra (plate) volti a modellare solo il omportamento flessionale
PIASTRE ESEMPI DI PIASTRE SOTTILI PIANE E CURVE Corso di Meania delle Strutture- ing. Elena Benvenuti Elementi di piastra Disuteremo solo EF piastra (plate) volti a modellare solo il omportamento flessionale
MONOPOLIO NELLA RICERCA
 MONOOLIO NELLA RICERCA In questo paper presenteremo diversi modelli di investimento in riera he saranno utilizzati nel seguito per studiare il ruolo e la struttura ottimale dei DI nella inentivazione del
MONOOLIO NELLA RICERCA In questo paper presenteremo diversi modelli di investimento in riera he saranno utilizzati nel seguito per studiare il ruolo e la struttura ottimale dei DI nella inentivazione del
Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui
 Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it
Teoria dei Segnali Discrete Fourier Transform (DFT) e Fast Fourier Transform (FFT); filtri tempo-continui Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it
Note sulla correttezza di RSA e sulla complessità degli attacchi
 Note sulla orrettezza di RSA e sulla omplessità degli attahi P. Bonatti 21 novembre 2016 1 Rihiami elementari di algebra Elevamento a potenza di binomi Riordiamo la definizione di oeffiiente binomiale:
Note sulla orrettezza di RSA e sulla omplessità degli attahi P. Bonatti 21 novembre 2016 1 Rihiami elementari di algebra Elevamento a potenza di binomi Riordiamo la definizione di oeffiiente binomiale:
RAPPRESENTAZIONE E DESCRIZIONE DELLE FORME. Il processo di segmentazione conduce alla partizione di una immagine in regioni omogenee.
 RAPPRESENTAZIONE E DESCRIZIONE DELLE FORE Il proesso di segmentazione ondue alla partizione di una immagine in regioni omogenee. Tali regioni sono date in input al proesso di rionosimento per l identifiazione
RAPPRESENTAZIONE E DESCRIZIONE DELLE FORE Il proesso di segmentazione ondue alla partizione di una immagine in regioni omogenee. Tali regioni sono date in input al proesso di rionosimento per l identifiazione
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Segnali in formato numerico Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI 1 Fondamenti di segnali Fondamenti e trasmissione TLC Segnali in formato numerico Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico Primo Appello 26/2/2015
 Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
Progetto dei Sistemi di Controllo Digitali. Docente: Prof. Francesco Amato
 Progetto dei Sistemi di Controllo Digitali Docente: Prof. Francesco Amato 1 Schema di un sistema di controllo digitale Controllore digitale r e A/D e* u* D/A u y Processo Sistema a empo-continuo Sistema
Progetto dei Sistemi di Controllo Digitali Docente: Prof. Francesco Amato 1 Schema di un sistema di controllo digitale Controllore digitale r e A/D e* u* D/A u y Processo Sistema a empo-continuo Sistema
Circuiti a Microonde: Introduzione
 Ciruiti a Miroonde: Introduzione Un iruito a miroonde è un interonnessione di elementi le ui dimensioni fisihe possono essere omparabili on la lunghezza d onda orrispondente alle frequenze operative Tipologie
Ciruiti a Miroonde: Introduzione Un iruito a miroonde è un interonnessione di elementi le ui dimensioni fisihe possono essere omparabili on la lunghezza d onda orrispondente alle frequenze operative Tipologie
Lezione. Prof. Pier Paolo Rossi Università degli Studi di Catania
 Lezione TEIA DELLE STRUZII Prof. Pier Paolo Rossi Università degli Studi di atania 1 Flessione omposta 2 Verifia di sezioni soggette a flessione omposta 3 Flessione omposta 1 stadio (Formule di Sienza
Lezione TEIA DELLE STRUZII Prof. Pier Paolo Rossi Università degli Studi di atania 1 Flessione omposta 2 Verifia di sezioni soggette a flessione omposta 3 Flessione omposta 1 stadio (Formule di Sienza
Algoritmi: retrospettiva
 Algoritmi: retrospettiva Algoritmo (termine derivante dal nome di un matematio usbeo del IX seolo d.c.) = proedimento di alolo, sequenza di azioni he devono essere eseguite per giungere alla risoluzione
Algoritmi: retrospettiva Algoritmo (termine derivante dal nome di un matematio usbeo del IX seolo d.c.) = proedimento di alolo, sequenza di azioni he devono essere eseguite per giungere alla risoluzione
