1. SIMMETRIA. 1.1 Operazioni ed elementi di simmetria puntuale
|
|
|
- Arturo Lelli
- 7 anni fa
- Visualizzazioni
Transcript
1 1. SIMMETRIA Molte proprietà molecolari sono determinate dalla simmetria delle molecole stesse, come del resto molte proprietà dei solidi sono determinate dalla simmetria del loro reticolo cristallino. Così, ad esempio, molecole centrosimmetriche non hanno un momento di dipolo elettrico permanente e solo molecole dissimmetriche sono otticamente attive. Per quanto riguarda i solidi cristallini, menzioniamo soltanto che fenomeni quali la piro- e la piezo-elettricità si riscontrano solo in reticoli cristallini non centrosimmetrici. Inoltre, importanti applicazioni dei concetti di simmetria si hanno nelle teorie del legame di valenza e degli orbitali molecolari, per determinare, ad esempio, quali orbitali atomici possano essere combinati per ottenere orbitali ibridi di prefissata geometria o orbitali molecolari. Lo studio della simmetria è poi di fondamentale importanza nella spettroscopia e nella cristallografia in genere. In questi appunti ci limiteremo ai principi fondamentali. 1.1 Operazioni ed elementi di simmetria puntuale Un operazione di simmetria è il movimento di un oggetto, tale che, dopo il movimento, ciascun punto dell oggetto coincide con un altro equivalente nella configurazione originale. Per configurazione intendiamo qui la disposizione dei punti dell oggetto e la loro orientazione nello spazio. In altre parole, se osserviamo la posizione e l orientazione di un corpo prima e dopo il movimento, quest ultimo è un operazione di simmetria se la posizione e l orientazione finale è indistinguibile da quella iniziale. Possiamo anche definire un operazione di simmetria dicendo che deve essere un movimento tale da portare il corpo in una configurazione equivalente, cioè sovrapponibile a quella originale. Un elemento di simmetria è un ente geometrico, quale una linea, un piano o un punto, rispetto al quale possono essere eseguite una o più operazioni di simmetria Assi di rotazione e rotazioni proprie Per fare un esempio, consideriamo un triangolo equilatero e una retta ad esso perpendicolare, passante per il suo centro: 5
2 La igura 1 mostra che per una rotazione di 120 (2π/3 rad) attorno a questo asse, il triangolo viene portato in una configurazione equivalente. Infatti, i triangoli I e II sono sovrapponibili. 3 2 I II ig Perciò, in base alle definizioni precedenti, possiamo dire che la retta è un asse di simmetria (asse di rotazione propria) e la rotazione di 120 (il movimento a cui è stato sottoposto il triangolo) un operazione di simmetria. Possiamo inoltre notare (ig. 2) che una configurazione equivalente si ottiene anche per rotazione di 240 ( 2x120 = 4π/3 rad), come pure per una rotazione di 360 ( 3x120 = 2π rad): triangoli III e IV, rispettivamente. In particolare, in quest ultimo caso, otteniamo una configurazione che è in tutto uguale a quella di partenza. Le configurazioni II e III sono equivalenti alla I perché senza i numeri sui vertici, che non fanno realmente parte del triangolo, esse sarebbero indistinguibili dalla I. Invece, la configurazione IV è in tutti i sensi indistinguibile dalla I, e pertanto è detta identica alla I. Per questa particolare operazione di simmetria, l identità, usiamo il simbolo E (dal tedesco Einheit, unità. In alcuni testi si trova il simbolo I, Identità). 3 1 I III I 360 IV = I ig. 2 6
3 Evidentemente, possiamo passare dalla configurazione I alla IV per tre successive rotazioni di 120, attorno all asse centrale, passando progressivamente dalla I alla II, dalla II alla III e dalla III alla IV (ig. 3) I II III IV ig.3 Il simbolo generale (simbolo di Schönflies) per un asse di rotazione è C n, dove n (numero intero positivo) denota l ordine dell asse. Per ordine intendiamo il valore di n tale che una rotazione di 360 /n (2π/n rad) porta a una configurazione equivalente. Possiamo anche definire l ordine n dell asse come il numero di volte che deve essere ripetuta la più piccola rotazione che porta a una configurazione equivalente per ritornare alla configurazione di partenza. Lo stesso simbolo C n viene usato anche per indicare l operazione di rotazione di 360 /n. Per il triangolo equilatero la rotazione di 120 (= 360 /3) è un operazione di simmetria e l asse di rotazione (propria), C 3, è detto asse ternario. Come detto, C 3 indica anche l operazione di rotazione che porta dalla configurazione I alla II, cosicché l operazione che dalla I porta alla III può venir scritta come C 3 x C 3 = C 2 3, e quella che dalla I porta alla IV come C 3 x C 2 3 = C 3 3. Il segno x indica qui la successione delle operazioni che porta ad un certo risultato; dopo aver effettuato l operazione indicata più a destra, si esegue quella che la precede. Il simbolo C 2 3 rappresenta quindi la rotazione di 2x120, mentre C 3 3 rappresenta la rotazione di 3x120. Poiché C 3 3 produce una configurazione identica, possiamo scrivere C 3 3 = E. Ė interessante osservare che la configurazione III può essere ottenuta, oltre che con l operazione C 2 3, anche con un operazione C 3, ma ruotando in verso opposto (ig. 4). 3 1 I 120 III ig Per questa operazione si usa il simbolo C 3-1 e diciamo che essa è l operazione inversa della C 3. Ė 7
4 -1 ovvio che C 3 x C 3 = C 3 x C -1 3 = E. A questo punto, possiamo facilmente generalizzare dicendo che un asse di rotazione di ordine n, come pure una rotazione di 360 /n, sono rappresentate dal simbolo C n. Se la rotazione di 360 /n viene eseguita in successione m volte, sempre nello stesso verso, l operazione è rappresentata dal simbolo C m n e avremo che C n n = E. Guardando ancora all esempio del triangolo è facile verificare che per rotazioni successive alla C n n si ritorna in ciclo, cioè C n+1 n =C n, C n+2 n =C 2 n,..., C n+m n =C m n. Si vede inoltre che un asse di ordine n genera n operazioni di rotazione, compresa l identità: C n, C 2 n, C 3 n,...,c n-1 n, C n n = E. Considerando la simmetria molecolare, n comunemente varia da 2 a 6; assi di ordine 7 e 8 sono meno comuni e si ritrovano, rispettivamente, in ioni del tipo C (ione tropilio) e C (ione cicloottatetraene). Nei seguenti esempi (ig.5), l asse di rotazione è perpendicolare al piano del foglio e passa per il baricentro della molecola. B Pt O C 2 C 3 C 4 binario ternario quaternario C 5 quinario ig. 5 C 6 senario La molecola d acqua possiede un asse binario, quella di trifluoruro di boro un asse ternario, lo ione tetracloroplatinato(ii), Pt 4 2-, un asse quaternario, lo ione ciclopentadienile un asse quinario e il benzene uno senario. 8
5 Da notare che anche molecole che non possiedono assi di rotazione di questo tipo, come ad esempio, il clorofluorotionile, SO, avranno comunque assi di ordine 1, C 1, corrispondenti all operazione di identità: C 1 = E. S O Consideriamo ora l operazione C 2 4, generata dall asse C 4. Questa corrisponde ad una rotazione 2 di 2x360 /4, cioè 180 che è la rotazione propria di un asse C 2, per cui l operazione C 4 coincide con l operazione C 2. Generalmente le operazioni vengono ricondotte ai minimi termini, per cui, ad esempio, le operazioni generate da un asse senario: C 6, C 2 6, C 3 6, C 4 6, C 5 6, C 6 6, vengono di solito scritte come: C 6, C 3, C 2, C 2 3, C 5 6, E. Le operazioni C 3 e C 2 3 sono proprie di un asse C 3, cosicché si vede che un asse senario implica la presenza di un asse ternario. In generale, se n è pari un asse C n implica l esistenza di un asse C n/2. In modo analogo, si verifica facilmente che l esistenza di un asse C 2 perpendicolare ad un asse di ordine n dispari, implica l esistenza di altri n-1 assi C 2. Infatti, nel caso del B 3 (ig. 6a), preso un legame B, si vede che esso giace su un asse binario, C 2, perpendicolare all asse C 3, a sua volta perpendicolare al piano della molecola, e, proprio per l esistenza di questo asse, si ritrovano, a 120 tra loro, altri due assi binari, C 2 e C 2. In effetti, ogni legame B giace su un asse C 2. C 2 ' C 2 ' C 2 " C 2 " B C 2 Pt C 2 C 2 " ig. 6a ig. 6b Nel caso invece, di un asse C n con n pari, se esiste un asse binario ad esso perpendicolare, vengono generati altri n/2 1 assi C 2 a 360 /n tra loro. Vengono inoltre generati altri n/2 assi binari, sempre a 360 /n tra loro, ma a 360 /2n dai precedenti. Ciò si verifica facilmente, ad esempio, in Pt 2-4. L asse passante per Pt e due in trans è un asse binario, C 2, perpendicolare all asse C 4. Una rotazione di 360 /4 = 90 genera l altro asse (n/2-1 = 1) C 2. Questi assi vengono indicati con il simbolo C 2. Dalla igura 6b si vede, inoltre, che si hanno altri due (n/2) assi binari, indicati con il simbolo C 2, a 90 tra loro, ma a 45 (360 /2n) dai precedenti. 9
6 Quanto detto sopra riguarda l asse C 2, che è il caso più frequente, ma il discorso è generale e si applica anche ad assi di ordine superiore, come è il caso degli assi C 3 generati da un asse C 4 in un cubo Piani di simmetria e riflessioni Una molecola possiede, come elemento di simmetria, un piano di riflessione, se, portata da ciascun atomo una perpendicolare al piano, si trova dall altra parte, alla stessa distanza, un atomo equivalente. Il simbolo di Schönflies per rappresentare il piano di simmetria è (sigma, probabilmente dal tedesco Spiegel, specchio), che è anche il simbolo per l operazione di riflessione attraverso un piano. Come esempio, consideriamo una molecola piana, quale il tetraossido di diazoto, N 2 O 4 : la retta indicata con è la traccia di un piano di simmetria della molecola (ig. 7a). O1 O3 O3 O1 N1 N2 N2 N1 ig. 7a O2 O4 O4 O2 Si vede chiaramente che l operazione, indicata dalla freccia, porta la molecola in una configurazione equivalente. A differenza degli assi di rotazione, un piano di simmetria genera un unica operazione di simmetria. Se sulla molecola a destra si ripete l operazione di riflessione attraverso il piano, si ritorna alla configurazione originale: x = 2 = E. In generale, n = E, se n è pari, n =, se n è dispari. La molecola N 2 O 4 possiede altri due piani di simmetria: uno, ancora perpendicolare al piano della molecola e passante per l asse N N, l altro coincidente con il piano della molecola (ig. 7b). O O N N O O ig. 7b 10
7 Considerazioni analoghe a quelle fatte per l asse C n e un asse C 2 perpendicolare, si applicano anche al caso di un asse C n e un piano di simmetria che lo contenga. Per n dispari, vengono generati altri n-1 piani, sempre contenenti C n, che formano angoli diedri di 360 /n; mentre, per n pari, vengono generati n/2-1 piani che contengono C n, e formano angoli diedri di 360 /n, e n/2 piani, sempre contenenti l asse e a 360 /n tra loro, ma che bisecano gli angoli diedri formati dai piani precedenti. Questi ultimi piani vengono definiti piani di simmetria diedri e indicati con d. Come esempio, consideriamo nuovamente B 3 e Pt 2-4 : la prima molecola (ig. 8a) con un asse C 3, e la seconda (ig. 8b) con un asse C 4, contenuti nel piano di simmetria. ig. 8a ig. 8b Nel primo caso vengono generati n-1=2 altri piani ( e ) a 120 tra loro; nel secondo caso, un piano (n/2-1=1),, a 90 da e n/2=2 piani ( e ) a 45 tra e. e sono i piani di simmetria diedri, d Centro di simmetria e inversione Una molecola possiede un centro di simmetria o centro di inversione (simbolo: i), se una retta tracciata da ciascun atomo, attraverso questo punto (centro), incontra un atomo equivalente alla stessa distanza dal centro. Così delle molecole viste prima, presentano un centro di simmetria: N 2 O 4 (nel punto medio tra i due atomi di azoto), Pt 2-4 (sull atomo di platino) e C 6 6 (al centro dell esagono). Non possiedono un centro di simmetria l acqua, il trifluoruro di boro, il ciclopentadienile e il clorofluorotionile. Il nome di inversione deriva dal fatto che, se fissiamo una terna di assi con origine sul centro, per effetto dell operazione, ogni atomo di coordinate x, y, z viene portato su un atomo equivalente di coordinate -x, -y, -z (ig. 9). 11
8 ig. 9 È interessante osservare che se esiste un centro di inversione vengono imposte delle restrizioni sul numero di atomi della molecola. Siccome il centro è un punto (il baricentro della molecola), soltanto un atomo può stare sul centro e tutti gli altri atomi devono esistere a coppie. In effetti, in Pt 2-4, solo Pt sta sul centro i, e ci sono due coppie di (a causa dell asse C 4 ); in C 6 6, nessun atomo sta su i, ma gli atomi di carbonio sono in numero pari (6 per la presenza dell asse senario). Come nel caso della riflessione, se l operazione di inversione viene eseguita più volte, avremo che i n = E se n è pari, i n = i se n è dispari. Anche per i esiste una sola operazione di simmetria Assi di rotazione impropria e operazioni di rotazione impropria Una rotazione impropria (simbolo S n ) può essere considerata come costituita da una rotazione propria (C n ) seguita da una riflessione () attraverso un piano perpendicolare all asse di rotazione. Per tale motivo gli assi di rotazione impropria vengono definiti anche assi di rotoriflessione. Attribuendo il significato dato precedentemente al simbolo x, possiamo perciò scrivere S n = x C n. È facile verificare che le due operazioni commutano, cioè che l ordine delle operazioni può essere invertito, e che quindi S n = x C n = C n x. Come esempio consideriamo la molecola ottaedrica dell esafluoruro di zolfo, S 6, e verifichiamo che essa possiede un asse S 6 perpendicolare alle facce triangolari dell ottaedro (antiprisma trigonale). Infatti, come mostrato in igura 10, una rotazione di 60 (360 /6) attorno a questo asse, seguita da una riflessione rispetto a un piano perpendicolare all asse e passante per l atomo centrale di zolfo, o scambiando l ordine delle operazioni, si arriva ad una configurazione equivalente. 12
9 S 3 Rotazione di S Riflessione 1 S 6 Riflessione S 4 Rotazione di S ig. 10 In effetti, la configurazione in basso a destra, ottenuta tramite le operazioni x C 6 o C 6 x, è equivalente a quella di partenza, in alto a sinistra. È importante osservare che la presenza di un asse di rotazione impropria non implica l esistenza di un asse di rotazione propria dello stesso ordine e/o l esistenza di un piano di simmetria ad esso perpendicolare. Infatti, nell esempio della molecola ottaedrica, esiste un asse S 6, ma non esiste un asse C 6 né un ad esso perpendicolare. Allo stesso modo nelle molecole tetraedriche esiste un asse S 4 senza che esista un asse C 4 o il ad esso perpendicolare. Il modo migliore per vedere l asse S 4 in un tetraedro è di considerare quest ultimo inscritto in un cubo; S 4 passa per l atomo centrale e i punti medi delle coppie di atomi superiori e inferiori (ig. 11). 90 Riflessione ig,11 13
10 In altri casi invece, un asse S n può coincidere con un asse C n. Ad esempio, in N 2 O 4 (ig. 12) esiste un asse S 2 passante per i due atomi di azoto, come pure un asse C 2 (coincidente con S 2 ) e un ad esso perpendicolare. O1 O3 N1 N2 C 2 ig. 12 O2 O4 La igura 13 mostra che S 2 = C 2 x coincide con i, per cui il centro di simmetria è in effetti un asse di rotoriflessione di ordine 2. O1 O3 O3 O1 N1 N2 C 2 N2 N1 O2 O4 O4 O2 S 2 O4 i O2 O4 C 2 O2 N2 N1 N2 N1 O3 O1 O3 O1 ig. 13 Possiamo inoltre osservare che l operazione di riflessione corrisponde all asse di rotoriflessione di ordine 1. Infatti: S 1 = C 1 x = E x =. Un asse S n genera n operazioni di simmetria se n è pari e 2n operazioni se n è dispari. Vediamo in dettaglio i due casi, con due esempi: 14
11 n pari: S 6 ; le operazioni S m n (fino a ritornare all identità) sono: 1. S 6 = C 6 x = S 6 2. S 2 6 = C 2 6 x 2 = C 3 x E = C 3 3. S 3 6 = C 3 6 x 3 = C 2 x = S 2 = i 4. S 4 6 = C 4 6 x 4 = C x E = C 3 5. S 5 6 = C 5 6 x 5 = C x = S 6 6. S 6 6 = C 6 6 x 6 = E x E = E Come si vede, si ritorna all identità dopo sei operazioni, di cui tre corrispondono all asse C 3, comprendendo in queste E (2., 4., 6.), e tre all asse S 6, comprendendo in queste i (1., 3., 5.). In generale, un asse S n di ordine pari genera n operazioni, di cui n/2 rotazioni proprie (asse C n/2 ) compresa E (= S n n ), e n/2 rotazioni improprie, compresa i (= S 2 ) se n/2 è dispari. In altre parole, un asse di rotoriflessione di ordine pari implica l esistenza di un asse di rotazione di ordine metà che coincide con l asse S n e un centro di simmetria se n/2 è dispari. Nel caso visto prima di S 6 è facile verificare dal disegno l esistenza dell asse C 3 coincidente con S 6 e la presenza del centro di simmetria (n/2=3) sull atomo di zolfo. n dispari: S 7 ; le operazioni S m n (fino a ritornare all identità) sono: 1. S 7 = C 7 x = S 7 2. S 2 7 = C 2 7 x 2 = C x E = C 7 3. S 3 7 = C 3 7 x 3 = C x = S 7 4. S 4 7 = C 4 7 x 4 = C x E = C 7 5. S 5 7 = C 5 7 x 5 = C x = S 7 6. S 6 7 = C 6 7 x 6 = C x E = C 7 7. S 7 7 = C 7 7 x 7 = E x = 8. S 8 7 = C 8 7 x 8 = C 7 x E = C 7 9. S 9 7 = C 9 7 x 9 = C x = S S 10 7 = C 10 7 x 10 = C x E = C S 11 7 = C 11 7 x 11 = C x = S S 12 7 = C 12 7 x 12 = C x E = C S 13 7 = C 13 7 x 13 = C x = S S 14 7 = C 14 7 x 14 = C 7 7 x E = E x E = E 15
12 e riordinando: C 7, C 2 7, C 3 7, C 5 7, C 6 7, E S 7, S 2 7, S 3 7, S 5 7, S 6 7,. Come si vede, per n=7, si ritorna all identità dopo 14 operazioni, di cui sette corrispondono all asse C 7 (compresa E, per m=14) e sette all asse S 7 (compresa, per m=7). In generale, un asse S n di ordine dispari genera 2n operazioni di cui n rotazioni proprie (asse C n ), 2n n n compresa E (S 2n = C n =E) e n rotazioni improprie, compresa (S n = ). Un esempio di asse S 7 si ha nello ione tropilio, C 7 + 7, mentre lo ione ciclopentadienile, C 5-5, ha un asse S 5, coincidenti, rispettivamente, con gli assi C 7 e C 5. Il piano di riflessione coincide col piano molecolare. In questi due esempi l asse di rotoriflessione non aggiunge niente agli elementi di simmetria già esistenti (C n e perpendicolare). In certi casi però l asse S n con n dispari porta a delle configurazioni equivalenti non ottenibili da 3- un asse C n o dal. Un esempio è dato dallo ione Zr 7 che ha una geometria a bipiramide pentagonale. Come riportato nella igura 14, l operazione S 5 dà una configurazione diversa dalla C 5 e dalla riflessione. ig. 14 Gli elementi di simmetria visti finora sono detti elementi di simmetria puntuale, perché nelle varie operazioni di simmetria, un punto, il baricentro della molecola, non viene mai spostato. Come vedremo in seguito, nel caso della simmetria nei cristalli bisogna considerare anche elementi di 16
13 simmetria traslazionale, che invece spostano le molecole. Nella Tabella 1, sono riassunti gli elementi e le operazioni di simmetria puntuale. Tabella 1 Simmetria puntuale Elemento Operazione Simbolo di Schönflies Numero di operazioni Asse di rotazione (propria) di ordine n Asse di rotazione impropria di ordine n Rotazione di 360 /n C n n Rotazione di 360 /n + Riflessione S n n, per n pari 2n, per n dispari Piano di simmetria Riflessione 1 Centro di simmetria Inversione i Rappresentazione matriciale delle operazioni di simmetria In molti casi è necessario conoscere come si trasformano le coordinate degli atomi di una molecola, sotto le varie operazioni di simmetria. A tale proposito, bisogna fissare un sistema di riferimento. Il sistema di assi standard è una terna cartesiana destra, cioè un sistema di assi cartesiani in cui i versi positivi degli assi x, y, z puntano, rispettivamente come il pollice, l indice e il medio della mano destra. Per l orientazione della terna nella molecola si seguono certe convenzioni, qui riportate schematicamente: L asse z coincide con l asse di rotazione, propria o impropria, di ordine maggiore. L asse z viene sempre considerato asse verticale, a prescindere dalla sua orientazione nel disegno. Se ci sono più assi di rotazione di ordine massimo, si prende come asse z quello che passa per più atomi. Se la molecola è planare e l asse z giace in questo piano, l asse x è perpendicolare al piano molecolare; se invece, l asse z è perpendicolare al piano, l asse x sta nel piano e viene scelto in modo da passare per il maggior numero di atomi. L asse y è perpendicolare a x e z, formando una terna destra. L origine viene generalmente posta sul baricentro della molecola. In alcuni casi però è conveniente porre l origine su un atomo o sul punto medio di un legame. 17
14 Alcuni esempi sono riportati nelle igure 15a e 15b. ig. 15a ig. 15b In base a queste definizioni, i piani di simmetria possono essere distinti in piani verticali ( v ) e piani orizzontali ( h ), a seconda che il piano contenga o sia perpendicolare all asse verticale z. 18
15 Così, ad esempio, dei tre piani di simmetria visti prima per la molecola N 2 O 4, due sono piani verticali, contenendo l asse C 2, e uno orizzontale, essendo perpendicolare a C 2 (ig. 16). h O O N N v C 2 ig. 16 O O v Ora, il nostro scopo è quello di trovare un operatore che permetta, note le coordinate di un atomo, di conoscere quelle degli atomi ad esso equivalenti, mediante opportune operazioni algebriche. Vediamo separatamente i seguenti casi: Rotazione Supponiamo che l asse di rotazione considerato coincida con l asse z. Se ruotiamo il vettore r di un angolo θ (θ>0 per rotazioni in senso antiorario), il punto P di coordinate x,y,z si sposta in P con coordinate x,y,z, con z = z (ig. 17). ig. 17 Dalla figura si ricava che: sviluppando si ha: x = r cos(α+θ) ig. 17 y = r sen(α+θ) z = z x = r cosα cosθ r senα senθ y = r senα cosθ + r cosα senθ z = z ma poiché x = r cosα e y = r senα, si avrà: x = x cosθ y senθ y = x senθ + y cosθ z = z 19
16 In forma matriciale possiamo scrivere: x = cosθ senθ 0 x y = senθ cosθ 0 y o r = R z (θ) r z = z che significa che la matrice R z (θ) applicata al vettore r(x,y,z) lo trasforma nel vettore r (x,y,z ). È importante osservare che R z (θ) è indipendente da α. La matrice R z (θ) esprime in termini matematici l effetto di una rotazione di un generico angolo θ intorno all asse z su di un punto di coordinate x,y,z. Per tale motivo, matrici di questo tipo sono dette matrici di rotazione. L operazione di rotazione C n sarà allora associata a una matrice di rotazione R w (360 /n), dove w = x, y o z, a seconda che l asse C n coincida, rispettivamente, con x, y o z. Consideriamo, ad esempio, una rotazione C 4, supponendo che l asse quaternario coincida con l asse z. La matrice R z (90 ) sarà: R z (90 ) = per cui: x x -y y = y = x z z z cosicché un punto di coordinate x, y, z avrà, dopo la rotazione di 90, coordinate -y, x, z. Per un operazione C 4 2 o C 2 (essendo in entrambi i casi θ = 180 ), avremo: R z (180 ) = per cui: x x -x y = y = -y z z z Si può verificare inoltre, algebricamente, che C 4 2 = C 4 x C 4 = C 2. Infatti: R z (90 ) R z (90 ) = = = R z (180 ) Come si vede da questo esempio, il prodotto di due operazioni di simmetria diventa un vero prodotto algebrico quando all operazione si sostituisce la corrispondente matrice. Con procedure analoghe si possono ricavare tutte le relazioni viste precedentemente. Possiamo 20
17 così verificare, ad esempio, che C 4 x C 2 = C 2 : = Le matrici di rotazione attorno agli assi x e y sono: cosθ 0 -senθ R x (θ) = 0 cosθ senθ R y (θ) = senθ cosθ senθ 0 cosθ La matrice relativa alla rotazione C 1 (θ = 360 ) e quindi all identità E è la matrice unità : E = da cui si vede che sotto l operazione E le coordinate non cambiano. Riflessione Supponiamo che il piano di simmetria passi per l asse z. La traccia del piano forma un angolo φ con l asse x. Il punto P(x,y,z) viene riflesso in P (x,y,z ) con z = z (ig. 18). Dalla figura si ricava che: x = r cos(2φ-α) y = r sen(2φ-α) z = z sviluppando si ha: ig. 18 x = r cos2φ cosα + r sen2φ senα y = r sen2φ cosα - r cos2φ senα z = z ma poiché x = r cosα e y = r senα, si avrà: x = x cos2φ + y sen2φ y = x sen2φ y cos2φ z = z In forma matriciale possiamo scrivere: x = cos2φ sen2φ 0 x y = sen2φ -cos2φ 0 y o r = M(φ) r z = z 21
18 Così, se il piano è un piano verticale contenente gli assi x,z (φ = 0 ) o gli assi y,z (φ = 90 ), avremo le matrici: M v (x,z) = e M v (y,z) = sarà: Per un piano orizzontale, come h = (x,y), dovendo essere x = x, y = y, z = -z, la matrice M h (x,y) = Possiamo ora verificare quanto detto precedentemente sulla generazione di piani diedri, e cioè che la coesistenza di un asse C 4 e di un piano di simmetria verticale, v, implica l esistenza di piani d. Infatti, in termini matriciali: R z (90 ) M v (x,z) = = = M v (45 ) Come si vede, la matrice ottenuta è proprio quella associata a un piano di simmetria a 45 da v. Rotoriflessione La matrice corrispondente a un operazione di rotoriflessione S n = C n x, si ottiene dal prodotto delle corrispondenti matrici di rotazione e riflessione rispetto al piano perpendicolare: S z (θ) = R z (θ) M h cosθ -senθ cosθ -senθ 0 S z (θ) = senθ cosθ = senθ cosθ Inversione Ricordando che l inversione corrisponde a S 2 (θ = 180 ) si ha che: I = Come già detto, l inversione cambia il segno delle coordinate x, y, z. 22
19 1.2 Simmetria e proprietà molecolari Esamineremo ora alcune proprietà molecolari che sono determinate dalla presenza o meno di certi elementi di simmetria. Così, nota la simmetria della molecola, potremo stabilire se quella proprietà è presente o no, oppure, dal valore sperimentale della grandezza relativa alla proprietà, potremo ottenere informazioni sulla presenza o meno di certi elementi di simmetria e quindi ottenere informazioni sulla struttura della molecola in esame Momento di dipolo elettrico Una molecola presenta un momento di dipolo elettrico se il baricentro della distribuzione della carica elettronica e di quella delle cariche positive dei nuclei non coincidono. Il momento di dipolo elettrico, µ, è una grandezza vettoriale, il cui modulo è dato dal prodotto della carica q, in valore assoluto, per la distanza, d, tra i due baricentri: µ = q d. µ viene misurato in Debye (D), dove 1 D = ues cm = C m. Una qualsiasi operazione di simmetria, compiuta su una molecola, non può portare ad alcuna variazione delle sue proprietà chimico-fisiche e quindi neanche del momento di dipolo, sia per quanto riguarda il modulo che la direzione e il verso. Se il vettore momento di dipolo deve rimanere inalterato quando si compiono delle operazioni di simmetria sulla molecola, esso deve giacere su tutti gli elementi di simmetria di quest ultima. Infatti, solo i punti che giacciono su un elemento di simmetria non subiscono spostamenti quando avviene la corrispondente operazione. Per tale ragione allora, le molecole che possiedono un centro di simmetria non hanno un momento di dipolo elettrico permanente, perché un vettore non può giacere su un punto. Analogamente, le molecole che hanno più assi C n (n>1) non coincidenti, non presentano un momento di dipolo, perché un vettore non può coincidere con più assi orientati in modo diverso. Lo stesso avviene se la molecola possiede un asse C n e un piano ad esso normale. Così, avremo un momento di dipolo permanente solo nelle molecole che hanno un solo asse C n, con n>1, come l 1,2-diclorociclopropano o un piano senza assi C n, come il metanolo. È possibile ancora avere un momento di dipolo permanente se la molecola presenta un asse C n formato dall intersezione di una serie di piani, come nel caso dell acqua (2, perpendicolari tra loro, che si intersecano formando un C 2 ) e dell ammoniaca (3, uno per ogni legame N, che si intersecano formando un C 3 ) (ig. 19a). 23
20 C 2 O O µ (D) = C 2 N C ig. 19a Nella igura 19b sono invece riportati i momenti di dipolo di alcuni derivati clorurati del benzene. µ (D) = ig. 19b Nel caso di assi C n, poiché il vettore µ giace su questi elementi di simmetria, questi ne definiscono la direzione. Ovviamente, non si hanno informazioni né sul verso né sul modulo Attività ottica Molecole che hanno la proprietà di provocare una rotazione del piano della luce polarizzata che le attraversa sono dette otticamente attive. Tale proprietà è stata scoperta e ampiamente studiata in composti organici ed è stata collegata alla presenza di atomi di carbonio asimmetrici, cioè legati a quattro atomi o gruppi diversi. In seguito però si è trovato che anche composti senza atomi di carbonio asimmetrici sono otticamente attivi. 24
21 Un criterio più generale per stabilire la presenza di attività ottica in una molecola è quello della non sovrapponibilità della molecola stessa con la sua immagine speculare. Tali molecole sono dette enantiomere (o enantiomorfi o antipodi ottici) e ruotano il piano della luce polarizzata dello stesso angolo, ma in verso opposto. Se la molecola in esame è piuttosto complessa non è sempre facile vedere da un disegno, soprattutto se non in prospettiva, se l immagine speculare di una molecola è sovrapponibile o meno con la molecola stessa, in quanto è spesso necessario compiere più rotazioni e traslazioni prima di arrivare all eventuale sovrapposizione. Un criterio più semplice per verificare la sovrapponibilità di due immagini speculari di una molecola è quello di stabilire la presenza nella molecola di un asse di rotoriflessione S n. La ragione di ciò sta nel fatto che l asse S n implica una riflessione attraverso un piano ad esso normale e non esiste alcun motivo per cui il piano che genera l immagine speculare debba essere esterno alla molecola. Ora, se scegliamo come piano di riflessione proprio il piano normale a S n, sarà sufficiente compiere una rotazione C n per portare l immagine in una configurazione equivalente, cioè a sovrapporsi alla molecola di partenza. Perciò, se la molecola possiede un asse S n essa è sovrapponibile alla propria immagine speculare e quindi è otticamente inattiva. Al contrario, molecole che non presentano assi di rotoriflessione non sono sovrapponibili con la propria immagine speculare e quindi sono otticamente attive. Una miscela dei due enantiomeri costituisce un racemo ed è otticamente inattiva. In base a tale criterio è facile vedere che la struttura tipo spirano del derivato schematizzato in igura 20a, con i due anelli a cinque termini perpendicolari tra loro, non è otticamente attivo in quanto possiede un asse S 4, passante per l atomo di azoto (tetraedrico) e i punti medi dei legami C(C 3 ) C(C 3 ). Invece, il complesso di zinco(ii), tetraedrico, con due anelli a sei termini perpendicolari tra loro (ig. 20b), è otticamente attivo se X è diverso da Y, mentre sarà inattivo se X è uguale a Y, per la presenza di un asse S 4. S 4 ig. 20a ig. 20b 25
22 Le molecole che non possiedono assi S n sono dette dissimmetriche, per distinguerle dalle asimmetriche, cioè da quelle molecole che non possiedono alcun elemento di simmetria tranne l asse C 1. È importante tenere presente che molte molecole possono esistere in una qualche conformazione che possiede solo assi C n e perciò se tutte le molecole di quel composto venissero congelate in quella conformazione, il composto sarebbe otticamente attivo. Così l 1,2-dicloroetano può esistere in diverse conformazioni: tre sfalsate (a, b, c della ig. 21), tre eclissate (d, e, f della ig. 21) e un numero infinito di conformazioni intermedie. Ora la a ha un centro di simmetria (i=s 2 ) e la f un piano di riflessione (=S 1 ), per cui sono otticamente inattive, ma tutte le altre conformazioni hanno solo l asse C 2 e sono quindi otticamente attive. Tuttavia, la barriera di potenziale per la rotazione attorno al legame singolo C C è sufficientemente bassa, per cui, a tutte le temperature ragionevolmente accessibili, il composto esiste come una miscela di tutti i conformeri (isomeri rotazionali), cosicché statisticamente ci sono tante molecole nella conformazione b, quante nella conformazione c (la sua immagine speculare). Lo stesso per d ed e. La probabilità di trovare popolazioni uguali di enantiomeri è vera in ogni istante per tutte le conformazioni e perciò l 1,2-dicloroetano è otticamente inattivo in quanto esso dà luogo a una miscela di miscele raceme. () a b c C 2 C 2 C 2 C 2 () () () () () () () () d e f ig. 21 A tale proposito, vale la pena osservare che nello schema della struttura del derivato spiranico, visto prima (ig. 20a), gli anelli a cinque termini, sono stati rappresentati come planari. In realtà 26
23 questi presentano una conformazione twist, ma la differenza di energia tra i due conformeri (δ e λ) è piccola per cui entrambi sono presenti in numero uguale, impartendo quindi alla molecola una simmetria media S 4. In pratica, per stabilire se una molecola è dissimmetrica, e quindi otticamente attiva, è sufficiente determinare se la molecola in esame non possiede un asse S n in una conformazione facilmente accessibile. Tuttavia, come accennato prima, la differenza tra conformeri e enantiomeri può dipendere dalla temperatura. Così, nello spettro NMR del 19 nel diclorofluoro derivato dell etano, 2 C C 2, si osserva un unico segnale a 32 C, ma due segnali a -120 C Atomi equivalenti e isomeria geometrica In molecole come metano, etano, benzene ed etilene, tutti gli atomi di idrogeno sono chimicamente equivalenti e diciamo che formano un insieme unico. L equivalenza chimica è verificata dal fatto che la sostituzione di un qualsiasi atomo di idrogeno dell insieme con un altro atomo porta a molecole identiche. Questo criterio dell equivalenza chimica può essere definito come test della sostituzione chimica. Così, negli esempi di cui sopra, sostituendo un qualsiasi con otterremo un unico monocloro derivato. Dal punto di vista della simmetria, atomi o gruppi di atomi, come ad esempio il metile, C 3, sono chimicamente equivalenti se possono essere scambiati dalla rotazione attorno ad un asse di simmetria della molecola. Così nel metano, tutti gli atomi di idrogeno possono essere scambiati dai tre assi C 2 che bisecano gli angoli C o dagli assi C 3, definiti dai legami C, oppure dai due piani di simmetria. Allora, i quattro atomi di idrogeno sono equivalenti e ci sarà, ad esempio, un unico monocloro derivato, il cloroformio, C 3. In quest ultimo c è un asse C 3 che passa per gli atomi C e, cosicché i tre sono equivalenti e perciò la sostituzione di un con un darà un unico prodotto, il diclorometano, C 2 2. Anche in quest ultimo gli atomi di idrogeno sono equivalenti perché riferiti da un asse C 2 e per sostituzione si avrà ovviamente solo C 3 (ig. 22). 27 ig. 22
24 L equivalenza chimica degli atomi di idrogeno in composti planari può essere accertata dallo scambio di idrogeni attraverso piani di riflessione, in quanto tali piani includono sempre assi C 2. Così nel caso del naftalene, vediamo che gli atomi di idrogeno 1 e 4, 5 e 8, 2 e 3, 6 e 7 sono scambiati per riflessione attraverso il piano x,y (o per rotazione C 2 attorno all asse y), mentre la riflessione attraverso il piano x,z (o per rotazione C 2 attorno all asse z) scambia 1 e 8, 2 e 7,3 e 6, 4 e 5 (ig. 23). x z 1 2 ig y Ci sono, quindi, due insiemi di idrogeni: 1, 8, 4, 5 e 2, 3, 6, 7 e perciò sono possibili due naftaleni monosostituiti. Se gli atomi vengono scambiati solo da un operazione, in quanto la molecola non possiede assi di rotazione propria, gli atomi, equivalenti per simmetria, non sono più chimicamente equivalenti. Vediamo (ig. 24) il caso generale RC 2 R : (a), la molecola non possiede nessun asse C n con n>1, ma solo un piano di riflessione che biseca l angolo C. Se sostituiamo un atomo di idrogeno con un altro atomo o gruppo atomico X, diverso da R e R otterremo (b), l enantiomorfo del composto ottenuto per sostituzione dell altro atomo di idrogeno con lo stesso X (c). Infatti d è l immagine speculare di c che, come si vede, coincide con b dopo una rotazione di 180. X X X X R R R R R R R R 180 R R a b c d b ig. 24 In questa situazione i due atomi di idrogeno, equivalenti per simmetria, ma non chimicamente equivalenti, vengono definiti pseudo-equivalenti o enantiotopici. L atomo di carbonio centrale 28
25 viene detto prochirale poiché, dopo scambio di uno degli atomi di idrogeno, si ottiene un composto otticamente attivo con un atomo di carbonio chirale (asimmetrico). La sostituzione di uno degli atomi di idrogeno porta all enantiomorfo di configurazione S, mentre la sostituzione dell altro porta alla configurazione R. Gli atomi di idrogeno sono perciò definiti Pro-S e Pro-R, come nel caso dell etilbenzene, C 6 5 C 2 C 3 (ig. 25). Pro-S Pro-R ig. 25 Senza entrare nei dettagli delle regole per definire la configurazione degli atomi di carbonio asimmetrici, per cui si rimanda ai testi di Chimica Organica, ricordiamo qui soltanto che la configurazione di un atomo, cioè l arrangiamento spaziale degli atomi che lo circondano, può essere definita considerando la sequenza dei sostituenti, in ordine decrescente di numero atomico degli atomi legati all atomo asimmetrico. Orientato il gruppo in modo che l atomo più leggero (in genere ) punti dalla parte opposta all osservatore, la configurazione sarà R se si passa dall atomo a numero atomico maggiore (considerati anche gli eventuali sostituenti) a quello minore, in senso orario; S se in senso antiorario. Come regola mnemonica si può osservare che la curva della sequenza dei sostituenti, in ordine decrescente di numero atomico, assomiglia alla parte superiore della lettera R o S, oppure a un volante e le frecce indicano la rotazione a destra o a sinistra, tenendo presente che i simboli R e S sono legati ai termini latini Rectus e Sinister, destra e sinistra, in relazione al verso della rotazione del piano della luce polarizzata. Ad esempio, nel caso dell acido lattico C(O)(C 3 )(COO), nell enantiomero a sinistra della igura 26, la configurazione è R, in quello a destra S. COO ig. 26 O C C 3 29 R S
26 Tornando al derivato del metano RC 2 R, se R = R = C 3, a causa della libera rotazione attorno ai legami C C 3, la molecola statisticamente possiede un asse C 2 e quindi nel propano l atomo di carbonio centrale non è prochirale. Ritornando alla determinazione del numero di isomeri geometrici ottenibili dai gruppi di atomi equivalenti, vediamo il 2- caso dello ione complesso ottaedrico Pt 6 e consideriamo la sostituzione di ioni cloruro con ioni idrossido. Data la struttura ottaedrica, in Pt 2-6 i tre assi C 4 (coincidenti con i legami Pt in trans tra loro) rendono equivalenti tutti e sei gli ioni cloruro. L esistenza di un unico set comporta la possibilità di avere un unico monoidrossoderivato, Pt 5 (O) 2- (ig. 27, a sinistra). In quest ultimo, la presenza di un O al posto di un, determina la scomparsa di due C 4 (oltre ad altri elementi di simmetria dell ottaedro). L asse C 4 residuo ( Pt O) rende ancora equivalenti i quattro nel piano ad esso perpendicolare, ma non esiste alcun elemento di simmetria che colleghi questi col assiale; quindi ci sono due gruppi di ione cloruro e perciò due possibili isomeri geometrici, a seconda che venga sostituito il assiale o uno basale. Nel primo caso si ottiene l isomero trans, nel secondo quello cis (ig. 27, al centro). O O O cis Pt Pt fac O O O Pt trans O Pt O O Pt O O mer ig. 27 L isomero cis ha perduto l ultimo asse C 4 e i quattro formano due gruppi equivalenti per simmetria, per la presenza dell asse C 2 (passante per i punti medi dei e O). Di conseguenza, l introduzione di un terzo O al posto di un porta ai due isomeri mer e fac (ig. 27). Nell isomero trans, i quattro sono equivalenti per la presenza dell asse C 4 (passante per i due O 30
27 in trans) e quindi l ulteriore sostituzione di un con un O dà il solo isomero mer (ig. 27). A differenza del caso ottaedrico, gli atomi ai vertici di una bipiramide trigonale non sono tutti equivalenti per simmetria, poiché non esiste alcuna operazione che scambi i tre atomi equatoriali con quelli assiali. Così, nel caso del P 5 (ig. 28 a), la sostituzione di un con un C 3, dovrebbe portare a due isomeri, P 4 C 3 (ig. 28 b, c). In realtà è noto solo l isomero con il metile in posizione equatoriale (ig. 28 c). Ciò evidentemente è dovuto alla diversa stabilità dei due isomeri, che la simmetria da sola non può prevedere. C 3 P P 3 C P a b c ig Gruppi puntuali Per una descrizione completa, ma nel contempo concisa, della simmetria molecolare vengono usati i cosiddetti gruppi puntuali, definiti dai possibili insiemi di operazioni di simmetria propri di una data molecola. Della teoria dei gruppi, qui riporteremo solo i concetti base, rimandando per una trattazione rigorosa e completa, a testi specifici di Matematica o Chimica quantistica Definizioni e teoremi della teoria dei gruppi Un insieme di elementi costituisce un gruppo se sono soddisfatte le seguenti condizioni: Il prodotto di due elementi qualsiasi del gruppo è ancora un elemento del gruppo. Qui prodotto non indica necessariamente un prodotto algebrico, ma una combinazione degli elementi. Se A e B sono due elementi del gruppo AB sarà generalmente diverso da BA. Esiste un elemento del gruppo che commuta con gli altri e li lascia inalterati. Questo elemento è l elemento identità (E) ed è tale che AE = EA = A. Vale la legge associativa della moltiplicazione, per cui A(BC) = (AB)C. Ogni elemento ha un reciproco (o inverso) che è ancora un elemento del gruppo. Se R è il reciproco di S, allora: RS = SR = E. Generalmente, per indicare che un elemento è il 31
28 reciproco dell altro, si scrive: R -1 = S, S -1 = R. Vale il teorema che dice che il reciproco di un prodotto di due o più elementi è uguale al prodotto dei reciproci, in ordine inverso: (ABC...YZ) -1 = Z -1 Y -1...C -1 B -1 A -1. I gruppi possono essere finiti e infiniti. Il numero di elementi di un gruppo finito definisce l ordine del gruppo. Un esempio di gruppo infinito è rappresentato dall insieme dei numeri interi, mentre un esempio di gruppo finito è dato dal numero di operazioni di simmetria di una molecola. Per verificare che le operazioni di simmetria di una molecola costituiscono effettivamente un gruppo, prendiamo come esempio l ammoniaca, che, come abbiamo visto precedentemente, possiede un asse C 3 e tre v, dando luogo alle seguenti sei operazioni di simmetria: E, C 3, C 2 3,,, (ig. 29a). N ig. 29a P5 P3 P2 N P1 ig. 29b P P4 Nella figura 29b è riportata la molecola di N 3, vista lungo l asse ternario, da cui si vede come un generico punto P si sposti in cinque altre posizioni equivalenti (P1 P5) sotto le varie operazioni di rotazione e riflessione. Costruiamo ora la cosiddetta tavola di moltiplicazione, cioè la tabella che indica il risultato del prodotto delle varie operazioni di simmetria. Per costruire tale tabella, poniamo le sei operazioni su una riga in alto e su una colonna a sinistra, e quindi combiniamo ogni operazione della riga con tutte le operazioni della colonna. Assumiamo di eseguire prima l operazione della riga, poi quella della colonna, ricordando che la prima operazione da eseguire è quella a destra del segno x. È ovvio che ogni operazione di moltiplicazione per E è uguale all operazione stessa, mentre il risultato delle altre combinazioni può essere ottenuto con l ausilio della figura o moltiplicando le 2 matrici associate alle varie operazioni di simmetria. Così ad esempio, E x C 3 = C 3 ; C 3 x C 3 = C 3 (infatti, C 3 sposta P in P5 e l altra C 3 in P1, ma P e P1 sono riferiti da una rotazione C 2 3, ovvero di 32
29 240 ); C 3 2 x C 3 = E; x C 3 = (C 3 sposta P in P5 e sposta P5 in P3, ma P e P3 sono riferiti appunto da ); x C 3 = (C 3 sposta P in P5 e sposta P5 in P2, ma P e P2 sono riferiti appunto da ). Continuando in questo modo si ottiene la Tabella 2. Tabella 2 Si è in questo modo verificato che ogni combinazione di due qualsiasi operazioni di simmetria produce un operazione di simmetria già presente nell insieme iniziale, come richiesto appunto dalla condizione di gruppo matematico Gruppi puntuali di simmetria Vediamo ora quali tipi di gruppi possono essere ottenuti da diversi insiemi di operazioni di simmetria molecolare. Nel caso più banale, in cui la molecola sia asimmetrica, l unica operazione di simmetria possibile è E, e il gruppo, di ordine 1, viene indicato con il simbolo C 1. Quando l unico elemento di simmetria è un piano di riflessione, vi sono due operazioni: e 2 = E. Il gruppo di ordine 2, viene indicato come C s. Se abbiamo solo il centro di simmetria, le operazioni sono i e i 2 = E. Il gruppo di ordine 2, viene indicato come C i. Se l unico elemento di simmetria è un asse di rotazione propria C n, avremo, come visto precedentemente, n operazioni di simmetria e quindi un gruppo di ordine n, indicato col simbolo C n. Se è presente solo un asse di rotazione impropria S n, con n pari, avremo, come già visto, n operazioni (E, S n, C n/2, S 3 n,..., S n-1 n ), e il gruppo viene indicato come S n. Se n è dispari avremo 2n operazioni, che includono C n e h, e il gruppo viene indicato come C nh. Il caso S 2 è un caso 33
30 speciale, perché essendo S 2 = i, il gruppo viene indicato come C i. Se oltre all asse di rotazione C n è presente un asse binario, ad esso perpendicolare, sappiamo che vengono generati altri n-1 assi C 2 e perciò il gruppo consiste di 2n elementi e ha il simbolo D n. Se all asse di rotazione C n vengono aggiunti dei piani di riflessione potremo avere diverse combinazioni delle operazioni di simmetria. Se esistono n v avremo il gruppo C nv, di ordine 2n; mentre se esistono n C 2, perpendicolari a C n, e un h, avremo il gruppo D nh, di ordine 4n. Se oltre al C n e agli n C 2, ci sono n d, si ha il gruppo D nd, di ordine 4n. Nel caso delle molecole lineari, abbiamo due gruppi speciali, indicati come C v e D h. Al primo appartengono molecole eteronucleari come o CN, che, oltre all asse di rotazione coincidente con l asse molecolare, possiedono infiniti piani verticali, mentre al secondo appartengono molecole omonucleari come 2 o eteronucleari come O=C=O, nelle quali, oltre all asse, esiste un piano h che taglia a metà l asse internucleare. Esistono infine altri tre gruppi puntuali speciali, a simmetria molto elevata, quali il T d, caratteristico delle molecole tetraedriche, l O h, delle molecole ottaedriche, e il gruppo I h, meno comune, cui appartengono il dodecaedro pentagonale e l icosaedro regolare. Riassumendo abbiamo i seguenti tipi di gruppi puntuali, di cui riportiamo il simbolo di Schönflies e gli elementi di simmetria caratteristici (tra parentesi sono riportati i valori di n più comuni nel caso delle molecole): 1. Gruppi non assiali: (a) C 1 : C 1 (b) C s : h (c) C i : i 2. Gruppi C n (3 < n 8): C n 3. Gruppi D n (2 < n 6): C n + n C 2 normali all asse C n 4. Gruppi C nv (2 < n 6): C n + n v 5. Gruppi C nh (2 < n 6): C n + h 6. Gruppi D nh (2 < n 6): C n + h + n C 2 normali all asse 7. Gruppi D nd (2 < n 6): C n + n d + n C 2 normali all asse 8. Gruppi S n (n = 4, 6, 8): S n 9. Gruppi cubici: (a) T d : 4 C 3, 4 C 2, 4 S 4, 2 v, 2 d (b) O h : 3 C 4, 4 C 3, S 6, 6 C 2, 3 h, 6 d 10. Gruppi delle molecole lineari: (a) C v : C + v (b) D h : C + h + C 2 normali all asse 11. Gruppo icosaedrico I h : 6 C 5, 10 C 3, 15 C 2, 15 34
31 I gruppi puntuali di generici oggetti geometrici sono illustrati nella igura 30. ig. 30 Di seguito, sono invece riportati, per i diversi gruppi puntuali, alcuni esempi relativi a molecole: C 1 : C 1 (molecole asimmetriche) C S : (S 1 ) 35
32 C i : i (S 2 ) C 2 : C 2 C 3 : C 3 S 4 : S 4 C nv : C n, n v C 2v 36
33 C 3v C 4v C 5v C 6v C v C nh : C n, h, (S n = C n x h ), i per n pari C 2h C 3h D n : C n, n C 2 D 2 (rotazione 90 ) 37
34 D 3 D nh : C n, n C 2, h, (n v ) D 2h D 3h D 4h D 5h D 6h D h D nd : C n, n C 2, n d D 2d D 3d 38
35 D 5d T d : 4 C 3, 4 C 2, 4 S 4, 2 v, 2 d molecole tetraedriche come metano O h : 3 C 4, 4 C 3, S 6, 6 C 2, 3 h, 6 d molecole ottaedriche: S 6, Cr(CO) 6, e(cn) 6 3- I h : simmetria dell icosaedro (20 facce triangolari), 6 C 5, 10 C 3, 15 C 2, 15 : ullerene (C 60 ), boro elementare e composti come B ullerene, boro elementare B Se nel gruppo T d si rimuovono le riflessioni, si ottiene il gruppo puntuale T, estremamente raro nelle molecole reali. Altrettanto rari sono anche i gruppi puntuali O e I che mantengono solo le operazioni di rotazione propria dei corrispondenti gruppi O h e I h. Per la determinazione del gruppo puntuale di una data molecola si può seguire la seguente procedura illustrata nella igura
36 Molecola D h Si i? No Si C v Lineare? Lineare? Si No Due o più C n, n>2? No Si i? No I h Si C 5? No O h T d D nh D nd Si Si h? n d? No C nh D n C nv Scegli C n con n più alto; ci sono n C 2 a C n? Si Si h? No n v? No C s C i Si Si C n? No? No i? No C 1 No S 2n Si S 2n? No C n ig
CHIMICA FISICA III (Modulo A)
 CHIMICA FISICA III (Modulo A) Prof. Giovanna Fronzoni, Dipartimento di Scienze Chimiche e Farmaceutiche fronzoni@units.it Testi consigliati : P. Atkins, J. De Paula : Chimica Fisica (per la parte generale
CHIMICA FISICA III (Modulo A) Prof. Giovanna Fronzoni, Dipartimento di Scienze Chimiche e Farmaceutiche fronzoni@units.it Testi consigliati : P. Atkins, J. De Paula : Chimica Fisica (per la parte generale
Elementi di strutturistica cristallina III
 Chimica fisica superiore Modulo 1 Elementi di strutturistica cristallina III Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i 14 reticoli di Bravais Basi cristalline Analogamente che al
Chimica fisica superiore Modulo 1 Elementi di strutturistica cristallina III Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i 14 reticoli di Bravais Basi cristalline Analogamente che al
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
CHIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA.
 CIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA. non simmetrica rispetto al piano piano di simmetria La mano destra non è sovrapponibile alla mano sinistra: ne è invece l'immagine
CIRALITA' E' una proprietà relativa ad oggetti PRIVI DI UN PIANO DI SIMMETRIA. non simmetrica rispetto al piano piano di simmetria La mano destra non è sovrapponibile alla mano sinistra: ne è invece l'immagine
Le simmetrie dei poliedri regolari
 Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) GRUPPO: insieme di elementi correlati dalle seguenti regole:
 APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
APPUNTI DI TEORIA DEI GRUPPI Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27) Dr. Andrea G. Marrani DEFINIZIONI GRUPPO: insieme di elementi correlati dalle seguenti regole: 1) PRODOTTO
Introduzione alla Simmetria Molecolare
 Scuola di Ingegneria Industriale e dell Informazione Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Introduzione alla Simmetria Molecolare Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/it/education/general-chemistry-lessons/
Scuola di Ingegneria Industriale e dell Informazione Insegnamento di Chimica Generale 083424 - CCS CHI e MAT Introduzione alla Simmetria Molecolare Prof. Dipartimento CMIC Giulio Natta http://iscamap.chem.polimi.it/citterio/it/education/general-chemistry-lessons/
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
02/10/2018. di catena. di posizione. strutturali. di gruppo funzionale. isomeri. geometrici. stereoisomeri. ottici
 Quando due composti organici sono costituiti dagli stessi atomi ma possiedono una struttura differente si definiscono ISOMERI. Esistono diversi tipi di isomeria: di catena strutturali di posizione isomeri
Quando due composti organici sono costituiti dagli stessi atomi ma possiedono una struttura differente si definiscono ISOMERI. Esistono diversi tipi di isomeria: di catena strutturali di posizione isomeri
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Simmetria Molecolare
 Simmetria Molecolare Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca simmetria: artefatti e natura elemento di simmetria operazione di simmetria piano di riflessione riflessione elementi
Simmetria Molecolare Chimica Generale ed Inorganica Chimica Inorganica 1 prof. Dario Duca simmetria: artefatti e natura elemento di simmetria operazione di simmetria piano di riflessione riflessione elementi
CONTENUTI DELLA LEZIONE:
 Stereochimica CONTENUTI DELLA LEZIONE: 1. La Chiralità: Molecole chirali e achirali 2. Identificare uno stereocentro 3. Enantiomeri 4. Regole per assegnare la configurazione R,S 5. Diastereoisomeri 6.
Stereochimica CONTENUTI DELLA LEZIONE: 1. La Chiralità: Molecole chirali e achirali 2. Identificare uno stereocentro 3. Enantiomeri 4. Regole per assegnare la configurazione R,S 5. Diastereoisomeri 6.
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
un legame covalente due legami covalenti? tre legami covalenti due legami covalenti un legame covalente
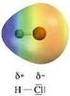 e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
Gli isomeri sono composti caratterizzati dalla stessa formula molecolare o bruta. Fino ad ora abbiamo conosciuto tre tipi di isomeria :
 Gli isomeri sono composti caratterizzati dalla stessa formula molecolare o bruta. Fino ad ora abbiamo conosciuto tre tipi di isomeria : ONFORMAZIONALE (eclissata, sfalsata) STRUTTURALE (pentano, 2 metil
Gli isomeri sono composti caratterizzati dalla stessa formula molecolare o bruta. Fino ad ora abbiamo conosciuto tre tipi di isomeria : ONFORMAZIONALE (eclissata, sfalsata) STRUTTURALE (pentano, 2 metil
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Teoria degli orbitali. Lo spazio intorno al nucleo in cui è possibile trovare con la massima probabilità gli elettroni viene chiamato orbitale.
 Teoria degli orbitali Lo spazio intorno al nucleo in cui è possibile trovare con la massima probabilità gli elettroni viene chiamato orbitale. orbitale nucleo STPA-Chimica Organica 1 L orbitale 1s Gli
Teoria degli orbitali Lo spazio intorno al nucleo in cui è possibile trovare con la massima probabilità gli elettroni viene chiamato orbitale. orbitale nucleo STPA-Chimica Organica 1 L orbitale 1s Gli
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Isomeria nelle molecole organiche
 Isomeria nelle molecole organiche 3 Cis/Trans o Z/E 1 4 Regole di priorità negli alcheni: 1. Numero atomico maggiore=maggiore priorità; 2. Maggiore priorità all isotopo più pesante; 3. Se il primo atomo
Isomeria nelle molecole organiche 3 Cis/Trans o Z/E 1 4 Regole di priorità negli alcheni: 1. Numero atomico maggiore=maggiore priorità; 2. Maggiore priorità all isotopo più pesante; 3. Se il primo atomo
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
La FORMA delle MOLECOLE
 La FORMA delle MOLECOLE Quando una molecola è costituita da due soli atomi, non vi è alcun dubbio sulla sua forma: gli atomi sono semplicemente disposti uno accanto all altro. Le molecole formate da tre
La FORMA delle MOLECOLE Quando una molecola è costituita da due soli atomi, non vi è alcun dubbio sulla sua forma: gli atomi sono semplicemente disposti uno accanto all altro. Le molecole formate da tre
LA STRUTTURA DELLE MOLECOLE. Orbitali molecolari e legame chimico
 LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
CENTRO DI MASSA. il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da:
 CENTRO DI MASSA il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da: dove M = m 1 + m 2 +... + m N è la massa totale del sistema e le quantità r i sono i raggi vettori
CENTRO DI MASSA il punto geometrico le cui coordinate, in un dato sistema di riferimento, sono date da: dove M = m 1 + m 2 +... + m N è la massa totale del sistema e le quantità r i sono i raggi vettori
CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA. - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES
 CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA TESTI: - John McMurry, CHIMICA ORGANICA, PICCIN - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES - Janice Gorzynski Smith, FONDAMENTI DI CHIMICA
CORSO DI LAUREA IN BIOTECNOLOGIE CHIMICA ORGANICA TESTI: - John McMurry, CHIMICA ORGANICA, PICCIN - Brown, Poon, INTRODUZIONE ALLA CHIMICA ORGANICA, EdiSES - Janice Gorzynski Smith, FONDAMENTI DI CHIMICA
H precedente. Procedendo come sopra, si costruisce la matrice del cambiamento di base
 Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
La matematica del CAD. Vettori e Matrici
 La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
Geometria molecolare
 Geometria molecolare Le molecole possono essere rappresentate disponendo gli atomi in posizioni definite nello spazio in modo da costruire una figura geometrica Il modo più semplice per assegnare la geometria
Geometria molecolare Le molecole possono essere rappresentate disponendo gli atomi in posizioni definite nello spazio in modo da costruire una figura geometrica Il modo più semplice per assegnare la geometria
IBRIDAZIONE e GEOMETRIA MOLECOLARE
 IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
Elementi di teoria degli insiemi
 ppendice Elementi di teoria degli insiemi.1 Introduzione Comincia qui l esposizione di alcuni concetti primitivi, molto semplici da un punto di vista intuitivo, ma a volte difficili da definire con grande
ppendice Elementi di teoria degli insiemi.1 Introduzione Comincia qui l esposizione di alcuni concetti primitivi, molto semplici da un punto di vista intuitivo, ma a volte difficili da definire con grande
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
1 Esercizi di ripasso 4
 Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
Esercizi con campi magnetici statici
 Esercizi con campi magnetici statici Il problema più generale è il calcolo del campo magnetico generato da uno o più fili percorsi da corrente. In linea di principio, questo tipo di problema dovrebbe essere
Esercizi con campi magnetici statici Il problema più generale è il calcolo del campo magnetico generato da uno o più fili percorsi da corrente. In linea di principio, questo tipo di problema dovrebbe essere
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Prisma retto. Generatrice. Direttrice. Prisma obliquo. Nel caso le generatrici non siano parallele. Generatrice
 Oggetti (identificati) nello spazio Una porzione di piano delimitata da una linea spezzata chiusa si chiama poligono, un solido delimitato da un numero finito di facce piane si chiama poliedro. In un poliedro
Oggetti (identificati) nello spazio Una porzione di piano delimitata da una linea spezzata chiusa si chiama poligono, un solido delimitato da un numero finito di facce piane si chiama poliedro. In un poliedro
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry)
 GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
06/03/2012. Elementi in chimica organica
 CORSO DI LAUREA IN BIOINFORMATICA CHIMICA ORGANICA E DELLE MACROMOLECOLE BIOLOGICHE MICHAEL ASSFALG Lezione: 6 CFU = 48 ORE Lun 14:30-16:30, 16:30, Mer 8:30-10:30 PROVA FINALE: SCRITTO (+ ORALE) TESTI:
CORSO DI LAUREA IN BIOINFORMATICA CHIMICA ORGANICA E DELLE MACROMOLECOLE BIOLOGICHE MICHAEL ASSFALG Lezione: 6 CFU = 48 ORE Lun 14:30-16:30, 16:30, Mer 8:30-10:30 PROVA FINALE: SCRITTO (+ ORALE) TESTI:
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici. Capitolo 10
 Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Laboratorio di informatica
 Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
LEZIONE 9. Figura 9.1.1
 LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
Elementi di Chimica Organica
 CORSO DI LAUREA IN BIOINFORMATICA Elementi di Chimica Organica Mariapina D Onofrio (mariapina.donofrio@univr.it) Orario ricevimento: mar e giov 11:30-13:30 Corso: 6 CFU = 48 ORE Lezioni: Mar 8:30-10:30,
CORSO DI LAUREA IN BIOINFORMATICA Elementi di Chimica Organica Mariapina D Onofrio (mariapina.donofrio@univr.it) Orario ricevimento: mar e giov 11:30-13:30 Corso: 6 CFU = 48 ORE Lezioni: Mar 8:30-10:30,
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
VETTORI E SCALARI DEFINIZIONI. Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura.
 VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo
 La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
Isomeri. Unità didattica 5. Isomeri cis-trans. La stereochimica. I composti achirali hanno immagini speculari sovrapponibili
 Isomeri Composti non identici ma che hanno la stessa formula molecolare Unità didattica 5 La stereochimica La disposizione degli atomi nello spazio; La stereochimica delle reazioni di addizione Isomeri
Isomeri Composti non identici ma che hanno la stessa formula molecolare Unità didattica 5 La stereochimica La disposizione degli atomi nello spazio; La stereochimica delle reazioni di addizione Isomeri
1 Congruenza diretta e inversa
 1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
FORMULE per la rappresentazione assonometrica della sfera e delle sue sezioni piane. 1 PREMESSE e convenzioni.
 Paolo Uccello. Studio prospettico. Galleria degli Uffizi, Firenze. FORMULE per la rappresentazione assonometrica della sfera e delle sue sezioni piane. 1 PREMESSE e convenzioni. È dato nello spazio un
Paolo Uccello. Studio prospettico. Galleria degli Uffizi, Firenze. FORMULE per la rappresentazione assonometrica della sfera e delle sue sezioni piane. 1 PREMESSE e convenzioni. È dato nello spazio un
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
GEOMETRIA ANALITICA 1 IL PIANO CARTESIANO
 GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
Matematica per Analisi dei Dati,
 Matematica per Analisi dei Dati, 230209 1 Spazio vettoriale R n Sia n un intero positivo fissato Lo spazio vettoriale R n e l insieme delle n ple ordinate di numeri reali, che rappresenteremo sempre come
Matematica per Analisi dei Dati, 230209 1 Spazio vettoriale R n Sia n un intero positivo fissato Lo spazio vettoriale R n e l insieme delle n ple ordinate di numeri reali, che rappresenteremo sempre come
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09
 NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
Le coniche retta generatrice
 Le coniche Consideriamo un cono retto a base circolare a due falde ed un piano. Le intersezioni possibili tra le due figure sono rappresentate dallo schema seguente Le figure che si possono ottenere sono
Le coniche Consideriamo un cono retto a base circolare a due falde ed un piano. Le intersezioni possibili tra le due figure sono rappresentate dallo schema seguente Le figure che si possono ottenere sono
Corso di Fisica. Lezione 2 Scalari e vettori Parte 1
 Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Il Legame Chimico e la Struttura Molecolare
 A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
Configurazione. Conformazione
 Configurazione Posizione relativa degli atomi nello spazio che caratterizza un particolare stereoisomero Sono in numero limitato (in genere 2) Conformazione Particolare geometria di una molecola che dipende
Configurazione Posizione relativa degli atomi nello spazio che caratterizza un particolare stereoisomero Sono in numero limitato (in genere 2) Conformazione Particolare geometria di una molecola che dipende
IL GRUPPO SO(3) , b a a R 2φ g R 1. a 2 + b 2 e i2φ N. Valendo a 2 + b 2 = 1, abbiamo dunque tr(r 2φ g R 1. Se diagonalizziamo R 2φ g R 1.
 IL GRUPPO SO3). Semplicità di SO3) Usando l omomorfismo suriettivo ρ : SU2) SO3) che abbiamo già descritto, possiamo dimostrare che SO3) è un gruppo semplice. In effetti, per far questo ci basta mostrare
IL GRUPPO SO3). Semplicità di SO3) Usando l omomorfismo suriettivo ρ : SU2) SO3) che abbiamo già descritto, possiamo dimostrare che SO3) è un gruppo semplice. In effetti, per far questo ci basta mostrare
Teoria degli orbitali ibridi
 Legami σ e π Teoria degli orbitali ibridi FORMAZIONE DEI LEGAMI CHIMICI COVALENTI L orbitale della molecola H 2 ha simmetria cilindrica intorno all asse internucleare H-H LEGAME SIGMA Gli orbitali molecolari
Legami σ e π Teoria degli orbitali ibridi FORMAZIONE DEI LEGAMI CHIMICI COVALENTI L orbitale della molecola H 2 ha simmetria cilindrica intorno all asse internucleare H-H LEGAME SIGMA Gli orbitali molecolari
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Geometria BAER Canale I Esercizi 10
 Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Progetto Matematica in Rete - Insiemi - Insiemi
 Insiemi Il concetto di insieme è molto importante in matematica. Cominciamo con lo stabilire cos è un insieme in senso matematico: un raggruppamento di oggetti è un insieme se si può stabilire in modo
Insiemi Il concetto di insieme è molto importante in matematica. Cominciamo con lo stabilire cos è un insieme in senso matematico: un raggruppamento di oggetti è un insieme se si può stabilire in modo
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI.
 VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
Geometria analitica: curve e superfici
 Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
La trasformazione di camera
 La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Figura. Stereochimica
 Figura Stereochimica Stereochimica: enantiomeri Differenze apparentemente insignificanti nella struttura 3-D possono causare proprietà molto differenti. Si può osservare questo considerando amido e cellulosa,
Figura Stereochimica Stereochimica: enantiomeri Differenze apparentemente insignificanti nella struttura 3-D possono causare proprietà molto differenti. Si può osservare questo considerando amido e cellulosa,
Piccola rassegna di Algebra delle Matrici
 Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Piccola rassegna di Algebra delle Matrici 1 Introduzione Questa nota va intesa semplicemente come un brevissimo sommario di alcuni concetti relativi alle Matrici, che dovete utilizzare nell ambito dello
Elementi di matematica - dott. I. GRASSI
 Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
1 Cambiamenti di riferimento nel piano
 1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Studio generale di una conica
 Studio generale di una conica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce conica C un equazione algebrica F (x 1, x 2, x 3 ) = 0 del secondo ordine omogenea. Detta A la matrice simmetrica
Studio generale di una conica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce conica C un equazione algebrica F (x 1, x 2, x 3 ) = 0 del secondo ordine omogenea. Detta A la matrice simmetrica
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
RETTE E PIANI NELLO SPAZIO
 VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
Trasformazioni geometriche del piano. 3 marzo 2013
 Trasformazioni geometriche del piano 3 marzo 2013 1 Indice 1 Trasformazioni geometriche del piano 3 1.1 Affinità............................... 4 1.2 Isometrie.............................. 8 1.2.1 Simmetrie..........................
Trasformazioni geometriche del piano 3 marzo 2013 1 Indice 1 Trasformazioni geometriche del piano 3 1.1 Affinità............................... 4 1.2 Isometrie.............................. 8 1.2.1 Simmetrie..........................
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
LEZIONE 9. k, tenendo conto delle formule che permettono di calcolare il prodotto scalare ed il prodotto vettoriale, otteniamo
 LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
Soluzioni dello scritto di Geometria del 28 Maggio 2009
 Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Il Legame Chimico e la Struttura Molecolare
 A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
A.A.2016 2017 CCS-Biologia CCS-Scienze Geologiche 1 Il Legame Chimico e la Struttura Molecolare Energia di interazione di due atomi di idrogeno Cap 8. 1-7, 9, 10(a/b), 17-20, 27-28, 31-33, 37-40, 52, 93-96
Cambiamenti di riferimento nel piano
 Cambiamenti di riferimento nel piano Stefano Capparelli November, 2013 Abstract Illustriamo con alcuni esempi il cambiamento di coordinate 1 Cambiamento di base Siano date due basi ortonormali ordinate
Cambiamenti di riferimento nel piano Stefano Capparelli November, 2013 Abstract Illustriamo con alcuni esempi il cambiamento di coordinate 1 Cambiamento di base Siano date due basi ortonormali ordinate
01 - Elementi di Teoria degli Insiemi
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 01 - Elementi di Teoria degli Insiemi Anno Accademico 2013/2014
7.1 LA TEORIA DEL LEGAME DI VALENZA INDICA CHE I LEGAMI SI FORMANO PER SOVRAPPOSIZIONE DEGLI ORBITALI
 7.1 LA TEORIA DEL LEGAME DI VALENZA INDICA CHE I LEGAMI SI FORMANO PER SOVRAPPOSIZIONE DEGLI ORBITALI Le strutture di Lewis non ci dicono nulla sul perché i legami covalenti si formano, né di come gli
7.1 LA TEORIA DEL LEGAME DI VALENZA INDICA CHE I LEGAMI SI FORMANO PER SOVRAPPOSIZIONE DEGLI ORBITALI Le strutture di Lewis non ci dicono nulla sul perché i legami covalenti si formano, né di come gli
Piano cartesiano e Retta
 Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
