Il modello relazionale. Il Modello Relazionale. Il modello relazionale. Relazione. Dominio. Esempio
|
|
|
- Ornella Bellucci
- 8 anni fa
- Visualizzazioni
Transcript
1 Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he permette i imostrre ormlmente proprietà i ti e operzioni le relzioni hnno un rppresentzione nturle per mezzo i telle 1 2 elzione, seene non si stto il moello usto nei primi DM, è ivenuto lentmente il moello più importnte l punto he è oggi omunemente usto in qusi tutti i DM isponiili livello ommerile l rgione priniple ell popolrità i questo moello è he ornise linguggi semplii e i tipo ihirtivo, m l tempo stesso potenti, on ui esprimere le operzioni per l'esso e l mnipolzione ei ti D 1, D 2,, D n (n insiemi nhe non istinti) il prootto rtesino D 1 D 2 D n, è l insieme i tutte le tuple orinte ( 1, 2,, n ) tli he 1 D 1, 2 D 2,, n D n un relzione su D 1, D 2,, D n è un sottoinsieme el prootto rtesino D 1 D 2 D n D 1, D 2,, D n sono i omini ell relzione un relzione su n omini h gro n il numero i tuple è l rinlità ell relzione nelle pplizioni reli, l rinlità è sempre init 3 4 Dominio Esempio Un ominio è un insieme (nhe ininito) i vlori: Esempi: l'insieme ei numeri interi l'insieme elle stringhe i rtteri i lunghezz 20 l'insieme {0,1} D 1 ={,} D 2 ={x,y,z} prootto rtesino D 1 D 2 un relzione r D 1 D 2 x y z x y z x z y z 5 6 1
2 elzione mtemti, proprietà Notzioni In se lle einizione, un relzione mtemti è un insieme i tuple orinte: ( 1, 2,, n ) tli he 1 D 1, 2 D 2,, n D n un relzione è un insieme, quini: non è einito lun orinmento r le tuple le tuple i un relzione sono istinte l un ll ltr un tupl è l proprio interno orint: l i-esimo vlore i isun proviene ll i -esimo ominio; è ioè einito un orinmento r i omini i r un relzione i gro k: si t un tupl i r si i un intero pprtenente ll'insieme {1,...,k} t[i] enot l i-esim omponente i t Esempio: i r={(0,), (0,),(1,)} i t=(0,) un tupl i r t[2] = t[1] = Moello relzionle Moello relzionle Un relzione può essere vist, lterntivmente, ome un tell, in ui ogni rig è un tupl e ogni olonn orrispone un omponente lle olonne sono ssoiti ei nomi, etti nomi i ttriuto l oppi (nome i ttriuto, ominio) è ett ttriuto l insieme egli ttriuti i un relzione ne ostituise lo shem e un relzione h nome e ttriuti i nomi rispettivmente 1, 2,..., k, lo shem è spesso inito on ( 1, 2,..., k ) inoltre U = { 1, 2,..., k } viene usto per enotre l'insieme i tutti i nomi i ttriuto ell relzione 9 10 Esempio Moello relzionle Ino_ittà ittà egione Popolzione om Lzio Milno Lomri Genov Liguri Pis Tosn hem: Ino_ittà(ittà,egione,Popolzione) In quest einizione el moello relzionle, le omponenti elle tuple sono enotte trmite i nomi i ttriuti (notzione per nome in ontrsto on l notzione per posizione) to uno shem i relzione ( 1, 2,..., k ), un tupl t su tle shem può essere rppresentt trmite l notzione [ 1 :v 1, 2 :v 2,..., k :v k ] ove v i (i=1,...,k) è un vlore pprtenente l ominio i i (inito on om( i )) inoltre t[ i ] enot il vlore ell'ttriuto i ell tupl t
3 Esempio Vlori nulli t=[ittà: om, egione: Lzio, Popolzione: ] è un tupl einit sullo shem Ino_ittà t[ittà] = om Il vlore ell ttriuto ittà per l tupl t è om Non sempre sono isponiili inormzioni sulle entità el ominio pplitivo rppresentto nell se i ti: lune tuple possono non vere un vlore per un qulhe ttriuto si introue un vlore speile (vlore nullo) he enot l mnnz i vlore (spesso enotto on '? ) Il onetto i hive Dt un relzione, l hive ell relzione è un insieme i ttriuti he istingue tr loro le tuple ell relzione più preismente, un insieme X i ttriuti i un relzione, è hive i se verii entrme le seguenti proprietà: 1 qulsisi si lo stto i, non esistono ue tuple istinte i he ino lo stesso vlore per tutti gli ttriuti in X 2 nessun sottoinsieme proprio i X verii l proprietà (1) 16 Esempio NNell'esempio preeente: hive(ino_ittà) = (ittà) e non esistono ittà on lo stesso nome in regioni iverse hive(ino_ittà) = (ittà,egione) se esistono ittà on lo stesso nome in regioni iverse Il onetto i hive hivi nite Un hive non può vere vlori nulli un relzione può vere più i un insieme X he verii le proprietà viste in luni si, può essere neessrio segliere un hive se il sistem usto non support più hivi in tl so, il termine hivi nite viene usto per inire le possiili hivi il termine hive primri viene usto per inire l hive seleziont Un riterio nell selt ell hive primri onsiste nello segliere tr le hivi nite quell più requentemente ust nelle interrogzioni un ltro riterio è segliere l hive he ontiene il minor numero i ttriuti
4 Il onetto i hive estern Il onetto i hive estern Dte ue relzioni e ' tli he: i un insieme i ttriuti X ' i ome hive un insieme Y i ttriuti Y è hive estern i su ' se Y è un sottoinsieme i X in ltre prole, se un relzione h tr i suoi ttriuti un insieme i ttriuti he ostituise l hive i un relzione, llor tle insieme i ttriuti è un hive estern i su ' ' è ett relzione rierit Le hivi esterne permettono i ollegre tr loro tuple i relzioni iverse e ostituisono un menismo, etto per vlore, per moellre le ssoizioni tr entità un tupl he eve rierire un'ltr tupl inlue tr i suoi ttriuti uno o più ttriuti il ui vlore è il vlore ell hive ell seon tupl Esempio Impiegti 21 Deinimo ue relzioni he ontengono inormzioni rigurnti i ipenenti i un'zien e i iprtimenti in ui l'zien è orgnizzt Le relzioni sono einite ome segue: Impiegti (Imp#, Nome, Mnsione, Dt_,tipenio, Premio_P,Dip#) hive(impiegti) = Imp# hive_estern(impiegti) = Dip# (relzione rierit: Diprtimenti) Diprtimenti(Dip#, Nome_Dip,Uiio#, Divisione#, Dirigente) hive(diprtimenti) = Dip# 22 Diprtimenti Integrità reerenzile L'integrità reerenzile rppresent un importnte vinolo i integrità semnti se un tupl t rierise ome vlori i un hive estern i vlori v 1,...,v n llor eve esistere nell relzione rierit un tupl t' on vlori i hive v 1,...,v n le relzioni Impiegti e Diprtimenti veriino l'integrità reerenzile
5 Integrit reerenzile Integrità reerenzile 25 Le operzioni he possono violre l integrit reerenzile sono: Inserimenti sull tell reerente i suppong he veng inserit l seguente tupl nell relzione Impiegti: [Imp#: 7899, Nome: mith, Mnsione: tenio, Dt_:03-Di-81, tipenio:2000,premio_p:100,dip#: 50] tle tupl viol l'integrità reerenzile in qunto non esiste un iprtimento (nell relzione Diprtimenti) he i numero 50 nellzioni o moiihe su tell rierit e si nell il iprtimento 10, le tuple egli impiegti he lvorno nel iprtimento 10 violno l integrit reerenzile e il oie el iprtimento 20 ivent 25, le tuple egli impiegti he lvorno nel iprtimento 20 violno l integrit reerenzile 26 I linguggi per si i ti (QL) permettono ll'utente i speiire per quli relzioni e quli ttriuti è neessrio mntenere l'integrità reerenzile (e le zioni eseguire in so i violzione) lger elzionle Operzioni nel Moello elzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori speilizzti lle relzioni lolo relzionle: le interrogzioni (query) sono espresse per mezzo i ormule logihe he evono essere veriite lle tuple ottenute ome rispost ll'interrogzione i ue ormlismi (sotto opportune ipotesi) sono equivlenti lger elzionle lger elzionle Esistono inque operzioni i se: Unione Dierenz Prootto rtesino Proiezione elezione queste operzioni einisono ompletmente l lger relzionle Ogni operzione restituise ome risultto un relzione: è pertnto possiile pplire un operzione l risultto i un'ltr operzione (proprietà i hiusur) esistono operzioni izionli, he possono essere espresse in termini elle inque operzioni i se
6 lger elzionle lger elzionle - Unione 31 Tli operzioni non ggiungono potere espressivo ll'insieme elle operzioni i se, m sono utili ome revizioni; i queste l più importnte è l'operzione i join rispetto ll notzione per nome el moello relzionle, può essere utile introurre un ulteriore operzione i renming he permette i moiire i nomi egli ttriuti 32 L unione i ue relzioni,, init on è l insieme elle tuple in, o in entrme l unione i ue relzione può essere tt solo se hnno lo stesso gro; inoltre il primo ttriuto i eve vere ominio omptiile on il primo ttriuto i, il seono ttriuto i eve vere ominio omptiile on il seono ttriuto i, e osì vi le tuple uplite vengono eliminte il gro ell relzione risultto è ugule l gro elle relzioni operni lger elzionle - Unione lger elzionle - Dierenz 33 Esempio: D E g F g 34 L ierenz i ue relzioni e, init on - è l insieme elle tuple he sono in m non in l ierenz (ome l unione) può essere eseguit solo se le relzioni hnno lo stesso gro e gli ttriuti hnno omini omptiili il gro ell relzione risultto è ugule l gro elle relzioni operni lger elzionle - Dierenz lger elzionle Prootto rtesino Esempio: D E g - F Il prootto rtesino i ue relzioni e, i gro k 1, k 2, inito on: X è un relzione i gro k 1 +k 2 le ui tuple sono tutte le tuple he hnno: ome prime k 1 omponenti le tuple i ome seone k 2 omponenti le tuple i
7 lger elzionle Prootto rtesino lger elzionle Prootto rtesino 37 Nell relzione risultto i nomi ei primi k 1 ttriuti sono i nomi egli ttriuti ell relzione e i nomi egli ultimi k 2 ttriuti sono i nomi egli ttriuti ell relzione se le ue relzioni hnno ttriuti on lo stesso nome, è neessrio rienominre gli ttriuti in un elle ue relzioni 38 Esempio: D E F g X D E g g g F lger elzionle - Proiezione lger elzionle - Proiezione 39 L proiezione i un relzione su un insieme i ttriuti ={ 1, m }, U, init on: è un relzione i gro m le ui tuple hnno ome ttriuti solo quelli speiiti in pertnto l proiezione gener un insieme T i m-tuple tli he se t=[ 1 :v 1, m :v m ] è in T llor esiste un tupl t in tle he per ogni i in, t[ i ]=t [ i ] nell relzione risultto gli ttriuti hnno l orine speiito in ( Π 1,, m ) 40 Esempio: Π, ( ) ( ) Π ( ) Π, lger elzionle - Preiti lger elzionle - Preiti Un preito F su un relzione h un elle seguenti orme: preito semplie ominzione oolen i preiti semplii (tli ominzioni sono ottenute on i onnettivi ND, O e NOT) Un preito semplie h un elle seguenti orme: op ostnte op e sono ttriuti i, op è un opertore relzionle i onronto >,<,>=,<=,=, e., ostnte è un ostnte omptiile on il ominio i
8 lger elzionle Esempi i preiti lger elzionle - elezione = preito semplie orm 1) = preito semplie orm 2) = O = ominzione oolen = ND = ominzione oolen NOT = ominzione oolen L selezione su un relzione, to un preito F, init on: σ F ( ) è un relzione he ontiene tutte e sole le tuple he veriino il preito F il gro ell relzione risultto è ugule l gro ell relzione operno; i nomi egli ttriuti ell relzione risultto sono gli stessi ell relzione operno se nessun tupl i verii il preito F, llor il risultto è un relzione vuot lger elzionle - elezione lger elzionle - elezione 45 e k è il gro i, l selezione gener un insieme T i k-tuple si t=[ 1 :v 1, k :v k ] un k-tupl in T t è tle he: F( 1 /t[ 1 ],, k /t[ k ]) è ver, ove l notzione i /t[ i ] ini l sostituzione in F el nome i ttriuto i (se tle nome ompre in F) on il vlore t[ i ] ell ttriuto i nome i in t 46 Esempio: = O= σ ( ) ( ) = σ NOT= σ ( ) σ ( ) = ND= lger elzionle - ienominzione lger elzionle - ienominzione L rienominzione i un relzione rispetto un list i oppie i nomi i ttriuti ( 1, 1 ),, ( m, m ) tle he i è un nome i ttriuto i, enott on: ρ 1, m 1,, m ( ) rienomin l ttriuto i nome i on il nome i l rienominzione è orrett se il nuovo shem ell relzione h ttriuti on nomi tutti istinti Esempio: L rienominzione: ρ,,,, ( ) mi lo shem (,,) in (,,)
9 lger elzionle Esempi lger elzionle - Esempi 49 Q1: selezionre i nomi egli impiegti he hnno uno stipenio mggiore i 2000 Π ( σ ( Impiegti) ) Nome tipenio> 2000 Nome osi lhi Neri Dre Veri 50 Π Q2: selezionre i nomi e i numeri i iprtimento egli impiegti he hnno uno stipenio mggiore i 2000 e hnno mnsione i ingegnere ( σ ( Impiegti) ) Nome, Dip# tipenio > 2000 ND Mnsione = 'ingegnere' Nome Neri Dre Dip# lger relzionle - Operzioni i se lger relzionle - Operzioni i se i = ( 1,..., k ) uno shem i relzione inihimo on () l'insieme i tutte le relzioni su tle shem _ _ : () () () r1 r2 = {t t r1 t r2} _ _ : (1) (2) (1 2) on 1 2 = r1 r2 = {t1 t2 t1 r1, t2 r2} _ π ' _ : () (') on ' π ' (r) = {t['] t r} 51 _ \ _ : () () () r1 \ r2 = {t t r1, t r2} 52 σ F _ : () () σ F (r) = {t t r, F(t)} lger elzionle - Join lger elzionle - Join Il join i ue relzioni e sugli ttriuti i e i, inito on θ ' è einito ome σ θ' ( ) il join è quini un prootto rtesino seguito un selezione il preito θ è etto preito i join Il gro ell relzione risultto è ugule ll somm ei gri elle relzioni operni spesso il join è inito on le seguenti notzioni:.θ. oppure [θ ] il join prene il nome i equijoin quno l opertore θ nel preito i join è l opertore i uguglinz
10 lger elzionle - Join lger elzionle Join nturle 55 Esempio: D E D = E E 1 D < D E L operzione i join nturle è un sempliizione el join si onsieri l interrogzione ritrovre tutti gli impiegti e gli uii ove lvorno. e usimo il join, tle interrogzione è espress ome: Π ( Impiegto Diprtimento) Nome, Uiio Impiegto.Dip# = Diprtimento.Dip# notre he questo join impone l uguglinz egli ttriuti he ppiono in entrme le relzioni lger elzionle Join nturle lger elzionle Join nturle E un tipo i join molto requente l operzione i join nturle ini un tipo i join sto sull eguglinz egli ttriuti omuni ue relzioni h senso solo nell notzione on nome, ierenz elle ltre operzioni, relzioni, { 1,, k }=U U insieme egli ttriuti presenti si nello shem i he nello shem i, {I 1,,I m }= U U insieme egli ttriuti nello shem i o nello shem i l espressione he einise il join nturle è Π I1,...,Im ( σ ( ( ρ ( ) )) 1,...,k.1,...,.k lger elzionle Join nturle lger elzionle Join nturle Nell ormul preeente ini l ormul Esempio: D 1=.1 ND 2 =.2 ND ND k =.k il join nturle esegue pertnto un join uguglino gli ttriuti on lo stesso nome elle ue relzioni e poi elimin gli ttriuti upliti il join nturle si ini on D e e e
11 lger relzionle - Intersezione lger relzionle - Intersezione 61 L intersezione i ue relzioni,, init on è l insieme elle tuple ontenute in e in l intersezione i ue relzione può essere tt solo se hnno lo stesso gro; inoltre il primo ttriuto i eve vere ominio omptiile on il primo ttriuto i, il seono ttriuto i eve vere ominio omptiile on il seono ttriuto i, e osì vi il gro ell relzione risultto è ugule l gro elle relzioni operni 62 L intersezione è un operzione erivt può intti essere einit ome segue: = - ( - ) ioè: si eterminno le tuple he stnno in m non in (-) si tolgono tutte le tuple he non stnno in ( - ( - )) le tuple risultnti stnno si in he in lger relzionle - Intersezione lger relzionle - Intersezione Esempio D E F g - - (-) lger relzionle - Divisione lger relzionle - Divisione 65 si suppong he gli impiegti ell se i ti i esempio sino ssegnti ei orsi i ggiornmento; ogni impiegto in genere prteip più orsi e vievers ogni orso è seguito più impiegti; vengono inoltre rppresentte le inormzioni reltivmente i orsi si suppong, pertnto, he sino einite le seguenti relzioni egue (Imp#, orso#) orsi (orso#, rgomento, Durt) 66 un possiile ontenuto elle ue relzioni è il seguente: egue orsi Imp# orso# orso# rgomento Durt D si i ti si i ti istemi oper
12 lger relzionle - Divisione lger relzionle - Divisione onsierimo l seguente interrogzione: "trovre il numero i impiegto egli impiegti he seguono tutti i orsi il ui rgomento è si i ti il numero i orso ei orsi il ui rgomento è si i ti è ottenuto ome segue: 1 = Π orso# (σ rgomento = 'si i ti' (orsi)) il risultto ell'espressione 1 è il seguente insieme i numeri i orso {10,30} il risultto ell interrogzione è to, pertnto, tutti quegli impiegti he ppiono nell relzione egue on ognuno ei numeri i orso eterminti 1 il risultto ell nostr interrogzione è pertnto solo l'impiegto il ui numero è 7369 l'operzione he permette i eseguire l'interrogzione preeente è l'operzione i ivisione lger relzionle - Divisione lger relzionle - Divisione Dte ue relzioni e on insiemi i ttriuti U e U, rispettivmente, e tli he U U, l'operzione i ivisione i per è enott e è espress ome segue: Π (U - U) () - Π (U - U) ((Π (U - U) () x ) - ) l'interrogzione ell'esempio preeente è espress ome segue = egue egue Π orso# (σ rgomento = 'si i ti' (orsi)) = Π orso# (σ rgomento = 'si i ti' (orsi)) 69 l'espressione estr el - etermin tutte le tuple i he non sono ssoite lmeno un tupl i 70 = {10, 30} U U = {Imp#, orso#} = {orso#} lger relzionle - Divisione lger relzionle - Divisione 1) Π (U - U) () = Π Imp# () = Imp# 3)(Π (U - U) () x ) - = (Π Imp# () x ) - = )Π (U - U) () x = Π Imp# () x = Imp# orso# Imp# orso# X = Imp# orso# Imp# orso# Imp# orso# - =
13 lger relzionle - Divisione lger relzionle - Operzioni erivte 73 4)Π (U - U) ((Π (U - U) () x ) - ) = Π Imp# ((Π Imp# () x ) - ) = Imp# )Π (U - U) () - lolto l psso (1) Π (U - U) ((Π (U - U) () x ) - ) lolto l psso (4) Imp# Imp# Imp# - = i = ( 1,..., k ) uno shem i relzione inihimo on () l'insieme i tutte le relzioni su tle shem _ _ : () () () r1 r2 = r1 \ (r1 \ r2) = {t t r1, t r2} _ x F _ : (1) (2) (1 2) on 1 2 = r1 x F r2 = σ F (r1 r2) = {t1 t2 t1 r1, t2 r2, F(t1,t2)} lger relzionle - Operzioni erivte lolo elzionle _ x _ : (1) (2) (1 2) r1 x r2 = {t t[1] r1, t[2] r2} - se 1 2 = r1 x r2 = r1 r2 - se 1 = 2 r1 x r2 = r1 r2 _ _ : (1) (2) (1 \ 2) on 1 2 r1 r2 = {t t2 r2 t1 r1 t.. t1[1\2] = t, t1[2] = t2} lger vs. lolo lolo relzionle - Vrinti L lger relzionle è un linguggio proeurle: nello speiire un espressione lgeri, oimo inire le operzioni neessrie per lolre il risultto ell query, insieme ll orine in ui queste operzioni evono essere svolte nel lolo relzionle viene t un esrizione ormle el risultto, senz speiire ome ottenerlo Due vrinti el lolo relzionle: Tuple reltionl lulus (T) le vriili rppresentno tuple Domin reltionl lulus (D) le vriili rppresentno vlori i omini veremo solo T
14 lolo relzionle lolo relzionle - Esempi In T un query è un espressione ell orm {t:u P(t)} ossi è einit ome l insieme i tutte le tuple einite su un insieme i ttriuti U tli he il preito P è vero per t notzione: t. ini il vlore ell tupl t per l ttriuto, t ini he t è nell relzione esempio: eterminre tutti gli impiegti il ui stipenio è mggiore i 2000 {t: U Impiegti t Impiegti t.tipenio>2000} Trovre il nome egli impiegti il ui stipenio è mggiore i 2000 {t:{nome} s(s Impiegti s.tipenio>2000 s.nome=t.nome)} t è un vriile he ini tuple pprtenenti un relzione he h ome shem {Nome} l notzione t(q(t)) ini he esiste un tupl t tle he Q(t) è ver lolo relzionle - Esempi lolo relzionle - Esempi Trovre i nomi e gli uii egli impiegti he hnno uno stipenio mggiore i 2000 {t:{nome,uiio} s(s Impiegti s.tipenio>2000 s.nome=t.nome u(u Diprtimenti s.dip#=u.dip# u.uiio=t.uiio))} Trovre i nomi egli impiegti he hnno uno stipenio mggiore i 2000 oppure lvorno in un iprtimento ell ivisione D1 {t:{nome} s(s Impiegti s.nome=t.nome ( s.tipenio>2000 u(u Diprtimenti s.dip#=u.dip# u.divisione= D1 )))} lolo relzionle - intssi lolo relzionle - sintssi tomi gli tomi sono: Formule 83 s ( è un nome i relzione e s è un vriile) l tupl s pprtiene ll relzione s.θu. (s e u sono vriili, θ è un opertore relzionle i onronto, e sono nomi i ttriuti) il vlore i nell tupl s è in relzione θ on il vlore i nell tupl u s. θ (s è un vriile, θ è un opertore relzionle i onronto, è un nome i ttriuto, è un ostnte) il vlore i nell tupl s è in relzione θ on il vlore 84 ogni tomo è un ormul, tutte le oorrenze elle vriili ell tomo sono liere se φ1 e φ2 sono ormule, llor φ1 φ2, φ1 φ2, φ1 sono ormule, le oorrenze elle vriili sono liere o legte seon i ome sono in φ1 e φ2 se φ è un ormul llor s(φ), s(φ) sono ormule tutte le oorrenze i s in φ sono legte l quntiitore (oppure ) se φ è un ormul llor (φ) è un ormul 14
15 lolo relzionle - intssi lolo relzionle - Esempi Vriili liere e legte t un ormul F e un vriile x, x è lier in F se e solo se x non è quntiit x (quntiizione universle) x (quntiizione esistenzile) s(s Impiegti s.tipenio>2000) è un ormul legle, tutte le oorrenze i s sono legte s(s Impiegti x.tipenio>2000 x.dip#= y.dip#) è un ormul legle, tutte le oorrenze i s sono legte mente quelle i x e y sono liere lolo relzionle - intssi lolo relzionle - Esempi Espressioni el lolo Un espressione (o query) el lolo su tuple h l orm {x:u (x)} ove U è un insieme i ttriuti, è un ormul legle el lolo, x è lier in (x) e è l uni vriile lier in (x) L espressione {y:{dip#} x(x Impiegti x.tipenio>2000 x.dip#=y.dip#)} è un espressione orrett i T he è soistt tutti i numeri ei iprtimenti he hnno lmeno un impiegto he gugn più i 2000 L espressione {y:u Impiegti y(y Impiegti y.mnsione= ingegnere )} non è un espressione orrett i T, in qunto y non è lier lolo relzionle Esprimere l lger on il T lolo relzionle Esprimere l lger on il T Unione: {t:u t t } Dierenz: - {t: U t t } Prootto rtesino: x sino U ={ 1,, n } e U ={ 1,, m } gli insiemi egli ttriuti i e {t: U U x( y(x y x. 1 =t. 1 x. n =t. n y. 1 =t. 1 y. m =t. m ))} Proiezione: Π 1, k () {t:{ 1,, k } x(x x. 1 =t. 1 x. k =t. k } elezione: σf() {t:u t F } ove F è l ormul F on ogni ttriuto sostituito t
16 lolo relzionle Potere espressivo lolo relzionle Potere espressivo L lger relzionle e il lolo relzionle hnno lo stesso potere espressivo? ioè: tutto le operzioni esprimiili meinte espressioni ell lger relzionle possono essere espresse meinte espressioni el lolo relzionle e vievers? L semnti i un interrogzione (in lger o in lolo) è un unzione he trsorm un se i ti relzionle (insieme i relzioni) in un nuov se i ti relzionle lger e lolo hnno lo stesso potere espressivo se per ogni interrogzione Q1 in uno ei ue ormlismi esiste un interrogzione Q2 nell ltro l ui semnti è l stess unzione lolo relzionle Potere espressivo lolo relzionle Potere espressivo 93 Non tutte le espressioni el lolo possono essere trotte in equivlenti espressioni ell lger esempio: l espressione {t:u t } seene sintttimente orrett, se lmeno uno ei omini egli ttriuti i è un insieme ininito, quest espressione è soistt un numero ininito i tuple il risultto non sree un relzione! 94 Nozione i ormul inipenente l ominio un ormul è inipenente l ominio se l su vlutzione gener sempre lo stesso risultto nhe supponeno i estenere i omini ssoiti gli ttriuti presenti nell se i ti on nuovi vlori, non presenti nell se i ti i prtenz si introue un onizione sinttti (sety) per grntire quest proprietà (non l veimo) Ie: mi restringo interrogzioni il ui risultto ipene solo vlori ontenuti nell se i ti i prtenz lolo relzionle - Potere espressivo lolo relzionle Potere espressivo l nozione i inipenenz l ominio è però ineiiile i introue quini un onizione sinttti (sety) suiiente grntire l inipenenz l ominio non veimo quest onizione L espressione {t:u t } non è se il lolo relzionle se e l lger relzionle hnno lo stesso potere espressivo l truzione un ormlismo ll ltro può essere eettut in tempo polinomile nell imensione ell espressione
17 Perhé ue linguggi? Esempio 97 lger relzionle linguggio proeurle utile per il sistem lolo relzionle linguggio ihirtivo utile per l utente i linguggi i interrogzione nei sistemi reli si sno sul lolo l lger relzionle viene utilizzt ome linguggio interno l interrogzione utente viene ompilt in un espressione ell lger relzionle il sistem utilizz le proprietà ell lger per stilire qule espressione permette i risolvere l interrogzione inizile nel moo più eiiente 98 Determinre i nomi egli impiegti he lvorno nell ivisione D1 lolo {t:{nome} s(s Impiegti s.nome=t.nome u(u Diprtimenti s.dip#=u.dip# u.divisione= D1 )))} lger () Π σ 1 Im piegti Diprtimenti ( ( )) Nome Divisione= D Esempio (ontinu) Poihé l ttriuto Divisione U Diprtimenti, è possiile ntiipre l selezione () Π Nome ( Impiegti σ Divisione= D1( Diprtimenti )) upponimo he: Impiegti onteng n 1 tuple Diprtimenti onteng n 2 tuple (rgionevolmente n 2 <= n 1 ) i iprtimenti ell ivisione D1 sono n 3 (n 3 <= n 2 ) osti (): join:n 1 x n 2, selezione: n 1, proiezione: n 1, totle: n 1 x n 2 +2n 1 99 (): selezione: n 2, join: n 1 x n 3, proiezione: n 1, totle: n 1 x n 3 +n 1 +n 2 osto() > osto() il sistem seglie l espressione () 17
Il modello relazionale. Il Modello Relazionale. Il modello relazionale. Relazione. Dominio. Esempio
 Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Algebra Relazionale. Operazioni nel Modello Relazionale
 lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
La rappresentazione per elencazione consiste nell elencare tutte le coppie ordinate che verificano la relazione
 RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
ESERCIZI IN PIÙ ESERCIZI DI FINE CAPITOLO
 L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
Unità D1.2 Selezione e proiezione
 (A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
(A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
Componenti per l elaborazione binaria dell informazione. Sommario. Sommario. Approfondimento del corso di reti logiche. M. Favalli.
 Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie
Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie
Esercitazione n. 2. Gian Carlo Bondi VERO/FALSO
 Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
A.A.2009/10 Fisica 1 1
 Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
F (r(t)), d dt r(t) dt
 Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
! è l'insieme A degli attributi di ! $ B IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI IL PROBLEMA DELLE VISTE MATERIALIZZATE
 IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
Numeri razionali COGNOME... NOME... Classe... Data...
 I numeri rzionli Cpitolo Numeri rzionli Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
I numeri rzionli Cpitolo Numeri rzionli Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
FUNZIONI MATEMATICHE. Una funzione lineare è del tipo:
 FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
] + [ ] [ ] def. ] e [ ], si ha subito:
![] + [ ] [ ] def. ] e [ ], si ha subito: ] + [ ] [ ] def. ] e [ ], si ha subito:](/thumbs/24/3548090.jpg) OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
3. Funzioni iniettive, suriettive e biiettive (Ref p.14)
 . Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
. Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
13. EQUAZIONI ALGEBRICHE
 G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
Monomi e polinomi. Verifica per la classe prima COGNOME... NOME... Classe... Data...
 Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Lezione 7: Rette e piani nello spazio
 Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
4 - TRASFORMAZIONI DI VARIABILI CASUALI
 4 - RASFORMAZIONI DI VARIABILI CASUALI 4 rsformzioni i vriili suli Cominimo un esempio Si l vriile sule lnio i un o non truto : / / / 4 / 5 / / e g() si l orrisponenz: pri test ispri roe Poihé g()g(4)g()test
4 - RASFORMAZIONI DI VARIABILI CASUALI 4 rsformzioni i vriili suli Cominimo un esempio Si l vriile sule lnio i un o non truto : / / / 4 / 5 / / e g() si l orrisponenz: pri test ispri roe Poihé g()g(4)g()test
Relazioni e funzioni. Relazioni
 Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Esercizi per il corso di Calcolatori Elettronici
 Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Scomposizione di polinomi 1
 Somposizione i un polinomio Cpitolo Somposizione i polinomi 1 erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Somposizione i un polinomio Cpitolo Somposizione i polinomi 1 erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quinto appello, 3 luglio 2017 Testi 1
 nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
VERIFICA DI UN CIRCUITO RESISTIVO CONTENENTE PIÙ GENERATORI CON UN TERMINALE COMUNE E SENZA TERMINALE COMUNE.
 FCA D UN CCUTO SSTO CONTNNT PÙ GNATO CON UN TMNAL COMUN SNZA TMNAL COMUN. Si verifino quttro iruiti on due genertori: genertori on polrità onorde e un terminle omune genertori on polrità disorde e un terminle
FCA D UN CCUTO SSTO CONTNNT PÙ GNATO CON UN TMNAL COMUN SNZA TMNAL COMUN. Si verifino quttro iruiti on due genertori: genertori on polrità onorde e un terminle omune genertori on polrità disorde e un terminle
Sondaggio piace l eolico?
 Songgio pie l eolio? Durnte l inugurzione i Stell sono stti istriuiti ei questionri per vlutre l inie i grimento ell eolio prte ell popolzione Sono stti ompilti e quini nlizzti 50 questionri Quest presentzione
Songgio pie l eolio? Durnte l inugurzione i Stell sono stti istriuiti ei questionri per vlutre l inie i grimento ell eolio prte ell popolzione Sono stti ompilti e quini nlizzti 50 questionri Quest presentzione
Il Modello Relazionale
 Il Modello Relazionale 1 Proposto da E. F. Codd nel 1970 per favorire l indipendenza dei dati e reso disponibile come modello logico in DBMS reali nel 1981 Si basa sul concetto matematico di relazione,
Il Modello Relazionale 1 Proposto da E. F. Codd nel 1970 per favorire l indipendenza dei dati e reso disponibile come modello logico in DBMS reali nel 1981 Si basa sul concetto matematico di relazione,
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
L insieme Q+ Le frazioni Operazioni con le frazioni Problemi con le frazioni
 L insieme Q+ Le frzioni Operzioni on le frzioni Prolemi on le frzioni Le frzioni Ini l rispost estt. In un frzione il numertore ini SEZ. C in qunte prti si ivie l unità. qunti interi si onsierno. qunte
L insieme Q+ Le frzioni Operzioni on le frzioni Prolemi on le frzioni Le frzioni Ini l rispost estt. In un frzione il numertore ini SEZ. C in qunte prti si ivie l unità. qunti interi si onsierno. qunte
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Analisi Matematica I per Ingegneria Gestionale, a.a Primo compitino, 18 novembre 2017 Testi 1
 Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
j Verso la scuola superiore Verso l algebra astratta
 j erso l suol superiore erso l lger strtt +nsiemi unzioni Operzioni inrie e strutture lgerihe Relzioni Logi Proilità +nsiemi ndividu l rispost estt. Un insieme è finito se: è formto d pohi elementi. è
j erso l suol superiore erso l lger strtt +nsiemi unzioni Operzioni inrie e strutture lgerihe Relzioni Logi Proilità +nsiemi ndividu l rispost estt. Un insieme è finito se: è formto d pohi elementi. è
Vettori - Definizione
 Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
8 Equazioni parametriche di II grado
 Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Politecnico di Milano Facoltà di Ingegneria dell Automazione INFORMATICA INDUSTRIALE Appello COGNOME E NOME. 11 febbraio 2008 RIGA COLONNA MATRICOLA
 Politecnico i Milno Fcoltà i Ingegneri ell Automzione INFORMATICA INDUSTRIALE Appello COGNOME E NOME ebbrio 2008 RIGA COLONNA MATRICOLA Il presente plico pinzto, composto i quttro ogli (ronte/retro)eve
Politecnico i Milno Fcoltà i Ingegneri ell Automzione INFORMATICA INDUSTRIALE Appello COGNOME E NOME ebbrio 2008 RIGA COLONNA MATRICOLA Il presente plico pinzto, composto i quttro ogli (ronte/retro)eve
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
GT Definizione di grafo orientato e non
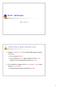 Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Calcolo del costo unitario FASE 1
 ESERCIZIO Definizione el pino ei entri i osto e eterminzione el osto unitrio i prootto Clolo el osto unitrio FASE 1 Azien i prouzione: proue i eni,,, Il proesso prouttivo prevee 3 fsi o proessi prinipli:
ESERCIZIO Definizione el pino ei entri i osto e eterminzione el osto unitrio i prootto Clolo el osto unitrio FASE 1 Azien i prouzione: proue i eni,,, Il proesso prouttivo prevee 3 fsi o proessi prinipli:
Minimizzazione di automi
 Minimizzzione di utomi Teorem e per ogni stto q di un DFA si re un loo tr q e tutti gli stti equivlenti q, llor l insieme dei lohi distinti rppresent un prtizione dell insieme degli stti. Ne deriv he ogni
Minimizzzione di utomi Teorem e per ogni stto q di un DFA si re un loo tr q e tutti gli stti equivlenti q, llor l insieme dei lohi distinti rppresent un prtizione dell insieme degli stti. Ne deriv he ogni
Disequazioni di primo grado
 Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equazioni di primo grado
 Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
d coulomb d volt b trasformatore d alternatore b amperometro d reostato
 ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Terza. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Terz Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Terz Suol..........................................................................................................................................
Disequazioni di secondo grado
 Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Corso di ELETTRONICA INDUSTRIALE
 0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
Teoria in sintesi ESPONENZIALI. Potenze con esponente reale. La potenza. Sono definite: Non sono definite: Casi particolari :
 Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >, per ogni R se, per tutti e soli gli R se
Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >, per ogni R se, per tutti e soli gli R se
ALGORITMI E COMPLESSITÀ CORSO DI LAUREA MAGISTRALE IN INFORMATICA UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
Corso di laurea in Informatica Applicata Fondamenti di Programmazione Appello 6/2/03
 Eserizio 1 Corso di lure in Informti Applit Fondmenti di Progrmmzione Appello 6/2/03 Prim prte i L(A) il linguggio sull lfeto {,,} he rionose le sequenze (nhe vuote) tli he il simolo è sempre seguito dl
Eserizio 1 Corso di lure in Informti Applit Fondmenti di Progrmmzione Appello 6/2/03 Prim prte i L(A) il linguggio sull lfeto {,,} he rionose le sequenze (nhe vuote) tli he il simolo è sempre seguito dl
Test di autovalutazione
 UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
COMBINAZIONI DI CARICO SOLAI
 COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
! Una gerarchia ricorsiva deriva dalla presenza di una ricorsione o ciclo (un anello nel caso più semplice) nello schema operazionale.
 Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Il piano cartesiano e la retta
 Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Piero Gallo Fabio Salerno. Task. Corso di informatica. Gli archivi sequenziali. il libro si estende sul web
 Piero Gllo Fio Slerno Tsk Corso i informti 2 il liro si estene sul we Gli rhivi sequenzili il liro si estene sul we LEZIONE L orgnizzzione sequenzile L orgnizzzione logi sequenzile Con rhivio logio sequenzile
Piero Gllo Fio Slerno Tsk Corso i informti 2 il liro si estene sul we Gli rhivi sequenzili il liro si estene sul we LEZIONE L orgnizzzione sequenzile L orgnizzzione logi sequenzile Con rhivio logio sequenzile
Elettronica dei Sistemi Digitali Disegno del layout di porte logiche combinatorie CMOS
 Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
01 Matematica Liceo \ Unità Didattica N 6 La retta 1
 Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
T16 Protocolli di trasmissione
 T16 Protoolli di trsmissione T16.1 Cos indi il throughput di un ollegmento TD?.. T16.2 Quli tr le seguenti rtteristihe dei protoolli di tipo COP inidono direttmente sul vlore del throughput? Impossiilità
T16 Protoolli di trsmissione T16.1 Cos indi il throughput di un ollegmento TD?.. T16.2 Quli tr le seguenti rtteristihe dei protoolli di tipo COP inidono direttmente sul vlore del throughput? Impossiilità
Ambiguità D 11 = SS ( S S S ( S (S ) S ( S ((S )) S ( + S (( )) S (S (( )) (S) (S (( )) ( ) ( (( )) ( )
 Amiguità D 11 = ( ( ( ) ( (( )) ( (( )) ( (( )) () ( (( )) ( ) ( (( )) ( )! ( ) ( )! Un Grmmti si die migu se medesime stringhe sono generte d leri sintttii di differente struttur ovvero on due distinte
Amiguità D 11 = ( ( ( ) ( (( )) ( (( )) ( (( )) () ( (( )) ( ) ( (( )) ( )! ( ) ( )! Un Grmmti si die migu se medesime stringhe sono generte d leri sintttii di differente struttur ovvero on due distinte
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe terza. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA
 VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA trtto Mtemti in zione, A. Arpinti, M. Musini Mettimoi ll prov! Suol..........................................................................................................................................
VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA trtto Mtemti in zione, A. Arpinti, M. Musini Mettimoi ll prov! Suol..........................................................................................................................................
Esercizi della 8 lezione sulla Geomeria Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ERCIZI SULL' IPERBOLE
 Eserizi dell lezione sull Geomeri Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ES ERCIZI SULL' IPERBOLE ESERCIZI SULLA CIRCONFERENZA. Determinre l equzione dell ironferenz
Eserizi dell lezione sull Geomeri Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ES ERCIZI SULL' IPERBOLE ESERCIZI SULLA CIRCONFERENZA. Determinre l equzione dell ironferenz
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE
 VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
La statistica nei test Invalsi
 L sttisti nei test Invlsi 1) Osserv il grfio seguente he rppresent l distriuzione perentule di fmiglie per numero di omponenti, in se l ensimento 2001.. Qul è l perentule di fmiglie on 2 omponenti? Rispost:..%.
L sttisti nei test Invlsi 1) Osserv il grfio seguente he rppresent l distriuzione perentule di fmiglie per numero di omponenti, in se l ensimento 2001.. Qul è l perentule di fmiglie on 2 omponenti? Rispost:..%.
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
a a = 1, a a = 0; a a = 1, a a = 0; e quindi, = (a a ) (a a ) = (a a) a = 0 a = a
 Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Ellisse ed iperbole. Osservazione. Considereremo sempre ellissi della forma + = 1 le quali hanno tutte centro nell origine degli
 Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
www.scuolaazienda.it MARIO FLORES L OPERATORE TURISTICO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi
 www.scuolaazienda.it MRIO FLORES L OPERTORE 4 TURISTIO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi VERO O FLSO? MOULO 1 1 V, 2 V, 3 F, 4 F 1 V, 2 V, 3 V, 4 F 1 V, 2 F, 3 F, 4 V 1 F, 2 F,
www.scuolaazienda.it MRIO FLORES L OPERTORE 4 TURISTIO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi VERO O FLSO? MOULO 1 1 V, 2 V, 3 F, 4 F 1 V, 2 V, 3 V, 4 F 1 V, 2 F, 3 F, 4 V 1 F, 2 F,
Geometria analitica +l piano cartesiano Le funzioni retta, parabola, iperbole Le trasformazioni sul piano cartesiano
 Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Barriere all entrata e modello del Prezzo Limite Economia industriale Università Bicocca
 Brriere ll entrt e modello del Prezzo imite onomi industrile Università Bio Christin Grvgli - Giugno 006 Brriere ll entrt definizioni Condizioni he permettono lle imprese opernti in un industri di elevre
Brriere ll entrt e modello del Prezzo imite onomi industrile Università Bio Christin Grvgli - Giugno 006 Brriere ll entrt definizioni Condizioni he permettono lle imprese opernti in un industri di elevre
MATRICI E DETERMINANTI
 MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
Sistemi Informativi Territoriali. La geometria imperfetta. Paolo Mogorovich Incoerenza monolayer Ricerca di una soluzione
 Inoerenz monolyer Rier i un soluzione Sistemi Informtivi Territorili Polo Mogorovih www.i.unipi.it/~mogorov L geometri imperfett Inoerenz monolyer Rier i un soluzione Vertii importnti e vertii meno importnti
Inoerenz monolyer Rier i un soluzione Sistemi Informtivi Territorili Polo Mogorovih www.i.unipi.it/~mogorov L geometri imperfett Inoerenz monolyer Rier i un soluzione Vertii importnti e vertii meno importnti
L'equazione di continuità
 L'equazione i continuità Una prima imostrazione. Consieriamo il volume occupato a una istribuzione i cariche ρ (t, x). È possibile esprimere la proprietà i conservazione ella carica nel seguente moo t
L'equazione i continuità Una prima imostrazione. Consieriamo il volume occupato a una istribuzione i cariche ρ (t, x). È possibile esprimere la proprietà i conservazione ella carica nel seguente moo t
Icone, finestre e strutture dati
 u t o n e n i t à i m r e n i p p Ione, finestre e strutture ti Competenze speifihe Il signifito elle prinipli ione, il loro spostmento e orinmento sul esktop I prinipli elementi elle finestre elle pplizioni
u t o n e n i t à i m r e n i p p Ione, finestre e strutture ti Competenze speifihe Il signifito elle prinipli ione, il loro spostmento e orinmento sul esktop I prinipli elementi elle finestre elle pplizioni
Esercizi per il corso di Calcolatori Elettronici. svolti da Mauro IACOVIELLO & Fabio LAUDANI
 Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
Verifica per la classe seconda COGNOME... NOME... Classe... Data...
 L rett Cpitolo Rett erifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt............................... Rett Rette
L rett Cpitolo Rett erifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt............................... Rett Rette
CORSO DI RAGIONERIA A.A. 2013/2014
 CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 10 LE SCRITTURE CONTABILI Il lesing IL CONTRATTO DI LEASING Il lesing è un contrtto tipico (non previsto dl Codice Civile) per mezzo del qule l ziend
CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 10 LE SCRITTURE CONTABILI Il lesing IL CONTRATTO DI LEASING Il lesing è un contrtto tipico (non previsto dl Codice Civile) per mezzo del qule l ziend
= det b, a, b, c R 3. In quest ottica, il determinante del terzo ordine e caratterizzato dalle seguenti proprieta : a a. c c
 Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Tecniche di Progettazione Digitale Progettazione e layout di porte logiche combinatorie CMOS p. 2
 Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
( ) 1. Scrivi l equazione della parabola ad asse verticale passante per il punto ( ) P e con vertice. Soluzione Dall equazione generica della parabola
 . Srivi l euzione dell prol d sse vertile pssnte per il punto ( ) ; P e on vertie ( ) ; V. Dll euzione generi dell prol e dll onosenze del vertie, le ui oordinte generihe sono V ; possimo srivere sostituendo
. Srivi l euzione dell prol d sse vertile pssnte per il punto ( ) ; P e on vertie ( ) ; V. Dll euzione generi dell prol e dll onosenze del vertie, le ui oordinte generihe sono V ; possimo srivere sostituendo
Unità Didattica N 08 I sistemi di primo grado a due incognite U.D. N 08 I sistemi di primo grado a due incognite
 66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
KIT ESTIVO MATEMATICA A.S. 2015/16 CLASSI SECONDE IeFP OPERATORE GRAFICO
 ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
Millenium 3 Interfaccia di comunicazione M3MOD Guida all'uso della Directory operativa 04/2006
 Millenium 3 Interfi i omunizione M3MOD Gui ll'uso ell Diretory opertiv 04/2006 160633105 Pnormi AGui ll'uso ell Diretory opertiv Introuzione L Diretory opertiv è un file i testo generto l softwre i progrmmzione
Millenium 3 Interfi i omunizione M3MOD Gui ll'uso ell Diretory opertiv 04/2006 160633105 Pnormi AGui ll'uso ell Diretory opertiv Introuzione L Diretory opertiv è un file i testo generto l softwre i progrmmzione
Allegato 3 Elenco BAT ed esempio interventi efficientamento
 Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Introduzione all algebra
 Introduzione ll lgebr E. Modic ersmo@glois.it Liceo Scientifico Sttle S. Cnnizzro Corso P.O.N. Modelli mtemtici e reltà A.S. 2010/2011 Premess Codificre e Decodificre Nell vit quotidin ci cpit spesso di
Introduzione ll lgebr E. Modic ersmo@glois.it Liceo Scientifico Sttle S. Cnnizzro Corso P.O.N. Modelli mtemtici e reltà A.S. 2010/2011 Premess Codificre e Decodificre Nell vit quotidin ci cpit spesso di
Momento di una forza rispettto ad un punto
 Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Definizione opposto: Somma. Definizione vettore 0:
 Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Ing. Alessandro Pochì
 Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
In generale i piani possono essere tra loro
 Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
VERIFICA DI MATEMATICA 1^F Liceo Sportivo 15 marzo 2018 Rispondere su un foglio protocollo e riconsegnare entro il 22 marzo 2018 NOME E COGNOME
 VERIFICA DI MATEMATICA 1^F Liceo Sportivo 15 mrzo 2018 Risponere su un foglio protocollo e riconsegnre entro il 22 mrzo 2018 NOME E COGNOME 1 Eseguire le seguenti moltipliczioni tr monomi, scriveno il
VERIFICA DI MATEMATICA 1^F Liceo Sportivo 15 mrzo 2018 Risponere su un foglio protocollo e riconsegnre entro il 22 mrzo 2018 NOME E COGNOME 1 Eseguire le seguenti moltipliczioni tr monomi, scriveno il
30 quesiti. 1 Febbraio 2011. Scuola... Classe... Alunno... Copyright 2011 Zanichelli Editore SpA, Bologna
 verso LA RILEVAZIONE INVALSI SCUOLA SECONDARIA DI secondo GRADO PROVA DI Mtemtic 30 quesiti Febbrio 0 Scuol... Clsse... Alunno... e b sono numeri reli che verificno quest uguglinz: Qunto vle il loro prodotto?
verso LA RILEVAZIONE INVALSI SCUOLA SECONDARIA DI secondo GRADO PROVA DI Mtemtic 30 quesiti Febbrio 0 Scuol... Clsse... Alunno... e b sono numeri reli che verificno quest uguglinz: Qunto vle il loro prodotto?
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
SISTEMI LINEARI. perché la prima equazione ha grado 3, la seconda 5, la terza 7 ( = 105)
 Autore: Enrio Mnfui - 5/4/ SISTEMI LINEARI Un sistem i equioni è un insieme i equioni i ui si vogliono lolre le soluioni omuni. un punto i vist ell teori egli insiemi questo vuol ire he se l prim equione
Autore: Enrio Mnfui - 5/4/ SISTEMI LINEARI Un sistem i equioni è un insieme i equioni i ui si vogliono lolre le soluioni omuni. un punto i vist ell teori egli insiemi questo vuol ire he se l prim equione
operazioni con vettori
 omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
Elettronica dei Sistemi Digitali Il test nei sistemi elettronici: guasti catastrofici e modelli di guasto (parte I)
 Elettronic dei Sistemi Digitli Il test nei sistemi elettronici: gusti ctstrofici e modelli di gusto (prte I) Vlentino Lierli Diprtimento di Tecnologie dell Informzione Università di Milno, 26013 Crem e-mil:
Elettronic dei Sistemi Digitli Il test nei sistemi elettronici: gusti ctstrofici e modelli di gusto (prte I) Vlentino Lierli Diprtimento di Tecnologie dell Informzione Università di Milno, 26013 Crem e-mil:
ALCUNE OSSERVAZIONI SUI TRIANGOLI
 LUNE OSSERVZIONI SUI TRINGOLI ataloghiamo i triangoli seondo i lati seondo gli angoli 115 3 67 81 Esiste sempre il triangolo? Selte a aso le misure dei lati, è sempre possibile ostruire il triangolo? Quali
LUNE OSSERVZIONI SUI TRINGOLI ataloghiamo i triangoli seondo i lati seondo gli angoli 115 3 67 81 Esiste sempre il triangolo? Selte a aso le misure dei lati, è sempre possibile ostruire il triangolo? Quali
