Algebra Trigonometrica
|
|
|
- Flaviana Lelli
- 7 anni fa
- Visualizzazioni
Transcript
1 Capitolo S-04 Algebra Trigonometrica Autore: Mirto Moressa Contatto: Sito: Data inizio: 19/10/009 Data fine: 08/1/009 Ultima modifica: 0/0/010 Versione:.3 Indice del capitolo 1) Nozioni preliminari: 1)def. angolo; )def. triangolo e classificazione; 3)propr.; 4)disuguaglianza triangolare; 5)Teorema di Pitagora; 6)triang. rett ; 7) triang. rett ; 8)angoli espressi in radianti; ) Seno e Coseno: 1)def.; )propr. fondamentale; 3)grafico; 4)periodicità; 3) Tangente e Cotangente: 1)def.; )grafico; 3)periodicità; 4) Altre funzioni: 1)funzioni reciproche; )funzioni inverse; 5) Formule: 1)angoli associati; )di sottrazione; 3)di addizione; 4)di duplicazione; 5)di bisezione; 6)di prostaferesi; 7)di Werner; 8)parametriche; 6) Equazioni goniometriche: 1)di 1º grado; )di º grado; 7) Disequazioni goniometriche: 1)di 1º grado; )di º grado; 8) Relazioni tra i lati di un triangolo rettangolo; 9) Relazioni tra i lati di un triangolo qualsiasi: 1)Teorema dei seni (Eulero); )Teorema del coseno (Carnot);
2
3 4.1) Nozioni preliminari Tutta la trigonometria si fonda su questi concetti ) Def: Un angolo è la parte di piano delimitata da due semirette, uscenti da uno stesso punto, detto vertice. L'unità di misura è il grado (º) e l'intero piano (angolo giro) misura 360º. In base alla misura, un angolo si dice acuto (<90º), retto (=90º), ottuso (>90º e < 180º), piatto (=180º). 4.1.) Def: Un triangolo è una figura piana di tre lati (e tre angoli). Un triangolo si può classificare: - in base ai lati: equilatero (3 lati uguali), isoscele ( lati uguali), scaleno (lati tutti diversi); - in base agli angoli: acutangolo (3 angoli acuti), rettangolo (1 angolo retto), ottusangolo (1 angolo ottuso); 4.1.3) Prop: In ogni triangolo la somma dei tre angoli è 180º. Ne consegue che in un triangolo rettangolo, la somma dei due angoli acuti è 90º ) Disuguaglianza triangolare In ogni triangolo la somma della misura di due lati è superiore alla misura del terzo lato (altrimenti il triangolo non si chiuderebbe). - I forma: abc - II forma: ac b (cioè un lato è maggiore della differenza degli altri due) Se bc la II forma è ovvia perché il secondo membro è negativo; se cb la II forma è già più interessante ) Teorema di Pitagora In un triangolo rettangolo, la somma dei quadrati costruiti sui cateti (lati adiacenti all'angolo retto) è uguale al quadrato costruito sull'ipotenusa (lato opposto all'angolo retto) ) Triangolo rettangolo È il primo triangolo notevole: è un triangolo rettangolo, i cui angoli acuti misurano entrambi 45º (è metà quadrato). Risulta, quindi, anche isoscele. 45º 1 45º 90º Se l'ipotenusa misura 1, i cateti devono misurare ciascuno, per il teorema di Pitagora. Infatti si ha: 1 =
4 4.1.7) Triangolo rettangolo È il secondo (e ultimo per quanto ci riguarda) triangolo notevole: è un triangolo rettangolo, i cui angoli acuti misurano uno 30º e l'altro 60º. È metà triangolo equilatero. 60º º 60º º 1 30º 90º 3 Se l'ipotenusa misura 1, il cateto di base deve misurare 1 (perché metà lato), mentre l'altro cateto deve misurare 3, sempre per il teorema di Pitagora. Infatti si ha: 1 = ) Angoli espressi in radianti Un'altra unità di misura per esprimere gli angoli sono i radianti. Per definirli si considera una circonferenza di raggio unitario (che è lunga ), si tracciano due assi perpendicolari (che suddividono il piano in 4 quadranti), si definisce l'estremo destro come lo 0 (punto di partenza) e il senso di rotazione antiorario come positivo (dunque il senso orario è negativo). L'angolo è espresso come lunghezza dell'arco di circonferenza che individua. All'angolo giro (360º) corrisponde la circonferenza completa ( ) II quadrante III quadrante I quadrante IV quadrante NOTA BENE: dopo aver fatto un giro completo (in senso antiorario), gli angoli cominciano a ripetersi; si vede, infatti, come in 0 ritorni : 0 è una quantità evidentemente diversa da, ma identifica lo stesso angolo; se avessimo continuato avremmo trovato che 6 identifica lo stesso angolo di, e così via. 6 Se ne deduce una periodicità angolare: misure in radianti che differiscono di, sono in realtà nomi diversi dello stesso angolo. Il discorso non cambia se giriamo in senso orario, ma in quel caso bisogna fare attenzione ai segni (es. 6 identifica lo stesso angolo di 11 6, ed infatti distano tra loro ).
5 4.) Seno e Coseno 4..1) Def: Dato un angolo sulla circonferenza di raggio unitario, si tracciano le proiezioni sugli assi verticale e orizzontale. La lunghezza del segmento verticale è il seno, mentre quella del segmento orizzontale è il coseno di quell'angolo. es.1) angoli = 0, es.) angolo = 6 sen0 = 0 cos0 = 1 sen 6 = 1 sen = 1 cos = 0 cos 6 = 3 (vedi triangolo rett ) es.3) angolo = 4 es.4) angolo = 3 sen 4 = cos 4 = sen 3 = 3 cos 3 = 1 (vedi triangolo rett ) (vedi triangolo rett ) Le cose si ripetono per i quadranti rimanenti, facendo, però, attenzione ai segni, visto che si tratta di segmenti orientati: il seno è positivo verso l'alto (I e II quadrante) e negativo verso il basso (III e IV quadrante); il coseno è positivo verso destra (I e IV quadrante) e negativo verso sinistra (II e III quadrante). 4..) Proprietà fondamentale sen xcos x = 1 Dove x è un qualsiasi angolo; la spiegazione di questa formula deriva dal Teorema di Pitagora e dal fatto che stiamo lavorando su una circonferenza di raggio unitario (e quindi l'ipotenusa vale sempre 1). C'è da aggiungere che i segni di seno e coseno non influiscono, visto che vengono persi con l'elevamento al quadrato. 4..3) Grafico delle funzioni seno e coseno Se si interpreta l'operazione di seno come una funzione (cioè si considera l'angolo come il valore di ingresso e il valore del seno come quello di uscita), si può disegnarne il grafico sul piano cartesiano (e così pure per il coseno):
6 y = sen x y = cos x OSSERVAZIONE: sono entrambe funzioni limitate tra -1 e 1, cioè non possono assumere valori nè maggiori di 1, nè minori di -1. OSSERVAZIONE: si vede dai grafici come si può interpretare cos x come una traslazione di particolare valgono le formule (ricavate utilizzando la traslazione degli assi di riferimento): cos x = sen x sen x = cos x sen x ; in 4..4) Periodicità Si sono disegnate le funzioni solo per i valori di ingresso x [0,], anziché per tutti i valori R ; questa scelta è giustificata dalla periodicità angolare (4.1.8): se l'angolo in ingresso si ripresenta con un altro valore, pur rappresentando lo stesso angolo, comunque darà lo stesso seno e lo stesso coseno. Così, disegnando un solo periodo, si è disegnato tutto ciò che c'era di interessante, perché nel resto del dominio, il grafico della funzione non è altro che una ripetizione di questo pattern. Le funzioni seno e coseno hanno periodo, e quindi avremmo potuto disegnarle in qualsiasi intervallo sull'asse delle x, purché fosse lungo almeno (es. [,], [,0 ], [8, 10 ], ecc.). NOTA BENE: se sen x ha periodo, sen x ha periodo ; per trovare la periodicità si eguaglia l'argomento (senza le traslazioni) alla periodicità della funzione in esame e si risolve rispetto ad x. es.1 sen 3 x 4 => 3 x = => x = 3 => periodicità 3
7 4.3) Tangente e Cotangente 4.3.1) Def: La tangente di un angolo x è definita come tg x = sen x cos x La cotangente di un angolo x è definita come ctg x = cos x sen x per x k ; per x 0k ;; Dunque tra loro vale la relazione: tg x = 1 ctg x Avendo denominatori che possono annullarsi, bisogna sempre considerare il C.E. es.1) angoli = 0, es.) angolo = 6 tg 0 = 0 ctg 0 = tg 6 = 3 3 tg = ctg 6 = 3 ctg = 0 es.3) angolo = 4 es.4) angolo = 3 tg 4 = 1 tg 3 = 3 ctg 4 = 1 ctg 3 = 3 3 Nel II quadrante tangente e cotangente sono negative, perché seno e coseno sono discordi. Nel III ritornano ad assumere gli stessi valori del I, perché seno e coseno sono entrambi negativi e quindi concordi. Nel IV assumono gli stessi valori del II. Si vede, allora, che la periodicità di queste funzioni è. 4.3.) Grafico delle funzioni tangente e cotangente y = tg x y = ctg x
8 OSSERVAZIONE: le funzioni sono state disegnate nell'intervallo x [,], corrispondente a due periodi. Si vede, infatti, come il grafico si ripeta. Ovviamente non è errore disegnare una funzione periodica in due suoi periodi (a dire il vero una funzione periodica di periodo P, sarà anche periodica di periodo np), ma generalmente per periodo si intende il più piccolo tra i periodi, per semplificare il più possibile le cose (il che equivale ad evitare di complicarle inutilmente). OSSERVAZIONE: si vede come tg x sia una funzione crescente perché quando si parte dall'angolo 0 e ci si sposta in senso antiorario lungo la circonferenza, seno cresce, mentre coseno decresce. Per lo stesso motivo ctg x, invece, decresce (proprio perché ha comportamento inverso della tangente, 1 essendo definita come tg x ) ) Periodicità Si è già discusso che tangente e cotangente hanno periodicità ; vediamo la periodicità di funzioni composte, secondo la regola esposta in 4..4: es.1 tg 5 x => 5 x = => x = 5 => periodicità 5
9 4.4) Altre funzioni 4.4.1) Funzioni reciproche di seno e coseno secante: sec x = 1 cos x cosecante: cosec x = 1 sen x per per x k x 0k 4.4.) Funzioni inverse Una funzione è invertibile se è iniettiva (cioè se l'intersezione del suo grafico con una retta orizzontale dà un solo punto di intersezione o nessuno). Si vede come le funzioni considerate in questa sezione (seno, coseno, tangente e cotangente), non verifichino questa condizione, perché nel momento in cui c'è un punto di intersezione con l'ipotetica retta orizzontale, allora ce ne saranno infiniti, per via della periodicità. Se consideriamo, però, queste funzioni all'interno di un opportuno intervallo, allora ci accorgiamo che sono in esso invertibili. es.1) sen x per x [, ] è invertibile, e l'inversa si chiama arcosen y in x [, ] ; arcosen1 = ; arcosen 1 = ; arcosen 1 = 6 ; arcosen = 4 ; es.) cos x per x [0,] è invertibile, e l'inversa si chiama arcocosen y in x [0,] ; arcocosen 1 = 0 ; arcocosen 1 = ; arcocosen 1 = 3 ; arcocosen = 3 4 ; es.3) tg x per x [, ] è invertibile, e l'inversa si chiama arctg y in x [, ] ; arctg 0 = 0 ; arctg 3 3 = 6 ; arctg 1 = 4 ; arctg 3 = 3 ; es.4) ctg x per x [0,] è invertibile, e l'inversa si chiama arcoctg y in x [0,] ; arcoctg 0 = ; arcoctg 3 3 = 3 ; arcoctg 1 = 3 4 ; arcoctg 3 = 6 ; NOTA BENE: quando si considera una di queste funzioni inverse, bisogna sempre indicare l'intervallo di inversione (es. arcosen y in x [, ] è una funzione diversa da arcosen y in x [, 3 ] ).
10 4.5) Formule 4.5.1) Angoli associati Queste formule si ricavano guardando la figura del punto Se consideriamo un generico angolo (che per concretizzare la cosa lo possiamo supporre = 6 ) osserviamo che sen è un segmento lungo 1 cos o ancora per cos. e lo stesso segmento lo troviamo per sen o per È più importante capire come ricavarle che sapere le formule in sè, anche perché ci sono infiniti modi di scriverle; riporto comunque le forme principali: sen = sen = sen = sen sen = cos = cos = cos = cos cos = cos = cos = cos cos = sen = sen = sen = sen = tg = tg = tg = tg tg = ctg = ctg = ctg = ctg ctg = ctg = ctg = ctg ctg = tg = tg = tg = tg 4.5.) Formule di sottrazione Ricavare queste formule è un po' difficile, e quindi vanno imparate a memoria alla perfezione, perché su queste si basano le formule che seguiranno: cos = cos cossen sen sen = sen cos cos sen (a memoria) tg = sen sen cos cos sen = cos cos cossen sen e dividendo numeratore e denominatore per cos cos : tg = tg tg 1tg tg (ricavabile dalle precedenti)
11 4.5.3) Formule di addizione cos = cos cos sen sen sen = sen coscos sen (a memoria) tg = sen sen cos cos sen = cos cos cos sen sen e dividendo numeratore e denominatore per cos cos : tg = tg tg 1 tg tg (ricavabile dalle precedenti) 4.5.4) Formule di duplicazione cos = cos = cos sen sen = sen = sen cos tg = tg = tg 1 tg (ricavabili dalle 4.5.3) 4.5.5) Formule di bisezione Dalle si ha: cos = cos = cos sen se in questa utilizziamo la relazione fondamentale 4.., prima per il seno e poi per il coseno, otteniamo: cos = 1 sen sen = 1 sen => sen = ± 1 cos cos = cos 1 cos = cos 1 => cos = ± 1cos tg = ± 1 cos 1cos Dove la scelta del segno + o - è data dalla conoscenza del quadrante di lavoro ) Formule di prostaferesi Di poca utilità generale, servono per trasformare somme (o differenze) in prodotti. Applicando le 4.5. e ottengo:
12 sensen = sen cos sen sen = cos sen coscos = cos cos cos cos = sen sen => sen psenq = sen pq p q cos sen p senq = cos pq p q sen cos pcosq = cos pq p q cos cos p cosq = sen pq p q sen Dove nell'ultimo passaggio si è fatto un cambio di variabili, ponendo = p; = q e conseguentemente (risolvendo il sistema delle due equazioni precedenti) = pq ; = p q ) Formule di Werner Di poca utilità generale, servono per trasformare prodotti in somme (o differenze). Dalle (prima versione) ottengo: sen cos = 1 [ sensen ] cos sen = 1 [ sen sen ] Notare come la prima e la seconda equazione abbiano lo stesso campo di applicazione, per via della proprietà commutativa della moltiplicazione (ecco perché solitamente le formule di Werner sono solo tre). cos cos = 1 [coscos ] sen sen = 1 [cos cos ] 4.5.8) Formule parametriche in tg Applicando le ottengo: cos = cos = cos cos sen = sen 1 cos sen = cos sen sen = sen = sen cos sen = cos 1 sen cos = cos sen
13 Se divido il numeratore e il denominatore delle ultime scritture per cos, e poi pongo un cambio di nome di variabili tg = t ottengo: cos = 1 tg 1tg => 1 t 1t tg sen = 1tg => t 1t
14 4.6) Equazioni goniometriche 4.6.1) Equazioni di I grado (lineari) (vedi.1) es.1) sen x = 1 => x = 6 ; x = 5 6 nel periodo scelto x [0, ] ; oppure x = 6 k; x = 5 6 k k Z se consideriamo le soluzioni su tutto R ; I due modi di esprimere le soluzioni sono equivalenti e la scelta può essere dettata dal particolare tipo di lavoro che si sta facendo (se si sta lavorando su un periodo in particolare ha più senso la prima, altrimenti la seconda), avendo cura, però, di proseguire poi con la stessa forma scelta. Negli esempi che seguiranno useremo la seconda forma, che risulta essere di carattere più generale, in quanto non prevede la scelta di un particolare periodo di studio (e sarà sottinteso k Z ). es.) sen x = => mai (perché seno e coseno sono limitate tra 1 e -1); es.3) cos x 3 = 3 => x 3 = 6 k; x 3 = 11 6 k => x = k6 ; x = 11 k6 es.4) sen 5 4 x = => 5 4 x = 4 k ; 5 4 x = 3 4 k => => 3 x = 80 k ; x = 7 80 k es.5) sen xcos x = 0 => sen x = cos x => x = 3 4 k ; x = 7 4 k 4.6.) Equazioni di II grado (vedi.6) es.1) tg x 1 = 0 ; pongo tg x = t => t 1 = 0 => t = ±1 => tg x = ±1 => => x = 4 k ; x = 3 4 k es.) 4 cos x 3 = 0 => cos x = 3 4 => cos x = ± 3 => x = 6 ; 11 6 ; 5 6 ; 7 6 ;tuttik ; es.3) cos x sen x1 = 0 => 1 sen x sen x1 = 0 => sen x sen x 1 = 0 => => pongo sen x = t => t t 1 = 0 => t = 1 ; t = 1 => sen x = 1 ; sen x = 1 => ecc... es.4) (omogenea) 3 sen x sen x cos x 3 = 0 - controllo se x = k è soluzione => = 3 0 => NON è soluzione; - ora pongo x k, cosicché sia possibile dividere per cos x : 3tg x tg x 3sen xcos x = 0 => cos 3 tg x tg x 3 tg x 3 = 0 => si pone tg x = t x ecc...
15 4.7) Disequazioni goniometriche 4.7.1) Disequazioni di I grado (lineari) (vedi.3) es.1) tg x 3 => 3 k x k (vedi il grafico 4.3.) es.) sen x 1 => 6 kx 5 6 k (vedi il grafico 4..3) es.3) sen xcos x 0 => sen x cos x => per via grafica (si sovrappone al grafico di sen x tra [0.], quello di cos x, e si individuano gli intervalli nei quali il primo sta sopra al secondo); soluzioni => 0x 3 4 ; 7 x; tuttik ; 4 NOTA BENE: il grafico di cos x si ottiene ribaltando il grafico di cos x lungo l'asse delle x. 4.7.) Disequazioni di II grado (vedi.7) es.1) sen x4 cos x 5 cos x => 1 cos x4cos x 5cos x 0 => si pone cos x = t ecc... es.) sen xcos x tg x 1 0 => si applica la regola dei segni (vedi ); NOTA BENE: nell'es., la disequazione che nasce dal denominatore dà soluzioni con periodicità ; conviene convertirle in soluzioni con periodicità, in modo che siano comparabili con le soluzioni del numeratore in un grafico di periodo appunto.
16 4.8) Relazioni tra i lati di un triangolo rettangolo In un triangolo rettangolo qualsiasi, valgono sempre le seguenti relazioni: c a b b = c sen a = c cos => b = c cos a = c sen => b a = tg b a = ctg Queste formule derivano da quanto definito in 4..1, solo che in questo caso immaginiamo di lavorare su una circonferenza di raggio c, anziché su una di raggio unitario. Per questo motivo, se ad esempio c1, il segmento verticale b, viene ad essere uguale non solo a sen (come solitamente avveniva), ma a qualcosa di più ( c sen ) cioè la stessa quantità amplificata di c. NOTA BENE: è bene ricordare che e non sono angoli qualsiasi, ma sono legati dalla relazione: =. APPROFONDIMENTO1: in questo paragrafo si è usato il Teorema di similitudine tra triangoli, che in breve dice che presi due triangoli T1 e T, aventi tutti gli angoli a due a due uguali, allora tutti i lati saranno a due a due proporzionali, cioè legati da un fattore di ampliamento costante c. Operativamente si inizia cercando gli angoli uguali e poi si stabiliscono i lati corrispondenti (che sono opposti agli angoli uguali); il tutto può essere solo formalmente complicato da rotazioni o ribaltamenti. APPROFONDIMENTO: per disegnare un triangolo rettangolo generico, si prende un punto su una semicirconferenza e si unisce con gli estremi del diametro; viceversa, preso un triangolo rettangolo generico e costruita una circonferenza sopra l'ipotenusa (cioè interpretandola come un diametro), detta circonferenza passerà pure per il rimanente vertice. Questo ci permette di concludere che tutti e soli i triangoli rettangoli esistenti di ipotenusa c, sono quelli inscritti nella semicirconferenza di diametro c.
17 4.9) Relazioni tra i lati di un triangolo qualsiasi 4.9.1) Teorema dei seni (o di Eulero) In un triangolo qualsiasi, valgono sempre le seguenti relazioni: a c b a sen = b sen = c sen 4.9.) Teorema del coseno (o di Carnot) In un triangolo qualsiasi, valgono sempre le seguenti relazioni: a c b a = b c bc cos b = a c ac cos c = a b ab cos
TRIGONOMETRIA. Un angolo si misura in gradi. Un grado è la novantesima parte di un angolo retto.
 TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
GONIOMETRIA. sin (x) = PH OP. ctg (x ) = cos (x) = CB sin (x) cosec (x ) = 1 = ON sin (x)
 GONIOMETRIA sin (x = PH OP cos (x = OH OP tg (x = sin(x = TA cos(x ctg (x = cos (x = CB sin (x sec (x = 1 = OM cos(x cosec (x = 1 = ON sin (x La tangente si calcola sempre sulla retta verticale passante
GONIOMETRIA sin (x = PH OP cos (x = OH OP tg (x = sin(x = TA cos(x ctg (x = cos (x = CB sin (x sec (x = 1 = OM cos(x cosec (x = 1 = ON sin (x La tangente si calcola sempre sulla retta verticale passante
APPUNTI DI GONIOMETRIA
 APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
che ci permette di passare da un sistema di misura all'altro con le:
 Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali (1 = 1/360 dell'angolo giro), anche se una Legge dello Stato italiano del 1960 impone di esprimerli in radianti.
Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali (1 = 1/360 dell'angolo giro), anche se una Legge dello Stato italiano del 1960 impone di esprimerli in radianti.
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016
 Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016 Le funzioni goniometriche La misura degli angoli Gli angoli e la loro ampiezza La misura in gradi La misura i radianti Dai
Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016 Le funzioni goniometriche La misura degli angoli Gli angoli e la loro ampiezza La misura in gradi La misura i radianti Dai
Teoria in sintesi 10. Teoria in sintesi 14
 Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
Appunti di Trigonometria per il corso di Matematica di base
 Appunti di Trigonometria per il corso di Matematica di base di Giovanna Neve Diploma accademico di primo livello per il corso di Tecnico di Sala di Registrazione Conservatorio C. Pollini Padova Indice
Appunti di Trigonometria per il corso di Matematica di base di Giovanna Neve Diploma accademico di primo livello per il corso di Tecnico di Sala di Registrazione Conservatorio C. Pollini Padova Indice
SENO, COSENO E TANGENTE DI UN ANGOLO
 Goniometria e trigonometria Misurare gli angoli nel sistema circolare L unità di misura del sistema circolare è il radiante def. Un radiante è la misura di un angolo alla circonferenza che sottende un
Goniometria e trigonometria Misurare gli angoli nel sistema circolare L unità di misura del sistema circolare è il radiante def. Un radiante è la misura di un angolo alla circonferenza che sottende un
Verifica di Topografia
 ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI " In Memoria dei Morti per la Patria " * CHIAVARI * ANNO SCOLASTICO 2010-2011 Verifica di Topografia classe 3^ Geometri 1) In un appezzamento a forma
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI " In Memoria dei Morti per la Patria " * CHIAVARI * ANNO SCOLASTICO 2010-2011 Verifica di Topografia classe 3^ Geometri 1) In un appezzamento a forma
Trigonometria angoli e misure
 Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
I TRIANGOLI. Esistono vari tipi di triangoli che vengono classificati in base ai lati e agli angoli.
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli o vertici e da tre lati. Il triangolo è la forma geometrica con il minor numero di lati perché tre è il numero minimo di lati con cui si può
I TRIANGOLI Il triangolo è un poligono formato da tre angoli o vertici e da tre lati. Il triangolo è la forma geometrica con il minor numero di lati perché tre è il numero minimo di lati con cui si può
IL TRIANGOLO. Teorema di Pitagora. Il triangolo è un poligono avente tre lati.
 IL TRIANGOLO Il triangolo è un poligono avente tre lati. FORMULE AREA: Il triangolo è equivalente a metà parallelogramma. A = (b x h) : da cui: b= A : h e h= A : b TRIANGOLO RETTANGOLO (a, b cateti; c
IL TRIANGOLO Il triangolo è un poligono avente tre lati. FORMULE AREA: Il triangolo è equivalente a metà parallelogramma. A = (b x h) : da cui: b= A : h e h= A : b TRIANGOLO RETTANGOLO (a, b cateti; c
Applicazioni dei teoremi di Pitagora ed Euclide
 Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Alcune nozioni di trigonometria 1
 Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
GEOMETRIA ANALITICA. Il Piano cartesiano
 GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
Corso di Analisi: Algebra di Base. 7^ Lezione
 Corso di Analisi: Algebra di Base 7^ Lezione Goniometria.Elementi di trigonometria piana. Unità di misura degli angoli. Misura di angoli orientati. Circonferenza goniometrica. Angoli e archi noti. Le funzioni,
Corso di Analisi: Algebra di Base 7^ Lezione Goniometria.Elementi di trigonometria piana. Unità di misura degli angoli. Misura di angoli orientati. Circonferenza goniometrica. Angoli e archi noti. Le funzioni,
I TRIANGOLI AB < AC + BC
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
Corso multimediale di matematica
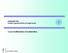 2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
La somma degli angoli interni di un triangolo è uguale a un angolo piatto (180 ).
 Il triangolo (UbiLearning) - 1 Triangoli Un triangolo è un poligono formato da tre lati. Rappresenta la più semplice figura piana formata dal minimo numero di lati utili a chiudere una superficie piana.
Il triangolo (UbiLearning) - 1 Triangoli Un triangolo è un poligono formato da tre lati. Rappresenta la più semplice figura piana formata dal minimo numero di lati utili a chiudere una superficie piana.
I TRIANGOLI AB < AC + BC
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
Risoluzione dei triangoli rettangoli
 Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Angolo. Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O.
 Angolo Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O. Trigonometria - Corso di matematica - Alessia Ceccato 1 Circonferenza goniometrica
Angolo Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O. Trigonometria - Corso di matematica - Alessia Ceccato 1 Circonferenza goniometrica
Corso multimediale di matematica
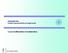 2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI
 Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI LATI: equilatero, isoscele, scaleno CLASSIFICAZIONE RISPETTO
Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni CLASSIFICAZIONE RISPETTO AI LATI: equilatero, isoscele, scaleno CLASSIFICAZIONE RISPETTO
Anno Scolastico:
 LICEO SCIENTIFICO DI STATO "G. BATTAGLINI" TARANTO PROGRAMMA DI MATEMATICA svolto nella Classe III Sezione A. Anno Scolastico: 2012-2013. Docente: Francesco Pantano. 1. Disequazioni. Richiami sulle disequazioni
LICEO SCIENTIFICO DI STATO "G. BATTAGLINI" TARANTO PROGRAMMA DI MATEMATICA svolto nella Classe III Sezione A. Anno Scolastico: 2012-2013. Docente: Francesco Pantano. 1. Disequazioni. Richiami sulle disequazioni
COMPENDIO TRIGONOMETRIA
 TORINO MAGGIO 2011 COMPENDIO DI TRIGONOMETRIA di Bart VEGLIA 1 FUNZIONI GONIOMETRICHE 1 Premessa La trigonometria ha lo scopo, come dice il nome, (dal greco, trigonon = triangolo e metron = misura) di
TORINO MAGGIO 2011 COMPENDIO DI TRIGONOMETRIA di Bart VEGLIA 1 FUNZIONI GONIOMETRICHE 1 Premessa La trigonometria ha lo scopo, come dice il nome, (dal greco, trigonon = triangolo e metron = misura) di
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
UNITÀ DIDATTICA 3 FUNZIONI GONIOMETRICHE
 UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA. PROGRAMMA DI Matematica. Classe IVB. Anno Scolastico
 LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IVB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 Le coniche nella discussione dei problemi (Richiami)
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IVB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 Le coniche nella discussione dei problemi (Richiami)
CORSO DI TECNOLOGIE E TECNICHE DI RAPPRESENTAZIONI GRAFICHE
 CORSO DI TECNOLOGIE E TECNICHE DI RARESENTAZIONI GRAFICHE ER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda ARTE RIMA Disegno del rilievo Unità Didattica:
CORSO DI TECNOLOGIE E TECNICHE DI RARESENTAZIONI GRAFICHE ER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda ARTE RIMA Disegno del rilievo Unità Didattica:
Note di trigonometria
 Note di trigonometria Daniel Gessuti indice Elementi di Trigonometria Seno, coseno e tangente Relazione fondamentale Secante, cosecante e cotangente 3 Le funzioni seno, coseno e tangente e le loro inverse
Note di trigonometria Daniel Gessuti indice Elementi di Trigonometria Seno, coseno e tangente Relazione fondamentale Secante, cosecante e cotangente 3 Le funzioni seno, coseno e tangente e le loro inverse
01 LE FUNZIONI GONIOMETRICHE
 0 LE FUNZIONI GONIOMETRICHE. LA MISURA DEGLI ANGOLI ESERCIZI Esprimi in forma sessadecimale le seguenti misure di angoli. A 4 9 ; 8 56 6 ; 57 59 B 44 ; 78 56 ; 9 4 0.,57 ; 8,97 ; 57,0. 4,4 ; 7,5 ; 9,569
0 LE FUNZIONI GONIOMETRICHE. LA MISURA DEGLI ANGOLI ESERCIZI Esprimi in forma sessadecimale le seguenti misure di angoli. A 4 9 ; 8 56 6 ; 57 59 B 44 ; 78 56 ; 9 4 0.,57 ; 8,97 ; 57,0. 4,4 ; 7,5 ; 9,569
Poligoni Un poligono è la parte di piano delimitata da una linea spezzata, semplice e chiusa.
 Poligoni Un poligono è la parte di piano delimitata da una linea spezzata, semplice e chiusa. Lato Vertice Angolo interno Angolo esterno I lati del poligono sono segmenti che costituiscono la linea spezzata.
Poligoni Un poligono è la parte di piano delimitata da una linea spezzata, semplice e chiusa. Lato Vertice Angolo interno Angolo esterno I lati del poligono sono segmenti che costituiscono la linea spezzata.
FUNZIONI TRIGONOMETRICHE
 FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che come sappiamo è 3.
 MODULO 3 LEZIONE 3 parte 2 Trigonometria: La risoluzione dei triangoli. Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che
MODULO 3 LEZIONE 3 parte 2 Trigonometria: La risoluzione dei triangoli. Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che
Proprietà di un triangolo
 Poligono con tre lati e tre angoli. Proprietà di un triangolo In un triangolo : I lati e i vertici sono consecutivi fra loro; La somma degli angoli interni è 180 ; La somma degli angoli esterni è 360 Ciascun
Poligono con tre lati e tre angoli. Proprietà di un triangolo In un triangolo : I lati e i vertici sono consecutivi fra loro; La somma degli angoli interni è 180 ; La somma degli angoli esterni è 360 Ciascun
Funzioni goniometriche di angoli notevoli
 Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE
 TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
Programma di Matematica Anno Scolastico 2012/2013 Classe III G
 Liceo Scientifico Statale G. BATTAGLINI Corso Umberto I 74100 Taranto Programma di Matematica Anno Scolastico 2012/2013 Classe III G Prof. Paolo Pantano Richiami di Algebra Equazioni e disequazioni Definizioni.
Liceo Scientifico Statale G. BATTAGLINI Corso Umberto I 74100 Taranto Programma di Matematica Anno Scolastico 2012/2013 Classe III G Prof. Paolo Pantano Richiami di Algebra Equazioni e disequazioni Definizioni.
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Test sui teoremi di Euclide e di Pitagora
 Test sui teoremi di Euclide e di Pitagora I test proposti in questa dispensa riguardano il teorema di Pitagora e i due teoremi di Euclide, con le applicazioni alle varie figure geometriche. Vengono presentate
Test sui teoremi di Euclide e di Pitagora I test proposti in questa dispensa riguardano il teorema di Pitagora e i due teoremi di Euclide, con le applicazioni alle varie figure geometriche. Vengono presentate
Nome.Cognome. 12 Febbraio 2009 Classe 4D. VERIFICA di MATEMATICA
 Nome.Cognome. Febbraio 009 Classe D VERIFIC di MTEMTIC Problemi ) Nel triangolo C si sa che ˆ 7 cos C =, tan C ˆ = e CM = a, essendo CM l altezza relativa ad. Determinare le misure dei lati del triangolo.
Nome.Cognome. Febbraio 009 Classe D VERIFIC di MTEMTIC Problemi ) Nel triangolo C si sa che ˆ 7 cos C =, tan C ˆ = e CM = a, essendo CM l altezza relativa ad. Determinare le misure dei lati del triangolo.
PROGRAMMA DI MATEMATICA
 A.S. 2015/2016 ALGEBRA - Equazioni letterali fratte PROGRAMMA DI MATEMATICA - Disequazioni di 1 grado ad una incognita intere e frazionarie - Sistemi di disequazioni di 1 o grado in una incognita - Sistemi
A.S. 2015/2016 ALGEBRA - Equazioni letterali fratte PROGRAMMA DI MATEMATICA - Disequazioni di 1 grado ad una incognita intere e frazionarie - Sistemi di disequazioni di 1 o grado in una incognita - Sistemi
La circonferenza e il cerchio
 La circonferenza e il cerchio Def. Circonferenza Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una
La circonferenza e il cerchio Def. Circonferenza Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una
MATEMATICA: Compiti delle vacanze Estate 2015
 MATEMATICA: Compiti delle vacanze Estate 2015 Classe II a PRIMA PARTE Ecco una raccolta degli esercizi sugli argomenti svolti quest anno: risolvili sul tuo quaderno! Per algebra ho inserito anche una piccola
MATEMATICA: Compiti delle vacanze Estate 2015 Classe II a PRIMA PARTE Ecco una raccolta degli esercizi sugli argomenti svolti quest anno: risolvili sul tuo quaderno! Per algebra ho inserito anche una piccola
La circonferenza e il cerchio
 La circonferenza e il cerchio Def.: Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una circonferenza
La circonferenza e il cerchio Def.: Si dice circonferenza una linea piana chiusa formata dall insieme dei punti che hanno la stessa distanza da un punto detto centro. Si dice raggio di una circonferenza
I triangoli. In questa dispensa presenteremo brevemente la definizione di triangolo e le proprietà principali.
 I triangoli In questa dispensa presenteremo brevemente la definizione di triangolo e le proprietà principali. Dopo aver introdotto la definizione e le classificazioni rispetto ai lati e rispetto agli angoli,
I triangoli In questa dispensa presenteremo brevemente la definizione di triangolo e le proprietà principali. Dopo aver introdotto la definizione e le classificazioni rispetto ai lati e rispetto agli angoli,
trasformazione grafico Cosa si deve fare Esempio goniometrico
 trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
Funzioni goniometriche
 Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
ANGOLI. ANGOLO OTTUSO ( β > 90 ) ANGOLO ACUTO ( β < 90 )
 ANGOLI Angolo è ciascuna delle due parti nelle quali un piano viene diviso da due semirette aventi la stessa origine. Le due semirette sono dette lati dei due angoli e l'origine comune il loro vertice.
ANGOLI Angolo è ciascuna delle due parti nelle quali un piano viene diviso da due semirette aventi la stessa origine. Le due semirette sono dette lati dei due angoli e l'origine comune il loro vertice.
CONGRUENZE TRA FIGURE DEL PIANO
 CONGRUENZE TRA FIGURE DEL PIANO Appunti di geometria ASSIOMI 15. La congruenza tra figure è una relazione di equivalenza 16. Tutte le rette del piano sono congruenti tra loro; così come tutti i piani,
CONGRUENZE TRA FIGURE DEL PIANO Appunti di geometria ASSIOMI 15. La congruenza tra figure è una relazione di equivalenza 16. Tutte le rette del piano sono congruenti tra loro; così come tutti i piani,
1 I solidi a superficie curva
 1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
1 I solidi a superficie curva PROPRIETÀ. Un punto che ruota attorno ad un asse determina una circonferenza. PROPRIETÀ. Una linea, un segmento o una retta che ruotano attorno ad un asse determinano una
Problema Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo.
 SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Copyright Esselibri S.p.A.
 .2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
.2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
Principali Definizioni e Teoremi di Geometria
 Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Principali Definizioni e Teoremi di Geometria Segmento (definizione) Si dice segmento di estremi A e B l insieme costituito dai punti A e B e da tutti i punti della retta AB compresi tra A e B. Angolo
Indice del vocabolario della Geometria euclidea
 Indice del vocabolario della Geometria euclidea 1 Postulati di appartenenza: piano, retta e punto nello spazio Punto, retta, piano nello spazio Punto, retta nel piano Punto nella retta Punto esterno alla
Indice del vocabolario della Geometria euclidea 1 Postulati di appartenenza: piano, retta e punto nello spazio Punto, retta, piano nello spazio Punto, retta nel piano Punto nella retta Punto esterno alla
Geometria euclidea. Alessio del Vigna
 Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Elementi di Geometria euclidea
 Elementi di Geometria euclidea Proprietà dei triangoli isosceli Il triangolo isoscele ha almeno due lati congruenti, l eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati
Elementi di Geometria euclidea Proprietà dei triangoli isosceli Il triangolo isoscele ha almeno due lati congruenti, l eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati
LA CIRCONFERENZA e IL CERCHIO
 LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
LA CIRCONFERENZA e IL CERCHIO La circonferenza è un poligono regolare con un numero infinito di lati Bisogna fare innanzitutto una distinzione: la circonferenza è la misura del perimetro; C (se sono più
Le caratteristiche dei poligoni. La relazione tra i lati e gli angoli di un poligono. Definizioni
 Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
FORMULARIO DEI TRIANGOLI
 RISOLUZIONE TRIANGOLI GENERICI Pagina 1 di 15 FORMULARIO DEI TRIANGOLI Teorema di Pitagora OP= 1 PP = sen OP = cos QQ = tan = Definizione seno Definizione coseno Definizione tangente TT = cotan = Consideriano
RISOLUZIONE TRIANGOLI GENERICI Pagina 1 di 15 FORMULARIO DEI TRIANGOLI Teorema di Pitagora OP= 1 PP = sen OP = cos QQ = tan = Definizione seno Definizione coseno Definizione tangente TT = cotan = Consideriano
Banca Dati Finale Senza Risposte
 Banca Dati Finale Senza Risposte TRG da 5451 a 6100 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (5/4) π radianti? A) 240 B) 270 C)
Banca Dati Finale Senza Risposte TRG da 5451 a 6100 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (5/4) π radianti? A) 240 B) 270 C)
TRIGONOMETRIA E COORDINATE
 Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Verifica di Matematica sommativa durata della prova : 2 ore. Punt. attr. Problema
 Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
Le funzioni periodiche e il ritmo della vita Molti fenomeni naturali hanno un andamento ciclico ( o periodico), cioè ad intervalli di tempo fissati,
 Le funzioni periodiche e il ritmo della vita Molti fenomeni naturali hanno un andamento ciclico ( o periodico), cioè ad intervalli di tempo fissati, detti periodi, si ripetono con le stesse modalità: il
Le funzioni periodiche e il ritmo della vita Molti fenomeni naturali hanno un andamento ciclico ( o periodico), cioè ad intervalli di tempo fissati, detti periodi, si ripetono con le stesse modalità: il
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
ˆ b, si usa la convenzione di prendere. come verso positivo quello antiorario e come verso negativo quello orario.
 Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
Capitolo 4 Le rotazioni 4.1 Richiami di teoria E' opportuno ricordare che, dato un angolo orientato ao ˆ b, si usa la convenzione di prendere come verso positivo quello antiorario e come verso negativo
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
Programma di Matematica svolto durante l anno scolastico nella classe 2 sez.e
 Programma di Matematica svolto durante l anno scolastico 2015-2016 nella classe 2 sez.e ALGEBRA 1) Richiami sul calcolo letterale e sulle equazioni algebriche lineari ad una incognita. 2) Disequazioni
Programma di Matematica svolto durante l anno scolastico 2015-2016 nella classe 2 sez.e ALGEBRA 1) Richiami sul calcolo letterale e sulle equazioni algebriche lineari ad una incognita. 2) Disequazioni
Corso di Matematica - Geometria. Geometria - 0. Ing. L. Balogh
 Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Classe III Aritmetica e Algebra Dati e previsioni Geometria Geometria
 Classe III U. D. 1 Equazioni e disequazioni (ripasso) Aritmetica e Algebra Equazioni algebriche numeriche con δ 2. Disequazioni algebriche numeriche con δ 2. Sistemi di equazioni e/o disequazioni algebriche
Classe III U. D. 1 Equazioni e disequazioni (ripasso) Aritmetica e Algebra Equazioni algebriche numeriche con δ 2. Disequazioni algebriche numeriche con δ 2. Sistemi di equazioni e/o disequazioni algebriche
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE
 QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a GEOMETRIA PIANA EQUAZIONI E DISEQUAZIONI a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1) Nel piano
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a GEOMETRIA PIANA EQUAZIONI E DISEQUAZIONI a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1) Nel piano
GEOMETRIA EUCLIDEA. segno lasciato dalla punta di una matita appena appoggiata sul foglio. P
 GEOMETRIA EUCLIDEA 1) GLI ENTI FONDAMENTALI: PUNTO, RETTA E PIANO Il punto, la retta e il piano sono gli ELEMENTI ( o ENTI ) GEOMETRICI FONDAMENTALI della geometria euclidea; come enti fondamentali non
GEOMETRIA EUCLIDEA 1) GLI ENTI FONDAMENTALI: PUNTO, RETTA E PIANO Il punto, la retta e il piano sono gli ELEMENTI ( o ENTI ) GEOMETRICI FONDAMENTALI della geometria euclidea; come enti fondamentali non
Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico.
 Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico. 1. Funzione esponenziale e logaritmica. a) Riepilogo delle proprietà delle potenze.
Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico. 1. Funzione esponenziale e logaritmica. a) Riepilogo delle proprietà delle potenze.
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Il Piano Cartesiano Goniometrico
 Valori di seno e coseno per angoli multipli di / Il Piano Cartesiano Goniometrico Seno e coseno: valori per angoli particolari September 1, 010 Valori di seno e coseno per angoli multipli di / Sommario
Valori di seno e coseno per angoli multipli di / Il Piano Cartesiano Goniometrico Seno e coseno: valori per angoli particolari September 1, 010 Valori di seno e coseno per angoli multipli di / Sommario
Classe 3 Sezione Indirizzo Liceo delle Scienze Applicate
 Alessandria, Settembre 2016 Anno scolastico 2016/2017 A Classe 3 Sezione C Indirizzo Liceo delle Scienze Applicate Materia Matematica Docente/i Nome e cognome PierCarlo Barbierato Nome e cognome Firma
Alessandria, Settembre 2016 Anno scolastico 2016/2017 A Classe 3 Sezione C Indirizzo Liceo delle Scienze Applicate Materia Matematica Docente/i Nome e cognome PierCarlo Barbierato Nome e cognome Firma
Problemi di geometria
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
Conoscenze. L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la regola di Ruffini, il teorema. del resto.
 Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1
 Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione.. Funzioni iniettive, suriettive e biiettive.. Le funzioni
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione.. Funzioni iniettive, suriettive e biiettive.. Le funzioni
Le grandezze fisiche scalari sono completamente definite da un numero e da una unità di misura.
 UNITÀ 3 LE GRANDEZZE FISICHE VETTORIALI E I VETTORI 1. Grandezze fisiche scalari e vettoriali. 2. I vettori. 3. Le operazioni con i vettori. 4. Addizione e sottrazione di vettori. 5. Prodotto di un numero
UNITÀ 3 LE GRANDEZZE FISICHE VETTORIALI E I VETTORI 1. Grandezze fisiche scalari e vettoriali. 2. I vettori. 3. Le operazioni con i vettori. 4. Addizione e sottrazione di vettori. 5. Prodotto di un numero
LICEO SCIENTIFICO STATALE GOBETTI - SEGRE DI TORINO. Anno scolastico Docente: Professor GILITOS LORENZO
 LICEO SCIENTIFICO STATALE GOBETTI SEGRE Via Maria Vittoria n. 39/bis 10123 Torino Tel. 011/817.41.57 011/839.52.19 - Fax 011/839.58.97 e-mail: dirigente@liceogobetti.it Succursale Via. Giulia di Barolo
LICEO SCIENTIFICO STATALE GOBETTI SEGRE Via Maria Vittoria n. 39/bis 10123 Torino Tel. 011/817.41.57 011/839.52.19 - Fax 011/839.58.97 e-mail: dirigente@liceogobetti.it Succursale Via. Giulia di Barolo
Costruzioni geometriche. (Teoria pag , esercizi )
 Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
EQUAZIONI E DISEQUAZIONI GONIOMETRICHE
 EQUAZIONI E DISEQUAZIONI GONIOMETRICHE Prerequisiti Saper risolvere le equazioni algebriche. Conoscere le definizioni delle funzioni goniometriche. Conoscere i valori delle funzioni goniometriche per gli
EQUAZIONI E DISEQUAZIONI GONIOMETRICHE Prerequisiti Saper risolvere le equazioni algebriche. Conoscere le definizioni delle funzioni goniometriche. Conoscere i valori delle funzioni goniometriche per gli
GEOMETRIA. Congruenza, angoli e segmenti
 GEOMETRIA Per affermare che un triangolo è isoscele o rettangolo oppure che un quadrilatero è un parallelogramma o un rettangolo o un rombo o un quadrato o un trapezio o un trapezio isoscele, c è sempre
GEOMETRIA Per affermare che un triangolo è isoscele o rettangolo oppure che un quadrilatero è un parallelogramma o un rettangolo o un rombo o un quadrato o un trapezio o un trapezio isoscele, c è sempre
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria. PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13
 Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
In un triangolo un lato è maggiore della differenza degli altri due, pertanto dal triangolo si ha > dividendo per =1.
 L iperbole L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi. Come si evince del grafico, la differenza delle distanze
L iperbole L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi. Come si evince del grafico, la differenza delle distanze
ISTITUTO ISTRUZIONE SUPERIORE
 ISTITUTO ISTRUZIONE SUPERIORE Federico II di Svevia Indirizzi: Liceo Scientifico Classico Linguistico Artistico e Scienze Applicate Via G. Verdi, 1 85025 MELFI (PZ) Tel. 097224434/35 Cod. Min.: PZIS02700B
ISTITUTO ISTRUZIONE SUPERIORE Federico II di Svevia Indirizzi: Liceo Scientifico Classico Linguistico Artistico e Scienze Applicate Via G. Verdi, 1 85025 MELFI (PZ) Tel. 097224434/35 Cod. Min.: PZIS02700B
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE
 QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a TRIGONOMETRIA a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1 1) Un angolo misura 315 o. La sua misura
QUESTIONARIO INIZIALE DI AUTOVALUTAZIONE relativo a TRIGONOMETRIA a cura di Mariacristina Fornasari, Daniela Mari, Giuliano Mazzanti, Valter Roselli, Luigi Tomasi 1 1) Un angolo misura 315 o. La sua misura
Il valore assoluto (lunghezza, intensita )
 Il valore assoluto (lunghezza, intensita ) = se 0 - se < 0 = 5 5-0, = 0 3, = 3 Il valore assoluto di un numero reale è quindi sempre un numero positivo. Geometricamente rappresenta la misura della distanza
Il valore assoluto (lunghezza, intensita ) = se 0 - se < 0 = 5 5-0, = 0 3, = 3 Il valore assoluto di un numero reale è quindi sempre un numero positivo. Geometricamente rappresenta la misura della distanza
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Il triangolo è una figura indeformabile ed è l'unico poligono cui è sempre circoscrivibile e in cui è sempre inscrivibile una circonferenza.
 I triangoli e il teorema di Pitagora (UbiLearning) - 1 Triangoli Un triangolo è un poligono formato da tre lati. Rappresenta la più semplice figura piana formata dal minimo numero di lati utili a chiudere
I triangoli e il teorema di Pitagora (UbiLearning) - 1 Triangoli Un triangolo è un poligono formato da tre lati. Rappresenta la più semplice figura piana formata dal minimo numero di lati utili a chiudere
Angoli e loro misure
 Angoli e loro misure R s Unità di misura: gradi, minuti, secondi 1 o =60' 1'=60'' Es: 35 o 41'1'' radianti α(rad) s R Angolo giro = 360 o = R/R = rad R=1 arco rad Es.: angolo retto R Arco 4 : se R=1 π
Angoli e loro misure R s Unità di misura: gradi, minuti, secondi 1 o =60' 1'=60'' Es: 35 o 41'1'' radianti α(rad) s R Angolo giro = 360 o = R/R = rad R=1 arco rad Es.: angolo retto R Arco 4 : se R=1 π
ISTITUTO TECNICO TECNOLOGICO STATALE G.
 ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2015/ 16 PROGRAMMA SVOLTO DI MATEMATICA 3 ore settimanali COMPLEMENTI DI MATEMATICA 1 ora settimanale Classe: 3^ INFORMATICA sez.
ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2015/ 16 PROGRAMMA SVOLTO DI MATEMATICA 3 ore settimanali COMPLEMENTI DI MATEMATICA 1 ora settimanale Classe: 3^ INFORMATICA sez.
