Lezione 4. Risposte canoniche dei sistemi del primo e del secondo ordine
|
|
|
- Bernadetta Carella
- 8 anni fa
- Visualizzazioni
Transcript
1 Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine
2 Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo, calino, rampa), ovvero quei egnali uilizzabili come e per evidenziare le proprieà dinamiche del iema. Ci concenreremo ui iemi del primo e econdo ordine in quano rappreenaivi dei modelli di prima approimazione di larga pare dei iemi fiici. Sul racciao di una generica ripoa allo calino poremo definire alcuni parameri caraeriici: () 0.9 S ±ε% 0.1 aε Fig. 1 : Parameri caraeriici della ripoa allo calino empo di alia : è il empo impiegao dalla ripoa a paare dal 10% al 90% del valore di regime. empo di aeameno al (100-ε)% aε : è il empo impiegao dalla ripoa ad enrare definiivamene in una facia comprea ra ±ε% del valore di regime. Sovraelongazione percenuale maima S E : è l ecurione maima della ripoa ripeo al valore di regime, rapporaa in percenuale al valore di regime eo: { ()} S max SE = 100 = 100. P. Rocco - Dipene di Auomaica Lez. 4-1
3 Siemi del primo ordine L epreione più generale della funzione di raferimeno per un iema del primo ordine (oia con un olo polo) è la eguene: ( ) G τ = g. Siemi reamene propri Sono i iemi in cui il grado del denominaore è maggiore del grado del numeraore. Siemi del primo ordine reamene propri non poono quindi preenare zeri: 1, g = 0 G ( ) = g =, g = 1 g = 0 ( ) G = 1 + Sudiamo la ripoa allo calino ( u () = ca() U() = 1 ): Y ( ) = GU ( ) ( ) = 1 = + + = / Aniraformando: () ( ) = 1 e, 0. A econda del egno di l andameno di riula molo divero 1 : > 0 < 0 Fig. : Ripoa allo calino per >0 e <0 1 Qui e nel eguio i aumerà, enza alcuna perdia di generalià, il paramero poiivo. P. Rocco - Dipene di Auomaica Lez. 4 -
4 Quando >0, la ripoa i aea u un valore finio, menre quando <0 la ripoa diverge all infinio. Si oervi che il iema di funzione di raferimeno G() preena un polo per = 1/. Perano il iema riula ainoicamene abile per >0, inabile per <0. 1/ 1/ > 0 < 0 Fig. 3 : Poizione del polo per >0 e <0 Coniderando olo il cao ainoicamene abile (>0), i può calcolare il valore limie (per ) della ripoa allo calino con il eorema del valore finale: lim () = lim[ Y ()] = lim =. Perano la ripoa allo calino ende al guadagno del iema: in alre parole il rapporo ra il valore limie dell ucia ed il valore limie dell ingreo (che in queo cao vale 1, eendo l ingreo uno calino), è pari al guadagno del iema. Ciò coiuice una circoanza generale. La forma del raniorio dipende invece olo dalla coane di empo. All iane iniziale (=0) la derivaa di vale /: perano inizialmene la curva è angene alla rea che paa per l origine e che inercea la rea orizzonale di ordinaa (oia la rea a cui ende la ripoa), in corripondenza dell iane = (fig. 1). Ne conegue che il raniorio è ano più veloce quano più piccolo è il valore della coane di empo. Si può verificare che la ripoa raggiunge praicamene (al 98 99%) il valore di regime dopo un empo pari a 4 5 vole la coane di empo. Si oervi che da quee coniderazioni emerge anche con mola evidenza un meodo grafico per racciare l andameno approimao della ripoa allo calino. Sudiamo anche la ripoa all impulo ( u () = imp() U() = 1 ): 1 Y ( ) = GU ( ) ( ) = = / Aniraformando: () e =, 0. Si noi che la ripoa all impulo riula uguale alla derivaa ripeo al empo della ripoa allo calino (circoanza generale). A econda del egno di i oiene: P. Rocco - Dipene di Auomaica Lez. 4-3
5 / > 0 < 0 Fig. 4 : Ripoa all impulo per >0 e <0 Coerenemene con la definizione di abilià, per >0 (iema ainoicamene abile), la ripoa converge a zero, per <0 (iema inabile) la ripoa diverge. g = 1 ( ) G =. Il iema ha un polo in =0: è perano emplicemene abile. Sudiamo la ripoa allo calino ( u () = ca() U() = 1 ): 1 Y ( ) = GU ( ) ( ) = = Aniraformando: () = ram ().. 1 Fig. 5 : Ripoa allo calino Per quano riguarda la ripoa all impulo: Y ( ) = GU ( ) ( ) =. P. Rocco - Dipene di Auomaica Lez. 4-4
6 e quindi: () = ca (). Fig. 6 : Ripoa all impulo In enrambi i cai l ucia equivale all inegrale dell ingreo, moliplicao per il faore. Siemi propri non reamene Sono i iemi in cui il grado del denominaore è uguale al grado del numeraore. Siemi del primo ordine propri non reamene preenano quindi uno zero: ( ) G τ = g = τ, τ,, g = 0 g = 1 g = 1 g = 0 τ G ( ) = Sudiando la ripoa allo calino i perviene alla eguene epreione: () τ = + e 1 1, 0. Al variare del valore relaivo di τ e (e quindi della poizione relaiva del polo e dello zero) la ripoa allo calino cambia enibilmene (i conidera olo il cao ainoicamene abile, >0): P. Rocco - Dipene di Auomaica Lez. 4-5
7 0 < τ < τ/ 1/τ 1/ Fig. 7 : Ripoa allo calino per 0<τ< τ/ 0 < < τ 1/ 1/τ Fig. 8 : Ripoa allo calino per 0<<τ τ < 0 < 1/ 1/τ τ/ Fig. 9 : Ripoa allo calino per τ<0< Uno zero nel emipiano iniro anicipa la ripoa ripeo al cao di iema privo di zero, nel eno che la ripoa ea i pora inizialmene ad un valore divero da zero, dello eo egno del valore di regime. Uno zero nel emipiano dero riarda la ripoa ripeo al cao di iema privo di zero, nel eno che la ripoa ea i pora inizialmene ad un valore divero da zero, di egno oppoo al valore di regime (ripoa invera). Queo ipo di comporameno è ipico dei P. Rocco - Dipene di Auomaica Lez. 4-6
8 iemi con zeri nel emipiano dero, che per ragioni che aranno chiare più avani nel coro, prendono anche il nome di iemi a fae non minima. g = 1 ( ) G τ = τ > 0 1/τ 1 Fig. 10 : Ripoa allo calino per τ>0 τ < 0 1 1/τ Fig. 11 : Ripoa allo calino per τ<0 g = 1 ( ) G = / 1/ Fig. 1 : Ripoa allo calino (zero in =0) P. Rocco - Dipene di Auomaica Lez. 4-7
9 Siemi del econdo ordine Per i iemi del econdo ordine (che preenano cioè due poli) ci limieremo ad eaminare alcuni cai paricolari, rinunciando alla caiica complea. Siemi con poli reali e neuno zero G ( ) = ( )( ) 1. Aumiamo 1 e poiivi, oia il iema ainoicamene abile (i uoi poli, in = 1/ 1, = 1/, ono nel emipiano iniro). La raformaa di Laplace della ripoa allo calino è daa da: Y ( ) =. ( 1)( ) In bae al eorema del valore iniziale, oeniamo: [ ] ( 0) = lim Y( ) = lim ( ) L( ) ( )( ) 1 = 0 [ ] ( ( ) ( ) [ )] [ ( )] & 0 = lim & = lim Y 0 = lim Y = lim ( ) L( ) 3 [ ] ( ) [ ] ( ( ) ( )) [ ] && 0 = lim && = lim Y & 0 = lim Y = lim menre in bae al eorema del valore finale: [ ] ( ) = lim Y( ) = lim 0 0 ( )( ) 1 =. ( )( ) 1 ( )( ) = 0 = > La ripoa pare quindi da zero, con angene orizzonale e concavià rivola vero l alo. ende poi al valore. L aniraformaa i può oenere con il meodo di Heaviide: () e e 1 = 1 1 +, L andameno ipico è a forma di S : P. Rocco - Dipene di Auomaica Lez. 4-8
10 Fig. 13 : Ripoa allo calino La duraa del raniorio può eere facilmene legaa alle due coani di empo 1 e olo e i due valori ono molo diveri ra loro: in al cao, infai, cona olo il valore della coane di empo più grande. Se, ad eempio 1 >>, allora: () [ ] 1 e 1, 0. raniorio veloce dovuo a 1 Fig. 14 : Ripoa allo calino con 1 >> Siemi con poli reali e uno zero G ( ) = τ ( )( ) 1. Aumiamo 1 e poiivi, oia il iema ainoicamene abile. La raformaa di Laplace della ripoa allo calino è daa da: τ Y ( ) = ( )( ) 1. In bae al eorema del valore iniziale, oeniamo: P. Rocco - Dipene di Auomaica Lez. 4-9
11 ( 0) = lim[ Y( ) ] = lim τ ( )( ) 1 = 0 ( ) [ ( )] [ ( ( ) ( ) & 0 = lim L & = lim Y 0 )] = lim[ Y( ) ] = lim menre in bae al eorema del valore finale: τ τ = ( )( ) 1 1 τ ( ) = lim[ Y( ) ] = lim =. 0 0 ( 1)( ) La ripoa pare quindi da zero, con angene rivola vero l alo per τ>0, vero il bao per τ<0. La ripoa ende poi al valore. Qualiaivamene, gli andameni della ripoa allo calino aranno: < < τ 1 < τ < oppure 1 0 < τ < < 1 Fig. 15 : Ripoa allo calino con τ>0 τ < 0 Fig. 16 : Ripoa allo calino con τ<0 Si oervi il rao di ripoa invera nel cao di zero nel emipiano dero (τ < 0). P. Rocco - Dipene di Auomaica Lez. 4-10
12 Siemi con poli complei e coniugai e neuno zero In queo cao è comodo ricrivere l epreione della funzione di raferimeno nella forma equivalene: ωn G ( ) =, + ζωn+ ωn dove ζ, morzameno, e ω n, pulazione naurale, ono ai definii nella precedene lezione. Si ricorda che il ignificao dei parameri ζ e ω n è illurao dalla eguene figura: ζω n ω α n ζ = co(α) Si oervi inolre che: Fig. 17 : Significao dei parameri ζ e ω n ζ>0: due poli nel emipiano iniro iema ainoicamene abile ζ=0: due poli ull ae immaginario iema emplicemene abile ζ<0: due poli nel emipiano dero iema inabile Sudiamo la ripoa allo calino: ωn Y ( ) =. + ζωn+ ωn In bae al eorema del valore iniziale, oeniamo: [ ] ( 0) = lim Y( ) = ( ) L( ) lim ωn + ζωn+ ωn = 0 [ ] ( ( ) ( ) [ )] [ ( )] & 0 = lim & = lim Y 0 = lim Y = lim ( ) L( ) 3 [ ] ( ) [ ] ( ( ) ( )) [ ] && 0 = lim && = lim Y & 0 = lim Y = lim menre, per ζ>0, in bae al eorema del valore finale: [ ] ( ) = lim Y( ) = lim 0 0 ωn + ζωn+ ωn =. ωn + ζω + ω n n ωn + ζω + ω n n = 0 n = ω > 0 L epreione analiica della ripoa allo calino, oenibile per aniraformazione, è la eguene: P. Rocco - Dipene di Auomaica Lez. 4-11
13 e in, 1 ζ 1 () = ζω n 1 ( ωn 1 ζ + α) dove ζ = co(α). Per ζ=0, i ha: [ n ] () = 1 co( ω ) oia una coinuoide di pulazione ω n : = π/ω n Fig. 18 : Ripoa allo calino per ζ=0 Per ζ 0, la ripoa ha l andameno di una inuoide inviluppaa da due eponenziali (convergeni nel cao ainoicamene abile, ζ>0, divergeni nel cao inabile, ζ<0). M ζω n (e ) = π/ω* n ζω n (1 e ) Fig. 19 : Ripoa allo calino per ζ>0 (ωn * = ωn 1 ζ ) Si può dimorare che, nel cao ainoicamene abile, la ovraelongazione percenuale maima, oia il rapporo percenuale ra l ecurione del primo picco della ripoa ripeo al valore di regime ed il valore di regime eo, dipende ecluivamene dal faore di morzameno ζ: P. Rocco - Dipene di Auomaica Lez. 4-1
14 S E M = 100 = 100e ζπ 1 ζ 100 S E ζ Fig. 19 : Sovraelongazione percenuale maima ripeo al faore di morzameno Per fare in modo che la ovraelongazione percenuale maima ia inferiore ad un valore aegnao, occorrerà quindi che i poli del iema apparengano ad un deerminao eore del emipiano iniro del piano compleo (come quello raeggiao in figura): Fig. 0 : Seore del piano compleo per limiare la ovraelongazione Il empo di aeameno può invece eere deerminao con buona approimazione (per ecceo) facendo riferimeno anziché alla ripoa ad uno dei uoi inviluppi. Volendo quindi calcolare ad eempio il empo di aeameno al 99% ( a1 ), i imporrà: ( ζωna ) ζω 1 n a1 1 e = e = ζω = ln100 e quindi: ln ζω ζω. a 1 = n n n a1 Il empo di aeameno riula quindi inveramene proporzionale al modulo della pare reale dei poli. Per limiare il empo di aeameno occorrerà quindi che i poli del iema iano caraerizzai da un prodoo ζω n ufficienemene grande, oia che apparengano ad un P. Rocco - Dipene di Auomaica Lez. 4-13
15 emipiano incluo nel emipiano iniro del piano compleo ufficienemene lonano dall ae immaginario (come quello raeggiao in figura): Fig. 1 : Semipiano del piano compleo per limiare il empo di aeameno Volendo conenere ia la ovraelongazione ia il empo di aeameno, i poli della funzione di raferimeno dovranno rovari in una regione del piano compleo inerezione delle due regioni raeggiae nelle precedeni figure. P. Rocco - Dipene di Auomaica Lez. 4-14
16 Eercizi Eercizio 4.1 Si racci l andameno qualiaivo della ripoa allo calino del iema decrio dalla eguene funzione di raferimeno: 4 G () = + Eercizio 4. Si racci l andameno qualiaivo della ripoa allo calino del iema decrio dalla eguene funzione di raferimeno: G () = Eercizio 4.3 Si racci l andameno qualiaivo della ripoa allo calino del iema decrio dalla eguene funzione di raferimeno: () G = 10 ( )( 01. ) Eercizio 4.4 Si racci l andameno qualiaivo della ripoa allo calino del iema decrio dalla eguene funzione di raferimeno: G () 18 = + 9 P. Rocco - Dipene di Auomaica Lez. 4-15
17 raccia delle oluzioni Eercizio 4.1 G() è della forma: ( ) G = 1 + con =, = 0.5. Perano: Eercizio 4. G() è della forma: τ G ( ) = con = 1, = 1, τ = 0.5. Perano: () () P. Rocco - Dipene di Auomaica Lez. 4-16
18 Eercizio 4.3 G() è della forma: G ( ) = ( )( ) 1 con = 10, 1 = 1, = 0.1. Perano la ripoa allo calino è dominaa dalla coane di empo 1 : Eercizio 4.4 G() è della forma: ( ) G = ωn + ζωn+ ωn con =, ω n =3, ζ=0. Perano: () () Il periodo dell ocillazione permanene vale: π = =. 094 ω n P. Rocco - Dipene di Auomaica Lez. 4-17
Metodo della trasformata di Laplace
 Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Meodo della raformaa di aplace Il meodo imbolico conene di affronare l analii di rei coneneni componeni reaivi (condenaori e induori) in regime inuoidale, aggirando la compleià maemaica inrodoa dalle relazioni
Metodo della Trasformata di Laplace (mtl)
 Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
Lezione 7 Meodo della raformaa di Laplace Lezione n.7 Meodo della raformaa di Laplace (ml). Inroduzione. Richiami ulla raformaa di Laplace. Proprieà della raformaa. Regola di derivazione.3 abella di raformae
REGISTRAZIONE DEL MOTO. Lo scopo è riempire una tabella t/s (istante di tempo/posizione occupata)
 REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
REGISTRAZIONE DEL MOTO Lo copo è riempire una abella / (iane di empo/poizione occupaa) (ec) (meri) Ciò i può fare in due modi: 1) Prefiare le poizioni e miurare a quale empo vengano raggiune. Si compila
Tema 3. Insiemi, elementi di logica, calcolo combinatorio, relazioni e funzioni
 Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
Tema 3 Iniemi, elemeni di logica, calcolo combinaorio, relazioni e funzioni 3.1 Queii di livello bae 3.1.1 Si coniderino i egueni enunciai: n è un muliplo di 3 o è un numero pari, e inolre è minore di
Problema 1: Una collisione tra meteoriti
 Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Lezione 12. Regolatori PID
 Lezione 1 Regolatori PD Legge di controllo PD Conideriamo un regolatore che eercita un azione di controllo dipendente dall errore attravero la eguente legge: t ut = K et K e d K de t P + τ τ+ D. dt La
Lezione 1 Regolatori PD Legge di controllo PD Conideriamo un regolatore che eercita un azione di controllo dipendente dall errore attravero la eguente legge: t ut = K et K e d K de t P + τ τ+ D. dt La
3. Catene di Misura e Funzioni di Trasferimento
 3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
CAPITOLO 9 - RETI DINAMICHE NEL DOMINIO DELLA FREQUENZA
 G. SUPT FUGA MT D TOA D T ovembre CAPTOO 9 - T DAMCH DOMO DA FQUZA pag. / CAPTOO 9 - T DAMCH DOMO DA FQUZA TODUZO l meodo della raformaa di aplace, chiamao anche analii nel dominio della frequenza, è una
G. SUPT FUGA MT D TOA D T ovembre CAPTOO 9 - T DAMCH DOMO DA FQUZA pag. / CAPTOO 9 - T DAMCH DOMO DA FQUZA TODUZO l meodo della raformaa di aplace, chiamao anche analii nel dominio della frequenza, è una
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
Paolo Rocco. Automatica
 Paolo Rocco Dipene ad uo degli tudenti del Politecnico di Milano per i cori da cinque crediti didattici Automatica Ingegneria Aeropaziale E vietato l uo commerciale di queto materiale Avvertenza Queta
Paolo Rocco Dipene ad uo degli tudenti del Politecnico di Milano per i cori da cinque crediti didattici Automatica Ingegneria Aeropaziale E vietato l uo commerciale di queto materiale Avvertenza Queta
Politica Economica Europea
 Poliica Economica Europea 2 Tao di cambio Obieivo: confronare il valore di uno eo bene denominao in due value divere Bene X P$ Bene X P Eprimere il valore di un bene denominao in una valua, in un alra
Poliica Economica Europea 2 Tao di cambio Obieivo: confronare il valore di uno eo bene denominao in due value divere Bene X P$ Bene X P Eprimere il valore di un bene denominao in una valua, in un alra
Capitolo. Il comportamento dei sistemi di controllo in regime permanente. 6.1 Classificazione dei sistemi di controllo. 6.2 Errore statico: generalità
 Capitolo 6 Il comportamento dei itemi di controllo in regime permanente 6. Claificazione dei itemi di controllo 6. Errore tatico: generalità 6. Calcolo dell errore a regime 6.4 Eercizi - Errori a regime
Capitolo 6 Il comportamento dei itemi di controllo in regime permanente 6. Claificazione dei itemi di controllo 6. Errore tatico: generalità 6. Calcolo dell errore a regime 6.4 Eercizi - Errori a regime
Trasformata di Laplace unilatera Teoria
 Definizione Tafomaa di Laplace unilaea Teoia L[f()] = f() $ e ($) d = F() Dove: f() = funzione eale afomabile. E nulla pe
Definizione Tafomaa di Laplace unilaea Teoia L[f()] = f() $ e ($) d = F() Dove: f() = funzione eale afomabile. E nulla pe
RISPOSTA NEL DOMINIO DEL TEMPO
 RISPOSTA NEL DOMINIO DEL TEMPO Nel dominio del empo le variabili sono esaminae secondo la loro evoluzione emporale. Normalmene si esamina la risposa del sisema a un segnale di prova canonico, cioè si sollecia
RISPOSTA NEL DOMINIO DEL TEMPO Nel dominio del empo le variabili sono esaminae secondo la loro evoluzione emporale. Normalmene si esamina la risposa del sisema a un segnale di prova canonico, cioè si sollecia
Introduzione allo studio delle reti elettriche
 Marco Panareo Inrodzione allo dio delle rei eleriche Unierià deli Sdi di Lecce - Facolà di Ineneria II Indice Rei eleriche lineari Lee di Kirchho per le correni Lee di Kirchho per le enioni Solzione di
Marco Panareo Inrodzione allo dio delle rei eleriche Unierià deli Sdi di Lecce - Facolà di Ineneria II Indice Rei eleriche lineari Lee di Kirchho per le correni Lee di Kirchho per le enioni Solzione di
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof Biani, BIO A-K 6 Seembre 7 Si conideri il eguene iema dinamico lineare a coefficieni coani a empo coninuo: u ( G ( y ( con G ( 5 a Di quale o quali, ra i iemi
Trasformata di Laplace ESEMPI DI MODELLIZZAZIONE
 Traformata di Laplace ESEMPI DI MODELLIZZAZIONE Introduzione La traformata di Laplace i utilizza nel momento in cui è tata individuata la funzione di traferimento La F.d.T è una equazione differenziale
Traformata di Laplace ESEMPI DI MODELLIZZAZIONE Introduzione La traformata di Laplace i utilizza nel momento in cui è tata individuata la funzione di traferimento La F.d.T è una equazione differenziale
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 21 Luglio 2008
 SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) Luglio 8. Si conideri il eguene iema dinamico lineare a empo coninuo: x () x() 36 x() + u() x () x() x 3() x() x3() u() y () 5 x() x().a Si
Analisi nei domini del tempo e della frequenza
 Elaborazione digiale dei egnali di miura - 1 Analii nei domini del empo e della requenza Ogni egnale reale può eere prodoo aggiungendo onde inuoidali a) Coordinae ridimenionali: empo, requenza ed ampiezza.
Elaborazione digiale dei egnali di miura - 1 Analii nei domini del empo e della requenza Ogni egnale reale può eere prodoo aggiungendo onde inuoidali a) Coordinae ridimenionali: empo, requenza ed ampiezza.
V AK. Fig.1 Caratteristica del Diodo
 1 Raddrizzaore - Generalià I circuii raddrizzaori uilizzano componeni come i Diodi che presenano la caraerisica di unidirezionalià, cioè permeono il passaggio della correne solo in un verso. In figura
1 Raddrizzaore - Generalià I circuii raddrizzaori uilizzano componeni come i Diodi che presenano la caraerisica di unidirezionalià, cioè permeono il passaggio della correne solo in un verso. In figura
Sintesi tramite il luogo delle radici
 Sintei tramite il luogo delle radici Può eere utilizzata anche per progettare itemi di controllo per itemi intabili Le pecifiche devono eere ricondotte a opportuni limiti u %, ta, t di W(), oltre quelle
Sintei tramite il luogo delle radici Può eere utilizzata anche per progettare itemi di controllo per itemi intabili Le pecifiche devono eere ricondotte a opportuni limiti u %, ta, t di W(), oltre quelle
Lezione 2. Campionamento e Aliasing. F. Previdi - Controlli Automatici - Lez. 2 1
 Lezione 2. Campionamento e Aliaing F. Previdi - Controlli Automatici - Lez. 2 1 Schema della lezione 1. Introduzione 2. Il campionatore ideale 3. Traformata di un egnale campionato 4. Teorema del campionamento
Lezione 2. Campionamento e Aliaing F. Previdi - Controlli Automatici - Lez. 2 1 Schema della lezione 1. Introduzione 2. Il campionatore ideale 3. Traformata di un egnale campionato 4. Teorema del campionamento
Definizione delle specifiche per un sistema di controllo a retroazione unitaria
 Definizione delle pecifiche per un itema di controllo a retroazione unitaria Obiettivi del controllo Il itema di controllo deve eere progettato in modo da garantire un buon ineguimento dei egnali di riferimento
Definizione delle pecifiche per un itema di controllo a retroazione unitaria Obiettivi del controllo Il itema di controllo deve eere progettato in modo da garantire un buon ineguimento dei egnali di riferimento
Lezione 5. Calcolo dell antitrasformata di Laplace. F. Previdi - Automatica - Lez. 5 1
 Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
SOLUZIONI PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 25 Settembre y=x 2 =i L
 .9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
.9.8.7.6.5.4... - 4 5 6 7 8 9 SOLUZIONI PROVA SRITTA DI AUTOMATIA I (Prof. Biani, BIO A-K) 5 Seembre 6. Si conideri il eguene circuio elerico conenene due reiori, un condenaore e un induore: u A B R v
ERRORE STATICO. G (s) H(s) Y(s) E(s) X (s) YRET(s)
 Preciione a regime: errore tatico ERRORE STATICO Alimentazione di potenza E() YRET() G() Y() H() Per errore tatico i intende lo cotamento, a regime, della variabile controllata Y() dal valore deiderato.
Preciione a regime: errore tatico ERRORE STATICO Alimentazione di potenza E() YRET() G() Y() H() Per errore tatico i intende lo cotamento, a regime, della variabile controllata Y() dal valore deiderato.
Capitolo IV L n-polo
 Capitolo IV L n-polo Abbiamo oervato che una qualiai rete, vita da due nodi, diventa, a tutti gli effetti eterni, un bipolo unico e queto è in qualche miura ovvio e abbiamo anche motrato come cotruire
Capitolo IV L n-polo Abbiamo oervato che una qualiai rete, vita da due nodi, diventa, a tutti gli effetti eterni, un bipolo unico e queto è in qualche miura ovvio e abbiamo anche motrato come cotruire
ANALISI STATISTICA DELLE VENDITE E METODI PER LA PREVISIONE
 La previione delle vendie ANALISI STATISTICA DELLE VENDITE E METODI PER LA PREVISIONE Prof. Domenico SUMMO. Premea Un imprendiore, nell eplicare la propria aivià economica, non fa alro che prevedere quali
La previione delle vendie ANALISI STATISTICA DELLE VENDITE E METODI PER LA PREVISIONE Prof. Domenico SUMMO. Premea Un imprendiore, nell eplicare la propria aivià economica, non fa alro che prevedere quali
6. Tassi di sostituzione lordi e netti del sistema pensionistico obbligatorio e complementare
 6. Tai di oiuzione lordi e nei del iema penioniico obbligaorio e complemenare 6.1. Premea Il capiolo è dedicao all analii dei ai di oiuzione del iema penioniico obbligaorio nell inero periodo di previione
6. Tai di oiuzione lordi e nei del iema penioniico obbligaorio e complemenare 6.1. Premea Il capiolo è dedicao all analii dei ai di oiuzione del iema penioniico obbligaorio nell inero periodo di previione
Operazioni finanziarie. Operazioni finanziarie
 Operazioni finanziarie Una operazione finanziaria è uno scambio di flussi finanziari disponibili in isani di empo differeni. Disinguiamo ra: operazioni finanziarie in condizioni di cerezza, quando ui gli
Operazioni finanziarie Una operazione finanziaria è uno scambio di flussi finanziari disponibili in isani di empo differeni. Disinguiamo ra: operazioni finanziarie in condizioni di cerezza, quando ui gli
Le ipotesi di base che si utilizzano sono le stesse quattro già viste con riferimento al caso della flessione semplice e cioè:
 LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
LEZIONI N 44 E 45 CALCOLO A ROTTURA DELLA SEZIONE PRESSOINFLESSA PROBLEMI DI VERIFICA La procedura di verifica dei pilatri di c.a., ottopoti a forzo normale e momento flettente, è baata ulla cotruzione
campionatore - converte un segnale a tempo continuo in una sequenza sono quindi presenti sia variabili a tempo discreto sia variabili a tempo
 Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
Ingegneria e ecnologie dei Siemi di Conrollo Campionameno e ricoruzione dei egnali Luigi Biagioi DEIS-Univerià di Bologna el. 5 9334 e-mail: lbiagioi@dei.unibo.i Ricoruore di ordine zero Ponendo la equenza
Controllo in retroazione
 Conrollo in reroazione E. regolaore di poraa: la miura della poraa (F) viene confronaa con il e-poin F p ed il comando di regolazione viene inviao all organo di auazione (valvola) L effeo della regolazione
Conrollo in reroazione E. regolaore di poraa: la miura della poraa (F) viene confronaa con il e-poin F p ed il comando di regolazione viene inviao all organo di auazione (valvola) L effeo della regolazione
L ipotesi di rendimenti costanti di scala permette di scrivere la (1) in forma intensiva. Ponendo infatti c = 1/L, possiamo scrivere
 DIPRTIMENTO DI SCIENZE POLITICHE Modello di Solow (1) 1 a. a. 2015-2016 ppuni dalle lezioni. Uso riservao Maurizio Zenezini Consideriamo un economia (chiusa e senza inerveno dello sao) in cui viene prodoo
DIPRTIMENTO DI SCIENZE POLITICHE Modello di Solow (1) 1 a. a. 2015-2016 ppuni dalle lezioni. Uso riservao Maurizio Zenezini Consideriamo un economia (chiusa e senza inerveno dello sao) in cui viene prodoo
Corso di Microonde II
 POITECNICO DI MIANO Coro di Microonde II ezi n. 3: Generalità ugli amplificatori ineari Coro di aurea pecialitica in Ingegneria delle Telecomunicazi Circuiti attivi a microonde (Amplificatori) V in Z g
POITECNICO DI MIANO Coro di Microonde II ezi n. 3: Generalità ugli amplificatori ineari Coro di aurea pecialitica in Ingegneria delle Telecomunicazi Circuiti attivi a microonde (Amplificatori) V in Z g
Dato un cammino P indichiamo con c(p ) il costo dell insieme di archi A(P ) del cammino, ovvero c(p )=c(a(p )) = uv P c uv. c 1
 Capiolo 7 Cammini minimi 7. Definizioni fondamenali Sia dao un grafo non orienao G(N,A) conneo, con coi aociai agli archi c uv R per ogni uv A. Siano anche dai due nodi peciali, N. Faremo la eguene: Aunzione
Capiolo 7 Cammini minimi 7. Definizioni fondamenali Sia dao un grafo non orienao G(N,A) conneo, con coi aociai agli archi c uv R per ogni uv A. Siano anche dai due nodi peciali, N. Faremo la eguene: Aunzione
Controllore Processo. Le principali componenti del sistema sono: il rivelatore di errore, il controllore che ha il compito di trasformare il segnale
 CONTROLLORI DI TIO ID rincipi di funzionamento Il termine controllo definice l azione volta per portare e mantenere ad un valore prefiato un parametro fiico di un impianto o di un proceo (ad eempio, la
CONTROLLORI DI TIO ID rincipi di funzionamento Il termine controllo definice l azione volta per portare e mantenere ad un valore prefiato un parametro fiico di un impianto o di un proceo (ad eempio, la
d y d u + u y des C(s) F(s) Esercizio 1 Si consideri lo schema di controllo riportato in figura:
 Eercizio Si conideri lo chema di controllo riportato in figura: y de e C() d u u F() d y y Applicando le regole di algebra dei blocchi, calcolare le eguenti funzioni di traferimento: y() a) W y,dy() =
Eercizio Si conideri lo chema di controllo riportato in figura: y de e C() d u u F() d y y Applicando le regole di algebra dei blocchi, calcolare le eguenti funzioni di traferimento: y() a) W y,dy() =
Università di Napoli Parthenope Facoltà di Ingegneria
 Universià di Napoli Parenope Facolà di Ingegneria Corso di Comunicazioni Elerice docene: Prof. Vio Pascazio a Lezione: 7/04/003 Sommario Caraerizzazione energeica di processi aleaori Processi aleaori nel
Universià di Napoli Parenope Facolà di Ingegneria Corso di Comunicazioni Elerice docene: Prof. Vio Pascazio a Lezione: 7/04/003 Sommario Caraerizzazione energeica di processi aleaori Processi aleaori nel
Slide del corso di. Controllo digitale
 Slide del coro di Controllo digitale Coro di Laurea in Ingegneria Informatica e dell Informazione Univerità di Siena, Dip. Ing. dell Informazione e Sc. Matematiche Parte III Sitemi a dati campionati Gianni
Slide del coro di Controllo digitale Coro di Laurea in Ingegneria Informatica e dell Informazione Univerità di Siena, Dip. Ing. dell Informazione e Sc. Matematiche Parte III Sitemi a dati campionati Gianni
Rappresentazione del sistema. Classificazione dei sistemi di controllo
 Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Rappreenazione del iema ẋ= f x,u, (equazione differenziale) y =g x,u, (equazione algebrica) Nomi delle variabili u: ingreo x: ao y: ucia Claificazione dei iemi di conrollo Ordine Il numero n delle variabili
Nome: Nr. Mat. Firma:
 Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Diagramma circolare di un motore asincrono trifase
 Diagramma circolare di un motore aincrono trifae l diagramma circolare è un diagramma che permette di leggere tutte le grandezze del motore aincrono trifae (potenza rea, perdite nel ferro, coppia motrice,
Diagramma circolare di un motore aincrono trifae l diagramma circolare è un diagramma che permette di leggere tutte le grandezze del motore aincrono trifae (potenza rea, perdite nel ferro, coppia motrice,
MACCHINE ELETTRICHE. Campo rotante. Stefano Pastore. Dipartimento di Ingegneria e Architettura Corso di Elettrotecnica (IN 043) a.a.
 MACCINE ELETTRICE Campo roane Sefano Pasore Diparimeno di Ingegneria e Archieura Corso di Eleroecnica (IN 043) a.a. 01-13 Inroduzione campo magneico con inensià ane che ruoa aorno ad un asse con velocià
MACCINE ELETTRICE Campo roane Sefano Pasore Diparimeno di Ingegneria e Archieura Corso di Eleroecnica (IN 043) a.a. 01-13 Inroduzione campo magneico con inensià ane che ruoa aorno ad un asse con velocià
Note su alcuni principi fondamentali di macroeconomia Versione parziale e provvisoria. Claudio Sardoni Sapienza Università di Roma
 Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
Basi di Elettronica (1 parte)
 Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
Bai di Eleronica ( pare) A TRASFORMATA DI APACE 2 Traformaa invera di aplace 2 Tabella: raformae di aplace di funzioni elemenari 2 Alcune proprieà noevoli della raformaa di aplace 3 Idenià di Pareval 5
PREMESSA In questa lezione verranno esposte le regole per l analisi dei sistemi continui con il metodo della Trasformata di Laplace.
 ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
ITIS G CARDANO PREMESSA In quea lezione verranno epoe le regole per l analii dei iemi coninui con il meodo della Traormaa di Laplace ANALISI DEI SISTEMI CONTINUI Per analizzare un iema di conrollo è neceario
velocità angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un intervallo di tempo)
 V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
ESEMPI DI ESERCIZI SU IRPEF ED IRES
 ESEMPI DI ESERCIZI SU IRPEF ED IRES 1. Irpef 1) Dopo avere definio il conceo di progressivià delle impose, si indichino le modalià per la realizzazione di un sisema di impose progressivo. 2) Il signor
ESEMPI DI ESERCIZI SU IRPEF ED IRES 1. Irpef 1) Dopo avere definio il conceo di progressivià delle impose, si indichino le modalià per la realizzazione di un sisema di impose progressivo. 2) Il signor
Struttura dei tassi per scadenza
 Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
LEZIONE 3 INDICATORI DELLE PRINCIPALI VARIABILI MACROECONOMICHE. Argomenti trattati: definizione e misurazione delle seguenti variabili macroecomiche
 LEZIONE 3 INDICATORI DELLE RINCIALI VARIABILI MACROECONOMICHE Argomeni raai: definizione e misurazione delle segueni variabili macroecomiche Livello generale dei prezzi, Tasso d inflazione, π IL nominale,
LEZIONE 3 INDICATORI DELLE RINCIALI VARIABILI MACROECONOMICHE Argomeni raai: definizione e misurazione delle segueni variabili macroecomiche Livello generale dei prezzi, Tasso d inflazione, π IL nominale,
Circuito Simbolico. Trasformazione dei componenti
 Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
VALORE EFFICACE DEL VOLTAGGIO
 Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
SEGNALI E SISTEMI 31 agosto 2017
 SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
SEGNALI E SISTEMI 31 agoto 2017 Eercizio 1. [3+3+3+4 punti] Si conideri il modello ingreo/ucita LTI e cauale decritto dalla eguente equazione differenziale: dove a è un parametro reale. d 2 v(t) 2 +(1
Richiami: funzione di trasferimento e risposta al gradino
 Richiami: funzione di trasferimento e risposta al gradino 1 Funzione di trasferimento La funzione di trasferimento di un sistema lineare è il rapporto di due polinomi della variabile complessa s. Essa
Richiami: funzione di trasferimento e risposta al gradino 1 Funzione di trasferimento La funzione di trasferimento di un sistema lineare è il rapporto di due polinomi della variabile complessa s. Essa
Esercizi sul moto del proiettile
 Eercizi ul moto del proiettile Riolvi li eercizi ul quaderno utilizzando la oluzione olo per controllare il tuo riultato. 1 Un fucile è puntato orizzontalmente contro un beralio alla ditanza di 30 m. Il
Eercizi ul moto del proiettile Riolvi li eercizi ul quaderno utilizzando la oluzione olo per controllare il tuo riultato. 1 Un fucile è puntato orizzontalmente contro un beralio alla ditanza di 30 m. Il
Lezione n.12. Gerarchia di memoria
 Lezione n.2 Gerarchia di memoria Sommario: Conceo di gerarchia Principio di localià Definizione di hi raio e miss raio La gerarchia di memoria Il sisema di memoria è molo criico per le presazioni del calcolaore.
Lezione n.2 Gerarchia di memoria Sommario: Conceo di gerarchia Principio di localià Definizione di hi raio e miss raio La gerarchia di memoria Il sisema di memoria è molo criico per le presazioni del calcolaore.
ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA 1 SETTIMANA 27
 ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA SETTIMANA 27.. Convergenza di inegrali generalizzai. () Per ognuno dei segueni inegrali impropri deerminae qual è l insieme dei valori del paramero α > per
ESERCIZI E ALCUNE SOLUZIONI ANALISI MATEMATICA SETTIMANA 27.. Convergenza di inegrali generalizzai. () Per ognuno dei segueni inegrali impropri deerminae qual è l insieme dei valori del paramero α > per
Lezione 9. Calcolo dell antitrasformata di Laplace. F. Previdi - Fondamenti di Automatica - Lez. 9 1
 ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
ezione 9. Calcolo dell aniraormaa di aplace. Previdi - ondameni di Auomaica - ez. 9 Schema della lezione. Inroduzione. Aniraormazione di aplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale
ELETTRONICA ANALOGICA INDUSTRIALE PARTE 4. Retroazione
 Retroazione Eetto della retroazione ul guadagno Riduzione della ditorione Impedenze di ingreo e di ucita Reti di retroazione Ripota in requenza Eetto della retroazione ui poli Margini di guadagno e di
Retroazione Eetto della retroazione ul guadagno Riduzione della ditorione Impedenze di ingreo e di ucita Reti di retroazione Ripota in requenza Eetto della retroazione ui poli Margini di guadagno e di
La programmazione aggregata nella supply chain. La programmazione aggregata nella supply chain 1
 La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
Stato limite ultimo di sezioni in c.a. soggette. SLU per sezioni rettangolari in c.a. con. determinazione del campo di rottura
 Univerità degli Studi di Roma Tre Coro di Progetto di trutture - A/A 2008-0909 Stato limite ultimo di ezioni in c.a. oggette a preoleione SLU per ezioni rettangolari in c.a. con doppia armatura determinazione
Univerità degli Studi di Roma Tre Coro di Progetto di trutture - A/A 2008-0909 Stato limite ultimo di ezioni in c.a. oggette a preoleione SLU per ezioni rettangolari in c.a. con doppia armatura determinazione
Distribuzione Weibull
 Disribuzione Weibull f() 6.6.4...8.6.4. 5 5 5 3 Disribuzione di Weibull Una variabile T ha disribuzione di Weibull di parameri α> β> se la sua densià di probabilià è scria nella forma: f ( ) exp da cui
Disribuzione Weibull f() 6.6.4...8.6.4. 5 5 5 3 Disribuzione di Weibull Una variabile T ha disribuzione di Weibull di parameri α> β> se la sua densià di probabilià è scria nella forma: f ( ) exp da cui
Soluzioni degli esercizi di Analisi Matematica I
 Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Sapienza - Universià di Roma - Corso di Laurea in Ingegneria Eleroecnica Soluzioni degli esercizi di Analisi Maemaica I A.A. 6 7 - Docene: Luca Baaglia Lezione del Dicembre 6 Argomeno: Equazioni differenziali,
Lezione 10. (BAG cap. 9) Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
 Lezione 10 (BAG cap. 9) Il asso naurale di disoccupazione e la curva di Phillips Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia In queso capiolo Inrodurremo uno degli oggei più conosciui
Lezione 10 (BAG cap. 9) Il asso naurale di disoccupazione e la curva di Phillips Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia In queso capiolo Inrodurremo uno degli oggei più conosciui
Lezione 11. Inflazione, produzione e crescita della moneta
 Lezione 11 (BAG cap. 10) Inflazione, produzione e crescia della monea Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia Tre relazioni ra produzione, disoccupazione e inflazione Legge di Okun
Lezione 11 (BAG cap. 10) Inflazione, produzione e crescia della monea Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia Tre relazioni ra produzione, disoccupazione e inflazione Legge di Okun
Fondamenti di Automatica
 Fondamenti di Automatica «Correzione Eonero 23/05/2019» Compito B Dario Maucci 28/05/2019 Traccia d eame (Eercizio 1 - Compito B) Dato il itema di controllo in figura u(t) + C() P 1 () + z + P 2 () y(t)
Fondamenti di Automatica «Correzione Eonero 23/05/2019» Compito B Dario Maucci 28/05/2019 Traccia d eame (Eercizio 1 - Compito B) Dato il itema di controllo in figura u(t) + C() P 1 () + z + P 2 () y(t)
LABORATORIO di ELETTRONICA SEGNALI ELETTRICI PERIODICI
 LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
LABORAORIO di ELERONICA SEGNALI ELERICI PERIODICI SEGNALI PERIODICI REANGOLARI (Recangular Waveform) Un egnale periodico avene una forma d onda reangolare è caraerizzao da un periodo [ec], una frequenza
Statica del corpo rigido: esercizi svolti dai compitini degli anni precedenti
 Statica de corpo riido: eercizi voti dai compitini dei anni precedenti II COMPITIO 00 003 Un ae di eno orizzontae omoenea, di maa M0 k e unhezza L m, è appoiata u due cavaetti. L ae pore di 60 cm otre
Statica de corpo riido: eercizi voti dai compitini dei anni precedenti II COMPITIO 00 003 Un ae di eno orizzontae omoenea, di maa M0 k e unhezza L m, è appoiata u due cavaetti. L ae pore di 60 cm otre
Calcolo della funzione di trasferimento P(s) Progetto del controllore in base alle specifiche
 Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
Esempio 1 Si consideri la sezione di un solaio latero-cementizio (1 m) di caratteristiche geometriche:
 Si riporta di eguito la rioluzione di alni eercizi riguardanti il calcolo del momento reitente e del dominio di preoleione di ezioni in cemento armato. In tutte le applicazioni ucceive i è utilizzato per
Si riporta di eguito la rioluzione di alni eercizi riguardanti il calcolo del momento reitente e del dominio di preoleione di ezioni in cemento armato. In tutte le applicazioni ucceive i è utilizzato per
Esempi Calcolo Antitrasformate
 Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Eempi Calcolo Antitraformate Note per il Coro di FdA - Info April, 05 Il punto focale del coiddetto metodo di Heaviide per l antitraformazione di un egnale regolare a traformata razionale conite nel riconocere
Errori di misura. è ragionevole assumere che una buona stima del valore vero sia la media
 Errori di miura Se lo trumento di miura è abbatanza enibile, la miura rietuta della tea grandezza fiica darà riultati diveri fra loro e fluttuanti in modo caratteritico. E l effetto di errori cauali, o
Errori di miura Se lo trumento di miura è abbatanza enibile, la miura rietuta della tea grandezza fiica darà riultati diveri fra loro e fluttuanti in modo caratteritico. E l effetto di errori cauali, o
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A )
 Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
Fondameni di comunicazioni eleriche (Ing. Eleronica - A.A.-) E. g (, ) rec / dipende dalla variabile aleaoria avene denià di probabilià uniforme nell inervallo [,]. rovare valor medio ed auocorrelazione
Domande di Affidabilità e controllo della qualità
 Domande di Affidabilià e conrollo della qualià QUALITÀ IL MAUALE DELLA QUALITÀ Si può cerificare che un'aienda è in qualià quando ha un iema di qualià ed un corripondene manuale della qualià valido e lo
Domande di Affidabilià e conrollo della qualià QUALITÀ IL MAUALE DELLA QUALITÀ Si può cerificare che un'aienda è in qualià quando ha un iema di qualià ed un corripondene manuale della qualià valido e lo
Trasformate e sistemi lineari
 Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod poa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca OMA
Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod poa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca OMA
DINAMICA STUDIA IL MOTO DEI CORPI E LE CAUSE CHE LO PRODUCONO. ITIS MAJORANA SERIATE (BG) Prof. E. Morandini
 DINAMICA STUDIA IL MOTO DEI CORPI E LE CAUSE CHE LO PRODUCONO DINAMICA SI BASA SU 3 PRINCIPI ONDAMENTALI PRINCIPIO DI INERZIA (ALILEI) ONI CORPO PERSEVERA NEL PROPRIO STATO DI QUIETE O DI MOTO INCHÈ NON
DINAMICA STUDIA IL MOTO DEI CORPI E LE CAUSE CHE LO PRODUCONO DINAMICA SI BASA SU 3 PRINCIPI ONDAMENTALI PRINCIPIO DI INERZIA (ALILEI) ONI CORPO PERSEVERA NEL PROPRIO STATO DI QUIETE O DI MOTO INCHÈ NON
Algebra vettoriale. risultante. B modulo, direzione e verso A punto di applicazione. Somma e differenza di vettori: a + b = c
 Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Algebra eoriale A B modulo, direzione e ero A puno di applicazione Somma e differenza di eori: a + b = c b a c meodo grafico: regola del parallelogramma Proprieà della omma: a + b = b + a (commuaia) (a
Il condensatore. Carica del condensatore: tempo caratteristico
 Il condensaore IASSUNTO: apacia ondensaori a geomeria piana, cilindrica, sferica La cosane dielerica ε r ondensaore ceramico, a cara, eleroliico Il condensaore come elemeno di circuio: ondensaori in serie
Il condensaore IASSUNTO: apacia ondensaori a geomeria piana, cilindrica, sferica La cosane dielerica ε r ondensaore ceramico, a cara, eleroliico Il condensaore come elemeno di circuio: ondensaori in serie
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI
 CAMPIONAMENO E RICOSRUZIONE DI SEGNALI CAMPIONAMENO E RICOSRUZIONE Numerizzazione dei egnali Nei Nei moderni iemi di di memorizzazione e ramiione i i egnali in in ingreo ono ono di di ipo ipo numerio,
CAMPIONAMENO E RICOSRUZIONE DI SEGNALI CAMPIONAMENO E RICOSRUZIONE Numerizzazione dei egnali Nei Nei moderni iemi di di memorizzazione e ramiione i i egnali in in ingreo ono ono di di ipo ipo numerio,
ALGEBRA DEGLI SCHEMI A BLOCCHI. La figura seguente rappresenta una relazione ingresso/uscita in forma grafica.
 Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
Lezioni di Teoria dei Siemi. CdL in Ingegneria dell Ambiene e del Terriorio (A.A. 00/0. Bozze). ALGEBRA DEGLI SCHEMI A BLOCCHI La figura eguene rappreena una relazione ingreo/ucia in forma grafica. U(
5. L integrale improprio x 2 : (a) diverge. (b) converge a 0 = lim. (c) converge a π 4 (d) è uguale al valore del limite
 INTEGRALI IMPROPRI Tes di auovaluazione. L inegrale improprio 5 d : (a) vale 4 5 (c) vale 5 4 (d) è negaivo.. L inegrale improprio 4 + 5 d : (a) vale 4 5 (c) vale 4 5 (d) ende a.. L inegrale improprio
INTEGRALI IMPROPRI Tes di auovaluazione. L inegrale improprio 5 d : (a) vale 4 5 (c) vale 5 4 (d) è negaivo.. L inegrale improprio 4 + 5 d : (a) vale 4 5 (c) vale 4 5 (d) ende a.. L inegrale improprio
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/10. Lecture 11: 13-14 Maggio 2010. Meccanismi per la Condivisione dei Costi
 Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/0 Lecture : 3-4 Maggio 200 Meccanimi per la Condiviione dei Coti Docente Paolo Penna Note redatte da: Paolo Penna Primo Eempio Vogliamo vendere
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/0 Lecture : 3-4 Maggio 200 Meccanimi per la Condiviione dei Coti Docente Paolo Penna Note redatte da: Paolo Penna Primo Eempio Vogliamo vendere
( ) ( ) Esempio di Prova di MATEMATICA E FISICA - MIUR PROBLEMA 1 (traccia di soluzione di S. De Stefani)
 Esempio di Prova di MATEMATICA E FISICA - MIUR - 8..9 PROBLEMA (raccia di soluzione di S. De Sefani) Assegnae due cosani reali a e (con >), si consideri la funzione ) così definia: )=. A seconda dei possiili
Esempio di Prova di MATEMATICA E FISICA - MIUR - 8..9 PROBLEMA (raccia di soluzione di S. De Sefani) Assegnae due cosani reali a e (con >), si consideri la funzione ) così definia: )=. A seconda dei possiili
Fisica Generale Modulo di Fisica II A.A. 2014-15 Esercitazione 7 CIRCUITI IN REGIME SINUSOIDALE
 Fisica Generale Modulo di Fisica II A.A. 4-5 Eserciazione 7 CICUII IN EGIME SINUSOIDALE Fa. Un generaore di correne alernaa con volaggio massimo di 4 e frequenza di 5 Hz è collegao a una resisenza 65 Ω.
Fisica Generale Modulo di Fisica II A.A. 4-5 Eserciazione 7 CICUII IN EGIME SINUSOIDALE Fa. Un generaore di correne alernaa con volaggio massimo di 4 e frequenza di 5 Hz è collegao a una resisenza 65 Ω.
ESAME DI STATO DI LICEO SCIENTIFICO 2006 Indirizzo Scientifico-Tecnologico Progetto Brocca
 Eame di tato 00 ESAME D STATO D LCEO SCENTFCO 00 ndirizzo Scientifico-Tecnologico rogetto Brocca Tema di: FSCA tracrizione del teto e redazione oluzione di Quintino d Annibale Secondo tema L'etto oule
Eame di tato 00 ESAME D STATO D LCEO SCENTFCO 00 ndirizzo Scientifico-Tecnologico rogetto Brocca Tema di: FSCA tracrizione del teto e redazione oluzione di Quintino d Annibale Secondo tema L'etto oule
MOTO RETTILINEO UNIFORMEMENTE ACCELERATO (M.R.U.A.) Giuseppe Frangiamore con la collaborazione di Francesco Garofalo
 MOTO RETTILINEO UNIFORMEMENTE ACCELERATO (M.R.U.A.) Giuseppe Frangiamore con la collaborazione di Francesco Garofalo Accelerazione Il moo reilineo uniformemene accelerao è il moo di un puno sooposo ad
MOTO RETTILINEO UNIFORMEMENTE ACCELERATO (M.R.U.A.) Giuseppe Frangiamore con la collaborazione di Francesco Garofalo Accelerazione Il moo reilineo uniformemene accelerao è il moo di un puno sooposo ad
APPLICAZIONE DELL UNSCENTED KALMAN FILTER ALLA
 APPLICAZIONE DELL UNSCENTED KALMAN FILTER ALLA SOLUZIONE DELLE EQUAZIONI DELLA NAVIGAZIONE STEFANO LAGRASTA TELESPAZIO S.P.A., VIA TIBURTINA, 965-56, ROME (ITALY) ABSTRACT Imporan GNSS applicaion ha are
APPLICAZIONE DELL UNSCENTED KALMAN FILTER ALLA SOLUZIONE DELLE EQUAZIONI DELLA NAVIGAZIONE STEFANO LAGRASTA TELESPAZIO S.P.A., VIA TIBURTINA, 965-56, ROME (ITALY) ABSTRACT Imporan GNSS applicaion ha are
6.5. La compressione
 6.5. La comreione rofondimenti 6.5.1. I materiali iotroi Mentre alcuni materiali (come l acciaio) hanno un uguale comortamento a trazione e a comreione (ono cioè «materiali iotroi») altri (come le ghie,
6.5. La comreione rofondimenti 6.5.1. I materiali iotroi Mentre alcuni materiali (come l acciaio) hanno un uguale comortamento a trazione e a comreione (ono cioè «materiali iotroi») altri (come le ghie,
PARTE 4: CINEMATICA DEL PUNTO MATERIALE
 PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
PARTE 4: CINEMATICA DEL PUNTO MATERIALE 4. INTRODUZIONE Fiaa una erna di ai careiani (muuamene orogonali fra loro) Oz, con origine nel puno O, i riferica il moo di un corpo maeriale a ale erna, cioè i
Università di Napoli Parthenope Facoltà di Ingegneria
 Universià di Napoi Parhenope Facoà di Ingegneria Corso di Comunicazioni Eeriche docene: Pro. Vio Pascazio 14 a Lezione: 8/5/3 Sommario Fasori Segnai passabanda Trasmissione di segnai passabanda in sisemi
Universià di Napoi Parhenope Facoà di Ingegneria Corso di Comunicazioni Eeriche docene: Pro. Vio Pascazio 14 a Lezione: 8/5/3 Sommario Fasori Segnai passabanda Trasmissione di segnai passabanda in sisemi
METODI DECISIONALI PER L'AZIENDA. www.lvproject.com. Dott. Lotti Nevio
 METODI DECISIONALI PER L'AZIENDA www.lvprojec.com Do. Loi Nevio Generalià sui sisemi dinamici. Variabili di sao, di ingresso, di uscia. Sisemi discrei. Sisemi lineari. Paper: Dynamic Modelling Do. Loi
METODI DECISIONALI PER L'AZIENDA www.lvprojec.com Do. Loi Nevio Generalià sui sisemi dinamici. Variabili di sao, di ingresso, di uscia. Sisemi discrei. Sisemi lineari. Paper: Dynamic Modelling Do. Loi
Controlli Automatici LA Risposte dei sistemi
 //8 Controlli Automatici LA Analii dei itemi dinamici lineari Ripote al gradino di itemi tipici Relazioni Funzione di Traferimento/Ripote Prof. Carlo Roi DEIS-Univerità di Bologna Tel. 5 93 Email: croi@dei.unibo.it
//8 Controlli Automatici LA Analii dei itemi dinamici lineari Ripote al gradino di itemi tipici Relazioni Funzione di Traferimento/Ripote Prof. Carlo Roi DEIS-Univerità di Bologna Tel. 5 93 Email: croi@dei.unibo.it
1 Generalità sui sistemi di controllo
 1 Generalità ui itemi di controllo Col termine proceo nell impiantitica chimica i intende un inieme di operazioni eeguite u una certa quantità di materia allo copo di modificarne in tutto o in parte alcune
1 Generalità ui itemi di controllo Col termine proceo nell impiantitica chimica i intende un inieme di operazioni eeguite u una certa quantità di materia allo copo di modificarne in tutto o in parte alcune
Esercizi & Domande per il Compito di Elettrotecnica del 1 giugno 2004
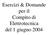 Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
Eercizi & Domande per il Compio di Eleroecnica del giugno Eercizio N Η Ω Solgimeno Deerminare i parameri z della ree due pore in figura: [ Z] Z Z Η Ω x X ω ω Z Z Z Z H Ω Z Z La ree non è reciproca come
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
Teoria dei Siemi e del Conrollo Compio A del 5 Febbraio 5 Domande ed eercizi Nome: Nr. Ma. Firma: C.L.: Info. Ele. Telec.. Scrivere la oluzione in forma chiua dell equazione differenziale ẋ() = Ax()+Bu()
Soluzione degli esercizi del Capitolo 2
 Sisemi di auomazione indusriale - C. Boniveno, L. Genili, A. Paoli 1 degli esercizi del Capiolo 2 dell Esercizio E2.1 Il faore di uilizzazione per i processi in esame è U = 8 16 + 12 48 + 6 24 = 1. L algorimo
Sisemi di auomazione indusriale - C. Boniveno, L. Genili, A. Paoli 1 degli esercizi del Capiolo 2 dell Esercizio E2.1 Il faore di uilizzazione per i processi in esame è U = 8 16 + 12 48 + 6 24 = 1. L algorimo
Nome..Cognome. classe 3D 26 Gennaio 2013. Verifica: Parabola e circonferenza
 Nome..Cognome. classe D Gennaio 0 erifica: Parabola e circonferenza. Dai la definizione di parabola. Considera la parabola di fuoco F(,) e direrice r:, deermina: a) l equazione dell asse b) le coordinae
Nome..Cognome. classe D Gennaio 0 erifica: Parabola e circonferenza. Dai la definizione di parabola. Considera la parabola di fuoco F(,) e direrice r:, deermina: a) l equazione dell asse b) le coordinae
3. MODELLI MATEMATICI
 3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
3. MODE MAEMA ASSFAZONE DE MODE iemi ono decrii da opporuni modelli maemaici. Poiamo claificarli in re caegorie: Modelli maemaici nel dominio del empo o in campo reale Decrivono il comporameno del iema
