Riproduzione vietata. Capitolo 1. Serie di funzioni. 1.1 Serie di funzioni
|
|
|
- Domenico Carraro
- 7 anni fa
- Visualizzazioni
Transcript
1 Capitolo 1 Serie di funzioni In questo capitolo trattiamo le serie di funzioni in generale e il primo importante esempio di tali serie: le serie di potenze. Nel capitolo precedente abbiamo visto la definizione e le proprietà delle serie numeriche, somme di infiniti numeri. In questo capitolo vediamo come sia possibile sommare infinite funzioni e che relazione esiste tra una serie di funzioni e la funzione somma. Questo discorso ha una grande importanza applicativa, perché consente di scrivere (ovviamente sotto ben precise ipotesi) una funzione come una somma infinita di funzioni più semplici ; molte operazioni che dovremmo svolgere sulla funzione somma, come la derivazione e l integrazione, sono eseguibili, in modo molto più agevole, sulle funzioni che compongono la serie. Nel primo paragrafo viene data la definizione di serie di funzioni e si presentano le problematiche relative a questo nuovo ente matematico; con la definizione di convergenza totale si introduce una proprietà che permette di stabilire alcune caratteristiche della funzione somma della serie a partire da quelle delle funzioni che sommiamo. Nel secondo e nel terzo paragrafo si studia un esempio particolarmente importante di serie di funzioni: le serie di potenze. Queste serie ci consentono di rappresentare solamente delle funzioni molto regolari, ma, d altra parte, sono estremamente maneggevoli perché consentono di ridurre le operazioni del calcolo differenziale e integrale sulla funzione somma ad analoghe operazioni su funzioni polinomiali. 1.1 Serie di funzioni Consideriamo una successione di funzioni {f n (x)}, con n = 0,1,2,..., definite in un intervallo I IR. Fissiamo un punto x I e consideriamo i valori assunti dalle funzioni f n in questo punto; risulta così definita la successione numerica {f n ( x)}, a partire dalla quale possiamo costruire (con il metodo visto nel capitolo precedente) la serie numerica 1
2 2 1 Serie di funzioni f n ( x), (1.1) che può essere convergente oppure divergente, oppure indeterminata. Questo procedimento si può ripetere per ogni punto dell intervallo I. Definizione 1.1 Se la serie numerica (1.1) è convergente diciamo che la serie di funzioni f n (x) (1.2) converge puntualmente nel punto x. L insieme E I dei punti in cui la serie (1.2) converge è detto insieme di convergenza (puntuale) della serie (1.2). Nell insieme E di convergenza puntuale possiamo associare a ogni punto x la somma della serie (1.2); in questo modo viene definita una nuova funzione, che indichiamo con f(x) e chiamiamo somma della serie (1.2); per indicare questo fatto scriviamo Definizione 1.2 Se la serie numerica f n ( x), f(x) = f n (x), x E. (1.3) è convergente diciamo che la serie di funzioni (1.2) converge assolutamente nel punto x. Osserviamo chese la serie (1.2) converge assolutamente in ogni punto di un determinato insieme ivi converge anche puntualmente. Esempio 1.3 Riferendoci alle notazioni introdotte sopra, con I = IR, consideriamo la successione di funzioni f n (x) = x n con n = 0,1,2,... (si intende che f 0 (x) = 1 per ogni x reale); sappiamo che scegliendo x ( 1,1) la serie numerica x n, (serie geometrica di ragione x) converge e ha come somma il numero 1 1 x, mentre essa diverge oppure oscilla se x (, 1] [1, + ). Possiamo quindi concludere che la serie di funzioni (detta anch essa serie geometrica) x n ha come insieme di convergenza puntuale l insieme E = ( 1,1) e che in esso risulta
3 1.1 Serie di funzioni 3 x n = 1 1 x. Assegnata una serie di funzioni, il primo problema che si pone è quello di determinarne l insieme di convergenza puntuale E; nell esempio precedente abbiamo visto che questo insieme non coincide necessariamente con l insieme I in cui sono definite le funzioni {f n (x)}. L insieme di convergenza può essere strano anche se sommiamo funzioni molto semplici, come si vede dai seguenti esempi. Esempio 1.4 Consideriamo la serie di funzioni definite in IR sin n x. (1.4) Se poniamo x = π/2 + 2kπ con k Z otteniamo la serie 1, che è divergente, mentre per x = 3π/2 + 2kπ si ha la serie ( 1) n, che è indeterminata. In tutti gli altri punti la serie è convergente; infatti, essendo sin x < 1, la (1.4) si riduce, con la sostituzione t = sin x, alla serie geometrica t n, di ragione t con t < 1. Quindi E = IR \ {x : x = π/2 + kπ}. Sapendo che la serie geometrica ha somma 1 1 t, possiamo concludere che nell insieme di convergenza E si ha sin n 1 x = 1 sin x. Esempio 1.5 Consideriamo la serie di funzioni definite in IR n!(x 2 x). (1.5) Questa serie di funzioni converge a zero per x = 0 e per x = 1, perché si riduce alla serie nulla; in tutti gli altri punti diverge, come si verifica immediatamente usando il criterio del rapporto.quindi E = {0,1}. Una volta determinato l insieme di convergenza, si pone il problema di calcolare la somma della serie. Questo problema è risolubile solo in casi molto particolari, per cui non vale la pena di affrontarlo in generale. Dobbiamo apparentemente accontentarci di qualcosa di meno; dal punto di vista matematico si tratta invece della domanda più interessante, perché riguarda una questione generale (e non dei casi particolari, come la ricerca della somma): la funzione somma eredita le proprietà delle funzioni che sommiamo? Ad esempio, la somma di una serie di funzioni continue è una funzione continua? Oppure
4 4 1 Serie di funzioni la somma di funzioni derivabili è una funzione derivabile? In caso affermativo, possiamo calcolare la sua derivata derivando termine a termine la serie che la esprime? Inoltre, se vale la relazione (1.3), ci chiediamo se è possibile integrare termine a termine, vale a dire, assegnati due punti a e b in E, se vale la relazione b ( b ) b f(x)dx = f n (x)dx = f n (x)dx. a a La risposta a queste domande è, in generale, negativa. Vediamo un esempio a riguardo delle prime due di esse. Esempio 1.6 Consideriamo, nell intervallo I = ( π,π), la serie di funzioni ( ) 4 sin 3x sin 5x sin x = 4 sin(2n + 1)x. π 3 5 π 2n + 1 Si tratta di funzioni di classe C (I) e quindi, in particolare, continue e derivabili; si può dimostrare (come faremo tra breve, trattando le serie di Fourier) che questa serie di funzioni converge puntualmente alla funzione 1 se π < x < 0 g(x) = 0 se x = 0 1 se 0 < x < π che nell origine non è continua e, quindi, neppure derivabile. Per rispondere positivamente alle domande che ci siamo posti, è necessario introdurre un nuovo concetto di convergenza: quello di convergenza totale. Definizione 1.7 Sia {f n (x)}, con n IN, una successione di funzioni definite nell intervallo I IR. Diciamo che la serie di funzioni f n (x) converge totalmente in I se: 1. si ha che f n (x) a n per ogni x I e per ogni n IN; 2. la serie numerica a n è convergente. La convergenza totale è più forte della convergenza puntuale: se una serie converge totalmente in I allora converge anche puntualmente in ogni punto di I, ma non vale il viceversa. Infatti, fissato x I la serie f n ( x) è convergente: è sufficiente applicare la condizione 1. nel punto x e il criterio del confronto per le serie numeriche tenendo conto della condizione 2. La serie f n ( x) è assolutamente convergente e quindi convergente. D altra parte esistono serie che convergono in ogni punto di un intervallo, ma non convergono totalmente in tale intervallo. a
5 1.1 Serie di funzioni 5 Esempio 1.8 Consideriamo la serie geometrica x n nell intervallo I = ( 1,1). Sappiamo che questa serie converge puntualmente in I; non c è però convergenza totale. Infatti per applicare la seconda condizione della Definizione 1.7 dovremmo determinare una successione a n, tale che 1. sia x n a n per ogni x ( 1,1) e per ogni n IN; 2. la serie numerica a n sia convergente. Questo è impossibile, perché la migliore maggiorazione che possiamo ottenere nell intervallo ( 1,1) è x n 1 e la serie 1 è divergente. L ipotesi di convergenza totale ci consente di risolvere il problema della continuità della funzione somma di funzioni continue e della derivabilità della funzione somma di funzioni derivabili. Vale infatti il seguente teorema. Teorema 1.9 Sia f n (x) una serie totalmente convergente di funzioni definite in un intervallo I IR e sia f(x) la sua somma; 1. se le funzioni f n (x) sono continue in I allora anche la funzione somma f(x) è continua in I; 2. se le funzioni f n (x) sono derivabili in I e la serie delle derivate f n (x) converge totalmente in I, allora anche la funzione f(x) è derivabile in I e la sua derivata può essere calcolata derivando termine a termine: [ f (x) = f n (x)] = f n(x). Nell ipotesi di convergenza totale è possibile anche integrare termine a termine; infatti vale il seguente teorema. Teorema 1.10 Sia f n (x) una serie totalmente convergente di funzioni continue in un intervallo I IR e sia f(x) la sua somma; comunque scelti a e b in I si ha che b ( b ) b f(x)dx = f n (x)dx = f n (x)dx. a a a
6 6 1 Serie di funzioni Esempio 1.11 Consideriamo la serie di funzioni Poiché per ogni x reale si ha sin nx n 3. (1.6) sin nx n 3 1 n 3, 1 la serie (1.6) è maggiorata dalla serie convergente 3 e quindi converge totalmente in n IR; indichiamo con f(x) la sua somma. Essendo le funzioni f n (x) continue in IR, grazie alla prima parte del Teorema 1.9, possiamo concludere che la funzione f(x) è continua in IR. Per dimostrare la derivabilità di f(x), dopo aver osservato che le funzioni f n (x) sono derivabili in IR, verifichiamo (con un procedimento analogo a quello appena utilizzato) la convergenza totale della serie delle derivate cos nx n 2. Applicando la seconda parte del Teorema 1.9, possiamo concludere che la funzione f(x) è derivabile in IR e che f cos nx (x) = n 2. Esempio 1.12 La serie di funzioni ( 1) n xn n 2 (1.7) converge totalmente in [ 1,1]; detta f(x) la sua somma, utilizzando il Teorema ( 1 ) ( f(x)dx = ( 1) n xn ) n 2 dx = ( 1) n xn 0 n 2 dx = = [( 1) n x n+1 ] 1 n 2 = ( 1) n 1 (n + 1) n 2 (n + 1). Osservazione 1.13 Mentre la definizione di convergenza puntuale di una serie di funzioni è abbastanza facile da capire dal punto di vista intuitivo, non altrettanto si può dire di quella di convergenza totale. Per interpretarla graficamente consideriamo una serie di funzioni f n (x) che converge totalmente alla funzione f(x), per x I. Consideriamo la somma parziale k-esima della serie; per la definizione di convergenza totale, si ha 0
7 1.1 Serie di funzioni 7 k f(x) f n (x) = f n (x) f n (x) a n. n=k+1 n=k+1 n=k+1 L ultima serie è il resto k-esimo della serie convergente a n e quindi tende a zero per k. La catena di disuguaglianze precedenti ci assicura quindi che, fissata una quantità ɛ > 0, pur di scegliere opportunamente l indice k, si ha la condizione k f(x) f n (x) < ɛ, x I. Dal punto di vista geometrico: fissato ɛ > 0, pur di scegliere opportunamente l indice k, il grafico della ridotta k-esima di una serie totalmente convergente è contenuto nella striscia compresa tra f(x) ɛ e f(x) + ɛ. Nella Figura 1.1 si vede un esempio di convergenza totale (la serie ( 1) n x2n = e x2 n! che converge totalmente in [ 1,1]) mentre nella Figura 1.2 è mostrato un esempio di serie che converge puntualmente, ma non totalmente (la serie ( 1) n x 2n = 1 x che converge puntualmente in ( 1,1)). PSfrag replacements Figura y 1 s(x) s 1 (x) s 2 (x) s 4 (x) x s 3 (x) Sono rappresentate le funzioni s(x) = e x2 e le ridotte s 1 (x) = 1 x 2, s 2 (x) = 1 x 2 + x4 2, s 3(x) = 1 x 2 + x4 2 x6 3!, s 4(x) = 1 x 2 + x4 2 x6 3! + x8 4!
8 8 1 Serie di funzioni PSfrag replacements 1 y s 4 (x) s 3 (x) s(x) 1 s 2 (x) s 1 (x) 1 Figura 1.2 Sono rappresentate le funzioni s(x) = x e le ridotte s 1(x) = 1 x 2, s 2 (x) = 1 x 2 + x 4, s 3 (x) = 1 x 2 + x 4 x 6, s 4 (x) = 1 x 2 + x 4 x 6 + x Serie di potenze Assegnati una successione {a n } di numeri reali e un punto x 0 dell asse reale si dice serie di potenze la serie di funzioni a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) a n (x x 0 ) n +... = a n (x x 0 ) n. (1.8) Il punto x 0 viene detto centro della serie e i numeri a n coefficienti della serie. In particolare concentriamo la nostra attenzione sulle serie di potenze con centro nell origine, che hanno la forma x a n x n. (1.9) Le definizioni e i risultati che seguono sono riferiti alle serie centrate nell origine; per adattarli al caso generale è sufficiente operare la sostituzione y = x x 0. Alle serie di potenze possono essere applicate le definizioni di convergenza che abbiamo introdotto nel paragrafo precedente; le ricordiamo, applicandole alle serie di potenze. Definizione 1.14 Assegnato un punto x 1 si dice che la serie (1.9) converge puntualmente in x 1 se risulta convergente la serie a n x n 1 ; converge assolutamente in x 1 se risulta convergente la serie a n x n 1. Assegnato un intervallo I si dice che la serie (1.9) converge totalmente in I se esiste una serie numerica convergente M n tale che a n x n M n, per ogni x I e per ogni n IN.
9 1.2 Serie di potenze 9 Ricordiamo che la convergenza totale in un intervallo implica la convergenza assoluta e quindi quella puntuale in ogni punto dell intervallo stesso. L insieme di convergenza Assegnata la serie di potenze (1.9) si pone il problema di determinare il suo insieme di convergenza; a differenza di quanto visto per le serie di funzioni in generale, possiamo ottenere risultati molto precisi a questo riguardo. Innanzitutto, l insieme di convergenza di una serie di potenze non è mai vuoto; infatti è immediato notare che la serie (1.9) converge nel suo centro x = 0. Prima di affrontare il problema della convergenza in punti diversi dall origine, esaminiamo alcuni esempi. Esempio 1.15 Consideriamo la serie di potenze, detta serie esponenziale, x n n! (1.10) e fissiamo un punto x 1 0. Studiamo la convergenza assoluta in x 1, vale a dire il comportamento di x 1 n. n! Per questa serie numerica a termini positivi possiamo utilizzare il criterio del rapporto; si tratta di calcolare il limite lim n x 1 n+1 n! (n + 1)! x 1 = lim n n x 1 n + 1 = 0. Il risultato è indipendente dal punto scelto; possiamo concludere che la serie (1.10) converge assolutamente (e quindi puntualmente) in ogni punto dell asse reale. Esempio 1.16 Consideriamo la serie di potenze, n!x n (1.11) e studiamo la convergenza assoluta in x 1 0. Utilizzando ancora il criterio del rapporto calcoliamo il limite lim n (n + 1)! x 1 n+1 n! x 1 n = lim (n + 1) x 1 = +. n La serie (1.11) non converge assolutamente in alcun punto dell asse reale, eccetto l origine. Può restare il dubbio che la serie converga semplicemente per x < 0, dove è una serie a segni alterni. Per dimostrare che questo non avviene basta fare vedere che il valore assoluto del termine generale della serie non tende a zero per n. La successione n n! x 1 n è a termini positivi ed è (almeno a partire da un certo punto in poi) monotona crescente e quindi non può tendere a zero. Infatti la disuguaglianza (n + 1)! x 1 n+1 > n! x 1 n
10 10 1 Serie di funzioni equivale alla disuguaglianza che è verificata almeno da un certo valore n 0 in poi. n + 1 > 1 x 1 Possiamo quindi concludere che la serie (1.11) converge solo per x = 0. Esempio 1.17 Consideriamo la serie di potenze, detta serie logaritmica, x n n. (1.12) Fissiamo x 1 0 e studiamo la convergenza assoluta, utilizzando il criterio della radice. Calcoliamo il limite x 1 lim n = x 1. n n Quindi la serie (1.12) converge assolutamente per x 1 < 1; per x 1 = 1 si riduce alla serie armonica (e quindi diverge), mentre per x 1 = 1 si riduce alla serie armonica a segni alterni, che converge semplicemente, ma non assolutamente. Con considerazioni analoghe a quelle dell esempio precedente si può far vedere che la serie non converge per x > 1 in quanto il suo termine generale non tende a zero. Possiamo concludere che la serie di potenze (1.12) converge nell intervallo [ 1,1). Esempio 1.18 Consideriamo la serie x n n 2. (1.13) Questa serie converge totalmente nell intervallo [ 1,1], essendo maggiorata, in tale intervallo, dalla serie convergente 1 2. Al di fuori di [ 1,1] non converge, in quanto il suo n termine generale non è infinitesimo. L insieme di convergenza della serie (1.13) è quindi l intervallo [ 1,1]. Gli esempi appena visti riassumono le possibili situazioni che si presentano: il comportamento di una serie di potenze è determinato dalla proprietà presentata nel seguente teorema. Teorema 1.19 Si consideri la serie di potenze (1.9) e due punti x 1 0 e x 2 0. Allora se la serie converge in x 1, allora essa converge assolutamente per tutti i punti x tali che x < x 1 ; se la serie non converge in x 2, allora essa non converge in tutti i punti x tali che x > x 2.
11 1.2 Serie di potenze 11 Dimostrazione Supponiamo che la serie converga in x 1 0; consideriamo un punto x 0, tale che x < x 1. Si ha che a n x n = a n x n 1 xn x n 1 = a nx n x n x 1 M n. L ultima disuguaglianza è giustificata dal fatto che la serie converge, per ipotesi, nel punto x 1 ; il suo termine generale è quindi infinitesimo e la quantità a n x n 1 è limitata. La disuguaglianza che abbiamo ottenuto ci dice che il termine generale della serie è maggiorato da quello della serie a n x n x M n, x 1 che è una serie geometrica di ragione minore di uno e quindi converge. Il criterio del confronto ci permette di concludere che la serie (1.9) è assolutamente convergente per ogni x tale che x < x 1. Per dimostrare la seconda parte, basta osservare che, per la prima parte del teorema, se la serie convergesse in x tale che x > x 2, allora dovrebbe convergere anche nel punto x 2, contrariamente all ipotesi. Osservazione 1.20 Si osservi che nel teorema precedente la convergenza (o la non convergenza) della serie in x 1 non fornisce nessuna informazione sul comportamento della serie nel punto x 1. Osservazione 1.21 Il teorema precedente si può interpretare intuitivamente dicendo che la convergenza in un punto x 1 0 ci fa guadagnare la convergenza in tutti i punti dell intervallo di centro l origine di cui x 1 è un estremo, mentre la non convergenza in x 2 0 ci fa perdere la convergenza nelle due semirette x > x 2. Nella determinazione dell insieme di convergenza di una serie di potenze, dal punto di vista operativo, ci troviamo quindi di fronte a questa casistica: 1. non si ha la convergenza per nessun x 1 0; 2. si ha la convergenza in un x 1 0; allora possiamo provare con un valore maggiore (in modulo) e ampliare l intervallo di convergenza; e anche qui abbiamo due casi: (1) possiamo verificare che c è convergenza per una successione di punti che diventa arbitrariamente grande in modulo (e quindi c è convergenza in tutto l asse reale) oppure x 1 x 1
12 12 1 Serie di funzioni (2) a un certo punto troviamo un valore per cui la serie non converge; allora necessariamente la convergenza è limitata a un intervallo. Possiamo concludere affermando che si presentano tre possibili situazioni per la convergenza di una serie di potenze: la serie converge solo in x = 0; la serie converge all interno di un intervallo ( R,R) e non converge per x > R e per x < R; la serie converge in ogni punto dell asse reale. Per descrivere queste tre situazioni si introduce il concetto di raggio di convergenza della serie di potenze. Definizione 1.22 Il raggio di convergenza R della serie (1.9) è l estremo superiore dell insieme dei numeri reali in cui la serie converge: R = sup{x IR : a n x n converge}. Se è noto il raggio di convergenza, sono note le principali caratteristiche della serie di potenze; infatti vale il seguente risultato. Teorema 1.23 Se la serie (1.9) ha raggio di convergenza R, allora 1. Se R = 0 la serie converge solo per x = Se R > 0 allora la serie converge assolutamente in ( R, R) e converge totalmente in ogni intervallo [a, b] ( R, R). 3. Se R = + allora la serie converge assolutamente per ogni x reale e converge totalmente in ogni intervallo [a, b]. Osservazione 1.24 Se la serie di potenze è centrata in x 0 0 il teorema precedente può essere riformulato nei seguenti termini: 1. Se R = 0 la serie converge solo per x = x Se R > 0 allora la serie converge assolutamente in (x 0 R, x 0 + R) e converge totalmente in ogni intervallo [a, b] (x 0 R, x 0 + R). 3. Se R = + allora la serie converge assolutamente per ogni x reale e converge totalmente in ogni intervallo [a, b].
13 1.2 Serie di potenze 13 Determinazione del raggio di convergenza Il risultato precedente ci mostra l utilità della conoscenza del raggio di convergenza per la determinazione delle proprietà di una serie di potenze. Per questo motivo, è importante trovare dei metodi che permettano di calcolarlo, senza ricorrere allo studio diretto della convergenza della serie nei vari punti dell asse reale. A questo scopo, si hanno i seguenti teoremi. Teorema 1.25 (Criterio della radice) Data la serie di potenze (1.9), se esiste n lim a n = l allora R = 0 se l = + ; R = + se l = 0; R = 1/l se l è finito e non nullo. n Teorema 1.26 (Criterio del rapporto) Data la serie di potenze (1.9), se a n 0, n IN, ed esiste a n+1 lim = l n a n allora R = 0 se l = + ; R = + se l = 0; R = 1/l se l è finito e non nullo. Dimostriamo il primo teorema; la dimostrazione del secondo può essere svolta in modo analogo. Dimostrazione Applichiamo il criterio della radice per le serie numeriche alla serie a n x n. Abbiamo, per l ipotesi del teorema, n lim a n x n = l x ; n Se l = 0 il limite precedente è sempre nullo e quindi, sempre per il criterio della radice, la serie è assolutamente convergente per ogni x. Se invece l è infinito la serie non converge per nessun x diverso da zero. Se infine l è un numero reale si ha la convergenza assoluta se l x < 1, vale a dire se x < 1/l; non si ha invece convergenza se risulta l x > 1, cioè se x > 1/l.
14 14 1 Serie di funzioni Esempio 1.27 Determiniamo il raggio di convergenza della serie (n 2 + 1)x n. n! Conviene applicare il criterio del rapporto e calcolare a n+1 lim n a n (n + 1) n! = n lim n (n + 1)! = lim n 2 + 2n n n n + 1 = 0. Il raggio di convergenza della serie è quindi infinito. Esempio 1.28 Determiniamo il raggio di convergenza della serie n n x n n + 1. In questo caso conviene utilizzare il criterio della radice; si tratta di calcolare lim n n an = lim n = +, n + 1 n n in quanto il numeratore tende all infinito, mentre il denominatore tende a uno. La serie di potenze considerata ha quindi raggio di convergenza nullo. Esempio 1.29 Calcoliamo il raggio di convergenza della serie nx 4n 3. n Questo esempio mostra come in alcuni casi il teorema precedente non sia applicabile direttamente, ma richieda una sostituzione preliminare nella serie. Nella serie proposta compaiono solo le potenze di x con esponenti che sono multipli di 4. La successione dei coefficienti comprende dei valori nulli, ripetuti con legge periodica. In particolare essa risulta (a partire dal termine costante) 0,0,0,0,1/3,0,0,0,2/9,0,0,0,3/27,.... Il limite della radice non esiste, mentre quello del rapporto non ha senso per la presenza di coefficienti nulli. Per ovviare a questa difficoltà si può operare un cambiamento di variabile e porre z = x 4, per cui la serie assegnata si trasforma nella nz n 3, n il cui raggio di convergenza può essere determinato calcolando n n lim n 3 = 1 3 ; la serie nella variabile z converge per z < 3; sostituendo si ottiene che la serie assegnata converge per x 4 < 3, cioè per x < 4 3.
15 1.2 Serie di potenze 15 Operazioni sulle serie di potenze Vogliamo qui esaminare la possibilità di sommare e moltiplicare serie di potenze e determinare il raggio di convergenza delle serie ottenute. A riguardo della somma, si ha il seguente risultato. Teorema 1.30 Assegnate due serie di potenze Σ 1 = a n x n, Σ 2 = b n x n, con raggio di convergenza R 1 ed R 2 rispettivamente, si ha che la serie somma (a n + b n )x n ha raggio di convergenza maggiore o uguale al minimo tra R 1 ed R 2. Osservazione 1.31 Nel caso in cui R 1 ed R 2 siano diversi (ad esempio R 1 < R 2 ) allora la serie somma ha come raggio di convergenza proprio il minimo dei due. Infatti, preso un punto x 1 tale che R 1 < x < R 2 la serie Σ 1 non converge in x, mentre la serie Σ 2 converge; per i risultati visti sulle serie numeriche, la serie somma non è convergente. Nel caso in cui R 1 = R 2 si possono invece avere, fuori dall intervallo di convergenza, delle cancellazioni in modo tale che la somma converga. Esempio 1.32 Le serie ( ) 1 Σ 1 = n! + 1 x n, Σ 2 = ( ) 1 n! 1 x n, hanno entrambe R = 1. Sommandole si ottiene la serie che ha raggio di convergenza infinito. ( ) 2 Σ 1 = x n, n! Assegnate due serie di potenze si può definirne il prodotto, detto prodotto alla Cauchy, delle due serie. Teorema 1.33 Assegnate due serie di potenze a nx n, b nx n, con raggio di convergenza R 1 ed R 2 rispettivamente, si ha che la serie prodotto ( n ) a ib n i ha raggio di convergenza maggiore o uguale al minimo tra R 1 ed R 2. i=0 x n
16 16 1 Serie di funzioni Serie di potenze, derivazione e integrazione In questo paragrafo studiamo le relazioni che esistono tra le serie di potenze e le operazioni di derivazione e integrazione, applicando alle serie di potenze i risultati che abbiamo visto per le serie di funzioni. Definizione 1.34 Assegnata la serie di potenze si dice sua serie derivata la serie a n x n na n x n 1, ottenuta derivando formalmente termine a termine la serie. Vale il seguente teorema. Teorema 1.35 Una serie di potenze e la sua serie derivata hanno lo stesso raggio di convergenza. Applicando i Teoremi 1.23 e 1.9 e il teorema precedente, otteniamo il seguente importante risultato, che ci dice che la somma di una serie di potenze è una funzione molto regolare. Teorema 1.36 Sia a n x n una serie di potenze con raggio di convergenza R > 0 e sia f(x) la sua somma in ( R,R). Allora la funzione f(x) è derivabile con derivate continue di ogni ordine in ( R,R) (vale a dire f(x) C ( R,R)) e la derivata n-esima di f(x) può essere calcolata derivando termine a termine n volte la serie a n x n. Esempio 1.37 Sappiamo che vale la relazione 1 1 x = x n, per x < 1. Il teorema precedente ci dice la funzione f (x) = dx d 1 1 x = 1 (1 x) 2 ammette per x < 1 lo sviluppo ottenuto derivando termine a termine la serie geometrica nx n 1, mentre la funzione f (x) ammette lo sviluppo n(n 1)x n 2 e così via. n=2 Il Teorema 1.10 di integrazione termine a termine assume una forma particolarmente semplice, quando è applicato alle serie di potenze.
17 1.2 Serie di potenze 17 Teorema 1.38 Sia a n x n una serie di potenze con raggio di convergenza R > 0 e sia f(x) la sua somma in ( R,R). Allora, per ogni x ( R,R), vale la relazione x ( x ) ( x ) f(t)dt = a n t n dt = a n t n a n x n+1 dt = n + 1. Esempio 1.39 Dalla relazione con la sostituzione z = x si ha 1 1 z = z n, per z < 1, x = ( x) n = ( 1) n x n, per x < 1. Applicando il teorema precedente otteniamo lo sviluppo della funzione log(1 + x): x ( 1 x ) log(1 + x) = t dt = ( x ) ( 1) n t n dt = ( 1) n t n dt 0 0 = ( 1) n xn+1, per x < 1. n + 1 Invece, con la sostituzione z = x 2, risulta x = ( x 2 ) n = 2 ( 1) n x 2n, per x < 1. Procedendo come prima, otteniamo lo sviluppo della funzione arcotangente: x ( 1 x ) arctan x = t dt = ( x ) ( 1) n t 2n dt = ( 1) n t 2n dt = ( 1) n x2n+1, per x < 1. 2n + 1 Osservazione 1.40 Il teorema specifica che i raggi di convergenza coincidono, ma non dice niente sul comportamento della serie agli estremi dell intervallo di convergenza. Si può, in modo impreciso, affermare che l operazione di derivazione può peggiorare il comportamento della serie agli estremi, mentre l operazione di integrazione lo può migliorare. La serie Σ 1 = ( 1) n xn+1 = log(1 + x) n + 1 e la sua serie derivata Σ 2 = ( 1) n x n = x ;
18 18 1 Serie di funzioni entrambe hanno raggio di convergenza uguale a uno. La serie Σ 1 converge in ( 1,1], mentre la Σ 2 converge in ( 1,1). 1.3 Serie di Taylor Nel paragrafo precedente abbiamo studiato le serie di potenze dal punto di vista formale, determinando le loro proprietà. Non abbiamo discusso in generale la relazione che esiste tra una serie di potenze e la sua somma. Ci siamo limitati a determinare esplicitamente la somma della serie geometrica e di alcune serie che da essa possono essere ricavate. Ora ci chiediamo se, in generale, data una funzione, sia possibile determinarne lo sviluppo in serie di potenze in un intervallo e, in caso affermativo, quale sia il procedimento per determinare questa serie. Il Teorema 1.36 fornisce una prima indicazione: poiché la somma di una serie di potenze è una funzione di classe C ( R,R) abbiamo che: condizione necessaria perché una funzione sia sviluppabile in serie di potenze in un intervallo è che sia di classe C in tale intervallo. Possiamo enunciare un primo risultato, che mette in relazione i coefficienti dello sviluppo in serie con le derivate della funzione somma della serie. Teorema 1.41 Sia f(x) C ( R,R) e supponiamo che in (x 0 R, x 0 + R) valga la relazione f(x) = a n (x x 0 ) n. Allora risulta che a n = f (n) (x 0 ), n IN. (1.14) n! Dimostrazione La dimostrazione di questo teorema è una conseguenza del Teorema Infatti dalle relazioni f(x) = a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) a n (x x 0 ) n +... f (x) = a 1 (x x 0 ) + 2a 2 (x x 0 ) na n (x x 0 ) n f (x) = 2a a 3 (x x 0 ) n(n 1)a n (x x 0 ) n f (n) (x) = n!a n + (n + 1)!a n+1 (x x 0 ) +... ponendo x = x 0 si ottengono la (1.14). Poiché si può dimostrare che se una funzione ammette uno sviluppo in serie di potenze, tale sviluppo è unico, possiamo concludere che: se una funzione di classe C ammette uno sviluppo in serie di potenze in un intervallo centrato in x 0 allora tale sviluppo è necessariamente della forma f (n) (x 0 ) (x x 0 ) n. (1.15) n!
19 1.3 Serie di Taylor 19 Data una funzione f(x) C (x 0 R, x 0 + R), possiamo calcolarne le derivate di ogni ordine in x 0 e costruire la serie (1.15); affinché questa serie rappresenti la f(x) almeno in un intorno (x 0 δ, x 0 + δ) di x 0 devono però verificarsi altre due condizioni: 1. la serie (1.15) deve essere convergente in (x 0 δ, x 0 + δ); 2. in tale intervallo la sua somma deve essere uguale a f(x). Queste due condizioni non sono sempre verificate. Esempio 1.42 Consideriamo la funzione: { h(x) = e 1/x 2 se x 0 0 se x = 0. Si può dimostrare che questa funzione è continua, con le sue derivate di ogni ordine, su tutto l asse reale e che tutte le derivate nell origine sono nulle. La serie (1.15) di h(x) centrata nell origine è quindi la serie identicamente nulla; questa serie ovviamente converge in tutto l asse reale, ma la sua somma non coincide con la funzione h(x) in nessun punto, tranne l origine. Introduciamo una definizione per le funzioni per cui le condizioni precedenti sono verificate. Definizione 1.43 Una funzione f(x) C (x 0 δ, x 0 + δ) si dice analitica oppure sviluppabile in serie di Taylor nel punto x 0 se la serie (1.15) converge in un intorno (x 0 δ, x 0 + δ) di x 0 e se per ogni x (x 0 δ, x 0 + δ) si ha f (n) (x 0 ) f(x) = (x x 0 ) n. (1.16) n! La serie (1.15) si chiama serie di Taylor della funzione f(x) centrata in x 0 e i numeri f (n) (x 0 ) sono detti coefficienti di Taylor della f(x) in x n! 0. Se x 0 = 0, la (1.15) è detta anche serie di McLaurin. Come abbiamo visto, la condizione f(x) C (x 0 δ,x 0 + δ) non è sufficiente ad assicurarci che f(x) sia sviluppabile in serie di Taylor in x 0 ; solo ulteriori condizioni sulla f(x) assicurano la sviluppabilità. Senza entrare nei dettagli di questo discorso, possiamo comunque capire quali possano essere queste condizioni con le seguenti considerazioni. Le somme parziali di ordine k della (1.15) non sono altro che i polinomi di Taylor P f,k,x0 (x) della funzione f(x) nel punto x 0 di ordine k. Il polinomio di Taylor approssima la funzione f(x) a meno di un resto, che indichiamo con R f,k,x0 (x): k f (n) (x 0 ) f(x) = (x x 0 ) n + R f,k,x0 (x). n!
20 20 1 Serie di funzioni La convergenza della serie di Taylor (1.15) alla funzione f(x) significa che ( k f (n) ) (x 0 ) lim f(x) (x x 0 ) n = 0, k n! vale a dire lim R f,k,x 0 (x) = 0 k x (x 0 δ, x 0 + δ). Esprimiamo il resto R f,k,x0 (x) nella forma di Lagrange; la condizione precedente diventa lim R f (k+1) (c) f,k,x 0 (x) = lim k k (k + 1)! (x x 0) k+1 dove c è un punto dell intervallo (x 0 δ, x 0 + δ); in tale intervallo x x 0 < δ e quindi possiamo eseguire la seguente maggiorazione: f (k+1) (c) (k + 1)! (x x 0) k+1 f (k+1) δ k+1 (c) (k + 1)!. (1.17) Il quoziente δ k+1 0 per k ; affinché l intera espressione (1.17) tenda a (k + 1)! zero è quindi sufficiente che le derivate successive non crescano troppo rapidamente nell intervallo (x 0 δ, x 0 + δ). Questa condizione è verificata, in particolare, quando le derivate sono maggiorate in modulo da una costante in tutto l intervallo considerato, come avviene negli esempi seguenti. Esempio 1.44 Mostriamo che la funzione f(x) = e x è sviluppabile in serie di McLaurin con raggio di convergenza infinito. Fissiamo un punto x e scegliamo un intervallo [ M,M] che contiene x. Scriviamo la formula di Taylor con il resto di Lagrange: k e x x n = n! + x k+1 ec (k + 1)! dove c è un punto dell intervallo [ M,M]. In tale intervallo e c e M e x M; quindi possiamo maggiorare il resto: x k+1 k+1 M ec em (k + 1)! (k + 1)!. Questa quantità tende a zero per k, per cui la somma della serie coincide con e x nel punto x. Il ragionamento può essere ripetuto per ogni x reale, scegliendo un M opportuno; concludiamo dunque che vale il seguente sviluppo di McLaurin su tutto IR e x x n = n!.
21 1.3 Serie di Taylor 21 Con un ragionamento analogo si dimostra che la funzione esponenziale è sviluppabile in serie di Taylor con centro in un punto x 0 0 e raggio di convergenza infinito. Dallo sviluppo di McLaurin dell esponenziale si ottengono immediatamente i seguenti sviluppi, validi anch essi in tutto l asse reale: cosh x = x 2n (2n)!, sinh x = x 2n+1 (2n + 1)!. Esempio 1.45 Mostriamo che la funzione f(x) = sin x è sviluppabile in serie di McLaurin con raggio di convergenza infinito. Come nell esempio precedente, fissiamo un punto x e un intervallo [ M,M] che contiene x. La formula di Taylor con il resto di Lagrange è: k sin x = ( 1) n x 2n+1 (2n + 1)! + x 2k+3 ( 1)k+1 (2k + 3)! g(c) dove con g(c) abbiamo indicato la derivata di ordine k + 1 della funzione seno nel punto c; essa ha quattro possibili valori: sin c, sin c, cos c e cos c; in ogni caso si tratta di una quantità minore di uno in modulo. Possiamo quindi maggiorare il resto: x 2k+3 ( 1)k+1 (2k + 3)! g(c) M 2k+3 k 0. (2k + 3)! Per l arbitrarietà di x, concludiamo che vale su tutto l asse reale il seguente sviluppo sin x = ( 1) n x 2n+1 (2n + 1)!. Con considerazioni analoghe si dimostra che la funzione coseno ammette il seguente sviluppo cos x = ( 1) n x2n (2n)!, x IR. Esempio 1.46 Vogliamo studiare lo sviluppo della funzione f(x) = ( 1 + x ) α. Osserviamo che se α IN, la funzione f(x) si riduce ad un polinomio; se α / IN, essa è sviluppabile in serie di McLaurin con raggio di convergenza R = 1. Vale, infatti, l uguaglianza ( ) ( ) α α 1 + x = x n, x ( 1,1), n dove ( ) α α(α 1)... (α n + 1) =. n n! La serie appena considerata viene detta serie binomiale.
22 22 1 Serie di funzioni Osservazione 1.47 Nello studio degli integrali indefiniti si è osservato che esistono delle funzioni elementari le cui primitive non possono essere espresse elementarmente. In alcuni casi, primitive di questo tipo assumono grande importanza applicativa, ad esempio in elettronica, in ottica o nel calcolo delle probabilità. Vediamo alcuni esempi: 1. la funzione seno integrale di x, Si(x), che è definita come Si(x) = x 0 sin t dt; t 2. la funzione degli errori, Erf(x), che è definita come Erf(x) = 2 x exp( t 2 )dt; π 3. la funzione integrale di Fresnel, S(x), che è definita come ( ) x πt 2 S(x) = sin dt. 0 2 Queste funzioni possono essere espresse come serie di potenze. Ad esempio, scriviamo lo sviluppo in serie di potenze della funzione Si(x) e calcoliamo Si(1) con un errore minore di Partiamo dallo sviluppo della funzione seno, che sappiamo essere convergente per ogni z reale: ( 1) n z 2n+1 sin z =. (2n + 1)! Scrivendo questo sviluppo nella variabile t e dividendo per t otteniamo: sin t = 1 t t ( 1) n t 2n+1 = (2n + 1)! 0 ( 1) n t 2n (2n + 1)!. Integriamo per serie (l operazione è senz altro possibile, perché lo sviluppo precedente ha raggio di convergenza infinito): x ( sin t x ( 1) n t 2n ) ( x ( 1) n t 2n ) Si(x) = dt = dx = 0 t 0 (2n + 1)! 0 (2n + 1)! dt [ ( 1) n t 2n+1 ] x ( 1) n x 2n+1 = = (2n + 1)!(2n + 1) (2n + 1)!(2n + 1). 0 Questo sviluppo ha raggio di convergenza infinito. Per calcolare Si(1), valutiamo la serie che abbiamo ottenuto per x = 1; otteniamo una serie numerica a segni alterni ( 1) n (2n + 1)!(2n + 1) = 1 1 3! !
23 1.3 Serie di Taylor 23 Affinché l errore sia minore di 10 3, per il Criterio di Leibniz, è sufficiente fermarci al terzo termine. Infatti il primo termine trascurato è minore di 10 3, poiché risulta 7!
24 24 1 Serie di funzioni 1.4 Esercizi svolti Esercizio 1.1 Data la serie di funzioni exp( nx), (1.18) determinarne l insieme di convergenza e verificare che essa converge totalmente in J = [1, + ). Soluzione Con la sostituzione z = exp( x) siamo ricondotti alla serie geometrica z n, che converge per 1 < z < 1. La serie (1.18) converge quindi per 1 < exp( x) < 1, cioè per x I = (0, + ). Nell insieme J I la serie converge puntualmente; per verificare la convergenza totale, osserviamo che in J si ha che exp( nx) exp( n) e che la serie exp( n) è convergente; sono quindi soddisfatte le ipotesi che ci permettono di concludere che la serie converge totalmente in J. Esercizio 1.2 Determinare il raggio di convergenza e l insieme di convergenza della serie Soluzione x n (n 2 + 2)2 n. (1.19) Per la determinazione del raggio di convergenza utilizziamo il criterio del rapporto, calcolando (n 2 + 2)2 n 1 n lim = lim n ((n + 1) 2 + 2)2n+1 n 2 n 2 + 2n + 3 = 1 2. Il raggio di convergenza è quindi R = 2. Nel punto x = 2 la serie (1.19) si riduce a 1 (n 2 + 2), che converge (è equivalente a 1/n 2 ), mentre per x = 2 abbiamo la serie ( 1) n (n 2 + 2),
25 1.4 Esercizi svolti 25 che è (assolutamente) convergente. Quindi la serie (1.19) converge in [ 2,2]. Esercizio 1.3 Determinare il raggio di convergenza e l insieme di convergenza della serie Soluzione n + 1 n + 2 Con la sostituzione z = x 3 ci riconduciamo alla serie n + 1 z n n n Applichiamo il criterio del rapporto, calcolando n + 2 n n lim n n + 3 n = 1 n+1 3. x 3n 3 n. (1.20) La serie (nella variabile z) ha raggio di convergenza R z = 3; quindi converge per z < 3; ricordando la sostituzione fatta, la serie (1.20) converge per x 3 < 3, cioè per x < 3 3. Ponendo nella (1.20) x = 3 3, otteniamo la serie numerica n + 1 n + 2, che non converge in quanto il suo termine generale non tende a zero (condizione necessaria di convergenza delle serie numeriche). Ponendo invece nella (1.20) x = 3 3, otteniamo la serie numerica ( 1) n n + 1 n + 2 ; anche questa serie non converge in quanto il suo termine generale non ammette limite (per n pari la successione dei suoi termini tende a 1, mentre per n dispari tende a -1). L insieme di convergenza della (1.20) è quindi ( 3 3, 3 3). Esercizio 1.4 Determinare il raggio di convergenza e l insieme di convergenza della serie dove a è un numero reale positivo. x n n a, (1.21)
26 26 1 Serie di funzioni Soluzione Determiniamo il raggio di convergenza con il criterio della radice. Dobbiamo calcolare lim n 1 n. n a Possiamo scrivere n n a =n a/n = exp a ln n. Ricordando che n lim n ln n n = 0 abbiamo che a ln n 0 e quindi exp a ln n 1. Il raggio di convergenza della (1.21) è n n quindi R = 1 per ogni valore a > 0. Studiamo il comportamento nell estremo x = 1; la serie 1 n a converge se a > 1 e non converge se a 1, Sostituendo x = 1, abbiamo la serie a segni alterni ( 1) n. n a Questa serie è convergente per ogni valore di a > 0, per il criterio di Leibniz. Infatti la successione {1/n a } è decrescente e infinitesima. L insieme di convergenza della (1.21) è quindi [ 1,1) se a 1 e [ 1,1] se a > 1. Esercizio 1.5 Determinare il raggio di convergenza e l insieme di convergenza della serie Soluzione x n! = x + x 2 + x 6 + x 24 + x (1.22) La successione dei coefficienti (sempre a partire dal termine costante) è 0,1,1,0,0,0,1,0,0,...,0,1,0,0,0,..., dove gli zeri non si ripetono con regolarità ma in blocchi sempre più grandi all aumentare di n. Non è quindi possibile operare una sostituzione z = x k allo scopo di ottenere una serie con coefficienti non nulli. Per studiare l insieme di convergenza della serie assegnata bisogna procedere direttamente. È immediato osservare che la serie diverge in x = 1 e in x = 1, mentre converge
27 1.4 Esercizi svolti 27 per x < 1. Infatti se x < 1 possiamo affermare che x n! = x + x 2 + x x + x 2 + x 3 + x 4 + x ; la serie maggiorante è la serie geometrica presa in modulo, che sappiamo essere convergente per x < 1. Dal criterio del confronto discende l assoluta convergenza della (1.22), che ha quindi raggio di convergenza uguale a uno e insieme di convergenza ( 1,1). Esercizio 1.6 Determinare il raggio di convergenza e l insieme di convergenza della serie Soluzione (2x 1) n 3 n + 1. (1.23) La serie assegnata non è della forma (1.8); per ricondurla a questa forma scriviamo (2(x 1/2)) n = 3 n n (x 1/2) n. 3 n + 1 Con la sostituzione z = x 1/2 ci riconduciamo a una serie centrata nell origine: 2 n z n 3 n + 1. Il raggio di convergenza di questa serie è R = 3/2, come si verifica con il criterio del rapporto; agli estremi dell intervallo la serie diverge (in entrambi i casi si ottiene una serie il cui termine generale non è infinitesimo), per cui l insieme di convergenza risulta {z : 3/2 < z < 3/2}. Tenendo conto della sostituzione z = x 1/2 la (1.23) ha come insieme di convergenza {x : 1 < x < 2}. Esercizio 1.7 Determinare lo sviluppo in serie di Taylor delle seguenti funzioni, centrato nei punti indicati, indicandone il raggio di convergenza: a) f(x) = exp(1 x 2 ) x 0 = 0 b) g(x) = 1 2x 3 x 0 = 0 c) h(x) = ln(1 + x) x 0 = 1
28 28 1 Serie di funzioni Soluzione a) Poiché f(x) = exp(1) exp( x 2 ), utilizzando lo sviluppo della funzione esponenziale exp(z) = z n e operando la sostituzione z = x 2, otteniamo ( x 2 ) n ( 1) n x 2n f(x) = exp(1) = exp(1). n! n! La serie esponenziale converge per ogni z reale e quindi la serie data converge per ogni x reale. b) Possiamo calcolare lo sviluppo di g(x), riconducendoci alla serie geometrica Scriviamo e sostituiamo z = 2x/3, ottenendo n! 1 1 z = z n, z < 1. (1.24) g(x) = 1 2x 3 = 1 3 ( ) = x 3 1 2x 3 3 g(x) = 1 ( ) 2x n = ( 2 n ) x n. 3 n Poiché la (1.24) converge per z < 1, tenendo conto della sostituzione effettuata, la serie che abbiamo ottenuto converge se 2x < 1, vale a dire per x < 3. È 3 2 immediato verificare che la serie non converge nei punti x = 3/2 e x = 3/2. c) Con la sostituzione t = x 1 ci riconduciamo allo sviluppo centrato in t 0 = 0 della funzione ln(2 + t), che scriviamo nella forma ( ( ln(2 + t) = ln t )) ( = ln 2 + ln 1 + t ). 2 2 Utilizzando lo sviluppo della funzione con la sostituzione z = t/2, otteniamo ( 1) n+1 z n ln(1 + z) =, z < 1 (1.25) n ( 1) n+1 t n ln(2 + t) = ln 2 +, n2 n
29 1.4 Esercizi svolti 29 che converge quando t/2 < 1, cioè quando t < 2, e infine ( 1) n+1 (x 1) n ln(1 + x) = ln 2 +. n2 n Questa serie converge se x 1 < 2, cioè nell intervallo ( 1,3). Nel punto x = 3 converge, in quanto si riduce alla serie armonica a segni alterni. Nel punto x = 1 si ottiene invece la serie che è divergente. Esercizio 1.8 ( 1) n+1 ( 1) n 2 n ( 1) 2n+1 ln 2 + = ln 2 + = ln 2 n2 n n Sviluppare in serie di McLaurin la funzione f(x) = 2x 8 x 2 8x n, precisando il raggio di convergenza. Utilizzare il risultato ottenuto per calcolare f (n) (0) per n generico. Soluzione Conviene decomporre la funzione f(x) in fratti semplici e sviluppare le due funzioni ottenute: 2x 8 f(x) = x 2 8x + 12 = 1 x x 2 = 1 6(1 x/6) + 1 2(1 x/2) Utilizzando la serie geometrica (1.24), con le sostituzioni z = x/6 e z = x/2, rispettivamente, otteniamo f(x) = 1 x n x n n 2 2 = x n n 6 x n n+1 2 = ( 1 n ) x n. n+1 2 n+1 Osserviamo che la prima serie ha raggio di convergenza R 1 = 6, mentre la seconda ha raggio R 2 = 2; quindi la serie somma ha raggio R = 2. Ricordando la formula dello sviluppo in serie di Taylor, si ha che e quindi f (n) (0) = 1 n! 6 1 n+1 2 n+1 f (n) (0) = n! n! 6n+1 2. n+1
30 30 1 Serie di funzioni Esercizio 1.9 Determinare l insieme di convergenza puntuale delle seguenti serie di funzioni: (1 x 2 ) n (2x 1) n a) ; b) n 3 n + 1 ; c) tan n x n ; d) Per ognuna di esser indicare (se possibile) un intervallo di convergenza totale. Soluzione a) Con la sostituzione z = 1 x 2 ci riconduciamo alla serie di potenze z n n, (x 2 + 1) n/2 3n che ha raggio di convergenza R z = 1 e converge in [ 1,1). La serie di funzioni converge allora per x tale che 1 1 x 2 < 1, vale a dire nell insieme [ 2,0) (0, 2]; osserviamo che questo insieme non è un intervallo. Un intervallo di convergenza totale è, ad esempio, un intervallo [a, b] con 0 < a < b < 2. b) Si tratta di un problema che abbiamo già trattato; vediamo qui un metodo alternativo di soluzione. Ponendo z = 2x 1 ci riconduciamo alla serie di potenze z n 3 n + 1, che converge per 3 < z < 3. La serie assegnata converge quindi per 3 < 2x 1 < 3, vale a dire per 1 < x < 2. Verifichiamo che si ha convergenza totale nell intervallo I = [0,1]. Tracciando il grafico della funzione y = 2x 1, si verifica che 2x 1 1 in I; possiamo quindi affermare che la serie (2x 1) n 3 n, maggiorata in I dalla serie convergente n, è totalmente convergente in I. + 1 c) Ponendo z = tan x, siamo ricondotti a studiare la serie di potenze z n n 2 + 1, che ha insieme di convergenza I = [ 1,1]. Quindi la serie di funzioni converge per 1 tan x 1, vale a dire per π/4 x π/4. Verifichiamo che la serie converge totalmente nell intervallo I = [ π/6,π/6]. In I si ha che tan x 1/ 3; quindi tan n x n (n 2 + 1)( 3) 1 n n
31 1.4 Esercizi svolti 31 d) Con la sostituzione z = x otteniamo la serie di potenze z n 3n 4 + 2, che converge in I = [ 1,1]. La serie di funzioni converge quindi per tutti gli x tali che 1 x Questa disuguaglianza è soddisfatta solamente per x = 0; l insieme di convergenza della serie di funzioni si riduce a un solo punto. Non esistono quindi intervalli di convergenza totale.
32 32 1 Serie di funzioni 1.5 Esercizi proposti 1. Determinare il raggio di convergenza e l insieme di convergenza delle seguenti serie di potenze: ( 1) n x n a) n 2 ; [R = 1, I = [ 1, 1]] (n + 5) 4 x n b) n! [R = ] c) n 2 (x 1) n [R = 1, I = (0, 2)] 3 n + 5 n d) 3 n + 7 n xn [R = 7/5, I = ( 7/5, 7/5)] n! e) 6 n + 2 xn [R = 0] n(x + 2) n f) 2 n [R = 2, I = ( 4, 0) ] + 1 g) ( 1) n x n 1 n n 2 [R = 1, I = ( 1, 1)] 5 n x 3n h) 2n(2n + 2) [R = 5 1/3, I = [ 5 1/3, 5 1/3 ]] i) ( 1) n 3n x 2n+1 n(n + 1) [R = 3 1/2, I = [ 3 1/2, 3 1/2 ]] l) ( 1) n 2n 1 + n2n x 1 + n 2 2 n [R = 1, I = [ 1, 1]]. 2. Data la serie di potenze con a parametro reale positivo, a n ln( n + 3 n + 2 )xn si determini a in modo che il suo raggio di convergenza valga 3; per il valore di a trovato si studi il comportamento della serie agli estremi dell intervallo di convergenza. [a = 1/3; per x = 3 la serie diverge, per x = 3 converge semplicemente] 3. Data la serie di potenze con b parametro reale positivo b n 1 sin( )x n n + 3
33 1.5 Esercizi proposti 33 si determini b in modo che il suo raggio di convergenza valga 2; per il valore di b trovato si studi il comportamento della serie agli estremi dell intervallo di convergenza. [b = 1/2; per x = 2 la serie diverge, per x = 2 converge semplicemente] 4. Il raggio di convergenza della serie a n x n è R = 5. Determinare il raggio di convergenza delle serie a) 3a n x 2n, b) a n x 4n+3. [a) R = 5, b) R = 4 5] 5. Sviluppare le seguenti funzioni in serie di McLaurin, indicando il raggio di convergenza degli sviluppi ottenuti. a) f(x) = sin(x 2 ( 1) n x 4n+2 ); [, R = ] (2n + 1)! b) f(x) = ln(1 + x 4 ); [ ( 1) n+1 x4n n, R = 1] c) f(x) = arctan(5x); [ ( 1) n 52n+1 x 2n+1 2n + 1, R = 1/5] d) f(x) = 2 3 5x ; [2 5 n x n n+1, R = 3/5] 3 e) f(x) = ln(2 + x 2 n+1 x2n ); [ln 2 + ( 1) n2 n, R = 2] f) x x 2 [ 1 (( 1) n 2 n )x n, R = 1] x 2 3 g) 3 2x (1 x) 2 [ (n + 3)x n, R = 1] h) log(x 2 ( 1) n 1 + 5x + 6) [ log 6 + ( 1 n 3 n n )xn, R = 2] 6. Sviluppare in serie di Taylor, con centro nei punti indicati seguenti funzioni, indicando l insieme I di convergenza degli sviluppi ottenuti. a) f(x) = 1 ; x x 0 = 2; n (x 2)n [ ( 1) 2 n+1, I = (0,4)] b) f(x) = 1 ; x x 0 = 3; (x + 3) n [ 3 n+1, I = ( 6,0)]
34 34 1 Serie di funzioni c) f(x) = x; x 0 = 1; [ I = (0,2)] d) f(x) = ln x 4 x x 0 = 1. [ ln 3 + ( ) 1/2 (x 1) n n, ( ( 1) n ) (x 1) n 2 3 n, I = (0,2]] n 7. Scrivere lo sviluppo in serie di potenze della funzione Erf(x) e calcolare Erf(1/2) e Erf(-1/2) con un errore minore di [Erf(x) = 2 ( 1) n π (2n + 1)n! x2n+1, Erf(1/2) 2 ( 12 1 π ), Erf(-1/2) = Erf(1/2), essendo la funzione Erf(x) dispari] 8. Scrivere lo sviluppo in serie di potenze della funzione S(x) e calcolare S(1/3) con un errore minore di [S(x) = ( 1) n π 2n+1 (2n + 1)!2 2n+1 (4n + 3) x4n+3, S(1/3) π/162] 9. Calcolare per serie con un errore minore di 10 3 i seguenti integrali. 1 sin x a) 0 x dx; [I = ( 1) n 1 (2n + 1)!(2n + 1) ] 1 b) cos(x 2 ( 1) n )dx; [I = 0 (2n)!(4n + 1) ] 1/2 ln(1 + x) c) dx. [I = ( 1) n x 2 n n ] 10. Determinare l insieme I di convergenza delle seguenti serie di funzioni, riconducendole, mediante un opportuna sostituzione a serie di potenze. a) ( 1) n e nx n 2 ; [e x = t, I = [0, + ) ] ln n x b) (n 2 + 1)2 n ; [ln x/2 = t, I = [e 2,e 2 ] ] c) (sin n x + cos n x). [Si studiano separatamente le due serie con sin x = t, cos x = t, I = IR \ {x = k π 2,k Z}]
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
SVILUPPI DI TAYLOR Esercizi risolti
 Esercizio 1 SVILUPPI DI TAYLOR Esercizi risolti Utilizzando gli sviluppi fondamentali, calcolare gli sviluppi di McLaurin con resto di Peano delle funzioni seguenti fino all ordine n indicato: 1. fx log1
Esercizio 1 SVILUPPI DI TAYLOR Esercizi risolti Utilizzando gli sviluppi fondamentali, calcolare gli sviluppi di McLaurin con resto di Peano delle funzioni seguenti fino all ordine n indicato: 1. fx log1
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
1. Scrivere il termine generale a n delle seguenti successioni e calcolare lim n a n:
 Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
Serie numeriche.6 Esercizi. Scrivere il termine generale a n delle seguenti successioni e calcolare a n: a),, 4, 4 5,... b), 9, 4 7, 5 8,... c) 0,,,, 4,.... Studiare il comportamento delle seguenti successioni
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Analisi Matematica. Serie numeriche, serie di potenze, serie di Taylor
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Serie numeriche, serie di potenze, serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Serie numeriche, serie di potenze, serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili
Serie Borlini Alex
 Serie numerica >> Prefazione Progressione lista ordinata e finita di elementi. Successione lista ordinata e infinita di elementi (numeri reali chiamati termini), {a n }=a 1, a 2, a 3 Successione di Fibonacci:
Serie numerica >> Prefazione Progressione lista ordinata e finita di elementi. Successione lista ordinata e infinita di elementi (numeri reali chiamati termini), {a n }=a 1, a 2, a 3 Successione di Fibonacci:
Analisi Matematica 1. Serie numeriche. (Parte 2) Dott. Ezio Di Costanzo.
 Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
Appunti di ANALISI MATEMATICA II Corso di Laurea Triennale in Matematica
 Appunti di ANALISI MATEMATICA II Corso di Laurea Triennale in Matematica Umberto Massari Anno accademico 3-4 SUCCESSIONI E SERIE DI FUNZIONI. Successioni di funzioni: convergenza puntuale ed uniforme Sia
Appunti di ANALISI MATEMATICA II Corso di Laurea Triennale in Matematica Umberto Massari Anno accademico 3-4 SUCCESSIONI E SERIE DI FUNZIONI. Successioni di funzioni: convergenza puntuale ed uniforme Sia
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
LIMITI - ESERCIZI SVOLTI
 LIMITI - ESERCIZI SVOLTI ) Verificare mediante la definizione di ite che a) 3 5) = b) = + ) c) 3n n + n+ = + d) 3+ = 3. ) Calcolare utilizzando i teoremi sull algebra dei iti a) 3 + ) b) + c) 0 + d) ±
LIMITI - ESERCIZI SVOLTI ) Verificare mediante la definizione di ite che a) 3 5) = b) = + ) c) 3n n + n+ = + d) 3+ = 3. ) Calcolare utilizzando i teoremi sull algebra dei iti a) 3 + ) b) + c) 0 + d) ±
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
1 Successioni di funzioni
 Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
Calcolo integrale. Regole di integrazione
 Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Calcolo integrale Linearità dell integrale Integrazione per parti Integrazione per sostituzione Integrazione di funzioni razionali 2 2006 Politecnico di Torino Proprietà Siano e funzioni integrabili su
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Dispense del corso di Analisi II
 Dispense del corso di Analisi II versione preliminare Paolo Tilli Dipartimento di Matematica Politecnico di Torino email: paolo.tilli@polito.it 2 dicembre 2004 Capitolo 2 Serie di potenze 2. Introduzione
Dispense del corso di Analisi II versione preliminare Paolo Tilli Dipartimento di Matematica Politecnico di Torino email: paolo.tilli@polito.it 2 dicembre 2004 Capitolo 2 Serie di potenze 2. Introduzione
Un paio di esempi su serie e successioni di funzioni
 Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Analisi Matematica per i corsi di Laurea in Ingegneria Energetica e Meccanica N-Z dell Università di Bologna. Anno Accademico 2003/2004.
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Analisi Matematica per i corsi di Laurea in Ingegneria Energetica e Meccanica N-Z dell Università di Bologna. Anno Accademico 2003/2004.
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Prove scritte di Analisi I - Informatica
 Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
F. Fagnani, A. Tabacco e P. Tilli. Versione 21 marzo. Introduzione all Analisi Complessa e Teoria delle distribuzioni.
 F. Fagnani, A. Tabacco e P. Tilli Introduzione all Analisi Complessa e Teoria delle distribuzioni 2 marzo 2006 3 Serie di Taylor e di Laurent. Residui 3. Successioni e serie di numeri complessi Una successione
F. Fagnani, A. Tabacco e P. Tilli Introduzione all Analisi Complessa e Teoria delle distribuzioni 2 marzo 2006 3 Serie di Taylor e di Laurent. Residui 3. Successioni e serie di numeri complessi Una successione
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti
 INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
Ingegneria civile - ambientale - edile
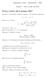 Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche
 C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
C.7 Serie Pag. 151 Dimostrazioni dei criteri per lo studio della convergenza di serie numeriche Teorema 5.29 (Criterio del confronto) Siano e due serie numeriche a termini positivi e si abbia 0, per ogni
ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI
 ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI Risolvere le seguenti disequazioni: ( 1 ) x < x + 1 1) 4x + 4 x ) x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) 0; ) x 1 x + 1 x
ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI Risolvere le seguenti disequazioni: ( 1 ) x < x + 1 1) 4x + 4 x ) x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) 0; ) x 1 x + 1 x
CORSO DI LAUREA IN FISICA
 CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
Esercizi riguardanti limiti di successioni e di funzioni
 Esercizi riguardanti iti di successioni e di funzioni Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno 0 Novembre 20. Come tali sono ben lungi dall essere esenti da errori,
Esercizi riguardanti iti di successioni e di funzioni Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno 0 Novembre 20. Come tali sono ben lungi dall essere esenti da errori,
Serie di funzioni: esercizi svolti
 Serie di funzioni: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. seguenti serie di funzioni: Studiare la convergenza normale, uniforme,
Serie di funzioni: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. seguenti serie di funzioni: Studiare la convergenza normale, uniforme,
PROGRAMMA. Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale.
 PROGRAMMA Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale. Gli insiemi numerici oggetto del corso: numeri naturali, interi relativi, razionali. Operazioni sui numeri
PROGRAMMA Capitolo 1 : Concetti di base: numeri reali, funzioni, funzioni reali di variabile reale. Gli insiemi numerici oggetto del corso: numeri naturali, interi relativi, razionali. Operazioni sui numeri
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 1 febbraio 2017 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
1 Primitive e integrali indefiniti
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 2 CALCOLO INTEGRALE Primitive e integrali indefiniti. Definizione di primitiva e di integrale indefinito Data una funzione
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 2 CALCOLO INTEGRALE Primitive e integrali indefiniti. Definizione di primitiva e di integrale indefinito Data una funzione
Università degli Studi della Calabria Facoltà di Ingegneria. 17 luglio 2012
 Università degli Studi della Calabria Facoltà di Ingegneria Correzione della Seconda Prova Scritta di nalisi Matematica 7 luglio cura dei Prof. B. Sciunzi e L. Montoro. Seconda Prova Scritta di nalisi
Università degli Studi della Calabria Facoltà di Ingegneria Correzione della Seconda Prova Scritta di nalisi Matematica 7 luglio cura dei Prof. B. Sciunzi e L. Montoro. Seconda Prova Scritta di nalisi
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA 1. Prova scritta del 14 gennaio 2017 Fila 1.
 Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del gennaio 207 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 6) Determinare
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del gennaio 207 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 6) Determinare
Soluzioni delle Esercitazioni VIII 21-25/11/2016. = lnx ln1 = lnx. f(t)dt.
 Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
CORSO DI LAUREA IN MATEMATICA
 CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1
 AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
Monomi L insieme dei monomi
 Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Massimo limite e minimo limite di una funzione
 Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
k=0 a k k=0 a k, quando si voglia precisare qual è l indice iniziale: si possono infatti considerare anche serie del tipo k=1 a k, k=50 a k,
 2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
b x 2 + c se x > 1 determinare a, b e c in modo che f sia continua in R, determinare a, b e c in modo che f sia anche derivabile in R
 9.. Esercizio. Data la funzione x tg( π x) se x < 4 f(x) = a se x = b x 2 + c se x > ANALISI Soluzione esercizi 9 dicembre 20 determinare a, b e c in modo che f sia continua in R, determinare a, b e c
9.. Esercizio. Data la funzione x tg( π x) se x < 4 f(x) = a se x = b x 2 + c se x > ANALISI Soluzione esercizi 9 dicembre 20 determinare a, b e c in modo che f sia continua in R, determinare a, b e c
Istituzioni di Matematiche, Integrali fratti. corso di laurea in Scienze geologiche. Mauro Costantini
 Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 005/06 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 9 settembre 005 Dimostrare
Università degli Studi di Udine Anno Accademico 005/06 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica Esercizi di Analisi Matematica Esercizi del 9 settembre 005 Dimostrare
STUDIO DI UNA FUNZIONE INTEGRALE. Z x. ln t ln t 2 2 dt. f(x) =
 STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
Esempi di soluzione di equazioni differenziali mediante serie di potenze
 Esempi di soluzione di equazioni differenziali mediante serie di potenze Cerchiamo una soluzione dell equazione differenziale nella forma 3y () + y () + y() 0 + y() σ n con σ,. Una serie di potenze generalizzata
Esempi di soluzione di equazioni differenziali mediante serie di potenze Cerchiamo una soluzione dell equazione differenziale nella forma 3y () + y () + y() 0 + y() σ n con σ,. Una serie di potenze generalizzata
Analisi matematica I. Sviluppi di Taylor e applicazioni. Sviluppi di Taylor. Operazioni sugli sviluppi di Taylor e applicazioni
 Analisi matematica I e applicazioni Operazioni sugli sviluppi di Taylor e applicazioni 2 2006 Politecnico di Torino 1 e applicazioni Formule di Taylor con resto di Peano: caso e n =0 n =1 Formule di Taylor
Analisi matematica I e applicazioni Operazioni sugli sviluppi di Taylor e applicazioni 2 2006 Politecnico di Torino 1 e applicazioni Formule di Taylor con resto di Peano: caso e n =0 n =1 Formule di Taylor
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI
 ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
2.9 Moltiplicazione di serie
 2.9 Moltiplicazione di serie A prima vista il problema di moltiplicare fra loro due serie sembra irrilevante. Fare il prodotto di due serie significa moltiplicare tra loro le successioni delle rispettive
2.9 Moltiplicazione di serie A prima vista il problema di moltiplicare fra loro due serie sembra irrilevante. Fare il prodotto di due serie significa moltiplicare tra loro le successioni delle rispettive
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93
 Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
1 - Estremo superiore ed estremo inferiore di insiemi
 - Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
- Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
Diario del corso di Analisi Matematica 1 (a.a. 2016/17)
 Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Diario del corso di Analisi Matematica 1 (a.a. 2016/17) 16 settembre 2016 (2 ore) Presentazione del corso. Numeri naturali, interi, razionali, reali. 2 non è razionale. Come si risolve 2 + 1 = 0? 19 settembre
Derivazione. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
ANALISI DI FOURIER. 2πk. è periodica di periodo T. Più precisamente, essendo. T x + 2π = cos. s(x) = s x + T ) T +α. f(x) dx
 ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti. April 5, 2006
 Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti April 5, 6 ESERCIZI. Studiare la convergenza della serie numerica al variare di γ IR.. Calcolare l integrale π n=
Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti April 5, 6 ESERCIZI. Studiare la convergenza della serie numerica al variare di γ IR.. Calcolare l integrale π n=
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti
 FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
FUNZIONI ELEMENTARI, DISEQUAZIONI, NUMERI REALI, PRINCIPIO DI INDUZIONE Esercizi risolti Discutendo graficamente la disequazione x > 3 + x, verificare che l insieme delle soluzioni è un intervallo e trovarne
Alcuni Teoremi sulle funzioni continue e uniforme continuità
 Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Alcuni Teoremi sulle funzioni continue e uniforme continuità Teorema 0. Una funzione f(x) è continua in x 0 se e solo se per ogni sucessione {x n } dom(f) con x n x 0 dom(f), risulta f(x n ) f(x 0 ). (Non
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Proposizioni. Negazione di una proposizione. Congiunzione e disgiunzione di due proposizioni. Predicati. Quantificatori.
 Corso di laurea in Ingegneria elettronica e informatica - A13 Programma di Analisi matematica 1 - A13106 Anno accademico 2015-2016 Prof. Giulio Starita 1 - Insiemi, logica, numeri I concetti primitivi.
Corso di laurea in Ingegneria elettronica e informatica - A13 Programma di Analisi matematica 1 - A13106 Anno accademico 2015-2016 Prof. Giulio Starita 1 - Insiemi, logica, numeri I concetti primitivi.
(1;1) y=2x-1. Fig. G4.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica) Simulazione compito d esame
 COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 16 febbraio 2016 - Soluzioni compito 1
 ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 6 febbraio 206 - Soluzioni compito E Calcolare, usando i metodi della variabile complessa, il seguente integrale
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 6 febbraio 206 - Soluzioni compito E Calcolare, usando i metodi della variabile complessa, il seguente integrale
INTEGRALI Test di autovalutazione
 INTEGRALI Test di autovalutazione. L integrale ln 6 è uguale a (a) vale 5 2 (b) (c) (d) 4 5 vale ln 256 2 è negativo 2 5 + 4 5 2 5 + 4 5 d d 2. È data la funzione = e 2. Allora: (a) se F() è una primitiva
INTEGRALI Test di autovalutazione. L integrale ln 6 è uguale a (a) vale 5 2 (b) (c) (d) 4 5 vale ln 256 2 è negativo 2 5 + 4 5 2 5 + 4 5 d d 2. È data la funzione = e 2. Allora: (a) se F() è una primitiva
Esercizi sulle equazioni differenziali a cura di Sisto Baldo, Elisabetta Ossanna e Sandro Innocenti
 Esercizi sulle equazioni differenziali a cura di Sisto Baldo, Elisabetta Ossanna e Sandro Innocenti 1. Verifica che y(t) = 1 t + e t è una soluzione dell equazione y (t) = y(t) + t.. Scrivi un equazione
Esercizi sulle equazioni differenziali a cura di Sisto Baldo, Elisabetta Ossanna e Sandro Innocenti 1. Verifica che y(t) = 1 t + e t è una soluzione dell equazione y (t) = y(t) + t.. Scrivi un equazione
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
DIFFERENZIAZIONE. Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim
 DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
Anno 5 Regole di derivazione
 Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Peccati, Salsa, Squellati, Matematica per l economia e l azienda, EGEA 2004
 1 Peccati, Salsa, Squellati, Matematica per l economia e l azienda, EGEA 004 Formula di Taylor Generalizziamo la formula che abbiamo introdotto nella sezione 11 del capitolo 5, cercando d approssimare
1 Peccati, Salsa, Squellati, Matematica per l economia e l azienda, EGEA 004 Formula di Taylor Generalizziamo la formula che abbiamo introdotto nella sezione 11 del capitolo 5, cercando d approssimare
Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica (1 modulo) - a.a.
 Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica ( modulo) - a.a. 00/04 APPUNTI INTEGRATIVI SUI CRITERI DI CONVERGENZA PER LE SERIE Serie
Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica ( modulo) - a.a. 00/04 APPUNTI INTEGRATIVI SUI CRITERI DI CONVERGENZA PER LE SERIE Serie
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Il Metodo di Newton, o delle Tangenti Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Il Metodo di Newton, o delle Tangenti 6 Novembre 2016 Indice 1 Metodo di Newton, o delle tangenti 2 1.1
Corso di Laurea in Ingegneria Edile-Architettura ANALISI MATEMATICA I. Prova scritta del 8 Gennaio 2014
 Corso di Laurea in Ingegneria Edile-Architettura ANALISI MATEMATICA I Prova scritta del 8 Gennaio 214 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile. (1) (Punti 8)
Corso di Laurea in Ingegneria Edile-Architettura ANALISI MATEMATICA I Prova scritta del 8 Gennaio 214 Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile. (1) (Punti 8)
Confronto locale di funzioni
 Confronto locale di funzioni Equivalenza di funzioni in un punto Sia A R ed f, g due funzioni definite in A a valori in R. Sia x 0 R un punto di accumulazione per A. Definizione. Si dice che f è equivalente
Confronto locale di funzioni Equivalenza di funzioni in un punto Sia A R ed f, g due funzioni definite in A a valori in R. Sia x 0 R un punto di accumulazione per A. Definizione. Si dice che f è equivalente
Integrali inde niti. F 2 (x) = x5 3x 2
 Integrali inde niti Abbiamo sinora studiato come ottenere la funzione derivata di una data funzione. Vogliamo ora chiederci, data una funzione f, come ottenerne una funzione, che derivata dia f. Esempio
Integrali inde niti Abbiamo sinora studiato come ottenere la funzione derivata di una data funzione. Vogliamo ora chiederci, data una funzione f, come ottenerne una funzione, che derivata dia f. Esempio
ORDINAMENTO SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
