24 IL RAPPORTO INCREMENTALE - DERIVATE
|
|
|
- Prospero Ventura
- 7 anni fa
- Visualizzazioni
Transcript
1 24 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y 2 domf con x 6= y, sidefinisceilrapporto incrementale di f tra x e y come P f (x, y) = f(x) x f(y). y OSSERVAZIONI: il rapporto incrementale ci permette di descrivere quantitativamente il comportamento di una funzione. Per esempio: i) f è non decrescente () P f è non negativa; ii) f è strettamente crescente () P f è strettamente positiva; iii) se f(x) =mx + q è a ne allora P f è il coe ciente angolare m. Più in generale, P f (x, y) rappresenta la tangente dell angolo che la retta (la secante al grafico) passante per i punti (x, f(x)) e (y, f(y)) forma con l asse coordinato orizzontale. Invece di studiare le proprietà di tutte le secanti è più comodo studiare le proprietà delle rette tangenti. Analiticamente, questo si traduce in un operazione di ite che porta alla seguente definizione. Definizione Sia I intervallo, f : I! R e x 0 un punto di I. Seesisteilite f(x) f(x 0 ) P f (x, x 0 )= 2 R, x!x 0 x!x 0 x x 0 esso viene chiamato la derivata di f nel punto x 0 e si indica con f 0 (x 0 ). Se f 0 (x 0 ) 2 R allora f si dice derivabile in x 0. ALTRE NOTAZIONI per f 0 d (x 0 ): Df(x 0 ), dx f(x dy 0), dx,y0 ESEMPI ) f = c costante Dc = 0 in ogni punto. Infatti P f (x, y) = 0 per ogni coppia di punti. 2) f(x) =x. Allora P f (x, y) = per ogni coppia di punti, per cui f 0 (x) =per ogni x. 3) f(x) =x n (n 2 N, n 2). Allora P f (x, y) =x n + x n 2 y xy n 2 x + y n,percuif 0 (x) =nx n. 4) f(x) = x. Allora (x 6= 0) f 0 (/x) (/x 0 ) (x 0 )= x!x 0 x x 0 (x 0 x)/(x 0 x) = = x!x 0 x x 0 x!x 0 x 0 x = x ) calcoliamo la derivata di e x.siha e x e x0 e (x x0) = e x0 = e x0. x!x 0 x x 0 x!x 0 x x 0 Dunque De x = e x. 75
2 sin t 6) dal ite fondamentale =sideduce t!0 t sin x = x + o(x) cos x = 2 x2 + o(x 2 ), da cui si ottiene subito la derivata di sin e cos. Per esempio si ha sin(x + t) sin x sin x cos t +sintcos x sin x D sin x = = t!0 t t!0 t sin t cos t t = cos x +sinx = cos x +sinx t!0 t t!0 t t!0 2 + o(t) = cos x. Analogamente D(cos x) = sinx. 7) Se f(x) =sgn x (il segno di x), allora f 0 (x) =0sex 6= 0, mentre per x =0 abbiamo f(x) f(0) = =+ = + x 0 + x equindif 0 (0) = +. x = f(x) f(0), x 0 Di erenziabilità Dalla derivabilità si ottengono alcune informazioni sul comportamento della funzione f vicino al punto x 0.Primadituttof è continua in x 0. Teorema. f derivabile in x 0 =) f continua in x 0. Dimostrazione Se f(x) =f(x 0 )+ (x x 0 )+o(x x 0 )perx! x 0, allora f(x) = f(x 0 )+ (x x 0 )=f(x 0 ). x!x 0 x!x 0 Ma il grafico di una funzione derivabile in x 0 ha una proprietà più forte: può essere approssimato con una retta (la sua retta tangente). Per specificare meglio come è definita questa retta introduciamo il concetto seguente. Definizione Sia I intervallo, f : I! R e x 0 2 I. Diciamo che f è differenziabile in x 0 quando esiste 2 R tale che si abbia f(x) =f(x 0 )+ (x x 0 )+o(x x 0 ) per x! x 0. SIGNIFICATO GEOMETRICO: la retta y = f(x 0 )+ (x x 0 ) approssima la curva y = f(x) ad un ordine superiore a x x 0 (questarettaètangente alla curva). Teorema. f di erenziabile in x 0 () f derivabile in x 0. In tal caso la retta tangente è data da y = f(x 0 )+f 0 (x 0 )(x x 0 ). = f 0 (x 0 ) e Dimostrazione f(x) =f(x 0 )+ (x x 0 )+o(x x 0 )perx! x 0 () f(x) f(x 0 ) (x x 0 ) f(x) f(x 0 ) =0() =. x!x 0 x x 0 x!x 0 x x 0 76
3 25 CALCOLO DI DERIVATE Dal teorema di linearità per i iti si ha subito: Teorema. (LINEARITÀ) Sia I intervallo e x 0 punto interno a I. Sef,g : I! R sono derivabili in x 0 e c 2 R, allora sono derivabili in x 0 anche f + g e cf esiha (f + g) 0 (x 0 )=f 0 (x 0 )+g 0 (x 0 ), (cf) 0 (x 0 )=c(f 0 (x 0 )). Teorema. (DERIVATA DI COMPOSIZIONE) Siano I e J intervalli; f : I! R, g : J! R x 0 un punto interno a I tale che f(x 0 ) è i n t e r n o a J. Sef è derivabile in x 0 e g è derivabile in f(x 0 ), allora g f è derivabile in x 0,esiha (g f) 0 (x 0 )=g 0 (f(x 0 )) f 0 (x 0 ). Dimostrazione Sia y 0 = f(x 0 ). Dalla di erenziabilità di g in y 0 si ha g(y) = g(y 0 )+g 0 (y 0 )(y y 0 )+o(y y 0 ), per y! y 0. In particolare per y = f(x) ex! x 0 si ha g(f(x)) = g(y 0 )+g 0 (y 0 )(f(x) y 0 )+o(f(x) y 0 ), ovvero (g f)(x) =(g f)(x 0 )+g 0 (y 0 )(f(x) y 0 )+o(f(x) y 0 ). Dalla di erenziabilità di f abbiamo f(x) y 0 = f(x) f(x 0 )=f 0 (x 0 )(x x 0 )+o(x x 0 )edunque (g f)(x) =(g f)(x 0 ) +g 0 (y 0 )(f 0 (x 0 )(x x 0 )+o(x x 0 )) + o(f 0 (x 0 )(x x 0 )) =(g f)(x 0 )+g 0 (y 0 )f 0 (x 0 )(x x 0 )+o(x x 0 ). Questo mostra che (g f) è di erenziabile in x 0 e la sua derivata è g 0 (y 0 )f 0 (x 0 ). ESEMPI: ) n 2 N D(x n )= nx n. La funzione x 7! x n si può considerare come composizione delle funzioni f(x) =x n e g(y) =/y; e sappiamo che f 0 (x) =nx n, g 0 (y) = /y 2.Dunque D(x n )=g 0 (f(x)) f 0 (x) = (x n ) 2 (nxn )= nx n ; 2) D = f f 2 f 0 (considerare come composizione di f e/y). f Teorema. (DERIVATA DEL PRODOTTO) Siano f,g : I! R derivabili in x 0 2 I; allora anche fg è derivabile in x 0,esiha (fg) 0 (x 0 )=f(x 0 )g 0 (x 0 )+f 0 (x 0 )g(x 0 ). Dimostrazione (fg)(x) (fg)(x 0 )=f(x)(g(x) g(x 0 )) + g(x 0 )(f(x) f(x 0 )), per cui P fg (x, x 0 )=f(x)p g (x, x 0 )+g(x 0 )P f (x, x 0 ). Passando al ite per x! x 0 (ricordando che f(x)! f(x 0 )) si ha la tesi. 77
4 f 0(x0 Esercizio. Provare la formula )= f 0 (x 0 )g(x 0 ) f(x 0 )g 0 (x 0 ) g (g(x 0 )) 2. (Applicare la derivazione del prodotto di f e/g ricordando che D(g )= g 2 g 0 ). Derivate delle funzioni elementari È utile imparare a memoria le derivate delle funzioni più usate. In particolare: D(e x )=e x, D=0, D(x )= x, D cos x = sin x Dsin x = cos x e quindi anche D tan x = + tan 2 x D cosh x =sinhx Dsinh x = cosh x, dove cosh x = ex + e x, sinh x = ex e x sono coseno e seno iperbolico. 2 2 Teorema. (DERIVAZIONE DELLA FUNZIONE INVERSA) Sia I intervallo e f : I! R continua e invertibile in I. Seesistef 0 (x 0 ), allora esiste anche la derivata di f nel punto y 0 = f(x 0 ),esiha D f (y 0 )= f 0 (x 0 ) ovvero f 0 (y 0 )= f 0 (f (y 0 )). NOTA: ) l ipotesi di invertibilità su f equivale alla stretta monotonia; 2) la formula per la derivata dell inversa vale anche se f 0 (x 0 )=0of 0 (y 0 )= ±, applicando le dovute convenzioni; 3) se f 0 (x 0 ) 6= 0, allora f è derivabile in f(x 0 ). Dimostrazione Si ha f (y) f (y 0 ) f (y) f (y 0 ) = y!y 0 y y 0 y!y 0 f(f (y)) f(f (y 0 )) = x x 0 x!x 0 f(x) f(x 0 ) = f 0 (x 0 ), per il teorema sul ite di composizione. Esempio. Ora possiamo calcolare la derivata di log x, usando il teorema della derivata della funzione inversa, con f(x) =e x,f (x) = log x. Si ha allora D(log x) =D(f )(x) = f 0 (f (x)) = exp(log x) = x. 78
5 Derivate delle funzioni inverse elementari D(log x) = x, Darctan x = +x 2 D(arcsin x) = p x 2 D(arccos x) = p x 2 (si intende che x appartiene al dominio della singola funzione). ESERCIZIO: ottenere le formule di derivazione delle funzioni trigonometriche inverse usando il teorema della derivazione dell inversa. Esercizi. Usando le derivate delle funzioni elementari e le regole di calcolo calcoliamo: ) D(sin 2x) = (cos 2x) 2; 2) D(log cos x) = sin x ( sin x) = = tan x; cos x cos x 3) la derivata di (log x) px (x>). Possiamo scrivere (log x) px =exp x /2 log(log x).siha D x /2 log(log x) = log(log x)dx /2 + x /2 D log(log x). Dato che Dx /2 = 2 x /2 = 2 p e D log(log x) = x log x x,sihadunque D x /2 log(log x) = log(log x) 2 p x + log x log(log x)+2 x/2 = x log x 2 p, x log x einfine D(log x) px log x log(log x)+2 =exp x /2 log(log x) 2 p = (log x) (p x ) log x log(log x)+2 x log x 2 p. x Esercizio: verificare la formula generale per la derivata di f g : D f g = f g f 0 g f + g0 log f. (scrivere f g =exp(g log f)...) Esercizi. ) D(log f) = f 0 f ; 2) D(e f )=e f f 0 ; 3) D(x )=D(e ( log x) )=x D( log x) = x ( 6= ). 79
6 26 PUNTI DI NON DERIVABILITÀ Definizione La funzione derivata Sia f : I! R una funzione tale che I 0 = {x 2 I : f è derivabile in x} 6= ;, allora si chiama derivata di f la funzione f 0 : I 0! R, x 7! f 0 (x) che associa ad ogni punto x 2 I 0 la derivata di f in x. ESEMPI: ) f(x) =x, dom f = dom f 0 = R; f 0 = ; 2) f(x) = x, dom f = dom f 0 = R \{0}; f 0 (x) = x 2 ; ( 3) f(x) = x 2 sin se x 6= 0 x 0 se x = 0. Allora dom f = dom f 0 = R e 8 < f 0 2x sin cos se x 6= 0 (x) = x x : 0 se x = 0. Notare che f 0 non è continua in 0. Definizione Derivate destre e sinistre Sia I intervallo, f : I! R e x 0 un punto di I. Seesisteilite f(x) f(x 0 ) P f (x, x 0 )= 2 R, x!x 0 x!x 0 x x 0 esso viene chiamato la derivata sinistra di f nel punto x 0 e si indica con f 0 (x 0 ). Se esiste il ite P f(x) f(x 0 ) f (x, x 0 )= 2 R, x!x 0+ x!x 0+ x x 0 esso viene chiamato la derivata destra di f nel punto x 0 e si indica con f 0 +(x 0 ). ) f(x) = x. Siax 0 > 0; allora P f (x, x 0 )= x x 0 = x x 0 = per tutti gli x>0, per cui f 0 (x 0 ) =. Se x x 0 x x 0 invece x 0 < 0, P f (x, x 0 )= x x 0 = x ( x 0) = per tutti gli x<0, per cui f 0 (x 0 )= x x 0 x x 0. 80
7 se x>0, Se x 0 =0sihaP f (x, 0) = se x<0, per cui f 0 (x 0 )= ef 0 +(x 0 ) = ; in particolare non esiste f 0 (x 0 ). Riassumendo D x = x x = x x. Dunque per f(x) = x, dom f 0 = R \{0} 6= dom f = R; f 0 = x x ; 2) f(x) =sgn(x) p x = p x 0 f+(0) 0 = + f 0 (0) = p p x se x 0. Allora x se x<0 x 0 = + p x 0 x 0 = p x =+, p x =+. Quindi f 0 (0) = +, ef non è derivabile in 0. Dunque per f(x) =sgn(x) p x dom f 0 6= dom f = R in quanto 0 62 dom f 0. n se x 0 3) f(x) = 0 se x<0. Allora f+(0) 0 = + x 0 = 0; f 0 (0) = 0 x 0 =+. Tipi di punti di non derivabilità Se la funzione f non è derivabile in un punto x 0 si possono presentare vari casi. Se f è continua in x 0 ed esistono le derivate destra e sinistra di f in x 0, allora si usa la seguente nomenclatura: ) 9 f 0 (x 0 ),f 0 +(x 0 ) 2 R e almeno uno dei due è finito. Allora x 0 si dice un punto angoloso. Esempi: (x 0 = 0) f(x) = x, f(x) = p x + x ; 2) 9 f 0 (x 0 )=±; allora x 0 si dice un punto di flesso a tangente verticale (o semplicemente punto a tangente verticale). Esempi: (x 0 = 0) f(x) = 3p x (l inversa di x 3 ), f(x) =sgn(x) p x ; 3) f 0 (x 0 ),f 0 +(x 0 ) 2{+, } f 0 (x 0 ) 6= f 0 +(x 0 ); allora x 0 si dice un punto di cuspide. Esempi: (x 0 = 0) f(x) = p x 8
8 NOTA: possono anche non esistere f 0 (x 0 )ef+(x 0 0 ); per esempio si prenda x sin(/x) se x 6= 0 f(x) = 0 se x = 0, e x 0 = 0. Esercizi. Descrivere i punti di non derivabilità delle seguenti funzioni.. f(x) = log x. Dato che log x è derivabile ovunque (nel suo dominio), e y non è derivabile in y = 0, la composizione PUÒ non essere derivabile solo per log x = 0, ovvero per x =, cioè x = ±. Si ha quindi questi due sono punti angolosi. 2. f(x) = p x 3 + x 2. f 0 (±) =, f 0 +(±) =, Dato che x 3 + x 2 è derivabile ovunque (nel suo dominio), e p y non è derivabile in y = 0, la composizione può non essere derivabile solo per x 3 + x 2 = 0, ovvero per x =0ex =. Si ha f 0 ±( ) = x! ± p x2 x + x + equindi èunpuntodicuspide. Si ha p f±(0) 0 x2 x + = ± x 0 y p y = = ±, y!0± y x p x + = = ±, ± x quindi 0 è punto angoloso. Notare che p y ha un punto di cuspide, quindi: non si può dedurre il tipo di non-derivabilità di una composizione sapendo solo i tipi di non-derivabilità delle funzioni separatamente. 3. f(x) = p sin x. Si ha f 0 ±(0) = ± p sin x = ±, x e analogamente ogni punto della forma k, quindi tutti questi sono punti di cuspide. 4. f(x) = p cos x. 82
9 Si ha p f±(0) 0 = ± cos x x = ± p 2, e analogamente ogni punto della forma 2k, quindi tutti questi sono punti angolosi. 5. f(x) = sin x x + x 2 nel intervallo [ 2, 2]. La funzione sin x ha un punto angoloso in 0 e la funzione x + x 2 ha due punti angolosi in 0 e, quindi i possibili punti di non derivabilità sono 0 e. Si ha quindi x = Si ha f±( 0 sin x x + x 2 ) = x! ± x + è punto angoloso. =sin x! ± x + x + f±(0) 0 sin x x + x 2 sin x x = = = ± x ± x ± = ± sin, sin x x =0, x equindif è derivabile in 0. Dunque x = 0 non è un punto di non derivabilità anche se lo era per entrambe le funzioni sin x e x + x 2. 8 x 2 sin x >< se x<0 6. f(x) = 0 se x =0 e >: x 2 sin + x se x>0. x L unico punto di non derivabilità possibile è x 0 = 0, dove per cui si ha un punto angoloso. f+(0) 0 = x sin += + x f 0 (0) = x sin =0, x 83
10 27 ALCUNI ESERCIZI SULLE DERIVATE Risolvere i seguenti esercizi:. Calcolare derivata destra e sinistra in x =0di f(x) =4 p sin x 2 +7 p cos x 2 ; 2. Calcolare derivata destra e sinistra in x = di f(x) = 3sin x 4 cos + x. (notare che per x! + siha f(x) = 4 cos( + x) 3sin(x ), mentre per x! si ha f(x) = 4 cos( + x) 3sin( x)); 3. Calcolare la retta tangente in x = al grafico di f(x) = + arctan(x2 x) ; 2x 4. Calcolare la retta tangente in x = 6 al grafico di f(x) =e x cos( x) log(x 5). (notare che D(f g h) =Df g h + f Dg h + f g Dh); 5. Calcolare la retta tangente al grafico di f(x) = ( + log x) 3x in x = 6. Calcolare la retta tangente al grafico di f(x) =(3x) log x in x = 7. Calcolare la retta tangente al grafico di f(x) = (cos x+sinx) cos x in x =2 8. Calcolare la derivata sinistra in x = 0 della funzione f(x) = p ( x + x) log( x + p cos x 2 ) 84
11 9. Trovare i punti di non-derivabilità di f(x) = p x (notare che 8 p >< p x per x< f(x) = p x + per <x<0 >: p x + per0<x< x per x> e che nei rispettivi intervalli queste funzion i sono derivabili. Dedurre che e sono punti di cuspide, 0 è punto angoloso). 0. Trovare i punti di non-derivabilità di f(x) = x 2 x p x 2 2x 85
12 28 IL TEOREMA DI De L Hôpital Una seconda applicazione delle derivate (oltre che dare informazioni sul grafico di una funzione) è il calcolo dei iti in caso di forme indeterminate. Come considerazione preinare notiamo che nel caso di iti 0/0 inx 0 echesiaf 0 (x 0 )che g 0 (x 0 ) siano finiti si ha f(x) g(x) = f 0 (x 0 )(x x 0 )+o(x x 0 ) g 0 (x 0 )(x x 0 )+o(x x 0 ) per cui il ite è banalmente f 0 (x 0 ) g 0 (x 0 ). Il seguente teorema generalizza questa osservazione. Teorema. Siano f,g : I! R funzioni definite e derivabili in un intorno destro I di x 0 2 [, +[. Supponiamo che sia verificata una delle due condizioni: i) (forma 0/0) f(x) = x!x 0+ ii) (forma /) x!x 0+ Se esiste il ite f 0 (x) x!x 0+ g 0 (x) = L, allora esiste anche il ite x!x 0+ f(x) g(x) = L. g(x) =0; x!x 0+ f(x) 2{+, }, x!x 0+ Le stesse conclusioni sono valide per il ite x! x 0 intorno sinistro di x 0 2 (, +]). g(x) 2{+, }. Non dimostreremo questo teorema, la cui dimostrazione non è di neanche particolarmente istruttiva. (se f,g sono definite in un cile, ma non è In seguito useremo la notazione (H) per intendere proviamo ad applicare il teorema dell Hôpital calcolandoci il ite del rapporto delle derivate. Se tale rapporto ha un ite, allora il conto è concluso. Se invece abbiamo di nuovo una forma indeterminata, possiamo di nuovo provare ad applicare il teorema, ecc. ESEMPI: tramite questo teorema possiamo ritrovare la maggior parte dei iti notevoli: sin x 0 x = cos x =(H) = = ; 0 e x 0 e = =(H) = x 0 x = ; log +x 0 = =(H) = x 0 x + = ; 86
13 x!+ >0 =(H) = e x + x = + log x + x!+ x = + log x x log x = /x = + e x =+; =(H) = x!+ /x =(H) = /x x = x!+ x = 0; /x 2 = ( x) = 0. Il Teorema di De L Hôpital può semplificare il calcolo di iti complicati: log(sin x 2 + cos x) x 2 = 0 =(H) 0 2x cos x 2 sin x = sin x 2 + cos x 2x cos x 2 sin x = 2x = cos x 2 sin x 2x = 2 = 2. Attenzione però a non eccedere nell uso: il ite sin 5 x x 5 è banalmente uguale a (applicando il ite fondamentale e la continuità di y 5 ); si può anche risolvere usando solo il teorema di De L Hôpital, ma si deve derivare 5 volte: sin 5 x x 5 =(H) 5sin 4 x cos x 5x 4 =(H) 4sin 3 x cos 2 x sin 5 x = 4x 3 =(H) = 2 sin 2 x cos 3 x 8sin 4 x cos x 5sin 4 x cos x 2x 2 =... Attenzione anche al fatto che se non esiste il ite del rapporto delle derivate allora non è detto che non esista il ite del rapporto delle funzioni: evidentemente, prendendo f(x) =x +sinx e g(x) =x, siha f(x) x!+ g(x) = +sin x x!+ x =, 87 2x
14 ma invece non esiste. f 0 (x) x!+ g 0 (x) = +cosx x!+ Esercizi.. Calcolare log(x 2 x + ) x! + log(3x 2 3x + ) in due modi: usando il teorema dell Hôpital e i iti fondamentali 2. Calcolare x!4 + p x +4 p 3x 4 p 3x +4 p 2x +8 in due modi: usando il teorema dell Hôpital e razionalizzando 3. Calcolare (dopo avere riscritto la funzione in base e) log x x!+ x 3 x 4 in due modi: usando il teorema dell Hôpital e mediante confronto di infiniti 4. Calcolare (dopo avere riscritto la funzione in base e) 2 log(x 2 log(x 3) 3x + ) x! Verificare che non si può applicare il teorema dell Hôpital al calcolo di x!+ log(x +3sinx) log(2x + 4 cos x). 6. Calcolare, se possibile, usando il teorema dell Hôpital il ite e + x 2 x 88
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
21 IL RAPPORTO INCREMENTALE - DERIVATE
 21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Derivate. Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come
 Lezioni 21-22 72 Derivate Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y) = f(x) f(y). x y OSSERVAZIONI:
Lezioni 21-22 72 Derivate Def. Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y) = f(x) f(y). x y OSSERVAZIONI:
Derivate. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33
 Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Calcolo differenziale I
 Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
41 POLINOMI DI TAYLOR
 4 POLINOMI DI TAYLOR DERIVATE DI ORDINI SUCCESSIVI Allo stesso modo della derivata seconda si definiscono per induzione le derivate di ordine k: la funzione derivata 0-ima di f si definisce ponendo f (0
4 POLINOMI DI TAYLOR DERIVATE DI ORDINI SUCCESSIVI Allo stesso modo della derivata seconda si definiscono per induzione le derivate di ordine k: la funzione derivata 0-ima di f si definisce ponendo f (0
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
29 IL TEOREMA DEL VALOR MEDIO
 29 IL TEOREMA DEL VALOR MEDIO Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto incrementale (positività,
29 IL TEOREMA DEL VALOR MEDIO Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto incrementale (positività,
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
La derivata. variabile indipendente x. Definiamo f := f(x) f(x 0 ) l incremento (positivo o negativo) della variabile dipendente.
 La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
ANALISI MATEMATICA 1 Commissione F. Albertini, P. Mannucci e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 Vicenza, 27 gennaio 214 TEMA Esercizio 1 (9 punti Si consideri la funzione f(x =xe x 2 x+2 (a Determinare il dominio, eventuali simmetrie ed il segno di f; (b determinare i iti agli estremi del dominio,
Vicenza, 27 gennaio 214 TEMA Esercizio 1 (9 punti Si consideri la funzione f(x =xe x 2 x+2 (a Determinare il dominio, eventuali simmetrie ed il segno di f; (b determinare i iti agli estremi del dominio,
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
y x y x A (x 1,y 1 ) = (c, f(c)) B(x 2,y 2 ) = (c+h, f(c+h)) m =
 DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare [cos x] x kπ/ al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
La formula di Taylor con resto di Peano. OSSERVAZIONE: se f è continua nel punto a possiamo scrivere (ricordando la definizione di o piccolo ) che
 109 Lezioni 9-40 La formula di Taylor con resto di Peano OSSERVAZIONE: se f è continua nel punto a possiamo scrivere (ricordando la definizione di o piccolo ) che f(x) =f(a)+o(1) per x a; se f è derivabile
109 Lezioni 9-40 La formula di Taylor con resto di Peano OSSERVAZIONE: se f è continua nel punto a possiamo scrivere (ricordando la definizione di o piccolo ) che f(x) =f(a)+o(1) per x a; se f è derivabile
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
DERIVATE. Rispondere ai seguenti quesiti. Una sola risposta è corretta. 1. Data la funzione f(x) =2+ x 7, quale delle seguente affermazioni èvera?
 DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Limiti di derivate. Punti angolosi e di cuspide. Ottobre 2012 Indice 1 Limiti della derivata e punti di non
Lezione 18 (8 gennaio) Limiti
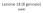 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Argomento 6: Derivate Esercizi. I Parte - Derivate
 6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
d f dx (x 0), (D f )(x 0 ), cui corrispondono vari modi di indicare la funzione derivata:
 Derivate Di solito, considereremo funzioni f : A R, dove A e un intervallo, o un unione di intervalli non ridotti a un punto. Indicato con B l insieme dei punti nei quali f e derivabile 1 si a una funzione
Derivate Di solito, considereremo funzioni f : A R, dove A e un intervallo, o un unione di intervalli non ridotti a un punto. Indicato con B l insieme dei punti nei quali f e derivabile 1 si a una funzione
(1;1) y=2x-1. Fig. G4.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
f (x) = f(x 2) f(x 1 ) x 2 x 1
 Lezioni 29-30 86 Il Teorema di Lagrange o del Valor Medio Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto
Lezioni 29-30 86 Il Teorema di Lagrange o del Valor Medio Abbiamo visto che molte proprietà importanti delle funzioni (crescenza, decrescenza, iniettività, ecc.) si esprimono tramite proprietà del rapporto
Lezione 11 (30 novembre)
 Lezione 11 (30 novembre) Teorema di De l Hopital Massimi e minimi assoluti e relativi Funzioni limitate superiormente e inferiormente Legame tra derivata prima e crescita e decrescita della funzione Derivata
Lezione 11 (30 novembre) Teorema di De l Hopital Massimi e minimi assoluti e relativi Funzioni limitate superiormente e inferiormente Legame tra derivata prima e crescita e decrescita della funzione Derivata
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Dispense di Matematica Analisi Matematica. Riccarda Rossi
 Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Dispense di Matematica Analisi Matematica Riccarda Rossi Corso di Laurea in Disegno Industriale Università degli Studi di Brescia Anno Accademico 2009/200 2 Capitolo Nozioni preinari 4 Riccarda Rossi Analisi
Equazione della retta tangente al grafico di una funzione
 Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Lezione 5 (9/10/2014)
 Lezione 5 (9/10/2014) Esercizi svolti a lezione Nota 1. La derivata di una funzione. Consideriamo una funzione f(x) : R R e definiamo il rapporto incrementale nel punto x 0 come r(h) = f(x 0 +h) f(x 0
Lezione 5 (9/10/2014) Esercizi svolti a lezione Nota 1. La derivata di una funzione. Consideriamo una funzione f(x) : R R e definiamo il rapporto incrementale nel punto x 0 come r(h) = f(x 0 +h) f(x 0
Derivazione. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
DERIVATE. Equazione della retta tangente al grafico di f nel suo punto P(x 0 ;y 0 ):
 DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 1
 Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. Es. Es. 3 Es. 4 Es. 5 AVVERTENZA: Scrivere le risposte scelte nello spazio in alto a destra. In ogni esercizio una sola risposta è corretta. Esercizio.
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. Es. Es. 3 Es. 4 Es. 5 AVVERTENZA: Scrivere le risposte scelte nello spazio in alto a destra. In ogni esercizio una sola risposta è corretta. Esercizio.
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Derivate di funzioni 1 / 40
 Derivate di funzioni 1 / 40 Variazione assoluta Sia data una funzione f (x) e due suoi valori in corrispondenza dei punti x 0 e x 0 + h, con h > 0. Supponiamo di voler determinare di quanto varia il valore
Derivate di funzioni 1 / 40 Variazione assoluta Sia data una funzione f (x) e due suoi valori in corrispondenza dei punti x 0 e x 0 + h, con h > 0. Supponiamo di voler determinare di quanto varia il valore
Matematica. Tutorato Attivo: Derivate. Alessio Bianchi. Matematica 20 maggio 2017
 Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Soluzioni del Foglio 6
 ANALISI Soluzioni del Foglio 6 1 novembre 2009 6.1. Esercizio. Calcolare le derivate delle seguenti funzioni: x + 1 x 2 + 1, ex (sin(x) + cos(x)), e x arcsin(x) 1 x 2, x arctan(x), ln(1 + e x2 ) x + 1
ANALISI Soluzioni del Foglio 6 1 novembre 2009 6.1. Esercizio. Calcolare le derivate delle seguenti funzioni: x + 1 x 2 + 1, ex (sin(x) + cos(x)), e x arcsin(x) 1 x 2, x arctan(x), ln(1 + e x2 ) x + 1
SOLUZIONI 3. f (x) = (x 2 1) 2/3 e x. (x 2 1) 2/3 e x 0 x R. x 4/3 e x = e 4/3 log x e x
 Domanda Si consideri la funzione SOLUZIONI f x = x 2 2/ e x. Determinare il campo di esistenza, il segno, i iti alla frontiera e gli eventuali asintoti. Classificare gli eventuali punti di discontinuità
Domanda Si consideri la funzione SOLUZIONI f x = x 2 2/ e x. Determinare il campo di esistenza, il segno, i iti alla frontiera e gli eventuali asintoti. Classificare gli eventuali punti di discontinuità
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Calcolo differenziale
 Calcolo differenziale L operazione di derivata Sia f: AR. Si vuole conoscere l equazione della retta tangente al grafico della funzione in un punto. Retta secante y f(+h) Q Rapporto incrementale y=f()
Calcolo differenziale L operazione di derivata Sia f: AR. Si vuole conoscere l equazione della retta tangente al grafico della funzione in un punto. Retta secante y f(+h) Q Rapporto incrementale y=f()
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
Matematica I, Derivate e operazioni algebriche.
 Matematica I, 6.0.202 Derivate e operazioni algebriche.. Prima di iniziare questa lezione, conviene rendere espliciti due fatti che sono impliciti nella definizione informale di derivata, banalmente verificabili
Matematica I, 6.0.202 Derivate e operazioni algebriche.. Prima di iniziare questa lezione, conviene rendere espliciti due fatti che sono impliciti nella definizione informale di derivata, banalmente verificabili
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Corso di Laurea in Scienze Biologiche Prova scritta di Matematica del 26/01/2007
 Corso di Laurea in Scienze Biologiche Prova scritta di Matematica del 6/0/007 COGNOME NOME MATRICOLA 3 sin( ) e 3 + ) Determinare ( cos()) Possibile svolgimento Il ite proposto si presenta nella forma
Corso di Laurea in Scienze Biologiche Prova scritta di Matematica del 6/0/007 COGNOME NOME MATRICOLA 3 sin( ) e 3 + ) Determinare ( cos()) Possibile svolgimento Il ite proposto si presenta nella forma
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
23 INVERTIBILITÀ E CONTINUITÀ
 23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
NOME:... MATRICOLA:... Corso di Laurea in Fisica, A.A. 2008/2009 Calcolo 1, Esame scritto del f(x) = cos
 NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 008/009 Calcolo, Esame scritto del 06.0.009 Consideriamo la funzione fx cos + x. a Determinare il dominio massimale di f. b Trovare tutti gli asintoti
NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 008/009 Calcolo, Esame scritto del 06.0.009 Consideriamo la funzione fx cos + x. a Determinare il dominio massimale di f. b Trovare tutti gli asintoti
Esercitazione 9 - Funzioni
 Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
sin(3x) 3 sinh(x) x 2 cos(3x + x 2 ) log(1 + x)
 Analisi Matematica LA - Primo appello e prova conclusiva CdL in Ingegneria per l Ambiente e il Territorio e CdL in Ingegneria per le Telecomunicazioni A.A. 24/25 Dott. F. Ferrari Dicembre 24 Gli esercizi
Analisi Matematica LA - Primo appello e prova conclusiva CdL in Ingegneria per l Ambiente e il Territorio e CdL in Ingegneria per le Telecomunicazioni A.A. 24/25 Dott. F. Ferrari Dicembre 24 Gli esercizi
Corso di Analisi Matematica 1 - professore Alberto Valli
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 07/8 Corso di Analisi Matematica - professore Alberto Valli 6 foglio di esercizi - 5 ottobre 07
Università di Trento - Corso di Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio - 07/8 Corso di Analisi Matematica - professore Alberto Valli 6 foglio di esercizi - 5 ottobre 07
Matematica generale CTF
 Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
Il calcolo differenziale 17 novembre 2015 Derivata della funzione inversa Primitiva Regole di derivazione Calcolo di limiti Derivate di ordine superiore Massimi e minimi locali Intervalli di concavità
Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO COGNOME: NOME: MATR.: (x 1); C: y = ; D: y = 2 x; E: N.A.
 Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO 10 marzo 017 COGNOME: NOME: MATR.: 1) La retta tangente al grafico di f(x) = e x 1 x+ nel punto (1, ) è A: y = x + 4; B: y = (4x+) (x 1); C:
Seconda prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO 10 marzo 017 COGNOME: NOME: MATR.: 1) La retta tangente al grafico di f(x) = e x 1 x+ nel punto (1, ) è A: y = x + 4; B: y = (4x+) (x 1); C:
Matematica con esercitazioni, Modulo 2. Analisi matematica. Diario delle lezioni.
 Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Università degli Studi di Verona
 Tipologia A 1.1 Si enunci il teorema di derivazione della funzione inversa e lo si applichi al calcolo della derivata della funzione log x. 1.2 Il ite vale 0; x + sin x 1 + xe x non esiste; vale + ; vale
Tipologia A 1.1 Si enunci il teorema di derivazione della funzione inversa e lo si applichi al calcolo della derivata della funzione log x. 1.2 Il ite vale 0; x + sin x 1 + xe x non esiste; vale + ; vale
17 LIMITI E COMPOSIZIONE
 17 LIMITI E COMPOSIZIONE L operazione di ite si comporta bene per composizione con funzioni continue. Teorema. Sia gx) = y 0 e sia f continua in y 0. Allora esiste fgx)) = fy 0 ). Questo teorema ci dice
17 LIMITI E COMPOSIZIONE L operazione di ite si comporta bene per composizione con funzioni continue. Teorema. Sia gx) = y 0 e sia f continua in y 0. Allora esiste fgx)) = fy 0 ). Questo teorema ci dice
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Derivate. Paola Mannucci e Alvise Sommariva. Università degli Studi di Padova Dipartimento di Matematica. 12 novembre 2014
 Derivate. Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 12 novembre 2014 Paola Mannucci e Alvise Sommariva Derivate. 1/ 106 Approssimazione Problema. Data
Derivate. Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 12 novembre 2014 Paola Mannucci e Alvise Sommariva Derivate. 1/ 106 Approssimazione Problema. Data
4.3 Teoremi sulle funzioni derivabili
 4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE
 ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE Determinare l incremento della funzione f (x) = x 2 relativo al punto x 0 e all incremento x x 0, nei seguenti casi:. x 0 =, x = 2 2. x 0 =, x =. 3. x 0 =,
ESERCIZIARIO SULL'APPLICAZIONE DELLE DERIVATE Determinare l incremento della funzione f (x) = x 2 relativo al punto x 0 e all incremento x x 0, nei seguenti casi:. x 0 =, x = 2 2. x 0 =, x =. 3. x 0 =,
Derivate e studio di funzioni di una variabile
 Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate di funzioni
 Derivate di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 9 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Derivate di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 9 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI
 40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI Derivate parziali e piani tangenti Scrivere l equazione del piano tangente al grafico delle funzioni: f(, y) = (y ) + log nel punto = y = y + f(,
40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI Derivate parziali e piani tangenti Scrivere l equazione del piano tangente al grafico delle funzioni: f(, y) = (y ) + log nel punto = y = y + f(,
Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli x R che verificano le condizioni:
 Studi di funzione 5) Studiare la funzione definita da f() = arcsin ( ) + 3 2 +. Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli R che verificano le condizioni: () : +,
Studi di funzione 5) Studiare la funzione definita da f() = arcsin ( ) + 3 2 +. Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli R che verificano le condizioni: () : +,
9.2 La Formula di Taylor
 Università Roma Tre L. Chierchia 149 9.2 La Formula di Taylor Formula di Taylor al secondo ordine Dal punto di vista geometrico, l Osservazione 7.5 può essere parafrasata dicendo che, se f è derivabile
Università Roma Tre L. Chierchia 149 9.2 La Formula di Taylor Formula di Taylor al secondo ordine Dal punto di vista geometrico, l Osservazione 7.5 può essere parafrasata dicendo che, se f è derivabile
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
(1;1) y=2x-1. Fig. G5.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G5. Derivate G5. Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente. Esempio G5.: La funzione = e la sua retta tangente per
G5. Derivate G5. Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente. Esempio G5.: La funzione = e la sua retta tangente per
Matematica Lezione 19
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
Università degli Studi di Verona
 Università degli Studi di Verona Dipartimento di Informatica Ca' Vignal Strada le Grazie 15 37134 Verona - Italia Tel. +39 045 80 7069 Fax +39 045 80 7068 Corso di Laurea in Matematica Applicata PROVA
Università degli Studi di Verona Dipartimento di Informatica Ca' Vignal Strada le Grazie 15 37134 Verona - Italia Tel. +39 045 80 7069 Fax +39 045 80 7068 Corso di Laurea in Matematica Applicata PROVA
Derivate. Capitolo Cos è la derivata?
 Capitolo 8 Derivate 8.1 Cos è la derivata? Consideriamo una funzione y f(x) e disegnamo il suo grafico. Sia x 0 nel dominio di f e consideriamo il punto (x 0, f(x 0 )) del grafico. Vogliamo determinare
Capitolo 8 Derivate 8.1 Cos è la derivata? Consideriamo una funzione y f(x) e disegnamo il suo grafico. Sia x 0 nel dominio di f e consideriamo il punto (x 0, f(x 0 )) del grafico. Vogliamo determinare
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Sviluppi di Taylor e applicazioni
 Sviluppi di Taylor e applicazioni Somma di sviluppi Prodotto di sviluppi Quoziente di sviluppi Sviluppo di una funzione composta Calcolo di ordini di infinitesimo e di parti principali Comportamento locale
Sviluppi di Taylor e applicazioni Somma di sviluppi Prodotto di sviluppi Quoziente di sviluppi Sviluppo di una funzione composta Calcolo di ordini di infinitesimo e di parti principali Comportamento locale
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Esercizio 1. Per quali valori di h e k le seguenti funzione sono derivabili? x 3 sin 1 x 0. 0 x = 0. x cos 1 x > 0
 Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 0/3 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi del 0 ottobre 0 La sottrazione
Università degli Studi di Udine Anno Accademico 0/3 Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi del 0 ottobre 0 La sottrazione
Domande. Analisi 1. Vincenzo De Felice. La matematica è più bella di Fujiko. Ziodefe
 Domande di Analisi Vincenzo De Felice La matematica è più bella di Fujiko. Ziodefe 2 Funzioni reali Domanda Si dia la definizione di funzione reale. Risposta Siano X e Y due sottoinsiemi di R e supponiamo
Domande di Analisi Vincenzo De Felice La matematica è più bella di Fujiko. Ziodefe 2 Funzioni reali Domanda Si dia la definizione di funzione reale. Risposta Siano X e Y due sottoinsiemi di R e supponiamo
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital
 Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Analisi Matematica 1
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 64555 - Fax +39 09 64558 Analisi Matematica Testi d esame e Prove parziali a prova - Ottobre
