Analisi della Dipendenza
|
|
|
- Agnolo Bonfanti
- 7 anni fa
- Visualizzazioni
Transcript
1 Aals della Dpedeza La correlazoe Il presete materale ddattco è stato parte estratto e adattato dal materale prodotto dal prof. Claudo Caplupp dell Uverst Uverstà d Veroa, che s rgraza. La resposabltà del coteuto resta comuque del docete ttolare del corso prof. Maro Bolza e o può essere dffuso seza autorzzazoe.
2 Aals della Dpedeza S parla d dpedeza tra due varablquattatve quado è potzzable ua relazoe, d qualsas tpo, tra valor pù geerale le modaltà assut dalle due varabl: la relazoe può essere d tpo causale, coè ua varazoe del valore assuto da ua delle due varabl provoca ua coseguete modfcazoe del valore dell altra varable X Y oppure o è detfcable ua causa e u effetto, ma s osserva solo ua assocazoe tra comportamet coè valor assut dalle due varabl X Y I asseza d qualuque relazoe, le due varabl s dcoo dpedet
3 Dpedeza E ecessaro sottoleare che ua relazoe d causaeffetto o è u dato d fatto, ma ua potes : l attrbuzoe d causaltà ad ua relazoe è ua operazoe cocettuale che va al d la de dat osservat, e ache dell aals statstca: la causaltà è ua categora del pesero umao: o s osserva... la possbltà d fare ua affermazoe d tpo causale che abba ua valdtà scetfca dpede essezalmete dal metodo d rcerca spermetale e dal grado d cotrollo eserctato sulle varabl esplcatve e d dsturbo 3
4 Aals della Dpedeza L attrbuzoe d u esso causale è comuque sempre ua ostra proezoe: a volte c rsulta aturale a torto o a ragoe, altre volte molto problematca. No è raro cofodere la causa co l effetto. D per se stess, dat osservat c permettoo d rlevare solo ua assocazoe o correlazoe, pù o meo forte, tra feome, comportamet, evet Osservare ua forte correlazoe tra due varabl rappreseta u dzo, ma o sgfca che la prma varable abba u effetto causale sulla secoda: coè che aumetadoe l valore testà s possa durre u aumeto o dmuzoe el valore assuto dall altra. 4
5 Dpedeza causale cotua Molte volte due varabl soo strettamete assocate, coè presetao adamet molto sml, ma essuo s sogerebbe d sosteere che esste ua relazoe causale, é ua drezoe e emmeo ell altra Altre volte vece avvee che, sulla base d ua correlazoe, s rtega d avere scoperto la causa d qualcosa es. HIV -> AIDS Ua forte assocazoe tra due varabl può essere dovuta ad es. a u terzo fattore, che agsce su etrambe: O essere l rsultato d ua be pù complessa catea d relazo e terazo tra molt fattor X Z Y 5
6 Aals della Dpedeza Per poter essere d tpo causale, coè dove l effetto certo è assocable ache modo o determstco ma cosstete, ad ua causa, elle relazo casual è vero l cotraro: l eveto certo o è ragoevolmete mputavble a essua causa eppure probablstcamete ua relazoe osservata deve avere seguet requst: 6
7 Il esso d causaltà Il esso d causaltà ell assocazoe tra feome s fa dscedere, ella rcerca scetfca, dal realzzars delle seguet codzo Sartwell, 959: Cossteza; Itestà; Specfctà; sequezaltà temporale degl evet; Logctà. 7
8 Il esso d causaltà cotua cossteza: l assocazoe causale deve essere dpedete dalla localtà e dal metodo seguto per rlevarla. Deve essere, partcolare, possble dmostrare la rlevaza dell assocazoe sa prospettcamete, rlevado l sorgeza d effett dvers e grupp dversamete espost alla possble causa, sa retrospettvamete, rcavado ua dversa esposzoe e soggett colpt dall effetto gradmeto/dao rspetto a cotroll utà statstche eset da quell effetto; testà: al varare, aumeto o dmuzoe dell esposzoe al fattore agete, deve varare adeguatamete l lvello dell effetto. Tale relazoe vee descrtta, laddove s rlev l testà e o solo la preseza del cambameto, dalla cosddetta curva d dose-effetto; 8
9 Il esso d causaltà, cotua specfctà: l rscho è specfco quado la relazoe tra l fattore e l effetto è orgale e pù forte d quelle tra l fattore cosderato e altr possbl effett e tra l effetto cosderato e altr potezal aget scateat; sequezaltà temporale degl evet: l esposzoe deve precedere l effetto. Ache l perodo d cubazoe, o lateza, che precede la mafestazoe dell effetto, va coteggato ello stablre la sequezaltà; logctà: l esso relazoale deve essere accettable dal puto d vsta sostatvo socale, ecoomco, sataro, ecc.. 9
10 Il esso d causaltà, cotua L essteza de presuppost a, b, c, è valutata base a metod e tecche statstche; crter d, e afferscoo alla coosceza della socologa, ecooma, ammstrazoe, satà, ecc..
11 Dpedeza casuale Queste codzo soo ecessare ma o suffcet: c possoo far potzzare ua relazoe causale, ma o soo suffcet a dmostrarla Cosa vuol dre dmostrato, provato scetfcamete? Per poter sosteere valdamete ua potes d causaeffetto, è dealmete ecessaro garatre: cotrollo dretto del presuto fattore causale asseza d fattor d cofusoe: che possoo compromettere la correttezza dell fereza >metodo spermetale dseg spermetal o quas
12 Relazoe d causa - effetto Se ua rcerca che ha msurato ua assocazoe tra due varabl o è stata codotta co metodo spermetale, coè o s è realzzata: cotrollado l assegazoe del presuto fattore causale prma: radomzzazoe -> gruppo/codzoe d cotrollo msurado po le evetual varazo della varable dpedete l assocazoe, per quato forte, o cosete ua terpretazoe seso causale
13 Aals della Dpedeza Sbaglare ell detfcazoe della causa, o addrttura cofodere la causa co l effetto, o è così raro. La stora della sceza è rcca d esemp d teore che hao domato la scea per molto tempo, e che ogg c sembrao credbl o addrttura rdcole L potes d causaltà deve essere sottoposta a verfca emprca deftamete: se le prevso della teora vegoo cotraddette dall osservazoe, l potes rsulta falsfcata e dovrebbe essere abbadoata No sempre ua potes falsfcata vee subto abbadoata dalla comutà scetfca: occorre avere ua potes alteratva, possblmete mglore l coseso, ache all tero della comutà scetfca, è ua damca socale soo talvolta goco ache teress ecoomc, poltc,... Solo molto tempo dopo che l potes è stata falsfcata, e solo dopo che la comutà scetfca l ha deftvamete abbadoata, essa dveta a ostr occh così assurda o rdcola... 3
14 Aals della Dpedeza Se potzzamo ua relazoe d causa-effetto, l valore assuto dalla varable X v. dpedete, v. esplcatva, fattore, trattameto può essere utlzzato per prevedere quello della Y v. dpedete, rsposta, esto, effetto Può ache dars l caso che ua varable possa essere utlzzata per prevedere l lvello assuto da u altra, pur o essedoe la causa, ma solo u dcatore, come el caso: X I effett, è sempre così: o o sappamo ma co certezza se la ostra potes 4 d causaltà è vera... Z Y
15 cotua Comuque sulla base della ostra potes costruamo u modello: fché l modello fuzoa, coè dà buo rsultat per l campo d applcazoe cu vee mpegato es. prevso corrette, terape effcac,..., o cofdamo ell potes, coè la rteamo valda e cofermata, e la utlzzamo c comportamo come se fosse vera. La prevsoe d ua varable dpedete Y fuzoe d u seme d predttor X vee codotta costruedo u modello es. matematco, coè ua rappresetazoe grado d descrvere l feomeo, ovvero la relazoe osservata: modell d regressoe leare/o leare, geeralzzato,... alber d classfcazoe/regressoe segmetazoe ret eural artfcal 5
16 Aals della Dpedeza Covarazoe o Correlazoe Nel caso d varabl quattatve, s defsce u partcolare tpo d assocazoe detta covarazoe o correlazoe: quado corrspodeza d valor alt d ua varable quattatva s osservao prevaletemete valor alt o bass dell altra quattatva e vceversa, s dce che esste ua correlazoe postva o egatva tra le varabl. Quado s vuole aalzzare la relazoe tra due varabl quattatve, è sempre opportuo partre dalla rappresetazoe grafca della stuazoe: a partre dalla sere doppa de dat osservat, s costrusce u grafco rappresetado dat come put sul pao cartesao, avet come coordate la coppa d valor, Dalla rappresetazoe grafca s può comcare a capre l tpo d relazoe 6
17 Aals della Dpedeza L seme de dat osservat è rappresetato sul pao cartesao come ua uvola d put Nell esempo a faco, l grafco mostra ua correlazoe postva o dretta tra le due varabl: a valor elevat della X s assocao prevaletemete valor alt della Y... per brevtà, s dce che al crescere d X cresce Y La relazoe sembra puttosto forte : la uvola d put è abbastaza stretta, coè put soo puttosto cocetrat lugo ua lea deale, e o molto dspers sul pao Quato è forte la relazoe? Voglamo quatfcare la forza della relazoe ovvero arrvare ad ua msura della dpedeza tra le due varabl 7
18 Aals della Dpedeza, Operamo la doppa trasformazoe d varabl: E equvalete a traslare gl ass cartesa el barcetro della uvola d put Nel uovo sstema d coordate traslato, cascu puto che prma aveva coordate,, ora avrà coordate:, 8
19 Aals della Dpedeza, Operamo la doppa trasformazoe d varabl: E equvalete a traslare gl ass cartesa el barcetro della uvola d put Nel uovo sstema d coordate traslato, cascu puto che prma aveva coordate,, ora avrà coordate:, 9
20 Aals della Dpedeza II quadrate I quadrate,, III quadrate IV quadrate Osservamo che quado put s trovao el: I quadrate: etrambe le coordate soo postve III quadrate: etrambe le coordate soo egatve II quadrate: ascssa egatva e ordata postva IV quadrate: ascssa postva e ordata egatva l prodotto è postvo l prodotto è egatvo Sommado prodott delle coordate trasformate per tutt put, abbamo u dcatore d come put s dstrbuscoo el pao u dce d covarazoe
21 Aals della Dpedeza II quadrate I quadrate, III quadrate IV quadrate Osservamo che quado put s trovao el: I quadrate: etrambe le coordate soo postve III quadrate: etrambe le coordate soo egatve II quadrate: ascssa egatva e ordata postva IV quadrate: ascssa postva e ordata egatva l prodotto è postvo l prodotto è egatvo Sommado prodott delle coordate trasformate per tutt put, abbamo u dcatore d come put s dstrbuscoo el pao u dce d covarazoe
22 Aals della Dpedeza La Covaraza E la meda de prodott degl scart d cascua varable dalla propra meda Cov, E u dce d covarazoe: l suo sego descrve l adameto della relazoe: è > quado la relazoe è postva è < quado è egatva è quado o c è correlazoe La covaraza cresce valore assoluto quato pù put tedoo ad allears lugo ua retta, e dmusce vece fo al suo mmo quato pù se e allotaao No è ua msura stadardzzata: dpede dalle utà d msura delle varabl, e dalle varabltà delle due sere d dat e
23 Aals della Dpedeza Propretà della Covaraza E ua quattà smmetrca, el seso che: Cov, Cov, La covarazoe è ua propretà recproca delle due varabl: è ua propretà della loro relazoe Se ua delle due varabl è costate, la covaraza è ulla, fatt se k : k k Cov, Se e soo statstcamete dpedet dstrbuzoe, la loro covaraza è ulla. La covaraza può però essere ulla ache seza che e sao dpedet La covaraza è effett ua msura della leartà della relazoe tra due varabl: altre forme d relazoe o lear o vegoo rlevate da questo dce La covaraza o è ua msura stadardzzata, dpede dalle utà d msura delle varabl, e dalle varabltà delle due sere d dat e : per superare questo dfetto, vee trodotto u altro dce d correlazoe, rcorredo acora ua volta alla stadardzzazoe E sempre ferore o uguale, valore assoluto, al prodotto degl scart quadratc med delle due varabl : Cov, 3
24 Aals della Dpedeza Il coeffcete d correlazoe leare Il coeffcete d correlazoe leare r, d Pearso è dato dal rapporto tra la covaraza e l prodotto degl scart quadratc med delle due varabl: E ua msura dell testà della dpedeza relazoe leare tra le due varabl E u dce relatvzzato o ormalzzato: è costruto come rapporto tra la covaraza e l valore massmo che essa può assumere è u umero puro admesoale coè seza utà d msura è compreso tra - e + ρ Iterpretazoe del valore d r,: è > quado la correlazoe è postva, < quado è egatva vale + o - quado la forza della correlazoe leare postva o egatva è massma, coè quado tutt put soo perfettamete alleat lugo ua retta 4 vale quado la correlazoe è ulla: le due varabl s dcoo correlate
25 Aals della Dpedeza Propretà del coeffcete d correlazoe leare E ua quattà smmetrca, el seso che: r, r, La co-relazoe è recproca Se e soo dpedet, allora r è uguale a zero. Tuttava r può essere uguale a zero ache seza che e sao dpedet Il coeffcete d correlazoe è ua msura della relazoe leare tra due varabl: o mette evdeza altre forme d relazoe parabolca, curvlee,... Pertato quado r è prossmo a zero può sgfcare che o c è relazoe tra le due varabl, ma s potrebbe ache essere vece preseza d ua relazoe d tpo o leare Il coeffcete d correlazoe leare è ua covaraza stadardzzata, coè è otteble come covaraza tra le due varabl e stadardzzate: Cov ρ, 5
26 Aals della Dpedeza 6
27 Aals della Dpedeza Eserczo. Studamo la dpedeza tra le varabl quattatve Yaltezza e Xpeso: Totale 6 44 Meda 75, 78, , Dal grafco s può otare ua relazoe postva abbastaza forte: solo ua osservazoe è puttosto dstate dalla lea deale toro alla quale s cocetrao dat 7
28 Aals della Dpedeza Prospetto d calcolo del coeffcete d correlazoe: -M -M [-M]² [-M]² -M-M , -4, 69, 96, 8, ,,,,, , -, 49, 4, 4, ,,,,, , 4, 9, 6,, ,, 5, 4,, , 4, 8, 6, 36, , 6, 96, 36, 84, Totale , 7, 338, Meda 75, 78, 8,5 34, 4,5 ρ 8,5 34 4,5 4,5,839 8,5 34 r è postvo e puttosto elevato, cosderato che l suo massmo è : qud msuramo ua forte dpedeza leare tra le due varabl 8
29 Aals della Dpedeza Eserczo. Studamo la dpedeza tra due varabl X e Y, legate dalla relazoe d dpedeza esatta : Y +, ² 3,8 5, 3 3 6, 4 4 6, , , 8 8 5, 9 9 3,8 Totale 45 5 Meda 5, 5, , Dal grafco s evdeza charamete la relazoe quadratca tra le due varabl, che dsega ua parabola co la cocavtà rvolta verso l basso 9 Vedamo cosa c dce l coeffcete d correlazoe...
30 Aals della Dpedeza Prospetto d calcolo: questa volta provamo l metodo dretto, molto pù veloce : M []² []² 3,8, 4,44 3,8 3,67 5 6,67 5, 4, 7,4,4 33,48 5,67 M 8,33 5 5,67, , 9, 38,44 8, ,8 6, 46,4 7, , 49, 35, 6 6 6,8 36, 46,4 4, , 49, 38,44 43, , 64, 7,4 4, ,8 8, 4,44 34, Totale ,3 55 Meda 5, 5,67 3,67 33,48 8,33 A meo d error d arrotodameto, r rsulta pratcamete par a zero, segalado asseza d relazoe leare Le due varabl soo vece strettssma relazoe, essedo, per costruzoe, fuzoe quadratca esatta d, ma: l coeffcete d correlazoe o è grado d rlevare relazo o lear 3
31 La regressoe Leare
32 Aals della Dpedeza La Regressoe Leare Quado tra due varabl c è ua relazoe d dpedeza, s può cercare d prevedere l valore d ua varable fuzoe del valore assuto dall altra. Questo ha sgfcato seso stretto quado s potzza ua relazoe d causaltà tra la varable dpedete, su cu s agsce, e quella dpedete, su cu s vuole produrre u effetto. Voledo costrure u modello statstco per prevedere Y fuzoe d X, s poe la questoe d quale relazoe fuzoale potzzare tra la varable dpedete X e la varable dpedete Y. Il modello pù semplce d relazoe tra due varabl è quello leare d prmo grado, rappresetato da ua retta, la cu equazoe è : a + b Ua volta determata la retta, l modello permetterà d stmare l valore della varable Y sulla base del valore assuto dalla X Per otteere u buo modello, e qud delle buoe prevso, occorre determare la retta che meglo descrve put osservat: pratca, s tratta d determare due coeffcet a e b che compaoo ell equazoe della retta: a + b 3
33 Aals della Dpedeza Rpassamo u po d geometra e d trgoometra... : l parametro a è l tercetta della retta co l asse delle ordate l parametro b è l coeffcete agolare: msura l clazoe della retta è la tagete dell agolo α formato dalla retta co l asse delle ascsse I pratca: a c dce quato vale Y quado X vale b c dce d quato aumeta Y all aumetare d ua utà d X a + b b a a α 33
34 Aals della Dpedeza Se put fossero solo due, o fossero tutt alleat, determare la retta terpolate sarebbe facle per due put passa ua sola retta, ma sfortuatamete ella realtà dat osservatv o soo ma esattamete alleat Per determare la retta d regressoe che meglo descrve dat osservat è allora ecessaro stablre u crtero statstco d valutazoe della botà del modello: a + b + ε L errore che s commette prevededo cascu Y osservato co l modello, può essere msurato come dffereza tra l dato reale e quello prevsto: ε a + b + ε coè, per cascua osservazoe, s commette u errore ε 34
35 Aals della Dpedeza Il Metodo de Mm Quadrat Il crtero detto de mm quadrat prevede d valutare la botà del modello sulla base della somma de quadrat d tutt error d stma commess: ε a b m La retta mglore, secodo questo crtero, è quella che mmzza la somma de quadrat degl scart de valor stmat da quell osservat, dett ache resdu della regressoe. Perché propro l quadrato de resdu? per evtare che resdu postv e egatv s compeso l valore assoluto è matematcamete pù scomodo da gestre e o sempre porta ad ua soluzoe uvoca l quadrato dà peso maggore agl scart pù grad, che soo ache quell che c dsturbao d pù: è meglo fare tat pccol error che o u errore molto grosso 35
36 Aals della Dpedeza Stma de parametr a mm quadrat Nel ostro caso voglamo mmzzare ua fuzoe fa,b rspetto ad a e b: dovremo mporre che sao ulle le dervate prme parzal della fuzoe rspetto ad a e b: Dervado la fuzoe prma rspetto ad a e po rspetto a b, e poedo a zero tal dervate, s ottee u sstema d due equazo d prmo grado due cogte a e b: Rsolvedo l sstema rspetto ad a e b, s determao le stme a mm quadrat de parametr della retta d regressoe m b a Sstema d equazo ormal d regressoe b a b a b a b a b b a a b a 36
37 Aals della Dpedeza Soluzoe del sstema d equazo ormal, Cov b b b b b b b b a b a b a b a b a b a b a b a + +,, M V M Cov 37
38 Aals della Dpedeza I coeffcet d regressoe I parametr del modello vegoo chamat ache coeffcet d regressoe: Equazoe della retta d regressoe: Bsoga calcolare prma l valore d b e po quello d a. Il cappello sopra a e b sottolea che s tratta delle stme, a mm quadrat, de parametr del modello. Il metodo d calcolo pù veloce per b è utlzzare l espressoe che compare ell ultmo passaggo della soluzoe del sstema d equazo ormal: che ha l vataggo d o rchedere l calcolo d scart pratca utlzza le formule drette per la varaza e la covaraza b a b,, M M Cov b b a + 38
39 Aals della Dpedeza Iterpretazoe de coeffcet d regressoe Il sego del coeffcete d regressoe dpede da quello della covaraza: e dca qud se la relazoe è dretta o versa Rcordamo che, ell equazoe della retta b rappreseta l coeffcete agolare, coè l clazoe della retta a + b b b > b b < relazoe dretta, coè cresce al crescere d asseza d relazoe leare, o vara al varare d relazoe versa, coè dmusce all aumetare d la retta è crescete, clazoe postva la retta è orzzotale, clazoe ulla la retta è decrescete, clazoe egatva Il valore assoluto d b dca d quato vara la Y al varare d ua utà della X Il coeffcete a rappreseta l tercetta della retta co l asse Y: dca quato vale Y quado X vale ; quado a, la retta passa per l orge degl ass cartesa, coè per l puto d coordate, 39
40 Aals della Dpedeza Propretà della regressoe a mm quadrat Stmat parametr, possamo produrre valor prevst dal modello corrspodeza degl osservat: a + b + ε La retta d regressoe passa per l barcetro del sstema, fatt quado assume l valore medo: a + b b + b a + b Per cascu possamo ora calcolare ache l errore commesso prevededo Y co l modello, come scarto tra l valore osservato e quello stmato: quest error soo dett resdu d regressoe ε I resdu soo mportat per la valutazoe della botà del modello, coè la sua capactà d adattars a dat osservat 4
41 Aals della Dpedeza Eserczo. Determamo la retta d regressoe a mm quadrat per la relazoe tra le varabl Yaltezza e Xpeso: b a b Osservamo che tutto quello che c serve per determare coeffcet d regressoe della retta, lo abbamo realtà gà calcolato per l coeffcete d correlazoe 4
42 Aals della Dpedeza Rpredamo l prospetto d calcolo del coeffcete d regressoe: -M -M [-M]² [-M]² -M-M , -4, 69, 96, 8, ,,,,, , -, 49, 4, 4, ,,,,, , 4, 9, 6,, ,, 5, 4,, , 4, 8, 6, 36, , 6, 96, 36, 84, Totale , 7, 338, Meda 75, 78, 8,5 34, 4,5 b 8,5 4,5 8,5 34,5 a 4,5 b 78, Il valore d b c dce che, al varare d ua utà d, l valore d vara d,5 Ora possamo dsegare la retta d regressoe, determadoe due put a scelta 4
43 Aals della Dpedeza Falmete scrvamo l equazoe della retta d regressoe: b a,5 b , , Per dsegare la retta d regressoe, è suffcete determare due put a scelta: uo realtà lo cooscamo gà: è l puto medo barcetro del sstema per l altro sceglamo ad es. 5, da cu 39 +,5 * 5 65 A vederla così o sembra che l tercetta sa 39: questo dpede dal fatto che put soo molto lota dall orge e o abbamo taglato la fgura 43
44 Aals della Dpedeza Se dsegamo l grafco e la retta d regressoe a partre dall orge degl ass, vedamo che tutto tora: La retta terseca l asse delle ordate propro el puto 39 L clazoe apparete della retta el dsego dpede dalla scala degl ass: abbamo usato due scale dverse per l asse X e per l asse Y Avevamo gà calcolato l coeffcete d correlazoe ρ 39 +, 5, , U coeffcete d correlazoe par a,8 c dce che put soo abbastaza be alleat lugo la retta, ma ora vedamo meglo come valutare la capacta del modello d descrvere dat osservat 44
45 Aals della Dpedeza Valutazoe del modello La botà dell terpolazoe forta dal modello s gudca sulla base della dspersoe de put osservat toro alla retta d regressoe: l terpolazoe è esatta quado la retta passa per tutt put osservat, che devoo essere qud perfettamete alleat pù put osservat s dscostao dalla retta -> more è la valdtà del modello, che dveta sempre meo effcace, fo a perdere pratcamete d sgfcato Il modello stmato può essere valutato, coeretemete co l crtero che è stato utlzzato per costrurlo, sulla base della somma de quadrat degl scart tra valor osservat e valor stmat, coè la somma de quadrat de resdu d regressoe: ε I resdu della regressoe leare a mm quadrat godoo d 4 mportat propretà: tutte queste propretà dervao dalle equazo ormal, ovvero dalle codzo che soo state mposte per determare parametr della retta d regressoe, modo da mmzzare la somma de quadrat de resdu stess 45
46 Aals della Dpedeza Le 4 Propretà de Resdu d Regressoe Le prme due propretà dervao drettamete, az o soo altro che le codzo mposte dalle equazo ormal d regressoe: ε ovvero b a b a b a + + ε ε 46
47 Aals della Dpedeza Dmostramo le altre due: soo propro le prme due propretà questa è la terza propretà Teamole preset: fra u attmo c torerao utl + + b a b a 47
48 Aals della Dpedeza Eserczo. Verfca emprca delle 4 propretà de resdu d regressoe a mm quadrat per l modello appea stmato: 39 +, 5 ^ ^-M -^ -^ -^ ^ -^^-M ,4-6,76-7,4-448,88-39, , ,8-5,7 5,7 366,8 985,446-3, ,36-3,64,64,5 85,954-5, ,,,,,, ,56,56,44 9,3 438,64 3, ,6,6 -,6-48, -8,36 -, ,68 4,68 -,68-57, -4,4-3, ,8 7,8 -,8-3,9-37,584-9,384 Totale ,,,,, Meda 75, 78, 78, 48
49 Aals della Dpedeza Devaza e Varaza Resdua Il modello vee valutato sulla base della somma de quadrat degl scart tra valor osservat e valor stmat: ε Questa quattà è detta devaza resdua, quato è la devaza de resdu d regressoe che rcordamo hao meda ulla Il terme devaza dca semplcemete la varaza o dvsa per, qud tutto quello che dcamo per la devaza vale ache per la varaza La quattà: M M a + b M + b M M b + b prede vece l ome d devaza spegata dal modello o devaza d regressoe, quato devaza de valor stmat dal modello: rappreseta la parte d varabltà della Y descrtta dal modello d regressoe Devaza spegata e devaza resdua soo legate tra loro e co la devaza totale della varable dpedete 49
50 Aals della Dpedeza Scomposzoe della Devaza e della Varaza d Y La devaza della varable Y può essere scomposta due compoet: coè come somma della devaza resdua e della devaza spegata dal modello Devaza spegata e resdua soo qud due quattà complemetar e la loro somma è par alla devaza totale della Y. Lo stesso vale ache per la varaza, basta dvdere tutto per : + + modello Capamo l sgfcato della scomposzoe: resdua ε a + b 5
51 Aals della Dpedeza Dmostrazoe: Lo stesso vale ovvamete ache per la varaza, basta dvdere tutto per, qud possamo scrvere ache la scomposzoe della varaza totale d Y: I vrtù d questa scomposzoe, s può costrure u dce stadardzzato compreso tra e per valutare la botà del modello d regressoe ] [ a b b a b a per la quarta propretà de resdu d regressoe devaza resdua + devaza spegata dal modello resdua modello + 5
52 Aals della Dpedeza Il Coeffcete d Determazoe R² Per valutare la botà del modello s troduce l coeffcete d determazoe R² rapporto tra la devaza del modello e la devaza totale della : R² msura la frazoe d varaza o d devaza della Y spegata dal modello R² s può scrvere ache come: Assume valor compres tra e : R vale quado l modello spega completamete la varaza della Y: resdu soo tutt ull, coè put soo perfettamete alleat vale quado la varaza descrtta dal modello è ulla: questo accade quado la retta d regressoe rsulta parallela all asse X, coè 5 R modello modello resdua resdua
53 Aals della Dpedeza Osservamo che per calcolare R² è ecessaro calcolare tutt gl stmat per og osservato, e tutt gl scart tra valor stmat e M Oppure, co la secoda formulazoe, dobbamo calcolare tutt gl scart tra gl stmat e quell osservat coè resdu Possamo però svluppare R² ache u altro modo: Il coeffcete d determazoe R² solo per l modello leare d prmo grado coè per la retta d regressoe è uguale al quadrato del coeffcete d correlazoe ρ² Qud l quadrato del coeffcete d correlazoe c forsce la frazoe d varaza spegata dal modello, seza calcolare resdu e emmeo gl stmat resdua modello R 4 ρ + modello b V V b V b a V V V R 53 53
54 Aals della Dpedeza Eserczo. Toramo al ostro esempo, per valutare la botà del modello stmato: determamo put stmat e calcolamo la varaza spegata e la varaza resdua Totale 6 44 Meda 75, 78, , R, Il modello spega crca l 65% della varaza complessva della Y: possamo rteerc soddsfatt? Nelle sceze socal e comportametal dffclmete s trovao modell che spegao molta varaza, perché feome soo compless e dpedoo da molt fattor dvers, oltre le relazo possoo essere o lear 54
55 Aals della Dpedeza Prospetto d calcolo del coeffcete d determazoe R²: ^ ^-M -^ -M [^-M]² [-^]² [-M]² ,4-6,76-7,4-4, 45,7 5,4 96, ,8-5,7 5,7, 3,7 3,7, ,36-3,64,64 -, 3,5,69 4, ,,,,,,, ,56,56,44 4,,43 5,95 6, ,6,6 -,6, 6,76,36 4, ,68 4,68 -,68 4,,9,46 6, ,8 7,8 -,8 6, 53,,64 36, Totale ,,, 75,76 96,4 7, Meda 75, 78, 78,,97,3 34, R modello,97 modello,97 34 resdua,3,646 oppure 34 R modello + resdua resdua,3 34,646 Cooscedo gà l valore del coeffcete d correlazoe, potevamo rsparmarc tutt quest calcol: R ρ,839,646 55
56 Aals della Dpedeza Esempo. U caso partcolare d retta d regressoe s verfca quado la stma d b rsulta uguale a : b a b La retta terseca l asse delle ordate el puto M La stma è sempre par a M, per qualuque valore d La varaza spegata dal modello è ulla ,5 R La varaza resdua è massma, coè uguale alla varaza totale d Y Il coeffcete d determazoe R²: R regress resd ρ
57 Aals della Dpedeza Eserczo. Rtoramo all esempo d due varabl legate da ua relazoe quadratca esatta: Y +, ² 3,8 5, 3 3 6, 4 4 6, , , 8 8 5, 9 9 3,8 Totale 45 5 Meda 5, 5, , Dal grafco s evdeza charamete la relazoe quadratca tra le due varabl, che dsega ua parabola co la cocavtà rvolta verso l basso Come rsulta la retta d regressoe? 57
58 Aals della Dpedeza Cosderazo sull applcabltà d u modello leare Quado R² è basso sgfca che l modello leare o resce a descrvere adeguatamete l feomeo, o s adatta bee a dat, e qud ache le ostre prevso sarao poco affdabl. Quado R² è elevato, dcamo prossmo a, l modello descrve bee dat emprc, spegado gra parte della varabltà osservata della varable dpedete. La capactà descrttva del modello è duque buoa, almeo relatvamete a dat osservat. S può allora rteere utlzzable l modello a scop prevsv? Il passaggo dalla descrzoe de dat osservat alla prevsoe d uov dat e comportamet è u problema d geeralzzabltà de rsultat d u modello valdtà estera La possbltà d operare geeralzzazo s basa su assuzo ragoevol come: orde della atura: se le cose soo adate u certo modo fora o c è ragoe che o fuzoo così ache futuro e passato: attualsmo determsmo degl evet: essu eveto avvee per caso, ma è determato da precedet evet; ovvero, se le cose fuzoao u certo modo, la ragoe c è sempre, e qud cotuerao Quest prcp soo plausbl, ma o asscurat: essuo può garatre che ache le prossme osservazo s comporterao allo stesso modo. 58
59 Aals della Dpedeza Cosderazo sull applcabltà d u modello leare Assa pù azzardato è utlzzare u modello per fare prevso per valor ester al campo d varazoe de dat osservat, su qual l modello è stato stmato: questo tpo d prevso, dette estrapolazo, portao spesso a cocluso errate es. sopravvalutare u tred d crescta postvo Raramete feome soo lear, oppure lo soo solo su ua parte lmtata del loro campo d essteza: utlzzare u modello leare è quas sempre ua semplfcazoe del feomeo reale, che può rsultare accettable per determate applcazo I rsultat del modello o devoo essere accettat cecamete: occorre sempre cosderare crtcamete le possbl lmtazo
60 Aals della Dpedeza La Colleartà U problema, detto colleartà, s verfca quado valor d X soo molto vc tra loro: questo caso la determazoe della retta d regressoe rsulta certa Vedamo cosa succede ella stuazoe lmte cu tutt gl vegao a cocdere esattamete: b Cov, Cov k, k La stma d b assume ua forma determata Cò equvale a dre che qualuque retta passate per l puto medo del sstema è la retta terpolate a mm quadrat No dmetchamo fatt che resdu vegoo calcolat parallelamete all asse Y I pratca o s verfcherà ma l caso lmte della cocdeza d tutt valor d X, ma basta che sao molto vc perché l calcolo d b rsult molto stable, e qud l modello sa prvo d sgfcato Sgfcato: se la X osservata o vara, o può eache spegare la varabltà d Y 6
61 Aals della Dpedeza L altra Retta d regressoe Cambamo le carte tavola, e questa volta stmamo, sempre sugl stess dat usat fora, l modello per prevedere X fuzoe d Y: c + d Totale 6 44 Meda 75, 78, ,9 +, Y Il grafco rsulta rovescato rspetto a prma, fatt questa volta trovamo la varable Y sull asse delle ascsse e la X sull asse delle ordate 6
62 Aals della Dpedeza Rportado valor stmat da due modell su uo stesso grafco, c accorgamo che la uova retta d regressoe o cocde co quella stmata precedeza Come s spega? Il metodo de mm quadrat valuta resdu lugo l asse della varable dpedete I resdu calcolat lugo l asse Y rsultao geerale dvers da quell calcolat lugo l asse X Qud s hao sempre due rette d regressoe, che geerale o cocdoo ,9 +, 46 La retta d regressoe per 6 stmare Y fuzoe d X è stata otteuta mmzzado la somma de quadrat de resdu d Y, calcolat parallelamete all asse Y 39 +, La retta d regressoe per stmare X fuzoe d Y s ottee mmzzado la somma de quadrat de resdu d X, calcolat parallelamete all asse X 6
63 Aals della Dpedeza Cosderamo le due rette d regressoe e vedamo cosa hao comue: Le rette regressoe a mm quadrat rsultao dverse, ma l coeffcete d determazoe R² o camba, essedo l quadrato del coeffcete d correlazoe, che è ua quattà smmetrca La frazoe d varabltà d Y spegata dalla regressoe d Y fuzoe d X è par alla frazoe d varabltà d X spegata dalla regressoe d X fuzoe d Y C è ua relazoe tra due coeffcet d regressoe b e d: Le due rette d regressoe cocdoo solo quado put soo perfettamete alleat, coè quado r. I questa stuazoe partcolare s ha: d d c b b a + + bd qud d b ρ ρ d b d b / ρ R ρ ρ 63
64 Aals della Dpedeza Il Modello seza tercetta Toramo alla stma d Y fuzoe d X, e cosderamo l modello rdotto elmado l parametro a, ovvero ua retta seza tercetta: b La stma d questo modello è molto semplce: dobbamo mmzzare la somma de quadrat de resdu, che questo caso soo ua fuzoe d ua sola varable b Totale 6 44 Meda 75, 78, La stma d b rsulta dversa da quella del modello completo : ε Per determare l puto d mmo, dervamo la fuzoe rspetto a b, otteedo ua sola equazoe: da cu: b b b b b 64 m
65 Aals della Dpedeza Prospetto d calcolo del coeffcete d regressoe: ² Totale Meda 75, 78, b M M, ,3469 E facle verfcare che questa retta d regressoe NON passa per l puto medo del sstema :, , 78 Adesso voglamo d valutare la botà del modello: calcolamo duque la varaza resdua e quella d regressoe spegata dal modello, e vedamo cosa succede... 65
66 Aals della Dpedeza Prospetto d calcolo del coeffcete d determazoe R²: ^ ^-M -^ -M [^-M]² [^-]² [-M]² ,5-3,49 8,49-4, 55,57 34,86 96, , -7,8 7,8, 77,59 77,59, ,59-8,4 6,4 -, 338,85 69, 4, , -,98,98, 3,9 3,9, ,6 5,6 -,6 4, 5,6,3 6, ,76 9,76-7,76, 95,7 6,5 4, ,4 9,4-5,4 4, 366,47 9,3 6, ,88 3,88-4,88 6, 953,45 68,9 36, Totale ,7-5,83 5,83, 36,63 97, 7, Meda 75, 78, 76, 45,45 87,4 34, modello 45,45 resdua 87,4 34 modello + resdua!! R modello resdua ρ La varaza resdua è maggore della varaza totale d Y... R² perde og sgfcato, perché o vale pù la scomposzoe della varaza 66
67 Aals della Dpedeza Rspetto al sstema d equazo ormal dervate per la stma de parametr del modello completo, pratca o è stata mposta la prma codzoe : Come cosegueza mmedata, o vale pù la prma propretà de resdu: la somma de resdu d regressoe del modello rdotto o rsulta uguale a o è ulla emmeo la somma degl scart de valor stmat dalla M la meda de valor stmat o cocde co la meda d Y la retta o passa per l barcetro del sstema La secoda propretà cotua a valere perché è la codzoe mposta dall uca equazoe ormale, dervata per la stma a mm quadrat del modello rdotto b a b a b a b a b a b a b a b a 67
68 Aals della Dpedeza Esempo. Verfca emprca delle 4 propretà de resdu d regressoe a mm quadrat: ^ ^-M -^ -^ -^ ^ -^^-M ,5-3,49 8,49 46, ,47-6, , -7,8 7,8 778, ,84-77, ,59-8,4 6,4 5,733 68,5567-3, , -,98,98 48, ,3785-3, ,6 5,6 -,6-8,88-94,346-5, ,76 9,76-7,76-6, ,439-75, ,4 9,4-5,4-7, ,48-89, ,88 3,88-4,88-4, , ,845 Totale ,7-5,83 5,83,, -88,3658 Meda 75, 78, 76, -35,957 Verfchamo che la varaza totale d Y è otteble come: modello + resdua , , ,83/ 8 45, ,4 + 35,
69 Aals della Dpedeza Il modello rdotto, per la macaza dell tercetta, obblga la retta a passare per l orge degl ass:, 3469 L troduzoe d questo vcolo peggora la capactà del modello d adattars a dat osservat, rspetto al modello completo I geerale, l troduzoe d u vcolo u modello e peggora sempre la capactà d adattameto 39 +, Possamo dre che, a partà d predttor, l aumeto d u parametro mglora sempre o almeo o peggora la capactà descrttva d u modello, metre l elmazoe d u parametro la rduce Per mglorare l adattameto e descrvere ache relazo o lear, potremmo ad esempo passare ad u modello d secodo grado, co tre parametr: 69 a + b + c
70 Aals della Dpedeza Stmamo a mm quadrat u modello d regressoe quadratco su dat gà aalzzat precedeza co l modello d prmo grado retta a + b + c 3,8 5, 3 3 6, 4 4 6, , , 8 8 5, 9 9 3,8 Totale 45 5 Meda 5, 5, , -, + + R I questo caso dovremo mmzzare la somma de quadrat de resdu del modello rspetto a tre parametr a, b, c otteedo u sstema d 3 equazo ormal Rsolvedo l sstema, trovamo u modello che s adatta perfettamete a dat osservat: R² 7
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
LA REGRESSIONE LINEARE SEMPLICE
 LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
Dott.ssa Marta Di Nicola
 RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Università degli Studi di Napoli Parthenope. Facoltà di Scienze Motorie a.a. 2011/2012. Statistica. Lezione IV
 Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Associazione tra due variabili quantitative
 Esempo (1) Assocazoe tra due varabl quattatve Suppoamo che u professore vogla dmostrare che eserctars a casa aut gl studet el superameto dell esame. esame. A tal fe regstra la votazoe de compt a casa e
Esempo (1) Assocazoe tra due varabl quattatve Suppoamo che u professore vogla dmostrare che eserctars a casa aut gl studet el superameto dell esame. esame. A tal fe regstra la votazoe de compt a casa e
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Corso di laurea in Scienze Motorie Corso di Statistica Docente: Dott.ssa Immacolata Scancarello Lezione 9: Covarianza e correlazione
 Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
Classi di reddito % famiglie Fino a 15 5.3 15-25 16.2 25-35 21.1 35-45 18.6 45-55 13.6 Oltre 55 25.2 Totale 100
 ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Indici di asimmetria. Elementi di Statistica descrittiva Parte IV. Simmetria di una distribuzione di frequenze. Primo indice di asimmetria (1/3)
 Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Variabili casuali ( ) 1 2 n
 Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
6. LA CONCENTRAZIONE
 UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTRAZIONE Prof. Maurzo Pertchett Statstca
UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTRAZIONE Prof. Maurzo Pertchett Statstca
Interpolazione. Definizione: per interpolazione si intende la ricerca di una funzione matematica che approssima l andamento di un insieme di punti.
 Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
INDICI DI VARIABILITA
 INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
Il modello di regressione lineare semplice (1) Studio della dipendenza riepilogo
 Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
CORSO DI STATISTICA I (Prof.ssa S. Terzi)
 CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
Aritmetica 2016/2017 Esercizi svolti in classe Quarta lezione
 Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Esercitazione 5 del corso di Statistica (parte 1)
 Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
TRATTAMENTO STATISTICO DEI DATI ANALITICI
 TRATTAMENTO STATISTICO DEI DATI ANALITICI Nell aals chmca u aalsta effettua u umero lmtato d prove e cosdera la meda de rsultat otteut per poter arrvare a determare o l valore VERO d ua determata gradezza
TRATTAMENTO STATISTICO DEI DATI ANALITICI Nell aals chmca u aalsta effettua u umero lmtato d prove e cosdera la meda de rsultat otteut per poter arrvare a determare o l valore VERO d ua determata gradezza
Lezione 13. Anelli ed ideali.
 Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Capitolo 2 Errori di misura: definizioni e trattamento
 Captolo Error d msura: )Geeraltà defzo e trattameto I cocett d meda, varaza e devazoe stadard s utlzzao ormalmete per otteere formazo sulla botà d ua msura. I geerale, s assume come msura m della gradezza
Captolo Error d msura: )Geeraltà defzo e trattameto I cocett d meda, varaza e devazoe stadard s utlzzao ormalmete per otteere formazo sulla botà d ua msura. I geerale, s assume come msura m della gradezza
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI QUANTITATIVE Indici di centralità, dispersione e forma
 Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI
Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI
CORSO DI STATISTICA I (Prof.ssa S. Terzi) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI. Esercitazione n 3
 ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Esercizi su Rappresentazioni di Dati e Statistica
 Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
dei quali si conoscono solo la media x e la deviazione standard σ e dato un valore reale positivo K, possiamo affermare che:
 Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Modulo di Fisica Tecnica. Differenze finite per problemi di conduzione in regime instazionario
 Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Regressione. Modelli statistici. Esempio: le automobili si vendono a peso? Esempio: le automobili si vendono a peso? prezzo=a+b*(peso-500)+errore
 Modell statstc Regressoe Ccchtell Cap. 0 La relazoe tra varabl può essere studata per mezzo d modell statstc varable (es. peso) Quato c s dscosta da u valore tpco modello varabl (peso-altezza) Quato c
Modell statstc Regressoe Ccchtell Cap. 0 La relazoe tra varabl può essere studata per mezzo d modell statstc varable (es. peso) Quato c s dscosta da u valore tpco modello varabl (peso-altezza) Quato c
STATISTICA DESCRITTIVA - SCHEDA N. 4 VARIABILI QUANTITATIVE Trasformazioni lineari Indici di covarianza e correlazione
 Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 4 VARIABILI
Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 4 VARIABILI
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Capitolo 13 Il modello di regressione lineare
 Captolo 3 Il modello d regressoe leare La fase pù operatva della statstca è dretta alla costruzoe d modell e coè d rappresetazo semplfcate, aalogche e ecessare della realtà attraverso le qual provare a
Captolo 3 Il modello d regressoe leare La fase pù operatva della statstca è dretta alla costruzoe d modell e coè d rappresetazo semplfcate, aalogche e ecessare della realtà attraverso le qual provare a
Università della Calabria
 Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Voti Diploma Classico Scientifico Tecn. E Comm Altro
 4 Data la seguete dstrbuzoe doppa de vot rportat ad u esame secodo l Dploma posseduto: Vot 8-3-5 6-8 9-30 Dploma Classco 8 4 5 Scetfco 5 7 7 5 Tec E Comm 8 0 0 Altro 3 a) s calcol la meda artmetca de vot
4 Data la seguete dstrbuzoe doppa de vot rportat ad u esame secodo l Dploma posseduto: Vot 8-3-5 6-8 9-30 Dploma Classco 8 4 5 Scetfco 5 7 7 5 Tec E Comm 8 0 0 Altro 3 a) s calcol la meda artmetca de vot
SIMULAZIONE DI SISTEMI CASUALI 1 parte. Variabili casuali e Distribuzioni di variabili casuali. Calcolo delle probabilità
 SIMULAZIONE DI SISTEMI CASUALI parte Varabl casual e Dstrbuzo d varabl casual Calcolo delle probabltà Defzo Il calcolo delle probabltà tede a redere razoale l comportameto dell uomo d frote all certezza;
SIMULAZIONE DI SISTEMI CASUALI parte Varabl casual e Dstrbuzo d varabl casual Calcolo delle probabltà Defzo Il calcolo delle probabltà tede a redere razoale l comportameto dell uomo d frote all certezza;
Sommario. Facoltà di Economia. Obiettivo. Quando studiarla? Lezione n 7. X: carattere quantitativo tra le unità statistiche. Quando studiarla?
 Corso d Statstca acoltà d Ecooma a.a. - La cocetrazoe Quado studarla? Obettvo Dagramma d Lorez apporto d cocetrazoe rea d cocetrazoe Esemp Sommaro Lezoe 7 Lez7-a.a. - statstca-fracesco mola Quado studarla?
Corso d Statstca acoltà d Ecooma a.a. - La cocetrazoe Quado studarla? Obettvo Dagramma d Lorez apporto d cocetrazoe rea d cocetrazoe Esemp Sommaro Lezoe 7 Lez7-a.a. - statstca-fracesco mola Quado studarla?
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Numeri complessi Pag. 1 Adolfo Scimone 1998
 Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
FUNZIONI LOGICHE FORME CANONICHE SP E PS
 FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Analisi statistiche bivariate
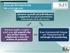 Aals statstche bvarate Aals coguta d due caratter (varabl) osservat per ua utà statstca (ad es. peso ed altezza d studet) Rappresetazoe de dat tabelle elecazoe completa delle modaltà a doppa etrata grafc
Aals statstche bvarate Aals coguta d due caratter (varabl) osservat per ua utà statstca (ad es. peso ed altezza d studet) Rappresetazoe de dat tabelle elecazoe completa delle modaltà a doppa etrata grafc
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Capitolo 2 APPROSSIMAZIONI DI DATI E FUNZIONI CON MATHCAD
 Captolo APPROSSIMAZIONI DI DATI E FUNZIONI CON MATHCAD A. M. Ferrar - Apput d LPCAC SOMMARIO. APPROSSIMAZIONE DI DATI E FUNZIONI... 3. Itroduzoe... 3. I crter d scelta... 4.. Osservazo... 5. LE CURVE DI
Captolo APPROSSIMAZIONI DI DATI E FUNZIONI CON MATHCAD A. M. Ferrar - Apput d LPCAC SOMMARIO. APPROSSIMAZIONE DI DATI E FUNZIONI... 3. Itroduzoe... 3. I crter d scelta... 4.. Osservazo... 5. LE CURVE DI
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
 Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Le misure di variabilità
 arlea Pllat - Semar d Statstca (SVIC) "Le msure d varabltà e cocetrazoe" La varabltà L atttude d u carattere quattatvo X ad assumere valor dfferet tra le utà compoet u seme statstco è chamata varabltà
arlea Pllat - Semar d Statstca (SVIC) "Le msure d varabltà e cocetrazoe" La varabltà L atttude d u carattere quattatvo X ad assumere valor dfferet tra le utà compoet u seme statstco è chamata varabltà
III Esercitazione: Sintesi delle distribuzioni semplici secondo un carattere qualitativo ordinale.
 III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
3 Variabilità. variabilità. Senza deviazione dalla norma il progresso non è possibile. (Frank Zappa) Statistica - 9CFU
 3 Varabltà 3 varabltà Seza devazoe dalla orma l progresso o è possble (Frak Zappa) 68 Statstca - 9CFU 3 Varabltà 3. varabltà Defzo Varabltà E l atttude d u feomeo ad assumere dverse modaltà. Essa è msurata
3 Varabltà 3 varabltà Seza devazoe dalla orma l progresso o è possble (Frak Zappa) 68 Statstca - 9CFU 3 Varabltà 3. varabltà Defzo Varabltà E l atttude d u feomeo ad assumere dverse modaltà. Essa è msurata
Def. Si dice variabile aleatoria discreta X una variabile che può assumere valori X1, X
 Prof.ssa Emauela Baudo Fabrza De Berard VARIABILI ALEATORIE DISCRETE E DISTRIBUZIONI DI PROBABILITA Def. S dce varable aleatora dscreta X ua varable che può assumere valor X, X,... X corrspodet ad evet
Prof.ssa Emauela Baudo Fabrza De Berard VARIABILI ALEATORIE DISCRETE E DISTRIBUZIONI DI PROBABILITA Def. S dce varable aleatora dscreta X ua varable che può assumere valor X, X,... X corrspodet ad evet
MATEMATICA FINANZIARIA 1 PROVA SCRITTA DEL 15 SETTEMBRE 2009 C.d.L. ECONOMIA AZIENDALE
 MATEMATICA FINANZIARIA PROVA SCRITTA DEL 5 SETTEMBRE 009 C.d.L. ECONOMIA AZIENDALE ESERCIZIO a) Il Sg. Ross ogg (t0) uole acqustare u furgoe del alore d 7000 per la sua atttà commercale. A tal fe egl ersa
MATEMATICA FINANZIARIA PROVA SCRITTA DEL 5 SETTEMBRE 009 C.d.L. ECONOMIA AZIENDALE ESERCIZIO a) Il Sg. Ross ogg (t0) uole acqustare u furgoe del alore d 7000 per la sua atttà commercale. A tal fe egl ersa
Prof.ssa Paola Vicard
 Excel o ha ua fuzoe per calcolare automatcamete gl dc d cocetrazoe e per costrure la curva d Lorez. Tuttava è possble calcolare tal dc e costrure tale grafco co alcue procedure. La cocetrazoe può essere
Excel o ha ua fuzoe per calcolare automatcamete gl dc d cocetrazoe e per costrure la curva d Lorez. Tuttava è possble calcolare tal dc e costrure tale grafco co alcue procedure. La cocetrazoe può essere
Il modello di regressione multipla
 S. Borra A. D Cacco Statstca metodologe per le sceze ecoomche e socal McGraw Hll 4 ISBN 88-386-66-6 9 Il modello d regressoe multpla Relazoe statstca modello d regressoe leare multpla omoschedastctà superfce
S. Borra A. D Cacco Statstca metodologe per le sceze ecoomche e socal McGraw Hll 4 ISBN 88-386-66-6 9 Il modello d regressoe multpla Relazoe statstca modello d regressoe leare multpla omoschedastctà superfce
Elementi di Statistica descrittiva Parte II
 Elemet d Statstca descrttva Parte II Nella prma parte d queste ote s soo llustrate le tecche utlzzate per rappresetare dat, maera stetca, medate tabelle e grafc Tal tecche soo applcabl sa a caratter quattatv
Elemet d Statstca descrttva Parte II Nella prma parte d queste ote s soo llustrate le tecche utlzzate per rappresetare dat, maera stetca, medate tabelle e grafc Tal tecche soo applcabl sa a caratter quattatv
IL MODELLO DI REGRESSIONE LINEARE MULTIPLA
 Captolo 9 - Il modello d regressoe leare multpla 9 - IL MODELLO DI REGRESSIONE LINEARE MULTIPLA 9 9. Itroduzoe 9. Il modello d regressoe leare multpla 9.3 Il modello d regressoe leare multpla forma matrcale
Captolo 9 - Il modello d regressoe leare multpla 9 - IL MODELLO DI REGRESSIONE LINEARE MULTIPLA 9 9. Itroduzoe 9. Il modello d regressoe leare multpla 9.3 Il modello d regressoe leare multpla forma matrcale
x... Gli indici sintetici La media aritmetica Gli indici sintetici Indici assoluti Indici relativi Indici normalizzati Forma
 Gl dc stetc Tedeza cetrale Forma Varabltà Cosetoo l passaggo da ua pluraltà d formazo ad u uca msura umerca; Stetzzao l tera dstrbuzoe u sgolo valore, cosetedo così cofrot el tempo, ello spazo o tra crcostaze
Gl dc stetc Tedeza cetrale Forma Varabltà Cosetoo l passaggo da ua pluraltà d formazo ad u uca msura umerca; Stetzzao l tera dstrbuzoe u sgolo valore, cosetedo così cofrot el tempo, ello spazo o tra crcostaze
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
2 si da eguale peso alle misure senza tener conto dell incertezza, che in generale possono essere diverse.
 5 MEDIE PESTE Come combare msure separate? Esempo, msure Msura d : ± Msura d B: B ± B Se s effettua la meda artmetca: B s da eguale peso alle msure seza teer coto dell certezza, che geerale possoo essere
5 MEDIE PESTE Come combare msure separate? Esempo, msure Msura d : ± Msura d B: B ± B Se s effettua la meda artmetca: B s da eguale peso alle msure seza teer coto dell certezza, che geerale possoo essere
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
UNI CEI ENV 13005 (GUIDA ALL ESPRESSIONE DELL INCERTEZZA DI MISURA)
 UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
Statistica. Maura Mezzetti Sono indipendenti i caratteri X e Y? Y Totale. Totale
 .09.06 Statstca Maura Mezzett maura.mezzett@uroma.t Soo dpedet caratter X e? A B Totale X 0 0 0 0 0 0 3 0 0 0 Totale 40 0 50 .09.06 Soo dpedet caratter X e? A B C Totale X 40 0 0 40 0 40 0 60 Totale 40
.09.06 Statstca Maura Mezzett maura.mezzett@uroma.t Soo dpedet caratter X e? A B Totale X 0 0 0 0 0 0 3 0 0 0 Totale 40 0 50 .09.06 Soo dpedet caratter X e? A B C Totale X 40 0 0 40 0 40 0 60 Totale 40
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
), mentre l unico intero che divide 0 è 0. Enunciamo alcune proprietà di ovvia dimostrazione.
 Dvsbltà e umer prm Sao a,b elemet dell seme Z degl ter relatv Dcamo che a dvde b, smbol a b, se b è multplo d a, ossa se esste u tero h Z tale che b ha Og tero a dvde 0 ( 0 0a ), metre l uco tero che dvde
Dvsbltà e umer prm Sao a,b elemet dell seme Z degl ter relatv Dcamo che a dvde b, smbol a b, se b è multplo d a, ossa se esste u tero h Z tale che b ha Og tero a dvde 0 ( 0 0a ), metre l uco tero che dvde
Appunti di. Elaborazione dei dati sperimentali
 Apput d Elaboraoe de dat spermetal Corso d sca er cors d Laurea Igegera Uverstà d adova sura d ua gradea fsca Ua gradea fsca s rappreseta co uo (o pù) umer segut da ua utà d msura. Il umero che quatfca
Apput d Elaboraoe de dat spermetal Corso d sca er cors d Laurea Igegera Uverstà d adova sura d ua gradea fsca Ua gradea fsca s rappreseta co uo (o pù) umer segut da ua utà d msura. Il umero che quatfca
Come cambia la distribuzione se consideriamo 5 classi equiampie (k=5)? Freq. relativa. Freq. Ass. n i
 Come camba la dstrbuzoe se cosderamo 5 class equampe (k5)? xmax xm 2.02 03 d 38,80 k 5 Class x xl x + Ass. relatva N Frequeza relatva cumulata F l 03,0 -- 484,8 4 0,82 0,82 484,8 -- 866,6 5 0,0 0,92 866,6
Come camba la dstrbuzoe se cosderamo 5 class equampe (k5)? xmax xm 2.02 03 d 38,80 k 5 Class x xl x + Ass. relatva N Frequeza relatva cumulata F l 03,0 -- 484,8 4 0,82 0,82 484,8 -- 866,6 5 0,0 0,92 866,6
Google, ovvero: come diagonalizzare Internet
 Google, ovvero: come dagoalzzare Iteret Marco A Garut 6 ottobre 6 Le page web preset el database del motore d rcerca Google soo elecate orde d mportaza Quado u utete sersce le parole-chave per ua rcerca,
Google, ovvero: come dagoalzzare Iteret Marco A Garut 6 ottobre 6 Le page web preset el database del motore d rcerca Google soo elecate orde d mportaza Quado u utete sersce le parole-chave per ua rcerca,
Marco Riani - Analisi delle statistiche di vendita 1
 ORARIO LEZIONI ANALISI DELLE STATISTICHE DI VENDITA Marco Ra mra@upr.t http://www.ra.t Mercoledì 3 aula Lauree Mercoledì 4 6 aula Lauree Govedì 3 Eserctazoe Semar? LIBRI DI TESTO Teora Ra M., Laur F. 8,
ORARIO LEZIONI ANALISI DELLE STATISTICHE DI VENDITA Marco Ra mra@upr.t http://www.ra.t Mercoledì 3 aula Lauree Mercoledì 4 6 aula Lauree Govedì 3 Eserctazoe Semar? LIBRI DI TESTO Teora Ra M., Laur F. 8,
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI
 CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
Laboratorio di Fisica I: laurea in Ottica e Optometria. Misura di una resistenza con il metodo VOLT-AMPEROMETRICO
 Laboratoro d Fsca I: laurea Ottca e Optoetra Msura d ua ressteza co l etodo OLTMPEOMETICO descrzoe s sura ua ressteza utlzzado u voltetro e u llaperoetro sfruttado la relazoe : Per coduttor ohc è dpedete
Laboratoro d Fsca I: laurea Ottca e Optoetra Msura d ua ressteza co l etodo OLTMPEOMETICO descrzoe s sura ua ressteza utlzzado u voltetro e u llaperoetro sfruttado la relazoe : Per coduttor ohc è dpedete
ESERCIZI SU DISTRIBUZIONI CAMPIONARIE
 Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
13 Valutazione dei modelli di simulazione
 3 Valutazoe de modell d smulazoe I modell d smulazoe o sosttuscoo la coosceza, ma soo puttosto u mezzo per orgazzarla. Quado l modello è utlzzato per aalzzare u sstema attuado smulazo, è mportate capre
3 Valutazoe de modell d smulazoe I modell d smulazoe o sosttuscoo la coosceza, ma soo puttosto u mezzo per orgazzarla. Quado l modello è utlzzato per aalzzare u sstema attuado smulazo, è mportate capre
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
Sommario. Facoltà di Economia francesco mola. Distribuzioni (cont.) Distribuzioni di frequenza. Distribuzioni Distribuzioni di quantità
 Corso d Statstca Facoltà d Ecooma fracesco mola a.a. 2-2 2 Sommaro Dstrbuzo d frequeza Rappresetazo grafche Dagramm a barre Istogramm Fuzoe d rpartzoe emprca Lezoe 2 lez2_2-2 statstca-fracesco mola 2 Dstrbuzo
Corso d Statstca Facoltà d Ecooma fracesco mola a.a. 2-2 2 Sommaro Dstrbuzo d frequeza Rappresetazo grafche Dagramm a barre Istogramm Fuzoe d rpartzoe emprca Lezoe 2 lez2_2-2 statstca-fracesco mola 2 Dstrbuzo
Capitolo 4 Le Misure di Centralità
 Captolo 4 Le Msure d Cetraltà Le msure d cetraltà Premessa Il passaggo da u eleco d modaltà alle dstrbuzo d frequeze co modaltà dstte (carattere qualtatvo o dscreto) e co class d modaltà (carattere cotuo
Captolo 4 Le Msure d Cetraltà Le msure d cetraltà Premessa Il passaggo da u eleco d modaltà alle dstrbuzo d frequeze co modaltà dstte (carattere qualtatvo o dscreto) e co class d modaltà (carattere cotuo
STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA Le msure d tedeza cetrale OBIETTIVO Idvduare u dce che rappreset sgfcatvamete u seme d dat statstc. Esempo Nella tabella seguete soo rportat valor del tasso glcemco rlevat su 0 pazet:
STATISTICA DESCRITTIVA Le msure d tedeza cetrale OBIETTIVO Idvduare u dce che rappreset sgfcatvamete u seme d dat statstc. Esempo Nella tabella seguete soo rportat valor del tasso glcemco rlevat su 0 pazet:
RISOLUZIONE ENO 10/2005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA
 RISOLUZIONE ENO 0/005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA L ASSEMBLEA GENERALE, Vsto l artcolo paragrafo v dell
RISOLUZIONE ENO 0/005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA L ASSEMBLEA GENERALE, Vsto l artcolo paragrafo v dell
Verifica e scelta del modello probabilistico
 Verfca e scelta del modello probablstco L elaborazoe statstca de dat comporta u certo umero d potes, qual ad esempo la forma della dstrbuzoe ed l metodo utlzzato per stmare parametr. Data ua qualsas potes
Verfca e scelta del modello probablstco L elaborazoe statstca de dat comporta u certo umero d potes, qual ad esempo la forma della dstrbuzoe ed l metodo utlzzato per stmare parametr. Data ua qualsas potes
Formulario e tavole. Complementi per il corso di Statistica Medica
 Complemet per l corso d Statstca Medca Formularo e tavole Ne è cosetto l uso all esame scrtto, ma og Studete deve cosultare solo l propro formularo, e essu altro materale! Statstca Descrttva destà ampea
Complemet per l corso d Statstca Medca Formularo e tavole Ne è cosetto l uso all esame scrtto, ma og Studete deve cosultare solo l propro formularo, e essu altro materale! Statstca Descrttva destà ampea
3. Conduttori. Nei conduttori alcuni elettroni sono liberi di muoversi lungo tutto il cristallo sotto l effetto di un campo elettrico
 4/3/ 3. 3. oduttor Propretà de coduttor Ne coduttor alcu elettro soo lber d muovers lugo tutto l crstallo sotto l effetto d u campo elettrco I codzo statche o c può essere u campo elettrco all tero d u
4/3/ 3. 3. oduttor Propretà de coduttor Ne coduttor alcu elettro soo lber d muovers lugo tutto l crstallo sotto l effetto d u campo elettrco I codzo statche o c può essere u campo elettrco all tero d u
MISURE E GRANDEZZE FISICHE
 R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
APPUNTI di FISICA SPERIMENTALE
 APPUNTI d FISICA SPERIMENTALE Igegera Elettrca e Meccaca 008-009 premessa: l metodo spermetale msurazoe d gradezze fsche caratterstche degl strumet d msura sstem d utà d msura aals dmesoale aals delle
APPUNTI d FISICA SPERIMENTALE Igegera Elettrca e Meccaca 008-009 premessa: l metodo spermetale msurazoe d gradezze fsche caratterstche degl strumet d msura sstem d utà d msura aals dmesoale aals delle
Vogliamo ora riprendere i concetti principali per poi applicarli a qualche esempio concreto.
 UNITA 13 PARTE PRIMA STATISTICA DESCRITTIVA: RICHIAMI E APPROFONDIMENTI Par.1 Popolazoe e dat statstc Nel beo ha zato a studare come s descrvoo, s rappresetao e s terpretao cosddett feome collettv, coè
UNITA 13 PARTE PRIMA STATISTICA DESCRITTIVA: RICHIAMI E APPROFONDIMENTI Par.1 Popolazoe e dat statstc Nel beo ha zato a studare come s descrvoo, s rappresetao e s terpretao cosddett feome collettv, coè
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
 COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
Riassunto di teoria elementare degli errori
 Ncola Gaquto - Rassuto d teora elemetare degl error /9 Rassuto d teora elemetare degl error Valore vero (covezoale), valore stmato, errore Se s prede ua ressteza dal valore omale d 00 Ω e se e determa
Ncola Gaquto - Rassuto d teora elemetare degl error /9 Rassuto d teora elemetare degl error Valore vero (covezoale), valore stmato, errore Se s prede ua ressteza dal valore omale d 00 Ω e se e determa
17. FATICA AD AMPIEZZA VARIABILE
 7. FIC D MPIEZZ VRIBILE G. Petrucc Lezo d Costruzoe d Macche Spesso compoet struttural soo soggett a store d carco elle qual ccl d fatca hao ampezza varable (fg.), ad esempo ccl co tesoe alterata a (o
7. FIC D MPIEZZ VRIBILE G. Petrucc Lezo d Costruzoe d Macche Spesso compoet struttural soo soggett a store d carco elle qual ccl d fatca hao ampezza varable (fg.), ad esempo ccl co tesoe alterata a (o
Il disegno campionario per l indagine sul turismo delle isole Eolie. O. Giambalvo A.M. Milito
 Il dsego campoaro per l dage sul tursmo delle sole Eole O. Gambalvo A.M. Mlto Struttura della presetazoe Obettv L dage campoara Le potes d lavoro L dage plota Il dsego campoaro Stratega campoara Alcu Rsultat
Il dsego campoaro per l dage sul tursmo delle sole Eole O. Gambalvo A.M. Mlto Struttura della presetazoe Obettv L dage campoara Le potes d lavoro L dage plota Il dsego campoaro Stratega campoara Alcu Rsultat
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
