Alberi. Cosa sono gli alberi? Strutture gerarchiche di ogni tipo. Corso di Informatica 2. Generale. Colonnello 1. Colonnello k
|
|
|
- Fabrizio Venturini
- 7 anni fa
- Visualizzazioni
Transcript
1 Alei Coso i Infomti 2 Cos sono gli lei? Stuttue gehihe i ogni tipo Genele Colonnello 1 Colonnello k Mggioe 1,1 Mggioe 1,m Cpitno Mggioe k,1 Mggioe k,n
2 Stuttue gehihe i ogni tipo Stuttue ti 1. Tipi i to e stuttue ti 1. Speifi e elizzzione 2. Rppesentzione in memoi 2. Liste 1. L ADT elle liste 2. Relizzzione on vettoi 3. Relizzzione on punttoi 3. Pile e oe 1. L ADT elle pile Definizioni Un leo èun gfo onnesso ilio; nel so finito può essee efinito inuttivmente ome un insieme tle he: è un leo; se k 0, T 1,, T k sono lei, v un vetie, llo {v, T 1,, T k è un leo Un insieme i lei è un foest. leo foest gfo ilio Stuttu inuttiv egli lei leo ie leo
3 Alei on ie e foglie L ie è un noo pivilegito i un leo; se l leo è un gfo non oientto qulunque noo può onsiesi ie; se l leo è oientto llo ue si: 1. l ie h solo hi in usit (leo sogente) 2. l ie h solo hi in entt (leo pozzo) Un fogli è un noo ui non ese lun o Alei sogente, lei pozzo sogente pozzo Pentele è pe i e è figlio i è ftello i e e f f è un isenente i ; è un vo i f
4 Cmmini Un mmino ll ie un fogli si ie mo Cmmino: sequenz i i hi isuno iniente sul sul vetie i i quello suessivo Livelli Livello: insieme i i vetii equiistnti ll ie L ltezz è l mssim istnz ll ie i un livello non vuoto Livello 0 Livello 1 Livello 2 Alei ointi Un Un leo è ointo quno lo lo sono (linemente) i i suoi livelli = Cont solo l oine, non sinist e est Come lei ointi simo ivesi
5 Alei k-i Aietà = mssimo num. ei ei figli i i qulhe noo Io sono un leo tenio Alei posizionli Un Un leo ointo è posizionle quno nell oine ei ei livelli si si tiene onto i i (si (si eve quini fisse l ietà) Un speifi Sintssi Tipi: Tee, Noe Opetoi: NewTee: voi Tee IsEmptyTee: Tee oolen InsAsRoot: Noe, Tee Tee Root: Tee Noe Pent: Noe, Tee Noe Lef: Noe, Tee oolen
6 Un speifi Sintssi Tipi: Tee, Noe Opetoi: Chil: Noe, Tee Noe HsSiling: Noe, Tee Boolen Siling: Noe, Tee Noe InsTee: Noe, Noe, Tee, Tee Tee DelTee: Noe, Tee Tee Semnti egli opetoi Con qulos si eve pu ominie InsAsRoot(, ) A os sevono queste nlità? InsAsRoot(n, T ) = T Pe: T = Post: T è l leo il ui unio noo è n Semnti egli opetoi T DelTee(, T ) DelTee(n, T ) = T Pe: n è un noo i T Post: T isult T eliminno il sottoleo on ie in n
7 Semnti egli opetoi z x v z T U x v InsTee(n, m, T, U ) = T InsTee(,, T, U ) Pe: m, n sono noi i T, U Post: T isult T inseeno U ome figlio i m e 1. ftello suessivo i n se n m 2. pimo figlio i m se n = m Semnti egli opetoi z x v z T U x v InsTee(n, m, T, U ) = T InsTee(,, T, U ) Pe: m, n sono noi i T, U Post: T isult T inseeno U ome figlio i m e 1. ftello suessivo i n se n m 2. pimo figlio i m se n = m Semnti egli opetoi Semnti NewTee () = (leo vuoto) Root(T) = l ie i T Pent (n, T) = m Pe: n T Post: m pe i n Chil (n, T) = m Pe: n T, Lef(n, T) = flse Post: m è il pimo figlio i n Siling (n, T) = m Pe: n T, HsSiling (n, T) = tue Post: m è il ftello suessivo i n IsEmptyTee(T) = tue se T =, flse lt. Lef(n, T) = Pe: n T, = tue sse n è un fogli HsSiling(n, T) = Pe: n T Post: = tue sse n h un ftello
8 Relizzzioni: vettoe ei pi e f Effiiente pe ppesente lei pozzo i inlità (numeo ei noi) fisst etihett el noo e 2 f 3 inie el pe inie el noo Alei ini: efinizione inuttiv L insieme egli lei ini etihettti in A, BT(A), è efinito inuttivmente: ) BT(A) (leo vuoto) ) A, l BT(A), BT(A) Si intoue l nozione i sottoleo sinisto e esto ConsTee(, l, ) BT(A) l Alei ini elizzti on punttoi info T left ight T
9 Coifi ini i lei k-i e f g e f g Nel so i lei non ointi l oifi non è univo! Relizzzioni: on punttoi pent info hil siling e f g e f g L inlità i un leo inio B Left(B) = l l Right(B) = Cinlità (B) if B = then etun 0 else etun 1 + Cinlità (Left(B)) + Cinlità (Right(B))
10 L ltezz i un leo inio Altezz (B) // Pe: B // Post: iton l ltezz i B etun Altezz_ux (B) Si us un funzione usilii pehé il so i se B = è essenzile ll iosione Altezz_ux (B) // Post: iton l ltezz i B, 0 se B = if B = then etun 0 else etun mx{altezz_ux(left(b), Altezz_ux(Right(B)) + 1 L iosione sugli lei ContFoglie (T) // Post: iton il numeo elle foglie i T if T = then etun 0 ue si i se else if T h un solo noo then etun 1 else sino T 1,, T k i sottolei on ii nei noi figli i ell ie i T k etun i = ContFoglie( T 1 i ) Questo pseuooie è lontno ll elizzzione L iosione sugli lei ContFoglie (T) // Post: iton il numeo elle foglie i T if IsEmptyTee(T) then etun 0 else etun Cf_ux(Root(T), T) Cf_ux (n, T) // Pe: n T // Post: iton il numeo elle foglie el sottoleo i T on ie in n
11 L iosione sugli lei Cf_ux (n, T) // Pe: n T // Post: iton il numeo elle foglie el sottoleo i T on ie in n if Lef(n, T) then etun 1 else // n h lmeno un figlio in T m Chil(n, T) foglie Cf_ux (m, T) while HsSiling (m, T) o m Siling (m, T) foglie foglie + Cf_ux (m, T) etun foglie Se m vev un ftello, llo l ttule vloe i m è un noo i T Visite: Depth Fist Seh DFS (T) // Post: visit i noi i T in pofonità if T then visit Root(T) sino T 1,, T k i sottolei on ii nei noi figli i ell ie i T fo i 1 to k o DFS (T i ) Visite: Depth Fist Seh DFS (T) // Post: visit i noi i T in pofonità if not IsEmtyTee(T ) then DFS_ux (Root(T), T) DFS_ux (n, T) // Post: visit in pofonità il sottoleo i T on ie in n
12 Visite: Depth Fist Seh DFS_ux (n, T) // Post: visit in pofonità il sottoleo i T on ie in n ominino ll ie visit n if not Lef (n, T) then m Chil (n, T) DFS_ux (m, T) while HsSiling (m, T) o m Siling(m, T) DFS_ux (m, T) Il tipo BinTee typeef stut tnoe { T info; // etihett stut tnoe *left, *ight; // punttoi i figli sinisto e esto tnoe; typeef stut inteefme { int ; // numeo ei noi ell leo tnoe* oot; // ie ell leo BinTeeFme typeef BinTeeFme* BinTee; Costuttoi tnoe* NewtNoe (T et, tnoe* l, tnoe* ) { tnoe* n = new tnoe; n->info = et; n->left = l; n->ight = ; etun n; BinTee NewBinTee (voi) { BinTee t = new BinTeeFme; t-> = 0; t->oot = NULL; etun t;
13 Un esempio: l funzione Altezz int Altezz (tnoe* n) // Pe: n!= NULL // Post: iton l ltezz ell leo on ie in n { etun Altezz_ux(n); int Altezz_ux (tnoe*) // Post: iton l ltezz i tnoe se!= NULL, 0 lt. { int hl = 0, h = 0; if (n->left == NULL && n->ight == NULL) etun 0; if (n->left!= NULL) hl = Altezz_ux (n->left); if (n->ight!= NULL) h = Altezz_ux (n->ight); if (hl > h) etun hl + 1; etun h + 1; Visite in pofonità voi peoe (tnoe* n) { if (n!= NULL) { visit(n); peoe(n->left); peoe(n->ight); voi inoe (tnoe* n) { if (n!= NULL) { inoe(n->left); visit(n); inoe(n->ight); L list ei vetii in peoine (1) l l
14 L list ei vetii in peoine (2) L soluzione ovvi è O(n 2 ): Noe* Peoe_List (tnoe* n) { if (n == NULL) etun NULL; etun NewNoe(n->info, ont (Peoe_List(n->left), Peoe_List(n->ight)); L omplessità quti eiv ll uso i ont nel so in ui l leo si egenee sinisto. L list ei vetii in peoine (3) Esiste un soluzione ottim O(n): Noe* Peoe_List2 (tnoe* n, Noe* l) { if (n == NULL) etun l; etun NewNoe(n->info, Peoe_List2(n->left, Peoe_List2(n->ight,l));
In generale i piani possono essere tra loro
 Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Alberi. ) è una sequenza ordinata, in cui a è l etichetta della radice, e
 Aleri Gli leri (finiti, ipotesi or in vnti sottintes) si possono veere ome un generlizzzione elle sequenze lineri (vettori o liste) nel senso he, mentre queste in ultime isun elemento possiee l più un
Aleri Gli leri (finiti, ipotesi or in vnti sottintes) si possono veere ome un generlizzzione elle sequenze lineri (vettori o liste) nel senso he, mentre queste in ultime isun elemento possiee l più un
ESERCIZI IN PIÙ ESERCIZI DI FINE CAPITOLO
 L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
Esercizi per il corso di Calcolatori Elettronici. svolti da Mauro IACOVIELLO & Fabio LAUDANI
 Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
Il problema da un milione di dollari
 Il prolem un milione i ollri SienzOrient: Informti Ginlu Rossi www.informti.unirom2.it (www.informti.unirom2.it) Prolem $ 000 000 / 9 Algoritmi Requisiti i un uon lgoritmo: Correttezz; Effiienz ovvero
Il prolem un milione i ollri SienzOrient: Informti Ginlu Rossi www.informti.unirom2.it (www.informti.unirom2.it) Prolem $ 000 000 / 9 Algoritmi Requisiti i un uon lgoritmo: Correttezz; Effiienz ovvero
Algebra Relazionale. Operazioni nel Modello Relazionale
 lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
La rappresentazione per elencazione consiste nell elencare tutte le coppie ordinate che verificano la relazione
 RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
Esercitazione n. 2. Gian Carlo Bondi VERO/FALSO
 Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
tan tan = angolo formato dalla normale p,q = lunghezze dei segmenti misurati a partire dall origine n = distanza della retta dall origine
 G. Di Mri Forulrio i geoetri nliti Forulrio i geoetri nliti G. Di Mri Rette For generle (ipliit) For riott (espliit) For norle 0 q For segentri os sin n 0 p q p,q = lunghezze ei segenti stti ll rett sugli
G. Di Mri Forulrio i geoetri nliti Forulrio i geoetri nliti G. Di Mri Rette For generle (ipliit) For riott (espliit) For norle 0 q For segentri os sin n 0 p q p,q = lunghezze ei segenti stti ll rett sugli
11. Geometria piana ( ) ( ) 1. Formule fondamentali. Rettangolo. A = b = h = = b h. b = base h = altezza. Quadrato
 11. Geometi pin 1. Fomule fonmentli Rettngolo = h = h = h p= + h p= + h h= p = p h + ( ) = h = h h = = se = igonle p = peimeto h = ltezz = e p = semipeimeto Quto = l l = = l l = l = lto = igonle = e p
11. Geometi pin 1. Fomule fonmentli Rettngolo = h = h = h p= + h p= + h h= p = p h + ( ) = h = h h = = se = igonle p = peimeto h = ltezz = e p = semipeimeto Quto = l l = = l l = l = lto = igonle = e p
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe terza. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
esercizi su controllo di accesso e sicurezza di sistema 2006-2008 maurizio pizzonia sicurezza dei sistemi informatici e delle reti
 eseizi su ontollo di esso e siuezz di sistem 2006-2008 muizio pizzoni siuezz dei sistemi infomtii e delle eti 1 ess mtix e onfidenzilità S={,,} O={f,f,} R={ed,ite} il modello è DAC o MAC? può sivee i file?
eseizi su ontollo di esso e siuezz di sistem 2006-2008 muizio pizzoni siuezz dei sistemi infomtii e delle eti 1 ess mtix e onfidenzilità S={,,} O={f,f,} R={ed,ite} il modello è DAC o MAC? può sivee i file?
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quinto appello, 3 luglio 2017 Testi 1
 nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
Il piano cartesiano e la retta
 Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Momento di una forza rispettto ad un punto
 Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Disequazioni di primo grado
 Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Elettronica dei Sistemi Digitali Disegno del layout di porte logiche combinatorie CMOS
 Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Organigramma Gerarchia. (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre
 Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
SOLUZIONE PROBLEMI Insegnamento di Fisica dell Atmosfera Seconda prova in itinere
 Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
Tecniche di Progettazione Digitale Progettazione e layout di porte logiche combinatorie CMOS p. 2
 Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Unità D1.2 Selezione e proiezione
 (A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
(A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
L Ω dell Ordinamento. Alberi N-ari completi. Confine inferriore alla complessità del problema dell ordinamento di sequenze lineari
 L Ω ell Orinamento Confine inferriore alla complessità el problema ell orinamento i sequenze lineari Alberi N-ari completi Un albero -ario è se se tutti i i noi interni hanno figli, e tutte le le foglie
L Ω ell Orinamento Confine inferriore alla complessità el problema ell orinamento i sequenze lineari Alberi N-ari completi Un albero -ario è se se tutti i i noi interni hanno figli, e tutte le le foglie
A.A.2009/10 Fisica 1 1
 Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
Le liste. ADT e strutture dati per la rappresentazione di sequenze. Ugo de' Liguoro - Algoritmi e Sperimentazioni 03/04 - Lez. 5
 Le liste ADT e strutture dati per la rappresentazione di sequenze L ADT delle liste Una lista di valori di tipo A è una sequenza finita: a1, a2, L, an dove ai A, per ogni i valore lunghezza posizione L
Le liste ADT e strutture dati per la rappresentazione di sequenze L ADT delle liste Una lista di valori di tipo A è una sequenza finita: a1, a2, L, an dove ai A, per ogni i valore lunghezza posizione L
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
capacità si può partire dalla sua definizione: C = e dalla relazione fra la differenza di potenziale ed il campo elettrico: V
 secizio (ll ppello 6/7/4) n conenstoe pino è costituito ue mtue qute i lto b septe un istnz. Il conenstoe viene completmente cicto ll tensione e poi scollegto ll bttei ust pe ciclo, così est isolto ll
secizio (ll ppello 6/7/4) n conenstoe pino è costituito ue mtue qute i lto b septe un istnz. Il conenstoe viene completmente cicto ll tensione e poi scollegto ll bttei ust pe ciclo, così est isolto ll
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Risoluzione dei sistemi di equazioni col metodo delle matrici
 Risoluzione ei sistemi i equzioni ol metoo elle mtrii Un sistem i n equzioni e n inonite può essere rppresentto ome mtrie formt i soli oeffiienti. Dto il sistem: x+ y+ z= x+ y+ z= x+ y+ z= L su mtrie srà:
Risoluzione ei sistemi i equzioni ol metoo elle mtrii Un sistem i n equzioni e n inonite può essere rppresentto ome mtrie formt i soli oeffiienti. Dto il sistem: x+ y+ z= x+ y+ z= x+ y+ z= L su mtrie srà:
Monomi e polinomi. Verifica per la classe prima COGNOME... NOME... Classe... Data...
 Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello dell 8 Febbraio 2005 Esercizio 1 (ASD) 1. Dire quale delle seguenti affermazioni è vera giustificando la risposta. (a) lg
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello dell 8 Febbraio 2005 Esercizio 1 (ASD) 1. Dire quale delle seguenti affermazioni è vera giustificando la risposta. (a) lg
Equazioni di primo grado
 Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
I vettori. Grandezze scalari e grandezze vettoriali
 I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
Indici con gli alberi
 Indici con gli alberi Alberi perfettamente bilanciati per indici su memorie di massa: B-alberi Indici su memorie secondarie Spesso i dati da ordinare sono in quantità tale da richiedere dispositivi di
Indici con gli alberi Alberi perfettamente bilanciati per indici su memorie di massa: B-alberi Indici su memorie secondarie Spesso i dati da ordinare sono in quantità tale da richiedere dispositivi di
Calcolo elettrico di linee con carichi distribuiti e diramati
 Ccoo eettico i inee con cichi istiuiti e imti /4 omenti mpeometici i consiei cut i tensione inustie i un ine in coente tent ung : V m ( ϕ senϕ) cos m m pe inee monofsi pe ineetifsi cut i tensione su un
Ccoo eettico i inee con cichi istiuiti e imti /4 omenti mpeometici i consiei cut i tensione inustie i un ine in coente tent ung : V m ( ϕ senϕ) cos m m pe inee monofsi pe ineetifsi cut i tensione su un
Algoritmi di Visita di Grafi. Damiano Macedonio mace@unive.it
 lgoritmi di Visita di rafi amiano Macedonio mace@unive.it Original work opyright lberto Montresor, Università di Trento, Italy Modifications opyright 00 0, Moreno Marzolla, Università di ologna, Italy
lgoritmi di Visita di rafi amiano Macedonio mace@unive.it Original work opyright lberto Montresor, Università di Trento, Italy Modifications opyright 00 0, Moreno Marzolla, Università di ologna, Italy
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
ALLEGATO TECNICO PER L USO DEL PROGRAMMA RICHIESTA DATI ALUNNI DISABILI
 1 ALLEGATO TECNICO PER L USO DEL PROGRAMMA RICHIESTA DATI ALUNNI DISABILI Il pr e s e n t e do c u m e n t o for ni s c e le info r m a z i o n i ne c e s s a r i e ed es s e n z i a l i a su p p o r t
1 ALLEGATO TECNICO PER L USO DEL PROGRAMMA RICHIESTA DATI ALUNNI DISABILI Il pr e s e n t e do c u m e n t o for ni s c e le info r m a z i o n i ne c e s s a r i e ed es s e n z i a l i a su p p o r t
Disequazioni di secondo grado
 Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Diffrazione & struttura
 Cimi fisi ei mterii Diffrzione & struttur Sergio Brutti Pini retiori prei Consierimo un generio pino retiore in un risto. Su te pino gie un motivo tomio (bse) regore e biimensione Te motivo srà ientio
Cimi fisi ei mterii Diffrzione & struttur Sergio Brutti Pini retiori prei Consierimo un generio pino retiore in un risto. Su te pino gie un motivo tomio (bse) regore e biimensione Te motivo srà ientio
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Heap Ordinamento e code di priorità. Ugo de' Liguoro - Algoritmi e Sperimentazioni 03/04 - Lez. 9
 Heap Ordinamento e code di priorità Heap: definizione Definizione. Uno Heap (binario) è un albero binario finito i cui vertici sono etichettati da elementi di un insieme linearmente ordinato (chiavi),
Heap Ordinamento e code di priorità Heap: definizione Definizione. Uno Heap (binario) è un albero binario finito i cui vertici sono etichettati da elementi di un insieme linearmente ordinato (chiavi),
Alberi ( GT. 7 ) In informatica, un albero è un modello astratto con cui viene rappresentata una struttura gerarchica
 Alberi ( GT. 7 ) Albero definizioni Albero ADT (Abstract Data Type) Algoritmi di base su alberi Alberi binari Strutture dati per rappresentare alberi Implementazione AlberoBinario 1 Alberi (GT. 7) In informatica,
Alberi ( GT. 7 ) Albero definizioni Albero ADT (Abstract Data Type) Algoritmi di base su alberi Alberi binari Strutture dati per rappresentare alberi Implementazione AlberoBinario 1 Alberi (GT. 7) In informatica,
Circonferenza e cerchio La circonferenza e il cerchio Poligoni inscritti e circoscritti a una circonferenza
 ironferenz e erhio L ironferenz e il erhio Poligoni insritti e irosritti un ironferenz L ironferenz e il erhio Stilisi se le seguenti ffermzioni sono vere o flse. SEZ. M e f g h Il rpporto tr l lunghezz
ironferenz e erhio L ironferenz e il erhio Poligoni insritti e irosritti un ironferenz L ironferenz e il erhio Stilisi se le seguenti ffermzioni sono vere o flse. SEZ. M e f g h Il rpporto tr l lunghezz
Informatica 3. Informatica 3. LEZIONE 14: Alberi binari: introduzione. Lezione 14 - Modulo 1. Definizioni. Introduzione. Definizioni e proprietà
 Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Le basi della geometria piana Punti, rette, piani Segmenti, angoli, rette parallele e perpendicolari
 Le si ell geometri pin Punti, rette, pini Segmenti, ngoli, rette prllele e perpeniolri SEZ. D Punti, rette, pini 1 Stilisi se le seguenti ffermzioni sono vere o flse. e f g Per un punto pssno infinite
Le si ell geometri pin Punti, rette, pini Segmenti, ngoli, rette prllele e perpeniolri SEZ. D Punti, rette, pini 1 Stilisi se le seguenti ffermzioni sono vere o flse. e f g Per un punto pssno infinite
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
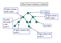 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Esercizi 5 Campo magnetico
 Esercizi 5 mpo mgnetico 1. Due lunghi fili rettilinei e prlleli, posti istnz, sono percorsi correnti uguli e opposte. lcolre il cmpo mgnetico nei punti equiistnti i fili. I θ I1 L sol componente che soprvvive
Esercizi 5 mpo mgnetico 1. Due lunghi fili rettilinei e prlleli, posti istnz, sono percorsi correnti uguli e opposte. lcolre il cmpo mgnetico nei punti equiistnti i fili. I θ I1 L sol componente che soprvvive
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Il lavoro è quindi una grandezza scalare le cui unita di misura sono: = Joule = J
 Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberto Montresor Università di Trento
 !! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
!! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
ALGORITMI E STRUTTURE DATI
 ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
Cinematica. Le equazioni del moto di A sono: v A = v 0 a A t ; s A = d + v 0 t ½ a A t 2
 Esercitzione n FISIC SPERIMENTLE I (C.L. In. Ei.) (Prof. Gbriele F).. / Cinemtic. Due uto e B iino con l stess elocità = 7 km/h su un str pin e rettiline, istnz l un ll ltr. un certo istnte t = il uitore
Esercitzione n FISIC SPERIMENTLE I (C.L. In. Ei.) (Prof. Gbriele F).. / Cinemtic. Due uto e B iino con l stess elocità = 7 km/h su un str pin e rettiline, istnz l un ll ltr. un certo istnte t = il uitore
Allegato 3 Elenco BAT ed esempio interventi efficientamento
 Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Verifica per la classe seconda COGNOME... NOME... Classe... Data...
 L rett Cpitolo Rett erifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt............................... Rett Rette
L rett Cpitolo Rett erifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt............................... Rett Rette
Ambiguità D 11 = SS ( S S S ( S (S ) S ( S ((S )) S ( + S (( )) S (S (( )) (S) (S (( )) ( ) ( (( )) ( )
 Amiguità D 11 = ( ( ( ) ( (( )) ( (( )) ( (( )) () ( (( )) ( ) ( (( )) ( )! ( ) ( )! Un Grmmti si die migu se medesime stringhe sono generte d leri sintttii di differente struttur ovvero on due distinte
Amiguità D 11 = ( ( ( ) ( (( )) ( (( )) ( (( )) () ( (( )) ( ) ( (( )) ( )! ( ) ( )! Un Grmmti si die migu se medesime stringhe sono generte d leri sintttii di differente struttur ovvero on due distinte
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
F (r(t)), d dt r(t) dt
 Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
LINEE GUIDA DELLE AUTORIZZAZIONI AL TRASPORTO RIFIUTI
 CASE STUDY LINEE GUIDA DELLE AUTORIZZAZIONI AL TRASPORTO RIFIUTI Soggetto Destinatario ella Domana i Autorizzazione: Sezione Regionale ell'alo Nazionale ei Gestori Amientali Categorie i isrizione per il
CASE STUDY LINEE GUIDA DELLE AUTORIZZAZIONI AL TRASPORTO RIFIUTI Soggetto Destinatario ella Domana i Autorizzazione: Sezione Regionale ell'alo Nazionale ei Gestori Amientali Categorie i isrizione per il
Lezione 9 Alberi binari di ricerca
 Lezione 9 Alberi binari di ricerca Rossano Venturini rossano.venturini@unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 1 Lista monodirezionale Scrivere
Lezione 9 Alberi binari di ricerca Rossano Venturini rossano.venturini@unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 1 Lista monodirezionale Scrivere
Cuscinetti assiali a rullini ed a rulli cilindrici
 Cuscinetti assiali a ullini e a ulli cilinici Cuscinetti assiali a ullini e a ulli cilinici Cuscinetti assiali a ullini e a ulli cilinici I cuscinetti assiali sono costituiti a una gabbia a ullini o a
Cuscinetti assiali a ullini e a ulli cilinici Cuscinetti assiali a ullini e a ulli cilinici Cuscinetti assiali a ullini e a ulli cilinici I cuscinetti assiali sono costituiti a una gabbia a ullini o a
! Una gerarchia ricorsiva deriva dalla presenza di una ricorsione o ciclo (un anello nel caso più semplice) nello schema operazionale.
 Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Geometria analitica +l piano cartesiano Le funzioni retta, parabola, iperbole Le trasformazioni sul piano cartesiano
 Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Algoritmi e Strutture Dati. Alberi
 Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Complessità algoritmi su strutture dati (riassunto)
 Complessità algoritmi su strutture dati (riassunto) Struttura di dato Algoritmo di ricerca Complessità (caso peggiore) applicabile Tavola come array non Ricerca sequenziale O(N) ordinato (N elementi) Tavola
Complessità algoritmi su strutture dati (riassunto) Struttura di dato Algoritmo di ricerca Complessità (caso peggiore) applicabile Tavola come array non Ricerca sequenziale O(N) ordinato (N elementi) Tavola
Appunti di Logica Ternaria: Operatori Monadici
 Appunti di Logi Ternri: Opertori Mondii Giuseppe Tlrio 11 Gennio 2014 Nell logi binri o Boolen il simbolo utilizzto è il Bit. Il numero di tutte le funzioni mondihe (di un simbolo binrio) è pri : 2 2 =4,
Appunti di Logi Ternri: Opertori Mondii Giuseppe Tlrio 11 Gennio 2014 Nell logi binri o Boolen il simbolo utilizzto è il Bit. Il numero di tutte le funzioni mondihe (di un simbolo binrio) è pri : 2 2 =4,
dizionari alberi bilanciati
 dizionari alberi bilanciati dizionari ADT che supportano le seguenti operazioni membership anche detta search insert delete o remove le liste e i BST sono dizionari maggio 2002 ASD2002 - Alberi bilanciati
dizionari alberi bilanciati dizionari ADT che supportano le seguenti operazioni membership anche detta search insert delete o remove le liste e i BST sono dizionari maggio 2002 ASD2002 - Alberi bilanciati
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
ALBERI : introduzione SOMMARIO ALBERI ALBERI. ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI
 SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
Esercizio su quadrati sovrapposti alternati: problema
 Esercizio su quadrati sovrapposti alternati: problema Riprodurre i disegni del tipo riportato in figura, in cui è possibile decidere il numero di quadrati da tracciare, il lato del quadrato più in basso
Esercizio su quadrati sovrapposti alternati: problema Riprodurre i disegni del tipo riportato in figura, in cui è possibile decidere il numero di quadrati da tracciare, il lato del quadrato più in basso
Implementazione ADT: Alberi
 Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Algoritmi e Strutture di Dati I 1. Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc
 Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc Algoritmi e Strutture di Dati I 2 Grafo Un grafo G è una coppia (V, E) ove V è un
Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc Algoritmi e Strutture di Dati I 2 Grafo Un grafo G è una coppia (V, E) ove V è un
Note su esperienza con il volano
 Note su espeienz con il olno 1 Cos è un olno? un mss più o meno "gnde" collegt solidlmente ll'lbeo motoe di un mcchin. A cos see un olno nelle mcchine? see d ccumule enegi cinetic nelle fsi di eccesso
Note su espeienz con il olno 1 Cos è un olno? un mss più o meno "gnde" collegt solidlmente ll'lbeo motoe di un mcchin. A cos see un olno nelle mcchine? see d ccumule enegi cinetic nelle fsi di eccesso
I PROBLEMI DI MASSIMO E DI MINIMO
 I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
! è l'insieme A degli attributi di ! $ B IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI IL PROBLEMA DELLE VISTE MATERIALIZZATE
 IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
Tav. E.007 ISTITUTO NAZIONALE DI FISICA NUCLEARE BARI. Quadro elettrico C.E.D. Schema unifilare
 ISTITUTO NZIONLE I FISI NULERE BRI LVORI I RISTRUTTURZIONE ELLE SLE S1, S, S5, S7 ed S9 EL IPRTIMENTO INTERTENEO I FISI ELL UNIVERSIT EGLI STUI I BRI PER L RELIZZZIONE ELL NUOV SL LOLO ELL SEZIONE I BRI
ISTITUTO NZIONLE I FISI NULERE BRI LVORI I RISTRUTTURZIONE ELLE SLE S1, S, S5, S7 ed S9 EL IPRTIMENTO INTERTENEO I FISI ELL UNIVERSIT EGLI STUI I BRI PER L RELIZZZIONE ELL NUOV SL LOLO ELL SEZIONE I BRI
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
d coulomb d volt b trasformatore d alternatore b amperometro d reostato
 ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
T R I BU N A L E D I T R E V IS O A Z I E N D A LE. Pr e me s so
 1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
Componenti per l elaborazione binaria dell informazione. Sommario. Sommario. Approfondimento del corso di reti logiche. M. Favalli.
 Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie
Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie
Problemi: dinamica. blocco M: blocco m: i due corpi hanno stressa accelerazione a!!! T + decimali e cifre significative!!
 Poblemi: inmic. Un blocco i mss M. k scoe su un supeicie oizzontle senz ttito. le blocco è leto meinte un une che pss ttveso un pulei un secono blocco i mss m. k. une e pulei sono pive i mss. Mente il
Poblemi: inmic. Un blocco i mss M. k scoe su un supeicie oizzontle senz ttito. le blocco è leto meinte un une che pss ttveso un pulei un secono blocco i mss m. k. une e pulei sono pive i mss. Mente il
Studio di una funzione razionale fratta (autore Carlo Elce)
 Stuio i funzioni Carlo Elce 1 Stuio i una funzione razionale fratta (autore Carlo Elce) Per rappresentare graficamente una funzione reale i una variabile reale bisogna seguire i seguenti passi: Passo 1)
Stuio i funzioni Carlo Elce 1 Stuio i una funzione razionale fratta (autore Carlo Elce) Per rappresentare graficamente una funzione reale i una variabile reale bisogna seguire i seguenti passi: Passo 1)
Il passo del gambero. La soluzione di problemi con la tecnica del Backtracking. Ugo de' Liguoro - Algoritmi e Sperimentazioni 03/04 - Lez.
 Il passo del gambero La soluzione di problemi con la tecnica del Backtracking Nel labirinto Nel labirinto In ogni posizione provo sistematicamente tutte le strade, ricordando ogni volta l ultima scelta
Il passo del gambero La soluzione di problemi con la tecnica del Backtracking Nel labirinto Nel labirinto In ogni posizione provo sistematicamente tutte le strade, ricordando ogni volta l ultima scelta
Capitolo 3. Modelli. Macchine combinatorie Macchine sequenziali asincrone sincrone
 Capitolo 3 Moelli Mahine ominatorie Mahine sequenziali asinrone sinrone Il moello el loo o satola nera i I: alfaeto i ingresso u U: alfaeto i usita ingresso ei ati i F u usita ei risultati F: relazione
Capitolo 3 Moelli Mahine ominatorie Mahine sequenziali asinrone sinrone Il moello el loo o satola nera i I: alfaeto i ingresso u U: alfaeto i usita ingresso ei ati i F u usita ei risultati F: relazione
B-Alberi Esercitazioni
 B-Alberi Esercitazioni Introduzione B-Trees: alberi bilanciati di ricerca progettati per essere memorizzati su dischi magnetici. Dischi magnetici molto più lenti delle memorie ad accesso casuale. La misura
B-Alberi Esercitazioni Introduzione B-Trees: alberi bilanciati di ricerca progettati per essere memorizzati su dischi magnetici. Dischi magnetici molto più lenti delle memorie ad accesso casuale. La misura
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Informatica 3. Informatica 3. LEZIONE 17: Alberi generici. Lezione 17 - Modulo 1. Introduzione. ADT dell albero generico.
 Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
B A N D O D I G A R A D A P P A L T O D I L A V O R I
 B A N D O D I G A R A D A P P A L T O D I L A V O R I S E Z I O N E I ) : A M M I N I ST R A Z I O N E A G G I U D I C A T R I C E I. 1 ) D e n o m i n a z i o ne, i n d ir i z z i e p u n t i d i c o
B A N D O D I G A R A D A P P A L T O D I L A V O R I S E Z I O N E I ) : A M M I N I ST R A Z I O N E A G G I U D I C A T R I C E I. 1 ) D e n o m i n a z i o ne, i n d ir i z z i e p u n t i d i c o
FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE
 FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE ALGEBRA LINEARE Operzioni tr mtrici Sino A = { ij } e B = {b ij } venti l stess imensione. L loro somm è l mtrice C i cui elementi sono {c ij
FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE ALGEBRA LINEARE Operzioni tr mtrici Sino A = { ij } e B = {b ij } venti l stess imensione. L loro somm è l mtrice C i cui elementi sono {c ij
Fisica II. 6 Esercitazioni
 Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
ADT Dizionario. Ordered search table. Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D:
 Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Esercizi II parte Esercizio 1 Discutere la correttezza di ciascuna delle seguenti affermazioni. Dimostrare formalmente la validità
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Esercizi II parte Esercizio 1 Discutere la correttezza di ciascuna delle seguenti affermazioni. Dimostrare formalmente la validità
INTERVENTO 1A - solaio di calpestio mezzanino (stanze 5 e 6)
 e-mail: ing.enrico@stuiomangoni.it INTERVENTO 1A - solaio i calpestio mezzanino (stanze 5 e 6) L intervento 1a consiste nella puntellatura con profili metallici el solaio i calpestio elle stanze 5 e 6.
e-mail: ing.enrico@stuiomangoni.it INTERVENTO 1A - solaio i calpestio mezzanino (stanze 5 e 6) L intervento 1a consiste nella puntellatura con profili metallici el solaio i calpestio elle stanze 5 e 6.
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
