Comunicazioni Radiomobili
|
|
|
- Martina Murgia
- 8 anni fa
- Visualizzazioni
Transcript
1 Università degli Studi di Siena Facoltà di Ingegneria Dipartimento di Ingegneria dell Informazione Comunicazioni Radiomobili Autore Abrardo Andrea Anno Accademico 2001/2002
2 Indice 1 Propagazione in ambiente radiomobile Attenuazioni deterministiche Attenuazioni aleatorie: shadowing Esercizio Attenuazioni aleatorie: Multipath fading Esercizio Fading selettivo in frequenza Esercizio Tecniche di trasmissione in presenza di fading non selettivo in frequenza Tecniche a diversità Esercizio Interleaving Esercizio Esercizio Sistemi Spread Spectrum Introduzione Sistemi Frequency Hopping Direct Sequence L interferenza nei sistemi radiomobili Introduzione Tecniche di accesso multiplo FDMA e TDMA Utilizzo delle tecniche SS per l accesso multiplo al canale Esercizio Esercizio Sistemi cellulari Introduzione Gestione delle risorse radio Esercizio Esercizio Cell Planning Esercizio Cell planning: modello statistico Esercizio Utilizzo di antenne direttive
3 Indice 6 Handover e mobilità Gestione della mobilità Hard Handover Esercizio Soft Handover Cell planning in sistemi DS-CDMA Il controllo di potenza Radio Link Budget Valutazione della capacità Esercizio ii
4 Capitolo 1 Propagazione in ambiente radiomobile 1.1 Attenuazioni deterministiche Nella trasmissione di segnali in ambiente radiomobile si ha a che fare con un antenna trasmittente che emette il segnale ed un antenna ricevente che lo riceve (Fig. 1.1). Qualora tale trasmissione avvenga nello spazio Figura 1.1 libero, la propagazione del segnale può essere efficacemente modellata dall equazione della tratta: G rx G tx P rx = P tx (4πR/λ) 2 (1-1) dove P tx, P rx, G tx, G rx, R, λ, sono rispettivamente la potenza trasmessa, la potenza ricevuta, il guadagno di antenna in trasmissione, il guadagno di antenna in ricezione, la distanza fra trasmettitore e ricevitore e la lunghezza d onda. Si definisce path-loss L p l attenuazione di potenza che è data in questo caso da: Se ci riferiamo al termine in (1-2) espresso in db 1, si ha: L p = (4πR/λ) 2 (1-2) L p = log 10 f + 20log 10 R. (1-3) dove f è la frequenza di trasmissione del segnale. Nella (1-3) si è tenuto conto della relazione che intercorre nello spazio libero: λf = c, essendo c la velocità della luce. 1 Adotteremo la convenzione di esprimere le quantità in db tramite una sopralineatura.
5 Capitolo 1. Propagazione in ambiente radiomobile La relazione (1-2), come detto, vale solo se la propagazione avviene nello spazio libero. Quando la propagazione avviene nell atmosfera terrestre, come nel caso dei sistemi radiomobili, tale relazione può essere ritenuta ancora valida in prima approssimazione solo se esiste un collegamento in vista fra trasmettitore e ricevitore. Nelle comunicazioni radiomobili terrestri questo non è quasi mai verificato. Infatti, a causa della presenza di ostacoli (colline, palazzi, alberi, etc.), il collegamento è spesso reso possibile soltanto attraverso riflessioni e diffrazioni da spigoli. Poiché in questo caso le condizioni di propagazione dipendono fortemente dal tipo di ambiente, risulta assai difficile trovare un equazione della tratta per i sistemi radiomobili. Se ad esempio consideriamo un ambiente urbano ed operiamo delle misure di path-loss ad una certa frequenza (ad esempio a 900 MHz), ci accorgiamo che il path-loss non dipende solo dalla distanza R ma risulta fortemente variabile nello spazio (fino ad oscillazioni di svariati db in pochi centimetri). Un metodo per studiare le condizioni di propagazione di un siffatto ambiente potrebbe essere quello di affidarsi a delle mappe geografiche (GIS, ovvero Geographical Information Systems) molto dettagliate del territorio con una risoluzione dell ordine di una frazione di lunghezza d onda 2, ottenute tramite campagne di misura. Effettuare delle campagne di misura con questo livello di dettaglio risulterebbe tuttavia praticamente impossibile. La soluzione è quella di affidarsi a dei modelli deterministici per caratterizzare il path-loss ad un livello di dettaglio grossolano (svariate lunghezze d onda) lasciando la caratterizzazione del livello di dettaglio più fine a modelli statistici. Sulla base di campagne di misura effettuate su vari ambienti (urbano, collinare, rurale) si è infatti visto che considerando un livello di dettaglio dell ordine dei 100 m (ad una frequenza di 900 MHz) si ottengono mappe in cui il path-loss dipende spazialmente soltanto dalla distanza R fra ricevitore e trasmettitore. Ovviamente, per ottenere questo risultato occorre che le misure di path-loss prese a intervalli di 100 m l una dall altra siano ottenute mediando su molte misure effettuate a distanze molto minori di 100 m. Il path-loss macroscopico, indicato per comodità semplicemente path-loss L p, è dato in generale da: L p = C 1 + C 2 log 10 f + C 3 log 10 R. (1-4) L p in (1-4) viene anche detto path-loss deterministico in quanto i parametri da cui dipende sono tutte grandezze deterministiche. In particolare, C 1, C 2, e C 3 sono costanti che dipendono strettamente dell ambiente di propagazione. A titolo di esempio si riporta la seguente tabella ottenuta per quattro tipologie di ambiente cellulare terrestre. Spazio libero Urbano Collinare Rurale C C C Tabella 1. I valori in Tabella possono essere considerati come valori di riferimento per la progettazione di sistemi cellulari qualora non siano disponibili mappe macroscopiche del territorio. Si può notare come, negli ambienti considerati, l attenuazione tenda a crescere più rapidamente con R e con f rispetto al caso dello spazio libero. Spesso interessa per il dimensionamento delle celle l andamento di L p con R. In accordo con la Tabella 1, si ha che la potenza decresce con R α, con α = 3.5. Questo vuol dire, per esempio, che la potenza misurata a distanza 2R risulta essere circa 11 volte inferiore alla potenza misurata a distanza R. 1.2 Attenuazioni aleatorie: shadowing La Tabella 1 consente di caratterizzare le condizioni di propagazione a livello macroscopico. Consideriamo ora ciò che accade in un intorno del ricevitore. Anche se l attenuazione media valutata in una zona di dimensioni elevate assume un certo valore fissato, a causa della presenza di ostacoli nelle vicinanze del ricevitore (o del 2 Alla frequenza di 900 MHz la lunghezza d onda vale 33 cm. 2
6 Capitolo 1. Propagazione in ambiente radiomobile trasmettitore) si possono avere forti variazioni in pochi metri delle condizioni di propagazione (si veda Fig. 1.2). Figura 1.2 In questo caso possiamo scrivere: N P rx = P tx L p + G tx + G tx + Γ n (1-5) i=1 dove Γ n rappresentano i guadagni espressi in db dovuti alla presenza o meno di ostacoli. Assumendo che tali contributi possano essere con eguale probabilità maggiori (guadagni) o minori (attenuazioni) di zero e che il loro numero sia molto elevato, il termine N L s = Γ n (1-6) i=1 denominato shadowing, può essere modellato come una variabile aleatoria Gaussiana a valor medio nullo e varianza σs. 2 In questo caso si ha: { } F s (x) = P rob. L s x = 1 [ 1 + erf 2 ( x 2σs )] f s (x) = df s(x) dx = 1 e x 2πσ 2 s 2 2σ 2 s (1-7) dove f s (x) e F s (x) sono rispettivamente la funzione densità di probabilità e la funzione distribuzione cumulativa di L s, mentre erf è la funzione errore definita come: erf(x) = 2 π x 0 e y2 dy (1-8) Per dare un idea dell effetto dello shadowing sulla propagazione del segnale e della sua differenza con l attenuazione di path-loss precedentemente definita, si faccia riferimento alla Fig. 1.3, dove viene riportato un 3
7 Capitolo 1. Propagazione in ambiente radiomobile Figura 1.3 tipico andamento dell attenuazione complessiva L p + L s per un ricevitore che si allontana dal trasmettitore (in ascisse viene riportata la distanza R fra tx e rx). Ovviamente lo shadowing sarà caratterizzato da una certa correlazione spaziale. Se infatti le dimensioni degli ostacoli sono molto grosse, ci si aspetta che la variazione dell attenuazione aleatoria dovuta allo shadowing sia trascurabile per piccoli spostamenti (shadowing molto correlato). Viceversa, quando gli ostacoli hanno piccole dimensioni si hanno grosse variazioni dello shadowing anche per piccoli spostamenti (shadowing poco correlato). Per caratterizzare matematicamente il comportamento spaziale dello shadowing si fa spesso riferimento al seguente modello molto semplice di correlazione: [ ] R Ls = E L s (x 1 )L s (x 2 ) = σs 2 R 1,2 D ɛd (1-9) dove L s (x 1 ) e L s (x 2 ) sono i valori dello shadowing in due punti dello spazio x 1 e x 2, D è la dimensione media degli ostacoli, R 1,2 rappresenta la distanza fra i punti x 1 e x 2, ɛ D rappresenta il coefficiente di correlazione a distanza D mentre E rappresenta l operatore di media statistica Esercizio Consideriamo uno shadowing caratterizzato da σ 2 s = 100, D = 100, ɛ D = 0.5. Supponiamo che tale shadowing in un certo punto dello spazio valga -20 db (L s (x 1 ) = -20). Valutare la probabilità che il valore dello shadowing a distanze R 1,2 = 10 m, R 1,2 = 100 m, e R 1,2 = 1000 m sia minore di -10 db. Per caratterizzare il comportamento congiunto di due variabili Gaussiane correlate a valor medio nullo (nel nostro caso L s (x 1 ) e L s (x 2 )) si può ricorrere al modello: L s (x 2 ) = ρl s (x 1 ) + n (1-10) dove ρ è il coefficiente di correlazione fra le due variabili aleatorie e n è una variabile aleatoria Gaussiana indipendente da L s con valor medio nullo e varianza σ 2 n. I termini ρ e σ 2 n possono essere valutati nel nostro caso dalle seguenti relazioni: [ ] E L s (x 2 )L s (x 1 ) = ρσs 2 = σs 2 R 1,2 D ɛd R 1,2 D ρ = ɛd { [ ] } 2 ( σs 2 = E L s (x 2 ) = ρ 2 σs 2 + σn 2 σn 2 = 1 ρ 2) σs 2 (1-11) 4
8 Capitolo 1. Propagazione in ambiente radiomobile Quindi, nel nostro caso si ha direttamente dalle (1-10) e (1-11): L s (x 2 ) = R 1, n (1-12) [ ( σn 2 = R 1,2 100 ) 2 ] Quindi valutare la probabilità che L s (x 2 ) sia minore di -10 db equivale a valutare la probabilità: { } { P rob. L s (x 2 ) < 10 = P rob. n < R 1,2 100 } = erf R1, σn (1-13) { } Nel nostro esempio si ha per R 1,2 = 10 m, R 1,2 = 100 m, e R 1,2 = 1000m, P rob. L s (x 2 ) < 10 = 0.992, 0.5, Attenuazioni aleatorie: Multipath fading Oltre allo shadowing esiste un altro fenomeno che comporta oscillazioni nella potenza ricevuta. Tale fenomeno è denominato multipath fading ed è dovuto al fatto che, a causa di fenomeni di riflessioni e diffrazioni, al ricevitore arrivano in genere una grande quantità di repliche dello stesso segnale trasmesso ciascuna ritardata ed attenuata in maniera indipendente dalle altre (si veda Fig. 1.4). Denominiamo con x(t) il segnale Figura 1.4 trasmesso. Il segnale ricevuto y(t) in presenza di fenomeni di multipath fading sarà dato da 3 y(t) = N 1 n=0 α n x(t τ n ) (1-14) 3 Nella rappresentazione del segnale ricevuto si trascura il rumore additivo bianco e Gaussiano per semplicità di trattazione. 5
9 Capitolo 1. Propagazione in ambiente radiomobile dove α n e τ n sono rispettivamente l attenuazione ed il ritardo del cammino n simo [ e N è il numero di cammini. Se rappresentiamo x(t) tramite il suo inviluppo complesso, cioè x(t) = Re x(t)e j2πf 0t ]4, si ottiene ovvero y(t) = Re ỹ(t) = [ N 1 n=0 N 1 n=0 α n x(t τ n )e j2πf 0τ n ] e j2πf 0t (1-15) α n x(t τ n )e j2πf 0τ n (1-16) Facciamo ora l ipotesi che il segnale trasmesso rimanga grossomodo costante in un intervallo di tempo pari alla massima dispersione temporale τ N τ 1. In questo caso x(t τ 1 ) = x(t τ 2 ),..., = x(t τ N ) ovvero ỹ(t) N 1 N 1 = x(t) α n e j2πf 0τ n = x(t) α n [cos(ϕ n ) jsin(ϕ n )] = (X + jy ) x(t) (1-17) n=0 n=0 dove ϕ n = 2πf 0 τ n. A causa dei valori molto elevati di frequenza che si considerano nelle applicazioni radiomobili (prossimi o addirittura superiori al GHz), anche i cammini che arrivano con differenze di ritardo molto piccole sono comunque sfasati in maniera del tutto indipendente fra loro. In altri termini, gli sfasamenti ϕ n possono essere modellati come variabili aleatorie indipendenti fra loro e uniformemente distribuite fra 0 e 2π. Ovviamente, data l imprevedibilità dei fenomeni coinvolti nel multipath fading, anche le attenuazioni α n possono essere considerate come variabili aleatorie indipendenti fra loro. Se in particolare le consideriamo come variabili aleatorie caratterizzate dalla stessa varianza e assumiamo N molto grande, il teorema del limite centrale consente di modellare il guadagno complesso X + jy come una variabile aleatoria Gaussiana, ovvero X e Y possono essere considerate variabili aleatorie Gaussiane indipendenti a valor medio nullo e con la stessa varianza. In questo caso, il modulo del segnale ricevuto diventa: ỹ(t) = A x(t) (1-18) dove A = X 2 + Y 2 è una variabile aleatoria distribuita secondo Rayleigh 5. Poiché la potenza di un segnale è proporzionale al modulo quadro del suo inviluppo complesso, dalla (1-18) possiamo scrivere: P rx = A 2 P tx. (1-19) Nel caso in cui A sia distribuita secondo Rayleigh, Ω = A 2 è distribuita in maniera esponenziale, ovvero F Ω (x) = P rob. {Ω x} = 1 e f Ω (x) = df Ω(x) dx = 1 E(Ω) e x E(Ω) x E(Ω) (1-20) dove E(Ω) è il valor medio del guadagno di canale che, tenendo conto delle perdite dovute a path-loss e shadowing, può essere espresso come: E(Ω) = G txg rx L p L s. (1-21) Tenendo conto della (1-21), la (1-19) può essere riscritta come: P rx = G f G tx G rx L p L s P tx (1-22) 4 f 0 è la frequenza di trasmissione che vale ad esempio circa 900 MHz nel sistema GSM. 5 Per questo motivo il modello di multipath fading esposto viene spesso indicato come fading di tipo Rayleigh. 6
10 Capitolo 1. Propagazione in ambiente radiomobile dove G f, definito guadagno di fading, è una variabile aleatoria a valor medio unitario (distribuita in maniera esponenziale nel caso Rayleigh). Osservando la (1-21) risulta evidente come il valor medio della potenza ricevuta debba essere in realtà considerato una variabile aleatoria a causa della presenza dello shadowing. Tuttavia, se consideriamo l attenuazione del segnale dovuta a path-loss e shadowing, questa può essere considerata costante su un area spaziale in cui lo shadowing risulta molto correlato (il raggio dell area è molto minore di D). All interno di tale area l attenuazione è soggetta a delle oscillazioni ulteriori distribuite in maniera esponenziale (nel caso in cui il fading sia di tipo Rayleigh). Il multipath fading comporta variazioni della potenza molto più repentine rispetto allo shadowing. Questo è dovuto al fatto che, spostandosi spazialmente di una certa distanza d, le varie repliche del segnale d vengono sfasate di una quantità che può assumere un qualsiasi valore aleatorio nell intervallo ±2πf 0 c. Basteranno allora spostamenti dell ordine di una frazione di lunghezza d onda (λ = c f 0 ) per variare in maniera consistente le fasi delle varie repliche, ovvero per scorrelare completamente il fading. Quindi, mentre le distanze di correlazione dello shadowing sono dell ordine delle decine di metri (grandezze degli ostacoli), quelle del fading sono dell ordine dei centimetri (frazioni di lunghezza d onda). A titolo di esempio, in Fig. 1.5 si riporta l esempio di Fig. 1.3 nel caso in cui si consideri anche l attenuazione dovuta a multipath ( fading. Con L f si è indicata l attenuazione dovuta al fading espressa in db, ovvero L f = 10log 1 10 G f ). Oltre alla correlazione spaziale, un altro parametro molto importante che caratterizza il fading è il tempo di correlazione t, che può essere definito come il tempo necessario affinché il fading si decorreli. Tale parametro dipende dalla distanza di decorrelazione d e dalla velocità v del mezzo mobile secondo la relazione: t = d v = λ v (1-23) dove si è considerato come distanza di decorrelazione la lunghezza d onda. frequenza Doppler f D = f 0 v/c, la (1-23) può essere riscritta come: Introducendo il parametro t = 1 f D (1-24) Figura 1.5 7
11 Capitolo 1. Propagazione in ambiente radiomobile Esercizio Consideriamo un collegamento uplink (da mobile a stazione radio base). Un problema spesso da affrontare è quello di stabilire la regione di copertura, ovvero la massima lontananza alla quale può trovarsi il mobile senza pregiudicare la qualità del collegamento. Questo problema viene detto radio link budget in uplink. I parametri noti in un problema del genere sono: P tx,max : massima potenza che il mobile può trasmettere G tx, G rx : Guadagni delle antenne L c1, L c2 : Perdite di potenza nel collegamento trasm. antenna e antenna ricevitore N 0 : Densità spettrale di potenza media di rumore al ricevitore F R : Figura di rumore del ricevitore W : Banda del segnale R : Bit rate utilizzato γ b,s : Rapporto E b /N 0 fra Energia per bit e densità spettrale di potenza media di rumore richiesto (come minimo) per garantire il collegamento P o,s : Probabilità di disservizio accettata, ovvero massimo valore della percentuale di tempo in cui il collegamento non è garantito Modello di path-loss (Tabella 1) o alternativamente mappa geografica del path-loss Modello di shadowing e fading Frequenza f 0 in cui avviene la trasmissione Supponiamo in un primo tempo di trascurare i fenomeni aleatori (shadowing e fading) e di avere i seguenti dati: P tx,max = W G tx = 0, G rx = 18 L c1 = L c2 = 2 N 0 = 204 (N 0 = KT, con K = , T = 290) F R = 5 W = 200 khz R = 270 kbit/s γ b,s = 10 P o,s = 0.01 Path-loss secondo modello urbano (Tabella 1) f 0 = 900 MHz (GSM) 8
12 Capitolo 1. Propagazione in ambiente radiomobile La prima cosa da fare è valutare la massima effettiva potenza trasmessa EIRP (Effective Isotropically Radiated Power): EIRP = P tx,max + G tx L c1 = (1-25) Adesso valutiamo la potenza di rumore in ingresso al ricevitore: P n = N 0 + W = 151. (1-26) Dal vincolo su E b /N 0, ricaviamo ora un vincolo sul rapporto segnale rumore minimo SNR o,min in uscita dal ricevitore di antenna: In ingresso al ricevitore di antenna sarà richiesto: SNR o,min = γ b,s R W = 13.5 SNR o,min = (1-27) SNR i,min = SNR o,min + F R = (1-28) Dato che il rapporto segnale rumore in (1-28) rappresenta la minima differenza fra la potenza di segnale e quella di rumore in ingresso al ricevitore di antenna, si ha che la potenza di segnale minima richiesta sarà: La massima potenza effettivamente ricevuta sarà: P rx,ric = P n + SNR i,min = (1-29) P rx,max = EIRP + G rx L c2 L p = 4.97 L p. (1-30) Affinché il collegamento sia garantito occorre che P rx,max > P rx,ric, ovvero L p < L p,max = (1-31) Si noti che in questo caso, avendo trascurato shadowing e fading, l attenuazione sul segnale risulta essere una variabile deterministica. Per cui la qualità del collegamento o è soddisfatta sempre (P o,s = 1) oppure mai (P o,s = 0). Il primo caso avviene quando è soddisfatta la (1-31). Considerando il modello di path-loss alla frequenza di 900 MHz per canale urbano si ha: Per cui dalla (1-31) si ricava la massima distanza R max : L p = log 10 (R) (1-32) log 10 (R max ) = 3.51 R max = 3235m (1-33) Assumiamo ora che vi sia un fading di tipo Rayleigh. In questo caso nell equazione della tratta compare l attenuazione di fading L f e la (1-31) va riscritta come L p + L f < (1-34) Il vincolo sulla probabilità di disservizio impone che la condizione (1-34) venga soddisfatta con probabilità 0.99, ovvero: } P rob. {G f > L p = (1-35) Chiamiamo con Γ la quantità Γ = L p. La (1-35) può essere riscritta come: P rob. {G f x 0 = 0.01} (1-36) dove x 0 = 10 Γ 10 9
13 Capitolo 1. Propagazione in ambiente radiomobile Come visto in precedenza nel caso di modello di Rayleigh la variabile G f può essere modellata come una variabile aleatoria distribuita in maniera esponenziale con valor medio 1. Allora la (1-36) può essere riscritta come: 1 e x 0 = 0.01 x 0 = 0.01 (1-37) e quindi ovvero Γ = 20 L p = (1-38) Ovviamente la (1-38) rappresenta il massimo path-loss ammissibile affinché la probabilità di disservizio rimanga al di sotto della soglia stabilita La massima distanza R max si ottiene ora semplicemente sostituendo nella (1-32) il valore di L p valutato in (1-38), cioè: log 10 (R max ) = 2.93 R max = 868m (1-39) Se dovessimo considerare oltre al fading anche lo shadowing il ragionamento sarebbe analogo salvo il fatto che nella (1-34) dovremmo considerare { L f + L s } in luogo di L f. Per risolvere il problema occorrerebbe avere a disposizione la funzione P rob. L f + L s < x che non è agevole da ricavare. Tuttavia, spesso il fading può essere combattuto efficacemente con opportune tecniche trasmissive che saranno oggetto del prossimo capitolo. Viceversa, lo shadowing non può essere combattuto con la stessa facilità per cui rimane di fatto il fenomeno che limita le prestazioni del ricevitore o, in questo caso, il raggio di copertura. Risolviamo allora ancora una volta l esercizio precedente assumendo di poter trascurare il fading e considerando uno shadowing caratterizzato da una σ s = 6. Il problema si può ovviamente formulare come { } P rob. L p + L s < = 0.99 (1-40) Il primo passo è trovare x 0 tale che F S (x 0 ) = 1 2 [ ( )] x0 1 + erf = 0.99 (1-41) 2σs Il termine x 0 in questo caso può essere denominato come margine di shadowing in quanto si tratta del margine di potenza che occorre imporre affinché la qualità del collegamento sia garantita con probabilità P o,s. Per valutare x 0 si fa riferimento alla curva di F S (x 0 ) riportata in Fig. 1.6 per diversi valori di σ s. Nel nostro caso (σ s = 6) si ottiene x 0 = 14. Dalla (1-40) si ricava ora direttamente: L p,max = = (1-42) E ora immediato derivare dalla (1-32) la massima distanza R max = 1289m. 1.4 Fading selettivo in frequenza Nel precedente paragrafo abbiamo visto che il multipath fading produce un attenuazione supplementare aleatoria sul segnale trasmesso. Tuttavia, il modello di disturbo moltiplicativo ricavato in (1-17) è valido solo nell ipotesi che il segnale trasmesso rimanga grossomodo costante in un intervallo di tempo pari alla massima dispersione temporale τ N τ 1. Vediamo adesso di rimuovere questa ipotesi. Consideriamo un caso semplice di multipath a due soli cammini con α 1 = α 2 = α: ỹ(t) = α x(t τ 1 )e j2πf 0τ 1 + α x(t τ 2 )e j2πf 0τ 2 (1-43) 10
14 Capitolo 1. Propagazione in ambiente radiomobile F S (x 0 ) σ s = 6 σ s = σ s = σ s = x 0 Figura 1.6 Il sistema canale è ovviamente un sistema lineare caratterizzato in questo caso dalla risposta impulsiva: h(t) = αδ(t τ 1 )e j2πf 0τ 1 + αδ(t τ 2 )e j2πf 0τ 2. (1-44) La risposta in frequenza equivalente passa basso del canale è data da: H(f) = αe j2π(f+f 0)τ 1 + αe j2π(f+f 0)τ 2 = 2αe jπ(f+f 0)(τ 1 +τ 2 ) cos [π(f + f 0 )(τ 1 τ 2 )]. (1-45) Il suo modulo normalizzato a 2α risulta quindi: H(f) = cos [π(f + f 0 )(τ 1 τ 2 )]. (1-46) In Fig. 1.7 viene riportato l andamento del modulo della risposta in frequenza per diversi valori della fase ϕ 0 = πf 0 (τ 1 τ 2 ). Si noti che, dato l alto valore di f 0 e l intrinseca natura aleatoria dei ritardi τ 1 e τ 2, il termine ϕ 0 va considerato come una variabile aleatoria uniformemente distribuita fra 0 e 2π. Quindi il comportamento in frequenza del sistema canale è anch esso aleatorio, nel senso che certe frequenze possono essere più o meno attenuate con una certa probabilità. Una caratteristica tipica del sistema canale non è tanto quindi la sua risposta in frequenza, quanto la correlazione della risposta in frequenza: R H ( f) = E[H(f+ f)h(f) ] = 4α 2 e jπ f(τ 1+τ 2 ) E {cos [π(f + f)(τ 1 τ 2 ) + ϕ 0 ] cos [πf(τ 1 τ 2 ) + ϕ 0 ]}. (1-47) Dalla (1-47), assumendo ϕ 0 uniformemente distribuito fra 0 e π, è facile ricavare: R H ( f) = 2α 2 e jπ f(τ 1+τ 2 ) cos [π f(τ 1 τ 2 )]. (1-48) La funzione di autocorrelazione in frequenza R H fornisce una misura di quanto il fading tenda a scorrelarsi in 1 frequenza. Nell esempio considerato, due frequenze che distano fra loro per una f molto minore di τ 1 τ 2 vengono trattate dal canale allo stesso modo (o entrambe attenuate o entrambre amplificate). Viceversa, 1 due frequenze che distano per una f dell ordine di τ 1 τ 2, o maggiore, vengono trattate in maniera del tutto indipendente. Si definisce banda di coerenza W l intervallo di frequenze entro il quale il canale rimane molto correlato. Tale termine viene generalmente posto uguale all inverso del delay spread σ, termine che indica a sua volta la dispersione temporale della risposta impulsiva (nel nostro esempio σ = 0.5 τ 1 τ 2 ). 11
15 Capitolo 1. Propagazione in ambiente radiomobile 1.5 H(f) f 0 (τ 1 τ2)=2kπ+π/4 f 0 (τ 1 τ2)=2kπ f 0 (τ 1 τ2)=2kπ+3π/4 f 0 (τ 1 τ2)=2kπ+π/ f(τ 1 τ 2 ) Figura 1.7 Nel caso in cui la banda del segnale trasmesso sia molto minore di W, il sistema si può considerare non selettivo in frequenza. In questo caso, si ha: ỹ(t) ) = H(0) x(t) = (αe j2πf 0τ 1 + αe j2πf 0τ 2 x(t) (1-49) ovvero si ritorna al caso di fading moltiplicativo analizzato nel paragrafo precedente. Se invece la banda del segnale è comparabile, o addirittura superiore a W, il sistema si dice selettivo in frequenza e il modello di fading moltiplicativo non è più adatto a descriverne il comportamento. In questo caso infatti il segnale trasmesso oltre ad essere eventualmente attenuato viene anche filtrato, ovvero distorto, dal canale. La distorsione del segnale viene generalmente combattuta al ricevitore tramite l utilizzo di filtri equalizzatori che comportano un notevole incremento della complessità del ricevitore. Diamo ora una caratterizzazione della banda di coerenza W nel caso generale. Dall espressione (1-16), si ricava l espressione generale della risposta impulsiva: h(t) = N 1 n=0 α n δ(t τ n )e j2πf 0τ n = N 1 n=0 Ψ n δ(t τ n ) (1-50) dove Ψ n = α n e j2πf 0τ n. Facciamo l assunzione che i ritardi τ n siano multipli di un tempo T c, cioè τ n = nt c. Allora: h(t) = N 1 n=0 Ψ n δ(t nt c ) (1-51) ovvero h(t) può essere vista come il campionamento, con passo di campionamento T c, del processo Ψ(t). Si noti che affinché la rappresentazione (1-51) abbia valore occorre che il passo di campionamento T c sia minore della metà della banda del processo Ψ(t). Dalla definizione di trasformata di Fourier di processi campionati si ha: H(f) = N 1 n=0 Ψ n e j2πfntc. (1-52) I termini Ψ n sono in generale modellabili come variabili aleatorie complesse scorrelate a valor medio nullo (Gaussiane nel caso di canale Rayleigh): E [Ψ nψ n+m ] = { 0 se m 0 A n altrimenti (1-53) 12
16 Capitolo 1. Propagazione in ambiente radiomobile dove la funzione discreta A n rappresenta la distribuzione temporale di energia delle repliche del segnale che arrivano con ritardi nt c e viene comunemente detta multipath intensity profile. Il modello di multipath intensity profile scorrelato (1-53) viene detto uncorrelated scattering. Calcoliamo ora la funzione di autocorrelazione in frequenza: R H (f) = E [H(f + f)h (f)] = Sfruttando la proprietà (1-53) è facile ricavare: N N n 1 =1 n 2 =1 R H ( f) = E [H(f + f)h (f)] = E [ Ψ n1 Ψ n 2 ] e j2π(f+ f)n 1 T c e j2πfn 2T c. (1-54) N 1 n=0 A n e j2π fntc. (1-55) La banda di coerenza è quindi data dalla larghezza di banda di R H (f), che corrisponde alla trasformata di Fourier del multipath intensity profile A n. Spesso si fa riferimento ad un multipath intensity profile esponenziale A n = e ntc σ, dove σ = LT c viene detto delay spread e rappresenta il ritardo temporale al quale la potenza del multipath è diminuita di un fatore 1/e. In questo caso si ha W = 1/σ Esercizio Determinare il valore massimo del bit rate di una segnale trasmesso con una modulazione BPSK su un canale radiomobile caratterizzato da σ = 3µs affinché il sistema non sia selettivo in frequenza (ovvero il segnale non venga distorto). Nel caso di modulazione BPSK si ha che la banda del segnale B è circa uguale al bit rate 6. Allora, occorre che il bit rate risulti minore della banda di coerenza W = 1/σ = 333 kbit/s. Se la trasmissione avvenisse in ambiente collinare (σ = 10µs), allora il massimo bit rate sarebbe 100 kbit/s (da questo semplice esercizio si intuisce come nel caso del GSM, dove il bit rate è pari a 270 kbit/s, il segnale può risultare fortemente distorto dal canale nel caso di trasmissione in ambiente collinare). 6 Nel caso invece di modulazione QPSK la banda è circa la metà del bit rate 13
17 Capitolo 2 Tecniche di trasmissione in presenza di fading non selettivo in frequenza 2.1 Tecniche a diversità Assumiamo che il canale sia non selettivo in frequenza. In questo caso l equazione della tratta può essere scritta come: P rx = G f G tx G rx L p L s P tx (2-1) dove G f è il guadagno (aleatorio) dovuto al fading. Come abbiamo visto il termine G f può comportare notevoli oscillazioni sul segnale ricevuto che a loro volta comportano un notevole deterioramento delle prestazioni del sistema (ad esempio nell esercizio si passa da una massima copertura di 3 km ad una di 800 m). Un modo per limitare gli effetti del fading è quello di utilizzare tecniche a diversità. Il concetto che sta alla base dei sistemi a diversità è quello di replicare per un numero di volte L la trasmissione del segnale su L canali indipendenti. Con la dizione canali indipendenti si intende il fatto che i canali sui quali si effettuano le trasmissioni multiple sono affetti da fading indipendenti. Abbiamo visto, ad esempio, che il fading tende a scorrelarsi temporalmente per effetto Doppler con un tempo di decorrelazione t = 1/f D. Quindi se si trasmettono due repliche dello stesso segnale a distanza temporale T > t l uno dall altra, i due segnali sono ricevuti con fading indipendenti. Si parla in questo caso di diversità nel tempo. Un altro modo per ottenere diversità è quello di trasmettere le repliche dello stesso segnale a frequenze diverse che distino fra loro più della banda di coerenza W (diversità in frequenza). Alternativamente possiamo ottenere la diversità semplicemente utilizzando più antenne in ricezione spaziate fra di loro per una distanza maggiore della distanza di decorrelazione d = λ (diversità di antenna). In qualunque modo venga realizzata la diversità, l effetto è quello di avere in ricezioni L segnali dati da (si veda (1-17)): ( ỹ (k) (t) = X (k) + jy (k)) x(t) per k = 1,..., L (2-2) dove X (k) + jy (k) sono i termini di rumore moltiplicativo (fading) introdotti nel canale k simo che per quanto detto possono essere considerati indipendenti fra loro. Il problema del ricevitore è a questo punto quello di ricombinare in qualche modo le repliche dello stesso segnale ricevute per ricostruire la sequenza informativa (bit) trasmessa. Il modo più semplice di effettuare tale ricombinazione è quello di selezionare fra tutti i segnali ricevuti solo quello caratterizzato da una potenza maggiore ed effettuare la demodulazione/decodifica solo su quel segnale. Tale tecnica di ricombinazione, detta selection diversity, è molto semplice da realizzare ma non è ottima, nel senso che non sfrutta al meglio le informazioni provenienti dai vari canali. Una tecnica alternativa è quella di effettuare una somma pesata dei vari contributi ricevuti dai vari canali dove i pesi sono scelti in maniera tale da pesare di più i segnali a maggiore potenza e meno gli altri. Nel caso in cui tali pesi siano direttamente proporzionali alle attenuazioni sperimentate nel canale si ottiene come risultato la massimizzazione del rapporto segnale rumore al ricevitore digitale; per questo motivo tale
18 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza tecnica viene detta maximal ratio combining. In questo caso la potenza ricevuta utile è pari alla somma delle potenze su tutti i canali. Nei due casi sopracitati si ottiene a valle della ricombinazione dei segnali ricevuti: per il caso Selection Diversity (SD), e P rx = max k P rx = L k=1 [ G (k) f G (k) f ] G tx G rx P (k) tx L p L s (2-3) G tx G rx P (k) tx (2-4) L p L s per il caso Maximal Ratio Combining (MRC), dove G (k) f e P (k) tx rappresentano rispettivamente il guadagno aleatorio dovuto al fading sul canale k simo e la potenza trasmessa sullo stesso canale. Si noti che nelle (2-4)(2-3) si è implicitamente assunto che i termini di shadowing e di path-loss (L s e L p ) siano gli stessi sugli L canali sui quali vengono trasmesse le repliche del segnale. Questo significa che tali termini sono molto correlati sugli L canali in questione. Tale assunzione è lecita in quanto lo shadowing, e a maggior ragione il path-loss, hanno tempi/distanze/frequenze di decorrelazione assai superiori al fading. Per valutare i benefici del sistema a diversità occorre considerare due casi distinti: a) La diversità è ottenuta trasmettendo più repliche dello stesso segnale su L canali (diversità in trasmissione). In questo caso P (k) tx = P tx/l. P (k) tx b) La diversità è ottenuta utilizzando più ricevitori in ricezione (diversità in ricezione). In questo caso = P tx. Consideriamo nel seguito per semplicità solo il caso MRC 1. Nel caso a) si ha: P rx = L k=1 G (k) f L G txg rx L p L s P tx (2-5) ovvero il sistema è equivalente ad un sistema senza diversità in cui il termine totale di fading è dato da: G f,t = L k=1 G (k) f L. (2-6) Quindi il fading è dato ora dalla somma di variabili aleatorie indipendenti ciascuna con media 1/L. Per capire l effetto che questo ha sulle prestazioni del sistema facciamo riferimento al caso di modello di fading di tipo Rayleigh in cui i termini G (k) f sono variabili aleatorie distribuite in maniera esponenziale. Si consideri a questo proposito la Fig. 2.1 dove viene riportato l andamento della funzione cumulativa di probabilità: F Gf,t (x) = P rob. {G f,t x} (2-7) per diversi valori di L. Si nota subito che l effetto della diversità è quello di diminuire la dispersione della variabile fading intorno al suo valor medio, ovvero di diminuirne la varianza. Questo comporta un miglioramento delle prestazioni del sistema. Si noti che tali benefici sono stati ottenuti grazie all indipendenza statistica delle variabili G (k) f. Se infatti consideriamo il caso limite in cui tali variabili sono tutte uguali (correlazione 1), è immediato verificare che le curve in Fig. 2.1 rimangono tutte uguali al variare di L, ovvero trasmettere su più canali non comporta nessun vantaggio. Si noti infine che nel caso in cui i canali siano indipendenti e andando al limite L, si ottiene una curva di probabilità che è esattamente un gradino, ovvero vale zero per x 0 < 1 mentre vale 1 altrove. In questo caso il sistema funziona come se il fading non ci fosse. 1 Il caso SD può essere trattato allo stesso modo semplicemente sostituendo la sommatoria con l operatore max. 15
19 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza F Gf,t (x) L = 1 L = L = log 10 (x) Figura 2.1 Analizzando il caso della diversità in ricezione è immediato verificare che oltre al guadagno di diversità c è un guadagno supplementare pari a 10log 10 L. Infatti, in questo caso l equazione della tratta radio può essere scritta come: Esercizio P rx = L k=1 G (k) f L LG txg rx L p L s P tx (2-8) Si consideri ancora l esercizio Si è visto nella (1-37) che nel caso di L = 1 la variabile fading sta sopra il livello x 0 = 0.01 nel 99% dei casi, da cui si ricava che la presenza del fading richiede un attenuazione minore di 20 db rispetto al caso senza fading (si ha cioè un margine di fading pari a 20 db). Considerando i casi L = 3 e L = 5 si valuti il margine di fading nel caso in cui si utilizzino tecniche di ricombinazione SD e MRD. Per quanto riguarda il caso MRD, si deriva dalla Fig. 2.1 per L = 3 x = 8 db mentre per L = 5 si ha x = 6, ovvero il margine di fading è nei due casi rispettivamente 8 e 6 db. Considerando ora il caso SD bisogna ricavare la distribuzione di probabilità di: G f,t = max k [ G (k) f 1 L ]. (2-9) Si tratta di trovare la distribuzione di probabilià del massimo di variabili aleatorie esponenziali indipendenti, ciascuna con valor medio 1/L. Si può facilmente ricavare: F Gf,t (x) = P rob. {G f,t x} = (1 e xl) L (2-10) Invertendo la (2-10) per F Gf,t (x) = 0.01 si ricava in questo caso rispettivamente per L = 3 e L = 5 x = db e x = 9.93 db, ovvero i margini di fading sono rispettivamente e 9.93 db. 2.2 Interleaving Come abbiamo visto il multipath fading comporta brusche oscillazioni della potenza del segnale ricevuto. Per limitare l effetto negativo di tali oscillazioni, un approccio alternativo a quello delle tecniche a diversità è quello di utilizzare tecniche di interleaving temporale. 16
20 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza Il problema delle oscillazioni causate dal fading consiste nel fatto che, nonostante la rapidità con la quale variano le condizioni del multipath, la presenza di una forte attenuazione sul segnale può protrarsi anche per moltissimi bit. Se ad esempio consideriamo un mezzo mobile che si sposta con velocità v = 10 m/s, ad una frequenza di 900 MHz, si ha t = 1/f D = 40 = 30 ms. Questo vuol dire che gli eventi cosiddetti di deep fading, ovvero gli eventi in cui il fading comporta pesanti attenuazioni della potenza ricevuta, hanno una durata di svariati ms. Durante questo tempo i bit ricevuti saranno sbagliati con elevata probabilità. Se consideriamo ad esempio un deep fading di durata T B = 10 ms ed una velocità trasmissiva di 270 kbit/s, si hanno sequenze di 2700 bit in cui la probabilità di errore è molto elevata. Denominiamo con L B la lunghezza dei periodi di deep fading, detta anche lunghezza del burst di errori 2. Se indichiamo ora con 0 l evento bit giusto e con 1 quello bit sbagliato, in ricezione si ottengono lunghissime sequenze di 0 intervallate da sequenze di 0 e di 1 della durata grossomodo pari a 2700 bit (Si veda Fig. 2.2 (a)). Durante Figura 2.2 un burst di errori, è molto probabile che il decodificatore di canale non riesca a fare bene il suo lavoro (la probabilità di errore è troppo elevata), ovvero che tutti i bit ricevuti in quell intervallo siano persi. L utilizzo di tecniche a diversità comporterebbe una diminuzione delle oscillazioni e quindi diminuirebbe la probabilità di avere burst errori molto lunghi. Un altra soluzione potrebbe essere quella di spalmare gli errori su tempi molto più lunghi di L B (Fig. 2.2 (b)). Mentre nel primo caso per un tempo L B i bit vengono tutti persi (errori a burst), nel secondo caso basterà utilizzare un decodificatore opportuno per poter correggere gli errori (errori isolati). Nell esempio mostrato in Fig. 9, si è assunto che durante il burst la probabilità di errore sia P e =0.3, troppo elevata per qualsiasi codificatore di complessità ragionevole. Nel caso in cui si riesca a spalmare il burst di errori su un tempo pari a 10 L B si ottiene una probabilià di errore pari a 0.03, senz altro compatibile con le prestazioni di un decodificatore di medie prestazioni Esercizio Consideriamo un segnale trasmesso con codifica di Hamming (7,4). Si assuma di avere due stati in ricezione: good, in cui la probabilità di errore per bit lorda (prima della decodifica) vale P e,g = 0.003, e bad in cui la probabilità di errore per bit lorda vale P e,b = 0.3. Si assuma che lo stato bad duri per un tempo pari al 5% dello stato good. Si valuti: La probabilità per bit lorda P e prima della decodifca La probabilità per bit netta P b dopo la decodifica 2 Se indichiamo con R b il bit rate di trasmissione, si ha L B = T B R b. 17
21 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza La probabilità per bit netta assumendo la probabilità per bit lorda valutata nel primo punto Per quanto riguarda il primo punto si ha molto semplicemente: P e = P e,g P e,b 0.05 = (2-11) Per quanto riguarda il secondo punto, occorre tenere presente che i codici di Hamming hanno la capacità di correggere 1 errore. Questo vuol dire che la probabilità P g di non commettere errori sulla parola di codice lunga 7 bit può essere calcolata come: ( ) 1 7 P g = (1 P k e ) 7 k Pe k = (1 P e ) 7 + 7(1 P e ) 6 P e. (2-12) k=0 Se il codice riesce a correggere gli errori la probabilità residua risulta P b = 0, altrimenti P b = 0.5. Perciò, la probabilità residua può essere calcolata come: P b = 0.5(1 P g ). (2-13) Allora si ha dalle (2-12) e (2-13), P b = 0.33 nel caso bad e P b = nel caso good, ovvero: P b = = (2-14) Per il calcolo del terzo punto richiesto si può ricorrere direttamente alle equazioni (2-13) e (2-12) considerando P e = Si ottiene in questo caso P b = Dall esercizio precedente si può notare come la presenza di uno stato bad caratterizzato da probabilità per bit molto elevate rende praticamente inefficace la protezione effettuata del codice. Nel caso invece in cui la probabilità d errore per bit sia uniforme (terzo punto), il codice riesce a migliorare notevolmente le prestazioni. Le tecniche di interleaving si propongono proprio lo scopo di rendere uniforme la probabilità di errore per bit in presenza di canali che introducono errori a burst. Lo scopo suddetto viene raggiunto utilizzando delle matrici m l, dette matrici di interleaving, sia in trasmissione (a monte del codificatore di canale) che in ricezione (a valle del decodificatore di canale). In trasmissione i bit da trasmettere vengono fatti passare nella matrice riempiendo quest ultima per righe. Quindi vengono mandati al trasmettitore leggendo la matrice per colonne. In ricezione avviene l operazione opposta, ovvero i bit ricevuti riempiono la matrice per colonne. La matrice viene poi riletta per righe ottenendo infine i bit da mandare in ingresso al decodificatore (si veda Fig. 2.3). Utilizzando una matrice Figura 2.3 di interleaving come quella mostrata in Fig. 2.3, si ottiene per effetto della ricombinazione in ricezione che m bit consecutivi vengono perfettamente sparpagliati su tutta la lunghezza della matrice di interleaving m l. Allora, se la lunghezza di un burst di errori L B risulta essere minore o uguale a m, il numero di bit 18
22 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza consecutivi soggetti a deep fading risulterà minore o uguale a m. In questo caso l interleaving riesce a isolare gli errori ottenendo una probabilità d errore perfettamente uniforme su tutti gli m l bit. Chiaramente se L B > m questo non è più vero. Si può facilmente ricavare ad esempio che nel caso in cui L B = hm, con h intero maggiore di 1, si ottengono in ricezione dei burst di errori di lunghezza residua L B,res = h. In altri termini, l interleaving riesce a diminuire la lunghezza dei burst di errori di un fattore m (numero di righe della matrice). Per ricavare il numero di righe di una matrice di interleaving occorre dunque conoscere il massimo L B,res sopportabile, ovvero la lunghezza del burst di errori residua che si può accettare affinché il decodificatore possa correttamente effettuare il suo lavoro. Se ad esempio abbiamo a che fare con un codice che corregge fino ad un massimo di t bit, occorre progettare la matrice di interleaving in modo tale che nelle parole di codice vi possano essere al massimo t bit appartenenti ad un burst di errori. In questo caso L B,res = t, ovvero m = L B /t. Per quanto riguarda il parametro l, ovvero il numero di colonne della matrice di interleaving, occorre tener presente che esso deve essere almeno uguale al numero di bit di una parola di codice. Il disegno di Fig. 2.4 chiarisce il motivo di questo requisito. Se infatti assumiamo che il burst di errori sia lungo hm, e che la parola di codice sia lunga 2l, si ottiene su ogni parola di codice in ingresso al decodificatore un numero di bit appartenenti al burst di errori pari a 2h, ovvero il doppio di quello che ci si sarebbe aspettati. Per avere quindi un effettiva diminuzione della lunghezza del burst di errori di un fattore m occorre che la parola di codice sia di lunghezza n l. Figura 2.4 Spesso il numero di colonne della matrice di interleaving viene preso esattamente uguale al minimo valore che soddisfa la condizione suddetta, ovvero l = n. Questo perché le dimensioni della matrice di interleaving D = m l sono un parametro critico che deve essere mantenuto il più piccolo possibile. Infatti, D rappresenta il numero di bit che occorre ricevere prima di iniziare la decodifica, ovvero il ritardo (espresso in bit) introdotto dall interleaving. In molte applicazioni (quali ad esempio la trasmissione della voce), tale ritardo non può superare un valore prefissato per non deteriorare la qualità della comunicazione. I codici di Hamming considerati precedentemente, che riescono a correggere un solo bit, non sono adatti a correggere errori a burst. In alternativa possono essere utilizzati codici capaci di correggere più di un errore. Una classe di codici di questo tipo è rappresentata dai codici BCH. Essi sono codici (n, k) capaci di correggere t errori; i valori possibili di n, k e t sono riportati in Fig
23 Capitolo 2. Tecniche di trasmissione in presenza di fading non selettivo in frequenza n k t n k t n k t Figura 2.5 Valori di n, k e t per i codici BCH Per fare un esempio si faccia riferimento ad un caso in cui la lunghezza del burst di errori residuo sia L B,res = 10. In questo caso, per essere sicuri che il decodificatore lavori correttamente, occorre utilizzare un codice capace di correggere fino ad un massimo di 10 bit. Considerando codici BCH, questo significa considerare ad esempio un codice (63, 18), caratterizzato da una bassissima efficienza (k/n = 0.28). In alternativa potremmo utilizzare un codice (511, 421) caratterizzato da un efficienza elevata (k/n = 0.82) ma al tempo stesso da un elevata complessità realizzativa (k elevato). Una classe di codici molto efficiente nel trattare errori a burst è quella dei codici Reed Solomon. I codici Reed Solomon lavorano su blocchi di bit di lunghezza p, con p intero maggiore o uguale a 3, e non su bit singoli. Un codice di Reed Solomon (n, k), con n = 2 p 1, è caratterizzato dall avere parole di codice lunghe n p bit dei quali k p bit costituiscono i bit informativi. Tali codici hanno la capacità di correggere fino ad un massimo di t blocchi di p bit, con t = n k 2. Una classe di codici Reed Solomon molto comune è quella in cui p è una potenza del 2, ed in particolare p = 8. In questo caso, per correggere ad esempio fino ad un massimo di 16 errori (t = 2), è sufficiente utilizzare un codice Reed Solomon (255, 251), che risulta di complessità compatibile con le capacità di calcolo dei moderni processori Esercizio Supponiamo di inviare dati con un bit rate al lordo della codifica pari a R b = 10 kbit/s su un canale radiomobile caratterizzato da un tempo di coerenza t = 10 ms. Progettare la matrice di interleaving ed il codice di canale tenendo conto che il massimo ritardo introdotto dall interleaving sia pari a 100 ms e assumendo di utilizzare un codice Reed Solomon caratterizzato da p = 4. Dalle specifiche sul massimo ritardo si trova m l R b = 100 ms, ovvero m l = 1000 bit. Inoltre, dal valore del tempo di coerenza t, si può ricavare la lunghezza del burst L B = t R b = 100 bit. Infine, imponendo un numero di colonne della matrice di interleaving pari alla lunghezza delle parole di codice, si ha l = n = 4(2 4 1) =
Università di Napoli Parthenope Facoltà di Ingegneria
 Università di Napoli Parthenope Facoltà di Ingegneria Corso di rasmissione Numerica docente: Prof. Vito Pascazio 18 a Lezione: 13/1/4 19 a Lezione: 14/1/4 Sommario rasmissione di segnali PM numerici su
Università di Napoli Parthenope Facoltà di Ingegneria Corso di rasmissione Numerica docente: Prof. Vito Pascazio 18 a Lezione: 13/1/4 19 a Lezione: 14/1/4 Sommario rasmissione di segnali PM numerici su
v in v out x c1 (t) Molt. di N.L. H(f) n
 Comunicazioni elettriche A - Prof. Giulio Colavolpe Compito n. 3 3.1 Lo schema di Fig. 1 è un modulatore FM (a banda larga). L oscillatore che genera la portante per il modulatore FM e per la conversione
Comunicazioni elettriche A - Prof. Giulio Colavolpe Compito n. 3 3.1 Lo schema di Fig. 1 è un modulatore FM (a banda larga). L oscillatore che genera la portante per il modulatore FM e per la conversione
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Lezione 28 Maggio I Parte
 Lezione 28 Maggio I Parte La volta scorsa abbiamo fatto un analisi dei fenomeni di diafonia e avevamo trovato che per la diafonia vicina il valore medio del quadrato del segnale indotto dalla diafonia
Lezione 28 Maggio I Parte La volta scorsa abbiamo fatto un analisi dei fenomeni di diafonia e avevamo trovato che per la diafonia vicina il valore medio del quadrato del segnale indotto dalla diafonia
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Il Campionameto dei segnali e la loro rappresentazione. 1 e prende il nome frequenza di
 Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08. Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2007-08 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/2005
 COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/005 1. Gli esercizi devono essere risolti su fogli separati: uno per la prima parte del compito (esercizi 1/4), uno per la seconda parte (esercizi
COMUNICAZIONI ELETTRICHE + TRASMISSIONE NUMERICA COMPITO 13/7/005 1. Gli esercizi devono essere risolti su fogli separati: uno per la prima parte del compito (esercizi 1/4), uno per la seconda parte (esercizi
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005
 Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Corso di Laurea in Ingegneria Biomedica Corso di Trasmissione Numerica (6 crediti) Prova scritta 16.02.2006
 Prova scritta 16.02.2006 D. 1 Si derivi l espressione dei legami ingresso-uscita, nel dominio del tempo per le funzioni di correlazione nel caso di sistemi LTI e di segnali d ingresso SSL. Si utilizzi
Prova scritta 16.02.2006 D. 1 Si derivi l espressione dei legami ingresso-uscita, nel dominio del tempo per le funzioni di correlazione nel caso di sistemi LTI e di segnali d ingresso SSL. Si utilizzi
Esercizi Multiplazione TDM Accesso Multiplo TDMA
 Esercizi Multiplazione TDM Accesso Multiplo TDMA Esercizio 1 Un sistema di multiplazione TDM presenta una trama di 10 slot e in ciascuno slot vengono trasmessi 128 bit. Se il sistema è usato per multiplare
Esercizi Multiplazione TDM Accesso Multiplo TDMA Esercizio 1 Un sistema di multiplazione TDM presenta una trama di 10 slot e in ciascuno slot vengono trasmessi 128 bit. Se il sistema è usato per multiplare
PROBLEMA SU COLLEGAMENTO WIRELESS CON ACCESS POINT
 PROBLEMA SU COLLEGAMENTO WIRELESS CON ACCESS POINT Il gestore di un ipermercato richiede l' installazione di un access point da utilizzare per il collegamento wireless delle casse automatiche alla rete
PROBLEMA SU COLLEGAMENTO WIRELESS CON ACCESS POINT Il gestore di un ipermercato richiede l' installazione di un access point da utilizzare per il collegamento wireless delle casse automatiche alla rete
Psicometria (8 CFU) Corso di Laurea triennale STANDARDIZZAZIONE
 Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Corso di Fondamenti di Telecomunicazioni
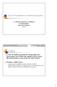 Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Propagazione in fibra ottica
 Propagazione in fibra ottica Struttura delle fibre ottiche In questa sezione si affronteranno: Modi in fibra ottica Dispersione multimodale Confronto multimodo-singolo modo. I modi in fibra ottica Il campo
Propagazione in fibra ottica Struttura delle fibre ottiche In questa sezione si affronteranno: Modi in fibra ottica Dispersione multimodale Confronto multimodo-singolo modo. I modi in fibra ottica Il campo
Elementi di teoria dei segnali /b
 Elementi di teoria dei segnali /b VERSIONE 29.4.01 Filtri e larghezza di banda dei canali Digitalizzazione e teorema del campionamento Capacità di canale e larghezza di banda Multiplexing e modulazioni
Elementi di teoria dei segnali /b VERSIONE 29.4.01 Filtri e larghezza di banda dei canali Digitalizzazione e teorema del campionamento Capacità di canale e larghezza di banda Multiplexing e modulazioni
IL FILTRAGGIO DEL SEGNALE
 CAPITOLO 4 IL FILTRAGGIO DEL SEGNALE 4.1 - SISTEMA LINEARE NON DISTORCENTE E un sistema lineare che restituisce in uscita una replica indistorta del segnale di entrata, intendendo x(t) y(t) = Ax(t-t 0
CAPITOLO 4 IL FILTRAGGIO DEL SEGNALE 4.1 - SISTEMA LINEARE NON DISTORCENTE E un sistema lineare che restituisce in uscita una replica indistorta del segnale di entrata, intendendo x(t) y(t) = Ax(t-t 0
La variabile casuale Binomiale
 La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
 Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione in virgola mobile
 Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
Problemi connessi all utilizzo di un numero di bit limitato Abbiamo visto quali sono i vantaggi dell utilizzo della rappresentazione in complemento alla base: corrispondenza biunivoca fra rappresentazione
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007
 RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Circuiti amplificatori
 Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Analisi di Protocolli
 Analisi di Protocolli Elenco di protocolli d accesso I principali protocolli di accesso si possono dividere in:. protocolli deterministici (accesso ordinato);. protocolli ad accesso casuale (o a contesa).
Analisi di Protocolli Elenco di protocolli d accesso I principali protocolli di accesso si possono dividere in:. protocolli deterministici (accesso ordinato);. protocolli ad accesso casuale (o a contesa).
ARCHITETTURA DI RETE FOLEGNANI ANDREA
 ARCHITETTURA DI RETE FOLEGNANI ANDREA INTRODUZIONE È denominata Architettura di rete un insieme di livelli e protocolli. Le reti sono organizzate gerarchicamente in livelli, ciascuno dei quali interagisce
ARCHITETTURA DI RETE FOLEGNANI ANDREA INTRODUZIONE È denominata Architettura di rete un insieme di livelli e protocolli. Le reti sono organizzate gerarchicamente in livelli, ciascuno dei quali interagisce
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/2/215 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema di
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/2/215 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema di
REGOLAZIONE (E TASSAZIONE OTTIMALE) DI UN MONOPOLIO CON PIÙ LINEE DI PRODUZIONE
 REGOLAZIONE (E TASSAZIONE OTTIMALE) DI UN MONOPOLIO CON PIÙ LINEE DI PRODUZIONE Nella Sezione 16.5 abbiamo visto come un regolatore che voglia fissare il prezzo del monopolista in modo da minimizzare la
REGOLAZIONE (E TASSAZIONE OTTIMALE) DI UN MONOPOLIO CON PIÙ LINEE DI PRODUZIONE Nella Sezione 16.5 abbiamo visto come un regolatore che voglia fissare il prezzo del monopolista in modo da minimizzare la
GUIDA ALLE SOLUZIONI
 Come posizionare una antenna indoor attiva o passiva per una ricezione ottimale? Come verificare in una stanza se il segnale digitale è presente? Perché effettuando la scansione con l antenna indoor non
Come posizionare una antenna indoor attiva o passiva per una ricezione ottimale? Come verificare in una stanza se il segnale digitale è presente? Perché effettuando la scansione con l antenna indoor non
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
Equivalenza economica
 Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
Ai fini economici i costi di un impresa sono distinti principalmente in due gruppi: costi fissi e costi variabili. Vale ovviamente la relazione:
 1 Lastoriadiun impresa Il Signor Isacco, che ormai conosciamo per il suo consumo di caviale, decide di intraprendere l attività di produttore di caviale! (Vuole essere sicuro della qualità del caviale
1 Lastoriadiun impresa Il Signor Isacco, che ormai conosciamo per il suo consumo di caviale, decide di intraprendere l attività di produttore di caviale! (Vuole essere sicuro della qualità del caviale
Un metodo per il rilevamento degli errori: la tecnica del Bit di Parità
 Appunti: Tecniche di rilevazione e correzione degli errori 1 Tecniche di correzione degli errori Le tecniche di correzione degli errori sono catalogabili in: metodi per il rilevamento degli errori; metodi
Appunti: Tecniche di rilevazione e correzione degli errori 1 Tecniche di correzione degli errori Le tecniche di correzione degli errori sono catalogabili in: metodi per il rilevamento degli errori; metodi
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Studio di una funzione ad una variabile
 Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Analisi di scenario File Nr. 10
 1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Segnali e Sistemi. Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici. Gianni Borghesan e Giovanni Marro
 Segnali e Sistemi Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici Gianni Borghesan e Giovanni Marro Indice Introduzione 2. Notazione............................. 2 2 Classificazione
Segnali e Sistemi Dispensa integrativa per l insegnamento di Elementi di Controlli Automatici Gianni Borghesan e Giovanni Marro Indice Introduzione 2. Notazione............................. 2 2 Classificazione
STATISTICA IX lezione
 Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Elementi di Telelocalizzazione
 Elementi di Telelocalizzazione Ing. Francesco Benedetto - Prof. Gaetano Giunta Laboratorio di Telecomunicazioni (COMLAB) Università degli Studi Roma Tre 1 Introduzione Proprietà della sequenza di spreading:
Elementi di Telelocalizzazione Ing. Francesco Benedetto - Prof. Gaetano Giunta Laboratorio di Telecomunicazioni (COMLAB) Università degli Studi Roma Tre 1 Introduzione Proprietà della sequenza di spreading:
1. Introduzione. 2. Simulazioni elettromagnetiche per la misura del SAR
 Relazione Tecnica Analisi simulative e misure con termocamera relative al confronto tra l utilizzo di un telefono smartphone in assenza e in presenza di dispositivo distanziatore EWAD Annamaria Cucinotta
Relazione Tecnica Analisi simulative e misure con termocamera relative al confronto tra l utilizzo di un telefono smartphone in assenza e in presenza di dispositivo distanziatore EWAD Annamaria Cucinotta
La trasformata Zeta. Marco Marcon
 La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
11. Analisi statistica degli eventi idrologici estremi
 . Analisi statistica degli eventi idrologici estremi I processi idrologici evolvono, nello spazio e nel tempo, secondo modalità che sono in parte predicibili (deterministiche) ed in parte casuali (stocastiche
. Analisi statistica degli eventi idrologici estremi I processi idrologici evolvono, nello spazio e nel tempo, secondo modalità che sono in parte predicibili (deterministiche) ed in parte casuali (stocastiche
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
C(f) : funzione di trasferimento del canale. Essa limita la banda del segnale trasmesso e quindi rappresenta un modello più realistico
 MODELLO DEL CANALE Modello gaussiano additivo a banda illimitata (considerato finora): s(t) + n(t) r(t) = s(t) + n(t) s(t) Canale C(f) + r(t) n(t) C(f) : funzione di trasferimento del canale. Essa limita
MODELLO DEL CANALE Modello gaussiano additivo a banda illimitata (considerato finora): s(t) + n(t) r(t) = s(t) + n(t) s(t) Canale C(f) + r(t) n(t) C(f) : funzione di trasferimento del canale. Essa limita
Scelte in condizioni di rischio e incertezza
 CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
Un sistema di controllo può essere progettato fissando le specifiche:
 3. Specifiche dei Sistemi Un sistema di controllo può essere progettato fissando le specifiche: nel dominio del tempo (tempo di salita, tempo di assestamento, sovraelongazione, ecc.); nel dominio della
3. Specifiche dei Sistemi Un sistema di controllo può essere progettato fissando le specifiche: nel dominio del tempo (tempo di salita, tempo di assestamento, sovraelongazione, ecc.); nel dominio della
2) Codici univocamente decifrabili e codici a prefisso.
 Argomenti della Lezione ) Codici di sorgente 2) Codici univocamente decifrabili e codici a prefisso. 3) Disuguaglianza di Kraft 4) Primo Teorema di Shannon 5) Codifica di Huffman Codifica di sorgente Il
Argomenti della Lezione ) Codici di sorgente 2) Codici univocamente decifrabili e codici a prefisso. 3) Disuguaglianza di Kraft 4) Primo Teorema di Shannon 5) Codifica di Huffman Codifica di sorgente Il
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
della funzione obiettivo. Questo punto dovrebbe risultare chiaro se consideriamo una generica funzione:
 Corso di laurea in Economia e finanza CLEF) Economia pubblica ************************************************************************************ Una nota elementare sulla ottimizzazione in presenza di
Corso di laurea in Economia e finanza CLEF) Economia pubblica ************************************************************************************ Una nota elementare sulla ottimizzazione in presenza di
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Regressione Mario Guarracino Data Mining a.a. 2010/2011
 Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il volume produttivo X per uno dei propri stabilimenti e il corrispondente costo mensile Y di produzione. Volume
Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il volume produttivo X per uno dei propri stabilimenti e il corrispondente costo mensile Y di produzione. Volume
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Soluzioni verifica 3 2009-10 parte 4
 Soluzioni verifica 3 2009-10 parte 4 1 Si consideri una rete ethernet a mezzo condiviso, costituita da un unico dominio di collisione in cui vi sono tre segmenti (costituiti da cavi diversi di
Soluzioni verifica 3 2009-10 parte 4 1 Si consideri una rete ethernet a mezzo condiviso, costituita da un unico dominio di collisione in cui vi sono tre segmenti (costituiti da cavi diversi di
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
Fondamenti di Automatica
 Fondamenti di Automatica Risposte canoniche e sistemi elementari Dott. Ing. Marcello Bonfè Dipartimento di Ingegneria - Università di Ferrara Tel. +39 0532 974839 E-mail: marcello.bonfe@unife.it pag. 1
Fondamenti di Automatica Risposte canoniche e sistemi elementari Dott. Ing. Marcello Bonfè Dipartimento di Ingegneria - Università di Ferrara Tel. +39 0532 974839 E-mail: marcello.bonfe@unife.it pag. 1
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
LE FINESTRE E L ISOLAMENTO ACUSTICO
 LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
b. Che cosa succede alla frazione di reddito nazionale che viene risparmiata?
 Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
Esercitazione 7 Domande 1. L investimento programmato è pari a 100. Le famiglie decidono di risparmiare una frazione maggiore del proprio reddito e la funzione del consumo passa da C = 0,8Y a C = 0,5Y.
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
