La rifrazione della luce: le lenti e gli strumenti ottici
|
|
|
- Stefano Masi
- 8 anni fa
- Visualizzazioni
Transcript
1 CPITOLO 4 La rifrazione della luce: le lenti e gli strumenti ottici Una fibra ottica è una specie di filo di vetro in grado di trasmettere impulsi luminosi a grandi distanze dalla sorgente che li ha generati. Grazie alla loro capacità di saper guidare ordinatamente la luce, le fibre ottiche hanno trovato svariate applicazioni nel settore della medicina, dell astronomia, ma soprattutto delle telecomunicazioni, dove vengono impiegate come canali di comunicazione privilegiati ad alta velocità. L ordine di grandezza Quante canzoni si riescono a scaricare in un ora, utilizzando una connessione internet a fibre ottiche? La risposta a pagina
2 CPITOLO 4 Tabella 4. Indice di rifrazione () di alcune sostanze comuni Sostanza Indice di rifrazione n Solidi a 20 C Cloruro di sodio,544 Diamante 2,49 Ghiaccio (a 0 C),309 Quarzo cristallino,544 Quarzo fuso,458 Vetro (ottico),523 Liquidi a 20 C cqua,333 lcol etilico,362 enzene,50 isolfuro di carbonio,632 Tetracloruro di carbonio,46 Gas a 0 C, atm ria, iossido di carbonio, Idrogeno (H 2 ), Ossigeno (O 2 ), () Misurati con una luce di lunghezza d onda nel vuoto pari a 589 nm. 4. L indice di rifrazione La luce si propaga nel vuoto alla velocità c 3, m/s. La luce si propaga anche in altri mezzi, come l aria, l acqua e il vetro. Tuttavia gli atomi della materia in parte la assorbono, in parte la riemettono e in parte la diffondono. Perciò la velocità della luce in un mezzo diverso dal vuoto è minore di c e il suo valore dipende dalla natura del materiale. La tabella 4. riporta gli indici di rifrazione di alcune sostanze comuni. I valori di n sono maggiori di perché la velocità della luce nel vuoto è maggiore di quella in qualunque altro materiale. Per esempio, l indice di rifrazione del diamante è n 2,49, perciò la velocità della luce nel diamante è: c 3,00 0 v 8 m/s, m/s n 2,49 L indice di rifrazione dell aria è così vicino a che per la maggior parte degli scopi pratici si può porre n aria. 4.2 La legge della rifrazione DEINIZIONE DELL INDICE DI RIRZIONE L indice di rifrazione n di un materiale è il rapporto tra la velocità della luce nel vuoto c e la velocità della luce v nel materiale: Legge di Snell n velocità della luce nel vuoto c velocità della luce nel materiale v (4.) Quando la luce colpisce la superficie di separazione tra due materiali trasparenti, in genere si divide in due parti, come mostra la figura 4.: una parte viene riflessa con un angolo di riflessione uguale all angolo di incidenza e una parte continua a propagarsi oltre la superficie di separazione. Se il raggio incidente non è perpendicolare alla superficie di separazione, il raggio che penetra nel secondo materiale ha una direzione diversa da quella del raggio incidente. igura 4.. Quando un raggio di luce passa dall aria all acqua, una parte della luce viene riflessa dalla superficie di separazione tra l aria e l acqua e una parte penetra nell acqua ma viene rifratta, cioè deviata dalla sua direzione originale. Il raggio rifratto si avvicina alla normale (θ 2 < θ ).. Quando la luce passa dall acqua all aria, il raggio rifratto si allontana dalla normale (θ 2 > θ ). 394 Raggio incidente ria (n =,00) cqua (n 2 =,33) Normale θ θ N θ 2 l Raggio riflesso Raggio rifratto Raggio rifratto ria (n 2 =,00) cqua (n =,33) Raggio riflesso Normale Raggio incidente Il raggio che penetra nel secondo materiale è chiamato raggio rifratto e mostra uno dei seguenti comportamenti: quando la luce passa da un mezzo con indice di rifrazione minore (l aria) a uno con indice di rifrazione maggiore (l acqua), il raggio rifratto si avvicina alla normale (figura 4.); quando la luce passa da un mezzo con indice di rifrazione maggiore (l acqua) a uno con indice di rifrazione minore (l aria), il raggio rifratto si allontana dalla normale (figura 4.). Sia il raggio incidente sia il raggio rifratto si comportano come previsto dal principio di reversibilità dei cammini ottici. Ciascuna delle situazioni illustrate può esse- θ 2 θ θ
3 CPITOLO 4 re ottenuta dall altra invertendo la direzione dei raggi. L unica differenza è dovuta al raggio riflesso, che una volta si propaga in aria e l altra in acqua. In entrambe le situazioni l angolo di incidenza, l angolo di riflessione e l angolo di rifrazione sono misurati rispetto alla normale alla superficie di separazione nel punto di incidenza. Osserviamo che nella parte della figura l indice di rifrazione dell aria è indicato con n, mentre nella parte è indicato con n 2 : il motivo di questa differenza è che indichiamo con il pedice tutte le variabili associate al raggio incidente (o al raggio riflesso) e con il pedice 2 tutte le variabili associate al raggio rifratto. L angolo di rifrazione θ 2 dipende dall angolo di incidenza θ e dagli indici di rifrazione n e n 2 dei due mezzi. La relazione tra queste grandezze è chiamata legge della rifrazione di Snell, dal nome del matematico olandese Willebrord Snell (59-626) che la scoprì sperimentalmente. LEGGE DELL RIRZIONE DI SNELL Quando la luce passa da un mezzo con indice di rifrazione n a un mezzo con indice di rifrazione n 2, il raggio incidente, il raggio rifratto e la normale alla superficie di separazione dei due mezzi nel punto di incidenza giacciono tutti nello stesso piano e l angolo di rifrazione θ 2 è legato all angolo di incidenza θ dalla relazione: n sen θ n 2 sen θ 2 (4.2) ESEMPIO Legge della rifrazione Determinazione dell angolo di rifrazione Un raggio incide sulla superficie di separazione tra aria e acqua con un angolo di incidenza di 46. L indice di rifrazione dell acqua è,33. Determina l angolo di rifrazione quando il raggio passa: dall aria all acqua. dall acqua all aria. Ragionamento pplichiamo la legge di Snell a entrambe le situazioni, ricordando che nella prima il raggio incidente proviene dall aria, mentre nella seconda proviene dall acqua. Teniamo conto di questa differenza indicando con il pedice le variabili associate al raggio incidente e con il pedice 2 le variabili associate al raggio rifratto. Soluzione Il raggio incidente proviene dall aria, perciò θ 46 e n,00. Il raggio rifratto è nell acqua, perciò n 2,33. Per trovare l angolo di rifrazione θ 2 possiamo usare la legge della rifrazione: n sen θ 2 sen θ (,00)(sen 46 ) 0,54,33 n 2 θ 2 sen (0,54) 33 Poiché θ 2 è minore di θ, il raggio rifratto si avvicina alla normale, come mostra la figura 4.. Quando il raggio incidente proviene dall acqua otteniamo: n sen θ 2 sen θ (,33)(sen 46 ) 0,96,00 n 2 θ 2 sen (0,96) Poiché θ 2 è maggiore di θ, il raggio rifratto si allontana dalla normale, come mostra la figura Problem solving Osservazione sugli angoli di incidenza e di rifrazione L angolo di incidenza θ e l angolo di rifrazione θ 2 che compaiono nella legge di Snell sono gli angoli che i raggi formano con la normale alla superficie di separazione nel punto di incidenza e non quelli che i raggi formano con la superficie di separazione. 395
4 CPITOLO 4 Cuneo di vetro trasparente Specchio argentato (superficie posteriore del cuneo) Conducente D Conducente C Levetta di regolazione giorno-notte Luce dall automobile che sta dietro C D Luce dall automobile che sta dietro Posizione per la guida diurna C Posizione per la guida notturna igura 4.2 Uno specchietto retrovisore interno di un automobile dotato di levetta per regolarne la posizione, in modo da adattarlo alla guida diurna e a quella notturna. isica quotidiana Effetto antiabbagliante negli specchietti retrovisori Quando un raggio di luce incide sulla superficie di separazione tra due mezzi, si formano sempre un raggio riflesso e un raggio rifratto. Questo fatto è utilizzato, per esempio, negli specchietti retrovisori delle automobili (figura 4.2), composti da un cuneo di vetro la cui superficie posteriore è argentata e con un forte potere riflettente. La parte della figura mostra lo specchietto regolato per la guida di giorno. La luce proveniente dall automobile che sta dietro arriva agli occhi del conducente lungo il cammino CD. Nei punti e C si formano raggi riflessi che non giungono all occhio del conducente. I raggi riflessi sono rappresentati con tratti molto sottili per indicare che in essi è contenuta solo una piccola percentuale (circa il 0%) della luce incidente. Quindi la maggior parte della luce è riflessa in e giunge all occhio del conducente, che vede un immagine molto nitida dell automobile che sta dietro. Durante la guida notturna, azionando una levetta si fa ruotare lo specchietto nella posizione indicata nella parte C della figura. L unica luce che il conducente vede è il debole raggio riflesso dalla superficie anteriore dello specchietto che segue il cammino D, con una notevole riduzione dell abbagliamento. Profondità apparente Una conseguenza interessante della rifrazione è il fatto che un oggetto sott acqua sembra più vicino alla supeficie di quanto è realmente. θ 3,3 m θ 2 ria (n =,00) cqua (n 2 =,33) Cassa 2,0 m igura 4.3 Il fascio di luce emesso dalla torcia viene rifratto quando penetra nell acqua. Problem solving Convenzione sull annotazione degli indici di rifrazione Ricorda che gli indici di rifrazione sono indicati con n per il mezzo in cui viaggia la luce incidente e con n 2 per il mezzo in cui viaggia la luce rifratta. ESEMPIO 2 Legge della rifrazione Trovare una cassa affondata Il faro di una barca è utilizzato per illuminare di notte una cassa affondata (figura 4.3). Con quale angolo di incidenza θ deve essere orientato il faro per illuminare la cassa? Ragionamento e soluzione nzitutto calcoliamo l angolo di rifrazione θ 2 : 2,0 m tg θ 2 per cui: θ 2 3 3,3 m Gli indici di rifrazione sono n,00 per l aria e n 2,33 per l acqua; dalla legge della rifrazione si ottiene: n sen θ 2 senθ 2 (,33)(sen 3 ) 0,69,00 n θ sen (0,69)
5 CPITOLO 4 Profondità reale Profondità apparente Immagine Osservatore Profondità apparente = d Profondità reale = d igura 4.4. Poiché i raggi di luce provenienti dalla cassa si allontanano dalla normale quando entrano nell aria e vengono rifratti, la profondità apparente dell immagine è minore della profondità reale.. L osservatore nell aria vede la cassa da un punto posto sulla verticale che passa per la cassa. Cassa La figura 4.4 mostra i cammini dei raggi luminosi emessi dalla cassa e osservati dalla barca. Prolungando dentro l acqua i raggi che viaggiano nell aria (osserva le rette tratteggiate), si vede che essi si intersecano in un punto che è l immagine virtuale della cassa vista dall osservatore e che questa immagine si trova a una profondità apparente minore della profondità reale. L immagine è virtuale perché i raggi luminosi non passano realmente per essa. Per la situazione rappresentata nella figura 4.4 è difficile determinare la profondità apparente. Nella parte della figura è rappresentata una situazione molto più semplice, in cui l osservatore è sulla verticale che passa per la cassa. In questo caso la profondità apparente d è legata alla profondità reale d dalla relazione: Profondità apparente, osservatore sulla verticale sopra l oggetto n 2 n d d (4.3) In questo risultato, n è l indice di rifrazione del mezzo in cui viaggiano i raggi incidenti (cioè il mezzo in cui si trova l oggetto che emette la luce) e n 2 è l indice di rifrazione del mezzo in cui viaggiano i raggi rifratti (cioè il mezzo in cui si trova l osservatore). Raggio di luce che attraversa una lastra di materiale trasparente Il vetro di una finestra è un esempio di una lastra di materiale trasparente a facce piane e parallele. Come mostra la figura 4.5, quando un raggio di luce attraversa il vetro, il raggio emergente è parallelo a quello incidente, ma spostato lateralmente rispetto a esso. Questo risultato può essere verificato applicando a ciascuna delle due superfici di separazione la legge della rifrazione, da cui si ottiene: n sen θ n 2 sen θ 2 n 3 sen θ 3 Poiché l aria circonda il vetro, si ha n n 3 e quindi sen θ sen θ 3. Perciò θ θ 3, e quindi il raggio incidente e il raggio emergente sono paralleli. Il raggio emergente risulta però spostato lateralmente rispetto a quello emergente. Lo spostamento dipende dall angolo di incidenza, dallo spessore della lastra e dall indice di rifrazione del materiale di cui è fatta la lastra. In particolare, quando lo spessore della lastra è piccolo, lo spostamento è trascurabile e la direzione del raggio incidente praticamente coincide con quella del raggio emergente. ria (n 3 = n ) Vetro (n 2 ) ria (n ) θ θ 2 Raggio incidente θ 2 Raggio emergente θ 3 Spostamento igura 4.5 Quando un raggio incidente attraversa una lastra di vetro a facce piane e parallele circondata dall aria, il raggio emergente è parallelo al raggio incidente (θ θ 3 ), ma è spostato lateralmente rispetto a esso. 397
6 CPITOLO 4 Dimostrazione della legge di Snell Per dimostrare la legge di Snell, possiamo considerare quello che succede ai fronti d onda quando la luce passa da un mezzo a un altro. La figura 4.6 mostra un raggio che passa dal mezzo al mezzo 2 in cui la velocità della luce è minore: poiché v v 2, risulta n n 2. Nella figura sono rappresentati i fronti d onda piani perpendicolari al raggio incidente e al raggio rifratto. Poiché la parte di ciascun fronte d onda della luce incidente che penetra nel mezzo 2 rallenta, le superfici dei fronti d onda nel mezzo 2 risultano ruotate in senso orario rispetto a quelle nel mezzo. Di conseguenza, come mostra la figura, il raggio incidente risulta deviato verso la nomale. igura 4.6. I fronti d onda vengono rifratti quando la luce passa dal mezzo al mezzo 2.. Vista ingrandita del fronte d onda incidente e del fronte d onda rifratto alla superficie di separazione dei due mezzi. Mezzo Raggio incidente ronti d onda incidenti che viaggiano a velocità maggiore λ θ θ h λ Mezzo 2 λ 2 λ 2 θ 2 ronti d onda rifratti che viaggiano a velocità minore Raggio rifratto θ 2 L onda incidente e l onda rifratta hanno la stessa frequenza. Possiamo renderci conto di questa proprietà in termini intuitivi osservando che ogni particella del mezzo 2 posta sulla superficie di separazione è fatta oscillare dall onda proveniente dal mezzo. Essa dunque oscilla con la frequenza della luce incidente ma genera a sua volta onde nel mezzo 2, che hanno quindi la stessa frequenza di quelle del mezzo. Scegliamo la distanza tra due fronti d onda successivi uguale alla lunghezza d onda λ (figura 4.6). Le frequenze sono uguali nei due mezzi ma le velocità di propagazione sono diverse; quindi le lunghezze d onda sono diverse: λ v f e λ 2 v 2 f Se v è maggiore di v 2, allora λ è maggiore di λ 2 e quindi i fronti d onda nel mezzo sono più distanti tra loro. La figura 4.6 mostra una visione ingrandita dei fronti d onda incidenti e rifratti alla superficie di separazione. Gli angoli indicati con θ e θ 2 nei triangoli rettangoli colorati della figura sono rispettivamente l angolo di incidenza e l angolo di rifrazione. Inoltre i due triangoli hanno in comune l ipotenusa h. Perciò si ha: λ sen θ v /f v λ v e sen θ /f h h hf h h v 2 hf Combinando queste due equazioni in un equazione unica ed eliminando il fattore comune hf, si ottiene: sen θ v sen θ 2 v 2 Moltiplicando entrambi i membri dell equazione per la velocità della luce nel vuoto c e ricordando che il rapporto c/v è l indice di rifrazione n, si ottiene l espressione della legge di Snell: n sen θ n 2 sen θ
7 CPITOLO La riflessione totale Quando la luce passa da un mezzo con indice di rifrazione maggiore a un mezzo con indice di rifrazione minore (per esempio dall acqua all aria), il raggio rifratto si allontana dalla normale, come mostra la figura 4.7. Quando aumenta l angolo di incidenza, aumenta anche l angolo di rifrazione. Quando l angolo di incidenza raggiunge un certo valore, chiamato angolo limite θ L, l angolo di rifrazione è di 90. In questo caso il raggio rifratto è radente alla superficie di separazione, come mostra la parte della figura. Quando l angolo di incidenza è maggiore dell angolo limite, il raggio rifratto manca: tutta la luce incidente viene riflessa all interno del mezzo da cui proveniva (figura 4.7C). Questo fenomeno è chiamato riflessione totale. Per ottenere il valore dell angolo limite imponiamo che l angolo di rifrazione sia θ 2 90 ; dalla legge della rifrazione n sen θ n 2 sen 90 otteniamo n sen θ n 2, quindi l angolo limite θ L è tale che è: ILM La riflessione totale ibre ottiche n 2 n sen θ L (n 2 n ) (4.4) Per esempio, l angolo limite per la luce che si propaga dall acqua (n,33) verso l aria (n 2,00) è:,00 θ L sen,33 48,8 ria (n 2 =,00) cqua (n =,33) θ θ Raggio incidente θ 2 Raggio rifratto Raggio riflesso n 2 n θ L θ L θ 2 = 90 n 2 n θ L Riflessione totale C ESEMPIO 3 Riflessione totale Luce attraverso un diamante Un raggio di luce attraversa un diamante (n 2,42) e colpisce la superficie di separazione tra l aria e il diamante con un angolo di incidenza di 28. Si ha riflessione totale? Che cosa avviene se il diamante è immerso in acqua (n 2,33)? Ragionamento e soluzione Dall equazione (4.4) si ricava che l angolo limite oltre il quale avviene la riflessione totale alla superficie di separazione tra il diamante e l aria è: n θ L sen 2,00 n sen 24,4 2,42 Poiché l angolo di incidenza di 28 è maggiore dell angolo limite, manca il raggio rifratto e il raggio di luce viene riflesso all interno del diamante. Quando il diamante è immerso nell acqua l angolo limite è: igura 4.7. Quando la luce passa da un mezzo con indice di rifrazione maggiore (per esempio l acqua) a un mezzo con indice di rifrazione minore (per esempio l aria), il raggio rifratto si allontana dalla normale.. Quando l angolo di incidenza è uguale all angolo limite θ L, l angolo di rifrazione è di 90. C. Quando θ è maggiore di θ L, il raggio rifratto manca e si verifica la riflessione totale. n θ L sen 2,33 n sen 33,3 2,42 Poiché l angolo di incidenza di 28 è minore dell angolo limite, alla superficie di separazione tra il diamante e l acqua il raggio di luce incidente viene rifratto nell acqua. 399
8 CPITOLO 4 isica quotidiana Perché i brillanti scintillano I brillanti, gemme che si ottengono sfaccettando i diamanti grezzi, sono famosi per lo scintillio che producono quando sono colpiti dalla luce. Per ottenere questo effetto le facce del brillante sono tagliate ad angoli tali che la quasi totalità dei raggi di luce all interno subiscono riflessione totale sul fondo del brillante e riemergono dalle facce superiori. θ = Normale Prismi Raggio luminoso C Masahiro Sano/Corbis Stock Market igura 4.8 La riflessione totale alla superficie di separazione vetro-aria può essere usata per far deviare un raggio di luce di 90 () o 80 (). C. pplicazione della doppia riflessione totale nei prismi di un binocolo. igura 4.9. La luce rimane confinata all interno di una fibra ottica grazie al fenomeno della riflessione totale.. Luce trasportata da varie fibre ottiche. 400 Raggio luminoso Mantello Nucleo isica quotidiana Le fibre ottiche Molti strumenti ottici come i binocoli, i periscopi e i telescopi impiegano prismi di vetro che provocano la riflessione totale per far ruotare di 90 o di 80 un fascio di luce. La figura 4.8 mostra un raggio di luce che entra in un prisma di vetro (n,5) con una sezione trasversale che ha la forma di un triangolo retto isoscele (cioè con angoli di 45, 45 e 90 ) e che va a colpire l ipotenusa di questo triangolo con un angolo di incidenza θ 45. L angolo limite per una superficie di separazione vetro-aria è: n θ L sen 2,0 n sen 42,5 Poiché l angolo di incidenza è maggiore dell angolo limite, la luce incidente sull ipotenusa viene totalmente riflessa all interno del prisma e il raggio emergente dal prisma mostrato in figura è diretto verticalmente verso l alto, cioè è ruotato di 90 rispetto al raggio entrato nel prisma. La parte della figura mostra come lo stesso prisma possa far ruotare il raggio di 80 quando si ha una doppia riflessione totale. I prismi possono anche essere usati in coppia per provocare uno spostamento laterale dei raggi di luce senza cambiarne la direzione originale. La figura 4.8C mostra un applicazione di questo tipo nel doppio prisma di un binocolo. Un importante applicazione della riflessione totale si trova nelle fibre ottiche, dove fili di vetro o di plastica sottili come capelli, chiamati appunto fibre ottiche, «guidano» la luce da un posto a un altro. La figura 4.9 mostra che una fibra ottica è formata da un nucleo cilindrico interno, attraverso il quale viaggia la luce, e da una parete esterna concentrica al nucleo, chiamata mantello. Il nucleo è fatto di vetro o di plastica trasparente con un indice di rifrazione relativamente grande. nche il mantello è fatto di vetro, ma di un tipo che ha un indice di rifrazione relativamente piccolo. La luce entra in un estremo del nucleo, colpisce la superficie di separazione nucleo-mantello con un angolo maggiore dell angolo limite e perciò viene riflessa totalmente all interno del nucleo. In questo modo la luce continua a viaggiare all interno della fibra ottica seguendo un percorso a zig-zag. In una fibra ottica ben progettata l assorbimento della luce da parte del nucleo è molto basso e quindi la luce può viaggiare per molti kilometri senza diminuire di intensità in quantità apprezzabili. Le fibre ottiche (figura 4.9) sono spesso raggruppate insieme in modo da formare dei cavi. Poiché le fibre sono sottilissime, anche i cavi di fibre ottiche sono molto sottili e flessibili e riescono a passare attraverso luoghi inaccessibili ai cavi metallici, che hanno un diametro molto maggiore. Inoltre la capacità di trasporto di informazioni delle fibre ottiche è migliaia di volte superiore a quella dei cavi elettrici.
9 CPITOLO La dispersione della luce La figura 4.0 mostra il fenomeno della dispersione della luce: un fascio di luce bianca incidente su un prisma è scomposto in una serie di raggi di diverso colore che formano lo spettro della luce. I colori dello spettro sono nell ordine: rosso, arancione, giallo, verde, azzurro, indaco e violetto. Prisma di vetro David Parker/Photo Researchers Luce incidente Normale Normale Luce incidente C Rosso (660 nm) Violetto (40 nm) igura 4.0. La luce bianca è dispersa nelle sue componenti colorate quando attraversa un prisma.. Quando un raggio di luce attraversa un prisma di vetro a sezione triangolare circondato dall aria viene rifratto due volte. C. Due colori diversi subiscono deviazioni diverse quando attraversano il prisma. Per maggiore chiarezza, nel disegno è stato esagerato l angolo di deviazione. Per comprendere l origine di questo fenomeno, scoperto da Newton alla fine del Seicento, consideriamo un raggio di luce di un dato colore, per esempio rosso, che incide sulla faccia di un prisma triangolare di vetro (figura 4.0). Il raggio rifratto è deviato verso la normale, perché l indice di rifrazione del vetro è maggiore di quello dell aria. Quando il raggio di luce esce dalla faccia di destra del prisma, il raggio rifratto si allontana dalla normale, perché l indice di rifrazione dell aria è minore di quello del vetro. Perciò l effetto complessivo del prisma è quello di cambiare la direzione del raggio, facendolo deviare verso il basso sia quando entra nel prisma sia quando ne esce. Poiché l indice di rifrazione del vetro dipende dal colore della luce e quindi, come vedremo, dalla lunghezza d onda della luce (tabella 4.2), i raggi luminosi di colori diversi sono deviati verso il basso con angoli diversi. Quanto maggiore è l indice di rifrazione per un dato colore, tanto maggiore è l angolo di deviazione: la parte C della figura mostra i raggi rifratti corrispondenti ai raggi incidenti di colore rosso e violetto, cioè i colori ai due estremi dello spettro della luce visibile. L arcobaleno Un esempio spettacolare di dispersione della luce è costituito dagli arcobaleni, in cui i diversi colori hanno origine dalla rifrazione della luce solare da parte delle gocce d acqua. In genere, capita di vedere un arcobaleno quando sta finendo un temporale e si guarda verso le ultime gocce di pioggia nell aria con le spalle al Sole. Quando la luce proveniente dal Sole entra in una goccia d acqua di forma sferica, come quella della figura 4., i diversi colori della luce vengono deviati di un angolo che dipende dall indice di rifrazione dell acqua per la luce di quel colore. Dopo essere stati riflessi dalla superficie posteriore della goccia, i raggi dei diversi colori vengono rifratti di nuovo quando riemergono nell aria. Tabella 4.2 Indici di rifrazione del vetro Crown per alcuni colori Colore Indice di rifrazione n Rosso,520 rancione,522 Giallo,523 Verde,526 lu,53 Violetto,538 isica quotidiana L arcobaleno Luce solare igura 4. Quando la luce solare emerge da una goccia d acqua viene dispersa nei colori che la compongono, di cui solo due sono rappresentati nella figura. Violetto Rosso Goccia d'acqua 40
10 CPITOLO 4 Sole Rosso Violetto Rosso Violetto Violetto Rosso Eric ean/the Image ank/getty Images igura 4.2. I colori dell arcobaleno hanno origine da gocce d acqua poste ad altezze diverse.. L arcobaleno ai piedi di una cascata. nche se ciascuna goccia disperde la luce solare in tutti i colori dello spettro della luce visibile, l osservatore della figura 4.2 vede solo un colore emergere da ciascuna goccia, perché solo uno dei colori viaggia nella direzione giusta per giungere al suo occhio. Tuttavia, in un arcobaleno si vedono tutti i colori dello spettro della luce solare (figura 4.2), perché ciascun colore proviene da gocce diverse poste ad altezze diverse. 4.5 Le lenti Le lenti sono impiegate in molti strumenti ottici, come gli occhiali, le macchine fotografiche e i telescopi. Una lente sferica è un corpo di materiale trasparente delimitato da due superfici sferiche (figura 4.3). La retta che passa per i centri di curvatura delle due superfici è detta asse ottico della lente. Il centro della lente è il punto sull asse ottico che ha la stessa distanza da ciascuna delle superfici. Nel seguito studieremo le proprietà delle lenti sottili, cioè di quelle lenti che hanno uno spessore molto più piccolo dei raggi delle superfici sferiche che le delimitano. igura 4.3. Lente convessa.. Lente concava. r r 2 r r 2 O C O 2 O C O 2 igura 4.4. I due prismi di vetro disposti come in figura fanno deviare i raggi paralleli all asse ottico che li attraversano in modo che i raggi emergenti intersechino l asse in punti diversi.. Quando i raggi parassiali paralleli all asse ottico attraversano una lente convergente, i raggi che emergono dalla lente convergono verso il fuoco della lente. superfici sferiche Lenti convergenti e lenti divergenti superfici sferiche Prendiamo in esame due tipi di lenti sottili: le lenti convergenti e le lenti divergenti. Una lente convergente devia i raggi che incidono su di essa parallelamente all asse ottico e li fa convergere in un punto sull asse ottico detto fuoco (figura 4.4). sse ottico Lente convergente sse ottico f = distanza focale 402
11 CPITOLO 4 Una lente divergente devia i raggi che incidono su di essa parallelamente all asse ottico e li fa divergere come se provenissero da un punto sull asse ottico, detto fuoco (figura 4.5). sse ottico La distanza tra il fuoco e il centro di una lente è chiamata distanza focale f della lente. Come mostra la figura 4.6, le lenti convergenti e divergenti possono avere varie forme. In generale, le lenti convergenti sono più spesse al centro che ai bordi, mentre le lenti divergenti sono più sottili al centro che ai bordi. Lente divergente f = distanza focale sse ottico igura 4.5. I due prismi di vetro disposti come in figura fanno deviare i raggi paralleli all asse ottico che li attraversano in modo che i raggi emergenti siano divergenti.. Quando i raggi parassiali paralleli all asse ottico attraversano una lente divergente, i raggi che emergono dalla lente sono divergenti e sembrano provenire dal fuoco della lente. iconvessa Menisco convesso Pianoconvessa Lenti convergenti iconcava Pianoconcava Lenti divergenti Menisco concavo igura 4.6 Le lenti convergenti e quelle divergenti possono avere varie forme. 4.6 Immagini formate da lenti I diagrammi dei raggi Per determinare la posizione e le dimensioni dell immagine formata da una lente sottile sono molto utili i diagrammi dei raggi, che abbiamo già visto nel capitolo precedente per le immagini formate dagli specchi. Le lenti sono però diverse dagli specchi, perché i raggi luminosi possono incidere su ciascuna delle due facce della lente. Perciò, quando si tracciano i diagrammi dei raggi, bisogna anzitutto conoscere i fuochi da entrambe le parti della lente: ognuno dei due fuochi si trova sull asse ottico a una distanza dalla lente uguale alla distanza focale. Per tracciare i diagrammi dei raggi sono particolarmente utili tre raggi parassiali che partono dal punto più alto dell oggetto e che sono indicati con, 2 e 3 nelle figure 4.7 e 4.8, in cui l oggetto è rappresentato da una freccia. Per tracciare i loro cammini usiamo le seguenti convenzioni. DIGRMM DEI RGGI PER LENTI CONVERGENTI (OGGETTO SINISTR DELL LENTE) (figura 4.7) Raggio. Questo raggio incidente è parallelo all asse ottico. Dopo aver attraversato la lente, il raggio rifratto passa per il fuoco a destra della lente (parte ). Raggio 2. Questo raggio incidente passa per il fuoco a sinistra della lente e viene rifratto in direzione parallela all asse ottico (parte ). Raggio 3. Questo raggio incidente è diretto verso il centro della lente sottile e la attraversa senza essere praticamente deviato (parte C). Lenti convergenti 2 C 3 igura 4.7 I raggi rappresentati in figura sono utili per determinare il tipo di immagine formato da una lente convergente. 403
12 CPITOLO 4 DIGRMM DEI RGGI PER LENTI DIVERGENTI (OGGETTO SINISTR DELL LENTE) (figura 4.8) Raggio. Questo raggio incidente è parallelo all asse ottico. Dopo aver attraversato la lente il raggio rifratto sembra provenire dal fuoco a sinistra della lente. Il raggio tratteggiato nella parte rappresenta il cammino apparente del raggio che esce dalla lente. Raggio 2. Questo raggio incidente è diretto verso il fuoco a destra della lente ed è rifratto parallelamente all asse ottico. Il raggio tratteggiato nella parte rappresenta il cammino che il raggio percorrerebbe se non ci fosse la lente. Raggio 3. Questo raggio incidente è diretto verso il centro della lente sottile e la attraversa senza essere praticamente deviato (parte C). Lenti divergenti 2 igura 4.8 I raggi rappresentati in figura sono utili per determinare il tipo di immagine formato da una lente divergente. C 3 Sia nelle lenti convergenti sia in quelle divergenti, il raggio 3 non viene deviato in modo apprezzabile da una lente sottile, in cui le superfici nella zona centrale sono praticamente parallele. Perciò la lente si comporta in entrambi i casi come una lastra piana a facce parallele (figura 4.5). Poiché lo spessore della lente è piccolo, le direzioni del raggio incidente e di quello rifratto sono praticamente coincidenti. isica quotidiana Una macchina fotografica Immagini formate da una lente convergente Nella figura 4.9 l oggetto si trova a una distanza da una lente convergente maggiore del doppio della distanza focale (cioè più lontana del punto indicato con 2). Per trovare l immagine si possono disegnare due qualunque dei tre raggi, 2 e 3 che partono dal punto superiore dell oggetto. Il punto a destra della lente in cui si intersecano i tre raggi rifratti è l immagine del punto da cui i raggi provengono. Il diagramma dei raggi mostra che l immagine dell oggetto è reale, capovolta e rimpicciolita rispetto all oggetto. La disposizione illustrata in figura 4.9 è simile a quella impiegata in una macchina fotografica, in cui una superficie sensibile alla luce, posta nella parte posteriore della macchina, raccoglie i raggi provenienti dalla lente (l obiettivo) e registra l immagine dell oggetto (figura 4.9) Immagine reale Pellicola Immagine reale (capovolta) igura 4.9. Quando l oggetto si trova a sinistra del punto indicato con 2, l immagine formata dalla lente è reale, capovolta e rimpicciolita.. La disposizione degli oggetti e delle lenti indicata nella parte della figura è simile a quella impiegata nelle macchine fotografiche. 404
13 CPITOLO 4 Lampada (capovolto) Schermo Immagine reale Immagine reale Proiettore igura Quando l oggetto si trova tra i punti e 2, l immagine formata dalla lente è reale, capovolta e ingrandita rispetto all oggetto.. La disposizione degli oggetti e delle lenti indicata nella parte della figura è simile a quella impiegata nei proiettori. Quando l oggetto si trova tra i punti e 2, come nel caso della figura 4.20 l immagine è reale e capovolta rispetto all oggetto, ma risulta più grande dell oggetto. Questo tipo di disposizione è impiegato nei proiettori di diapositive o di pellicole, in cui l oggetto è una piccola parte di pellicola e l immagine ingrandita viene raccolta su uno schermo (figura 4.20). Naturalmente, per ottenere un immagine diritta, la pellicola va inserita nel proiettore capovolta. Quando l oggetto si trova tra il fuoco e la lente, come nella figura 4.2, i raggi divergono dopo aver attraversato la lente. un osservatore che li guarda, questi raggi sembrano provenire da un immagine posta dietro la lente, cioè a sinistra della lente. Poiché nessuno di questi raggi proviene realmente dall immagine, l immagine è virtuale. Inoltre il diagramma dei raggi mostra che l immagine è diritta e ingrandita. Come si può vedere nella parte della figura, le lenti di ingrandimento sfruttano questa disposizione. isica quotidiana Un proiettore per diapositive Immagine virtuale 3 EGHI Lente d'ingrandimento OPQRSTUVWXYZ igura 4.2. Quando un oggetto è posto tra il fuoco di una lente convergente e la lente, si forma un immagine virtuale, diritta e ingrandita dell oggetto.. Questo tipo di immagine si può vedere quando si guarda attraverso una lente d ingrandimento. Immagini formate da una lente divergente Dopo aver attraversato una lente divergente, i raggi divergono come mostra la figura 4.22, e il diagramma dei raggi indica che si forma un immagine virtuale a sinistra della lente. In effetti, indipendentemente dalla posizione dell oggetto, una lente divergente forma sempre un immagine virtuale, diritta e rimpicciolita rispetto all oggetto. Immagine virtuale 3 C C DE Lente divergente DE igura Una lente divergente forma sempre un immagine virtuale di un oggetto reale. L immagine è diritta e rimpicciolita rispetto all oggetto.. Un immagine vista attraverso una lente divergente. 405
14 CPITOLO L equazione delle lenti sottili Equazione delle lenti sottili. Ingrandimento lineare Per determinare con precisione le caratteristiche dell immagine di un oggetto formata da una lente sottile si possono usare le due seguenti equazioni: Equazione delle lenti sottili p (4.5) q f Equazione dell ingrandimento lineare altezza dell immagine h q G i (4.6) altezza dell immagine h o p La figura 4.23 mostra il significato dei simboli che compaiono nelle due equazioni precedenti con riferimento a una lente sottile convergente, ma le equazioni sono valide anche per una lente divergente, purché sottile. igura 4.23 La figura mostra la distanza focale f, la distanza dell oggetto p e la distanza dell immagine q per una lente convergente. Le altezze dell oggetto e dell immagine sono indicate rispettivamente con h o e h i. h o p f q Immagine reale h i Per utilizzare correttamente le due equazioni precedenti bisogna ricordare alcune convenzioni sui segni, elencate nel caso di raggi che provengono da un oggetto reale a sinistra della lente. RIEPILOGO DELL CONVENZIONE SUI SEGNI PER LE LENTI SOTTILI Distanza focale f 0 per una lente convergente f 0 per una lente divergente Distanza dell oggetto p 0 se l oggetto è a sinistra della lente (oggetto reale), come avviene di solito p 0 se l oggetto è a destra della lente (oggetto virtuale) () Distanza dell immagine q 0 se l immagine di un oggetto reale è reale e si forma a destra della lente q 0 se l immagine di un oggetto reale è virtuale e si forma a sinistra della lente Ingrandimento lineare G 0 se l immagine è diritta rispetto all oggetto G 0 se l immagine è capovolta rispetto all oggetto ESEMPIO 4 Equazione delle lenti sottili L immagine reale formata dall obiettivo di una macchina fotografica Una persona alta,70 m è in piedi davanti a una macchina fotografica a una distanza di 2,50 m da essa. La macchina fotografica ha un obiettivo formato da una lente convergente con una distanza focale di 0,0500 m. () Questa situazione può verificarsi quando un sistema ottico contiene più di una lente e l immagine formata dalla prima lente funziona come oggetto per la seconda. In questo caso l oggetto della seconda lente può trovarsi alla sua destra e la convenzione dei segni stabilisce che la distanza dell oggetto sia negativa e che l oggetto sia considerato un oggetto virtuale. 406
15 CPITOLO 4 Trova la distanza dell immagine (cioè la distanza tra l obiettivo e la pellicola) e determina se l immagine è reale o virtuale. Calcola l ingrandimento e l altezza dell immagine sulla pellicola. Ragionamento La posizione dell oggetto è simile a quella della figura 4.9, in cui la distanza dell oggetto dalla lente è maggiore del doppio della distanza focale. Perciò ci aspettiamo che l immagine sia reale, capovolta e rimpicciolita. Soluzione Usando l equazione delle lenti sottili con p 2,50 m e f 0,0500 m, otteniamo: Problem solving Osservazione sull equazione delle lenti sottili Dall equazione delle lenti sottili si ricava che il reciproco della distanza dell immagine q è q f p, dove f è la distanza focale e p è la distanza dell oggetto. Perciò, dopo aver combinato i valori di f e p, è importante non dimenticare di calcolare il reciproco del risultato trovato per determinare q. q 9,6 m da cui: f p 0,0500 m 2,50 m q 0,050 m Poiché il valore di q è positivo, l immagine che si forma sulla pellicola è reale. Dall equazione dell ingrandimento troviamo che il valore di G è: q 0,050 m G 0,0204 p 2,50 m L immagine è più piccola dell oggetto (perché G ) ed è capovolta (perché G 0). Poiché l altezza dell oggetto è h o,70 m, l altezza dell immagine è: h i Gh o (0,0204)(,70 m) 0,0347 m ESEMPIO 5 Equazione delle lenti sottili L immagine virtuale formata da una lente divergente Un oggetto è posto a una distanza di 7,0 cm a sinistra di una lente divergente che ha una distanza focale f 5,08 cm. Trova la distanza dell immagine e dimostra che l immagine è virtuale. Calcola l ingrandimento. Ragionamento La situazione è simile a quella della figura Il diagramma dei raggi mostra che l immagine è virtuale, diritta e rimpicciolita rispetto all oggetto. Soluzione Per trovare la distanza dell immagine possiamo usare l equazione delle lenti sottili: q 0,338 cm da cui: f p 5,08 m 7,0 m q 2,96 m Il valore negativo di q indica che l immagine è virtuale e si forma a sinistra della lente. Poiché q e p sono note, dall equazione dell ingrandimento si ottiene: q 2,96 m G p 7,0 m 0,47 L immagine è diritta (perché G 0) e rimpicciolita rispetto all oggetto (perché G ). 407
16 CPITOLO 4 Dimostrazione delle equazioni delle lenti sottili e dell ingrandimento lineare Consideriamo i raggi e 3 della figura Il raggio è rappresentato separatamente nella parte della figura, in cui l angolo θ è uguale nei due triangoli rettangoli colorati. Perciò anche tg θ è uguale nei due triangoli: tg θ h o f Il segno meno del numeratore della frazione h i /(q f) è stato inserito per il seguente motivo: nella figura 4.24 l angolo θ è considerato positivo e, poiché l immagine è capovolta, l altezza dell immagine h i è negativa. Inserendo il segno meno il valore di h i /(q f), e quindi anche quello di tg θ, è un numero positivo. Il raggio 3 è rappresentato separatamente nella parte C della figura, in cui sono uguali gli angoli θ dei triangoli rettangoli colorati. Perciò si ha: h i q f tg θ h o p h i q Il segno meno del numeratore della frazione h i /q è stato inserito, come nel caso precedente, per assicurare che tg θ sia un numero positivo. Dalle due equazioni precedenti si ottiene rispettivamente: h i h o q f h q e i f p h o Uguagliando le due espressioni di h i /h o e disponendo opportunamente i termini, si ottiene l equazione delle lenti sottili: p q f L equazione dell ingrandimento si ricava direttamente dall equazione h i /h o q/p ricordando che il rapporto h i /h o è l ingrandimento G della lente. h o 3 Immagine h i f p q h o h o θ θ h i f q igura 4.24 Questi diagrammi dei raggi sono utilizzati nel testo per ricavare l equazione delle lenti sottili e l equazione dell ingrandimento. C h o p θ 3 θ q h i 408
17 CPITOLO Combinazioni di lenti Gli strumenti ottici, come il microscopio o il telescopio, usano particolari combinazioni di lenti per ottenere immagini degli oggetti con un ingrandimento maggiore di quello fornito da ciascuna singola lente. Per esempio, la figura 4.25 mostra il sistema a due lenti usato nei microscopi. La lente più vicina all oggetto è detta obiettivo, mentre quella più vicina all occhio dell osservatore è detta oculare. L oggetto è posto appena oltre il fuoco o dell obiettivo. L immagine formata dall obiettivo, indicata in figura come prima immagine, è reale, capovolta e ingrandita rispetto all oggetto. La prima immagine serve come oggetto per l oculare. Poiché la prima immagine si forma fra l oculare e il suo fuoco e, l oculare ne forma un immagine virtuale e ingrandita che è raccolta dall occhio dell osservatore. Immagine finale (virtuale) o Lente (obiettivo) o Prima immagine (reale) e Lente 2 (oculare) e igura La combinazione di due lenti convergenti raffigurata può essere usata come microscopio composto per produrre un immagine virtuale, ingrandita e capovolta di un oggetto.. L obiettivo forma la prima immagine. C. L oculare forma l immagine finale. o Obiettivo o Prima immagine f o p q 6,0 mm C Prima immagine e Oculare e Immagine finale f e p 2 q 2 La posizione dell immagine finale formata da una combinazione di lenti può essere determinata applicando l equazione delle lenti sottili a ciascuna di esse separatamente. L importante è ricordare che l immagine prodotta da una lente serve come oggetto per la lente successiva. Inoltre si può dimostrare quanto segue: INGRNDIMENTO LINERE DELL COMINZIONE DI DUE LENTI L ingrandimento lineare G di una combinazione di due lenti è il prodotto degli ingrandimenti G e G 2 di ciascuna di esse: G G G 2 (4.7) 409
18 CPITOLO 4 ESEMPIO 6 Combinazione di lenti L unione fa la forza: due lenti diventano un microscopio L obiettivo e l oculare del microscopio composto della figura 4.25 sono lenti convergenti con distanze focali f o 5,0 mm e f e 25,5 mm. La distanza fra le due lenti è 6,0 mm. Un oggetto è posto a 24, mm dall oculare. Calcola a quale distanza il microscopio forma l immagine dell oggetto. Ragionamento e soluzione Mediante l equazione delle lenti sottili, calcoliamo la distanza della prima immagine, quella formata dall obiettivo (parte della figura): 0,0252 mm q f o p 5,0 mm 24, mm e quindi q 39,7 mm. La prima immagine diventa l oggetto per l oculare (parte C della figura), da cui dista: p 2 6,0 mm 39,7 mm 2,3 mm pplicando l equazione delle lenti sottili all oculare, otteniamo: 0,0077 mm 25,5 mm 2,3 mm e quindi: q 2 f e p 2 q 2 30 mm Il segno meno indica che l immagine è virtuale e si forma a sinistra dell oculare. 4.9 L occhio Umor acqueo Cornea Iride Iride igura 4.26 Cristallino Legamento sospensore Muscolo ciliare Retina Umor vitreo Un occhio umano visto in sezione verticale. Nervo ottico natomia L occhio, di cui la figura 4.26 mostra alcune delle componenti anatomiche principali, ha una forma approssimativamente sferica, con un diametro di circa 25 mm. La luce entra nell occhio attraverso una membrana trasparente chiamata cornea, che delimita una regione piena di un liquido trasparente (l umor acqueo), dietro la quale si trovano un diaframma (l iride), una lente chiamata cristallino, una regione riempita con una stanza gelatinosa (l umor vitreo) e infine la retina. La retina è la parte dell occhio sensibile alla luce ed è formata da milioni di cellule chiamate coni e bastoncelli. Quando sono stimolate dalla luce, queste cellule inviano tramite il nervo ottico, impulsi elettrici al cervello, che interpreta l immagine formata sulla retina. L iride è la parte colorata dell occhio e regola la quantità di luce che raggiunge la retina; si comporta infatti come un diaframma muscolare con un apertura centrale di dimensioni variabili, chiamata pupilla, attraverso cui entra la luce. Il diametro della pupilla può variare circa da 2 a 7 mm, restringendosi quando c è molta luce e dilatandosi quando c è poca luce. Una caratteristica di importanza fondamentale per il funzionamento dell occhio è che il cristallino è flessibile e la sua forma può essere modificata dai muscoli ciliari, che sono collegati a esso attraverso i legamenti sospensori. La capacità del cristallino di cambiare forma è alla base della capacità dell occhio di mettere a fuoco gli oggetti. 40 isica quotidiana L occhio umano Ottica Dal punto di vista ottico, l occhio umano è simile a una macchina fotografica: entrambi hanno un sistema di lenti e un diaframma con un apertura di dimensioni variabili al centro. Inoltre la retina dell occhio e la pellicola della macchina foto-
19 CPITOLO 4 grafica svolgono funzioni simili, perché entrambe registrano l immagine formata dal sistema di lenti. L immagine che si forma sulla retina è reale, capovolta e più piccola dell oggetto, e lo stesso avviene per l immagine che si forma sulla pellicola di una macchina fotografica. nche se l immagine che si forma sulla retina è capovolta, il cervello la interpreta come diritta. Per vedere un oggetto nitidamente, l occhio deve rifrangere i raggi incidenti che entrano nella pupilla in modo che vadano a formare un immagine nitida sulla retina. Per raggiungere la retina i raggi luminosi attraversano cinque mezzi diversi, ciascuno con un indice di rifrazione n diverso: l aria (n,00), la cornea (n,38), l umor acqueo (n,33), il cristallino (n,40 in media) e l umor vitreo (n,34). Ogni volta che la luce passa da un mezzo all altro, essa viene rifratta. Circa il 70% della deviazione totale avviene nel passaggio tra l aria e la cornea, perché questi due mezzi hanno indici di rifrazione molto diversi. Il cristallino contribuisce solo a un quarto della rifrazione totale, però la sua funzione è molto importante. Infatti la distanza tra cristallino e retina è fissa: l unico modo di formare sulla retina immagini di oggetti situati a distanze diverse dall occhio è quello di variare la distanza focale del cristallino. lontano vicino Cristallino rilassato Immagine sulla retina igura Quando è completamente rilassato, il cristallino ha la distanza focale massima e riesce a formare sulla retina un immagine nitida di un oggetto lontano.. Quando il muscolo ciliare è contratto, il cristallino ha la distanza focale minima e riesce a formare sulla retina un immagine nitida di un oggetto vicino. Cristallino contratto Immagine sulla retina Quando l occhio guarda un oggetto molto lontano, i muscoli ciliari non sono contratti e il cristallino ha la curvatura minima e, di conseguenza, la distanza focale massima. In queste condizioni si dice che l occhio è «completamente a riposo» (figura 4.27). Quando l oggetto è più vicino all occhio, i muscoli ciliari si contraggono, per aumentare la curvatura del cristallino e quindi diminuire la sua distanza focale (figura 4.27). Quando sulla retina si forma un immagine nitida di un oggetto, si dice che l occhio è «messo a fuoco» sull oggetto. Il meccanismo con cui il cristallino cambia la sua distanza focale per mettere a fuoco oggetti a distanze diverse è chiamato accomodamento. La distanza minima dall occhio a cui si può trovare un oggetto che forma un immagine nitida sulla retina è chiamata punto prossimo dell occhio. Quando un oggetto si trova nel punto prossimo, i muscoli ciliari sono completamente contratti. Per una persona giovane il punto prossimo si trova a circa 25 cm dall occhio. Questa distanza aumenta notevolmente con il passare degli anni: diventa di circa 50 cm a quarant anni e di circa 500 cm a sessant anni. Il punto remoto dell occhio è la distanza massima a cui può trovarsi un oggetto per essere messo a fuoco da un occhio completamente a riposo. Le persone con una vista normale riescono a vedere oggetti molto lontani, come i pianeti e le stelle, e perciò si dice che il loro punto remoto è all infinito. Miopia Una persona miope riesce a mettere a fuoco gli oggetti vicini ma non a vedere bene gli oggetti lontani, perché il punto remoto del suo occhio non è all infinito, ma può trovarsi a tre o quattro metri di distanza. La distanza focale di un occhio miope è minore di quella di un occhio normale e quindi i raggi che provengono da un ogget- isica quotidiana La miopia 4
20 CPITOLO 4 to lontano formano un immagine nitida davanti alla retina, come mostra la figura 4.28, e di conseguenza l immagine sulla retina è sfocata. La miopia può essere corretta con lenti divergenti, come indica la figura I raggi provenienti dall oggetto divergono dopo aver attraversato la lente; quando vengono rifratti dall occhio verso l asse ottico, l immagine si forma più lontano e cade sulla retina. Poiché un occhio miope, quando è rilassato, riesce a mettere a fuoco un oggetto situato nel suo punto remoto ma non più lontano, le lenti divergenti usate per correggere la miopia sono progettate in modo da formare l immagine di un oggetto lontano nel punto remoto dell occhio (figura 4.28C). igura Quando una persona miope guarda un oggetto lontano, l immagine dell oggetto si forma davanti alla retina e di conseguenza risulta sfocata.. Mettendo una lente divergente davanti all occhio, l immagine si sposta sulla retina e viene vista nitidamente. C. La lente divergente è sagomata in modo da formare un immagine virtuale di un oggetto lontano nel punto remoto di un occhio miope. lontano lontano Punto remoto di un occhio miope Punto remoto di un occhio miope Cristallino rilassato Lente divergente Immagine formata davanti alla retina lontano Immagine virtuale formata dalla lente divergente Immagine formata sulla retina C Punto remoto di un occhio miope Problem solving pplicazione dell equazione delle lenti sottili in presenza di occhiali La distanza abituale tra gli occhiali e gli occhi è di 2 cm. Se necessario, ricorda di tenere conto di questi 2 cm quando devi determinare la distanza dell oggetto e quella dell immagine (p e q) da usare nell equazione delle lenti sottili. ESEMPIO 7 Equazione delle lenti sottili Occhiali per miopi Il punto remoto di una persona miope si trova a soli 52 cm di distanza dall occhio. La distanza tra le lenti degli occhiali e l occhio è di 2 cm. Calcola la distanza focale delle lenti divergenti che permettono a questa persona di vedere gli oggetti molto lontani. Ragionamento e soluzione Il punto remoto è a 52 cm 2 cm 59 cm di distanza dalla lente e a sinistra di essa (figura 4.28C). La distanza dell immagine è perciò q 59 cm (il segno meno indica che l immagine è virtuale e si forma a sinistra della lente). L oggetto si trova molto lontano dalla lente, in pratica a distanza infinita: quindi p. La distanza focale f si ricava dall equazione delle lenti sottili: da cui: f 59 cm f p q 59 cm 42 isica quotidiana L ipermetropia Ipermetropia Una persona ipermètrope vede bene gli oggetti lontani ma non mette a fuoco gli oggetti vicini. Mentre il punto prossimo dell occhio di una persona giovane e con una vista normale è a circa 25 cm dall occhio, il punto prossimo di una persona ipermetrope può trovarsi notevolmente più lontano, fino a diverse centinaia di centimetri. La distanza focale minima di un occhio ipermetrope è maggiore di quella di un occhio normale, quindi i raggi provenienti da un oggetto molto vicino formerebbero un immagine nitida dietro la retina come mostra la figura In realtà la luce non può attraversare la retina, di conseguenza l immagine che si forma su di essa è sfocata.
Radiazione elettromagnetica
 Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
1.Visione_01 Ottica geometrica. Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona
 1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
1.Visione_01 Ottica geometrica Prof. Carlo Capelli Fisiologia Corso di Laurea in Scienze delle Attività Motorie e Sportive Università di Verona Obiettivi Principi di refrazione delle lenti, indice di refrazione
Ottica geometrica. L ottica geometrica tratta i. propagazione in linea retta e dei. rifrazione della luce.
 Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Ottica geometrica L ottica geometrica tratta i fenomeni che si possono descrivere per mezzo della propagazione in linea retta e dei fenomeni di riflessione e la rifrazione della luce. L ottica geometrica
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Laboratorio per il corso Scienza dei Materiali II
 UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
UNIVERSITÀ DI CAMERINO Corso di Laurea Triennale in Fisica Indirizzo Tecnologie per l Innovazione Laboratorio per il corso Scienza dei Materiali II a.a. 2009-2010 Docente: E-mail: Euro Sampaolesi eurosampaoesi@alice.it
Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
 Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Lenti sottili: Definizione
 Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili: Definizione La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
28/05/2009. La luce e le sue illusioni ottiche
 La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
OTTICA TORNA ALL'INDICE
 OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
PROGRAMMA OPERATIVO NAZIONALE
 PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
- Formazione delle immagini per riflessione: specchio sferico
 Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
Ottica geometrica: - condizione di validità: o occorre conrontare la lunghezza d onda λ della luce e le dimensioni degli oggetti su cui la luce incide. Se λ è MINORE, valgono le leggi dell ottica geometrica.
PERCORSO DIDATTICO DI OTTICA GEOMETRICA
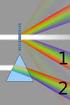
 PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
PERCORSO DIDATTICO DI OTTICA GEOMETRICA Tipo di scuola e classe: Liceo Scientifico, classe II Nodi concettuali: riflessione della luce; rifrazione della luce, riflessione totale, rifrazione attraverso
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La lente singola rimane ancora in uso nelle macchine più economiche e, entro certi limiti, dà dei risultati accettabili.
 O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti
 L occhio MPZ 1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti retina muscolo cornea iride pupilla cristallino nervo
L occhio MPZ 1. Come funziona l occhio normale? Cosa caratterizza i difetti della vista? Come correggerli? Prova ad osservare con le diverse lenti retina muscolo cornea iride pupilla cristallino nervo
Costruirsi un cannocchiale galileiano
 Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
1 Introduzione 1. Ottica Geometrica
 1 Introduzione 1 1 Introduzione Ottica Geometrica 1.1 Estratto Lo scopo di questa esperienza è quello di apprendere come la luce interagisce con elementi ottici quali le lenti, e come, in sequito alla
1 Introduzione 1 1 Introduzione Ottica Geometrica 1.1 Estratto Lo scopo di questa esperienza è quello di apprendere come la luce interagisce con elementi ottici quali le lenti, e come, in sequito alla
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale...
 IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
19 Il campo elettrico - 3. Le linee del campo elettrico
 Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Prof. Gian Piero Pugliese Lezioni di Fisica
 Prof. Gian Piero Pugliese Lezioni di Fisica Il miraggio Fin dai tempi più remoti, il miraggio è stato un fenomeno che ha destano nell uomo paura e al tempo stesso meraviglia, proprio perché non conosciuto
Prof. Gian Piero Pugliese Lezioni di Fisica Il miraggio Fin dai tempi più remoti, il miraggio è stato un fenomeno che ha destano nell uomo paura e al tempo stesso meraviglia, proprio perché non conosciuto
Dai colori alle stelle: un excursus tra Fisica e Ottica
 Dai colori alle stelle: un excursus tra Fisica e Ottica Martina Giordani Facoltà di Scienze matematiche, fisiche e naturali Corso di Laurea in Ottica e Optometria Federica Ricci Facoltà di Scienze matematiche,
Dai colori alle stelle: un excursus tra Fisica e Ottica Martina Giordani Facoltà di Scienze matematiche, fisiche e naturali Corso di Laurea in Ottica e Optometria Federica Ricci Facoltà di Scienze matematiche,
Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione
 Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione 1. L elettrone ha una massa di 9.1 10-31 kg ed una carica elettrica di -1.6 10-19 C. Ricordando che la forza gravitazionale
Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione 1. L elettrone ha una massa di 9.1 10-31 kg ed una carica elettrica di -1.6 10-19 C. Ricordando che la forza gravitazionale
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
SCIENTIA MAGISTRA VITAE
 1 -Argomento Lenti fatte in casa Esperimenti usando lenti realizzate con materiali a costo nullo o basso o di riciclo. Cosa serve: acqua, bottiglie di plastica trasparente (es. quelle dell acqua minerale
1 -Argomento Lenti fatte in casa Esperimenti usando lenti realizzate con materiali a costo nullo o basso o di riciclo. Cosa serve: acqua, bottiglie di plastica trasparente (es. quelle dell acqua minerale
Ciao!! Un cielo stellato così come lo puoi vedere con i tuoi occhi. Il cielo visto da un potente telescopio molto lontano dalle città
 1 Ciao!! Quando guardi il cielo ogni volta che si fa buio, se è sereno, vedi tanti piccoli punti luminosi distribuiti nel cielo notturno: le stelle. Oggi si apre l immaginario Osservatorio per guardare...
1 Ciao!! Quando guardi il cielo ogni volta che si fa buio, se è sereno, vedi tanti piccoli punti luminosi distribuiti nel cielo notturno: le stelle. Oggi si apre l immaginario Osservatorio per guardare...
INTRODUZIONE: PERDITE IN FIBRA OTTICA
 INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto
 Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto rimanda indietro arriva ai nostri occhi. Dipende da: SI PROPAGA
Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto rimanda indietro arriva ai nostri occhi. Dipende da: SI PROPAGA
4.6 Lenti Capitolo 4 Ottica
 4.6 Lenti Esercizio 04 Due lenti biconvesse sono posizionate lungo il cammino ottico di un fascio di luce, separate da una distanza d. Il fascio di luce è parallelo e esce parallelo dopo le due lenti.
4.6 Lenti Esercizio 04 Due lenti biconvesse sono posizionate lungo il cammino ottico di un fascio di luce, separate da una distanza d. Il fascio di luce è parallelo e esce parallelo dopo le due lenti.
2.1 CAPITOLO 2 I RAGGI E LE LORO PROPRIETÀ
 2.1 CAPITOLO 2 I RAGGI E LE LORO PROPRIETÀ 2.2 Riflettendo sulla sensazione di calore che proviamo quando siamo esposti ad un intensa sorgente luminosa, ad esempio il Sole, è naturale pensare alla luce
2.1 CAPITOLO 2 I RAGGI E LE LORO PROPRIETÀ 2.2 Riflettendo sulla sensazione di calore che proviamo quando siamo esposti ad un intensa sorgente luminosa, ad esempio il Sole, è naturale pensare alla luce
All interno dei colori primari e secondari, abbiamo tre coppie di colori detti COMPLEMENTARI.
 Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
OTTICA. Ottica geometrica. Riflessione e rifrazione
 Ottica geometrica OTTICA Sappiamo che la luce è un onda elettromagnetica. Essa perciò può non propagarsi in linea retta, analogamente alle altre onde (p. es. quelle sonore). Però, come avviene per tutte
Ottica geometrica OTTICA Sappiamo che la luce è un onda elettromagnetica. Essa perciò può non propagarsi in linea retta, analogamente alle altre onde (p. es. quelle sonore). Però, come avviene per tutte
Ottica fisiologica (2): sistemi ottici
 Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
IL MICROSCOPIO OTTICO. DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011
 IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
IL MICROSCOPIO OTTICO DOWNLOAD Il pdf di questa lezione (microscopio2.pdf) è scaricabile dal sito http://www.ge.infn.it/ calvini/fistrum/ 09/03/2011 Lo scopo di questi appunti è la descrizione dei principi
Specchio parabolico: MIRASCOPE. a cura di Pietro Pozzoli
 Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
Specchio parabolico: MIRASCOPE Proprietà coinvolte: Rifrazione dei raggi partenti dal fuoco lungo rette parallele all asse Focalizzazione dei raggi paralleli all asse sul fuoco PUNTO DI VISTA FISICO: Quali
Interazione & Multimedia 1
 Il nostro viaggio nell image processing deve iniziare con lo studio di come l occhio umano percepisce una immagine e come la elabora. Ci interessa capire quali sono i limiti della visione umana al fine
Il nostro viaggio nell image processing deve iniziare con lo studio di come l occhio umano percepisce una immagine e come la elabora. Ci interessa capire quali sono i limiti della visione umana al fine
SISTEMA NERVOSO E ORGANI DI SENSO
 Unità SISTEMA NERVOSO E ORGANI DI SENSO Il sistema nervoso Un uomo viaggia in autostrada. E molto attento: guarda le auto che gli stanno davanti, guarda lo specchietto retrovisore, controlla la velocità,
Unità SISTEMA NERVOSO E ORGANI DI SENSO Il sistema nervoso Un uomo viaggia in autostrada. E molto attento: guarda le auto che gli stanno davanti, guarda lo specchietto retrovisore, controlla la velocità,
Definizione di lente. Tipi di lenti
 LENTI Sommario Definizione di lente... 2 Tipi di lenti... 2 Punti e piani principali... 5 Punti e piani nodali... 10 Terminologia... 12 Focale, distanze coniugate ed ingrandimento... 19 Immagine generata
LENTI Sommario Definizione di lente... 2 Tipi di lenti... 2 Punti e piani principali... 5 Punti e piani nodali... 10 Terminologia... 12 Focale, distanze coniugate ed ingrandimento... 19 Immagine generata
La propagazione della luce in una fibra ottica
 La propagazione della luce in una fibra ottica La rifrazione della luce Consideriamo due mezzi trasparenti alla luce, separati da una superficie piana. Il primo mezzo ha indice di rifrazione n, il secondo
La propagazione della luce in una fibra ottica La rifrazione della luce Consideriamo due mezzi trasparenti alla luce, separati da una superficie piana. Il primo mezzo ha indice di rifrazione n, il secondo
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE
 I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
L elemento fondamentale è l obiettivo, ovvero la lente o lo specchio che forniscono l immagine dell oggetto.
 Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Risultati Esercizi volume Ottica Visuale
 Risultati Esercizi volume Ottica Visuale Zeri F, Rossetti A, Fossetti A, Calossi A. Capitolo 2 Es.2.1: Effettuare il calcolo del potere della cornea, attraverso la formula per lenti sottili usando i dati
Risultati Esercizi volume Ottica Visuale Zeri F, Rossetti A, Fossetti A, Calossi A. Capitolo 2 Es.2.1: Effettuare il calcolo del potere della cornea, attraverso la formula per lenti sottili usando i dati
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni?
 La natura della luce Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni? Se si potesse fotografare un fotone in un certo istante vedremmo una deformazione
La natura della luce Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni? Se si potesse fotografare un fotone in un certo istante vedremmo una deformazione
MOTO DI UNA CARICA IN UN CAMPO ELETTRICO UNIFORME
 6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini
 SSIS indirizzo Fisico - Informatico - Matematico 2 anno - a.a.. 2006/2007 Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini LA LUCE La luce è un onda elettromagnetica Il principio
SSIS indirizzo Fisico - Informatico - Matematico 2 anno - a.a.. 2006/2007 Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini LA LUCE La luce è un onda elettromagnetica Il principio
Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica
 Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica Richiami teorici Equazione della lente sottile in approssimazione parassiale: p + q = () f dove: p = distanza oggetto-lente q = distanza
Corso di Laurea in Ottica e Optometria Laboratorio di Ottica Geometrica Richiami teorici Equazione della lente sottile in approssimazione parassiale: p + q = () f dove: p = distanza oggetto-lente q = distanza
Il controllo della visualizzazione
 Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Capitolo 3 Il controllo della visualizzazione Per disegnare in modo preciso è necessario regolare continuamente l inquadratura in modo da vedere la parte di disegno che interessa. Saper utilizzare gli
Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE
 Titolo: Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE Autore: Elisabetta Caroti Percorsi didattici associati: 1. Investigazioni sul modello particellare AVVERTENZA: Le domande che
Titolo: Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE Autore: Elisabetta Caroti Percorsi didattici associati: 1. Investigazioni sul modello particellare AVVERTENZA: Le domande che
Lunghezza ocale. Donato Di Bello
 F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
Spettrofotometria. Le onde luminose consistono in campi magnetici e campi elettrici oscillanti, fra loro perpendicolari.
 Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Gli strumenti ottici. Capitolo. Concetti da rivedere 22.1 I SISTEMI DI LENTI
 22txtI:GIAMBATTISTA 4-2-2007 2:03 Pagina 865 Capitolo 22 Gli strumenti ottici La distinzione tra immagini reali e virtuali (Paragrafo 2.6) L ingrandimento (Paragrafo 2.8) La rifrazione (Paragrafo 2.3)
22txtI:GIAMBATTISTA 4-2-2007 2:03 Pagina 865 Capitolo 22 Gli strumenti ottici La distinzione tra immagini reali e virtuali (Paragrafo 2.6) L ingrandimento (Paragrafo 2.8) La rifrazione (Paragrafo 2.3)
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
4 La Polarizzazione della Luce
 4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini 1.1 Caratteristiche ottiche dei materiali oftalmici
 1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini Esaminiamo in questo capitolo le principali caratteristiche dei vari materiali utilizzati nel campo dell'ottica oftalmica,
1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini Esaminiamo in questo capitolo le principali caratteristiche dei vari materiali utilizzati nel campo dell'ottica oftalmica,
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA
 EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
CONOSCERE LA LUCE. Propagazione nello spazio di un onda elettromagnetica.
 FOTODIDATTICA CONOSCERE LA LUCE Le caratteristiche fisiche, l analisi dei fenomeni luminosi, la temperatura di colore. Iniziamo in questo fascicolo una nuova serie di articoli che riteniamo possano essere
FOTODIDATTICA CONOSCERE LA LUCE Le caratteristiche fisiche, l analisi dei fenomeni luminosi, la temperatura di colore. Iniziamo in questo fascicolo una nuova serie di articoli che riteniamo possano essere
Energia potenziale elettrica e potenziale. In queste pagine R indicherà una regione in cui è presente un campo elettrostatico.
 Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Colori e Arcobaleno. La composizione della luce
 Colori e Arcobaleno Noi vediamo grazie alla luce, ma che cosa sono tutti i colori che ci circondano? La luce del Sole è proprio bianca come la vediamo? Come si forma l arcobaleno? Perché il cielo è azzurro?
Colori e Arcobaleno Noi vediamo grazie alla luce, ma che cosa sono tutti i colori che ci circondano? La luce del Sole è proprio bianca come la vediamo? Come si forma l arcobaleno? Perché il cielo è azzurro?
Appunti sul galleggiamento
 Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
APPENDICE 1 DISPOSITIVI OBBLIGATORI DISPOSITIVI FACOLTATIVI
 APPENDICE 1 M O T O C I C L I A - Luce posizione anteriore; B - Luce posizione posteriore; D - Luce targa; E - Proiettore; G - Luce di arresto; O - Catadiottro rosso. I - Proiettore fendinebbia Tutti i
APPENDICE 1 M O T O C I C L I A - Luce posizione anteriore; B - Luce posizione posteriore; D - Luce targa; E - Proiettore; G - Luce di arresto; O - Catadiottro rosso. I - Proiettore fendinebbia Tutti i
Oggetto SEZIONE O «ONDE. Muscoli. ciliare. Cornea. Retina. Nervo ottico. Umore acqueo. A Figura 1. Gli elementi fondamentali dell'occhio
 SEZIONE O «ONDE Cornea Umore acqueo Muscolo ciliare Retina Nervo ottico A Figura 1. Gli elementi fondamentali dell'occhio umano. La luce entra nell'occhio attraverso la cornea e il cristallino. Viene fecalizzata
SEZIONE O «ONDE Cornea Umore acqueo Muscolo ciliare Retina Nervo ottico A Figura 1. Gli elementi fondamentali dell'occhio umano. La luce entra nell'occhio attraverso la cornea e il cristallino. Viene fecalizzata
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Traduzioni & Corsi di Lingue Udine. Via Cussignacco 27/4. P. IVA: 02159420302 tel/fax: 0432-229621 scuola@jmi.it
 APPUNTI PRIMO INCONTRO Sono passati quasi duecento anni dall invenzione dei primi strumenti in grado di registrare immagini ma si può dire che la fotocamera è costituita dagli stessi elementi basilari
APPUNTI PRIMO INCONTRO Sono passati quasi duecento anni dall invenzione dei primi strumenti in grado di registrare immagini ma si può dire che la fotocamera è costituita dagli stessi elementi basilari
Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) Prof. Gianluca Todisco
 Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) 1 LA LUCE NELLA STORIA Nell antica Grecia c era chi (i pitagorici) pensavano che ci fossero dei fili sottili che partono dagli
Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) 1 LA LUCE NELLA STORIA Nell antica Grecia c era chi (i pitagorici) pensavano che ci fossero dei fili sottili che partono dagli
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Qual è la differenza fra la scala Celsius e la scala assoluta delle temperature?
 ISTITUTO DI ISTRUZIONE SECONDARIA DANIELE CRESPI Liceo Internazionale Classico e Linguistico VAPC02701R Liceo delle Scienze Umane VAPM027011 Via G. Carducci 4 21052 BUSTO ARSIZIO (VA) www.liceocrespi.it-tel.
ISTITUTO DI ISTRUZIONE SECONDARIA DANIELE CRESPI Liceo Internazionale Classico e Linguistico VAPC02701R Liceo delle Scienze Umane VAPM027011 Via G. Carducci 4 21052 BUSTO ARSIZIO (VA) www.liceocrespi.it-tel.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it
 LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
Ottica geometrica. Superfici rifrangenti e lenti
 Nome ile d:\scuola\corsi\corso isica\ottica\lenti.doc Creato il 09/05/003 0.33 Dimensione ile: 48640 byte Andrea Zucchini Elaborato il 8/05/003 alle ore.54, salvato il 8/05/03 0.54 stampato il 8/05/003.54
Nome ile d:\scuola\corsi\corso isica\ottica\lenti.doc Creato il 09/05/003 0.33 Dimensione ile: 48640 byte Andrea Zucchini Elaborato il 8/05/003 alle ore.54, salvato il 8/05/03 0.54 stampato il 8/05/003.54
Scuola Media Piancavallo 2
 LA CELLULA Una caratteristica di quasi tutti gli esseri viventi è quella di possedere una struttura più o meno complessa in cui parti diverse, gli organi, sono adatte a svolgere funzioni specifiche. Il
LA CELLULA Una caratteristica di quasi tutti gli esseri viventi è quella di possedere una struttura più o meno complessa in cui parti diverse, gli organi, sono adatte a svolgere funzioni specifiche. Il
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Orietta Bay - Sestri Levante 2011
 Per -corso Orietta Bay - Sestri Levante 2011 Per -corso Fotografare è saper cogliere l essenza delle cose e degli avvenimenti e Scriverli con la luce La macchina fotografica Il cuore originario della
Per -corso Orietta Bay - Sestri Levante 2011 Per -corso Fotografare è saper cogliere l essenza delle cose e degli avvenimenti e Scriverli con la luce La macchina fotografica Il cuore originario della
LA FASE MONOCULARE DELL ESAME VISIVO. Relatore: Silvio Maffioletti
 LA FASE MONOCULARE DELL ESAME VISIVO Relatore: Silvio Maffioletti La fase monoculare Sistemare il forottero davanti al soggetto Metterlo in bolla Regolare la distanza interpupillare Controllare la distanza
LA FASE MONOCULARE DELL ESAME VISIVO Relatore: Silvio Maffioletti La fase monoculare Sistemare il forottero davanti al soggetto Metterlo in bolla Regolare la distanza interpupillare Controllare la distanza
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
la luce 14.1 La propagazione della luce n La propagazione della luce
 online.zanichelli.it/ruffo_fisica, pagina Prerequisiti 4unità 4 la luce 4. La propagazione della luce IDE-CHIVE In un mezzo omogeneo, la luce si propaga in linea retta con velocità costante; il valore
online.zanichelli.it/ruffo_fisica, pagina Prerequisiti 4unità 4 la luce 4. La propagazione della luce IDE-CHIVE In un mezzo omogeneo, la luce si propaga in linea retta con velocità costante; il valore
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Luce e colore A cura di Ornella Pantano e Enrica Giordano
 Cosa serve per vedere Didattica della Fisica A.A. 2009/10 Luce e colore A cura di Ornella Pantano e Enrica Giordano Per poter vedere un oggetto è necessario che un fascio di luce emesso da una sorgente
Cosa serve per vedere Didattica della Fisica A.A. 2009/10 Luce e colore A cura di Ornella Pantano e Enrica Giordano Per poter vedere un oggetto è necessario che un fascio di luce emesso da una sorgente
Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza assiale)
 Ovvero le ametropie che possiamo riscontrare nell occhio Ametropia Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza
Ovvero le ametropie che possiamo riscontrare nell occhio Ametropia Condizione oculare in cui la potenza refrattiva dell occhio non è proporzionata alla distanza fra l apice corneale e la retina (lunghezza
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
