Elementi di meccanica dei fluidi
|
|
|
- Graziano Dante Righi
- 8 anni fa
- Visualizzazioni
Transcript
1 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Caitolo 3 Elementi di meccanica dei fluidi 3.
2 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE Introduzione In molti imianti il collegamento fra i vari comonenti è costituito da una tubazione in grado di contenere un fluido. Lo scoo del fluido uò essere quello del trasorto di una qualsiasi delle grandezze di stato che lo caratterizzano; la finalità dell imianto uò quindi essere quella del trasorto di una massa (collegata quindi alla densità) come ad esemio nell imianto combustibile o nell imianto di ventilazione, del trasorto di una forza (collegata quindi alla ressione) come ad esemio nell imianto oleodinamico, del trasorto di calore (collegato quindi alla temerature) come ad esemio nell imianto antighiaccio. Le leggi che reggono il funzionamento dell imianto sono le stesse indiendentemente dalle sue finalità; otranno al massimo assumere maggiore o minore imortanza, e quindi essere in ratica trascurabili, alcuni termini. Verranno in seguito richiamate le leggi fondamentali er il calcolo del flusso interno utili er il rogetto e la verifica degli imianti a fluido. 3. Caratteristiche rinciali dei fluidi idraulici I fluidi in genere sono caratterizzati da un certo numero di rorietà fisiche di cui qui si elencano le iù rilevanti, indicando le unità di misura utilizzate secondo il sistema metrico internazionale ed in ratica. Densità La densità (o massa volumica) è la massa dell'unità di volume di una determinata sostanza. Essa diende dalla ressione e dalla temeratura (fig. 3.), ha dimensioni [ML -3 ] ed ha le seguenti misure: sistema metrico internazionale kg/m 3 sistema tecnico kg f s /m 4 sistema anglosassone lb f s /ft DENSITA' [kg/m3] TEMPERATURA [ C] 3.
3 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Fig Densità in funzione della temeratura (liquido a base etrolifera) Peso secifico Il eso secifico è il eso dell'unità di volume. Ha dimensioni [FL -3 ] o, iù formalmente, [ML - T - ]. E' legato alla densità dalla relazione γ = ρg, dove g è l'accelerazione di gravità. Pure esso è diendente da ressione e temeratura. Il eso secifico ha le seguenti misure: sistema metrico internazionale N/m 3 sistema tecnico kg f /m 3 sistema anglosassone lb f /ft 3 Pressione La ressione è data dal raorto fra una forza e l'area su cui questa agisce. Dimensionalmente è quindi [FL - ], le unità di misura utilizzate sono varie: sistema metrico internazionale N/m o Pa sistema tecnico kg f /m sistema tecnico anglosassone si = lb f /in Il Pascal è un'unità di misura iccola er cui vengono iù usati il kpa o il MPa, anche se sono ancora molto in uso le vecchie unità, comrese quelle che misurano la ressione come altezza equivalente di una colonna di acqua o mercurio: atm 035 Pa at 9806 Pa kg/cm bar Pa 0 baria baria 0. Pa dyne/cm kg/m 9.8 Pa si 6890 Pa mmhg 33.3 Pa mh O 9.8 Pa Viscosità La viscosità è la caacità di un fluido a resistere a forze tangenziali. Per far scorrere l uno risetto all altro due iani aralleli searati da un fluido, è necessaria una forza F roorzionale alla suerficie di contatto A, alla velocità relativa v ed inversamente roorzionale alla distanza h delle due suerfici: da cui: F = µ Av h µ = Fh Av Le dimensioni della viscosità sono quindi [FL - T]. Le unità di misura della viscosità sono le seguenti: 3.3
4 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 sistema metrico internazionale Ns/m o Pa s sistema tecnico kg f s/m sistema anglosassone lb f s/m ma in ratica vengono semre usati il oise P o il centioise cp, essendo: P = dyne s/cm = 0. Pa s. E sesso usata anche la viscosità cinematica, data dal raorto fra la viscosità e la densità: ν µ = ρ ed avente le dimensioni di una lunghezza er una velocità [L T - ], è usualmente misurata in stokes St: St = cm /s o iù comunemente in centistokes cst: cst = 0-6 m /s La viscosità diende fortemente dalla temeratura, come evidente nel diagramma di fig VISCOSITA' CINEMATICA [cst] TEMPERATURA [ C] Fig Viscosità in funzione della temeratura (liquido a base etrolifera) Tensione di vaore La tensione di vaore è la grandezza iù significativa er descrivere la volatilità di un liquido. Un fluido allo stato liquido è caratterizzato dall'avere un volume rorio; se il fluido viene osto in un reciiente di volume maggiore del volume del liquido, nel reciiente il fluido si trova arzialmente allo stato liquido e arzialmente allo stato gassoso. La ressione alla quale 3.4
5 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 viene a trovarsi lo stato gassoso è detta tensione di vaore e diende dalla temeratura (fig. 3.3); er esemio la tensione di vaore dell acqua a 00 C è notoriamente di bar. La tensione di vaore è un arametro fondamentale er l'equilibrio fra le due fasi del fluido ed è un indice della tendenza del liquido ad evaorare. La tensione di vaore viene misurata con le stesse unità di misura della ressione. Una grandezza correlata alla tensione di vaore è il unto di ebollizione, la temeratura cioè alla quale il liquido tende a assare allo stato gassoso, questa temeratura è funzione della ressione TENSIONE DI VAPORE [Pa] TEMPERATURA [ C] Fig Tensione di vaore in funzione della temeratura (liquido a base etrolifera) Infiammabilità L infiammabilità è una caratteristica molto imortante er la sicurezza dell'imianto e del velivolo stesso; viene caratterizzata attraverso tre temerature caratteristiche:. unto di infiammabilità: temeratura minima alla quale il liquido, vaorizzato in modo definito, crea una miscela caace di incendiarsi in resenza di una fiamma;. unto di fiamma: temeratura minima alla quale si genera vaore sufficiente a mantenere la combustione; 3. unto di autoignizione: temeratura alla quale si crea una fiamma sontaneamente in resenza di aria senza essere innescata. Comrimibilità I fluidi imiegati negli imianti idraulici sono liquidi e quindi caratterizzati dall'avere un volume rorio; in realtà sotto effetto della ressione il fluido tende a comrimersi e a ridurre il rorio volume; una misura di questo effetto è data dal modulo di comrimibilità definito come raorto fra la variazione ercentuale di volume e la variazione di ressione che la ha rodotta, come meglio descritto in seguito (ar 3.3). 3.5
6 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Resistenza all aria L aria uò essere resente nel fluido sotto 3 forme: disciolta, disersa in bollicine ben distinte e in schiuma, ossia bolle agglomerate in suerficie. Gli ultimi due casi sono da evitare er il corretto funzionamento dell imianto, in quanto vengono radicalmente modificate le caratteristiche fisiche del liquido. Stabilità La stabilità chimica è la tendenza a mantenere invariate le rinciali caratteristiche. Si arla in genere di: stabilità all ossidazione, ossia alla reazione con l ossigeno; stabilità termica, ossia alla decomosizione rodotta dalla temeratura; stabilità all idrolisi, ossia alla reazione con l acqua. Corrosione Indica l aggressività del fluido sui materiali usati negli imianti. Può essere di due tii: corrosione chimica, in genere ossidazione o attacco acido; corrosione elettrochimica, tiicamente quella galvanica, che interviene nel contatto di due metalli bagnati da un elettrolito. 3.3 Equazione di stato e modulo di comrimibilità Le grandezze fondamentali che definiscono lo stato di un fluido sono, come noto: ressione [FL - ]=[MLT - ] densità ρ [ML -3 ] temeratura T [ ] Le grandezze di stato non sono indiendenti, ma legate dall equazione di stato che nel caso dei gas erfetti assume la nota forma: = Rρ T questa relazione è valida er gas erfetti, in un ben reciso camo di ressioni e temerature; il coefficiente di roorzionalità R ha un valore diendente dalla comosizione del gas ed in articolare dal eso molecolare degli elementi che lo comongono. Per i gas esistono formulazioni dell equazione di stato iù comlesse valide anche in condizioni iù amie. Per i liquidi non è invece ossibile determinare un equazione di stato che abbia un sufficiente camo di validità; si ricorre quindi ad una linearizzazione che orta ad un equazione di stato valida solo nell intorno di un unto noto. Tale equazione, esressa iù comunemente in funzione del volume secifico, ha la forma: V = + α T V β 3.6
7 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 La arte dell equazione di stato che fornisce il legame densità - ressione (sia ure questo esresso in termini volumetrici), a temeratura costante, diventa così in termini finiti: /b V = β V PRESSIONE Fig Andamento qualitativo del modulo di comrimibilità con la ressione o in termini differenziali : d = β dv V Come noto si ammette normalmente che i liquidi siano incomrimibili; questo orterebbe da un unto di vista matematico ad un valore infinito di β; fisicamente è invece evidente che, er quanto iccola, esista una certa comrimibilità nei liquidi, anche se questa è talmente iccola che er molte alicazioni ratiche risulta trascurabile. Il modulo di comrimibilità β (bulk modulus nella letteratura anglosassone) è diendente in modo non lineare dalla ressione, secondo un andamento qualitativamente descritto in fig. 3.4; er l utilizzo della relazione in termini finiti occorrerà quindi considerarne un valore medio. β ha le dimensioni di una ressione ed il suo valore diende dalla ressione; si uò assumere er V V [MPa] Tab Contrazione del volume in funzione del salto di ressione i vari fluidi utilizzati negli imianti oleodinamici, imianti oeranti alle iù alte ressioni, dove quindi la comrimibilità è in grado di far sentire i suoi effetti, valori dell ordine di grandezza di 500 MPa. Assumendo tale valore come valore medio indiendente dalla ressione ne derivano le variazioni di volume del fluido riortate in tab. 3.. Variazioni di ressione dell ordine di grandezza dei 0 MPa, che sono valori utilizzati negli imianti oleodinamici di bordo, sono quindi in grado di ridurre il volume del fluido già di una quantità sueriore all.3%; d altra arte variazioni di volume dell ordine dell % sono in grado di far nascere variazioni di ressione dell ordine dei 5 MPa. In effetti l equazione di stato deve essere vista come l analoga dell equazione di Hooke er i solidi; la ressione definisce lo stato di sforzo e la variazione di volume corrisonde alle deformazioni. Per quanto riguarda il termine legato alla temeratura: 3.7
8 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 V V = α T Il valore di α è circa C - er un olio idraulico. Le conseguenze dalla dilatazione rovocate da variazioni di temeratura sono in incremento di ressione se il liquido è contenuto in un volume chiuso, o in una variazione di volume del contenitore se questa è ossibile come avviene er esemio nei cilindri attuatori. 3.4 Modulo di comrimibilità effettivo Per quanto riguarda i valori del modulo di comrimibilità, occorre fare attenzione che nella ratica si deve tenere conto anche del fatto che in un imianto, nonostante tutte le recauzioni che si ossono rendere, è inevitabilmente contenuto oltre al liquido anche una frazione di gas e che i comonenti dell imianto, er quanto rigidi, ossono resentare una certa elasticità e quindi er effetto della ressione si deformano aumentando il loro volume. Il comortamento del gas esresso in termini di modulo di comrimibilità è facilmente ottenibile dato che questo è ricavato in condizioni isoterme; er un gas quindi: V dv + Vd = 0 d = β = = cost Se un certo volume V tot è occuato arzialmente da liquido V l e arzialmente da gas V g, si uò ricavare un modulo di comrimibilità effettivo: V = V + V tot l g V = V + V tot l g 3.8 dv V V V V V V tot l l g g = = + β e Vtot Vtot Vl Vtot Vg V V l g = + β V β V β e tot l tot g Dato che normalmente il volume di gas contenuto nel reciiente è iccolo risetto a quello del liquido, il modulo di comrimibilità effettivo uò essere arossimato con: Vg = + β β V β e l Evidentemente il modulo di comrimibilità diende dalla quantità di gas contenuto nel volume in esame, quantità che deve essere normalmente iccola. La tab. 3. riorta i valori di variazione di volume che si ottengono con varie ercentuali di gas, considerando er il modulo tot g
9 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 di comrimibilità del gas il valore corrisondente alla ressione media. Si uò notare che l effetto corrisondente alla ressione di 30 MPa con solo liquido si ha alla ressione di.5 MPa con una ercentuale dell % di gas, di 5 MPa con una ercentuale del % e sotto i.5 MPa con ercentuali sueriori. V/V V g /V tot [MPa] Tab Contrazione del volume in diendenza della concentrazione di gas Effetti nello stesso senso si hanno er la dilatazione dei comonenti che contengono il liquido, er cui è ossibile definire un modulo di comrimibilità dovuto in effetti all incremento di volume del reciiente ed avere in definitiva: β c tot Vg = + + β β V β β e V = V l tot g c In ratica quindi il modulo di comrimibilità è normalmente iù basso di quanto atteso in base ai valori del solo liquido e questo ha conseguenze, er quanto iccole, sulla quantità di liquido necessario a riemire un dato volume. Inoltre il legame ressione - volume è da vedersi come una rigidezza e questa in ratica risulta iù bassa di quanto di cometenza del solo liquido. 3.5 Idrostatica: il rinciio di Pascal L idrostatica è governata dal rinciio di Pascal: se si considera un iccolo elemento di fluido in condizioni statiche, la ressione che si misura sulle areti di quell elemento si trasmette a tutto il fluido, con eguale intensità ed in ogni direzione: = cost 3.9
10 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Ricordiamo che quando si arla di misura di ressione molte volte si trascura di recisare se si tratta di una misura di ressione assoluta o relativa; in moltissimi casi questo è chiaro dal contesto o è inessenziale; occorre comunque ricordare che la misura uò essere eseguita in entrambi i modi e sesso gli strumenti misurano la ressione relativa risetto a quella atmosferica nel luogo di misura. Se la misura è utilizzata er valutare differenze di ressioni fra due unti diversi o le sollecitazioni indotte dalla ressione, l una o l altra misura ortano agli stessi risultati, dato che conta solo la differenza fra le due ressioni; esistono erò fenomeni legati alla ressione assoluta: uno di questi è il fatto che la ressione assoluta non uò diventare negativa: si avrebbe infatti il assaggio da uno stato di comressione ad uno di trazione, stato di sforzo al quale i fluidi non ossono resistere; in articolare er i liquidi esiste un valore di ressione minimo al disotto del quale il fluido assa allo stato gassoso. Il valore di ressione al quale questo fenomeno avviene è detto tensione di vaore ed è in genere fortemente influenzato dalla temeratura. Si consideri, er meglio chiarire la ortata del rinciio di Pascal, il sistema in fig. 3.5, costituito essenzialmente da due cilindri differenti muniti di istone, collegati tra loro da un condotto, il tutto riemito di liquido. F A S A F S Fig Torchio idraulico All equilibrio deve essere: F = = A F A il che significa che un sistema del genere è in grado di trasmettere forze variandone l intensità a seconda del raorto tra le aree dei istoni (torchio idraulico). D altro canto, se non ci sono erdite di liquido, il volume sostato da una arte deve ritrovarsi dall altra: V = sa = V = sa 3.0
11 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 ossia gli sostamenti ure vengono variati dal raorto delle aree. Ma ovviamente il lavoro si conserva: L = A s = A s = L Con tale disositivo, che sta alla base della trasmissione idraulica, si uò trasmettere lavoro variandone l intensità della forza e dello sostamento, ovvero si uò amlificare la forza a atto di ridurre lo sostamento, e viceversa. 3.6 Equazione di continuità Sotto questo termine si intende l equazione che esrime il rinciio di conservazione della massa, e del quale già si è vista un esressione elementare nel aragrafo recedente. L esressione classica è: dm = 0 dt dv t ρ V + ρvda = 0 A dove V è il volume considerato ed A sono le aree attraverso le quali uò aversi entrata o uscita di massa nel volume considerato, alla velocità v. Quando il fluido uò essere ritenuto incomrimibile ρ è costante e uò quindi essere eliminata; er le alicazioni imiantistiche non ha quasi mai interesse l effettiva distribuzione di velocità nelle sezioni di assaggio er cui si considera una velocità media: v = A A vda da l equazione di continuità si riduce quindi a: o, introducendo la ortata volumetrica: dv dt Q t + va = 0 = va dv + Q t = 0 dt n dv = Q i dt i= 3.
12 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 dove Q i sono le singole ortate volumetriche, ositive entranti. Per tutti i comonenti dove non si ha variazione di volume si ha infine: n Q i = i = 0 Una classe imortante di comonenti nei quali si uò avere variazione di volume è costituita dagli attuatori lineari (normalmente detti martinetti); in questi l incremento o decremento di volume è ottenuto a sezione costante e quindi si ha un legame di roorzionalità fra la ortata entrante o uscente e la velocità di azionamento del martinetto: Q = Ax& 3.7 Conservazione dell energia Il rimo rinciio della termodinamica imone la conservazione dell energia; ragionamenti energetici ortano a formulazioni estremamente utili er il calcolo del flusso in tubazioni. Esso infatti ossiede energia in forma cinetica, dovuta cioè alla sua velocità, ed in forma otenziale, dovuta cioè all elevazione del condotto ed alla ressione del fluido. Quando si studia il moto del fluido in un condotto (e in genere le correnti fluidodinamiche) si osservano le varie grandezze fisiche in sezioni di controllo fisse. L energia che assa attraverso una sezione del condotto è ovviamente crescente, semlicemente erché col assare del temo semre iù fluido assa quella sezione. Viene quindi utile riferirsi all energia er unità di massa, o di eso, o di volume del fluido. Vediamo di seguito le varie forme di energia ossedute dal fluido, er unità di volume. Energia cinetica L energia cinetica di qualsiasi massa m che viaggi alla velocità v è notoriamente data da: E = mv Nel caso in esame, riferendosi all unità di volume ed essendo ρ la densità, sarà: E = ρ v Energia otenziale L energia otenziale, in senso classico, di una articella di fluido di massa m diende dalla sua altezza z misurata da un iano arbitrario di riferimento. L energia otenziale er unità di volume è quindi: Energia di ressione E = ρ gz 3.
13 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 L energia di ressione è ancora un energia otenziale, che uò essere elementarmente definita nel seguente modo. Si consideri un reciiente come quello indicato nella fig. 3.6, contenente del liquido. Ad una certa distanza dal elo libero si suonga vi sia un tubo che si stacca dal contenitore, chiuso da un istone mobile di area A. La forza esercitata dal liquido su tale istone, dovuta alla sua ressione idrostatica, è A. Il lavoro comiuto dal fluido er sostare il istone di una lunghezza L, dalla sezione alla sezione, sarà A L; il volume di fluido che comie tale lavoro è quello che assa er la sezione, ossia A L. Il lavoro er unità di volume risulta quindi: E = L A Fig Lavoro di ressione Energia interna L energia interna è legata alla temeratura del fluido ed al calore secifico a volume costante e, er unità di volume, ossiamo scriverla come insegna la termodinamica: E i = c T v Conservazione dell energia Il rimo rinciio della termodinamica assicura che l energia viene conservata o meglio che le variazioni di energia in un sistema sono uguali al lavoro che viene esercitato sul sistema stesso. Per un tubo di flusso le variazioni comlessive delle quattro energie sora viste devono quindi uguagliare il lavoro fornito dalle ressioni nelle sezioni di entrata e uscita ed i calori rovenienti dall esterno: + ρ v + ρ gz + c vt = + ρ v + ρ gz + c vt + L + q dove lavoro e calore sono considerati er unità di volume. Si ossono esrimere tutti i termini er unità di eso; se γ è il eso secifico: 3.3
14 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 γ + v z + v cvt z cvt L q g + = γ + + g In tale esressione le dimensioni sono quelle di una lunghezza. Questo modo di esrimere la conservazione dell energia è sfruttato sorattutto nell idraulica classica dove i termini legati ai dislivelli resenti negli acquedotti e quindi all energia otenziale hanno imortanza redominante. Consideriamo in seguito alcuni casi articolari. 3.8 Moto stazionario di un fluido incomrimibile Se il fluido è incomrimibile γ è costante: γ + v z + v cvt z cvt L q g + = γ + + g oure, esrimendo le energie er unità di volume: + ρgz + ρv + c vt = + ρgz + ρ v + c vt + L + q 3.9 Fluido in quiete Se la velocità è nulla, il fluido in equilibrio termico, non si verifica scambio di lavoro e di calore con l esterno, ci si riduce a: + ρgz = + ρgz = ρg z Quando le ressioni sono consistenti e le variazioni di quota iccole, il termine dell energia otenziale uò essere trascurato risetto al termine della ressione e ci si riduce al rinciio di Pascal er i fluidi in quiete: = cost 3.0 Perdite di carico distribuite Rirendiamo dall esressione della conservazione energetica er un fluido incomrimibile in moto stazionario in una tubazione: + ρgz + ρv + c vt = + ρgz + ρ v + c vt + L + q 3.4
15 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 In assenza di lavoro e calore scambiato con l esterno, considerando trascurabile l energia otenziale risetto alle altre grandezze in gioco ed iotizzando il condotto a sezione costante (il che imlica la conservazione della velocità), si ottiene: = +, dove il termine c v (T -T ) è stato sostituito dal generico. Questo termine è legato al fatto che esistono fenomeni dissiativi, er cui arte dell energia iniziale viene ersa dal unto di vista meccanico, erché trasformata in energia termica. Questa erdita viene vista come una erdita di ressione ed è usuale chiamarla erdita di carico. Le tubazioni sono state amiamente studiate dagli idraulici nel diciannovesimo secolo. L'intensità delle erdite di carico risente molto della resenza di un moto regolare, caratterizzato dall'avere nelle singole articelle velocità sensibilmente dirette come l'asse del condotto e nel verso del moto, o moto irregolare con comonenti di velocità in tutte le direzioni; il rimo tio di moto è detto moto laminare, il secondo moto turbolento. Se si osserva serimentalmente il moto del fluido, si vede che in certe condizioni il moto è di tio laminare ed in altre diventa turbolento. La transizione del moto da laminare a turbolento è dominata dal raorto fra le forze di massa e le forze viscose, esrimibile da una grandezza adimensionale, il numero di Reynolds, definito da: Re = ρ vd µ dove ρ è la densità, v la velocità media, D il diametro idraulico e µ la viscosità. La caduta di ressione lungo la linea è quindi dovuta a disuniformità nella velocità che rovoca conseguenti effetti viscosi. E stata riconosciuta una relazione tra la caduta di ressione e l energia cinetica: = + α ρ v e si è giunti er via serimentale a determinare er α la seguente esressione: α = λ dove λ è un coefficiente di erdite distribuite, L è la lunghezza della tubazione e D il diametro idraulico. La caduta di ressione sull intera tubazione è quindi data dalla legge di Darcy - Weisbach: L D L = λ ρ v D Il diametro idraulico corrisonde al diametro geometrico nel caso di tubi a sezione circolare, er altre forme della sezione è definito come: 3.5
16 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 D S = 4 C dove S è l area della sezione e C il erimetro; nel caso di sezione circolare: πd 4 4S = 4 = D C πd Il coefficiente λ diende dal tio di moto, indicato dal numero di Reynolds, e dalla rugosità suerficiale del condotto, definita come raorto tra lo sessore medio delle irregolarità ed il diametro del tubo. Il diagramma di Moody di fig. 3.7 riorta l andamento del coefficiente in funzione del numero di Reynolds della corrente fluida e arametrizzato sulla rugosità suerficiale. Fig Diagramma di Moody Reynolds number 3.6
17 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Si riconosce che er Re < 000 il moto è laminare, la velocità è nulla al contorno, diretta come l asse della tubazione e massima al centro del tubo (fig. 3.8), con una distribuzione arabolica; in questo caso è ossibile ricavare anche teoricamente il valore di λ che risulta: e quindi: λ = 64 Re 64 L 64µ L L v v D vd D D v = = ρ = ρ = 3µ Re ρ Nel moto laminare la erdita di carico risulta diendente, oltre che dai arametri geometrici, in modo lineare dalla viscosità e dalla velocità del fluido. La diendenza dalla viscosità orta ad una diendenza dalla temeratura dato che la viscosità è fortemente influenzata da questa. Quando il numero di Reynolds suera il valore di 4000, il moto diventa turbolento, la distribuzione di velocità nella sezione si aiattisce (fig. 3.8), la velocità massima si avvicina quindi alla velocità media, ma la velocità ha comonenti anche erendicolari alla tubazione: in questo caso i valori di λ sono desumibili da curve serimentali o da formule emiriche. LAMINARE TURBOLENTO Fig Profili di velocità laminare e turbolento Per numeri di Reynolds molto alti, λ è sensibilmente indiendente dal numero di Reynolds e diende solo dalla rugosità. In tale camo di moto la erdita di carico risulta quindi diendente dal quadrato della velocità ed indiendente dalla viscosità del fluido (questa interviene comunque nel calcolo del numero di Reynolds!). Per i valori del numero di Reynolds fra 000 e 4000 si ha una zona di transizione non ben definita, dato che il assaggio dallo stato laminare a quello turbolento è un fenomeno di instabilità che uò avere quindi un certo margine di indeterminazione. Per le tubazioni si arla comunemente di erdite distribuite dato che la caduta di ressione è distribuita uniformemente su tutta la linea; la ressione ha quindi sulla linea un andamento lineare: x = λ ρ v D In realtà le erdite di carico così determinate avvengono quando il moto nella tubazione è a regime; se consideriamo l inizio del tubo si ha una zona di una certa lunghezza nella quale la velocità assa da una distribuzione iniziale nella sezione alla distribuzione tiica del moto 3.7
18 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 laminare o turbolento che si ha oi nell intero tubo; er tubazioni di una certa lunghezza questo fenomeno non orta a differenze significative, ma er tubazioni corte questo uò non essere iù vero. 3. Comonenti discreti Le erdite di carico sono dovute agli effetti viscosi causati da differenze di velocità nei vari unti nel fluido; questo avviene tutte le volte che il fluido trova nel suo cammino un ostacolo di natura qualsiasi o comunque la geometria del condotto orta a variazioni del vettore velocità (fig. 3.9). Nell idraulica classica, dove le tubazioni hanno una lunghezza molto elevata, queste erdite ossono essere di entità molto minore risetto a quelle nelle tubazioni, tanto che nella letteratura anglosassone vengono definite erdite minori; negli imianti di nostro interesse le tubazioni sono invece relativamente corte ed esistono molti comonenti in grado di causare erdite di valore significativo. Verranno genericamente indicate come erdite concentrate. Fig Cause di erdite di carico concentrate Anche in questo caso le erdite ossono essere esresse come funzione di un energia cinetica: o: = α ρ v = KQ e stabiliscono quindi un legame fra la ortata che attraversa il comonente e la ressione alle estremità di esso (ovviamente nell iotesi che nel comonente non vi sia scambio di lavoro con l esterno). I coefficienti necessari er il calcolo delle erdite di carico concentrate sono ovviamente funzione della geometria del comonente, ma anche di un numero di Reynolds di riferimento. La letteratura secializzata riorta i coefficienti er gomiti, sbocchi, divergenti, convergenti, raccordi, valvole, ecc. 3.8
19 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE Analogia elettrica Può essere conveniente esrimere le erdite di carico in funzione della ortata, sostituendo al termine di velocità il corrisondente raorto tra ortata ed area del condotto: L L Q 8L v D D D D Q KQ = = λ ρ = λ ρ = λ ρ = 5 π π 4 Questa esressione definisce il legame fra ressione e ortata, le due grandezze caratteristiche della otenza idraulica. La relazione è in analogia con l equazione di Ohm utilizzata nel camo elettrico, con erò la comlicazione che il legame ressione - ortata è quadratico anziché lineare. Q k M k Q Q k Q Q k Q Fig Linee in serie e in arallelo L analogia uò erò essere alicata e le regole utilizzate er il collegamento in serie o in arallelo restano analoghe considerando il coefficiente K come una resistenza. Nel collegamento in serie, essendo uguali le ortate nelle due tubazioni, si ha (fig. 3.0): M M = K Q = K = ( K + K ) Q Nel collegamento in arallelo, essendo uguali le ressioni alle due estremità, si ha (fig. 3.0): Q = KQ = KQ 3.9
20 IMPIANTI AEROSPAZIALI DISPENSE DEL CORSO, VERSIONE 005 Q = Q + Q = K + K = K + K = KQ K = K + K relazione che ricorda quella delle resistenze in arallelo, con la differenza che il legame è quadratico anziché lineare. 3.3 Bibliografia G.Rigamonti, Oleodinamica e Pneumatica, Hoeli, 987. R.W.Jeson, Analysis of Flows in Pie Networks, Ann Arbor Science Publishers,
Legge del gas perfetto e termodinamica
 Scheda riassuntia 5 caitoli 9-0 Legge del gas erfetto e termodinamica Gas erfetto Lo stato gassoso è quello di una sostanza che si troa oltre la sua temeratura critica. La temeratura critica è quella oltre
Scheda riassuntia 5 caitoli 9-0 Legge del gas erfetto e termodinamica Gas erfetto Lo stato gassoso è quello di una sostanza che si troa oltre la sua temeratura critica. La temeratura critica è quella oltre
FISICA. V [10 3 m 3 ]
![FISICA. V [10 3 m 3 ] FISICA. V [10 3 m 3 ]](/thumbs/24/2838543.jpg) Serie 5: Soluzioni FISICA II liceo Esercizio 1 Primo rinciio Iotesi: Trattiamo il gas con il modello del gas ideale. 1. Dalla legge U = cnrt otteniamo U = 1,50 10 4 J. 2. Dal rimo rinciio U = Q+W abbiamo
Serie 5: Soluzioni FISICA II liceo Esercizio 1 Primo rinciio Iotesi: Trattiamo il gas con il modello del gas ideale. 1. Dalla legge U = cnrt otteniamo U = 1,50 10 4 J. 2. Dal rimo rinciio U = Q+W abbiamo
CBM a.s. 2012/2013 PROBLEMA DELL UTILE DEL CONSUMATORE CON IL VINCOLO DEL BILANCIO
 CM a.s. /3 PROLEMA DELL TILE DEL CONSMATORE CON IL VINCOLO DEL ILANCIO Il consumatore è colui che acquista beni er destinarli al rorio consumo. Linsieme dei beni che il consumatore acquista rende il nome
CM a.s. /3 PROLEMA DELL TILE DEL CONSMATORE CON IL VINCOLO DEL ILANCIO Il consumatore è colui che acquista beni er destinarli al rorio consumo. Linsieme dei beni che il consumatore acquista rende il nome
Progettazione di un motore Ringbom Stirling per la produzione di energia elettrica nei paesi in via di sviluppo
 Progettazione di un motore Ringbom Stirling er la roduzione di energia elettrica nei aesi in via di sviluo C. M. Invernizzi, G. Incerti, S. Parmigiani, V. Villa Diartimento di Ingegneria Meccanica e Industriale
Progettazione di un motore Ringbom Stirling er la roduzione di energia elettrica nei aesi in via di sviluo C. M. Invernizzi, G. Incerti, S. Parmigiani, V. Villa Diartimento di Ingegneria Meccanica e Industriale
I NUMERI INDICI. Numeri indici indici (misurano il livello di variabilità, concentrazione, dipendenza o interdipendenza, ecc.)
 NUMER NDC Numeri indici indici (misurano il livello di variabilità, concentrazione, diendenza o interdiendenza, ecc.) si utilizzano er confrontare grandezze nel temo e nello sazio e sono dati dal raorto
NUMER NDC Numeri indici indici (misurano il livello di variabilità, concentrazione, diendenza o interdiendenza, ecc.) si utilizzano er confrontare grandezze nel temo e nello sazio e sono dati dal raorto
Una proposizione è una affermazione di cui si possa stabilire con certezza il valore di verità
 Logica 1. Le roosizioni 1.1 Cosa studia la logica? La logica studia le forme del ragionamento. Si occua cioè di stabilire delle regole che ermettano di assare da un'affermazione vera ad un'altra affermazione
Logica 1. Le roosizioni 1.1 Cosa studia la logica? La logica studia le forme del ragionamento. Si occua cioè di stabilire delle regole che ermettano di assare da un'affermazione vera ad un'altra affermazione
Corso di Componenti e Impianti Termotecnici LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE
 LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Portata Q - è il volume di liquido mosso dalla pompa nell'unità di tempo; l'unità di misura della portata è m 3 /sec (l/s; m 3 /h).
 OME ER FLUIDI ALIMENARI Definizione Sono macchine oeratrici oeranti su fluidi incomrimibili in grado di trasformare l energia meccanica disonibile all albero di un motore in energia meccanica del fluido
OME ER FLUIDI ALIMENARI Definizione Sono macchine oeratrici oeranti su fluidi incomrimibili in grado di trasformare l energia meccanica disonibile all albero di un motore in energia meccanica del fluido
CAPITOLO 5 IDRAULICA
 CAPITOLO 5 IDRAULICA Cap. 5 1 FLUIDODINAMICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO'
CAPITOLO 5 IDRAULICA Cap. 5 1 FLUIDODINAMICA STUDIA I FLUIDI, IL LORO EQUILIBRIO E IL LORO MOVIMENTO FLUIDO CORPO MATERIALE CHE, A CAUSA DELLA ELEVATA MOBILITA' DELLE PARTICELLE CHE LO COMPONGONO, PUO'
LABORATORIO DI CHIMICA GENERALE E INORGANICA
 UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
Pressione. Esempio. Definizione di pressione. Legge di Stevino. Pressione nei fluidi EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI
 Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Proprieta meccaniche dei fluidi
 Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Gas perfetti e sue variabili
 Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Dilatazione termica. Δl=α l o Δt. ΔA = 2 α A o Δt. ( ) Δl=α l o Δt. α = coefficiente di dilatazione termica lineare
 Acroolis Atene Eretteo: sostituzione di armature in acciaio con strutture in itanio. Esemi di restauro negativo acciaio contro ferro sigillato in iombo. Recuero di restauri inoortuni con sostituzione mediante
Acroolis Atene Eretteo: sostituzione di armature in acciaio con strutture in itanio. Esemi di restauro negativo acciaio contro ferro sigillato in iombo. Recuero di restauri inoortuni con sostituzione mediante
Il trasporto di materia. Principi di Ingegneria Chimica Ambientale
 Il trasporto di materia Principi di Ingegneria Chimica Ambientale 1 Considerazioni preliminari Il nostro studio sarà limitato a: miscele binarie miscele diluite (ossia in cui la frazione molare di uno
Il trasporto di materia Principi di Ingegneria Chimica Ambientale 1 Considerazioni preliminari Il nostro studio sarà limitato a: miscele binarie miscele diluite (ossia in cui la frazione molare di uno
LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante
 IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
RICHIAMI DI TERMOCHIMICA
 CAPITOLO 5 RICHIAMI DI TERMOCHIMICA ARIA TEORICA DI COMBUSTIONE Una reazione di combustione risulta completa se il combustibile ha ossigeno sufficiente per ossidarsi completamente. Si ha combustione completa
CAPITOLO 5 RICHIAMI DI TERMOCHIMICA ARIA TEORICA DI COMBUSTIONE Una reazione di combustione risulta completa se il combustibile ha ossigeno sufficiente per ossidarsi completamente. Si ha combustione completa
CORRENTE E TENSIONE ELETTRICA LA CORRENTE ELETTRICA
 CORRENTE E TENSIONE ELETTRICA La conoscenza delle grandezze elettriche fondamentali (corrente e tensione) è indispensabile per definire lo stato di un circuito elettrico. LA CORRENTE ELETTRICA DEFINIZIONE:
CORRENTE E TENSIONE ELETTRICA La conoscenza delle grandezze elettriche fondamentali (corrente e tensione) è indispensabile per definire lo stato di un circuito elettrico. LA CORRENTE ELETTRICA DEFINIZIONE:
Pressione. www.easymaths.altervista.org. 01 - Pressione.
 Pressione 01 - Pressione La forza è una grandezza fisica caratterizzata dal fatto di essere in grado di modificare lo stato di moto di un corpo o di modificarne la struttura interna Supponiamo che una
Pressione 01 - Pressione La forza è una grandezza fisica caratterizzata dal fatto di essere in grado di modificare lo stato di moto di un corpo o di modificarne la struttura interna Supponiamo che una
Statica e dinamica dei fluidi. A. Palano
 Statica e dinamica dei fluidi A. Palano Fluidi perfetti Un fluido perfetto e incomprimibile e indilatabile e non possiede attrito interno. Forza di pressione come la somma di tutte le forze di interazione
Statica e dinamica dei fluidi A. Palano Fluidi perfetti Un fluido perfetto e incomprimibile e indilatabile e non possiede attrito interno. Forza di pressione come la somma di tutte le forze di interazione
DISTRIBUZIONE di PROBABILITA. Si dice variabile aleatoria (o casuale) discreta X una quantità variabile che può assumere i
 DISTRIBUZIONE di PROBABILITA Si dice variabile aleatoria (o casuale) discreta X una quantità variabile che uò assumere i valori: ; ;, n al verificarsi degli eventi incomatibili e comlementari: E ; E ;..;
DISTRIBUZIONE di PROBABILITA Si dice variabile aleatoria (o casuale) discreta X una quantità variabile che uò assumere i valori: ; ;, n al verificarsi degli eventi incomatibili e comlementari: E ; E ;..;
LA CORRENTE ELETTRICA CONTINUA
 LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Si classifica come una grandezza intensiva
 CAP 13: MISURE DI TEMPERATURA La temperatura È osservata attraverso gli effetti che provoca nelle sostanze e negli oggetti Si classifica come una grandezza intensiva Può essere considerata una stima del
CAP 13: MISURE DI TEMPERATURA La temperatura È osservata attraverso gli effetti che provoca nelle sostanze e negli oggetti Si classifica come una grandezza intensiva Può essere considerata una stima del
LO STATO GASSOSO. Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi
 LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
COMPONENTI TERMODINAMICI APERTI
 CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
L Q = 1. e nel ciclo di Carnot questo rendimento assume valore massimo pari a : η =
 CICLI ERMODINAMICI DIREI: Maccine termice Le maccine ce anno come scoo uello di trasformare ciclicamente in lavoro il calore disonibile da una sorgente termica sono dette maccine termice o motrici e il
CICLI ERMODINAMICI DIREI: Maccine termice Le maccine ce anno come scoo uello di trasformare ciclicamente in lavoro il calore disonibile da una sorgente termica sono dette maccine termice o motrici e il
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
L H 2 O nelle cellule vegetali e
 L H 2 O nelle cellule vegetali e il suo trasporto nella pianta H 2 O 0.96 Å H O 105 H 2s 2 2p 4 tendenza all ibridizzazione sp 3 H δ+ O δ- δ+ 1.75 Å H legame idrogeno O δ- H H δ+ δ+ energia del legame
L H 2 O nelle cellule vegetali e il suo trasporto nella pianta H 2 O 0.96 Å H O 105 H 2s 2 2p 4 tendenza all ibridizzazione sp 3 H δ+ O δ- δ+ 1.75 Å H legame idrogeno O δ- H H δ+ δ+ energia del legame
LA CORRENTE ELETTRICA
 L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI
 9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI 9. Introduzione I rocessi termodinamici che vengono realizzati nella ratica devono consentire la realizzazione di uno scambio di energia termica o di energia
9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI 9. Introduzione I rocessi termodinamici che vengono realizzati nella ratica devono consentire la realizzazione di uno scambio di energia termica o di energia
GLI STATI DI AGGREGAZIONE DELLA MATERIA. Lo stato gassoso
 GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
Capitolo Ventitrè. Offerta nel breve. Offerta dell industria. Offerta di un industria concorrenziale Offerta impresa 1 Offerta impresa 2 p
 Caitolo Ventitrè Offerta dell industria Offerta dell industria concorrenziale Come si combinano le decisioni di offerta di molte imrese singole in un industria concorrenziale er costituire l offerta di
Caitolo Ventitrè Offerta dell industria Offerta dell industria concorrenziale Come si combinano le decisioni di offerta di molte imrese singole in un industria concorrenziale er costituire l offerta di
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Politecnico di Milano Dipartimento di Ingegneria Aerospaziale Impianti e Sistemi Aerospaziali CALCOLO D IMPIANTO IDRAULICO
 Politecnico di Milano Dipartimento di Ingegneria Aerospaziale Impianti e Sistemi Aerospaziali CALCOLO D IMPIANTO IDRAULICO 1 1. Premessa La presente relazione riporta il calcolo della rigidezza del comando
Politecnico di Milano Dipartimento di Ingegneria Aerospaziale Impianti e Sistemi Aerospaziali CALCOLO D IMPIANTO IDRAULICO 1 1. Premessa La presente relazione riporta il calcolo della rigidezza del comando
CORSO DI FORMAZIONE DOCENTI NEOIMMESSI IN RUOLO. a.s. 2011/12. Istituto attuatore: IPSEOA Duca di Buonvicino. Napoli
 CORSO DI FORMAZIONE DOCENTI NEOIMMESSI IN RUOLO a.s. 2011/12 Istituto attuatore: IPSEOA Duca di Buonvicino Naoli COGNOME MONE NOME Mariangela Assunta E-TUTOR : Guidotti Ugo AREA TEMATICA: Elettronica,
CORSO DI FORMAZIONE DOCENTI NEOIMMESSI IN RUOLO a.s. 2011/12 Istituto attuatore: IPSEOA Duca di Buonvicino Naoli COGNOME MONE NOME Mariangela Assunta E-TUTOR : Guidotti Ugo AREA TEMATICA: Elettronica,
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Trigonometria (tratto dal sito Compito in classe di Matematica di Gilberto Mao)
 Trigonometria (tratto dal sito Comito in classe di Matematica di Gilberto Mao) Teoria in sintesi Radiante: angolo al centro di una circonferenza che sottende un arco di lunghezza rettificata uguale al
Trigonometria (tratto dal sito Comito in classe di Matematica di Gilberto Mao) Teoria in sintesi Radiante: angolo al centro di una circonferenza che sottende un arco di lunghezza rettificata uguale al
L E L E G G I D E I G A S P A R T E I
 L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
Termodinamica: legge zero e temperatura
 Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti.
 Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Michele D'Amico (premiere) 6 May 2012
 Michele D'Amico (premiere) CORRENTE ELETTRICA 6 May 2012 Introduzione La corrente elettrica può essere definita come il movimento ordinato di cariche elettriche, dove per convenzione si stabilisce la direzione
Michele D'Amico (premiere) CORRENTE ELETTRICA 6 May 2012 Introduzione La corrente elettrica può essere definita come il movimento ordinato di cariche elettriche, dove per convenzione si stabilisce la direzione
CALCOLO EFFICACIA ED EFFICIENZA DI TERMOCAMINETTI A GIRI DI FUMO
 Pag. 1 di 7 CALCOLO EFFICACIA ED EFFICIENZA DI TERMOCAMINETTI A GIRI DI FUMO Introduzione La resente relazione ha obiettivo di calcolare indicativamente funzionamento efficacia ed efficienza di termocaminetti
Pag. 1 di 7 CALCOLO EFFICACIA ED EFFICIENZA DI TERMOCAMINETTI A GIRI DI FUMO Introduzione La resente relazione ha obiettivo di calcolare indicativamente funzionamento efficacia ed efficienza di termocaminetti
F S V F? Soluzione. Durante la spinta, F S =ma (I legge di Newton) con m=40 Kg.
 Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
ESERCITAZIONE N. 1 (11 Ottobre 2007) Verifica di un impianto di pompaggio
 ESERCITAZIONE N. 1 (11 Ottobre 2007) Verifica di un impianto di pompaggio È dato un pozzo con piano campagna H posto a 90 m s.l.m., dal quale l acqua è sollevata verso un serbatoio il cui pelo libero H
ESERCITAZIONE N. 1 (11 Ottobre 2007) Verifica di un impianto di pompaggio È dato un pozzo con piano campagna H posto a 90 m s.l.m., dal quale l acqua è sollevata verso un serbatoio il cui pelo libero H
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
6.5. Risultati simulazioni sistema rifiuti e riscaldamento
 Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Correnti e circuiti a corrente continua. La corrente elettrica
 Correnti e circuiti a corrente continua La corrente elettrica Corrente elettrica: carica che fluisce attraverso la sezione di un conduttore in una unità di tempo Q t Q lim t 0 t ntensità di corrente media
Correnti e circuiti a corrente continua La corrente elettrica Corrente elettrica: carica che fluisce attraverso la sezione di un conduttore in una unità di tempo Q t Q lim t 0 t ntensità di corrente media
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
CORRENTE ELETTRICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V 2 isolati tra loro V 2 > V 1 V 2
 COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
TEORIA CINETICA DEI GAS
 TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
LA FORZA. Il movimento: dal come al perché
 LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6
 28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
MASSA VOLUMICA o DENSITA
 MASSA VOLUMICA o DENSITA Massa volumica di una sostanza: è la massa di sostanza, espressa in kg, che occupa un volume pari a 1 m 3 1 m 3 di aria ha la massa di 1,2 kg 1 m 3 di acqua ha la massa di 1000
MASSA VOLUMICA o DENSITA Massa volumica di una sostanza: è la massa di sostanza, espressa in kg, che occupa un volume pari a 1 m 3 1 m 3 di aria ha la massa di 1,2 kg 1 m 3 di acqua ha la massa di 1000
Sessione live #2 Settimana dal 24 al 30 marzo. Statistica Descrittiva (II): Analisi congiunta, Regressione lineare Quantili.
 Sessione lie # Settimana dal 4 al 30 marzo Statistica Descrittia (II): Analisi congiunta, Regressione lineare Quantili Lezioni CD: 3 4-5 Analisi congiunta Da un camione di 40 studenti sono stati rileati
Sessione lie # Settimana dal 4 al 30 marzo Statistica Descrittia (II): Analisi congiunta, Regressione lineare Quantili Lezioni CD: 3 4-5 Analisi congiunta Da un camione di 40 studenti sono stati rileati
Termodinamica. Sistema termodinamico. Piano di Clapeyron. Sistema termodinamico. Esempio. Cosa è la termodinamica? TERMODINAMICA
 Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
SISTEMA BINARIO DI DUE LIQUIDI VOLATILI TOTALMENTE MISCIBILI che seguono Raoult
 SISTEM INRIO DI DUE IQUIDI OTII MENTE MISCIII che seguono Raoult Consideriamo due liquidi e totalmente miscibili di composizione χ e χ presenti in un contenitore ad una certa temperatura T=T 1. o strato
SISTEM INRIO DI DUE IQUIDI OTII MENTE MISCIII che seguono Raoult Consideriamo due liquidi e totalmente miscibili di composizione χ e χ presenti in un contenitore ad una certa temperatura T=T 1. o strato
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it
 LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
Ripasso di microeconomia ECONOMIA E FINANZA PUBBLICA. Teoria del consumatore. Lezione n. 1. Teoria del consumatore. Le preferenze.
 Università degli Studi di erugia Corso di Laurea Magistrale in Scienze della olitica e dell'mministrazione Lezione n. Riasso di microeconomia CONOMI FINNZ ULIC nza Caruso Le referenze Come i consumatori
Università degli Studi di erugia Corso di Laurea Magistrale in Scienze della olitica e dell'mministrazione Lezione n. Riasso di microeconomia CONOMI FINNZ ULIC nza Caruso Le referenze Come i consumatori
GAS. I gas si assomigliano tutti
 I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
Università di Roma Tor Vergata
 Università di oma Tor Vergata Facoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TEMOTECNIC 1 IMPINTI DI ISCLDMENTO D CQU: DIMENSIONMENTO Ing. G. Bovesecchi gianluigi.bovesecchi@gmail.com
Università di oma Tor Vergata Facoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TEMOTECNIC 1 IMPINTI DI ISCLDMENTO D CQU: DIMENSIONMENTO Ing. G. Bovesecchi gianluigi.bovesecchi@gmail.com
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Lezione 4: I profili alari e le forze
 Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione 4: I profili alari e le forze aerodinamiche Prof. D. P. Coiro coiro@unina.itit www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni
Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione 4: I profili alari e le forze aerodinamiche Prof. D. P. Coiro coiro@unina.itit www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni
Valvole di regolazione
 Valvole di Regolazione Valvole di regolazione Sono attuatori che servono a modulare la portata di fluido (liquido o gassoso) nei circuiti idraulici Diffusissime nel controllo di processo industriale (es:
Valvole di Regolazione Valvole di regolazione Sono attuatori che servono a modulare la portata di fluido (liquido o gassoso) nei circuiti idraulici Diffusissime nel controllo di processo industriale (es:
Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ]
![Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ] Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ]](/thumbs/33/15874186.jpg) Idrogeologia Oltre alle proprietà indici del terreno che servono a classificarlo e che costituiscono le basi per utilizzare con facilità l esperienza raccolta nei vari problemi geotecnici, è necessario
Idrogeologia Oltre alle proprietà indici del terreno che servono a classificarlo e che costituiscono le basi per utilizzare con facilità l esperienza raccolta nei vari problemi geotecnici, è necessario
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Risposta: 2009 2010 Quantità Prezzo ( ) Quantità Prezzo ( ) Automobili 8.000 15.000 6.500 14.500 Biciclette 80.000 195,52 94.
 1. Domanda Si consideri un sistema economico che roduce solo due beni: automobili e biciclette. È noto che nel 009 sono state rodotte 8.000 automobili che sono state venduto al rezzo di 15.000 e 80.000
1. Domanda Si consideri un sistema economico che roduce solo due beni: automobili e biciclette. È noto che nel 009 sono state rodotte 8.000 automobili che sono state venduto al rezzo di 15.000 e 80.000
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
CONTROLLO TERMICO DEI SISTEMI DI CALCOLO Fluidodinamica UNITA' 07 - SOMMARIO 7. EQUAZIONI INTEGRALI DI BILANCIO PER FLUIDI IN MOTO (B)
 U.07/0 UNITA' 07 - SOMMARIO 7. EQUAZIONI INTEGRALI DI BILANCIO PER FLUIDI IN MOTO (B) 7. BILANCIO DELL ENERGIA 7.. Bilancio dell energia stazionario er sistemi a due correnti 7... Bilancio dell energia
U.07/0 UNITA' 07 - SOMMARIO 7. EQUAZIONI INTEGRALI DI BILANCIO PER FLUIDI IN MOTO (B) 7. BILANCIO DELL ENERGIA 7.. Bilancio dell energia stazionario er sistemi a due correnti 7... Bilancio dell energia
CALCOLO ELETTRICO DELLE LINEE ELETTRICHE
 CALCOLO ELETTRICO DELLE LINEE ELETTRICHE Appunti a cura dell Ing. Stefano Usai Tutore del corso di ELETTROTECNICA per meccanici e chimici A. A. 2001/ 2002 e 2002/2003 Calcolo elettrico delle linee elettriche
CALCOLO ELETTRICO DELLE LINEE ELETTRICHE Appunti a cura dell Ing. Stefano Usai Tutore del corso di ELETTROTECNICA per meccanici e chimici A. A. 2001/ 2002 e 2002/2003 Calcolo elettrico delle linee elettriche
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Q t CORRENTI ELETTRICHE
 CORRENTI ELETTRICHE La corrente elettrica è un flusso di particelle cariche. L intensità di una corrente è definita come la quantità di carica netta che attraversa nell unità di tempo una superficie: I
CORRENTI ELETTRICHE La corrente elettrica è un flusso di particelle cariche. L intensità di una corrente è definita come la quantità di carica netta che attraversa nell unità di tempo una superficie: I
Temperatura e Calore
 Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
PRINCIPI DI TRASMISSIONE DEL CALORE
 PRINCIPI DI TRASMISSIONE DEL CALORE La trasmissione del calore può avvenire attraverso tre meccanismi: - Conduzione; - Convezione; - Irraggiamento; Nella conduzione la trasmissione del calore è riconducibile
PRINCIPI DI TRASMISSIONE DEL CALORE La trasmissione del calore può avvenire attraverso tre meccanismi: - Conduzione; - Convezione; - Irraggiamento; Nella conduzione la trasmissione del calore è riconducibile
I CIRCUITI ELETTRICI. Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi.
 I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
Capitolo 03 LA PRESSIONE ATMOSFERICA. 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni
 Capitolo 03 LA PRESSIONE ATMOSFERICA 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni 12 3.1 Peso dell aria I corpi solidi hanno un loro peso, ma anche i corpi gassosi e quindi l aria,
Capitolo 03 LA PRESSIONE ATMOSFERICA 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni 12 3.1 Peso dell aria I corpi solidi hanno un loro peso, ma anche i corpi gassosi e quindi l aria,
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
La combustione ed i combustibili
 La combustione ed i combustibili Concetti di base Potere calorifico Aria teorica di combustione Fumi: volume e composizione Temperatura teorica di combustione Perdita al camino Combustibili Gassosi Solidi
La combustione ed i combustibili Concetti di base Potere calorifico Aria teorica di combustione Fumi: volume e composizione Temperatura teorica di combustione Perdita al camino Combustibili Gassosi Solidi
Energia nelle reazioni chimiche. Lezioni d'autore di Giorgio Benedetti
 Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
Scambio termico 6.1. 6.1.1 Introduzione. 6.1.2 Conduzione
 6. Scambio termico 6.. Introduzione Lo studio dei fenomeni di scambio termico si uò ricondurre a due variabili: la temeratura e il flusso di calore. La temeratura indica l energia molecolare media di un
6. Scambio termico 6.. Introduzione Lo studio dei fenomeni di scambio termico si uò ricondurre a due variabili: la temeratura e il flusso di calore. La temeratura indica l energia molecolare media di un
Estensimetro. in variazioni di resistenza.
 Estensimetro La misura di una forza incidente su di un oggetto può essere ottenuta misurando la deformazione o la variazione di geometria che l oggetto in questione subisce. L estensimetro estensimetro,
Estensimetro La misura di una forza incidente su di un oggetto può essere ottenuta misurando la deformazione o la variazione di geometria che l oggetto in questione subisce. L estensimetro estensimetro,
6.1. Risultati simulazioni termovalorizzatore Osmannoro2000
 pag. 217 6. Risultati Di seguito si riportano i risultati relativi alle diverse simulazioni di diffusione atmosferica degli inquinanti effettuate. In particolare sono riportati i risultati sotto forma
pag. 217 6. Risultati Di seguito si riportano i risultati relativi alle diverse simulazioni di diffusione atmosferica degli inquinanti effettuate. In particolare sono riportati i risultati sotto forma
SOLUZIONE ESAME DI STATO TEMA NR.1 TECNICO DEI SISTEMI ENERGETICI ANNO 2015
 SOLUZIONE ESAME DI STATO TEMA NR.1 TECNICO DEI SISTEMI ENERGETICI ANNO 2015 PREFAZIONE AL TEMA Nella parte sottostante è rappresentato lo schema circuitale dell impianto idraulico, dove, vengono raffigurate:
SOLUZIONE ESAME DI STATO TEMA NR.1 TECNICO DEI SISTEMI ENERGETICI ANNO 2015 PREFAZIONE AL TEMA Nella parte sottostante è rappresentato lo schema circuitale dell impianto idraulico, dove, vengono raffigurate:
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Gas e gas perfetti. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Gas e gas perfetti 1 Densita Densita - massa per unita di volume Si misura in g/cm 3 ρ = M V Bassa densita Alta densita Definizione di Pressione Pressione = Forza / Area P = F/A unita SI : 1 Nt/m 2 = 1
Gas e gas perfetti 1 Densita Densita - massa per unita di volume Si misura in g/cm 3 ρ = M V Bassa densita Alta densita Definizione di Pressione Pressione = Forza / Area P = F/A unita SI : 1 Nt/m 2 = 1
Cenni di Teoria Cinetica dei Gas
 Cenni di Teoria Cinetica dei Gas Introduzione La termodinamica descrive i sistemi termodinamici tramite i parametri di stato (p, T,...) Sufficiente per le applicazioni: impostazione e progettazione di
Cenni di Teoria Cinetica dei Gas Introduzione La termodinamica descrive i sistemi termodinamici tramite i parametri di stato (p, T,...) Sufficiente per le applicazioni: impostazione e progettazione di
Unità di misura e formule utili
 Unità di misura e formule utili Lezione 7 Unità di misura Il Sistema Internazionale di unità di misura (SI) nasce dall'esigenza di utilizzare comuni unità di misura per la quantificazione e la misura delle
Unità di misura e formule utili Lezione 7 Unità di misura Il Sistema Internazionale di unità di misura (SI) nasce dall'esigenza di utilizzare comuni unità di misura per la quantificazione e la misura delle
sorgente di lavoro meccanico operante in maniera ciclica internamente reversibile esternamente reversibile termostato T
 CICLI MOORI Utilizzando un motore (sorgente di lavoro meccanico oerante in maniera ciclica) che evolve secondo il ciclo isotermo-adiabatico di Carnot in maniera internamente reversibile, scambiando calore
CICLI MOORI Utilizzando un motore (sorgente di lavoro meccanico oerante in maniera ciclica) che evolve secondo il ciclo isotermo-adiabatico di Carnot in maniera internamente reversibile, scambiando calore
Anche nel caso che ci si muova e si regga una valigia il lavoro compiuto è nullo: la forza è verticale e lo spostamento orizzontale quindi F s =0 J.
 Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
BILANCI DI ENERGIA. Capitolo 2 pag 70
 BILANCI DI ENERGIA Capitolo 2 pag 70 BILANCI DI ENERGIA Le energie in gioco sono di vario tipo: energia associata ai flussi entranti e uscenti (potenziale, cinetica, interna), Calore scambiato con l ambiente,
BILANCI DI ENERGIA Capitolo 2 pag 70 BILANCI DI ENERGIA Le energie in gioco sono di vario tipo: energia associata ai flussi entranti e uscenti (potenziale, cinetica, interna), Calore scambiato con l ambiente,
Stati di aggregazione della materia unità 2, modulo A del libro
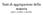 Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
 ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione
 REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
2014 2015 CCS - Biologia CCS - Fisica I gas e loro proprietà. I liquidi e loro proprietà
 2014 2015 CCS - Biologia CCS - Fisica I gas e loro proprietà 1 I liquidi e loro proprietà 2 Proprietà Generali dei Gas I gas possono essere espansi all infinito. I gas occupano i loro contenitori uniformemente
2014 2015 CCS - Biologia CCS - Fisica I gas e loro proprietà 1 I liquidi e loro proprietà 2 Proprietà Generali dei Gas I gas possono essere espansi all infinito. I gas occupano i loro contenitori uniformemente
