Compressione Dati. Teorema codifica sorgente: Entropia fornisce un limite sia inferiore che superiore al numero di bit per simbolo sorgente.. p.

Transcript

1 Compressione Dati Teorema codifica sorgente: Entropia fornisce un limite sia inferiore che superiore al numero di bit per simbolo sorgente.. p.1/21

2 Compressione Dati Teorema codifica sorgente: Entropia fornisce un limite sia inferiore che superiore al numero di bit per simbolo sorgente. Risultato non pratico risultati valgono per n codifica basata su insieme sequenze tipiche. p.1/21

3 Compressione Dati Teorema codifica sorgente: Entropia fornisce un limite sia inferiore che superiore al numero di bit per simbolo sorgente. Risultato non pratico risultati valgono per n codifica basata su insieme sequenze tipiche Vedremo: limite teorico è raggiunto da codici di uso comune.. p.1/21

4 Notazione Assumiamo per semplicità la seguente notazione : D = {0, 1,..., D 1} D : insieme di tutte le possibili sequenze finite sull alfabeto D D = D D 2 D 3... C : codice C(x) : parola codice associata al simbolo x X l(x) : lunghezza della parola x. p.2/21

5 Codici a lunghezza variabile Def. Un codice sorgente D-ario per una v.c. X è una funzione da X in D. Esempio X = ( testa 1 2 croce C(testa) = 00, C(croce) = 11, l(testa) = 2, l(croce) = ), D = {0, 1}. p.3/21

6 Lunghezza media di un codice Def. La lunghezza media L(C) di un codice C per una v.c. X con d.d.p. P (x) è data da L(C) = x X p (x) l (x) = E[l(X)] Esempio X v.c. con valori in {1, 2, 3, 4}, D = {0, 1}, P (X = 1) = 1/2 C(1) = 0 P (X = 2) = 1/4 C(2) = 10 P (X = 3) = 1/8 C(3) = 110 P (X = 4) = 1/8 C(4) = 111 L(C) = = 1.75 = H(X). p.4/21

7 Nell esempio precedente si ha H(X) = L(C) ma questa uguaglianza non è vera in generale. Esempio X v.c. con valori in {1, 2, 3}, D = {0, 1}, P (X = 1) = 1/3 C(1) = 0 P (X = 2) = 1/3 C(2) = 10 P (X = 3) = 1/3 C(3) = 11 H(X) = log 3, L (C) = ( ) = 5 3 = p.5/21

8 Codici non singolari Def. Un codice è detto non singolare se ad ogni x X viene assegnata una diversa stringa in D, cioè x i x j C (x i ) C (x j ) I codici presentati negli esempi precedenti sono tutti non singolari.. p.6/21

9 Estensione di un codice Def. L estensione k ma C k di un codice C è una funzione che associa ad ogni x 1... x k X la stringa in D C k (x 1,..., x k ) = C(x 1 )C(x 2 )... C(x k ), L estensione C di C associa a ciascuna sequenza x 1... x n di lunghezza finita su X una stringa in D : C = C 1 C 2 C 3... Esempio C(x 1 ) = 00, C(x 2 ) = 11 C (x1x2) = p.7/21

10 Codici univocamente decodificabili Osservazione: Associare a parole sorgente diverse parole codice diverse non garantisce che il codice sia univocamente decodificabile: Può succedere C (x 1,..., x m ) = C (x 1,..., x n) nonostante si abbia C(x i ) C(x j ) per ogni i e j. Es. C = {10, 100, 01, 101} = = p.8/21

11 Codici univocamente decodificabili Osservazione: Associare a parole sorgente diverse parole codice diverse non garantisce che il codice sia univocamente decodificabile: Può succedere C (x 1,..., x m ) = C (x 1,..., x n) nonostante si abbia C(x i ) C(x j ) per ogni i e j. Es. C = {10, 100, 01, 101} = = Def. Un codice si dice univocamente decodificabile se la sua estensione è non singolare.. p.8/21

12 Codici prefissi Osservazione: Puó accadere che occorre attendere che la sequenza codificata sia trasmessa quasi interamente prima di poter iniziare la decodifica Es. C = {10, 100, 01, } = ? = p.9/21

13 Codici prefissi Osservazione: Puó accadere che occorre attendere che la sequenza codificata sia trasmessa quasi interamente prima di poter iniziare la decodifica Es. C = {10, 100, 01, } = ? = Def. Un codice si dice prefisso se nessuna parola di codice è prefissa di un altra.. p.9/21

14 Codici prefissi Osservazione: Puó accadere che occorre attendere che la sequenza codificata sia trasmessa quasi interamente prima di poter iniziare la decodifica Es. C = {10, 100, 01, } = ? = Def. Un codice si dice prefisso se nessuna parola di codice è prefissa di un altra. Un codice prefisso é univocamente decodificabile con ritardo finito. p.9/21

15 . p.10/21

16 Esempi di codici X Singolare Non Singolare U.D. non prefisso Prefisso Ambiguo Ambiguo Per decodificare Es. occorre scandire l intera sequenza Es Si det. I simbolo solo alla fine. p.11/21

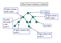
17 Alberi e Codici Prefissi Dato un codice D-ario C prefisso è possibile associare a C un albero D-ario: i rami dell albero sono etichettati con le lettere dell alfabeto D-ario {0,..., D 1} ciascuna parola di C possa essere ottenuta leggendo le etichette dei rami lungo il percorso dalla radice ad una certa foglia dell albero.. p.12/21

18 Esempio Dato il codice {111, 110, 10, 0} sull alfabeto D = {0, 1}, possiamo costruire l albero D-ario:. p.13/21

19 Disuguaglianza di Kraft La disuguaglianza di Kraft lega la lunghezza delle parole codice alla cardinalità dell alfabeto. (Parte Diretta) Per ogni codice prefisso D-ario, le lunghezze delle parole codice l 1,..., l m devono soddisfare la seguente disugluaglianza: m D l i 1 i=1 (Parte Inversa) Se l 1,..., l m soddisfano la disuguaglianza di Kraft, allora esiste un codice prefisso D-ario le cui parole hanno lunghezze l 1..., l m.. p.14/21

20 Dimostrazione parte diretta Dim. C: codice prefisso D-ario con lunghezze delle parole codice l 1,..., l m. l max : lunghezza massima delle parole di C altezza massima dell albero D-ario associato a C T : albero D-ario completo di altezza l max (T ha D l max foglie). Trasformiamo T nell albero associato a C.. p.15/21

21 Esempio. p.16/21

22 per ogni lunghezza l i, i = 1,..., m, dobbiamo eliminare un sottoalbero di altezza l max l i per ogni i = 1,..., m, vengono eliminate D l max l i foglie in totale vengono eliminate i D l max l i foglie poichè il numero di foglie eliminate non può superare il numero totale delle foglie di T si ha D l max l i D l max i i D l i 1. p.17/21

23 Dimostrazione parte inversa Dim. Supponiamo che l 1,..., l m soddisfano la disuguaglianza di Kraft l 1... l m (se così non fosse potremmo sempre riordinarle). Consideriamo l albero D-ario completo di altezza l m e proviamo a trasformarlo in un albero che rappresenta un codice D-ario prefisso: Prima di tutto etichettiamo i rami uscenti da ciascun nodo interno con gli interi 0, 1,..., D 1.. p.18/21

24 Per ogni i = 1,..., m: consideriamo il primo nodo disponibile di profondità l i (primo secondo l ordine lessicografico delle parole che si leggono andando dalla radice ai nodi). Eliminiamo il sottoalbero di questo nodo dall albero ed associamo alla foglia che abbiamo appena creato la parola codice i (vedi esempio). Eliminiamo D l m l i foglie Al passo i-esimo in totale abbiamo eliminato i j=1 Dl m l j foglie.. p.19/21

25 Esempio Lunghezze 1,2,2,2,2,2,3,3,3 che soddisfano la disuguaglianza di Kraft, D = {0, 1, 2}.. p.20/21

26 Il numero di foglie eliminte nei primi i (i < m) passi è i D l m l j = i+1 D l m l j D l m l i+1 D l m m D l j D l m l i+1 j=1 j=1 j=1 Poichè l 1,..., l m soddisfano la dis. di Kraft si ha D l m m j=1 D l j D l m l i+1 D l m D l m l i+1 D l m foglie eliminate al passo i-esimo D l m l i+1 possiamo eseguire il passo (i + 1)-esimo.. p.21/21