Analisi del circuito di stabilizzazione in ampiezza dell'oscillatore a ponte di Wien
|
|
|
- Annabella Martini
- 6 anni fa
- Visualizzazioni
Transcript
1 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 nalisi del circuito di stabilizzazione in ampiezza dell'oscillatore a ponte di Wien ota: nel testo sono riportati dei richiami a alcuni approfondimenti riportati alla fine di questo laoro La presente trattazione fa riferimento allo schema di Fig. doe è rappresentato un oscillatore a ponte di Wien con la rete di stabilizzazione dell'ampiezza. L'analisi è solta con l'obiettio di dimensionare correttamente la rete di stabilizzazione dell'ampiezza e alutare la distorsione da essa prodotta sulla tensione di uscita. L'analisi si basa sulla sostituzione del ramo non lineare del circuito (il ramo contenente gli zener) con due generatori di corrente equialenti. Il primo generatore I contiene la sola componente fondamentale, alla frequenza dell'oscillatore, della corrente che circola negli zener, mentre il secondo generatore I contiene tutta la componente armonica della suddetta corrente. In questo modo la somma delle correnti dei due generatori coincide con la totale corrente che circola negli zener. ei calcoli si utilizza l'ipotesi semplificatia che la tensione di uscita dell'oscillatore sia pressoché sinusoidale e sia pressoché sinusoidale anche la tensione ai capi del ramo del circuito che contiene gli zener. Fig. - Schema dell'oscillatore a ponte di Wien con rete di stabilizzazione dell'ampiezza Fig. - Sostituzione della rete non lineare con due generatori di corrente: I per la componente fondamentale e I per la componente armonica
2 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 La corrente che circola negli zener è diersa da zero solo quando la tensione supera la tensione di zener. Essa può essere calcolata a partire dalla tensione sulla resistenza _ di Fig. e ale: _ 0 + per per per In una rappresentazione normalizzata rispetto a, la forma d'onda della tensione ai capi di _, mostrata in Fig.3, Limitandoci al primo semiperiodo tale tensione assume un alore nullo per e alore non nullo altroe ( a) _ per α < α e α > 80 0 α sin( α) _ sin( α) b per α < α < 80 elle precedenti equazioni sono state fatte le seguenti assunzioni: α asin ( b ) e b α 0.5 x i y i 4, 0 y i 8, i Fig.3 - Tensione sulla resistenza _ per diersi rapporti tra la tensione di zener e l'ampiezza della sinusoide Continuando ad operare su grandezze normalizzate, dalla forma d'onda di Fig.3 si ricaa la componente armonica fondamentale, parametrizzata con b della tensione su _. Sfruttando la simmetria della forma d'onda, l'integrale è calcolato su un quarto di periodo:
3 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett π. π α sin( α ). sin( α ) b dα 4 π.. 4 π. cos α ( ). sin ( α ). α. b cos( α) ora, sostituendo l'espressione di α, si ottiene 4 π.. 4 π. b.. b asin b Questa espressione fornisce il alore normalizzato della componente fondamentale (prima armonica) della tensione sulla resistenza _, in funzione del rapporto b fra la tensione degli zener e l'ampiezza della tensione ai capi del circuito. Il suo andamento è riportato in Fig. 4 in funzione del rapporto b 0.8 i bi Fig.4 - ndamento della componente di prima armonica della tensione sulla resistenza _ normalizzata rispetto alla tensione in funzione del rapporto b fra la tensione di zener z e l'ampiezza della tensione PPOFODIMETI Linearizzazione della caratteristica Dall'analisi precedente risulta che il generatore I impone una corrente sinusoidale in fase con la tensione, anch'essa sinusoidale (per ipotesi di laoro), presente ai suoi capi. Quindi è equialente ad una resistenza equi di alore:
4 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 equi I _ da cui si può scriere equi _ quindi il grafico di Fig.4 può anche rappresentare l'andamento del rapporto _ / equi in funzione di b. Il risultato dell'analisi precedente è che la rete non lineare può essere sostituita con un circuito parallelo costituito da una resistenza di alore equi e da un generatore di corrente I. Per aere la condizione di oscillazione del ponte di Wien l'amplificatore dee aere guadagno pari a 3 quindi si dee porre // equi *_ e questo consente di definire una procedura di progetto: Sia dato out (ampiezza della tensione di uscita dell'oscillatore). Dalla condizione di oscillazione si ottiene /3 out. Si sceglie il alore per il rapporto z / 3. Si impone un alore arbitrario per _ 4. Si impone il alore _ leggermente maggiore (+0%) del alore teorico *_ per garantire la partenza dell'oscillazione 5. Dall'espressione * // equi si calcola equi 6. Dal grafico, noto z /, si determina equi /_ 7. esta determinato il alore di _ 8. Ora si possono riscalare proporzionalmente i alori di resistenza _, _ e _ per aere dei alori compatibili con la corrente erogabile dall'operazionale (che fissa un alore minimo per le resistenze) e la corrente di polarizzazione negli zener (che fissa un alore massimo) PPOFODIMETI Criteri di progettazione nalisi del contenuto armonico Per analizzare il contenuto armonico della tensione di uscita occorre alutare la funzione di trasferimento fra il generatore I e la tensione di uscita out dell'oscillatore. Essa risulta W ( s) I out + s3c + ( sc) + ( sc) Si ede che la FdT ha due poli complessi coniugati alla frequenza di oscillazione che le danno un guadagno infinito, ed una coppia di zeri reali. Il segnale di ingresso (I ) non ha componenti alla frequenza fondamentale dell'oscillatore ma contiene armoniche dispari.osserando il diagramma asintotico, si troa che, per le componenti armoniche, il guadagno risulta costante. Infatti il secondo zero, oltre al quale il modulo della FdT è costante su tale diagramma, è a circa.6 olte la fondamentale e la prima armonica è a 3 olte la fondamentale. In pratica tutte le armoniche presenti sulla tensione su _ sono riportate in uscita con un rapporto pari a quello delle resistenze _/_ e che ale. β β
5 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 Per migliorare la situazione è anche possibile modificare lo schema nel modo mostrato in Fig.6 doe si sfrutta l'effetto filtrante della rete di Wien per ottenere un segnale a distorsione inferiore. La nuoa uscita out presenta ancora la stessa ampiezza di segnale alla componente fondamentale in quanto i due amplificatori hanno lo stesso guadagno sulla tensione presente agli ingressi inertenti. Però questa tensione è meno corrotta dalla presenza del generatore I. La nuoa funzione di trasferimento risulta: W ( s) sc + ( sc) che presenta un solo zero nell'origine e quindi il suo modulo continua a diminuire all'aumentare della frequenza e le armoniche in uscita engono attenuate in modo proporzionale al loro ordine. Il risultato di una simulazione di ponte di Wien progettato secondo i criteri appena esposti, è riportato in Fig.7. Si ede la tensione sulla uscita a bassa distorsione out e la tensione differenza fra le due uscite (bassa distorsione e uscita naturale), amplificata di 0 olte. Questa differenza mostra la cancellazione della componente fondamentale, praticamente coincidente per le due uscite, mentre mostra un residuo sostanzialmente di terza armonica che è presente sull'uscita naturale dell'oscillatore a ponte di Wien e non sulla nuoa uscita. Esistono molte arianti dell'oscillatore a ponte di Wien che sono intese a migliorarne le prestazioni, ma, generalmente sono tutte facilmente riconducibili alla topologia di base. Lo stesso si può dire per il circuito di limitazione del guadagno e quindi anche la teoria di analisi proposta con questo laoro può facilmente essere estesa anche a situazioni dierse. Fig.6 - Schema dell'oscillatore a ponte di Wien con rete di stabilizzazione dell'ampiezza e con uscita a bassa distorsione
6 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 Fig.7 - Tensione di uscita dell'oscillatore a ponte di Wien (out_) e differenza fra la tensione fra l'uscita a bassa distorsione e quella "naturale". Questa tensione è amplificata di 0 olte (0(out- - out_)).
7 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett PPOFODIMETI Linearizzazione della caratteristica Per aere una linearizzazione della cura per piccoli alori di b si può deriare l'espressione troata in precedenza ottenendo: 4 π b ( ) b b che, come mostrato in Fig.5, ale circa -.5 per b prossimi a zero. Tale espressione può quindi essere approssimata dall'equazione:. 5 alida per tensioni di zener non superiori al 30% della tensione ai capi del circuito di limitazione. b y i bi Fig.5 - alutazione della pendenza della cura di Fig Criteri di progettazione el progetto così definito dee essere scelta (punto ) la tensione di zener z. E' interessante aere un criterio per la sua scelta. isulta coneniente che tale scelta sia per alori di tensione possibilmente bassi (rispetto a ) in base alle seguenti considerazioni:. Il alore di equi non dipende dalla tensione degli zener ma solo da _ ed _. Di conseguenza anche la corrente I dipende solo dalla scelta di _ ed _.. E' coneniente che la componente I sia il più piccola possibile per aere meno distorsione sulla tensione di uscita 3. Dai punti precedenti risulta coneniente che il rapporto I / I sia massimo cioè che la corrente sugli zener sia il più sinusoidale possibile e questo si ottiene se la caduta sugli zener è minima e quella su _ è massima.
8 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 Come si edrà a bree, il alore minimo di risulta limitato dal fatto di aere fissato il guadagno massimo per consentire di far funzionare il circuito anche in considerazione delle tolleranze dei componenti e della non idealità dell'amplificatore operazionale. Finché < gli zener sono spenti e il guadagno dell'amplificatore risulta massimo e tale condizione è necessaria per far iniziare l'oscillazione. Il guadagno ale: _ max + + β + β doe rappresenta l'incremento di _ dal suo alore nominale _ che fornisce l'aumento di guadagno necessario ad iniziare l'oscillazione. Il suo alore risulta: β _ max Fissato il alore di β, si può ottenere il alore della equi che garantisce l'oscillazione sapendo che il suo parallelo con dee alere : equi β β Scegliendo ora il rapporto / si impone, dal grafico di Fig. 4, il rapporto _ / equi dal quale il alore di risulta: concludendo così il progetto. _ equi _ β β Fissati ora i alori di,,, si può determinare l'andamento del guadagno (riferito alle sole componenti fondamentali di tensione e di corrente) al ariare dell'ampiezza del segnale di uscita. Tale guadagno sarà maggiore di 3 per ampiezze prossime a zero, e sarà minore di 3 per alori eleati di. + // equi equi ( β + β β β ) // β + β + ( β ) L'andamento del guadagno è infine riportato in Fig.6 sempre al ariare del rapporto b fra la tensione di zener z e l'ampiezza della tensione. Si ede che per alori eleati di, il alore di b è basso e il guadagno risulta inferiore a 3. iceersa il guadagno aumenta per alori bassi di. L'ampiezza (stabile) dell'oscillazione sarà quindi in corrispondenza del punto di intersezione fra le due cure di Fig. 6.
9 Stabilizzazione dell'mpiezza nell'oscillatore a Ponte di Wien leopoldo rossetto - 5 sett. 00 Fig.6 - ndamento del guadagno in funzione del rapporto b fra la tensione di zener z e l'ampiezza della tensione (K0.6, β.) Dalle precedenti equazioni si troa che i alori minimo e massimo del guadagno risultano: _ min _ max + β + β + ( β ) tali alori deono essere in grado di coprire le ariazioni di guadagno richieste dal fatto che i componenti utilizzati nella realizzazione dell'oscillatore a ponte di Wien non sono ideali e quindi la condizione di oscillazione richiederà un alore di guadagno dierso da quello teorico (3). olendo porre una ariazione simmetrica δ di guadagno attorno al alore nominale dee risultare: _ max _ min + β 3 ( + δ ) + β 3 ( δ ) + ( β ) ricaando δ dalla prima equazione e sostituendolo nella seconda, risulta δ ( β ) 3 _ + β 3 ( ( β )) + ( β ) 3 da cui β 4 Quindi, per aere una escursione simmetrica del guadagno intorno al suo alore teorico, il rapporto fra la tensione di zener z e l'ampiezza della tensione risulta inferiore a / e tanto più basso quanto è alto il alore massimo del guadagno che si sceglie. Si ossera che potrebbe non essere possibile garantire una escursione simmetrica del guadagno intorno al alore teorico
Amplificatori in classe A con accoppiamento capacitivo
 Ottobre 00 Amplificatori in classe A con accoppiamento capacitivo amplificatore in classe A di Fig. presenta lo svantaggio che il carico è percorso sia dalla componente di segnale, variabile nel tempo,
Ottobre 00 Amplificatori in classe A con accoppiamento capacitivo amplificatore in classe A di Fig. presenta lo svantaggio che il carico è percorso sia dalla componente di segnale, variabile nel tempo,
Amplificatori operazionali
 mplificatori operazionali - - O ( - - ) (*) >> (*) nella zona ad alto guadagno Per amplificatori operazionali (OP-MP) si intende quella categoria di dispositii integrati che presentano due morsetti di
mplificatori operazionali - - O ( - - ) (*) >> (*) nella zona ad alto guadagno Per amplificatori operazionali (OP-MP) si intende quella categoria di dispositii integrati che presentano due morsetti di
Amplificatori elementari con carico attivo MOSFET E connesso a diodo
 Amplificatori elementari con carico attio MOSFET E connesso a diodo i ( ) = K g = µ C W L I V t m n OX G. Martines MOSFET DE connesso a diodo GS = 0, il transistore può funzionare in regione di triodo
Amplificatori elementari con carico attio MOSFET E connesso a diodo i ( ) = K g = µ C W L I V t m n OX G. Martines MOSFET DE connesso a diodo GS = 0, il transistore può funzionare in regione di triodo
Multivibratore astabile con Amp. Op.
 Multivibratore astabile con Amp. Op. Il multivibratore astabile è un generatore di onde quadre e rettangolari; esso è un circuito retroazionato positivamente, avente due stati entrambi instabili, che si
Multivibratore astabile con Amp. Op. Il multivibratore astabile è un generatore di onde quadre e rettangolari; esso è un circuito retroazionato positivamente, avente due stati entrambi instabili, che si
Principi di ingegneria elettrica. Analisi delle reti resistive. Lezione 8 a. Teorema di Thévenin Teorema di Norton
 Principi di ingegneria elettrica ezione 8 a Analisi delle reti resistie eorema di héenin eorema di Norton eorema di héenin Una rete lineare attia (comprendente generatori ideali di tensione e/o corrente)
Principi di ingegneria elettrica ezione 8 a Analisi delle reti resistie eorema di héenin eorema di Norton eorema di héenin Una rete lineare attia (comprendente generatori ideali di tensione e/o corrente)
Amplificatori. (versione del ) Amplificatore
 mplificatori www.die.ing.unibo.it/pers/mastri/didattica.htm (ersione del 8--0) mplificatore Un amplificatore è un dispositio a due porte in grado di aumentare l ampiezza del segnale s i (t) applicato alla
mplificatori www.die.ing.unibo.it/pers/mastri/didattica.htm (ersione del 8--0) mplificatore Un amplificatore è un dispositio a due porte in grado di aumentare l ampiezza del segnale s i (t) applicato alla
FONDAMENTI DI ELETTRONICA - 2 a prova 4 febbraio 2003
 Ù FONDAMENTI DI ELETTRONICA - 2 a prova 4 febbraio 2003 Esercizio 1 1) Si consideri il circuito riportato in figura. Si supponga che l amplificatore operazionale sia ideale (A, Z in, Z out =0).Si determini
Ù FONDAMENTI DI ELETTRONICA - 2 a prova 4 febbraio 2003 Esercizio 1 1) Si consideri il circuito riportato in figura. Si supponga che l amplificatore operazionale sia ideale (A, Z in, Z out =0).Si determini
4.4 Il regolatore di tensione a diodo zener.
 4.4 l regolatore di tensione a diodo zener. n molte applicazioni il valore del fattore di ripple ottenibile con un alimentatore a raddrizzatore e filtro capacitivo non è sufficientemente basso. Per renderlo
4.4 l regolatore di tensione a diodo zener. n molte applicazioni il valore del fattore di ripple ottenibile con un alimentatore a raddrizzatore e filtro capacitivo non è sufficientemente basso. Per renderlo
Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA AC2. Circuiti in corrente alternata
 Scopo dell'esperienza: Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA AC2 Circuiti in corrente alternata. Uso di un generatore di funzioni (onda quadra e sinusoidale); 2.
Scopo dell'esperienza: Corso di Laurea in Scienza dei Materiali Laboratorio di Fisica II ESPERIENZA AC2 Circuiti in corrente alternata. Uso di un generatore di funzioni (onda quadra e sinusoidale); 2.
Convertitori da tensione a impulsi
 Misure basate sul conteggio di impulsi Conertitori da tensione a impulsi - Conertitori da tensione a impulsi - Conertitore tensione-frequenza Schema di principio Il conertitore tensione-frequenza consente
Misure basate sul conteggio di impulsi Conertitori da tensione a impulsi - Conertitori da tensione a impulsi - Conertitore tensione-frequenza Schema di principio Il conertitore tensione-frequenza consente
Il blocco amplificatore realizza la funzione di elevare il livello (di tensione o corrente) del segnale (in tensione o corrente) in uscita da una
 l blocco amplificatore realizza la funzione di elevare il livello (di tensione o corrente) del segnale (in tensione o corrente) in uscita da una sorgente. Nel caso, come riportato in figura, il segnale
l blocco amplificatore realizza la funzione di elevare il livello (di tensione o corrente) del segnale (in tensione o corrente) in uscita da una sorgente. Nel caso, come riportato in figura, il segnale
ELETTROTECNICA T - A.A. 2014/2015 ESERCITAZIONE 1
 ELETTROTECNICA T - A.A. 2014/2015 ESERCITAZIONE 1 ESERCIZIO 1 Dopo aver risolto il circuito lineare tempo-invariante mostrato Fig. 1.1, calcolare la potenza erogata/assorbita da ogni componente. Fig. 1.1
ELETTROTECNICA T - A.A. 2014/2015 ESERCITAZIONE 1 ESERCIZIO 1 Dopo aver risolto il circuito lineare tempo-invariante mostrato Fig. 1.1, calcolare la potenza erogata/assorbita da ogni componente. Fig. 1.1
I.P.S.I.A. Di BOCCHIGLIERO Oscillatori ad alta frequenza ---- Materia: Elettronica. prof. Ing. Zumpano Luigi
 I.P.S.I.A. Di BOHIGLIERO a.s. 2010/2011 classe III Materia: Elettronica Oscillatori ad alta frequenza alunni : hindamo Michelangelo Bossio Salvatore prof. Ing. Zumpano Luigi IPSIA Bocchigliero Elettronica
I.P.S.I.A. Di BOHIGLIERO a.s. 2010/2011 classe III Materia: Elettronica Oscillatori ad alta frequenza alunni : hindamo Michelangelo Bossio Salvatore prof. Ing. Zumpano Luigi IPSIA Bocchigliero Elettronica
Curva caratteristica del transistor
 Curva caratteristica del transistor 1 AMPLIFICATORI Si dice amplificatore un circuito in grado di aumentare l'ampiezza del segnale di ingresso. Un buon amplificatore deve essere lineare, nel senso che
Curva caratteristica del transistor 1 AMPLIFICATORI Si dice amplificatore un circuito in grado di aumentare l'ampiezza del segnale di ingresso. Un buon amplificatore deve essere lineare, nel senso che
Compito di Fondamenti di Automatica - 13 luglio 2006 Versione A Esercizio 1A. Dato lo schema seguente (operazionali ideali)
 Compito di Fondamenti di Automatica - 1 luglio 2006 Versione A Esercizio 1A. Dato lo schema seguente (operazionali ideali) C v in 2 vout é richiesto di calcolare la funzione di trasferimento G(s) tra v
Compito di Fondamenti di Automatica - 1 luglio 2006 Versione A Esercizio 1A. Dato lo schema seguente (operazionali ideali) C v in 2 vout é richiesto di calcolare la funzione di trasferimento G(s) tra v
Studio di circuiti contenenti diodi Uso di modelli semplificati
 STUDIO DI CIRCUITI CONTENENTI DIODI USO DI MODELLI SEMPLIFICATI 1 Primo modello 2 Secondo modello 4 Terzo modello 6 La caratteristica e la retta di carico 8 Studio di circuiti contenenti diodi Uso di modelli
STUDIO DI CIRCUITI CONTENENTI DIODI USO DI MODELLI SEMPLIFICATI 1 Primo modello 2 Secondo modello 4 Terzo modello 6 La caratteristica e la retta di carico 8 Studio di circuiti contenenti diodi Uso di modelli
OSCILLATORE. Fig.1 - Sistema retroazionato positivamente
 OSCILLATORE La forma d'onda sinusoidale riveste una particolare importanza negli sviluppi teorici ed applicativi dell'elettronica e delle telecomunicazioni. Infatti ogni altra forma d'onda può essere pensata,
OSCILLATORE La forma d'onda sinusoidale riveste una particolare importanza negli sviluppi teorici ed applicativi dell'elettronica e delle telecomunicazioni. Infatti ogni altra forma d'onda può essere pensata,
1 Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli R 2. v out R 1
 Prova scritta di fine corso di Meccanica Applicata alle Macchine, modulo da 5CFU Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC Il circuito mostrato in figura è uno
Prova scritta di fine corso di Meccanica Applicata alle Macchine, modulo da 5CFU Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC Il circuito mostrato in figura è uno
Prova scritta Fondamenti di Elettronica B / BC 26 Gennaio 2011 COGNOME: NOME: CORSO DI LAUREA: INGEGNERIA
 Prova scritta Fondamenti di Elettronica B / BC 26 Gennaio 2011 A COGNOME: NOME: CORSO DI LAUREA: INGEGNERIA MATRICOLA: Negli esercizi, ove necessario e salvo indicazioni contrarie, si consideri che i circuiti
Prova scritta Fondamenti di Elettronica B / BC 26 Gennaio 2011 A COGNOME: NOME: CORSO DI LAUREA: INGEGNERIA MATRICOLA: Negli esercizi, ove necessario e salvo indicazioni contrarie, si consideri che i circuiti
Circuiti elettrici non lineari. Il diodo
 Circuiti elettrici non lineari Il diodo Misure con l oscilloscopio e con il multimetro Edgardo Smerieri Laura Faè PLS - AIF - Corso Estivo di Fisica Genova 009 Individuazione dei pin del diodo Anodo Anodo
Circuiti elettrici non lineari Il diodo Misure con l oscilloscopio e con il multimetro Edgardo Smerieri Laura Faè PLS - AIF - Corso Estivo di Fisica Genova 009 Individuazione dei pin del diodo Anodo Anodo
Teoria dei circuiti reazionati
 Teoria dei circuiti reazionati Differenze tra lo schema di reazione ideale e il circuito con retroazione: Ogni blocco dello schema a blocchi ha una direzione e un trasferimento che non dipende dai blocchi
Teoria dei circuiti reazionati Differenze tra lo schema di reazione ideale e il circuito con retroazione: Ogni blocco dello schema a blocchi ha una direzione e un trasferimento che non dipende dai blocchi
L Amplificatore Operazionale
 L mplificatore perazionale ommario L amplificatore perazionale: Introduzione agli.. Caratteristiche degli.. ideali mplificatore Inertente e NN Inertente Inseguitore Differenziale (mpl. da strumentazione)
L mplificatore perazionale ommario L amplificatore perazionale: Introduzione agli.. Caratteristiche degli.. ideali mplificatore Inertente e NN Inertente Inseguitore Differenziale (mpl. da strumentazione)
Amplificatori operazionali
 Amplificatori operazionali Parte 3 www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 6--) Integratore Dato che l ingresso invertente è virtualmente a massa si ha vi ( t) ir ( t) R Inoltre i
Amplificatori operazionali Parte 3 www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 6--) Integratore Dato che l ingresso invertente è virtualmente a massa si ha vi ( t) ir ( t) R Inoltre i
I.T.I.S. Max Planck Verifica di Elettronica Oscillatori classe 5 A/Tel a.s. 2013/14 COGNOME E NOME Data: 27/11/2013
 I.T.I.. Max Planck Verifica di Elettronica Oscillatori classe 5 A/Tel a.s. 03/4 OGNOME E NOME Data: 7//03 Quesito ) (50%) Dato il circuito qui a fianco che rappresenta un oscillatore sinusoidale a ponte
I.T.I.. Max Planck Verifica di Elettronica Oscillatori classe 5 A/Tel a.s. 03/4 OGNOME E NOME Data: 7//03 Quesito ) (50%) Dato il circuito qui a fianco che rappresenta un oscillatore sinusoidale a ponte
Gli alimentatori stabilizzati
 Gli alimentatori stabilizzati Scopo di un alimentatore stabilizzato è di fornire una tensione di alimentazione continua ( cioè costante nel tempo), necessaria per poter alimentare un dispositivo elettronico
Gli alimentatori stabilizzati Scopo di un alimentatore stabilizzato è di fornire una tensione di alimentazione continua ( cioè costante nel tempo), necessaria per poter alimentare un dispositivo elettronico
Valutazione della capacità dissipativa di un sistema strutturale
 Tecniche innovative per l identificazione delle caratteristiche dinamiche delle strutture e del danno Valutazione della capacità dissipativa di un sistema strutturale Prof. Ing. Felice Carlo PONZO - Ing.
Tecniche innovative per l identificazione delle caratteristiche dinamiche delle strutture e del danno Valutazione della capacità dissipativa di un sistema strutturale Prof. Ing. Felice Carlo PONZO - Ing.
SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE
 CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE Ing. e-mail: luigi.biagiotti@unimore.it
CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE Ing. e-mail: luigi.biagiotti@unimore.it
Amplificatori Differenziali
 Amplificatori Differenziali nei simboli non si esplicitano gli alimentatori DC, cioè Normalmente i circuiti che realizzano l amplificatore differenziale e operazionale non contengono un nodo elettricamente
Amplificatori Differenziali nei simboli non si esplicitano gli alimentatori DC, cioè Normalmente i circuiti che realizzano l amplificatore differenziale e operazionale non contengono un nodo elettricamente
Lezione 2: Amplificatori operazionali. Prof. Mario Angelo Giordano
 Lezione 2: Amplificatori operazionali Prof. Mario Angelo Giordano L'amplificatore operazionale come circuito integrato è uno dei circuiti lineari maggiormente usati. L'amplificatore operazionale è un amplificatore
Lezione 2: Amplificatori operazionali Prof. Mario Angelo Giordano L'amplificatore operazionale come circuito integrato è uno dei circuiti lineari maggiormente usati. L'amplificatore operazionale è un amplificatore
Risposta temporale: esempi
 ...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
Schemi e caratteristiche dei principali amplificatori a BJT
 Schemi e caratteristiche dei principali amplificatori a BJT Sommario argomenti trattati Schemi e caratteristiche dei principali amplificatori a BJT... 1 Amplificatore emettitore comune o EC... 1 Amplificatore
Schemi e caratteristiche dei principali amplificatori a BJT Sommario argomenti trattati Schemi e caratteristiche dei principali amplificatori a BJT... 1 Amplificatore emettitore comune o EC... 1 Amplificatore
AMPLIFICATORI OPERAZIONALI DEFINIZIONI AMPLIFICATORE INVERTENTE AMPLIFICATORE NON INVERTENTE INTEGRATORE DERIVATORE SOMMATORE
 AMPLIFICATOI OPEAZIONALI DEFINIZIONI AMPLIFICATOE INVETENTE AMPLIFICATOE NON INVETENTE INTEGATOE DEIVATOE SOMMATOE 2 Buona parte dei circuiti elettronici è costituita da componenti integrati, composti
AMPLIFICATOI OPEAZIONALI DEFINIZIONI AMPLIFICATOE INVETENTE AMPLIFICATOE NON INVETENTE INTEGATOE DEIVATOE SOMMATOE 2 Buona parte dei circuiti elettronici è costituita da componenti integrati, composti
La struttura circuitale del multivibratore monostabile deriva da quella dell astabile modificata nel seguente modo:
 Generalità Il multivibratore monostabile è un circuito retroazionato positivamente, che presenta una tensione di uscita V out stabile che può essere modificata solo a seguito di un impulso esterno di comando
Generalità Il multivibratore monostabile è un circuito retroazionato positivamente, che presenta una tensione di uscita V out stabile che può essere modificata solo a seguito di un impulso esterno di comando
Elaborazione aut. dei dati
 Programma Elaborazione aut. dei dati Sistema interattivo MATLAB Risoluzione di sistemi lineari e di equazioni non lineari Interpolazione e smoothing di dati Opzioni finanziarie Approssimazione di integrali
Programma Elaborazione aut. dei dati Sistema interattivo MATLAB Risoluzione di sistemi lineari e di equazioni non lineari Interpolazione e smoothing di dati Opzioni finanziarie Approssimazione di integrali
RELAZIONE DI TELECOMUNICAZIONI ITIS Vobarno Titolo: Oscillatori sinusoidali
 RELAZIONE DI TELECOMUNICAZIONI ITIS Vobarno Titolo: Oscillatori sinusoidali Nome: Samuele Sandrini 4AT 7/3/5 Gli oscillatori sinusoidali sono circuiti che producono un segnale sinusoidale di ampiezza e
RELAZIONE DI TELECOMUNICAZIONI ITIS Vobarno Titolo: Oscillatori sinusoidali Nome: Samuele Sandrini 4AT 7/3/5 Gli oscillatori sinusoidali sono circuiti che producono un segnale sinusoidale di ampiezza e
ANALISI DEI SISTEMI DI CONTROLLO A TEMPO CONTINUO. Schema generale di controllo in retroazione
 ANALISI DEI SISTEMI DI CONTROLLO A TEMPO CONTINUO Schema generale di controllo in retroazione Requisiti di un sistema di controllo Stabilità in condizioni nominali Margine di guadagno e margine di fase
ANALISI DEI SISTEMI DI CONTROLLO A TEMPO CONTINUO Schema generale di controllo in retroazione Requisiti di un sistema di controllo Stabilità in condizioni nominali Margine di guadagno e margine di fase
SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo. RETI CORRETTRICI
 SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html RETI CORRETTRICI Ing. Luigi Biagiotti e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html RETI CORRETTRICI Ing. Luigi Biagiotti e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
Liberamente tratto da Prima Legge di Ohm
 Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Liberamente tratto da www.openfisica.com Prima Legge di Ohm Agli estremi di due componenti elettrici di un circuito (che si possono chiamare conduttore X ed Y) è applicata una differenza di potenziale
Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni
 Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni Definizioni e breve richiamo alle principali leggi dei circuiti elettrici Risolvere un circuito elettrico significa determinare i
Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni Definizioni e breve richiamo alle principali leggi dei circuiti elettrici Risolvere un circuito elettrico significa determinare i
Esercizi sul luogo delle radici
 FA Esercizi 6, 1 Esercizi sul luogo delle radici Analisi di prestazioni a ciclo chiuso, progetto di regolatori facendo uso del luogo delle radici. Analisi di prestazioni FA Esercizi 6, 2 Consideriamo il
FA Esercizi 6, 1 Esercizi sul luogo delle radici Analisi di prestazioni a ciclo chiuso, progetto di regolatori facendo uso del luogo delle radici. Analisi di prestazioni FA Esercizi 6, 2 Consideriamo il
VELOCITA' CRITICHE FLESSIONALI
 VELOCITA' CRITICHE FLESSIONALI Si consideri un albero privo di massa recante in posizione intermedia un corpo puntiforme di massa "M". Se la massa viene spostata dalla sua posizione di equilibrio in direzione
VELOCITA' CRITICHE FLESSIONALI Si consideri un albero privo di massa recante in posizione intermedia un corpo puntiforme di massa "M". Se la massa viene spostata dalla sua posizione di equilibrio in direzione
OSCILLATORE A SFASAMENTO
 Elettronica Applicata a.a. 2013/2014 Esercitazione N 5 OSCILLATORE A SFASAMENTO Fabio Cioria Andrea Giombetti Giulio Pelosi (fabio.cioria@insono.com) (giombetti@unifi.it) (giulio.pelosi@insono.it) www.echommunity.com/courses.htm
Elettronica Applicata a.a. 2013/2014 Esercitazione N 5 OSCILLATORE A SFASAMENTO Fabio Cioria Andrea Giombetti Giulio Pelosi (fabio.cioria@insono.com) (giombetti@unifi.it) (giulio.pelosi@insono.it) www.echommunity.com/courses.htm
APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts
 Università degli Studi di Trieste Facoltà di Ingegneria Laurea in Ingegneria dell Informazione a.a. 2004/2005 APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts docente: Stefano Pastore
Università degli Studi di Trieste Facoltà di Ingegneria Laurea in Ingegneria dell Informazione a.a. 2004/2005 APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts docente: Stefano Pastore
a.a. 2014/2015 Docente: Stefano Bifaretti
 a.a. 2014/2015 Docente: Stefano Bifaretti email: bifaretti@ing.uniroma2.it Gli schemi circuitali impiegati per la realizzazione dei convertitori statici sono molteplici. Infatti, la struttura del convertitore
a.a. 2014/2015 Docente: Stefano Bifaretti email: bifaretti@ing.uniroma2.it Gli schemi circuitali impiegati per la realizzazione dei convertitori statici sono molteplici. Infatti, la struttura del convertitore
In elettronica un filtro elettronico è un sistema o dispositivo che realizza
 Filtri V.Russo Cos è un Filtro? In elettronica un filtro elettronico è un sistema o dispositivo che realizza delle funzioni di trasformazione o elaborazione (processing) di segnali posti al suo ingresso.
Filtri V.Russo Cos è un Filtro? In elettronica un filtro elettronico è un sistema o dispositivo che realizza delle funzioni di trasformazione o elaborazione (processing) di segnali posti al suo ingresso.
PROGETTO DI UN FILTRO PASSA BASSO
 orso di elettronica per telecomunicazioni - esercitazione POGETTO DI UN FILTO PASSA BASSO Docente del corso: prof. Giovanni Busatto Galletti iccardo Matr. 65 relazione elettronica per telecomunicazioni
orso di elettronica per telecomunicazioni - esercitazione POGETTO DI UN FILTO PASSA BASSO Docente del corso: prof. Giovanni Busatto Galletti iccardo Matr. 65 relazione elettronica per telecomunicazioni
I convertitori c.a.-c.a. possono essere suddivisi in tre categorie: convertitori a controllo di fase, cicloconvertitori, convertitori a matrice.
 Tra i vari tipi di convertitori monostadio, i convertitori c.a.-c.a. sono quelli che presentano il minore interesse applicativo, a causa delle notevoli limitazioni per quanto concerne sia la qualità della
Tra i vari tipi di convertitori monostadio, i convertitori c.a.-c.a. sono quelli che presentano il minore interesse applicativo, a causa delle notevoli limitazioni per quanto concerne sia la qualità della
a.a. 2015/2016 Docente: Stefano Bifaretti
 a.a. 2015/2016 Docente: Stefano Bifaretti email: bifaretti@ing.uniroma2.it Controllo ad anello aperto Il filtro LC è necessario per ridurre le ondulazioni di corrente e di tensione ed è dimensionato in
a.a. 2015/2016 Docente: Stefano Bifaretti email: bifaretti@ing.uniroma2.it Controllo ad anello aperto Il filtro LC è necessario per ridurre le ondulazioni di corrente e di tensione ed è dimensionato in
CONTROLLI AUTOMATICI Ingegneria Gestionale ANALISI ARMONICA
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANALISI ARMONICA Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANALISI ARMONICA Ing. Federica Grossi Tel. 059 2056333 e-mail: federica.grossi@unimore.it
Filtri passivi Risposta in frequenza dei circuiti RC-RL-RLC
 23. Guadagno di un quadripolo Filtri passivi isposta in frequenza dei circuiti C-L-LC In un quadripolo generico (fig. ) si definisce guadagno G il rapporto tra il valore d uscita e quello d ingresso della
23. Guadagno di un quadripolo Filtri passivi isposta in frequenza dei circuiti C-L-LC In un quadripolo generico (fig. ) si definisce guadagno G il rapporto tra il valore d uscita e quello d ingresso della
2 Alimentazione. +Vdc. Alimentazione 1 IGBT1 GND1. Alimentazione 2 IGBT2 GND2. -Vdc. Fig.1 - Alimentazione corretta degli switchs di uno stesso ramo
 2 Alimentazione In un convertitore di potenza l alimentazione rappresenta un elemento fondamentale di tutto il progetto. L alimentatore deve essere in grado di fornire il livello di tensione e la corrente
2 Alimentazione In un convertitore di potenza l alimentazione rappresenta un elemento fondamentale di tutto il progetto. L alimentatore deve essere in grado di fornire il livello di tensione e la corrente
LA RISPOSTA ARMONICA DEI SISTEMI LINEARI (regime sinusoidale) S o (t)
 ELETTRONICA E TELECOMUNICAZIONI CLASSE QUINTA A INF LA RISPOSTA ARMONICA DEI SISTEMI LINEARI (regime sinusoidale) S i (t) Sistema LINEARE S o (t) Quando si considerano i sistemi lineari, per essi è applicabile
ELETTRONICA E TELECOMUNICAZIONI CLASSE QUINTA A INF LA RISPOSTA ARMONICA DEI SISTEMI LINEARI (regime sinusoidale) S i (t) Sistema LINEARE S o (t) Quando si considerano i sistemi lineari, per essi è applicabile
ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
STABILITÀ DEI SISTEMI Metodo di Bode e Nyquist
 I.T.I. Modesto PANETTI B A R I Via Re David, 186-70125 BARI 080-542.54.12 - Fax 080-542.64.32 Internet http://www.itispanetti.it email : BATF05000C@istruzione.it INTRODUZIONE STABILITÀ DEI SISTEMI Metodo
I.T.I. Modesto PANETTI B A R I Via Re David, 186-70125 BARI 080-542.54.12 - Fax 080-542.64.32 Internet http://www.itispanetti.it email : BATF05000C@istruzione.it INTRODUZIONE STABILITÀ DEI SISTEMI Metodo
12. F.d.T. con uno ZERO nell'origine ed un POLO non nell origine: Derivatore invertente reale. Per prima cosa troviamo Z 1. Quindi: eq
 Appunti di ELETTONIA lassi QUINTE Integratori e Derivatori attivi:.d.t., diagrammi di Bode, risposte nel tempo A.S. 999-000 - martedì 7 dicembre 999 Pagina n. 53..d.T. con uno EO nell'origine ed un POLO
Appunti di ELETTONIA lassi QUINTE Integratori e Derivatori attivi:.d.t., diagrammi di Bode, risposte nel tempo A.S. 999-000 - martedì 7 dicembre 999 Pagina n. 53..d.T. con uno EO nell'origine ed un POLO
Esercitazione n 3: Amplificatore a base comune
 Esercitazione n 3: Amplificatore a base comune 1) Per il circuito in Fig. 1 determinare il valore delle resistenze di polarizzazione affinché si abbia: I C = 0,2 ma; V C = 3 V; V E = 1,9 V. Sia noto che:
Esercitazione n 3: Amplificatore a base comune 1) Per il circuito in Fig. 1 determinare il valore delle resistenze di polarizzazione affinché si abbia: I C = 0,2 ma; V C = 3 V; V E = 1,9 V. Sia noto che:
P4 OSCILLATORI SINUSOIDALI
 P4 OSILLATOI SINUSOIDALI P4. Dimensionare un oscillatore a ponte di Wien con amplificatore operazionale, per una frequenza f 6 khz, utilizzando un termistore NT per il controllo automatico di guadagno.
P4 OSILLATOI SINUSOIDALI P4. Dimensionare un oscillatore a ponte di Wien con amplificatore operazionale, per una frequenza f 6 khz, utilizzando un termistore NT per il controllo automatico di guadagno.
Esercitazione Multimetro analogico e digitale
 Esercitazione Multimetro analogico e digitale - 1 Esercitazione Multimetro analogico e digitale 1 - Oggetto Confronto tra multimetro analogico (OM) e digitale (DMM). Misure di tensioni alternate sinusoidali
Esercitazione Multimetro analogico e digitale - 1 Esercitazione Multimetro analogico e digitale 1 - Oggetto Confronto tra multimetro analogico (OM) e digitale (DMM). Misure di tensioni alternate sinusoidali
Esperimentazioni di Fisica 3. Appunti sugli. Amplificatori Differenziali. M De Vincenzi
 Esperimentazioni di Fisica 3 Appunti sugli. Amplificatori Differenziali M De Vincenzi 1 Introduzione L amplificatore differenziale è un componente elettronico che (idealmente) amplifica la differenza di
Esperimentazioni di Fisica 3 Appunti sugli. Amplificatori Differenziali M De Vincenzi 1 Introduzione L amplificatore differenziale è un componente elettronico che (idealmente) amplifica la differenza di
Sistemi vibranti ad 1 gdl
 Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Università degli Studi di Bergamo Dipartimento di Ingegneria Sistemi vibranti ad 1 gdl - vibrazioni forzate - rev. 1. Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ
Diodi e transistor sono spesso utilizzati in circuiti ad elementi discreti, insieme a R, C, L. Il diodo è spesso utilizzato nei circuiti
 Diodi e transistor sono spesso utilizzati in circuiti ad elementi discreti, insieme a R, C, L. Il diodo è spesso utilizzato nei circuiti raddrizzatori per convertire la corrente alternata, fornita dalla
Diodi e transistor sono spesso utilizzati in circuiti ad elementi discreti, insieme a R, C, L. Il diodo è spesso utilizzato nei circuiti raddrizzatori per convertire la corrente alternata, fornita dalla
Diagrammi asintotici di Bode: esercizi. Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): s 2. s(s 30)(1+ s
 .. 3.2 1 Nyquist: Diagrammi asintotici di Bode: esercizi Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): 6(s2 +.8s+4) s(s 3)(1+ s 2 )2. Pendenza iniziale: -2 db/dec. Pulsazioni critiche:
.. 3.2 1 Nyquist: Diagrammi asintotici di Bode: esercizi Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): 6(s2 +.8s+4) s(s 3)(1+ s 2 )2. Pendenza iniziale: -2 db/dec. Pulsazioni critiche:
Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie.
 Circuiti RC ed RL Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie. Figura A In figura vi è lo schema riferito ad un generatore
Circuiti RC ed RL Consideriamo ora circuiti in cui siano presenti più componenti. Circuito ohmico-induttivo R-L con resistenza e reattanza in serie. Figura A In figura vi è lo schema riferito ad un generatore
Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE
 Automation Robotics and System CONTROL Università degli Studi di Modena e Reggio Emilia Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL o E 2 o ORDINE CA 5 Cesare Fantuzzi (cesare.fantuzzi@unimore.it)
Automation Robotics and System CONTROL Università degli Studi di Modena e Reggio Emilia Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL o E 2 o ORDINE CA 5 Cesare Fantuzzi (cesare.fantuzzi@unimore.it)
Le configurazioni della reazione
 Capitolo 2 Le configurazioni della reazione Nel capitolo precedente si è visto che la reazione ha effetto diametralmente opposto tra l amplificatore non invertente (par. 9.5) e quello invertente (par.
Capitolo 2 Le configurazioni della reazione Nel capitolo precedente si è visto che la reazione ha effetto diametralmente opposto tra l amplificatore non invertente (par. 9.5) e quello invertente (par.
Elettronica generale - Santolo Daliento, Andrea Irace Copyright The McGraw-Hill srl
 1 1. Per il circuito raddrizzatore a doppia semionda di Fig. 3.21 si valuti la massima tensione inversa che può esser presente su ogni diodo e si disegni l uscita del raddrizzatore nel caso in cui il valore
1 1. Per il circuito raddrizzatore a doppia semionda di Fig. 3.21 si valuti la massima tensione inversa che può esser presente su ogni diodo e si disegni l uscita del raddrizzatore nel caso in cui il valore
per la matrice R, e: I 1 = G 11 V 1 + G 12 V 2, I 2 = G 21 V 1 + G 22 V 2,
 100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
100 Luciano De Menna Corso di Elettrotecnica Il caso N = 2 è particolarmente interessante tanto da meritare un nome speciale: doppio bipolo I parametri indipendenti saranno tre: R 11, R 22 ed R 12 =R 21
CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi. SINTESI E APPUNTI Prof.ssa Elena Spera
 CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi SINTESI E APPUNTI Prof.ssa Elena Spera 1 SISTEMI DI RIFERIMENTO Il moto è relatio Ogni moto a studiato dopo aere fissato un sistema di riferimento,
CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi SINTESI E APPUNTI Prof.ssa Elena Spera 1 SISTEMI DI RIFERIMENTO Il moto è relatio Ogni moto a studiato dopo aere fissato un sistema di riferimento,
AMPLIFICATORE DIFFERENZIALE
 AMPLIFICATORE DIFFERENZIALE Per amplificatore differenziale si intende un circuito in grado di amplificare la differenza tra due segnali applicati in ingresso. Gli ingressi sono due: un primo ingresso
AMPLIFICATORE DIFFERENZIALE Per amplificatore differenziale si intende un circuito in grado di amplificare la differenza tra due segnali applicati in ingresso. Gli ingressi sono due: un primo ingresso
Esercitazione n 2: Circuiti di polarizzazione (2/2)
 Esercitazione n 2: Circuiti di polarizzazione (2/2) 1) Per il circuito di in Fig. 1 dimensionare R in modo tale che la corrente di collettore di Q 1 sia 5 ma. Siano noti: V CC = 15 V; β = 150; Q1 = Q2
Esercitazione n 2: Circuiti di polarizzazione (2/2) 1) Per il circuito di in Fig. 1 dimensionare R in modo tale che la corrente di collettore di Q 1 sia 5 ma. Siano noti: V CC = 15 V; β = 150; Q1 = Q2
FILTRI ANALOGICI L6/1
 FILTRI ANALOGICI Scopo di un filtro analogico è l eliminazione di parte del contenuto armonico di un segnale, lasciandone inalterata la porzione restante. In funzione dell intervallo di frequenze del segnale
FILTRI ANALOGICI Scopo di un filtro analogico è l eliminazione di parte del contenuto armonico di un segnale, lasciandone inalterata la porzione restante. In funzione dell intervallo di frequenze del segnale
Capitolo. Stabilità dei sistemi di controllo. 8.1 Generalità. 8.2 Criterio generale di stabilità. 8.3 Esercizi - Criterio generale di stabilità
 Capitolo 7 Stabilità dei sistemi di controllo 8.1 Generalità 8. Criterio generale di stabilità 8.3 Esercizi - Criterio generale di stabilità 8.4 Criterio di stabilità di Nyquist 8.5 Esercizi - Criterio
Capitolo 7 Stabilità dei sistemi di controllo 8.1 Generalità 8. Criterio generale di stabilità 8.3 Esercizi - Criterio generale di stabilità 8.4 Criterio di stabilità di Nyquist 8.5 Esercizi - Criterio
In conduzione continua si ottiene una tensione sul carico v c proporzionale al valore desiderato v i.
 Controllo ad anello aperto Il filtro LC è necessario per ridurre le ondulazioni di corrente e di tensione ed è dimensionato in modo da mantenere v c circa costante. R rappresenta le perdite sugli avvolgimenti
Controllo ad anello aperto Il filtro LC è necessario per ridurre le ondulazioni di corrente e di tensione ed è dimensionato in modo da mantenere v c circa costante. R rappresenta le perdite sugli avvolgimenti
Progetto del controllore
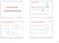 Parte 10, 1 - Problema di progetto Parte 10, 2 Progetto del controllore Il caso dei sistemi LTI a tempo continuo Determinare in modo che il sistema soddisfi alcuni requisiti - Principali requisiti e diagrammi
Parte 10, 1 - Problema di progetto Parte 10, 2 Progetto del controllore Il caso dei sistemi LTI a tempo continuo Determinare in modo che il sistema soddisfi alcuni requisiti - Principali requisiti e diagrammi
Amplificatori a retroazione negativa
 I.T.I.S. "Antonio Meucci" di Roma Amplificatori a retroazione negativa a cura del Prof. Mauro Perotti Anno Scolastico 2011-2012 Sommario 1. Schemi a blocchi...3 1.1. Caratteristiche degli schemi a blocchi...
I.T.I.S. "Antonio Meucci" di Roma Amplificatori a retroazione negativa a cura del Prof. Mauro Perotti Anno Scolastico 2011-2012 Sommario 1. Schemi a blocchi...3 1.1. Caratteristiche degli schemi a blocchi...
! "#$%"#&'&" ( ) *( +, ''-'. / (0 *123,4 5, %, 1,%""" / / (*6 7, 48 5,8 9-1,'$$:
 ! "#$%"#&'&" ( ) *( +, ''-'. 1 / (0 *13,4 5, %, 1,%""" / / (*6 7, 48 5,8 9-1,'$$: / ' % 0. ; < # 8=< 8= 3 ' < %. 0 5? 6? 9?
! "#$%"#&'&" ( ) *( +, ''-'. 1 / (0 *13,4 5, %, 1,%""" / / (*6 7, 48 5,8 9-1,'$$: / ' % 0. ; < # 8=< 8= 3 ' < %. 0 5? 6? 9?
ELETTRONICA II. Prof. Dante Del Corso - Politecnico di Torino. Parte E: Circuiti misti analogici e digitali Lezione n E - 1:
 ELETTRONICA II Prof. Dante Del Corso - Politecnico di Torino Parte E: Circuiti misti analogici e digitali Lezione n. 19 - E - 1: Comparatori di soglia Comparatori con isteresi Circuiti misti analogici
ELETTRONICA II Prof. Dante Del Corso - Politecnico di Torino Parte E: Circuiti misti analogici e digitali Lezione n. 19 - E - 1: Comparatori di soglia Comparatori con isteresi Circuiti misti analogici
Esercitazione Oscilloscopio
 Esercitazione Oscilloscopio - 1 Esercitazione Oscilloscopio 1 - Oggetto Uso dell oscilloscopio. Rilievo della caratteristica tensione-corrente di un diodo. Misure di capacità mediante misure di sfasamento.
Esercitazione Oscilloscopio - 1 Esercitazione Oscilloscopio 1 - Oggetto Uso dell oscilloscopio. Rilievo della caratteristica tensione-corrente di un diodo. Misure di capacità mediante misure di sfasamento.
Problemi di Fisica. ONDE Moto Ondulatorio
 Problemi di Fisica ONDE Moto Ondulatorio Una corda ha una densità lineare 8,0 g/m ed è soggetta a una tensione 00 N. Calcoliamo la lunghezza d'onda λ di un'onda trasersale armonica di frequenza f440 Hz
Problemi di Fisica ONDE Moto Ondulatorio Una corda ha una densità lineare 8,0 g/m ed è soggetta a una tensione 00 N. Calcoliamo la lunghezza d'onda λ di un'onda trasersale armonica di frequenza f440 Hz
ELETTRONICA APPLICATA E MISURE
 Ingegneria dell Informazione ELETTRONICA APPLICATA E MISURE Dante DEL CORSO De3 ESERCIZI PARTI B e D» Esempi di esercizi da scritti di esame AA 2015-16 01/12/2015-1 ElapDe2-2014 DDC Page 1 2014 DDC 1 De3:
Ingegneria dell Informazione ELETTRONICA APPLICATA E MISURE Dante DEL CORSO De3 ESERCIZI PARTI B e D» Esempi di esercizi da scritti di esame AA 2015-16 01/12/2015-1 ElapDe2-2014 DDC Page 1 2014 DDC 1 De3:
Per equazione lineare nelle incognite x, y intendo un equazione del tipo. ax = b,
 Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
VERIFICA DELLE PROPRIETÀ E DELLE CARATTERISTICHE DEL CIRCUITO APERTO E DEL CORTO CIRCUITO
 VEFCA DELLE POPETÀ E DELLE CAATTESTCHE DEL CCUTO APETO E DEL COTO CCUTO Le caratteristiche di un circuito aperto sono: A. Tensione massima: V ca Max B. Corrente nulla: ca 0 C. Tutti i bipoli passivi che
VEFCA DELLE POPETÀ E DELLE CAATTESTCHE DEL CCUTO APETO E DEL COTO CCUTO Le caratteristiche di un circuito aperto sono: A. Tensione massima: V ca Max B. Corrente nulla: ca 0 C. Tutti i bipoli passivi che
s + 6 s 3, b) i valori di K per i quali il sistema a ciclo chiuso risulta asintoticamente stabile;
 1 Esercizi svolti Esercizio 1. Con riferimento al sistema di figura, calcolare: ut) + K s s + 6 s 3 yt) a) la funzione di trasferimento a ciclo chiuso tra ut) e yt); b) i valori di K per i quali il sistema
1 Esercizi svolti Esercizio 1. Con riferimento al sistema di figura, calcolare: ut) + K s s + 6 s 3 yt) a) la funzione di trasferimento a ciclo chiuso tra ut) e yt); b) i valori di K per i quali il sistema
Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo
 Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 603 Crema email:
Elettronica I Leggi di Kirchhoff; risoluzione dei circuiti elettrici in continua; serie e parallelo Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 603 Crema email:
8. Analisi delle principali configurazioni circuitali a BJT e FET
 8. Analisi delle principali configurazioni circuitali a BJT e FET 8. Concetti generali Esamineremo nel seguito i principali montaggi che si utilizzano per i circuiti a transistori, che differiscono tra
8. Analisi delle principali configurazioni circuitali a BJT e FET 8. Concetti generali Esamineremo nel seguito i principali montaggi che si utilizzano per i circuiti a transistori, che differiscono tra
ANALISI DEI SISTEMI IN RETROAZIONE E FUNZIONI DI SENSITIVITA
 SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html ANALISI DEI SISTEMI IN RETROAZIONE E FUNZIONI DI SENSITIVITA Schema di riferimento
SISTEMI DI CONTROLLO Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/sistemicontrollo.html ANALISI DEI SISTEMI IN RETROAZIONE E FUNZIONI DI SENSITIVITA Schema di riferimento
ELETTRONICA APPLICATA
 Università degli Studi di oma Tor ergata Dipartimento di ng. Elettronica corso di ELETTONCA APPLCATA ng. occo Giofrè Esercizi su semiconduttori e diodi / CHAMO SU DOD Linearizzazione a tratti f D + Circuito
Università degli Studi di oma Tor ergata Dipartimento di ng. Elettronica corso di ELETTONCA APPLCATA ng. occo Giofrè Esercizi su semiconduttori e diodi / CHAMO SU DOD Linearizzazione a tratti f D + Circuito
Analisi e dimensionamento di amplificatori a retroazione multipla con controllo dell impedenza d uscita
 Università degli Studi di Padova DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Corso di Laurea Magistrale in Ingegneria Elettronica Tesi di Laurea Magistrale Analisi e dimensionamento di amplificatori a
Università degli Studi di Padova DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Corso di Laurea Magistrale in Ingegneria Elettronica Tesi di Laurea Magistrale Analisi e dimensionamento di amplificatori a
Il comportamento di un amplificatore ideale, ad esempio di tensione, è descritto dalla relazione lineare V out = A V in (3.1)
 Capitolo 3 Amplificazione 3.1 Circuiti attivi Gli elementi circuitali considerati sino ad ora, sia lineari (resistenze, capacità, induttanze e generatori indipendenti), sia non lineari (diodi), sono detti
Capitolo 3 Amplificazione 3.1 Circuiti attivi Gli elementi circuitali considerati sino ad ora, sia lineari (resistenze, capacità, induttanze e generatori indipendenti), sia non lineari (diodi), sono detti
= A v1 A v2 R o1 + R i2 A v A v1 A v2. se R i2 R o1
 Amplificatori a due stadi STADIO 1 STADIO 2 R s R o1 R o2 v s + _ vi1 R i1 + A v1 v i1 _ v i2 R i2 + Av2vi2 _ vo2 RL A v v o2 v i1 = A v1 A v2 R i2 R o1 + R i2 A v A v1 A v2 se R i2 R o1 A.Nigro Laboratorio
Amplificatori a due stadi STADIO 1 STADIO 2 R s R o1 R o2 v s + _ vi1 R i1 + A v1 v i1 _ v i2 R i2 + Av2vi2 _ vo2 RL A v v o2 v i1 = A v1 A v2 R i2 R o1 + R i2 A v A v1 A v2 se R i2 R o1 A.Nigro Laboratorio
DIODO. La freccia del simbolo indica il verso della corrente.
 DIODO Si dice diodo un componente a due morsetti al cui interno vi è una giunzione P-N. Il terminale del diodo collegato alla zona P si dice anodo; il terminale collegato alla zona N si dice catodo. Il
DIODO Si dice diodo un componente a due morsetti al cui interno vi è una giunzione P-N. Il terminale del diodo collegato alla zona P si dice anodo; il terminale collegato alla zona N si dice catodo. Il
Esercizi svolti di termodinamica applicata
 0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
L amplificatore operazionale
 L amplificatore operazionale terminali di input terminale di output Alimentazioni: massa nodo comune L amplificatore operazionale ideale Applichiamo 2 tensioni agli input 1 e 2 L amplificatore è sensibile
L amplificatore operazionale terminali di input terminale di output Alimentazioni: massa nodo comune L amplificatore operazionale ideale Applichiamo 2 tensioni agli input 1 e 2 L amplificatore è sensibile
ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2016/2017
 ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2016/2017 CLASSE 4 I Disciplina: Elettrotecnica ed Elettronica PROGETTAZIONE DIDATTICA ANNUALE Elaborata dai docenti: Linguanti Vincenzo,
ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2016/2017 CLASSE 4 I Disciplina: Elettrotecnica ed Elettronica PROGETTAZIONE DIDATTICA ANNUALE Elaborata dai docenti: Linguanti Vincenzo,
Università degli studi di Bergamo Facoltà di Ingegneria
 Università degli studi di ergamo Facoltà di Ingegneria Corso di elettrotecnica Soluzione tema d esame del 16 giugno 1998 Esercizio n 1 Data la rete in figura determinare le correnti I 1,I 2,I,I 5 e la
Università degli studi di ergamo Facoltà di Ingegneria Corso di elettrotecnica Soluzione tema d esame del 16 giugno 1998 Esercizio n 1 Data la rete in figura determinare le correnti I 1,I 2,I,I 5 e la
ELETTRONICA CdS Ingegneria Biomedica
 ELEONICA CdS Ingegneria Biomedica LEZIONE A.03 Circuiti a diodi: configurazioni, analisi, dimensionamento addrizzatori a semplice e doppia semionda addrizzatori a filtro (L, C e LC) Moltiplicatori di tensione
ELEONICA CdS Ingegneria Biomedica LEZIONE A.03 Circuiti a diodi: configurazioni, analisi, dimensionamento addrizzatori a semplice e doppia semionda addrizzatori a filtro (L, C e LC) Moltiplicatori di tensione
RISONANZA. Fig.1 Circuito RLC serie
 RISONANZA Risonanza serie Sia dato il circuito di fig. costituito da tre bipoli R, L, C collegati in serie, alimentati da un generatore sinusoidale a frequenza variabile. Fig. Circuito RLC serie L impedenza
RISONANZA Risonanza serie Sia dato il circuito di fig. costituito da tre bipoli R, L, C collegati in serie, alimentati da un generatore sinusoidale a frequenza variabile. Fig. Circuito RLC serie L impedenza
1 a PROVA PARZIALE DI FONDAMENTI DI AUTOMATICA A.A. 2004/ novembre Soluzione
 a PROVA PARZIAE DI FONDAMENTI DI AUTOMATIA A.A. 24/25 9 novembre 24 Esercizio on riferimento alla funzione di trasferimento G(s) = 7s2 + 36s + 48 (s + 3)(s + 4) 2 Domanda.. Indicare i valori del guadagno,
a PROVA PARZIAE DI FONDAMENTI DI AUTOMATIA A.A. 24/25 9 novembre 24 Esercizio on riferimento alla funzione di trasferimento G(s) = 7s2 + 36s + 48 (s + 3)(s + 4) 2 Domanda.. Indicare i valori del guadagno,
IL DIODO. 1 - Generalità
 IL DIODO 1 - Generalità Un cristallo di materiale semiconduttore, drogato in modo da creare una giunzione pn, costituisce un diodo a semiconduttore. In fig. 1 sono illustrati la struttura e il simbolo
IL DIODO 1 - Generalità Un cristallo di materiale semiconduttore, drogato in modo da creare una giunzione pn, costituisce un diodo a semiconduttore. In fig. 1 sono illustrati la struttura e il simbolo
UNIVERSITÀ DEGLISTUDIDIPAVIA Laurea in Ingegneria Elettronica e Informatica
 7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
7.09.0 Problema L interruttore indicato nel circuito in figura commuta nell istante t 0 dalla posizione AA alla posizione BB. Determinare le espressioni delle tensioni v (t) ev (t) per ogni istante di
