Particella Libera. ne deriva che l Hamiltoniano è dato dalla somma degli Hamiltoniani rispettivi:
|
|
|
- Roberta Cecilia Pini
- 6 anni fa
- Visualizzazioni
Transcript
1 9 Particella Libera Una seplice applicaione dell equaione di Scrödinger riguarda una particella il cui poteniale è costante (V=0). Scriviao l equaione di Scrödinger nella sua fora copleta: V V 8 per cui 0 a 8
2 9 Particella Libera Se una funione è espriibile coe un prodotto di più funioni ne deriva ce l Hailtoniano è dato dalla soa degli Hailtoniani rispettivi: ˆ ˆ ˆ ˆ e l energia è data dalla soa delle energie lungo i tre assi. Queste uguagliane vanno sotto il noe di tecnica di separaione delle variabili
3 93 Particella Libera Aettiao ce la nostra funione abbia queste caratteristice e sostituiao alla i valori e dividiao per i edesii Tale equaione è separabile in tre diverse equaioni del tipo così per e
4 94 Particella Libera 8 L equaione precedente rappresenta l equaione di Scrödinger per il caso di una particella libera in una situaione onodiensionale le cui soluioni sono del tipo A senk e verificando d d A k cosk; d d A k senk
5 95 Particella Libera Sostituendo la soluione particolare nell equaione agli autovalori, otteniao Da cui L unica liitaione al valore dell energia per una particella libera è ce 0 ) ( 8 ) ( ) ( 8 ) ( ) ( 8 senk A senk A k senk A senk k A senk A senk A 8 8 k k
6 96 Particella Libera stendiao il caso ad una situaione tridiensionale Questo può essere ridotto ad una soa di funioni sinusoidali e quindi globalente è una funione sinusoidale. Quindi esisterà un onda ce, nel caso onodiensionale, sarà assia per certi valori di. quaione di de Broglie senk senk senk A A A p p p v p v p k con 8
7 97 Particella Libera L equaione differeniale da risolvere 0 8 è un equaione differeniale lineare oogenea del II ordine a coefficienti costanti. Le sue soluioni si ottengono con l aiuto di una equaione ausiliaria ce in questo caso è 8 0 Le cui radici sono 8 Per cui la soluione più generale dell equaione differeniale è c Ae e ik i Be ik c e i 0
8 98 Particella Libera Verificiao sulla soluione particolare: Ae ik Se l operatore oento e posiione sono calcolabili esattaente. p ˆ i ˆ pae ˆ Ae ˆ ik ik i Ae ik Ae cae ik ik i Abbiao trovato ce l indeterinaione sul oento p è nulla e quella sulla posiione è infinita e cioè p 0 ik Ae ik fora indeterinata
9 onodiensionale 99 Prendiao in consideraione il problea di una particella vincolata a uoversi in una buca ad una diensione. Questo esepio ci perette di applicare i postulati quantistici e ostra conteporaneaente coe anno origine i livelli energetici discreti di una particella vincolata a uoversi in una regione discreta dello spaio. Consideriao la situaione illustrata. La particella è vincolata a uoversi in una buca ad una diensione di lungea a. V Per trovare le energie peresse e le funioni d onda della particella si deve risolvere l equaione agli autovalori ˆ n nn V 0 a
10 00 Particella in una scatola onodiensionale La ricerca della soluione è più conveniente se si divide il sistea in tre parti: ) ) Particella all esterno della buca ) ) Particella all interno della buca 3) 3) Particella ai confini della buca 4) ) L equaione in questo caso sarà (posto V= ): d d d d d d per oltiplicando V d d ovvero ) ( 8 0 ) ( 8 8
11 onodiensionale 0 Consideraioni: Dal punto di visto ateatico, non esiste una funione ce derivata due volte sia uguale ad infinito per la stessa funione. Dal punto di vista geoetrico, la derivata seconda della funione rappresenta la sua curvatura ce non può avere valore infinito. Dal punto di vista fisico, dato ce la probabilità di trovare la particella è data da * e l unica possibilità in questo caso è ce =0. Per cui la probabilità di trovare la particella fuori della buca è ero.
12 onodiensionale 0 ) All interno della buca l equaione agli autovalori assue la fora (posto V=0): d 8 d d d 8 0 Questa è un equaione differeniale del II ordine le cui soluioni sono funioni ce, differeniate due volte contengono le funioni iniiali oltiplicate per una costante, coe le funioni seno e coseno. A senk
13 onodiensionale 03 3) In terini ateatici, il problea consiste nella applicaione delle condiioni al contorno. La condiione ce sia ad un sol valore ipone ce la funione si annulli agli estrei della buca, vale a dire ( a) (0) 0 (0) A senk 0 0 ( a) A senk a 0 ce è verificato per ka n dove n è un nuero intero e da cui k n a e k 8 n a
14 onodiensionale 04 Ne consegue ce le energie peresse della particella sono: n n 8 a 8a n=,,3 I vincoli iposti dalle condiioni al contorno liitano l energia a valori discreti. Il valore di è inversaente proporionale al quadrato delle diensioni della buca e alla assa della particella. Quando le diensioni della buca sono grandi il valore dell energia diinuisce e all auentare della assa ance la distana tra i livelli diinuisce.
15 onodiensionale 05 Dobbiao definire i valori della costante A in A senk per far questo si adotta un processo detto di noraliaione. Una funione si dice noraliata quando a 0 * d Sostituendo e* con le rispettive espressioni analitice e tenendo conto ce è a coefficienti reali: a n 0 A sen d a
16 06 Particella in una scatola onodiensionale Il risultato finale è: AUTOFUNZION AUTOVALOR 8 sen a n a n a a A a A aa n
17 07 Particella in una scatola onodiensionale n 3 n 9 8a a 8a n n Un aspetto interessante è la relaione tra l energia dello stato e il nuero di nodi della funione d onda. Un nodo è un punto in cui la funione d onda si annulla. Trascurando i nodi agli estrei della buca, nello stato caratteriato da n= c è un nodo, per n=3 due nodi, ecc. Al crescere del nuero dei nodi della funione auenta l energia dello stato corrispondente. 0
18 onodiensionale 08 Consideraioni: Per il edesio valore del nuero quantico n l energia risulta inversaente proporionale alla assa della particella ed al quadrato della lungea della buca. Così, coe la particella diventa più pesante e la buca più larga i livelli energetici diventano sepre più vicini. Solaente quanto la quantità a è dello stesso ordine di è possibile isurare sperientalente i livelli energetici quantiati. Quando si a a ce fare con diensioni dell ordine del grao e del centietro i livelli sono così poco separati da apparire un continuo. Pertanto la forula quantoeccanica porta ad una risultato ce coincide con quello classico per sistei di diensioni tali ce a >>. Questo è un odo di espriere il principio di corrispondena.
19 09 Particella in una scatola onodiensionale Un altro aspetto iportante esso in luce dalle soluioni del problea della particella nella buca è la relaione tra l energia dello stato ed il nuero di nodi della funione d onda. Un nodo è un punto in cui la funione d onda si annulla. Trascurando i nodi agli estrei della buca, nello stato caratteriato da n= vi è un solo nodo; per n=3 vi sono due nodi e in generale nello stato caratteriato dal nuero quantico n sono presenti n- nodi. una proprietà generale delle funioni d onda ce al crescere del nuero dei nodi della funione auenta l energia dello stato corrispondente. Ricordandoci la relaione di de Broglie p v Se la lungea d onda diinuisce, il oento, e quindi l energia cinetica della particella, diventano più grandi. T v p
20 onodiensionale 0 Misuriao, ora, la coponente del oento lungo la direione di un insiee di particelle identice ce si trovano nello stato ad energia più bassa. i L operatore adatto per il calcolo del oento è i d d d d ed opera sulla funione così: p ˆ i d Asen d i A cos a a a È evidente ce non è autofunione di p ˆ e pertanto per il IV postulato una serie di isure di ˆ non daranno il edesio risultato. p Si deve quindi ricorrere al teorea del valor edio per calcolare il valore di aspettaione di ˆ : p ˆ p 0 a p ˆ d a 0 d 0
21 onodiensionale Sostituendo: ˆ p 0 a e risolvendo l integrale: Asen a i A a cos a d A sen a a d 0 0 ˆ p 0 a Asen a i A a cos a d A sen a a d 0 i 0 a a sen a 0 a cos a d a sen a d a
22 onodiensionale t per = 0 t = 0 per = a t = p a i a 0 sent costdt i a 0 sent costdt i 0 sentdt a a 0 sen a tdt sen a cost 0 tdt 0 dt cost poicè sent i a = i 0 0 sentd(t) dt a 4 0 i 4 0 send a cos tdt 0 costdt 4 cos a a 4 i = a cosd 4 sen 0 a 0 0 a a se t = il valor edio del oento isurato su un gran nuero di particelle è ero.
23 onodiensionale 3 Consideriao ora il quadrato del oento nella direione : p ˆ d 4 d p ˆ d 4 d Asen a 4 a Asen a Questa volta risulta autofunione di ˆ ed una serie di isure di ˆ su un insiee sistei identici darà sepre il edesio risultato, in pratica l autovalore è p p (p ) a (p )
24 onodiensionale 4 Il postulato del valor edio vuol significare ce se vengono eseguite olte isure di p la frequena con cui si ottiene è uguale a quella del risultato (p ) (p ) ed il valor edio di p ˆ sarà uguale a ero. L aspetto significativo è l ipossibilità di conoscere a priori se il risultato sarà positivo o negativo. Si può dire ce esiste una indeterinaione nella conoscena del oento ed il valore di questa indeterinaione è uguale a
25 onodiensionale 5 In odo analogo si può dire ce se è noto ce la particella nella buca è nello stato n la sola cosa ce possiao dire sulla posiione della particella è ce si trova in qualce punto della buca, cioè l indeterinaione della coordinata della particella è la diensione a della buca. È interessante calcolare il prodotto dell indeterinaione della posiione e del oento di una particella nella buca, ce risulta: p a ( ) a n n a 8a a n L indeterinaione assuerà il valore inio per n= e con questo valore si ottiene: p Questa è una delle forulaionu del principio di indeterinaione di Heiseberg, ce affera ce la isura siultanea della posiione e del oento di una particella non può essere realiata con un accuratea superiore alla costante di Planck.
26 onodiensionale 6 Un altra proprietà delle soluioni di una particella in una buca è ce l integrale < > è nullo. Infatti si può diostrare ce per tutte le funioni d onda ce caratteriano il oto della particella nella buca vale la relaione seguente: 0 per i j Quando vale una relaione di questo tipo si dice ce le funioni sono ortogonali. NOTA: il valore dell integrale relativo ad una coppia qualsiasi di funioni della particella nella buca può essere espresso sinteticaente ediante la relaione: ij dove ij è la delta di Kronecker Quest ultia grandea gode delle seguenti proprietà: ij per i j e ij 0 per i j. L espressione precedente vuol dire ce ciascuna funione è noraliata e ce tutte le coppie di funioni sono ortogonali. Quando è verificata una relaione di questo tipo si dice ce le funioni forano un insiee ortonorale.
27 tridiensionale 7 stendiao il problea di una particella nella buca al caso tridiensionale cioè consideriao il problea di una particella in una scatola a tre diensioni. L equaione agli autovalori ce descrive il oto della particella all interno della scatole assue la fora: c V 0 Con la tecnica di separaione delle variabili: a b ovvero nella fora più esplicita: e
28 tridiensionale 8 La generica autofunione noraliata ce avevao precedenteente ricavato era: n sen a a Ce per e sarà: n sen b b n sen c c Da cui n n 8 abc senn a senn b senn c
29 tridiensionale 9 d n 8 a n b n c a, b, c sono le diensioni della buca rispetto ai tre assi, ovviaente se la buca è cubica a=b=c e si potrà scrivere: Se n n n 8 n n n avreo il livello energetico più basso possibile.
30 tridiensionale 0 Vediao ora lo stato ce segue iediataente quello a più bassa energia. Questo stato è caratteriato da un nuero quantico uguale a e da due nueri quantici uguale a e conseguenteente 3 4 a Questa energia può essere ottenuta attraverso tre cobinaione dei nueri quantici n n n 8a n n n 8a ( 4) 3 4 a Questi tre stati anno il edesio valore dell energia e si dicono degeneri
31 tridiensionale SMPIO: Consideriao una olecola di butadiene: H H C C C C H H H H essendo gli elettroni delocaliati, essi si trovano in una scatola onodiensionale di lungea pari alla soa delle lungee di due doppi legai più uno seplice,cioè: C C C C (,35 Å)+,54 Å=5,78 Å I livelli di energia del butadiene sono dati dalla forula n n 37,59 ev 37,59 ev,n a (5,78) ev
32 tridiensionale Per il principio di esclusione di Pauli, ogni livello può ospitare al assio due elettroni con spin opposto, per cui quattro elettroni andranno ad occupare i prii due livelli. ccitando la olecola, un elettrone passa dallo stato n= allo stato n=3. 3,(3 ) 5,60eV c n=3 n= eccitaento La particella nella scatola è un ottio odello ateatico per descrivere i fenoeni ce si osservano sperientalente. n= e - e -
33 3 Teoria delle perturbaioni Solo per poci sistei è possibile ottenere le soluioni esatte dell equaione di Scrödinger. Per tutti gli altri problei è necessario cercare ed ottenere soluioni approssiate. Due etodi approssiati servono essenialente allo scopo: -il etodo della variaione lineare e -la teoria delle perturbaioni. La teoria delle perturbaioni si rivela olto utile quando il problea da risolvere è siile ad un problea già risolto esattaente. In terini ateatici ciò significa ce le soluioni all ordine ero del problea ˆ 0 sono note e deve essere risolto il nuovo problea ˆ 0 0 0
34 4 Teoria delle perturbaioni Si scrive l Hailtoniano nella fora seguente ˆ ˆ 0 ˆ... dove il secondo terine rappresenta una perturbaione del prio. Il terine è un oltiplicatore arbitrario.
m O Esercizio (tratto dal Problema 4.29 del Mazzoldi 2)
 Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
PRINCIPIO DI INDUZIONE. k =. 2. k 2 n(n + 1)(2n + 1) 6
 PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn + ) ). 2 Esercizio 2. Diostrare che per ogni n si ha 2) 2 nn + )2n + ). Soluzione. Procediao per induzione: la 2) è ovviaente
PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn + ) ). 2 Esercizio 2. Diostrare che per ogni n si ha 2) 2 nn + )2n + ). Soluzione. Procediao per induzione: la 2) è ovviaente
1 Simulazione di prova d Esame di Stato
 Siulazione di prova d Esae di Stato Problea Risolvi uno dei due problei e 5 dei 0 quesiti in cui si articola il questionario Sia y = f) una funzione reale di variabile reale tale che la sua derivata seconda
Siulazione di prova d Esae di Stato Problea Risolvi uno dei due problei e 5 dei 0 quesiti in cui si articola il questionario Sia y = f) una funzione reale di variabile reale tale che la sua derivata seconda
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
I moti. Daniel Gessuti
 I oti Daniel Gessuti 1 introduzione Uno dei problei che ha interessato gli scienziati fin dall antichità e che costituisce un notevole capo d indagine della Fisica è senza dubbio quello che riguarda il
I oti Daniel Gessuti 1 introduzione Uno dei problei che ha interessato gli scienziati fin dall antichità e che costituisce un notevole capo d indagine della Fisica è senza dubbio quello che riguarda il
2. calcolare l energia cinetica del corpo e tracciare il suo andamento nel tempo;
 1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
Frequenze proprie di una catena unidimensionale
 UNIVERSITA DEGLI STUDI DI CATANIA Dipartiento di Scienze MM FF NN Corso di Laurea di prio livello in Fisica Frequenze proprie di una catena unidiensionale Cristalli e quasicristalli Oscillazioni e onde
UNIVERSITA DEGLI STUDI DI CATANIA Dipartiento di Scienze MM FF NN Corso di Laurea di prio livello in Fisica Frequenze proprie di una catena unidiensionale Cristalli e quasicristalli Oscillazioni e onde
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti scelti nel questionario.
 LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE ORDINARIA Il candidato risolva uno dei due problei e 5 dei quesiti scelti nel questionario. N. De Rosa, La prova di ateatica per il liceo PROBLEMA t La funzione
LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE ORDINARIA Il candidato risolva uno dei due problei e 5 dei quesiti scelti nel questionario. N. De Rosa, La prova di ateatica per il liceo PROBLEMA t La funzione
Le molecole ed il legame chimico
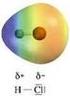 LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
Capitolo 1 Fisica, grandezze, unità di misura, metodo scientifico.
 Capitolo 1 Fisica, grandezze, unità di isura, etodo scientifico. Fisica e etodo Il terine fisica deriva dal greco physiké che letteralente significa riguardante la natura. Tale definizione, corretta dal
Capitolo 1 Fisica, grandezze, unità di isura, etodo scientifico. Fisica e etodo Il terine fisica deriva dal greco physiké che letteralente significa riguardante la natura. Tale definizione, corretta dal
Esercizio (tratto dal Problema 4.7 del Mazzoldi 2)
 1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
LAVORO ED ENERGIA Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
PROBLEMA 1 Nel piano cartesiano Oxy è data la circonferenza C con centro O e raggio r = 3.
 Sessione ordinaria all estero (AMERICHE) 8 - ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO AMERICHE CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tea di: MATEMATICA Il candidato risolva
Sessione ordinaria all estero (AMERICHE) 8 - ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO AMERICHE CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tea di: MATEMATICA Il candidato risolva
POLITECNICO DI TORINO 1 a Facoltà di Ingegneria A.A. 2011/2012. Progetto di Infrastrutture Viarie. Corso di Laurea Magistrale in Ingegneria Civile
 POLITECNICO DI TOINO a Facoltà di Ingegneria A.A. 0/0 Corso di Laurea Magistrale in Ingegneria Civile Progetto di Infrastrutture Viarie prof. Marco Bassani ing. oberto Melotti Esercizio : Progetto di una
POLITECNICO DI TOINO a Facoltà di Ingegneria A.A. 0/0 Corso di Laurea Magistrale in Ingegneria Civile Progetto di Infrastrutture Viarie prof. Marco Bassani ing. oberto Melotti Esercizio : Progetto di una
PROBABILITÀ E VARIABILI CASUALI
 PROBABILITÀ E VARIABILI CASUALI Fondaenti di segnali Fondaenti e trasissione TLC Frequenza relativa e probabilità Mediante le le probabilità si si descrivono i i fenoeni che che possono essere essere pensati
PROBABILITÀ E VARIABILI CASUALI Fondaenti di segnali Fondaenti e trasissione TLC Frequenza relativa e probabilità Mediante le le probabilità si si descrivono i i fenoeni che che possono essere essere pensati
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Oscillazioni e Onde Forza elastica
 Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica,
 Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Gli strumenti necessari per lo studio
 La potenza di un fucile a olla Sunto E possibile deterinare la potenza di un fucile a olla quando sono note la costante elastica K della olla, la isura d della copressione e la assa del proiettile sparato?
La potenza di un fucile a olla Sunto E possibile deterinare la potenza di un fucile a olla quando sono note la costante elastica K della olla, la isura d della copressione e la assa del proiettile sparato?
Fondamenti di Informatica. Cosa è l informazione. A cosa serve. Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a.
 Fondaenti di Inforatica Prof.V.L.Plantaura Inforatica e Counicazione Digitale a.a. 2005-2006 Cosa è l inforazione L inforazione è qualcosa che si possiede e si può dare ad un altro senza perderne il possesso.
Fondaenti di Inforatica Prof.V.L.Plantaura Inforatica e Counicazione Digitale a.a. 2005-2006 Cosa è l inforazione L inforazione è qualcosa che si possiede e si può dare ad un altro senza perderne il possesso.
Esercizi di Analisi Matematica L-B
 Esercii di Analisi Matematica L-B Marco Alessandrini Gennaio-Maro 7 Indice Funioni di più variabili reali. Calcolo differeniale........................................... Ricerca di massimi e minimi.......................................
Esercii di Analisi Matematica L-B Marco Alessandrini Gennaio-Maro 7 Indice Funioni di più variabili reali. Calcolo differeniale........................................... Ricerca di massimi e minimi.......................................
Soluzione del compito di Fisica 2. 2 febbraio 2012 (Udine)
 del copito di isica febbraio 1 (Udine) Elettrodinaica E` data una spira conduttrice quadrata di lato L e resistenza R, vincolata sul piano xy, in oto lungo x con velocita` iniziale v. Nel punto x la spira
del copito di isica febbraio 1 (Udine) Elettrodinaica E` data una spira conduttrice quadrata di lato L e resistenza R, vincolata sul piano xy, in oto lungo x con velocita` iniziale v. Nel punto x la spira
Misura delle distanze
 Prof. V. Franco: Topografia e tecniche cartografiche Corso di laurea in Ingegneria per l Abiente e il Territorio a.a. 006-007 Misura delle distanze Le isure di distanze vengono suddivise in: - isure dirette:
Prof. V. Franco: Topografia e tecniche cartografiche Corso di laurea in Ingegneria per l Abiente e il Territorio a.a. 006-007 Misura delle distanze Le isure di distanze vengono suddivise in: - isure dirette:
G Mm 2. otteniamo R = 11 Perché la forza di gravitazione è diretta parallelamente. 12 Falso. Lo sarebbero se fosse costante il rapporto
 La gravitazione. La gravitazione Doande sui concetti er la terza legge di Keplero, il rapporto fra la distanza Sole-pianeta e quella Sole-erra è pari alla radice cubica del rapporto fra i quadrati dei
La gravitazione. La gravitazione Doande sui concetti er la terza legge di Keplero, il rapporto fra la distanza Sole-pianeta e quella Sole-erra è pari alla radice cubica del rapporto fra i quadrati dei
Il campo magnetico. 1. Fenomeni magnetici 2. Calcolo del campo magnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz
 Il capo agnetico 1. Fenoeni agnetici 2. Calcolo del capo agnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz Prof. Giovanni Ianne 1/21 Fenoeni agnetici La agnetite è un inerale
Il capo agnetico 1. Fenoeni agnetici 2. Calcolo del capo agnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz Prof. Giovanni Ianne 1/21 Fenoeni agnetici La agnetite è un inerale
Isometrie Ad ogni simmetria delle Natura corrisponde una quantità conservata (Emmy Noether)
 Isoetrie Ad ogni sietria delle Natura corrisponde una quantità conservata (E Noether) Le isoetrie sono particolari affinità cioè trasforazioni lineari del piano in sé, che lasciano invariata la distanza
Isoetrie Ad ogni sietria delle Natura corrisponde una quantità conservata (E Noether) Le isoetrie sono particolari affinità cioè trasforazioni lineari del piano in sé, che lasciano invariata la distanza
Amperometri analogici passivi
 ppunti di Misure Elettriche peroetri analogici passivi NTODUZONE L aperoetro è, in generale, lo struento atto a isurare una corrente elettrica. Parliao invece di galvanoetro quando tale corrente è di intensità
ppunti di Misure Elettriche peroetri analogici passivi NTODUZONE L aperoetro è, in generale, lo struento atto a isurare una corrente elettrica. Parliao invece di galvanoetro quando tale corrente è di intensità
LA MISURA. Le grandezze fisiche e le loro misure. FISICA - Prof. Massimiliano Bacchi
 LA MISURA Le grandezze fisiche e le loro isure 1 Le grandezze fisiche Si può isurare la bellezza? Si può isurare la bontà? Si può isurare la felicità? 2 Le grandezze fisiche Si può isurare il peso? Si
LA MISURA Le grandezze fisiche e le loro isure 1 Le grandezze fisiche Si può isurare la bellezza? Si può isurare la bontà? Si può isurare la felicità? 2 Le grandezze fisiche Si può isurare il peso? Si
Potenze, logaritmi, equazioni esponenziali e logaritmiche.
 Potenze, logariti, equazioni esponenziali e logaritiche Potenza con esponente intero di un nuero reale Sia a R ed n Z Ricordiao, anzitutto, le seguenti definizioni: ) se n >, si chiaa potenza ennesia (che,
Potenze, logariti, equazioni esponenziali e logaritiche Potenza con esponente intero di un nuero reale Sia a R ed n Z Ricordiao, anzitutto, le seguenti definizioni: ) se n >, si chiaa potenza ennesia (che,
Istituzioni di Economia Laurea Triennale in Ingegneria Gestionale Lezione 4 Il Vincolo di Bilancio
 UNIVERSITÀ DEGLI STUDI DI BERGAMO Laurea Triennale in Ingegneria Gestionale Lezione 4 Il Vincolo di Bilancio Prof. Gianaria Martini Insiee delle scelte di consuo In un sistea econoico in cui vengono prodotti
UNIVERSITÀ DEGLI STUDI DI BERGAMO Laurea Triennale in Ingegneria Gestionale Lezione 4 Il Vincolo di Bilancio Prof. Gianaria Martini Insiee delle scelte di consuo In un sistea econoico in cui vengono prodotti
SUI SISTEMI LINEARI. 1. Richiami.Il metodo di Gauss. Un equazione nelle incognite. si dice lineare o di primo grado se si può ridurre. R.
 SUI SISTEMI LINEARI. Richiami.Il metodo di Gauss Un equaione nelle incognite..., n si dice lineare o di primo grado se si può ridurre alla forma: a a... an n b con a, a... an, b R. I numeri a, a... an
SUI SISTEMI LINEARI. Richiami.Il metodo di Gauss Un equaione nelle incognite..., n si dice lineare o di primo grado se si può ridurre alla forma: a a... an n b con a, a... an, b R. I numeri a, a... an
Le molecole ed il legame chimico
 La meccanica quantistica è in grado di determinare esattamente i livelli energetici dell atomo di idrogeno e con tecniche matematiche più complesse è anche in grado di descrivere l atomo di elio trovando
La meccanica quantistica è in grado di determinare esattamente i livelli energetici dell atomo di idrogeno e con tecniche matematiche più complesse è anche in grado di descrivere l atomo di elio trovando
I POSTULATI DELLA MECCANICA QUANTISTICA
 68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
MODELLO ATOMISTICO PER I DATI OCSE SULL ISTRUZIONE
 MODELLO ATOMISTICO PER I DATI OCSE SULL ISTRUZIOE Arturo Marcello Allega 1 Dirigente scolastico ITIS Giovanni XXIII di Roa Via di Tor Sapienza 160, 00155 Roa Abstract I dati OCSE sull istruzione sono distribuiti
MODELLO ATOMISTICO PER I DATI OCSE SULL ISTRUZIOE Arturo Marcello Allega 1 Dirigente scolastico ITIS Giovanni XXIII di Roa Via di Tor Sapienza 160, 00155 Roa Abstract I dati OCSE sull istruzione sono distribuiti
Equazioni di grado superiore al II
 Equaioni di grado superiore al II Equaioni binomie Un equaione binomia è un equaione che, ridotta a forma normale, è del tipo a n + b 0. Per risolvere una tale equaione, volendo cercare anche le soluioni
Equaioni di grado superiore al II Equaioni binomie Un equaione binomia è un equaione che, ridotta a forma normale, è del tipo a n + b 0. Per risolvere una tale equaione, volendo cercare anche le soluioni
TRASLAZIONI E DILATAZIONI
 TRASLAZIONI E DILATAZIONI Prof. Fabio Breda Abstract. Lo scopo di questo articolo è fare chiarezza sulla odalità di costruzione del graco di funzioni attraverso traslazioni o dilatazioni del graco di altre
TRASLAZIONI E DILATAZIONI Prof. Fabio Breda Abstract. Lo scopo di questo articolo è fare chiarezza sulla odalità di costruzione del graco di funzioni attraverso traslazioni o dilatazioni del graco di altre
Ingegneria dei Sistemi Elettrici_3d
 Ingegneria dei Sistemi Elettrici_3d Soluioni di problemi elettrostatici I problemi elettrostatici riguardano lo studio degli effetti delle cariche elettriche fisse. I principi dei campi elettrostatici
Ingegneria dei Sistemi Elettrici_3d Soluioni di problemi elettrostatici I problemi elettrostatici riguardano lo studio degli effetti delle cariche elettriche fisse. I principi dei campi elettrostatici
1. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE
 8 SISTEMI DI GRADO SUPERIORE AL. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE Si dice grado di un sistema il prodotto fra i gradi delle sue equaioni. + y ( grado) + y ( grado) sistema di 6 grado
8 SISTEMI DI GRADO SUPERIORE AL. GRADO DI UN SISTEMA. METODI GENERALI DI RISOLUZIONE Si dice grado di un sistema il prodotto fra i gradi delle sue equaioni. + y ( grado) + y ( grado) sistema di 6 grado
tempo trascorso T numero dei cicli svolti
 Capitolo X Oscillazioni 1. Il oto periodico In natura sono olto frequenti dei fenoeni che si ripetono con uguali caratteristiche: le oscillazioni di un pendolo, l alternanza di giorno e notte, il oto orbitale
Capitolo X Oscillazioni 1. Il oto periodico In natura sono olto frequenti dei fenoeni che si ripetono con uguali caratteristiche: le oscillazioni di un pendolo, l alternanza di giorno e notte, il oto orbitale
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Equazioni Polinomiali II Parabola
 Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
LA TEORIA CINETICA DEI GAS
 LA TEORIA CINETICA DEI GAS Le teorie microscopiche Le proprietà degli atomi e delle molecole spiegano le proprietà che riscontriamo nei sistemi macroscopici. Grandee microscopiche Massa di una molecola
LA TEORIA CINETICA DEI GAS Le teorie microscopiche Le proprietà degli atomi e delle molecole spiegano le proprietà che riscontriamo nei sistemi macroscopici. Grandee microscopiche Massa di una molecola
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria III esonero pariale A.A. 6 Cognome Nome Matricola Codice
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria III esonero pariale A.A. 6 Cognome Nome Matricola Codice
Tonzig Fondamenti di Meccanica classica
 Capitolo 14 Urti 1 Il significato del terine «urto» non è, in Fisica, rigidaente codificato, a, quanto eno a liello acroscopico, è sostanzialente quello stesso del linguaggio corrente: si pensi all urto
Capitolo 14 Urti 1 Il significato del terine «urto» non è, in Fisica, rigidaente codificato, a, quanto eno a liello acroscopico, è sostanzialente quello stesso del linguaggio corrente: si pensi all urto
CAPITOLO 6 DURATA OTTIMALE
 CAPITOLO 6 DURATA OTTIMALE I diritti di proprietà intellettuale proteggono gli innovatori, a la protezione è liitata in durata ed apiezza. In durata, perché i diritti di proprietà intellettuale hanno una
CAPITOLO 6 DURATA OTTIMALE I diritti di proprietà intellettuale proteggono gli innovatori, a la protezione è liitata in durata ed apiezza. In durata, perché i diritti di proprietà intellettuale hanno una
INDICE 1. PREMESSA 1 2. COMPATIBILITA IDRAULICA 3
 INDICE 1. PREMESSA 1. COMPATIBILITA IDRAULICA 3.1. CALCOLO DELLA PORTATA 3.. IL MODELLO IDRAULICO 4.3. CARATTERIZZAZIONE GEOMETRICA DELLE SEZIONI. 6.4. DEFINIZIONI DELLE CONDIZIONI AL CONTORNO E DELLE
INDICE 1. PREMESSA 1. COMPATIBILITA IDRAULICA 3.1. CALCOLO DELLA PORTATA 3.. IL MODELLO IDRAULICO 4.3. CARATTERIZZAZIONE GEOMETRICA DELLE SEZIONI. 6.4. DEFINIZIONI DELLE CONDIZIONI AL CONTORNO E DELLE
1 Oscillazioni libere (oscillatore armonico)
 C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
ANALISI DI SERIE TEMPORALI CAOTICHE
 ANALISI DI SERIE TEMPORALI CAOTICHE Probleatiche Ricostruzione dello stato Diensione di ebedding Calcolo della diensione frattale Modelli di previsione Calcolo degli esponenti di Liapunov C. Piccardi e
ANALISI DI SERIE TEMPORALI CAOTICHE Probleatiche Ricostruzione dello stato Diensione di ebedding Calcolo della diensione frattale Modelli di previsione Calcolo degli esponenti di Liapunov C. Piccardi e
Lezione 12. Sottogruppi finiti di ordine fissato. I Teoremi di Sylow.
 Lezione 1 Prerequisiti: Lezioni, 7. ruppi di perutazioni. Riferienti ai testi: [Fd] Sezione.1; [H] Sezione.7; [PC] Sezione 5.1 Sottogruppi finiti di ordine fissato. I Teorei di Sylow. Dal Teorea di Lagrange
Lezione 1 Prerequisiti: Lezioni, 7. ruppi di perutazioni. Riferienti ai testi: [Fd] Sezione.1; [H] Sezione.7; [PC] Sezione 5.1 Sottogruppi finiti di ordine fissato. I Teorei di Sylow. Dal Teorea di Lagrange
8.4 Calcolo di tensori di inerzia
 1 CAPITL 8. IL CRP RIGID Infatti B I ( u) (P )(P ) [ u (P )] dτ(p ) B (P )(P ) [ u (P )] dτ(p ) B 1 + ρ(p )(P ) [ u (P )] dτ(p ) B B = 1 B I + I Analoga proprietà vale per i oenti di inerzia. 8. Calcolo
1 CAPITL 8. IL CRP RIGID Infatti B I ( u) (P )(P ) [ u (P )] dτ(p ) B (P )(P ) [ u (P )] dτ(p ) B 1 + ρ(p )(P ) [ u (P )] dτ(p ) B B = 1 B I + I Analoga proprietà vale per i oenti di inerzia. 8. Calcolo
Equazioni di secondo grado
 Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
Liceo Classico D. Alighieri A.S Studio di Funzione. Prof. A. Pisani. Esempio
 Liceo Classico D. Alighieri A.S. 0-3 y Data la funzione: Studio di Funzione tracciatene il grafico nel piano cartesiano. Prof. A. Pisani Esempio ) Tipo e grado della funzione La funzione è analitica, data
Liceo Classico D. Alighieri A.S. 0-3 y Data la funzione: Studio di Funzione tracciatene il grafico nel piano cartesiano. Prof. A. Pisani Esempio ) Tipo e grado della funzione La funzione è analitica, data
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Prima parte. giustificando le a operazioni fatte con le proprietà delle congruenze utilizzate. Poiché ax b mod n (a mod n) x (b mod n) mod n
 Soluione del copito di Fondaenti di Mateatica del discreto laurea OnLine 6 aio 7 Per la soluione si è posto: N = 7354 n=n od =354; =G od 4)+4=7; =M od 6)+=5; a=a od =86 Pria parte 3 96 od). Deterinare
Soluione del copito di Fondaenti di Mateatica del discreto laurea OnLine 6 aio 7 Per la soluione si è posto: N = 7354 n=n od =354; =G od 4)+4=7; =M od 6)+=5; a=a od =86 Pria parte 3 96 od). Deterinare
Ingegneria Meccanica; Algebra lineare e Geometria 2008/2009
 Capitolo Ingegneria Meccanica; Algebra lineare e Geometria 8/9. Esercii svolti su rette e piani Eserciio. Stabilire se le due rette r e s sono coincidenti oppure no: ( ( ( ( ( ( 7 r : = + t ; s : = + t
Capitolo Ingegneria Meccanica; Algebra lineare e Geometria 8/9. Esercii svolti su rette e piani Eserciio. Stabilire se le due rette r e s sono coincidenti oppure no: ( ( ( ( ( ( 7 r : = + t ; s : = + t
= τ MOTO ROTOTRASLATORIO DI UN CORPO RIGIDO. Equazioni cardinali. Prima equazione cardinale:
 MOTO ROTOTRASLATORO D UN CORPO RGDO Equaioni cardinali Prima equaione cardinale: dv c M Fet Esprime il teorema del moto del centro di massa: il moto del centro di massa del corpo rigido è quello di un
MOTO ROTOTRASLATORO D UN CORPO RGDO Equaioni cardinali Prima equaione cardinale: dv c M Fet Esprime il teorema del moto del centro di massa: il moto del centro di massa del corpo rigido è quello di un
Alcuni esercizi sulla diagonalizzazione di matrici. campo dei reali. Se lo è calcolare una base spettrale e la relativa forma diagonale di A.
 Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
Alcuni esercii sulla diagonaliaione di matrici Eserciio Dire se la matrice A 4 8 è diagonaliabile sul 3 3 campo dei reali Se lo è calcolare una base spettrale e la relativa forma diagonale di A Svolgimento
asse fuoco vertice direttrice Fig. D3.1 Parabola.
 D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
Sistemi lineari. 1. Generalità. a 1 x 1 + a 2 x 2 + a 3 x a n x n = k (matrice completa)
 Sistemi lineari. Generalità La teoria dei sistemi di equaioni lineari costituisce uno dei capitoli molto importanti della matematica pura e applicata. Infatti molte questioni teoriche o tecniche si traducono
Sistemi lineari. Generalità La teoria dei sistemi di equaioni lineari costituisce uno dei capitoli molto importanti della matematica pura e applicata. Infatti molte questioni teoriche o tecniche si traducono
Nota metodologica Strategia di campionamento e livello di precisione dei risultati
 Nota etodologica Strategia di capionaento e livello di precisione dei risultati 1. Obiettivi conoscitivi La popolaione di interesse dell indagine in oggetto, ossia l insiee delle unità statistiche intorno
Nota etodologica Strategia di capionaento e livello di precisione dei risultati 1. Obiettivi conoscitivi La popolaione di interesse dell indagine in oggetto, ossia l insiee delle unità statistiche intorno
PLASMONI SUPERFICIALI
 PLASMONI SUPERFICIALI Un possibile approccio nello studio delle proprietà fisiche dei etalli consiste nel considerare gli elettroni liberi presenti all interno del loro volue coe un liquido ad alta densità,
PLASMONI SUPERFICIALI Un possibile approccio nello studio delle proprietà fisiche dei etalli consiste nel considerare gli elettroni liberi presenti all interno del loro volue coe un liquido ad alta densità,
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
Anno 3 Equazione dell'ellisse
 Anno Equazione dell'ellisse 1 Introduzione In questa lezione affronteremo una serie di problemi che ci chiederanno di determinare l equazione di un ellisse sotto certe condizioni. Al termine della lezione
Anno Equazione dell'ellisse 1 Introduzione In questa lezione affronteremo una serie di problemi che ci chiederanno di determinare l equazione di un ellisse sotto certe condizioni. Al termine della lezione
Soluzioni delle Esercitazioni VIII 21-25/11/2016. = lnx ln1 = lnx. f(t)dt.
 Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercizi di Fisica Generale Foglio 3. Forze
 31.01.11 Esercizi di Fisica Generale Foglio 3. Forze 1. Un corpo di assa viene sospeso da una olla con costante elastica k, coe in figura (i). La olla si allunga di 0.1. Se ora due corpi identici di assa
31.01.11 Esercizi di Fisica Generale Foglio 3. Forze 1. Un corpo di assa viene sospeso da una olla con costante elastica k, coe in figura (i). La olla si allunga di 0.1. Se ora due corpi identici di assa
Equazioni di 2 grado
 Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
7. Integrazione delle funzioni di più variabili (II)
 7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
Geometria analitica del piano pag 32 Adolfo Scimone
 Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
VII. AREA E PERIMETRO ELLISSE
 VII. AREA E PERIMETRO ELLIE Area e Perietro Ellisse Cap. VII Pag. AREA DEL ETTORE DELL'ELLIE I )ia ( x) y dx l area OCAA. La funzione (x) deve essere tale d( x) che y x e poiché dx è ( x) xy area settoreoaa'
VII. AREA E PERIMETRO ELLIE Area e Perietro Ellisse Cap. VII Pag. AREA DEL ETTORE DELL'ELLIE I )ia ( x) y dx l area OCAA. La funzione (x) deve essere tale d( x) che y x e poiché dx è ( x) xy area settoreoaa'
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
ẋ 1 = 2x 1 + (sen 2 (x 1 ) + 1)x 2 + 2u (1) y = x 1
 Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
17. Elettromagnetismo
 1 quaioni di Mawell 17. lettromagnetismo Nelle leioni precedenti abbiamo considerato i campi elettrico e magnetico statici, cioè abbiamo considerato fenomeni indipendenti dal tempo. I campi elettrico e
1 quaioni di Mawell 17. lettromagnetismo Nelle leioni precedenti abbiamo considerato i campi elettrico e magnetico statici, cioè abbiamo considerato fenomeni indipendenti dal tempo. I campi elettrico e
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
(1;1) y=2x-1. Fig. G4.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
La retta nel piano cartesiano
 La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Esercizi di Fisica Matematica 3, anno , parte di meccanica hamiltoniana e quantistica
 Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
Esercizi di Fisica Matematica 3, anno 014-015, parte di meccanica hamiltoniana e quantistica Dario Bambusi 09.06.015 Abstract Gli esercizi dei compiti saranno varianti dei seguenti esercizi. Nei compiti
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Determinazione della densità di solidi.
 Deterinazione della densità di solidi. Scopo dell esperienza Lo scopo di questa esperienza è quello di deterinare la densità di alcuni corpi solidi, per poi confrontare il valore ottenuto sperientalente
Deterinazione della densità di solidi. Scopo dell esperienza Lo scopo di questa esperienza è quello di deterinare la densità di alcuni corpi solidi, per poi confrontare il valore ottenuto sperientalente
Tipologia delle funzioni studiate: 1. y= ax n + bx n y= e x 3. y= (ax + b)/ (cx + d) 4. y= (ax 2 + b) (cx + d)
 - ricerca dei punti di flesso - ricerca dell asintoto orizzontale - ricerca dell asintoto verticale - ricerca dell asintoto obliquo - ricerca dei punti di intersezione con gli assi Tipologia delle funzioni
- ricerca dei punti di flesso - ricerca dell asintoto orizzontale - ricerca dell asintoto verticale - ricerca dell asintoto obliquo - ricerca dei punti di intersezione con gli assi Tipologia delle funzioni
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Lezione n.15. Doppi bipoli
 Lezione 5 Doppi bipoli Lezione n.5 Doppi bipoli. Definizione di N-polo. Definizione di doppio-bipolo 3. Doppi-bipoli in regie stazionario (doppi-bipoli di resistenze 4. Problei di analisi 5. Problei di
Lezione 5 Doppi bipoli Lezione n.5 Doppi bipoli. Definizione di N-polo. Definizione di doppio-bipolo 3. Doppi-bipoli in regie stazionario (doppi-bipoli di resistenze 4. Problei di analisi 5. Problei di
Elettronica dello Stato Solido Lezione 5: L equazione di Schrödinger. Daniele Ielmini DEI Politecnico di Milano
 Elettronica dello Stato Solido Lezione 5: L equazione di Schrödinger Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 05 Outline Argomenti qualitativi
Elettronica dello Stato Solido Lezione 5: L equazione di Schrödinger Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 05 Outline Argomenti qualitativi
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Problema 1. m F. che è un sistema di due equazioni e due incognite (a e µ s ). Risolvendo si ottiene:
 1 Problea 1 Un blocchetto di assa = 1 kg è appoggiato sopra un blocco di assa M = 4 kg e lunghezza d = 0.8, alla sua estreità sinistra (vedi figura). Tra i due blocchi vi è attrito (µ d = 0.6µ s ) entre
1 Problea 1 Un blocchetto di assa = 1 kg è appoggiato sopra un blocco di assa M = 4 kg e lunghezza d = 0.8, alla sua estreità sinistra (vedi figura). Tra i due blocchi vi è attrito (µ d = 0.6µ s ) entre
Appello di Meccanica Quantistica I
 Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
2. FUNZIONI REALI DI n VARIABILI REALI
 FUNZIONI REALI DI n VARIABILI REALI Determinaione del dominio Y Sia D un sottoinsieme dell insieme R R indicato anche con R Graficamente possiamo pensare a D come ad una ona del piano cartesiano secondo
FUNZIONI REALI DI n VARIABILI REALI Determinaione del dominio Y Sia D un sottoinsieme dell insieme R R indicato anche con R Graficamente possiamo pensare a D come ad una ona del piano cartesiano secondo
Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni
 Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni Definizioni e breve richiamo alle principali leggi dei circuiti elettrici Risolvere un circuito elettrico significa determinare i
Risoluzione dei circuiti elettrici col metodo dei sistemi di equazioni Definizioni e breve richiamo alle principali leggi dei circuiti elettrici Risolvere un circuito elettrico significa determinare i
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
ILLUMINAZIONE NATURALE
 CAPITOLO 9 ILLUMINAZIONE NATURALE 9.1 Generalità Un corretto utilizzo della luce diurna rende più gradevoli abienti agli occupanti e conteporaneaente può contribuire a contenere durante il giorno i consui
CAPITOLO 9 ILLUMINAZIONE NATURALE 9.1 Generalità Un corretto utilizzo della luce diurna rende più gradevoli abienti agli occupanti e conteporaneaente può contribuire a contenere durante il giorno i consui
LE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE
 LE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE 1. EQUAZIONI DIFFERENZIALI LE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE ESEMPIO Della funzione y = f(x) si sa che y' 2x = 1. Che cosa si può dire della funzione
LE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE 1. EQUAZIONI DIFFERENZIALI LE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE ESEMPIO Della funzione y = f(x) si sa che y' 2x = 1. Che cosa si può dire della funzione
SOLUZIONE La presente soluzione verrà redatta facendo riferimento al manuale:
 SOLUZIONE La presente soluzione verrà redatta facendo riferiento al anuale: Caligaris, Fava, Toasello Manuale di Meccanica Hoepli. PRIMA PARTE Diensionaento delle ruote dentate Si calcola il rapporto di
SOLUZIONE La presente soluzione verrà redatta facendo riferiento al anuale: Caligaris, Fava, Toasello Manuale di Meccanica Hoepli. PRIMA PARTE Diensionaento delle ruote dentate Si calcola il rapporto di
La circonferenza nel piano cartesiano
 La circonferenza nel piano cartesiano 1. Definizione ed equazione. Si chiama circonferenza C, di centro C( α, β ) e raggio r, l insieme di tutti e soli i punti del piano che hanno distanza r da C. L equazione
La circonferenza nel piano cartesiano 1. Definizione ed equazione. Si chiama circonferenza C, di centro C( α, β ) e raggio r, l insieme di tutti e soli i punti del piano che hanno distanza r da C. L equazione
