SCOMMESSE SPORTIVE 1 LA PROBABILITÀ. Se indichiamo con A l evento lancio un dado ed esce il numero 6 abbiamo che ( ) 2 LE VARIABILI ALEATORIE
|
|
|
- Luigi Antonella
- 8 anni fa
- Visualizzazioni
Transcript
1 SCOMMESSE SPORTIVE In questo manuale tenterò cercherò di illustrare il meccanismi che a grandi linee regolano il mondo delle scommesse sportive ed indicherò alcuni possibili punti deboli del sistema. Per farlo mi avvarrò il più possibile di grafici e tabelle che a mio parere risultano molto più chiari di una sequenza di parole. Le formule matematiche utilizzate saranno il più possibile semplificate. Tutta questa prima parte introduttiva ha come scopo quello di giungere ad una formulazione della Legge dei Grandi Numeri e di comporre la base per le considerazioni successive. 1 LA PROBABILITÀ Tutti abbiamo dimestichezza con il concetto di probabilità. Sappiamo ad esempio che lanciando un moneta c è una probabilità del 50% che esca testa ed una probabilità del 50% che esca croce. In generale possiamo dire che la probabilità è un valore compreso tra zero e uno che comunemente viene espresso in percentuale oppure con la dicitura c è una possibilità su... La probabilità misura la possibilità che si verifichi un dato evento. Se la probabilità è uguale a zero l evento è impossibile, se la probabilità è uno l evento accadrà certamente. Esempio. Se indichiamo con A l evento lancio un dado ed esce il numero 6 abbiamo che ( ) dove ( ) indica la probabilità dell evento A e il simbolo 1/6 è stata approssimata al secondo decimale. significa circa dal momento che la frazione 2 LE VARIABILI ALEATORIE Un fenomeno aleatorio è un fenomeno che non si può prevedere a priori. L etimologia dell aggettivo deriva da alea che in latino significa dado ( alea iacta est cioè il dado è tratto è la frase che pronunciò Cesare quando varcò il Rubicone ). Una variabile aleatoria è una variabile che ha associata una descrizione di tipo probabilistico. Le variabili aleatorie modellano i processi. Esempio Processo : LANCIO DI UN DADO. Il processo è modellato da una variabile aleatoria che può assumere i valori {1,2,3,4,5,6 }. Possiamo indicare con p(n) la probabilità che la variabile aleatoria assuma il valore n. In questo caso abbiamo che ( ) ( ) ( ) ( ) ( ) ( ) La somma delle probabilità dei valori che una variabile aleatoria può assumere deve essere ovviamente uguale a 1. La funzione p può essere rappresentata in diverse maniere. Una maniera chiara ed elegante sono gli istogrammi (facilmente realizzabili in Excel)
2 Ogni barra dell istogramma rappresenta la probabilità che la variabile aleatoria assuma quel determinato valore. Una variabile aleatoria di questo tipo, dove tutti i possibili valori hanno la stessa probabilità, si dice equidistribuita. Per avere una variabile aleatoria che non sia equidistributia consideriamo il lancio di 2 dadi. In questo caso la variabile aleatoria x rappresenta la somma dei punteggi dei due dadi e può assumere i valori compresi tra 2 e 12. Per calcolare la probabilità di ogni singolo valore dobbiamo distinguere i due dadi, fare ad esempio conto che siano uno rosso e uno verde, e considerare tutte le coppie di valori (punteggio dado rosso, punteggio dado verde). Queste sono in tutto 36. Le rappresentiamo in una tabella di 6 righe per 6 colonne dove all interno mettiamo la somma dei sue valori Come si vede i punteggi totali si dispongono sul linee diagonali all interno della tabella. Abbiamo così che ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
3 Come si vede il valore più probabile è 7 seguito dai due nelle immediate vicinanze 6 e 8. Una distribuzione di probabilità di questo tipo è ben presente a chi pratica con assiduità il gioco del Monopoli. In questo gioco ogni giocatore acquista dei terreni sui quali può edificare case ed alberghi. I giocatori muovono il proprio segnalino lanciando due dadi. Quando un giocator finisce su un terreno di proprietà di un avversario deve versargli una certa somma che aumenta in funzione degli edifici che sul terreno sono stati realizzati. Il valore dei terreni e di conseguenza il prezzo da corrispondere aumenta man mano che si procede nel giro. I terreni che richiedono un esborso più economico sono i due siti sulla casella 1 e 3 del gioco (vicolo stretto de vicolo corto) mentre la mazzate più toste si prendono quando si giunge sugli ultimi due terreni, Parco della Vittoria e Viale dei Giardini. Nella casa 10 sita nell angolo in basso a sinistra c è la prigione. Si finisce in essa quando si raggiunge la casa diagonalmente opposta ad essa oppure quando si pesca un cartellino arancione degli imprevisti che vi ci manda. Dalla prigione si esce facendo un numero doppio (11,22, ecc) oppure al terzo tiro con il punteggio realizzato dai dadi pagando un ammenda. Di primo impatto verrebbe da dire che i terreni che rendono maggiormente sono i sue terreni viola ma in realtà simulazioni fatte con il calcolatore hanno dimostrato che non è così. I terreni più redditizi sono quelli sul lato sinistro della figura (gli arancioni ed i marron) dal momento che sono quelli dove si finisce con maggiore
4 probabilità quando si esce di prigione. Allo stesso modo un giocatore che parte dalla casella VIA sa che con una probabilità intorno al 50% finirà o su un terreno azzurro o nella casella degli imprevisti. Nel caso del lancio di 3 dadi la variabile aleatoria che modella la somma dei punti può assumere valori compresi tra 3 e 18. La corrispondente distribuzione delle probabilità è quella illustrata nell istogramma qui sopra. Avevo una professoressa di matematica al liceo che per decidere chi interrogare apriva a caso una pagina del libro e faceva la somma delle cifre del numero di pagina andando poi a pescare il nome corrispondente a quel numero sul registro di classe. Supponendo che la professoressa aprisse il libro in un pagina casuale compresa tra la numero 50 e la numero 100 e che guardasse unicamente le pagine numerate pari si ottiene un istogramma di questo tipo Come si vede la procedura non era delle più eque. I numeri 3 4 e 5 del registro e quelli oltre il 17 (non mi ricordo in quanti fossimo) erano al sicuro mentre coloro che rischiavano di più erano i numeri 9 11 e 13.
5 3 LA MEDIA La media è un parametro statistico fondamentale per avere l ordine di grandezza di una variabile aleatoria. Per calcolare la media di una variabile aleatoria occorre moltiplicare tutti i suoi possibili valori per le corrispondenti probabilità. Esempio La variabile aleatoria x assume i valori 3,4,5 e,6 con ( ) ( ) ( ) ( ) Calcoliamo la sua media ( )( ) ( )( ) ( )( ) ( )( ) Nel caso di variabili aleatorie equidistribuite su un numero n di valori abbiamo che la probabilità che la variabile aleatoria assuma un dato valore è 1/n e dunque la media della variabile aleatoria è data dalla somma di tutti i suoi valori divisa per n. Nel caso di una distribuzione di probabilità simmetrica come quella che si ha nel lancio di due dadi si può verificare che la media coincide con il valore centrale cioè 7. 4 FREQUENZE STATISTICHE Supponiamo ora di eseguire realmente il processo modellato dalla variabile aleatoria per esempio di eseguire 10 lanci di un dado ed ottenere i punteggi Fare la statistica dei risultati ottenuti significa calcolare le frequenze con le quali si sono ottenuti i vari valori cioè contare il numero di volte che è uscito ciascun valore e dividerlo per il numero di prove. In questo caso, se la funzione f indica la frequenza abbiamo ( ) ( ) ( ) ( ) ( ) ( ). La media dei risultati ottenuti invece è data dalla somma di essi divisa per il numero delle prove. In questo caso abbiamo La lettera maiuscola M è stata usata per distinguere questo concetto di media da quello di media di una variabile aleatoria. 5 LA LEGGE DEI GRANDI NUMERI Chiamiamo probabilità teoriche le probabilità p(x) relative ad una certa variabile aleatoria x mentre le frequenze teoriche ( ) le frequenze che si sono ottenute facendo la statistica su n prove del processo modellato dalla variabile x (nell esempio precedente era n=10). La legge dei grandi numeri dice in sostanza che all aumentare del numero delle prove n le frequenze statistiche tendono sempre più ad avvicinarsi alle medie teoriche. In pratica proseguendo nell esempio di prima si avrebbe che facendo la statistica su un numero maggiore di lanci del dado (1000, 5000, 10000) ecc. le frequenze tenderebbero sempre più ad appiattirsi avvicinandosi al valore 0.17 che è la probabilità teorica.
6 In figura sono stati simulati lanci di un dado con un calcolatore e sono state messe su un grafico le frequenze di uscita del numero 1 via via ottenute. Si vede che a partire da circa il 5000 esimo lancio la frequenza in pratica è indistinguibile dalla probabilità teorica rappresentata dalla linea rossa. Discorso analogo vale anche per le medie. All aumentare del numero delle prove la media statistica M dei valori ottenuti si avvicina sempre di più alla media teorica m della variabile aleatoria che modella il processo. La legge dei grandi numeri viene di sovente citata a sproposito. Per esempio un allenatore potrebbe dire abbiamo perso le prime 4 partite e quindi per la legge dei grandi numeri la quinta dovremmo vincerla. In questo caso si può muovere l obiezione che 5 non è un grande numero. In altri contesti quali il gioco del lotto la legge dei grandi numeri è associata alla teoria dei ritardi. Se ad esempio il numero 1 non esce da 50 estrazioni sulla ruota di Bari si ritiene allora che all estrazione successiva abbia più probabilità degli altri di uscire dal momento che per la legge dei grandi numeri tutte le frequenze di uscita devono tendere a riequilibrarsi. In realtà la probabilità che il numero 1 esca alla 51 estrazione è sempre 5/90 (la ruota del lotto non ha memoria). 6 GIOCHI CON PREMIO PROPORZIONALE ALLA GIOCATA Il lotto, la roulette, le scommesse stesse seguono tutte lo stesso schema di gioco. Il giocatore gioca (o punta ne caso delle scommesse) una certa cifra sull esito di un dato evento (l uscita di una certa combinazione al lotto, un numero della roulette o il risultato di una partita). Il gestore del gioco (banco o agenzia di scommesse) intasca subito la somma giocata. Se il giocatore indovina l esito dell evento gli viene restituita una somma pari all importo che ha giocato moltiplicato per un certo fattore (nelle scommesse questo fattore prende il nome di quota). Se ad esempio giochiamo un euro ed il fattore moltiplicativo è pari a 5 abbiamo che se non indoviniamo perdiamo l euro giocato mentre se vinciamo ci vengono restituiti 5 euro e pertanto il guadagno che ne otteniamo è di 4 euro. Esistono anche altri giochi, quali il superenalotto od il totocalcio, che seguono un altro schema. In questi giochi il numero totale delle puntate dei giocatori forma il monte giocate. Di questo solo una parte, il 38% circa va a formare il montepremi mentre il rimanente 62% viene trattenuto netto dal gestore del gioco. In pratica per ogni euro giocato al superenalotto la SISAL sa già che 62 centesimi saranno suoi mentre i rimanenti 38 dovrà metterli a disposizione dei vincitori. Il montepremi viene suddiviso tra le varie categorie di vincita e di lì spartito tra tutti i vincitori di quella categoria. La differenza tra i due sistemi di gestione del gioco è evidente. La SISAL sa che comunque vadano le cose ad ogni estrazione sarà sempre in attivo di un capitale pari al 62% del monte giocate. La LOTTOMATICA che gestisce il gioco del lotto ha invece un margine di guadagno variabile. Per assurdo potrebbe accadere che un guru vada in televisione suggerendo i 5 numeri vincenti su una data ruota, che un gran numero di giocatori li giochi e che questi escano davvero. In questo caso la LOTTOMATICA fallirebbe. 7 I GIOCHI D AZZARDO Nessun gestore di giochi d azzardo fa della beneficenza e quindi ognuno si tiene un proprio margine di guadagno. Il guadagno deriva dal corrispondere quale fattore moltiplicativo della puntata un valore inferiore a quello onesto. Ad esempio se si partecipa ad un gioco che può avere solo due possibili esiti entrambi con la stessa probabilità il fattore moltiplicativo non sarà 2 ma sarà sempre un valore un po inferiore. In pratica giocando un euro al 50% lo perderemmo mentre al 50% ci verrebbero ridati ad esempio 1.90 euro con un conseguente nostro guadagno di soli 90 centesimi. Il gioco più onesto al mondo è la roulette. Essa si compone di 37 numeri (da 0 a 36) e quindi la probabilità di vincere puntando su di un numero vale 1/37. In caso di vittoria viene restituita la puntata moltiplicata per 36. Facciamo che la variabile aleatoria x rappresenti il nostro guadagno unitario (cioè quello che si ha giocando un euro) ad ogni puntata. Se x è positiva abbiamo effettivamente un guadagno mentre se è negativa abbiamo una perdita. La variabile aleatoria x può assumere solo 2 valori
7 1) Se vinciamo x vale 36-1=35. Ciò avviene con probabilità ( ) 2) Se perdiamo x vale -1. Ciò avviene con probabilità 36/37 Calcoliamo la media della variabile aleatoria x e la chiamiamo guadagno medio g ( ) ( ) ( ) ( ) All aumentare del numero delle giocate il guadagno per ogni euro puntato si attesterà sempre più verso questo valore. Se per esempio facessimo 1000 giocate da un euro ci ritroveremmo a fine serata con una perdita attorno ai 27 euro. La perdita che si ha su grandi numeri di giocate va ovviamente a vantaggio del banco che si ritroverà a fine serata con un guadagno circa pari al 2.7% del totale delle giocate effettuate.
8 In queste 2 figure sono mostrate due simulazioni fatte al calcolatore. Tre giocatori effettuano puntate da un euro. I corrispondenti guadagno sono rappresentati dalle 3 linee rossa blue e verde. La linea nera rappresenta il guadagno del banco. Nella prima simulazione alla fine i 3 giocatori si ritrovano tutti in perdita mentre il banco realizza un forte guadagno. Nella seconda due dei giocatori hanno alla fine un leggero guadagno ma ciò non basta a mandare in perdita il banco dal momento che le vincete sono compensate dalle perdite del giocatore rosso. In generale non è vero che ai giochi d azzardo alla fine ci si rimette sempre (andatelo a chiedere al tipo che vinse 70 milioni di euro al superenalotto). Sta di fatto che nella stragrande maggioranza dei casi con il gioco d azzardo non ci si arricchisce e talvolta ci si rovina. Per dare un idea dell onestà del gioco della roulette consideriamo invece il gioco del lotto. In esso è possibile ad esempio puntare sull estratto semplice (cioè sul fatto che un dato numero esca su una data ruota). Dal momento che gli estratti di una ruota sono 5 ed i numeri 90 abbiamo che la probabilità che un dato numero sia estratto vale 5/90=1/18. La vincita è pagata volte la somma giocata. Come prima, giocando un euro, abbiamo il guadagno x che può assumere 2 valori e cioè con un probabilità pari a 1/18 e -1 con probabilità 17/18. Abbiamo allora che ( ) ( ) Come si vede in questo caso il guadagno del banco è del 38%. Per altre combinazioni giocate (ambo, terno ecc.) i guadagni del banco sono ancora maggiori. 8 LE SCOMMESSE Le scommesse seguono come già detto lo stesso schema dei giochi d azzardo. Il fattore moltiplicativo della puntata si dice quota. A differenza che nei giochi d azzardo la quota non è fissa ma varia da evento ad evento a seconda delle valutazioni che l agenzia di scommesse fa riguardo all esito dell evento. Se la
9 vittoria di una squadra è abbastanza probabile verrà pagata una quota bassa mentre se è improbabile verrà pagata una quota alta. A differenza che nei giochi d azzardo nelle scommesse subentra una componente di abilità. In teoria siamo in grado di guadagnare soldi se siamo più abili della compagnia ad interpretare gli esiti degli eventi sportivi e se puntiamo su quelli secondo noi più favorevoli. Vediamo innanzi tutto il meccanismo di formazione delle quote. Vi sono incontri di calcio dove è possibile praticamente scommettere su tutto (prima squadra che segnerà, minuto del primo gol, numero degli ammoniti ecc ). Talvolta viene quotata anche quale delle squadre tirerà il calcio di inizio. In questo caso la probabilità che sia una o l altra squadra è del 50%. La quota proposta varia da 1.85 a Poniamoci nella migliore delle ipotesi. Stiamo scommettendo su JUVENUS-INTER e puntiamo un euro sul fatto che il calcio di inizio sarà tirato dalla Juventus. Il meccanismo di calcolo del guadagno è lo stesso visto prima. Se la Juventus tira effettivamente il calcio di inizio vinciamo =0.90 euro, se il calcio di inizio è tirato dall Inter perdiamo un euro. ( )( ) ( )( )( ) In pratica in media perdiamo 5 centesimi (cioè il 5% di quanto giocato). Tale perdita corrisponde al guadagno dell agenzia di scommesse. Supponiamo adesso che le opinioni circa l esito finale dell incontro siano sintetizzate in un valore probabilistico. Siano le probabilità che il lo scommettitore assegna ai 3 possibili esiti e le corrispondenti probabilità assegnate dall agenzia di scommesse. Ad esempio potremmo avere una situazione di questo tipo JUVENTUS -INTER p p' 1 50% 40% X 30% 30% 2 20% 30% Come si vede l agenzia di scommesse prevede una partita molto equilibrata mentre lo scommettitore magari per ragioni di tifo vede la Juventus più favorita. Consideriamo una generica quota q data dall agenzia di scommesse per uno dei 3 esiti avente probabilità p. Quanto vale il guadagno della compagnia nell ipotesi di una scommessa da un euro? Identifichiamo questo guadagno come g. In questo caso abbiamo che se lo scommettitore indovina il risultato, cosa che può accadere secondo l agenzia con una probabilità pari a p l agenzia ci rimette q- 1 mentre se lo scommettitore sbaglia il pronostico, cosa che accade con probabilità 1-p l agenzia guadagna 1 euro. Quindi ( )( ) ( ) Adesso supponiamo che l agenzia voglia determinare la quota q che le garantisca un certo guadagno g. Invertendo la formula abbiamo Consideriamo l esempio precedente e che l agenzia voglia un guadagno di 0.05 euro per ogni euro giocato (come nel caso del calcio di inizio visto sopra). Avremo che : Queste sono le quote che l agenzia proporrà agli scommettitori. Ora consideriamo le nostre probabilità p ed andiamo a valutare la scommessa per noi più conveniente In generale se q è la quota proposta e p la corrispondente probabilità da noi assegnata a quell evento abbiamo che scommettendo un euro vinciamo q-1 euro con probabilità p e ne perdiamo 1 con probabilità 1-p
10 Quindi ( ) ( )( ) Quindi con riferimento alla partita in questione avremo ( )( ) ( )( ) ( )( ) Come si vede la scommessa più conveniente, che poi è l unica a guadagno positivo, è per noi quella sul segno 1. Può anche darsi che su di un dato evento nessuna delle possibili opzioni di scommessa risulti conveniente. Ciò accade quando le probabilità che lo scommettitore assegna ai 3 esiti sono uguali o molto vicine a quelle assegnate dall agenzia. Il modello proposto è semplificato all essenziale. Talvolta le quote date dall agenzia vengono determinate sulla base di meccanismi diversi. Per esempio in presenza di una forte concentrazione di puntate su di una dato esito l agenzia ritoccherà quella quota verso il basso ed alzerà le quote degli altri esiti in modo da riequilibrare la situazione ed evitare di rimetterci una somma ingente di denaro nella peggiore delle condizioni. 8.1 TIPOLOGIE DI SCOMMESSE Su di un incontro di calcio sono quotati tutta una serie di tipi di scommesse. Le più comuni, quelle che prenderemo in considerazione sono le seguenti 1) Risultato finale 1 X 2 2) Doppia Chance. Si scommette su due possibili esiti (come le doppie del gioco del totocalcio). Abbiamo quindi 1X (doppia chance in) X2 (doppia chance out) e 12 (doppia chance in-out) 3) Risultato esatto. Negli esempi considereremo le quote date per tutti i possibili risultati nei quali una delle due squadre segna da zero a 4 reti. In totale abbiamo 25 possibili risultati con l aggiunta di un opzione ALTRO che considera tutti gli altri possibili risultati. Quindi in tutto è possibile scommettere su 26 esiti 4) GOL-NON GOL. L opzione GOL significa che tutte e due le squadre segneranno almeno una rete mentre l opzione NON-GOL significa che almeno una delle due squadre non segnerà. 5) UNDER. Le scommesse UNDER 1.5, UNDER 2.5, UNDER 3.5 e UNDER 4.5 comprendono i casi in cui la somma delle reti dell incontro sia inferiore a 1,2,3 o 4 gol rispettivamente. Se ad esempio l esito di un incontro è 1-1 la scommessa fatta su una UNDER 1.5 è persa mentre le scommesse fatte sulle UNDER 2.5, UNDER 3.5 e UNDER 4.5 sono vinte. 6) OVER. Sono il contrario delle under. Le scommesse OVER 1.5, OVER 2.5, OVER 3.5 e over 4.5 comprendono i casi in cui il numero totale di reti sia maggiore di 1,2,3 o 4 reti rispettivamente. Nell esempio dell esito finale 1-1 vincono gli scommettitori che hanno puntato sulle over 1.5 e perdono quelli che hanno giocato le OVER 2.5, OVER 3.5 e over DETERMINAZIONE DELLE PROBABILITÀ CHE L AGENZIA ASSEGNA AGLI ESITI DI UN EVENTO E DEL CORRRISPONDENTE GUADAGNO. In questo paragrafo ci poniamo nell ipotesi che su una data tipologia di scommessa l agenzia si riservi un guadagno g uguale per tutte le opzioni. È possibile esaminando unicamente quote risalire alle probabilità che l agenzia assegna ai vari esiti e al guadagno g? Sappiamo che per un generico evento avente probabilità p e quota q il guadagno g vale. Se consideriamo gli esiti 1X2 abbiamo che deve essere
11 A questo va aggiunto che la somma delle probabilità dei 3 eventi deve essere 1. Ne deriva un sistema di 4 equazioni nelle incognite { Consideriamo un esempio reale JUVENTUS-REAL MADRID Il sistema diventa { Questo sistema può essere risolto con il metodo di sostituzione. Per chi ha dimestichezza con il calcolo matriciale si può utilizzare la funzione che calcola la matrice inversa della matrice del sistema (tale funzione è presente ad esempio in Excel). Nella fattispecie si ottiene Come si vede l agenzia vede la sfida molto equilibrata con la Juventus leggermente favorita (per la cronaca l incontro terminerà con un pareggio). Il guadagno dell agenzia è dell 8%. La matrice del sistema è in generale questa [ ] Se n sono i possibili esiti la matrice ha dimensione n+1 per n+1. Le quote sono sulla diagonale. L ultima riga e l ultima colonna sono una fila di valori 1. Fa eccezione l elemento in basso a destra che è sempre zero. La colonna dei termini noti invece è formata da n+1 valori ANALISI GENERALE DELLE QUOTE DATE PER UNA CERTA PARTITA Facciamo riferimento all incontro UCRAINA-FRANCIA (per la cronaca il risultato finale è stato 2-0) Le quote fornite sono le seguenti quelle riportate in tabella. Evidenziati in blu vi sono possibili esiti e sotto ciascuno di essi la quota corrispondente.
12 SEGNO 1 X 2 1X X2 12 GOL NO GOL 2,90 3,20 2,40 1,52 1,37 1,31 1,90 1,80 U/O U 1,5 U 2,5 U 3,5 U 4,5 O 1,5 O 2,5 O 3,5 O 4,5 2,70 1,57 1,18 1,04 1,38 2,25 4,00 7,00 RIS ,00 16,00 12,00 50,00 25,00 RIS ,00 80,00 66,00 75,00 150,00 RIS ,50 12,00 10,00 40,00 20,00 RIS ,00 50,00 50,00 66,00 100,00 RIS ALTRO 7,50 6,00 15,00 66,00 200,00 33,00 Come si vede le quote massime si hanno sui risultati esatti altamente improbabili (in questo caso il 4-4 quotato a 2). Un altra osservazione che si può fare riguarda l andamento delle quote delle under e delle over. Come si vede le under diminuiscono all aumentare del valore di riferimento mentre le over aumentano e ciò in ragione del fatto che un incontro termina con maggiore probabilità con una somma delle reti bassa anziché alta. Con il metodo visto prima calcoliamo le probabilità assegnate ed i guadagni per le varie tipologie di scommesse. 1) Esito finale. Abbiamo
13 2) Doppia chance. Per calcolare le probabilità delle doppie chance sommiamo tra loro le probabilità ottenute per i singoli esiti Le quote sono calcolate su queste probabilità ed applicando lo stesso guadagno dei pronostici singoli 3) UNDER/OVER P'.UNDER P'.OVER g' 1,5 33,82% 66,18% 8,68% 2,5 58,90% 41,10% 7,53% 3,5 77,22% 22,78% 8,88% 4,5 87,06% 12,94% 9,45% Come si vede i guadagni dell agenzia per le under e le over sono superiori rispetto a quelli che l agenzia realizza sulle opzioni 1X2 e sulle doppie chance. In generale quindi le under e over sono opzioni meno convenienti da giocare rispetto alle precedenti. 4) GOL-NON GOL Anche in questo caso il guadagno della compagnia è superiore a quello che si ha nelle opzioni 1X2 5) RISULTATO ESATTO In questo caso occorre costruire una matrice di 27 righe per 27 colonne e mettere disporre le quote secondo i criteri prima illustrati. Si ottiene la tabella seguente RIS prob 9.65% 4.70% 6.43% 1.54% 3.09% RIS prob 1.54% 0.96% 1.17% 1.03% 0.51% RIS prob 10.29% 6.43% 7.72% 1.93% 3.86% RIS Prob. 1.93% 1.54% 1.54% 1.17% 0.77% RIS ALTRO Prob % 12.86% 5.14% 1.17% 0.39% 2.34% Il guadagno vale %. Puntare sul risultato significa quindi ambire a vincite alte ( si può anche vincere 200 volte la posta in gioco). Si tratta però unicamente di un esca per attirare lo scommettitore. Le quote date dall agenzia sui risultati esatti sono abbondantemente sottostimate ed è lì che l agenzia medesima ha il maggior margine di guadagno. Per avere un idea più chiara di quali siano i risultati più probabili e meno probabili è opportuno utilizzare ancora un istogramma
14 In questo caso i dati sono stati raggruppati sull asse orizzontale per somma totale di reti. Per mancanza di dati non si è potuto proseguire oltre le 4 reti totali segnate (il risultato 5-0 ad esempio non è preso in considerazione dall agenzia) e pertanto tutte le opzioni con più di 4 reti segnate sono raggruppate nella barra ALTRO. Si cede comunque che il risultato più comune è UN CALCOLO ALTERNATIVO DELLE PROBABILITÀ E DEI GUADAGNI La tabella precedente con le probabilità assegnate ad ogni singolo esito ci permette di calcolare le probabilità delle varie altre opzioni (1,X,2, under, over ecc.) in una maniera diversa e confrontare i risultati. Per esempio per calcolare la probabilità di uscita del segno 1 basta sommare le probabilità tutti i risultati nei quali prevale la squadra di casa. Nel caso 1X2 si è fatta l ipotesi che ne caso nell incontro una squadra segni più di 5 gol questa è sempre quella di casa e dunque la probabilità dell opzione ALTRO è stata aggiunta alla probabilità del segno 1. Si sono ottenuti i risultati seguenti 1 X 2 1X X2 12 GOL NOGOL 32,97% 29,85% 37,18% 62,82% 67,03% 70,15% 52,66% 47,34% U1,5 O21,5 U2,5 O2,5 U3,5 O3,5 U4,5 O4,5 30,22% 69,78% 54,22% 45,78% 71,84% 28,16% 86,95% 13,05% Anche in questo caso le righe blu indicano il tipo di giocata e sotto ciascuna opzione vi è la corrispondente probabilità calcolata. Adesso facciamo un confronto tra le probabilità ottenute con questo metodo e quelle ottenute precedentemente analizzando le varie tipologie di scommesse singolarmente.
15 Come si nota esistono delle discrepanze. Le massime si hanno sulle under/over 2.5 e 3.5 e sono dell ordine del 4%-5%. Tali differenze sono dovute ad imperfezioni del nostro modello (il guadagno su ogni possibile opzione di un evento non è costante, l agenzia cerca di indirizzare le giocate su una certa tipologia ecc.) 8.6 LA SCELTA DELLA SCOMMESSA DA EFFETTUARE Come abbiamo visto per scegliere la scommessa a guadagno medio più alto dobbiamo avere una stima delle probabilità dei veri eventi. Questa può venire da considerazioni personali, dalla consultazione di riviste specializzate o quant altro. In ogni caso per vincere dobbiamo essere più bravi degli esperti dell agenzia di scommesse in modo da compensare il margine di guadagno che le agenzie si riservano nelle quotazioni. Un possibile criterio di valutazione è quello di calcolare la media delle probabilità assegnate agli eventi che si sono effettivamente verificati. Esempio GIOCATORE AGENZIA P1 PX P2 P1' PX' P2' ESITO PARTITA 1 45% 25% 30% 40% 30% 30% 1 PARTITA 2 26% 51% 23% 25% 50% 25% X PARTITA 3 22% 52% 26% 20% 50% 30% 1 PARTITA 4 40% 30% 30% 33% 33% 34% 2 PARTITA 5 60% 20% 20% 60% 30% 10% X PARTITA 6 55% 30% 15% 50% 30% 20% 1 PARTITA 7 20% 20% 60% 20% 20% 60% 1 PARTITA 8 55% 40% 5% 50% 40% 10% 1 PARTITA 9 50% 25% 25% 50% 30% 20% 2 PARTITA 10 40% 30% 30% 34% 33% 33% X PARTITA 11 15% 25% 60% 20% 20% 60% X PARTITA 12 35% 45% 20% 30% 40% 30% X prob. Esiti media 35,25% prob. Esiti media 33,92%
16 In tabella sono riportati 12 ipotetici incontri. Sulle prime tre colonne sono riportate le probabilità che il giocatore assegna ad ognuno dei tre esiti mentre sulle colonne dalla quarta alla sesta sono riportate le probabilità assegnate dall agenzia di scommesse. Sull ultima colonna in rosso sono riportati gli esiti effettivi degli incontri. In base a questi è possibile fare un controllo a posteriori cioè andare a vedere che probabilità erano state assegnate dal giocatore e dall agenzia agli eventi che si sono effettivamente verificati e valutare chi sia stato il più bravo. Le probabilità degli esiti che si sono verificati sono evidenziate in verde. Se facciamo la somma delle probabilità evidenziate in verde relative al giocatore otteniamo un media del 35.25%. Se facciamo lo stesso per l agenzia otteniamo il valore 33.92%. Vuol dire che il giocatore ha un metodo di valutare le probabilità migliore di quello dell agenzia e quindi può avere qualche chance di guadagnare scommettendo. Se un test come questo dà esiti negativi, cioè le probabilità medie assegnate dal giocatore sono peggiori od uguali a quelle dell agenzia allora conviene non giocare secondo questi criteri dal momento che ciò comporterebbe alla lunga una perdita sicura come avviene per i giochi d azzardo. Possiamo provare a sfruttare la discrepanza vista prima, cioè quella tra le probabilità degli eventi calcolata direttamente dalle quote di essi e le probabilità degli eventi calcolata in base alle probabilità dei singoli risultati. Facciamo cioè conto che le probabilità sui singoli risultati siano quelle più affidabili e nelle nostre valutazioni prendiamo quali nostre probabilità di riferimento quelle che derivano da essi. Riconsideriamo la tabella relativa ad UCRAINA-FRANCIA. Aggiungiamo le righe con le probabilità delle varie opzioni ed i relativi guadagni medi 1 X 2 1X X2 12 GOL NO GOL 2,90 3,20 2,40 1,52 1,37 1,31 1,90 1, % 29.85% 37.18% 62.82% 67.03% 70.15% 52.66% 47.34% U 1,5 U 2,5 U 3,5 U 4,5 O 1,5 O 2,5 O 3,5 O 4,5 2,70 1,57 1,18 1,04 1,38 2,25 4,00 7, % 44.57% 71.84% 86.95% 69.78% 55.43% 28.16% 13.05% Come si vede la scommessa più conveniente in questo risulta essere la OVER LE MULTIPLE Una scommessa multipla è una scommessa effettuata su più partite ed equivale ad una scommessa nella quale la quota è pari al prodotto delle quote delle opzioni giocate. La scommessa multipla è vinta se tutte le opzioni sulle quali si scommette si realizzano. Esempio Giochiamo il segno 1 su JUVENTUS-UDINESE quotato a 1.70, 1X su ROMA CHIEVO quotato a 1.01 e la OVER 2.5 su NAPOLI-LAZIO quotata a La quota della multipla vale (1.70)(1.01)(2.50)=4.29. Puntando un euro ne riceviamo di ritorno se tutte e 3 le opzioni giocate. Supponiamo ora di avere il solito euro da scommettere e di avere a disposizione due opzioni relative a partite diverse entrambe a guadagno positivo. Esempio ATALANTA-LAZIO segno 1 quotato a 1.52 con probabilità 70 % (guadagno 0.06) e BOLOGNA-FIORENTINA con la OVER 2.5 quotata a 2.30 e probabilità 55% (guadagno 0.23). Conviene giocare l euro sull opzione più conveniente, in questo caso la OVER oppure giocare la multipla?
17 Se giochiamo la multipla la quota vale (1.52)(2.30)=3.50 mentre la probabilità di indovinare entrambi i risultati è pari al prodotto delle due probabilità e cioè (0.70)(0.55)=38.5%. Calcoliamo il guadagno medio della multipla ( )( ) Come si vede il guadagno della multipla è maggiore e quindi la giocata è conveniente. Questo è vero in generale Se e postivi con sono i guadagni medi di due giocate abbiamo che il guadagno medio della multipla vale. Dalle prime due equazioni ricaviamo e e quindi abbiamo ( )( ) Essendo i guadagni positivi per ipotesi si ha che A è positivo e quindi il guadagno della multipla è più grande del guadagno sulla scommessa singola. La multipla tra opzioni a guadagno positivo è sempre conveniente. 8.8 LA STRATEGIA DI GIOCO Le multiple sono dei moltiplicatori di guadagno. Grazie ad esse si possono ottenere dei guadagni medi elevati. All aumentare del guadagno medio abbiamo che diminuisce la probità di vincita (in pratica per avere un guadagno medio pari a 1000 occorre scommettere si tante partite e gli esiti della scommessa si devono realizzare tutti). A questo conviene domandarsi se sia opportuno puntare a guadagni elevati, con la prospettiva di fare magari una sola vincita nella vita come nel caso di un 14 al totocalcio oppure se sia più opportuno accontentarsi di guadagni modesti con vincite più frequenti. Occorre considerare vari fattori 1) La soddisfazione. Vincere un paio di volte nell arco di un campionato è più gratificante che realizzare una vincita sia pur più consistente dopo 10 anni di tentativi. 2) Le eventuali piccole vincite possono essere reinvestite aumentando l importo delle puntate. Un parametro fondamentale per la determinazione della strategia di gioco è la probabilità minima di vincita accettabile. Si tratta della minima probabilità di vincita in un singola scommessa che fa sì che con un alta probabilità vi sia almeno una vincita entro un dato numero di scommesse Esempio Trovare la probabilità minima per la quale si ha con probabilità del 99.9% almeno una vincita in 100 scommesse. Se è la probabilità di vincita in una singola scommessa abbiamo che quella di non vincita vale. Non ho un vincita per 100 scommesse quando per 100 volte si ripete un evento di probabilità e dunque la probabilità che ciò accada vale ( ). Ne deriva che si ha almeno una vincita in 100 concorsi con probabilità ( ). Voglio che ( ) Risolvendo la disequazione ( ) ( ) ( ) Dunque la probabilità minima vale 6.7% e giocando sempre delle multiple la cui probabilità è maggiore od uguale al 6.7% siamo pressoché certi di avere almeno una vincita in 100 giocate. In generale dove è il numero di scommesse che stiamo considerando (nell esempio 100) e è la probabilità di avere almeno una vincita (nell esempio 0.999).
18 In questo grafico la probabilità minima è stata rappresentata in funzione della probabilità di almeno una vincita e parametrizzata con i valori di n 50,100 e 150 che corrispondono all incirca ad un anno, due anni o tre anni di scommesse. Le linee rosse verticali evidenziano delle percentuali di vincita di riferimento. In questo grafico viceversa sono state messe in ascissa il numero delle scommesse che si intendono fare in totale e la probabilità minima è stata parametrizzata in funzione della probabilità di avere almeno una vincita. 8.9 UN MODELLO SEMPLIFICATO Modelliamo il gioco delle scommesse come un gioco d azzardo a guadagno positivo (tipo una roulette nin caso di vittoria 10.5 volte la posta in modo da avere un guadagno medio positivo di 0.05 euro. È concesso
19 anche di giocare delle multiple cioè di scommettere una certa cifra sul fatto che indovineremo l esito esatto per un certo numero consecutivo di giocate. Supponiamo di avere a disposizione 1000 euro da investire. PRIMA STRATEGIA È la più banale. Giochiamo un euro alla volta per 1000 giocate. Mal che vada perdo tutta la somma perdendo le prime 1000 puntate ma ciò è praticamente impossibile. Dal momento che il guadagno medio su un euro giocato è di 5 centesimi dopo 1000 giocate mi ritroverò con un guadagno medio di 50 euro. SECONDA STRATEGIA Giochiamo per 100 volte 10 euro una multipla su 10 puntate. La probabilità di vittoria scende all 1% e la vittoria è pagata volte. Il guadagno medio vale ( )( ). L inconveniente di questa strategia è che il procedimento potrebbe bloccarsi all inizio cioè potrei avere più di 100 giocate senza vincere. Ciò può accadere con una probabilità pari a ( ).Quindi all incirca con una probabilità pari ad 1/3 ci rimettiamo tutti 1000 gli euro e con una probabilità di 2/3 vinciamo in media euro cioè 16 miliardi di euro. TERZA STRATEGIA Faccio una giocata progressiva puntando sempre su una singola. In pratica all inizio e dopo ogni vincita considero il capitale che ho a disposizione e regolo la giocata in modo poter puntare fino alla fine delle 1000 giocate anche senza vincere più. Quindi de C è il capitale che ho a disposizione e n le giocate residue che mi restano da fare giocherò ogni volta C/n euro. Facciamo ad esempio di realizzare una vincita esattamente ogni 10 giocate. Inizialmente giochiamo un euro alla volta. Alla decima giocata abbiamo giocato 10 euro e ne vinciamo Il capitale diviene di Restano da fare 990 giocate e quindi ad goni puntata metteremo 1050/ euro. Dopo 10 giocate sono stati messi 10.6 euro e quindi il capitale è sceso a = euro. Vinciamo (1.06)(10.5)=11.13 e euro ed il capitale sale a euro e così via. Come si vede l incremento del capitale è modesto. Simulazioni fatte al calcolatore indicano un guadagno compreso medio compreso tra i 200 e i 700 euro I CONDIZIONAMENTI Supponiamo di essere assolutamente certi di uno degli esiti di un dato incontro. Questo può derivare da nostre convinzioni personali oppure perché abbiamo saputo che le squadre si sono messe d accordo. Il modo migliore per truccare le partite è farlo sull opzione GOL NON GOL o sulle OVER. In pratica si può dire alle due squadre lasciatevi fare un gol per parte nel primo tempo e nel secondo vinca il migliore. Il condizionamento mette a zero tutte le probabilità delle opzioni che non vanno d accordo con l evento condizionante. Riconsideriamo la tabella relativa alle probabilità dell incontro UCRAINA-FRANCIA e condizioniamo essendo sicuri che entrambe le squadre segneranno almeno una rete RIS prob 9.65% 4.70% 6.43% 1.54% 3.09% RIS prob 1.54% 0.96% 1.17% 1.03% 0.51% RIS prob 10.29% 6.43% 7.72% 1.93% 3.86% RIS Prob. 1.93% 1.54% 1.54% 1.17% 0.77% RIS ALTRO Prob % 12.86% 5.14% 1.17% 0.39% 2.34% Come prima nell opzione ALTRO si dà per scontato che una delle due squadre segni almeno una rete.
20 La somma delle probabilità che restano dopo il condizionamento vale 52.66%. Per trovare le probabilità condizionate dobbiamo dividere le probabilità rimaste per questo valore. Abbiamo questa tabella RIS prob 9.65% 4.70% 12.21% 1.54% 5.87% RIS prob 2.92% 0.96% 2.22% 1.96% 0.97% RIS prob 10.29% 6.43% 14.66% 1.93% 7.33% RIS Prob. 3.67% 1.54% 2.92% 2.22% 1.46% RIS ALTRO Prob % 24.42% 9.76% 2.22% 0.76% 4.44% Come si vede le probabilità degli eventi rimasti sono all incirca raddoppiate. Ora calcoliamo le probabilità dei vari eventi sui quali si può scommettere ed i relativi guadagni.. 1 X 2 1X X2 12 GOL NOGOL 2,9 3,2 2,4 1,52 1,37 1,31 1,9 1,8 30,59% 37,14% 32,26% 67,74% 69,41% 62,86% 100% 0% -0,11 0,19-0,23 0,03-0,05-0,18 0,90-1,00 U 1,5 U 2,5 U 3,5 U 4,5 O 1,5 O 2,5 O 3,5 O 4,5 2,70 1,57 1,18 1,04 1,38 2,25 4,00 7,00 0% 24,42% 51,29% 74,25% 100% 75,58% 48,71% 25,75% -1,00-0,62-0,39-0,23 0,38 0,70 0,95 0,80 Come si vede scommettendo un euro sull opzione sicura GOL si guadagno certamente 90 centesimi. Tuttavia questa non è la scommessa statisticamente più conveniente. Giocando un OVER 3.5 si vince all incirca con una probabilità del 50% ma la quota è alta con un guadagno medio di 0.95 centesimi. Esistono anche forme di condizionamento più complesse che prevedono doppie opzioni. Per esempio potremmo essere al corrente che le due squadre si sono messe d accordo di pareggiare segnando entrambe almeno una rete. In questo caso sono ammissibili unicamente i risultati RIS prob 9.65% 4.70% 12.21% 1.54% 5.87% RIS prob 2.92% 0.96% 2.22% 1.96% 0.97% RIS prob 10.29% 6.43% 14.66% 1.93% 7.33% RIS Prob. 3.67% 1.54% 2.92% 2.22% 1.46% RIS ALTRO Prob % 65.75% 26.28% 5.98% 1.99% 4.44%
21 La tabella per calcolare i guadagni diviene questa 1 X 2 1X X2 12 GOL NOGOL 2,9 3,2 2,4 1,52 1,37 1,31 1,9 1,8 0,00% 100,00% 0,00% 100,00% 100,00% 0,00% 100% 0% -1,00 2,20-1,00 0,52 0,37-1,00 0,90-1,00 U 1,5 U 2,5 U 3,5 U 4,5 O 1,5 O 2,5 O 3,5 O 4,5 2,70 1,57 1,18 1,04 1,38 2,25 4,00 7,00 0% 12,86% 12,86% 92,02% 100% 87,14% 87,14% 7,98% -1,00-0,80-0,85-0,04 0,38 0,96 2,49-0,44 Anche in questo caso l opzione più conveniente è la OVER LE ASSICURAZIONI Supponiamo che due agenzie di scommesse A e B abbiano opinioni diverse sull esito della medesima partita e quindi propongano quote diverse. Esempio agenzia A agenzia B P1 PX P2 P1 PX P2 ROMA-LAZIO 40% 30% 30% 30% 50% 20% Q1 QX Q2 Q1 QX Q2 2,33 3,10 3,10 3,10 1,86 4,65 Abbiamo a disposizione 100 euro. Ci proponiamo di disporre la somma in maniera da essere certi di non rimetterci mai soldi e, sotto questa condizione, massimizziamo il guadagno medio. Chiamiamo con i che può essere A o B e j che può essere 1,X o 2 una delle possibili puntate. Condizioni di non perdita. Se si verifica l esito 1 deve essere Se si verifica l esito X deve essere Se si verifica l esito 2 deve essere Un altra condizione è data dal fatto che la somma di tutte le possibili puntate deve ammontare a 100 euro Il guadagno medio è la quantità da massimizzare Assumiamo che la valutazione che noi diamo dell evento sia una via di mezzo tra quella delle due compagnie. Sia allora che per noi. Dunque ( ) ( ) ( )
22 Dobbiamo quindi risolvere questo problema ( ) soggetto ai vincoli con le variabili tutte non negative. Un problema di questo tipo è detto problema di programmazione lineare (PPL) e viene risolto dall algoritmo del simplesso disponibile nel componente aggiuntivo Risolutore di Excel. La soluzione ottima in questo caso è con massimo di Come era da aspettarsi la soluzione ottima suddivide le puntate tra i tre possibili esiti dell incontro. Se l esito è 1 ho una vincita pari a (32.26)(3.10)-100=0.00 euro. Se l esito dell incontro è X ho una vincita pari a (46.23)(3.10)-100=43.39 mentre se l esito è 2 ho una vincita pari a (21.51)(4.65)-100=0.00 euro. Quindi ho una vincita solo se l esito della partita è X mentre le altre due puntate mi assicurano di non rimetterci nel caso in cui questo esito non si verifichi IL GIOCO SU AGENZIE DIFFERENTI Con il metodo visto sopra guadagnare con le scommesse sarebbe semplice, basterebbe trovare due compagnie che danno quote differenti sul medesimo incontro. In realtà le varie agenzie tendono a fare cartello ed a proporre quote che differiscono di poco Il sito confronta le varie quota ed evidenzia quella più alta per ogni possibile opzione. Riportiamo i dati in una tabella per maggior chiarezza. Indichiamo le varie agenzie con le lettere dell alfabeto. A B C D E F 1 2,50 2,50 2,55 2,40 2,50 2,45 X 2,85 2,80 3,00 2,88 2,90 2,95 2 3,00 3,10 2,95 3,00 3,10 3,10 Applichiamo il metodo del simplesso. Abbiamo i 2 vincoli Occorre decidere quali probabilità assegnamo ai 3 esiti per calcolare il guadagno medio. Le ricaviamo dalle quote della prima compagnia. Abbiamo Calcoliamo in guadagno medio ( )
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
VINCERE AL BLACKJACK
 VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Sarà del tutto identico a come se giocassimo 4 schedine da 2 euro ciascuna così fatte, avremo quindi 4 combinazioni:
 SISTEMISTICA. Prefazione. Il mio consiglio è quello di giocare in base al budget di cui si dispone. Se in budget è limitato si può optare di giocare più persone insieme. Sia chiaro che bisogna sempre avere
SISTEMISTICA. Prefazione. Il mio consiglio è quello di giocare in base al budget di cui si dispone. Se in budget è limitato si può optare di giocare più persone insieme. Sia chiaro che bisogna sempre avere
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Vincere a testa o croce
 Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
TERMINI E CONDIZIONI DELLA PROMOZIONE SNAI RUNNER 2
 TERMINI E CONDIZIONI DELLA PROMOZIONE SNAI RUNNER 2 1. DESTINATARI DELLA PROMOZIONE Possono partecipare alla promozione tutti i Clienti che abbiano sottoscritto un Contratto per la partecipazione al gioco
TERMINI E CONDIZIONI DELLA PROMOZIONE SNAI RUNNER 2 1. DESTINATARI DELLA PROMOZIONE Possono partecipare alla promozione tutti i Clienti che abbiano sottoscritto un Contratto per la partecipazione al gioco
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Regole di gioco Roulette Mobile
 Regole di gioco Roulette Mobile European Classic Roulette European Premium Roulette European VIP Roulette Regole di gioco European Classic Roulette Il gioco si svolge esclusivamente nella modalità a solitario,
Regole di gioco Roulette Mobile European Classic Roulette European Premium Roulette European VIP Roulette Regole di gioco European Classic Roulette Il gioco si svolge esclusivamente nella modalità a solitario,
Scelte in condizioni di rischio e incertezza
 CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
CAPITOLO 5 Scelte in condizioni di rischio e incertezza Esercizio 5.1. Tizio ha risparmiato nel corso dell anno 500 euro; può investirli in obbligazioni che rendono, in modo certo, il 10% oppure in azioni
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
1 tabellone di gioco 4 set di carte (4 colori diversi, numerati da 1 a 20) 8 cani (2 di ogni colore) 1 blocco di fogli di scommessa Soldi Regolamento
 GREYHOUNDS (Levrieri) Componenti 1 tabellone di gioco 4 set di carte (4 colori diversi, numerati da 1 a 20) 8 cani (2 di ogni colore) 1 blocco di fogli di scommessa Soldi Regolamento L'obiettivo del gioco
GREYHOUNDS (Levrieri) Componenti 1 tabellone di gioco 4 set di carte (4 colori diversi, numerati da 1 a 20) 8 cani (2 di ogni colore) 1 blocco di fogli di scommessa Soldi Regolamento L'obiettivo del gioco
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
Determinare la grandezza della sottorete
 Determinare la grandezza della sottorete Ogni rete IP possiede due indirizzi non assegnabili direttamente agli host l indirizzo della rete a cui appartiene e l'indirizzo di broadcast. Quando si creano
Determinare la grandezza della sottorete Ogni rete IP possiede due indirizzi non assegnabili direttamente agli host l indirizzo della rete a cui appartiene e l'indirizzo di broadcast. Quando si creano
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL
 LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
LABORATORIO DI MATEMATICA RENDITE, AMMORTAMENTI, LEASING CON EXCEL ESERCITAZIONE GUIDATA: LE RENDITE 1. Il montante di una rendita immediata posticipata Utilizzando Excel, calcoliamo il montante di una
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Traduzione e adattamento a cura di Gylas per Giochi Rari
 Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
Traduzione e adattamento a cura di Gylas per Giochi Rari Versione 1.0 Luglio 2001 NOTA. La presente traduzione non sostituisce in alcun modo il regolamento originale del gioco; il presente documento è
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti. Enrico Saltari Università di Roma La Sapienza
 MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Un modello matematico di investimento ottimale
 Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Pertanto la formula per una prima approssimazione del tasso di rendimento a scadenza fornisce
 A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
A. Peretti Svolgimento dei temi d esame di MDEF A.A. 015/16 1 PROVA CONCLUSIVA DI MATEMATICA per le DECISIONI ECONOMICO-FINANZIARIE Vicenza, 9/01/016 ESERCIZIO 1. Data l obbligazione con le seguenti caratteristiche:
Un gioco con tre dadi
 Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Un gioco con tre dadi Livello scolare: biennio Abilità interessate Costruire lo spazio degli eventi in casi semplici e determinarne la cardinalità. Valutare la probabilità in diversi contesti problematici.
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Regolamento CAMPIONATO e COPPA THE BEST TWENTY 2014-2015:
 Regolamento CAMPIONATO e COPPA THE BEST TWENTY 2014-2015: 1. Il THE BEST TWENTY comprende un CAMPIONATO e una COPPA. Il campionato è un torneo composto da 20 CONCORRENTI, con la durata di 80 giornate (la
Regolamento CAMPIONATO e COPPA THE BEST TWENTY 2014-2015: 1. Il THE BEST TWENTY comprende un CAMPIONATO e una COPPA. Il campionato è un torneo composto da 20 CONCORRENTI, con la durata di 80 giornate (la
Psicometria (8 CFU) Corso di Laurea triennale STANDARDIZZAZIONE
 Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Numeri naturali numeri naturali minore maggiore Operazioni con numeri naturali
 1 Numeri naturali La successione di tutti i numeri del tipo: 0,1, 2, 3, 4,..., n,... forma l'insieme dei numeri naturali, che si indica con il simbolo N. Tale insieme si può disporre in maniera ordinata
1 Numeri naturali La successione di tutti i numeri del tipo: 0,1, 2, 3, 4,..., n,... forma l'insieme dei numeri naturali, che si indica con il simbolo N. Tale insieme si può disporre in maniera ordinata
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Aspetti probabilistici del gioco d azzardo
 Università degli Studi di Genova Scuola di Scienze Sociali Dipartimento di Economia Perché il banco vince sempre? Aspetti probabilistici del gioco d azzardo Enrico di Bella (edibella@economia.unige.it)
Università degli Studi di Genova Scuola di Scienze Sociali Dipartimento di Economia Perché il banco vince sempre? Aspetti probabilistici del gioco d azzardo Enrico di Bella (edibella@economia.unige.it)
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
I giochi delle Gioc-Arte
 I giochi delle Gioc-Arte Giochi basati sulla capacità di osservazione e di attenzione. Indovina l opera Numero di giocatori: da 2 a tutta la classe. Ognuno col suo mazzo, o una parte di esso, senza le
I giochi delle Gioc-Arte Giochi basati sulla capacità di osservazione e di attenzione. Indovina l opera Numero di giocatori: da 2 a tutta la classe. Ognuno col suo mazzo, o una parte di esso, senza le
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
Vincere a testa o croce
 Vincere a testa o croce Liceo B. Russell - Cles (TN) Classe 3D Insegnante di riferimento: Claretta Carrara Ricercatrice: Ester Dalvit Partecipanti: Alessio, Christian, Carlo, Daniele, Elena, Filippo, Ilaria,
Vincere a testa o croce Liceo B. Russell - Cles (TN) Classe 3D Insegnante di riferimento: Claretta Carrara Ricercatrice: Ester Dalvit Partecipanti: Alessio, Christian, Carlo, Daniele, Elena, Filippo, Ilaria,
ANALISI DELLE FREQUENZE: IL TEST CHI 2
 ANALISI DELLE FREQUENZE: IL TEST CHI 2 Quando si hanno scale nominali o ordinali, non è possibile calcolare il t, poiché non abbiamo medie, ma solo frequenze. In questi casi, per verificare se un evento
ANALISI DELLE FREQUENZE: IL TEST CHI 2 Quando si hanno scale nominali o ordinali, non è possibile calcolare il t, poiché non abbiamo medie, ma solo frequenze. In questi casi, per verificare se un evento
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
COPPA DEI PRONOSTICI REGOLAMENTO PER LA STAGIONE 2014/2015
 COPPA DEI PRONOSTICI REGOLAMENTO PER LA STAGIONE 2014/2015 Generalità sul gioco. Il gioco consiste nel pronosticare correttamente dei risultati legati alle partite di calcio della Champions League 2014/2015;
COPPA DEI PRONOSTICI REGOLAMENTO PER LA STAGIONE 2014/2015 Generalità sul gioco. Il gioco consiste nel pronosticare correttamente dei risultati legati alle partite di calcio della Champions League 2014/2015;
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
CAPITOLO 10 I SINDACATI
 CAPITOLO 10 I SINDACATI 10-1. Fate l ipotesi che la curva di domanda di lavoro di una impresa sia data da: 20 0,01 E, dove è il salario orario e E il livello di occupazione. Ipotizzate inoltre che la funzione
CAPITOLO 10 I SINDACATI 10-1. Fate l ipotesi che la curva di domanda di lavoro di una impresa sia data da: 20 0,01 E, dove è il salario orario e E il livello di occupazione. Ipotizzate inoltre che la funzione
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Test statistici di verifica di ipotesi
 Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
I CIRCUITI ELETTRICI. Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi.
 I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti
 da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
REGOLAMENTO ROULETTE 3D
 REGOLAMENTO ROULETTE 3D La Roulette 3D appartiene alla famiglia dei Giochi di sorte a quota fissa. Il gioco della Roulette 3D prevede una pallina che, lanciata in direzione opposta rispetto ad una ruota
REGOLAMENTO ROULETTE 3D La Roulette 3D appartiene alla famiglia dei Giochi di sorte a quota fissa. Il gioco della Roulette 3D prevede una pallina che, lanciata in direzione opposta rispetto ad una ruota
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Macroeconomia, Esercitazione 2. 1 Esercizi. 1.1 Moneta/1. 1.2 Moneta/2. 1.3 Moneta/3. A cura di Giuseppe Gori (giuseppe.gori@unibo.
 acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
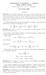 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
I SISTEMI DI NUMERAZIONE
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA I SISTEMI DI NUMERAZIONE Prof. G. Ciaschetti Fin dall antichità, l uomo ha avuto il bisogno di rappresentare le quantità in modo simbolico. Sono nati
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA I SISTEMI DI NUMERAZIONE Prof. G. Ciaschetti Fin dall antichità, l uomo ha avuto il bisogno di rappresentare le quantità in modo simbolico. Sono nati
BLACK SLOT COME SI GIOCA A BLACK SLOT:
 BLACK SLOT COME SI GIOCA A BLACK SLOT: Questo videogioco utilizza quattro display per informare il giocatore lungo tutto il corso della partita. Indicheremo questi display con le lettere A) B) C) D) per
BLACK SLOT COME SI GIOCA A BLACK SLOT: Questo videogioco utilizza quattro display per informare il giocatore lungo tutto il corso della partita. Indicheremo questi display con le lettere A) B) C) D) per
REGOLAMENTO LIVE ROULETTE
 REGOLAMENTO LIVE ROULETTE La Live Roulette appartiene alla famiglia dei Giochi di sorte a quota fissa svolto con live dealer. Il gioco della Live Roulette prevede una pallina che, lanciata in direzione
REGOLAMENTO LIVE ROULETTE La Live Roulette appartiene alla famiglia dei Giochi di sorte a quota fissa svolto con live dealer. Il gioco della Live Roulette prevede una pallina che, lanciata in direzione
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 14 marzo 2013 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2013.html IL PARI O DISPARI I II S T S (-1, 1) (1, -1)
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 14 marzo 2013 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2013.html IL PARI O DISPARI I II S T S (-1, 1) (1, -1)
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Dipartimento di Economia Aziendale e Studi Giusprivatistici. Università degli Studi di Bari Aldo Moro. Corso di Macroeconomia 2014
 Dipartimento di Economia Aziendale e Studi Giusprivatistici Università degli Studi di Bari Aldo Moro Corso di Macroeconomia 2014 1. Assumete che = 10% e = 1. Usando la definizione di inflazione attesa
Dipartimento di Economia Aziendale e Studi Giusprivatistici Università degli Studi di Bari Aldo Moro Corso di Macroeconomia 2014 1. Assumete che = 10% e = 1. Usando la definizione di inflazione attesa
15. Antico gioco russo
 15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL
 RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
INTRODUZIONE AI CICLI
 www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Totoquote totocalcio expert. ( per Windows XP, Vista, 7 )
 Totoquote totocalcio expert. ( per Windows XP, Vista, 7 ) Software portatile per calcolo quote e picchetti. Diventa autonomo nella generazione di picchetti. Licenza Shareware nominativa senza scadenza
Totoquote totocalcio expert. ( per Windows XP, Vista, 7 ) Software portatile per calcolo quote e picchetti. Diventa autonomo nella generazione di picchetti. Licenza Shareware nominativa senza scadenza
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di
 STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
Pinella Singolo ASC-CAAM 2013/14
 Pinella Singolo ASC-CAAM 2013/14 Vedi Calendario Premi del campionato ( si svolge in 4/5 tappe di qualificazione ) : > Trofei per i primi nr 4 ( quattro ) > Ai prmi due omaggio pernottamento in residence
Pinella Singolo ASC-CAAM 2013/14 Vedi Calendario Premi del campionato ( si svolge in 4/5 tappe di qualificazione ) : > Trofei per i primi nr 4 ( quattro ) > Ai prmi due omaggio pernottamento in residence
