COIN TOSSINGS. Contents. 1 Sistemi dinamici a tempo discreto 2. 2 Bernoulli shifts 4. 3 Equivalenza tra sistemi deterministici e stocastici 8
|
|
|
- Agnolo Masi
- 6 anni fa
- Visualizzazioni
Transcript
1 COIN TOSSINGS Contents 1 Sistemi dinamici a tempo discreto 2 2 Bernoulli shifts 4 3 Equivalenza tra sistemi deterministici e stocastici 8 4 Large and small deviations 9 5 From coin tossing to statistical mechanics 14
2 1 Sistemi dinamici a tempo discreto Talvolta è conveniente considerare dinamiche a tempo discreto, con φ = φ τ che rappresenta l evoluzione del sistema in un dato tempo caratteristico τ. Allora, la dinamica di uno stato iniziale X 0 è data da X 0 X 1 = φ(x 0 ) X 2 = φ(x 1 ) = φ(φ(x 0 )) φ (2) (X 0 )... Mappa di Bernoulli σ(x) = 2X ( mod 1), X [0, 1] (1) nell intervallo [0, 1], cioè con spazio delle fasi Γ = [0, 1] Si lascia come esercizio mostrare che l usuale misura dx nell intervallo [0, 1] è invariante rispetto a questa dinamica.
3
4 2 Bernoulli shifts Consideriamo la mappa (1). genera la successione Data la condizione iniziale x 0, la mappa x 0, x 1 = σ(x 0 ), x 2 = σ(x 1 ) = σ(σ(x 0 )).... Scriviamo x 0 in rappresentazione binaria: 1 x 0 = a n 2 n = 0, a 1a 2 a 3 n=0 dove a n assume i valori 0 o 1. Per x 0 < 1/2, abbiamo a 1 = 0, e x 0 > 1/2 implica a 1 = 1. Quindi { } 2x 0 per a 1 = 0 σ(x 0 ) = = 0, a 2 a 3 a 4, 2x 0 1 per a 1 = 1 vale a dire, l azione di σ sulla rappresentazione binaria di x è di cancellare la prima cifra e spostare la successione rimanente verso sinistra.
5 Dipendenza sensibile dalle condizioni iniziali: anche se due punti x ed x differiscono solo dopo la loro ennesima cifra, questa differenza diventa amplificata sotto l azione di σ(x), e le loro iterazioni σ (n) (x) e σ (n) (x ) già differiscono nella prima cifra perché σ (n) (x) = 0, a n La successione delle iterazioni σ (n) (x) ha le stesse proprietà casuali dei lanci successivi di una moneta associamo a σ (n) (x) il simbolo D o S a seconda che l iterazione è contenuto nella parte destra o sinistra del intervallo unitario. Se ora prescriviamo una successione DSDDSDSD arbitraria, per es., lanciando una moneta, possiamo sempre trovare un x 0 per il quale la serie di iterazioni x 0, σ(x 0 ), σ(σ(x 0 )).... genera questa successione. Questo segue perché σ (n) (x) = 0, a n a n+1 corrisponde a D o S se e solo se a n = 1 o a n = 0, cioè la successione DSDDSDSD è isomorfa alla rappresentazione binaria di x 0 x 0 = 0, D S D D S D S D (2)
6 Così, la prescrizione di una successione lanciando una moneta diventa equivalente alla scelta di un particolare valore di x 0. Consideriamo adesso la frequenza relativa fn D che in N iterazioni dello stato iniziale x 0 il sistema si trovi a destra, Allora f D N (x 0 ) = #(la prima cifra binaria di σ(n) (x 0 ) è uguale a 1 per n = 1, 2,..., N) N f D N (x 0 ) = 1 N N a n (x 0 ), dove a n (x 0 ) è l ennesima cifra binaria dell espansione binaria di x 0. Per determinare a che valore converge fn D quando N diventa infinitamente grande, usiamo un teorema classico di Borel sui numeri normali. Un numero è detto normale se in una qualunque base b le sue cifre hanno una n=1 distribuzione uniforme 1/b, tutte le coppie possibili di cifre hanno distribuzione 1/b 2, tutte le terne possibili hanno distribuzione 1/b 3 e così via. Il teorema di Borel stabilisce che in un intervallo quasi tutti i numeri sono normali, fatta eccezione per un insieme di numeri hanno misura
7 di Lebesgue µ nulla. Quindi f D N (x 0 ) = 1 N N n=1 a n (x 0 ) 1, quasi ovunque rispetto a µ in [0, 1]. 2 (legge forte dei grandi numeri). Da cui segue la legge debole { µ x 0 [0, 1] f N D (x 0 ) 1 } N 0 (3) 2 Un analisi più fine permette di stabilire che la convergenza è esponenzialmente rapida. Risulta così dimostrato che per grandi tempi, il sistema spende circa metà del tempo a destra (e l altra metà a sinistra). e che questo è un comportamento tipico. Il sistema è ergodico.
8 3 Equivalenza tra sistemi deterministici e stocastici La (2) permette di stabilire un equivalenza tra la dinamica deterministica di Bernoulli e la dinamica completamente stocastica del lancio di una moneta con facce D ( testa ) e S ( croce ). La probabilità di ottenere D all ennesimo lancio è in corrispondenza la misura delle successioni di numeri in [0, 1] la cui n-esima cifra binaria è pari a 1, che è chiaramente 1/2. La dinamica è lo spostamento di Bernoulli a 1 a 2 a 3 a 2 a 3 a 4... e la (3) è semplicemente la legge dei grandi numeri per i lanci una moneta: { numero di teste in N lanci P 1 } N 0 (4) N 2
9 4 Large and small deviations Binomial distribution Let S n = B B n, where each variable of the sum is bernoulli(p) distributed. Then ( ) ( ) n n IP {S n = k} = p k (1 p) n k n!, with = k k k!(n k)!. (5) This is the binomial distribution b(n, k, p). IE{S n } = np, Var (S n ) = npq, q (1 p) (6) IE{Ȳn} = p, Var ( ) pq Ȳ n = n. (7)
10 p = 1/3 Asymptotics Fair coin: p = q = 1/2. Stirling s formula: n! 2πn n n e n
11 IP {S n = k} 2πe n n n+1/2 2 n 2πe (n k) (n k) n k+1/2 2πe k k k+1/2 log IP {S n = k} 1 ( 2 log(2π) + n + 1 ) ( log n n k + 1 ) log(n k) 2 2 ( ) If k ny, then Thus k + 1 log k n log 2 2 = 1 2 log(2π) 1 ( 2 log n n k + 1 ) ( log 1 k ) 2 n ( ) k log k n n log 2 log IP {S n = k} n [log 2 + y log y + (1 y) log(1 y)] + o(n) log IP {S n = k} ni(y) + o(n) with I(y) = log 2 + y log y + (1 y) log(1 y)
12 the rate function of bernoulli (1/2) Asymptotic decay-rate of tail Point at which tail starts Figure 5: Measured decay-rates with the rate-function superimposed. for each positive number ɛ. Howdowesetaboutprovingthis?First,letus write out P( M n 1/2 > ɛ )indetailandseeifwecanapproximateitor get a bound on it: P( M n 1/2 > ɛ )=P(M n < 1/2 ɛ )+P(M n > 1/2+ɛ ). Now we have found that, for coin tossing, the tails of the distribution of M n decay exponentially fast: P( M n >x) e ni(x) for x>1/2,
13 Exercise Consider bernoulli (p) Show that: M(k) = (q + pe k ) C(k) = log(q + pe k ) I(y) = y log y p + (1 y) log 1 y 1 p for y (0, 1) I(y) = outside of (0, 1). Small deviations Fair coin: p = q = 1/2. Taylor series: I(y) = log 2 + y log y + (1 y) log(1 y) = ( ) y The mean of each toss of a coin is 1/2, and the variance of each toss is 1/4; thus the rate function for coin tossing gives us the Central Limit Theorem. In general, whenever the rate function can be approximated near its maximum by a quadratic form, we can expect the Central Limit Theorem to hold.
14 5 From coin tossing to statistical mechanics Phase space In contains 2 n points. Event: Γ = {x = (x 1,..., x n ) x i = 0 or 1} A Γ = set of points x Random variables: functions Y, Z,... on Γ. We reserve the notation X for the random vector X(x) = x. So, any random variable Y can written as Uniform measure Uniform probability measure Y = F (X) A = number of points in A IP {A} = A Γ = A 2 n
15 Basic problem: find the probabilities IP {Z = z Y = y} = {Z = y} {Y = y} {Y = y} IP {A {S n = k}} = A {S n = k} {S n = k}
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
! X (92) X n. P ( X n X ) =0 (94)
 Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Limiti della Distribuzione Binomiale
 Limiti della Distribuzione Binomiale Giuseppe Sanfilippo 11 maggio 2012 1 Teorema di Bernoulli Sia X 1, X 2,..., X n... una successione di variabili aleatorie bernoulliane stocasticamente indipendenti
Limiti della Distribuzione Binomiale Giuseppe Sanfilippo 11 maggio 2012 1 Teorema di Bernoulli Sia X 1, X 2,..., X n... una successione di variabili aleatorie bernoulliane stocasticamente indipendenti
College Algebra. Logarithms: Denitions and Domains. Dr. Nguyen November 9, Department of Mathematics UK
 College Algebra Logarithms: Denitions and Domains Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK November 9, 2018 Agenda Logarithms and exponents Domains of logarithm functions Operations
College Algebra Logarithms: Denitions and Domains Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK November 9, 2018 Agenda Logarithms and exponents Domains of logarithm functions Operations
ESERCIZI EPOS. { C x 3 (1 x) 0 x 1 0 altrove
 ESERCIZI EPOS 1. Sia X una v.c. con densità f X (x) = { C x 3 (1 x) 0 x 1 0 altrove (a) Determinare il valore della costante C (b) Calcolare la funzione di ripartizione F X (x) (c) Calcolare P (X > 1/2)
ESERCIZI EPOS 1. Sia X una v.c. con densità f X (x) = { C x 3 (1 x) 0 x 1 0 altrove (a) Determinare il valore della costante C (b) Calcolare la funzione di ripartizione F X (x) (c) Calcolare P (X > 1/2)
Neyman Construction. θ s true. pdf f (x θ) is known for each prospectiveθ generate x construct an int erval in DATA phase space.
 Neyman Construction θ s true x s measured pdf f (x θ) is known for each prospectiveθ generate x construct an int erval in DATA phase space Interval = x h xl repeat for each θ f (x θ)dx = 68% 158!60 Figure
Neyman Construction θ s true x s measured pdf f (x θ) is known for each prospectiveθ generate x construct an int erval in DATA phase space Interval = x h xl repeat for each θ f (x θ)dx = 68% 158!60 Figure
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2006/07
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
Distribuzione Binomiale
 Statistica e analisi dei dati Data: 2 Maggio 2016 Distribuzione Binomiale Docente: Prof. Giuseppe Boccignone Scriba: Nicoló Pisaroni 1 Conteggi e tempi di attesa Consideriamo il seguente schema, facendo
Statistica e analisi dei dati Data: 2 Maggio 2016 Distribuzione Binomiale Docente: Prof. Giuseppe Boccignone Scriba: Nicoló Pisaroni 1 Conteggi e tempi di attesa Consideriamo il seguente schema, facendo
Finite Model Theory / Descriptive Complexity: bin
 , CMPSCI 601: Recall From Last Time Lecture 19 Finite Model Theory / Descriptive Compleity: Th: FO L DSPACE Fagin s Th: NP SO. bin is quantifier-free.!#"$&% ('*), 1 Space 0 1 ) % Time $ "$ $ $ "$ $.....
, CMPSCI 601: Recall From Last Time Lecture 19 Finite Model Theory / Descriptive Compleity: Th: FO L DSPACE Fagin s Th: NP SO. bin is quantifier-free.!#"$&% ('*), 1 Space 0 1 ) % Time $ "$ $ $ "$ $.....
X (o equivalentemente rispetto a X n ) è la
 Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Variabili aleatorie. Richiami e uso del Matlab T T T. ω 2. ω 1. ω 3. ω 4. ω 5. ω 6. ω 7. ω 8
 ω Variabili aleatorie Richiami e uso del Matlab X ( ω) x R S In molte situazioni, si vuole assegnare un valore numerico ad ogni possibile risultato di un esperimento. Tale assegnamento viene chiamato variabile
ω Variabili aleatorie Richiami e uso del Matlab X ( ω) x R S In molte situazioni, si vuole assegnare un valore numerico ad ogni possibile risultato di un esperimento. Tale assegnamento viene chiamato variabile
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 14
 Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
Constant Propagation. A More Complex Semilattice A Nondistributive Framework
 Constant Propagation A More Complex Semilattice A Nondistributive Framework 1 The Point Instead of doing constant folding by RD s, we can maintain information about what constant, if any, a variable has
Constant Propagation A More Complex Semilattice A Nondistributive Framework 1 The Point Instead of doing constant folding by RD s, we can maintain information about what constant, if any, a variable has
Calcolo delle Probabilità 2017/18 Foglio di esercizi 8
 Calcolo delle Probabilità 07/8 Foglio di esercizi 8 Catene di Markov e convergenze Si consiglia di svolgere gli esercizi n 9,,,, 5 Catene di Markov Esercizio (Baldi, Esempio 5) Si consideri il grafo costituito
Calcolo delle Probabilità 07/8 Foglio di esercizi 8 Catene di Markov e convergenze Si consiglia di svolgere gli esercizi n 9,,,, 5 Catene di Markov Esercizio (Baldi, Esempio 5) Si consideri il grafo costituito
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x)
![1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x) 1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x)](/thumbs/97/134407840.jpg) Esercizi di Calcolo delle Probabilità della 3 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio.. Sia (X, Y ) un vettore aleatorio bidimensionale con densità uniforme
Esercizi di Calcolo delle Probabilità della 3 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio.. Sia (X, Y ) un vettore aleatorio bidimensionale con densità uniforme
Il Corso di Fisica per Scienze Biologiche
 Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 75-585 278 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 75-585 278 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
Discrete Parabolic Anderson Model with Heavy Tailed Potential
 Discrete Parabolic Anderson Model with Heavy Tailed Potential F. Caravenna 1, P. Carmona 2 and N. Pétrélis 2 1 Università degli Studi di Milano-Bicocca 2 Laboratoire Jean Leray, Université de Nantes 1March2011
Discrete Parabolic Anderson Model with Heavy Tailed Potential F. Caravenna 1, P. Carmona 2 and N. Pétrélis 2 1 Università degli Studi di Milano-Bicocca 2 Laboratoire Jean Leray, Université de Nantes 1March2011
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 4: Variabili aleatorie continue
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 4: Variabili aleatorie continue Definizione di variabile aleatorie continua Se il risultato di un esperimento
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 4: Variabili aleatorie continue Definizione di variabile aleatorie continua Se il risultato di un esperimento
P(X > 0) = P(X 1 = 1) + P(X 1 = 1, X 2 = 1, X 3 = 1) =
 1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
1 Esercizi settimana 3 Esercizio 1. Un urna contiene 8 palline bianche, 4 nere e rosse. Si assuma di vincere e ogni volta che si estragga una pallina nera, si perda 1e per ogni pallina bianca e non succeda
Esercizi di riepilogo Lezioni
 Esercizi di riepilogo Lezioni 9-10-11 Es1: Aspettazioni iterate Siano X, Y, e Z v.a. discrete. Dimostrare le seguenti generalizzazioni della legge delle aspettazioni iterate a) b) c) Es2: Bacchetta Abbiamo
Esercizi di riepilogo Lezioni 9-10-11 Es1: Aspettazioni iterate Siano X, Y, e Z v.a. discrete. Dimostrare le seguenti generalizzazioni della legge delle aspettazioni iterate a) b) c) Es2: Bacchetta Abbiamo
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini e Leonardo Bertini. Lezione 4:
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini e Leonardo Bertini Lezione 4: Variabili aleatorie continue Definizione di variabile aleatorie continua Se il
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini e Leonardo Bertini Lezione 4: Variabili aleatorie continue Definizione di variabile aleatorie continua Se il
Serie di numeri di diverse origini. Marcata asimmetria in favore dei digits bassi nella prima cifra. Legge di Benford. Processi moltiplicativi
 Serie di numeri di diverse origini Marcata asimmetria in favore dei digits bassi nella prima cifra Legge di Benford Processi moltiplicativi Primi 3 digits dei titoli di borsa: 60%,2 e 3 40% da 4 a 9 s
Serie di numeri di diverse origini Marcata asimmetria in favore dei digits bassi nella prima cifra Legge di Benford Processi moltiplicativi Primi 3 digits dei titoli di borsa: 60%,2 e 3 40% da 4 a 9 s
I Appello di Processi Stocastici Cognome: Laurea Magistrale in Matematica 2014/15 Nome: 23 Giugno
 I Appello di Processi Stocastici Cognome: Laurea Magistrale in Matematica 014/15 Nome: 3 Giugno 015 Email: Quando non è espressamente indicato il contrario, per la soluzione degli esercizi è possibile
I Appello di Processi Stocastici Cognome: Laurea Magistrale in Matematica 014/15 Nome: 3 Giugno 015 Email: Quando non è espressamente indicato il contrario, per la soluzione degli esercizi è possibile
CP410: Esonero 1, 7 novembre, 2018
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2018-19, I semestre 7 novembre, 2018 CP410: Esonero 1, 7 novembre, 2018 Cognome Nome Matricola Firma 1. Sia X una variabile aleatoria su uno spazio di
Dipartimento di Matematica, Roma Tre Pietro Caputo 2018-19, I semestre 7 novembre, 2018 CP410: Esonero 1, 7 novembre, 2018 Cognome Nome Matricola Firma 1. Sia X una variabile aleatoria su uno spazio di
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale a.a. 2016/17
 Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci
 Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha. P {X = a, Y = b} = P {X = a}p {Y = b}
 Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19
 DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
ESERCIZI DI ANALISI FUNZIONALE. T(f) = g(x)f(x)dx
 ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
Variabile casuale E 6 E 5 E 4. R S x1 E 2
 Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE. 1. La variabile aleatoria di Bernoulli e la variabile aleatoria binomiale
 PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE In questa scheda vedremo due famiglie di variabili aleatorie (una discreta e una continua), che ci serviranno per descrivere uno dei risultati
PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE In questa scheda vedremo due famiglie di variabili aleatorie (una discreta e una continua), che ci serviranno per descrivere uno dei risultati
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini e Leonardo Bertini. Lezione 1: Probabilità: fondamenti
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini e Leonardo Bertini Lezione 1: Probabilità: fondamenti Progettazione probabilistica: Considerazione delle incertezze
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini e Leonardo Bertini Lezione 1: Probabilità: fondamenti Progettazione probabilistica: Considerazione delle incertezze
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 3: Variabili aleatorie discrete notevoli
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 3: Variabili aleatorie discrete notevoli Esperimenti binari ripetuti o esperimenti bernoulliani (Bernoulli
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 3: Variabili aleatorie discrete notevoli Esperimenti binari ripetuti o esperimenti bernoulliani (Bernoulli
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ o modulo - PROVA d esame del 9/02/200 - Laurea Quadriennale in Matematica - Prof. Nappo Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ o modulo - PROVA d esame del 9/02/200 - Laurea Quadriennale in Matematica - Prof. Nappo Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate
Problema Posto s = n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000
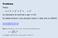 Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
Foglio di Esercizi 10 con Risoluzione 18 dicembre 2017
 Matematica per Farmacia, a.a. 07/8 Foglio di Esercizi 0 con Risoluzione 8 dicembre 07 ATTENZIONE: in alcuni degli esercizi di Probabilità puó essere utile usare il Teorema di Bayes. Esercizio (Vedere il
Matematica per Farmacia, a.a. 07/8 Foglio di Esercizi 0 con Risoluzione 8 dicembre 07 ATTENZIONE: in alcuni degli esercizi di Probabilità puó essere utile usare il Teorema di Bayes. Esercizio (Vedere il
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE CATENE DI MARKOV TEMPO CONTINUE Definizioni Sia dato un processo stocastico x(t) che può assumere valori discreti appartenenti ad un insieme se accade che il processo è una catena
RETI DI TELECOMUNICAZIONE CATENE DI MARKOV TEMPO CONTINUE Definizioni Sia dato un processo stocastico x(t) che può assumere valori discreti appartenenti ad un insieme se accade che il processo è una catena
Stima della qualità dei classificatori per l analisi dei dati biomolecolari
 Stima della qualità dei classificatori per l analisi dei dati biomolecolari Giorgio Valentini e-mail: valentini@dsi.unimi.it Rischio atteso e rischio empirico L` apprendimento di una funzione non nota
Stima della qualità dei classificatori per l analisi dei dati biomolecolari Giorgio Valentini e-mail: valentini@dsi.unimi.it Rischio atteso e rischio empirico L` apprendimento di una funzione non nota
Variabili aleatorie: parte 1. 1 Definizione di variabile aleatoria e misurabilitá
 Statistica e analisi dei dati Data: 11 Aprile 2016 Variabili aleatorie: parte 1 Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori 1 Definizione di variabile aleatoria e misurabilitá Informalmente,
Statistica e analisi dei dati Data: 11 Aprile 2016 Variabili aleatorie: parte 1 Docente: Prof. Giuseppe Boccignone Scriba: Noemi Tentori 1 Definizione di variabile aleatoria e misurabilitá Informalmente,
Author: Raffaele Cogoni born in Assemini on 21/02/1954
 Author: Raffaele Cogoni born in Assemini on 21/02/1954 raff54cog@libero.it Title: Simplification of the Sieve of Eratosthenes Abstract It is a procedure to find the prime numbers, in practice it is a simplification
Author: Raffaele Cogoni born in Assemini on 21/02/1954 raff54cog@libero.it Title: Simplification of the Sieve of Eratosthenes Abstract It is a procedure to find the prime numbers, in practice it is a simplification
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 2 maggio 2017
 SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 2 maggio 217 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 2 maggio 217 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
Definizione formale di probabilitá
 Definizione formale di probabilitá 10 marzo 2017 Si introducono la definizione assiomatica di probabilitá e alcune proprietá elementari che ne derivano 1 Eventi e insiemi Poiché un evento é definito come
Definizione formale di probabilitá 10 marzo 2017 Si introducono la definizione assiomatica di probabilitá e alcune proprietá elementari che ne derivano 1 Eventi e insiemi Poiché un evento é definito come
Variabili aleatorie parte 2. 1 Definizione di funzione di ripartizione o funzione cumulativa (CDF)
 Statistica e analisi dei dati Data: 11 aprile 2016 Variabili aleatorie parte 2 Docente: Prof. Giuseppe Boccignone Scriba: Alessandra Birlini 1 Definizione di funzione di ripartizione o funzione cumulativa
Statistica e analisi dei dati Data: 11 aprile 2016 Variabili aleatorie parte 2 Docente: Prof. Giuseppe Boccignone Scriba: Alessandra Birlini 1 Definizione di funzione di ripartizione o funzione cumulativa
Corsi di Laurea in Ingegneria Civile e Edile Analisi Matematica II e Probabilita Lezioni A.A. 2000/01, prof. G. Stefani 9 Ottobre Gennaio 2001
 Corsi di Laurea in Ingegneria Civile e Edile Analisi Matematica II e Probabilita Lezioni A.A. 2000/01, prof. G. Stefani 9 Ottobre 2000-28 Gennaio 2001 1 Nona settimana 76. Lun. 4 Dic. Generalita. Spazi
Corsi di Laurea in Ingegneria Civile e Edile Analisi Matematica II e Probabilita Lezioni A.A. 2000/01, prof. G. Stefani 9 Ottobre 2000-28 Gennaio 2001 1 Nona settimana 76. Lun. 4 Dic. Generalita. Spazi
Probabilità: teoremi e distribuzioni
 Probabilità: teoremi e distribuzioni OBIETTIVO DIDATTICO DELLA LEZIONE Illustrare le più importanti distribuzioni di probabilità che vengono utilizzate in statistica Distribuzioni di probabilità 1. La
Probabilità: teoremi e distribuzioni OBIETTIVO DIDATTICO DELLA LEZIONE Illustrare le più importanti distribuzioni di probabilità che vengono utilizzate in statistica Distribuzioni di probabilità 1. La
AA Decima lezione, seconda del secondo modulo
 AA 2010-11 http://people.na.infn.it/palladin/lezioni2010-11/100314lezione10.pdf Decima lezione, seconda del secondo modulo Comiciamo ad applicare alle misure La piu semplice misura il conteggio n-k x x
AA 2010-11 http://people.na.infn.it/palladin/lezioni2010-11/100314lezione10.pdf Decima lezione, seconda del secondo modulo Comiciamo ad applicare alle misure La piu semplice misura il conteggio n-k x x
Distribuzione di Probabilità
 Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Lezione 11 Ugo Vaccaro
 Teoria dell Informazione II Anno Accademico 207 208 Lezione Ugo Vaccaro Abbiamo visto finora che in vari problemi collegati alla codifica di emissioni di una sorgente di informazione la entropia H(P )
Teoria dell Informazione II Anno Accademico 207 208 Lezione Ugo Vaccaro Abbiamo visto finora che in vari problemi collegati alla codifica di emissioni di una sorgente di informazione la entropia H(P )
PNI 2005 QUESITO 1
 www.matefilia.it PNI 2005 QUESITO 1 Consideriamo il lato AB del decagono regolare inscritto nella circonferenza e indichiamo con AC la bisettrice dell angolo alla base A. Essendo l angolo in O di 36 (360
www.matefilia.it PNI 2005 QUESITO 1 Consideriamo il lato AB del decagono regolare inscritto nella circonferenza e indichiamo con AC la bisettrice dell angolo alla base A. Essendo l angolo in O di 36 (360
Il sistema dei tipi in ML. cenni
 Il sistema dei tipi in ML cenni Inferenza tipi ML - val f = fn x => x+1; val f = fn : int -> int - f 2; val it = 3 : int - - fun f(x) = x+1; val f = fn : int -> int - f 2; val it = 3 : int - - val g =
Il sistema dei tipi in ML cenni Inferenza tipi ML - val f = fn x => x+1; val f = fn : int -> int - f 2; val it = 3 : int - - fun f(x) = x+1; val f = fn : int -> int - f 2; val it = 3 : int - - val g =
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Vedi: Probabilità e cenni di statistica
 Vedi: http://www.df.unipi.it/~andreozz/labcia.html Probabilità e cenni di statistica Funzione di distribuzione discreta Istogrammi e normalizzazione Distribuzioni continue Nel caso continuo la probabilità
Vedi: http://www.df.unipi.it/~andreozz/labcia.html Probabilità e cenni di statistica Funzione di distribuzione discreta Istogrammi e normalizzazione Distribuzioni continue Nel caso continuo la probabilità
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
3.1 La probabilità: eventi e variabili casuali
 Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
A.S. 2011/2012. Circuito semaforico da incrocio. Corso di Elettronica. Dipartimento di Elettrotecnica
 A.S. 2011/2012 Circuito semaforico da incrocio Corso di Elettronica Dipartimento di Elettrotecnica Alunno: Bari Aldo 3E 1 Relazione Elettronica Realizzazione di un impianto semaforico da incrocio 2 Relazione
A.S. 2011/2012 Circuito semaforico da incrocio Corso di Elettronica Dipartimento di Elettrotecnica Alunno: Bari Aldo 3E 1 Relazione Elettronica Realizzazione di un impianto semaforico da incrocio 2 Relazione
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Esercizi - Fascicolo IV
 Esercizi - Fascicolo IV Esercizio Una compagnia di assicurazioni emette una polizza che pagherà n euro se l evento E si verificherà entro un anno. Se la compagnia stima che l evento E si verificherà entro
Esercizi - Fascicolo IV Esercizio Una compagnia di assicurazioni emette una polizza che pagherà n euro se l evento E si verificherà entro un anno. Se la compagnia stima che l evento E si verificherà entro
1! 4! = 5. Quindi la probabilità di ottenere 1 successo su 5 lanci sarà 5 2 = 5! 2! 3! = 10
 Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
Variabili aleatorie discrete. Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia
 Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
A.A. 2006/2007 Laurea di Ingegneria Informatica. Fondamenti di C++ Horstmann Capitolo 3: Oggetti Revisione Prof. M. Angelaccio
 A.A. 2006/2007 Laurea di Ingegneria Informatica Fondamenti di C++ Horstmann Capitolo 3: Oggetti Revisione Prof. M. Angelaccio Obbiettivi Acquisire familiarità con la nozione di oggetto Apprendere le proprietà
A.A. 2006/2007 Laurea di Ingegneria Informatica Fondamenti di C++ Horstmann Capitolo 3: Oggetti Revisione Prof. M. Angelaccio Obbiettivi Acquisire familiarità con la nozione di oggetto Apprendere le proprietà
()Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Energia immessa da un white noise Ricordiamo la motivazione applicativa della volta scorsa: un white noise additivo, messo in un equazione che nel caso deterministico
Probablità, Statistica e Processi Stocastici Energia immessa da un white noise Ricordiamo la motivazione applicativa della volta scorsa: un white noise additivo, messo in un equazione che nel caso deterministico
CALCOLO DELLE PROBABILITÀ 2 (Laurea Specialistica) 28 giugno Motivare dettagliatamente le risposte su fogli allegati
 CALCOLO DELLE PROBABILITÀ 2 (Laurea Specialistica) 28 giugno 2006 Motivare dettagliatamente le risposte su fogli allegati 1.- Sia X un numero aleatorio a valori { α, 0, α}, con α > 0 e P (X = α) = P (X
CALCOLO DELLE PROBABILITÀ 2 (Laurea Specialistica) 28 giugno 2006 Motivare dettagliatamente le risposte su fogli allegati 1.- Sia X un numero aleatorio a valori { α, 0, α}, con α > 0 e P (X = α) = P (X
Esercitazione 5 del corso di Statistica 2 Prof. Domenico Vistocco
 Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Secoli di probabilità. Marta Lucchini, IIS Bertrand Russell, Milano
 Secoli di probabilità Marta Lucchini, IIS Bertrand Russell, Milano Venezia, 15 Aprile 2018 Il 1600, Pascal e gli altri Cardano, Liber de ludo aleae (1663, postumo) Galilei, Sopra le scoperte dei dadi (1630)
Secoli di probabilità Marta Lucchini, IIS Bertrand Russell, Milano Venezia, 15 Aprile 2018 Il 1600, Pascal e gli altri Cardano, Liber de ludo aleae (1663, postumo) Galilei, Sopra le scoperte dei dadi (1630)
Soluzione Esercizio 1 (pag 1):
 8 - Test di Ipotesi Esercizio 1: Dopo anni di esperienza e noto che la distribuzione della concentrazione di rame nel sangue umano e ben descritta da una distribuzione gaussiana di parametri μ=3.2 10-5
8 - Test di Ipotesi Esercizio 1: Dopo anni di esperienza e noto che la distribuzione della concentrazione di rame nel sangue umano e ben descritta da una distribuzione gaussiana di parametri μ=3.2 10-5
AA Prof. V. Palladino. Undicesima lezione, seconda del secondo modulo
 AA 2016-17 Prof. V. Palladino http://people.na.infn.it/palladin/lezioni2016-17/161205lezione11.pdf Undicesima lezione, seconda del secondo modulo Possiamo predire le distribuzioni di probabilita' delle
AA 2016-17 Prof. V. Palladino http://people.na.infn.it/palladin/lezioni2016-17/161205lezione11.pdf Undicesima lezione, seconda del secondo modulo Possiamo predire le distribuzioni di probabilita' delle
La distribuzione binomiale o di Bernoulli
 La distribuzione binomiale o di Bernoulli La distribuzione di probabilità binomiale, de/a così perché richiama la potenza n-esima di un binomio, riguarda lo schema successo-insuccesso Ha diverse applicazioni
La distribuzione binomiale o di Bernoulli La distribuzione di probabilità binomiale, de/a così perché richiama la potenza n-esima di un binomio, riguarda lo schema successo-insuccesso Ha diverse applicazioni
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
CP410: Esame 2, 30 gennaio Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 23-4, I semestre 3 gennaio, 24 CP4: Esame 2, 3 gennaio 24 Testo e soluzione Cognome Nome Matricola Firma . Per ogni n N, sia X n la variabile aleatoria
Dipartimento di Matematica, Roma Tre Pietro Caputo 23-4, I semestre 3 gennaio, 24 CP4: Esame 2, 3 gennaio 24 Testo e soluzione Cognome Nome Matricola Firma . Per ogni n N, sia X n la variabile aleatoria
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Exam of ELECTRONIC SYSTEMS June 15 th, 2012 Prof. Marco Sampietro
 Exam of ELECTRONIC SYSTEMS June 15 th, 2012 Prof. Marco Sampietro Matr. N NAME Problem 1 Operational Amplifier circuit 1. Considerare l amplificatore della figura seguente. Supporre inizialmente di usare
Exam of ELECTRONIC SYSTEMS June 15 th, 2012 Prof. Marco Sampietro Matr. N NAME Problem 1 Operational Amplifier circuit 1. Considerare l amplificatore della figura seguente. Supporre inizialmente di usare
ANNO ACCADEMICO 2016/2017 CORSO di LAUREA in BIOTECNOLOGIE MATEMATICA IV appello 12/1/2017 1
 ANNO ACCADEMICO 016/017 CORSO di LAUREA in BIOTECNOLOGIE MATEMATICA IV appello 1/1/017 1 Esercizio 1. Una scatola contiene 10 monete; 8 di queste sono equilibrate, mentre le altre danno testa con probabilità
ANNO ACCADEMICO 016/017 CORSO di LAUREA in BIOTECNOLOGIE MATEMATICA IV appello 1/1/017 1 Esercizio 1. Una scatola contiene 10 monete; 8 di queste sono equilibrate, mentre le altre danno testa con probabilità
Fiori di campo. Conoscere, riconoscere e osservare tutte le specie di fiori selvatici più note
 Fiori di campo. Conoscere, riconoscere e osservare tutte le specie di fiori selvatici più note M. Teresa Della Beffa Click here if your download doesn"t start automatically Fiori di campo. Conoscere, riconoscere
Fiori di campo. Conoscere, riconoscere e osservare tutte le specie di fiori selvatici più note M. Teresa Della Beffa Click here if your download doesn"t start automatically Fiori di campo. Conoscere, riconoscere
Analisi Reale. Anno Accademico Roberto Monti. Versione del 13 Ottobre 2014
 Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
CP410: Esonero 1, 31 ottobre 2013
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2013-14, I semestre 31 ottobre, 2013 CP410: Esonero 1, 31 ottobre 2013 Cognome Nome Matricola Firma 1. Fare un esempio di successione di variabili aleatorie
Dipartimento di Matematica, Roma Tre Pietro Caputo 2013-14, I semestre 31 ottobre, 2013 CP410: Esonero 1, 31 ottobre 2013 Cognome Nome Matricola Firma 1. Fare un esempio di successione di variabili aleatorie
Le coniche furono studiate già 2000 anni fa dagli antichi Greci in particolare da Apollonio (III secolo a.c) che ne scoprì numerose proprietà.
 Coniche 1 3 Ci sono alcune curve, dette coniche, che fanno la loro comparsa in moltissimi ambiti, apparentemente diversi fra loro; per esempio: le traiettorie dei pianeti sono coniche; le superficie delle
Coniche 1 3 Ci sono alcune curve, dette coniche, che fanno la loro comparsa in moltissimi ambiti, apparentemente diversi fra loro; per esempio: le traiettorie dei pianeti sono coniche; le superficie delle
Compiti tematici capp. 5,6
 Compiti tematici capp. 5,6 a cura di Giovanni M. Marchetti 2016 ver. 0.6 Indice Esercizi dai compiti a casa (HW..................................... 8 1. Se X e Y sono due variabili casuali independenti,
Compiti tematici capp. 5,6 a cura di Giovanni M. Marchetti 2016 ver. 0.6 Indice Esercizi dai compiti a casa (HW..................................... 8 1. Se X e Y sono due variabili casuali independenti,
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Algoritmi Priority-Driven RT. Corso di Sistemi RT Prof. Davide Brugali Università degli Studi di Bergamo
 Algoritmi Priority-Driven RT Corso di Sistemi RT Prof. Davide Brugali Università degli Studi di Bergamo 2 Algoritmi Real Time Earliest Due Date (statico) Seleziona il task con la deadline relativa più
Algoritmi Priority-Driven RT Corso di Sistemi RT Prof. Davide Brugali Università degli Studi di Bergamo 2 Algoritmi Real Time Earliest Due Date (statico) Seleziona il task con la deadline relativa più
6.6 ARIMA Model. Autoregressive Integrated Moving Average (ARIMA ) Model. ARIMA(p, d, q) Process
 128 6.6 ARIMA Model Autoregressive Integrated Moving Average (ARIMA ) Model ARIMA(p, d, q) Process φ(l) d y t = θ(l)ɛ t, where d y t = d 1 (1 L)y t = d 1 y t d 1 y t 1 = (1 L) d y t for d = 1, 2,, and
128 6.6 ARIMA Model Autoregressive Integrated Moving Average (ARIMA ) Model ARIMA(p, d, q) Process φ(l) d y t = θ(l)ɛ t, where d y t = d 1 (1 L)y t = d 1 y t d 1 y t 1 = (1 L) d y t for d = 1, 2,, and
Comunicazioni Elettriche anno accademico Esercitazione 1
 Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
I CAMBIAMENTI PROTOTESTO-METATESTO, UN MODELLO CON ESEMPI BASATI SULLA TRADUZIONE DELLA BIBBIA (ITALIAN EDITION) BY BRUNO OSIMO
 I CAMBIAMENTI PROTOTESTO-METATESTO, UN MODELLO CON ESEMPI BASATI SULLA TRADUZIONE DELLA BIBBIA (ITALIAN EDITION) BY BRUNO OSIMO READ ONLINE AND DOWNLOAD EBOOK : I CAMBIAMENTI PROTOTESTO-METATESTO, UN MODELLO
I CAMBIAMENTI PROTOTESTO-METATESTO, UN MODELLO CON ESEMPI BASATI SULLA TRADUZIONE DELLA BIBBIA (ITALIAN EDITION) BY BRUNO OSIMO READ ONLINE AND DOWNLOAD EBOOK : I CAMBIAMENTI PROTOTESTO-METATESTO, UN MODELLO
CAPITOLO QUINTO DISTRIBUZIONE NORMALE
 CAPITOLO QUINTO DISTRIBUZIONE NORMALE 1. Probabilità nel continuo Fino ad ora abbiamo considerato casi in cui l insieme degli eventi elementari è finito. Vediamo, mediante due semplici esempi, come si
CAPITOLO QUINTO DISTRIBUZIONE NORMALE 1. Probabilità nel continuo Fino ad ora abbiamo considerato casi in cui l insieme degli eventi elementari è finito. Vediamo, mediante due semplici esempi, come si
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di 2 - EQUAZIONI NON LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Elementi introduttivi 2 3 4 Introduzione Problema: trovare le soluzioni di
Corso di Laurea in Ingegneria Informatica Corso di 2 - EQUAZIONI NON LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Elementi introduttivi 2 3 4 Introduzione Problema: trovare le soluzioni di
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Diario Complementi di Probabilità a.a. 2017/2018
 Diario Complementi di Probabilità a.a. 2017/2018 Testi di riferimento: [W] Probability with martingales, D.Williams [Bi] Probability and measure, P.Billingsley [Ba] Appunti del corso di Calcolo delle Probabilità
Diario Complementi di Probabilità a.a. 2017/2018 Testi di riferimento: [W] Probability with martingales, D.Williams [Bi] Probability and measure, P.Billingsley [Ba] Appunti del corso di Calcolo delle Probabilità
Vi prego di segnalare ogni inesattezza o errore tipografico a Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi
 ESERCIZI DI GEOMETRIA 3 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi Esercizio 1. Sia (X, d) uno spazio
ESERCIZI DI GEOMETRIA 3 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Spazi metrici, spazi topologici, applicazioni continue ed omeomorfismi Esercizio 1. Sia (X, d) uno spazio
Laboratorio di Calcolo B 68
 Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 2010-11 P.Baldi Lista di esercizi 3. Corso di Laurea in Biotecnologie Esercizio 1 Una v.a. X segue una legge N(2, ). Calcolare a1) P(X 1) a2) P(2
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 2010-11 P.Baldi Lista di esercizi 3. Corso di Laurea in Biotecnologie Esercizio 1 Una v.a. X segue una legge N(2, ). Calcolare a1) P(X 1) a2) P(2
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La variabile casuale normale Da un analisi di bilancio è emerso che, durante i giorni feriali
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La variabile casuale normale Da un analisi di bilancio è emerso che, durante i giorni feriali
Metodi Matematici Probabilità e Statistica. Correzione Compitino del
 Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
Metodi Matematici Probabilità e Statistica Correzione Compitino del.4.04 nota: Una sola risposta è esatta. 4 punti per una risposta esatta, -2 per una sbagliata, 0 per una non data. Gli esercizi sono divisi
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
