Laboratorio di Giochi Matematici
|
|
|
- Caterina Caselli
- 8 anni fa
- Visualizzazioni
Transcript
1 Unità operativa di Milano Città Studi Laboratorio di Giochi Matematici (responsabile Prof. Stefania De Stefano) Incontri presso il Dipartimento di Matematica "F. Enriques" 3. Soluzioni proposte dei giochi Versione estesa (*) (*) Agli studenti sono state consegnate solo le soluzioni dei giochi effettivamente svolti durante i quattro incontri
2 Soluzioni dei Giochi dell incontro N o 1 Preliminari 1. Il gioco delle tre carte Il gioco delle tre carte consiste nell indovinare quale sia, fra tre carte coperte, una carta prefissata. Una volta che lo scommettitore ha puntato su una delle tre carte, il banditore (che conosce quale sia la carta da indovinare) scopre, fra le due rimaste, quella, o una di quelle, che non è la carta prefissata, consentendo poi allo scommettitore di modificare la sua scelta, qualora lo desideri. Qual è la strategia più vantaggiosa per lo scommettitore? Soluzione: Modificare la scelta; si passa dalla probabilità 1/3 di vincere alla probabilità 2/3. Per convincersene, si supponga che le carte, invece di tre, siano 1000 e che il banditore ne scopra 998 Se si decide di non modificare la scelta, non viene tenuta in alcun conto l informazione ricevuta, quindi la probabilità rimane quella iniziale. 2. Achille e la Tartaruga: riproposizione di un quesito (N o 1) già affrontato nel quarto incontro in classe, ma poco compreso. 3. Il sacchetto di monete truccate: riproposizione di un quesito (N o 7) già affrontato da alcuni gruppi nel quarto incontro in classe. Parte A 1. Ho dimenticato il numero di cellulare di un amico. Ricordo che è un numero di 7 cifre, che nessuna è 0 e che ogni cifra (tranne l ultima a destra) è maggiore quella che si trova alla sua destra. Quanti tentativi saranno necessari al massimo per parlare con il mio amico? Soluzione: 36. Si tratta di prendere, tra le disposizioni semplici di 9 cifre a 7 a 7, solo quelle in cui le cifre sono in ordine decrescente; tale numero coincide con quello delle combinazioni di 9 cifre a 7 a 7 (prefissare un ordine equivale a dire che non teniamo conto dell ordine per distinguere due disposizioni). Come visto nel gioco dei gelati, ciò significa considerare (3 4 9)/(1 2 7) = 8 9/2 = 4 9 sequenze decrescenti di cifre. In modo più elementare: Visto che le cifre del numero di cellulare si susseguono in ordine decrescente, basta decidere quali cifre provare ad utilizzare. Allo scopo pensate di aver scritto le nove cifre 9,8,,1 in ordine decrescente: in quanti modi se ne possono scartare due (in modo da ottenere un numero di 7 cifre)? Si può scegliere la prima cifra tra nove in 9 modi differenti: ciò fatto restano otto cifre tra le quali scegliere la seconda cifra, e questo può essere fatto in 8 modi diversi: complessivamente ci sono quindi 9 8 = 72 modi di scegliere una coppia ordinata di cifre da scartare, ma per il problema è significativo solo l insieme delle due cifre, non l ordine in cui si scartano: quindi ci sono 36=72/2 modi in cui scartare due delle nove cifre. 2. Considerate un esagono regolare P. Quanti sono complessivamente i suoi lati e le sue diagonali? Soluzione: da ogni vertice partono 5 tra lati e diagonali; in tutto 15 segmenti, visto che ogni segmento è condiviso da due vertici. 13
3 3. Una compagnia ferroviaria gestisce una linea con m stazioni. Ne fa poi costruire altre n (con n > 1). Sapendo che per ogni nuova tratta viene stampato un nuovo tipo di biglietto e che in totale vengono stampati 46 nuovi biglietti, determinare m e n. Soluzione: n = 4 ed m = 10. Infatti il numero di tutte le possibili tratte che uniscono k stazioni è k (k 1) /2 (infatti ciascuna delle k stazioni può essere unita con le restanti k 1, ma in questo modo ogni tratta resta contata due volte). Il numero delle tratte nuove si ottiene sottraendo, da quelle presenti alla fine, le tratte di vecchia costruzione. Dunque: 46 = [(m + n) (m + n 1) m (m 1)] /2 cioè 46 x 2 = n (2m + n 1) I numeri che entrano in gioco sono tutti interi: quindi n deve essere un numero che divide 92 = 2 2 x 23. Esaminiamo i vari casi possibili: n = 4: allora (2m + n 1) = 2m + 3 = 23, che significa m = 10 n = 2: allora si dovrebbe avere (2m + n 1) = 2m + 1 = 46, ma questo è impossibile poiché 2m + 1 è sicuramente un numero dispari n = 1 è escluso dai vincoli del problema, mentre palesemente se n = 23 oppure 46 oppure 92 la seconda equazione 2m + n 1 = 92 /n non ha soluzioni intere e positive. Parte B 4. In un area pedonale alcune lastre di pietra sono poste in modo da formare un quadrato Q di lato 3 metri. Due ragazzi giocano a tirare sassolini al suo interno: 37 sassolini cadono in Q e di essi 5 cadono in un quadrato di lato un metro. È un caso o di 37 sassolini caduti in Q almeno 5 cadono sempre in un quadrato di lato 1 e perché? Soluzione: non è un caso. Se i sassolini si distribuissero uniformemente sulla superficie del quadrato (che misura 9 metri quadrati) su ogni metro quadrato ne dovrebbero cadere 4 e ne avanzerebbe ancora 1, che dovrebbe comunque cadere in Q e quindi in uno dei quadrati di lato 1 metro in cui ne cadono già 4. Se la distribuzione non è uniforme la situazione non può che essere più favorevole. 14
4 Soluzioni dei Giochi dell incontro N o 2 1. Supponete di avvolgere (una volta) attorno alla Terra un filo perfettamente adagiato sull'equatore. Allungate il filo di un metro e sollevatelo uniformemente lungo l'equatore. L'altezza raggiunta dal filo sulla superficie terrestre è maggiore o minore di dieci centimetri? (supponete la superficie terrestre perfettamente sferica). Soluzione: maggiore di 10 centimetri. Se R è la misura in metri del raggio della Terra, la lunghezza iniziale del filo è 2πR. Aumentando tale lunghezza di 1 metro il raggio della corrispondente circonferenza diventa R+1/(2π) e quindi l altezza in metri del filo sulla superficie terrestre è 1/(2π), che è sicuramente maggiore di 10 cm (approssimare per eccesso 2π con 7). 2. All'interno di una scatola cubica di cartone, in uno dei vertici, è posta una briciola di pane; all'esterno della scatola, nel vertice opposto al precedente, si trova una formica. La scatola ha spigolo di lunghezza 30 cm, e la sua unica apertura è un foro quadrato, di lato 10 cm, praticato al centro di una delle facce laterali. Qual è la lunghezza del più breve percorso possibile con cui la formica può raggiungere la briciola, assumendo che le pareti della scatola siano di spessore trascurabile? Soluzione: 30 5 cm. Visto che lavoriamo sulla superficie (esterna o interna) della scatola, ciò che importa per misurare le distanze è lo sviluppo piano della scatola di cartone, che è quello indicato a lato. A meno di simmetrie, la formica deve andare da A a B o viceversa, passando da una parte all altra del cartone. Se non ci fosse da attraversare il cartone, il cammino minimo da A a B sarebbe B rappresentato esattamente dalla lunghezza del segmento AB. D altra parte tale segmento passa esattamente per il vertice C del quadratino interno (per C la similitudine dei triangoli rettangoli di ipotenusa AC ed AB, che hanno cateti lunghi rispettivamente 20 e 10 A cm, 60 e 30 cm) e quindi permette il passaggio dall esterno all interno. Quindi la lunghezza del percorso più breve con cui la formica raggiunge la briciola è di 30 5 cm. 3. Osservate la figura: stando su un pontile alto sull'acqua che termina con una ringhiera, un uomo tiene tesa una fune a cui è legata una barca. L'uomo arretra di un metro verso terra tirando con sé la fune. La barca si avvicina al pontile di più di un metro? di esattamente un metro? di meno di un metro? Soluzione: di più di un metro. In figura, A indica la posizione iniziale dell'uomo, A la sua posizione dopo lo spostamento, C la sommità della ringhiera, B la posizione iniziale della prua, B C A A la posizione finale della prua: D vogliamo stimare la lunghezza l(bb ) di BB. La fune può essere vista come unione dei B B due tratti BC e CA (situazione prima dello spostamento) oppure dei tre tratti B C, CA e AA (situazione dopo lo spostamento). Allora, se denotiamo con D il punto del segmento BC tale che CD sia lungo quanto B C, si 15
5 vede che il segmento BD misura tanto quanto il segmento AA, cioè un metro. Per la disuguaglianza triangolare, deve essere l(bb )+ l(b C) > l(bc) = 1 + l(cd) = 1 + l(b C) Dunque l(bb ) > 1, cioè la barca si avvicina al pontile di più di un metro. 4. In figura vedete un esagono regolare. Potete suddiverlo in 8 parti di ugual forma e dimensioni? In caso di risposta negativa dovete motivarla, in caso di risposta affemativa, illustrate direttamente sulla figura la suddivisione che proponete. Soluzione: la figura documenta che la suddivisione richiesta è possibile. I trapezi evidenziati, costruiti congiungendo i punti medi dei segmenti che collegano vertici adiacenti al centro, hanno effettivamente le stesse dimensioni: infatti il lato di un esagono regolare è lungo quanto il raggio della circonferenza circoscritta all esagono stesso fiammiferi di uguale lunghezza sono disposti un modo da rappresentare un pesce, come indicato nella figura. L'area della regione occupata dal pesce vale 24. Quanto vale l'area del triangolo ombreggiato, delimitato utilizzando il segmento tracciato in figura fra due dei "vertici" del pesce? Soluzione: 2. È facile vedere che il pesce è costituito accostando 8 triangoli equilateri di lato un fiammifero (6 formano l esagono regolare, 2 la coda ), ciascuno dei quali viene dunque ad avere area 3. Visto che i due triangoli DCK e DKE hanno uguale altezza, le loro aree stanno nello stesso rapporto di proporzionalità delle basi CK e KE: mostriamo che tale rapporto è 2:1. A B C D K E Per vederlo, osserviamo che i triangoli CDK e FHK sono simili (infatti gli angoli in F e C misurano 60 o e gli angoli in K sono uguali) con le misure dei lati che stanno nel rapporto 1:2. Allora H G F CK è lungo la metà di KF e dunque il doppio di KE (infatti CF è lungo quanto due fiammiferi). Alternativamente si può procedere come segue: esternamente all esagono aggiungiamo due triangoli equilateri (di lato un fiammifero) rispettivamente di base AB e terzo vertice D e di base GH e terzo vertice F : il triangolo DD F è equilatero di lato 3 fiammiferi e quindi DH taglia sulla base D F due segmenti D H e HF che stanno in rapporto 2:1. Per similitudine, anche sulla base CE di CDE il segmento DH taglia due segmenti CK e KE che stanno in rapporto 2:1. 6. I nove punti rappresentati in figura sono distribuiti nei nodi di un reticolo quadrato 3 3. Sapete congiungerli (senza staccare la matita dal foglio e senza percorrere due volte lo stesso tratto) con una spezzata che comprenda il minor numero di segmenti? Soluzione: 16
6 Soluzioni dei Giochi dell incontro N o 3 1. Una comitiva di 20 persone in cui ci sono uomini, donne e bambini - parte per una passeggiata. Dovendo trasportare cibarie, indumenti ed attrezzature per il picnic, per un totale di 40 kg, viene deciso che ogni uomo porterà uno zaino da esattamente 6 kg, ogni donna uno zaino da esattamente 3 kg ed ogni bambino uno zaino da esattamente 1 kg. Come è composta la comitiva? Soluzione: 2 uomini, 5 donne e 13 bambini. Denotato con u il numero degli uomini e con d quello delle donne si deve avere 6u + 3d + (20 u d) = 40. Dunque 5u + 2d = 20 che, se u e d non sono nulli, comporta u = 2 e d = 5, poiché 5u = 20 2d deve essere un numero pari. Dunque i bambini sono L'orologio di un campanile batte allo scoccare di ogni ora un numero di rintocchi corrispondente al valore numerico dell'ora stessa (da 1 a 12), e batte un solo rintocco allo scoccare di ogni quarto d'ora, di ogni mezz'ora, e di ogni tre quarti d'ora. Si sente suonare un rintocco. Quanto tempo occorre aspettare al massimo per sapere che ore sono (basandosi unicamente sul numero dei rintocchi uditi)? Soluzione: 60 minuti. Infatti tanto se il rintocco è quello delle 0:15 che se è quello delle 1:00 seguiranno altri 3 rintocchi isolati: ma nel primo caso anche alle 1:15 risuonerà un rintocco solo, nel secondo, alle 2:00 risuoneranno 2 rintocchi. Tutti gli altri casi sono ovviamente più favorevoli. 3. Avete due micce, identiche fra loro, ognuna delle quali brucia in un'ora esatta. Come potete farle bruciare in modo da misurare 45 minuti di tempo se avete a disposizione un solo fiammifero e le micce non possono essere tagliate? Soluzione. Piegate a metà una miccia e date fuoco contemporaneamente ai due capi di questa e ad un capo dell altra: quando la prima si sta esaurendo, piegate a metà la seconda e fate prender fuoco anche al capo rimasto intatto di questa: al suo esaurimento sono passati 45 minuti. 4. Avete una tanica piena d acqua: in tutto sono 8 litri che volete dividere esattamente a metà, ma avete a disposizione solo una tanica da 5 litri ed una da 3. Qual è il minimo numero di travasi da fare? Soluzione: 7. Per essere sicuri della quantità d acqua misurata bisogna riempire le singole taniche ed eventualmente travasarne in seguito il contenuto in altra tanica. Indichiamo con una terna ordinata i litri di acqua presenti in ogni tanica, nell ordine (Grande, Media, Piccola). Mediante travasi successivi si ha la sequenza di terne: (8,0,0), (3,5,0), (3,2,3), (6,2,0), (6,0,2), (1,5,2), (1,4,3), (4,4,0), per un totale di 7 travasi. L altra maniera plausibile di muoversi dà la sequenza di terne (8,0,0), (5,0,3), (5,3,0), (2,3,3), (2,5,1), (7,0,1), (7,1,0), (4,1,3), (4,4,0), per un totale di 8 travasi, che sono in numero maggiore di quelli appena trovati. 5. Un allevatore si accorge di avere munto del latte molto denso e decide così di annacquarlo. Avendo a disposizione due bidoni, uno contenente il latte fresco, l'altro contenente acqua pura, procede nel seguente modo. 1) Travasa dal bidone A al bidone B tanto liquido da raddoppiare il volume del liquido contenuto in B. 2) Poi travasa da B in A in modo da raddoppiare il volume del liquido ora contenuto in A. 3) Infine versa ancora il liquido da A a B raddoppiando il volume del liquido al momento contenuto in B. Ora i due bidoni contengono la stessa quantità di liquido e in B l'acqua è 1 litro in più del latte. Non vi è stato detto se il latte fosse inizialmente in A oppure in B: potete ugualmente stabilire quanta acqua e quanto latte si avevano inizialmente e in che quantità i due liquidi sono presenti nei due bidoni alla fine? (Supponete che i liquidi si mescolino sempre perfettamente.) Soluzione: in A c erano 5,5 litri di acqua ed in B 2,5 litri di latte. Chiamiamo α il liquido inizialmente contenuto in A e β quello contenuto in B. Possiamo risolvere il problema in termini di proporzioni: nel primo passaggio in A resta una parte di α (e nessuna di β) mentre in B i liquidi α e β sono in rapporto 17
7 1:1. Ora si deve versare in A il liquido contenuto in B in quantità pari a quella contenuta in A: dunque se in A ci sono 2 unità di liquido α, verrà aggiunta una unità di liquido α ed una di β che quindi restano in rapporto 3:1. Ora si deve travasare parte di questo liquido in B: supponendo (per comodità) che in B ci siano 2 unità di liquido α e 2 di liquido β (di valore non necessariamente uguale a quello della precedente unità), ne aggiungiamo 3 di liquido α e 1 di liquido β, ottenendo alla fine una miscela in cui i liquidi α e β sono in rapporto 5:3. Ora visto che sappiamo che alla fine l acqua presente in B è un litro più del latte, possiamo innanzitutto dedurre che α è l acqua e β il latte. Inoltre se le unità k di liquido in B sono 8, si ha 5k - 3k = 1 litro. Quindi l unità in esame è il mezzo litro. alla fine in B ci sono 1,5 litri di latte e 2,5 litri di acqua, mentre in A ci sono 3 litri di acqua ed uno di latte inizialmente in A c erano 5,5 litri di acqua ed in B 2,5 litri di latte Formalmente si potrebbe organizzare il discorso così. Indichiamo le quantità di liquido nei due bidoni A e B come coppie ordinate ; se denotiamo con a la quantità di liquido presente inizialmente in A e con b quella presente in B, si parte da (a, b); al primo passaggio si ha (a -b, 2b), al secondo (2a - 2b, 3b - a), al terzo (3a - 5b, 6b - 2a) e so che 3a - 5b = 6b - 2a cioè 5a = 11b. Questo è possibile se le due quantità a e b si possono scrivere come multiple di un altra quantità k: a = 11k e b = 5k. Al primo passaggio in B c è una quantità di α e di β pari a 5k (quindi in un rapporto 1:1); al secondo passaggio in A c è una quantità di α pari a 6k + 3k e di secondo liquido pari a 3k (quindi in un rapporto 3:1). Alla fine in B c è una quantità di α pari a 2k + 3k = 5k e di β pari a 2k + k = 3k. Visto che β è in quantità inferiore, esso è il latte e 2k = 1 litro.. 6. Avendo a disposizione una bilancia a due piatti e cinque pesi da 1, 3, 9, 27 e 81 grammi, quanti pesi diversi si possono misurare? Soluzione: 121. Osserviamo che mettere un peso A su un piatto ed un peso B sull altro (insieme a quanto da pesare) equivale a misurare il peso A B. Si hanno dunque le seguenti possibili misure: 1, 3 1, 3, 3+1, 9 (3+1), 9 3, 9 (3 1), 9 1, 9; sommando i primi 4 a 9 si arriva a 9+(3+1)=13; sottraendo da 27 i primi 13 in ordine inverso si va da a 27 1 mentre sommandoli si arriva a 27+[9+(3+1)]=40; sottraendo da 81 i primi 40 in ordine inverso si va da a 81 1 mentre sommandoli si arriva a 81+40=121. [Implicazione della serie geometrica: per ogni numero intero n 0 la somma ( n 1 ) delle prime n potenze di 3 è la metà di 3 n 1.] 7. In uno stesso mese tre domeniche sono cadute in giorni pari. Quale giorno della settimana era il 20 di quel mese? Soluzione: giovedì. Infatti due domeniche consecutive non cadono entrambe in un giorno pari (o dispari). Di conseguenza nel mese ci sono state 5 domeniche, la prima il 2, l ultima il 30. Quindi il 20 del mese era giovedì. 8. Nel mese di dicembre di un certo anno vi furono esattamente quattro domeniche e quattro mercoledì. In quale giorno della settimana cadde il 3 febbraio dell'anno successivo? Soluzione: venerdì. In quel dicembre c erano 5 giovedì, venerdì e sabati, cioè il mese finì di sabato; il 29 gennaio cadde quindi di domenica ed il 3 febbraio di venerdì. 9. Alla fine di un torneo di pallavolo con un solo girone all italiana (dove ogni squadra incontra una sola volta tutte le altre), esiste sempre almeno una squadra A che negli incontri con ogni altra squadra B o ha vinto o ha battuto una squadra che ha battuto B? Motivate la risposta. (N.B. nella pallavolo nessuna partita si conclude in parità). Soluzione: ogni squadra A a punteggio massimo è in questa condizione. Infatti, se A non avesse battuto B e non avesse battuto alcuna delle squadre che hanno battuto B (cioè se A è stata battuta, oltre che da B, anche da tutte le squadre che hanno battuto B) il punteggio di A sarebbe sicuramente inferiore a quello di B. 18
8 Soluzioni dei Giochi dell incontro N o 4 1. Considerate un esagono regolare P. Nel primo incontro avete trovato che il numero di segmenti che uniscono a due a due i vertici di P sono 15. a) Quanti sono i triangoli i cui vertici sono vertici di P (e i cui lati sono lati o diagonali di P)? b) Se avete a disposizione due colori (rosso e blu) per colorare i lati e le diagonali di P (i vertici possono essere soggetti a doppia colorazione), in quanti modi diversi potete colorare i lati e le diagonali di P? (pensate l esagono fisso). c) Considerate ora tutti i possibili triangoli i cui vertici sono vertici di P: c è una colorazione che eviti i triangoli monocromatici? Soluzione. a) I triangoli i cui vertici sono vertici di P sono quanti i modi di prendere i vertici dell esagono a 3 a 3, cioè (6 5 4):(2 3) = 20. b) Ogni segmento può essere colorato in 2 modi diversi e quindi in totale ci sono 2 15 = colorazioni distinte. c) Quindi, a meno dello scambio dei colori, per vedere se esiste una colorazione che eviti i triangoli monocromatici dovremmo esaminare 2 14 = colorazioni. È chiaro che, considerando configurazioni ruotate, il numero di colorazioni può essere ulteriormente ridotto e non è utopistico pensare che, con molta pazienza, si possa arrivare alla soluzione del problema esaminando tutti i casi possibili; certamente sarebbe lavoro di poco conto per un computer. La seguente semplice considerazione può comunque evitare tutto questo. Si isoli un vertice qualunque v di P: da esso si staccano 5 segmenti ad almeno 3 dei quali deve essere assegnato uno stesso colore α (l altro sia β). Si consideri il triangolo T i cui vertici coincidono con i secondi estremi di questi 3 segmenti: se uno almeno dei suoi lati è colorato in α, esiste un triangolo monocromatico con un vertice in v; in caso contrario, T stesso è un triangolo monocromatico (colorato in β). In questo caso dunque non si possono evitare triangoli monocromatici. Può sorprendere il fatto che il problema analogo con n = 45 e k = 5 sia tuttora aperto: una stima grossolana, non difficile da ottenere, rivela che un computer tradizionale potrebbe fornire la risposta in un ora, esaminando tutte le configurazioni possibili, solo assorbendo un quantitativo di energia pari a quello prodotto dall uomo sull intera superficie terrestre nell arco di 20 anni. Altri giochi in cui contare elementi di una figura geometrica si trovano ai numeri 11, Dieci ragazzi vogliono giocare a pallacanestro. In quanti modi diversi è possibile formare le due squadre (5 ragazzi ciascuna), tenendo conto che Matteo vuole giocare con Stefano e che Beppe non vuole giocare con Andrea? (Tutti i ragazzi hanno nomi diversi fra loro.) Soluzione: 30. Denotiamo Matteo, Stefano, Andrea e Beppe con le iniziali dei loro nomi. Visto che A e B vogliono stare in squadre diverse, denotiamo ognuna delle due squadre con la loro iniziale. Se MS fanno parte della squadra A, gli altri due componenti della squadra possono essere scelti, tra i restanti 6, in (6 5):2 modi (si divide per 2 poiché è indifferente se X e Y entrano a far parte della squadra in quest ordine o nell ordine inverso: anche in questo gioco, come in quello dei gelati, si considerano le combinazioni di 6 elementi a 2 a 2). Analogamente se MS fanno parte della squadra B. Quindi sommando si arriva a 30 modi di formare le squadre. 3. In un urna vi sono 17 palline numerate da 1 a 17. Avete la possibilità di effettuare un unica estrazione di un numero di palline a vostra scelta. Volendo essere certi che, fra le palline che estraete, ve ne siano almeno due la somma dei cui numeri sia 18, quante ne dovete estrarre? 19
9 Soluzione: 10. Vi sono 8 coppie non ordinate di interi fra 1 e 17 che sommati danno 18, e questi interi sono tutti diversi fra loro, dunque sono 16 in tutto. Se si estraggono 9 numeri, può accadere che uno sia 9 e che di ognuna di queste coppie sia presente un solo numero. Estraendone 10 invece, necessariamente fra questi si devono ritrovare entrambi gli interi di una coppia di cui sopra. 4. Maria ha 6 cartoncini di colore diverso, su ciascuno dei quali è segnato un numero naturale. Sceglie tre cartoncini e calcola la somma dei numeri corrispondenti. Dopo aver fatto questa operazione in tutti i 20 modi possibili, scopre che in 10 casi ha ottenuto 16, e negli altri ha ottenuto 18. Quanto vale il più piccolo dei numeri segnati sui cartoncini? Soluzione: 4. Il punteggio complessivo ottenuto con le venti estrazioni è =340. D'altra parte ogni cartoncino viene estratto 10 volte (poiché, pensandolo come primo cartoncino, ci sono 10 modi per scegliere gli altri): quindi la somma dei valori dei cartoncini è 34. Tre di questi cartoncini comunque scelti hanno somma che non supera 18. Supponiamo che ci sia un 1 tra i numeri segnati sui cartoncini: la somma dei rimanenti 5 numeri deve dare 33 e quindi il valore medio di ogni cartoncino deve superare 6, per cui ci saranno almeno 3 cartoncini la cui somma è >18 (ad es. 21 come succede scomponendo così 33 = = = ). In modo analogo si vede che non ci può essere un 2 o un 3. Invece ci può essere un 4, visto che 34 = : e tra l'altro si vede che se i cartoncini hanno questi valori in metà dei casi 3 cartoncini hanno somma 16 e nell'altra metà hanno somma 18. D'altra parte è chiaro che il più piccolo numero segnato sui cartoncini non può essere 6 (la somma di tutti i cartoncini darebbe almeno 36) e neppure 5 poiché è vero che 34 = , ma in questo caso si avrebbero anche estrazioni in cui il punteggio è 17. Altri giochi di strategia si trovano ai numeri 7, 8, 9, Un giocatore professionista di dadi accetta di scommettere sull uscita, con 4 lanci di 1 solo dado, di un 6. Lo stesso giocatore non accetterà mai di scommettere sull uscita di un doppio 6 con 24 lanci di 2 dadi. Perché? Soluzione. Sa che, su 6 4 = 1296 eventi, il 6 ha solo (6 1) 4 = 625 occasioni di non uscire pari ad una probabilità di circa il 48,2%. Invece, su (6 6) 24 eventi, il doppio 6 ha (36 1) 24 occasioni di non uscire pari a una probabilità di circa il 50,8%. 6. Permutando in tutti i modi possibili le cifre del numero si ottengono 7! numeri interi di 7 cifre. Qual è la somma di questi 7! numeri? Soluzione: Può essere utile cominciare a capire come organizzare il discorso con un numero più piccolo: In questo caso le possibili permutazioni sono 24: di esse 6 hanno come cifra delle unità 1, altre 6 hanno 2, altre 6 hanno 3 ed altre 6 hanno 4. Per avere la cifra delle unità della somma basta quindi sommare 6 ( ) = 60: la cifra delle unità è 0 e si ha un riporto di 6. Lo stesso ragionamento sulle decine porta come risultato 66: cifra delle decine 6, e riporto 6. Proseguendo così anche per le centinaia e le migliaia si arriva a dire che la somma vale Ora si può estendere questo ragionamento al numero proposto: Qui ogni cifra comparirà in ogni colonna 6! = 720 volte e la somma delle cifre vale = 28, quindi la cifra delle unità è quella del numero = e, riportando successivamente 2016, 2217, 2237 e per tre volte 2239, si ottiene che la somma vale
10 Altri quesiti 7. In un urna vi sono 35 palline. Compiamo delle estrazioni successive seguendo rigorosamente questa procedura: - alla prima estrazione si prende una pallina; - a ogni successiva estrazione (ultima inclusa) va presa una pallina in più o una in meno rispetto all estrazione precedente. Qual è il numero minimo di estrazioni sufficiente perché l urna resti vuota? Motiva la risposta. Soluzione: 9. Non bastano 7 estrazioni, poiché al massimo si potrebbero estrarre = 28 palline. Non ne bastano neppure 8, poiché = 36 mentre = 34, il che significa che, se ad anche una sola delle estrazioni estraessimo una pallina in meno rispetto all estrazione precedente anziché una in più, non arriveremmo a svuotare l urna. D altra parte 9 estrazioni sono sufficienti: basta estrarre, per esempio, nell ordine 1, 2, 3, 4, 5, 6, 5, 4, 5 palline, oppure 1, 2, 3, 4, 5, 4, 5, 6, 5 palline. 8. Indicate come può essere individuato un insieme di 200 numeri interi compresi fra 1 e 300, estremi inclusi, in modo che sia rispettata la seguente clausola: se nell insieme è presente un numero, allora non è presente il suo doppio. Soluzione. Possiamo scegliere tutti i numeri da 151 a 300 inclusi, quelli da 38 a 75 inclusi, quelli da 10 a 18 inclusi e infine i numeri 3, 4, 1. Oppure possiamo scegliere tutti i 150 numeri dispari (da 1 a 299), poi i multipli di 4 ma non di 8 (da 4 a 300: 38 numeri), quindi i multipli di 16 ma non di 32 (da 16 a 272: 9 numeri), quindi i multipli di 64 ma non di 128 (64 e 192: 2 numeri) e infine 256, per un totale di Considerate una successione di numeri interi positivi, tale che ogni numero dal terzo in poi sia la somma di tutti quelli che lo precedono, il primo numero sia 1 e l ultimo sia Nella più lunga successione che si può costruire con questa legge, quanto vale il secondo numero? Soluzione Infatti, si chiami x il secondo numero che compare nella successione; i numeri che compaiono nella successione sono: 1, x, 1 + x, 1 + x + (1 + x) = 2(1 + x), 1 + x + (1 + x) + 2(1 + x) = 4(1 + x), 1 + x + (1 + x) + 2(1 + x) + 4(1 + x) = 8(1 + x) In sostanza i numeri della successione dal quarto in poi si ottengono moltiplicando il precedente per 2. Ora 1000 è divisibile per 8 ma non per 16: quindi la più lunga sequenza di questo tipo che termini con 1000 si ha prendendo x in modo che sia 8(1 + x) = 1000, cioè x = Presi 5 interi qualsiasi, è sempre possibile trovarne 3 la cui somma è un multiplo di 3? Soluzione. Sì. Ci sono solo tre possibili resti nella divisione di un numero intero per 3: 0, 1, 2. Se almeno 3 dei 5 numeri hanno lo stesso resto nella divisione per 3 (cioè hanno la forma 3m + r, 3n + r, 3p + r) la loro somma è certamente multiplo di 3; in caso contrario ci deve essere almeno un numero con ciascuno dei resti possibili (cioè della forma 3m, 3n + 1, 3p + 2) e ancora la loro somma è un multiplo di Quanti sono i triangoli non degeneri di perimetro 20 cm, le misure dei cui lati sono date da un numero intero di centimetri? Soluzione: 8. In base alla disuguaglianza triangolare - che afferma che la somma delle lunghezze di due lati di un triangolo non degenere è maggiore della lunghezza del terzo lato - si devono trovare tutte le partizioni in numeri interi del numero 20 in cui nessun numero sia maggiore di 9: (9,9,2), (9,8,3), (9,7,4), (9,6,5), (8,8,4), (8,7,5), (8,6,6), (7,7,6). 21
11 12. Quanti triangoli non degeneri con lati tutti diversi si possono costruire con 10 segmenti lunghi rispettivamente 1, 2,, 10 centimetri? Soluzione: 50. Infatti denotiamo con m la lunghezza del lato più corto e con n e p (n < p) quella degli altri: per la disuguaglianza triangolare si deve avere m + n > p ed in particolare m > 1. Contiamo ora le terne ammissibili: m = 2: (2,3,4), (2,4,5), (2,5,6), (2,6,7), (2,7,8), (2,8,9), (2,9,10): totale 7 m = 3: (3,4,5), (3,4,6); (3,5,6), (3,5,7); (3,6,7), (3,6,8); (3,7,8), (3,7,9); (3,8,9), (3,8,10); (3,9,10): totale 11 m = 4: (4,5,6), (4,5,7), (4,5,8); (4,6,7), (4,6,8), (4,6,9); (4,7,8), (4,7,9), (4,7,10); (4,8,9), (4,8,10), (4,9,10): totale 12 da m = 5 a m = 8 la disuguaglianza triangolare è automaticamente soddisfatta e quindi basta fare il conto delle combinazioni di 10 m oggetti a due a due: =
Laboratorio di Giochi Matematici
 Unità operativa di Milano Città Studi Laboratorio di Giochi Matematici (responsabile Prof. Stefania De Stefano) Incontri presso il Dipartimento di Matematica "F. Enriques" 2. Schede di lavoro per gli studenti
Unità operativa di Milano Città Studi Laboratorio di Giochi Matematici (responsabile Prof. Stefania De Stefano) Incontri presso il Dipartimento di Matematica "F. Enriques" 2. Schede di lavoro per gli studenti
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado
 Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
Kangourou Italia Gara del 15 marzo 2001 Categoria Student Per studenti di quarta e quinta superiore
 Kangourou Italia Gara del 1 marzo 001 Categoria Student Per studenti di quarta e quinta superiore Regole:! La prova è individuale. E vietato l uso di calcolatrici di qualunque tipo.! Vi è una sola risposta
Kangourou Italia Gara del 1 marzo 001 Categoria Student Per studenti di quarta e quinta superiore Regole:! La prova è individuale. E vietato l uso di calcolatrici di qualunque tipo.! Vi è una sola risposta
Kangourou Italia Gara del 15 marzo 2012 Categoria Student Per studenti di quarta o quinta della secondaria di secondo grado
 Testi_12Mat_5-8-Ecolier.qxd 24/06/12 17:29 Pagina 27 Kangourou Italia Gara del 15 marzo 2012 Categoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono
Testi_12Mat_5-8-Ecolier.qxd 24/06/12 17:29 Pagina 27 Kangourou Italia Gara del 15 marzo 2012 Categoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
Terza Edizione Giochi di Achille (13-12-07) - Olimpiadi di Matematica Soluzioni Categoria M1 (Alunni di prima media)
 Il Responsabile coordinatore dei giochi: Prof. Agostino Zappacosta Chieti tel. 087 65843 (cell.: 340 47 47 95) e-mail:agostino_zappacosta@libero.it Terza Edizione Giochi di Achille (3--07) - Olimpiadi
Il Responsabile coordinatore dei giochi: Prof. Agostino Zappacosta Chieti tel. 087 65843 (cell.: 340 47 47 95) e-mail:agostino_zappacosta@libero.it Terza Edizione Giochi di Achille (3--07) - Olimpiadi
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
I Giochi di Archimede - Soluzioni Biennio 22 novembre 2012
 PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE I Giochi di Archimede - Soluzioni Biennio novembre 0 Griglia delle risposte corrette Problema Risposta
PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE I Giochi di Archimede - Soluzioni Biennio novembre 0 Griglia delle risposte corrette Problema Risposta
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
IGiochidiArchimede--Soluzionibiennio
 PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLA NORMALE SUPERIORE IGiochidiArchimede--Soluzionibiennio 17 novembre 2010 Griglia delle risposte
PROGETTO OLIMPIADI DI MATEMATICA U.M.I. UNIONE MATEMATICA ITALIANA MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLA NORMALE SUPERIORE IGiochidiArchimede--Soluzionibiennio 17 novembre 2010 Griglia delle risposte
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
GIOCHI A SQUADRE. 30 marzo 2012
 Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno
 Kangourou Italia Gara del 19 marzo 2015 Categoria Cadet Per studenti di terza della scuola secondaria di primo grado e prima della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti
Kangourou Italia Gara del 19 marzo 2015 Categoria Cadet Per studenti di terza della scuola secondaria di primo grado e prima della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti
Kangourou Italia Gara del 22 marzo 2011 Categoria Ecolier Per studenti di quarta o quinta della scuola primaria
 Testi_11Mat.qxp 19-05-2011 21:20 Pagina 5 Kangourou Italia Gara del 22 marzo 2011 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1.
Testi_11Mat.qxp 19-05-2011 21:20 Pagina 5 Kangourou Italia Gara del 22 marzo 2011 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1.
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
Kangourou Italia Gara del 21 marzo 2013 Categoria Junior Per studenti di seconda e terza della secondaria di secondo grado
 Kangourou Italia Gara del 21 marzo 2013 Categoria Junior Per studenti di seconda e terza della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Il numero 200013 2013
Kangourou Italia Gara del 21 marzo 2013 Categoria Junior Per studenti di seconda e terza della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Il numero 200013 2013
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Calcolo combinatorio
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Soluzioni del giornalino n. 16
 Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014
 Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
Kangourou della Matematica 2011 Coppa a squadre Kangourou Semifinale turno A Cervia, 7 maggio 2011. Quesiti
 Kangourou della Matematica 2011 Coppa a squadre Kangourou Semifinale turno A Cervia, 7 maggio 2011 Quesiti 1. Un lungo viaggio Quando a Londra sono le 17.00, a S. Francisco sono le 09.00 (dello stesso
Kangourou della Matematica 2011 Coppa a squadre Kangourou Semifinale turno A Cervia, 7 maggio 2011 Quesiti 1. Un lungo viaggio Quando a Londra sono le 17.00, a S. Francisco sono le 09.00 (dello stesso
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Rilevazione degli apprendimenti. Anno Scolastico 2006 2007 PROVA DI MATEMATICA. Scuola Secondaria di II grado. Classe Terza Tipo A. Codici. Scuola:...
 Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti
 da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti
 di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti Contenuto: 44 Carte percorso, 27 Carte azione, 28 Carte oro, 7 Cercatori d oro, 4 Sabotatori. Idea del gioco I
di Frederic Moyersoen Giocatori: 3-10 Età: a partire dagli 8 anni Durata: circa 30 minuti Contenuto: 44 Carte percorso, 27 Carte azione, 28 Carte oro, 7 Cercatori d oro, 4 Sabotatori. Idea del gioco I
Primo allenamento per i Giochi Kangourou della Matematica
 Primo allenamento per i Giochi Kangourou della Matematica Per gli alunni di prima e seconda media i quesiti sono dal numero 1 al numero 11 Per gli alunni di terza media i quesiti sono dal numero 7 al numero
Primo allenamento per i Giochi Kangourou della Matematica Per gli alunni di prima e seconda media i quesiti sono dal numero 1 al numero 11 Per gli alunni di terza media i quesiti sono dal numero 7 al numero
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI
 DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
DA GIOCHI D AUTUNNO 2006 SOLUZIONI E COMMENTI 1. GIOCO DI CUBI L altezza della piramide di Luca è 95 cm. = (14 + 13 + 12 + + 7 + 6 + 5) 2. LA PARTENZA Anna saluterà le amiche nel seguente ordine: S-I-G-C
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
GIOCHI D AUTUNNO 2003 SOLUZIONI
 GIOCHI D AUTUNNO 2003 SOLUZIONI 1) MARATONA DI MATHTOWN Pietro arriva alle 16.56, Renato alle 17.01, Desiderio alle 16.54 e Angelo alle 17.04. L ultimo ad arrivare è Angelo che arriva alle 17.04 2) PARI
GIOCHI D AUTUNNO 2003 SOLUZIONI 1) MARATONA DI MATHTOWN Pietro arriva alle 16.56, Renato alle 17.01, Desiderio alle 16.54 e Angelo alle 17.04. L ultimo ad arrivare è Angelo che arriva alle 17.04 2) PARI
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
GIOCHI MINIBASKET. 1) Il gioco dei nomi. 2) Il gambero
 GIOCHI MINIBASKET Questi giochi sono stati tratti da alcuni libri e talvolta modificati per adattarli al nostro gioco. Adatti per diverse età. Buon lavoro. 1) Il gioco dei nomi Obiettivi: conoscere i compagni,
GIOCHI MINIBASKET Questi giochi sono stati tratti da alcuni libri e talvolta modificati per adattarli al nostro gioco. Adatti per diverse età. Buon lavoro. 1) Il gioco dei nomi Obiettivi: conoscere i compagni,
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Anna Montemurro. 2Geometria. e misura
 Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Rilevazione degli apprendimenti. Anno Scolastico 2006 2007 PROVA DI MATEMATICA. Scuola Secondaria di II grado. Classe Terza Tipo A. Codici. Scuola:...
 Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
Ministero della Pubblica Istruzione Rilevazione degli apprendimenti Anno Scolastico 2006 2007 PROVA DI MATEMATICA Scuola Secondaria di II grado Classe Terza Tipo A Codici Scuola:..... Classe:.. Studente:.
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Kangourou Italia Gara del 19 marzo 2009 Categoria Ecolier Per studenti di quarta o quinta della scuola primaria
 Testi_09.qxp 15-04-2009 20:23 Pagina 5 Kangourou Italia Gara del 19 marzo 2009 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1. Hai
Testi_09.qxp 15-04-2009 20:23 Pagina 5 Kangourou Italia Gara del 19 marzo 2009 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1. Hai
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Regolamento Ravennate 200/400
 Regolamento Ravennate 200/400 L INIZIO Il tavolo è composto da 4 giocatori dove ognuno gioca per sé stesso. Controllare la propria posta in fiches,, deve risultare un totale di 2000 punti. ( 1 da 1.000,
Regolamento Ravennate 200/400 L INIZIO Il tavolo è composto da 4 giocatori dove ognuno gioca per sé stesso. Controllare la propria posta in fiches,, deve risultare un totale di 2000 punti. ( 1 da 1.000,
THE BOXER. www.stamping.it
 Misura, cordona e piega accuratamente con questa innovativa tavola per fare scatole! Da un lato trovi le misure in centimetri con incrementi di 1/2 cm. e sull altro quelle in pollici con incrementi di
Misura, cordona e piega accuratamente con questa innovativa tavola per fare scatole! Da un lato trovi le misure in centimetri con incrementi di 1/2 cm. e sull altro quelle in pollici con incrementi di
Esercizi di calcolo combinatorio
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
La prof.ssa SANDRA VANNINI svolge da diversi anni. questo percorso didattico sulle ARITMETICHE FINITE.
 La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Kangourou Italia Gara del 19 marzo 2015 Categoria Student Per studenti di quarta e quinta della secondaria di secondo grado
 Kangourou Italia Gara del 19 marzo 2015 Categoria Student Per studenti di quarta e quinta della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Angela è nata nel 1997,
Kangourou Italia Gara del 19 marzo 2015 Categoria Student Per studenti di quarta e quinta della secondaria di secondo grado I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Angela è nata nel 1997,
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
ESAME DI QUALIFICA TRIENNALE (II LIVELLO EUROPEO)
 Nome e ognome Id Azione Data.. Tipo prova MATEMATIA - III anno - sessione 1 a.f. 008/009 ESAME DI QUALIFIA TRIENNALE (II LIVELLO EUROPEO) 1 M0 Data l equazione x + 3 = 3x + b quale valore si deve dare
Nome e ognome Id Azione Data.. Tipo prova MATEMATIA - III anno - sessione 1 a.f. 008/009 ESAME DI QUALIFIA TRIENNALE (II LIVELLO EUROPEO) 1 M0 Data l equazione x + 3 = 3x + b quale valore si deve dare
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Indovinelli Algebrici
 OpenLab - Università degli Studi di Firenze - Alcuni semplici problemi 1. L EURO MANCANTE Tre amici vanno a cena in un ristorante. Mangiano le stesse portate e il conto è, in tutto, 25 Euro. Ciascuno di
OpenLab - Università degli Studi di Firenze - Alcuni semplici problemi 1. L EURO MANCANTE Tre amici vanno a cena in un ristorante. Mangiano le stesse portate e il conto è, in tutto, 25 Euro. Ciascuno di
12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005.
 Logica matematica 12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005. In quale anno cadrà la prossima data nella
Logica matematica 12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005. In quale anno cadrà la prossima data nella
3 IL CRUCIVERBA NUMERICO Trova i numeri e inseriscili nel cruciverba (una cifra in ogni casella). Buon divertimento!
 GIOCHI MATEMATICI 1 I PALLONCINI NUMERICI Inserisci nei palloncini i numeri da 1 a 6 in modo che la somma su ogni lato sia uguale a 10. GIOCHI MATEMATICI 2 IL QUADRATO NUMERICO Disponi i numeri da 1 a
GIOCHI MATEMATICI 1 I PALLONCINI NUMERICI Inserisci nei palloncini i numeri da 1 a 6 in modo che la somma su ogni lato sia uguale a 10. GIOCHI MATEMATICI 2 IL QUADRATO NUMERICO Disponi i numeri da 1 a
Kangourou Italia Gara del 20 marzo 2003 Categoria Cadet Per studenti di terza media o prima superiore
 15-20-.qxd 29/03/2003 8.22 Pagina 16 Kangourou Italia Gara del 20 marzo 2003 Categoria Per studenti di terza media o prima superiore I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Quale dei seguenti
15-20-.qxd 29/03/2003 8.22 Pagina 16 Kangourou Italia Gara del 20 marzo 2003 Categoria Per studenti di terza media o prima superiore I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. Quale dei seguenti
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda
 PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda Rilevazione degli apprendimenti Anno Scolastico 2011 2012 PROVA DI MATEMATICA Scuola Primaria Classe Seconda Spazio per l etichetta autoadesiva ISTRUZIONI
PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda Rilevazione degli apprendimenti Anno Scolastico 2011 2012 PROVA DI MATEMATICA Scuola Primaria Classe Seconda Spazio per l etichetta autoadesiva ISTRUZIONI
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
CENTRO PRISTEM-UNIVERSITÀ BOCCONI
 CENTRO PRISTEM-UNIVERSITÀ BOCCONI 1 Compleanni e ritardi Carla ha festeggiato il suo compleanno di domenica, il 28 marzo, con due giorni di ritardo rispetto alla data esatta. Milena è nata (in un altro
CENTRO PRISTEM-UNIVERSITÀ BOCCONI 1 Compleanni e ritardi Carla ha festeggiato il suo compleanno di domenica, il 28 marzo, con due giorni di ritardo rispetto alla data esatta. Milena è nata (in un altro
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
ALTRI SUGGERIMENTI PER IL PERCORSO AD OSTACOLI
 ALTRI SUGGERIMENTI PER IL PERCORSO AD OSTACOLI Con l intento di proseguire l osservazione sulle competenze che i bambini posseggono nei confronti della matematica è stata intrapresa una rivisitazione del
ALTRI SUGGERIMENTI PER IL PERCORSO AD OSTACOLI Con l intento di proseguire l osservazione sulle competenze che i bambini posseggono nei confronti della matematica è stata intrapresa una rivisitazione del
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta
 Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Soluzioni del Certamen Mathematicum
 Soluzioni del Certamen Mathematicum dicembre 2004 1. Notiamo che un qualsiasi quadrato modulo 4 è sempre congruo o a 0 o a 1. Infatti, se tale numero è pari possiamo scriverlo come 2k, seè dispari invece
Soluzioni del Certamen Mathematicum dicembre 2004 1. Notiamo che un qualsiasi quadrato modulo 4 è sempre congruo o a 0 o a 1. Infatti, se tale numero è pari possiamo scriverlo come 2k, seè dispari invece
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Capitolo 25: Lo scambio nel mercato delle assicurazioni
 Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
Capitolo 25: Lo scambio nel mercato delle assicurazioni 25.1: Introduzione In questo capitolo la teoria economica discussa nei capitoli 23 e 24 viene applicata all analisi dello scambio del rischio nel
2. Un teorema geniale e divertente anche per la scuola elementare
 051-056 BDM 56 Maurizi imp 21.5.2008 11:49 Pagina 51 II. Didattica 2. Un teorema geniale e divertente anche per la scuola elementare Lorella Maurizi 1 51 Ho proposto ai bambini di una classe quinta della
051-056 BDM 56 Maurizi imp 21.5.2008 11:49 Pagina 51 II. Didattica 2. Un teorema geniale e divertente anche per la scuola elementare Lorella Maurizi 1 51 Ho proposto ai bambini di una classe quinta della
Cenni sul calcolo combinatorio
 Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo.
 Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
Capitolo 1 9 Ottobre 00 Calcolo delle Probabilita, INGEGNERIA INFORMATICA, semestre II, laurea (ord. Leonardo. 000, Milano Esercizio 1.0.1 (svolto in classe [II recupero Ing. Matematica aa.00-0-rivisitato]nel
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
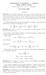 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
Giochi matematici. Slot machine
 Giochi matematici di Luca Barletta Slot machine Una slot machine ha 5 finestre; da ogni finestra si può affacciare uno dei 6 simboli possibili. All inizio tutti i simboli sono diversi; lo scopo è quello
Giochi matematici di Luca Barletta Slot machine Una slot machine ha 5 finestre; da ogni finestra si può affacciare uno dei 6 simboli possibili. All inizio tutti i simboli sono diversi; lo scopo è quello
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Appunti ed esercizi di combinatoria. Alberto Carraro
 Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
Appunti ed esercizi di combinatoria Alberto Carraro December 2, 2009 01 Le formule principali per contare Disposizioni Sia A un insieme di n 1 elementi distinti Le sequenze di 1 k n elementi scelti senza
LA STATISTICA NEI TEST INVALSI
 LA STATISTICA NEI TEST INVALSI 1 Prova Nazionale 2011 Osserva il grafico seguente che rappresenta la distribuzione percentuale di famiglie per numero di componenti, in base al censimento 2001. Qual è la
LA STATISTICA NEI TEST INVALSI 1 Prova Nazionale 2011 Osserva il grafico seguente che rappresenta la distribuzione percentuale di famiglie per numero di componenti, in base al censimento 2001. Qual è la
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
GIOCHI A SQUADRE 2013
 GIOCHI A SQUADRE 2013 1. Trovate il più piccolo intero naturale che, diviso per 3, dà come resto 1; diviso per 4, dà il resto di 2, diviso per 5, dà il resto di 3 e, diviso per 6, dà il resto di 4. 58
GIOCHI A SQUADRE 2013 1. Trovate il più piccolo intero naturale che, diviso per 3, dà come resto 1; diviso per 4, dà il resto di 2, diviso per 5, dà il resto di 3 e, diviso per 6, dà il resto di 4. 58
4 LA PALETTA È possibile «svuotare» la paletta spostando solo due segmenti. Sai dire come?
 GIOCHI MATEMATICI 1 CUORI, QUADRI, PICCHE E FIORI Riempi le caselle della griglia con i simboli,, e in modo che ogni simbolo compaia una sola volta in ogni riga e in ogni colonna. GIOCHI MATEMATICI 2 LA
GIOCHI MATEMATICI 1 CUORI, QUADRI, PICCHE E FIORI Riempi le caselle della griglia con i simboli,, e in modo che ogni simbolo compaia una sola volta in ogni riga e in ogni colonna. GIOCHI MATEMATICI 2 LA
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Vincere a testa o croce
 Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
Vincere a testa o croce Liceo Scientifico Pascal Merano (BZ) Classe 2 Liceo Scientifico Tecnologico Insegnante di riferimento: Maria Elena Zecchinato Ricercatrice: Ester Dalvit Partecipanti: Jacopo Bottonelli,
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
