5. Metodo semiprobabilistico agli stati limite per il cemento armato

Transcript

1 5. Metodo emiprobabilitio agli tati limite per il emento armato Per la determinazione delle olleitazioni di alolo, oneguenti alle ombinazioni di ario previte, la Normativa vigente prevede l adozione di modelli lineari e modelli non lineari del omportamento trutturale. Agli SLE, in partiolare, l analii deve eere ondotta in ampo elatio lineare; agli SLU è poibile eeguire anhe un alolo non lineare. Rinviando a diipline più peialitihe la derizione dei proedimenti di analii non lineare, in queta ede la valutazione delle olleitazioni verrà eeguita ipotizzando un omportamento elatio-lineare delle trutture. L unia ondizione da oddiare per l adozione di un modello elatio-lineare agli SLU, ondizione peraltro non impota dall attuale Normativa ma previta dal preedente D.M. del 1996 e dall Euroodie 2 (UNI EN , novembre 2005), onite nell evitare ituazioni di ragilità loale nella truttura, onerendo alla tea opportuni requiiti di duttilità. Sulla bae di tale aunzione, e le ezioni hanno un omportamento duttile le olleitazioni he i ottengono tramite l analii elatia, ome già detto nel Capitolo 1, ono uperiori a quelle he eettivamente agiono nelle ezioni in virtù del loro omportamento elato-platio eettivo. L adozione di queto metodo pertanto omporta un ulteriore margine di iurezza nelle trutture Legami otitutivi Caletruzzo Convenendo di aumere poitive per il aletruzzo le tenioni di ompreione e le deormazioni di aoriamento, ai ini della valutazione della reitenza della ezione a orzo normale e leione la Normativa propone l adozione dei eguenti legami otitutivi σ ε per lai di reitenza non uperiori a C50/55 (Fig. 5.1): a) modello parabola-rettangolo (Fig. 5.1a) di equazioni: () ε ε( 1 ε) σ 1000 d 250 per ε ε 0.2% (tratto parabolio) () ε d 0 2 σ per ε.2% ε ε 0.35% (tratto otante) 2 0 u b) modello triangolo-rettangolo (Fig. 5.1b) di equazioni: () ε σ ε d ε 3 per ε ε 0.175% (tratto lineare) 0 3 () ε d σ per ε.175% ε ε 0.35% (tratto otante) 3 0 u Metodo emiprobabilitio agli tati limite 32

2 ) modello rettangolo (tre blok) (Fig. 5.1) di equazioni: () ε 0 σ per ε ε 0.07% () ε d 0 4 σ per ε.07% ε ε 0.35% (tratto otante) 4 0 u % % % d d d 2 u 3 u 4 u a) b) ) Fig. 5.1 L epreione della reitenza di alolo a ompreione d è la eguente: d α dove: k è la reitenza aratteritia ilindria a ompreione del aletruzzo a 28 giorni di tagionatura ( k 0.83Rk on R k reitenza aratteritia ubia a ompreione); α 0.85 è il oeiiente riduttivo per le reitenze di lunga durata; γ 1.5 è il oeiiente parziale di iurezza relativo al aletruzzo. γ k E emplie veriiare he nel modello parabola-rettangolo la tangente alla parabola in orripondenza di ε ε 2 0.2% è orizzontale: dσ( ε) d d ε ε mentre quella nell origine ha oeiiente angolare: dσ( ε) d ε [ 1000 ( ε) ] 0 ε d Aiaio Per il diagramma tenione-deormazione dell aiaio è poibile adottare opportuni modelli rappreentativi del reale omportamento del materiale, modelli deiniti in bae al Metodo emiprobabilitio agli tati limite 33

3 valore di alolo nervamento ε 0 ε della deormazione ultima, al valore di alolo della tenione di ud. 9 uk ed al rapporto di ovrareitenza ( t y ) k k. (k-1) ud k. E E ud uk ud a) b) Fig. 5.2 Si aume un legame perettamente elatio ino alla maima tenione di alolo, on pendenza pari ad E, modulo di elatiità longitudinale dell aiaio (E MPa per tutti gli aiai); da queto valore in poi i può aumere un legame on inrudimento ino alla deormazione maima ε ud (Fig. 5.2a) oppure perettamente platio indeinito. Si ritiene opportuno, anhe in quet ultimo ao, porre lo teo limite uperiore ε ud all allungamento dell aiaio (Fig. 5.2b), enza he iò omporti otanziali modiihe a quanto verrà epoto nel eguito. Peraltro tale aunzione onentirà di rendere più omogenea la trattazione, in maniera indipendente dal partiolare legame adottato per l aiaio. Si ha: yk / γ dove: yk è la tenione aratteritia di nervamento, unzione della qualità dell aiaio, determinata nei Laboratori Uiiali Prove eondo rigoroe proedure ornite dalla normativa (è ompito del produttore eettuare tali prove e ornire i relativi ertiiati all atto della onegna del materiale, a dierenza del aletruzzo per il quale i ontrolli ono aidati in antiere al direttore dei lavori). γ è il oeiiente parziale di iurezza relativo al materiale, pari a 1.15 (valore notevolmente minore di quello del aletruzzo ia perhé l aiaio è ottopoto a più rigidi ontrolli ed è prodotto in onderia on proedimenti rigoroi, ia perhé il uo omportamento è più prevedibile: omogeneità, iotropia). La deormazione in orripondenza della reitenza di alolo è: ε / E. Metodo emiprobabilitio agli tati limite 34

4 Per l unia qualità di aiaio per.a. laminato a aldo (B450C) previta dalla Normativa vigente riulta: ε ε yk uk 450MPa E % ; ; γ ( A ) 7.5% ; ε 0.9 ε 6.75% gt k ud yk t k y k uk 391.3MPa 5.2. Ipotei di alolo alla bae del metodo emiprobabilitio agli SLU Le ipotei pote alla bae del proedimento di alolo ono: 1) onervazione delle ezioni piane; 2) peretta aderenza tra aiaio e aletruzzo; 3) reitenza a trazione del aletruzzo nulla; 4) diagrammi otitutivi dei materiali ome deritti in preedenza. Si può oervare he le prime tre ipotei ono le tee aunte ome bae della teoria tatia del.a. in ampo elatio. La quarta ipotei dierie in quanto per l aiaio i onidera anhe il ramo inrudente o perettamente platio (nell analii elatia i onidera olo il ramo elatio iniziale), mentre per il aletruzzo i onidera un legame otitutivo parabola-rettangolo, triangolo-rettangolo o rettangolo più viino al omportamento reale ripetto alla peretta proporzionalità in zona omprea aunta nell analii lineare L aderenza tra aiaio e aletruzzo L eperienza prova he una barra rettilinea di aiaio ad aderenza migliorata (a.m.), immera in un bloo di aletruzzo (l) indurito e ottopota ad una orza di trazione, i oppone all azione di ilamento: e la lunghezza del tratto di barra immero nel l è maggiore di un erto valore minimo (lunghezza di anoraggio), i arriva al ollao della barra per nervamento enza etrazione dalla ua ede. Vievera, e la lunghezza del tratto immero è minore di un erto valore minimo, i veriia lo ilamento della barra, prima he la tenione nell aiaio arrivi allo nervamento. In quet ultimo ao il enomeno dominante è la rii del ollegamento ra la barra ed il l irotante. Nel primo ao invee il enomeno dominante è la rii della barra. Il enomeno di interazione tra l armatura ed il l irotante viene denominato aderenza. Eo è dovuto eenzialmente alla rugoità artiiiale della uperiie laterale della barra (ad a.m.), uniormemente diua lungo lo viluppo lineare della barra. Metodo emiprobabilitio agli tati limite 35

5 L aderenza tra aiaio e l i viluppa in bae alle eguenti aratteritihe meanihe: l adeione, l attrito, la reitenza al taglio del l. L adeione rappreenta l inollaggio vero e proprio della pata di emento indurita all aiaio; dipende da orze apillari e moleolari e otituie una razione molto eigua dell aderenza ompleiva. L attrito ornie il prinipale ontributo di reitenza allo orrimento nel ao delle barre lie (non più previte dalle norme vigenti) ed in miura ineriore nel ao delle barre ad a.m.. E attribuito all azione di erraggio eeritato dal l he diminuie di volume per ritiro ed alle imperezioni geometrihe delle barre (non perettamente rettilinee) e alla rugoità uperiiale dei tratti omprei tra i rialti. La reitenza al taglio del l interluo ra le otole porgenti dalle barre ornie il ontributo eenziale. σ σ σ P τ T T τ σ σ σ σ1 τ σ2 σir P σrad τ Fig. 5.3 Alle tenioni tangenziali τ agenti ul ilindro oaiale alla barra ad a.m., he irorive le otole porgenti, orripondono le tenioni prinipali ompreione (Fig. 5.3). σ 1 τ di trazione e σ 2 τ di Quando σ 1 raggiunge il valore della reitenza a trazione del l ( 1/10 di quella a ompreione), il l teo i eura ed il meanimo reitente i modiia, in quanto reta oltanto il ampo delle tenioni di ompreione verranno eeritate delle tenioni di ompreione oppote alle σ. Sul l di rioprimento della barra σ indiate in igura e quindi delle omponenti radiali σ rad vero l eterno (pinte a vuoto) he rihiedono l adozione di appoite armature traverali (le tae) o un opportuno peore di rioprimento della barra. Alle tenioni radiali di ompreione i aompagnano tenioni di trazione ironerenziali σir he, in preenza di un eiguo rioprimento, poono auare eurazioni radiali e ondurre quindi allo ilamento della barra. Metodo emiprobabilitio agli tati limite 36

6 Le prove di aderenza he vengono eeguite in laboratorio ono: a) la prova di ilamento per trazione entrata (pull-out-tet); b) la prova di ilamento per trazione dovuta a leione e taglio (beam tet). Si deinie lunghezza di anoraggio il tratto terminale di una barra tea, miurato oltre la ezione nella quale la barra deve eere aoggettata alla tenione maima orripondente alla qualità dell aiaio di ui ea è otituita. La lunghezza di anoraggio deve eere tale da onentire il traerimento della orza normale πφ P 4 ( tenione di nervamento di alolo dell aiaio; φ diametro della barra) dalla barra al l, per il tramite delle tenioni tangenziali di aderenza bd, nell ipotei he ee abbiano una ditribuzione uniorme (Fig. 5.4). 2 Zona di anoraggio Zona di utilizzazione della barra P Diagramma tenioni nella barra l b bd Diagramma tenioni di aderenza bdπφ l b 2 πφ /4 Fig. 5.4 La ondizione uddetta è eprea dalla eguente equazione di equilibrio lungo la direzione della barra: bd π φl b πφ 4 2 Metodo emiprobabilitio agli tati limite 37

7 da ui i riava: l b φ. 4 Cira la tenione tangenziale di aderenza la Normativa tenia nazionale ornie l epreione: dove: bd bd γ γ 1.5 è il oeiiente parziale di iurezza relativo al aletruzzo; bk è la reitenza tangenziale aratteritia di aderenza data da: in ui: bk bk tk 2.25 η η 1.0 per barre di diametro φ 32mm ( 132 φ) 100 η per barre di diametro uperiore tk tm 2 / 3 k 2 / 3 k reitenza a trazione del l per lai C50 60 [ + 10] ln[ 1+ ( 8) 10] tk 0.7 tm ln 1 m k + per lai >C50/60. Nel ao di armature molto addenate o anoraggi in zone di aletruzzo teo, la reitenza di aderenza va ridotta dividendola almeno per 1.5. I parametri he inluenzano la tenione tangenziale di aderenza bd ono: la qualità del l da ui dipende la tk tk,0.05 ; le ondizioni di rugoità della uperiie delle barre; il diametro φ della barra ( η ); la direzione delle barre ripetto al getto: l aderenza è minore nelle barre orizzontali e maggiore in quelle vertiali, perhé in quete ultime è meno entita l inluenza dei enomeni di eudazione (bleeding); la poizione delle barre ripetto alla ezione di l. Nel ao delle travi l aderenza delle barre uperiori, viino all etradoo, è minore di quella delle barre ineriori, anora una volta a aua dell eudazione, he rende più poroo il l viino all etradoo; la quantità di armature traverali (tae), le quali aorbono le pinte radiali vero l eterno ed equilibrano le tenioni ironerenziali di trazione tramite la loro azione di oninamento del l; la preenza di eventuali tati di tenione di ompreione, opportunamente diretti, in modo da ontratare le pinte radiali a vuoto. L aderenza aumenta e le tenioni di Metodo emiprobabilitio agli tati limite 38

8 ompreione agiono perpendiolarmente all ae della barra. E il ao delle zone terminali delle travi appoggiate, dove ono loalizzate le reazioni vertiali, he premono ul oprierro dell intradoo e i oppongono alle tenioni ironerenziali di trazione. Nella eguente Tabella ono riportati intetiamente i valori della tenione tangenziale di aderenza e della lunghezza di anoraggio per barre aventi diametro φ 32mm in unzione della lae di l e delle ondizioni di aderenza (nel ao di attiva aderenza i è adottata la tenione ridotta bd bd 1. 5 ). bd [MPa] l b buona aderenza altri ai buona aderenza altri ai C25/30 C28/35 C32/40 C35/45 C40/50 γ 1.5 γ 1.5 γ 1.5 γ 1.5 γ φ 34 φ 31 φ 29 φ 27 φ 54 φ 50 φ 46 φ 44 φ 40 φ L anoraggio delle barre può eere utilmente migliorato mediante unini terminali. Se preenti, gli unini dovranno avere raggio interno pari ad almeno 6 diametri e, ai ini dell aderenza, ei poono eere omputati nella eettiva miura del loro viluppo in ae alla barra. Con rierimento alla Fig. 5.5, nella quale ono indiate le prerizioni geometrihe eenziali, lo viluppo lineare dell unino (emierhio + prolungamento) è equivalente ad un tratto rettilineo pari a 20 Φ (eattamente 3.14x6Φ + 3Φ 21.84Φ). L impiego dell unino terminale quindi a ì he la lunghezza di anoraggio in rettilineo i ridua a (l b 20 Φ) ZONA DI ANCORAGGIO ZONA DI UTILIZZO DELLA BARRA lb - 20 Fig. 5.5 In aenza degli unini la lunghezza di anoraggio deve eere in ogni ao non minore di 20 diametri, on un minimo di 150 mm. Metodo emiprobabilitio agli tati limite 39

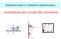
9 5.3. Condizioni ritihe di rottura (ampi di rottura) Nel metodo di alolo agli tati limite i individuano le ondizioni limite deormative, per le quali i veriia la rii nel aletruzzo o nell aiaio. Si raggiunge una ondizione ritia deormativa della ezione in.a. ogni qualvolta: 1) la deormazione nell aiaio teo raggiunge il valore limite ε ud (6.75% per il B450C); 2) la deormazione maima nel aletruzzo ompreo attinge il valore ε u 0.35% nel ao di diagramma delle deormazioni bitriangolare (l ae neutro taglia la ezione) o, al limite, triangolare (l ae neutro è radente la ezione); 3) la deormazione maima nel aletruzzo è omprea tra lo 0.35% e lo 0.2% e la ezione è tutta omprea (l ae neutro è eterno alla ezione) ed aume il valore 0.2% nella ituazione di uniorme aoriamento. Data una ezione rettangolare di altezza h e oprierro d, on rierimento alla Fig. 5.6, ono pertanto rette limite deormative tutte quelle: del aio di entro A, a partire dalla retta a, aratterizzata da ε ε ud ot, ino alla retta, aratterizzata da ε ε ud e ε,up ε u ( rottura per deormazione limite nell aiaio); del aio di entro B, a partire dalla retta, on ε ε ud e ε,up ε u, ino alla retta e on diagramma triangolare delle ε (rottura per deormazione limite nel aletruzzo); del aio di entro C (interezione della retta e e della retta on ε ε 2 0.2% ot) a partire dalla retta e ino alla (rottura per aoriamento limite nel aletruzzo). La ditanza x C del punto C dal lembo maggiormente ompreo i ottiene dalla imilitudine xc h 0.35% 0.2% 3 dei triangoli KBC e OBH : xc h h. ε ε ε 0.35% 7 u 2 u Per gli viluppi ueivi è onveniente eettuare le eguenti ulteriori uddiviioni: - del ampo ompreo tra le rette a e (aio di rette limite di entro A) nel ampo 1, tra le rette a e b, nel quale la ezione è tutta tea, e nel ampo 2, tra le rette b e, nel quale la ezione è in parte tea e in parte omprea; - del ampo ompreo tra le rette e e (aio di entro B) nel ampo 3, tra le rette e d, nel quale l aiaio ineriore è teo e nervato e nel ampo 4, tra le rette d ed e, nel quale l aiaio ineriore è teo o ompreo ma elatio. Il aio di entro C (ampo ompreo tra le rette e e ) prende il nome di ampo 5. Si india on ξx/d il rapporto tra la ditanza dell ae neutro dal bordo maggiormente ompreo e l altezza utile d della ezione. Metodo emiprobabilitio agli tati limite 40

10 h d A' d' a 1 b O d K u B C 5 3 h 7 d' A b A ud 2 e H x Fig. 5.6 Campo 1: aio di rette di rottura on entro in A, ompree tra la retta a e la retta b. La rii avviene per deormazione limite nell aiaio teo (ε ε ud ) on ezione tutta tea. L ordinata x è omprea tra x a - (ξ a - retta limite a ) e x b 0 (ξ b 0 retta limite b ). Le olleitazioni he i poono preentare in queto Campo ono la tenoleione e la trazione. Si ha trazione pura allorquando la riultante degli orzi di trazione nelle armature è appliata nel barientro della ezione in aletruzzo. Campo 2: aio di rette di rottura on entro in A, ompree tra la retta b e la retta. La rii avviene per deormazione limite nell aiaio teo (ε ε ud ); in partiolare, in orripondenza della retta limite i ha la ontemporanea rii nell aiaio teo, per raggiungimento della deormazione limite ε ud, e nel aletruzzo ompreo per raggiungimento della deormazione limite ε u. La ezione è empre parzializzata. L ordinata x è omprea tra x b 0 (ξ b 0 retta limite b ) e x d (ξ retta limite ). Inatti per emplie imilitudine tra triangoli, aumendo ε ud 6.75% (B450C), riulta: x εu 0.35% ξ d ε + ε 0.35% % u ud Eendo la ezione parzializzata, le olleitazioni he i poono avere ono la tenoleione, la preoleione e la leione. Però, oprattutto in viinanza della retta b, è poo probabile he i abbiano le olleitazioni di preoleione e leione emplie, poihé quete rihiedono ripettivamente he gli orzi di ompreione iano uperiori o uguali a quelli di trazione. In queto ao lo orzo di ompreione è generato da un eiguo trato di aletruzzo al di opra dell'ae neutro, per di più oggetto ad un aoriamento limitato (e, dunque, ad una tenione limitata in virtù del legame otitutivo σ-ε) e da un ontributo, anh eo eiguo, oerto dall armatura uperiore e omprea. Lo orzo di trazione, invee, raggiunge il valore maimo, eendo l armatura ineriore nervata. Metodo emiprobabilitio agli tati limite 41

11 Si potrebbe avere preoleione nel ao in ui ia preente un eigua quantità di armatura tea, ma iò è in ontrato on quanto preritto dalle norme tenihe. Quete inatti prevedono una perentuale minima di armatura da diporre nelle travi in zona tea al ine di oddiare il ondamentale requiito di robutezza nei onronti di azioni eezionali, oia la apaità della truttura di evitare danni proporzionati ripetto all entità delle aue inneanti (inendio, eploioni, urti). Si ritiene importante inoltre aggiungere alune ondamentali oniderazioni in bae alle quali arebbe opportuno traurare nel Campo 2 il ontributo del aletruzzo. E ben noto innanzitutto he il materiale aletruzzo, miela di emento, aqua ed inerti di varia pezzatura, i può oniderare omogeneo olo a livello maroopio, aumendo dei valori medi delle aratteritihe himihe, iihe e meanihe. Inoltre per eigenze di protezione delle armature le norme tenihe prevedono, in unzione della lae di epoizione ambientale del manuatto (ondizioni ambientali ordinarie, aggreive o molto aggreive), della poroità del aletruzzo e della enibilità delle armature alla orroione, dei valori minimi del oprierro, omunque empre dell ordine di pohi entimetri (minimo aoluto 20 millimetri). In onluione, poihé nel Campo 2 la poizione dell ae neutro è tale da ridurre l altezza della aia di aletruzzo ompreo a dimenioni addirittura ineriori a quelle del pietrio utilizzato per il onezionamento del miuglio, è da ritenere aolutamente inattendibile l aunzione di omogeneità del onglomerato. Nel ueivo apitolo verrà omunque meo in onto nel Campo 2 il modeto ontributo oerto dal aletruzzo, ma olo per motivi di ompletezza ed uniormità di trattazione on gli altri Campi di rottura. Campo 3: aio di rette di rottura on entro in B, ompree tra la retta e la retta d. La rii avviene per deormazione limite nel aletruzzo ompreo (ε u 0.35%) on aiaio teo nervato. La x è omprea tra x 0.049d (ξ retta limite ) e, per l aiaio B450C, x εu 0.35% d d 0.65d ( ξ d 0.65 retta limite d ). ε + ε 0.35% % d u Eendo la ezione parzializzata, anhe in queto ao le olleitazioni poibili ono tenoleione, preoleione e leione emplie. Campo 4: aio di rette di rottura on entro in B, ompree tra la retta d e la retta e. La rii avviene per deormazione limite nel aletruzzo ompreo (ε u 0.35%) on Metodo emiprobabilitio agli tati limite 42

12 armatura ineriore tea oppure omprea ma empre in ampo elatio. La x è omprea tra x d 0.65d (ξ d 0.65 retta limite d ) e x e h altezza ompleiva della ezione ( ξ h d ( d + d' ) d 1+ δ e retta limite e, avendo indiato on δ d' d il valore del oprierro adimenionalizzato). Eendo la ezione parzializzata, i tipi di olleitazione poibili ono tenoleione, preoleione e leione. Va però evidenziato he per x d, ioè quando ia la ezione di l he le armature ono ompree, è poibile olo la olleitazione di preoleione. Campo 5: aio di rette di rottura on entro in C, ompree tra la retta e e la retta. La rii avviene per deormazione limite nel aletruzzo ompreo (ε 2 ε ε u ) on aiaio ineriore ompreo. La x è omprea tra x e h (ξ e 1+δ retta limite e ) e x + (ξ + retta limite ). La retta limite e è aratterizzata dalla deormazione limite nel aletruzzo ompreo pari a ε u 0.35% (diagramma triangolare), mentre la retta limite dalla deormazione nel aletruzzo ompreo otante e pari a ε 2 0.2% (diagramma rettangolare). In quet ultimo ao la rii avviene per raggiungimento ontemporaneo della deormazione limite in tutte le ibre della ezione, ituazione notevolmente più perioloa ripetto al ao di rii per deormazione limite di una ola orda. Le olleitazioni poibili ono preoleione e ompreione pura. Quet ultima i ha in orripondenza della retta limite e il barientro delle armature oinide on quello della ezione di aletruzzo. Nella tabella eguente è intetizzato quanto inora epoto. Campo ξx/d Caletruzzo Deormazioni Arm. in. Tipo di olleitazione 1 < ξ ξ b 0 ε >0 ε ε ud 6.75% Tenoleione Trazione pura 2 ξ b 0 ξ ξ ε ε u 0.35% ε ε ud 6.75% 3 ξ ξ ξ d 0.65 ε ε u 0.35% ε 0.19% ε ε ud 6.75% Tenoleione Fleione Preoleione Tenoleione Fleione Preoleione Tipo di rottura Deorm. limite nell aiaio teo Deorm. limite nell aiaio teo Deorm. limite nel l 4 ξ d 0.65 ξ 1+δ ε ε u 0.35% ε ε 0.19% 5 1+δ ξ < + ε 2 0.2% ε ε u 0.35% -0.2% ε Tenoleione Fleione Preoleione Preoleione Compreione pura Deorm. limite nel l Deorm. limite nel l Metodo emiprobabilitio agli tati limite 43