Intervalli di Fiducia
|
|
|
- Floriana Massa
- 6 anni fa
- Visualizzazioni
Transcript
1 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica Sio ad ora si soo cosiderati diversi stimatori putuali: per esempio la media Y è u oggetto il cui valore atteso coicide co il parametro cercato μ. D altrode l osservazioe di Y sarà (sempre) u po più grade o u po più piccola del valore vero o possiamo affermare che y è esattamete uguale a μ. Si potrebbe costruire u itervallo del tipo μ = y ± Δy i cui riteiamo molto otoprobabile ecada il valore vero di μ. Δy dipederà dall ampiezza delle fluttuazioi Y di Tale tipo di itervallo prede il ome di itervallo o itervallo fiduciario o itervallo di cofideza
2 di Fiducia Itroduzioe Determiare l itervallo di ua gradezza misurata θ, equivale alla determiazioe di due umeri θ e θ, tali che icludao il valore vero co certezza. Comuque, si è visto che o è possibile, da u campioe fiito di dati sperimetali, trarre delle coclusioi riguardo alla popolazioe che siao certe al % E possibile stabilire però u itervallo i cui il valore vero ha probabilità molto elevata (esempio: 95% o 99%) di cadere. 3 di Fiducia Procedura Si sceglie ua probabilità γ vicia a. Tale probabilità prede il ome di livello. Si determiao quidi due quatità Θ e Θ tali che la probabilità che Θ e Θ racchiudao il valore esatto Θ sia eguale a γ. L itervallo di estremi Θ e Θ si chiama itervallo e si idica co il simbolo: CONF { Θ Θ Θ } Θ 4
3 di Fiducia Procedura Scegliere γ = 95% equivale a dire che i preseza di u campioe di dati c è ua probabilità del 95% che il valore vero ricada ell itervallo determiato. La scelta di γ implica ua differete ampiezza dell itervallo di fiducia calcolato. All aumetare di γ, quale è il comportameto della larghezza dell itervallo? 5 della Media el caso di variaza ota. Sia dato u certo campioe di dati sperimetali y, y,..., Ipotesi: Tutte le gradezze misurate soo caratterizzate dalla stessa variabile aleatoria (eguale media e variaza) e soo idipedeti. La variaza della variabile aleatoria è ota (per esempio da pregresse misure) La media, ivece, è igota. y 6 3
4 di Fiducia Caso di variaza ota La determiazioe dell itervallo passa per i segueti puti:. Scegliere u livello γ. Calcolare il valore c tale che: 3. Calcolare F X ( c) F ( c) = γ dove F è la distribuzioe cumulativa della ormale di tipo stadard, ovvero X ~ N(,) X k = cσ. L itervallo per la popolazioe sarà: { y k μ y k} cof + 7 di Fiducia Caso di variaza ota Gli campioi dei dati sperimetali possoo essere visti come sigole osservazioi della stessa variabile aleatoria Y (co eguale distribuzioe, eguale variaza, eguale media). La variabile media del campioe è quidi ua variabile aleatoria di media μ e variaza σ /. La variabile aleatoria Y X = σ ~ N μ, Y μ σ È ua variabile aleatoria ormale di tipo stadard. ~ N(,) 8 4
5 di Fiducia Caso di Variaza Nota Il valore y è quidi u valore osservato della variabile Y Determiiamo iazitutto il valore di c tale che ( c X c) = γ Questa ieguagliaza può essere scritta come: P P c Y μ σ c = γ 9 di Fiducia Caso di Variaza Nota Da cui: σ σ P c Y μ c = γ Co qualche passaggio si ottiee ifie: dove ( k μ Y + k) = γ P Y σ k = c Questo passaggio merita u po di attezioe! (riflettere sulle VA i gioco) La relazioe di prima si legge: La probabilità che il valore vero della media μ sia racchiuso i u itervallo cetrato sulla stima Y co uo spessore k è pari a γ 5
6 - Media aritmetica Caso Variaza a priori ota Importate: Nella diseguagliaza μ è sempre costate. È l itervallo che varia co il campioe. Per chiarire il cocetto, si cosideri il caso (poco realistico) i cui si abbia la coosceza della popolazioe i termii di media e variaza. La popolazioe sia, per esempio, di tipo Gaussiao co media e variaza: μ Y σ Y = 69 = 3.3 Si prelevi da questa popolazioe u campioe di elemeti per cui la variabile aleatoria media sia: μ Y σy = 69 σy = =. N - Media aritmetica Caso Variaza a priori ota Se uo statistico ripete il calcolo dell itervallo più volte (ovviamete su campioi differeti): calcolati Solo ua volta su l itervallo o racchiude il valore vero 6
7 di Fiducia Caso di Variaza Nota L itervallo rappreseta u itervallo di umeri reali i cui ricada il valore vero della media (μ), co ua probabilità pari al 95%. Nel caso i cui l itervallo sia del 99%, l itervallo è più grade o più piccolo di quello determiato precedetemete? Quale sarebbe l itervallo di cofideza per u livello γ del %? 3 - Media aritmetica Caso Variaza a priori ota All aumetare del umero di prove, la variaza della media aritmetica (ovvero l icertezza ella stima) decresce L itervallo di valori i cui soo più ricorreti le stime per la media aritmetica si restrige: N > N. σ = Y σ N. σ = Y σ N μ c μ μ+c μ c μ μ+c 7
8 - Media aritmetica Caso Variaza a priori ota Come valutare lo spessore c dell itervallo La costate c γ può essere valutata dalla seguete probabilità: P ( c < Z < c ) = γ γ Essedo Z la variabile aleatoria Gaussiaa stadard (di media e variaza ) γ.5 Valori tipici di c γ per differeti livelli γ γ c γ γ=.95 γ=.99 - Media aritmetica Caso Variaza o ota Il calcolo dell itervallo emerge i maiera aturale dalla atura Gaussiaa dello stimatore media aritmetica Tale derivazioe è possibile grazie alla coosceza pregressa della variaza dell errore sperimetale Nella realtà, questo è raramete possibile e si coosce solo ua stima della variaza dell errore sperimetale: s = N ( y i y) i = Tale evetualità implica u ulteriore sorgete di icertezza da teere i coto el calcolo dell itervallo I maiera ituitiva, dovremmo cosiderare degli itervalli più ampi di quelli registrati el caso di coosceza della variaza 8
9 della Media Caso di Variaza o ota. I passi per la determiazioe dell itervallo soo i segueti:. Scegliere u livello γ. Calcolare il valore c tale che: F T () c = ( + γ) Dove F T (y) è la fuzioe di distribuzioe cumulativa della T di studet ad (-) gradi di libertà 3. Calcolare la media y e la variaza s del campioe dei dati 4. sperimetali. s Calcolare k = c 5. L itervallo sarà: { y k μ y k} cof + 7 della Media Caso di Variaza o ota. La variabile aleatoria: Y μ X = σ È ua variabile ormale di tipo stadard Si è gia visto che lo stimatore imparziale variaza s può essere correlata ad ua variabile aleatoria χ a - gradi di libertà : σ χ s ( i ) χ = = = i= σ s Y Y 8 9
10 della Media Caso di Variaza o ota. I coclusioe la variabile aleatoria: Y μ Z Y T = = σ = χ s σ μ s È ua variabile aleatoria di tipo T di studet ad - gradi di libertà Il passaggio alla T di studet è ecessario per la semplificazioe della variaza σ igota. 9 della Media Caso di Variaza o ota. Il campioe di risultati sperimetali può quidi essere visto, el suo isieme, come u risultato della variabile aleatoria T di studet, ua volta ota la media dei dati sperimetali e la variaza stimata. È possibile quidi determiare quale è la probabilità che tale variabile assumi valori compresi i u certo itervallo. P ( Θ Θ ) = γ Θ
11 y della Media Caso di Variaza o ota. È ecessario quidi determiare, data la simmetria della distribuzioe, u umero c tale che P ( c T c) = F ( c) F ( c) = γ Data la simmetria della distribuzioe, F(-c) = -F(c) e quidi T T Da cui P ( c T c) = F T ( c) = γ F T c = + γ ( ) ( ) della Media Caso di Variaza o ota. La distribuzioe T di studet è geeralmete più larga della distribuzioe ormale di tipo stadard x Pertato ci attediamo u itervallo di ampiezza più grade, rispetto al caso i cui la variaza sia ota i modo esatto.
12 per stimatori Caso geerica per variaza o ota. Dato uo stimatore geerico (N.B. di tipo gaussiao), la variabile aleatoria ˆθ ˆ θ θ s θ Rappreseta sempre ua variabile aleatoria di tipo T di studet. Ituitivamete, tale gradezza è la distaza tra valore osservato e valore vero, ormalizzata per la radice della variaza La gradezza s θ è il valore osservato della variaza dello stimatore Il umero di gradi di libertà della T di studet dipede ivece da caso a caso. Si deve fare riferimeto ai gradi di libertà della stima della variaza 3 per i coefficieti di regressioe Oltre alle stime putuali sui coefficieti di regressioe è possibile valutare u itervallo per i coefficieti stimati della regressioe. Lo spessore dell itervallo è ua misura della qualità della regressioe. 4
13 per i coefficieti di regressioe Nel caso della regressioe lieare, è ecessaria ua stima imparziale della variaza dell errore sperimetale: s = MSE = i= ( y b b x ) I parecchi libri di testo tale espressioe prede ache il ome di Errore Quadratico Medio (i iglese: Mea Square Errore, acroimo MSE) i i 5 per i coefficieti di regressioe Si è gia visto che gli stimatori b e b soo delle variabili aleatorie Gaussiae, ell ipotesi che l errore ella misura all esperimeto i- esimo sia Gaussiao. Si può dimostrare che le segueti variabili aleatorie: b β MSE S e b β x MSE + xx S xx soo delle distribuzioi T di studet ad - gradi di libertà. 6 3
14 per i coefficieti di regressioe Procedura: Si sceglie u livello γ Calcolare il valore c tale che: () = ( + γ) F T c Dove F è la distribuzioe t di studet ad - gradi di libertà. Calcolare MSE k = c k S Gli itervalli sarao: = c x MSE + xx S xx { b k β b + k } e cof { b k β b } cof + k 7 per i coefficieti di regressioe La quatità: ( b ) se = MSE S xx Si chiama errore stadard della pedeza e misura la precisioe co cui β è stata stimata. I modo aalogo, la quatità: se x ( b ) = MSE + Si chiama errore stadard dell itercetta e misura la precisioe co cui β è stata stimata. S xx 8 4
15 per la risposta media U ulteriore esempio è la determiazioe dell itervallo per la risposta media E(y=b +b x) per u particolare valore della variabile regressore x La stima putuale forisce u valore: y ˆ = b + b x Ci si poe il problema della determiazioe di u itervallo di fiducia per la variabile y i corrispodeza del valore x 9 per la risposta media Il primo passaggio cosiste ella determiazioe della variaza della variabile aleatoria La variaza è: V [ ] ( yˆ ) V ( b + b x ) = V Y + b ( x x) σ ( x x) ( x x) σ + = = Si può dimostrare che le VA Y e b = σ + + Cov( Y, b ) soo S xx S xx idipedeti Se per σ prediamo lo stimatore MSE si può dimostrare che la variabile aleatoria: y yˆ ( x x) MSE + S xx È ua distribuzioe T di studet ad - g.d.l. 3 5
16 per la risposta media Procedura: Scegliere u livello γ Calcolare il valore c tale che: () = ( + γ) F T c Dove F è la distribuzioe T di studet ad - gradi di libertà. Calcolare ( x ) = c L itervallo sarà: k MSE ( ) x x + S xx { yˆ k( x ) y y k( x )} cof + ˆ 3 per la risposta media L itervallo è variabile co x, esso assumerà valore miimo i corrispodeza del cetroide dei dati
17 per i Coefficieti di ua regressioe multilieare Problema: Regressioe multilieare: y = F α T a = ( ) ( p)( p ) T ( F F) F y Ipotesi: Gli errori ε i soo idipedeti e ormalmete distribuiti. La variaza degli errori è uguale a σ Ne segue che la stima a è ormalmete distribuita co vettore media α e matrice di covariaza σ (F T F) - Questo implica che la margiale di ogi coefficiete di regressioe è ormale co media α j evariazaσ C jj,l elemeto diagoale della matrice (F T F) - 33 per i Coefficieti di ua regressioe multilieare Ne cosegue che la geerica statistica: a j α j MSE C jj È ua distribuzioe t di studet ad -p gradi di libertà, dove MSE è la stima di σ, così come defiito el semplice caso della regressioe lieare. 34 7
18 per i Coefficieti di ua regressioe multilieare Procedura: Scegliere u livello γ Calcolare il valore c tale che: () = ( + γ) F T c Dove F è la distribuzioe t di studet ad -p gradi di libertà. Calcolare k = c MSE C jj L itervallo sarà: cof { a k α a k} j j j
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
CONCETTI BASE DI STATISTICA
 CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
iovanella@disp.uniroma2.it http://www.disp.uniroma2.it/users/iovanella Intervalli di confidenza
 iovaella@disp.uiroma.it http://www.disp.uiroma.it/users/iovaella Itervalli di cofideza Itroduzioe Note geerali La stima putuale permette di otteere valori per i parametri di ua fuzioe ma i alcui casi può
iovaella@disp.uiroma.it http://www.disp.uiroma.it/users/iovaella Itervalli di cofideza Itroduzioe Note geerali La stima putuale permette di otteere valori per i parametri di ua fuzioe ma i alcui casi può
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA. Prof.ssa Donatella Siepi tel:
 UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
Titolo della lezione. Dal campione alla popolazione: stima puntuale e per intervalli
 Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Metodi statistici per l analisi dei dati
 Metodi statistici per l aalisi dei dati due ttameti Motivazioi ttameti Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ttameti) per cui soo stati codotti gli esperimeti. due ttameti Esempio itroduttivo
Metodi statistici per l aalisi dei dati due ttameti Motivazioi ttameti Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ttameti) per cui soo stati codotti gli esperimeti. due ttameti Esempio itroduttivo
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA
 UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Metodi statistici per l'analisi dei dati
 Metodi statistici per l aalisi dei dati due Motivazioi Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ) per cui soo stati codotti gli esperimeti. Metodi tatistici per l Aalisi dei Dati due Esempio
Metodi statistici per l aalisi dei dati due Motivazioi Obbiettivo: Cofrotare due diverse codizioi (ache defiiti ) per cui soo stati codotti gli esperimeti. Metodi tatistici per l Aalisi dei Dati due Esempio
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
Y = ln X è normalmente distribuita. (y) = dg(x) dx. f Y. (x) = dy dx f Y. f X. (g(x)) & exp$ dx x - $ % ( x) DISTRIBUZIONE LOG-NORMALE.
 DISTRIBUZIONE LOG-NORMALE. La variabile si dice log-ormalmete distribuita se: l è ormalmete distribuita g( l g ( e 0 +. uzioe di desità di probabilità: f ( d d f ( dg( d f (g( dg( d f (. & ep$ - / $ %,
DISTRIBUZIONE LOG-NORMALE. La variabile si dice log-ormalmete distribuita se: l è ormalmete distribuita g( l g ( e 0 +. uzioe di desità di probabilità: f ( d d f ( dg( d f (g( dg( d f (. & ep$ - / $ %,
Lezione 5. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 5. A. Iodice.
 La Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 26 Outlie La 1 2 La 3 4 () Statistica 2 / 26 Trimmed mea - La aritmetica risete della preseza di valori
La Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 26 Outlie La 1 2 La 3 4 () Statistica 2 / 26 Trimmed mea - La aritmetica risete della preseza di valori
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Statistica 1 A.A. 2015/2016
 Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
Corso di Laurea i Ecoomia e Fiaza Statistica 1 A.A. 2015/2016 (8 CFU, corrispodeti a 48 ore di lezioe frotale e 24 ore di esercitazioe) Prof. Luigi Augugliaro 1 / 21 Misura della dipedeza di u carattere
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
La correlazione e la regressione. Antonello Maruotti
 La correlazioe e la regressioe Atoello Maruotti Outlie 1 Correlazioe 2 Associazioe tra caratteri quatitativi Date due distribuzioi uitarie secodo caratteri quatitativi X e Y x 1 x 2 x y 1 y 2 y associate
La correlazioe e la regressioe Atoello Maruotti Outlie 1 Correlazioe 2 Associazioe tra caratteri quatitativi Date due distribuzioi uitarie secodo caratteri quatitativi X e Y x 1 x 2 x y 1 y 2 y associate
Teoria dei Fenomeni Aleatori AA 2012/13
 Statistica Matematica: Cocetti Fodametali Nell esperieza quotidiaa e ella pratica della professioe dell igegere occorre: predere decisioi e ciò ormalmete richiede la dispoibilità di specifiche iformazioi
Statistica Matematica: Cocetti Fodametali Nell esperieza quotidiaa e ella pratica della professioe dell igegere occorre: predere decisioi e ciò ormalmete richiede la dispoibilità di specifiche iformazioi
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
INFERENZA o STATISTICA INFERENTE
 INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
Lezione III: Variabilità. Misure di dispersione o di variabilità. Prof. Enzo Ballone. Lezione 3a- Misure di dispersione o di variabilità
 Lezioe III: Variabilità Cattedra di Biostatistica Dipartimeto di Scieze Biomediche, Uiversità degli Studi G. d Auzio di Chieti Pescara Prof. Ezo Balloe Lezioe a- Misure di dispersioe o di variabilità Misure
Lezioe III: Variabilità Cattedra di Biostatistica Dipartimeto di Scieze Biomediche, Uiversità degli Studi G. d Auzio di Chieti Pescara Prof. Ezo Balloe Lezioe a- Misure di dispersioe o di variabilità Misure
STATISTICA 1 ESERCITAZIONE 5
 STATISTICA ESERCITAZIONE 5 Dott. Giuseppe Padolfo 28 Ottobre 203 VARIABILITA IN TERMINI DI DISPERSIONE DA UN CENTRO Cetro Me o μ La dispersioe viee misurata come sitesi delle distaze tra le uità statistiche
STATISTICA ESERCITAZIONE 5 Dott. Giuseppe Padolfo 28 Ottobre 203 VARIABILITA IN TERMINI DI DISPERSIONE DA UN CENTRO Cetro Me o μ La dispersioe viee misurata come sitesi delle distaze tra le uità statistiche
Anemia. Anemia - percentuali
 1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
Metodi statistici per l analisi dei dati
 Metodi statistici per l aalisi dei dati Massimiliao Grosso Dipartimeto di Igegeria Meccaica, Chimica e dei Materiali E-mail: massimiliao.grosso@dimcm.uica.it Web: http://people.uica.it/massimiliaogrosso
Metodi statistici per l aalisi dei dati Massimiliao Grosso Dipartimeto di Igegeria Meccaica, Chimica e dei Materiali E-mail: massimiliao.grosso@dimcm.uica.it Web: http://people.uica.it/massimiliaogrosso
Diagramma polare e logaritmico
 Diagramma polare e aritmico ariatori discotiui del moto di taglio Dalla relazioe π D c si ota che la velocità di taglio dipede, oltre che dal umero di giri del madrio, ache dal diametro dell elemeto rotate
Diagramma polare e aritmico ariatori discotiui del moto di taglio Dalla relazioe π D c si ota che la velocità di taglio dipede, oltre che dal umero di giri del madrio, ache dal diametro dell elemeto rotate
Inferenza statistica. Popolazione. Camp. Statistiche campionarie basate sulle osservazioni del campione. Estrazione casuale. Parametro e statistica
 6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
INTRODUZIONE ALLA INFERENZA STATISTICA
 INTRODUZIONE ALLA INFERENZA STATISTICA 1) CONCETTO DI INFERENZA STATISTICA E SCOPI : L ifereza statistica è il procedimeto iduttivo che, avvaledosi del calcolo delle probabilità, cosete di estedere all
INTRODUZIONE ALLA INFERENZA STATISTICA 1) CONCETTO DI INFERENZA STATISTICA E SCOPI : L ifereza statistica è il procedimeto iduttivo che, avvaledosi del calcolo delle probabilità, cosete di estedere all
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
6 Stima di media e varianza, e intervalli di confidenza
 Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE
 DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
DEFINIZIONE PROCESSO LOGICO E OPERATIVO MEDIANTE IL QUALE, SULLA BASE DI UN GRUPPO DI OSSERVAZIONI O DI ESPERIMENTI, SI PERVIENE A CERTE CONCLUSIONI, LA CUI VALIDITA PER UN COLLETTIVO Più AMPIO E ESPRESSA
Lezione 10 - Tensioni principali e direzioni principali
 Lezioe 10 - Tesioi pricipali e direzioi pricipali ü [A.a. 2011-2012 : ultima revisioe 23 agosto 2011] I questa lezioe si studiera' cio' che avviee alla compoete ormale di tesioe s, al variare del piao
Lezioe 10 - Tesioi pricipali e direzioi pricipali ü [A.a. 2011-2012 : ultima revisioe 23 agosto 2011] I questa lezioe si studiera' cio' che avviee alla compoete ormale di tesioe s, al variare del piao
PROBLEMI DI INFERENZA SU MEDIE
 PROBLEMI DI INFERENZA SU MEDIE STIMA PUNTUALE Il problema della stima di ua media si poe allorchè si vuole cooscere, sulla base di osservazioi campioarie, il valore medio μ che u dato carattere preseta
PROBLEMI DI INFERENZA SU MEDIE STIMA PUNTUALE Il problema della stima di ua media si poe allorchè si vuole cooscere, sulla base di osservazioi campioarie, il valore medio μ che u dato carattere preseta
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
LABORATIORIO 3. Taratura statica
 LABORATIORIO 3 Taratura statica Obiettivi dell esercitazioe Obiettivo di questa esercitazioe è lo svolgimeto di ua serie di esperieze di laboratorio per verificare e applicare le coosceze relative alle
LABORATIORIO 3 Taratura statica Obiettivi dell esercitazioe Obiettivo di questa esercitazioe è lo svolgimeto di ua serie di esperieze di laboratorio per verificare e applicare le coosceze relative alle
Matematica e Statistica: Modulo di Statistica - Prof. Federico Di Palma - Appello del 12 Febbraio
 Matematica e Statistica: Modulo di Statistica - Prof. Federico Di Palma - Appello del 1 Febbraio 014 - Esercizio 1) I ua ricerca si è iteressati a verificare le dimesioi i micrometri di u graulocita eutrofilo.
Matematica e Statistica: Modulo di Statistica - Prof. Federico Di Palma - Appello del 1 Febbraio 014 - Esercizio 1) I ua ricerca si è iteressati a verificare le dimesioi i micrometri di u graulocita eutrofilo.
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
STUDIO DEL LANCIO DI 3 DADI
 Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
 Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
LE MISURE DI TENDENZA CENTRALE
 STATISTICA DESCRITTIVA LE MISURE DI TENDENZA CENTRALE http://www.biostatistica.uich.itit OBIETTIVO Esempio: Nella tabella seguete soo riportati i valori del tasso glicemico rilevati su 0 pazieti: Idividuare
STATISTICA DESCRITTIVA LE MISURE DI TENDENZA CENTRALE http://www.biostatistica.uich.itit OBIETTIVO Esempio: Nella tabella seguete soo riportati i valori del tasso glicemico rilevati su 0 pazieti: Idividuare
Esame di Statistica A-Di Prof. M. Romanazzi
 1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
Regressione e correlazione
 Regressioe e correlazioe Regressioe e correlazioe I molti casi si osservao gradezze che tedoo a covariare, ma () Se c è ua relazioe di dipedeza fra due variabili, ovvero se il valore di ua variabile (dipedete)
Regressioe e correlazioe Regressioe e correlazioe I molti casi si osservao gradezze che tedoo a covariare, ma () Se c è ua relazioe di dipedeza fra due variabili, ovvero se il valore di ua variabile (dipedete)
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2005/06
 PROVE SCRITTE DI MTEMTIC PPLICT, NNO 5/6 Esercizio 1 Prova scritta del 14/1/5 Sia X ua successioe I.I.D. di variabili aleatorie co distribuzioe uiforme cotiua, X U(, M), ove M = umero lettere del cogome.
PROVE SCRITTE DI MTEMTIC PPLICT, NNO 5/6 Esercizio 1 Prova scritta del 14/1/5 Sia X ua successioe I.I.D. di variabili aleatorie co distribuzioe uiforme cotiua, X U(, M), ove M = umero lettere del cogome.
Argomenti trattati: Capitolo 12 libro di testo. Statistica - Metodologie per le scienze economiche e sociali A. Di Ciaccio, S.
 1 GLI INTERVALLI DI CONFIDENZA Argometi trattati: Stima per itervallo Aalogie tra la stima putuale e per itervallo Itervallo di cofideza per la media Itervallo di cofideza per la proporzioe Itervallo di
1 GLI INTERVALLI DI CONFIDENZA Argometi trattati: Stima per itervallo Aalogie tra la stima putuale e per itervallo Itervallo di cofideza per la media Itervallo di cofideza per la proporzioe Itervallo di
Titolo della lezione. Campionamento e Distribuzioni Campionarie
 Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
STATISTICA INFERENZIALE SCHEDA N. 2 INTERVALLI DI CONFIDENZA PER IL VALORE ATTESO E LA FREQUENZA
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
CAPITOLO 2 Semplici esperimenti comparativi
 Douglas C. Motgomer Progettazioe e aalisi degli esperimeti 006 McGraw-Hill CAPITOLO emplici esperimeti comparativi Metodi statistici e probabilistici per l igegeria Corso di Laurea i Igegeria Civile A.A.
Douglas C. Motgomer Progettazioe e aalisi degli esperimeti 006 McGraw-Hill CAPITOLO emplici esperimeti comparativi Metodi statistici e probabilistici per l igegeria Corso di Laurea i Igegeria Civile A.A.
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Esercizi di econometria: serie 2
 Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
16 - Serie Numeriche
 Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Uiversità degli Studi di Palermo Facoltà di Ecoomia CdS Statistica per l Aalisi dei Dati Apputi del corso di Matematica 6 - Serie Numeriche Ao Accademico 03/04 M. Tummiello, V. Lacagia, A. Cosiglio, S.
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Confronto di due misure Campioni indipendenti
 Statistica7 /11/015 Cofroto di due misure Campioi idipedeti o meglio.. rispodere al quesito Due serie di misure soo state estratte dalla stessa popolazioe (popolazioe comue o idetica) o soo state estratte
Statistica7 /11/015 Cofroto di due misure Campioi idipedeti o meglio.. rispodere al quesito Due serie di misure soo state estratte dalla stessa popolazioe (popolazioe comue o idetica) o soo state estratte
Consideriamo un insieme di n oggetti di natura qualsiasi. Indicheremo questi oggetti con
 Calcolo Combiatorio Adolfo Scimoe pag 1 Calcolo combiatorio Cosideriamo u isieme di oggetti di atura qualsiasi. Idicheremo questi oggetti co a1 a2... a. Co questi oggetti si voglioo formare dei gruppi
Calcolo Combiatorio Adolfo Scimoe pag 1 Calcolo combiatorio Cosideriamo u isieme di oggetti di atura qualsiasi. Idicheremo questi oggetti co a1 a2... a. Co questi oggetti si voglioo formare dei gruppi
Approfondimento 2.1 Scaling degli stimoli mediante il metodo del confronto a coppie
 Approfodimeto 2.1 Scalig degli stimoli mediate il metodo del cofroto a coppie Il metodo del cofroto a coppie di Thurstoe (Thurstoe, 1927) si basa sull assuzioe che la valutazioe di u oggetto o di uo stimolo
Approfodimeto 2.1 Scalig degli stimoli mediate il metodo del cofroto a coppie Il metodo del cofroto a coppie di Thurstoe (Thurstoe, 1927) si basa sull assuzioe che la valutazioe di u oggetto o di uo stimolo
Materiale didattico relativo al corso di Matematica generale Prof. G. Rotundo a.a.2009/10
 Materiale didattico relativo al corso di Matematica geerale Prof. G. Rotudo a.a.2009/10 ATTENZIONE: questo materiale cotiee i lucidi utilizzati per le lezioi. NON sostituisce il libro, che deve essere
Materiale didattico relativo al corso di Matematica geerale Prof. G. Rotudo a.a.2009/10 ATTENZIONE: questo materiale cotiee i lucidi utilizzati per le lezioi. NON sostituisce il libro, che deve essere
STATISTICA INFERENZIALE - SCHEDA N. 1 CAMPIONAMENTO E STIMA
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
Matematica e statistica: dai dati ai modelli alle scelte www.dima.uige/pls_statistica Resposabili scietifici M.P. Rogati e E. Sasso (Dipartimeto di Matematica Uiversità di Geova) STATISTICA INFERENZIALE
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
STATISTICA A K (63 ore)
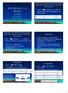 STATISTICA A K (63 ore) Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto =400 X =34.000 Km; s cor =9000 Km Calcolare l
STATISTICA A K (63 ore) Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto =400 X =34.000 Km; s cor =9000 Km Calcolare l
Esercitazione 6 del corso di Statistica 2
 Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Esercitazioni di Statistica Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it
 Esercitazioi di Statistica Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Cocetrazioe Esercizio 1. Nell'ultima settimaa ua baca ha erogato i segueti importi (i migliaia di euro) per prestiti a imprese:
Esercitazioi di Statistica Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Cocetrazioe Esercizio 1. Nell'ultima settimaa ua baca ha erogato i segueti importi (i migliaia di euro) per prestiti a imprese:
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
NOTE DALLE LEZIONI DI STATISTICA MEDICA ED ESERCIZI
 NOTE DALLE LEZIONI DI TATITICA MEDICA ED EERCIZI I METODI PER IL CONFRONTO DI MEDIE (Campioi idipedeti) IL PROBLEMA oo stati rilevati i dati relativi alla frequeza cardiaca (misurata i battiti al miuto)
NOTE DALLE LEZIONI DI TATITICA MEDICA ED EERCIZI I METODI PER IL CONFRONTO DI MEDIE (Campioi idipedeti) IL PROBLEMA oo stati rilevati i dati relativi alla frequeza cardiaca (misurata i battiti al miuto)
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Università di Napoli Federico II, DISES, A.a , CLEC, Corso di Statistica (L-Z) Lezione 22 La verifica delle ipotesi. Corso di Statistica (L-Z)
 Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE
 DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
DETERMINANTI (SECONDA PARTE). NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 21 DICEMBRE 2010 1. Sviluppi di Laplace Proposizioe 1.1. Sia A M, (K), allora per ogi idice i = 1,..., fissato vale lo sviluppo
Esercitazioni del corso: ANALISI MULTIVARIATA
 A. A. 9 1 Esercitazioi del corso: ANALISI MULTIVARIATA Isabella Romeo: i.romeo@campus.uimib.it Sommario Esercitazioe 4: Verifica d Ipotesi Test Z e test T Test d Idipedeza Aalisi Multivariata a. a. 9-1
A. A. 9 1 Esercitazioi del corso: ANALISI MULTIVARIATA Isabella Romeo: i.romeo@campus.uimib.it Sommario Esercitazioe 4: Verifica d Ipotesi Test Z e test T Test d Idipedeza Aalisi Multivariata a. a. 9-1
Intervalli di confidenza
 Itervalli di cofideza Fracesco Lagoa Itroduzioe Questa dispesa riassume schematicamete i pricipali risultati discussi a lezioe sulla costruzioe di itervalli di cofideza. Itervalli di cofideza per la media
Itervalli di cofideza Fracesco Lagoa Itroduzioe Questa dispesa riassume schematicamete i pricipali risultati discussi a lezioe sulla costruzioe di itervalli di cofideza. Itervalli di cofideza per la media
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO Che cosa sigifica cotare Tutti coosciamo la successioe dei umeri iteri Naturali N = {0, 1,,, } si tratta di ua struttura metale fodametale, chiaramete presete alla ostra ituizioe che
CALCOLO COMBINATORIO Che cosa sigifica cotare Tutti coosciamo la successioe dei umeri iteri Naturali N = {0, 1,,, } si tratta di ua struttura metale fodametale, chiaramete presete alla ostra ituizioe che
Corso di laurea in STATISTICA MATEMATICA E TRATTAMENTO INFORMATICO DEI DATI
 Corso di laurea i STATISTICA MATEMATICA E TRATTAMENTO INFORMATICO DEI DATI Raccolta delle prove scritte degli esami del corso di STATISTICA INFERENZIALE STATISTICA INFERENZIALE SMID a.a. 00/3 Prova scritta
Corso di laurea i STATISTICA MATEMATICA E TRATTAMENTO INFORMATICO DEI DATI Raccolta delle prove scritte degli esami del corso di STATISTICA INFERENZIALE STATISTICA INFERENZIALE SMID a.a. 00/3 Prova scritta
Precorso di Matematica. Parte IV : Funzioni e luoghi geometrici
 Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
converge in probabilità alla v.a. X e si scrive: converge in media quadratica alla v.a. X e si scrive: m n
 98 Covergeza i probabilità Si dice che la successioe X coverge i probabilità alla v.a. X e si scrive: se, per qualsiasi ε > 0, si ha: X p X oppure plim X = X limp( X X < ε)= Covergeza i media quadratica
98 Covergeza i probabilità Si dice che la successioe X coverge i probabilità alla v.a. X e si scrive: se, per qualsiasi ε > 0, si ha: X p X oppure plim X = X limp( X X < ε)= Covergeza i media quadratica
Quartili. Esempio Q 3 Q 1. Distribuzione unitaria degli affitti settimanali in euro pagati da 19 studenti U.S. A G I F B D L H E M C
 Quartili Primo quartile Q 1 : modalità che ella graduatoria (crescete o decrescete) bipartisce il 50% delle osservazioi co modalità più piccole o al più uguali alla Me Terzo quartile Q 3 : modalità che
Quartili Primo quartile Q 1 : modalità che ella graduatoria (crescete o decrescete) bipartisce il 50% delle osservazioi co modalità più piccole o al più uguali alla Me Terzo quartile Q 3 : modalità che
Teoremi limite classici
 Capitolo 4 Teoremi limite classici I Teoremi limite classici, la Legge dei Gradi Numeri e il Teorema Limite Cetrale, costituiscoo il ucleo del Calcolo delle Probabilità, per la loro portata sia teorica
Capitolo 4 Teoremi limite classici I Teoremi limite classici, la Legge dei Gradi Numeri e il Teorema Limite Cetrale, costituiscoo il ucleo del Calcolo delle Probabilità, per la loro portata sia teorica
Scheda n.6: legame tra due variabili; correlazione e regressione
 Scheda.6: legame tra due variabili; correlazioe e regressioe October 26, 2008 Covariaza e coefficiete di correlazioe Date due v.a. X ed Y, chiamiamo covariaza il umero Cov (X, Y ) = E [(X E [X]) (Y E [Y
Scheda.6: legame tra due variabili; correlazioe e regressioe October 26, 2008 Covariaza e coefficiete di correlazioe Date due v.a. X ed Y, chiamiamo covariaza il umero Cov (X, Y ) = E [(X E [X]) (Y E [Y
Esercizi sulle successioni
 Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
Esercizi sulle successioi 1 Verificare, attraverso la defiizioe, che la successioe coverge a 2 3. a := 2 + 3 3 7 2 Verificare, attraverso la defiizioe, che la successioe coverge a 0. a := 4 + 3 3 5 + 7
5. INDICI DI VARIABILITA'
 UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso di Laurea i Scieze per l'ivestigazioe e la Sicurezza. INDICI DI VARIABILITA' Prof. Maurizio Pertichetti
UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso di Laurea i Scieze per l'ivestigazioe e la Sicurezza. INDICI DI VARIABILITA' Prof. Maurizio Pertichetti
Distribuzioni di probabilità
 Itroduzioe Distribuzioi di robabilità Fio ad ora abbiamo studiato ua secifica fuzioe desità di robabilità, la fuzioe di Gauss, che descrive variabili date dalla somma di molti termii idiedeti es. ua misura
Itroduzioe Distribuzioi di robabilità Fio ad ora abbiamo studiato ua secifica fuzioe desità di robabilità, la fuzioe di Gauss, che descrive variabili date dalla somma di molti termii idiedeti es. ua misura
Programma (orientativo) secondo semestre 32 ore - 16 lezioni
 Programma (orietativo) secodo semestre 32 ore - 6 lezioi 3 lezioi: successioi e serie 4 lezioi: itegrali 2-3 lezioi: equazioi differeziali 4 lezioi: sistemi di equazioi e calcolo vettoriale e matriciale
Programma (orietativo) secodo semestre 32 ore - 6 lezioi 3 lezioi: successioi e serie 4 lezioi: itegrali 2-3 lezioi: equazioi differeziali 4 lezioi: sistemi di equazioi e calcolo vettoriale e matriciale
Radici, potenze, logaritmi in campo complesso.
 SOMMARIO NUMERI COMPLESSI... Formula di Eulero... Coiugato di u umero complesso... 3 Poteza -esima di u umero complesso z (formula di De Moivre... 3 Radice -esima di z... 3 Osservazioi... Logaritmo di
SOMMARIO NUMERI COMPLESSI... Formula di Eulero... Coiugato di u umero complesso... 3 Poteza -esima di u umero complesso z (formula di De Moivre... 3 Radice -esima di z... 3 Osservazioi... Logaritmo di
RISOLUZIONE MODERNA DI PROBLEMI ANTICHI
 RISOLUZIONE MODERNA DI PROBLEMI ANTICHI L itelletto, duque, che o è la verità, o comprede mai la verità i modo così preciso da o poterla compredere (poi acora) più precisamete, all ifiito, perché sta alla
RISOLUZIONE MODERNA DI PROBLEMI ANTICHI L itelletto, duque, che o è la verità, o comprede mai la verità i modo così preciso da o poterla compredere (poi acora) più precisamete, all ifiito, perché sta alla
1 Statistica Inferenziale
 1 Statistica Ifereziale Cosideriamo u tipico problema che coduce a cosiderazioi di tipo statistico: Problema: Ua moeta, di cui si igora l oestà, viee laciata 1000 volte otteedo 447 teste. Si può affermare
1 Statistica Ifereziale Cosideriamo u tipico problema che coduce a cosiderazioi di tipo statistico: Problema: Ua moeta, di cui si igora l oestà, viee laciata 1000 volte otteedo 447 teste. Si può affermare
