DISEGNO TECNICO INDUSTRIALE
|
|
|
- Leonora Bruno
- 8 anni fa
- Visualizzazioni
Transcript
1 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico
2 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione e costruzione di organi di macchine, assume una funzione basilare la conoscenza della geometria elementare ed euclidea e della geometria proiettiva e descrittiva. Con la geometria elementare si introducono certi enti primitivi (punti, rette e piani) e si enunciano certe proporzioni riguardanti le varie relazioni interconnesse con la esplicita loro rappresentazione sul piano. A tale scopo, quindi, vanno finalizzate le costruzioni geometriche, intese a formalizzare graficamente, secondo convenzioni date, la rappresentazione sul piano di oggetti spaziali e, viceversa, intese a ricostruire la visione tridimensionale degli oggetti deducendola dalle loro rappresentazioni simboliche piane.
3 Le Costruzioni Geometriche Per esempio la costruzione geometrica sul piano di un poligono esagonale ci consente di rappresentare virtualmente la testa di una vite e/o la configurazione di un dado. Il tracciamento di tangenti e la costruzione di raccordi consente la rappresentazione sul piano di meccanismi fondamentali (eccentrici) costituiti da una coppia cinematica intesa a trasmettere per contatto reciproco un moto alternativo traslatorio o rotatoria da un corpo detto movente, ad un altro detto cedente. L applicazione più comune si trova negli alberi della distribuzione dei motori a combustione interna, in cui il movente prende il nome di camma.
4 Le Costruzioni Geometriche Gli eccentrici trovano impiego assai vasto nelle costruzioni meccaniche. Importanti sono gli impieghi nelle macchine utensili, tessili e simili e vengono con sempre più frequenza applicati nelle macchine utensili automatiche, in cui camme intercambiabili possano comandare tempi e modalità di intere sequenze operative. Altro importante ed interessante esempio di applicazione delle costruzioni geometriche, con particolare riferimento alle curve ad evolvente epicicloide ed ipocicloide si ha nel tracciamento del profilo delle ruote dentate. Per la ruota dentata con dentatura ad evolvente il profilo del dente si ottiene mediante il tracciamento della curva evolvente rispetto ad una circonferenza concentrica della primitiva della ruota. Per le ruote dentate con dentatura epicicloidale, il profilo del dente si ottiene tracciando rispetto alla circonferenza primitiva o di base una curva epicicloidale.
5 Le costruzioni geometriche si possono così suddividere: costruzioni fondamentali (costruzioni 1 11); curve notevoli (costruzioni 12 33); curve nello spazio (costruzioni 34 37); poligoni (costruzioni 38 63); raccordi (costruzioni 64 95).
6 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI FONDAMENTALI Anno Accademico
7
8
9
10
11
12
13
14
15 DISEGNO TECNICO INDUSTRIALE CURVE NOTEVOLI Anno Accademico
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 DISEGNO TECNICO INDUSTRIALE CURVE NELLO SPAZIO Anno Accademico
38
39
40
41 DISEGNO TECNICO INDUSTRIALE COSTRUZIONE GRAFICA DI POLIGONI Anno Accademico
42
43
44
45
46
47
48
49 DISEGNO TECNICO INDUSTRIALE COSTRUZIONE GRAFICA DI RACCORDI E TANGENTI Anno Accademico
50 DEFINIZIONE DI RACCORDO Dati due tratti di linea (curvi e/o rettilinei) si definisce curva di raccordo (o semplicemente raccordo) l arco (o gli archi) di curva, avente, in corrispondenza del punto di contatto con ciascuno dei due tratti di linea assegnati, la tangente comune. Due linee complanari sono tangenti in un punto (punto appartenente ad entrambe le linee) quando da esso passa la retta normale comune alle due linee.
51 Le costruzioni dei raccordi risultano di fondamentale importanza in parecchie applicazioni meccaniche. A tal proposito dalla definizione della curva di raccordo si evince una vasta tipologia di raccordi: una prima classificazione porta a distinguere i raccordi piani dai raccordi nello spazio; è poi possibile differenziare gli stessi in raccordi parabolici, iperbolici, ellittici ecc. a seconda del tipo di arco di curva che li definisce. Nelle tavole che seguono sono presi in considerazione solo i raccordi circolari piani, senz altro i più utilizzati nelle applicazioni tecniche ed industriali. Vengono considerati cioè solo i casi in cui i tratti di curva utilizzati per raccordare le linee complanari date sono archi di circonferenza. In particolare vengono descritti tutti i possibili raccordi costituiti da un solo arco di circonferenza e i casi più significativi di raccordi costituiti da due archi.
52 Nelle varie tavole sono evidenziate con un tratto più spesso la curva di raccordo finale e le linee date. Inoltre si indica con R (R e R nei raccordi costituiti da due archi) il raggio e con C (C e C nei raccordi costituiti da due archi) il centro dell arco di circonferenza che costituisce il raccordo, mentre con T1 e T2 si indicano i punti in cui la curva di raccordo ha la tangente comune con ciascuna delle due linee (curve o rettilinee) assegnate. Nei raccordi costituiti da una doppia curva si indica con T3 il punto di tangenza tra i due archi che costituiscono la curva di raccordo. Le costruzioni delle tangenti possono essere considerate come dei casi limite di raccordo quando il raggio dell arco assume valore infinito.
53 Da un punto di vista analitico la costruzione di un raccordo circolare piano consiste nel determinare in un sistema piano di assi cartesiani ortogonali (0, x, y) l equazione della circonferenza che contiene l arco di raccordo cercato. Tale equazione ha la forma x 2 +y 2 + ax + by + c = 0 (dove a, b, c sono tre numeri reali). Per individuare in maniera univoca la circonferenza occorre, quindi, imporre tre condizioni (passaggi per determinati punti, tangenze, condizioni sul centro e sul raggio della circonferenza). I raccordi determinati da due o più archi di circonferenza costituiscono una generalizzazione del problema dei raccordi tra due tratti di linea e permettono di raccordare gli stessi fissando ulteriori condizioni di vincolo, quali il punto di tangenza T3 tra i due archi e la lunghezza del raggio R2 del secondo arco che costituisce il raccordo.
54 Nei disegni che illustrano le costruzioni si utilizzano vari colori e tipi di linee e precisamente: la linea continua grossa di colore nero, per le curve di raccordo cercate; la linea continua di colore ciano, per le linee di costruzione; la linea mista fine di colore ciano, per gli assi di simmetria; la linea continua di colore rosso, per le linee di riferimento e di misura delle quote. Sempre di colore rosso sono le indicazioni delle quote, delle frecce unitamente alle lettere e ai numeri.
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86 Tracciare il segmento O 1 O 2 e determinare su di esso il punto medio M. Con centri in O 1 e M e con raggi rispettivamente R 4 =R 1 R 2 e R 3 =O 1 M tracciare due archi di circonferenza che si incontrano nei punti A e B. I punti di tangenza T 1 e T 2 con la circonferenza c 1 si determinano tracciando rispettivamente la retta congiungente i punti O 1 e A e la retta congiungente i punti O 1 e B. I punti di tangenza T 3 e T 4 con la circonferenza c 2 si determinano tracciando da O 2 le rette parallele rispettivamente ad O 1 T 1 e ad O 1 T 2. Le rette r e s congiungenti rispettivamente i punti T 1 con T 3 e T 2 con T 4 sono le tangenti cercate.
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni
 Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
Ruote Dentate. Ing. Alessandro Carandina A.A. 2014/2015. Disegno Tecnico Industriale per Ingegneria Meccanica
 Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
RUOTE DENTATE. Introduzione
 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Esercizio Decorazioni
 Nome Cognome Classe Data La riproduzione di questa pagina tramite fotocopie è autorizzata ai soli fini dell utilizzo nell attività didattica degli alunni delle classi che hanno adottato il testo. Esercizio
Nome Cognome Classe Data La riproduzione di questa pagina tramite fotocopie è autorizzata ai soli fini dell utilizzo nell attività didattica degli alunni delle classi che hanno adottato il testo. Esercizio
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico
 La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
Spline Nurbs. IUAV Disegno Digitale. Camillo Trevisan
 Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
Esercizi complementari al corso di DISEGNO TECNICO INDUSTRIALE (MECL, AUTL, MATL), a.a. 2005/06.
 UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
UNIVERSITÀ DI BRESCIA - FACOLTA DI INGEGNERIA DIPARTIMENTO DI INGEGNERIA MECCANICA Gabriele Baronio, Valerio Villa. Esercizi complementari al corso di (MECL, AUTL, MATL), a.a. 2005/06. La presente raccolta
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI
 DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
Programmazione per competenze del corso Matematica, Secondo biennio
 Programmazione per del corso Matematica, Secondo biennio Competenze di area Traguardi per lo sviluppo delle degli elementi del calcolo algebrico algebriche di primo e secondo grado di grado superiore al
Programmazione per del corso Matematica, Secondo biennio Competenze di area Traguardi per lo sviluppo delle degli elementi del calcolo algebrico algebriche di primo e secondo grado di grado superiore al
6. Moto in due dimensioni
 6. Moto in due dimensioni 1 Vettori er descriere il moto in un piano, in analogia con quanto abbiamo fatto per il caso del moto in una dimensione, è utile usare una coppia di assi cartesiani, come illustrato
6. Moto in due dimensioni 1 Vettori er descriere il moto in un piano, in analogia con quanto abbiamo fatto per il caso del moto in una dimensione, è utile usare una coppia di assi cartesiani, come illustrato
Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008
 Alma Mater Studiorum Università di Bologna Seconda Facoltà di Ingegneria con Sede a Cesena Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008 Docente: Tutor:
Alma Mater Studiorum Università di Bologna Seconda Facoltà di Ingegneria con Sede a Cesena Disegno Tecnico Aerospaziale L (A-L) Disegno Tecnico Industriale L (A-L) Anno Accademico 2007/2008 Docente: Tutor:
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI
 MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI Obiettivi del triennio: ; elaborando opportune soluzioni; 3) utilizzare le reti e gli strumenti informatici
MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI Obiettivi del triennio: ; elaborando opportune soluzioni; 3) utilizzare le reti e gli strumenti informatici
SymCAD/C.A.T.S. modulo Antincendio
 SymCAD/C.A.T.S. modulo Antincendio Potente ed aggiornato strumento di progettazione di reti idranti e sprinkler secondo le norme UNI EN 12845, UNI 10779 e NFPA 13 - - - - - - - - - - - - - - - - - - -
SymCAD/C.A.T.S. modulo Antincendio Potente ed aggiornato strumento di progettazione di reti idranti e sprinkler secondo le norme UNI EN 12845, UNI 10779 e NFPA 13 - - - - - - - - - - - - - - - - - - -
Corso di Automazione industriale
 Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
Corso di Automazione industriale Lezione 11 Macchine utensili e controllo numerico Programmazione CNC Università degli Studi di Bergamo, Automazione Industriale, A.A. 2015/2016, A. L. Cologni 1 Introduzione
L Unità didattica in breve
 L Unità didattica in breve Trasmissione del moto mediante ruote dentate Si definisce ingranaggio l accoppiamento di due ruote dentate ingrananti fra loro, montate su assi la cui posizione relativa resta
L Unità didattica in breve Trasmissione del moto mediante ruote dentate Si definisce ingranaggio l accoppiamento di due ruote dentate ingrananti fra loro, montate su assi la cui posizione relativa resta
STANDARD MINIMI DI RIFERIMENTO MATEMATICA LICEO TECNICO
 STANDARD MINIMI DI RIFERIMENTO MATEMATICA LICEO TECNICO CLASSE 1^ CONOSCENZE Insiemi numerici N, Z, Q, R; rappresentazioni, operazioni, ordinamento Espressioni algebriche; principali operazioni Equazioni
STANDARD MINIMI DI RIFERIMENTO MATEMATICA LICEO TECNICO CLASSE 1^ CONOSCENZE Insiemi numerici N, Z, Q, R; rappresentazioni, operazioni, ordinamento Espressioni algebriche; principali operazioni Equazioni
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
Proiezioni Grafica 3d
 Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Docente: DI LISCIA F. CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI
 Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
PROGRAMMAZIONE della M.U. CNC
 PROGRAMMAZIONE della M.U. CNC 1 La programmazione delle M.U. CNC 1 Generalità 2 Geometrie di riferimento 3 Grammatica 4 Lessico 5 Sintassi 6 Esempi 7 Linguaggio APT 2 La programmazione delle M.U. CNC Le
PROGRAMMAZIONE della M.U. CNC 1 La programmazione delle M.U. CNC 1 Generalità 2 Geometrie di riferimento 3 Grammatica 4 Lessico 5 Sintassi 6 Esempi 7 Linguaggio APT 2 La programmazione delle M.U. CNC Le
Fig. 2. Proiezioni ortogonali di un parallelepipedo su piani esterni alla figura
 3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
TRASFORMAZIONI GEOMETRICHE NEL PIANO. Parte 1
 TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
.y 6. .y 4. .y 5. .y 2.y 3 B C C B. B f A B f -1
 Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. x 1. x..y B C.y 5 x 4..y 4 L elemento è
Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. x 1. x..y B C.y 5 x 4..y 4 L elemento è
Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti. Equazioni e Disequazioni
 Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti Equazioni e Disequazioni Ripasso generale relativo alla risoluzione di equazioni, disequazioni,
Liceo Scientifico F. Lussana Bergamo Programma di MATEMATICA A.S. 2014/2015 Classe 3 A C Prof. Matteo Bonetti Equazioni e Disequazioni Ripasso generale relativo alla risoluzione di equazioni, disequazioni,
Corso di. Dott.ssa Donatella Cocca
 Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
INTRODUZIONE AI SISTEMI CAD
 INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Disegno di Macchine. Lezione n 7 Componentistica di base: alberi. corso per I anno della laurea in ing. meccanica Docente: ing.
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 7 Componentistica di base: alberi Introduzione ai componenti di macchine I componenti meccanici
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 7 Componentistica di base: alberi Introduzione ai componenti di macchine I componenti meccanici
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO
 ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO vittorio.scialla@strumentiperleaziende.com Attuatore per traiettorie non lineari dotato di
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO vittorio.scialla@strumentiperleaziende.com Attuatore per traiettorie non lineari dotato di
 6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
RUGOSITÀ. Introduzione
 RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
 Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
PROVA N 1. 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(x) PROVA N 2. è monotona in R?
 PROVA N 1 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(). Studiare la funzione f()= 8+ 7 9 (Sono esclusi i flessi) 3. Data la funzione f()= 1 6 3 - +5-6
PROVA N 1 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(). Studiare la funzione f()= 8+ 7 9 (Sono esclusi i flessi) 3. Data la funzione f()= 1 6 3 - +5-6
I NUMERI DECIMALI. che cosa sono, come si rappresentano
 I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
www.atoolsoftware.it
 www.atoolsoftware.it import / export dxf import ascii import macchine (configurazione attrezzaggio) Aspan è un programma che tramite il suo CAD/CAM interno permette di realizzare in modo semplice ed immediato
www.atoolsoftware.it import / export dxf import ascii import macchine (configurazione attrezzaggio) Aspan è un programma che tramite il suo CAD/CAM interno permette di realizzare in modo semplice ed immediato
Disegno di Macchine. corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Amministrazione, finanza e marketing - Turismo Ministero dell Istruzione, dell Università e della Ricerca PROGRAMMAZIONE DISCIPLINARE PER U. di A.
 UdA n. 1 Titolo: Disequazioni algebriche Saper esprimere in linguaggio matematico disuguaglianze e disequazioni Risolvere problemi mediante l uso di disequazioni algebriche Le disequazioni I principi delle
UdA n. 1 Titolo: Disequazioni algebriche Saper esprimere in linguaggio matematico disuguaglianze e disequazioni Risolvere problemi mediante l uso di disequazioni algebriche Le disequazioni I principi delle
PLANIMETRIA E PROFILO INSIEME
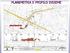 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
2) Sul piano coordinato z = 0 studiare il fascio Φ di coniche di equazione. determinando in particolare le sue coniche spezzate ed i suoi punti base.
 DPARTMENTO D MATEMATCA E NFORMATCA Corso di Laurea in ngegneria Telematica Prova scritta di Elementi di Algebra e Geometria assegnata il 18/7/02 È assegnato l endomorfismo f : R 3 R 3 definito dalle relazioni
DPARTMENTO D MATEMATCA E NFORMATCA Corso di Laurea in ngegneria Telematica Prova scritta di Elementi di Algebra e Geometria assegnata il 18/7/02 È assegnato l endomorfismo f : R 3 R 3 definito dalle relazioni
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
COMANDI PER CICLI. Ciclo: un insieme di operazioni (movimentazioni, ecc.) che evolvono secondo una sequenza prestabilita.
 COMANDI PER CICLI Ciclo: un insieme di operazioni (movimentazioni, ecc.) che evolvono secondo una sequenza prestabilita. Tipologie di comandi per cicli: 1. MANUALI o ARBITRARI : ogni azione della sequenza
COMANDI PER CICLI Ciclo: un insieme di operazioni (movimentazioni, ecc.) che evolvono secondo una sequenza prestabilita. Tipologie di comandi per cicli: 1. MANUALI o ARBITRARI : ogni azione della sequenza
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Università degli Studi della Calabria. Ruote dentate
 Trasmissione di moto rotatorio mediante ruote di frizione (ad assi paralleli od anche sghembi) Accoppiamento ruota/dentiera Coppia di ruote dentate fra loro ingrananti: la distanza fra i denti lungo la
Trasmissione di moto rotatorio mediante ruote di frizione (ad assi paralleli od anche sghembi) Accoppiamento ruota/dentiera Coppia di ruote dentate fra loro ingrananti: la distanza fra i denti lungo la
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
Disegno 2D, rappresentazioni
 CAD 2D/3D Disegno 2D, rappresentazioni piane Disegno 2D, rappresentazioni piane Il CAD 2D è il livello base per il disegno bidimensionale, cioè quello che consente di rappresentare un oggetto mediante
CAD 2D/3D Disegno 2D, rappresentazioni piane Disegno 2D, rappresentazioni piane Il CAD 2D è il livello base per il disegno bidimensionale, cioè quello che consente di rappresentare un oggetto mediante
Strumenti di controllo degli organi meccanici
 Strumenti di controllo degli organi meccanici Il controllo dello spessore dei denti di un ingranaggio, può essere effettuato mediante il calibro a doppio nonio o mediante un micrometro a piattelli. Calibro
Strumenti di controllo degli organi meccanici Il controllo dello spessore dei denti di un ingranaggio, può essere effettuato mediante il calibro a doppio nonio o mediante un micrometro a piattelli. Calibro
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
CLASSE 1ª Manutenzione e Assistenza Tecnica
 CLASSE 1ª Manutenzione e Assistenza Tecnica Programma svolto di MATEMATICA Anno scolastico 2013/14 ELEMENTI DI RACCORDO CON LA SCUOLA MEDIA GLI INSIEMI CALCOLO LETTERALE GEOMETRIA - Ordinamento, proprietà,
CLASSE 1ª Manutenzione e Assistenza Tecnica Programma svolto di MATEMATICA Anno scolastico 2013/14 ELEMENTI DI RACCORDO CON LA SCUOLA MEDIA GLI INSIEMI CALCOLO LETTERALE GEOMETRIA - Ordinamento, proprietà,
Modello matematico PROGRAMMAZIONE LINEARE PROGRAMMAZIONE LINEARE
 PRGRMMZIN LINR Problemi di P.L. in due variabili metodo grafico efinizione: la programmazione lineare serve per determinare l allocazione ottimale di risorse disponibili in quantità limitata, per ottimizzare
PRGRMMZIN LINR Problemi di P.L. in due variabili metodo grafico efinizione: la programmazione lineare serve per determinare l allocazione ottimale di risorse disponibili in quantità limitata, per ottimizzare
/H]LRQH,OFRQIURQWRGHOOHVXSHUILFL,O SUREOHPD GHO FRQIURQWR GL VXSHUILFL H OD WUDVIRUPD]LRQH GL SROLJRQLHTXLYDOHQWL
![/H]LRQH,OFRQIURQWRGHOOHVXSHUILFL,O SUREOHPD GHO FRQIURQWR GL VXSHUILFL H OD WUDVIRUPD]LRQH GL SROLJRQLHTXLYDOHQWL /H]LRQH,OFRQIURQWRGHOOHVXSHUILFL,O SUREOHPD GHO FRQIURQWR GL VXSHUILFL H OD WUDVIRUPD]LRQH GL SROLJRQLHTXLYDOHQWL](/thumbs/27/11668192.jpg) /H]LRQH,OFRQIURQWRGHOOHVXSHUILFL,O SUREOHPD GHO FRQIURQWR GL VXSHUILFL H OD WUDVIRUPD]LRQH GL SROLJRQLHTXLYDOHQWL Il confronto della lunghezza tra due segmenti è un problema molto semplice. Infatti tutti
/H]LRQH,OFRQIURQWRGHOOHVXSHUILFL,O SUREOHPD GHO FRQIURQWR GL VXSHUILFL H OD WUDVIRUPD]LRQH GL SROLJRQLHTXLYDOHQWL Il confronto della lunghezza tra due segmenti è un problema molto semplice. Infatti tutti
Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica
 Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica Classe: 5 Meccanica Docente prof. Angelo Rinaldi Ore settimanali previste: 4 ore ro totale di ore 4x33=132 ore Libro di testo Corso di Meccanica
Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica Classe: 5 Meccanica Docente prof. Angelo Rinaldi Ore settimanali previste: 4 ore ro totale di ore 4x33=132 ore Libro di testo Corso di Meccanica
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI PROGRAMMAZIONE ANNUALE ANNO SCOLASTICO 2014 /2015
 ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI PROGRAMMAZIONE ANNUALE ANNO SCOLASTICO 2014 /2015 A047 MATEMATICA CLASSE PRIMA PROFESSIONALE DOCENTI : CARAFFI ALESSANDRA, CORREGGI MARIA GRAZIA, FAZIO ANGELA,
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI PROGRAMMAZIONE ANNUALE ANNO SCOLASTICO 2014 /2015 A047 MATEMATICA CLASSE PRIMA PROFESSIONALE DOCENTI : CARAFFI ALESSANDRA, CORREGGI MARIA GRAZIA, FAZIO ANGELA,
Classificazione. Dispensa per istruttori di primo Livello parte seconda
 Classificazione Dispensa per istruttori di primo Livello parte seconda Vittorio Brizzi-2014 Diverse geometrie di archi, diversi grafici Cultura e ambiente nella storia hanno condizionato l evoluzione del
Classificazione Dispensa per istruttori di primo Livello parte seconda Vittorio Brizzi-2014 Diverse geometrie di archi, diversi grafici Cultura e ambiente nella storia hanno condizionato l evoluzione del
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Corso Integrato di DISEGNO A Prof.ssa Anna De Santis
 Prima Facoltà di Architettura Ludovico Quaroni Corso di Laurea in DISEGNO INDUSTRIALE A.A. 2007-08 - 1 Semestre Corso Integrato di DISEGNO A Prof.ssa Anna De Santis Calendario del corso con argomenti svolti
Prima Facoltà di Architettura Ludovico Quaroni Corso di Laurea in DISEGNO INDUSTRIALE A.A. 2007-08 - 1 Semestre Corso Integrato di DISEGNO A Prof.ssa Anna De Santis Calendario del corso con argomenti svolti
Il valore assoluto. F. Battelli Università Politecnica delle Marche, Ancona. Pesaro, Precorso di Analisi 1, 22-28 Settembre 2005 p.
 Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
PROGRAMMAZIONE di MATEMATICA CLASSE PRIMA
 PROGRAMMAZIONE di MATEMATICA 1.NUMERI CLASSE PRIMA Comprende il significato Comprendere il significato Insiemi numerici NQZ Utilizzare le tecniche e le procedure del calcolo aritmetico e algebrico rappresentandole
PROGRAMMAZIONE di MATEMATICA 1.NUMERI CLASSE PRIMA Comprende il significato Comprendere il significato Insiemi numerici NQZ Utilizzare le tecniche e le procedure del calcolo aritmetico e algebrico rappresentandole
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Mete e coerenze formative. Dalla scuola dell infanzia al biennio della scuola secondaria di II grado
 Mete e coerenze formative Dalla scuola dell infanzia al biennio della scuola secondaria di II grado Area disciplinare: Area Matematica Finalità Educativa Acquisire gli alfabeti di base della cultura Disciplina
Mete e coerenze formative Dalla scuola dell infanzia al biennio della scuola secondaria di II grado Area disciplinare: Area Matematica Finalità Educativa Acquisire gli alfabeti di base della cultura Disciplina
09 - Funzioni reali di due variabili reali
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 09 - Funzioni reali di due variabili reali Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 09 - Funzioni reali di due variabili reali Anno Accademico 2013/2014
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Esercizi svolti sui numeri complessi
 Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
Introduzione al 3D con Autocad
 2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
Progetto e costruzione di macchine Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas Copyright 2005 The McGraw-Hill Companies srl
 Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE
 100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE Queste domande sono state tratte dai registri delle sessioni d'esame orale degli scorsi anni. L'esame orale, di regola, viene svolto ponendo tre domande:
100 DOMANDE PER L'ESAME ORALE DI DISEGNO DI MACCHINE Queste domande sono state tratte dai registri delle sessioni d'esame orale degli scorsi anni. L'esame orale, di regola, viene svolto ponendo tre domande:
