Figure piane. Due figure sono congruenti se sovrapposte coincidono perfettamente. figure a contorno mistilineo
|
|
|
- Riccardo Antonini
- 6 anni fa
- Visualizzazioni
Transcript
1
2 Figure piane poigoni cerci figure a contorno curviineo figure a contorno mistiineo I due poigoni sono congruenti I due cerci non sono congruenti ue figure sono congruenti se sovrapposte coincidono perfettamente
3 F F F Le figure F, F ed F non anno a stessa forma, non sono quindi congruenti, ma sono formate dao stesso numero di parti congruenti; diciamo ce sono equicomposte composte dao stesso numero di parti congruenti). Essendo equicomposte, anno tutte a stessa estensione, in quanto occupano a stessa parte di superficie; e ciamiamo aora equivaenti e indiciamo ciò ne seguente modo: F & F & F eggi: F equivaente a F equivaente a F )
4 onsideriamo un rettangoo avente a ase unga 5 cm e atezza unga 3 cm. Per cacoare a sua area asterà vedere quante vote un unità di misura è contenuta in esso. Se scegiamo come unità di misura i centimetro quadrato e o riportiamo in esso, osserviamo ce ci sono 15 quadratini, cioè area è di 15 cm². tae risutato arriviamo motipicando fra oro i numeri 5 e 3 ce esprimono, in centimetri, a ungezza dea ase e de atezza. 1cm L area de rettangoo si ottiene motipicando a misura dea ase per quea de atezza. La formua è quindi: formua diretta) formue inverse)
5 I quadrato è un particoare rettangoo avente a ase congruente a atezza. Per cacoare a sua area possiamo appicare a stessa formua de rettangoo: dove, cioè L area de quadrato si ottiene motipicando a misura de ato per se stessa. La formua è: formua diretta) formua inversa)
6 Osserva i paraeogramma ; se da esso ritagiamo i triangoo H e o spostiamo daa parte opposta, otteniamo un rettangoo equivaente a paraeogramma. Possiamo quindi affermare ce: H H Un paraeogramma è equivaente a un rettangoo avente a stessa ase e a stessa atezza. L area de paraeogramma si ottiene motipicando a misura dea ase per quea de atezza. La formua è: formua diretta) formue inverse)
7 Un triangoo è equivaente aa metà di un paraeogramma avente a stessa ase e a stessa atezza. L area de triangoo si ottiene motipicando a misura dea ase per quea de atezza a essa reativa e dividendo tae prodotto per due. La formua è: formua diretta) formue inverse)
8 E H Un romo è equivaente aa metà di un rettangoo ce a per ase e per atezza rispettivamente e due diagonai de romo. L area de romo si ottiene motipicando e misure dee due diagonai e dividendo tae prodotto per due. F d d1 O G d d1 O La formua è: d1 d d1 d formua diretta) d formue d 1 inverse)
9 1 1 Un trapezio è equivaente aa metà di un paraeogramma ce a come ase a somma dee asi de trapezio e come atezza a stessa atezza. H isegniamo i trapezio 1 isegniamone due congruenti e sistemiamoi in modo da far coincidere un ato oiquo. L area di un trapezio si ottiene motipicando a somma dee asi per a misura de atezza e dividendo tae prodotto per due ) 1 La formua sarà: formua + 1 diretta) Otteniamo un paraeogramma ce a per ase a somma dee asi de trapezio e per atezza a stessa atezza. formue inverse)
10 H G onsideriamo un poigono regoare, per esempio ottagono EFGH. ome vedi si può dividere in 8 triangoi congruenti. In ognuno di questi triangoi a ase coincide con un ato de ottagono e atezza è apotema de poigono. Per cacoare area de ottagono asterà cacoare area di uno dei triangoi e motipicare i risutato per otto: a F E a a t da cui : o 6 ma 6 ) non è atro ce i perimetro de' esagono, quindi a p a formua diventa :
11 iremo quindi ce: L area di un poigono regoare si ottiene motipicando a misura de perimetro per a misura de apotema e dividendo tae prodotto per due. La formua è: acoare a misura de apotema f e φ sono due costanti, detti impropriamente numeri fissi, i oro vaore dipende da tipo di poigono. p p a a a formua diretta) ) p a ϕ f ϕ formue e a f formua formua H inverse) a diretta) inversa) G F E
12
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
Equivalenza di figure piane +soperimetria ed equivalenza di figure piane Area di triangoli e quadrilateri Teorema di Pitagora e sue applicazioni
 Equivaenza i figure piane +soperimetria e equivaenza i figure piane rea i triangoi e quariateri Teorema i itagora e sue appiazioni +soperimetria e equivaenza i figure piane Staiisi se e seguenti affermazioni
Equivaenza i figure piane +soperimetria e equivaenza i figure piane rea i triangoi e quariateri Teorema i itagora e sue appiazioni +soperimetria e equivaenza i figure piane Staiisi se e seguenti affermazioni
Triangolo rettangolo
 Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Triangoo rettangoo Le paroe dea matematica Cateto minore C i ipotenusa C1 Cateto maggiore Verificiamo i teorema di Pitagora Enunciato: In un triangoo rettangoo area de quadrato costruito su ipotenusa è
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
Percorsi di Matematica on line ESERCIZI DI RECUPERO 3
 Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
L AREA DELLE FIGURE PIANE
 L AREA DELLE FIGURE PIANE Segna il completamento corretto. 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie, cioè hanno la stessa
L AREA DELLE FIGURE PIANE Segna il completamento corretto. 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie, cioè hanno la stessa
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
Le equazioni e le disequazioni lineari
 MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
Il piano cartesiano, la retta e le funzioni di proporzionalità
 MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
MATEMATICAperTUTTI I piano cartesiano, a retta e e funzioni di proporzionaità ESERCIZIO SVOLTO I piano cartesiano. Per fissare un sistema di riferimento ne piano si considerano due rette orientate fra
a. Le due figure sono equivalenti?...sì... Perchè? sono equicomposte. b. Due figure equicomposte sono sempre equivalenti? sì..
 Segna il completamento corretto. L AREA DELLE FIGURE PIANE (in rosso i risultati) 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie,
Segna il completamento corretto. L AREA DELLE FIGURE PIANE (in rosso i risultati) 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie,
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
si usa in geometria per definire due figure uguali per forma ma non per dimensioni.
 FIGURE PIANE EQUIESTESE Due figure piane si definiscono equivalenti (o equiestese) se hanno la stessa superficie, la stessa estensione cioè la stessa area. OSSERVA CHE 1- Due figure congruenti saranno
FIGURE PIANE EQUIESTESE Due figure piane si definiscono equivalenti (o equiestese) se hanno la stessa superficie, la stessa estensione cioè la stessa area. OSSERVA CHE 1- Due figure congruenti saranno
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Geometria 2
 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 2 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 2 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
Le funzioni goniometriche
 CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
CAPITOLO 1 MATEMATICA PER LA FISICA Le funzioni goniometriche Obiettivi definire e funzioni goniometriche fondamentai in riferimento ai triangoi rettangoi e aa circonferenza goniometrica risovere triangoi
l B 1. la velocità angolare dell asta un istante prima dell urto; 2. la velocità v 0 ; 3. l energia cinetica dissipata nell urto;
 1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
1 Esercizio (tratto da Probema 8.29 de Mazzodi 2) Un asta di unghezza 1.2 m e massa M 0.5 Kg è incernierata ne suo estremo A ad un perno fisso e può osciare senza attrito in un piano verticae. A istante
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. CLASSE 1TGC2
 ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
Organi di collegamento
 Organi di coegamento Linguette Ciavette Aeri scanaati Organi di coegamento - Carmine apoi pag. 1 di 10 LIGUETTA Per inguetta si intende un organo meccanico caettato in opportune cave degi aeri ed utiizzato
Organi di coegamento Linguette Ciavette Aeri scanaati Organi di coegamento - Carmine apoi pag. 1 di 10 LIGUETTA Per inguetta si intende un organo meccanico caettato in opportune cave degi aeri ed utiizzato
Un poligono può avere tre, quattro, cinque o più lati. Il vertice è il punto d incontro di due lati; i vertici si indicano
 Pagina 1 di 13 I poligoni I poligoni sono figure piane che hanno come contorno una linea spezzata chiusa formatada almeno tre segmenti consecutivi. Un poligono può avere tre, quattro, cinque o più lati.
Pagina 1 di 13 I poligoni I poligoni sono figure piane che hanno come contorno una linea spezzata chiusa formatada almeno tre segmenti consecutivi. Un poligono può avere tre, quattro, cinque o più lati.
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Il rapporto fra la lunghezza di una circonferenza qualsiasi e la lunghezza del suo diametro è costante. in conclusione:
 La circonferenza è una linea curva e misurarla, per esempio, con il righello è un procedimento impossibile. ome fare allora? Vediamo di trovare un procedimento adeguato. 1. Procuriamoci un oggetto il cui
La circonferenza è una linea curva e misurarla, per esempio, con il righello è un procedimento impossibile. ome fare allora? Vediamo di trovare un procedimento adeguato. 1. Procuriamoci un oggetto il cui
LIMITI E CONTINUITA. 1. Sul concetto di limite
 LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
LIMITI E CONTINUITA. Su concetto di imite I concetto di imite nasce da esigenza di conoscere i comportamento di una funzione agi estremi de suo insieme di definizione D. Quaora esso sia costituito da unione
Il Tetraedro regolare
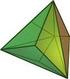 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Gli angoli corrispondenti sono congruenti; I lati corrispondenti, che si dicono lati omologhi, sono in rapporto costante:
 ome sai, se vuoi riprodurre una figura, puoi disegnarla perfettamente uguale rispettandone la forma e le dimensioni e cambiandone quindi solo la posizione. In questo caso la riproduci isometricamente,
ome sai, se vuoi riprodurre una figura, puoi disegnarla perfettamente uguale rispettandone la forma e le dimensioni e cambiandone quindi solo la posizione. In questo caso la riproduci isometricamente,
Parallelogrammi, trapezi e poligoni regolari
 CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTICA
 http://www.itimarconi.ct.it/sezioni/didatticaonine/edie/ostruzioni/linea%0eastic... Pagina di 06/0/006 L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTIA. BREVI RIHIAMI SULLA TEORIA DELLE TRAVI INFLESSE Si
http://www.itimarconi.ct.it/sezioni/didatticaonine/edie/ostruzioni/linea%0eastic... Pagina di 06/0/006 L EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTIA. BREVI RIHIAMI SULLA TEORIA DELLE TRAVI INFLESSE Si
I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e spigoli del poliedro.
 1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
C = d x π (pi greco) 3,14. d = C : π (3,14) r = C : (π x 2)
 circonferenza rettificata significa messa su una retta è un segmento che ha la stessa lunghezza della circonferenza formule: C = d x π (pi greco) 3,14 d = C : π (3,14) r = C : (π x 2) area del cerchio
circonferenza rettificata significa messa su una retta è un segmento che ha la stessa lunghezza della circonferenza formule: C = d x π (pi greco) 3,14 d = C : π (3,14) r = C : (π x 2) area del cerchio
I poligoni e la circonferenza
 CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
CAPITOLO 2 I poigoni e a circonferenza 1. POLIGONI INSCRITTI E CIRCOSCRITTI CON GEOGEBRA Esercitazione 1. I teoremi sui quadriateri con GeoGebra Facciamo a seguente costruzione: disegniamo un triangoo
VERIFICA DI MATEMATICA 11 febbraio 2016 classe 2 a D. Nome...Cognome... ARITMETICA
 VERIFICA DI MATEMATICA 11 febbraio 016 classe a D Nome...Cognome... ARITMETICA 1. Scrivi l enunciato delle proprietà fondamentale, dell invertire e del permutare. Applicale alla seguente proporzione, dimostrando
VERIFICA DI MATEMATICA 11 febbraio 016 classe a D Nome...Cognome... ARITMETICA 1. Scrivi l enunciato delle proprietà fondamentale, dell invertire e del permutare. Applicale alla seguente proporzione, dimostrando
Figura 1.1. La struttura illustrata in figura risulta essere, dall analisi cinematica, una struttura due volte iperstatica a nodi spostabili.
 TEMI ESAME Esercizio 1 Tema d esame de 1/09/1998 Si consideri a struttura iustrata in figura, con EJ costante. I vaore de azione concentrata F è pari a: Figura 1.1 1 F p 4 La struttura iustrata in figura
TEMI ESAME Esercizio 1 Tema d esame de 1/09/1998 Si consideri a struttura iustrata in figura, con EJ costante. I vaore de azione concentrata F è pari a: Figura 1.1 1 F p 4 La struttura iustrata in figura
Percorsi di Matematica on line
 Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERIZI I POTENZIMENTO -- IREZIONE EITORILE: avide asteano RELIZZTO : RG& S.R.L. SOLUZIONI PER L EITORI che ha curato per a casa editrice
Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERIZI I POTENZIMENTO -- IREZIONE EITORILE: avide asteano RELIZZTO : RG& S.R.L. SOLUZIONI PER L EITORI che ha curato per a casa editrice
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
I TRIANGOLI AB < AC + BC
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
2B GEOMETRIA. Isoperimetria, equivalenza e calcolo delle aree. Esercizi supplementari di verifica
 2 GEOMETRI Isoperimetria, equivalenza e calcolo delle aree Esercizi supplementari di verifica Esercizio 1 Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F ue poligoni isoperimetrici
2 GEOMETRI Isoperimetria, equivalenza e calcolo delle aree Esercizi supplementari di verifica Esercizio 1 Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F ue poligoni isoperimetrici
Compito scritto di Elettricità e Magnetismo ed Elettromagnetismo 24 Giugno 2004
 Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
Compito scritto di Eettricità e Magnetismo ed Eettromagnetismo 4 Giugno 4 ecupero I (II) esonero di Eettromagnetismo: esercizio C (D) in due ore Prova scritta di Eettricità e Magnetismo: esercizi A e B
Poligoni inscritti e circoscritti ad una circonferenza
 Poligoni inscritti e circoscritti ad una circonferenza Def: 1. Un poligono si dice inscritto in una circonferenza se tutti i suoi vertici sono punti della La circonferenza si dice circoscritta al poligono.
Poligoni inscritti e circoscritti ad una circonferenza Def: 1. Un poligono si dice inscritto in una circonferenza se tutti i suoi vertici sono punti della La circonferenza si dice circoscritta al poligono.
Equilibrio del corpo rigido
 Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
Equiibrio de corpo rigido Probema1 Due sbarrette omogenee AB e BC aventi a stessa unghezza e a stessa massa di 6 kg, vengono sadate ne punto B in modo da formare un angoo di 90. Le due sbarrette così unite
CONOSCENZE 1. le proposizioni 2. i connettivi logici 3. le espressioni logiche
 ALGEBRA LOGICA E CONNETTII PREREQUISITI conoscere gi insiemi e i oro inguaggio conoscere i significato di soggetto e predicato di una frase conoscere i significato di congiunzione, disgiunzione e negazione
ALGEBRA LOGICA E CONNETTII PREREQUISITI conoscere gi insiemi e i oro inguaggio conoscere i significato di soggetto e predicato di una frase conoscere i significato di congiunzione, disgiunzione e negazione
Anno 1. Poligoni equivalenti
 Anno 1 Poligoni equivalenti 1 Introduzione Una qualsiasi figura geometrica piana è costituita da una linea spezzata chiusa che, a sua volta, delimita una parte di piano. In questa lezione introdurremo
Anno 1 Poligoni equivalenti 1 Introduzione Una qualsiasi figura geometrica piana è costituita da una linea spezzata chiusa che, a sua volta, delimita una parte di piano. In questa lezione introdurremo
Nicola De Rosa, Liceo scientifico sperimentale sessione straordinaria 2012, matematicamente.it
 Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
Nicoa De Rosa Liceo scientiico sperimentae sessione straordinaria matematicamente.it PROBLEMA La sezione trasversae di un canae di imgazione ha a orma di un trapezio isoscee con a base maggiore in ato.
Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece
 Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece ha lasciato inalterato. Si chiama trasformazione geometrica un
Studiare una trasformazione geometrica significa prendere in esame i cambiamenti che ha prodotto nella figura trasformata e ciò che invece ha lasciato inalterato. Si chiama trasformazione geometrica un
Si definisce poligono la parte di piano delimitata da una spezzata semplice chiusa. D contorno
 I POLIGONI Si definisce poligono la parte di piano delimitata da una spezzata semplice chiusa. E D contorno La linea spezzata chiusa che delimita il F C poligono si chiama contorno I punti A, B, C, D,
I POLIGONI Si definisce poligono la parte di piano delimitata da una spezzata semplice chiusa. E D contorno La linea spezzata chiusa che delimita il F C poligono si chiama contorno I punti A, B, C, D,
Sfruttando le considerazioni appena fatte come misureresti il coefficiente di attrito statico μ s?
 MISURA DEL COEFFICIENTE DI ATTRITO STATICO Materiae occorrente: piano incinato monete Nota a unghezza de piano, qua è a reazione che sussiste fra i coefficiente di attrito statico μ s e a configurazione
MISURA DEL COEFFICIENTE DI ATTRITO STATICO Materiae occorrente: piano incinato monete Nota a unghezza de piano, qua è a reazione che sussiste fra i coefficiente di attrito statico μ s e a configurazione
MAPPA 8 FIGURE. Area dei poligoni e figure equivalenti. Misura dell estensione superficiale. Il metro quadrato. Figure equivalenti
 Misua de estensione supeficiae L aea è a misua de estensione supeficiae di una figua ispetto a unità di misua fissata. Indiciamo aea con a ettea. Esempio: R MPP 8 u 1 è aea de ettangoo R secondo unità
Misua de estensione supeficiae L aea è a misua de estensione supeficiae di una figua ispetto a unità di misua fissata. Indiciamo aea con a ettea. Esempio: R MPP 8 u 1 è aea de ettangoo R secondo unità
Le figure che abbiamo ottenuto prendono il nome di spezzate o poligonali. Una spezzata può essere: H S T U
 Prendiamo in considerazione le figure geometriche nel piano, cioè le figure piane, intendendo con questo termine un qualsiasi insieme di punti appartenenti a uno stesso piano. Disegniamo più segmenti consecutivi:
Prendiamo in considerazione le figure geometriche nel piano, cioè le figure piane, intendendo con questo termine un qualsiasi insieme di punti appartenenti a uno stesso piano. Disegniamo più segmenti consecutivi:
La trasformata di Fourier
 La trasformata di Fourier (Metodi Matematici e Cacoo per Ingegneria) Enrico Bertoazzi DIMS Università di Trento anno accademico 2005/2006 La trasformata di Fourier 1 / 15 Outine 1 La serie di Fourier La
La trasformata di Fourier (Metodi Matematici e Cacoo per Ingegneria) Enrico Bertoazzi DIMS Università di Trento anno accademico 2005/2006 La trasformata di Fourier 1 / 15 Outine 1 La serie di Fourier La
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 14
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 14 L equivalenza di figure piane Due figure piane si dicono equivalenti (o equiestese) se hanno la stessa estensione nel piano. L area
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 14 L equivalenza di figure piane Due figure piane si dicono equivalenti (o equiestese) se hanno la stessa estensione nel piano. L area
Si supponga ora che, con le stesse condizioni iniziali, l urto avvenga elasticamente. Calcolare in questo caso:
 1 Esercizio (tratto da Probema 8.21 de Mazzodi 2) Un asta rigida di sezione trascurabie, unga = 1 m e di massa M = 12 Kg è imperniata ne centro ed è ibera di ruotare in un piano orizzontae xy. Contro un
1 Esercizio (tratto da Probema 8.21 de Mazzodi 2) Un asta rigida di sezione trascurabie, unga = 1 m e di massa M = 12 Kg è imperniata ne centro ed è ibera di ruotare in un piano orizzontae xy. Contro un
CIRCONFERENZA E CERCHIO
 CIRCONFERENZA E CERCHIO CERCHIO Perimetro (circonferenza) Area La circonferenza è circa 3 volte ( ) la lunghezza del diametro C= d oppure C=2 r A = r 2 Formule inverse d=c: r=c:(2 ) SETTORE CIRCOLARE È
CIRCONFERENZA E CERCHIO CERCHIO Perimetro (circonferenza) Area La circonferenza è circa 3 volte ( ) la lunghezza del diametro C= d oppure C=2 r A = r 2 Formule inverse d=c: r=c:(2 ) SETTORE CIRCOLARE È
Geometria euclidea. Alessio del Vigna
 Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Geometria figure piane Raccolta di esercizi
 Geometria figure piane Raccolta di esercizi RETTANGOLO 1. Calcola il perimetro e l area di un rettangolo le cui dimensioni misurano rispettivamente 13 cm e 22 cm. [70 cm; 286 cm 2 ] 2. Un rettangolo ha
Geometria figure piane Raccolta di esercizi RETTANGOLO 1. Calcola il perimetro e l area di un rettangolo le cui dimensioni misurano rispettivamente 13 cm e 22 cm. [70 cm; 286 cm 2 ] 2. Un rettangolo ha
ROTAZIONI DEGLI ESTREMI DI UNA TRAVE PRISMATICA APPOGGIATA ALLE ESTREMITÁ E SOGGETTA AD UN CARICO VERTICALE
 M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
LA CIRCONFERENZA DEFINIZIONI. Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro.
 LA CIRCONFERENZA DEFINIZIONI Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro. Un cerchio è una figura piana formata dai punti di una circonferenza
LA CIRCONFERENZA DEFINIZIONI Una circonferenza è l insieme dei punti del piano che hanno distanza assegnata da un punto, detto centro. Un cerchio è una figura piana formata dai punti di una circonferenza
Anno 2. Equivalenza fra triangoli, parallelogramma e trapezio
 Anno 2 Equivalenza fra triangoli, parallelogramma e trapezio 1 Introduzione In questa lezione parleremo dell equivalenza tra alcune figure piane; in particolare parleremo di triangoli, trapezi e parallelogrammi.
Anno 2 Equivalenza fra triangoli, parallelogramma e trapezio 1 Introduzione In questa lezione parleremo dell equivalenza tra alcune figure piane; in particolare parleremo di triangoli, trapezi e parallelogrammi.
Circonferenze e cerchi
 Alunno/a... Geometria Classe... Sez.... Data... Circonferenze e cerchi 1 Definisci la circonferenza: 2 Definisci il settore circolare: 3 Definisci la figura che nel disegno è colorata in grigio: 4 Osserva
Alunno/a... Geometria Classe... Sez.... Data... Circonferenze e cerchi 1 Definisci la circonferenza: 2 Definisci il settore circolare: 3 Definisci la figura che nel disegno è colorata in grigio: 4 Osserva
De Poligonorum Inscriptione
 De oigonorum Inscriptione Ovvero: come trascorrere i mese di settembre fra i, coi, radicai doppi e financo tripi De oigonorum Inscriptione / 0 De oigonorum Inscriptione / 0 INDIC INTRODUZION... IMOSTZION
De oigonorum Inscriptione Ovvero: come trascorrere i mese di settembre fra i, coi, radicai doppi e financo tripi De oigonorum Inscriptione / 0 De oigonorum Inscriptione / 0 INDIC INTRODUZION... IMOSTZION
IL PENDOLO REVERSIBILE DI KATER
 IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
IL PENDOLO REVERSIBILE DI KATER I periodo dee osciazioni de pendoo sempice è dato daa formua: T 0 = π g Questa reazione è vaida per e piccoe osciazioni, quando, cioè, si può assimiare i seno de'angoo massimo
Equivalenza e aree. Circonferenza e cerchio
 Indice Geometria e misura VIII Indice unità 1 Equivalenza e aree Figure piane equivalenti L area del rettangolo e del quadrato 8 L area del parallelogramma 14 L area del triangolo 17 La formula di Erone
Indice Geometria e misura VIII Indice unità 1 Equivalenza e aree Figure piane equivalenti L area del rettangolo e del quadrato 8 L area del parallelogramma 14 L area del triangolo 17 La formula di Erone
POLIGONI REGOLARI. ( Libro : teoria pag ; esercizi pag ) Un poligono è detto regolare quando.
 POLIGONI REGOLARI. ( Libro : teoria pag. 54 61; esercizi pag. 120 128) Un poligono è detto regolare quando. Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
POLIGONI REGOLARI. ( Libro : teoria pag. 54 61; esercizi pag. 120 128) Un poligono è detto regolare quando. Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
AREE DEI POLIGONI. b = A h
 AREE DEI POLIGONI 1. RETTANGOLO E un parallelogramma avente quattro angoli retti, i lati opposti uguali e paralleli, le diagonali uguali non perpendicolari che si scambiano vicendevolmente a metà. Def.
AREE DEI POLIGONI 1. RETTANGOLO E un parallelogramma avente quattro angoli retti, i lati opposti uguali e paralleli, le diagonali uguali non perpendicolari che si scambiano vicendevolmente a metà. Def.
COS È UN PRISMA. Due POLIGONI congruenti e paralleli, come basi. È UN POLIEDRO DELIMITATO DA
 PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
PRISMI E PIRAMIDI COS È UN PRISMA È UN POLIEDRO DELIMITATO DA Due POLIGONI congruenti e paralleli, come basi. Tanti PARALLELOGRAMMI quanti sono i lati del poligono di base (come facce laterali). PRISMA
I TRIANGOLI AB < AC + BC
 I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
I TRIANGOLI Il triangolo è un poligono formato da tre angoli e da tre lati: rappresenta la figura più semplice in assoluto, in quanto 3 è il numero minimo di segmenti necessari per delimitare una superficie
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 10
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
REGOLA DELLA SEMPLIFICAZIONE DELLE AREE
 REGOLA DELLA SEMPLIFICAZIONE DELLE AREE Ogni formula di calcolo delle aree dei poligoni può essere espressa tramite una frazione avente al numeratore un prodotto di due valori e un unico valore al denominatore.
REGOLA DELLA SEMPLIFICAZIONE DELLE AREE Ogni formula di calcolo delle aree dei poligoni può essere espressa tramite una frazione avente al numeratore un prodotto di due valori e un unico valore al denominatore.
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Le caratteristiche generali di un quadrilatero
 1 Le caratteristiche generali di un quadrilatero Nel quadrilatero (poligono di quattro lati) si distinguono:! i vertici,,, ;! gli angoli α, β, γ, δ;! i lati,,, ;! le diagonali e. EFINIZIONE. ue angoli
1 Le caratteristiche generali di un quadrilatero Nel quadrilatero (poligono di quattro lati) si distinguono:! i vertici,,, ;! gli angoli α, β, γ, δ;! i lati,,, ;! le diagonali e. EFINIZIONE. ue angoli
Buone Vacanze! Compiti per le vacanze. Classe II A
 Compiti per le vacanze Classe II A Indicazioni Procurati un quaderno a quadretti, dove eseguirai tutti gli esercizi. Se le espressioni non ti dovessero riuscire ritenta almeno tre volte sul quaderno Nei
Compiti per le vacanze Classe II A Indicazioni Procurati un quaderno a quadretti, dove eseguirai tutti gli esercizi. Se le espressioni non ti dovessero riuscire ritenta almeno tre volte sul quaderno Nei
INDICE EQUIVALENZA E MISURA DELLE FIGURE
 INIE 2 Unità di apprendimento 5 EQUIVLENZ E MISUR ELLE FIGURE 3 ttività per iniziare verso le competenze fondamentali 4 1 Equivalenza delle figure piane Equicomposizione ed equivalenza delle figure geometriche,
INIE 2 Unità di apprendimento 5 EQUIVLENZ E MISUR ELLE FIGURE 3 ttività per iniziare verso le competenze fondamentali 4 1 Equivalenza delle figure piane Equicomposizione ed equivalenza delle figure geometriche,
GEOMETRIA CLASSE IV B A.S.
 GEOMETRIA CLASSE IV B A.S. 2014/15 Insegnante: Stallone Raffaella RETTA, SEMIRETTA E SEGMANTO La retta è illimitata, non ha né inizio né fine. Si indica con una lettera minuscola. La semiretta è ciascuna
GEOMETRIA CLASSE IV B A.S. 2014/15 Insegnante: Stallone Raffaella RETTA, SEMIRETTA E SEGMANTO La retta è illimitata, non ha né inizio né fine. Si indica con una lettera minuscola. La semiretta è ciascuna
Esercizi di geometria per il corso PAS A059
 Esercizi di geometria per il corso PAS A059 1. Dato un rombo con un angolo di 60 trovare il rapporto tra il raggio del cerchio inscritto nel rombo e il raggio del piu piccolo cerchio che contiene interamente
Esercizi di geometria per il corso PAS A059 1. Dato un rombo con un angolo di 60 trovare il rapporto tra il raggio del cerchio inscritto nel rombo e il raggio del piu piccolo cerchio che contiene interamente
Esempio di risoluzione di struttura iperstatica col metodo misto. Complemento alla lezione 47/50: Telai a nodi mobili
 Esempio di risouzione di struttura iperstatica co metodo misto ompemento aa ezione 47/50: Teai a nodi mobii La struttura in figura è soggetta ad un cedimento verticae dea cerniera. Tutto i teaio ha sezione
Esempio di risouzione di struttura iperstatica co metodo misto ompemento aa ezione 47/50: Teai a nodi mobii La struttura in figura è soggetta ad un cedimento verticae dea cerniera. Tutto i teaio ha sezione
non ha significato in R ¼
 MATEMATICAerTUTTI I radicai ESERCIZIO SVOLTO Potenze e radici. Saiamo che si uò estrarre a radice quadrata soo di numeri ositivi o nui e che i risutato è un numero ositivo o nuo. La radice cubica di un
MATEMATICAerTUTTI I radicai ESERCIZIO SVOLTO Potenze e radici. Saiamo che si uò estrarre a radice quadrata soo di numeri ositivi o nui e che i risutato è un numero ositivo o nuo. La radice cubica di un
Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa.
 IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
Anno 4 Superficie e volume dei solidi
 Anno 4 Superficie e volume dei solidi Introduzione In questa lezione parleremo del volume e della superficie dei solidi, imparando a trattare con semplicità il loro calcolo tramite le formule Al termine
Anno 4 Superficie e volume dei solidi Introduzione In questa lezione parleremo del volume e della superficie dei solidi, imparando a trattare con semplicità il loro calcolo tramite le formule Al termine
CALCOLO MATEMATICO E GEOMETRIA GEOMETRIA PIANA
 CALCOLO MATEMATICO E GEOMETRIA GEOMETRIA PIANA Nella prima parte del corso si ripasseranno le caratteristiche principali delle figure di geometria piana, per poi passare nella seconda parte dell'anno alla
CALCOLO MATEMATICO E GEOMETRIA GEOMETRIA PIANA Nella prima parte del corso si ripasseranno le caratteristiche principali delle figure di geometria piana, per poi passare nella seconda parte dell'anno alla
Area dei poligoni. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA.
 Area dei poligoni AREA DEI POLIGONI 1 Def: si dice area di una superficie piana la parte delimitata di piano che essa occupa. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA. Proprietà:
Area dei poligoni AREA DEI POLIGONI 1 Def: si dice area di una superficie piana la parte delimitata di piano che essa occupa. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA. Proprietà:
Un poligono è inscritto in una circonferenza se tutti i suoi vertici appartengono alla circonferenza
 1. I poligoni inscritti Quando un poligono è inscritto in una Un poligono è inscritto in una circonferenza se tutti i suoi vertici appartengono alla circonferenza Se un poligono è inscritto in una circonferenza,
1. I poligoni inscritti Quando un poligono è inscritto in una Un poligono è inscritto in una circonferenza se tutti i suoi vertici appartengono alla circonferenza Se un poligono è inscritto in una circonferenza,
7. Travi appoggiate: metodo generale
 7. Travi aoggiate: metodo generae Se si riesce a trasformare a trave aoggiata in una mensoa, e sue deformazioni si ossono cacoare con gi stessi criteri de aragrafo recedente. Deve trattarsi naturamente
7. Travi aoggiate: metodo generae Se si riesce a trasformare a trave aoggiata in una mensoa, e sue deformazioni si ossono cacoare con gi stessi criteri de aragrafo recedente. Deve trattarsi naturamente
a b a : b Il concetto di rapporto
 1 Il concetto di rapporto DEFINIZIONE. Il rapporto fra due valori numerici a e b è costituito dal loro quoziente; a e b sono i termini del rapporto, il primo termine si chiama antecedente, il secondo si
1 Il concetto di rapporto DEFINIZIONE. Il rapporto fra due valori numerici a e b è costituito dal loro quoziente; a e b sono i termini del rapporto, il primo termine si chiama antecedente, il secondo si
Inflessione nelle travi
 Ifessioe ee travi Caso dea trave icastrata ad u estremità Data a trave a mesoa AB di ughezza, sottoposta a azioe de carico cocetrato F appicato a estremo ibero B, questa risuta soecitata, i ogi sezioe,
Ifessioe ee travi Caso dea trave icastrata ad u estremità Data a trave a mesoa AB di ughezza, sottoposta a azioe de carico cocetrato F appicato a estremo ibero B, questa risuta soecitata, i ogi sezioe,
Un metodo di calcolo per le strutture monodimensionali piane
 www.carosantagata.it n metodo di cacoo per e strutture monodimensionai piane bstract. Si propone un metodo di cacoo per a determinazione dea configurazione di equiibrio dee strutture monodimensionai piane.
www.carosantagata.it n metodo di cacoo per e strutture monodimensionai piane bstract. Si propone un metodo di cacoo per a determinazione dea configurazione di equiibrio dee strutture monodimensionai piane.
Cap 1. LA CIRCONFERENZA
 Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
Cap 1. LA CIRCONERENZA Rivedi a teoria I uoghi geometrici Un uogo eá 'insieme di tutti e soi gi oggetti geometrici che possiedono una proprietaá P; se gi oggetti sono punti, si para di uogo di punti. Esempi
IL Calcolo letterale (o algebrico). (teoria pag ;esercizi pag , es.59 66) 1) Premessa: Al posto dei numeri posso utilizzare delle..
 IL Calcolo letterale (o algebrico). (teoria pag. 29 31;esercizi pag. 100 103, es.59 66) 1) Premessa: Al posto dei numeri posso utilizzare delle.. Esempi:. 2) Introduzione. a) Un numero qualsiasi: b) Il
IL Calcolo letterale (o algebrico). (teoria pag. 29 31;esercizi pag. 100 103, es.59 66) 1) Premessa: Al posto dei numeri posso utilizzare delle.. Esempi:. 2) Introduzione. a) Un numero qualsiasi: b) Il
POLIGONI REGOLARI. ( Libro : teoria pag ; esercizi pag )
 POLIGONI REGOLARI. ( Libro : teoria pag. 52 61; esercizi pag. 120 128) Un poligono è detto regolare quando Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
POLIGONI REGOLARI. ( Libro : teoria pag. 52 61; esercizi pag. 120 128) Un poligono è detto regolare quando Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
Le caratteristiche dei poligoni. La relazione tra i lati e gli angoli di un poligono. Definizioni
 Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
Le caratteristiche dei poligoni 1. Si dice poligono la parte del piano delimitata da una spezzata chiusa. 2. Il perimetro di un poligono è la somma delle misure del suoi lati, si indica cm 2p. 3. Un poligono
Problemi di geometria
 1 2 6 7 9 Calcola la misura dell ipotenusa di un triangolo rettangolo i cui cateti misurano 11,2 cm e 1 cm. [1,7 cm] In un triangolo rettangolo l ipotenusa misura cm, un cateto è dell ipotenusa. Calcola
1 2 6 7 9 Calcola la misura dell ipotenusa di un triangolo rettangolo i cui cateti misurano 11,2 cm e 1 cm. [1,7 cm] In un triangolo rettangolo l ipotenusa misura cm, un cateto è dell ipotenusa. Calcola
LE FRAZIONI. 1 Scrivi la frazione corrispondente alla parte colorata. cinque settimi. dieci quindicesimi. nove diciottesimi. dodici ventiquattresimi
 LE FRAZIONI Scrivi la frazione corrispondente alla parte colorata. 3 7 9 Riscrivi la frazione in cifre e colora la parte indicata. cinque settimi dieci quindicesimi nove diciottesimi dodici ventesimi quattordici
LE FRAZIONI Scrivi la frazione corrispondente alla parte colorata. 3 7 9 Riscrivi la frazione in cifre e colora la parte indicata. cinque settimi dieci quindicesimi nove diciottesimi dodici ventesimi quattordici
Sandra Bernecoli - Luigi Tomasi CABRIRRSAE. I poliedri regolari: un tema di geometria dello spazio rivisitato con Cabri-géomètre.
 BRIRRSE quaderni di Sandra Bernecoi - Luigi Tomasi I poiedri regoari: un tema di geometria deo spazio rivisitato con abri-géomètre n 1 Sandra Bernecoi Liceo Scientifico Statae P. Paeocapa di Rovigo Luigi
BRIRRSE quaderni di Sandra Bernecoi - Luigi Tomasi I poiedri regoari: un tema di geometria deo spazio rivisitato con abri-géomètre n 1 Sandra Bernecoi Liceo Scientifico Statae P. Paeocapa di Rovigo Luigi
Corso di Matematica - Geometria. Geometria - 0. Ing. L. Balogh
 Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Geometria - 0 Triangoli qualunque somma degli angoli interni, calcolo del perimetro e dell area Oggetti Vertici Lati Angoli Altezza Raggio Simbolo A, B, C a, b, c,, h S, r Perimetro = + + Somma angoli
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
1. CALCOLARE LA FRAZIONE DI UNA GRANDEZZA O DI UN NUMERO:
 PROBLEMI FONDAMENTALI CON LE FRAZIONI/RAPPORTI Le frazioni hanno applicazioni in moltissimi problemi. I tipi di problemi più frequenti sono: 1. Calcolare la frazione di un numero 2. Calcolare un numero
PROBLEMI FONDAMENTALI CON LE FRAZIONI/RAPPORTI Le frazioni hanno applicazioni in moltissimi problemi. I tipi di problemi più frequenti sono: 1. Calcolare la frazione di un numero 2. Calcolare un numero
GEOMETRIA SOLIDA PIRAMIDE. Prof.ssa M. Rosa Casparriello
 GEOMETRIA SOLIDA PIRAMIDE Prof.ssa M. Rosa Casparriello Scuola media di Cervinara 2007/2008 DEFINIZIONE La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati
GEOMETRIA SOLIDA PIRAMIDE Prof.ssa M. Rosa Casparriello Scuola media di Cervinara 2007/2008 DEFINIZIONE La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati
Geometria e misura. Indice. esercizi. mi autovaluto 26. mi autovaluto 38. Il calcolo delle aree 3. Il teorema di Pitagora 27
 Indice Geometria e misura Per orientarti 2 unità di apprendimento 1 Il calcolo delle aree 3 Equivalenza di figure piane 4 Figure piane prevalenti e subvalenti, p. 9 alcoliamo le aree 10 rea del rettangolo,
Indice Geometria e misura Per orientarti 2 unità di apprendimento 1 Il calcolo delle aree 3 Equivalenza di figure piane 4 Figure piane prevalenti e subvalenti, p. 9 alcoliamo le aree 10 rea del rettangolo,
