Insegnamento di Fondamenti di Infrastrutture viarie
|
|
|
- Nicolo Agostini
- 8 anni fa
- Visualizzazioni
Transcript
1 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto Dall equazione generale del moto alle caratteristiche di moto Sistemi di trazione e motori di trazione Trazione ferroviaria: studio di una fase completa di moto Trazione stradale: studio di una fase completa di moto La frenatura in ferrovia e su strada Legislazione e Normativa Norme funzionali e geometriche per la costruzione delle strade Andamento planimetrico di un tracciato stradale: 1) elementi del tracciato planimetrico, rettifili e curve circolari, pendenza trasversale in curva, curve a raggio variabile 2) allargamento in curva e diagramma di velocità Distanze di visibilità e andamento altimetrico di un tracciato stradale Volume del solido stradale: metodi di calcolo
2 Fondamenti di Infrastrutture viarie Volume del solido stradale Generalità Il quaderno delle sezioni Il diagramma delle aree Il diagramma dei volumi Determinazione analitica del volume del solido stradale
3 Volume del solido stradale Generalità Il problema della determinazione (misura e distribuzione) dei volumi lungo il tracciato stradale è di fondamentale importanza, sia per stabilire il costo dello scavo o del riporto, sia per ricavare il costo del trasporto dei movimenti di terra lungo l asse stradale. Per solido stradale s intende il solido delimitato dal piano di campagna, dalla piattaforma stradale, dalle scarpate del rilevato o della trincea e dalle due sezioni terminali del tronco considerato. Se assimiliamo il solido stradale ad un prismoide il suo volume è calcolabile con la formula del Torricelli: V = d/6 (F 1 + F 2 + 4F m ) Dove: F 1 e F 2 sono le aree delle sezioni d estremità (poste a distanza d) e F m è l area della sezione a distanza d/2 dalle sezioni d estremità. In questo caso occorre conoscere non solo le aree delle sezioni d estremità, ma anche l area della sezione F m.
4 Volume del solido stradale Il quaderno delle sezioni Le sezioni trasversali sono ottenute con piani verticali normali all asse stradale posti in corrispondenza dei singoli picchetti individuati in planimetria e che caratterizzano il modello del terreno (profilo longitudinale dell asse stradale). Nella figura 1 di due sezioni successive viene riportata la collocazione planimetrica e le sezioni trasversali (entrambe in rilevato). Per il progetto preliminare si utilizzano di solito le sezioni ricavate dalla carta a curve di livello, mentre per quello definitivo è sempre opportuno che ci si serva delle sezioni direttamente rilevate sul terreno. Per un conteggio analitico delle diverse parti (sterro e riporto) che caratterizzano una sezione trasversale occorre predisporre, oltre alla loro rappresentazione grafica anche delle tabelle analitiche per il calcolo degli sterri e dei riporti. Nelle sezioni trasversali, oltre all asse verticale in corrispondenza del picchetto dell asse stradale, è bene indicare il cassonetto relativo alla sovrastruttura stradale in quanto la sua area trasversale inciderà solo per la sua quota parte in trincea (e non in per la quota parte in rilevato). In figura 2 è riportato un esempio di sezione trasversale.
5 Diagrammi dei volumi Esempio di due sezioni trasversali successive Due sezioni successive: collocazione planimetrica e sezioni trasversali (entrambe in rilevato).
6 Diagrammi dei volumi Esempio di sezione trasversale
7 Volume del solido stradale Il metodo delle sezioni ragguagliate Se si ipotizza che F m = (F 1 + F 2 )/2 la formula del Torricelli diventa: V = d/2 (F 1 + F 2 ) Dove: F 1 e F 2 sono le aree delle sezioni d estremità (poste a distanza d). In questo caso occorre tener presente che il metodo delle sezioni ragguagliate fornisce un volume maggiore rispetto a quello del Torricelli. Tale metodo è utilizzato per costruire il diagramma delle aree: in ascissa vengono riportate le distanze (tra sezioni stradali), in ordinata vengono riportate le aree delle sezioni stradali. La congiungente delle ordinate relative alle sezioni di diversa area ha un andamento lineare (tra due sezioni) riducendosi quindi ad una spezzata. Per convenzione le aree di sterro si riportano nell ordinata positiva (verso l alto), le aree di riporto nell ordinata negativa (verso il basso). L area sottesa al diagramma delle aree tra due sezioni rappresenta il volume del solido stradale tra le due sezioni stesse.
8 Costruzione del diagramma delle aree 1 Occorre distinguere tra sezioni omogenee (entrambe di riporto o di sterro), sezioni non omogenee (una di sterro e l altra di riporto) e sezioni parzializzate (mezza costa). Sezioni omogenee: Con riferimento alla figura 3 (3 sezioni in sterro: F 0, F 1, F 2 ) il diagramma delle aree è dato dalla spezzata congiungente le trae ordinate (aree) relative alle tre sezioni in sterro considerate (distanti rispettivamente d 1 e d 2 ). Il volume di sterro, graficamente rappresentato dall area sottesa alla spezzata congiungente gli estremi superiori delle 3 ordinate (gli estremi inferiori appoggiano sull ascissa), è dato dall espressione: V = d 1 (F 0 + F 1 )/2 + d 1 (F 1 +F 2 )/2. Sezioni non omogenee: Metodo delle sezioni ragguagliate Con riferimento alla figura 4 (un sezione di sterro e l altra di riporto) il diagramma delle aree, che in questo caso individua due distinti volumi (aree): uno di sterro e l altro di riporto, interseca l ascissa in un punto P di passaggio (in corrispondenza del quale V = 0). In questo caso: V s = d 1 F 1 /2 e V r = d 1 F 2 /2.
9 Metodo delle sezioni ragguagliate Sezioni omogenee e non omogenee Diagramma delle aree: sezioni omogenee. Diagramma delle aree: sezioni non omogenee.
10 Costruzione del diagramma delle aree 2 Sezioni parzializzate (vedi figura 5): Metodo delle sezioni ragguagliate Nel caso in cui una sezione (la 1) è omogenea (riporto) mentre l altra (la 2) è parzializzata (a mezza costa), la costruzione del diagramma delle aree avviene per passi successivi (figura 3): a) Poste le sezioni una (la 2) sotto l altra (la 1) (rispetto la congiungente dei rispettivi assi stradali), rispetto al punto T si traccia la verticale y-y che divide la sezione 1 in due parti A 1 e A 2 (entrambe aree di riporto) cui corrispondono nella sezione 2 rispettivamente le due parti B 1 (area di sterro) e B 2 (area di riporto). b) Poste le due sezioni 1 e 2 alla distanza d lungo una retta orizzontale, prima si riportano in ordinata le due aree A 1 e B 1 e se ne congiungono le estremità per determinare il punto di passaggio P (in quanto le due aree non sono omogenee), poi si riportano in ordinata le due aree omogenee A 2 e B 2 congiungendone le estremità. (Vedi casi precedenti, ma rappresentati sovrapponendone i diagrammi). c) Abbassata da P la verticale sino in P, resta da sommare nella sezione 1 all area A 2 l area A 1 e congiungere il nuovo estremo con P.
11 Metodo delle sezioni ragguagliate Sezioni parzializzate Determinazione del volume del solido stradale tra una sezione in rilevato e la successiva a mezza costa. Costruzione del diagramma delle aree nel caso di sezioni parzializzate.
12 Sezioni parzializzate: Metodo delle sezioni ragguagliate Costruzione del diagramma delle aree 3 In figura 6 è rappresentato un caso più complesso: Successione di tre sezioni: 1) in trincea 2) e 3) a mezza costa. Diagramma delle aree delle tre sezioni.
13 Diagramma delle aree Diagramma delle aree con e senza aree di paleggio Una volta costruito il diagramma delle aree, prima di procedere al compenso trasversale, occorre aumentare le ordinate positive (di sterro) della differenza percentuale tra il volume dopo lo scavo e quello nel rilevato (figura 7). Semprechè i terreni provenienti dagli scavi risultino idonei per costruire i rilevati, si procede ad individuare quelle zone del diagramma delle aree che presentano contemporaneamente ordinate in sterro (trincea) e in riporto (rilevato). Per la ricerca del volume compensato trasversalmente (aree di paleggio) è sufficiente ribaltare i contorni del diagramma delle aree intorno all asse delle ascisse. L area priva di tratteggio rappresenta il volume compensato trasversalmente e l area tratteggiata rappresenta invece il volume depurato dai paleggi (figura 8). Nel caso che la strada sia interrotta da un ponte, il diagramma delle aree sarà anch esso interrotto tra le sezioni in corrispondenza delle due spalle.
14 Diagramma delle aree Aumenti (per scavo) e diminuzioni (per riporto) di volume per diversi tipi di terreno
15 Diagramma delle aree Diagramma delle aree con compensi trasversali e depurato
16 Volume del solido stradale Diagramma dei volumi o profilo di Brukner Integrando graficamente il diagramma delle aree depurato (dei paleggi) si ottiene il diagramma dei volumi (Brukner) che ha per ascisse le distanze fra le successive sezioni e per ordinate la somma algebrica dei volumi di terra dall origine alla sezione considerata. Tale diagramma (volumi) è di fondamentale importanza per lo studio di un progetto stradale. Infatti indica come si alternano i volumi di sterro e di riporto lungo la strada, così da poter stabilire il posizionamento dei cantieri di lavoro e le modalità di esecuzione dei compensi longitudinali (delle terre dalle zone di scavo verso le zone di riporto). In figura 9 sono rappresentati due esempi di diagramma dei volumi: a) con esubero di sterro (occorre quindi un luogo di deposito) b) con esubero di riporto (occorre quindi una cava di prestito). Il diagramma dei volumi corrisponde alla curva integrale del diagramma delle aree in cui i rami ascendenti corrispondono a tratti in trincea (sterri) ed i rami discendenti corrispondono a tratti in rilevato (riporti).
17 Diagrammi dei volumi Esempi a) con esubero di sterro (occorre quindi un luogo di deposito). b) con esubero di riporto (occorre quindi una cava di prestito).
18 Diagramma dei volumi Cantiere di compenso e distanza media del trasporto In figura 10 si mostra che si ha un cantiere di compenso quando il volume di sterro risulta uguale al volume di riporto e se ne illustra il tipico andamento del diagramma dei volumi. In presenza di un cantiere di compenso l area A (racchiusa tra la curva dei volumi e limitata dalla fondamentale) rappresenta il momento di trasporto (prodotto del volume per la distanza). Il rapporto tra l area A e l ordinata Y max (volume massimo di sterro che è utilizzato nel riporto) si chiama distanza media del trasporto ed è rappresentata in figura 11 dal segmento d m. La determinazione della distanza media esemplifica il calcolo del costo dei movimenti di materiale. Il costo complessivo di trasporto per tale cantiere di compenso è dato da: C = c γ d m Y max Dove: c = costo unitario della tkm, γ = peso specifico del materiale, d m = distanza media del trasporto, Y max = massimo volume di sterro utilizzato nel riporto.
19 Diagramma dei volumi Diagramma dei volumi del cantiere di compenso Cantiere di compenso e distanza media del trasporto
20 Diagramma dei volumi Ricerca della fondamentale di minima spesa Per quanto detto in precedenza, risulta evidente che le aree racchiuse dal diagramma dei volumi sono proporzionali alle entità dei trasporti. Quindi se il costo del trasporto è proporzionale al momento del trasporto, la distanza più economica è quella che rende minimo tale momento. Inoltre lo spostamento verticale dell orizzontale di riferimento produce una variazione del momento di trasporto nei singoli cantieri. Il problema quindi si riduce a ricercare la posizione dell orizzontale predetta che rende minimo il momento. In figura 13 si mostra come un abbassamento z provochi una variazione del costo di trasporto: in corrispondenza dei segmenti v 1, v 2, (valli) si avrà una riduzione, mentre in corrispondenza dei segmenti m 1, m 2, (monti) si avrà un aumento. La variazione di costo complessiva è quindi data da: S = (c 1 m 1 + c 2 m 2 c 1 v 1 c 2 v 2 ) z Perchè il costo S sia minimo, occorre che S = 0 e quindi: c 1 m 1 + c 2 m 2 = c 1 v 1 + c 2 v 2 Se il sistema di trasporto ed il relativo costo unitario sono uguali (c 1 =c 2 =c 1 =c 2 ), si ha: m 1 + m 2 = v 1 + v 2 In generale il minimo della funzione momento di trasporto corrisponderà con il minimo di v i - m i, cioè quando v i = m i. La fondamentale di minima spesa sarà quella per cui la somma dei segmenti v i (valli) sia eguale alla somma dei segmenti m i (monti). In figura 14 si riporta un esempio di diagramma dei volumi con secondarie di compenso.
21 Diagramma dei volumi Fondamentale di minima spesa
22 Diagramma dei volumi Diagramma dei volumi con secondarie di compenso
23 Diagramma dei volumi Metodo grafico per la costruzione del diagramma dei volumi Il diagramma delle aree (depurato) è costituito da una spezzata, per cui l area racchiusa fra essa e la fondamentale è, in ogni caso, scomponibile in rettangoli, in triangoli e in trapezi. Il diagramma dei volumi è un diagramma ottenuto per integrazione e quindi sarà costituito da una serie di archi di parabole. Nelle figure: 15, 16, e 17 sono rispettivamente le costruzioni dei diagrammi dei volumi nel caso di sezioni di area: rettangolare triangolare trapezoidale In figura 18 è illustrata la costruzione del diagramma dei volumi relativo ad un generico diagramma delle aree.
24 Diagramma dei volumi Esempio di costruzione del diagramma dei volumi
25 Volume del solido stradale Determinazione analitica del volume del solido stradale Per impostare il computo dei volumi di scavo e di riporto ci si serve di appositi stampati (vedere figura 19) nei quali il volume si determina applicando il metodo delle sezioni ragguagliate. Nella compilazione quindi della tabella occorrerà tenere conto delle tre diverse tipologie di sezioni a due a due considerate: 1) se le sezioni sono omogenee: V = d (A 1 + A 2 )/2 (sterro o riporto); 2) se le sezioni sono non omogenee: V s = d s A s / 2 (sterro), V r = d r A r / 2 (riporto) e tali sezioni determinano un punto di passaggio P tale per cui: d s + d r = d; 3) se le sezioni sono parzializzate (una sola delle due od entrambe): occorre tenere conto delle aree parzializzate corrispondenti. Una volta calcolati i volumi tra due sezioni, occorrerà determinare i volumi compensati là dove esiste la possibilità di compenso trasversale. La somma algebrica dei volumi compensati sarà positiva sin tanto che i volumi di scavo sono maggiori di quelli di riporto e diventerà negativa quando i volumi di riporto supereranno quelli di scavo. Tali valori, quindi, non sono altro che le successive ordinate del diagramma dei volumi.
26 Volume del solido stradale Tabella per il calcolo analitico dei volumi
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
Q4 Ripercorriamo dunque i casi fondamentali esaminati nei precedenti paragrafi relativi al calcolo analitico dei volumi.
 4. Rappresentazione grafica dei volumi Il problema del calcolo dei volumi, oltre alla soluzione analitica proposta nei paragrafi 3 e 4, può essere anche sviluppato per via grafica con una semplice ed elegante
4. Rappresentazione grafica dei volumi Il problema del calcolo dei volumi, oltre alla soluzione analitica proposta nei paragrafi 3 e 4, può essere anche sviluppato per via grafica con una semplice ed elegante
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
PLANIMETRIA E PROFILO INSIEME
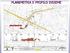 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
Parte I: Meccanica della locomozione ed armamento
 Parte I: Meccanica della locomozione ed armamento 1) Meccanica della locomozione: equazione del moto, resistenze al moto, dinamica del veicolo, andamento planoaltimetrico, sopraelevazione in curva, accelerazione
Parte I: Meccanica della locomozione ed armamento 1) Meccanica della locomozione: equazione del moto, resistenze al moto, dinamica del veicolo, andamento planoaltimetrico, sopraelevazione in curva, accelerazione
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione Dall equazione alle
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione Dall equazione alle
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
Statistica. Le rappresentazioni grafiche
 Statistica Le rappresentazioni grafiche Introduzione Le rappresentazioni grafiche costituiscono uno dei mezzi più efficaci, sia per descrivere in forma visiva i risultati di numerose osservazioni riguardanti
Statistica Le rappresentazioni grafiche Introduzione Le rappresentazioni grafiche costituiscono uno dei mezzi più efficaci, sia per descrivere in forma visiva i risultati di numerose osservazioni riguardanti
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
METODO PER LA DESCRIZIONE DEL CAMPO MAGNETICO ROTANTE
 Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
ISTITUTO TECNICO PER GEOMETRI "P.L. NERVI"
 ISTITUTO TECNICO PER GEOMETRI "P.L. NERVI" ALUNNO: FRANCESCO FRIZZALE DOCENTE: ING. DOMENICO TAMBONE CLASSE : V SEZ. D ANNO SCOLASTICO: 2000/2001 1 1. PREMESSA Il progetto consiste nella realizzazione
ISTITUTO TECNICO PER GEOMETRI "P.L. NERVI" ALUNNO: FRANCESCO FRIZZALE DOCENTE: ING. DOMENICO TAMBONE CLASSE : V SEZ. D ANNO SCOLASTICO: 2000/2001 1 1. PREMESSA Il progetto consiste nella realizzazione
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico e Scientifico opzione scienze applicate Tema di matematica
 wwwmatematicamenteit maturità 5 Esame di stato di istruzione secondaria superiore Indirizzi: Scientiico e Scientiico opzione scienze applicate Tema di matematica Il candidato risolva uno dei due problemi
wwwmatematicamenteit maturità 5 Esame di stato di istruzione secondaria superiore Indirizzi: Scientiico e Scientiico opzione scienze applicate Tema di matematica Il candidato risolva uno dei due problemi
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Soluzione di equazioni quadratiche
 Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione dell esercizio del 2 Febbraio 2004
 Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Svolgimento 1 Scriviamo la funzione f(x) che rappresenta la spesa totale in un mese: Figura 2 Il grafico di f(x).
 Problema 1 Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per ogni minuto di conversazione. Indicando con
Problema 1 Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per ogni minuto di conversazione. Indicando con
Premessa: Nella traccia non è specificato cosa accade se si effettuano per esempio 2,3 minuti di conversazione.
 Esame di stato 5 - Proposta di risoluzione del problema Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per
Esame di stato 5 - Proposta di risoluzione del problema Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per
L ingombro ed il numero delle corsie si calcola attraverso lo schema e la tabella riportata a seguito.
 4.2 IL COLLAUDO STATICO DEI PONTI 4.2.1 Ponti stradali Per i ponti stradali le norme per l effettuazione del collaudo statico sono contenute nel D.M. LL. PP. del 4 maggio 1990 Aggiornamento delle norme
4.2 IL COLLAUDO STATICO DEI PONTI 4.2.1 Ponti stradali Per i ponti stradali le norme per l effettuazione del collaudo statico sono contenute nel D.M. LL. PP. del 4 maggio 1990 Aggiornamento delle norme
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Laboratorio di Rappresentazione e Modellazione dell Architettura
 Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
DIAGRAMMA DELLE VELOCITA ESERCITAZIONE
 PROGETTI DI INFRSTRUTTURE VIRIE DIGRMM DELLE VELOCIT ESERCITZIONE Il capitolo 5.4 del Decreto Ministeriale del 5/11/2001 prevede che per la verifica della correttezza della progettazione si debba redigere
PROGETTI DI INFRSTRUTTURE VIRIE DIGRMM DELLE VELOCIT ESERCITZIONE Il capitolo 5.4 del Decreto Ministeriale del 5/11/2001 prevede che per la verifica della correttezza della progettazione si debba redigere
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
.y 6. .y 4. .y 5. .y 2.y 3 B C C B. B f A B f -1
 Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. x 1. x..y B C.y 5 x 4..y 4 L elemento è
Funzioni FUNZIONI Una funzione è una relazione fra due insiemi non vuoti e, che associa ad ogni elemento uno e un solo elemento. In simboli si scrive: = oppure. x 1. x..y B C.y 5 x 4..y 4 L elemento è
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
LE TRASFORMAZIONI GEOMETRICHE NEL PIANO
 LE TRASFORMAZIONI GEOMETRICHE NEL PIANO Una trasformazione geometrica è una funzione che fa corrispondere a ogni punto del piano un altro punto del piano stesso Si può pensare come MOVIMENTO di punti e
LE TRASFORMAZIONI GEOMETRICHE NEL PIANO Una trasformazione geometrica è una funzione che fa corrispondere a ogni punto del piano un altro punto del piano stesso Si può pensare come MOVIMENTO di punti e
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Lezione 27: L offerta di moneta e la LM
 Corso di Economia Politica prof. S. Papa Lezione 27: L offerta di moneta e la LM Facoltà di Economia Università di Roma Sapienza Offerta di moneta Offerta di moneta. È la quantità di mezzi di pagamento
Corso di Economia Politica prof. S. Papa Lezione 27: L offerta di moneta e la LM Facoltà di Economia Università di Roma Sapienza Offerta di moneta Offerta di moneta. È la quantità di mezzi di pagamento
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni
 Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Indicando con x i minuti di conversazione effettuati in un mese, con la spesa totale nel mese e con il costo medio al minuto:
 PROBLEMA 1. Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di 10 euro al mese, più 10 centesimi per ogni minuto di conversazione. Indicando
PROBLEMA 1. Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di 10 euro al mese, più 10 centesimi per ogni minuto di conversazione. Indicando
COMUNE DI RAVENNA GUIDA ALLA VALUTAZIONE DELLE POSIZIONI (FAMIGLIE, FATTORI, LIVELLI)
 COMUNE DI RAVENNA Il sistema di valutazione delle posizioni del personale dirigente GUIDA ALLA VALUTAZIONE DELLE POSIZIONI (FAMIGLIE, FATTORI, LIVELLI) Ravenna, Settembre 2004 SCHEMA DI SINTESI PER LA
COMUNE DI RAVENNA Il sistema di valutazione delle posizioni del personale dirigente GUIDA ALLA VALUTAZIONE DELLE POSIZIONI (FAMIGLIE, FATTORI, LIVELLI) Ravenna, Settembre 2004 SCHEMA DI SINTESI PER LA
Esame di Stato 2015 - Tema di Matematica
 Esame di Stato 5 - Tema di Matematica PROBLEMA Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per ogni minuto
Esame di Stato 5 - Tema di Matematica PROBLEMA Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per ogni minuto
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
1. PREMESSA 2. CALCOLI E VERIFICHE FOGNATURA ACQUE REFLUE
 1. PREMESSA La presente verifica idraulica fa riferimento alla precedente verifica allegata al progetto preliminare approvato con Deliberazione del Giunta Municipale n. 113 del 19.09.2011, con la quale
1. PREMESSA La presente verifica idraulica fa riferimento alla precedente verifica allegata al progetto preliminare approvato con Deliberazione del Giunta Municipale n. 113 del 19.09.2011, con la quale
Dipartimento di Economia Aziendale e Studi Giusprivatistici. Università degli Studi di Bari Aldo Moro. Corso di Macroeconomia 2014
 Dipartimento di Economia Aziendale e Studi Giusprivatistici Università degli Studi di Bari Aldo Moro Corso di Macroeconomia 2014 1. Assumete che = 10% e = 1. Usando la definizione di inflazione attesa
Dipartimento di Economia Aziendale e Studi Giusprivatistici Università degli Studi di Bari Aldo Moro Corso di Macroeconomia 2014 1. Assumete che = 10% e = 1. Usando la definizione di inflazione attesa
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta
 Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
LA CRESCITA DELLE POPOLAZIONI ANIMALI
 LA CRESCITA DELLE POPOLAZIONI ANIMALI Riccardo Scipioni Generalmente, con il termine crescita di una popolazione si intende l aumento, nel tempo, del numero di individui appartenenti ad una stessa popolazione.
LA CRESCITA DELLE POPOLAZIONI ANIMALI Riccardo Scipioni Generalmente, con il termine crescita di una popolazione si intende l aumento, nel tempo, del numero di individui appartenenti ad una stessa popolazione.
Il modello generale di commercio internazionale
 Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
Capitolo 6 Il modello generale di commercio internazionale [a.a. 2013/14] adattamento italiano di Novella Bottini (ulteriore adattamento di Giovanni Anania) 6-1 Struttura della presentazione Domanda e
Aprile (recupero) tra una variazione di velocità e l intervallo di tempo in cui ha luogo.
 Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Capitolo 4. Elasticità. Principi di economia (seconda edizione) Robert H. Frank, Ben S. Bernanke. Copyright 2007 - The McGraw-Hill Companies, srl
 Capitolo 4 Elasticità In questa lezione introdurremo il concetto di elasticità: un indicatore dell entità con cui domanda e offerta reagiscono a variazioni di prezzo, reddito ed altri elementi. Nella lezione
Capitolo 4 Elasticità In questa lezione introdurremo il concetto di elasticità: un indicatore dell entità con cui domanda e offerta reagiscono a variazioni di prezzo, reddito ed altri elementi. Nella lezione
CORSO DI IDRAULICA esercizi svolti di correnti a superficie libera
 08/0/000 CORSO DI IDRAULICA esercizi svolti di correnti a superficie libera Prof. E. Larcan - Ing. F. Ballio collaborazione dell'ing. Sara Marcante Sulla base dell'esperienza didattica nell'ambito dei
08/0/000 CORSO DI IDRAULICA esercizi svolti di correnti a superficie libera Prof. E. Larcan - Ing. F. Ballio collaborazione dell'ing. Sara Marcante Sulla base dell'esperienza didattica nell'ambito dei
DALLE CARTE ALLE SEZIONI GEOLOGICHE
 DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
Insegnamento di Progetto di Infrastrutture viarie
 Insegnamento di Progetto di Infrastrutture viarie Opere in terra Caratteristiche di un terreno Compressibilità e costipamento delle terre Portanza sottofondi e fondazioni stradali Instabilità del corpo
Insegnamento di Progetto di Infrastrutture viarie Opere in terra Caratteristiche di un terreno Compressibilità e costipamento delle terre Portanza sottofondi e fondazioni stradali Instabilità del corpo
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 25 NOVEMBRE 2010 DURATA ORE 2:00
 VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 5 NOVEMBRE 010 DURATA ORE :00 QUESITI A RISPOSTA MULTIPLA Una sola risposta è esatta fra le 4 proposte per ciascun quesito. Ogni risposta esatta vale
VII GARA DI MATEMATICA CON LE TECNOLOGIE SELEZIONE 5 NOVEMBRE 010 DURATA ORE :00 QUESITI A RISPOSTA MULTIPLA Una sola risposta è esatta fra le 4 proposte per ciascun quesito. Ogni risposta esatta vale
DIAGRAMMA CARTESIANO
 DIAGRAMMA CARTESIANO Imparerai ora a costruire con excel un diagramma cartesiano. Inizialmente andremo a porre sul grafico un solo punto, lo vedremo cambiare di posizione cambiando i valori nelle celle
DIAGRAMMA CARTESIANO Imparerai ora a costruire con excel un diagramma cartesiano. Inizialmente andremo a porre sul grafico un solo punto, lo vedremo cambiare di posizione cambiando i valori nelle celle
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
Capitolo 26. Stabilizzare l economia: il ruolo della banca centrale. Principi di economia (seconda edizione) Robert H. Frank, Ben S.
 Capitolo 26 Stabilizzare l economia: il ruolo della banca centrale In questa lezione Banca centrale Europea (BCE) e tassi di interesse: M D e sue determinanti; M S ed equilibrio del mercato monetario;
Capitolo 26 Stabilizzare l economia: il ruolo della banca centrale In questa lezione Banca centrale Europea (BCE) e tassi di interesse: M D e sue determinanti; M S ed equilibrio del mercato monetario;
ELENCO PREZZI STANDARD ALLEGATO ALLA BOZZA DI CONVENZIONE
 ELENCO PREZZI STANDARD ALLEGATO ALLA BOZZA DI CONVENZIONE DEFINIZIONI CLIENTE FINALE Persona fisica o giuridica che acquista gas naturale per uso proprio CODICE DI RETE codice contenente regole e modalità
ELENCO PREZZI STANDARD ALLEGATO ALLA BOZZA DI CONVENZIONE DEFINIZIONI CLIENTE FINALE Persona fisica o giuridica che acquista gas naturale per uso proprio CODICE DI RETE codice contenente regole e modalità
Appunti sul galleggiamento
 Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007
 RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE.
 IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE. Lezione 5 Castellanza, 17 Ottobre 2007 2 Summary Il costo del capitale La relazione rischio/rendimento
IL RISCHIO D IMPRESA ED IL RISCHIO FINANZIARIO. LA RELAZIONE RISCHIO-RENDIMENTO ED IL COSTO DEL CAPITALE. Lezione 5 Castellanza, 17 Ottobre 2007 2 Summary Il costo del capitale La relazione rischio/rendimento
Master della filiera cereagricola. Impresa e mercati. Facoltà di Agraria Università di Teramo. Giovanni Di Bartolomeo Stefano Papa
 Master della filiera cereagricola Giovanni Di Bartolomeo Stefano Papa Facoltà di Agraria Università di Teramo Impresa e mercati Parte prima L impresa L impresa e il suo problema economico L economia studia
Master della filiera cereagricola Giovanni Di Bartolomeo Stefano Papa Facoltà di Agraria Università di Teramo Impresa e mercati Parte prima L impresa L impresa e il suo problema economico L economia studia
L aggiornamento di valore deve riguardare tutti i beni appartenenti alla stessa categoria omogenea.
 Supporto On Line Allegato FAQ FAQ n.ro MAN-7PTCTV28338 Data ultima modifica 06/03/2009 Prodotto Sistema Professionista Modulo Cespiti Oggetto Rivalutazione D.L. 185/2008 Riferimenti normativi - D.L. 185/2008
Supporto On Line Allegato FAQ FAQ n.ro MAN-7PTCTV28338 Data ultima modifica 06/03/2009 Prodotto Sistema Professionista Modulo Cespiti Oggetto Rivalutazione D.L. 185/2008 Riferimenti normativi - D.L. 185/2008
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
Metodi risolutivi per le disequazioni algebriche
 Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
 ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
LA CORRELAZIONE LINEARE
 LA CORRELAZIONE LINEARE La correlazione indica la tendenza che hanno due variabili (X e Y) a variare insieme, ovvero, a covariare. Ad esempio, si può supporre che vi sia una relazione tra l insoddisfazione
LA CORRELAZIONE LINEARE La correlazione indica la tendenza che hanno due variabili (X e Y) a variare insieme, ovvero, a covariare. Ad esempio, si può supporre che vi sia una relazione tra l insoddisfazione
Ipotesi sulle preferenze
 La teoria delle scelte del consumatore La teoria delle scelte del consumatore Descrive come i consumatori distribuiscono i propri redditi tra differenti beni e servizi per massimizzare il proprio benessere.
La teoria delle scelte del consumatore La teoria delle scelte del consumatore Descrive come i consumatori distribuiscono i propri redditi tra differenti beni e servizi per massimizzare il proprio benessere.
Il Taeg = 0. Trasparenza e credito ai consumatori. 2011 ABISERVIZI S.p.A. - Riproduzione vietata - Tutti i diritti sono riservati.
 e credito ai consumatori 5 Il Taeg k = n 1 1 + TAEG TAEG ( F k )) tk tk = 0 2011 ABISERVIZI S.p.A. - Riproduzione vietata - Tutti i diritti sono riservati. INDICE La formula finanziaria Le ipotesi di calcolo
e credito ai consumatori 5 Il Taeg k = n 1 1 + TAEG TAEG ( F k )) tk tk = 0 2011 ABISERVIZI S.p.A. - Riproduzione vietata - Tutti i diritti sono riservati. INDICE La formula finanziaria Le ipotesi di calcolo
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
UD 7.2. Risparmio, investimento e sistema finanziario
 UD 7.2. Risparmio, investimento e sistema finanziario Inquadramento generale In questa unità didattica analizzeremo come i risparmi delle famiglie affluiscono alle imprese per trasformarsi in investimenti.
UD 7.2. Risparmio, investimento e sistema finanziario Inquadramento generale In questa unità didattica analizzeremo come i risparmi delle famiglie affluiscono alle imprese per trasformarsi in investimenti.
