LA SECONDA PROVA SCRITTA
|
|
|
- Violetta Anna Maria Caselli
- 8 anni fa
- Visualizzazioni
Transcript
1 L SEOND PROV SRITT 1 L SEOND PROV SRITT 1 Sessione unica 1975 Un tronco stradale è composto da tre tratti rettilinei, e D che si vogliono raccordare con due curve circolari. Per determinare la posizione dei punti,,, D si è fatto uso di un tacheometro sessagesimale a graduazione destrorsa e cannocchiale centralmente anallattico, di costante distanziometrica K = 100. Si conosce la quota del punto, Q = 320,80 m. Le osservazioni eseguite sono riportate nella seguente tabella: ,701 2,351 2, ,452 1,984 1, D ,906 1,493 1,080 Note. h = 1,50 m; h = 1,51 m. I rettifili e si raccordano con una curva monocentrica di raggio R = 62,50 m mentre si sa che i punti di tangenza del secondo raccordo distano dal vertice di 26,15 m. Il candidato determini: a) gli sviluppi delle due curve e la lunghezza totale del tronco stradale; b) le quote del terreno nei punti di tangenza delle due curve, ritenendo il terreno a pendenza costante lungo i lati della poligonale d asse. Sapendo inoltre che il tronco stradale deve avere pendenza 2% da verso D e che in la quota di progetto coincide con quella del terreno, si determinino le quote di progetto nei suddetti punti di tangenza, la quota rossa in D e la posizione dell eventuale punto di passaggio. Si esegua quindi il disegno planimetrico in scala 1:1000 e il profilo longitudinale della strada nella scala 1:1000 per le lunghezze e 1:100 per le altezze. [Esercizio svolto] 2 Prova suppletiva 1975 Un appezzamento di terreno D è definito altimetricamente dalle falde piane e D. L appezzamento è attraversato da una fognatura il cui asse ha la proiezione coincidente con la diagonale e il cui letto è situato a una profondità costante di 2,50 m dalla superficie del terreno. Sull appezzamento devono essere costruiti altri due tronchi di fognatura: uno rettilineo HG sulla falda, l altro bilatero EFG sulla falda D. Entrambi i tronchi dovranno avere i letti alla profondità costante di 2,50 m dalla superficie del terreno e gli assi confluenti nel punto G dell asse della fognatura. Il punto H è situato lungo il lato, il punto E lungo D e il punto F all interno della falda D. Dal vertice sono stati misurati gli angoli di direzione: () = 0 c,00 () = 44 c,52 (D) = 84 c,86 e, nei punti G, E, gli angoli orizzontali: HĜ = 30 c,05 ĜF = 38 c,52 FÊ = 53 c,26 Sono poi state misurate le distanze: = 50,85 m = 76,18 m G = 27,30 m D = 77,69 m DE = 9,50 m Sono state inoltre determinate le quote del terreno in corrispondenza dei vertici dell appezzamento: Q = 100,00 m Q = 101,20 m Q = 102,68 m Q D = 102,60 m Il candidato: a) determini la posizione planimetrica e la quota dei punti E, F, G, H del terreno; b) calcoli le pendenze dei tratti della fognatura da costruire; c) disegni la planimetria in scala 1:500 e il profilo longitudinale lungo la poligonale EFGH nelle scale 1:500 e 1:50. [ = 49,60 m; D = 47,97 m; G = 48,88 m; Q E = 102,323 m; Q G = 100,430 m; p HG = 4,273%; p EF = 3,812%]
2 2 L SEOND PROV SRITT 3 Sessione unica 1977 Un appezzamento di terreno di forma quadrilatera D è stato rilevato dal vertice D con un tacheometro sessagesimale anallattico (K = 100) a graduazione destrorsa. I dati ottenuti dal rilievo sono riportati nel seguente registro: ,400 1,013 0,626 D ,280 1,777 1, ,560 1,131 0,702 Nota. h D = 1,56 m. La quota del punto D è Q D = 120,45 m; l altezza strumentale, sempre nel punto D,è h D = 1,56 m. Si vuole staccare dall appezzamento dato, mediante una dividente MN parallela al lato (con M su D ed N su ), un area di 1300 m 2 dalla parte del lato. Lungo tale dividente si deve realizzare una stradella interpoderale avente la stessa come asse, da raccordare a una stradella corrente lungo il lato con una curva circolare avente vertice in N e il punto di tangenza T 2 sul lato a 30,00 m da. Il candidato determini: a) la posizione dei punti M ed N in cui la dividente incontra i lati D e dell appezzamento mediante le distanze M e N; b) le quote dei punti,, dell appezzamento e quelle dei punti M ed N nell ipotesi che il terreno formi due falde triangolari piane D e D; c) la pendenza della livelletta stradale MT 1 T 2 nell ipotesi che le quote di progetto nei punti estremi M e coincidano con quelle del terreno; d) l area compresa tra le due tangenti (T 1 N e NT 2 ) e l arco circolare T 1 T 2 di cui è prevista una particolare destinazione. Il candidato rappresenti la planimetria quotata dell appezzamento in scala 1:1000. [Esercizio svolto] 4 Sessione unica 1984 Una cava estrattiva di sabbia e ghiaia, posta nelle vicinanze di un bacino fluviale, è delimitata dal contorno pentagonale di vertici 1, 2, 3, 4 e 5. La ditta di rilievi fotogrammetrici incaricata di redigere la carta topografica dell intero bacino in scala 1:1000, decide di utilizzare, mediante adeguati segnali che risulteranno visibili anche sui fotogrammi, i cinque vertici del contorno anzidetto integrati da due altri punti e posti all interno della concessione, come punti d appoggio dei primi due fotogrammi. Facendo stazione nei punti 2, 3, 4, 5 e, mediante un distanziometro a onde e teodolite, si sono misurati gli elementi riportati nella tabella seguente: St P.b. ltezze Distanze Letture Letture prismi (m) inclinate (m) azimutali zenitali 1 1,80 21 = 319, c, c, ,75 23 = 191, c, c, c, c, ,75 43 = 206, c, c, ,70 45 = 159, c, c, c, c, ,70 5 = 144, c, c,0410 1,64 = 140, c, c,8224 Note. h 2 = 1,61 m; h 4 = 1,56 m; h = 1,62 m. La graduazione dei cerchi è destrorsa e centesimale; l origine del sistema è nel punto 1; l asse X coincide con il lato 1-2; la quota del punto 1 è Q 1 = 251,837 m. Si determinino anzitutto: a) le coordinate cartesiane ortogonali dei vertici del contorno delimitante la concessione, nonché le coordinate dei punti e ; b) le quote dei punti 2,3,4,5, e ;c) l area della concessione. Sapendo che le riprese aeree nadirali verranno effettuate utilizzando una camera grandangolare con distanza principale p = 15,2 cm e larghezza utile di lastra l = 23 cm, dopo aver scelto adeguatamente la scala dei fotogrammi, determinare: d) l altezza di volo; e) la lunghezza della zona di terreno ripresa da un fotogramma e quella comune a due successivi, assumendo come ricoprimento longitudinale il valore 0,7. Dovendo costruire lungo l asse un canale scolmatore di pendenza uniforme (quota rossa in pari a 2,5 m, quota rossa in pari a 1,3 m), si dà disposizione al tecnico restitutore di determinare sul modello stereoscopico le quote dei quattro punti, D, E ed F individuati planimetricamente sul disegno nel seguente modo: e D si trovano sulla perpendicolare per alla ( a sinistra, D a destra di guardando ); E ed F si trovano sulla perpendicolare per alla (E a sinistra, F a destra di sempre guardando da ). Le distanze grafiche sono: = D = E = F = 1 cm. Si sono ottenuti i seguenti valori: Q = 250,270 m Q D = 251,000 m Q E = 247,500 m Q F = 248,000 m Determinare la pendenza del canale nonché il volume di terreno da rimuovere sapendo che la larghezza del fondo è pari a 1,00 m e che le pendenze delle scarpate sono tutte uguali a 1:1. Disegnare, infi-
3 L SEOND PROV SRITT ne, la planimetria con gli elementi desunti dal rilievo e con quelli derivanti da calcolo (nella scala suddetta) e le due sezioni trasversali del canale in e in, nella scala 1:50. [Esercizio svolto] 5 Sessione unica di ddis beda 1984 Un appezzamento di terreno di forma poligonale DE è stato rilevato con un tacheometro centralmente anallattico (K = 100) e stadia verticale. Sono stati ottenuti gli elementi riportati nella seguente tabella: 082 c, c,708 1,248 1,439 1, c, c,939 1,475 1,707 1, c,774 D 200 c, c,194 1,743 1,932 2, c,460 D E 222 c, c,239 1,348 1,964 2,580 Note. h = 1,48 m; h = 1,55 m; h D = 1,50 m. La graduazione è centesimale e destrorsa; la quota del punto è Q = 37,54 m. Il candidato: a) assunto un sistema di riferimento cartesiano ortogonale, con origine nel vertice e l asse delle ascisse orientato positivamente secondo il lato, calcoli le coordinate ortogonali e le quote dei vertici; b) considerato l appezzamento di uguale valore unitario, lo divida, con una dividente rettilinea perpendicolare al lato ED, in due parti equivalenti, determinando la posizione dei punti M ed N di intersezione della dividente col perimetro dell appezzamento stesso; c) considerando, inoltre, l appezzamento costituito dalle tre falde piane triangolari D, D, DE, determini le pendenze del terreno lungo la dividente MN; d) rappresenti, infine, la planimetria quotata dell appezzamento con la posizione della dividente, nella scala 1:500. [S = 4471,803 m 2 ; MN = 52,174 m; Q M = 25,363 m; Q N = 36,452 m; p MP = 5,35%; p PN = 43,86%] 6 Sessione unica di aracas 1984 La poligonale D è stata rilevata mediante tacheometro centralmente anallattico (K = 100) e stadia verticale, facendo stazione nei punti e. Le misure eseguite sono riportate nella seguente tabella: 312 c, c,750 1,315 1,826 2, c, c,093 1,025 1,501 1, c,728 D 187 c, c,505 1,410 2,080 2,750 Note. h = 1,50 m; h = 1,52 m. La quota del punto è Q = 125,000 m, mentre le altezze strumentali sono: h = 1,50 m, h = 1,52 m. Il punto, riferito a un particolare sistema di assi cartesiani ortogonali,ha coordinate:x = 30,75 m,y = 33,27 m. L angolo di direzione, riferito alla parallela all asse Y, è () = 63 c,158. Determinare le coordinate cartesiane ortogonali e le quote degli altri vertici della poligonale. I lati della suddetta poligonale sono i rettifili di una strada in progetto che vanno raccordati con due curve circolari di uguale raggio. La livelletta stradale in e in D avrà la stessa quota del terreno e dovrà mantenere per tutto il percorso la stessa pendenza: 2,8%. alcolare: a) il raggio delle due curve di raccordo; b) le coordinate cartesiane e le quote dei punti di tangenza; c) la posizione e la quota del punto di passaggio fra il profilo del terreno e la livelletta di progetto. Disegnare, in scala opportuna, la planimetria e il profilo longitudinale. Nel caso, infine, che la livelletta sopra definita non dia compenso sul profilo longitudinale fra l area di sterro e quella di riporto, si sposti la livelletta parallelamente a se stessa e si determini la quota rossa occorrente in e in D per ottenere tale compenso. [R = 60,438 m; q T1 = 1,385 m; q T2 = 0,089 m; q T3 = 2,643 m; q T4 = 3,792 m; d = 1,095 m] 7 Sessione unica 1986 Si deve realizzare una carta topografica in scala 1:5000 per lo studio e la progettazione di un bacino idrico. Sono note le coordinate planimetriche e le quote dei quattro punti,, e D: X = 1175,12 m Y = 3025,36 m Q = 2340,38 m X = 4400,56 m Y = 4349,83 m Q = 1826,08 m X = 2425,38 m Y = 3901,12 m Q = 1936,54 m X D = 7358,26 m Y D = 2488,84 m Q D = 1736,12 m Per poter posizionare e orientare la carta si sono scelti due punti P e Q posti agli estremi del bacino, la cui larghezza massima sarà di circa un chilometro. Dal punto P (h = 1,58 m), con un teodolite centesimale de- 3
4 4 L SEOND PROV SRITT strorso, si sono collimati i suddetti punti effettuando tre reiterazioni e ottenendo le letture riportate nel seguente specchietto: erchio orizzontale Strati erchio verticale c, c, c, c, = 35 = P 265 c, c, c, c, = 54 = 296 c, c, c, c, = 07 = D 346 c, c, c, c, = 75 = alcolare le coordinate planimetriche e la quota, compensate empiricamente, del punto P. Per il calcolo della quota si consideri il coefficiente di rifrazione atmosferica K pari a 0,14 e il raggio della sfera locale pari a m. naloghe operazioni sono state eseguite per determinare il punto Q che, a calcoli effettuati, risulta possedere le seguenti coordinate: X Q = 6070,24 m Y Q = 108,36 m Q Q = 1451,72 m Il candidato, sapendo che per il rilievo aerofotogrammetrico verrà usata una camera grandangolare di focale pari a 152 mm e formato lastra cm, scelti adeguatamente i ricoprimenti longitudinale e trasversale, nonché la scala media dei fotogrammi, determini: a) l altezza di volo; b) il tempo di scatto (velocità dell aereo 200 km/h); c) il numero della strisciate; d) il numero dei fotogrammi. Descriva inoltre quelle operazioni topografiche che intende adottare per determinare le posizioni plano-altimetriche dei punti (dire all incirca quanti) utili per l orientamento assoluto dei modelli. [X P = 3328,719 m; Y P = 90,388 m; Q P = 1526,909 m; H volo = 1976 m; t = 21,5 sec; n. fot. = 12] 8 Prova suppletiva 1986 Gli appezzamenti contigui di due proprietari sono separati da un confine poligonale DE e lateralmente sono delimitati dai confini rettilinei coincidenti con gli allineamenti ed EF. Partendo dal punto, sul primo confine rettilineo, e terminando nel punto F, sul secondo confine rettilineo EF, si è rilevata la poligonale DEF. Si sono effettuate le misure riportate nella tabella seguente. La graduazione è centesimale destrorsa (K = 100), mentre la quota del punto è Q = 75,48 m. Il candidato: a) calcoli le coordinate cartesiane e le quote dei vertici della poligonale DEF, assumendo il sistema di riferimento cartesiano ortogonale con origine nel punto e l asse delle ascisse orientato secondo il lato ; b) disegni nelle appropriate scale il D 078 c, c,3618 1,547 1,224 0, c, c, c,0000 2,371 2,157 1,942 D 118 c, c, c,4529 1,643 1,362 1,082 E 387 c,2539 D 126 c, c,0000 1,845 1,428 1,010 E F 195 c, c,0000 2,838 2,210 1,585 Note. h = 1,48 m; h = 1,52 m; h D = 1,50 m; h E = 1,54 m. profilo longitudinale del terreno lungo la poligonale DEF; c) dovendosi rettificare il confine poligonale DE, determini, lasciando immutate le aree (di uguale valore unitario) dei due poderi, il nuovo confine rettilineo MN, in modo che risulti parallelo alla congiungente i punti ed F, calcolandone la posizione. [X F = 1,503 m; Y F = 161,986 m; Q F = 72,269 m; NM = 129,49 m; M = 83,741 m; FN = 89,55 m] 9 Prova suppletiva di ddis beba 1986 È in progetto la costruzione di un bacino idrico; a tal fine si rileva la poligonale MNP, lungo i lati della quale, verso valle, saranno costruite le opere di sbarramento. La poligonale si appoggia ai vertici trigonometrici e, le cui coordinate spaziali sono: X = 140,50 m Y = +405,25 m Q = 1315,25 m X = +242,72 m Y = +410,71 m Q = 1324,25 m Usando un teodolite integrato, sono state effettuate le seguenti letture: Distanze M = 149,55 m MN = 411,95 m orizzontali NP = 336,80 m P = 264,555 m ngoli azimutali ÂM = MˆN = destrorsi MNˆP = NPˆ = Pˆ = ngoli zenitali Z M = Z MN = (misurati con altezza del segnale uguale Z NP = Z P = all altezza strumentale) Determinare le coordinate spaziali compensate dei vertici della poligonale. Per il calcolo delle quote si consideri il coefficiente di rifrazione K pari a 0,14 e il raggio della sfera locale R = m. Inoltre, con-
5 L SEOND PROV SRITT siderando il terreno altimetricamente costituito dalle tre falde piane NP, NM, M, e stabilito il livello di massimo invaso alla quota del punto medio del lato NP, determinare la capacità del bacino. [X P = 362,347 m; Y P = 174,746 m; Q P = 1320,042 m; S = ,33 m 2 ; V = m 3 ] 10 Sessione unica di aracas 1986 L appezzamento di forma poligonale DEF è costituito da due parti di valore unitario diverso, e precisamente: la zona DEF ha il valore di lire 8500 al metro quadrato e la zona D ha il valore di lire 5000 al metro quadrato. Le due zone sono separate dall allineamento D. Dovendo dividere l intero appezzamento in tre parti aventi lo stesso valore, con dividenti parallele all allineamento D di separazione delle due parti di valore unitario diverso, il candidato calcoli le coordinate dei punti d incontro delle dividenti con il perimetro dell appezzamento. Le coordinate dei vertici di quel terreno sono: X = 34,80 m X = +50,12 m X = +49,75 m Y = 19,95 m Y = 41,30 m Y = +56,78 m X D = 7,25 m X E = 70,20 m X F = 59,15 m Y D = 82,10 m Y E = +76,10 m Y F = +9,88 m [MN = 104,81 m; M = 19,19 m; PQ = 93,63 m; P = 18,19 m] 11 Prova suppletiva di aracas 1986 Si deve progettare uno spianamento di una zona di terreno con un piano orizzontale creante compenso fra sterro e riporto. Sono note le coordinate cartesiane ortogonali e le quote dei vertici delle falde piane triangolari costituenti l appezzamento. Tali falde sono: F, FG, G, GD, DGF, DFE, EF. I vertici di esse hanno le seguenti coordinate: X = 5,10 m X = 42,50 m Y = 19,85 m Y = 3,90 m Q = 132,38 m Q = 131,96m X = 82,40 m Y = 1,50 m Q = 130,84 m X D = 88,50 m Y D = 61,40 m Q D = 127,47 m X E = 29,80 m X F = 41,10 m X G = 68,60 m Y E = 53,60 m Y F = 35,20 m Y G = 23,40 m Q E = 129,60 m Q F = 137,15 m Q G = 134,25 m Il candidato dopo aver calcolato la quota del piano richiesto, determini analiticamente le posizioni dei punti di passaggio e disegni, in scala opportuna, la planimetria, indicando le zone di sterro e quelle di riporto. [S = 3538,66 m 2 ; Q = 132,67 m] 12 Prova suppletiva 1989 Per la sistemazione di un area destinata a bacino montano, si rileva la poligonale chiusa DE alla quale si appoggiano i vertici del poligono LMNOP che delimita il bacino stesso. Per il rilevamento della poligonale si sono misurati i lati e gli angoli centesimali destrorsi seguenti: = 280,58 m D = 274,06 m DE = 400,00 m E = 481,70 m ˆ = 162 c,7885 ĈD = 110 c,1000 DˆE = 139 c,6225 DÊ = 87 c,3870 EÂ = 100 c,2040 Sono poi note le coordinate cartesiane dei punti e e le quote dei punti,, E: X = 80,12 m Y = 40,05 m X = 348,36 m Y = 72,98 m Q = 725,80 Q = 730,95 m Q E = 723,85 m Per rilevare i punti L, M, N, O, P si sono eseguite le misure raccolte nel registro riportato di seguito. Le misure sono state realizzate mediante un tacheometro di lunghezza costante (praticamente anallattico), avente costante distanziometrica K = 100 e cerchi con graduazione centesimale destrorsa. 035 c,55 L 120 c, c,85 1,085 1,595 2, c,40 M 074 c, c,15 0,973 1,493 2,013 N 120 c, c,00 1,476 1,966 2,456 D 000 c,00 E O 020 c, c,00 1,598 2,084 2,570 P 051 c, c,80 1,113 1,713 2,314 Note. h = 1,55 m; h = 1,58 m; h E = 1,53 m. alcolare: a) le coordinate cartesiane compensate della poligonale DE, riferite al sistema di assi cui sono riferiti i punti e ; b) le coordinate cartesiane, rispetto agli stessi assi, e le quote dei vertici del poligono LMNOP; c) l area del bacino. Dovendo, inoltre, rettificare la bilatera LMN con un lato RT parallelo a LN e tale che l area del bacino rimanga immutata, determinare la posizione degli estremi R e T del nuovo lato e la pendenza di RT,es- 5
6 6 L SEOND PROV SRITT sendo R e T rispettivamente sui prolungamenti di PL e di ON, ritenuti, a loro volta, di pendenza uniforme. Disegnare la planimetria in scala opportuna. Determinare, infine, la quota alla quale sarebbe stato conveniente effettuare il volo fotogrammetrico dell area DEF e il numero dei fotogrammi occorrenti, con l ipotesi della restituzione nella scala 1:1000, scegliendo opportunamente le caratteristiche della camera da presa, la scala dei fotogrammi e il ricoprimento. [S = ,60 m 2 ; LN = 213,03 m; RT = 222,58 m; NT = 23,24 m; p RT = 2,04%; scala fotog. 1:3000; p =152 mm; l = 230 mm; = 0,60; H = 456 m; L = 690 m; t = 4,5; n = 3] 13 Sessione unica di ddis beba 1989 È stata rilevata la poligonale DEFG che delimita un podere. Le misure, eseguite con un teodolite integrato a graduazione centesimale destrorsa, sono raccolte nella seguente tabella: Stazioni Punti battuti Letture al.o. Distanze (m) D E F G G 074 c, c, , c, c, , c,8518 D 186 c, , c,5887 E 397 c, ,44 D 032 c,9438 F 151 c, ,10 E 094 c,7527 G 258 c, ,28 F 239 c, c, ,34 Si calcolino le coordinate dei vertici suddetti, compensandole empiricamente, rispetto a un sistema di riferimento avente l origine nel vertice e l asse positivo delle ascisse orientato secondo il lato.sapendo che la proprietà è divisa dall allineamento E in due parti di valore unitario diverso, risultando la zona EFG di valore u 1 pari a lire/m 2,e la zona DE di valore u 2 uguale a lire/m 2,si esegua la divisione del podere in tre parti dello stesso valore con dividenti uscenti dal vertice E, calcolando le coordinate dei punti di incontro di esse con il peri- metro della proprietà. Si esegua poi la rappresentazione grafica in scala opportuna. [S 1 = 7699,54 m 2 ; S 2 = 7359,21 m 2 ; X P = 22,772 m; Y P = 15,67 m; X T = 53,00 m; Y T = 4,34 m] 14 Sessione unica di aracas 1989 Due proprietà confinanti sono separate dalla poligonale DE, entrambe limitate lateralmente dagli allineamenti PP e QQ. Dovendo procedere alla costruzione di una strada, si conviene di rettificare il vecchio confine, sostituendolo con un confine rettilineo di compenso, perpendicolare all allineamento PP, e di assumere il nuovo confine come asse della strada in progetto. tale scopo, mediante un tacheometro a graduazione centesimale e cannocchiale centralmente anallattico K = 100, si sono fatte le misure riportate nella tabella seguente: D 137 c,780 P 200 c, c, c,59 1,325 1,630 1, c, c,95 1,428 1,584 1, c,108 D 352 c, c, c,90 1,743 1,915 2,088 E 122 c, c,00 1,975 2,160 2,345 D 150 c,000 E Q 47 c,285 Note. h = 1,55 m; h D = 1,58 m. Sapendo che la quota del punto è Q = 100,00 m, determinare il nuovo confine MN mediante le distanze dei suoi estremi rispettivamente da e da E lungo i confini laterali. onsiderando i lati del confine DE ciascuno di pendenza uniforme e i confini laterali P di pendenza +3% da verso P ed EQ di pendenza 3% da E verso Q, determinare gli elementi del profilo longitudinale del terreno lungo il nuovo confine. Stabilito che la livelletta stradale debba avere pendenza p = 1%, in salita da M verso N, e debba essere tale da compensare nel profilo longitudinale le aree di scavo e quelle di riporto, determinare la posizione dei punti di passaggio e le relative quote.disegnare in scale opportune la planimetria e il profilo longitudinale. [S = 3205,71 m 2 ; MN = 136,38 m; M = 22,38 m; EN = 7,43 m; QT M = 100,671 m; QT N = 100,706 m; QP M = 99,366 m; QP N = 100,744 m]
7 L SEOND PROV SRITT 7 erchio orizzontale Strati erchio verticale Distanze ridotte (m) c, c, c, c, c, = 50 = 44 = S = 94,832 S 351 c, c, c, c, c, = 28 = 25 = S = 71, c, c, c, c, c, = 09 = 20 = S = 66, Sessione unica 1992 Due rettifili devono essere raccordati con una curva circolare monocentrica il cui asse dovrà passare per i punti, e, essendo e i punti di tangenza. I punti e individueranno i punti d asse posti sulle spalle di un ponte che, costruttivamente, realizzerà la prima parte di quel raccordo. Il topografo a cui è stata affidata la determinazione degli elementi geometrici della curva ha fatto ricorso a un teodolite integrato, a graduazione destrorsa, ponendolo sul punto S, caposaldo di una livellazione di alta precisione. Ha deciso di effettuare, per le misure angolari, quattro reiterazioni in maniera da compensare gli errori accidentali e da scartare eventuali errori grossolani. Dopo aver collimato i punti, e, ha registrato le misure riportate nella tabella a inizio pagina. La quota del punto S è Q S = 124,3018 m, l altezza strumentale h S = 1,62 m e l altezza del prisma h p = 1,50 m. Il candidato, dopo aver calcolato i valori più probabili degli angoli azimutali e zenitali, nonché i loro errori quadratici medi, e avere accertato se rientrano nelle relative tolleranze, determini: a) il raggio della curva; b) lo sviluppo del ponte e quello dell intero raccordo; c) la quota rossa del punto sapendo che l altezza delle travi del ponte (massicciata compresa) è di 1,10 m e che la pendenza dovrà essere costante; d) le coordinate di cinque punti dell asse, esclusi e, equidistanti fra di loro, che consentiranno il picchettamento di quel tratto col metodo delle ordinate alla corda. ponte ultimato, il collaudatore, non potendo eseguire misure flessimetriche, affida allo stesso topografo il compito di determinare per via indiretta le frecce nelle due condizioni di carico: su una sola corsia e su tutta la carreggiata. Il candidato descriva strumenti e metodi che permetteranno quelle determinazioni relativamente ai due punti posti in mezzeria su entrambi i marciapiede, tenendo presente che, oltre alle frecce sotto carico, si dovranno determinare anche quelle residue e che tutte dovranno essere fornite con l incertezza dell ordine di m. [R = 106,146 m; = 155,0730 m (corda); S = 48,646 m; S = 173,869 m; p = +1,9983%; q = +2,2491 m; X 5 = 40,674 m; Y 5 = 9,835 m] 16 Prova suppletiva 1992 È stato eseguito il rilievo di una zona di terreno con un teodolite integrato a graduazione destrorsa. I risultati dello stesso sono elencati nel registro riportato nella colonna seguente. Il terreno si può ritenere formato dalle seguenti falde piane: P, P, PQ, QPM, MNP, NPO, OP, QD, DQR, RQL, LQM. L altezza del prisma riflettente è uguale all altezza strumentale delle relative stazioni. La quota del punto P è Q P = 74,58 m s.l.m. Dovendo utilizzare quella zona di terreno per spazio attrezzato, il candidato progetti lo spianamento orizzontale di quota 76,00 m, determinando analiticamente i punti di passaggio. alcoli i volumi di sterro e di riporto e disegni, in scala opportuna, la planimetria della zona medesima, mettendo in evidenza la linea di passaggio. [q = +5,367 m; q = 1,992 m; q D = 3,467 m; V ST. = 14402,43 m 3 ; V RIP. = 26979,64 m 3 ] Letture angolari Distanze azimutali zenitali orizzontali (m) 000 c, c,365 57, c, c,254 45, c, c,328 81,24 P Q 203 c, c,157 64,12 Q M 281 c, c,548 42,19 N 303 c, c,289 59,43 O 364 c, c,187 82,77 P 000 c, c,187 78,54 D 116 c, c,743 58,67 R 233 c, c,654 73,28 L 312 c, c,253 50,15 M 357 c,305 64,09
8 8 L SEOND PROV SRITT 17 Sessione unica di ddis beba 1992 Per il progetto di una galleria MN si fa stazione in due punti e D. Da essi, con un teodolite a graduazione destrorsa, si collimano i vertici trigonometrici e le cui coordinate cartesiane sono: X = 105,75 m X = 915,50 m Y = 1115,00 m Y = 1241,54 m Le misure angolari sono registrate nel registro 1. Gli estremi M ed N della galleria in progetto sono stati collegati ai punti e D attraverso un punto E. Mediante un distanziometro elettro-ottico, montato sul teodolite, sono state fatte le misure riportate nel registro 2. Il candidato determini le coordinate cartesiane, le quote dei punti M ed N,la lunghezza e la pendenza della galleria ed esegua la planimetria in scala opportuna. Nell ipotesi che dell intera zona interessata al progetto si dovesse redigere la carta topografica nella scala 1:2000 mediante rilievo fotogrammetrico, il candidato stabilisca tutte le caratteristiche del volo nonché il numero delle strisciate e dei fotogrammi occorrenti. [X M = 37,43 m; Y M = 99,69 m; X N = 621,93 m; Y N = 326,75 m; Q N = 916,14 m; MN = 627,05 m; scala dis. 1:2000; scala fotog. 1:7500; p = 152 mm; l = 230 mm; V = 165 km/h; = 0,60; H = 1140 m, L = 1725 m; t = 15,3; n = 3] Registro 1 Stazione P.b. Letture al.o. Letture al.v. h = 1,60 m D , , , D , ,8 h = 1,58 m ,7 Note. Q = 1007,95 m; K = 0,14; R = m. Registro 2 Stazione P.b. Distanze reali (m) Letture zenitali E 439, M 301, M 380, E N 505, D 440, D N 549, Note.L altezza del prisma in M è uguale all altezza strumentale in e quella del prisma in N è uguale all altezza strumentale in D. 18 Prova suppletiva di ddis beba 1992 La poligonale d asse di una strada in progettazione ha per vertici i punti 1, 2, 3, 4 e 5 le cui coordinate e quote sono le seguenti: X 1 = 74,96 m X 2 = 55,87 m X 3 = 20,74 m X 4 = 36,38 m X 5 = 155,68 m Y 1 = 25,64 m Y 2 = 55,23 m Y 3 = 20,10 m Y 4 = 59,45 m Y 5 = 61,30 m Z 1 = 60,35 m Z 2 = 63,10 m Z 3 = 61,00 m Z 4 = 57,80 m Z 5 = 60,40 m Tra i vertici suddetti sono inseriti, nei rispettivi allineamenti, alcuni picchetti corrispondenti all intersezione della poligonale d asse piano a curve di livello (si veda la tabella seguente). La poligonale suddetta deve essere raccordata con tre curve circolari monocentriche delle quali si conoscono le quote dei punti M, N, P e le distanze dei vertici dei rettilinei: 2M = 15,11 m 3N = 4,70 m 4P = 13,72 m Q M = 62,52 m Q N = 61,00 m Q P = 58,30 m llineamenti Picchetti Distanze (m) Quote (m) = 16,50 61,00 1 = 48,28 62, = 41,80 62, D 3D = 30,22 60,00 E 3E = 50,47 59,00 F 4F = 51,79 59,00 G 4G = 116,36 60,00 Si calcolino tutti gli elementi necessari per poter disegnare il profilo longitudinale dell asse della strada nelle opportune scale. Si determini, infine, la quota di progetto nel punto 5 della livelletta di compenso che nel punto 1 avrà quota rossa uguale a zero. [L = 397,457 m; QP 5 = 60,505 m; p = 0,04%] 19 Prova assegnata agli esami di abilitazione 1994 Due appezzamenti confinano fra di loro lungo l asse di una strada vicinale della quale non sono più reperibili gli atti progettuali. Nella zona che ci interessa, la strada, tutta a pendenza costante, è costituita dai due tratti rettilinei M e N raccordati da una curva circolare monocentrica i cui punti di tangenza sono e. I due proprietari, per meglio utilizzare i loro fondi, decidono di sostituire quel raccordo con uno, pure circolare monocentrico, i cui punti di tangenza T 1 (su M) e T 2 (su N) sono arretrati rispetto ai primi di
9 L SEOND PROV SRITT 70 m. Per stabilire le caratteristiche geometriche della curva esistente il tecnico preposto alla riconfinazione fa stazione sul punto con un teodolite con distanziometro elettro-ottico e, dopo aver collimato il prisma posto su e su (il punto si trova sull asse della curva), effettua le seguenti letture: Letture ai cerchi Distanze ltezza orizz. vert. (m) prisma (m) 10 c, c, ,50 1, c, c, ,30 1,50 Nota. h = 1,60 m. Il candidato, dopo aver calcolato gli elementi caratteristici del raccordo esistente, determini quelli necessari per la progettazione della nuova curva, includendo fra essi anche la pendenza. alcoli l area che col nuovo tracciato viene a passare di proprietà. Descriva, inoltre, una possibile metodologia di rilievo e una coerente procedura di elaborazione per ottenere la planimetria, il profilo longitudinale e il quaderno delle sezioni trasversali del progetto esecutivo del tracciato in oggetto. In base alla natura del terreno, proceda infine al picchettamento del nuovo raccordo. [R = 13,37 m; R 1 = 44,21 m; p = 7,27%; S = 1978,20 m 2 ] 20 Prova assegnata agli esami di abilitazione 1997 Due appezzamenti confinano fra di loro lungo l asse di una strada vicinale. Nella zona che ci interessa, la strada è costituita dai due tratti rettilinei e D raccordati da una curva circolare monocentrica i cui punti di tangenza sono e.i due proprietari decidono di dismetterne l uso e di sostituire quel confine curvilineo con uno formato dalla spezzata MND, essendo M ed N situati rispettivamente sui prolungamenti di e di D, con M distante 20,00 m da. Per stabilire le caratteristiche geometriche della curva esistente il tecnico preposto alla riconfinazione misura direttamente le distanze P, P e, essendo P un punto del raccordo circolare, e ottiene i seguenti valori: P = 32,22 m P = 69,98 m = 90,18 m Il candidato, dopo aver calcolato gli utili elementi geometrici che caratterizzano il raccordo, determini la posizione dei punto N mediante la distanza N,imponendo che le superfici scambiate siano equivalenti. Stabilito che la nuova dividente MN si trova all interno del triangolo fiduciale PF4, PF5, PF9 (si scelgano a piacere questi tre punti), il candidato descriva il metodo del rilievo catastale di aggiornamento e la relativa strumentazione che intende adottare per l inquadramento di questa riconfinazione. Descriva, inoltre, gli elaborati tecnici da predisporre ed esegua lo schema del rilievo, redatto in scala 1:1000, corredato di tutti gli eventuali sviluppi esplicativi per una completa interpretabilità delle operazioni di inquadramento, con evidenziazione anche simbolica dei PF utilizzati, dei punti generatori delle osservazioni e degli eventuali punti ausiliari. Per quanto riguarda il libretto delle misure, le righe di informazione standardizzate saranno formulate secondo lo schema previsto dalle norme in vigore. [R = 51,633 m; N = 29,45 m] 21 Prova assegnata agli esami di abilitazione 1998 La proprietà fondiaria quadrilatera di vertici 1, 2, 3, 4, per motivi di successione testamentaria, deve essere divisa in due parti equivalenti. I beneficiari decidono di realizzare il frazionamento con una dividente MN parallela al lato 12 e convengono, altresì, che quella dividente rappresenti l asse di un canale per uso irriguo, di comune proprietà. Il tecnico preposto all espletamento dell incarico professionale decide, indipendentemente dalle coordinate cartografiche planimetriche lette sugli atti catastali, di ridefinire la geometria di quel fondo mediante un opportuno rilevamento i cui risultati, comprensivi delle quote, conseguenti alle misurazioni e ai relativi calcoli, sono i seguenti: X 1 = 236,80 m Y 1 = 172,40 m Q 1 = 201,00 m X 3 = 616,00 m Y 3 = 960,10 m Q 3 = 202,80 m X 2 = 576,10 m Y 2 = 368,40 m Q 2 = 207,90 m X 4 = 208,50 m Y 4 = 840,20 m Q 4 = 191,10 m Le due falde piane 124 e 234 definiscono l orografia del fondo. L asse del canale sarà costituito da un unica livelletta con quota rossa uguale a zero nel punto N e con pendenza negativa da N verso M. Il valore di essa sarà scelto dal candidato che fisserà anche la larghezza del fondo del canale e le scarpe delle sue sponde. Il candidato, dopo aver determinato le distanze 1M e 2N (M sulla 14, N sulla 23), disegni, per la definizione di quel progetto, la planimetria della proprietà fondiaria e del frazionamento, il profilo longitudinale lungo l asse del canale e un congruo numero di sezioni trasversali adottando opportune scale di rappresentazione. [1M = 320 m; 2N = 341,60 m; MN = 434,05 m] 22 Prova assegnata agli esami di abilitazione 2000 Due fondi X e Y sono compresi fra due strade e confinano fra loro secondo il segmento lungo 256,20 m. Dati gli angoli che la linea di confine forma con il margine di una strada nel punto 9
10 10 L SEOND PROV SRITT ( =59 c,3704) e l angolo che la stessa linea forma con il margine dell altra strada nel punto ( = 108 c,7240), indicando V il punto di convergenza dei predetti tratti rettilinei delle due strade, si proceda alla rettifica del confine attuale con una dividente perpendicolare alla bisettrice dell angolo di convergenza delle strade. Il candidato determini la posizione del nuovo confine mediante le distanze delle due estremità T e Z rispettivamente da e da e ne calcoli la lunghezza. alcoli inoltre la pendenza della nuova linea dividente conoscendo le pendenze p 1 = 3,60% e p 2 = 3,05% in salita rispettivamente da e da verso V e le quote altimetriche Q = 242,20 m e Q = 253,45 m. La zona in cui sono situati i due fondi diverrà edificabile; le norme di attuazione del PRG hanno fissato l indice di edificabilità pari a 1 m 3 /m 2 e un altezza massima dei fabbricati di 7 m. Un impresa di costruzioni è interessata all acquisto di due porzioni dei fondi X e Y, della superficie rispettiva di ha e ha per realizzarvi un complesso residenziale. Il proprietario del fondo X è disponibile alla vendita, mentre il proprietario del fondo Y, che conduce un azienda orticola, intende proseguire nella sua attività, ma è disposto alla cessione della cubatura edificabile di sua competenza. Il candidato, assunto liberamente ogni elemento ritenuto utile o indispensabile, determini il giusto prezzo che l impresa dovrebbe pagare ai proprietari dei fondi X e Y, per acquistarne rispettivamente la proprietà e il diritto di edificabilità. È facoltà del candidato di integrare la prova illustrando le operazioni da compiere e gli elaborati da redigere per l aggiornamento degli atti catastali. [TV = 475,64 m; TZ = 235,89 m; Q T = 244,094 m; Q Z = 252,005 m; p = 3,35%] 23 Sessione unica 2001 Facendo riferimento alla planimetria di figura 1, si devono collegare i due punti e con una strada comunale le cui principali caratteristiche, fissate dopo un attenta analisi del traffico, sono le seguenti: larghezza della sede stradale: 6,00 m; raggio minimo dei raccordi circolari: 60,00 m; pendenza massima: 5%. Il candidato rediga il progetto corredandolo coi prescritti allegati. Sarà facoltà del candidato schematizzare le eventuali opere d arte necessarie al corpo stradale (muri di sostegno, di sottoscarpa, di controripa, ponte ecc. ) senza che ci si soffermi alle loro progettazioni. [Esercizio svolto] 24 Sessione unica 2004 (Progetto cinque) Dovendosi realizzare il restauro di un edificio storico a pianta rettangolare, si decide di eseguire un rilevo topofotogrammetrico dell edificio, rilevando una poligonale chiusa D (i cui vertici si susseguono in Scala 1: m Figura 1 Rappresentazione grafica allegata all esercizio 23.
11 L SEOND PROV SRITT senso orario) ai fini del suo inquadramento plano-altimetrico; da punto, inoltre, si sono collimati tre trigonometrici P, R, S le cui coordinate sono: X P = 419, 023 m Y P = 494,908 m Z P = 175,277 m X R = 486,811 m Y R = 291,606 m Z R = 175,726 m X S = 344,650 m Y S = 74,988 m Z S = 188,056 m Gli elementi, misurati con un teodolite elettronico centesimale, sono raccolti nel seguente libretto: Stazione h = 1,609 m Punti.O..V. Distanze Prisma coll. (gon) (gon) (m) (m) P 110, ,2547 R 144, ,8895 S 192, ,6843 D 221, , , , ,350 1,70 379, ,350 h = 1,609 m 251, , ,650 1,70 174, ,650 h = 1,609 m D 174, , ,880 1,70 D 259, ,880 h D = 1,609 m 163, , ,050 1,70 Il candidato, dopo aver relazionato brevemente sulla funzione dell inquadramento plano-altimetrico ai fini del rilievo topofotogrammetrico dell edificio, determini: 1. Le coordinate planimetriche del punto. 2. La quota del punto, compensata empiricamente, tenendo conto delle diverse distanze alle quali sono stati misurati i dislivelli (si assuma K = 0,13 e R = m). 3. alcoli le coordinate planimetriche e le quote compensate dei vertici della poligonale, rappresentando il relativo piano quotato a scala adeguata. Si utilizzino le seguenti tolleranze prefissate: tolleranza angolare: T a = 0,025 n (gon); tolleranza lineare: T L = 0,025 L (m); tolleranza altimetrica: T D = 0,004 L (m). 4. Descriva le successive operazioni di campagna relative al rilievo dell edificio, la procedura di ripresa fotogrammetrica che intende adottare, nonché i mezzi necessari ai fini della presa e della restituzione del rilievo fotogrammetrico. [X = 177,663 m; Y = 408,131 m; Q = 178,727 m; X D = 57,486 m; Y D = 407,106 m; Q D = 178,834 m] Sessione unica 2004 (ordinamento) un Geometra viene affidato l incarico di frazionare un terreno DE, i cui vertici si susseguono in senso orario, in vista di due diversi futuri interventi di natura altimetrica. Da un precedente rilievo, della cui attendibilità il Tecnico è certo, viene a conoscenza della superficie reale del terreno, che è di ,26 m 2,e di alcuni elementi, misurati con un teodolite elettronico centesimale, raccolti nel seguente libretto: Stazione h = 1,544 E Punti.O..V. Distanze Prisma coll. (gon) (gon) (m) (m) 110, , ,328 P 258, ,5764 1,60 R 289, ,6449 1,60 S 348, ,1620 1,60 110, ,328 E 121, , , ,393 D 105,3125 D 110, ,8513 dove i punti P, R, S sono elementi visibili dal vertice e di coordinate note rispetto a un sistema di riferimento locale (il punto si trova alla destra di un osservatore che da P guarda il vertice R): X P = 501,027 m Y P = 398,198 m Z P = 109,116 m X R = 532,769 m Y R = 390,325 m Z R = 108,100 m X S = 587,964 m Y S = 397,768 m Z S = 106,886 m Il Tecnico incaricato, ritenendo sufficienti i dati a disposizione per la risoluzione del frazionamento, rimandando a una fase successiva la scelta di un idoneo schema di rilievo per l atto di aggiornamento catastale, effettua una livellazione geometrica dal mezzo composta lungo la linea chiusa DE, ottenendo i seguenti dislivelli: = +1,735 m = 0,928 m D = 0,875 m DE = +0,574 m E = 0,531 m Il candidato determini: 1. Le misure dei lati incogniti del terreno (, D, DE). 2. Relativamente al vertice, le coordinate compensate (rispetto al sistema di riferimento locale assegnato) e la quota compensata.
12 12 L SEOND PROV SRITT Stazione Punto Letture azimutali Letture zenitali Distanza inclinata ltezza prisma battuto (gon) (gon) (m) (m) Note 300, , ,254 1,60 Primo vertice (h = 1,50 m) 154, , ,372 1,60 Stazione avanti 289,3250 1,60 Stazione indietro (h = 1,48 m) D 149, , ,945 1,60 Stazione avanti D 187,4520 1,60 Stazione indietro (h = 1,52 m) E 351, , ,166 1,60 Ultimo vertice 3. Le coordinate planimetriche e le quote compensate dei vertici della poligonale chiusa DE. tal fine si utilizzi la seguente tolleranza prefissata: T = 0,004 P (m), con P perimetro della poligonale espresso in metri. 4. Frazioni il terreno in tre parti proporzionali ai numeri 2, 3, 5 con dividenti uscenti dal vertice,in maniera tale che l area minore contenga il vertice E, e la maggiore il vertice. 5. Rediga infine il relativo piano quotato, con l esplicazione grafica del frazionamento, in scala opportuna. Il candidato ha facoltà, inoltre, di elencare o descrivere quali elaborati tecnici sarebbero da predisporre per l atto di aggiornamento catastale, scegliendo un opportuno schema di rilievo. [X = 539,943 m; Y = 346,624 m; Q = 101,602 m; X D = 738,906 m; Y D = 214,709 m; EM = 94,619 m; N = 67,482 m] 26 Prova assegnata agli esami di abilitazione 2006 I vertici ed E sono il primo e l ultimo picchetto di una strada in progetto di tipo F, locale extraurbana ai sensi delle «Norme funzionali e geometriche per la costruzione delle strade» elaborate dal NR. Tra di essi si è eseguita la poligonale d asse DE per il rilievo della quale si è fatta stazione sui vertici, e D con un teodolite integrato a graduazione centesimale destrorsa. Si è ottenuto il registro delle misure illustrato a inizio pagina. ssumendo per il primo vertice della poligonale d asse coordinate plano-altimetriche di comodo (0,00; 0,00; 100,00) m, e sapendo che il primo lato della poligonale si trova sul semiasse positivo delle ascisse, si richiedono: il disegno di una planimetria in scala opportuna; il calcolo delle coordinate plano-altimetriche (X, Y, Q) dei vertici della poligonale d asse; lo studio del raccordo tra il rettifilo e il rettifilo con una curva circolare monocentrica avente tangente t 1 = 18,00 m; lo studio del raccordo tra i rettifili, D e DE con un unica curva circolare monocentrica; il calcolo della lunghezza complessiva della strada e il calcolo dell area di esproprio, considerando una fascia di rispetto media di 1,5 m per lato. [X E = 151,228 m; Y E = 23,697 m; Q E = 101,272 m; X D = 738,906 m; Y D = 214,709 m; R 1 = 48,477 m; R 2 = 37,628 m; S ES = 1788,22 m 2 ] 27 Sessione unica 2007 Dovendosi realizzare lavori di natura planimetrica (frazionamenti) ed altimetrica (spianamenti) in un terreno DEFG, i cui vertici si susseguono in senso orario, sono stati misurati tutti i lati, alcuni angoli interni del terreno, in quanto non tutti i vertici risultano reciprocamente visibili, ed alcune quote. I risultati del rilievo sono riportati nella seguente tabella: Lati (m) ngoli (gon) Quote (m) = 527,321 EÂ = 92,3258 Del vertice : 601,454 = 358,396 ÊD = 58,3215 Del vertice E: 619,327 D = 456,321 GFˆE = 135,2215 Del vertice F: 605,327 DE = 495,398 ĈD = 85,3215 Del vertice G: 590,328 EF = 402,528 FG = 597,421 G = 728,429 Il candidato: 1. alcoli le coordinate dei vertici del terreno rispetto a un sistema di assi cartesiani che ha origine in E e semiasse positivo delle Y passante per il vertice. 2. Frazioni il terreno DE, di uguale valore in tutta la sua estensione, in tre parti, S 1, S 2, S 3, rispettivamente proporzionali ai numeri m = 1, n = 2, p = 3, con dividenti parallele al lato E, sapendo che S 1 deve contenere il lato E e S 3 il vertice.
13 L SEOND PROV SRITT 3. Progetti la sistemazione altimetrica del terreno EFG, formato dalle falde triangolari EG ed EFG, con uno spianamento orizzontale di compenso, determinando i relativi volumi di scavo e di riporto. 4. Nell ipotesi di voler realizzare del territorio una carta in scala 1:500 e si stabilisca: di effettuare il volo per la presa dei fotogrammi secondo parallele all asse delle x; il tempo di esposizione dell obiettivo, pari a 0,001 s; un trascinamento massimo di 0,03 mm; una sovrapposizione longitudinale tra i fotogrammi di una stessa strisciata del 60%; una sovrapposizione trasversale tra due strisciate consecutive del 20%; 13 l utilizzo di una camera da presa grandangolare, con distanza principale di 153,000 mm; il formato dei fotogrammi mm; calcoli: la quota media del volo, la velocità massima che potrà tenere l aereo e il corrispondente intervallo di tempo tra due scatti successivi; il numero delle strisciate, quello dei fotogrammi per ciascuna strisciata e quello complessivo. 5. lleghi i seguenti disegni in scala opportuna: esplicazione grafica del frazionamento del terreno DE; il piano quotato del terreno EFG, evidenziando la parte di scavo da quella di riporto; il grafico del piano di volo. [Esercizio svolto]
LA SECONDA PROVA SCRITTA
 L SEOND PROV SRITT 1 L SEOND PROV SRITT 1 Sessione unica 1975 Un tronco stradale è composto da tre tratti rettilinei, e D che si vogliono raccordare con due curve circolari. Per determinare la posizione
L SEOND PROV SRITT 1 L SEOND PROV SRITT 1 Sessione unica 1975 Un tronco stradale è composto da tre tratti rettilinei, e D che si vogliono raccordare con due curve circolari. Per determinare la posizione
ELEMENTI DI TOPOGRAFIA - ESERCIZI
 ELEMENTI I TOPOGRFI ESERIZI 1. ato il quadrilatero, i cui vertici si seguono in senso antiorario, di cui si conoscono le coordinate dei vertici e rispetto a un sistema di assi ortogonali: E = 23,55 m N
ELEMENTI I TOPOGRFI ESERIZI 1. ato il quadrilatero, i cui vertici si seguono in senso antiorario, di cui si conoscono le coordinate dei vertici e rispetto a un sistema di assi ortogonali: E = 23,55 m N
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
PLANIMETRIA E PROFILO INSIEME
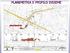 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
PERCORSO ESTIVO PER STUDENTI CON DEBITO FORMATIVO IN TOPOPGRAFIA
 I. I. S."MOREA-VIVARELLI" ----- FABRIANO ********************************************************* sez. COSTRUZIONI AMBIENTE TERRITORIO - a.s.2013/2014 corso di TOPOGRAFIA prof. FABIO ANDERLINI nella classe
I. I. S."MOREA-VIVARELLI" ----- FABRIANO ********************************************************* sez. COSTRUZIONI AMBIENTE TERRITORIO - a.s.2013/2014 corso di TOPOGRAFIA prof. FABIO ANDERLINI nella classe
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico
 La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
IL SISTEMA CARTOGRAFICO NAZIONALE
 IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Unità Didattica 3 ESERCITAZIONE IL PLASTICO. Unità Didattica 1 CURVE DI LIVELLO. Unità Didattica 2 PROFILO ALTIMETRICO
 ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
-Rilievo diretto Laboratori -Rilievo Aula 9 edificio A. Alessio Tirapelle Mirko Mondini Daniel Colombelli Irene Gregori
 -Rilievo diretto Laboratori -Rilievo Aula 9 edificio A Alessio Tirapelle Mirko Mondini Daniel Colombelli Irene Gregori Operazioni di misura a diretto contatto con l oggetto da rilevare; è possibile il
-Rilievo diretto Laboratori -Rilievo Aula 9 edificio A Alessio Tirapelle Mirko Mondini Daniel Colombelli Irene Gregori Operazioni di misura a diretto contatto con l oggetto da rilevare; è possibile il
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
DALLE CARTE ALLE SEZIONI GEOLOGICHE
 DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
DALLE CARTE ALLE SEZIONI GEOLOGICHE PROFILO TOPOGRAFICO Il profilo topografico, detto anche profilo altimetrico, è l intersezione di un piano verticale con la superficie topografica. Si tratta quindi di
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
L ingombro ed il numero delle corsie si calcola attraverso lo schema e la tabella riportata a seguito.
 4.2 IL COLLAUDO STATICO DEI PONTI 4.2.1 Ponti stradali Per i ponti stradali le norme per l effettuazione del collaudo statico sono contenute nel D.M. LL. PP. del 4 maggio 1990 Aggiornamento delle norme
4.2 IL COLLAUDO STATICO DEI PONTI 4.2.1 Ponti stradali Per i ponti stradali le norme per l effettuazione del collaudo statico sono contenute nel D.M. LL. PP. del 4 maggio 1990 Aggiornamento delle norme
11 - Rilievo tridimensionale di un edificio con distanziometro senza prisma e restituzione dei prospetti in 2D
 11 - Rilievo tridimensionale di un edificio con distanziometro senza prisma e restituzione dei prospetti in 2D Vediamo in questo capitolo una procedura molto importante di PFCAD CATASTO quale il disegno
11 - Rilievo tridimensionale di un edificio con distanziometro senza prisma e restituzione dei prospetti in 2D Vediamo in questo capitolo una procedura molto importante di PFCAD CATASTO quale il disegno
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
Ministero delle Infrastrutture e dei Trasporti
 Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Produzione e collaudo di cartografia tecnica numerica verso i DB topografici
 Ufficio Cartografico Servizio Cartografia e Gis della Provincia di Brescia Produzione e collaudo di cartografia tecnica numerica verso i DB topografici Ing. Antonio Trebeschi L attività dell Ufficio Cartografico
Ufficio Cartografico Servizio Cartografia e Gis della Provincia di Brescia Produzione e collaudo di cartografia tecnica numerica verso i DB topografici Ing. Antonio Trebeschi L attività dell Ufficio Cartografico
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Rilievo e Rilevamento
 Rilievo e Rilevamento I metodi di rilevamento si basano sulla determinazione della posizione di un certo numero di punti dell oggetto che ne permettano la rappresentazione ed un successivo utilizzo di
Rilievo e Rilevamento I metodi di rilevamento si basano sulla determinazione della posizione di un certo numero di punti dell oggetto che ne permettano la rappresentazione ed un successivo utilizzo di
Anna Montemurro. 2Geometria. e misura
 Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
GIOCHI A SQUADRE. 30 marzo 2012
 Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
Ministero delle Infrastrutture e dei Trasporti
 Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
Ministero delle Infrastrutture e dei Trasporti UNITÀ DI GESTIONE DELLE INFRASTRUTTURE PER LA NAVIGAZIONE ED IL DEMANIO MARITTIMO S.I.D. SISTEMA INFORMATIVO DEMANIO MARITTIMO GUIDA ALLA COMPILAZIONE DEL
LA RETTA. b) se l equazione si presente y=mx+q (dove q è un qualsiasi numero reale) si ha una retta generica del piano.
 LA RETTA DESCRIZIONE GENERALE Nella GEOMETRIA ANALITICA si fa sempre un riferimento rispetto al piano cartesiano Oxy; questa riguarda lo studio della retta, delle trasformazioni lineari piane e delle coniche.
LA RETTA DESCRIZIONE GENERALE Nella GEOMETRIA ANALITICA si fa sempre un riferimento rispetto al piano cartesiano Oxy; questa riguarda lo studio della retta, delle trasformazioni lineari piane e delle coniche.
LEZIONI DI TOPOGRAFIA
 Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
Che cos è il Centro di Gravità
 Che cos è il Centro di Gravità Chiunque si è sempre posto domande del tipo: dove si trova il centro di gravità del mio modello? oppure: Dovrò avanzarlo o arretrarlo?. In questa pagina cercherò di spiegare
Che cos è il Centro di Gravità Chiunque si è sempre posto domande del tipo: dove si trova il centro di gravità del mio modello? oppure: Dovrò avanzarlo o arretrarlo?. In questa pagina cercherò di spiegare
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Tutorial 3DRoom. 3DRoom
 Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Aprile (recupero) tra una variazione di velocità e l intervallo di tempo in cui ha luogo.
 Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Il monitoraggio degli spostamenti
 Il monitoraggio degli spostamenti Introduzione Lo studio del monitoraggio di un opera d Ingegneria Civile nasce con l opera stessa in quanto fisiologicamente connesso ai problemi strutturali che il progetto
Il monitoraggio degli spostamenti Introduzione Lo studio del monitoraggio di un opera d Ingegneria Civile nasce con l opera stessa in quanto fisiologicamente connesso ai problemi strutturali che il progetto
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
INDICE. Pregeo Rilievo Crea righe 3 2. Pregeo Rilievo Crea righe 4, 5 3. Pregeo Rilievo Crea righe 7 9
 Prodotto da INDICE Pregeo Rilievo Crea righe 3 2 Pregeo Rilievo Crea righe 4, 5 3 Pregeo Rilievo Crea righe 7 9 Pregeo Rilievo Crea righe 7 vertice/direzione 11 Pregeo Rilievo Crea righe per frazionamento
Prodotto da INDICE Pregeo Rilievo Crea righe 3 2 Pregeo Rilievo Crea righe 4, 5 3 Pregeo Rilievo Crea righe 7 9 Pregeo Rilievo Crea righe 7 vertice/direzione 11 Pregeo Rilievo Crea righe per frazionamento
Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente.
 Linee Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente. a. curva spezzata retta mista aperta chiusa b. curva spezzata
Linee Che tipo di linee riconosci in questi quadri? Ripassale con una matita colorata e, con la stessa tinta, colora il pallino corrispondente. a. curva spezzata retta mista aperta chiusa b. curva spezzata
Geoute. Versione 8.01 Gestione dati da Stazioni Totali PENTAX. GUIDO VERONESI S.r.l.
 Geoute Versione 8.01 Gestione dati da Stazioni Totali PENTAX GUIDO VERONESI S.r.l. Via Caselle, 46 40068 San Lazzaro di S. (BOLOGNA) +39 (051) 454733-453229 Fax +39 (051) 453181 Web site: www.veronesi.org
Geoute Versione 8.01 Gestione dati da Stazioni Totali PENTAX GUIDO VERONESI S.r.l. Via Caselle, 46 40068 San Lazzaro di S. (BOLOGNA) +39 (051) 454733-453229 Fax +39 (051) 453181 Web site: www.veronesi.org
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
La misura in topografia
 La misura in topografia In questa dispensa di fornisce un cenno agli strumenti e alle tecniche di misura impiegate in topografia. Vengono descritti gli strumenti per misurare le lunghezze, quali il flessometro,
La misura in topografia In questa dispensa di fornisce un cenno agli strumenti e alle tecniche di misura impiegate in topografia. Vengono descritti gli strumenti per misurare le lunghezze, quali il flessometro,
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
GUIDA RAPIDA PER LA COMPILAZIONE DELLA SCHEDA CCNL GUIDA RAPIDA PER LA COMPILAZIONE DELLA SCHEDA CCNL
 GUIDA RAPIDA BOZZA 23/07/2008 INDICE 1. PERCHÉ UNA NUOVA VERSIONE DEI MODULI DI RACCOLTA DATI... 3 2. INDICAZIONI GENERALI... 4 2.1. Non modificare la struttura dei fogli di lavoro... 4 2.2. Cosa significano
GUIDA RAPIDA BOZZA 23/07/2008 INDICE 1. PERCHÉ UNA NUOVA VERSIONE DEI MODULI DI RACCOLTA DATI... 3 2. INDICAZIONI GENERALI... 4 2.1. Non modificare la struttura dei fogli di lavoro... 4 2.2. Cosa significano
Mappe catasto terreni Mappe catasto edifici Planimetria chiesa
 1 E una rappresentazione in piano di una superficie, di un terreno o di un edificio. Equivale al concetto di pianta nel disegno tecnico (PO). Tutti i beni immobili vengono registrati al CATASTO, ufficio
1 E una rappresentazione in piano di una superficie, di un terreno o di un edificio. Equivale al concetto di pianta nel disegno tecnico (PO). Tutti i beni immobili vengono registrati al CATASTO, ufficio
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ALLEGATO II Dispositivi di attacco
 ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
ORGANIZZATORE PER BORSA GRANDE
 ORGANIZZATORE PER BORSA GRANDE Lavorando a circa cinquanta chilometri da dove vivo, la borsa risulta per me è essere uno strumento di sopravvivenza! Dentro di essa deve trovare spazio tutto ciò che ipoteticamente
ORGANIZZATORE PER BORSA GRANDE Lavorando a circa cinquanta chilometri da dove vivo, la borsa risulta per me è essere uno strumento di sopravvivenza! Dentro di essa deve trovare spazio tutto ciò che ipoteticamente
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON
 PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Tabella A.1 Classificazione generale degli edifici per categorie
 Appendice A Modalità di installazione degli impianti fotovoltaici sugli edifici Ai fini dell applicabilità della tariffa incentivante competente agli impianti fotovoltaici realizzati sugli edifici si adotta
Appendice A Modalità di installazione degli impianti fotovoltaici sugli edifici Ai fini dell applicabilità della tariffa incentivante competente agli impianti fotovoltaici realizzati sugli edifici si adotta
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Sistema di diagnosi CAR TEST
 Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Istituto Tecnico Commerciale Statale e per Geometri E. Fermi Pontedera (Pi)
 Istituto Tecnico Commerciale Statale e per Geometri E. Fermi Pontedera (Pi) Via Firenze, 51 - Tel. 0587/213400 - Fax 0587/52742 http://www.itcgfermi.it E-mail: mail@itcgfermi.it PIANO DI LAVORO Prof. Michele
Istituto Tecnico Commerciale Statale e per Geometri E. Fermi Pontedera (Pi) Via Firenze, 51 - Tel. 0587/213400 - Fax 0587/52742 http://www.itcgfermi.it E-mail: mail@itcgfermi.it PIANO DI LAVORO Prof. Michele
Tracciamento di fabbricati
 Standard di qualità ai fini della qualificazione professionale della categoria dei geometri Specifica T10 Geomatica e attività catastali Tracciamento di fabbricati Sommario Il presente documento specifica
Standard di qualità ai fini della qualificazione professionale della categoria dei geometri Specifica T10 Geomatica e attività catastali Tracciamento di fabbricati Sommario Il presente documento specifica
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA
 SCUOLA PRIMARIA DI CORTE FRANCA MATEMATICA CLASSE QUINTA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA L ALUNNO SVILUPPA UN ATTEGGIAMENTO POSITIVO RISPETTO ALLA MATEMATICA,
SCUOLA PRIMARIA DI CORTE FRANCA MATEMATICA CLASSE QUINTA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA L ALUNNO SVILUPPA UN ATTEGGIAMENTO POSITIVO RISPETTO ALLA MATEMATICA,
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
ISTITUTO D'ISTRUZIONE SUPERIORE. PROGRAMMAZIONE DIDATTICA DI DIPARTIMENTO Primo biennio Secondo biennio e quinto anno
 PROGRAMMAZIONE DIDATTICA DI DIPARTIMENTO Primo biennio Secondo biennio e quinto anno TOPOGRAFIA 2014/15 Iiritano A. Dipartimento Anno scolastico Data della riunione Coordinatore SCIENTIFICO-TECNOLOGICO
PROGRAMMAZIONE DIDATTICA DI DIPARTIMENTO Primo biennio Secondo biennio e quinto anno TOPOGRAFIA 2014/15 Iiritano A. Dipartimento Anno scolastico Data della riunione Coordinatore SCIENTIFICO-TECNOLOGICO
P R O G E T T O D I R I S O L U Z I O N E D E L L E I N T E R F E R E N Z E
 P R O G E T T O D I R I S O L U Z I O N E D E L L E I N T E R F E R E N Z E La presente relazione si riferisce al progetto dell intervento pubblico in attuazione Programmi Urbani Complessi - PUC2 Sistemazione
P R O G E T T O D I R I S O L U Z I O N E D E L L E I N T E R F E R E N Z E La presente relazione si riferisce al progetto dell intervento pubblico in attuazione Programmi Urbani Complessi - PUC2 Sistemazione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
Sistema di riferimento
 Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Introduzione. 001_007_pagine_iniziali.indd 7 22/01/14 11.21
 7 Introduzione Questo volume si propone di riorganizzare i percorsi di aritmetica e di geometria del corso principale adattandoli a studenti con esigenze specifiche. Il progetto grafico originale del corso
7 Introduzione Questo volume si propone di riorganizzare i percorsi di aritmetica e di geometria del corso principale adattandoli a studenti con esigenze specifiche. Il progetto grafico originale del corso
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri. rel. 0.1. Esercizi di Topografia distribuzione gratuita 1/6
 ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
. Si determina quindi quale distanza viene percorsa lungo l asse y in questo intervallo di tempo: h = v 0y ( d
 Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Studio di Geologia Applicata - Dott. Geol. Pier Luigi Amadori
 Studio di Geologia Applicata - Dott. Geol. Pier Luigi Amadori Viale della Repubblica, 4-47014 Meldola (FC) Tel-Fax. 0543/49 03 36 - C. F. MDR PLG 44L06 A 565 O - P. IVA 00627450406 PREMESSA La presente
Studio di Geologia Applicata - Dott. Geol. Pier Luigi Amadori Viale della Repubblica, 4-47014 Meldola (FC) Tel-Fax. 0543/49 03 36 - C. F. MDR PLG 44L06 A 565 O - P. IVA 00627450406 PREMESSA La presente
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
