Diario del Corso di Analisi Matematica I - Mod. 1
|
|
|
- Aniello Palumbo
- 6 anni fa
- Visualizzazioni
Transcript
1 Dirio del Corso di Anlisi Mtemtic I - Mod. 1 Corso di Lure: Mtemtic Applict Docente: Sisto Bldo ATTENZIONE: Il presente Dirio del Corso vuole essere un rissunto bbstnz dettglito di quello che è stto detto in ul, e come tle può essere un utile sussidio per chi vogli sistemre i propri ppunti, o per chi si stto ssente e vogli ricostruire i contenuti di un lezione. D ltr prte, queste brevi pginette NON possono sostituire completmente un libro di testo, l lezione in ul o un interzione dirett con il docente o l esercittore: siete quindi invitti servirvi ANCHE di queste ltre opportunità per pprofondire le vostre conoscenze! 1
2 Indice 1 Lezione del 1/10/2015 (2 ore) 5 Numeri reli: perché ne bbimo bisogno? Modelli dei numeri reli e definizione ssiomtic. 2 Lezione del 2/10/2015 (2 ore) 7 Estremo superiore. Estremo inferiore, crtterizzzione di sup e inf. 3 Lezione del 5/10/2015 (3 ore) 10 Crtterizzzione di sup e inf. Funzione esponenzile. Funzioni circolri. Funzioni e relzioni. Comportmento dell funzione f(x) = sin x x vicino 0. 4 Lezione del 7/10/2015 (1 or) 14 Definizione di limite. Funzioni continue. 5 Lezione del 8/10/2015 (3 ore) 16 Teorem dei crbinieri. Teoremi elementri sui limiti. Continuità di lcune funzioni elementri. Limiti destri, sinistri, infiniti. 6 Lezione del 9/10/2015 (2 ore) 19 Forme indeterminte. Limiti di funzioni composte. Successioni e loro limiti. Limite di un successione monoton. Forme indeterminte. Numero di Nepero. 7 Lezione del 14/10/2015 (2 ore) 22 Altri limiti fondmentli con esponenzili. 8 Lezione del 15/10/2015 (2 ore) 25 Teorem di esistenz degli zeri. Teorem dei vlori intermedi. Continuità dell funzione invers di funzioni continue e strettmente crescenti su un intervllo. Teorem di Bolzno Weierstrss. 9 Lezione del 16/10/2015 (2 ore) 29 Teorem di Weierstrss. Derivte: euristic, definizione, interpretzione geometric e fisic. 10 Lezione del 21/10/2015 (2 ore) 33 Clcolo di derivte. Derivte di funzioni elementri. Derivt di funzione compost e invers. 2
3 11 Lezione del 22/10/2015 (3 ore) 36 Concvità e convessità. Alcuni controesempi. Principio di Fermt. Teoremi di Rolle e Lgrnge e conseguenze. Rett tngente come rett di migliore pprossimzione vicino l punto di tngenz. 12 Lezione del 23/10/2015 (2 ore) 42 Polinomi di Tylor. Teorem di l Hôpitl. Teorem di Tylor con resto di Peno. 13 Lezione del 28/10/2015 (2 ore) 45 Derivte successive e punti di estremo reltivo. Teorem di Cuchy. Teorem di Tylor con resto di Lgrnge. Approssimzione di funzioni elementri con polinomi di Tylor. Serie di Tylor. 14 Lezione del 29/10/2015 (2 ore) 49 Irrzionlità di e. Serie geometric. Funzioni non nlitiche. Cenni sulle serie di potenze. Serie logritmic. Euristic dell integrle. Integrle di Riemnn: funzioni scl e loro integrle. 15 Lezione del 30/10/2015 (2 ore) 55 Integrle superiore e inferiore, integrbilità nel senso di Riemnn. Uniforme continuità. Teorem di Heine-Cntor. Integrbilità delle funzioni continue. 16 Lezione del 4/11/2015 (2 ore) 59 Linerità dell integrle. Additività rispetto ll intervllo dell integrle. Enuncito del teorem fondmentle del clcolo integrle e prime conseguenze.teorem dell medi integrle, dimostrzione del teorem fondmentle del clcolo integrle. Primitive e loro clcolo: tbell degli integrli immediti. 17 Lezione del 5/11/2015 (3 ore) 65 Integrzione per prti e per sostituzione. Esempi di tecniche di integrzione. Integrzione di funzioni rzionli. Integrli impropri. 18 Lezione del 6/11/2015 (2 ore) 69 Principio del confronto e dell equivlenz sintotic per gli integrli impropri. Convergenz ssolut e convergenz degli integrli impropri. 19 Lezione del 11/11/2015 (2 ore) 72 Criteri di convergenz per le serie. Criteri del rpporto e dell rdice. 20 Lezione del 12/11/2015 (3 ore) 78 3
4 Serie di potenze. Rggio di convergenz. Teorem di regolrità dell somm di un serie di potenze. Appliczioni. 21 Lezione del 13/11/2015 (2 ore) 85 Mssimo e minimo limite. Successioni di Cuchy e completezz di R. Esercizi sugli intergrli impropri. 22 Lezione del 18/11/2015 (2 ore) 90 Successioni di Cuchy. Esercizi su integrli impropri e serie. 23 Lezione del 26/11/2015 (2 ore) 93 Esercitzione strordinri in preprzione dell prov intermedi. 24 Lezione del 2/12/2015 (1 or) 94 Correzione dell prov intermedi. 25 Lezione del 21/1/2016 (2 ore) 94 Esercizi. 4
5 1 Lezione del 1/10/2015 (2 ore) Buon prte dell prim or di lezione è stt dedict ll presentzione del corso: orrio, esercitzioni, esmi... Argomento del corso: clcolo differenzile per funzioni reli di vribile rele. Visto che nel corso ci occuperemo di funzioni reli di vribile rele, srà bene cpire esttmente cos sono i numeri reli! Considerimo l seguente cten di insiemi numerici, sempre più grndi: N Z Q R C. Ogni volt che pssimo d un insieme l successivo, gudgnmo qulcos... Nell insieme N = {0, 1, 2,...} dei numeri nturli non è possibile trovre l elemento inverso di un numero rispetto ll somm (l opposto): perché questo si poss fre dobbimo llrgrci ll insieme Z = {0, ±1, ±2,...} dei numeri interi. Anlogmente, in Z non è possibile definire l operzione invers del prodotto: per questo, si introduce l insieme Q dei numeri rzionli (Q = {m/n : m, n Z, n 0}). Con l insieme dei numeri rzionli potremmo dirci soddisftti, lmeno dl punto di vist delle quttro operzioni! E llor, perché sentimo il bisogno di llrgre ulteriormente l insieme dei numeri? Quest necessità divenne evidente già gli lbori dell mtemtic grec (nche se i greci vevno un visione più geometric che lgebric dell mtemtic): i pitgorici si ccorsero che l lunghezz dell digonle di un qudrto di lto 1 non è un numero rzionle. In termini moderni (e grzie l teorem di Pitgor), questo equivle dire che 2 non è un numero rzionle... In seguito ci divertiremo dimostrre questo ftto! Per i pitgorici, l scopert dell irrzionlità di 2 ebbe sconvolgenti conseguenze filosofiche...per noi, signific solo che dobbimo trovre un insieme più mpio di numeri, in modo che lmeno uno di essi bbi qudrto ugule 2 (e in cui mgri si possibile risolvere ltri interessnti problemi!). Un buon rispost queste necessità è l insieme R dei numeri reli, che noi ben conoscimo. Vero? Cos sono i numeri reli di cui bbimo prlto (e che bbimo usto) per buon prte dell nostr crrier scolstic? Un possibile rispost: sono tutti i numeri decimli, eventulmente con infinite cifre dopo l virgol. Questo è un buon modello dei numeri reli, che present però un piccolo problem: se definimo i reli come numeri decimli infiniti, non è poi fcilissimo definire le operzioni e l relzione d ordine, 5
6 e mostrre poi che esse godono di tutte le proprietà che ci spettimo... Comunque, questo è possibile senz eccessive difficoltà. Un pproccio lterntivo (dottto d molti testi di nlisi mtemtic) è quello ssiomtico: i numeri reli sono per definizione un cmpo ordinto e completo. Questo signific che i numeri reli sono un insieme su cui sono definite due operzioni (l somm e il prodotto), ed un relzione d ordine che godono di tutt un serie di buone proprietà che elencheremo meglio tr poco. Un tle oggetto si dice cmpo ordinto...m nche Q è un cmpo ordinto! Quel che distingue R d Q è l ssiom di completezz, che vedremo l prossim volt in un delle sue possibili formulzioni. Riprendimo i nostri discorsi sull insieme dei numeri reli. Siccome bbimo ffermto che l rdice qudrt di 2 non è un numero rzionle, vedimo di dimostrrlo! In termini precisi, dire che 2 è rzionle equivle d ffermre che esiste un numero rzionle q = m/n tle che q > 0 e q 2 = 2. Riducendo l frzione i minimi termini, non è restrittivo supporre che i numeri nturli m e n non bbino fttori primi in comune. Or, l nostr supposizione equivle m 2 = 2n 2, d cui segue che m 2 è un numero pri. Poiché ogni fttore primo di m 2 deve essere presente nche in m, ne deriv che m è pri. Dunque, m = 2r per qulche numero nturle r, e l nostr identità divent 4r 2 = 2n 2, d cui 2r 2 = n 2. Ripetendo esttmente il rgionmento ppen ftto, questo mostr che n è pri. Assurdo perché bbimo supposto che m e n non bbino fttori in comune, e quindi essi non possono essere entrmbi pri! In sostnz, il teorem ppen dimostrto ci dice che esistono tutt un serie di problemi nturli per l mtemtic che non si possono risolvere nel cmpo Q dei rzionli. È per questo che risult necessrio introdurre l insieme R dei numeri reli, del qule dimo l seguente definizione: DEFINIZIONE: l insieme R dei numeri reli è un cmpo ordinto completo. Questo signific che i numeri reli sono un insieme su cui sono definite due operzioni (l somm e il prodotto), entrmbe ssocitive e commuttive. Inoltre, entrmbe le operzioni hnno un elemento neutro (0 e 1 rispettivmente) e sono invertibili (cioè per ogni x R esiste un ltro elemento che denotimo ( x) tle che x + ( x) = 0; per ogni x R, x 0 esiste un ltro elemento x 1 tle che x x 1 = 1). Vle inoltre l proprietà distributiv, che leg l somm l prodotto. Un insieme con due operzioni che godono di queste proprietà è detto cmpo. 6
7 C è poi un relzione d ordine, che dti due numeri reli ci consente di dire qul è il più grnde. Quest relzione d ordine è comptibile con le operzioni (nel senso che possimo mnipolre le disuguglinze nel modo in cui simo bituti: sommndo uno stesso numero rele d mbo i membri di un disuguglinz ess rimne ver, così come se moltiplichimo mbo i membri per uno stesso numero rele positivo). Un cmpo che gode di queste proprietà è un cmpo ordinto: m nche Q è un cmpo ordinto! Il cmpo ordinto R è poi completo: in soldoni, questo signific che l rett rele non h buchi, m vedremo domni uno dei possibili modi equivlenti di formlizzre quest ffermzione! 2 Lezione del 2/10/2015 (2 ore) Dimo finlmente due formulzioni dell ssiom di completezz (in clsse bbimo visto solo l second di quelle che seguono, l prim viene propost gli interessti...): ASSIOMA DI COMPLETEZZA, I FORMULAZIONE (Dedekind): Se A e B sono sottinsiemi di R, entrmbi non vuoti e tli che b A, b B, llor esiste un numero rele c tle che c b A, b B. Un tle numero c si dice elemento seprtore di A e B. In soldoni, se bbimo due sottinsiemi non vuoti A e B dell rett rele tli che A st tutto sinistr di B, possimo trovre un numero rele che st si destr di A che sinistr di B. In ltre prole, e sempre in modo informle, possimo dire che l rett rele non h buchi! ASSIOMA DI COMPLETEZZA, II FORMULAZIONE (Esistenz dell estremo superiore): Ogni sottoinsieme non vuoto e superiormente limitto di R mmette estremo superiore in R. Per cpire l formulzione dell ssiom di completezz che si rifà l concetto di estremo superiore, bbimo bisogno di lcune definizioni: DEFINIZIONI: Se A R, un mggiornte di A è un numero rele M tle che M per ogni A. Un sottinsieme di R si dice superiormente limitto se mmette lmeno un mggiornte. L estremo superiore di un sottinsieme A di R è il minimo dei mggiornti di A, se questo minimo esiste. 7
8 Cerchimo di comprendere il significto di quest definizione di estremo superiore (che per inciso si indic col simbolo sup A...). Se l insieme A mmette mssimo, llor l estremo superiore coincide col mssimo. Inftti il mssimo dell insieme è un mggiornte per definizione, e inoltre nessun numero più piccolo del mssimo può essere un mggiornte (perché è superto dl mssimo stesso, che è un elemento dell insieme). D ltr prte, un insieme infinito non è detto che possegg mssimo nche se è superiormente limitto: per esempio, l semirett A = {x R : x < 2} = (, 2) non possiede un elemento mssimo. Inftti, dto un qulunque elemento A, il numero +2 è ncor minore di 2, ed è mggiore di : non 2 può essere dunque l elemento mssimo dell semirett. Invece, è immedito verificre che sup A = 2... L estremo superiore è l nturle generlizzzione del concetto di mssimo gli insiemi superiormente limitti che non hnno mssimo! L ssiom di completezz nell su second formulzione dice un cos non ovvi: qulunque sottinsieme non vuoto e superiormente limitto A R mmette il sup. L cos non è immedit perché il sup è definito come minimo di un insieme infinito (l insieme dei mggiornti di A), e non sempre un insieme infinito mmette minimo! Per gli studenti interessti, mostrimo l equivlenz delle due formulzioni dell ssiom di completezz. Fermo restndo che gli studenti non interessti possono limitrsi studire quell che predic l esistenz del sup... Comincimo col mostrre che se vle l ssiom di Dedekind, llor ogni sottinsieme non vuoto e superiormente limitto di R mmette estremo superiore. Si inftti A R, A, A superiormente limitto. Definimo B = {b R : b è un mggiornte di A}. L coppi di insiemi A e B soddisf le richieste dell ssiom di Dedekind (B è non vuoto perché A è superiormente limitto, e gice destr di A perché contiene solo mggiornti di A), quindi esiste un elemento seprtore c R tle che c b per ogni A e per ogni b B. L disuguglinz di sinistr dice che c è un mggiornte di A, mentre quell di destr ssicur che è più piccolo di ogni ltro mggiornte: in conclusione, c = sup A. Mostrimo che l second formulzione dell ssiom di completezz implic l prim. Sino A, B due sottinsiemi come nell ssiom di Dedekind (cioè sono non vuoti e A gice tutto sinistr di B). Ponimo c = sup A (esiste per ipotesi, visto che A è non vuoto, ed è nche superiormente limitto perché B è non vuoto ed è tutto ftto di mggiornti di A). Dico che c è un elemento seprtore tr A e B: inftti, c è un mggiornte di A per definizione di sup. Inoltre, è minore o ugule di ogni elemento di B perché è il minimo dei mggiornti di A, e B è costituito intermente d mggiornti di A. Q.E.D. Evidentemente, l ssiom di completezz (in un qulunque delle sue formulzioni equivlenti) non è vero nel cmpo dei rzionli: per esempio, l insieme A = {q Q : q 0, q 2 2} è un sottinsieme di Q non vuoto e superiormente limitto (per esempio, 2 è un mggiornte), m esso non h estremo superiore in Q: il problem è che possimo trovre mggiornti rzionli rbitrrimente vicini 2, che peró non pprtiene i rzionli. Ovvimente, se vedimo questo insieme come sottinsieme di R, l estremo superiore c è ed è ugule 2. 8
9 L ffermzione ppen ftt è un conseguenz prticmente immedit dell seguente, importnte proprietà di densità dei numeri rzionli in R: PROPOSIZIONE (Proprietà rchimede e densità di Q in R): Sino, b numeri reli con 0 < < b. Allor esiste un numero nturle n tle che n > b (proprietà rchimede). Se poi, b R, < b (di segno qulunque), esiste un numero rzionle q tle che < q < b (densità di Q in R). DIM.: Provimo che vlgono l proprietà rchimede e l densità dei rzionli. Per provre l proprietà rchimede, bst osservre che esiste un numero nturle n tle che n > b : bst prendere n = [ b ] + 11 Moltiplicndo per si h l tesi. Provimo poi l densità dei rzionli nel cso 0 < < b. Intnto, per l proprietà rchimede esiste n N tle che n(b ) > 1, d cui nb > 1 + n. Ne segue che c è un numero nturle m compreso tr nb e n (possimo prendere semplicemente [nb], trnne nel cso in cui nb è intero: in quel cso prendimo nb 1). M llor n < m < nb, d cui < m < b, come volevsi. n Se poi < 0 < b, bst prendere q = 0. Se invece < b < 0, bst cmbire di segno... Q.E.D. In mtemtic, oltre ll estremo superiore si us spesso l estremo inferiore che è l oggetto simmetrico: DEFINIZIONE: Un minornte di un insieme A R è un numero rele c tle che c per ogni A. A si dice inferiormente limitto se possiede un minornte. L estremo inferiore di A (se esiste) è il mssimo dei minornti di A, e si indic con inf A. Ovvimente, l estremo inferiore coincide con il minimo di A qundo questo esiste. Inoltre, un ulteriore formulzione equivlente dell ssiom di completezz consiste nel chiedere che ogni insieme inferiormente limitto mmette estremo inferiore (esercizio)! Per comodità, vle nche l pen di introdurre un notzione per indicre l estremo superiore e l estremo inferiore di insiemi illimitti, e dell insieme vuoto: DEFINIZIONE: Il ftto che un insieme A non si superiormente limitto si esprime con l scrittur sup A = +. Anlogmente, per un insieme illimitto inferiormente scriveremo inf A =. Ponimo poi sup =, inf = +. 1 Con [x] indichimo l prte inter di un numero rele x, ossi il più grnde numero intero minore o ugule x. 9
10 L definizione ssiomtic di R è comod (è sostnzilmente un menù delle proprietà che possimo utilizzre qundo mnipolimo i numeri reli), m rimne il problem di mostrre che esiste lmeno un insieme, dotto di operzioni e relzione d ordine, che soddisf tutti gli ssiomi: bbimo bisogno di un modello dei numeri reli. Come ccennvmo, un tle modello è costituito di numeri decimli infiniti. Non è difficile convincersi che con tle modello si possono definire le operzioni e l relzione d ordine, e che esse godono di tutte le proprietà che ci servono... Per gli studenti interessti, cerchimo di mostrre che in questo modello vle l ssiom di completezz: precismente, supponimo di vere un insieme A R (cioè A è un collezione di decimli infiniti) non vuoto e inferiormente limitto, e mostrimo come si possibile identificrne l estremo inferiore come decimle infinito. Evidentemente, non è restrittivo supporre che 0 si un minornte di A (bst compiere un trslzione, cioè ggiungere tutti gli elementi di A uno stesso numero, per esempio l opposto di un minornte: nche l estremo inferiore risulterà modificto nello stesso modo...). Ci trovimo nell seguente situzione: bbimo un sottinsieme dell rett rele che gice tutto destr di 0, e ci chiedimo come clcolre le cifre decimli del mssimo dei suoi minornti. Evidentemente, per trovre l estremo inferiore meno di un unità, ci bst prendere il mssimo dei numeri nturli che sono minornti di A, per trovrlo meno di un decimo ci bst prendere il mssimo dei numeri decimli finiti con un cifr dopo l virgol che sono minornti di A, per trovrlo meno di un centesimo troveremo il mssimo dei numeri decimli finiti con due cifre dopo l virgol che sono minornti di A, e così vi... Ogni volt, dobbimo trovre il mssimo di un insieme finito. Inoltre, ogni volt che rffinimo l suddivisione è evidente che le cifre che vevmo già trovto in precedenz non cmbino. Proseguendo indefinitmente, bbimo un ricett per trovre tutte le cifre che voglimo di un numero decimle infinito c, che gode di quest proprietà: se rrestimo c ll k-esim cifr dopo l virgol e chimimo c k il numero decimle finito così ottenuto 2, c k è un minornte di A ed esiste un elemento di A che dist meno di 1/10 k d c k (ltrimenti vrei potuto umentre di lmeno un unità l k-esim cifr decimle di c). Siccome k può essere preso rbitrrimente grnde, questo ci dice che esistono punti di A rbitrrimente vicini c. In conclusione, c è per costruzione un minornte di A, ed è il mssimo perché l insieme A possiede punti rbitrrimente vicini c, per cui un qulunque numero più grnde di c non può essere più un minornte di A. L esistenz dell rdice qudrt di un numero rele positivo può essere recupert usndo l estremo superiore: se R, > 0, definimo = sup{x R : x 2 }. Questo definisce un numero rele positivo, il cui qudrto si può dimostrre che è ugule d. Non dimostrimo questo ftto, perché esso è un conseguenz immedit del teorem di esistenz degli zeri per le funzioni continue, che verrà enuncito e dimostrto tr poche lezioni in questo corso... Durnte questo breve periodo, fremo un tto di fede e continueremo confidre nell esistenz delle rdici n-esime, dell funzione esponenzile, dell funzione logritmo, etc... 3 Lezione del 5/10/2015 (3 ore) È utile ricordre le seguenti crtterizzzione di estremo superiore ed estremo inferiore: sino A R, M, m R. Allor si h sup A = M se e solo se M per ogni A (M è un mggiornte); 2 c k non è ltro che il numero decimle ottenuto l k-psso del nostro lgoritmo 10
11 per ogni ε > 0 esiste A tle che > M ε (nessun numero strettmente minore di M è un mggiornte). Anlogmente si h m = inf A se e solo se m per ogni A (m è un minornte); per ogni ε > 0 esiste A tle che < m + ε (nessun numero strettmente mggiore di m è un minornte). Usndo quest crtterizzzione, si può fr vedere per esempio che dto l insieme A = { n2 1 : n = 1, 2, 3,...} n si h inf A = min A = 0, mentre sup A = 1. Ci simo dedicti d un ripsso critico sulle potenze: potenze d esponente nturle, intero, rzionle (l definizione è obbligt se voglimo che vlgno le proprietà delle potenze!). Potenze ed esponente rele: se > 1 e x R, definimo x = sup{ q : q Q, q x}. Si può dimostrre che questo oggetto h tutte le proprietà dell funzione esponenzile che ben conoscimo (omettimo però l dimostrzione). Abbimo prlto brevemente di come sono definite le funzioni trigonometriche seno e coseno: in prticolre, ci simo resi conto che c è un difficoltà dovut l ftto che è necessrio definire in modo rigoroso l lunghezz di un rco di curv. Fccimo quindi un brevissimo ripsso sul concetto di funzione e su quello di grfico di un funzione: un funzione f : A B, dove A, B sono insiemi (A si chim dominio, B codominio) può essere penst come un sctol ner o un regol che d ogni elemento A ssoci uno ed un solo elemento f() B. Qulche esempio di funzioni che esistono in ntur : l tempertur nell nostr ul o il vlore di un cert zione ll Bors di Milno (entrmbe in funzione del tempo), l forz elstic esercitt d un moll in funzione dell elongzione, il segnle custico rccolto d un microfono in funzione del tempo, l funzione che ssoci d ogni sedi presente in quest ul il nome di chi l occup... Cso prticolrmente importnte per noi: le funzioni reli di vribile rele, cioè quelle per cui A R e B R. Grfico di un funzione f : R R: è il sottinsieme del pino crtesino G f = {(x, y) : x R, y = f(x)}. 11
12 Tr i sottinsiemi del pino crtesino, come distinguere quelli che sono grfici di un funzione rele di vribile rele? Sono i sottinsiemi G tli che per ogni x R trovimo un ed un sol y R tle che (x, y) G. Nel cso generle in cui A e B sono insiemi qulunque, si introduce il prodotto crtesino A B di due insiemi A e B come l insieme delle coppie ordinte (, b) in cui A e b B: A B = {(, b) : A, b B}. Il grfico di un funzione f : A B è llor il sottinsieme di A B definito esttmente come sopr: G f = {(, b) A B : b = f()}. Identifichimo i sottinsiemi di A B che sono grfici di un funzione f : A B: ottenimo un ricett, simile quell sopr, che può essere dottt come definizione rigoros di funzione tr due insiemi. Riportimo di seguito quest definizione DEFINIZIONE (corrispondenz, funzione): Dti due insiemi A, B, un corrispondenz tr A e B è, per definizione, un sottinsieme del prodotto crtesino A B. Un corrispondenz R tr A e B si dice funzione se per ogni A esiste un unico B B tle che (, b) R. Dimostrimo un pio di disuguglinze che tornernno utili nel seguito: ttrverso semplici considerzioni geometriche, scoprimo che per 0 < x < π/2 vlgono le disuguglinze x tn x e sin x < x: 12
13 P K x O H M 1 L second disuguglinz si ottiene osservndo che l rco P M (lungo x) è più lungo dell cord P M, che su volt è più lung del segmento P H = sin x (sono rispettivmente cteto e ipotenus del tringolo rettngolo OHP ). Per ottenere l prim disuguglinz, osservimo che il settore circolre OMP è contenuto nel tringolo rettngolo OMK, per cui l re del settore circolre è minore dell re del tringolo. D ltr prte, l re del settore circolre è x/2, mentre l re del tringolo è tn x/2. Voglimo or introdurre, dpprim in modo ssolutmente informle, le nozioni di limite di un funzione rele di vribile rele e di funzione continu. Cerchimo or di ffrontre un esercizio piuttosto difficile: voglimo cpire come è ftto il grfico dell funzione f(x) = sin x, funzione rele definit x su R \ {0}. Osservimo che quest è un funzione pri (cioè f( x) = f(x)) e che per x > 0 h lo stesso segno dell funzione seno ed è compres tr le funzioni 1/x e 1/x. Quello che non è per niente chiro priori, è come si comport l funzione per vlori piccoli dell x... Per 0 < x < π/2 sppimo poi che sin x < x < tn x (lo bbimo mostrto l volt scors...) Ne segue subito che cos x < sin x x < 1 se 0 < x < π/2. 13
14 Si noti che le disuguglinze rimngono vlide nche per π/2 < x < 0 perché tutte le funzioni coinvolte sono pri. Geometricmente, questo dice che il grfico dell funzione f(x), per ngoli piccoli, è compreso tr i grfici dell funzione cos x e dell funzione costnte 1: possimo quindi concludere che qundo x si vvicin 0, il vlore dell funzione f(x) deve necessrimente vvicinrsi d 1. Esprimimo questo ftto scrivendo sin x lim x 0 x = 1. Possimo dire, in ltre prole, che l funzione f(x) = sin x x tende 1 qundo x tende 0. 4 Lezione del 7/10/2015 (1 or) Cerchimo di dre un prim pseudodefinizione di limite: DEFINIZIONE INFORMALE: l scrittur lim x x 0 f(x) = l esprime il ftto che, se si vvicin sufficientemente l x x 0 (con x x 0 ), il vlore di f(x) divent rbitrrimente vicino l numero l. Osservimo che non è fftto necessrio che l funzione f si definit in x 0 (e, se lo fosse, convenimo comunque di non tenerne conto qundo ndimo verificre l relzione di limite). Quel che serve, è solo che l funzione f si definit in punti rbitrrimente vicini d x 0 e diversi d x 0 (in mtemtichese, x 0 deve essere un punto di ccumulzione del dominio di f). Attendimo ncor qulche istnte per dre un definizione precis di limite: ess rriverà inesorbilmente tr non molto. Piuttosto, vendo disposizione il concetto di limite si può introdurre quello di funzione continu: DEFINIZIONE: Si f : [, b] R un funzione rele di vribile rele definit su un intervllo. Se x 0 [, b], dicimo che f è continu in x 0 se lim f(x) = f(x 0 ). x x 0 Se f è continu in ogni punto del suo dominio [, b], dicimo semplicemente che ess è continu. 14
15 Ci si convince fcilmente che l ide geometric dietro l concetto di continuità è piuttosto semplice: il grfico di un funzione continu è un curv continu, cioè può essere disegnto senz stccre l penn dl foglio. Inftti, se rileggimo l definizione di continuità ll luce dell nostr pseudodefinizione di limite, vedimo che un funzione è continu in x 0 qundo f(x) divent rbitrrimente vicino f(x 0 ) ptto di prendere x sufficientemente vicino x 0. In mnier ncor più informle possimo dire che un funzione continu f(x) h l proprietà di cmbire di poco il suo vlore qundo si cmbi di poco l vribile indipendente x. A questo punto, viene nturle chiedersi se già conoscimo delle funzioni continue... L rispost è ffermtiv: si pensi ll funzione costnte f(x) = k, o ll funzione identic f(x) = x. In questi due csi, le (pseudo)-definizioni dte sopr diventno delle tutologie! Dopo questi discorsi informli, è ormi or di rrivre d un definizione rigoros del concetto di limite: vle l pen di sottolinere che nei prossimi pochi secondi... percorreremo un iter che storicmente h richiesto moltissimo tempo ed un cces discussione nell comunità mtemtic! Dremo inftti l definizione di limite dovut Weierstrss. Avevmo detto che lim f(x) = l se succede che, vvicinndo sufficientemente x x 0 (con x x 0 ), f(x) divent rbitrrimente vicin l. Possimo x x0 trdurre quest frse nell seguente DEFINIZIONE: Si f un funzione definit in un intorno 3 di x 0. Dicimo che lim x x0 f(x) = l se e soltnto se, comunque sceglimo un intervllo I l centrto in l, piccolo qunto voglimo, è possibile trovre un intervllo J x0 centrto in x 0 tle che f(x) I l per ogni x J x0, x x 0. Se scrivimo I l = (l ε, l+ε) e J x0 = (x 0 δ, x 0 +δ), l definizione si può trdurre nell seguente (che è ssolutmente equivlente quell sopr, ed è quell che h sempre riscosso il mggior successo di pubblico e di critic): DEFINIZIONE: Si f un funzione definit in un intorno di x 0. Dicimo che lim f(x) = l se e soltnto se, per ogni ε > 0, è possibile trovre δ > 0 x x0 tle che 0 < x x 0 < δ f(x) l < ε. (P ) x 0. 3 Un intorno di x 0 è, per definizione, un insieme che contiene un intervllo centrto in 15
16 Vi sottopongo un mio tenttivo di illustrre l definizione di limite con un grfico interttivo 4 sul qule si può scegliere il proprio ε picere, e verificre poi l esistenz di δ... Non sono però completmente convinto dell efficci del risultto!) 5 Lezione del 8/10/2015 (3 ore) Osservimo, che l definizione di limite h senso nche se f è definit su un insieme qulunque A, purchè A possegg punti distinti d x 0 e vicini qunto si vuole x 0 : questo si esprime dicendo che x 0 è un punto di ccumulzione di A. Ovvimente, in tl cso l disuguglinz nell definizione di limite ndrà verifict solo per gli x A. Verifichimo che con l definizione di limite ppen vist, vlgono lcune proprietà dei limiti e delle funzioni continue che suonno bbstnz nturli e che si rivelernno utilissime: Continuità delle costnti e dell funzione identic: Per mostrre che lim x = x 0 bst prendere δ = ε nell definizione di limite. Dimostrre x x 0 che il limite di un costnte è l costnte stess è ltrettnto fcile! TEOREMA (dei crbinieri): Se f, g, h sono tre funzioni definite in un intorno di x 0, f(x) h(x) g(x) in tle intorno e lim f(x) = x x0 lim g(x) = l, llor esiste il limite x x 0 lim h(x) = l. x x
17 DIM.: si ε > 0, e sceglimo δ > 0 tle che f(x) l < ε, g(x) l < ε ogni qul volt 0 < x x 0 < δ ( priori, l definizione di limite potrebbe drci due vlori diversi di δ per f e per g: perché si vero qunto ppen scritto, bst prendere il più piccolo dei due). Le due disuguglinze per f e per g possono nche essere scritte: l ε < f(x) < l + ε, l ε < g(x) < l + ε. Usndo l ipotesi f(x) h(x) g(x) ottenimo llor (per ogni x tle che 0 < x x 0 < δ): cioè h(x) l < ε, Q.E.D. l ε < f(x) h(x) g(x) < l + ε, Continumo nell nostr dimostrzione di risultti elementri che seguono dll definizione di limite: Un funzione che mmette limite finito in un punto è limitt in un intorno di quel punto: se lim x x0 f(x) = l R, llor esiste un intervllo I centrto in x 0 e un costnte M > 0 tle che f(x) M per ogni x I \ {x 0 } (che pprteng nche l dominio di f). Anlogmente, se f è come sopr e l 0, llor esiste un intervllo J centrto in x 0 tle che f(x) l /2 per ogni x J \ {x 0 } (che pprteng nche l dominio di f). Per provre queste ffermzioni bst pplicre l definizione di limite, per l prim con ε = 1 e per l second con ε = l /2. Algebr dei limiti: Se lim x x0 f(x) = l 1, lim x x0 g(x) = l 2 si h lim x x 0 (f(x) + g(x)) = l 1 + l 2, lim x x 0 (f(x) g(x)) = l 1 l 2, 1 lim x x 0 f(x) = 1 se l 1 0. l 1 Questi risultti, pplicti lle funzioni continue, ci dicono d esempio che i polinomi sono funzioni continue! Dimostrimo le ffermzioni sull lgebr dei limiti, comincindo dll prim: per definizione di limite, scelto ε > 0 esiste δ > 0 tle che se 17
18 0 < x x 0 < δ si h f(x) l 1 < ε, g(x) l 2 < ε. M llor (f(x) + g(x)) (l 1 + l 2 ) f(x) l 1 + g(x) l 2 < 2ε, che implic l nostr tesi. Per qunto rigurd il limite del prodotto, osservimo dpprim che grzie l punto precedente possimo trovre un costnte positiv M tle che f(x) M, g(x) M in un opportuno intorno di x 0 ( x x 0 ). Fissto poi ε > 0, si δ come sopr: evidentemente non è restrittivo supporre che δ si tnto piccolo d fr vlere le nostre limitzioni f(x) M, g(x) M per 0 < x x 0 < δ. Allor f(x)g(x) l 1 l 2 = f(x)g(x) f(x)l 2 + f(x)l 2 l 1 l 2 f(x) g(x) l 2 + f(x) l 1 l 2 2Mε, che implic l tesi. Infine, mostrimo l ultim delle proprietà elencte: fissimo ε > 0 e osservimo che 1 f(x) 1 l 1 = f(x) l 1 f(x) l 1. Usndo il punto precedente: in un opportuno intervllino centrto in x 0, dicimo di rggio δ 1, si h f(x) l /2 (per x x 0 ). A questo punto, bst ripplicre l definizione di limite con ε qulunque per stimre il numertore: trovimo così un δ < δ 1 tle che f(x) l 1 f(x) l 1 < 2ε l 1 2 ogni qul volt x x 0 < δ, x x 0. Abbimo sostnzilmente usto il teorem dei crbinieri per fr vedere = 1... nche se rigore vremmo vuto bisogno di mostrre che sin x che lim x 0 x l funzione cos x è continu in 0: bbimo dto per scontto che cos x si vvicin 1 qundo x si vvicin 0. Questo, fortuntmente, può essere dedotto dlle considerzioni ppen ftte: dimostrimo dunque l continuità delle funzioni seno e coseno sull inter rett rele. Anzitutto, bbimo visto che per ngoli cuti si h 0 < sin x x (mentre per rgioni di simmetri vremo x sin x < 0 per x ( π, 0)): grzie l 2 teorem dei crbinieri deducimo che lim sin x = 0. x 0 In ltre prole, l funzione seno è continu in 0. 18
19 Sempre per ngoli cuti (e positivi), d semplici considerzioni geometriche si ricv che 1 cos x < x, d cui deducimo subito che 1 x < cos x < 1. Dl teorem dei crbinieri bbimo llor lim cos x = 1 (per il limite x 0 sinistr di 0, si ricordi che l funzione coseno è pri). In reltà seno e coseno sono funzioni continue ovunque: se x 0 R possimo scrivere sin x = sin(x 0 + (x x 0 )) = sin x 0 cos(x x 0 ) + cos x 0 sin(x x 0 ) d cui si deduce fcilmente che sin x è continu in x 0. In mnier nlog, l funzione cos x è continu in tutti i punti. Introducimo lcune vrizioni sul tem: limiti destro e sinistro, limiti ll infinito e limiti infiniti (e mostrimo qulche esempio di ciscuno): se f : A R, diremo che lim x x + 0 f(x) = l (limite destro) se l restrizione di f ll insieme A (x 0, + ) h limite l nel punto x 0 (ovvimente x 0 dovrà essere di ccumulzione per tle insieme). Anlogmente si definisce il limite sinistro, restringendosi ll semirett (, x 0 ). I limiti infiniti si definiscono come segue: lim f(x) = + se per ogni x x0 M > 0 esiste δ > 0 tle che 0 < x x 0 < δ implic f(x) > M (e c è un definizione nlog per il limite ). Limiti ll infinito: dicimo che lim x + f(x) = l se per ogni ε > 0 esiste N > 0 tle che x > N implic f(x) l < ε. Anlogmente, si definisce il limite, e nche i limiti infiniti ll infinito... 6 Lezione del 9/10/2015 (2 ore) Osservimo che il clcolo del limite di rpporti, prodotti e somme divent complicto in lcuni csi prticolrmente delicti, detti forme indeterminte. Inftti non è difficile convincersi che se lim f(x) = l 0 e lim g(x) = x x0 x x0 +, llor lim f(x)/g(x) = 0. Invece, se lim f(x) = lim g(x) = 0, (form x x0 x x0 x x0 indetermint 0/0) non è cosí chiro cos succed l limite del rpporto! Questo per un buon motivo: il limite del rpporto di due funzioni che tendono entrmbe 0 può combinre qulunque cos. Può essere un qulunque numero rele, essere infinito o non esistere. Per vederlo prendimo x 0 = 0 e (i) f(x) = g(x) = x: in questo cso il limite del rpporto è 1; (ii) f(x) = x, g(x) = x 3 : in questo cso il limite è + ; (iii) f(x) = x sin(1/x), g(x) = x: in questo cso il limite non esiste. Altre forme indeterminte (cioè situzioni come quell ppen vist, in cui l sol conoscenz del limite delle funzioni f e g non permette di stbilire 19
20 qunto f il limite di f/g, f g, f + g oppure f g ) sono /, 0,, 0 0, 1, 0... Il lettore può provre ripetere l esercizio sopr per l form indetermint 0 (prodotto di un funzione che tende 0 e di un che tende ll infinito), mostrndo che nche in questo cso il limite del prodotto può essere finito, infinito o non esistere. Anlizzimo or il limite di funzioni composte. Nel cso delle funzioni continue, l enuncito è piuttosto semplice: l composizione di due funzioni continue è continu. In ltre prole f, g : R R sono due funzioni definite (per semplicità) su tutto R, ovunque continue, llor l funzione compost (funzione di funzione) f(g(x)) è pure lei continu: un risultto del tutto plusibile se ricordimo l nostr pseudo-definizione di continuità. Per i limiti, occorre un cert cutel dovut l ftto che nell definizione di limite non voglimo tener conto del comportmento dell funzione nel punto in cui si clcol il limite. Dimo un enuncito preciso, che implic evidentemente qunto detto sopr sulle funzioni continue: TEOREMA: Si f definit in un intorno (ev. bucto) di x 0 tle che lim x x0 f(x) = y 0, g definit in un intorno (ev. bucto) di y 0 tle che lim y y0 g(y) = l. Supponimo poi che g si (definit e) continu in y 0, oppure che si bbi f(x) y 0 in un intorno di x 0. Allor si h lim x x 0 g(f(x)) = l. DIM.: Dimostrimo il risultto nel secondo cso: dto ε > 0, trovimo η > 0 tle che g(y) l < ε se 0 < y y 0 < η. Trovimo poi δ tle che, se 0 < x x 0 < δ, llor f(x) y 0 < η (e quest quntità è positiv, ptto di prendere η bbstnz piccolo, grzie ll ipotesi che f(x) y 0 in un intorno di x 0 ). Usndo dunque l disuguglinz vlid per g, ottenimo g(f(x)) l < ε se 0 < x x 0 < δ, Se poi g è continu in y 0, con l stess notzione ust sopr vremo g(y 0 ) = l, per cui l disuguglinz g(y) l < ε vle per y y 0 < η (non c è più bisogno di supporre y y 0 ). Q.E.D. OSSERVAZIONE: Se f : [, b] R è un funzione continu e strettmente crescente (oppure strettmente decrescente), llor esiste l funzione invers g : [f(), f(b)] [, b], (rispettivmente g : [f(b), f()] [, b]), nch ess 20
21 continu. Questo risultto è geometricmente evidente, ed un su dimostrzione rigoros srà dedott fcilmente dl teorem di esistenz degli zeri e d un notevole proprietà delle funzioni crescenti o decrescenti. Per il momento, bsti dire che questo implic d esempio l continuità dell funzione rdice qudrt... Si noti che per prlre di limite + di un funzione f, bst che il dominio di f si un insieme illimitto superiormente: in prticolre, dt un funzione f : N R, h senso chiedersi se esiste il lim f(n). n + Abbimo poi visto che purtroppo non esiste sempre. Ad esempio non esiste lim sin 1 (quest funzione compie infinite oscillzioni tr 1 e 1 in x 0 x ogni intorno comunque piccolo di 0). Ecco di seguito un cso prticolre importnte di limite ll infinito... Un funzione definit su N si chim successione. Di solito, per le successioni si dott un notzione differente d quell ust per le funzioni: piuttosto che scrivere f(n), si us un scrittur del tipo { n }, dove il simbolo n rppresent il vlore dell successione in n N. Fcendo l opportun trduzione dell definizione di limite in questo prticolre cso, scoprimo che lim n = l se e solo se per ogni ε > 0 esiste n + n N tle che per n n si bbi n l < ε. Abbimo già visto che il limite di un funzione in un punto non necessrimente esiste, così come non necessrimente esiste il limite di un successione per n + : per esempio, l successione n = ( 1) n non h limite. Ci picerebbe vere un risultto che dic lmeno che le successioni ftte in un certo modo hnno limite. Ancor un volt, ci viene in iuto l completezz di R: TEOREMA: Si { n } un successione crescente (cioè n+1 n per ogni n). Allor { n } mmette limite per n +, e si h lim n = sup{ n : n N}. n + Anlogo risultto vle per successioni decrescenti: in questo cso il limite coincide con l estremo inferiore dell immgine dell successione. Dimostrzione: Si S = sup{ n : n N}. Supponimo dpprim che si S R: vedremo poi il cso S = +. Fissimo ε > 0. Siccome S è un mggiornte dei vlori ssunti dll successione, bbimo che n S < S + ε per ogni n. D ltr prte, S ε non è più un mggiornte (per definizione di sup), per cui esiste un elemento dell successione, chimimolo n, tle che n > S ε. Siccome l successione è crescente, se n n si h n n > S ε. 21
22 Mettendo insieme le due disuguglinze ottenute sopr, bbimo che per n > n si h n S < ε. Se poi S = +, l immgine dell successione non mmette mggiornti. Dunque, per ogni fissto M > 0 esiste n tle che n > M. Per l crescenz dell successione bbimo llor n n > M per ogni n n e dunque lim n + n = + Q.E.D. In mnier del tutto nlog, si mostr che un funzione crescente mmette limite +, e che questo limite è ugule l sup. Ancor, un funzione crescente f : R R mmette limite destro e sinistro in ogni punto: precismente, lim x x 0 f(x) = sup{f(x) : x < x 0 }, lim f(x) = inf{f(x) : x > x 0 }. x x + 0 Usimo or il teorem sui limiti delle successioni monotone per definire il numero di Nepero e (l bse dei logritmi nturli): ponimo per definizione e = lim n + ( 1 ) n. 1 + n Nturlmente, occorre fr vedere che questo limite esiste ed è finito! L ide dell dimostrzione non è difficile: mostrimo dpprim che l successione n = (1 + 1/n) n è crescente (e quindi il limite esiste!), ed è poi limitt superiormente (e quindi il limite è finito). Come vedremo l volt prossim, il tutto può essere dimostrto usndo l disuguglinz di Bernoulli 5. 7 Lezione del 14/10/2015 (2 ore) L volt scors bbimo definito il numero di Nepero e = lim n, ove n + n = ( n. 1 + n) 1 Per mostrre che questo limite esiste finito, mostrimo che l successione n è crescente e superiormente limitt. Dobbimo fr vedere che n n 1 per ogni numero nturle n > 1. Or, mnipolndo un po l disuguglinz d dimostrre si vede che quest equivle ( n2 1) n ( n 1), cioè (1 1 ) n (1 1 ): m questo è esttmente n 2 n n 2 n 5 L disuguglinz di Bernoulli fferm che (1 + ) n 1 + n se > 1 e n N. Ess può essere dimostrt fcilmente utilizzndo il principio di induzione, procedendo come segue. Per n = 0 l disuguglinz è ovvimente ver. Supponimol ver per un certo n: llor (1 + ) n+1 = (1 + ) n (1 + ) (1 + n)(1 + ) = 1 + (n + 1) + n (n + 1), che dimostr il psso induttivo. Si noti che, in reltà, per n 2, 0 l disuguglinz è strett! 22
23 quel che ci dice l disuguglinz di Bernoulli! (In reltà, tenendo conto dei csi in cui l disuguglinz di Bernoulli è strett, bbimo mostrto che l successione n è strettmente crescente...) Per mostrre poi che il limite è finito, occorre mostrre che l successione è superiormente limitt. Per fr questo prendimo l successione b n = (1 + 1/n) n+1, e mostrimo che quest è decrescente. Inftti, mnipolndol un po ci si rende conto che l disuguglinz b n b n 1 è equivlente ll seguente: ( n ) n. n 2 1 D ltr prte, grzie ll disuguglinz di Bernoulli bbimo ( ) n 1 + n n 2 1 n 2 1 = n n, n come volevmo. Si h llor 2 = 1 < n < b n < b 1 = 4, e possimo essere certi che e è un numero rele compreso tr 2 e 4. Evidentemente, si possono vere stime migliori prendendo n grnde, in qunto n < e < b n... Dll definizione del numero di Nepero e deriv il seguente limite fondmentle (di funzione rele!): lim (1 + x + 1/x)x = e. L cos può essere dimostrt senz tropp difficoltà giocndo con le prti intere: ricordo che il simbolo [x] indic il più grnde numero intero minore o ugule x, d cui si h evidentemente lim (1 + 1 x + [x] )[x] = e grzie ll definizione del numero e. Inoltre, per x > 0 vlgono le ovvie disuguglinze ( ) [x] ( x ( 1 + [x] + 1 x) 1 ) [x]+1. [x] Or, è immedito verificre che l funzione sinistr e quell destr tendono entrmbe d e (grzie ll osservzione ftt sopr), e il risultto voluto segue dl teorem dei crbinieri. Usndo il limite fondmentle ppen dimostrto e l continuità dell funzione esponenzile e dell funzione logritmo (per il momento dimol per buon: l dimostreremo tr poco!), possimo dimostrre senz eccessiv difficoltà che log(1 + x) lim = 1 x 0 x 23
24 e che e x 1 lim = 1. x 0 x Per ( dimostrre il primo limite, possimo comincire fr vedere che lim x x x) = e (questo è un semplice esercizio), d cui lim (1 + x) 1/x = e x 0 (bst cmbire vribile ponendo y = 1/x... è nche opportuno distinguere il limite destro e il limite sinistro). Il limite voluto segue llor prendendo il logritmo in bse e (ricordndo nche il teorem sul limite di funzione compost: prendimo per buon l continuità dell funzione logritmo!). Il secondo dei due limiti fondmentli segue invece dl primo con il cmbio di vribile y = e x 1 (nche in questo cso, ci serve l continuità dell funzione esponenzile per dire che y 0 qundo x 0). Verifichimo finlmente che le funzioni esponenzili f(x) = x (con > 0, 1) sono continue. Grzie lle proprietà delle potenze, è sufficiente verificrne l continuità in x 0 = 0: ci bst fr vedere che lim x = 1. x 0 Supponimo per fissre le idee che si > 1 (l generlizzzione l cso 0 < < 1 è lscit per esercizio: bsti osservre che x = (1/) x...). Comincimo col mostrre che vle il limite di successione lim 1 n = 1. n + Definimo b n = 1 n 1: quest è un successione positiv, ed il nostro limite srà provto se fccimo vedere che b n 0 per n +. Or, si vede subito che = (1 + b n ) n 1 + nb n (dove per l ultimo pssggio usimo l disuguglinz di Bernoulli), d cui 0 < b n 1. Il limite segue llor dl n teorem dei crbinieri. Si or ε > 0. Trovimo n N tle che 1/n < 1+ε. Siccome l funzione esponenzile è crescente, se ne deduce che 1 < x < 1+ε se 0 < x < 1, per cui lim n x = 1. Per mostrre che nche il limite sinistro x 0 + h lo stesso vlore, bst osservre che x = 1... x Dll continuità di esponenzile e logritmo si deducono molte proprietà importnti, d esempio l continuità dell funzione f(x) = x b (x 0): bst scrivere x b = e b log x e usre l continuità di esponenzile e logritmo. Ecco un ltro esercizio guidto per dimostrre due limiti fondmentli molto utili: visto che bbimo prlto dell funzione esponenzile e delle sue proprietà, questo è un buon momento per frlo! ESERCIZIO: Si provino i due seguenti limiti fondmentli: x lim x + x = +, b per ogni > 1 e per ogni b > lim log x = 0 x + x b
25 [SUGGERIMENTO: Comincimo con l osservre che, grzie ll disuguglinz di Bernoulli, n / n = (1 + ( 1)) n / n (1 + n( 1))/ n = 1/ n + n( 1) +, e quindi lim n n + n = +. Si h poi, per x > 0, x x [x] [x] + 1 = [x]+1 [x] + 1. L quntità destr, per x + tende + grzie l limite di successione ppen visto. Ne consegue che x x = +. lim x + D questo segue fcilmente il primo dei due limiti fondmentli scritti sopr, in qunto ( ) 2b x x = ( 1 2b ) x... b x Per verificre il secondo limite fondmentle, è sufficiente cmbire vribile ponendo y = log x.] 8 Lezione del 15/10/2015 (2 ore) Uno dei risultti fondmentli sulle funzioni continue, è il TEOREMA DI ESISTENZA DEGLI ZERI: Si f : [, b] R un funzione continu tle che f() < 0 e f(b) > 0. Allor esiste un punto c (, b) tle che f(c) = 0. Questo teorem dll ri innocu si rivel in reltà ssi utile. Per esempio, considerimo l funzione continu f(x) = x 2 (con > 0) sull intervllo [0, +1]. Si vede subito che f(0) = < 0, mentre f(+1) = > 0. Il teorem ci ssicur che esiste un punto c dell intervllo tle che c 2 = 0: bbimo così dimostrto che esiste l rdice qudrt di. Ess è poi unic perché l funzione considert è strettmente crescente sull semirett dei reli positivi (e quindi non si può nnullre due volte). In mnier nlog possimo dimostrre l esistenz del logritmo, delle funzioni trigonometriche inverse, delle rdici di ogni ordine...non srà nemmeno difficile verificre che tutte queste funzioni sono continue. Propongo due diverse dimostrzioni del teorem di esistenz degli zeri (in ul bbimo visto l second!). PRIMA DIMOSTRAZIONE (lunghett m istruttiv...): Usimo il cosiddetto metodo di bisezione. Si d = (b )/2 il punto medio dell intervllo [, b]: se f(d) = 0 simo felicissimi perché bbimo trovto il punto voluto, in cso 25
26 contrrio vremo f(d) < 0 oppure f(d) > 0. In ogni cso, in uno dei due mezzi intervlli [, d] oppure [d, b] si ripropone l situzione di prtenz: f è negtiv nell estremo sinistro dell intervllo, positiv nell estremo destro. Chimimo [ 1, b 1 ] il semiintervllo che gode di quest proprietà. Ripetimo poi l stess costruzione: prendimo il punto di mezzo dell intervllo [ 1, b 1 ] e osservimo che se l funzione non si nnull nel punto di mezzo (m se così fosse vremmo finito), in uno dei due mezzi intervlli che chimeremo [ 2, b 2 ] si ripropone l situzione di prtenz: f( 2 ) < 0 e f(b 2 ) > 0. Iterimo quest costruzione: se il processo non si rrest perché trovimo un punto in cui l funzione si nnull, vremmo individuto un successione infinit di intervlli [ n, b n ], ciscuno contenuto nel precedente e tli che f( n ) < 0, f(b n ) > 0. Per costruzione bbimo che l successione degli estremi sinistri n è crescente, l successione degli estremi destri b n è decrescente e inoltre b n n = (b )/2 n. Siccome un successione crescente e limitt mmette limite finito, esisterà il limite c [, b]. È evidente che si h nche lim n = c, ed evidentemente n + lim b n = c per qunto osservto sopr sull n + differenz tr n e b n. Grzie ll continuità di f, si h poi lim f( n) = f(c) n + lim f(b n) = f(c). n + D ltr prte, il primo limite deve essere necessrimente 0 in qunto limite di un successione di numeri negtivi, mentre il secondo deve essere 0 in qunto limite di un successione di numeri positivi: siccome i due limiti sono entrmbi uguli f(c), ne deriv che f(c) = 0. Q.E.D. DIMOSTRAZIONE ALTERNATIVA: Voglimo proporre un ltr dimostrzione del teorem, leggermente più rpid. Ponimo c = sup A, dove A = {x [, b] : f(x) < 0}. Questo è evidentemente un numero rele compreso tr e b. Dico che f(c) = 0. Inftti, se per ssurdo vessimo f(c) > 0, per definizione di limite vremmo f(x) > 0 nche per tutti gli x in un certo intorno sinistro [c δ, c] di c 6. Quindi c δ srebbe un mggiornte di A più piccolo di c, contro l definizione di estremo superiore. Se poi fosse f(c) < 0, dovrebbe essere c < b (perché f(b) > 0). Per lo stesso motivo di prim, troveremmo δ > 0 tle che f(x) < 0 per x [c, c+δ], e c non srebbe più un mggiornte di A. Q.E.D. 6 Questo semplice ftto è noto come teorem dell permnenz del segno: se un funzione h limite positivo in x 0, llor è positiv in un intorno di x 0 (con l possibile esclusione di x 0 ). 26
27 Un immedito corollrio del teorem di esistenz degli zeri è il seguente TEOREMA (dei vlori intermedi): Se f : [, b] R è un funzione continu, ess ssume tutti i vlori compresi tr f() e f(b). Dimostrzione: Si y 0 un vlore compreso tr f() e f(b). Bst pplicre il Teorem di esistenz degli zeri ll funzione g(x) = f(x) y 0... Q.E.D. Questo teorem è prticolrmente utile per dimostrre che certe funzioni continue sono invertibili. DEFINIZIONE: Un funzione f : A B (A, B insiemi) si dice iniettiv o uno uno se f( 1 ) = f( 2 ) implic 1 = 2 : in ltre prole, dto b B esiste l più un A tle che f() = b (oppure nessuno!). f si dice poi suriettiv se per ogni b B esiste A tle che f() = b, ossi se l immgine coincide col codominio: f(a) = B. Infine, f si dice biiettiv o biunivoc o invertibile se è si iniettiv che suriettiv. In tl cso, esiste un unic funzione g : B A tle che g(f()) = per ogni A e f(g(b)) = b per ogni b B. Tle g si chim invers di f. Vle evidentemente nche il vicevers: esiste dunque l invers se e soltnto se f è biiettiv. Dl teorem dei vlori intermedi segue che se f : [, b] R è un funzione continu e strettmente crescente (che è evidentemente iniettiv!), ess è suriettiv sull intervllo [f(), f(b)]: in ltre prole, ess è invertibile. Questo ci ssicur l esistenz di rdici, logritmi, funzioni inverse delle funzioni trigonometriche... Ecco un teomer che ssicur l continuità dell funzione invers: TEOREMA (Continuità delle funzioni monotone): Un funzione crescente f : [, b] R è continu se e solo se f([, b]) = [f(), f(b)]. Un risultto nlogo vle per le funzioni decrescenti. DIM.: Se f è continu, l tesi è un conseguenz immedit del Teorem dei vlori intermedi. Vicevers, supponimo che f non si continu, e si x 0 un suo punto di discontinuità (supponimo per semplicità x 0 (, b): le semplici modifiche necessrie nei csi x 0 = o x 0 = b sono lscite per esercizio). Abbimo osservto che le funzioni crescenti mmettono sempre limite destro e sinistro, che evidentemente devono essere diversi in x 0 : l 1 = lim x x 0 f(x) = sup{f(x) : x < x 0 } < l 2 = lim f(x) = inf{f(x) : x 0 < x b}. x x
28 Per l crescenz di f, segue subito che f([, b]) contiene l più un punto dell intervllo perto (l 1, l 2 ), ossi il vlore f(x 0 ) se questo non coincide con uno dei due limiti: per questo motivo f non può essere suriettiv. Q.E.D. D quest ultimo teorem segue che l funzione invers di un funzione continu e strettmente crescente definit su un intervllo [, b], è nch ess continu. Inftti, l funzione invers è strettmente crescente e suriettiv d [f(), f(b)] in [, b]. Sono in prticolre continue le rdici, i logritmi, le funzioni trigonometriche inverse... Un ltro, importnte risultto sulle funzioni continue è il TEOREMA (di Weierstrss): Un funzione continu f : [, b] R mmette mssimo e minimo. (Attenzione: è importnte che il dominio dell funzione si un intervllo chiuso e limitto, e che l funzione si continu. Abbimo visto con qulche esempio che senz queste ipotesi l tesi può nche essere fls!). Per dimostrre il teorem di Weierstrss useremo un risultto che si rivelerà utilissimo in molte ltre occsioni: il teorem di Bolzno-Weierstrss. Oggi è rimsto soltnto il tempo per enuncire tle teorem: premettimo un importnte definizione che srà necessri comprenderlo. DEFINIZIONE: Dt un successione { n } n N, un su sottosuccessione è un nuov successione del tipo { nk } k N, dove n k è su volt un successione strettmente crescente di numeri nturli. Per esempio, d un dt successione si può estrrre l sottosuccessione dei termini di indice pri, dei termini di indice dispri, di quelli il cui indice è divisibile per Evidentemente, se lim n = l, mggior rgione si vrà lim n n + k = l k + per ogni sottosuccessione dell prim. È però interessnte notre che nche d un successione che non h limite si può estrrre un sottosuccessione che ce l h: enuncimo e dimostrimo il Teorem di Bolzno-Weierstrss che fferm proprio questo! TEOREMA (di Bolzno-Weierstrss): D un successione limitt { n } n N è sempre possibile estrrre un sottosuccessione { nk } k N che mmette limite finito. Vedremo domni l dimostrzione. 28
29 9 Lezione del 16/10/2015 (2 ore) Dimostrimo il teorem di Bolzno-Weierstrss usndo il buon vecchio metodo di bisezione. Per ipotesi, l nostr successione è limitt, cioè esiste un intervllo [α, β] tle che n [α, β] per ogni n N. Se dividimo l intervllo [α, β] in due metà, ce ne dovrà essere lmeno un (che chimeremo [α 1, β 1 ]) tle che n [α 1, β 1 ] per infiniti indici n. Anlogmente, se dividimo [α 1, β 1 ] in due prti uguli, ce ne srà un che chimeremo [α 2, β 2 ] tle che n [α 2, β 2 ] per infiniti indici n. Proseguendo in questo modo, costruimo un successione infinit di intervlli [α k, β k ], ciscuno dei quli è un delle due metà del precedente, con l proprietà che l successione { n } cde entro [α k, β k ] per infiniti indici n. Evidentemente, {α k } k N è un successione crescente per cui esisterà lim α k = l [α, β]. k + Inoltre, vremo nche lim β k = l poiché β k α k = (β α)/2 k. k + Costruimo un sottosuccessione { nk } di { n } nel modo seguente: come n 1 prendimo il più piccolo indice n per cui n pprtiene [α 1, β 1 ], come n 2 il più piccolo indice n > n 1 per cui n [α 2, β 2 ] (esisterà certmente: di indici sifftti ce ne sono infiniti per costruzione di [α 2, β 2 ])... Proseguimo llo stesso modo: n k srà il più piccolo indice n > n k 1 per cui n [α k, β k ]. In questo modo, vremo individuto un sottosuccessione { nk } di { n } tle che α k nk β k per ogni k. Grzie l teorem dei crbinieri, si vrà quindi lim n k = l. Q.E.D. k + DIM. DEL TEOREMA DI WEIERSTRASS: Si M = sup{f(x) : x [, b]}. Dobbimo mostrre che M è finito ed è il mssimo di f, cioè che esiste x [, b] tle che f(x) = M. L esistenz del minimo si dimostr poi in modo nlogo. Innnzitutto, dll definizione di sup segue che possimo trovre un successione {x n } [, b] tle che lim f(x n) = M. n + Inftti, se M è finito e n N, bst osservre che M 1 non è un mggiornte n dell immgine di f per trovre x n [, b] tle che M 1/n < f(x n ) M. 29
30 Se vicevers M = + e n N, llor n non è un mggiornte dell immgine di f (perché ess è illimitt superiormente): esiste dunque x n tle che f(x n ) > n. L successione {x n } è limitt (perché lo è l intervllo [, b]): il teorem di Bolzno-Weierstrss ci fornisce un sottosuccessione {x nk } k tle che lim x n k = x. Evidentemente, x [, b] (e per questo è essenzile l chiusur k + dell intervllo...). Allor, grzie ll continuità di f in x si h: M = lim f(x n k ) = f(x), k + e x è il punto di mssimo cercto. Q.E.D. Concluso il nostro studio delle funzioni continue, è giunto il momento di vvicinrci l clcolo differenzile. Comincimo dunque introdurre il fondmentle concetto di derivt di un funzione. Supponimo di vere un funzione f : R R, e di voler cpire come è ftto il suo grfico: questo può vere un notevole interesse pplictivo, per esempio se voglimo mssimizzre o minimizzre un quntità fisic rppresentt d f. Se gurdimo il grfico di un funzione cso (che si però bbstnz regolre: supponimo che il grfico si un line continu e senz spigoli vivi), ci ccorgimo che ci srebbe estremmente utile sper identificre i trtti in slit e i trtti in disces del grfico dell funzione! Per fr questo, bbimo bisogno di un definizione di pendenz del nostro grfico in un punto. Se l funzione è un polinomio di primo grdo, cioè se f(x) = mx + q, il grfico è un rett e l rispost è fcilissim: l pendenz del grfico (in senso strdle : rpporto tr qunto si sle e qunto ci si spost in orizzontle!) è dt dl coefficiente ngolre m. In sostnz, per chi si spost d sinistr verso destr, se m > 0 il grfico è in slit, se m = 0 è pino e se m < 0 è in disces! Se prendimo però un funzione il cui grfico non si un rett, l pendenz non srà più costnte, m potrà cmbire d punto punto. Vedremo l prossim volt come fre definire in modo rigoroso quest pendenz nel punto! Vedimo come possimo definire l pendenz del grfico di un funzione rele di vribile rele in un suo punto di sciss x 0 : se prendimo due punti bbstnz vicini sull rett rele, x 0 e x 0 + h, è rgionevole pensre che l pendenz del grfico di f in x 0 (qulunque cos questo significhi!), si 30
31 vicin ll pendenz dell rett che pss per i due punti corrispondenti sul grfico, (x 0, f(x 0 )) e (x 0 +h, f(x 0 )+h). Tle pendenz è dt dll espressione f(x 0 + h) f(x 0 ), h dett rpporto incrementle. E rgionevole supporre che prendendo h sempre più piccolo (e quindi i due punti sempre più vicini), vremo un pprossimzione sempre migliore dell pendenz del grfico di f nel punto (x 0, f(x 0 )). Dimo dunque l seguente DEFINIZIONE: L pendenz del grfico di f per x = x 0 si chim derivt di f in x 0 e si indic con f (x 0 ). Ess si definisce ponendo f f(x 0 + h) f(x 0 ) (x 0 ) = def lim, h 0 h purché il limite esist finito. Se il limite non esiste o è infinito, non è definit l pendenz e dicimo che l funzione non è derivbile in x 0. In prticolre, se f (x 0 ) esiste, l rett tngente l grfico di f per x = x 0 srà l rett pssnte per (x 0, f(x 0 )) l cui pendenz coincide con quell del grfico stesso: ess vrà dunque equzione y = f (x 0 )(x x 0 ) + f(x 0 ). Per visulizzre meglio l definizione di derivt, vi propongo un nimzione interttiv 7 che illustr il concetto I più curiosi potrnno trovre nche un modo lterntivo di vedere l rett tngente, come limite di ingrndimenti del grfico di f ttorno (x 0, f(x 0 )) :
32 Dimo ltre possibili interpretzioni del rpporto incrementle e dell derivt: velocità medi e velocità istntne di un corpo che si muove di moto rettilineo, velocità medi e istntne di un rezione chimic, tsso di interesse (o tsso di inflzione...). Un risultto ssi semplice m importnte è il seguente TEOREMA: Se f è un funzione definit in un intorno di x 0 derivbile in x 0, llor f è nche continu in x 0. Dimostrzione: Si h lim (f(x f(x 0 + h) f(x 0 ) 0 + h) f(x 0 )) = lim h = 0. h 0 h 0 h Inftti, nell ultim espressione l frzione tende f (x 0 ), mentre il fttore h tende 0. Q.E.D. Osservimo che il vicevers non è vero: un funzione può essere continu m non derivbile in un punto, come d esempio l funzione f(x) = x in 0. In reltà, può suggedere ben di peggio: nel 1872 Krl Weierstrss costruì un funzione ovunque continu sull rett rele, m non derivbile in lcun punto. L costruzione di quest funzione richiede conoscenze un po più rffinte di quelle che possedimo in questo momento. Nel frttempo, però, possimo mmirrne il grfico (cliccndo sull immgine prte un filmto!): 32
33 Abbimo osservto nche che l derivbilità in x 0 non implic l continuità in un intorno di x 0 : ci sono esempi di funzioni derivbili e continue in un punto m discontinue in tutti gli ltri. In concreto, l funzione { 0 se x Q, f(x) = x 2 se xi R \ Q è continu e derivbile in 0 (con f (0) = 0), m discontinu in tutti gli ltri punti. 10 Lezione del 21/10/2015 (2 ore) Come bbimo ftto con i limiti, possimo chiederci cos si l derivt dell somm, del prodotto o del rpporto di due funzioni: TEOREMA (Algebr delle derivte): Sino f(x), g(x) due funzioni definite in un intorno di x 0, derivbili in x 0. (i) L somm di f e g è derivbile in x 0, e (f + g) (x 0 ) = f (x 0 ) + g (x 0 ); (ii) Il prodotto di f e g è derivbile in x 0, e (fg) (x 0 ) = f (x 0 )g(x 0 ) + f(x 0 )g (x 0 ); (iii) se g(x 0 ) 0, llor f/g è derivbile in x 0 e ( ) f (x 0 ) = f (x 0 )g(x 0 ) f(x 0 )g (x 0 ). g [g(x 0 )] 2 33
34 Dimostrzione: L (i) è prticmente ovvi (il rpporto incrementle dell somm è l somm dei rpporti incrementli... Dimostrimo l (ii): bbimo f(x 0 + h)g(x 0 + h) f(x 0 )g(x 0 ) = h f(x 0 + h)g(x 0 + h) f(x 0 )g(x 0 + h) + f(x 0 )g(x 0 + h) f(x 0 )g(x 0 ) h f(x 0 + h) f(x 0 ) g(x 0 + h) + f(x 0 ) g(x 0 + h) g(x 0 ) h h = e pssndo l limite per h 0 (tenendo conto nche dell continuità delle funzioni derivbili) si ottiene (ii). Per dimostrre l (iii), clcolimoci l derivt di 1/g(x): dobbimo fre ( ) 1 (x 0 ) = lim g h 0 1 g(x 0 +h) 1 g(x 0 ) h = g(x 0 + h) g(x 0 ) 1 lim h 0 h g(x 0 + h)g(x 0 ) = g (x 0 ) g(x 0 ). 2 L (iii) segue llor immeditmente usndo l formul ppen ricvt e l (ii). Q.E.D. Usndo queste semplici regole, e l stess definizione di derivt, verifichimo senz difficoltà che (x n ) = nx n 1 per n Z, (sin x) = cos x, (cos x) = sin x, (tn x) 1 = cos 2 (x) (ex ) = e x (e nlogmente ( x ) = x log ), (log x) = 1. x Vedimo or come si deriv un funzione compost: TEOREMA (Chin Rule): Si f un funzione definit in un intorno di x 0, derivbile in x 0, e si g un funzione definit in un intorno di y 0 = f(x 0 ), derivbile in y 0. Allor l funzione compost g f(x) = g(f(x)) è derivbile in x 0 e si h (g f) (x 0 ) = g (f(x 0 ))f (x 0 ). DIM.: Introducimo l seguente funzione usiliri, definit in un intorno di 0: { g(y0 + k) g(y 0 ) A(k) = se k 0, k g (y 0 ) se k = 0. Evidentemente, quest funzione è continu in 0, per definizione di derivt. 34
35 Costruimo or il rpporto incrementle dell funzione g f, e pssimo l limite per h 0: g(f(x 0 + h)) g(f(x 0 )) = h A(f(x 0 + h) f(x 0 )) f(x 0 + h) f(x 0 ) h g (f(x 0 ))f (x 0 ). Q.E.D. Usndo quest formul possimo clcolrci ltre derivte. Per esempio, se x > 0 e R bbimo: (x ) = (e log x ) = x = x x 1. Anlogmente ( ) f(x) g(x) ( ) = e g(x) log f(x) =... Ci ponimo or l questione dell derivbilità dell invers di un funzione derivbile(ed invertibile). TEOREMA (Derivt dell funzione invers): Si f : I R un funzione continu e strettmente crescente su un intervllo perto I, g : J I l su invers (definit sull intervllo J = f(i)). Se f è derivbile in x 0 I e f (x 0 ) 0, llor g è derivbile in y 0 = f(x 0 ), e g (y 0 ) = 1/f (x 0 ). In ltre prole, g 1 (y 0 ) = f (g(y 0 )). Dimostrzione: Osservimo che se spessimo già che l funzione invers g è derivbile in y 0, l formul per l derivt di g srebbe fcilissim d trovre. Inftti g(f(x)) = x, e derivndo mbo i membri si h g (f(x 0 )) f (x 0 ) = 1, d cui l formul volut. Siccome però non sppimo che g è derivbile in y 0, dobbimo proprio trovre il limite del rpporto incrementle (g(y 0 + h) g(y 0 ))/h per h 0. Se ponimo y 0 +h = f(x 0 +k), pplicndo l g d mbo i membri trovimo g(y 0 +h) = x 0 +k = g(y 0 )+k, d cui g(y 0 +h) g(y 0 ) = k. Siccome sppimo che con le nostre ipotesi l funzione invers g è continu, vedimo che qundo h 0 nche k 0. Dunque Q.E.D. g (y 0 ) = lim h 0 g(y 0 + h) g(y 0 ) h k = lim k 0 f(x 0 + k) f(x 0 ) = 1 f (x 0 ). 35
36 Utilizzimo il teorem di derivzione dell funzione invers per trovre l derivt di rcsin y: (rcsin y) = 1 (sin) (rcsin y) = 1 cos rcsin y = 1 1 sin 2 (rcsin y) = 1. 1 y 2 In mnier del tutto nlog trovimo che (rccos y) = 1/ 1 y 2, e che (rctn y) = 1/(1 + y 2 ) (per quest ultim formul, si ricordi l identità cos 2 α = 1/(1 + tn 2 α). Or bbimo disposizione un rsenle di risultti sufficiente clcolre le derivte di tutte le funzioni esprimibili in termini di funzioni elementri trmite operzioni lgebriche e di composizione. Quindi, in line di principio, simo in grdo di studire l ndmento di un grn numero di funzioni studindo il segno delle loro derivte Lezione del 22/10/2015 (3 ore) Per determinre in modo più ccurto l ndmento del grfico di un funzione, è utile sper trovre gli intervlli di concvità e di convessità del grfico stesso: bisogn cioè sper determinre se, in un certo intervllo, l funzione f l pnci verso il bsso o verso l lto... Prim di proseguire nell lettur, potete esminre l seguente introduzione interttiv lle funzioni convesse... 9 Comincimo con un definizione rigoros di convessità per un funzione derivbile: in reltà, si può dre un definizione più generle, vlid nche per funzioni non derivbili. 8 A rigore, bisogn dire che per or bbimo solo intuito che un funzione con derivt positiv su un intervllo è crescente in tle intervllo: l effettiv dimostrzione di questo plusibilissimo ftto verrà dt in seguito!
37 Definizione: Dicimo che un funzione derivbile f : [, b] R è convess sull intervllo [, b] se il grfico di f gice tutto l di sopr di ogni rett tngente l grfico stesso, condott per un punto qulunque di [, b]. Con linguggio simbolico, voglimo che per ogni x 0 [, b] e per ogni x [, b] vlg f(x) f (x 0 )(x x 0 ) + f(x 0 ). Se vle sempre l disuguglinz oppost, diremo che l funzione è concv. Se disegnmo il grfico di un funzione convess, osservimo come l pendenz delle rette tngenti cresc mn mno che il punto di tngenz si spost verso destr: in effetti, quest è un crtterizzzione dell convessità per funzioni derivbili: TEOREMA: Si f : [, b] R un funzione derivbile. Allor f è convess se e solo se l funzione derivt f è crescente sull intervllo [, b]. Dimostrzione: Supponimo che f si convess, e prendimo x 1, x 2 in [, b]. Per l disuguglinz di convessità bbimo f(x) f (x 1 )(x x 1 ) + f(x 1 ), f(x) f (x 2 )(x x 2 ) + f(x 2 ), disuguglinze vlide per ogni x [, b]. In prticolre, prendimo x = x 2 nell prim disuguglinz, x = x 1 nell second, e sommimo: si ottiene (f (x 1 ) f (x 2 )) (x 2 x 1 ) 0, che è proprio l crescenz dell funzione derivt. Vicevers, supponimo che l funzione f si crescente e prendimo x 0 [, b]. Considerimo l funzione derivbile g(x) = f(x) f (x 0 )(x x 0 ) f(x 0 ). Si h g (x) = f (x) f (x 0 ), per cui g è un funzione crescente che è negtiv per x < x 0, mentre è positiv per x > x 0. Ne deducimo che l funzione g h un minimo ssoluto per x = x 0 : ess è inftti decrescente nell intervllo sinistr di x 0, crescente nell intervllo destr di x Poichè g(x 0 ) 0, bbimo g(x) 0 per ogni x [, b]: quest è proprio l disuguglinz di convessità! Q.E.D. Grzie questo teorem, bbimo un comodo criterio di convessità per funzioni l cui derivt si ncor derivbile (ossi per funzioni derivbili due volte): un funzione f derivbile due volte in un intervllo srà convess se 10 Abbimo usto ncor un volt il ftto che un funzione derivbile è crescente su un intervllo se e solo se l su derivt è non negtiv. 37
38 f (x) 0 per ogni x nell intervllo, srà invece concv se f (x) 0 in ogni punto x dell intervllo. Pssimo or d esminre con le dovute cutele un ftto che bbimo usto sinor con indebit disinvoltur. Inftti, bbimo osservto che siccome l derivt corrisponde geometricmente ll pendenz del grfico, se un funzione h derivt positiv in un intervllo, ess srà crescente in esso. Questo ftto è intuitivmente molto plusibile, perché non si vede come un funzione poss vere il grfico in slit in tutti i punti di un intervllo senz essere nche crescente! D ltr prte, non ne bbimo vist lcun dimostrzione rigoros: tle dimostrzione è lo scopo dei discorsi che seguono. Per pprezzre mggiormente l portt del teorem che fferm l crescenz di un funzione con derivt positiv in un intervllo, vle l pen di vedere un pio di esempi ptologici...che sottolineno qunto l derivt si un oggetto intrinsecmente locle: vere un teorem che consente di ottenere informzioni globli dll derivt è quindi prticolrmente interessnte! ESEMPIO: Come primo esempio, bbimo considerto l funzione { x + x f(x) = 2 sin(1/x 2 ) se x 0 0 se x = 0 Clcolndo esplicitmente l derivt per x 0, bbimo verificto che quest cmbi di segno infinite volte in un intorno di 0: non esiste lcun intorno di 0 in cui l funzione è crescente o decrescente. D ltr prte, un clcolo diretto usndo l definizione di derivt mostr che f è derivbile in 0 con f (0) = 1. Dunque, dl ftto che l derivt si strettmente positiv in un punto non possimo dedurre che l funzione è crescente in un intorno di quesl punto! Si noti però che l esempio funzion perché l derivt di f è discontinu in 0: se l derivt fosse continu, dovrebbe essere positiv in un intervllino centrto in 0 e l funzione srebbe crescente in tle intervllo. 38
39 ESEMPIO: Vedimo un funzione ncor più ptologic. Un funzione può essere derivbile (e quindi continu) in un punto, m essere discontinu in tutti gli ltri punti del suo dominio. Considerimo l funzione { x + x 2 se x Q f(x) = x se x R \ Q Grzie ll densità di rzionli e di irrzionli in R, si vede subito che quest funzione è discontinu per ogni x 0. D ltr prte, ess è derivbile in 0 con derivt 1 (si usi l definizione di derivt). Anche quest funzione h ovvimente l proprietà di vere derivt strettmente positiv in 0, m di non essere crescente in lcun intorno di 0. Tornimo dunque l nostro risultto teorico! Comincimo col ricordre l seguente definizione: DEFINIZIONE: Si f : [, b] R. Un punto x 0 [, b] si dice di mssimo reltivo (risp., di minimo reltivo) per f se esiste un intorno I x0 di x 0 tle che f(x) f(x 0 ) (risp., f(x) f(x 0 )) per ogni x I x0 [, b]. Venimo d un primo, semplice risultto: se un funzione è derivbile in un punto di mssimo o minimo reltivo interno ll intervllo di definizione, in quel punto l derivt si deve nnullre: TEOREMA (Principio di Fermt): Si f : [, b] R, x 0 (, b) un punto di mssimo o minimo reltivo per f. Se f è derivbile in x 0, llor f (x 0 ) = 0. DIMOSTRAZIONE: Supponimo per fissre le idee che x 0 si di minimo reltivo. Considerimo il rpporto incrementle per f in x 0 : f(x 0 + h) f(x 0 ). h Se prendimo h bbstnz piccolo, in modo che x 0 +h pprteng ll intorno I x0 nell definizione di minimo reltivo, vedimo subito che il numertore è mggiore o ugule 0. Ne consegue che il rpporto incrementle srà positivo (o nullo) per h > 0 bbstnz piccolo, e negtivo (o nullo) per h < 0 bbstnz piccolo in modulo. Ne segue che e contempornemente f (x 0 ) = lim x x + 0 f (x 0 ) = lim x x 0 f(x 0 + h) f(x 0 ) h f(x 0 + h) f(x 0 ) h 39 0, 0.
40 Dunque, f (x 0 ) = 0, Q.E.D. Si noti che questo teorem può essere flso per punti di mssimo o minimo reltivo che sino gli estremi dell intervllo su cui f è definit. Per esempio, si consideri l funzione f(x) = x sull intervllo [0, 1]... Due conseguenze del principio di Fermt sono i teoremi di Rolle e di Lgrnge, che sono tr i risultti più importnti del clcolo differenzile per funzioni di un vribile: TEOREMA (di Rolle): Si f : [, b] R un funzione continu, derivbile nell intervllo (, b). Se f() = f(b), llor esiste un punto c (, b) tle che f (c) = 0. DIMOSTRAZIONE: Grzie l teorem di Weierstrss, l funzione possiede un punto di mssimo ssoluto x M, e uno di minimo ssoluto x m. Se uno di questi punti pprtiene ll interno dell intervllo, esso è nche di mssimo o minimo reltivo, e per il principio di Fermt l derivt si deve nnullre in quel punto (che srà dunque il punto c cercto). In cso contrrio, x m e x M coincidono con gli estremi e b dell intervllo. Allor, per ogni x [, b] si h f() = f(x m ) f(x) f(x M ) = f(b) = f(), per cui il mssimo e il minimo di f coincidono. Ne segue che f è costnte, e l su derivt si nnull in tutti i punti dell intervllo. Q.E.D. TEOREMA (di Lgrnge): Si f : [, b] R un funzione continu, derivbile nell intervllo (, b). Esiste un punto c (, b) tle che f (c) = f(b) f() b. DIM.: Considerimo l funzione usiliri g(x) = f(x) f(b) f() (x ). b Quest è un funzione continu in [, b] e derivbile in (, b). Inoltre g() = f() = g(b), per cui possimo pplicre il teorem di Rolle e ottenere un punto c (, b) tle che g (c) = 0. Questo è proprio il punto cercto. Q.E.D. A lezione, bbimo visto che le ipotesi dei teoremi di Rolle e Lgrnge non possono essere in generle indebolite, e bbimo discusso il significto geometrico di questi risultti. Quel che è più importnte, è comunque l seguente conseguenz del teorem di Lgrnge, d noi già mpimente utilizzt: COROLLARIO: Si f : [, b] R un funzione derivbile. Se f (x) 0 per ogni x [, b], llor f è crescente in [, b]. 40
41 Se f è invece minore o ugule 0, l funzione è decresente in [, b]. Infine, se f = 0 in tutto l intervllo, l funzione è costnte. DIMOSTRAZIONE: Fccimo vedere per esempio che vle l prim delle nostre ffermzioni: supponimo che f (x) 0 per ogni x [, b]. Sino poi x 1 e x 2 due punti di [, b], con x 1 < x 2. Applichimo il teorem di Lgrnge f sull intervllo [x 1, x 2 ]: trovimo c (x 1, x 2 ) tle che f(x 2 ) f(x 1 ) = (x 2 x 1 )f (c). Per l ipotesi sull derivt, il membro di destr è mggiore o ugule zero. Q.E.D. Ci occuperemo or del problem di pprossimre un funzione regolre, in un intorno di un punto, medinte polinomi. Supponimo di vere un funzione f derivbile in x 0 : se ci chiedessero qul è l rett che meglio pprossim il grfico di f vicino x 0, probbilmente risponderemmo tutti che è l rett tngente y = f (x 0 )(x x 0 ) + f(x 0 ): l cos è ncor più plusibile se fccimo un disegno! Vedimo però di precisre meglio (in mnier quntittiv) in che senso l rett tngente è quell che pprossim meglio f in un intorno di x 0 : se g(x) = x + b è un polinomio di primo grdo che pprossim f, possimo scrivere che f(x) = g(x) + R(x), dove R(x) è un resto che voglimo si il più piccolo possibile qundo x si vvicin x 0. Siccome R(x) = f(x) (x x 0 ) b, notimo subito che lim x x 0 R(x) = 0 b = f(x 0 ). In questo senso, tutte le rette che pssno per il punto (x 0, f(x 0 ) pprossimno f, nel senso che il resto tende zero qundo x si vvicin x 0! Perché, dunque, l rett tngente è meglio delle ltre? Perché è l unic per cui il resto tende zero più rpidmente di x x 0, cioè è l unic per cui si bbi lim x x 0 R(x) (x x 0 ) = 0. Inftti, siccome bbimo già osservto che deve essere b = f(x 0 ), l quntità di cui dobbimo fre il limite divent: R(x) x x 0 = f(x) f(x 0) x x 0 f (x 0 ). Dunque, il limite è zero se = f (x 0 ), mentre è non nullo in tutti gli ltri csi. 41
42 Concludimo dunque che l rett tngente è l rett di migliore pprossimzione intorno x 0, nel senso che è quell per cui il resto tende 0 più rpidmente qundo x x 0! 12 Lezione del 23/10/2015 (2 ore) Nel tenttivo di generlizzre qunto ppen scoperto, divent nturle chiedersi qul è il polinomio di grdo n che meglio pprossim un cert funzione f (che supporremo derivbile qunte volte si vuole) in un intorno di x 0. Ci viene il sospetto che si un polinomio simile ll rett tngente, nel senso che le sue derivte fino ll n esim nel punto x 0 dovrnno coincidere con quelle di f... Per semplificrci l vit, supponimo che si x 0 = 0: ci si può sempre ridurre quest situzione con un trslzione lungo l sse delle x. Il polinomio di Tylor di grdo n per f centrto in 0 è definito d P n (x) = f(0) + f (0)x + f (0) 2! x f (n) (0) x n = n! n k=0 f (k) (0) x k. k! (Si noti che, ironi dell sorte, il polinomio di Tylor di grdo n h in reltà grdo minore o ugule n...) LEMMA 1: Si f un funzione derivbile n volte in 0. Tr tutti i polinomi P (x) di grdo minore o ugule n, il polinomio di Tylor P n (x) è l unico tle che P (0) = f(0), P (0) = f (0), P (0) = f (0),..., P (n) (0) = f (n) (0). DIM.: Il generico polinomio di grdo minore o ugule n srà dell form P (x) = x + 2 x n x n. Or, derivndo h volte il monomio x k si ottiene k(k 1)... (k h+1)x k h se h < k, k! per h = k, mentre si ottiene 0 per h > k. Tle funzione è sempre null in 0, trnne che nell unico cso in cui h = k, in cui vle k!. Dunque, sostituendo nelle relzioni che bbimo si ottiene P (0) = 0 = f(0), P (0) = 1 = f (0), P (0) = 2 2 = f (0), e in generle (per k n) P (k) (0) = k! k = f (k) (0). Di conseguenz, i coefficienti del polinomio devono essere proprio quelli che bbimo ttribuito l polinomio di Tylor di grdo n. Q.E.D. Per dimostrre che il polinomio di Tylor di grdo n è quello che meglio pprossim il grfico di f vicino x 0 (tr tutti i polinomi di grdo n), ci srà molto utile il Teorem di l Hôpitl, che è più in generle utilissimo 42
43 per il clcolo del limite di forme indeterminte. Esso è pplicbile limiti di rpporti nell form 0/0 o / : TEOREMA (l Hôpitl): Sino f, g funzioni derivbili in un intorno di x 0, trnne eventulmente in x 0 (dove possono nche non essere definite). Supponimo inoltre che g (x) 0 in tle intorno e che oppure lim f(x) = lim g(x) = 0 x x 0 x x0 lim f(x) = lim g(x) =. x x 0 x x0 Se esiste (finito o infinito) il limite llor esiste nche il limite f (x) lim x x 0 g (x), f(x) lim x x 0 g(x), e questi due limiti sono uguli. L enuncito del teorem rimne vero nche se x 0 = ± e per limiti destri/sinistri (con le ovvie modifiche delle ipotesi). A lezione, bbimo visto un esempio di ppliczione di questo teorem. Attenzione: il limite del rpporto f(x)/g(x) (in un delle due forme indeterminte suddette) può benissimo esistere nche se non esiste il limite del rpporto delle derivte. Ad esempio, si prend f(x) = x 2 sin(1/x), g(x) = x con x 0 = 0: il rpporto si present nell form 0/0 e tende 0, m non esiste il limite del rpporto delle derivte. Non vedremo l dimostrzione del teorem. Come conseguenz dell regol di l Hôpitl bbimo nche ottenuto un risultto semplice e utile: Si f un funzione derivbile in un intorno I x0 di x 0, trnne eventulmente in x 0. Se f è continu in x 0, e se esiste lim f (x) = x x0 l, llor f è derivbile nche in x 0 e f (x 0 ) = l. Risultto simile se il limite l è infinito: in quel cso l è il limite del rpporto incrementle di f in x 0 (solo che in quel cso...non lo chimimo derivt!). Infine, il risultto vle nche per limiti destri e sinistri dell derivt (e in quel cso fornisce informzioni sull derivt destr e sinistr). Per ottenere questo risultto è sufficiente pplicre il teorem di l Hôpitl l rpporto incrementle di f in x 0. In lterntiv, il risultto si può dimostrre utilizzndo direttmente il teorem di Lgrnge. Proseguimo l nostr discussione sull pprossimzione di funzioni medinte polinomi. Ci servirà il seguente lemm: 43
44 LEMMA 2: Si g(x) un funzione derivbile n 1 volte in un intorno di 0, con derivt n-esim in 0. Se g(0) = g (0) = g (0) =... = g (n) (0) = 0, llor bbimo g(x) lim x 0 x = 0. n DIM.: Bst pplicre n 1 volte il teorem di L Hôpitl (grzie lle nostre ipotesi, d ogni psso bbimo un form indetermint 0/0) ed infine l definizione di derivt come limite del rpporto incrementle: Q.E.D. g(x) lim x 0 lim x 0 x n 1 n! = lim x 0 g (x) =... = lim nxn 1 x 0 g (n 1) (x) g (n 1) (0) x g (n 1) (x) n!x = 1 n! g(n) (0) = 0. OSSERVAZIONE: Se g è come nel lemm, m qulcun delle derivte di ordine minore o ugule n è divers d 0, il limite non può essere 0: rifcendo lo stesso clcolo, si trov che è infinito, oppure è un numero diverso d zero. Come corollrio, ottenimo un prim form del Teorem di Tylor: TEOREMA (Di Tylor con resto di Peno): Si f un funzione derivbile n 1 volte in un intorno di 0 con derivt n-esim in 0. Se P n (x) denot il polinomio di Tylor di grdo n centrto in 0, llor f(x) P n (x) lim = 0. x 0 x n Tr tutti i polinomi di grdo minore o ugule n, il polinomio di Tylor è l unico d vere quest proprietà. DIM.: Grzie l Lemm 1, l funzione g(x) = f(x) P n (x) soddisf le ipotesi del Lemm 2, e il teorem risult dimostrto. L unicità del polinomio di Tylor rispetto quest proprietà segue dll Osservzione ftt dopo l dimostrzione del Lemm 2. Q.E.D. OSSERVAZIONE: Se l posto di 0 prendimo un generico punto x 0, il polinomio di Tylor di grdo n centrto in x 0 srà = P n (x) = n k=0 f (k) (x 0 ) (x x 0 ) k. k! 44
45 In questo cso, il teorem di Tylor dice che se f è derivbile (n 1) volte in un intorno di x 0, e possiede derivt n-esim in x 0, llor f(x) = P n (x) + R n (x), con lim x x0 R n (x) (x x 0 ) n = Lezione del 28/10/2015 (2 ore) A proposito dell formul di Tylor con resto di Peno, torn comod l definizione di o piccolo : DEFINIZIONE: Dte due funzioni f, g definite in un intorno di x 0, diremo che f è un o piccolo di g per x x 0, e scriveremo f(x) = o(g(x)) se f(x) lim x x 0 g(x) = 0, cioè se f(x) tende zero più rpidmente di g(x) per x 0. Con il linguggio degli o piccoli, il teorem di Tylor con resto di Peno dice che f(x) = P n (x) + o((x x 0 ) n )... Applichimo or l formul di Tylor con resto di Peno llo studio dei mssimi e dei minimi reltivi di un funzione. L ide è che spesso, per cpire se un punto in cui l derivt prim si nnull è di mssimo o minimo reltivo, bst studire il segno dell derivt second: TEOREMA: Si f un funzione derivbile k volte in x 0 (k 2), e supponimo che le prime k 1 derivte esistno in un intorno di x 0. Supponimo nche che f (k) (x 0 ) 0, mentre f (h) (x 0 ) = 0 per h = 1,..., k 1 (in ltre prole, l prim derivt che non si nnull è l k-esim). Allor se k è dispri, x 0 non è né di mssimo reltivo né di minimo reltivo; se k è pri e f (k) (x 0 ) > 0, llor x 0 è un punto di minimo reltivo; se k è pri e f (k) (x 0 ) < 0, llor x 0 è un punto di mssimo reltivo. DIM.: Si trtt di studire il segno dell funzione f(x) f(x 0 ) qundo x vri in un intorno sufficientemente piccolo di x 0 : se tle funzione è positiv simo in presenz di un punto di minimo reltivo, se è negtiv di un mssimo 45
46 (mentre se ess cmbi di segno in ogni intorno, comunque piccolo, di x 0, il punto non è né di mssimo né di minimo). Se prendimo x bbstnz vicino x 0 in modo che vlgno le ipotesi del teorem di Tylor, ottenimo f(x) f(x 0 ) = f (k) (x 0 ) (x x 0 ) k + R k (x) = [ f (k) (x 0 ) + R k(x) ] (x x0 ) k. k! k! (x x 0 ) k Siccome R k (x)/(x x 0 ) k 0, l quntità tr prentesi qudre tende f (k) (x 0 )/k! per x x 0. Di conseguenz, ess vrà lo stesso segno di f (k) (x 0 ) qundo x vri in un intorno sufficientemente piccolo di x 0. Poiché è invece chiro che il polinomio (x x 0 ) k è sempre positivo per k pri, mentre cmbi di segno per k dispri ( second che x sti destr o sinistr di x 0 ), l tesi segue immeditmente. Q.E.D. Osservzione: Il teorem ppen dimostrto ci dice che se f (x 0 ) = 0, f (x 0 ) > 0, llor f(x) > f(x 0 ) (con l disuguglinz strett) se x x 0 è sufficientemente vicino x 0 : in ltre prole, il punto in questione è un punto di minimo reltivo stretto, e dunque non può di sicuro essere di mssino reltivo. Questo ci permette di invertire in prte il risultto precedente: se f è derivbile due volte in un intorno di x 0 e x 0 è di mssimo reltivo, llor f (x 0 ) = 0 e f (x 0 ) 0 (L derivt prim si nnull per il principio di Fermt, mentre l second non può essere positiv perché se lo fosse il risultto precedente mi drebbe un punto di minimo reltivo stretto, il che srebbe ssurdo!). Anlogmente, in un punto di minimo reltivo deve essere f (x 0 ) = 0 e f (x 0 ) 0. In molti csi, il nostro teorem permette di stbilire se un punto in cui si nnull l derivt prim corrisponde d un mssimo o minimo reltivo: bst trovre l prim derivt divers d zero ( ptto che l funzione si derivbile bbstnz volte)! Può però cpitre che l funzione si derivbile infinite volte, m tutte le derivte si nnullino nel punto che ci interess: ESEMPIO: Si consideri l funzione { e 1/x 2 se x 0 f(x) = 0 se x = 0 Con un po di ftic si vede che f è derivbile infinite volte in 0, e che tutte le derivte si nnullno. D ltr prte, siccome l funzione f è non negtiv, è evidente che 0 è un punto di minimo reltivo. 46
47 Conviene tenere presente l funzione f di questo esempio: tornerà utile tr non molto! Dimostrimo or un versione leggermente più generle del teorem di Lgrnge, che ci tornerà utile per trovre subito dopo un espressione molto precis del resto nell formul di Tylor. TEOREMA (di Cuchy): Sino f, g : [, b] R due funzioni continue, derivbili in (, b). Supponimo poi che g (x) 0 per ogni x (, b). Allor esiste c (, b) tle che f (c) g (c) = f(b) f() g(b) g(). DIM.: Si noti che risult g(b) g() (ltrimenti otterremo un ssurdo col teorem di Rolle): di conseguenz, il denomintore del secondo membro nell tesi non si nnull, e il teorem h perfettmente senso. Per dimostrrlo, bst pplicre il teorem di Rolle ll funzione usiliri h(x) = (f(x) f())(g(b) g()) (g(x) g())(f(b) f()). Q.E.D. Il teorem di Cuchy permette di dimostrre l regol di l Hôpitl (m non lo fremo...), ed nche di dimostrre un vrinte prticolrmente utile del teorem di Tylor. Il prossimo teorem esprime ppunto in modo molto preciso il resto che si h nell formul di Tylor: questo permette di vlutre l errore che si commette, in un fissto punto x x 0, sostituendo f(x) il vlore del suo polinomio di Tylor di ordine n centrto in x 0. TEOREMA (Formul di Tylor con resto di Lgrnge): Si f un funzione derivbile (n + 1) volte in un intervllo centrto in x 0, e si x un punto pprtenente tle intervllo. Allor esiste un punto c, compreso tr x 0 e x, tle che f(x) = P n (x) + f (n+1) (c) (n + 1)! (x x 0) n+1, dove P n (x) = n k=0 f (k) (x 0 ) (x x 0 ) k k! è il polinomio di Tylor di grdo n centrto in x 0. DIM.: Considerimo l funzione g(x) = f(x) P n (x) (cioè il resto n-esimo). 47
48 Abbimo visto l volt scors che ess h l fondmentle proprietà di vere g(x 0 ) = g (x 0 ) =... = g (n) (x 0 ) = 0. Inoltre, g (n+1) (x) = f (n+1 (x) perché l derivt (n + 1)-esim del polinomio P n si nnull identicmente. L ide è or di pplicre (n + 1) volte il teorem di Cuchy, prtire dl rpporto g(x) (x x 0 ) = g(x) g(x 0 ) n+1 (x x 0 ) n+1 (x 0 x 0 ). n+1 Inftti, il teorem di Cuchy pplicto tle espressione ci grntisce l esistenz di un punto c 1 compreso tr x 0 e x, tle che l espressione stess è ugule g (c 1 ) (n + 1)(c 1 x 0 ) n. L ultim quntità può essere nche riscritt g (c 1 ) g (x 0 ) (n + 1)(c 1 x 0 ) n (n + 1)(x 0 x 0 ) n, e possimo ripplicre il teorem di Cuchy... Ripetendo questo pssggio per (n + 1) volte trovimo: g(x) (x x 0 ) =... = g(n) (c n ) g (n) (x 0 ) n+1 (n + 1)!(c n x 0 ) = g(n+1) (c) (n + 1)! = f (n+1) (c) (n + 1)!, dove c 1,..., c n, c sono opportuni punti compresi tr x 0 e x. Q.E.D. ESERCIZIO: Supponimo che un funzione f soddisfi le ipotesi del teorem ppen dimostrto, e che inoltre l derivt f (n+1) si continu in x 0. Mostrre che llor f(x) P n+1 (x) lim = 0. x x 0 (x x 0 ) n+1 (In buon sostnz, vremo ridimostrto il Teorem di Tylor con resto di Peno, nche se con ipotesi leggermente più forti perché chiedimo l continuità dell derivt (n + 1)-esim...) Mettimo subito frutto il teorem dimostrto, usndolo per pprossimre lcune importnti funzioni con polinomi. Comincimo col prendere f(x) = e x (e x 0 = 0): l formul di Tylor con resto di Lgrnge ci dice che esiste un punto c compreso tr 0 e x tle che e x = n k=0 x k k! + e c (n + 1)! xn+1. 48
49 Dimostrimo or che il resto, qulunque si x R, tende 0 per n + : e c lim n + (n + 1)! xn+1 = 0 x R. Si noti che, nche se c dipende in generle si d x che d n, l quntità e c è mggiort d e x, per cui ci bsterà fr vedere che x n+1 /(n + 1)! 0 per n +. Questo ftto, su volt, si dimostr immeditmente ricordndo l stim n! ( n) n, 3 che bbimo provto per induzione. In conclusione, bbimo ftto vedere che e x = lim n + L ultimo limite si chim serie di Tylor di e x, e si denot usulmente con k=0 x k k! : n k=0 x k k!. In generle, si h l seguente definizione di serie: DEFINIZIONE: Se { k } è un successione di numeri reli, col simbolo (che si legge serie degli k, si intende per definizione il limite lim n + n k, k=0 k k=0 ptto che tle limite esist. Se il limite è finito, si dice che l serie converge, se è infinito che diverge, se infine non esiste si dice che l serie è indetermint. 14 Lezione del 29/10/2015 (2 ore) Come ulteriore ppliczione del teorem di Tylor con resto di Lgrnge, dimostrimo che il numero di Nepero e è irrzionle. Supponimo inftti per ssurdo che si bbi e = p/q, con p e q numeri nturli. Applichimo il teorem di Tylor con resto di Lgrnge ll funzione esponenzile, con x 0 = 0 e x = 1: per ogni n N trovimo un punto c (0, 1) tle che e = p q = ! n! + ec 1 n + 1!. 49
50 Prendimo n > q, e moltiplichimo mbo i membri dell identità per n!. Ottenimo: ( p q n! = ! ) n! + ec n! n + 1. Il membro di sinistr dell uguglinz è evidentemente un intero, così come il primo pezzo del membro di destr (l quntità tr prentesi tonde moltiplict per n!). Invece, l ultimo termine è non nullo e si mggior con e/(n + 1) (perché c < 1), e quest ultim quntità è strettmente minore di 1 per n bbstnz grnde: questo è evidentemente ssurdo (un intero non può essere ugule d un intero più un quntità minore di 1). Con lo stesso tipo di conti, bbimo poi verificto che si h nche sin x = cos x = ( 1) k x 2k+1 (2k + 1)!, ( 1) k x2k (2k)! k=0 k=0 per ogni x R. Nell figur, tnto per rendere visivmente l cos, bbimo disegnto i primi polinomi di Tylor dell funzione seno: Ricordimo poi l formul per l somm di un progressione geometric: 1 + x + x 2 + x x n = 1 xn+1 1 x, x 1. L si può dimostrre fcilmente per induzione oppure moltiplicndo mbo i membri per 1 x... 50
51 Cerchimo poi di determinre un ltr serie di Tylor interessnte in modo un po bizzrro. Precismente, studimo l serie x k. Per definizione di serie, bbimo x k = k=0 lim n + n x k = k=0 1 x n+1 lim n + 1 x = k=0 1 se 1 < x < 1, 1 x + se x 1, se x 1. dove bbimo usto l formul per l somm di un progressione geometric. In conclusione, per 1 < x < 1 si h 1 1 x = x k, mentre l di fuori di questo intervllo l serie non converge d un limite finito (o non converge fftto). Or, non è fftto difficile verificre che quest è proprio l serie di Tylor (centrt in 0) dell funzione f(x) = 1 : inftti bbimo f (k) k! (x) =, 1 x (1 x) k+1 d cui f (k) (0) = k!... Oppure, bst osservre che 1 + x + x x n è il polinomio di Tylor di grdo n di 1/(1 x) perché soddisf il Teorem di Tylor con resto di Peno (conto immedito!). Questo è un esempio di funzione l cui serie di Tylor centrt in zero converge ll funzione stess su un intervllo centrto nell origine, m non sull inter rett rele. Sostituendo x con x nell serie precedente si ottiene k= x = ( 1) k x k 1 < x < 1. k=0 A questo punto, sorge spontne l seguente questione: se f è un funzione derivbile infinite volte in x 0, è sempre possibile trovre un intorno di x 0 tle che f (k) (x 0 ) f(x) = (x x 0 ) k? k! L rispost è negtiv: k=0 ESEMPIO: Si consideri l funzione { e 1/x 2 se x 0 f(x) = 0 se x = 0 51
52 si può fr vedere che ess è derivbile infinite volte in 0, e che tutte le derivte si nnullno (trlscimo l dimostrzione: il punto chive srebbe fr vedere, per esempio per induzione, che per x 0 si h per ogni n f (n) (x) = g n(x) x 3n e 1/x2, dove g n (x) è un polinomio... A questo punto, bst pssre l limite per x 0 per concludere che l derivt n-esim esiste ed è null nell origine). Ne segue che l serie di Tylor centrt in 0 per f è identicmente null, e quindi evidentemente ess coincide con f solo per x = 0. Le funzioni l cui serie di Tylor converge ll funzione stess in un intorno di x 0 si dicono nlitiche in x 0 : l funzione dell esempio non è nlitic, mentre l funzione esponenzile, il seno ed il coseno lo sono. Per concludere l prte sui polinomi e sulle serie di Tylor, voglimo dre un brevissim pnormic, senz dimostrzioni, dell teori delle serie di potenze: studieremo queste cose in mggior dettglio più vnti! Un serie di potenze è per definizione un serie del tipo k x k, k=0 dove { k } è un successione not di numeri reli. Questo è proprio il tipo di serie che si ottiene come serie di Tylor (centrt nell origine) di un funzione derivbile infinite volte! Nel cso peggiore, un serie di potenze converge solo per x = 0... In tutti gli ltri csi, converge in un intervllo centrto nell origine, del tipo ( r, r) (oppure [ r, r], ( r, r] o [ r, r)... r può nche essere infinito). Il numero r si chim rggio di convergenz dell serie di potenze, e ci sono metodi piuttosto semplici per clcolrlo. Supponimo dunque che l nostr serie di potenze bbi rggio di convergenz positivo, e chimimo f(x) l somm dell serie (per x nell intervllo in cui quest converge): f(x) = k x k. k=0 Allor si può dimostrre che f(x) è un funzione derivbile infinite volte, e che l serie di potenze non è ltro che l serie di Tylor dell su somm f(x) (...e dunque quel che vevmo visto nel cso dell funzione 1/(1 x) 52
53 non er csule). Inoltre, l derivt si clcol semplicemente derivndo l serie termine termine: f (x) = k k x k 1, k=1 con l serie delle derivte che converge nello stesso intervllo dell serie originle (trnne, eventulmente, gli estremi). Si noti che quest ultim ffermzione non è immeditmente ovvi: stimo derivndo un somm infinit di funzioni! Come conseguenz di questo teorem, si può mostrre che log(1 + x) = ( 1) n=1 n+1 xn n per x ( 1, 1). Inftti, si può fr vedere, con i semplici metodi che vedremo più vnti, che l serie dt converge nell intervllo indicto d un qulche funzione. D ltr prte, l serie delle derivte è l serie geometric di rgione ( x), scritt poco sopr: quest sppimo che converge 1/(1 + x). Siccome quest ultim è proprio l derivt di log(1 + x), deducimo che l serie originle converge proprio quest funzione (più un eventule costnte: m l costnte è evidentemente 0, come si verific clcolndo funzione e serie per x = 0...). Conclusi per or i nostri discorsetti sull formul di Tylor, cominceremo studire un definizione rigoros di re per certe figure pine delimitte d un contorno curvilineo. Questo ci porterà dre l definizione di integrle nel senso di Riemnn per un funzione f : [, b] R. Prtimo d un esempio concreto: supponimo di voler dre un senso ll re dell regione limitt del pino delimitt dll sse delle x, dl grfico dell funzione f(x) = e x, dll sse delle y e dll rett x = : si trtt di un specie di trpezio rettngolo, solo che il lto obliquo è curvo (è inftti il grfico dell funzione e x. Un ide potrebbe essere l seguente: dividimo l intervllo [0, ] in n intervllini uguli (che vrnno quindi estremi 0, /n, 2/n, 3/n,..., ). Per ciscuno di questi intervllini, costruimo un rettngolo che h l intervllino stesso come bse, e ltezz ugule l vlore dell funzione esponenzile nell estremo di sinistr: in ltre prole, sull intervllino [k/n, (k + 1)/n] costruimo un rettngolo di ltezz e k/n. 53
54 In questo modo ottenimo un figur scl che è tutt contenut nell figur curviline di cui voglimo clcolre l re: l re di quest scl inscritt si clcol subito, e vle n 1 k=0 n ek/n = n e 1 e /n 1. L ultim espressione, per n +, tende l numero (e 1), che rppresent quindi il limite delle nostre pprossimzioni per difetto. In mnier nlog, possimo costruire un scl circoscritt ll regione che ci interess, prendendo su ciscun intervllino [k/n, (k + 1)/n] un rettngolo di ltezz e (k+1)/n. In tl cso, l re dell sclint srà e /n n e 1 e /n 1, che tende ncor l limite e 1. Possimo dunque legittimmente ffermre che l re del trpezoide curvilineo sotto l funzione esponenzile tr 0 e, vle esttmente e 1: tle numero si chim integrle dell funzione esponenzile tr 0 e, e si indic 0 e x dx = e 1. Vedimo or come l ide soggicente questo conticino con l funzione esponenzile si estendibile d un grn numero di funzioni! DEFINIZIONE: Un funzione φ : [, b] R si dice scl se esiste un suddivisione di [, b] in un numero finito di intervllini di estremi = x 0 < 54
55 x 1 < x 2 <... < x N = b, in modo tle che φ ssum vlore costnte c i su ciscun intervllino (x i, x i+1 ) (per i = 0,..., N 1). L integrle dell suddett funzione scl si definisce come N 1 φ(x) dx = (x i+1 x i )c i. i=0 Come si vede, un funzione scl è crtterizzt dl ftto che il suo grfico è un istogrmm. Si noti che se φ è positiv, l integrle dell funzione scl è semplicemente l re dell unione finit di rettngoli delimitt dl grfico di φ, l sse delle x e le rette verticli x = e x = b. Se φ h nche trtti negtivi, l unic differenz è che gli sclini con ltezz negtiv si contno con re negtiv. Le funzioni scl ed il loro integrle godono delle seguenti proprietà, l cui dimostrzione è lscit ll riflessione del lettore: LEMMA: Se φ 1 e φ 2 sono funzioni scl su [, b], e c R, llor cφ 1 e φ 1 + φ 2 sono funzioni scl; l integrle è linere: (cφ 1 (x)) dx = c (φ 1 (x) + φ 2 (x)) dx = φ 1 (x) dx φ 1 (x) dx + φ 2 (x) dx; l integrle è monotono: se φ 1 (x) φ 2 (x) per ogni x [, b], llor φ 1 (x) dx φ 2 (x) dx. 15 Lezione del 30/10/2015 (2 ore) Simo or in grdo di definire l integrle superiore, l integrle inferiore ed eventulmente l integrle di un funzione limitt: DEFINIZIONE: Si f : [, b] R un funzione limitt. L integrle superiore di f si definisce come f(x) dx = inf{ φ(x) dx : φ scl, φ f in [, b]}. 55
56 Anlogmente, l integrle inferiore di f si definisce come f(x) dx = sup{ ψ(x) dx : ψ scl, ψ f in [, b]}. Se l integrle superiore e l integrle inferiore coincidono, diremo che l funzione f è integrbile secondo Riemnn in [, b], ed indicheremo il vlore comune dei due integrli con f(x) dx, integrle secondo Riemnn di f su [, b]. Vle un semplice crtterizzzione dell integrle di Riemnn, che permette tr l ltro di verificre l correttezz di qunto trovto sopr per l integrle dell funzione esponenzile: PROPOSIZIONE: Si f : [, b] R un funzione limitt. f è integrbile secondo Riemnn se e solo se per ogni ε > 0 si possono trovre due funzioni scl φ, ψ con ψ f φ in [, b] tli che φ(x) dx ψ(x) dx < ε. Prim di dre l semplice dimostrzione di questo risultto, vedimo un esempio di funzione non integrbile secondo Riemnn: ESEMPIO (Funzione di Dirichlet): Si consideri l funzione f : [0, 1] R definit d { 1 se x Q f(x) = 0 se x R \ Q Abbimo già incontrto quest funzione, ed bbimo osservto che ess è ovunque discontinu. Attulmente, invece, ci preme di osservre che un funzione scl mggiore o ugule f srà ovunque mggiore o ugule 1, e che un funzione scl minore o ugule f è ovunque minore o ugule 0. Questo segue dll densità dei rzionli e degli irrzionli: in ogni sclino di qulunque funzione scl, esistono si punti rzionli in cui l funzione vle 1, che punti irrzionli in cui ess vle 0. Se ne deduce che 1 0 f(x) dx = 1, 1 0 f(x) dx = 0, 56
57 e l funzione non è integrbile secondo Riemnn. DIM. dell crtterizzzione delle funzioni integrbili: Se f è integrbile, per definizione di integrle superiore e di integrle inferiore possimo trovre due funzioni scl φ e ψ, l prim mggiore o ugule e l second minore o ugule f, tli che φ(x) dx < ψ(x) dx > f(x) dx + ε/2, f(x) dx ε/2, d cui φ(x) dx ψ(x) dx < ε. Vicevers, prendimo ε > 0 e considerimo le due funzioni scl φ, ψ che ci vengono ssicurte dll ipotesi. Per definizione di integrle superiore e di integrle inferiore vremo φ(x) dx ψ(x) dx f(x) dx, f(x) dx, per cui 0 f(x) dx f(x) dx φ(x) dx ψ(x) dx < ε. Per l rbitrrietà di ε, ne deriv che l integrle superiore e l integrle inferiore sono uguli. Q.E.D. A questo punto, divent importnte fr vedere che tutte le funzioni bbstnz decenti sono integrbili. Per esempio, sono integrbili le funzioni monotone: TEOREMA: Se f : [, b] R è crescente (decrescente), llor è integrbile secondo Riemnn. DIM.: Per fissre le idee, trttimo il cso in cui f si crescente. Dividimo l intervllo [, b] in n prti uguli (lunghe (b )/n), di estremi = x 0 < x 1 < x 2 <... < x n = b. Definimo un funzione scl mggiornte φ n e un funzione scl minornte ψ n nel modo seguente: nell i-esimo intervllino [x i, x i+1 ), ponimo φ n ugule f(x i+1 ), e ψ n ugule f(x i ). 57
58 Si h b n φ n (x) dx n 1 i=0 ψ n (x) dx = n 1 i=0 [f(x i+1 ) f(x i )] = b n b n [f(x i+1) f(x i )] = [f(b) f()], e l ultim quntità può essere res piccol picere ptto di prendere n bbstnz grnde. Q.E.D. Verificre che sono integrbili nche le funzioni continue non srà ltrettnto fcile... TEOREMA (Integrbilità delle funzioni continue): Si f : [, b] R un funzione continu. Allor f è integrbile secondo Riemnn. L dimostrzione di questo teorem è molto meno semplice di quell che bbimo dto per le funzioni monotone: in effetti, bbimo bisogno di un concetto nuovo, quello di uniforme continuità. DEFINIZIONE: Un funzione f si dice uniformemente continu su un intervllo I se per ogni ε > 0 esiste δ > 0 tle che per ogni x, y I con x y < δ, si h f(x) f(y) < ε. In quest definizione chiedimo qulcos di più dell continuità in tutti i punti di I: stimo inftti pretendendo che δ dipend d ε, m non dl punto in cui ndimo vlutre l continuità. Lo stesso δ deve funzionre in tutti i punti dell intervllo I! In effetti, se è vero che ogni funzione uniformemente continu in I è nche continu in I, il vicevers può essere flso: per esempio, l funzione f(x) = x 2 è continu in tutti i punti dell rett rele, m non è uniformemente continu su R. Se però considerimo soltnto intervlli chiusi e limitti, i due concetti coincidono: TEOREMA (di Heine-Cntor): Un funzione continu f : [, b] R è nche uniformemente continu. DIM.: Rgionimo per ssurdo. Se f non fosse uniformemente continu, dovrebbe esistere ε 0 > 0 tle che per ogni δ > 0 esistno x, y [, b] con x y < δ e tli che f(x) f(y) ε 0. Ponimo δ = 1 (δ può essere scelto rbitrrimente...): per qunto ppen visto possimo trovre due punti x n, y n [, b] con x n y n < 1 e n n f(x n ) f(y n ) ε 0. 58
59 Or, l successione {x n } [, b] è limitt, per cui possimo estrrre un successione {x nk } tle che esiste lim x n k = x. Evidentemente, visto che si k + h x nk 1 n k < y nk < x nk + 1 n k vremo nche lim y n k = x. k + Per l continuità di f in x vremo llor e in prticolre lim f(x n k ) = lim f(y n k ) = f(x), k + k + lim f(x n k ) f(y nk ) = 0. k + Questo è ssurdo perché per costruzione l disuguglinz f(x nk ) f(y nk ) ε 0 deve vlere per ogni k. Q.E.D. DIM. dell integrbilità di f : [, b] R continu: Si ε > 0. Per il teorem di Heine-Cntor, f è uniformemente continu su [, b], e possimo trovre δ > 0 tle che f(x) f(y) < ε qundo x, y [, b] e x y < δ. In prticolre, se I è un qulunque sottointervllo chiuso di [, b] di lunghezz minore di δ, vremo mx{f(x) : x I} min{f(x) : x I} ε. Sceglimo or n bbstnz grnde, in modo che (b )/n < δ, e suddividimo [, b] in n prti uguli trmite i punti = x 0 < x 1 < x 2 <... < x n = b. Definimo un funzione scl mggiornte φ n ed un minornte ψ n nel modo seguente: sull i-esimo intervllino [x i, x i+1 ), l funzione φ n vle M i = mx{f(x) : x [x i, x i+1 ]}, mentre ψ n vle m i = min{f(x) : x [x i, x i+1 ]}. Per qunto visto sopr, srà M i m i ε. Abbimo φ n (x) dx ψ n (x) dx = n 1 i=0 b n (M n 1 i m i ) ε e quest quntità può essere res piccol picere. Q.E.D. i=0 b n = ε(b ), 16 Lezione del 4/11/2015 (2 ore) Avendo or un grnde bbondnz di funzioni integrbili, pssimo verificre che l integrle gode delle stesse proprietà di linerità dell integrle delle funzioni scl: 59
60 PROPOSIZIONE: Sino f, g : [, b] R due funzioni integrbili secondo Riemnn, c R. Allor le funzioni c f e f + g sono integrbili secondo Riemnn e si h c f(x) dx = c [f(x) + g(x)] dx = f(x) dx f(x) dx + g(x) dx. DIM.: Supponimo dpprim c > 0. L integrbilità dell funzione c f (e l prim delle due identità nell tesi) segue subito se si osserv che l insieme delle funzioni scl mggiori o uguli c f coincide con l insieme delle funzioni scl mggiori o uguli f moltiplicte per c. Poiché per le funzioni scl è lecito portre l costnte c fuori dl segno di integrle (si ved il lemm enuncito l volt scors), ne deducimo che c f(x) dx = c f(x) dx. Un identità del tutto nlog vle per l integrle inferiore, d cui l tesi. Se invece c < 0 (il cso c = 0 è ovvio!), l unico cmbimento d fre viene dl ftto che un funzione scl mggiornte per f moltiplict per c, drà un funzione scl minornte per c f. Ci rimne d dimostrre l integrbilità dell somm di due funzioni integrbili: osservimo che {Φ : Φ scl, Φ f + g} {φ 1 + φ 2 : φ 1, φ 2 scl, φ 1 f, φ 2 g}, d cui, ricordndo l definizione di integrle superiore: [f(x) + g(x)] dx f(x) dx + g(x) dx. (A lezione bbimo visto un esempio che mostr come, se toglimo l ipotesi che f e g sino integrbili, poss nche succedere che vlg l disuguglinz strett). Anlogmente, per gli integrli inferiori si ottiene [f(x) + g(x)] dx f(x) dx + g(x) dx. 60
61 Mettendo ssieme le due disuguglinze e ricordndo l integrbilità di f e g ottenimo f(x) dx + f(x) dx + g(x) dx g(x) dx, [f(x) + g(x)] dx [f(x) + g(x)] dx d cui l tesi. Q.E.D. Un proprietà dell integrle che ci srà piuttosto utile, è l dditività rispetto ll intervllo di integrzione: PROPOSIZIONE: Se f : [, b] R è integrbile, c (, b) si h f(x) dx = c f(x) dx + c f(x) dx. Lscimo per esercizio l fcile dimostrzione. È comodo definire l integrle nche su intervlli orientti ll rovesci : se f : [, b] R è integrbile secondo Riemnn, ponimo per definizione b f(x) dx = f(x) dx. Con quest posizione, l proprietà di dditività dell integrle rispetto ll intervllo vle in generle, nche se c non è compreso tr e b (in tl cso, f dovrà essere integrbile sul più grnde tr gli intervlli coinvolti...). Per il clcolo effettivo degli integrli, lo strumento fondmentle risult il seguente TEOREMA (teorem fondmentle del clcolo integrle): Si f : [, b] R un funzione continu, e definimo l funzione integrle F (x) = x f(t) dt. Allor F è derivbile, e F (x) = f(x) per ogni x [, b]. Evidentemente, se simo in grdo di clcolre l funzione integrle F (x) ssocit f, simo mggior rgione in grdo di clcolre l integrle f(x) dx (che srà ugule semplicemente F (b)). 61
62 Il teorem fondmentle del clcolo integrle dice che l funzione integrle F (x) è d ricercrsi tr le funzioni l cui derivt è dt d f(x) (che si chimno primitive di f). Si cpisce quindi che se simo in grdo di trovre le primitive di un dt funzione f(x), sremo nche in condizione di trovre l funzione integrle d ess ssocit: vedimo or come fre! L dimostrzione del teorem fondmentle, invece, l vedremo tr un po. DEFINIZIONE: Se f : [, b] R, un primitiv di f è un funzione G : [, b] R tle che G (x) = f(x) per ogni x [, b]. Il teorem fondmentle del clcolo integrle dice che l funzione integrle è un primitiv dell integrnd. Or, spesso è fcile indovinre un primitiv di un funzione f (e vedremo presto delle tecniche per trovre in modo più sistemtico le primitive di moltissime funzioni elementri). Se ci riuscimo, simo nche in grdo di clcolre l integrle di f: PROPOSIZIONE: Si f : [, b] R un funzione continu, G : [, b] R un qulunque primitiv di f. Allor f(x) dx = G(b) G(). DIM.: Per il Teorem fondmentle, nche l funzione integrle F (x) = x f(t) dt è un primitiv di f. Ne segue che l funzione F (x) G(x) h derivt null in [, b], e quindi è costnte: esiste C R tle che F (x) = G(x) + C per ogni x [, b]. Siccome F () = f(t) dt = 0, ponendo x = nell ultim identità trovimo C = G(), d cui F (x) = G(x) G(). In prticolre, per x = b si h l tesi. Q.E.D. Vedimo subito degli esempi di ppliczione dell formul fondmentle del clcolo integrle. ESEMPI: Se f(x) = e x, riconoscimo subito che un primitiv è dt dll funzione G(x) = e x, e quindi 0 e x dx = G() G(0) = e 1. Abbimo così rpidmente riottenuto un risultto che ci ervmo conquistti con un cert ftic prtire dll definizione di integrle! 62
63 Se f(x) = mx, si vede che un primitiv è G(x) = mx 2 /2, quindi mx dx = m(b 2 2 )/2. Possimo convincerci dell veridicità di quest formul se osservimo che geometricmente l integrle ppen clcolto rppresent l re di un trpezio rettngolo di ltezz (b ) e bsi m e mb. Se f(x) = sin x, un primitiv srà G(x) = cos x. Quindi π 0 sin x dx = cos(π) ( cos(0)) = 2, risultto che non srebbe stto fcile prevedere in ltro modo! Per dimostrre il teorem fondmentle ci servirà il seguente risultto: TEOREMA (Dell medi integrle): Si f : [, b] R un funzione continu. Esiste un punto c [, b] tle che f(x) dx = f(c) (b ). DIM.: Si M = mx{f(x) : x [, b]}, m = min{f(x) : x [, b]}. Per l monotoni dell integrle, vremo m(b ) f(x) dx M(b ), per cui l quntità 1 b f(x) dx b (che è dett medi integrle) è compres tr m e M. Per il teorem dei vlori intermedi, f ssume tutti i vlori compresi tr m e M, e quindi nche il vlore corrispondente ll medi integrle! Q.E.D. DIM. DEL TEOREMA FONDAMENTALE: Considerimo il rpporto incrementle dell funzione F nel punto x. Ricordndo l dditività dell integrle rispetto ll intervllo si h: F (x + h) F (x) h = 1 h [ x+h f(t) dt x ] f(t) dt = 1 h x+h x f(t) dt. Applicndo il Teorem dell medi ll ultimo integrle trovimo un punto c compreso tr x e x + h tle che F (x + h) F (x) h 63 = f(c).
64 Pssndo l limite per h 0, vremo c x e f(c) f(x) (perché f è continu), d cui F F (x + h) F (x) (x) = lim = f(x). h 0 h Q.E.D. Cerchimo or di studire un mnier un po più sistemtic per trovre le primitive di un dt funzione elementre. 11 Conviene stbilire un notzione per l insieme di tutte le primitive di un funzione f: DEFINIZIONE: Se f : [, b] R è un funzione continu, l insieme delle primitive G : [, b] R (cioè l insieme delle funzioni derivbili l cui derivt è ugule d f), si denot con il simbolo f(x) dx: f(x) dx = {G : [, b] R : G (x) = f(x) x [, b]}. L insieme delle primitive di f si chim tlvolt integrle indefinito di f. Grzie l teorem fondmentle del clcolo integrle e qunto osservto l volt scors, sppimo che l funzione integrle è un primitiv di f, e nche che due primitive diverse definite su uno stesso intervllo differiscono per un costnte, dunque: x f(x) dx = { f(t) dt + C : C R}. Con lieve buso di notzione, se G è un qulunque primitiv di f si scrive f(x) dx = G(x) + C, con C costnte rbitrri. Se prendimo un tbell delle derivte delle funzioni elementri, e l leggimo l contrrio, trovimo l seguente tbell di integrli indefiniti immediti : f(x) f(x) dx x 1 (con 1) +1 x+1 + C 1/x log x + C e x e x + C sin x cos x + C cos x sin x + C 1 tn x + C cos 2 x 1 cotn x + C sin 2 x 1 rctn x + C 1+x 2 1 rcsin x + C 1 x 2 11 L prte che segue srà corredt d numerosi esempi nelle esercitzioni. In prticolre, lezione non riusciremo vedere tutti gli integrli che seguono. 64
65 17 Lezione del 5/11/2015 (3 ore) Altre regole di integrzione vengono direttmente dlle regole di derivzione dell somm e del prodotto: (f(x) + g(x)) dx = f(x) dx + g(x) dx (dditività), cf(x) dx = c f(x) dx, f(x)g (x) dx = f(x)g(x) f (x)g(x) dx (formul di integrzione per prti). Dll formul per l derivt dell funzione compost viene un utile formul di integrzione per sostituzione: se F (x) è un primitiv di f(x), llor f(g(x))g (x) dx = F (g(x)) + C. Se cmbimo vribile ponendo y = g(x), l identità ppen scritt divent f(y) dy = f(g(x))g (x) dx. Quest formul può essere ricordt nel seguente modo, poco ortodosso m efficce: usndo l notzione di Leibniz per l derivt, bbimo dy dx = d(g(x)) dx = g (x), e moltplicndo mbo i membri per dx (cos che ovvimente non h lcun senso!) ottenimo l identità dy = d(g(x)) = g (x) dx, che sostituit nell integrle f(y) dy ci restituisce l formul volut... Evidentemente, bbimo commesso più di un crimine mtemtico: l derivt NON è un rpporto, e il simbolo dx nell integrle NON h un significto mtemtico ben definito (se non quello di indicre l vribile indipendente rispetto ll qule si integr). D ltr prte, l notzione per l derivt e l integrle si è rivelt suggestiv: gendo senz frci troppi scrupoli, bbimo comunque ottenuto un risultto corretto (inftti lo vevmo già giustificto prtendo dll formul di derivzione di funzioni composte!). ESEMPI: 1. Si vogli clcolre cos 2 x dx. Per un not identità trigonometric, bbimo cos 2 1+cos 2x x = d cui cos 2x cos 2 x dx = dx = x cos 2x d(2x) = x 2x +sin +C
66 2. Clcolimo poi 1 x 2 dx. Ponimo x = sin y, d cui (OK, non è ortodosso m bbimo verificto che funzion): dx = cos y dy e 1 x2 dx = 1 sin 2 y cos y dy = cos 2 y dy = y 2y +sin +C. 2 4 Or, y = rcsin x e cos y = 1 x 2, d cui sin 2y = 2x 1 x 2 e l integrle cercto vle 1 rcsin x + 1x 1 x C. L integrle definito di quest funzione tr 1 e 1 vle llor π/2... e questo h un semplice significto geometrico: qule? Quest è un ulteriore conferm del ftto che l integrle di Riemnn è l oggetto giusto per definire l re di oggetti curvilinei del pino dl contorno bbstnz regolre! 3. Clcolimo log x dx. Integrndo per prti si h: log x dx = 1 log x dx = (x) log x dx = x log x x 1 dx = x log x x + C. x 4. Clcolimo e x sin x dx. Integrndo due volte per prti si ottiene: e x sin x dx = e x sin x e x cos x dx = e x sin x e x cos x e x sin x dx. Portndo l ultimo integrle primo membro si ottiene subito e x sin x = ex sin x e x cos x + C Clcolimo x 1 x 2 dx. Ponimo y = 1 x 2, d cui: dy = 2x dx e l integrle divent 1 dy = y + C = 1 x C. y Oppure, con un uso disinvolto dell formul di integrzione per sostituzione: x d(1 x 2 dx = 1 ) 1 x 2 2 = 1 (1 x 2 ) 1/2 d(1 x 2 ) = 1 x 1 x C. 6. Si vogli clcolre sin x dx. Si ottiene subito il risultto ponendo x = y, e integrndo per prti. 7. Per clcolre l integrle 1 + x 2 dx, si operi l sostituzione 1 + x 2 = y x... 66
67 8. Integrzione di funzioni rzionli: f(x) = A(x)/B(x), con A(x), B(x) polinomi. Possimo supporre che il grdo di A si strettmente minore del grdo di B (ltrimenti fccimo l divisione e scrivimo A(x)/B(x) = Q(x) + R(x)/B(x), dove Q ed R sono rispettivmente il quoziente ed il resto dell divisione (e deg(r) < deg(b)). Siccome un polinomio è di integrzione immedit, ci simo ricondotti l cso di cui sopr). Vedimo per semplicità come si ffront il cso in cui il polinomio denomintore bbi grdo 2: l situzione è nettmente divers second che B(x) bbi due rdici reli distinte, un rdice doppi, nessun rdice rele. Comincimo dl primo cso: si vogli clcolre 2x+5 dx. Abbimo x 2 3x+2 x2 3x+2 = (x 2)(x 1): l tecnic d usre è quell dell decomposizione in somm di frzioni przili, cerchimo cioè di scrivere 2x + 5 x 2 3x + 2 = x 2 + b x 1. Si trov subito che dobbimo scegliere = 9, b = 7 per cui 2x + 5 x 2 3x + 2 dx = 9 x 2 dx + 7 x 1 dx = 9 log x 2 7 log x Cso delle rdici reli coincidenti: si vogli clcolre 3x+5 dx = x 2 2x+1 3x+5 dx. Scrivimo 3x + 5 = 3(x 1) + 8. L integrle divent (x 1) 2 immedito e vle: 3 log x 1 8/(x 1) + C. 10. Cso del polinomio di secondo grdo irriducibile: voglimo clcolre 2x+5 dx. In questo cso, l moss vincente è scrivere il denomintore come somm di qudrti: x 2 + 2x + 6 = (x + 1) Cmbimo x 2 +2x+6 poi vribile, ponendo y = x Tecniche simili sino pplicbili funzioni rzionli con denomintore di grdo qulunque. In generle, il denomintore può essere decomposto in fttori irriducibili di primo e secondo grdo. L tecnic dell decomposizione in frzioni przili funzion ncor: d esempio x 2 + 2x + 3 (x 1) 2 (x 2) = A (x 1) + B 2 x 1 + C x 2 x (x 1)(x 2 + 1) = A x 1 + Bx + C x
68 Questi due esempi mostrno cos succede qundo c è un fttore linere ripetuto, oppure qundo ci sono fttori di secondo grdo irriducibili. Altro esempio esotico x = Ax + B 4 x 2 + 2x Cx + D x 2 2x Per integrle funzioni rzionli in seno e coseno, l tecnic stndrd è utilizzre l sostituzione t = tn(x/2) e le note formule prmetriche sin x = 2t, cos x = 1 t2. 1+t 2 1+t 2 Come bbimo già osservto in precedenz, l nostr definizione di integrle di Riemnn è bbstnz soddisfcente, m nell prtic può essere utile definire l integrle di un funzione su intervlli che sino illimitti. Precismente, proponimo in modo bbstnz nturle l seguente definizione: DEFINIZIONE: Si f : [, + ) R un funzione continu. L integrle (improprio o generlizzto) di f sull semirett [, + ) si definisce come + ptto che il limite esist f(x) dx = M lim f(x) dx M + A titolo di esempio, bbimo verificto che x 2 dx = 1, mentre dx = + e infine + sin x dx non esiste. x 0 In modo nlogo possimo definire l integrle (generlizzto) di un funzione continu su un intervllo perto in uno dei suoi estremi: se per esempio f : (, b] R è continu, definimo f(x) dx = lim δ + δ f(x) dx, ptto che il limite esist. Anche in questo cso, l integrle può essere finito, infinito o non esistere. Per esempio, un semplice conticino mostr che l integrle 1 1 dx è finito 0 x α se e soltnto se α < 1, mentre + 1 dx è finito se e solo se α > 1 (e per 1 x α α = 1, entrmbi gli integrli sono infiniti). Invece, l integrle dell funzione f(x) = 1 sin(1/x) non esiste su (0, 1]. x 2 A questo proposito, vle l pen di notre che se f 0, l integrle improprio esiste sempre (si nel cso delle semirette che nel cso degli intervlli 68
69 semiperti). Inftti, in quel cso il limite nell definizione di integrle improprio è il limite di un funzione monoton, e sppimo bene che questo esiste sempre (finito o infinito). Dunque, nel cso delle funzioni non negtive, l integrle improprio può essere finito (e in quel cso diremo che converge), oppure può divergere Lezione del 6/11/2015 (2 ore) Un semplicissim osservzione (che deriv dll proprietà monotoni dell integrle) è l seguente PROPOSIZIONE (Principio del confronto per gli integrli impropri): Sino f, g : [, + ) [0, + ) due funzioni continue non negtive, e supponimo di spere che f(x) g(x) per ogni x [, + ). Allor, se l integrle di g converge, converge nche l integrle di f. Se invece l integrle di f diverge, diverge nche l integrle di g. Un nlogo principio di confronto vle nche per gli integrli impropri di funzioni continue su intervlli semiperti. Come conseguenz del principio del confronto bbimo l seguente Proposizione, che h nch ess un ovvi estensione gli integrli impropri di funzioni continue su intervlli semiperti: PROPOSIZIONE (Principio dell equivlenz sintotic): Sino f, g : [, + ) [0, + ) due funzioni continue non negtive tli che f(x) g(x) per x + (questo signific che f(x)/g(x) = 1, e si legge f è sintoticmente lim x + equivlente g ). Allor gli integrli impropri + f(x) dx, + g(x) dx hnno lo stesso comportmento: sono entrmbi convergenti, oppure entrmbi divergenti +. DIM.: Per definizione di limite ll infinito, visto che f g esisterà tle che 1 2 g(x) f(x) 3 g(x) x. 2 L tesi segue llor dl principio del confronto pplicto gli integrli impropri sull semirett [, + ). Q.E.D. 69
70 Meno ovvi è l seguente versione del principio del confronto, vlid per un funzione f di segno qulunque: PROPOSIZIONE (dell convergenz ssolut): Si f : [, + ) R un funzione continu. Allor, se l integrle improprio + f(x) dx converge, esiste finito nche l integrle improprio di f. Possimo pplicre questo risultto, d esempio, per verificre che + 1 sin x x 2 converge: inftti il modulo dell integrnd h integrle convergente perché è mggiorto d 1 x 2, che già sppimo vere integrle convergente. DIM.del teorem sull convergenz ssolut degli integrli impropri: Considerimo l funzione h(x) = f(x) + f(x). Segue subito che 0 h(x) 2 f(x), per cui l integrle improprio di h è convergente. Possimo scrivere llor: + lim M + f(x) dx = lim M + [ M h(x) dx dx M M f(x) dx = ] f(x) dx, e l ultimo limite esiste finito perché i due integrli impropri coinvolti sono convergenti. Q.E.D. Il teorem del confronto si rivel spesso utilissimo per dimostrre l convergenz (o l divergenz, nel cso di funzioni non negtive) dell integrle improprio di un funzione di cui non si sppi clcolre esplicitmente un primitiv. Purtroppo, però, l convergenz ssolut è un condizione sufficiente, m non necessri, per l convergenz di un integrle improprio: ESEMPIO: L integrle improprio Inftti, integrndo per prti si h M 1 sin x [ x dx = cos x x ] M 1 M 1 sin x dx esiste finito, mentre + sin x dx = x 1 x cos x x 2 70 dx cos cos x x 2 dx.
71 L integrle improprio + cos x dx converge per il principio del confronto, 1 x 2 cos x perché 1 e bbimo visto che l integrle dell ultim funzione è finito. x 2 x 2 Dunque, + sin x dx esiste finito. 1 x Fccimo vedere che + sin x dx = +. 1 x Inftti, per ogni n N (n 2) vremo nπ π sin x x n 1 dx k=1 (k+1)π kπ sin x (k + 1)π dx = 2 n 1 1 π (k + 1). k=1 Pssndo l limite per n + bbimo quindi trovto l seguente disuguglinz: + π sin x x 2 π + k=1 1 k + 1 = 2 π ( ) L serie nell ultim disuguglinz (cioè l serie dei reciproci dei numeri nturli) si chim serie rmonic: mostreremo domni che ess diverge +, concludendo così l dimostrzione dell divergenz del nostro integrle. Per dimostrre che l serie rmonic diverge, useremo ncor un volt il principio del confronto per gli integrli impropri! Inftti, possimo interpretre l serie rmonic come l integrle tr 2 e + dell funzione scl (con infiniti sclini) φ(x) = [x] 12 Si noti che l definizione di integrle improprio si può estendere senz cmbire null funzioni nche non necessrimente continue, che sino però integrbili secondo Riemnn su tutti gli intervlli limitti. Quindi, è perfettmente lecito fre l integrle improprio di φ. 71
72 Visto che φ(x) 1, e visto che + 1 dx = +, il principio del confronto ci x 2 x dice che l integrle di φ (che è poi l serie rmonic) diverge. L discussione ftt per mostrre l divergenz dell integrle improprio di sin x, ci suggerisce un utilissimo criterio di convergenz per le serie. Ricordimo questo proposito, l fondmentle definizione di serie che bbimo x già visto prlndo di polinomi di Tylor: se { n } n N è un successione di numeri reli, ponimo per definizione + k=1 k = lim n + n k, ptto che il limite secondo membro esist. L successione k=1 s n = n k=1 k si chim successione delle somme przili dell serie, per cui l somm dell serie è semplicemente il limite delle somme przili! PROPOSIZIONE (Criterio integrle di convergenz per le serie): Si f : [1, + ) [0, + ) un funzione non negtiv e decrescente. Allor l integrle improprio + h lo stesso comportmento dell serie 1 f(x) dx f(k). k=1 Con questo voglimo dire che se l integrle converge, converge nche l serie, mentre se l integrle diverge +, diverge nche l serie. Vedremo l dimostrzione l prossim volt. 19 Lezione del 11/11/2015 (2 ore) DIM.: Bst osservre che f([x + 1]) f(x) f([x]), e interpretre l serie come l integrle dell funzione costnte trtti f([x]): f(k) = k= f([x]) dx.
73 Il risultto segue llor immeditmente dl principio del confronto tr gli integrli impropri. Q.E.D. ESEMPIO: L serie rmonic generlizzt + k=1 converge se e solo se α > 1: bst usre il criterio integrle con l funzione f(x) = 1/x α. D qunto bbimo ppen visto, non ci stupirà scoprire che esistono delle nlogie tr integrli impropri e serie! Comincimo inftti con un elenco di lcune proprietà delle serie che ricordno qunto bbimo già visto per gli integrli: Se n k k=1 0, l serie + 1 k α esiste sempre, finit o infinit: inftti, le somme przili costituiscono un successione monoton. In sostnz un serie termini positivi converge un somm finit, oppure diverge +. Vle il seguente criterio del confronto per le serie termini positivi: se 0 n b n, llor l convergenz di + b k implic l convergenz di + k=1 k, mentre l divergenz di + k implic l divergenz di + b k. Vle nche un criterio dell equivlenz sintotic: se n, b n > 0 e k=1 k=1 n lim = 1, n + b n k=1 k=1 llor le serie + k e + b k hnno lo stesso comportmento. Bst inftti osservre che per n bbstnz grnde 1 2 b n n 3 2 b n, e pplicre il criterio del confronto. 13 Un ltr proprietà interessnte (che per gli integrli impropri non vle) è l seguente: 13 Questo criterio è flso per le serie termini di segno qulunque. Inftti, le serie di termine generle n = ( 1) n 1 n + 1 n e b n = ( 1) n 1 n sono sintoticmente equivlenti. Grzie un criterio di convergenz che vedremo l prossim volt (criterio di Leibniz), si verific che l prim serie diverge +, mentre l second converge. 73 k=1
74 PROPOSIZIONE: Se l serie ( termini di segno qulunque) + k converge, llor. lim k = 0 k + DIM.: Se s n denot l somm przile n-esim dell serie e s l su somm (cioè s n s), si h n = s n s n 1, e pssndo l limite per n + si h l tesi. Q.E.D. Si noti che il vicevers non è vero: il termine generle dell serie può essere infinitesimo senz che l serie converg. Come esempio, bbimo visto il cso dell serie rmonic: + 1 = +. k k=1 Quest condizione necessri non vle per gli integrli impropri: ESEMPIO/ESERCIZIO: Si f : [, + ) R un funzione continu. Mostrre che l convergenz dell integrle improprio + f(x) dx non implic necessrimente che lim f(x) = 0. In questo, gli integrli impropri si x + comportno in modo diverso dlle serie! Non bbimo visto l soluzione in clsse, comunque eccol! Ci si convince fcilmente che se il limite f(x) esiste, llor deve essere proprio 0: lim x + usndo l definizione di integrle improprio, si vede senz difficoltà che se il limite è un numero diverso d zero, llor l integrle diverge ± (stimo inftti clcolndo l re di un regione che contiene un strisci di ltezz fiss e lunghezz infinit!). Voglimo dunque esibire un funzione f che bbi integrle improprio convergente e per l qule non esist il limite +. Se non fosse richiest l continuità di f, potremmo prendere l funzione seguente: f(x) = { 1 se x N 0 ltrimenti Quest funzione h integrle improprio nullo (l integrle non si ccorge che ess vle 1 su un insieme discreto di punti: l re del sottogrfico è proprio 0!), m non mmette limite ll infinito. Volendo f continu, simo costretti complicre un po questo esempio. Un possibilità è l funzione dell figur: k=0 74
75 Si trtt di un funzione linere trtti che vle 0 qusi sempre, trnne nelle vicinnze dei numeri nturli: nel punto x = n {1, 2, 3,...} ess cominci slire linermente fino 1, dove rriv per x = n + 1, per poi 2n 2 ridiscendere linermente 0 dove rriv per x = n+1/n 2. In sintesi, destr del punto x = n, il grfico di f produce un tringolo isoscele di bse 1/n 2 e ltezz 1. Quest funzione non mmette limite per x +. M qunto vle il suo integrle improprio? Esso è l somm delle ree dei tringoli isosceli, cioè n=1 : quest è un serie rmonic generlizzt convergente (perché n 2 l esponente è mggiore di 1)! Sfruttndo ncor l interpretzione delle serie come integrli impropri (un serie è l integrle improprio di un funzione scl con sclini di lrghezz unitri... ), bbimo il seguente risultto: PROPOSIZIONE: Se un serie è ssolutmente convergente, cioè se converge + k, llor nche l serie + k esiste finit 14. k=1 k=1 Un ltro utilissimo criterio, prticolrmente semplice d pplicre, è il seguente: 14 Anche in questo cso, non vle il vicevers: vedremo che un serie può convergere nche se non converge ssolutmente. 75
76 PROPOSIZIONE (Criteri dell rdice e del rpporto): Si n generle di un serie, + k. k=1 Supponimo che esist il limite il termine lim n + n n = l 1. Allor, se l 1 > 1 l serie non converge, se l 1 < 1 converge ssolutmente. Si n 0, e supponimo che esist il limite lim n+1 n + n = l 2. Allor, se l 2 > 1 l serie non converge, se l 2 < 1 converge ssolutmente 15. OSSERVAZIONE: I criteri dell rdice e del rpporto flliscono se i limiti l 1, l 2 sono uguli d 1. Per esempio, si consideri l serie rmonic generlizzt di termine generle n = 1/n α. In questo cso, i limiti di rdice e rpporto sono entrmbi uguli 1, m bbimo visto che l serie converge se α > 1, mentre diverge per α 1. Per dimostrre i criteri del rpporto e dell rdice occorre ricordre il seguente ESEMPIO FONDAMENTALE (Serie geometric): Come già bbimo visto, possimo usre l formul per l somm dell progressione geometric per studire l serie geometric + k, k=0 15 Si può fr vedere che se esiste il limite del rpporto, llor esiste nche il limite dell rdice, e questi due limiti sono uguli: per questo, il criterio del rpporto è in reltà un conseguenz del criterio dell rdice. Mostrimo dunque che se n+1 / n l, llor si h nche n n l. Usndo l stim ottenut nell dimostrzione del criterio del rpporto (vedi sotto), scoprimo che per qulunque ε > 0 esiste ν > 0 tle che ν (l ε) n ν n ν (l + ε) n ν n > ν d cui n ν (l ε) 1 ν/n n n n ν (l + ε) 1 ν/n. Il membro di sinistr e quello di destr tendono l ε e l + ε rispettivmente, quindi per n bbstnz grnde si vrà l 2ε n n l + 2ε. Dll rbitrrieà di ε segue che n n l. 76
77 in cui è un numero rele chimto rgione dell serie. Se s n = n k denot l somm przile n-esim dell serie, bbimo visto k=0 che s n = 1 n+1. Se studimo il limite di quest espressione per n +, 1 vedimo che l serie converge 1/(1 ) per < 1, diverge + per 1, non esiste per 1. DIM. dei criteri del rpporto e dell rdice: Comincimo dl criterio dell rdice. Se l 1 > 1, sceglimo ε > 0 in modo che l 1 ε > 1. Per l definizione di limite, sppimo che per n bbstnz grnde vremo n n > l 1 ε, ossi n > (l 1 ε) n. Pssndo l limite per n + ottenimo n +, e l serie non può convergere perché il suo termine generle non tende zero. Se l 1 < 1, sceglimo ε > 0 in modo che l 1 + ε < 1. Per n bbstnz grnde vremo n n < l 1 + ε, d cui n < (l 1 + ε) n. Poiché l serie geometric di rgione l 1 +ε converge, converge ssolutmente nche l nostr serie (criterio del confronto), e quindi ess converge. L prossim volt concluderemo dimostrndo nche il criterio del rpporto Dimostrimo il criterio del rpporto: supponimo l 2 > 1, e sceglimo ε tnto piccolo che l 2 ε > 1. Per definizione di limite, trovimo ν N tle che n+1 n > l2 ε per n ν. Allor, se n > ν: n = ν ν+1 ν... n 1 n 2 n n 1 ν (l 2 ε) n ν. Pssndo l limite vedimo che n +, e l serie non converge di sicuro. Se poi l 2 < 1, sceglimo ε > 0 in modo che l 2 + ε < 1. Trovimo ν N tle che n+1 n < l2 + ε per n ν. Rifcendo il conto di prim bbimo n = ν ν+1 n... ν ν (l 2 + ε) n ν, n 1 e l serie dei moduli risult mggiort d un serie geometric convergente. Q.E.D. Che ltro dire delle serie termini di segno qulunque? Se esse non convergono ssolutmente, bbimo ben pochi strumenti nostr disposizione. Uno di questi è il seguente: PROPOSIZIONE (Criterio di Leibniz): Si { n } un successione di numeri non negtivi, e si consideri l serie termini di segno lterno + n=0 ( 1) n n. 77
78 Se n è decrescente e tende zero, llor l serie converge. Vedremo l dimostrzione domni. 20 Lezione del 12/11/2015 (3 ore) DIM.: Al solito, si s n = n ( 1) k k l successione delle somme przili. Si h k=0 s 2n+2 = s 2n 2n+1 + 2n+2 s 2n, cioè l successione delle somme przili di indice pri è decrescente. Anlogmente, s 2n+3 s 2n+1 : l successione delle somme przili di indice dispri è crescente. Inoltre, evidentemente s 1 0 e s 2n s 2n 1 : ne segue che l successione delle somme przili pri è non negtiv, e tenderà un limite finito l (ugule l suo inf). Anche le somme przili dispri tendernno llo stesso limite: lim s 2k+1 = lim (s 2k 2k+1 ) = l 0. k + k + Ne segue che l è proprio l somm dell serie. Q.E.D. Il criterio di Leibniz ci dice d esempio che l versione segni lterni dell serie rmonic, + ( 1) n+1, è convergente (in reltà, si può fr vedere n n=1 che converge log 2). Per visulizzre il comportmento di quest serie (e l ide dell dimostrzione del criterio di Leibniz), potete dre un occhit d un nimzione 16 costruit con GeoGebr che ho messo in rete. Si ricorderà che bbimo incontrto per l prim volt le serie qundo ci simo ccorti che lcune funzioni infinitmente derivbili possono essere sviluppte in serie di Tylor: l serie che si ottiene in quel cso è del tipo + n=0 n x n, e si chim serie di potenze. Abbimo visto che se f(x) è un funzione nlitic e sceglimo n = f (n) (0) n!, llor l serie di potenze converge in un intorno di 0, e converge
79 proprio f(x)... dire il vero, quest er proprio l definizione di funzione nlitic! È però interessnte nche studire il problem inverso: se ci viene dt un serie di potenze + n x n, cos possimo dire del suo insieme di n=0 convergenz? E se scoprimo che ess converge per gli x in un opportuno intorno di 0, srà poi vero che l su somm f(x) è un funzione infinitmente derivbile, l cui serie di Tylor coincide con l serie di prtenz? Comincimo con un osservzione semplice m interessnte: LEMMA: Se l serie di potenze + n x n converge per x = x 0, llor converge n=0 ssolutmente per tutti gli x con x < x 0. DIM.: Siccome l serie converge per x = x 0, bbimo necessrimente lim nx n 0 = 0. In prticolre, per n bbstnz grnde vremo n x n 0 1. n + Se poi x < x 0 si h (sempre per n bbstnz grnde) n n n x n = n x n 0 x x, e l serie + n x n converge perché è mggiort d un serie geometric n=0 convergente. Q.E.D. Il lemm ci suggerisce di dre l seguente, fondmentle DEFINIZIONE: Il rggio di convergenz dell serie di potenze + n x n è l estremo superiore dei vlori di x per cui l serie converge. Si r il rggio di convergenz dell nostr serie di potenze. lemm visto sopr, possimo concludere che + n=0 Se r = +, l serie converge ssolutmente per ogni x R. x 0 x 0 n=0 Grzie l Se r > 0, l serie converge ssolutmente nell intervllo perto ( r, r),mentre non converge per x > r. Se r = 0, l serie converge soltnto per x = 0. Tutti e tre questi comportmenti sono possibili: l serie esponenzile x n converge per ogni x R, l serie geometric + x n h rggio di n! 79 n=0
80 convergenz 1, mentre l serie + n n x n h rggio di convergenz 0 come si n=0 può fcilmente verificre con il criterio dell rdice. Si noti nche che il nostro lemm non dice null sul comportmento dell serie per x = ±r, cioè gli estremi dell intervllo di convergenz: in effetti, in quei due punti può succedere qulunque cos (l serie può convergere in tutti e due i punti, in uno solo di essi, oppure in nessuno dei due). L convergenz di un serie di potenze gli estremi dell intervllo di convergenz è spesso l cos più difficile d vlutre, e lo studio deve essere condotto cso per cso. Vedimo or come è possibile trovre il rggio convergenz di un serie di potenze: in qusi tutti i csi è possibile dre un rispost grzie l criterio dell rdice o del rpporto. Supponimo inftti di spere che lim n + n n = l (oppure che lim n+1 n + n = l). Usndo il criterio dell rdice (del rpporto) vedimo subito che l serie converge per x < 1, mentre non converge per l x > 1 (nei csi l = 0 e l = +, l insieme di convergenz è rispettivmente l R e {0}...). L unic situzione in cui questo metodo non funzion, è quell in cui non esiste il limite dell rdice n-esim di n (nche in questo cso, tuttvi, è possibile ggirre il problem: se volete spere come fre, leggete l not 17 qui sotto...). Nei csi in cui questo metodo funzion, l insieme di convergenz è un intervllo simmetrico rispetto ll origine (trmite eventulmente gli estremi: l serie può convergere in uno, entrmbi o nessuno degli estremi dell intervllo!). Vedremo domni che quest proprietà di simmetri è sempre ver, nche qundo non esiste il limite del rpporto o dell rdice, e che il rggio di questo intervllo si chim rggio di convergenz dell serie di potenze. 17 L semplice osservzione ppen ftt può essere trsformt in un ricett universle per trovre il rggio di convergenz: se è vero che non sempre esiste il limite dell successione n n, è però sempre possibile frne il mssimo limite, un oggetto di cui vi infliggerò breve l definizione. Or, il criterio dell rdice vle pri pri (e nche l dimostrzione non cmbi grnché) se si sostituisce il limite con il mssimo limite: possimo quindi ffermre che il rggio di convergenz dell nostr serie di potenze è dto dl reciproco di n l = lim sup n. Dimostrzione complet tr poche lezioni! n + 80
81 Supponimo di vere un serie di potenze con rggio di convergenz r > 0. Possimo llor definire un funzione f : ( r, r) R nel modo seguente: f(x) = + n=0 n x n. Ci chiedimo quli sino le proprietà dell funzione f(x): vedremo l prossim volt che f è derivbile infinite volte, e che l serie di potenze coincide con l serie di Tylor di f. Tornimo llo studio dell funzione somm f(x) di un serie di potenze con rggio di convergenz r > 0. Vle il seguente: TEOREMA (Regolrità delle serie di potenze): Si f(x) = + n x n l somm di un serie di potenze con rggio di convergenz r > 0. Allor f(x) è continu e derivbile in ( r, r). Inoltre l serie delle derivte n=1 n nx n 1 h ncor rggio di convergenz r, e nell intervllo ( r, r) converge proprio ll derivt f di f. Il teorem dice dunque che un serie di potenze si può derivre termine termine. Inoltre, iterndo il procedimento si ottiene che f(x) è derivbile infinite volte, e che l serie di prtenz non è ltro che l serie di Tylor di f centrt in 0. L dimostrzione del teorem sull regolrità dell somm delle serie di potenze è piuttosto complict...m siccome siete degli studenti di mtemtic ho deciso di non risprmirvel! L vedremo l prossim volt. Questo risultto è meno ovvio di qunto poss sembrre: se bbimo un serie di funzioni continue, è in generle flso che l somm dell serie si continu, come mostr l esempio seguente. ESEMPIO: Ponimo g n (x) = rctn(nx), f n (x) = g n (x) g n 1 (x). Allor l somm przile N-esim dell serie di funzioni continue f n (x) n=1 è g N (x), che tende chirmente d un funzione discontinu per N +. Per concludere l lezione, bbimo verificto l prte più semplice dell enuncito, ossi bbimo eseguito l semplice verific che l serie derivt n=1 n n x n 1 h ncor rggio di convergenz r. Inftti, il reciproco 81 n=0
82 del rggio di convergenz dell serie derivt è dto d lim sup n 1 n n = n + n lim sup n, e l ultim espressione sppimo che vle 1/r. n + DIM. dell regolrità dell somm di un serie di potenze. Per poter dimostrre il teorem di regolrità, bbimo bisogno di lcuni lemmi. Il primo di essi rigurd l velocità con cui il resto N-esimo di un serie di potenze v zero. Se prendimo un serie numeric convergente n, il resto N-esimo è per definizione R N = n : è immedito verificre che lim R N = 0. n=n+1 N + Se poi considerimo il cso dell nostr serie di potenze n x n di rggio di convergenz r > 0, il resto N-esimo R N (x) = n=1 n=n+1 n=0 n x n tenderà zero per ogni x ( r, r). Il primo lemm dice che se 0 < ρ < r e x [ ρ, ρ], llor possimo stimre l velocità con cui R N (x) tende zero in mnier indipendente d x: in mtemtichese, si dice che l serie di potenze converge uniformemente in [ ρ, ρ]. LEMMA 1: Si n=0 n x n r > 0, ρ (0, r). Allor, per ogni x [ ρ, ρ] si h un serie di potenze con rggio di convergenz R N (x) n=n+1 n ρ n. In ltre prole, il resto N-esimo dell serie è mggiorto, per ogni x [ ρ, ρ], dl resto N-esimo dell serie numeric convergente (l serie di potenze converge ssolutmente per x = ρ...) n=0 Dim.: Si x [ ρ, ρ], M N. ottenimo: M M n x n n=n+1 n=n+1 n ρ n. Usndo l disuguglinz tringolre n x n M n=n+1 e pssndo l limite per M + si h l tesi. Q.E.D. n ρ n, Il prossimo lemm constituisce l prim prte del teorem di regolrità che voglimo dimostrre: l somm di un serie di potenze è un funzione continu. 82
83 LEMMA 2: Si f(x) = n x n l somm di un serie di potenze con rggio n=0 di convergenz r > 0. Allor l funzione f è continu in ( r, r). Dim.: Si x 0 ( r, r): mostrimo che f è continu in x 0. A questo scopo, sceglimo ρ > 0 con x 0 < ρ < r. Se x ρ e N è un qulunque numero nturle possimo scrivere: f(x) f(x 0 ) = n x n n x n 0 n=0 n=0 N n (x n x n 0) + n=0 n=n+1 n x n n=n+1 N n (x n x n 0) + R N (x) + R N (x 0 ) n=0 N n (x n x n 0) + 2 n=0 n=n+1 n ρ n, n x n 0 dove nell ultimo pssggio bbimo ftto uso del Lemm 1. Fissimo ε > 0 e osservimo l ultim rig dell nostr stim: il secondo ddendo può essere reso minore di ε/2 ptto di prendere N bbstnz grnde (si trtt del resto N-esimo di un serie numeric convergente). A questo punto, prendendo x bbstnz vicino x 0 il primo ddendo può essere reso minore di ε/2 (perché il polinomio N n x n è un funzione continu): in conclusione, se x n=0 è bbstnz vicino x 0 si h f(x) f(x 0 ) < ε, Q.E.D. Il terzo lemm dice che possimo integrre termine termine un serie di potenze sugli intervlli chiusi contenuti in ( r, r). LEMMA 3: Si f(x) = n x n l somm di un serie di potenze con rggio n=0 di convergenz r > 0, [x 1, x 2 ] ( r, r). Denotimo con S N (x) = N n x n le somme przili dell serie. Allor x2 x 1 f(x) dx = lim N + x2 x 1 S N (x) dx. In mnier più espressiv, questo è equivlente scrivere x2 x2 n x n dx = n x n dx, x 1 n=0 83 n=0 x 1 n=0
84 cioè si poò scmbire il segno di serie con quello di integrle 18 ). Dim: L funzione f(x) è integrbile perché bbimo dimostrto nel Lemm 2 che è continu. Si ρ = mx{ x 1, x 2 }: grzie l Lemm 1 bbimo x2 x2 x 1 x 1 (f(x) S N (x)) dx = R N (x) dx x2 x 1 n=n+1 x2 x 1 R N (x) dx n ρ n = (x 2 x 1 ) n=n+1 n ρ n, e l ultim espressione tende zero per N +. Q.E.D. Abbimo così concluso il lvoro sporco : vedimo come l regolrità dell somm di un serie di potenze segu fcilmente dgli ultimi due lemmi! Abbimo visto inftti che l funzione somm f(x) è continu, rimngono d dimostrre solo le ffermzioni sull derivbilità. Innnzitutto, bbimo già visto che l serie derivt n n x n 1 h ncor rggio di convergenz r. Grzie l Lemm 2, sppimo dunque che le somme przili S N (x) dell serie derivt convergono d un cert funzione continu g(x) (l somm dell serie derivt). Or, sino S N (x) le somme przili dell serie di potenze non derivt: grzie l teorem fondmentle del clcolo integrle, se fissimo si h S N (x) = S N (0) + x 0 S N (t) dt. Pssimo l limite per N + : il primo mebro tende f(x), mentre il secondo membro tende f(0) + x g(t) dt grzie l Lemm 0 3. In conclusione, bbimo mostrto che f(x) = f(0) + x 0 g(t) dt, per cui f è derivbile e l su derivt è proprio g (teorem fondmentle del clcolo integrle). Q.E.D. 18 Inftti questo è chirmente possibile per le somme przili (dditività dell integrle): il lemm dice che è lecito pssre l limite per N + ed estendere l ffermzione ll serie di potenze. n=1 84
85 ESEMPIO: Come ppliczione del teorem sull somm delle serie di potenze, verifichimo che log(1 + x) = rctn(x) = + n=1 + n=0 ( 1) n+1 xn n ( 1) n x2n+1 2n < x < 1; 1 < x < 1. Inftti, non è difficile vedere che entrmbe le serie hnno rggio di convergenz 1. Se chimimo f(x) l somm dell prim e g(x) l somm dell second, derivndo termine termine si ottiene f (x) = g (x) = + n=1 + n=0 ( 1) n+1 x n 1 = ( 1) n x 2n = + k=0 + n=0 ( x) k = x, ( x 2 ) n = x 2, dove bbimo usto l formul per l somm dell serie geometric. Integrndo e tenendo conto del ftto che f(0) = g(0) = 0, si ottiene f(x) = log(1+x) e g(x) = rctn x. 21 Lezione del 13/11/2015 (2 ore) ESEMPIO: Considerimo l serie binomile + n=0 ( α n) x n, in cui α R e i coefficienti binomili sono definiti d ( α ) ( α α (α 1) (α 2)... (α n + 1) = 1, = 0 n) n! (n 1). Usndo il criterio del rpporto, si verific subito che il quest serie h rggio di convergenz A meno che non si bbi α N: in tl cso solo i primi α coefficienti binomili sono diversi d 0, e l serie si riduce un polinomio. 85
86 Mostrimo or che l somm f(x) dell serie è ugule (1 + x) α per ogni x ( 1, 1). Derivndo termine termine l serie si ottiene inftti f (x) = + n=0 ( α n) nx n 1 = + n=0 ( α n) (α n)x n (l second espressione si ottiene osservndo che ( ) ( α n n = α n 1) (α n + 1) e cmbindo l indice, (n 1) n). Utilizzndo queste due scritture equivlenti di f (x) si ottiene subito (1 + x)f (x) = αf(x), ovvero f (x) f(x) = α 1 + x. Integrndo, si h llor log f(x) = log(1 + x) α + C, d cui (osservndo che f(0) = 1) f(x) = (1 + x) α. C è un unico punto dell dimostrzione del teorem di regolrità delle serie di potenze che è rimsto un po in sospeso: per fr vedere che l serie derivt h lo stesso rggio di convergenz dell serie originle, bbimo usto un formulett per clcolre il rggio di convergenz trmite il mssimo limite dell rdice... È giunto il momento di vedere cos sono il mssimo ed il minimo limite di un successione! Si dt dunque un successione rele { n }: in generle, non è fftto detto che ess mmett limite per n +. In compenso, è sempre possibile clcolre due mezzi limiti noti come mssimo e minimo limite di n : DEFINIZIONE (Mssimo e minimo limite): Dt un successione rele { n } n N, definimo il suo mssimo e minimo limite come segue lim sup n := lim sup m, n + n + m n lim inf n := lim inf m. n + n + m n Si noti che i due limiti nell definizione esistono sempre: le successioni b n = inf m e c n = sup m sono inftti rispettivmente crescente e decrescente m n m n (stimo fcendo l inf ed il sup di insieme sempre più piccoli... ). Possimo llor scrivere l seguente definizione, del tutto equivlente quell dt sopr: lim sup n := inf sup m, n + n N m n lim inf n := sup inf m. n + m n n N 86
87 Il mssimo limite si indic nche con le scritture mx lim n, oppure n + lim n. Anlogmente, il minimo limite si indic nche con le scritture n + min lim n, oppure lim n. n + n + Vedimo or un crtterizzzione del mssimo e minimo limite, che iut cpire meglio questi strni oggetti. Per rendere ncor più espressiv l nostr crtterizzzione, è utile spiegre cos vuol dire che un cert proposizione P(n) (indicizzt d un numero nturle n N) è ver definitivmente oppure frequentemente. Si dice che P(n) è ver definitivmente qundo è ver per tutti gli n bbstnz grndi, cioè se esiste ν N tle che P(n) è ver per ogni n ν. Si dice invece che P(n) è ver frequentemente se è ver per infiniti n. In modo equivlente, per ogni n N esiste m n tle che P(m) è ver. Tnto per fre degli esempi semplici, l ffermzione l = lim n è equivlente dire che per ogni ε > 0 si h definitivmente n l < ε. L n + successione ( 1) n ssume frequentemente il vlore 1. Enuncimo l crtterizzzione di mssimo e minimo limite: PROPOSIZIONE (Crtterizzzione di lim inf e lim sup): Dt un successione { n } n N si h l 1 = lim inf n se e soltnto se per ogni ε > 0 vle che n + n > l 1 ε definitivmente e che n < l 1 + ε frequentemente. In mnier del tutto nlog, l 2 = lim sup n + n se e solo se per ogni ε > 0 vle che n < l 2 + ε definitivmente e che n > l 2 ε frequentemente. Il seguente foglio dinmico GeoGebr 20 illustr l crtterizzzione:
88 Dimostrimo l crtterizzzione del lim inf con gli ε: per il lim sup l music è l stess... nche perché potete fcilmente dimostrre (esercizio!) che lim sup n = lim inf( n )... Si dunque l = lim inf n + n, ε > 0. Per definizione il lim inf è il limite dell successione b n = inf m n m : grzie ll definizione di limite vremo llor che ( ) l ε < b n < l + ε definitivmente. Siccome si h evidentemente n b n (perché n pprtiene ll insieme di numeri di cui prendimo l inf), srà nche vero che n > l ε definitivmente. Fissimo poi n bbstnz grnde, in modo che vlg ( ). Allor inf m < m n l+ε, dunque l+ε non è un minornte dell insieme di cui fccimo l inf. Esiste dunque m n tle che m < l + ε. Siccome n può essere scelto rbitrrimente grnde, possimo concludere che m < l + ε frequentemente. Le due ffermzioni che costituiscono l crtterizzzione sono dunque dimostrte. Vicevers, supponimo che per ogni ε > 0 vlgno entrmbe le proprietà richieste dll nostr crtterizzzione. Dll prim di esse segue subito che b n = inf m l ε definitivmente. L second dice poi che b n < l + 2ε: m n inftti l + 2ε non può essere un minornte dell insieme { m : m n perché vle frequentemente l disuguglinz oppost! Concludimo llor che l 2ε b n l + 2ε definitivmente, d cui l = lim b n = lim inf n, Q.E.D. ESEMPI: Grzie ll definizione o ll crtterizzzione, si può immeditmente verificre che lim inf n + ( 1)n = 1, lim sup( 1) n = 1, lim inf n + ( 1)n + 88 n +
Diario del Corso di Analisi Matematica I - Mod. 1
 Dirio del Corso di Anlisi Mtemtic I - Mod. 1 Corso di Lure: Mtemtic Applict Docente: Sisto Bldo ATTENZIONE: Il presente Dirio del Corso vuole essere un rissunto bbstnz dettglito di quello che è stto detto
Dirio del Corso di Anlisi Mtemtic I - Mod. 1 Corso di Lure: Mtemtic Applict Docente: Sisto Bldo ATTENZIONE: Il presente Dirio del Corso vuole essere un rissunto bbstnz dettglito di quello che è stto detto
Diario del Corso di Analisi Matematica I - Mod. 1
 Dirio del Corso di Anlisi Mtemtic I - Mod. 1 Corso di Lure: Mtemtic Applict Docente: Sisto Bldo ATTENZIONE: Il presente Dirio del Corso vuole essere un rissunto bbstnz dettglito di quello che è stto detto
Dirio del Corso di Anlisi Mtemtic I - Mod. 1 Corso di Lure: Mtemtic Applict Docente: Sisto Bldo ATTENZIONE: Il presente Dirio del Corso vuole essere un rissunto bbstnz dettglito di quello che è stto detto
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
1 Integrale delle funzioni a scala
 INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
Laurea triennale in Scienze della Natura a.a. 2009/2010. Regole di Calcolo
 Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
Integrali dipendenti da un parametro e derivazione sotto il segno di integrale.
 1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
Il lemma di ricoprimento di Vitali
 Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Matematica I, Funzione integrale
 Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
Capitolo 5. Integrali. 5.1 Integrali di funzioni a gradinata
 Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
Esercizi svolti Limiti. Prof. Chirizzi Marco.
 Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI
 FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
Erasmo Modica. : K K K
 L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
Osserviamo che per trovare le costanti A e B possiamo anche ragionare così: se moltiplichiamo l equazione x + 1 (x + 2)(x + 3) = A.
 88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
7. Derivate Definizione 1
 7. Derivte Il concetto di derivt è importntissimo e molto nturle. Per vere un esempio concreto, penste l moto di un mcchin: se f(t) è l funzione che esprime qunt strd vete percorso fino d un certo istnte
7. Derivte Il concetto di derivt è importntissimo e molto nturle. Per vere un esempio concreto, penste l moto di un mcchin: se f(t) è l funzione che esprime qunt strd vete percorso fino d un certo istnte
1 Il problema del calcolo dell area di una regione piana limitata
 Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Modulo o "valore assoluto" Proprietà del Valore Assoluto. Intervalli
 Modulo o "vlore ssoluto" Dto x definimo modulo o vlore ssoluto di x il numero rele positivo x se x 0 x = x se x < 0 Es. 5 è 5. 2.34 è 2.34 Dl punto di vist geometrico x rppresent l distnz di x d 0. x x
Modulo o "vlore ssoluto" Dto x definimo modulo o vlore ssoluto di x il numero rele positivo x se x 0 x = x se x < 0 Es. 5 è 5. 2.34 è 2.34 Dl punto di vist geometrico x rppresent l distnz di x d 0. x x
CORSO ANALISI MATEMATICA 1 A.A. 2015/2016. Testo consigliato
 Università degli studi di Cgliri CORSO ANALISI MATEMATICA 1 A.A. 2015/2016 Docente: Monic Mrrs 1 Anlisi Mtemtic 1 Testo consiglito con elementi di geometri e lgebr linere. M. Brmnti, C.D. Pgni, S. Sls
Università degli studi di Cgliri CORSO ANALISI MATEMATICA 1 A.A. 2015/2016 Docente: Monic Mrrs 1 Anlisi Mtemtic 1 Testo consiglito con elementi di geometri e lgebr linere. M. Brmnti, C.D. Pgni, S. Sls
1 Espressioni polinomiali
 1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
Integrali. Il concetto di integrale nasce per risolvere due classi di problemi:
 Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
SPAZI VETTORIALI. 1. Spazi e sottospazi vettoriali
 SPAZI VETTORIALI 1. Spzi e sottospzi vettorili Definizione: Dto un insieme V non vuoto e un corpo K di sostegno si dice che V è un K-spzio vettorile o uno spzio vettorile su K se sono definite un operzione
SPAZI VETTORIALI 1. Spzi e sottospzi vettorili Definizione: Dto un insieme V non vuoto e un corpo K di sostegno si dice che V è un K-spzio vettorile o uno spzio vettorile su K se sono definite un operzione
1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =
![1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) = 1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =](/thumbs/19/319521.jpg) Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Integrali. Il concetto di integrale nasce per risolvere due classi di problemi:
 Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Corso di Analisi Matematica Calcolo integrale per funzioni di una variabile
 Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Serie di Potenze. Introduciamo il concetto di convergenza puntuale ed uniforme per successioni. { 0 se 1 < x < 1
 Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
INTERVALLI NELL INSIEME R
 INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
1 Equazioni e disequazioni di secondo grado
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma
![INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma](/thumbs/17/120065.jpg) INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
8. Prodotto scalare, Spazi Euclidei.
 8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
DISPENSE DI ANALISI MATEMATICA. Indice
 DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
Corso di Analisi Matematica. Calcolo integrale
 .. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
.. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
Analisi matematica. Materiale didattico
 Anlisi mtemtic. Mterile didttico Lure triennle F.A.I. Rimini 7 ottobre 23 Indice Linguggio, funzioni elementri 2. Il linguggio degli insiemi.................................... 2.2 Numeri reli, vlore ssoluto,
Anlisi mtemtic. Mterile didttico Lure triennle F.A.I. Rimini 7 ottobre 23 Indice Linguggio, funzioni elementri 2. Il linguggio degli insiemi.................................... 2.2 Numeri reli, vlore ssoluto,
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
2. Teoremi per eseguire operazioni con i limiti in forma determinata
 . Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
. Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
Pietro Baldi Successioni e serie di funzioni. 1 Convergenza puntuale
 Pietro Bldi Successioni e serie di funzioni Testi di riferimento: W. Rudin, Principi di Anlisi Mtemtic, McGrw-Hill Libri Itli; N. Fusco, P. Mrcellini, C. Sbordone, Anlisi Mtemtic Due, Liguori Editore;
Pietro Bldi Successioni e serie di funzioni Testi di riferimento: W. Rudin, Principi di Anlisi Mtemtic, McGrw-Hill Libri Itli; N. Fusco, P. Mrcellini, C. Sbordone, Anlisi Mtemtic Due, Liguori Editore;
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
INTEGRALI IMPROPRI. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Integrali impropri cap10.pdf 1
 INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
ANALISI REALE E COMPLESSA a.a. 2007-2008
 ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Esercizio 1. Dimostrare che se (X, d) è uno spazio metrico anche (X, d ) lo è, dove d =
 I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
Corso di Laurea in Ingegneria Civile ed Ambientale Prima prova scritta di Analisi Matematica 1 del 10/01/2011 A
 Prim prov scritt di Anlisi Mtemtic 1 del 10/01/2011 A (1) Fornire l definizione di funzione integrbile secondo Riemnn e di integrle di Riemnn. (2) Enuncire e dimostrre il Teorem di Rolle. (3) Dimostrre
Prim prov scritt di Anlisi Mtemtic 1 del 10/01/2011 A (1) Fornire l definizione di funzione integrbile secondo Riemnn e di integrle di Riemnn. (2) Enuncire e dimostrre il Teorem di Rolle. (3) Dimostrre
Corso di Analisi: Algebra di Base. 4^ Lezione. Radicali. Proprietà dei radicali. Equazioni irrazionali. Disequazioni irrazionali. Allegato Esercizi.
 Corso di Anlisi: Algebr di Bse ^ Lezione Rdicli. Proprietà dei rdicli. Equzioni irrzionli. Disequzioni irrzionli. Allegto Esercizi. RADICALI : Considerto un numero rele ed un numero intero positivo n,
Corso di Anlisi: Algebr di Bse ^ Lezione Rdicli. Proprietà dei rdicli. Equzioni irrzionli. Disequzioni irrzionli. Allegto Esercizi. RADICALI : Considerto un numero rele ed un numero intero positivo n,
Differenziale. Consideriamo la variazione finita, x della variabile indipendente a cui corrisponde una variazione finita della funzione f x, f x y
 Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Esponenziali e logaritmi
 Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Campi. Una funzione F di n variabili reali e a valori in R n è detta campo di vettori. Nel seguito considereremo F : A R n con A aperto di R n.
 Cmpi Ultimo ggiornmento: 18 febbrio 217 Un funzione F di n vribili reli e vlori in R n è dett cmpo di vettori. Nel seguito considereremo F : A R n con A perto di R n. 1. Integrli curvilinei di second specie
Cmpi Ultimo ggiornmento: 18 febbrio 217 Un funzione F di n vribili reli e vlori in R n è dett cmpo di vettori. Nel seguito considereremo F : A R n con A perto di R n. 1. Integrli curvilinei di second specie
{ 1, 2,3, 4,5,6,7,8,9,10,11,12, }
 Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Il problema delle aree. Metodo di esaustione.
 INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
2 Numeri reali. M. Simonetta Bernabei & Horst Thaler
 2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
26/03/2012. Integrale Definito. Calcolo delle Aree. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi:
 ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
Appunti di Analisi Matematica
 Appunti di Anlisi Mtemtic Stefno Med e Alberto Peretti Appunti per il corso di Mtemtic I I semestre,.. 2001/2002 Fcoltà di Scienze Sttistiche Università di Milno-Bicocc c Stefno Med e Alberto Peretti,
Appunti di Anlisi Mtemtic Stefno Med e Alberto Peretti Appunti per il corso di Mtemtic I I semestre,.. 2001/2002 Fcoltà di Scienze Sttistiche Università di Milno-Bicocc c Stefno Med e Alberto Peretti,
si definisce Funzione Integrale; si chiama funzione integrale in quanto il suo * x
 Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
Area del Trapezoide. f(x) A f(a) f(b) f(x)
 Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
Are del Trpezoide y o A f() trpezoide h B f() f() L're del trpezoide S puo' essere pprossimt dll're del trpezio AB. Per vere un migliore pprossimzione possimo suddividere il trpezio in trpezi piu' piccoli.
5 2d x x >12. con a, b, c e d parametri reali. Il grafico di f (x) passa per l origine del sistema di riferimento
 Questionrio Risolvi quttro degli otto quesiti: L Città dello sport è un struttur sportiv progettt dll rchitetto Sntigo Cltrv e mi complett, situt sud di Rom Rispetto l sistem di riferimento indicto in
Questionrio Risolvi quttro degli otto quesiti: L Città dello sport è un struttur sportiv progettt dll rchitetto Sntigo Cltrv e mi complett, situt sud di Rom Rispetto l sistem di riferimento indicto in
Integrali. all integrale definito all integrale indefinito. Integrali: riepilogo
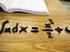 Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
dr Valerio Curcio Le affinità omologiche Le affinità omologiche
 1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
ipotenusa cateto adiacente ad α cateto opposto ad α ipotenusa cateto adiacente ad α ipotenusa cateto adiacente ad α
 Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
INTEGRALI IMPROPRI. c Paola Gervasio - Analisi Matematica 1 - A.A. 17/18 Integrali impropri cap10.pdf 1
 INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 7/8 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 7/8 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
Integrali curvilinei (integrali di densità) Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli curvilinei di prim specie (integrli di densità) 15 Dicembre 215 Indice 1 Integrli di line di prim specie
Politecnico di Milno orso di Anlisi e Geometri 1 Federico Lstri federico.lstri@polimi.it Integrli curvilinei di prim specie (integrli di densità) 15 Dicembre 215 Indice 1 Integrli di line di prim specie
corrispondenza dal piano in sé, che ad ogni punto P del piano fa corrispondere il punto P' in
 Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
II-8 Integrale di Riemann
 II-8 INTEGRALE DI RIEMANN DEFINIZIONE DI INTEGRALE DI RIEMANN II-8 Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle
II-8 INTEGRALE DI RIEMANN DEFINIZIONE DI INTEGRALE DI RIEMANN II-8 Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle
1 Integrali generalizzati su intervalli illimitati
 Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Si noti che da questa definizione segue che il punto C è il punto medio del segmento PP'. Figura 1
 APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
Ellisse riferita al centro degli assi
 Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
Successioni di Funzioni e Serie di Potenze
 Successioni di Funzioni e Serie di Potenze 1 Successioni di Funzioni e Serie di Potenze 1 Successioni di Funzioni Nel corso di nlisi di bse si sono studite le successioni numeriche. Qui considerimo un
Successioni di Funzioni e Serie di Potenze 1 Successioni di Funzioni e Serie di Potenze 1 Successioni di Funzioni Nel corso di nlisi di bse si sono studite le successioni numeriche. Qui considerimo un
FUNZIONI IPERBOLICHE
 FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
1 Funzioni continue: definizioni e prime proprietà. 2 Continuità delle funzioni elementari 2
 FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 2 3 Funzioni continue
FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 2 3 Funzioni continue
Pietro Baldi. Analisi matematica I. Programma d esame, anno accademico Corso di Laurea Triennale in Ingegneria Biomedica, cognomi A-I.
 Pietro Bldi Anlisi mtemtic I Progrmm d esme, nno ccdemico 2012-2013 Corso di Lure Triennle in Ingegneri Biomedic, cognomi A-I. Il libro di testo dottto durnte il corso è Anlisi Mtemtic Uno, P. Mrcellini,
Pietro Bldi Anlisi mtemtic I Progrmm d esme, nno ccdemico 2012-2013 Corso di Lure Triennle in Ingegneri Biomedic, cognomi A-I. Il libro di testo dottto durnte il corso è Anlisi Mtemtic Uno, P. Mrcellini,
ELEMENTI DI TEORIA DEI NUMERI
 ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
5. Funzioni elementari trascendenti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
PNI SESSIONE SUPPLETIVA QUESITO 1
 www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
Equazioni di 2 grado. Definizioni Equazioni incomplete Equazione completa Relazioni tra i coefficienti della equazione e le sue soluzioni Esercizi
 Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Appunti di Analisi Matematica 1
 Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
Scheda Sei ESPONENZIALI E LOGARITMI. 0,+. Inoltre valgono le
 Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Minimi quadrati e problemi di distanza minima
 Minimi qudrti e problemi di distnz minim Considerimo un mtrice rettngolre B, con elementi b ij, i 1,..., n, j 1,..., m, con m < n (quindi, più righe che colonne. Voglimo risolvere il sistem linere (1 Bx
Minimi qudrti e problemi di distnz minim Considerimo un mtrice rettngolre B, con elementi b ij, i 1,..., n, j 1,..., m, con m < n (quindi, più righe che colonne. Voglimo risolvere il sistem linere (1 Bx
1 Definizione di integrale di Riemann 1. 2 Condizioni di esistenza dell integrale di Riemann 3. 3 Proprietà dell integrale di Riemann 4
 DEFINIZIONE DI INTEGRALE DI RIEMANN Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle di Riemnn 4 4 Clcolo dell integrle
DEFINIZIONE DI INTEGRALE DI RIEMANN Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle di Riemnn 4 4 Clcolo dell integrle
TEST DI MATEMATICA. Funzioni in una, Funzioni in due variabili Integrali Equazioni differenziali. 1) Il valore del limite seguente. e e. e 1.
 TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
ESPONENZIALI E LOGARITMI
 Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
Lezione 16 Derivate ed Integrali
 Lezione 16 Derivte ed Integrli Frnk Sullivn 1 Dicembre 11 1 Prim Or Compiti di letture ed esercizi per 3 Dicembre Durnte l lezione di oggi pplicheremo le regole per differenzire funzioni l clcolo di integrli.
Lezione 16 Derivte ed Integrli Frnk Sullivn 1 Dicembre 11 1 Prim Or Compiti di letture ed esercizi per 3 Dicembre Durnte l lezione di oggi pplicheremo le regole per differenzire funzioni l clcolo di integrli.
acuradi Luca Cabibbo e Walter Didimo Esercizi di Informatica teorica - Luca Cabibbo e Walter Didimo 1
 curdi Luc Cio e Wlter Didimo Esercizi di Informtic teoric - Luc Cio e Wlter Didimo 1 pumping lemm proprietà di chiusur dei linguggio regolri notzioni sul livello degli esercizi:(*)fcile, (**) non difficile
curdi Luc Cio e Wlter Didimo Esercizi di Informtic teoric - Luc Cio e Wlter Didimo 1 pumping lemm proprietà di chiusur dei linguggio regolri notzioni sul livello degli esercizi:(*)fcile, (**) non difficile
Funzioni razionali fratte
 Funzioni rzionli frtte Per illustrre l medizione che AlNuSet fornisce per lo studio delle funzioni rzionli frtte, inizimo con il considerre l funzione f ( ) l vrire del prmetro. L su rppresentzione nell
Funzioni rzionli frtte Per illustrre l medizione che AlNuSet fornisce per lo studio delle funzioni rzionli frtte, inizimo con il considerre l funzione f ( ) l vrire del prmetro. L su rppresentzione nell
Funzioni 1. 3) una legge che ad un elemento x di X associa al più un unico elemento ( x)
 Funzioni Un funzione f d X in Y è costituit d un tern di elementi ) un insieme X, detto dominio di f 2) un insiemey, detto codominio di f f di Y. Nel cso, in cui X,Y sino sottinsiemi di R, generlmente
Funzioni Un funzione f d X in Y è costituit d un tern di elementi ) un insieme X, detto dominio di f 2) un insiemey, detto codominio di f f di Y. Nel cso, in cui X,Y sino sottinsiemi di R, generlmente
Siano A e B due insiemi non vuoti. Una funzione f da A a B è un assegnamento di esattamente un elemento di B ad ogni elemento di A
 Funzioni Definizione di funzione: Sino A e B due insiemi non vuoti. Un funzione f d A B è un ssegnmento di esttmente un elemento di B d ogni elemento di A Scrivimo f() = b se b è l unico elemento dell
Funzioni Definizione di funzione: Sino A e B due insiemi non vuoti. Un funzione f d A B è un ssegnmento di esttmente un elemento di B d ogni elemento di A Scrivimo f() = b se b è l unico elemento dell
Formulario di Analisi Matematica 1
 Formulrio di Anlisi Mtemtic Indice degli rgomenti Punti interni, isolti, di ccumulzione e di frontier Alcune costnti Proprietà delle potenze Proprietà degli esponenzili Proprietà dei logritmi Proprietà
Formulrio di Anlisi Mtemtic Indice degli rgomenti Punti interni, isolti, di ccumulzione e di frontier Alcune costnti Proprietà delle potenze Proprietà degli esponenzili Proprietà dei logritmi Proprietà
II-5 Funzioni continue
 II-5 FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ II-5 Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 3 3 Funzioni
II-5 FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ II-5 Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 3 3 Funzioni
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 9 Sommrio. Crtterizzimo l equivlenz elementre in termini di sistemi di isomorfismi przili e di giochi di Ehrenfeucht-Frïssé. 1. Giochi di Ehrenfeucht-Frïssé
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 9 Sommrio. Crtterizzimo l equivlenz elementre in termini di sistemi di isomorfismi przili e di giochi di Ehrenfeucht-Frïssé. 1. Giochi di Ehrenfeucht-Frïssé
Sistemi principali di normali ad una varietà giacenti nel suo o 2. Nota di
 Sistemi principli di normli d un vrietà gicenti nel suo o 2. Not di Giuseppe Vitli Pdov. In un mio recente lvoro *) ho considerto, per ogni superficie il cui j si di 2 k dimensioni (k 2, 3), un sistem
Sistemi principli di normli d un vrietà gicenti nel suo o 2. Not di Giuseppe Vitli Pdov. In un mio recente lvoro *) ho considerto, per ogni superficie il cui j si di 2 k dimensioni (k 2, 3), un sistem
LEZIONE 20. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
" Osservazione. 6.1 Integrale indefinito. R Definizione (Primitiva) E Esempio 6.1 CAPITOLO 6
 CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
c a (seno di alfa); (coseno di alfa); (tangente di alfa).
 Sito Personle di Ettore Limoli Lezioni di Mtemtic Prof. Ettore Limoli Sommrio Elementi di trigonometri... 1 Angoli e loro misur... Funzioni e loro grfici... 4 Usre i grfici... 5 Funzioni inverse delle
Sito Personle di Ettore Limoli Lezioni di Mtemtic Prof. Ettore Limoli Sommrio Elementi di trigonometri... 1 Angoli e loro misur... Funzioni e loro grfici... 4 Usre i grfici... 5 Funzioni inverse delle
Anno 5. Applicazione del calcolo degli integrali definiti
 Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
B8. Equazioni di secondo grado
 B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accdemico 07/8 Diprtimento di Scienze Mtemtic, Informtiche e Fisiche Corsi di Lure in Informtic e in IBW Esercizi di Anlisi Mtemtic Esercizi del 7 ottobre 07. Nell
Università degli Studi di Udine Anno Accdemico 07/8 Diprtimento di Scienze Mtemtic, Informtiche e Fisiche Corsi di Lure in Informtic e in IBW Esercizi di Anlisi Mtemtic Esercizi del 7 ottobre 07. Nell
Micol Amr ANALISI MATEMATICA I - 999/2000 Dim. Considerimo il cso in cui l successione si crescente; l dimostrzione procede in modo del tutto nlogo, q
 TEOREMI DIMOSTRATI NEL CORSO. Successioni e serie numeriche. Teorem. (Unicit del ite) Si ( n ) n2in un successione di numeri reli convergente. Allor il suo ite e unico. Dim. Assumimo per ssurdo che n =
TEOREMI DIMOSTRATI NEL CORSO. Successioni e serie numeriche. Teorem. (Unicit del ite) Si ( n ) n2in un successione di numeri reli convergente. Allor il suo ite e unico. Dim. Assumimo per ssurdo che n =
3. Funzioni iniettive, suriettive e biiettive (Ref p.14)
 . Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
. Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
Strumenti Matematici per la Fisica
 Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
1. Elementi di analisi funzionale Esercizi
 . Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
. Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
Nome.Cognome classe 5D 18 Marzo 2014. Verifica di matematica
 Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
