Appunti di informatica. Lezione 2 anno accademico Mario Verdicchio
|
|
|
- Ottaviano Vitale
- 8 anni fa
- Visualizzazioni
Transcript
1 Appunti di informatica Lezione 2 anno accademico Mario Verdicchio
2 Sistema binario e logica C è un legame tra i numeri binari (0,1) e la logica, ossia la disciplina che si occupa del ragionamento Noi ragioniamo intorno a delle affermazioni, che possono essere vere oppure false* I valori di verità delle affermazioni sono due: vero o falso e possiamo costruire una codifica binaria 0 corrisponde al falso, 1 al vero *si tratta naturalmente di un idealizzazione: esistono anche affermazioni dal valore di verità incerto o impossibile da verificare
3 Codifica binaria Codifica: corrispondenza biunivoca tra un insieme di elementi e un insieme di numeri naturali Per biunivoca si intende una corrispondenza tra due insiemi (chiamati dominio e codominio) che è sia iniettiva sia suriettiva Una corrispondenza si dice iniettiva quando a elementi diversi del dominio corrispondono elementi diversi del codominio Una corrispondenza si dice suriettiva quando tutti gli elementi del codominio sono coinvolti nella corrispondenza In un corrispondenza biunivoca, quindi, a ogni elemento del dominio corrisponde uno e un solo elemento del codominio e viceversa In una codifica, gli elementi del codominio sono numeri naturali Un esempio di codifica nella vita quotidiana è il sistema di immatricolazione in un università: a ogni studente corrisponde una e una sola matricola e a una matricola corrisponde uno e un solo studente Una codifica in cui il codominio è costituito da due soli elementi si dice codifica binaria
4 Operatori logici Come in algebra si eseguono operazioni sui numeri per ottenere altri numeri (esempio banale: applichiamo l operazione somma a 3 e 5 e otteniamo 8) così in logica si eseguono operazioni sui valori di verità Le operazioni sui valori di verità si eseguono mediante i cosiddetti operatori logici: congiunzione, disgiunzione, negazione
5 Congiunzione Date due affermazioni A e B, applicando una congiunzione si ottiene un affermazione composta che indichiamo con A e B (oppure A and B, A && B, A B ) che è vera solo quando sia A sia B sono vere, e falsa in tu8 gli altri casi
6 Disgiunzione Date due affermazioni A e B, applicando una disgiunzione si ottiene un affermazione composta che indichiamo con A o B (oppure A or B, A B, A B ) che è falsa solo quando sia A sia B sono false, e vera in tu8 gli altri casi
7 Negazione Date una affermazione A, applicando una negazione si ottiene un affermazione composta che indichiamo con non A (oppure not A,!A, A ) che è falsa quando A è vera e viceversa A differenza di congiunzione e disgiunzione, che sono operatori binari perché si applicano a due operandi, la negazione è un operatore unario perché si applica a un solo operando
8 Disgiunzione esclusiva Chiamato anche or esclusivo e indicato con xor (oppure ), è l operatore logico con cui costruire una affermazione A xor B che è vera quando A (oppure B) è vera e l altra è falsa, mentre è falsa quando sia A sia B hanno lo stesso valore di verità
9 Tavole di verità Con le tavole di verità si possono rappresentare graficamente le definizioni dei diversi operatori logici
10 Precedenze degli operatori! precede &&, che precede, che precede!a&&b C è equivalente a ((!A)&&B) C Le parentesi vincono sulle precedenze: in!((a B)&&C) la disgiunzione viene eseguita per prima, poi la congiunzione, da ultimo la negazione
11 Uso delle tavole di verità Le tavole di verità possono essere usate per dimostrare l equivalenza di certe affermazioni Due affermazioni si dicono (logicamente) equivalenti quando hanno lo stesso valore di verita in tutti i casi Ad esempio, A xor B e equivalente a (A or B) and not(a and B)
12
13 Altre equivalenze logiche nota and A falso nota or A vero falso and A falso falso or A A vero or A vero vero and A A not(a and B) not A or not B not(a or B) not A and not B Tramite le equivalente logiche certe affermazioni possono essere semplificate in affermazioni equivalenti Ad esempio: (not A and A) or (not B and C) è equivalente a not B and C
14 Regole di inferenza Una regola di inferenza è un meccanismo con cui ottenere da una o più affermazioni una nuova affermazione. Ad esempio: A B A B La regola introduzione di congiunzione dice che, a partire da A e B, possiamo ottenere A B.
15 Regole di inferenza corrette Una regola di inferenza si dice corretta se, a partire da affermazioni vere, ci permette di ottenere affermazioni vere La regola introduzione di congiunzione è corretta. Lo si può verificare mediante opportune tavole di verità Una regola come eliminazione di disgiunzione, invece, non è corretta: A B A perché esiste un caso in cui A B è vera ma A è falsa A noi interessano solo regole di inferenza corrette La equivalente logiche sono un caso speciale di regole di inferenza
16 Uso della logica in informatica Tipicamente i sistemi informatici sono attivati per eseguire delle operazioni A volte alcune operazioni devono essere eseguite solo se certe condizioni si verificano Tali operazioni si chiamano istruzioni condizionali Le condizioni che devono essere verificate sono di fatto affermazioni che all istante della verifica hanno un valore di verità (cioè sono vere oppure false)
17 Condizioni semplici Si definisce condizione semplice un affermazione che confronta due valori Ha tipicamente la forma: valore operatore di confronto valore Esempi (con relativo valore di verità): 4 < 10 (vera) (falsa) x < 100 (dipende dal valore di x al momento della verifica)
18 Condizioni composte Si costruisce una condizione composta a partire da condizioni semplici per mezzo di operatori logici Esempi [e relativi valori di verità]: (4 < 10) and (50 400) [falsa] (10 10) or (100 > 100) [vera] not (x 5) [dipende dal valore di x]
19 Tipi di condizioni in base alla verità Tautologie: condizioni, come nota or A, che sono sempre vere (qualunque sia il valore di A) Contraddizioni: condizioni, come nota and A, che sono sempre false (qualunque sia il valore di A) Tutte le altre condizioni che possono essere sia vere sia false, a seconda dei valori delle loro componenti, si dicono contingenze
20 Porte logiche (1) Negazione, NOT,! IN OUT IN OUT
21 Porte logiche (2) Congiunzione, AND, && IN1 IN2 OUT= IN1 AND IN IN1 IN2 OUT
22 Porte logiche (3) Disgiunzione, OR, IN1 IN2 OUT= IN1 OR IN IN1 IN2 OUT
23 Porte logiche (4) Disgiunzione esclusiva, XOR, IN1 IN2 OUT= IN1 XOR IN IN1 IN2 OUT
24 Codifica binaria Il processore, abbiamo detto, lavora solo con segnali elettrici Segnali elettrici a valori alti di tensione vengono fatti corrispondere al numero 1 Segnali elettrici a valori bassi di tensione vengono fatti corrispondere al numero 0 Questa si chiama codifica binaria Da questo punto di vista, il calcolatore opera solo con due cifre: 0 e 1 Tutta l informazione che un calcolatore elabora viene espressa con queste due cifre, per mezzo della codifica binaria
25 Numerazione: le basi Noi siamo abituati a una numerazione basata su 10 cifre: da 0 a 9 La base della nostra numerazione è il 10: 147 = 7 x x x 10 2 La base del sistema binario è il 2: 1011 = 1 x x x x 2 3 Se si svolge il calcolo si ottiene il numero che, in base 10, corrisponde a 1011 in base 2.
26 Base 2 -> Base , ossia 1011 in base 2, a che numero in base 10 corrisponde? Stiamo cercando la x tale che: = x 10 Basta ricordarsi la definizione di base 2: 1011 = 1 x x x x 2 3 = 11 Perciò 1011 in base 2 vuol dire 11 in base 10: = Il nostro 11 è per il calcolatore 1011
27 Base 10 -> Base 2 Il metodo per esprimere in base 2 un numero dato in base 10 è il seguente Cerchiamo la x tale che: = x 2 Si procede con una sequenza di divisioni per 2, fintantoché il quoziente non diventa 0, e scrivendo la sequenza dei resti in ordine inverso
28 Come si scrive 25 in base 2? 25 : 2 = 12 con resto 1 12 : 2 = 6 con resto 0 6 : 2 = 3 con resto 0 3 : 2 = 1 con resto 1 1 : 2 = 0 con resto 1 Una volta ottenuto il quoziente pari a 0, scriviamo i resti in ordine inverso: =
29 Verifica del metodo è davvero la codifica in base 2 di 25? Basta svolgere i calcoli basati sulla definizione di sistema binario = 1 x x x 2 4 = = (gli addendi con lo 0 sono stati omessi perché ovviamente non influiscono sulla somma)
30 Numeri binari in memoria In un calcolatore, i numeri binari sono tipicamente memorizzati in sequenze di caselle (note anche come parole) di lunghezza fissa dipendente dalla struttura del calcolatore stesso. Ad esempio, una parola di 4 bit può contenere il numero
31 Combinazioni possibili di numeri Una parola di 4 bit può contenere 2 4 = 16 numeri binari diversi: da 0000 a 1111 In generale, una parola di n bit può contenere 2 n numeri binari diversi
32 Dimensioni delle memorie 8 bit = 1 Byte (1B) 2 10 Byte = 1024 Byte = 1 KiloByte (1KB) 2 20 Byte = Byte = 1 MegaByte (1MB) 2 30 Byte = Byte = 1 GigaByte (1GB) 2 40 Byte = Byte = 1 TeraByte (1TB)
33 Dimensioni delle memorie (2) Oramai è sempre più diffusa la seguente approssimazione: 1000 (10 3 ) Byte (o bit) = 1 KiloByte o KiloBit (1KB o 1Kb) (10 6 ) Byte (o bit) = 1 MegaByte o MegaBit (1MB o 1Mb) 1 miliardo (10 9 ) Byte (o bit) = 1 GigaByte o GigaBit (1GB o 1Gb) 1000 miliardi (10 12 ) Byte (o bit) = 1 TeraByte o TeraBit (1TB o 1Tb)
Informazione analogica e digitale
 L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Calcolatori: Algebra Booleana e Reti Logiche
 Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Algebra di Boole ed Elementi di Logica
 Algebra di Boole ed Elementi di Logica 53 Cenni all algebra di Boole L algebra di Boole (inventata da G. Boole, britannico, seconda metà 8), o algebra della logica, si basa su operazioni logiche Le operazioni
Algebra di Boole ed Elementi di Logica 53 Cenni all algebra di Boole L algebra di Boole (inventata da G. Boole, britannico, seconda metà 8), o algebra della logica, si basa su operazioni logiche Le operazioni
Laurea Specialistica in Informatica
 Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
BIT? Cosa c è dietro a questo nome? Che cos è il bit? Perché si usa? Come si converte un numero binario?
 BIT? Cosa c è dietro a questo nome? Che cos è il bit? Perché si usa? Come si converte un numero binario? Cosa c è dietro a questo nome? BIT è un acronimo e deriva da BInary digit, cioè cifra binaria Che
BIT? Cosa c è dietro a questo nome? Che cos è il bit? Perché si usa? Come si converte un numero binario? Cosa c è dietro a questo nome? BIT è un acronimo e deriva da BInary digit, cioè cifra binaria Che
Algebra booleana. Si dice enunciato una proposizione che può essere soltanto vera o falsa.
 Algebra booleana Nel lavoro di programmazione capita spesso di dover ricorrere ai principi della logica degli enunciati e occorre conoscere i concetti di base dell algebra delle proposizioni. L algebra
Algebra booleana Nel lavoro di programmazione capita spesso di dover ricorrere ai principi della logica degli enunciati e occorre conoscere i concetti di base dell algebra delle proposizioni. L algebra
4. Operazioni aritmetiche con i numeri binari
 I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
I Numeri Binari 4. Operazioni aritmetiche con i numeri binari Contare con i numeri binari Prima di vedere quali operazioni possiamo effettuare con i numeri binari, iniziamo ad imparare a contare in binario:
Convertitori numerici in Excel
 ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
ISTITUTO DI ISTRUZIONE SUPERIORE G. M. ANGIOY CARBONIA Convertitori numerici in Excel Prof. G. Ciaschetti Come attività di laboratorio, vogliamo realizzare dei convertitori numerici con Microsoft Excel
Informatica per la comunicazione" - lezione 7 -
 Informatica per la comunicazione - lezione 7 - Campionamento La codifica dei suoni si basa sulla codifica delle onde che li producono, a sua volta basata su una procedura chiamata campionamento.! Il campionamento
Informatica per la comunicazione - lezione 7 - Campionamento La codifica dei suoni si basa sulla codifica delle onde che li producono, a sua volta basata su una procedura chiamata campionamento.! Il campionamento
A L'operatore NOT si scrive con una linea sopra la lettera indicante la variabile logica A ; 0 1 1 0. NOT di A =
 ALGEBRA DI BOOLE L'algebra di Boole è un insieme di regole matematiche; per rappresentare queste regole si utilizzano variabili logiche, funzioni logiche, operatori logici. variabili logiche: si indicano
ALGEBRA DI BOOLE L'algebra di Boole è un insieme di regole matematiche; per rappresentare queste regole si utilizzano variabili logiche, funzioni logiche, operatori logici. variabili logiche: si indicano
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013
 Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Operazioni Aritmetiche e Codici in Binario Giuseppe Talarico 23/01/2013 In questo documento vengono illustrate brevemente le operazioni aritmetiche salienti e quelle logiche ad esse strettamente collegate.
Lezione 2 Circuiti logici. Mauro Piccolo piccolo@di.unito.it
 Lezione 2 Circuiti logici Mauro Piccolo piccolo@di.unito.it Bit e configurazioni di bit Bit: una cifra binaria (binary digit) 0 oppure 1 Sequenze di bit per rappresentare l'informazione Numeri Caratteri
Lezione 2 Circuiti logici Mauro Piccolo piccolo@di.unito.it Bit e configurazioni di bit Bit: una cifra binaria (binary digit) 0 oppure 1 Sequenze di bit per rappresentare l'informazione Numeri Caratteri
Università degli Studi di Cassino Corso di Fondamenti di Informatica Codifica di dati e istruzioni. Anno Accademico 2010/2011 Francesco Tortorella
 Corso di Fondamenti di Informatica Codifica di dati e istruzioni Anno Accademico 2010/2011 Francesco Tortorella La codifica dei dati e delle istruzioni La più piccola unità di informazione memorizzabile
Corso di Fondamenti di Informatica Codifica di dati e istruzioni Anno Accademico 2010/2011 Francesco Tortorella La codifica dei dati e delle istruzioni La più piccola unità di informazione memorizzabile
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Informatica B a.a 2005/06 (Meccanici 4 squadra) PhD. Ing. Michele Folgheraiter
 Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Informatica B a.a 2005/06 (Meccanici 4 squadra) Scaglione: da PO a ZZZZ PhD. Ing. Michele Folgheraiter Architettura del Calcolatore Macchina di von Neumann Il calcolatore moderno è basato su un architettura
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Fondamenti di calcolo booleano
 Breve introduzione storica Nel 1854, il prof. Boole pubblica un trattato ormai famosissimo: Le leggi del pensiero. Obiettivo finale del trattato è di far nascere la matematica dell intelletto umano, un
Breve introduzione storica Nel 1854, il prof. Boole pubblica un trattato ormai famosissimo: Le leggi del pensiero. Obiettivo finale del trattato è di far nascere la matematica dell intelletto umano, un
Informa/ca. Codifica binaria
 Informa/ca Appun/ della lezione 2 Codifica binaria Il processore, abbiamo de>o, lavora solo con segnali ele>rici Segnali ele>rici a valori al/ di tensione vengono fac corrispondere al numero 1 Segnali
Informa/ca Appun/ della lezione 2 Codifica binaria Il processore, abbiamo de>o, lavora solo con segnali ele>rici Segnali ele>rici a valori al/ di tensione vengono fac corrispondere al numero 1 Segnali
Codifica binaria dei numeri relativi
 Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
Codifica binaria dei numeri relativi Introduzione All interno di un calcolatore, è possibile utilizzare solo 0 e 1 per codificare qualsiasi informazione. Nel caso dei numeri, non solo il modulo ma anche
Dispense di Informatica per l ITG Valadier
 La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
Teoria degli insiemi
 Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio
 Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio Rappresentazione dell Informazione
Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Fondamenti di Informatica Laurea in Ingegneria Civile e Ingegneria per l Ambiente e il Territorio Rappresentazione dell Informazione
PROVA INTRACORSO TRACCIA A Pagina 1 di 6
 PROVA INTRACORSO DI ELEMENTI DI INFORMATICA MATRICOLA COGNOME E NOME TRACCIA A DOMANDA 1 Calcolare il risultato delle seguenti operazioni binarie tra numeri interi con segno rappresentati in complemento
PROVA INTRACORSO DI ELEMENTI DI INFORMATICA MATRICOLA COGNOME E NOME TRACCIA A DOMANDA 1 Calcolare il risultato delle seguenti operazioni binarie tra numeri interi con segno rappresentati in complemento
Anno 1. Definizione di Logica e operazioni logiche
 Anno 1 Definizione di Logica e operazioni logiche 1 Introduzione In questa lezione ci occuperemo di descrivere la definizione di logica matematica e di operazioni logiche. Che cos è la logica matematica?
Anno 1 Definizione di Logica e operazioni logiche 1 Introduzione In questa lezione ci occuperemo di descrivere la definizione di logica matematica e di operazioni logiche. Che cos è la logica matematica?
Architettura hardware
 Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri.
 Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri. A partire da questa lezione, ci occuperemo di come si riescono a codificare con sequenze binarie, quindi con sequenze di 0 e 1,
Codici Numerici. Modifica dell'informazione. Rappresentazione dei numeri. A partire da questa lezione, ci occuperemo di come si riescono a codificare con sequenze binarie, quindi con sequenze di 0 e 1,
Variabili e tipi di dato
 Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
Variabili e tipi di dato Tutte le variabili devono essere dichiarate, specificandone il tipo La dichiarazione deve precedere l uso Il tipo è un concetto astratto che esprime: L allocazione di spazio per
11010010 = 1*2^7 + 1*2^6 + 0*2^5 + 1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 210
 Il sistema BINARIO e quello ESADECIMALE. Il sistema di numerazione binario è particolarmente legato ai calcolatori in quanto essi possono riconoscere solo segnali aventi due valori: uno alto e uno basso;
Il sistema BINARIO e quello ESADECIMALE. Il sistema di numerazione binario è particolarmente legato ai calcolatori in quanto essi possono riconoscere solo segnali aventi due valori: uno alto e uno basso;
I sistemi di numerazione
 I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
I sistemi di numerazione 01-INFORMAZIONE E SUA RAPPRESENTAZIONE Sia dato un insieme finito di caratteri distinti, che chiameremo alfabeto. Utilizzando anche ripetutamente caratteri di un alfabeto, si possono
RAPPRESENTAZIONE BINARIA DEI NUMERI. Andrea Bobbio Anno Accademico 1996-1997
 1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
1 RAPPRESENTAZIONE BINARIA DEI NUMERI Andrea Bobbio Anno Accademico 1996-1997 Numeri Binari 2 Sistemi di Numerazione Il valore di un numero può essere espresso con diverse rappresentazioni. non posizionali:
Sistemi di Numerazione
 Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Fondamenti di Informatica per Meccanici Energetici - Biomedici 1 Sistemi di Numerazione Sistemi di Numerazione I sistemi di numerazione sono abitualmente posizionali. Gli elementi costitutivi di un sistema
Logica binaria. Porte logiche.
 Logica binaria Porte logiche. Le porte logiche sono gli elementi fondamentali su cui si basa tutta la logica binaria dei calcolatori. Ricevono in input uno, due (o anche più) segnali binari in input, e
Logica binaria Porte logiche. Le porte logiche sono gli elementi fondamentali su cui si basa tutta la logica binaria dei calcolatori. Ricevono in input uno, due (o anche più) segnali binari in input, e
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Numeri naturali numeri naturali minore maggiore Operazioni con numeri naturali
 1 Numeri naturali La successione di tutti i numeri del tipo: 0,1, 2, 3, 4,..., n,... forma l'insieme dei numeri naturali, che si indica con il simbolo N. Tale insieme si può disporre in maniera ordinata
1 Numeri naturali La successione di tutti i numeri del tipo: 0,1, 2, 3, 4,..., n,... forma l'insieme dei numeri naturali, che si indica con il simbolo N. Tale insieme si può disporre in maniera ordinata
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Anno 3. Classificazione delle funzioni
 nno 3 Classificazione delle funzioni 1 Introduzione In questa lezione affronteremo lo studio delle principali proprietà delle funzioni, imparando a classificarle e a compiere alcune operazioni su esse.
nno 3 Classificazione delle funzioni 1 Introduzione In questa lezione affronteremo lo studio delle principali proprietà delle funzioni, imparando a classificarle e a compiere alcune operazioni su esse.
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
SCHEDA DI RECUPERO SUI NUMERI RELATIVI
 SCHEDA DI RECUPERO SUI NUMERI RELATIVI I numeri relativi sono l insieme dei numeri negativi (preceduti dal segno -) numeri positivi (il segno + è spesso omesso) lo zero. Valore assoluto di un numero relativo
SCHEDA DI RECUPERO SUI NUMERI RELATIVI I numeri relativi sono l insieme dei numeri negativi (preceduti dal segno -) numeri positivi (il segno + è spesso omesso) lo zero. Valore assoluto di un numero relativo
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Informatica per la comunicazione" - lezione 8 -
 Informatica per la comunicazione - lezione 8 - Esercizio Convertire i seguenti numeri da base 10 a base 2: 8, 23, 144, 201. Come procedere per risolvere il problema? Bisogna ricordarsi che ogni sistema,
Informatica per la comunicazione - lezione 8 - Esercizio Convertire i seguenti numeri da base 10 a base 2: 8, 23, 144, 201. Come procedere per risolvere il problema? Bisogna ricordarsi che ogni sistema,
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE
 Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
La somma. Esempio: Il prodotto. Esempio:
 La somma L algoritmo della operazione di somma non cambia qualunque sia la base considerata. Naturalmente, le regole da imparare nel caso di una base b sono relative alle sole b 2 posssibili combinazioni
La somma L algoritmo della operazione di somma non cambia qualunque sia la base considerata. Naturalmente, le regole da imparare nel caso di una base b sono relative alle sole b 2 posssibili combinazioni
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
(71,1), (35,1), (17,1), (8,1), (4,0), (2,0), (1,0), (0,1) 0, 7155 2 = 1, 431 0, 431 2 = 0, 862 0, 896 2 = 1, 792 0, 724 2 = 1, 448 0, 448 2 = 0, 896
 2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
2 Esercizio 2.2 La rappresentazione esadecimale prevede 16 configurazioni corrispondenti a 4 bit. Il contenuto di una parola di 16 bit può essere rappresentato direttamente con 4 digit esadecimali, sostituendo
I.I.S. Primo Levi Badia Polesine A.S. 2012-2013
 LGEBR DI BOOLE I.I.S. Primo Levi Badia Polesine.S. 2012-2013 Nel secolo scorso il matematico e filosofo irlandese Gorge Boole (1815-1864), allo scopo di procurarsi un simbolismo che gli consentisse di
LGEBR DI BOOLE I.I.S. Primo Levi Badia Polesine.S. 2012-2013 Nel secolo scorso il matematico e filosofo irlandese Gorge Boole (1815-1864), allo scopo di procurarsi un simbolismo che gli consentisse di
Algebra di Boole: Concetti di base. Fondamenti di Informatica - D. Talia - UNICAL 1. Fondamenti di Informatica
 Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
Fondamenti di Informatica Algebra di Boole: Concetti di base Fondamenti di Informatica - D. Talia - UNICAL 1 Algebra di Boole E un algebra basata su tre operazioni logiche OR AND NOT Ed operandi che possono
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Operatori logici e porte logiche
 Operatori logici e porte logiche Operatori unari.......................................... 730 Connettivo AND........................................ 730 Connettivo OR..........................................
Operatori logici e porte logiche Operatori unari.......................................... 730 Connettivo AND........................................ 730 Connettivo OR..........................................
Quanto può essere veloce un upload e un download?
 Quanto può essere veloce un upload e un download? Download trasferimento di dati da un computer remoto al computer locale Upload trasferimento dei dati da un computer locale a un computer remoto Velocità
Quanto può essere veloce un upload e un download? Download trasferimento di dati da un computer remoto al computer locale Upload trasferimento dei dati da un computer locale a un computer remoto Velocità
la scienza della rappresentazione e della elaborazione dell informazione
 Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Sistema binario Sommario informatica rappresentare informazioni la differenza Analogico/Digitale i sistemi di numerazione posizionali il sistema binario Informatica Definizione la scienza della rappresentazione
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione dell informazione negli elaboratori
 Informazione e computer Si può rappresentare l informazione attraverso varie forme: Numeri Testi Suoni Immagini 0001010010100101010 Computer Cerchiamo di capire come tutte queste informazioni possano essere
Informazione e computer Si può rappresentare l informazione attraverso varie forme: Numeri Testi Suoni Immagini 0001010010100101010 Computer Cerchiamo di capire come tutte queste informazioni possano essere
Informatica Generale (Prof. Luca A. Ludovico) Presentazione 5.1 Operazioni aritmetiche nel sistema binario
 Operazioni aritmetiche nel sistema binario Operazioni aritmetiche basilari Le regole da imparare nel caso di una base b sono relative alle b 2 possibili combinazioni delle cifre da 0 a b- 1. Ad esempio,
Operazioni aritmetiche nel sistema binario Operazioni aritmetiche basilari Le regole da imparare nel caso di una base b sono relative alle b 2 possibili combinazioni delle cifre da 0 a b- 1. Ad esempio,
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
CODIFICA BINARIA. ... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità.
 I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
I METODI DI NUMERAZIONE I numeri naturali... sono rappresentati ricorrendo a simboli che sintezzano il concetto di numerosità. Il numero dei simboli usati per valutare la numerosità costituisce la base
Corso di Informatica
 Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Linguaggio del calcolatore. Algebra di Boole AND, OR, NOT. Notazione. And e or. Circuiti e reti combinatorie. Appendice A + dispense
 Linguaggio del calcolatore Circuiti e reti combinatorie ppendice + dispense Solo assenza o presenza di tensione: o Tante componenti interconnesse che si basano su e nche per esprimere concetti complessi
Linguaggio del calcolatore Circuiti e reti combinatorie ppendice + dispense Solo assenza o presenza di tensione: o Tante componenti interconnesse che si basano su e nche per esprimere concetti complessi
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
L INNOVAZIONE SCIENTIFICO-TECNOLOGICA NEI PROCESSI PRODUTTIVI
 L INNOVAZIONE SCIENTIFICO-TECNOLOGICA NEI PROCESSI PRODUTTIVI Scienza ed industria hanno oggi costituito legami molto forti di collaborazione che hanno portato innovazione tecnologica sia a livello organizzativo-amministrativo
L INNOVAZIONE SCIENTIFICO-TECNOLOGICA NEI PROCESSI PRODUTTIVI Scienza ed industria hanno oggi costituito legami molto forti di collaborazione che hanno portato innovazione tecnologica sia a livello organizzativo-amministrativo
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Algebra di Boole. Le operazioni, nell algebra booleana sono basate su questi tre operatori: AND ( ), OR ( + ),NOT ( )
 Algebra di Boole L algebra di Boole prende il nome da George Boole, matematico inglese (1815-1864), che pubblicò un libro nel 1854, nel quale vennero formulati i principi dell'algebra oggi conosciuta sotto
Algebra di Boole L algebra di Boole prende il nome da George Boole, matematico inglese (1815-1864), che pubblicò un libro nel 1854, nel quale vennero formulati i principi dell'algebra oggi conosciuta sotto
C. P. U. MEMORIA CENTRALE
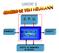 C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
Rappresentazione dei numeri in un calcolatore
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Corso di Calcolatori Elettronici I A.A. 2010-2011 Rappresentazione dei numeri in un calcolatore Lezione 2 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Rappresentazione dei numeri
Utilizzo I mintermini si usano quando si considererà la funzione di uscita Q come Somma di Prodotti (S. P.) ossia OR di AND.
 IPSI G. Plana Via Parenzo 46, Torino efinizione di Mintermine onsiderata una qualunque riga della tabella di verità in cui la funzione booleana di uscita Q vale, si definisce mintermine il prodotto logico
IPSI G. Plana Via Parenzo 46, Torino efinizione di Mintermine onsiderata una qualunque riga della tabella di verità in cui la funzione booleana di uscita Q vale, si definisce mintermine il prodotto logico
Funzioni. Funzioni /2
 Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Memorie ROM (Read Only Memory)
 Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
Memorie ROM (Read Only Memory) Considerando la prima forma canonica, la realizzazione di qualsiasi funzione di m variabili richiede un numero di porte AND pari al numero dei suoi mintermini e di prolungare
Dall Algoritmo al Programma. Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni
 Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
Dall Algoritmo al Programma Prof. Francesco Accarino IIS Altiero Spinelli Sesto San Giovanni IL PROGRAMMA Gli algoritmi sono modelli di descrizione astratti e per controllarne il funzionamento devono essere
SOMMARIO. 13.1 I radicali pag. 3. 13.2 I radicali aritmetici pag. 5. 13.3 Moltiplicazione e divisione fra radicali aritmetici pag.
 SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
CONCETTI BASE dell'informatica Cose che non si possono non sapere!
 CONCETTI BASE dell'informatica Cose che non si possono non sapere! Pablo Genova I. I. S. Angelo Omodeo Mortara A. S. 2015 2016 COS'E' UN COMPUTER? È una macchina elettronica programmabile costituita da
CONCETTI BASE dell'informatica Cose che non si possono non sapere! Pablo Genova I. I. S. Angelo Omodeo Mortara A. S. 2015 2016 COS'E' UN COMPUTER? È una macchina elettronica programmabile costituita da
La Logica Proposizionale. (Algebra di Boole)
 1 ISTITUTO DI ISTRUZIONE SUPERIORE ANGIOY La Logica Proposizionale (Algebra di Boole) Prof. G. Ciaschetti 1. Cenni storici Sin dagli antichi greci, la logica è intesa come lo studio del logos, che in greco
1 ISTITUTO DI ISTRUZIONE SUPERIORE ANGIOY La Logica Proposizionale (Algebra di Boole) Prof. G. Ciaschetti 1. Cenni storici Sin dagli antichi greci, la logica è intesa come lo studio del logos, che in greco
La misura degli angoli
 La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
Predicati e Quantificatori
 Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
Algoritmi e strutture dati. Codici di Huffman
 Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
Operazioni binarie fondamentali
 Operazioni binarie fondamentali Operazioni fondamentali: operazioni elementari sui bit. Sono definite le operazioni aritmetiche più le operazioni logiche (AND, OR, NOT). Le operazioni possono essere descritte
Operazioni binarie fondamentali Operazioni fondamentali: operazioni elementari sui bit. Sono definite le operazioni aritmetiche più le operazioni logiche (AND, OR, NOT). Le operazioni possono essere descritte
Semantica operazionale dei linguaggi di Programmazione
 Semantica operazionale dei linguaggi di Programmazione Oggetti sintattici e oggetti semantici Rosario Culmone, Luca Tesei Lucidi tratti dalla dispensa Elementi di Semantica Operazionale R. Barbuti, P.
Semantica operazionale dei linguaggi di Programmazione Oggetti sintattici e oggetti semantici Rosario Culmone, Luca Tesei Lucidi tratti dalla dispensa Elementi di Semantica Operazionale R. Barbuti, P.
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Obiettivi dell Analisi Numerica. Avviso. Risoluzione numerica di un modello. Analisi Numerica e Calcolo Scientifico
 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
Gian Luca Marcialis studio degli algoritmi programma linguaggi LINGUAGGIO C
 Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
Università degli Studi di Cagliari Corso di Laurea in Ingegneria Biomedica (Industriale), Chimica, Elettrica, e Meccanica FONDAMENTI DI INFORMATICA 1 http://www.diee.unica.it/~marcialis/fi1 A.A. 2010/2011
Comparatori. Comparatori di uguaglianza
 Comparatori Scopo di un circuito comparatore é il confronto tra due codifiche binarie. Il confronto può essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo "maggiore",
Comparatori Scopo di un circuito comparatore é il confronto tra due codifiche binarie. Il confronto può essere effettuato per verificare l'uguaglianza oppure una relazione d'ordine del tipo "maggiore",
Anno 1. Le relazioni fondamentali (equivalenza, d'ordine, inverse, fra insiemi)
 Anno 1 Le relazioni fondamentali (equivalenza, d'ordine, inverse, fra insiemi) 1 Introduzione In questa lezione imparerai a utilizzare le diverse tipologie di relazione e a distinguerle a seconda delle
Anno 1 Le relazioni fondamentali (equivalenza, d'ordine, inverse, fra insiemi) 1 Introduzione In questa lezione imparerai a utilizzare le diverse tipologie di relazione e a distinguerle a seconda delle
APPUNTI DI ELETTRONICA DIGITALE
 APPUNTI DI ELETTRONICA DIGITALE ITIS MARCONI-GORGONZOLA docente :dott.ing. Paolo Beghelli pag.1/24 Indice 1.ELETTRONICA DIGITALE 4 1.1 Generalità 4 1.2 Sistema di numerazione binario 4 1.3 Operazioni con
APPUNTI DI ELETTRONICA DIGITALE ITIS MARCONI-GORGONZOLA docente :dott.ing. Paolo Beghelli pag.1/24 Indice 1.ELETTRONICA DIGITALE 4 1.1 Generalità 4 1.2 Sistema di numerazione binario 4 1.3 Operazioni con
Ancora sugli insiemi. Simbologia
 ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
Reti Logiche. Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali.
 Reti Logiche Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali. - Elaborano informazione rappresentata da segnali digitali, cioe
Reti Logiche Le reti logiche sono gli elementi architettonici di base dei calcolatori, e di tutti gli apparati per elaborazioni digitali. - Elaborano informazione rappresentata da segnali digitali, cioe
Codifica delle Informazioni
 Codifica delle Informazioni Luca Bortolussi Dipartimento di Matematica e Informatica Università degli studi di Trieste Panoramica Le informazioni gestite dai sistemi di elaborazione devono essere codificate
Codifica delle Informazioni Luca Bortolussi Dipartimento di Matematica e Informatica Università degli studi di Trieste Panoramica Le informazioni gestite dai sistemi di elaborazione devono essere codificate
Algebra Booleana ed Espressioni Booleane
 Algebra Booleana ed Espressioni Booleane Che cosa è un Algebra? Dato un insieme E di elementi (qualsiasi, non necessariamente numerico) ed una o più operazioni definite sugli elementi appartenenti a tale
Algebra Booleana ed Espressioni Booleane Che cosa è un Algebra? Dato un insieme E di elementi (qualsiasi, non necessariamente numerico) ed una o più operazioni definite sugli elementi appartenenti a tale
Compito DA e BD. Tempo concesso: 90 minuti 12 giugno 03 Nome: Cognome: Matricola: Esercizio 1
 Compito DA e BD. Tempo concesso: 90 minuti 12 giugno 03 Nome: Cognome: Matricola: Esercizio 1 Si considerino le seguenti specifiche relative alla realizzazione della base di dati di una facoltà e si definisca
Compito DA e BD. Tempo concesso: 90 minuti 12 giugno 03 Nome: Cognome: Matricola: Esercizio 1 Si considerino le seguenti specifiche relative alla realizzazione della base di dati di una facoltà e si definisca
Una proposizione è una affermazione di cui si possa stabilire con certezza il valore di verità
 Logica 1. Le roosizioni 1.1 Cosa studia la logica? La logica studia le forme del ragionamento. Si occua cioè di stabilire delle regole che ermettano di assare da un'affermazione vera ad un'altra affermazione
Logica 1. Le roosizioni 1.1 Cosa studia la logica? La logica studia le forme del ragionamento. Si occua cioè di stabilire delle regole che ermettano di assare da un'affermazione vera ad un'altra affermazione
