PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2005/06
|
|
|
- Vittore Guerra
- 6 anni fa
- Visualizzazioni
Transcript
1 PROVE SCRITTE DI MTEMTIC PPLICT, NNO 5/6 Esercizio 1 Prova scritta del 14/1/5 Sia X ua successioe I.I.D. di variabili aleatorie co distribuzioe uiforme cotiua, X U(, M), ove M = umero lettere del cogome. Si deoti poi per ogi > co Y la v.a. defiita da Y = 1 max{x 1,..., X }. Per ciascu itero si calcolio E(Y ), E(Y ), V (Y ), e si trovi la desita di Y ; si studi ifie se, a cosa, e i che modo la successioe (Y ) coverge. Esercizio 1 palle umerate vegoo iserite a caso i 3 scatole, seza alcua limitazioe. Per k = 1,, 3, si deoti co X k la variabile aleatoria che deota il umero di palle capitate ella scatola k-esima. Cosiderato che le v.a. X k hao tutte la stessa distribuzioe (di tipo biomiale), si valutio le quatita : E(X 1 ), E(X 1 X = j ), E(X 1 X X = j ). Si deduca ifie la covariaza cov(x 1, X ). Esercizio 3 La seguete tabella riporta i risultati di u idagie codotta su u campioe di 6 itervistati tra i 3 e i 35 ai di ua certa regioe rispetto ai caratteri titolo di studio e stato occupazioale : Occupati Disoccupati Laureati 6 15 No laureati a) Da u idagie precedete e oto che, tra tutti coloro che lavorao, la percetuale dei laureati e pari al 38%. Verificare tale ipotesi (H ) cotro l alterativa (H 1 ) che la percetuale sia iferiore al 38%, co u test di livello di sigificativita del 5%. b) Verificare l ipotesi di idipedeza tra il titolo di studio e lo stato occupazioale, co a =.1. (Detta Φ la fuzioe di ripartizioe della distribuzioe ormale N(, 1), utilizzare la seguete tabella: 1
2 Φ(1.645).95 Φ(1.96).975 Φ(.33).99 Φ(.58).995) Soluzioi compito 14/1/5 Esercizio 1 F : Iazitutto, troviamo la fuzioe di ripartizioe di Y, che deotiamo co F (x) = [P ( X 1 x )] = ( x M ), aturalmete per < x < M. Ne deriva che la desita di Y é la fuzioe φ defiita da per < x < M, e ulla altrove. Ne deriva E(Y ) = M M x dx = M V (Y ) = M Di cosegueza, si ha E(Y ) = φ (x) = M x 1, M + 1, E((Y ) ) = M x+1 dx = M + M ( + 1) = M ( + 1) ( + ). M + 1, V (Y ) = M ( + 1) ( + ). Per ote regole, deotado co f la desita di Y, avremo poi +, per x [, M/], e altrove. f (x) = φ (x) = +1 M x 1, Per quato riguarda la covergeza, si sa gia per motivi teorici che (Y ) coverge q.c. e i L a M, per cui (Y ) coverge q.c. e i L a. Esercizio Evidetemete, ciascua variabile X k ha distribuzioe B(1, 1 ). 3 Di cosegueza, E(X 1 ) = 1. 3 Supposto che si abbia X = j, per le altre due scatole restao 1 j palle dispoibili, quidi la distribuzioe codizioata per X 1 é di tipo B(1 j, 1 ). Duque E(X 1 X = j ) = 1 j, e E(X 1 X X = j ) = j 1 j.
3 Ora, si puo calcolare E(X 1 X ), come segue: E(X 1 X ) = 1 j= E(X 1 X X = j )P ( X = j ) = 1 j= j 1 j ( ) 1 ( 1 j 3 )j ( 1 3 )1 j = = 5E(X ) 1 E(X ) = (V (X ) + E (X )) = ( = 1. Ifie, cov(x 1, X ) = E(X 1 X ) E(X 1 )E(X ) = ) = 1 9. Esercizio 3 a) Viee richiesto u test uidirezioale dove l ipotesi ulla e H : p = p =.38, cotro l ipotesi alterativa H 1 : p < p. Essedo grade si puo sfruttare l approssimazioe ormale. Si rifiuta pertato l ipotesi ulla se p (1 p ) p < p z a dove = 195 e, dalla tabella, risulta z a 1.645, duque la zoa di rifiuto e R = {ˆp : ˆp <.3}. Poiche, dai dati del campioe, risulta ˆp.38, l ipotesi ulla va rifiutata e si propede per ua dimiuzioe della percetuale. b) Completado la tabella co le margiali si ottiee Occupati Disoccupati Totale Laureati No laureati Totale Viee richiesto u test per l idipedeza, duque la statistica test e X = r s ( i,j i,,j /) j=1 i,,j / che puo essere approssimata co ua χ co (r 1)(s 1) = 1 gradi di liberta. Pertato la zoa di rifiuto del test e R = {X : X > χ a} dove, essedo a =.1, e χ a = χ.1 = Sulla base dei dati risulta X = ( /6) /6 ( /6) /6 duque si accetta l ipotesi ulla di idipedeza. ( /6) ( /6) / /6 1.45, Prova scritta del 11/1 /6 3
4 Esercizio 1 Si deoti co B il umero di lettere del cogome. Siao X e Y due variabili aleatorie idipedeti, co distribuzioe cotiua, di tipo U(, 1). Posto U = log X, e Z = Y + U, si determii la desita di Z, e si calcoli la probabilita che risulti Z < B. Esercizio Sia il umero delle lettere del ome. U recipiete cotiee iizialmete palle biache e 4 ere. Si effettua ua prima estrazioe casuale, e si poe X 1 = 1, se esce palla biaca, altrimeti X 1 =. Successivamete, si aggiugoo el recipiete altre 4 palle ere, e si procede ad ua secoda estrazioe casuale: si porra X = 1 se ella secoda estrazioe esce palla biaca, e altrimeti. Si prosegue i questo modo, raddoppiado ogi volta il umero di palle ere ell ura, e lasciadovi sempre palle biache, e segado X = 1 se all estrazioe -esima esce palla biaca, altrimeti. Posto per ogi : si calcoli S = X i, a) se e a cosa coverge q.c. la successioe (X ) ; b) se e a cosa coverge q.c. la successioe delle medie (X ) = ( S ) ; c) se e a cosa coverge la successioe umerica E(S ). Esercizio 3 Si cosideri la fuzioe f(x; λ, θ) = { λe k(x θ), x θ, x < θ co k IR, λ >. Dopo aver determiato k tale che f(x; λ, θ) sia la fuzioe di desita di ua variabile aleatoria X, si chiede di (a) determiare h IR tale che Y = X + h, co Y exp(λ); (b) forire uo stimatore di λ co il metodo della massima verosimigliaza sulla base di u campioe casuale X 1,..., X ; (c) forire uo stimatore di θ co il metodo della massima verosimigliaza sulla base di u campioe casuale X 1,..., X. Soluzioi compito 11/1 /6 4
5 Esercizio 1 E oto che la variabile U ha distribuzioe Γ(1, 1), co desita { e u, u > f U (u) =, u <. Poiché X e Y soo idipedeti, lo soo ache U e Y, e quidi, per determiare la desita di Z, basta usare la formula di covoluzioe: f Z (z) = + f U (z y)f Y (y)dy = 1 f U (z y)dy, i quato la desita di Y o é altro che la fuzioe idicatrice dell itervallo [, 1]. Ioltre, poiché f U é o ulla solo quado l argometo é positivo, dobbiamo vicolare l itegrale alla codizioe y < z (e duque z >, com é aturale). L itegrale da risolvere é quidi 1 z e y z dy = e z (e 1 z 1), dove sta per miimo. Duque, z < f Z (z) = 1 e z, < z < 1 e z (e 1), z > 1. La probabilita che risulti Z < B o é altro che l itegrale Esercizio B f Z (z)dz = 1 (1 e z )dz + B 1 (e 1)e z dz = eb e + 1 e B. Chiaramete, ciascua variabile X ha distribuzioe B(1, p ), ove p 1 = 4 +, p = 8 + = 4 +, p 3 = Di cosegueza, risulta E(X ) = +1 +, V (X ) = per ogi. Da cio segue subito che : 4 +,..., p = +1 + ( ), E(S ) = +1 +,... j=1 + j+1 1) la serie delle variaze di X é covergete; di cosegueza, dato ache che lim E(X ) =, e segue che la successioe (X ) coverge quasi certamete a. Pertato, ache la successioe delle medie (X ) coverge q.c. a. ) + =1 E(X ) coverge; di cosegueza, la successioe (E(S )) coverge alla somma di tale serie. 5
6 Esercizio 3 Osserviamo iazitutto che si deve avere quidi k = λ. + θ λe k(x θ) dx = λ k = 1, (a) E immediato verificare che F Y (y) = F X (y + h), per cui la desita di Y é f Y (y) = { λe λ(y+h θ), y θ h, y < θ h e duque Y ha ua distribuzioe espoeziale co parametro λ se h = θ. (b) I virtu dell idipedeza la fuzioe di verosimigliaza é e duque L(x 1,..., x ; λ, θ) = λ e λ(x i θ), log L(x 1,..., x ; λ, θ) = log λ λ Dallo studio della derivata prima si ha mi x i θ 1 i, mi 1 i x i < θ (x i θ). λ log L(x 1,..., x ; λ, θ) = λ (x i θ) = se ˆλ = Essedo λ log L(x 1,..., x ; λ, θ) = λ <, lo stimatore di massima verosimigliaza di λ é ˆλ = x i θ. x i θ. (c) Voledo massimizzare rispetto a θ, si osserva immediatamete che la fuzioe di verosimigliaza é crescete al crescere di θ, fitato che θ mi x i, metre 1 i si aulla o appea θ > mi x i. Cio implica che lo stimatore di massima 1 i verosimigliaza é ˆθ = mi x i. 1 i Prova scritta del 4/3 /6 6
7 Esercizio 1 Ua gallia depoe ogi gioro N uova, dove N ha distribuzioe di Poisso co parametro λ. Ciascu uovo ha, idipedetemete da ogi altro, probabilita p di schiudersi dado vita ad u pulcio. Detto X il umero di pulcii ati, si determii E(X). Si dica ioltre se X ha distribuzioe di Poisso, e co quale parametro. Esercizio Siao X e Y due v.a. idipedeti, etrambe di tipo N(, 1). Si determii la distribuzioe della v.a. Z = X + Y, e se e valutio valor medio e variaza. Si trovi ifie la mediaa di Z, ossia quel valore reale x m tale che P (Z < x m ) = P (Z > x m ). Esercizio 3 Su ati i u ospedale i u ao, 9 bambii hao i capelli chiari, di cui co gli occhi scuri; tra i bimbi co i capelli scuri, hao gli occhi chiari. a) Nell ambito dei bambii co gli occhi scuri, costruire u itervallo di cofideza al 95% per la proporzioe di quelli che hao i capelli scuri. b) Sia p la probabilità di ascere co i capelli chiari e ˆp la sua stima campioaria. ssumedo che la variaza campioaria sia.4/, quato deve essere grade il campioe affiché l errore ˆp p sia iferiore a.1 co probabilità.98? (Detta Φ la fuzioe di ripartizioe della distribuzioe ormale N(, 1), utilizzare la seguete tabella: Φ(1.645).95 Φ(1.96).975 Φ(.33).99 Φ(.58).995) Soluzioi compito 4/3/6 Esercizio 1 Utilizzado il teorema del valor medio iterato, si ha E(X) = + j= E(X N = j)p (N = j) = + j= pj λj e λ j! = pe(n) = pλ. Per determiare la distribuzioe di X, si puo procedere i maiera aaloga: si ha, per ogi itero k : P (X = k) = + j=k P (X = k N = j)p (N = j) = 7 + j=k ( j )p k j k λj (1 p) k j! e λ =
8 + = h= (pλ) k k! λ h (1 p) h h! e λ = (pλ)k k! Cio dimostra che i effetti si ha X P (λp). e λ e λ(1 p) = (pλ)k k! e (λp). Esercizio Com é oto, la v.a. U = X + Y ha distribuzioe χ, quidi ha desita f U (u) = 1 e u, aturalmete per u >. Per determiare la distribuzioe di Z = U, cerchiamo la sua fuzioe di ripartizioe: F Z (z) = P (U z ) = F U (z ) (sempre co z > ). Duque, la desita di Z é f Z (z) = zf U (z ) = z e z, z >. Per valutare E(Z), basta itegrare: E(Z) = + z e z dz = + v 1 e v dv = Γ( 3 ) = π. Chiaramete poi si ha E(Z ) = E(U) =, da cui V (Z) = E(Z ) E (Z) = π. Ifie, la mediaa x m di Z si trova mediate la relazioe: 1 xm = u e u / du = 1 e x m /. Risolvedo, si ha facilmete il risultato: x m = log. Esercizio 3 a) Se X è la variabile aleatoria dei bimbi co i capelli scuri, all itero della popolazioe co gli occhi scuri, X ha ua distribuzioe biomiale co probabilità di successo p. Sfruttado l approssimazioe ormale, l itervallo di cofideza ha ˆp(1 ˆp) estremi ˆp±z a, dove ˆp = 8/11 =.8, = 11 e, dalla tabella, z a Pertato l itervallo di cofideza cercato è [ ] , [.75,.875]
9 Occhi Chiari Occhi Scuri Totale Capelli Chiari 7 9 Capelli Scuri Totale 9 11 b) Voledo per semplicità rappresetare i dati co ua tabella dove sulle righe abbiamo il carattere colore dei capelli, metre sulle coloe troviamo il carattere colore degli occhi, risulta Vogliamo determiare tale che P ( ˆp p <.1) =.98, ovvero P ˆp p.4 ˆp p.98. Essedo.4 N(, 1), dalla tabella si ottiee.1.4 = , e duque il campioe deve essere almeo di 18 bambii. <.1.4 = =.33, da cui Esercizio 1 Prova scritta del 8/9/6 Soo date tre variabili aleatorie IID, X, Y, Z, tutte co distribuzioe cotiua uiforme i [, 1]. Si calcoli la probabilita dell eveto X Y Z. Esercizio U recipiete cotiee iizialmete due pallie umerate, la.1 e la.. Si estrae ua palla a caso, e si deota co X 1 il umero della palla estratta. Idi, la palla estratta si rimette ell ura, isieme co ua terza palla, segata co il.3. lla secoda estrazioe, si deota co X il umero della palla estratta, e poi si procede allo stesso modo, cosi al mometo della terza estrazioe ell ura soo preseti 4 palle, co i umeri da 1 a 4. Si va avati cosi idefiitamete, idicado ogi volta co X il umero della palla estratta alla -esima estrazioe, umero che varia tra 1 e + 1. Posto poi Y = X +1 per ogi, si studi la covergeza delle variabili Y, per. Esercizio 3 I segueti dati campioari si riferiscoo alla durata (i migliaia di ore) di due tipi di lampadie, e B, prodotti da ua ditta B
10 ssumedo che le due popolazioi abbiao distribuzioe ormale co variaze σ = 1, σb = 9.5, rispettivamete, si chiede di: a) costruire u itervallo di cofideza al 99% per la durata media delle lampadie ella popolazioe ; b) sottoporre a verifica l ipotesi (H ) che i due prodotti abbiao la stessa durata media, cotro l alterativa (H 1 ) che sia u prodotto migliore di B, al livello di sigificatività a =.5. (Detta Φ la fuzioe di ripartizioe della distribuzioe ormale N(, 1), utilizzare la seguete tabella: Φ(1.645).95 Φ(1.96).975 Φ(.33).99 Φ(.58).995) Soluzioi compito 8/9/6 Esercizio 1 Per ogi valore possibile z [, 1] si ha P ( X Y z) = 1 (1 z), come varie volte osservato. Cosiderata l idipedeza, e la distribuzioe supposta per Z, la probabilita cercata é data da: Esercizio P ( X Y Z) = 1 (1 (1 z) )dz = = 3. Chiaramete, si ha X U( + 1) per ogi (distribuzioe discreta uiforme). Di cosegueza, si ha Y [, 1], sempre co distribuzioe discreta. Per ogi reale positivo t 1, avremo P ([Y t]) = P ([X ( + 1)t]) = [( + 1)t] + 1, ove la scrittura [x] sta ad idicare, per x reale, la parte itera di x, ossia il piu grade umero itero che sia miore o uguale a x. Duque, la quatita [( + 1)t] differisce da ( + 1)t al piu per 1. Ne segue che lim P ([Y t]) = t e quidi le fuzioi di ripartizioe delle Y covergoo a quella della distribuzioe cotiua U(, 1). Duque, le Y covergoo i distribuzioe alla uiforme cotiua U(, 1). 1
11 Esercizio 3 a) Se X è la variabile aleatoria che rappreseta la durata di, si trova che la media campioaria è pari a: X = 6 x,i Sotto l ipotesi ormale si ha X X σ N(, 1), da cui l itervallo di cofideza ha estremi X ± z a cofideza cercato è [ σ, dove, dalla tabella, z a , Pertato l itervallo di ] [31.837, ]. b) Si tratta di u test uidirezioale dove l ipotesi ulla è H : µ µ B =, cotro l ipotesi alterativa H 1 : µ µ B >, idicado co µ e µ B le medie delle due popolazioi. Poiché le due popolazioi hao distribuzioe ormale, si rifiuta l ipotesi ulla se z > z a dove z = X X 6 B. Essedo X e X B = x B,i σ 6 + σ B 3.333, risulta z.68, metre i base alla tabella z a 1.645; l ipotesi ulla pertato va rifiutata e si è portati a cocludere che è effettivamete u prodotto migliore di B. 11
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL 1/2/2011
 CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Esercizi di Probabilità e Statistica Samuel Rota Bulò 24 maggio 26 Desità e distribuzioi cogiute e codizioate. Covergeza e approssimazioe Esercizio Uo studio dice che l ivestimeto i titoli di stato, rappresetato
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 07/02/2017
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 07/02/207 COGNOME e NOME... N. MATRICOLA... Esercizio. Sia {X } N ua martigala rispetto ad ua filtrazioe {F } N co P (X N) = per ogi
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di econometria: serie 2
 Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Il risultato di una prova è un n. aleatorio Funzioni degli esiti: Ω IR X, Y, Z,... funzioni, X(ω), Y (ω), Z(ω)
 Variabili aleatorie (v.a.) Il risultato di ua prova è u. aleatorio Fuzioi degli esiti: Ω IR X, Y, Z,... fuzioi, X(ω), Y (ω), Z(ω) se B IR, P(X B) = = P({ω Ω : X(ω) B}) = P(X 1 (B)) I geerale iteressa B
Variabili aleatorie (v.a.) Il risultato di ua prova è u. aleatorio Fuzioi degli esiti: Ω IR X, Y, Z,... fuzioi, X(ω), Y (ω), Z(ω) se B IR, P(X B) = = P({ω Ω : X(ω) B}) = P(X 1 (B)) I geerale iteressa B
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Università degli Studi di Salerno Pietro Coretto. Corso di Statistica FORMULARIO
 Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
P(X = k) = (k 1). 2 Infatti, le uniche sequenze di lunghezza k (di T e C) possibili sono
 Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
Prima Prova Itermedia testo co soluzioi 5 Aprile 09 Elemeti di Probabilità e Statistica, Laurea Trieale i Matematica, 08-9 M Romito, M Rossi Problema 0 Ua moeta equa viee laciata fio alla prima volta i
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Probabilità 1, laurea triennale in Matematica II prova scritta sessione estiva a.a. 2008/09
 Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Probabilità, laurea trieale i Matematica II prova scritta sessioe estiva a.a. 8/9. U ura cotiee dadi di cui la metà soo equilibrati, metre gli altri soo stati maipolati i modo che, per ciascuo di essi,
Esercitazione X Complementi di Probabilità a.a. 2011/2012
 Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Esercitazioe X Complemeti di Probabilità a.a. 20/202 Argometi: covergeza e TLC. Esercizio. Sia {X k } k ua successioe di v.a. i.i.d. di legge Exp(. Sia G = S,. a Scrivere la fuzioe caratteristica φ di
Traccia delle soluzioni degli esercizi del fascicolo 3
 Traccia delle soluzioi degli esercizi del fascicolo 3 Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo,
Traccia delle soluzioi degli esercizi del fascicolo 3 Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo,
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Soluzioni quarta esercitazione
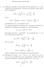 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Esercitazione n Supponendo che i giorni lavorativi in un anno siano 340, quanti chilometri percorre mediamente un tir in un anno?
 Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Traccia delle soluzioni degli esercizi del fascicolo 6
 Traccia delle soluzioi degli esercizi del fascicolo 6 Esercizio Vegoo geerati umeri casuali tra 0 e, co distribuzioe uiforme. Quati umeri è ecessario geerare affiché la probabilità che la somma di essi
Traccia delle soluzioi degli esercizi del fascicolo 6 Esercizio Vegoo geerati umeri casuali tra 0 e, co distribuzioe uiforme. Quati umeri è ecessario geerare affiché la probabilità che la somma di essi
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
ESERCITAZIONE N. 6 corso di statistica
 ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
IV Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2011/12 Nome: 17 luglio
 IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
IV Appello di Calcolo delle Probabilità Cogome: Laurea Trieale i Matematica / Nome: 7 luglio Email: Quado o è espressamete idicato il cotrario, per la soluzioe degli esercizi è possibile usare tutti i
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Capitolo Parte V
 Capitolo 1 1.1 Parte V Exercise 1.1. Sia X ua variabile aleatoria, defiita su (Ω,P a valori i E, quasi certamete costate, ossia esiste c E tale che P(X = c = 1. Si mostri che esiste u uico elemeto c E
Capitolo 1 1.1 Parte V Exercise 1.1. Sia X ua variabile aleatoria, defiita su (Ω,P a valori i E, quasi certamete costate, ossia esiste c E tale che P(X = c = 1. Si mostri che esiste u uico elemeto c E
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA
 UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a Esame del STATISTICA
 FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
Caso studio 9. Distribuzioni doppie. Esempi
 7/3/16 Caso studio 9 Si cosideri la seguete tabella che riporta i dati dei Laureati el 4 dei tre pricipali gruppi di corsi di laurea, per codizioe occupazioale a tre ai dalla laurea (Fote: ISTAT, Idagie
7/3/16 Caso studio 9 Si cosideri la seguete tabella che riporta i dati dei Laureati el 4 dei tre pricipali gruppi di corsi di laurea, per codizioe occupazioale a tre ai dalla laurea (Fote: ISTAT, Idagie
Lezioni del Corso di Fondamenti di Metrologia Meccanica
 Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Facoltà di Igegeria Lezioi del Corso di Fodameti di Metrologia Meccaica A.A. 005-006 Prof. Paolo Vigo Idice. Frequeza e Probabilità. 3. Curva di Gauss 4. Altre Distribuzioi Frequeza e Probabilità Me spiego:
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Formulario (versione del 3/10/2015)
 Uiversità degli Studi della Basilicata C.d.L. Ecoomia Aziedale Statistica a.a. 04/05 Docete: E. Di Nardo Frequeze Formulario versioe del 3/0/05 taglia campioe casuale x,..., x campioe casuale ordiato x...
Uiversità degli Studi della Basilicata C.d.L. Ecoomia Aziedale Statistica a.a. 04/05 Docete: E. Di Nardo Frequeze Formulario versioe del 3/0/05 taglia campioe casuale x,..., x campioe casuale ordiato x...
Test Statistici. In termini statistici, agli eventi appena indicati viene attribuita una probabilità ed una specifica definizione:
 Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
ESERCITAZIONE VII. H 0 : μ = 500. H 1 : μ > /3.16 = = 3.403
 ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Esercizi - Fascicolo III
 Esercizi - Fascicolo III Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo, idipedetemete dagli altri,
Esercizi - Fascicolo III Esercizio I ua procedura di cotrollo di produzioe, processori prodotti da u processo idustriale vegoo sottoposti a cotrollo Si assuma che ogi pezzo, idipedetemete dagli altri,
Tutoraggio AM1 17/12/2015. sin(x) arctan(x) 2) lim sup / inf x 0 + cos(x) sin( 1 x ) e x2 cos 2 (x 3 ) x 2 + ln(3x + 2) δ(x) δ(x) =
 Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
