Algoritmi e strutture dati
|
|
|
- Rosa Mazza
- 6 anni fa
- Visualizzazioni
Transcript
1 Algoritmi e strutture dati Roberto Cordone A. A
2 Capitolo 3 Implementazioni dei dizionari ordinati Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio In buona parte ripetono gli argomenti delle dispense del prof. Goldwurm, con alcune aggiunte, qualche piccola modifica nella presentazione, qualche esempio. Chi notasse errori, incoerenze, oscurità o avesse dubbi è invitato a contattarmi per segnalarli. 3.3 Alberi 2-3 Il problema fondamentale degli alberi binari di ricerca è la possibilità di incontrare il proprio caso pessimo (dati inseriti in modo ordinato), che rendono le operazioni inefficienti, cioè O (n) anziché O (log n). Per evitare questo problema esistono altre strutture la cui topologia viene dinamicamente aggiornata per conservare il bilanciamento. Un albero 2-3 si definisce come un albero con foglie tutte allo stesso livello; nodi interni tutti dotati di 2 o 3 sottoalberi: indicheremo i sottoalberi del nodo r con T 1 (r), T 2 (r) e T 3 (r); etichette sulle foglie associate agli elementi di un dizionario: E (r) A; tutte le foglie di un sottoalbero hanno etichette inferiori a quelle delle foglie di un sottoalbero successivo: E (u) < E (v) per ogni u T i (r), v T j (r) tale che i < j (i = 1, 2 e j = 2, 3). Negli alberi 2-3, le informazioni stanno sulle foglie, e i nodi interni servono solo a guidare la ricerca. Un albero di altezza h (livelli da 0 a h) ha almeno 2 h foglie e al massimo 3 h foglie. Se indichiamo con n gli elementi del dizionario, l altezza è compresa fra log 3 n e log 2 n. Se invece indichiamo con n tutti i nodi, compresi quelli interni, l espressione è più complicata: log 3 1 h log 2 n Ogni nodo v interno di un albero 2-3 contiene due informazioni ausiliarie: la chiave massima L v di tutte le foglie del primo sottoalbero T 1 (v) la chiave massima M v di tutte le foglie del secondo sottoalbero T 2 (v) 1
3 Un albero 2-3 radicato in v rappresenta una specie di sequenza ordinata divisa in tre sottosequenze; L v e M v sono gli elementi massimi delle prime due sottosequenze, cioè i punti di separazione fra le tre sottosequenze. Si noti che si può usare in alternativa la convenzione che L v e M v siano le chiavi degli elementi minimi delle ultime due sottosequenze. Esempio: disegnare (1, 2, 3, 4, 6, 8) come albero 2-3 di altezza h = 2, con tre coppie o due terne di foglie. Un implementazione diretta è quella con puntatori: struct _elemento A *a; int L; int M; struct _elemento *T1; struct _elemento *T2; struct _elemento *T3; struct _elemento *father; ; typedef struct _elemento *node; typedef struct _elemento *tree2_3; tree2_3 T; dove un albero T è visto come un puntatore al nodo radice, e i nodi contengono un puntatore a all informazione di tipo A (usato solo nelle foglie), due chiavi intere L e M, massime dei primi due sottoalberi (nel caso delle foglie, entrambe pari alla chiave dell elemento), tre sottoalberi e un puntatore father verso il nodo padre. Al solito, è possibile un implementazione alternativa, che fa uso di un vettore di strutture, ed è praticamente identica, salvo sostituire i puntatori con indici numerici struct _elemento A *a; int L; int M; int T1; int T2; int T3; int father; ; typedef int node; typedef struct _elemento *tree2_3; tree2_3 T; La funzione MIN è identica a quella degli alberi binari: il primo elemento del dizionario certamente è una foglia e sta nel primo sottoalbero di tutti i suoi antenati, per cui si può trovare scorrendo i primi sottoalberi finché ce ne sono: 2
4 A *MIN(tree_23 T) if (T == NULL) return NULL; else r = ROOT(T); if (r->t1 == NULL) return r->a; else return MIN(r->T1); Ne esiste una semplice versione iterativa: A *MIN(tree T) if (T!= NULL) while (T->T1!= NULL) T = ROOT(T)->T1; return ROOT(T)->a; La funzione MEMBER (e la funzione SEARCH che fa le stesse cose, ma restituisce un puntatore a un elemento anziché un valore logico) sono molto simili alle corrispondenti funzioni per gli alberi binari, salvo che: 1. i nodi interni possono avere tre figli, per cui la chiave dell elemento cercato va confrontata con L (r) e M (r), anziché con una singola chiave; 2. nei nodi interni non ci sono informazioni, per cui non ci si ferma fino alle foglie. A *SEARCH (A *a, tree2_3 T) if (T == NULL) return NULL; k = KEY(a); r = ROOT(T); if (r->t1 == NULL) /* se il nodo corrente e una foglia */ if (k == r->l) return r->a; else return NULL; else if (k <= r->l) return SEARCH(a,r->T1); else if (k <= r->m) return SEARCH(a,r->T2); else /* (k > r->m) */ 3
5 return SEARCH(a,r->T3); Esempio: si costruisca l albero 2-3 con una radice avente due figli, ciascuno con due nipoti, e le seguenti foglie: 2, 5 e 9 appese al primo nipote, 23 e 34 appesi al secondo, 45, 47 e 50 appesi al terzo e 67, 80, 85 appesi al quarto. Si cerchino le seguenti chiavi: 1 47, 23, 85, 90. La funzione INSERT ha bisogno di conoscere il nodo che farà da padre al nuovo elemento. Tale nodo è un nodo interno al livello più basso, subito sopra le foglie, ed è tale che il nuovo elemento cade entro la sua sottosequenza, o subito prima o subito dopo, cioè cade dopo l ultimo elemento che la precede e prima del primo elemento che le segue. Figura 3.1: FIGURA DA FARE: DATO L ALBERO (1,2) (3,4) (6,8), I NODI 2.5, 3 E 5 HANNO TUTTI COME PADRE IL NODO CENTRALE DEL LIVELLO 1, PERCHE CADONO FRA 2 E 5. La funzione SEARCH FATHER determina questo nodo padre. funzione SEARCH, salvo che È identica alla 1. non si ferma in una foglia, ma al livello immediatamente superiore; 2. quando il terzo sottoalbero è vuoto, scende nel secondo. Questo perché non sta cercando l elemento, ma il posto in cui metterlo (quindi si ferma nel nodo padre potenziale, ed evita i sottoalberi vuoti, in cui non ci sono padri potenziali). node SEARCH_FATHER (A *a, tree2_3 T) if (T == NULL) return NULL; k = KEY(a); p = ROOT(T); if (p->t1->t1 == NULL) /* se il primo figlio e una foglia */ return p; else if (k <= p->l) return SEARCH_FATHER(a,p->T1); else if ( (k <= p->m) (p->t3 == NULL) ) return SEARCH_FATHER(a,p->T2); else /* (k > p->m) && (p->t3!= NULL) */ return SEARCH_FATHER(a,p->T3); Trovato il padre potenziale, il nuovo elemento andrebbe semplicemente appeso ad esso nella posizione giusta in base alla chiave: se il nuovo elemento è uguale a uno dei vecchi, non occorre fare nulla; se k < p->l (il nuovo elemento ha chiave minore del primo sottoalbero), bisogna scalare in avanti tutti i sottoalberi; 4
6 altrimenti, se p->l < k < p->m (il nuovo elemento ha chiave minore del secondo sottoalbero), bisogna scalare in avanti il secondo e terzo sottoalbero; altrimenti, se k > p->m, bisogna scalare il terzo; Il problema è che in questo modo i sottoalberi potrebbero diventare quattro! Occorre quindi una procedura REDUCE che rimetta a posto le cose. tree2_3 INSERT (A *a, tree2_3 T) if (T == NULL) T = CREATE_TREE2_3(a); else p = SEARCH_FATHER(a,T); if ( (p->e!= p->t1->e) && (p->e!= p->t2->e) && (p->e!= p->t2->e) ) APPEND(a,p,T); REDUCE(p,T); return T; La funzione REDUCE(node p, tree2 3 T) ripara l albero T nel caso in cui il nodo p abbia quattro figli. L idea è di spezzare p in due nodi fratelli ciascuno con due figli, e poi risalire l albero per vedere se la scomposizione crea problemi al padre. In caso positivo, si ripete il procedimento. Nel caso della radice, si spezza la radice in due e si aggiunge una superradice che faccia loro da padre. In dettaglio: 1. si crea un nuovo albero formato da un solo nodo ˆp; 2. si appende a ˆp gli ultimi due figli di p, tenendo i primi due in p; 3. se p era la radice dell albero, ora abbiamo due radici: si crea una nuova radice ˆr con figli p e ˆp (e terzo sottoalbero vuoto) 4. se p non era la radice, determiniamo il nodo pp padre di p e aggiungiamo ˆp come figlio di pp subito dopo p; 5. eseguiamo REDUCE anche su pp Sistemata la topologia, bisogna correggere le etichette L e M in tutti i nodi da p su fino alla radice. Gli altri nodi dell albero sono intatti. La complessità della funzione INSERT è O (h) = O (log n). Esempio: dato un albero la cui radice ha tre figli e le seguenti foglie: 2, 5 e 9 appese al primo figlio, 23 e 34 appese al secondo e 45, 47 e 50 appese al terzo, si aggiunga l elemento con chiave 6: 1. si cerca il nodo padre, che è il primo figlio della radice; 2. si appende 6 come suo terzo figlio, ma in totale sono quattro; 5
7 3. la funzione REDUCE spacca il primo figlio in due, tenendo 2 e 5 appesi al primo e 6 e 9 alla copia; 4. si calcolano le soglie della copia, che sono L = 6 e M = 9 5. la copia del primo figlio viene appesa alla radice dopo il primo figlio, ma ora in totale sono quattro; 6. la funzione REDUCE spacca la radice in due, tenendo primo figlio e copia appesi alla vecchia radice e secondo e terzo figlio appesi alla copia; 7. si calcolano le soglie della copia, che sono L = 34 e M = 50; 8. si crea una nuova radice e le si appendono la vecchia radice e la copia; 9. si ricalcolano le soglie a partire dal nodo padre di inserimento, che era il primo figlio della radice: le sue nuove soglie sono: L = 2 e M = 5; le nuove soglie della vecchia radice sono: L = 5 e M = 9; le soglie della nuova radice sono: L = 9 e M = 50. Esempio: dato un albero la cui radice ha due figli, ognuno con due nipoti e le seguenti foglie: 2, 5 e 9 appese al primo nipote, 23 e 34 appese al secondo, 45, 47 e 50 al terzo e 67, 80 e 85 al quarto, si aggiunga l elemento con chiave 44: 1. si cerca il nodo padre, che è il terzo nipote (primo figlio del secondo figlio della radice); 2. si appende 44 come suo primo figlio, ma in totale sono quattro; 3. la funzione REDUCE spacca il terzo nipote in due, tenendo 44 e 45 appesi al terzo nipote e 47 e 50 alla copia; 4. si calcolano le soglie della copia, che sono L = 47 e M = 50; 5. la copia del terzo nipote viene appesa dopo il terzo nipote; diventano tre figli del secondo figlio e va bene così; 6. si ricalcolano le soglie a partire dal nodo padre di inserimento, che era il terzo nipote della radice: le sue nuove soglie sono: L = 44 e M = 45; le nuove soglie del secondo figlio sono: L = 45 e M = 50; le soglie della radice restano: L = 34 e M = 85. La funzione DELETE applica la funzione SEARCH per trovare l elemento. Se non lo trova, non fa nulla. Se lo trova ed è l unico nodo, l albero diventa vuoto. Se lo trova, lo cancella. Questo è semplice (il nodo è una foglia), ma può portare a un nodo padre con un solo figlio. Se il padre rimane con un figlio solo, consideriamo i fratelli del padre: se il fratello precedente o successivo ha tre figli, se ne ruba uno se entrambi hanno due figli, si sposta il figlio unico su un fratello con due figli e si cancella il padre. Può essere che questo lasci il nonno con un solo figlio: nel caso, si ripete. se si arriva a una radice con un solo figlio, si cancella la radice. Esempio: dato un albero la cui radice ha due figli, ognuno con due nipoti e le seguenti foglie: 2 e 9 appese al primo nipote, 23 e 34 appese al secondo, 45, 47 e 50 al terzo e 67, 80 e 85 al quarto, si cancelli l elemento con chiave 50: 6
8 1. si cerca il nodo padre, che è il terzo nipote (primo figlio del secondo figlio della radice); 2. si cerca il nodo fra i figli e lo si cancella; restano due figli e tutto va bene; 3. si ricalcolano le soglie a partire dal nodo padre di cancellazione, che era il terzo nipote della radice: le sue soglie non cambiano: L = 45 e M = 47; le nuove soglie del secondo figlio sono: L = 47 e M = 85; le soglie della radice restano: L = 34 e M = 85. Esempio: dato un albero la cui radice ha due figli, ognuno con due nipoti e le seguenti foglie: 2 e 9 appese al primo nipote, 23 e 34 appese al secondo, 45 e 47 al terzo e 67, 80 e 85 al quarto, si cancelli l elemento con chiave 47: 1. si cerca il nodo padre, che è il terzo nipote (primo figlio del secondo figlio della radice); 2. si cerca il nodo fra i figli e lo si cancella; resta un solo figlio; 3. si cerca un fratello del padre (terzo nipote) che abbia tre figli: è il quarto nipote; 4. si sottrae il primo figlio al fratello del padre e lo si appende al padre; 5. si aggiornano le soglie del fratello del padre: L = 80 e M = 85; 6. si ricalcolano le soglie a partire dal nodo padre di cancellazione, che era il terzo nipote della radice: le sue soglie diventano: L = 45 e M = 67; le nuove soglie del secondo figlio sono: L = 67 e M = 85; le soglie della radice restano: L = 34 e M = 85. Esempio: dato un albero la cui radice ha due figli, ognuno con due nipoti e le seguenti foglie: 2 e 9 appese al primo nipote, 23 e 34 appese al secondo, 45 e 67 al terzo e 80 e 85 al quarto, si cancelli l elemento con chiave 9: 1. si cerca il nodo padre, che è il primo nipote (primo figlio del primo figlio della radice); 2. si cerca il nodo fra i figli e lo si cancella; resta un solo figlio; 3. si cerca un fratello del padre (primo nipote) che abbia tre figli: non ce n è; 4. si appende l unico figlio al fratello successivo (secondo nipote), che ora ha tre figli; 5. si cancella il primo nipote; ora il primo figlio ha un solo figlio; 6. si cerca un fratello del padre (primo figlio) che abbia tre figli: non ce n è; 7. si appende l unico figlio al fratello successivo (secondo figlio), che ora ha tre figli; 8. si cancella il primo figlio; ora la radice ha un solo figlio; 9. si cancella la radice, e il secondo figlio diventa radice; 10. si ricalcolano le soglie a partire dal fratello del padre cancellato, che era il secondo nipote della radice: le sue soglie diventano: L = 9 e M = 23; le nuove soglie del secondo figlio, che ora è la radice, sono: L = 34 e M = 50. 7
Algoritmi e strutture dati
 Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 4 Implementazioni delle partizioni Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio 2016.
Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 4 Implementazioni delle partizioni Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio 2016.
Per semplicità eliminiamo le ripetizioni nell'albero.
 Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Organigramma Gerarchia. (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre
 Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Indici multilivello dinamici (B-alberi e B + -alberi) Alberi di ricerca - 1. Un esempio. Alberi di ricerca - 3. Alberi di ricerca - 2
 INDICI MULTILIVELLO DINAMICI Indici multilivello dinamici (B-alberi e B + -alberi) Gli indici multilivello dinamici (B-alberi e B + -alberi) sono casi speciali di strutture ad albero. Un albero è formato
INDICI MULTILIVELLO DINAMICI Indici multilivello dinamici (B-alberi e B + -alberi) Gli indici multilivello dinamici (B-alberi e B + -alberi) sono casi speciali di strutture ad albero. Un albero è formato
Implementazione ADT: Alberi
 Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
In questa lezione Alberi binari di ricerca: la cancellazione
 In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
Esercitazione 6. Alberi binari di ricerca
 Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Un esempio: l ADT Dizionario (mutabile) Definizione. Alberi binari di ricerca (BST = binary search tree) search(chiave k) -> elem
 Un esempio: l ADT Dizionario (mutabile) Algoritmi e Laboratorio a.a. 2006-07 Lezioni Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Parte 19-D Alberi
Un esempio: l ADT Dizionario (mutabile) Algoritmi e Laboratorio a.a. 2006-07 Lezioni Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Parte 19-D Alberi
Alberi di ricerca. Alberi binari di ricerca. F. Damiani - Alg. & Lab. 04/05 (da C. Demetrescu et al - McGraw-Hill)
 Alberi di ricerca Alberi binari di ricerca Un esempio: l ADT Dizionario (mutabile) Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Alberi binari di
Alberi di ricerca Alberi binari di ricerca Un esempio: l ADT Dizionario (mutabile) Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato astratto dizionario Alberi binari di
Un esempio di mutua ricorsione
 Inserimento in un ABR n-bilanciato Un esempio di mutua ricorsione con gli alberi bilanciati in altezza, proprietà più debole, si ottiene maggiore semplicità delle operazioni di ribilanciamento (niente
Inserimento in un ABR n-bilanciato Un esempio di mutua ricorsione con gli alberi bilanciati in altezza, proprietà più debole, si ottiene maggiore semplicità delle operazioni di ribilanciamento (niente
Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica. Modulo di Laboratorio di Algoritmi e Strutture Dati
 Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica Modulo di Laboratorio di Algoritmi e Strutture Dati Alberi binari Giovanna Melideo melideo@di.univaq.it 1 Alberi
Università degli Studi di L Aquila Facoltà di Scienze M.F.N. Corso di Laurea in Informatica Modulo di Laboratorio di Algoritmi e Strutture Dati Alberi binari Giovanna Melideo melideo@di.univaq.it 1 Alberi
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Alberi Binari di Ricerca e Alberi Rosso-Neri
 Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
Alberi binari di ricerca
 Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità
 Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Alberi. Se x è il genitore di y, allora y è un figlio di x. Un albero binario è un albero in cui ogni nodo ha al massimo due figli.
 Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree
 Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
ricerca di un elemento, verifica dell appartenenza di un elemento
 Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
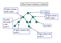 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
GLI ALBERI BINARI DI RICERCA. Cosimo Laneve
 GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
Divide et impera su alberi
 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Heap e code di priorità
 Heap e code di priorità Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica AA 2009/2010
Heap e code di priorità Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica AA 2009/2010
ADT Dizionario. Ordered search table. Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D:
 Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
ALGORITMI E STRUTTURE DATI
 ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
Indici con gli alberi
 Indici con gli alberi Alberi perfettamente bilanciati per indici su memorie di massa: B-alberi Indici su memorie secondarie Spesso i dati da ordinare sono in quantità tale da richiedere dispositivi di
Indici con gli alberi Alberi perfettamente bilanciati per indici su memorie di massa: B-alberi Indici su memorie secondarie Spesso i dati da ordinare sono in quantità tale da richiedere dispositivi di
Informatica 3. Informatica 3. LEZIONE 17: Alberi generici. Lezione 17 - Modulo 1. Introduzione. ADT dell albero generico.
 Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
Informatica 3 Informatica 3 LEZIONE 17: lberi generici Lezione 17 - Modulo 1 Modulo 1: Definizione e DT Modulo 2: Implementazione Modulo 3: lberi e classi di equivalenza Definizione e DT Politecnico di
Laboratorio di Algoritmi e Strutture Dati. Code con Priorità
 Laboratorio di Algoritmi e Strutture Dati Code con Priorità Teresa M.A. Basile basile@di.uniba.it Dipartimento di Informatica Università degli Studi di Bari Aldo Moro Materiale di base gentilmente concesso
Laboratorio di Algoritmi e Strutture Dati Code con Priorità Teresa M.A. Basile basile@di.uniba.it Dipartimento di Informatica Università degli Studi di Bari Aldo Moro Materiale di base gentilmente concesso
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
alberi completamente sbilanciati
 alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
Alberi binari. Alberi binari di ricerca
 Alberi binari Alberi binari Alberi binari di ricerca Cause: Inserimenti Sbilanciamento Cancellazioni Alberi binari Alberi binari di ricerca Alberi binari di ricerca bilanciati Alberi binari Alberi binari
Alberi binari Alberi binari Alberi binari di ricerca Cause: Inserimenti Sbilanciamento Cancellazioni Alberi binari Alberi binari di ricerca Alberi binari di ricerca bilanciati Alberi binari Alberi binari
Alberi di ricerca binari
 Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Introduzione Gli alberi di ricerca binari (Binary Search Tree, o BST) sono una struttura di dati che supporta in modo
Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Introduzione Gli alberi di ricerca binari (Binary Search Tree, o BST) sono una struttura di dati che supporta in modo
Lezione 9 Alberi binari di ricerca
 Lezione 9 Alberi binari di ricerca Rossano Venturini rossano.venturini@unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 1 Lista monodirezionale Scrivere
Lezione 9 Alberi binari di ricerca Rossano Venturini rossano.venturini@unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 1 Lista monodirezionale Scrivere
Verificare se un albero binario è bilanciato
 Verificare se un albero binario è bilanciato Definizione: Un albero è bilanciato nel Numero dei Nodi, brevemente n- bilanciato, quando, per ogni sottoalbero t radicato in un suo nodo, il numero dei nodi
Verificare se un albero binario è bilanciato Definizione: Un albero è bilanciato nel Numero dei Nodi, brevemente n- bilanciato, quando, per ogni sottoalbero t radicato in un suo nodo, il numero dei nodi
Un albero completamente bilanciato o pieno (full) alberi completamente sbilanciati. Un albero binario completo
 alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Alberi binari di ricerca 2 1 Alberi L albero è un tipo astratto di dato utilizzato per rappresentare
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Alberi binari di ricerca 2 1 Alberi L albero è un tipo astratto di dato utilizzato per rappresentare
Algoritmi e Strutture Dati
 Alberi AVL Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 26/7 Alberi AVL Definizione (bilanciamento in altezza): un albero è bilanciato
Alberi AVL Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 26/7 Alberi AVL Definizione (bilanciamento in altezza): un albero è bilanciato
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni.
 Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Algoritmi e Strutture Dati
 Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
ALBERI : introduzione SOMMARIO ALBERI ALBERI. ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI
 SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
Lezione 7 Alberi binari: visite e alberi di ricerca
 Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Strutture di accesso ai dati: B + -tree
 Strutture di accesso ai dati: B + -tree A L B E R T O B E L U S S I S E C O N D A P A R T E A N N O A C C A D E M I C O 2 0 0 9-2 0 0 Osservazione Quando l indice aumenta di dimensioni, non può risiedere
Strutture di accesso ai dati: B + -tree A L B E R T O B E L U S S I S E C O N D A P A R T E A N N O A C C A D E M I C O 2 0 0 9-2 0 0 Osservazione Quando l indice aumenta di dimensioni, non può risiedere
ADT Coda con priorità
 Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
Implementazione dell albero binario in linguaggio C++
 Implementazione dell albero binario in linguaggio C++ Costruire il programma per gestire le operazioni su un albero binario. Ogni nodo dell albero contiene un codice e una descrizione; il programma deve
Implementazione dell albero binario in linguaggio C++ Costruire il programma per gestire le operazioni su un albero binario. Ogni nodo dell albero contiene un codice e una descrizione; il programma deve
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Informatica 3. Informatica 3. LEZIONE 14: Alberi binari: introduzione. Lezione 14 - Modulo 1. Definizioni. Introduzione. Definizioni e proprietà
 Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Laboratorio di Python
 Laboratorio di Python Alberi binari Lab15 12 Maggio 2017 Outline Correzione esercizi per oggi Alberi binari Teoria Esercizi Esercizi per casa Saluti Esercizio 1 per casa Scrivere una funzione palindroma(s)
Laboratorio di Python Alberi binari Lab15 12 Maggio 2017 Outline Correzione esercizi per oggi Alberi binari Teoria Esercizi Esercizi per casa Saluti Esercizio 1 per casa Scrivere una funzione palindroma(s)
23/10/2016. gli alberi. alcune definizioni. un esempio. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica.
 gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
Alberto Montresor Università di Trento
 !! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
!! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
 Da libro di testo Cormen et al. CAP 21: par 21.1, 21.2, 21.3 pagg. 468-477 Strutture dati per insiemi disgiunti Una struttura dati per insiemi disgiunti mantiene una collezione S={S 1,S 2,,S k } di insiemi
Da libro di testo Cormen et al. CAP 21: par 21.1, 21.2, 21.3 pagg. 468-477 Strutture dati per insiemi disgiunti Una struttura dati per insiemi disgiunti mantiene una collezione S={S 1,S 2,,S k } di insiemi
Strutture dati dinamiche in C (II)
 Strutture dati dinamiche in C (II) Laboratorio di Linguaggi di Programmazione a.a. 2001/2002 dott.ssa Francesca A. Lisi lisi@di.uniba.it Sommario Le liste concatenate (ancora ma in modo più formale) L
Strutture dati dinamiche in C (II) Laboratorio di Linguaggi di Programmazione a.a. 2001/2002 dott.ssa Francesca A. Lisi lisi@di.uniba.it Sommario Le liste concatenate (ancora ma in modo più formale) L
Laboratorio di Informatica
 Liste semplici (semplicemente linkate) Una lista semplice e costituita da nodi Laboratorio di Informatica 7. Strutture complesse di dati in C++ Ogni nodo e una struttura che contiene : Dati Un riferimento
Liste semplici (semplicemente linkate) Una lista semplice e costituita da nodi Laboratorio di Informatica 7. Strutture complesse di dati in C++ Ogni nodo e una struttura che contiene : Dati Un riferimento
Algoritmi Greedy. Tecniche Algoritmiche: tecnica greedy (o golosa) Un esempio
 Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Esercizi Strutture dati di tipo astratto
 Salvatore Cuomo Esercizi Strutture dati di tipo astratto Lezione n. 20 Parole chiave: Strutture dati, pile code, liste Corso di Laurea: Informatica Insegnamento: Programmazione II, modulo di Laboratorio
Salvatore Cuomo Esercizi Strutture dati di tipo astratto Lezione n. 20 Parole chiave: Strutture dati, pile code, liste Corso di Laurea: Informatica Insegnamento: Programmazione II, modulo di Laboratorio
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Algoritmi (9 CFU) (A.A ) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1
 Algoritmi (9 CFU) (A.A. 2009-10) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1 Overview Definiamo la struttura dati heap Operazioni di costruzione e gestione di un heap Algoritmo Heapsort Code
Algoritmi (9 CFU) (A.A. 2009-10) Heap e Algoritmo HeapSort. Prof. V. Cutello Algoritmi 1 Overview Definiamo la struttura dati heap Operazioni di costruzione e gestione di un heap Algoritmo Heapsort Code
Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato
 Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
Laboratorio di Programmazione
 Laboratorio di Programmazione (Laurea triennale in matematica) Lezione 21 Strutture dinamiche Gli array ci permettono di memorizzare un insieme di dati dello stesso tipo Deve essere noto staticamente il
Laboratorio di Programmazione (Laurea triennale in matematica) Lezione 21 Strutture dinamiche Gli array ci permettono di memorizzare un insieme di dati dello stesso tipo Deve essere noto staticamente il
Memorizzazione di una relazione
 Heap file File ordinati Indici o Hash o B+-tree Costo delle operazioni algebriche Simboli: NP: numero di pagine NR: numero record LP: lunghezza pagina LR: lunghezza record Memorizzazione di una relazione
Heap file File ordinati Indici o Hash o B+-tree Costo delle operazioni algebriche Simboli: NP: numero di pagine NR: numero record LP: lunghezza pagina LR: lunghezza record Memorizzazione di una relazione
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari.
 Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Algoritmi e strutture dati
 Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 2 Implementazione dei dizionari: tabelle hash Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 2 Implementazione dei dizionari: tabelle hash Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Array e Oggetti. Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1. Dispensa 12. A. Miola Dicembre 2006
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
lezione 9 min-heap binario Heap e Alberi posizionali generali
 lezione 9 Heap e Alberi posizionali generali min-heap binario Un min-heap è un albero binario quasi completo in cui ogni nodo i diverso dalla radice soddisfa la seguente proprietà: il valore memorizzato
lezione 9 Heap e Alberi posizionali generali min-heap binario Un min-heap è un albero binario quasi completo in cui ogni nodo i diverso dalla radice soddisfa la seguente proprietà: il valore memorizzato
INDICI PER FILE. Accesso secondario. Strutture ausiliarie di accesso
 INDICI PER FILE Strutture ausiliarie di accesso 2 Accesso secondario Diamo per scontato che esista già un file con una certa organizzazione primaria con dati non ordinati, ordinati o organizzati secondo
INDICI PER FILE Strutture ausiliarie di accesso 2 Accesso secondario Diamo per scontato che esista già un file con una certa organizzazione primaria con dati non ordinati, ordinati o organizzati secondo
Esercitazioni di Algoritmi e Strutture Dati
 Esercitazioni di Algoritmi e Strutture Dati III esercitazione, 17/03/2016 Tong Liu 1 ESERCIZIO PRECEDENTE Es 2.5, Il rango di un elemento di una lista di interi é la somma degli elementi successivi piú
Esercitazioni di Algoritmi e Strutture Dati III esercitazione, 17/03/2016 Tong Liu 1 ESERCIZIO PRECEDENTE Es 2.5, Il rango di un elemento di una lista di interi é la somma degli elementi successivi piú
Alberi rosso-neri. Oltre ad essere alberi binari di ricerca, gli alberi rosso-neri soddisfano le seguenti proprietà:
 Alberi rosso-neri Gli alberi rosso-neri sono alberi binari di ricerca in cui le operaioni Insert e Delete sono opportunamente modificate in modo tale da garantire un altea dell albero h = O(log n). A tale
Alberi rosso-neri Gli alberi rosso-neri sono alberi binari di ricerca in cui le operaioni Insert e Delete sono opportunamente modificate in modo tale da garantire un altea dell albero h = O(log n). A tale
B-Alberi Esercitazioni
 B-Alberi Esercitazioni Introduzione B-Trees: alberi bilanciati di ricerca progettati per essere memorizzati su dischi magnetici. Dischi magnetici molto più lenti delle memorie ad accesso casuale. La misura
B-Alberi Esercitazioni Introduzione B-Trees: alberi bilanciati di ricerca progettati per essere memorizzati su dischi magnetici. Dischi magnetici molto più lenti delle memorie ad accesso casuale. La misura
Union-find. Insiemi disgiunti. F. Damiani - Alg. & Lab. 04/05 (da C. Demetrescu et al - McGraw-Hill)
 Union-find Insiemi disgiunti Il problema Union-find Mantenere una collezione di insiemi disgiunti di elementi distinti (interi in 1 n) durante una sequenza delle seguenti operazioni: union(a,b) = unisce
Union-find Insiemi disgiunti Il problema Union-find Mantenere una collezione di insiemi disgiunti di elementi distinti (interi in 1 n) durante una sequenza delle seguenti operazioni: union(a,b) = unisce
Nell informatica esistono alcuni problemi particolarmente rilevanti, poiché essi:
 Pag 24 3) Il problema della ricerca Nell informatica esistono alcuni problemi particolarmente rilevanti, poiché essi: si incontrano in una grande varietà di situazioni reali; appaiono come sottoproblemi
Pag 24 3) Il problema della ricerca Nell informatica esistono alcuni problemi particolarmente rilevanti, poiché essi: si incontrano in una grande varietà di situazioni reali; appaiono come sottoproblemi
Tipi di dato e Strutture dati elementari
 Tipi di dato e Strutture dati elementari Ing. Paolo Craca Anno accademico 2007/2008 Tipi di dato e Strutture dati elementari 1 / 40 Cosa vedremo in questo seminario 1 Introduzione 2 Pile 3 Code 4 5 Bibliografia
Tipi di dato e Strutture dati elementari Ing. Paolo Craca Anno accademico 2007/2008 Tipi di dato e Strutture dati elementari 1 / 40 Cosa vedremo in questo seminario 1 Introduzione 2 Pile 3 Code 4 5 Bibliografia
liste ogni nodo ha un successore, tranne l ultimo della lista che ne ha zero; alberi binari ogni nodo ha zero, uno oppure due figli
 Alberi generali Gli alberi visti fino a questo momento erano insiemi di nodi collegati fra di loro, in cui ogni nodo poteva avere al massimo due figli. Negli alberi generali, ogni nodo può avere un numero
Alberi generali Gli alberi visti fino a questo momento erano insiemi di nodi collegati fra di loro, in cui ogni nodo poteva avere al massimo due figli. Negli alberi generali, ogni nodo può avere un numero
dizionari alberi bilanciati
 dizionari alberi bilanciati dizionari ADT che supportano le seguenti operazioni membership anche detta search insert delete o remove le liste e i BST sono dizionari maggio 2002 ASD2002 - Alberi bilanciati
dizionari alberi bilanciati dizionari ADT che supportano le seguenti operazioni membership anche detta search insert delete o remove le liste e i BST sono dizionari maggio 2002 ASD2002 - Alberi bilanciati
ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA)
 ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA) Definizione induttiva: un albero vuoto è un albero di ricerca binario un albero non vuoto avente per radice l'elemento (di chiave) x e per sottoalberi
ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA) Definizione induttiva: un albero vuoto è un albero di ricerca binario un albero non vuoto avente per radice l'elemento (di chiave) x e per sottoalberi
Alberi rosso-neri. Le operazioni sugli alberi binari di ricerca hanno complessità proporzionale all altezza h dell albero.
 Alberi rosso-neri Le operazioni sugli alberi binari di ricerca hanno complessità proporzionale all altezza h dell albero. Gli alberi rosso-neri sono alberi binari di ricerca in cui le operazioni Insert
Alberi rosso-neri Le operazioni sugli alberi binari di ricerca hanno complessità proporzionale all altezza h dell albero. Gli alberi rosso-neri sono alberi binari di ricerca in cui le operazioni Insert
Le precondizioni e postcondizioni aggiunte al prototipo, consentono di fornire una specificazione precisa della funzione
 OBIETTIVO CORRETTEZZA: specificazione completa con precondizioni e postcondizioni Le precondizioni e postcondizioni aggiunte al prototipo, consentono di fornire una specificazione precisa della funzione
OBIETTIVO CORRETTEZZA: specificazione completa con precondizioni e postcondizioni Le precondizioni e postcondizioni aggiunte al prototipo, consentono di fornire una specificazione precisa della funzione
Indice come albero binario di ricerca!
 Indice come albero binario di ricerca! n Obiettivo: Utilizzare una struttura dati del tipo albero binario di ricerca per realizzare un indice su file Ricerca sull indice in memoria centrale, poi accesso
Indice come albero binario di ricerca! n Obiettivo: Utilizzare una struttura dati del tipo albero binario di ricerca per realizzare un indice su file Ricerca sull indice in memoria centrale, poi accesso
Alberi binari. Esercizi su alberi binari
 Alberi binari Definizione della struttura dati: struct tree int dato; struct tree *sx, *dx; ; typedef struct tree tree; Esercizi su alberi binari 1. Scrivere una funzione che cerchi un intero k all'interno
Alberi binari Definizione della struttura dati: struct tree int dato; struct tree *sx, *dx; ; typedef struct tree tree; Esercizi su alberi binari 1. Scrivere una funzione che cerchi un intero k all'interno
B-alberi. Strutture dati avanzate
 Strutture dati avanzate Strutture dati avanzate B-alberi B-alberi Vedremo alcune strutture dati che permettono di eseguire in modo particolarmente efficiente un determinato insieme di operazioni. Ognuna
Strutture dati avanzate Strutture dati avanzate B-alberi B-alberi Vedremo alcune strutture dati che permettono di eseguire in modo particolarmente efficiente un determinato insieme di operazioni. Ognuna
Algoritmi e Strutture Dati. Alberi
 Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Dizionari Liste invertite e Trie
 Dizionari Liste invertite e Trie Lucidi tratti da Crescenzi Gambosi Grossi, Strutture di dati e algoritmi Progettazione, analisi e visualizzazione Addison-Wesley, 2006 Dizionari Universo U delle chiavi
Dizionari Liste invertite e Trie Lucidi tratti da Crescenzi Gambosi Grossi, Strutture di dati e algoritmi Progettazione, analisi e visualizzazione Addison-Wesley, 2006 Dizionari Universo U delle chiavi
