DISPENSA DI PROGETTO DEL TELAIO
|
|
|
- Nicolo Bassi
- 8 anni fa
- Visualizzazioni
Transcript
1 DISPENSA DI PROGETTO DEL TELAIO Capitolo 7 Analisi Dinaia Analitia e Nueria 7. - Introduzione La gran parte delle strutture reali è soggetta a eitazioni vibratorie. Gli senari appliativi sono i più vasti: da vibrazioni indotte da arihi aerodinaii su strutture ivili oe ponti o edifii, alle vibrazioni indotte da otore e strada sulla soa di una autoobile, a abienti vibrazionali oplessi oe quelli a ui è soggetta la struttura di un satellite al lanio. Il oportaento di un sistea eanio in ondizioni vibrazionali può essere effiaeente siulato, a partire dal alolo delle frequenze proprie e dei odi propri di vibrare, traite siulazioni di dinaia strutturale oe la FRF (risposta in frequenza), l analisi shok e rando. L analisi di base nel apo dello studio delle vibrazioni è la riera delle risonanze (analisi odale), he tendenzialente debbono essere tenute a suffiiente distanza dalle frequenze portanti delle eitazioni periodihe he agisono sul oponente o sul sistea di interesse. L analisi FEM perette di individuare sia le frequenze di risonanza he le fore odali ad esse assoiate, e pertanto onsente di apire oe eventualente intervenire a livello progettuale per spostare (innalzare o abbassare) le frequenze proprie del sistea stesso. Una volta opreso il oportaento dinaio di base della struttura traite l analisi odale, è possibile siulare la risposta dinaia rispetto a eitazioni sinusoidali (FRF, sine analysis), eitazioni rando o shok, analisi più oplesse e oputazionalente più intensive (si parla di dinaia avanzata ), he rihiedono la sheatizzazione dello sorzaento della struttura in esae. Gli sopi prinipali dell analisi dinaia vibrazionale sono: evitare he le eitazioni adano in viinanza di risonanze della struttura;
2 valutare il fattore di aplifiazione della struttura (Q fator) e gli stress assii rispetto a arihi variabili in odo noto in frequenza; valutare risposte RMS di aelerazione e stress PSD nel aso di analisi rando; valutare stress di pio e equivalenti in analisi di risposta shok SRS; effettuare studi di fatia vibrazionale; effettuare studi di onfort vibro-austio (ad esepio di NVH nel settore dei trasporti) Teoria dell analisi odali: la eania delle vibrazioni Per eglio oprendere i prinipi he perettono di eseguire siulazioni nuerihe per il oportaento dinaio dei sistei e delle strutture, è neessario riprendere la teoria analitia standard della Meania delle Vibrazioni he perette di srivere le equazioni dalle quali partire per trovare la soluzione di oto del sistea. In partiolare, il aso più seplie e quindi di pria appliazione dal punto di vista analitio risulta quello dell analisi del oportaento libero e forzato di sistei eanii lineari aratterizzati da un solo grado di libertà. Le equazioni he regolano la dinaia di tali sistei sono equazioni differenziali lineari, a oeffiienti ostanti di seondo ordine, ovvero si ha he i terini dell equazione ontengono solo la funzione inognita e le due derivate elevate ad esponente. Nel aso in ui il sistea non sia sottoposto a forzanti (f(t)), si analizzerà il oportaento libero. Qualora invee vi siano forzanti (f(t) ), si parlerà di oportaento forzato. Nell abito del oportaento forzato di un sistea è neessario fare una ulteriore distinzione. In effetti la risposta forzata di un qualsiasi sistea lineare è ostituita dalla soa di due funzioni he rappresentano l una il osiddetto transitorio e l altra il oportaento a regie. Il transitorio è quella parte del oportaento del sistea he tende ad estinguersi on il passare del tepo in funzione dello sorzaento del sistea. Il oportaento a regie del sistea è vieversa quella parte del oportaento he non si estingue (ed anzi riane inalterata se la forzante è periodia) finhé la forzante non essa oppure varia il suo ontributo. Per quanto riguarda le azioni forzanti, i si riferirà sepre a forzanti di tipo aronio in quanto tutte le funzioni di interesse tenio (forzanti periodihe e transitorie) possono essere espresse in terini di soatorie o integrali di funzioni aronihe. Poihé inoltre le equazioni sono eslusivaente lineari, è possibile sfruttare il prinipio di sovrapposizione degli effetti, per ui lo studio eslusivo di tale tipo di funzione forzante non risulta riduttivo. Nel aso di una forzante non aronia, si sopone quindi la forzante stessa nelle sue oponenti aronihe (f, f,.., f i ) e si trovano le soluzioni delle equazioni del sistea sottoposto alle singole oponenti aronihe (x, x,.., x i ); la soluzione generale è la soa delle soluzioni del sistea sottoposto alle singole oponenti aronihe xx +x +..+x i.
3 7.3 - Equazioni di oto per sistei lineari Le equazioni di oto dei sistei vibranti on uno o più gradi di libertà disendono direttaente dalle Equazioni Cardinali della Dinaia. Tuttavia una fora assai più oune di queste, è quella nota ouneente oe Legge di Newton, he disende direttaente dalle Equazioni Cardinali, appliando il Prinipio di D Alabert: F a Dove F rappresenta la risultante delle forze (esterne) appliate al orpo in analisi, la sua assa, a la sua aelerazione assoluta (rispetto a un riferiento inerziale). Questa risulta essere una equazione vettoriale nello spazio artesiano a 3 diensioni (F ed a sono vettori). Ovviaente, se per sepliità al fine dell analisi ateatia si onsidera il oto in una unia direzione rettilinea, se si prende l asse x del sistea di riferiento parallelo alla traiettoria di un qualunque punto del orpo, allora lo studio del oto del sistea può essere effettuato traite la risoluzione dell unia equazione salare: F x a x Poihé inoltre la aelerazione assoluta del orpo a x altro non è he la derivata seonda della sua posizione x rispetto al tepo, e onsiderando tra le forze esterne solo quelle he hanno oponenti lungo la direzione x, la preedente può essere risritta nella più onsueta fora: F x & Nella suddetta forula (solo foralente identia alla forula F a presentata in preedenza), a prio ebro il terine F rappresenta la risultante delle forze esterne aventi sul sistea in direzione x. Poihé si è preesso he l equazione differenziale he onsentirà lo studio del oto del sistea dovrà risultare lineare (nella funzione inognita x(t)), all interno del terine F poteo trovare eslusivaente: Funzioni di qualunque tipo a dipendenti eslusivaente dal tepo F(t), he hiaereo forzanti; Forze elastihe; Forze sorzanti. Delle forzanti si è già parlato: possono esservi (e quindi si studia il oto forzato del sistea), oppure no (e si studia quindi il oto libero). Pur essendo teoriaente di fora qualsiasi (deterinistihe o aleatorie, periodihe o aperiodihe, transitorie, e ) sfruttando i risultati dell Analisi Aronia e le proprietà derivanti dalla linearità delle equazioni, i si liiterà allo studio di forzanti aronihe del tipo ff e i ω t
4 7.4 - Forze elastihe Le forze elastihe sono forze onservative he tendono ad opporsi alle ause he le deterinano. E per tale otivo he vengono anhe dette forze di rihiao. Si parlerà di forza elastia oe di una forza he ha un odulo proporzionale (traite la ostante di elastiità generalente indiata on k) allo spostaento del orpo rispetto alla sua posizione di equilibrio. Il verso della forza (e quindi il suo segno), sarà quello he ontribuirà a far ritornare il orpo nella sua posizione di equilibrio. Indiando on x l asse lungo ui avviene il oto, se si india on x la posizione di equilibrio (statio) del orpo, la forza elastia varrà quindi: F el (t)-k(x(t)-x ) F el x x(t) x F el x(t) x x Tuttavia, se si prende la posizione di equilibrio (statio) oe origine del sistea di riferiento, allora x, e quindi si ottiene la più lassia fora: F el -kx Va tuttavia riarato he in questo aso (diversaente da quanto sritto in preedenza), la variabile x(t) rappresenta lo spostaento del orpo rispetto alla posizione di equilibrio, e non più seplieente la posizione del orpo rispetto ad un riferiento qualsiasi. Il aso più oune di forza elastia è quello della forza sviluppata da una olla a spirale (a patto he non sia né troppo opressa né troppo allungata). E proprio da questo oponente he trae origine il sibolo grafio onvenzionale per tale tipo di forze. A B Da quanto detto in preedenza risulta hiaro he la forza sviluppata da un tale eleento è proporzionale traite la ostante di elastiità k (N/) alla distanza tra gli estrei indiati on le lettere A e B. Soltanto nel aso in ui on s si intenda la deforazione della olla rispetto alle sue ondizioni a riposo, è sepre possibile indiare la forza elastia di una olla traite:
5 F el -k s E infine utile riordare he una forza elastia è anhe onservativa: per deforare la olla è neessario opiere lavoro (fornire energia) he viene auulato oe energia potenziale (di deforazione). Tale energia può essere trasforata in energia inetia (durante il oto) e viene restituita integralente se si riporta la olla alla sua lunghezza di riposo in ondizioni di veloità nulla Forze sorzanti: lo sorzaento visoso A differenza delle forze elastihe, le forze sorzanti sono forze dissipative, he onsuano energia. E proprio a ausa dell inevitabile presenza di forze di questo tipo he un orpo, una volta posto in oviento e lasiato uoversi senza ulteriori apporti energetii, è inesorabilente destinato a ferarsi dopo un tepo più o eno lungo. Se gli spostaenti sono di tipo aronio si osserva he, in orrispondenza del assio (o inio) spostaento la forza sorzante è nulla; la forza sorzante assia (in odulo), si ha invee quando gli spostaenti sono nulli. Le forze sorzanti sono aratterizzate dal fatto di essere in quadratura on gli spostaenti del sistea. Faendo riferiento alla notazione vettoriale, le forze sorzanti sono sepre sfasate di 9 (π/) rispetto alle forze elastihe. L unia forza sorzante he verrà presa in onsiderazione (e he perette di soddisfare l ipotesi di linearità dell equazione di oto) è lo sorzaento visoso. Si definise forza di sorzaento visoso, una forza il ui odulo è direttaente proporzionale (traite la ostante detta oeffiiente di sorzaento visoso Ns/) alla veloità di deforazione. Le forze di sorzaento visoso odellano assai bene le forze he agisono su un orpo he si uove on veloità relativaente basse all interno di un fluido. Un eleento a ui è ben appliabile tale odello è uno sorzatore oleodinaio, oe quello presente nelle sospensioni autoobilistihe. Da tale eleento trae origine il sibolo onvenzionale di una forza di tale tipo. x A B Poihé anhe tale forza tende ad opporsi alla variazione della veloità di deforazione, ed in analogia a quanto già detto per la forza elastia, se si india on s la distanza tra gli ohielli A e B dello sorzatore, la forza di sorzaento visoso vale quindi: F s vis - s& Se l ohiello A è fisso, e se si india on x la posizione dell ohiello B, la forza he lo sorzatore applia al orpo adiaente in orrispondenza dell ohiello B vale: F s vis - x&
6 Si osservi inoltre he a parità di apiezza di spostaenti (a parità di x ), la forza sorzante auenta linearente on la pulsazione degli spostaenti stessi. Se quindi il sistea opie vibrazioni aratterizzate da frequenze olto basse (spostaenti quasi-statii), a volte può anhe essere aettabile trasurare tali forze. Se vieversa gli spostaenti sono aratterizzati da frequenze piuttosto elevate, non onsiderare tali forze può portare ad errori del tutto inaettabili Sistei a Grado di Libertà I sistei vibranti ad un gradi di libertà sono ovviaente i asi più seplii per quanto riguarda la trattazione analitia. Ovviaente, per i vasi a più gradi di libertà, i prinipi alla base della teoria della eania delle vibrazioni riangono gli stessi, a seplieente oorrerà passare da una fora analitia ostituita da una singola equazione differenziale del oto ad una fora atriiale più oplessa, he nel aso di un elevato nuero di gradi di libertà, può essere risolta sfruttando eslusivaente gli struenti del alolo nuerio. Nei asi di analisi dinaia FEM i software sfruttano proprio i prinipi della eania delle vibrazioni appliati su ognuno dei nodi e quindi ognuno degli eleenti he ostituisono il odello, asseblando opportune atrii di assa, di sorzaento, e di rigudezza, e risolvendo il problea on etodi nuerii. La veloità del alolatore perette ovviaente di gestire sistei atriiali di diensioni anhe parehio elevate. In ogni aso, il fatto iportante è he i prinipi della teoria della vibraziione riangono i edesii per ui l analisi FEM seplieente prende questa teoria e la applia sui odelli ad eleenti finiti, ottenendo i sistei atriiali he, risolti, fornisono le soluzioni del problea. Per la teoria analitia fareo quindi riferiento prinipalente ai sistei a un grado di libertà, sapendo he per i sistei a più gradi di libertà sarà seplieente senessario passare alla fora atriiale delle equazioni, stando attenti a riwspettare opportune etodologie di passaggio per ostruire, per esepio, la atrie di assa del odello ad eleenti finiti. In sostanza, la più generihe equazione di oto a ui un sistea on un solo grado di libertà potrebbe essere riondotto è del tipo: & x kx x& + f (t) Dallo studio delle soluzioni delle equazioni differenziali lineari possono essere deterinati il oportaento libero (se f(t)) o quello forzato (se f(t) ) di un qualsiasi sistea on un solo grado di libertà. Un sistea di tale tipo può essere sheatizzato attraverso il seguente disegno:
7 x k Un orpo rigido di assa è ollegato a un basaento fisso traite una olla di ostante di rigidezza k e uno sorzatore visoso di ostante. Il orpo rigido può solo opiere traslazioni nella direzione vertiale per ui, per desriverne il oto, si seglie di utilizzare un sistea di riferiento inerziale onoassiale x, rivolto verso l alto, e on origine in orrispondenza del barientro del orpo nella posizione di equilibrio del sistea, supposta nota. In questo aso, poihé non sono presenti forzanti e uno degli estrei sia dello sorzatore he della olla sono fissi (al basaento), l equazione he regola le vibrazioni del sistea è: & x kx & x + x& + kx x& Osservazione: è hiaro he la soluzione x(t) soddisfa l equazione differenziale, il he giustifia il fatto, noto a tutti, he un orpo non sottoposto ad aluna forzante può rianere fero nella sua posizione di equilibrio. Tuttavia vedreo he questa non è l unia soluzione possibile, in quanto non è detto he all istante iniziale (per t) il orpo si trovi nella posizione di equilibrio (x) e on veloità nulla ( x& ). Se infatti la posizione iniziale oppure la veloità sono non nulle, è evidente he il sistea si uoverà, tendendo peraltro a ritornare sepre nella sua posizione di equilibrio Analisi del oto libero Per onosere oe si possa uovere un sistea on GdL in assenza di forzanti, è suffiiente risolvere la seplie equazione differenziale ordinaria, del seondo ordine, oogenea. & x + x& + kx E noto he se una funzione x(t) è effettivaente una soluzione dell equazione differenziale, questa, introdotta nell equazione stessa insiee alle sue derivate, deve dar luogo ad una identità. Dalle teoria delle equazioni differenziali ordinarie lineari e oogenee, risulta he tutte soluzioni dell equazione oogenea sono una obinazione lineare seondo due ostanti arbitrarie reali (he hiaereo A e B), delle due funzioni
8 quindi x λ t e e x e λ t x( t) λt λ t Ae + Be, in ui λ e λ sono le due soluzioni dell equazione aratteristia: λ + λ + k Sfruttando le ben note forule risolutive si ha he: λ, ± 4k A questo punto si presentano tre possibilità in funzione del valore del radiando ( -4k). Prio aso: -4k (Sistea Critio) Questo aso, assai diffiile da realizzarsi nella pratia, è utile da analizzare solo per via del suo arattere di onfine. In tale aso si ha he vi sono due radii reali oinidenti (una unia radie reale doppia), peraltro negative, he valgono: La soluzione generale è quindi: x( t) λ Ae λ t + Bte λt on A e B ostanti arbitrarie (he saranno deterinate solo traite le ondizioni iniziali). Poihé λ è negativa la soluzione è una funzione onotona deresente (essendo soa di due funzioni esponenziali negative). Si può quindi onludere he il oto libero di un sistea on sorzaento visoso per ui 4k è un transitorio aperiodio: il sistea tende a ritornare nella sua posizione di equilibrio senza aluna osillazione. La ostante di sorzaento visoso he deterina, a parità di assa e rigidezza, una soluzione di tale tipo viene detta ostante di sorzaento ritio del sistea. Seondo aso: -4k> (Sistea Sovrasorzato) In questo aso, he si verifia quando lo sorzaento del sistea è elevato, ovvero aggiore dello sorzaento ritio, si ha he l equazione aratteristia aette due soluzioni reali negative in quanto risulta sepre: In questo aso quindi la soluzione generale è: > 4k λt λt x( t) Ae + Be
9 on A e B ostanti arbitrarie. Poihé entrabe le funzione esponenziali sono negative, la soluzione totale è anora una volta una funzione onotona deresente. Anhe in questo aso si può onludere he il oto libero di un sistea on sorzaento visoso per ui >4k è un transitorio aperiodio: il sistea quindi tende a ritornare nella sua posizione di equilibrio senza aluna osillazione. Terzo aso: -4k< Questo terzo aso si verifia quindi quando lo sorzaento del sistea è liitato, ovvero inferiore dello sorzaento ritio, si ha he l equazione aratteristia non aette soluzioni reali. Tuttavia, introduendo i nueri oplessi, e in partiolare l unità iaginaria i, è possibile srivere ) (4 ) (4 ) (4 4 k i k k k espressione in ui il radiando risulta positivo, ed è quindi possibile alolarne la radie quadrata. In questo aso quindi le soluzioni dell equazione aratteristia risultano:, 4 4 k i k ± ± λ e la soluzione generale è: t k i t k i t t Be Ae Be Ae t x ) ( λ λ on A e B ostanti arbitrarie. La soluzione, on faili passaggi, può quindi essere risritta oe: + + t k i t k i t t t Be Ae e Be Ae t x 4 4 ) ( λ λ La parte dell ultio ebro tra parentesi quadre, sfruttando forulazioni siili alle Forule di Eulero (in ui si riade direttaente se AB), può essere inoltre risritta nella seguente fora: + + ϕ t k X Be Ae t k i t k i sin in ui le due ostanti X e ϕ dipendono eslusivaente dalle due ostanti arbitrarie A e B, e quindi sono arbitrarie anh esse. Naturalente tali ostanti potranno essere deterinate on la onosenza delle ondizioni iniziali (posizione e veloità della assa nell istante t). A questo punto la soluzione generale dell equazione differenziale può essere espressa nella sua fora definitiva:
10 x( t) X t e 4 sin k t + ϕ in ui, si può notare, sono soparsi i nueri oplessi, utilizzati solo oe struento per la risoluzione dell equazione differenziale: il oto in effetti deve essere realizzato da una funzione reale. 8 6 Posizione () Tepo (s) Dalla fora ateatia della soluzione si possono quindi trarre le seguenti onlusioni: Il oto libero è un oto osillatorio sorzato; t L apiezza delle osillazioni, deterinata dal terine X e, è deresente on il tepo in dipendenza dalla assa e dallo sorzaento del sistea. Poihé l apiezza tende a zero on il tepo, si evine he il sistea opie osillazioni sorzate (he diinuisono di apiezza on il tepo) nell intorno della posizione di equilibrio; Mentre l apiezza e la fase delle osillazioni dipendono dalle ondizioni iniziali, la pulsazione del oto libero è una ostante dipendente uniaente dalle aratteristihe del sistea. Essa prende il noe di pulsazione propria del sistea. Si osservi appena he è evidente he la soluzione per ui X (derivante dal aso in ui AB) soddisfa l equazione; questa soluzione, detta soluzione banale, i onfera il fatto, di oune esperienza, he un sistea non sottoposto a forze può rianere fero Paraetri vibrazionali adiensionali
11 Per paraetri adiansionali si intendono quei paraetri ottenuti on partiolari forulazioni partendo dalle aratteristihe note del sistea, he perettono di risrivere le soluzioni analitihe delle equazioni di oto in fore eglio interpretabili e quindi più oode per una valutazione ritia. Queste sono date da: k. la pulsazione naturale, indiata on ω n, e he assue il valore ω n ;. il fattore di sorzaento visoso, indiato on ξ, he assue il valore di ξ. k La pulsazione naturale è un nuero (dotato di diensioni fisihe) dipendente eslusivaente dalla assa e dalla rigidezza del sistea. Se proprio si vuole attribuire a questo nuero un signifiato fisio, si può dire he la pulsazione propria di un sistea è pari alla pulsazione propria (e anhe alla pulsazione di risonanza, he verrà introdotta nel seguito) di un sistea siile a quello preso in esae, a privo di sorzaento (). Il fattore di sorzaento visoso, oe risulta evidente dalla stessa definizione, è un nuero puro he india il rapporto tra lo sorzaento effettivaente presente nel sistea, e quello ritio. Se si riorda il signifiato dello sorzaento ritio, si evine he solo sistei aratterizzati da un fattore di sorzaento visoso inore di, sono aratterizzati da un oportaento libero di tipo osillante. Introduendo tali paraetri, la soluzione del oto libero del sistea può essere risritta oe: x( t) X e quindi la pulsazione propria varrà: ξω t e sin ( ωn ξ t + ϕ ) n ω p k 4k 4k ωn ξ Dereento logaritio La onosenza dello sorzaento è sepre il fattore più ritio per la odellazione di un sistea eanio: entre per la isura (o la stia) della assa e della rigidezza esistono più tenihe, e di elevata preisione, spesso l identifiazione del valore dello sorzaento on un errore assio del % (inaettabile per asse e rigidezza) ostituise un risultato più he soddisfaente. Traite l analisi del oportaento libero del sistea, note he siano la sua assa e la rigidezza, è possibile ottenere ounque una buona stia di tale valore. Si onsiderino due assii relativi onseutivi della soluzione del oto libero. Tali assii si avranno in orrispondenza degli istanti in ui il seno raggiunge il suo valore assio, ovvero il valore unitario. Se si suppone he il prio assio si avrà in orrispondenza dell istante t, allora il seondo assio si avrà in orrispondenza del tepo:
12 t t + T t + π ω p t + ω n π ξ in ui T è il periodo dell osillazione libera. L apiezza della osillazione in tali istanti varrà allora: x ( ) ξωnt x t X e ξω nt ξω n (t+ T) ξω nt ξω nt ( t ) X e X e X e e Effettuando il logarito naturale del rapporto di tali due apiezze si ottiene dunque: x( t) X e ln ln ( ) x t X e ξωnt ξω t ξω T n e n ln e ξω T n ln ξω T π πξ n ( e ) ξω nt ξω n ω n ξ ξ Il logarito del rapporto delle apiezze delle vibrazioni in orrispondenza di due assii suessivi (appunto detto dereento logaritio) è quindi dipendente eslusivaente dal fattore di sorzaento visoso. Noto quindi il valore del dereento (da prove sperientali), è possibile riavare il fattore di sorzaento visoso on la preisione desiderata attraverso tenihe di alolo nuerio. Una volta alolato di fattore di sorzaento visoso ξ, noti i valori della assa e della rigidezza, è possibile riavare il valore della ostante di sorzaento visoso Posizione () Moto forzato Tepo (s) Un sistea on un solo grado di libertà on sorzaento visoso su ui agise una forzante di tipo aronio può essere sheatizzato attraverso il seguente disegno:
13 x F(t) k Un orpo rigido di assa è ollegato a un basaento fisso traite una olla di ostante di rigidezza k e uno sorzatore visoso di ostante. Il orpo rigido può solo opiere traslazioni nella direzione vertiale e si seglie di utilizzare un sistea di riferiento inerziale onoassiale x, rivolto verso l alto, e on origine in orrispondenza del barientro del orpo nella posizione di equilibrio del sistea. In questo aso è presente una forzante aronia he supporreo di pulsazione generia Ω e apiezza generia F. A seonda he si vogliano utilizzare i nueri oplessi (la notazione esponenziale) oppure i si voglia liitare ai nueri reali, la forzante può essere espressa nelle due fore seguenti: F(t)F os(ω t) F(t)F e i Ω t In ogni aso, poihé il basaento è fisso, l equazione he regola le vibrazioni del sistea è: Ovvero & x kx x& + F (t) & x + x& + kx F (t) E noto ounque he tutte le soluzioni di una equazione differenziale opleta si ottengono soando a tutte le soluzioni dell equazione oogenea assoiata, una qualsiasi soluzione della equazione opleta. Per quanto onerne l equazione oogenea assoiata, ovvero: & x + x& + kx le sue soluzioni sono già state studiate in preedenza, laddove si è rierato il oportaento libero del sistea. In tale oasione si è visto he le vibrazioni he soddisfano la preedente equazione sono sorzate; queste quindi (ad eezione del aso in ui non vi sia aluno sorzaento), in un tepo più o eno lungo tendono ad annullarsi. E proprio per tale otivo he tale parte della soluzione del sistea forzato viene hiaata soluzione di transitorio, o più seplieente transitorio.
14 Da quanto detto in preedenza si ha he nei prii istanti del oto del sistea,le vibrazioni sono ottenibili oe soa del transitorio e della soluzione partiolare. Con il passare del tepo il transitorio tende ad estinguersi, e quindi dopo un erto periodo (in dipendenza dallo sorzaento) le vibrazioni forzate sono ostituite eslusivaente dalla soluzione partiolare. Tale soluzione perarrà inalterata, senza estinguersi, finhé non intervengano variazioni della forzante. Per tali otivi la soluzione partiolare dell equazione di oto ostituise il oportaento a regie del sistea Transitorio Regie Risposta opleta Da adesso in poi quando si parlerà di oportaento forzato, si farà ipliito riferiento al solo al oportaento a regie. Se per la risoluzione dell equazione differenziale si sfrutta la tenia dei nueri oplessi e la linearità del sistea, è faile verifiare he se la forzante è del tipo F(t)F e i Ω t, allora neessariaente per verifiare identiaente l equazione differenziale la soluzione dovrà essere del tipo x(t)x e i Ω t. Ciò signifia he le vibrazioni della assa dovranno avere la stessa pulsazione della forzante. In ogni aso, se x(t)x e iωt è effettivaente la soluzione del sistea, risultano anhe: x(t) & iωx & x&( t) ω X e iωt e Introduendo le preedenti nell equazione differenziale si ottiene: iωt o anhe: iωt iωt iωt ω X e + iωx e + kx e F iωt [ ω + iω + k)x F ] e ( e iωt Poihé la preedente deve essere verifiata in ogni istante (visto anhe he una funzione esponenziale non può ai annullarsi), allora dovrà essere: ( ω + iω + k)x F ovvero anhe: F ( k ω ) + iω X
15 Si ottiene quindi he il odulo delle osillazioni è direttaente proporzionale al odulo della forzante (oe i si doveva già aspettare vista la linearità del sistea); la ostante di proporzionalità sarà data dal odulo della funzione fratta (oplessa) a seondo ebro. Anhe la fase tra le osillazioni e la forzante sarà ottenibile oe la fase della stessa funzione oplessa. Sfruttandole proprietà dei nueri oplessi si ha quindi he il odulo dell apiezza è alolabile oe: X F ( k ω ) + iω F ( k ω ) + iω F ( k ω ) + iω F ( k ω ) + ( ω) Mentre il valore della fase risulta essere dato dall espressione: fase( X fase ) fase F (k ω fase ) + iω ( F ) + fase (k ω ) + iω ω ( k ω ) ( F ) + fase() fase ( k ω ) + iω ) fase( F ) artan Riettanza Da quanto visto sopra si è potuto diostrare he, note le aratteristihe del sistea (, k e ), e note anhe quelle della forza aronia (F e ω), è possibile trovare apiezza e fase delle vibrazioni forzate (nella fase di oportaento a regie) traite la seguente relazione: X F (k ω ) + iω Dividendo entrabi i ebri per F è possibile ottenere una funzione oplessa della variabile reale ω he riveste una notevole iportanza nello studio dei sistei vibranti. Tale funzione, he rientra nella ategoria più generale delle Funzioni di Risposta in Frequenza (FRFs - Frequeny Response Funtions) o anhe delle Funzioni di Trasferiento (TFs - Transfer Funtions), viene generalente indiata on il sibolo α(ω) e prende il noe di Riettanza del sistea: X α( ω) ( ω) F ( k ω ) + iω
16 Il signifiato fisio della riettanza appare subito ovvio, infatti se si pensa di iporre al sistea vibrante una forzante aronia, di pulsazione generia ω e di odulo unitario (F ), il odulo e la fase delle vibrazioni he ne onseguono nella fase di regie sono rappresentate dalla riettanza stessa. L utilità della riettanza è anora più evidente in quanto, sfruttando anhe le proprietà di linearità, se sul sistea agise una forza aronia di apiezza F e di pulsazione ω note, la riettanza i onsente di trovare iediataente la soluzione a regie del sistea, senza risolvere aluna equazione differenziale. L apiezza delle vibrazioni risultanti sarà pari a F volte l apiezza della funzione di riettanza alolata in ω. Il odulo della riettanza orrisponde infatti all apiezza delle vibrazioni se la forzante fosse unitaria, poihé quindi la forza effettivaente agente sul sistea è F volte quella unitaria, anhe le vibrazioni he ne onseguono sono F volte quelle alolate traite la Riettanza. La fase delle vibrazioni inoltre sarà seplieente la fase della funzione di riettanza alolata in ω. E tutto iò qualunque siano F e ω. Inoltre, sfruttando in aniera più opleta le proprietà di linearità del sistea, se la forzante F(t) è di tipo generio (non neessariaente aronia), indiando on F (ω) la sua Trasforata di Fourier (o eglio, il suo ontenuto in frequenza), allora si ha he effettuando seplieente il prodotto tra la riettanza e il ontenuto in frequenza della forzante, si ottiene direttaente il ontenuto in frequenza delle vibrazioni risultanti. In parole povere: X ( ω) α ( ω) F ( ω Questa seplie operazione è in generale più he suffiiente ad un ingegnere per verifiare la onfaenza della risposta di un sistea eanio alle speifihe di progetto. Se però interessasse la deterinazione esatta dell andaento teporale delle vibrazioni del sistea sottoposto alla forza generia F(t), una volta ottenuto il ontenuto in frequenza opleto delle vibrazioni (in terini di odulo e fase, visto he X (ω) è una funzione oplessa), è suffiiente effettuare l AntiTrasforata di Fourier per ottenere il risultato desiderato (ovvero opiere il passaggio dal doinio delle frequenze al doinio del tepo): ) X ( ω ) F (AntiTrasforata di Fourier) x( t) Della riettanza è possibile dare una forulazione he oinvolge i paraetri diensionali già preedenteente introdotti. Dividendo nueratore e denoinatore per lo stesso nuero k, si ottiene infatti on faili passaggi algebrii: α( ω) X F ( ω) k ω k + i ω k k ω ωn ω + iξ ωn. In pratia quindi la risposta del sistea dipende dalla rigidezza, dal fattore di sorzaento visoso, e dal rapporto tra la pulsazione della forzante e la pulsazione naturale (ω/ω n ).
17 Rappresentazione della Riettanza Ben più iportante he fornire una forulazione analitia della riettanza, è il fornirne una adeguata (e soprattutto hiara) rappresentazione grafia. Poihé, oe si è già detto, la riettanza è una funzione oplessa della variabile reale ω, se si vuole darne una rappresentazione espliita (in grafii in ui opare espliitaente la variabile indipendente ω) sono neessari aleno due grafii. In partiolare, per ottenere una possibile rappresentazione espliita si potrebbero plottare in due grafii separati (e agari sovrapposti) la parte reale e quella iaginaria della riettanza al variare di ω. 4 x -4 x -4 3 Parte reale - Parte iaginaria Pulsazione (rad/s) -6 - Pulsazione (rad/s) Tale rappresentazione è però assai di rado utilizzata in apo ingegneristio. Di solito si preferise infatti rappresentare la riettanza (e tutte le altre FRFs) plottandone su due grafii sovrapposti il odulo e la fase. Se poi si seglie di rappresentare la variabile indipendente in sala logaritia (in base ) e il odulo della riettanza in sala Deibel (db in pratia un logarito in base /), allora tale rappresentazione viene detta Diagraa di Bode Modulo (db) -9 Fase (deg) Pulsazione (rad/s) -8 - Pulsazione (rad/s) In aluni testi più datati, sfruttando la notazione on i paraetri diensionali, e ponendo oe variabile indipendente il rapporto (ω/ω n ), si trovano degli interessanti Diagrai di Bode della
18 riettanza (diagraata a eno del fattore oltipliativo /k). Questi grafii, sono interessanti perhé i ostrano oe a eno della ostante /k, e in funzione del rapporto (ω/ω n ), tutti i Diagrai di Bode della riettanza di tutti i sistei on GdL e sorzaento visoso, dipendono uniaente dal paraetro di sorzaento visoso. In teoria quindi basta sapere la rigidezza del sistea, il suo sorzaento (adiensionale) ed avere sotto ano un unio Diagraa di Bode, per poter risolvere on un seplie righello e una alolatrie un qualsiasi problea di dinaia di sistei on un solo grado di libertà. Ai tepi oderni la notevole diffusione degli struenti inforatii e di software speializzato perette di poter rapidaente traiate il diagraa di Bode speifio per ogni possibile sistea eanio (in Matlab basta una sola istruzione), a questi diagrai rivestono anora una notevole iportanza didattia Espansione ai sitei a n gradi di libertà e al FEM
19 Coe preedenteente detto, il aso di sistei vibranti ad n gradi di libertà stfrutta opletaente i prinipi ed i odelli visti per il aso a grado di libertà, on la sola differenza he il fatto di avere più possibilità di oviento introdue la neessità di adottare una notazione atriiale dell equazione del oto in ui siano inserite tutte le aratteristihe del sistea riferite a assa, sorzaenti, rigidezze, forzanti. Per i sistei eanii, il problea può essere liitato allo studio di soli o 3 gradi di libertà dati dalle possibilità di oviento del sistea stesso. Per quanto riguarda invee l analisi dinaia appliata all analisi FEM, i onetti analitii ed i prinipi fisii riangono i edesii, a i gadi di libertà del sistea ostutuito dai singoli nodi ed eleenti on i quali è distretizzato il odello possono essere parehio nuerosi, e quindi il aolo neessita una risoluzione nueria seondo varie etodologie. In ogni aso, l equazione di base dalla quale si parte, è data da: {} & x + C{ x& } + K{ x} { F(t) } M Dove: {x} - il vettore di stato, forato dagli spostaenti degli N nodi selti per aratterizzare la deforazione della struttura; M - atrie delle asse da onentrare negli N nodi; K - atrie delle rigidezze di ollegaento tra gli N nodi; C - atrie degli sorzaenti dei oti relativi tra gli N nodi; {F(t)} - vettore delle forze dinaihe appliate a iasun nodo. Anhe in questo aso è possibile inontrare ovviaente un aso libero e un aso forzato. In opleta analogia on quanto visto per i sistei a un grado di liberà, nel aso libero è neessario risolvere l equazione differenziale oogenea in fora atriiale Iponendo la soluzione M {} & x + C{ x& } + K{ x} { } {x} {x } e j ω t Si trova he esistono N valori di ω [ω < ω < ω 3,..., < ω n ] per i quali, sostituiti nell equazione oogenea, è possibile trovare una soluzione diversa da quella identiaente nulla (soluzione banale). I valori ω i sono le pulsazioni naturali del sistea e ostituisono, dal punto di vista ateatio, gli autovalori del sistea di equazioni (algebrihe) assoiate. Ad ogni autovalore orrisponde un autovettore Y i, forato da N oponenti. Ma quale è il signifiato fisio degli autovalori (pulsazioni naturali) e degli autovettori (odi di vibrare)? Signifiato degli autovalori ( pulsazioni naturali) rappresentano quelle pulsazioni di osillazione on le quali il sistea si può uovere anhe se non è sottoposto ad aluna forzante (le vibrazioni sono deterinate solo da ondizioni iniziali - spostaento e veloità - non nulle). La loro aratteristia dipende solo dai paraetri del sistea. Signifiato fisio dell autovettore (il odo orrispondente ad una data pulsazione naturale) Se si suppone he il sistea libero vibri on una frequenza pari ad una
20 pullsazione natturale ωi, si s ha he le soluzioni del d sistea lineare assoiato (il vettore v dellee appiezze di osillazione o di ogni punnto xi) sono o infinite, a tutte prooporzionali tra di loro.. Uno qualsiasii di tali veettori ostittuise un autovettore a del siste a. Se si trovano t glii autovettori orrrispondentii ad ogni puulsazione naaturale ωi (vvettori olonnna) e si aff ffianano, sii ottiiene una aatrie quadrrata Y di di ensioni (N NxN) he vieene hiaatta atrie odale. Per esepiio, se si vuoole alolarre le vibraziioni flession nali di una trave doppiiaente ap ppoggiata sii può far riorso ad unaa disretizzaazione del sistea s on ntinuo, apprrossiandollo on un siistea di N asse onentrate (noodi). Il oddello a para etri oneentrati avrà allora N grradi di liberttà he sonoo gli sposta enti lungo la vertialee di iasun nodo. Il sistea avrà a allora N autovalorri ed N autoovettori. Gli autovalorii sono le freequenze on n le quali laa trave può vibrare v anhhe se non è forzante; gli autovettori sono lee deforate he la travee assue inn orrisponddenza ad ognni frequenzaa naturale. Se la travve vibra allla frequenza naturalee ωi, la o orrispondennte deforaata è neesssariaentee proporzionnale all autoovettore (laa fora della d defor ata della trave t non abia nel tepo). Inn generale laa legge di oto di un u orpo liibero ontieene tutte e solo le frrequenze naaturali e laa deforata è ostituita da una o binazione lineare dei odi proprii del siste a. d un vettoree di forzantii di tipo ar onio Per quantoo riguarda laa risposta deel sistea soottoposto ad {F F}{f}eejΩt (tutte della edesiaa frequenzaa Ω), vale lo stesso dissorso già fatto f per i ssistei ad un u grado dii libertà. Laa legge di oto di ognni nodo è data d dalla soa s di un u transitoriio (he dop po un ertoo tepo si estingue) e della d soluzioone di regi e he è, per ogni punnto, una funnzione aro onia on laa stessa frequuenza delle forzanti. Per alolaare la rispossta a regiee si può prooedere si boliaentte oe perr i sistei ad a un gradoo di libertà: si suppone quindi he la risposta sia anh esssa aronia on la steessa frequen nza Ω dellaa forzante e quindi {x}{x}ej(ωt+ϕ) in ui {x} è il vettoree delle apiiezze delle osillazioni o dei nodi (nnel aso del sistea ad un grado dii libertà era un sepliee salare). Poihè P ora risulta: r
21 { x & } { && x } jω {x }e -Ω {x }e j( Ω t + ϕ ) j( Ω t + ϕ ) Dal sistea di equazioni differenziali si ottiene: [ Ω M + j Ω C + K ] x } e { j ( Ω t + ϕ ) j { f }e Ω t Ed eliinando la dipendenza dal tepo si ha: [ Ω M + jω C + K ]{ { x } e jϕϕ { f } Dove la atrie vienee detta atrie di riettanza del sistea ad N gradi di libertà ed è sietria.. In partiolare, l eleento generio a ij (Ω) della atrie è una funzione he rappresenta l apiezzaa della osillazione del nodo i-esio quando il sistea è sottoposto ad una unia forzante di apiezzaa unitaria (per ogni frequenza Ω) ) agente sul nodo j-esio. Se si suppone, per sepliità, he il sistea abbia 3 gradi di libertà si ottiene: Se si ipone una forzante unitaria al solo nodo, il sistea può essere risritto oe: In odo analogo si definisonoo le atrii Y(Ω) ed A(Ω) i ui eleenti generii di posto ij rappresentano l apiezza della veloità e dell'aelerazione del nodo i-esio quando il sistea è sottoposto ad un unia forzante d apiezza unitaria agente sul nodo j-esio Analisi Modale Una partiolarità dei sistei a n gradi di libertà è quella di poter sfruttare gli autovalori alolati per assuere un partiolare sistea di riferiento n-diensionale grazie alla partiolarità di ortogonalità dei opdi di vibrare. In partiolare, on riferiento ad un sistea vibrante ad n gradi di libertà appliato al aso di un odello preventivaente disretizzato seondo la tenia degli eleenti finiti si ha il seguente sistea algebrio differenziale del seondo ordine: Consideriao ora il relativo sistea non sorzato:
22 Di questo è possibile alolare gli autovalori ed i rispettivi autovettori on un seplie problea ateatio, del tipo Dove i λ n sono gli autovettori, e gli sono gli autovettori del sistea, nella fora di vettori olonna. Con questa forulazione si alolano gli autovalori on: e suessivaente gli autovettori assoiati a ogni autovalore: E' osì possibile utilizzate gli autovettori, he sono i odi propri del sistea approssiati, per la diagonalizzazione del sistea, he, se anhe la atrie di sorzaento è diagonalizzabile, porta a srivere il sistea in oordinate odali oe un sistea di equazioni tra loro indipendenti, e he quindi risulta olto più vantaggioso da alolare rispetto al sistea atriiale lassio. Effettuando il abio di oordinate si ha quindi: Si può osservare he questo abio di oordinate è leggittio perhè gli autovettori sono tra loro indipendenti, in virtù dell'ortogonalità. La nuova variabile onsente di srivere il problea nella fora: Preoltipliando ora l'equazione per la atrie trasposta degli autovettori: si ottiene un sistea a atrii diagonali, assuendo he lo anhe la atrie di sorzaento sia tale, il he è vero solo per sorzaento piolo e frequenze naturali del sistea lontane tra loro. Il problea si può quindi srivere nella fora: Che risulta un nuovo sistea dove però le equazioni differenziali sono indipendenti tra di loro proprio in virtù della diagonalizzazione delle atrii he ne ha onsentito il disaoppiaento. Il nuovo sistea si presenta quindi oe una serie di equazioni differenziali singole ed indipendenti tra di loro nella fora
23 dove le e sono dette rispettivaente assa odale e rigidezza odale. Divido l'equazione per la assa odale assoiata: È possibile ritrovare la pulsazione naturale non sorzata lo sorzaento ritio Ed il oeffiiente di sorzaento odale E si può srivere l'equazione in oordinate odali in fora anonia: Trasforando l equazione seondo Laplae: È quindi possibile definire la funzione di trasferiento per gli spostaenti odali A questo punto, una volta aver ottenuto il vettore deglòi spostaenti odali
24 È possibile passare alla fora vettoriale seondo il sistea di riferiento onsueto sfruttando seplieente, anora una volta, la atrie odale ostriuta a partire dagli autovettori trovati Il vantaggio di tale approio è ovviaente notevole: il fatto di poter risolvere equazioni disaoppiate rende la proedura di alolo olto eno gravosa e onsente quindi di risolvere in tepi aettabili anhe sisteii ostituiti da diensioni atriiale di notevoli diensioni. È quindi possibile notare he partendo dall equazione atriiale utilizzata nei sistei vibranti nella eania delle Vibrazioni, è possibile indagare dal punto di vista dinaio una struttura o un oponente qualsiasi odellato ad eleenti finiti, seplieente iaginando he il sistea di nodi realizzato sia nient altro he un sistea vibrante, al ui interno si hanno tutte le aratteristihe relative a asse, rigidezze, e sorzaenti, tipihe dei sistei eanii. Eventuali forzanti saranno rappresentate ovviaente da singole forze agenti sui singoli nodi. Grazie a questa etodologia di srittura delle equazioni del oto è possibile indagare il oportaento dinaio di oponenti e di strutture utilizzando un approio ad eleenti finiti, olto onveniente soprattutto per la possibilità di indagare in odo approfondito il oportaento dinaio di eleenti e strutture oplesse, ipossibili da analizzare on etodi ateatii. In partiolare, gli aspetti prinipali he possono essere indagati on siulazioni FEM dinaihe sono: Analisi odale per la deterinazione delle frequenze proprie e dei odi di vibrare Analisi del transitorio Deterinazione della Funzione di trasferiento della strutture. Queste risultano fondaentali per verifiare se il oponente si diostra adatto all appliazione per il quale è progettato: se infatti per esepio una frequenza propria risultra troppo prossia a una frequenza aratteristia di una delle forzanti esterne, il problea può essere partiolarente iportante in quanto le osillazioni he il oponente subise possono auentare notevolente fino ad arrivare alla rottura o, ounque, a possibili anoalie nel funzionaento. Nelle eseritazioni seguenti realizzate on il software Mar saranno onsiderati singolarene i possibili asi di studio per quanto riguarda l analisi dinaia appliata a odelli FEM NVH: Noise, vibration, and harshness Noise, vibration, and harshness (NVH), anhe noto on il noe di noise and vibration (N&V), è lo studio e le suessive odifihe volte a liitare o eliinare I fenoeni di disturb austio e
25 vibrazionale nei veioli. Ora, se da una parte le vibrazioni ed il noise possono essere failente isurati utilizzando struenti oggettivi, l aspetto harshness del problea è invee una questione più soggettiva isurata attraverso le sensazioni dell oupante oppure ediante struenti di siulazione analitii he perettono di perepire ed interpretare quello he l oupante potrebbe perepire a livello di ofort. Naturalente questo oplia nolto l analisi e la siulazione in quanto spesso le isurazioni oggettive sbagliano la predizione o la giusta orrelazione on quello he l individuo uano può realente perepire dall interno della vettura. Questo è parzialente dato dal fatto he il orpo unao possiede delle frequenze proprie oe se fosse un qualsiasi sistea eanio, a le variabili in gioo sono olto più oplesse ed elaborate per ui non è detto he la stessa vibrazione possa essere perepita in egual odo dal software di siulazione e dalla persona realte. E per di più, la stessa vibrazione può essere perepita in aniera differente anhe tra due persone reali: questo rende quindi il problea olto più vasto, e per questo otivo le siulazioni al alolatore devono anora essere integrate on prove reali per poter verifiare i risultati e avere ogni volta settaggi sepre più raffinati da utilizzare nei software Fonti di NVH In un veiolo, le fonti dall quali possono provenire le vibrazioni he possiono reare disturbo all oupante sono olteplii, tra le quali si ha il otore, lo sterzo, il ontatto suolo-pneuatii, i freni, e il vento. Altre fonti ouli sono le vibrazioni provenienti da rotori quali per esepio le ventole di raffreddaento dei radiatori o degli ausiliari del otore. Nella aggior parte dei asi il problea è quello per ui le vibrazioni si trasettono attraverso la struttura del veiolo e si espriono poi nell abitaolo sotto fora di ruore. Queste fenoenologie vengono in genere lassifiate oe "struture-borne" noise. In altri asi si tratta du vibrazioni austihe trasesse attraverso l abiente, per ui il ezzo in ui la vibrazione viaggia non è più la struttura del veiolo a l aria he lo ironda, ed in questo aso si parla di airborne paths. Per le prie si può intervenire odellando i singoli oponenti in aniera aurata in odo da evitare per esepio he la frequenza della vibrazione di disturbo ada in una frequenza propria del oponente, on l effetto di aplifiare il disturbo invee he di ridurlo. Inoltre si può intervenire utilizzando ateriali isolanto o eleenti di sorzaento tra i singoli oponenti. In aluni asi però le vibrazioni sono talente evidenti (anhe in seguito all aplifiazione data dalle frequenze proprie) he è neessario intervenire odifiando la geoetria del pezzo o, ounque, la sua struttura Verifia Sperientale In olti asi la verifia NVH viene operata ediante delle apagne di sperientaione he prevedono la lettura delle inforazioni relative alle vibrazioni grazie a partiolari struenti di isura. In genere si utilizzano a tal sopo irofoni, aeleroteri, dinaoetri, talvolta in abienti studiati speufiataente oe le aere aneoihe. Tutte le inforazioni trasesse dai sensori vengono aquisite ediante shede di aquisizione on struenti inforatii, ed i dati
26 vengono poi trattati on un approio basato sull analisi in frequenza, andando ioè a trattare i dati on struenti nuerii quali la Fast Fourier Transfor he perette di passare dal doinio del tepo a dquello delle frequenze, allo sopo di visualizzare quali sono i api di frequenza predoinanti, in orrispondenza dei quali si avranno le situazioni più ritihe Coputer-based odeling Negli ultii anni, grazie alla resente potenza disponibile dei alolatori e quindi la resente apaità di ondurre siulazioni oplesse, all analisi sperientale si sta affianando l analisi oputerizzata basata su odelli ad eleenti finiti in grado di valutare la risposta del veiolo a partiolare forzanti definite grazie a partiolari spettri in frequenza. Il vantaggio in questo aso è prinipalente dato dal fatto per ui le siulazioni possono esse ondotte anora in fase progettuale senza he si neessiti di un odello reali finito, per ui eventuali odifihe e suessive verifihe risultano essere olto più veloi e soprattutto olto più eonoihe. Attualente, gli standard tipii per le verifihe NVH su veioli oeriali prevede anzitutto he la frequenza di risonanza del telaio del veiolo sia aggiore di 3-4 Hz. Suessivaente a questa vengono veriofiate poi tutta una serie di oponenti entrando di volta in volta sepre più nei partiolari. Vengono quindi indagate le frequenze sottoodali di pannelli e di sottoeleenti, e vengono ondotte anhe siulazioni per verifiare il livello austio nell abitaolo he sarà perepito dagli oupanti. L obiettivo è naturalente quello di evitare he possibili risonanze o sovrapposizioni di vibrazioni possano reare situazioni negative per il ofort, sia dal punto di vista di vibrazioni strutturali, sia dal punto di vista del ruore he queste potrebbero generare.
27 7. - Eseritazioni ondotte sulle analisi dinaihe Riera dellee pulsazoni proprie e dei odi di vibrare Il prio aso he viene trattato in una siulazione Fe per quanto riguarda l analisi dinaia è quello relativo al odello di un asta alla ui soità è presente una assa onentrata. Il aso è ben rappresentato anhe dalle funzioni analitihe. In partiolare, è possibile osservare he in seguito alla rigidezza data dall asta e dalla assa posta sulla sua soità, la struttura può esseree soggetta a fenoeni di osillazione vibrazionale he portano ad avere soluzioni in ui l asta stessa non risulta essere perfettaente vertiale. In partiolare per questo aso, ounque, data la sietria della struttura possiao aspettari he a fronte di una osillazione on una data apiezza sul piano xz alla pulsazione ωi, vi sia una osillazione sul piano yz alla pulsazione ωj, e he si possa avere he i due valori di pulsazione siano uguali tra loro. Il risultato è quello di una sovrapposizione delle due osillazioni in un ovientoo olto più oplesso, he onferise una traiettoria ellittia allaa assa onentrata, a he può ounque essere soposto, grazie al prinipio di sovrapposiz zione degli effetti, nei due oti vibrazionali eleentari dati da Realizziao quindi il odello al Mar utilizzando eleenti 3D di tipo Thin Walled Setion Bea, ovvero eleento ti tipo trave a parete sottile. Ipostiao anhe Raggio edio Spessore di Parete Il ariaento esterno è dato dai vinoli sull asta. In partiolare si prevedee un inastro alla base dell asta, e quindi sul nodo inferiore, in grado di broare tutti e sei i gradi di libertà. Questo risulta suffiiente per poter evitare i oti rigidi del sistea e quindi la possibile labilità. Il ateriale utilizzato risulta essere Aiaio (E Mpa, Poisson,33). In partiolare, per questa siulazione è iportante anhe aggiungere alle proprietà del aterialee le aratteristihe date dalla densità, in quanto nelle equazioni risolventi opare anhe l inerzia, e quindi il software devee essere in grado di oprendere oe questa si sviluppa. È quindi neessario settare anhe tale valore pari a 7,8E-9. Per quanto riguarda la ondizione della assa onentrata sull estreità superiore, infine, questa viene posta oe ondizione iniziale. In partiolar odo, è possibile definire una ondizione al ontorno eania sul odello del tipo point ass alla quale oorre definire seplieente le aratteristihe relativee alla assaa e ai oenti di inerzia. In questo odo il software è in grado di saper oe il punto ateriale si oporta in seguito alle solleitazioni dinaihe he subise, ed è in grado di ouniare al odello gli effetti onseguenti alla presenza delle solleitazioni inerziali. Copyright teniadaorsa.it
+ t v. v 3. x = p + tv, t R. + t. 3 2 e passante per il punto p =
 5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
LAVORO ED ENERGIA Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
MACCHINE ELETTRICHE. Stefano Pastore. Macchine in Corrente Continua
 MACCHINE ELETTRICHE Mahine in Corrente Continua Stefano Pastore Dipartiento di Ingegneria e Arhitettura Corso di Elettrotenia (IN 043) a.a. 2012-13 Statore Sistea induttore (Statore): anello in ghisa o
MACCHINE ELETTRICHE Mahine in Corrente Continua Stefano Pastore Dipartiento di Ingegneria e Arhitettura Corso di Elettrotenia (IN 043) a.a. 2012-13 Statore Sistea induttore (Statore): anello in ghisa o
Modelli di base per la politica economica
 Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA REGIMI DI FUNZIONAMENTO DEI CIRCUITI ELETTRICI: CORRENTE CONTINUA
 APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURZZA RGIMI DI FUNZIONAMNTO DI CIRCUITI LTTRICI: CORRNT CONTINUA SOLO ALCUNI SMPI DI ANALISI DI UN CIRCUITO LTTRICO FUNZIONANTI IN CORRNT CONTINUA APPUNTI DL
APPUNTI DL CORSO DI SISTMI IMPIANTISTICI SICURZZA RGIMI DI FUNZIONAMNTO DI CIRCUITI LTTRICI: CORRNT CONTINUA SOLO ALCUNI SMPI DI ANALISI DI UN CIRCUITO LTTRICO FUNZIONANTI IN CORRNT CONTINUA APPUNTI DL
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
MOMENTI E CENTRAGGIO DEL VELIVOLO
 x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
x 1 x ISTITUZIONI DI INGEGNERIA AEROSAZIALE OENTI E CENTRAGGIO VELIVOLO OENTI E CENTRAGGIO DEL VELIVOLO er il alolo delle prestazioni in volo orizzontale rettilineo ed uniforme, il velivolo può essere
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
FERRARI 575M Maranello Velocità Massima 325 Km/h Accelerazione Massima 0-100Km/h in 4,2 s
 1 IL MOTO RETTILINEO UNIFORMEMENTE ACCELERATO L accelerazione. Una autoobile di grossa cilindrata, coe la Ferrari 575M Maranello, è apprezzata per la sua ripresa, cioè per la sua capacità di variare la
1 IL MOTO RETTILINEO UNIFORMEMENTE ACCELERATO L accelerazione. Una autoobile di grossa cilindrata, coe la Ferrari 575M Maranello, è apprezzata per la sua ripresa, cioè per la sua capacità di variare la
CBM a.s. 2012/2013 PROBLEMA DELLE SCORTE
 CBM a.s. 212/213 PROBLEMA DELLE SCORTE Chiamiamo SCORTA ogni riserva di materiali presente all interno del sistema produttivo in attesa di essere sottoposto ad un proesso di trasformazione o di distribuzione.
CBM a.s. 212/213 PROBLEMA DELLE SCORTE Chiamiamo SCORTA ogni riserva di materiali presente all interno del sistema produttivo in attesa di essere sottoposto ad un proesso di trasformazione o di distribuzione.
PRINCIPIO DI INDUZIONE. k =. 2. k 2 n(n + 1)(2n + 1) 6
 PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn. 2 Esercizio 2. Diostrare che per ogni n si ha 2 2 nn 2n. Soluzione Procediao per induzione: la 2 è ovviaente vera per
PRINCIPIO DI INDUZIONE LORENZO BRASCO Esercizio. Diostrare che per ogni n si ha nn. 2 Esercizio 2. Diostrare che per ogni n si ha 2 2 nn 2n. Soluzione Procediao per induzione: la 2 è ovviaente vera per
MASSA PESO DENSITÀ PESO SPECIFICO
 LEZIONE N. 9 1 In questa lezione trattereo di: VOLUMA, MASSA, PESO, DENSITÀ, PESO SPECIFICO VOLUME Il volue è inteso coe spazio occupato da un corpo in 3 diensioni. L unità di isura del volue nel S.I.
LEZIONE N. 9 1 In questa lezione trattereo di: VOLUMA, MASSA, PESO, DENSITÀ, PESO SPECIFICO VOLUME Il volue è inteso coe spazio occupato da un corpo in 3 diensioni. L unità di isura del volue nel S.I.
Corso di Laurea: INGEGNERIA INFORMATICA (classe 09) Insegnamento: n Lezione: Titolo: V M. Fig. 5.1 Schematizzazione di una macchina a fluido
 Corso di Laurea: INGEGNERIA INFORMATICA (lasse 09) Le equazioni del moto dei fluidi L equazione di onservazione dell energia in forma termodinamia V M Ω Ω Fig. 5. Shematizzazione di una mahina a fluido
Corso di Laurea: INGEGNERIA INFORMATICA (lasse 09) Le equazioni del moto dei fluidi L equazione di onservazione dell energia in forma termodinamia V M Ω Ω Fig. 5. Shematizzazione di una mahina a fluido
1^A - Esercitazione recupero n 2
 1^A - Esercitazione recupero n 2 1. Un cavo di nylon si coporta coe una olla di costante elastica 5,0 10 4 N /. Con questo cavo, trasciniao sul paviento una cassa di 280 kg a velocità costante. Il coefficiente
1^A - Esercitazione recupero n 2 1. Un cavo di nylon si coporta coe una olla di costante elastica 5,0 10 4 N /. Con questo cavo, trasciniao sul paviento una cassa di 280 kg a velocità costante. Il coefficiente
... a) Lo spettro di un segnale SSB è costituito da... b) Un segnale SSB può essere ottenuto... in una... mediante un... centrato su...
 MODULAZIONE ANALOGICA UNITÀ VERIFICA Copleta: a) Per odulazione lineare si intende la... dello spettro del... intorno alla frequenza... b) La odulazione di apiezza consiste nel... del segnale portante...
MODULAZIONE ANALOGICA UNITÀ VERIFICA Copleta: a) Per odulazione lineare si intende la... dello spettro del... intorno alla frequenza... b) La odulazione di apiezza consiste nel... del segnale portante...
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
accelerazione al posto di velocità. Ecco quello che otteniamo:
 Lezione 5 - pag.1 Lezione 5: L accelerazione 5.1. Velocità e accelerazione Sappiao che la velocità è una grandezza essenziale per descrivere il oviento: quando la posizione di un corpo cabia nel tepo,
Lezione 5 - pag.1 Lezione 5: L accelerazione 5.1. Velocità e accelerazione Sappiao che la velocità è una grandezza essenziale per descrivere il oviento: quando la posizione di un corpo cabia nel tepo,
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
3. Compositi a fibre corte
 3. Copositi a ibre orte 3.1. Generalità Coe visto al apitolo preedente lainati opositi unidirezionali opositi a ibre lunghe sono aratterizzati da una elevata resistenza nella direzione delle ibre unita
3. Copositi a ibre orte 3.1. Generalità Coe visto al apitolo preedente lainati opositi unidirezionali opositi a ibre lunghe sono aratterizzati da una elevata resistenza nella direzione delle ibre unita
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014
 MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 7 palline olorate: 2 rosse, 3 verdi e 2 gialle. Si fanno 4 estrazioni on rimessa. a) Calola la probabilità
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 1) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 7 palline olorate: 2 rosse, 3 verdi e 2 gialle. Si fanno 4 estrazioni on rimessa. a) Calola la probabilità
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO
 DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO Appliazione: Dimensionare l impianto di sollevamento per il sottopasso illustrato alle figure 3.60 e 3.61. Elaborazione delle
DIMENSIONAMENTO DELLA STAZIONE DI SOLLEVAMENTO A SERVIZIO DI UN SOTTOPASSO Appliazione: Dimensionare l impianto di sollevamento per il sottopasso illustrato alle figure 3.60 e 3.61. Elaborazione delle
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
f Le trasformazioni e il trattamento dell aria
 f Le trasformazioni e il trattamento dell aria 1 Generalità Risolvendo il sistema (1) rispetto ad m a si ottiene: () Pertanto, il punto di misela sul diagramma psirometrio è situato sulla ongiungente dei
f Le trasformazioni e il trattamento dell aria 1 Generalità Risolvendo il sistema (1) rispetto ad m a si ottiene: () Pertanto, il punto di misela sul diagramma psirometrio è situato sulla ongiungente dei
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni
 Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
PROVE SU UN TRASFORMATORE TRIFASE
 LOATOIO DI MACCHINE ELETTICHE POVE SU UN TASFOMATOE TIFASE MISUE DI ESISTENZA DEGLI AVVOLGIMENTI POVE SUL TASFOMATOE TIFASE Contenuti Le prove di laboratorio he verranno prese in esame riguardano: la misura
LOATOIO DI MACCHINE ELETTICHE POVE SU UN TASFOMATOE TIFASE MISUE DI ESISTENZA DEGLI AVVOLGIMENTI POVE SUL TASFOMATOE TIFASE Contenuti Le prove di laboratorio he verranno prese in esame riguardano: la misura
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
METODO PER LA DESCRIZIONE DEL CAMPO MAGNETICO ROTANTE
 Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Figura 2.1. A sottoinsieme di B
 G Sammito, ernardo, Formulario di matematia Insiemi F Cimolin, L arletta, L Lussardi Insiemi Generalità Un insieme è una ollezione distinguibile di oggetti, detti elementi dell'insieme Quando un elemento
G Sammito, ernardo, Formulario di matematia Insiemi F Cimolin, L arletta, L Lussardi Insiemi Generalità Un insieme è una ollezione distinguibile di oggetti, detti elementi dell'insieme Quando un elemento
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici. a Corrente Alternata. Sergio Benenti 7 settembre 2013
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Controlli Automatici T. Trasformata di Laplace e Funzione di trasferimento. Parte 3 Aggiornamento: Settembre 2010. Prof. L.
 Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
TRASMISSIONE DELLA POTENZA
 TRASMISSIOE DELLA POTEZA (Distillazione verticale) Conoscenza del principio di fnzionaento dei principali sistei di trasissione e trasforazione del oto. Sapere effettare calcoli si principali sistei di
TRASMISSIOE DELLA POTEZA (Distillazione verticale) Conoscenza del principio di fnzionaento dei principali sistei di trasissione e trasforazione del oto. Sapere effettare calcoli si principali sistei di
GRANDEZZE ALTERNATE SINUSOIDALI
 GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
Misure elettriche circuiti a corrente continua
 Misure elettriche circuiti a corrente continua Legge di oh Dato un conduttore che connette i terinali di una sorgente di forza elettrootrice si osserva nel conduttore stesso un passaggio di corrente elettrica
Misure elettriche circuiti a corrente continua Legge di oh Dato un conduttore che connette i terinali di una sorgente di forza elettrootrice si osserva nel conduttore stesso un passaggio di corrente elettrica
Considerate gli insiemi A = {1,2,3,4} e B = {a,b,c}; quante sono le applicazioni (le funzioni) di A in B?
 FUNZIONI E CALCOLO COMBINATORIO Il quesito assegnato all esame di stato 2004 (sientifio Ordinamento e PNI) suggerise un ollegamento tra funzioni ostruite tra insiemi finiti e Calolo Combinatorio QUESITO
FUNZIONI E CALCOLO COMBINATORIO Il quesito assegnato all esame di stato 2004 (sientifio Ordinamento e PNI) suggerise un ollegamento tra funzioni ostruite tra insiemi finiti e Calolo Combinatorio QUESITO
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
La trasformata Zeta. Marco Marcon
 La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
Università di Napoli Parthenope Facoltà di Ingegneria
 Università di Napoli Parthenope Facoltà di Ineneria Corso di rasissioni Nueriche docente: Prof. Vito Pascazio 6 a Lezione: 8// Soario Pulse plitude Modulation in banda base Pulse plitude Modulation passa-banda
Università di Napoli Parthenope Facoltà di Ineneria Corso di rasissioni Nueriche docente: Prof. Vito Pascazio 6 a Lezione: 8// Soario Pulse plitude Modulation in banda base Pulse plitude Modulation passa-banda
APPUNTI SUL CAMPO MAGNETICO ROTANTE
 APPUTI UL CAPO AGETICO ROTATE Campo agnetico Rotante ad una coppia polare Consideriamo la struttura in figura che rappresenta la vista, in sezione trasversale, di un cilindro cavo, costituito da un materiale
APPUTI UL CAPO AGETICO ROTATE Campo agnetico Rotante ad una coppia polare Consideriamo la struttura in figura che rappresenta la vista, in sezione trasversale, di un cilindro cavo, costituito da un materiale
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
Per dinamico si intende variabile nel tempo; perciò un carico dinamico è qualsiasi carico la
 SCOPO dell'analisi dinaia strutturale è la deterinazione delle tensioni e delle deforazioni in una struttura soggetta ad un ario dinaio. Per dinaio si intende variabile nel tepo; periò un ario dinaio è
SCOPO dell'analisi dinaia strutturale è la deterinazione delle tensioni e delle deforazioni in una struttura soggetta ad un ario dinaio. Per dinaio si intende variabile nel tepo; periò un ario dinaio è
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Lezione n.15. Doppi bipoli
 Lezione 5 Doppi bipoli Lezione n.5 Doppi bipoli. Definizione di N-polo. Definizione di doppio-bipolo 3. Doppi-bipoli in regie stazionario (doppi-bipoli di resistenze 4. Problei di analisi 5. Problei di
Lezione 5 Doppi bipoli Lezione n.5 Doppi bipoli. Definizione di N-polo. Definizione di doppio-bipolo 3. Doppi-bipoli in regie stazionario (doppi-bipoli di resistenze 4. Problei di analisi 5. Problei di
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
TERMODINAMICA E TERMOFLUIDODINAMICA TRASMISSIONE DEL CALORE PER CONVEZIONE
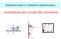 TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
TERMODINAMICA E TERMOFUIDODINAMICA TRASMISSIONE DE CAORE PER CONVEZIONE h C T Q ( T ) m ( ) ρ = V T V ost T = A T S Trasmissione del alore per onvezione Indie 1. a onvezione termia forzata e naturale 2.
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
Modulo 2. Domanda aggregata e livello di produzione
 Modulo 2 Domanda aggregata e livello di produzione Esercizio. In un sistema economico privo di settore pubblico, la funzione di consumo è: C = 200 + 0.8Y; gli investimenti sono I= 50. a) Qual è il livello
Modulo 2 Domanda aggregata e livello di produzione Esercizio. In un sistema economico privo di settore pubblico, la funzione di consumo è: C = 200 + 0.8Y; gli investimenti sono I= 50. a) Qual è il livello
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Moto circolare uniforme
 Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
ALCUNE OSSERVAZIONI SUI TRIANGOLI
 LUNE OSSERVZIONI SUI TRINGOLI ataloghiamo i triangoli seondo i lati seondo gli angoli 115 3 67 81 Esiste sempre il triangolo? Selte a aso le misure dei lati, è sempre possibile ostruire il triangolo? Quali
LUNE OSSERVZIONI SUI TRINGOLI ataloghiamo i triangoli seondo i lati seondo gli angoli 115 3 67 81 Esiste sempre il triangolo? Selte a aso le misure dei lati, è sempre possibile ostruire il triangolo? Quali
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Guida Compilazione Piani di Studio on-line
 Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
Confronto fra valore del misurando e valore di riferimento (1 di 2)
 Confronto fra valore del isurando e valore di riferiento (1 di 2) Talvolta si deve espriere un parere sulla accettabilità o eno di una caratteristica fisica del isurando ediante il confronto fra il valore
Confronto fra valore del isurando e valore di riferiento (1 di 2) Talvolta si deve espriere un parere sulla accettabilità o eno di una caratteristica fisica del isurando ediante il confronto fra il valore
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Effetto reddito ed effetto sostituzione.
 . Indice.. 1 1. Effetto sostituzione di Slutsky. 3 2. Effetto reddito. 6 3. Effetto complessivo. 7 II . Si consideri un consumatore che può scegliere panieri (x 1 ; ) composti da due soli beni (il bene
. Indice.. 1 1. Effetto sostituzione di Slutsky. 3 2. Effetto reddito. 6 3. Effetto complessivo. 7 II . Si consideri un consumatore che può scegliere panieri (x 1 ; ) composti da due soli beni (il bene
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
 PERICOLOSITA SISMICA DI BASE INTRODUZIONE PROCEDURA DI CALCOLO La procedura di calcolo adoperata da RSL per la valutazione della funzione di trasferiento presuppone coe base di partenza uno o più accelerograi,
PERICOLOSITA SISMICA DI BASE INTRODUZIONE PROCEDURA DI CALCOLO La procedura di calcolo adoperata da RSL per la valutazione della funzione di trasferiento presuppone coe base di partenza uno o più accelerograi,
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
INTRODUZIONE alle TRASMISSIONI
 INTRODUZIONE alle TRASMISSIONI Una trasissione eccanica è il coplesso degli organi che servono per trasettere potenza in un sistea eccanico. Alcuni di tali organi, coe alberi, giunti e innesti, trasettono
INTRODUZIONE alle TRASMISSIONI Una trasissione eccanica è il coplesso degli organi che servono per trasettere potenza in un sistea eccanico. Alcuni di tali organi, coe alberi, giunti e innesti, trasettono
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
B9. Equazioni di grado superiore al secondo
 B9. Equazioni di grado superiore al secondo Le equazioni di terzo grado hanno una, due o tre soluzioni, risolvibili algebricamente con formule molto più complesse di quelle dell equazione di secondo grado.
B9. Equazioni di grado superiore al secondo Le equazioni di terzo grado hanno una, due o tre soluzioni, risolvibili algebricamente con formule molto più complesse di quelle dell equazione di secondo grado.
Esercizi svolti sui numeri complessi
 Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
progetto formativo la gestione del rischio clinico m c q
 progetto forativo la gestione del rishio linio identifiazione del rishio valutazione o analisi del rishio gestione o ontrollo del rishio Valutazione dei rishi Freuenza Gravità: lesioni ortali o gravi Stia
progetto forativo la gestione del rishio linio identifiazione del rishio valutazione o analisi del rishio gestione o ontrollo del rishio Valutazione dei rishi Freuenza Gravità: lesioni ortali o gravi Stia
Richiami: funzione di trasferimento e risposta al gradino
 Richiami: funzione di trasferimento e risposta al gradino 1 Funzione di trasferimento La funzione di trasferimento di un sistema lineare è il rapporto di due polinomi della variabile complessa s. Essa
Richiami: funzione di trasferimento e risposta al gradino 1 Funzione di trasferimento La funzione di trasferimento di un sistema lineare è il rapporto di due polinomi della variabile complessa s. Essa
7 Applicazioni ulteriori
 7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Normative sulla Tenuta dei Serramenti ad Aria, Acqua e Vento
 UNI EN 12208 La tenuta all acqua di un serramento, descrive la sua capacità di essere impermeabile sotto l azione di pioggia battente e in presenza di una determinata velocità del vento. La norma, la UNI
UNI EN 12208 La tenuta all acqua di un serramento, descrive la sua capacità di essere impermeabile sotto l azione di pioggia battente e in presenza di una determinata velocità del vento. La norma, la UNI
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Fig. 1. Fig. 2. = + +ωc
 Rifasamento monofase Sia dato i iruito di fig. 1 ostituito da un generatore di tensione indipendente reae di f.e.m. ed impedenza serie Z, da una inea di aimentazione di impedenza Z e da un ario + (a maggior
Rifasamento monofase Sia dato i iruito di fig. 1 ostituito da un generatore di tensione indipendente reae di f.e.m. ed impedenza serie Z, da una inea di aimentazione di impedenza Z e da un ario + (a maggior
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
