Funzioni reali di 2 variabili reali
|
|
|
- Leopoldo Alberti
- 6 anni fa
- Visualizzazioni
Transcript
1 Funzioni reali di 2 variabili reali Sono funzioni del tipo: f :domf R 2 R Ad ogni punto P =(x, y) di un sottoinsieme dom f P =(x, y) f (P )=f (x, y) di R 2 associano un numero reale f (P )=f (x, y). Se f (x, y) è un espressione in x, y, salvo diversa indicazione si conviene che: dom f = {(x, y) R 2 : f (x, y) esiste in R}. Si chiama immagine di f il sottoinsieme di R deivaloriassuntidaf, cioè l insieme im f := {f (x, y) R :(x, y) dom f}. Grafico di una f :domf R 2 R È il sottoinsieme di R 3 definito da G f = {(x, y, f (x, y)) R 3 :(x, y) dom f} = luogo dei punti (x, y, z) di equazione z = f (x, y). Proiezione ortogonale di G f sul piano xy =domf. Proiezione ortogonale di G f sull asse z =imf. Esempio. Il grafico di f (x, y) =ax + by èilpianoz = ax + by (non verticale, ortogonale a N =(a, b, 1)).
2 Insiemidilivellodiunaf :domf R 2 R Sono i sottoinsiemi di dom f definiti da L f,c = {(x, y) dom f : f (x, y) =c},cr = l insieme dei punti su cui f ècostanteevalec. Esempio. Gli insiemi L f,c di f (x, y) =ax + by (a, b non entrambi nulli) sono L f,c : f (x, y) =c, cioè le rette ax + by = c del piano xy. Ovviamente L f,c = se e solo se c im f. L f,c èlaproiezionesulpianoxy dell intersezione tra il grafico z = f (x, y) ed il piano z = c. Gli insiemi di livello danno una rappresentazione bidimensionale dell andamento di f, alternativa a quella tridimensionale data dal grafico. Insiemi di livello della funzione f (x, y) = x2 1 esuografico x 2 +y 2 Rappresentadole per valori equidistanziati di c, si visualizzano anche informazioni sulla velocità di variazione dei valori di f.
3 Continuità Definizione. Sia f :domf R 2 R. Sidiceche: f è continuainunpuntop 0 dom f se: > 0, > 0 tale che P dom f B (P 0 ) = f (P ) f (P 0 ) < ; cioè f (P ) I (f (P 0 )) f è continua (o continua ovunque) se è continua in tutti i punti di dom f; f è continuasuuninsiemea dom f se la restrizione f A è continua. L insieme delle funzioni reali continue su A si indica con C (A) o C 0 (A). Per stabilire la continuità di una funzione di più variabili, sono di solito sucienti i risultati seguenti. Ogni funzione continua di una variabile è anche continua come funzione di più variabili. Esempio. (y) =logy continua su dom =(0, +) = f (x, y) =logy continua su dom f = {(x, y) :y>0} = R (0, +). Combinazioni lineari, prodotti, rapporti e composizioni di funzioni continue risultano funzioni continue. Esempio. f (x, y) = y e x ècontinuasudom f = {(x, y) :y e x },perché f (x, y) = (g (x, y)) con (t) = t e g (x, y) =y e x sono continue (dove g ècontinuasudom g = R 2 perché c.l. di funzioni continue).
4 Segue che le funzioni polinomiali (cioè i polinomi in x, y) sono continue su tutto R 2 e le funzioni razionali (cioè i rapporti di polinomi in x, y) sono continue in tutti i punti in cui sono definite (cioè i punti di R 2 in cui il denominatore non si annulla). Sia f :domf R 2 R. Valgono i seguenti teoremi: Teorema(dellapermanenzadelsegno).Se f ècontinuainp 0 ed f (P 0 ) = 0, allora esiste un intorno B r (P 0 ) in cui f ha lo stesso segno di f (P 0 ). Teorema (dei valori intermedi). Se f è continua e dom f è connesso, allora im f è un intervallo. Teorema (di Weierstrass). Se f è continua e dom f è compatto, allora f ammette massimo e minimo assoluti (cioè li ammette im f): A, B dom f tali che f (A) = max f (P ) e f (B) = min f (P ). P dom f P dom f In particolare, f è limitata (cioè lo è im f): a, b R tali che P dom f : a f (P ) b.
5 Limiti Definizione. Siano f :domf R 2 R e P 0 =(x 0,y 0 ) un punto di accumulazione per dom f. Si dice che f (P ) tende al limite (finito o infinito) per P che tende a P 0 esiscrive lim f (P )= o lim f (x, y) = P P 0 (x,y)(x 0,y 0 ) se 2 per ogni intorno I () esiste > 0 tale che P dom f B (P 0) f (P ) I (). Limiti e continuità. f :domf R 2 R ècontinuainp 0 dom f se e solo se: P 0 è punto di accumulazione per dom f P 0 è un punto isolato di dom f oppure lim f (P )=f(p 0 ). P P 0 Per un approfondimento sul calcolo di limiti in 2 variabili, si veda il file apposito. 2 Ricordiamo che I () =(, + ) se R, mentrei (+) =(a, +) e I () =(,b). Inoltre poniamo B (P 0):=B (P 0 ) \{P 0 }. Derivate parziali e gradiente Definizione. Siano f :domf R 2 R e P 0 =(x 0,y 0 ) un punto interno a dom f. Si dice che f è derivabile parzialmente nel punto P 0 rispetto alla variabile x se la funzione f (x, y 0 ) della sola variabile x è derivabile in x = x 0, cioè esiste la derivata d dx f (x, y 0) f (x 0 + h, y 0 ) f (x 0,y 0 ) =lim. h0 x=x0 h In tal caso, tale derivata è indicata con f x (x 0,y 0 ) o f x (x 0,y 0 ) o D x f (x 0,y 0 ) ed è detta derivata parziale di f rispetto ad x nel punto P 0. f (x, y 0 ) è definita almeno in (x 0 r, x 0 + r)
6 Analogamente per la derivata parziale rispetto ad y: f y (x 0,y 0 ):= d dy f (x 0,y) f (x 0,y 0 + h) f (x 0,y 0 ) = lim. h0 y=y0 h Definizione. Siano f :domf R 2 R e P 0 un punto interno a dom f. Se f è derivabile in P 0 rispetto ad entrambe le sue variabili, si chiama gradiente di f in P 0 il vettore f f (P 0 ):= x (P 0), f y (P 0) R 2. Esempio. Siaf (x, y) =x y 2 + xy. dom f = {(x, y) :xy 0}, malederivateparzialidif hanno senso solo nei punti di (dom f) = {(x, y) :xy > 0} (unione dei quadranti I e III, assi esclusi). Prendiamo P 0 =(1, 3) (dom f) e calcoliamo f (1, 3) = f f (1, 3),.Siha (1, 3) x y f d (1, 3) = f (x, 3) x dx = d x=1 dx f y (1, 3) = d dy f (1,y) = d y=3 dy equindif (1, 3) = , y=3 3 2, x 9+ 3x =1+ 3 x=1 2 3x =1+ x=1 1+y 2 + y =2y + 1 y=3 2 =6+ 1 y 2 3
7 Se f è derivabile rispetto a tutte le sue variabili in tutti i punti di un aperto dom f, allora le derivate parziali di f sono a loro volta funzioni di due variabili, definite su : f x f f : P (P ) R, x y : P f y (P ) R. Se tali funzioni sono continue su, diciamo che f è di classe C 1 f C 1 (). su e scriviamo Esempio. Riprendiamo f (x, y) =xy 2 + xy e prendiamo un generico (x, y) (dom f). Guardando la funzione x xy 2 + xy della sola variabile x (y va vista come costante), si ha f d (x, y) = x y 2 + xy d =10+ x dx dx ( xy) =1+ y 2 xy se xy > 0 e dunque f =1+ y x 2 è una funzione reale definita sull aperto =(domf). xy Analogamente, immaginando x come costante, si ottiene f y (x, y) = d x y 2 + xy = 2y + dy equindif (x, y) = 1+ y 2 xy, 2y + x 2 xy x 2 xy per ogni (x, y) per ogni (x, y). Le funzioni f x e f y sono continue su e perciò risulta f C1 ().
8 Significato geometrico delle derivate parziali Siano f :domf R 2 R e (x 0,y 0 ) interno a dom f. La funzione y f (x 0,y) è la restrizione di f ai punti della retta x = x 0 (del piano xy). Il suo grafico z = f (x 0,y) si visualizza in R 3 intersecando z = f (x, y) con il piano x = x 0 (verticale e contenente la retta). La derivata f y (x 0,y 0 )= d dy f (x 0,y) èilcoeciente angolare della retta del piano verticale x = x 0 tangente al grafico z = f (x 0,y) nel punto (x 0,y 0,f(x 0,y 0 )). y=y0 In figura: f y (x 0,y 0 )=tan.
9 Dunque f x (x 0,y 0 ) e f y (x 0,y 0 ) sono una misura numerica (con segno) della velocità con cui variano i valori f (x, y) muovendo il punto (x, y) nell intorno di (x 0,y 0 ) parallelamente e concordemente agli assi. E muovendolo secondo altre direzioni? Derivate direzionali Sia f :domf R 2 R esianop 0 un punto interno a dom f ed u R 2 un versore (potremmo scrivere u =(cos, sin )). Consideriamo parametricamente la retta (del piano xy) passante per P 0 e parallela ad u: P (t) =P 0 + tu. Consideriamo la funzione del parametro t ottenuta calcolando f sui punti della retta: (t) =f (P (t)) = f (P 0 + tu). Se esiste, la derivata (0) = d dt f (P 0 + tu) f (P 0 + tu) f (P 0 ) =lim t0 t=0 t (t) è definita almeno in un intorno di t =0 esiha (0) = f (P 0 ) è indicata con f u (P 0) ed è detta derivata direzionale di f secondo il versore u nel punto P 0.
10 Significato geometrico della derivata direzionale La funzione (t) =f (P 0 + tu) è la restrizione di f ai punti della retta r : P (t) =P 0 + tu (del piano xy). Il suo grafico z = (t) si visualizza in R 3 intersecando z = f (x, y) con il piano verticale contenente la retta r. La derivata f u (x 0,y 0 )= (0) èilcoeciente angolare della retta del piano verticale contenente r tangente al grafico z = (t) (=f (P 0 + tu)) nel punto (x 0,y 0,f(x 0,y 0 )). Dunque f u (P 0) èunamisura numerica (con segno) 3 della velocità con cui variano i valori f (P ) muovendo P vicino a P 0 lungolarettap 0 + tu e concordemente con u. Si noti che f i (P 0)= f x (P 0) e f j (P 0)= f y (P 0). 3 muovendo P nel verso di u, i valori f (P ) crescono se f u (P 0) > 0 e decrescono se f u (P 0) < 0
11 Dierenziabilità Definizione. Siano f :domf R 2 R e P 0 un punto interno a dom f. Si dice che f è dierenziabile in P 0 se: (i) esiste f (P 0 ) (cioè esistono entrambe le derivate parziali di f in P 0 ); (ii) si ha f (P ) f (P 0 ) f (P 0 ) (P P 0 ) lim =0, P P 0 P P 0 cioè (estendendo la ben nota definizione di o piccolo) f (P )=f (P 0 )+f (P 0 ) (P P 0 )+o (P P 0 ) P P0. Più esplicitamente, la formula f (P )=f (P 0 )+f (P 0 ) (P P 0 )+o (P P 0 ) P P0 diventa f (x, y) =f (x 0,y 0 )+ f x (x 0,y 0 )(x x 0 )+ f y (x 0,y 0 )(y y 0 )+ +o (x x 0 ) 2 +(y y 0 ) 2 (x,y)(x 0,y 0 ) ed è detta formuladitaylordiordine1 di f in P 0 (MacLaurin se P 0 =(0, 0)). Il polinomio (nelle variabili x, y) T 1 (x, y) :=f (x 0,y 0 )+ f x (x 0,y 0 )(x x 0 )+ f y (x 0,y 0 )(y y 0 ) èdettopolinomio di Taylor di ordine 1 di f in P 0 (MacLaurin se P 0 =(0, 0)).
12 Se f èdierenziabile in P 0,ilgraficoz = T 1 (x, y) del polinomio T 1,cioèilpiano z = f (x 0,y 0 )+ f x (x 0,y 0 )(x x 0 )+ f y (x 0,y 0 )(y y 0 ), èdettopiano tangente al grafico di f nel punto (x 0,y 0,f(x 0,y 0 )). Tratuttiipianiper(x 0,y 0,f(x 0,y 0 )), è quello che meglio approssima il grafico di f nelle vicinanze di tale punto (nel senso che è l unico piano tale che, per P P 0, lo scarto tra le quote su grafico e piano tende a 0 più velocemente della distanza d (P, P 0 )=P P 0 ). Stabilire se una funzione è dierenziabile tramite la definizione non è agevole e di solito si ricorre al seguente: Teorema (condizione suciente di dierenziabilità). Sia f :domf R 2 R. Se f èdiclassec 1 in un aperto dom f, allora f èdierenziabile in tutti i punti di. La nozione di dierenziabilità svolge in più variabili molti dei ruoli che la derivabilità svolge in una variabile. Ad esempio: Teorema. Se f :domf R 2 R èdierenziabile in P 0,alloraf ècontinuainp 0. Nota: la sola derivabilità parziale non assicura la continuità ( funzioni, anche semplici, che hanno derivate parziali in un punto, ma non sono continue in quel punto).
13 Il seguente risultato segue facilmente dalle formule di derivazione di funzioni composte, che vedremo tra poco. Teorema (dierenziabilità e derivate direzionali). Se f :domf R 2 R è dierenziabile in P 0, allora: (i) f è derivabile in P 0 secondo tutte le direzioni; (ii) per ogni versore u R 2,risulta Note: f u (P 0)=f (P 0 ) u. la derivabilità in ogni direzione non implica la dierenziabilità ( funzioni con tutte le derivate direzionali in un punto, che non sono dierenziabili, e nemmeno continue, in quel punto); continuità e derivabilità direzionale non implicano la dierenziabilità ( funzioni continue che hanno tutte le derivate direzionali in un punto, ma non sono dierenziabili in quel punto). Significato geometrico del gradiente: massima crescita Problema. Allontanando P da P 0, secondo quale direzione e verso devo muovermi per avere massima velocità di crescita dei valori f (P )? Cerco un versore v tale che f v (P f 0)=max u=1 u (P 0). Se esiste, v è detto direzione di massima crescita nel punto P 0.
14 Supponiamo f :domf R 2 R dierenziabile in P 0 esiau R 2 un generico versore. Si ha f u (P 0)=f (P 0 ) u = f (P 0 )ucos = f (P 0 ) cos, dove è l angolo tra u e f (P 0 ). Allora, poiché 1 cos 1, f u (P 0) èmassima quando cos =1,cioè =0,cioè quando u è parallelo e concorde con f (P 0 ). Dunque v = f (P 0) f (P 0 ) è la direzione di massima crescita in P 0. Derivazione di funzioni composte Vediamo due regole di derivazione (casi particolari della più generale regola della catena, che sarà vista più avanti). 1 Sia t f (x (t),y(t)) la composta di f :domf R 2 R con x, y : I R R. Se x, y sono derivabili in t 0 ed f èdierenziabile in P 0 =(x (t 0 ),y(t 0 )), allora d f (x (t),y(t)) dt = f (P 0 ) (x (t 0 ),y (t 0 )) = f t0 x (P 0) x (t 0 )+ f y (P 0) y (t 0 ). 2 Sia (x, y) g (f (x, y)) la composta di g : I R R con f :domf R 2 R. Se f èdierenziabile in P 0 e g è derivabile in f (P 0 ),allora g (f (x, y)) x = g (f (P 0 )) f P0 x (P 0), g (f (x, y)) y = g (f (P 0 )) f P0 y (P 0).
15 Sono regole di valenza teorica (nella pratica si deriva l espressione della composta), dalle quali segue, ad esempio, la formula su gradiente e derivate direzionali. Dimostrazione del teorema su dierenziabilità e derivate direzionali. Sia f :domf R 2 R esianop 0 =(x 0,y 0 ) (dom f) ed u =(a, b) un versore. Consideriamo la retta (x (t),y(t)) = (x 0 + at, y 0 + bt) passante per P 0 e parallela ad u. Se f èdierenziabile in P 0, allora la regola derivazione composta 1 implica d f (x (t),y(t)) dt = f (x (0),y(0)) (x (0),y (0)) = f (P 0 ) u. t=0 = f(x 0,y 0 ) =(a,b) f = u (P 0) Derivate successive e formula di Taylor di ordine 2 Se f :domf R 2 R ammette gradiente in tutti i punti di un aperto dom f, allora le derivate parziali delle funzioni f e f in un punto P x y 0, se esistono, sono indicate con 2 f x (P f 2 f 0):= (P 2 0 ), x x yx (P f 0):= (P 0 ), y x 2 f xy (P f 2 f 0):= (P 0 ), x y y (P f 0):= (P 2 0 ) y y e vengono dette derivate parziali seconde (pure la prima e l ultima, miste le altre) di f in P 0.Siusanoancheisimbolif xx, f xy, f yx, f yy, rispettivamente.
16 Le derivate seconde sono 4 edè molto utile disporle in una matrice 2 2 (vedremo perché): H f (P 0 ):= 2 f x 2 (P 0) 2 f xy (P 0) 2 f yx (P 0) 2 f. y (P 0) 2 H f (P 0 ) si chiama matrice hessiana di f in P 0. Se le seconde esistono in tutti i punti di, esse sono nuovamente funzioni definite su e, se derivabili ulteriormente, forniscono le 2 3 =8derivate parziali terze di f. E così via, fino a definire le eventuali 2 k derivate parziali di ordine k di f. Nei casi più comuni, le miste non sono così tante come sembra. Vale infatti il seguente: Teorema (di Schwarz, sull indipendenza delle miste dall ordine di derivazione). Sia R 2 un aperto e sia f C 1 () tale che 2 f esiste ed è continua su. Allora xy P : 2 f yx (P )= 2 f xy (P ) (analogamente se esiste ed è continua 2 f yx ). Nei casi più comuni, il teorema può essere applicato ripetutamente e allora si riduce anche il numero delle miste di ordine superiore al secondo. Inoltre, la matrice hessiana H f risulta essere una matrice simmetrica.
17 Definizione (classi C k ). Sia f :domf R 2 R esia dom f un aperto. Diciamo che f è di classe C k su se tutte le 2 k derivate parziali di ordine k di f esistono e sono continue su. Diciamo che f è di classe C su se f è di classe C k su per ogni k 1. L insieme delle funzioni di classe C k su un aperto si indica con C k () (1 k ). Ogni C k () è sottospazio vettoriale dello spazio vettoriale delle funzioni da in R e valgono le inclusioni C 0 () C 1 () C 2 ()... C () (basta applicare ripetutamente l implicazione f C 1 () f C 0 ()). Teorema. Sia f :domf R 2 R di classe C 2 in un intorno di un punto P 0 =(x 0,y 0 ). Allora vale la seguente formula f (x, y) =f (P 0 )+ f x (P 0)(x x 0 )+ f y (P 0)(y y 0 ) f x 2 (P 0)(x x 0 ) f xy (P 0)(x x 0 )(y y 0 )+ 2 f y 2 (P 0)(y y 0 ) 2 + o (x x 0 ) 2 +(y y 0 ) 2 (x,y)(x 0,y 0 ), + detta formuladitaylordiordine2 di f in P 0 (MacLaurin se P 0 =(0, 0)).
18 Ottimizzazione di funzioni reali di 2 variabili È il problema della ricerca di eventuali punti di massimo o minimo di una funzione f :domf R 2 R. Definizione. Diciamo che P 0 èunpunto di massimo (minimo) relativo per f se esiste B r (P 0 ) tale che P B r (P 0 ) dom f risulta f (P ) f (P 0 ) (rispettivamente f (P ) f (P 0 )). Si parla di punto di massimo o minimo stretto se le disuguaglianze sono strette per P = P 0. punto di massimo relativo stretto (non assoluto) Non c è una tecnica che sia definitiva in generale. Però, in ipotesi di buona regolarità di f, il problema della ricerca di eventuali punti di massimo o minimo interni a dom f èrisolto quasi completamente dai teoremi di Fermat e della matrice hessiana. Definizione. P 0 èunpuntocriticoostazionario per f se 4 f (P 0 )=0. Teorema (di Fermat). Se i) P 0 è un punto di max o min per f ii) f (P 0 ) esiste ( P 0 interno a dom f), allora P 0 è punto critico per f (cioè f (P 0 )=0). Conseguenza: sedom f èapertoedf è derivabile parzialmente ovunque, allora ogni punto di massimo o minimo è punto critico. Se f èdierenziabile in P 0,allora P 0 è punto critico se e solo se il piano tangente in P 0 èorizzontale 4 Alcuni autori richiedono anche che f sia dierenziabile in P 0, cioè che esista il piano tangente in P 0.
19 Attenzione! Un punto critico può non essere né di massimo né di minimo. Ad esempio, f (x, y) =x 3 + y 3 ha un punto critico in P 0 =(0, 0), ma in ogni intorno B r (P 0 ) ci sono sia un punto P 1 in cui f (P 1 ) <f(p 0 ) che un punto P 2 in cui f (P 2 ) >f(p 0 ) (ad esempio perché f (x, 0) = x 3 è positiva per x>0 enegativaperx<0). Teorema (della matrice hessiana). Supponiamo che P 0 (dom f) sia punto critico per f echef sia di classe C 2 in un intorno di P 0.Risultache: se det H f (P 0 ) < 0, allora P 0 non è punto di massimo né di minimo per f ed è detto punto di sella; se det H f (P 0 ) > 0 e tr H f (P 0 ) > 0, allora P 0 è punto di minimo stretto per f; se det H f (P 0 ) > 0 e tr H f (P 0 ) < 0, allora P 0 è punto di massimo stretto per f. Attenzione! Se det H f (P 0 )=0, il teorema non permette di concludere nulla (nel senso che P 0 potrebbe essere punto di max, di min o di nessuno dei due tipi). Per studiare P 0 si deve allora ragionare caso per caso, ricorrendo alle definizioni di punto di max e min. Il caso det H f (P 0 ) > 0 e tr H f (P 0 )=0, invece, non si può presentare.
20 Il teorema precedente comprende anche la seguente definizione 5 : un punto P 0 è detto punto di sella per f se f è di classe C 2 in un intorno di P 0, f (P 0 )=0 e det H f (P 0 ) < 0. La definizione è motivata dal fatto che, nell intorno di un punto di sella, il grafico di f ha un andamento simile a quello dell esempio in figura. grafico e piano tangente di f (x, y) =y 2 x 2 nell intorno dell orgine (punto sella per f) 5 Alcuni autori danno definizioni più generali di punto di sella, ad esempio come punto critico P 0 che sia di max relativo stretto lungo una retta passante per P 0 e di min relativo stretto lungo un altra, oppure, ancora più in generale, come puntocriticochenonsianédimaxnédimin. Attenzione: è importante distinguere il problema della ricerca di punti di max o min interni a dom f (detti liberi), da quello, assai più complicato, della ricerca di punti di max o min appartenenti all eventuale frontiera di dom f (detti vincolati). dom f = R 2 dom f =[1, 1] [1, 1]
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Punti di estremo e Teorema di Fermat
 Punti di estremo e Teorema di Fermat Nello studio di una funzione, le derivate sono (tra le altre cose) uno strumento utile per la determinazione di intervalli di monotonia e puntidiestremo. Definizione.
Punti di estremo e Teorema di Fermat Nello studio di una funzione, le derivate sono (tra le altre cose) uno strumento utile per la determinazione di intervalli di monotonia e puntidiestremo. Definizione.
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
CURVE E SUPERFICI / RICHIAMI
 M.GUIDA, S.ROLANDO, 2016 1 CURVE E SUPERFICI / RICHIAMI Di seguito ricordiamo brevemente come curve e superfici in R 2 o R 3 vengano rappresentate classicamente come insiemi di livello di campi scalari
M.GUIDA, S.ROLANDO, 2016 1 CURVE E SUPERFICI / RICHIAMI Di seguito ricordiamo brevemente come curve e superfici in R 2 o R 3 vengano rappresentate classicamente come insiemi di livello di campi scalari
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011
 Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011 08- Estremi: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 4.1. Esercizi 4.1 Estremi liberi: punti
Appunti sul corso di Complementi di Matematica mod.analisi prof. B.Bacchelli a.a. 2010/2011 08- Estremi: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 4.1. Esercizi 4.1 Estremi liberi: punti
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Prima parte: DOMINIO E INSIEMI DI LIVELLO
 FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Limiti di funzioni di due variabili
 Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Equazione della retta tangente al grafico di una funzione
 Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
y (b) f(x, y) = y log x sin x (c) f(x, y) = tan y (d) f(x, y) = e x y (f) f(x, y) = cos(x 2 + y 2 )
 FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
Esempio di grafico di una funzione reale di due variabili reali
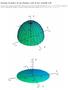 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
R. Capone Analisi Matematica Calcolo Differenziale Funzioni di due variabili
 Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini.
 Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Programma delle lezioni svolte nel corso CLEM di Matematica Generale, Lettere M-Z, Prof. F. Manzini. 1. Generalità sul corso e sulle modalità di esame. Insiemi ed operazioni sugli insiemi. Applicazioni
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi:
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, itati, convessi, connessi per archi; punti di frontiera
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, itati, convessi, connessi per archi; punti di frontiera
Svolgimento. f y (x, y) = 8 y 2 x. 1 x 2 y = 0. y 2 x = 0. (si poteva anche ricavare la x dalla seconda equazione e sostituire nella prima)
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Gestionale Canale PZ Secondo codocente: Dott. Salvatore Fragapane Lezione 1-04/10/2016 - Serie Numeriche (1): definizione e successione
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital
 Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Calcolo Differenziale. Corsi di Laurea in Tecniche di Radiologia ecc... A.A Analisi Matematica - Calcolo Differenziale - p.
 Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Funzioni derivabili in un intervallo
 Funzioni derivabili in un intervallo Studiamo le proprietà delle funzioni derivabili in un intero intervallo, tramite due teoremi fondamentali e le conseguenze che portano. Teorema (di Rolle). Sia f continua
Funzioni derivabili in un intervallo Studiamo le proprietà delle funzioni derivabili in un intero intervallo, tramite due teoremi fondamentali e le conseguenze che portano. Teorema (di Rolle). Sia f continua
1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, () December 30, / 26
 ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
ANALISI 1 1 UNDICESIMA LEZIONE DODICESIMA LEZIONE TREDICESIMA LEZIONE Derivata - definizione e teoremi di calcolo delle derivate Massimi e minimi relativi e teorema di Fermat Teorema di Lagrange Monotonia
Derivate parziali, derivate direzionali, differenziabilità. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) =
 Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
Derivate parziali, derivate direzionali, differenziabilità 1. a) Calcolare le derivate direzionali e le derivate parziali in (0, 1) di f(x, y) = 3 x (y 1) + 1. b) Calcolare D v f(0, 1), dove v è il versore
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Estremi liberi. (H x, x) x 2 (1) F (x) =
 Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo compito in itinere 3 Febbraio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
ESERCIZIO SVOLTO N 1 ESERCIZIO SVOLTO N 2. Determinare e rappresentare graficamente il dominio della funzione
 ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
21 IL RAPPORTO INCREMENTALE - DERIVATE
 21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
21 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
Note sulle funzioni convesse/concave
 Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Geometria analitica: rette e piani
 Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
Analisi Matematica II. Esercizi per le vacanze pasquali
 Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
Analisi Matematica II Esercizi per le vacanze pasquali Corso di laurea in Ingegneria Meccanica. A.A. 2008-2009. Esercizio 1. Stabilire se la funzione reale f di due variabili reali, definita come sin(
REGISTRO DELLE ESERCITAZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
STUDIO DI UNA FUNZIONE INTEGRALE. Z x. ln t ln t 2 2 dt. f(x) =
 STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Circonferenze del piano
 Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Analisi Matematica T1 (prof.g.cupini) (CdL Ingegneria Edile Polo Ravenna) REGISTRO DELLE LEZIONI A.A
 Analisi Matematica T1 (prof.g.cupini) (CdL Ingegneria Edile Polo Ravenna) REGISTRO DELLE LEZIONI A.A.2012-2013 (Grazie agli studenti del corso che comunicheranno eventuali omissioni o errori) 25 SETTEMBRE
Analisi Matematica T1 (prof.g.cupini) (CdL Ingegneria Edile Polo Ravenna) REGISTRO DELLE LEZIONI A.A.2012-2013 (Grazie agli studenti del corso che comunicheranno eventuali omissioni o errori) 25 SETTEMBRE
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Esercizi sulle funzioni di due variabili: parte II
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
DERIVATE SUCCESSIVE E MATRICE HESSIANA
 FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
By Fabriziomax. Storia del concetto di derivata:
 By Fabriziomax Storia del concetto di derivata: Introduzione: La derivata fu inventata da Newton per risolvere il problema pratico di come definire una velocita e un accelerazione istantanea a partire
By Fabriziomax Storia del concetto di derivata: Introduzione: La derivata fu inventata da Newton per risolvere il problema pratico di come definire una velocita e un accelerazione istantanea a partire
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
y x y x A (x 1,y 1 ) = (c, f(c)) B(x 2,y 2 ) = (c+h, f(c+h)) m =
 DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale per funzioni in più variabili.
 Calcolo differenziale per funzioni in più variabili. Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 14 dicembre 2014 Paola Mannucci e Alvise Sommariva Calcolo
Calcolo differenziale per funzioni in più variabili. Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 14 dicembre 2014 Paola Mannucci e Alvise Sommariva Calcolo
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Teoremi fondamentali dell'analisi Matematica versione 1
 Teoremi fondamentali dell'analisi Matematica versione 1 Roberto Boggiani 7 novembre 2012 1 Richiami di geometria analitica Dalla geometria analitica sulla retta sappiamo che dati due punti del piano A(x
Teoremi fondamentali dell'analisi Matematica versione 1 Roberto Boggiani 7 novembre 2012 1 Richiami di geometria analitica Dalla geometria analitica sulla retta sappiamo che dati due punti del piano A(x
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1
 AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
AM210 - Analisi Matematica 3: Soluzioni Tutorato 1 Università degli Studi Roma Tre - Dipartimento di Matematica Docente: Luca Biasco Tutori: Patrizio Caddeo, Davide Ciaccia 19 ottobre 2016 1 Se z = (1
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Mauro Sassetti. Calcolo differenziale ed integrale. per funzioni di due variabili reali.
 Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
25 IL RAPPORTO INCREMENTALE - DERIVATE
 25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
25 IL RAPPORTO INCREMENTALE - DERIVATE Definizione Sia f una funzione reale di variabile reale. Allora, dati x, y domf con x y, si definisce il rapporto incrementale di f tra x e y come P f (x, y = f(x
ORDINAMENTO SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
www.matefilia.it ORDINAMENTO 2003 - SESSIONE SUPPLETIVA QUESTIONARIO QUESITO Tra i rettangoli aventi la stessa area di 6 m 2 trovare quello di perimetro minimo. Indicate con x ed y le misure della base
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
3 ) (5) Determinare la proiezione ortogonale del punto (2, 1, 2) sul piano x + 2y + 3z + 4 = 0.
 1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi:
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
