I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
|
|
|
- Vittoria Bernasconi
- 6 anni fa
- Visualizzazioni
Transcript
1 I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può ssr confrontata con un valor critico tipico dl matrial. L sprssion analitica dlla funzion scalar dipnd dal critrio adottato. Può ssr utilizzata pr confrontar tra loro stati di tnsion gnrici ma soprattutto pr confrontar uno stato gnrico con il caso monoassial.
2 Conctto di tnsion quivalnt I du stati di tnsion sono ugualmnt pricolosi s F F' F f (,, ) F f,, ) ( Particolarmnt significativo è il confronto con lo stato di tnsion ch si vrifica nlla prova dl matrial,, caso monoassial (prova di trazion) caso gnral triassial Dduzion dlla tnsion quivalnt dai critri di rsistnza F f (,, ) Du stati di tnsion possono ssr confrontanti sulla bas dl valor dlla funzion scalar f ch stabilisc il critrio di confronto ch prnd il nom di critrio di rsistnza F f In particolar s f è applicato allo stato di tnsion assial ch si ha nlla prova di trazion, si può scrivr ch: F f (,0,0) f ( ass ) F f (,, ) (,0,0) Pr cui si ha lo stsso grado di pricolosità tra i primo il trzo caso quando: F F f ( ass ) f (,, ) da cui sgu ch il valor dlla tnsion monoassial ( ) ch gnra uno stato di tnsion quivalnt a qullo dfinito da, può ssr ricavata com: f ass [ f (,, )]
3 Cofficint di sicurzza pr sollcitazioni multiassiali [ f (, )] f ass, La tnsion quivalnt è ora confrontabil con il valor limit dl matrial. Nl caso gnral di sollcitazion multiassial il cofficint di sicurzza assum dunqu il sgunt significato: X lim Dov pr tnsion limit gnralmnt si assum: lim s r Tnsion di snrvamnto pr matriali duttili Tnsion di rottura pr matriali fragili I critri di rsistnza possono ssr divisi in tr gruppi, sulla bas dl loro principio ispirator: Critri dirttamnt basati sullo stato di tnsion Massima tnsion normal (Ranin-Lamé-Navir) Massima tnsion tangnzial (Trsca-Gust) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima tnsion tangnzial ottadrica (Rôs ichingr) Critri basati sullo stato di dformazion Massima dformazion normal (Ponclt-d St. Vnant-Grashof) Critri basati sulla nrgia di dformazion Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima nrgia di distorsion (Hubr-von Miss-Hncy)
4 I critri di rsistnza possono ssr divisi in du gruppi, sulla bas dl loro campo di applicazion: Critri utilizzati pr i matriali duttili Massima tnsion tangnzial (Trsca-Gust) Massima nrgia di distorsion (Hubr-von Miss-Hncy) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima tnsion tangnzial ottadrica (Rôs ichingr) Critri utilizzati pr i matriali fragili Massima tnsion normal (Ranin-Lamé-Navir) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima dformazion normal (Ponclt-d St. Vnant-Grashof) 6- Critri di rsistnza Massima tnsion normal (Ranin) suprfici critica dfinita dal critrio di Ranin nllo spazio dll tnsioni principali Il matrial subisc danno quando la massima tnsion principal raggiung un valor critico. tnsion limit a trazion tnsion limit a comprssion Si ha rottura s: la suprfici è la zona critica all strno dl volum c è rottura > < all intrno dl volum il matrial rsist 6-8 4
5 Critri di rsistnza Massima tnsion tangnzial (Trsca-Gust) τ τ τ τ max τ Il matrial subisc danno quando la massima tnsion tangnzial raggiung un valor critico. Si ha rottura s: ( ) τmax > τ > τ L, L Valori critici dl matrial L L 6-4 all intrno dll ara il matrial rsist all strno dll ara c è rottura Critri di rsistnza Massima tnsion tangnzial (Trsca-Gust) Nl caso gnral di stato di tnsion triassial il valor dlla tnsion tangnzial massima val: τ max Quando la sollcitazion è monoassial solo è divrsa da zro si avrà: max ( ) τmax (, 0,0) τ a Si può, quindi, ricavar l sprssion dlla tnsion quivalnt dalla rlazion: [ τ (, )] τa max max, 5
6 Critri di rsistnza Massima tnsion tangnzial (Trsca-Gust) N sgu ch: τ a max [ τ (,, )] max Si avrà prciò rottura quando: > L Casi particolari: torsion pura: τ xy torsion trazion: x 4 τ xy Critri di rsistnza Massima tnsion tangnzial (Trsca-Gust) suprfici critica dfinita dal critrio di Trsca nllo spazio dll tnsioni principali β γ α Nllo spazio dll tnsioni principali la suprfici critica è un prisma a szion sagonal indfinito. L ass coincid con la tristtric. α β γ 6
7 Critri di rsistnza τ Curva di rsistnza intrinsca (Mohr) Ipotsi dll attrito intrno Curva intrinsca dl matrial 6-6 il taglio massimo sopportabil dal matrial è maggior in prsnza di uno stato di comprssion Critri di rsistnza τ Curva di rsistnza intrinsca (Mohr) D A O ϕ B ϕ C LC LT Smplificando la curva intrinsca con du rtt, si ottin ch la rottura avvin s: > 7
8 Critri di rsistnza Curva di rsistnza intrinsca (Mohr) τ La curva intrinsca può ssr approssimata da du rtt tangnti ai crchi di Mohr rlativi all condizioni limit a trazion comprssion AD sin ϕ AB D A O ϕ B ϕ C tnsion limit a trazion tnsion limit a comprssion Critri di rsistnza Curva di rsistnza intrinsca (Mohr) D A τ O ϕ B Posto: Si ottin: ϕ sin ϕ C Quindi si può sprimr la lunghzza dl sgmnto OC in funzion di : OC OB BC sin ϕ 8
9 Critri di rsistnza τ d Curva di rsistnza intrinsca (Mohr) Il matrial subisc danno quando il maggior di crchi di Mohr rapprsntativi dl suo stato di tnsion raggiung la tangnza con la curva intrinsca. O δ ρ ϕ C Quindi, ponndo il raggio la posizion dl cntro dl crchio massimo pari rispttivamnt a ρ δ, la distanza d dalla curva intrinsca può ssr sprssa com: ( OC δ) ϕ ρ d sin Critri di rsistnza Curva di rsistnza intrinsca (Mohr) Ricordando l sprssioni di OC, sinϕ, ρ δ, OC, sin ϕ, ρ d ( OC δ) sin ϕ ρ [ ( ) ], δ l sprssion di d pr uno stato di tnsion triassial divnta: Pr una stato di tnsion monoassial, l'sprssion prcdnt divnta: da ( ) d(, 0,0) ( ) Si può, quindi, ricavar il valor dlla tnsion quivalnt dalla rlazion: [ d(, )] d a, 9
10 Critri di rsistnza Curva di rsistnza intrinsca (Mohr) N sgu ch: d a [ d(,, )] [ ( ) ] Si avrà prciò rottura quando: > L Casi particolari: torsion pura: τ xy torsion trazion: x x 4 τ xy Critri di rsistnza suprfici critica dfinita dal critrio di St. Vnant nllo spazio dll tnsioni principali Massima dformazion normal (d St. Vnant) Il matrial subisc danno quando la massima dformazion principal raggiung un valor critico. Nl caso triassial si ha: ε ε [ -ν ( ) ] [ -ν ( y ) ] > ε L < -ε L Nl caso monoassial si ha: ε > ε L Dal confronto si ottin ch si ha rottura s: ν ν ( ) > L ( ) 0
11 Critri di rsistnza Massima nrgia di dformazion (Bltrami) Il matrial subisc danno quando l nrgia accumulata pr dformazion raggiung un valor critico. F In campo lastico, pr la trazion smplic, l nrgia di dformazion Nl caso triassial si avrà quindi: pr unità di volum val : U ε U tot U U U ( ε ε ε ) Avndosi dallo studio dlla rlazion tnsion-dformazion in campo lastico ch: ε [ ν( )] ε [ ν( )] ε [ ν( )] Si potrà scrivr l nrgia di dformazion total com: U tot [ ν( )] [ ν( )] [ ν( )] [ ν( )] Critri di rsistnza Massima nrgia di dformazion (Bltrami) Il matrial subisc danno quando l nrgia accumulata pr dformazion raggiung un valor critico. F Nl caso triassial si ha: U s [ - ν( )] Nl caso monoassial si ha: U s Dal confronto si ottin ch si ha rottura s: ( ) > L ν
12 Critri di rsistnza Massima nrgia di dformazion (Bltrami) all strno dl volum c è rottura la suprfici rapprsnta la condizion limit all intrno dl volum il matrial rsist Nllo spazio dll tnsioni principali la suprfici critica è un llissoid. L ass coincid con la tristtric. Critri di rsistnza stato di tnsion triassial Massima nrgia di distorsion (von Miss) Il matrial subisc danno quando l nrgia di distorsion accumulata raggiung un valor critico. stato di tnsion sfrico (idrostatico): variazion di volum stato di tnsion dviatorico: variazion di forma L nrgia di distorsion nl caso triassial si può scrivr: ( ν) ( ) ( ) [ ( ) U dist ] 6 ( ν ) Nl caso monoassial si ha: U dist > Si ha rottura s: ( ) ( ) ( ) L 6-5
13 Critri di rsistnza stato di tnsion triassial Massima nrgia di distorsion (von Miss) Il matrial subisc danno quando l nrgia di distorsion accumulata raggiung un valor critico. Stato di tnsion triassial: S d d d S S stato di tnsion sfrico (idrostatico): variazion di volum Componnt idrostatica: S stato di tnsion dviatorico: variazion di forma Componnti dviatorich: d d d Critri di rsistnza Massima nrgia di distorsion (von Miss) In campo lastico, pr la trazion F smplic, l nrgia di dformazion pr unità di volum val : U ε Nl caso triassial si avrà quindi: U tot U U U ( ε ε ε ) Avndosi dallo studio dlla rlazion tnsion-dformazion in campo lastico ch: ε [ ν( )] ε ν( ) [ ] ε [ ν( )] Si potrà scrivr l nrgia di dformazion total com: U tot [ ν( )] [ ν( )] [ ν( )] [ ν( )]
14 Critri di rsistnza Massima nrgia di distorsion (von Miss) Quindi, pr uno stato di tnsion triassial l nrgia total di dformazion val: U tot [ ν( )] La part dovuta alla componnt sfrica dllo stato di tnsion varrà: ν U S S S ( S S S ) sf ν [ ] ( ) S Ricordando l sprssion di S si ottin: U sf ( ν) ( ν) S Quindi, pr diffrnza si ottin l nrgia di distorsion: U dist U tot U sf Critri di rsistnza Massima nrgia di distorsion (von Miss) U dist U tot U sf [ ( )] ( ν) ν Ch può ssr scritta nlla forma: (la stssa sprssion potva ssr ricavata introducndo l componnti dviatorich dllo stato di tnsion nll sprssion dll nrgia di dformazion) U dist [ ] ( ν) ( ) ( ) ( ) 6 Nl caso in cui solo sia divrsa da zro si avrà: ( ) ( ) ( ν) ( ) ( ) ν U ass dist U dist, 0,0 6 Si può, quindi, ricavar l sprssion dlla tnsion quivalnt dalla formula: [ U (, )] U ass dist dist, [ ] ( ) 4
15 Critri di rsistnza Massima nrgia di distorsion (von Miss) Quindi: U ass dist [ ] [ U (,, )] ( ) ( ) ( ) ( ) ( ) ( ) dist Si avrà prciò rottura quando: ν ν 6 ( ) ( ) ( ) > L Casi particolari: torsion pura: τ xy torsion trazion: x τ xy Critri di rsistnza Massima nrgia di distorsion (von Miss) suprfici critica dfinita dal critrio di von Miss nllo spazio dll tnsioni principali β γ α Nllo spazio dll tnsioni principali la suprfici critica è un cilindro a szion circolar indfinito. L ass coincid con la tristtric. α β γ 5
16 Critri di rsistnza Confronto tra l vari tori pr un stato di tnsion piano Trsca Ranin von Miss Critri di rsistnza Confronto tra l vari tori sulla bas dl rapporto carattristico L /τ L Massima tnsion normal (Ranin-Lamé-Navir) Massima tnsion tangnzial (Trsca-Gust) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima dformazion normal (Ponclt-d St. Vnant-Grashof) Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima nrgia di distorsion (Hubr-von Miss-Hncy) Matriali fragili.5 Valori sprimntali di L /τ L Matriali duttili
17 Critri di rsistnza: ripilogo Massima tnsion normal (Ranin) > < Massima tnsion tangnzial (Trsca) Curva di rsistnza intrinsca (Mohr) Massima nrgia di df. (Bltrami) Massima nrgia di distorsion (von Miss) > L > Massima df. normal (d St. Vnant) ν ( ) > L ν ( ) ( ) > L ν ( ) ( ) ( ) > L 7
0.1. CIRCONFERENZA 1. La 0.1.1, espressa mediante la formula per la distanza tra due punti, diviene:
0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
w(r)=w max (1-r 2 /R 2 ) completamente sviluppato in un tubo circolare è dato da wmax R w max = = max
16-1 Copyright 009 Th McGraw-Hill Companis srl RISOLUZIONI CAP. 16 16.1 Nl flusso laminar compltamnt sviluppato all intrno di un tubo circolar vin misurata la vlocità a r R/. Si dv dtrminar la vlocità
ESERCIZI PARTE I SOLUZIONI
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
Progetto di cinghie trapezoidali
Progtto i cinghi trapzoiali L cinghi trapzoiali sono utilizzat frquntmnt pr la trasmission i potnza Vantaggi Basso costo Smplicità i installazion Capacità i assorbir vibrazioni torsionali picchi i coppia
Compito di Fisica Generale I (Mod. A) Corsi di studio in Fisica ed Astronomia 4 aprile 2011
Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico Comunicazione Opzione Sportiva Tema di matematica
wwwmatmaticamntit Nicola D Rosa maturità Esam di stato di istruzion scondaria suprior Indirizzi: Scintifico Comunicazion Opzion Sportiva Tma di matmatica Il candidato risolva uno di du problmi risponda
PROVA EDOMETRICA A.A
PROA EDOMETRICA La prova domtrica riproduc in laboratorio l condizioni di consolidazion monodimnsional PROA A INCREMENTO DI CARICO (IL) La consolidazion monodimnsional è simulata applicando una squnza
Teoria. Tale retta limite non sempre esiste. Si veda il grafico sottostante. Matematica 1
LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
Le coniche e la loro equazione comune
L conich la loro quazion comun L conich com ombra di una sra Una sra ch tocca il piano π nl punto F è illuminata da una sorgnt puntiorm S. Nl caso dlla igura l'ombra dll sra risulta una suprici dlimitata
STABILITÀ DELL EQILIBRIO 5. Tensione critica e snellezza. Al carico critico euleriano (1) N cr =
Tnsion critica snllzza Al carico critico ulriano STABILITÀ DELL EQILIBRIO 5 π EI cr () l do l è la lunghzza libra di inflssion corrispondnt alla smilunghzza d onda dlla sinusoid formata dalla lina lastica,
RISOLUZIONI cap (a) La resistenza termica totale dello scambiatore di calore, riferita all'unità di lunghezza, è
"Trmodinamica trasmission dl calor 3/d" 1 - Yunus A. Çngl RISOLUZIONI cap.19 19.1 (a) La rsistnza trmica total dllo scambiator di calor, rifrita all'unità di lunghzza, è (b) Il cofficint global di scambio
Test di autovalutazione
UNITÀ FUNZINI E LR RAPPRESENTAZINE Tst di autovalutazion 0 0 0 0 0 50 60 70 80 90 00 n Il mio puntggio, in cntsimi, è n Rispondi a ogni qusito sgnando una sola dll 5 altrnativ. n Confronta l tu rispost
= l. x 0. In realtà può aversi una casistica più amplia potendo sia x che f ( x) tendere ad un elemento dell insieme
LIMITI DI FUNZINI. CNCETT DI LIMITE Esula dallo scopo di qusto libro la trattazion dlla toria sui iti. Tuttavia, pnsando di far cosa gradita allo studnt, ch dv possdr qusta nozion com background, ritniamo
Corso di Teoria delle Strutture Dispense - parte #1 Richiami di Elasticità Lineare
Corso di Toria dll Struttur Dispns - part # Richiami di Elasticità Linar A.A. 26 27 Vrsion.. Indic Sistma di Rifrimnto 3. Cambio di bas..................................... 4.2 Cambio dlla bas di Lin...............................
Ministero dell Istruzione, dell Università e della Ricerca
Pag. 1/5 Sssion straordinaria 2017 I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE (Tsto valvol anch pr la corrispondnt
Problema. caso uniassiale prova di trazione. caso multiassiale (carico generico)
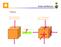Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Numeri complessi - svolgimento degli esercizi
Numri complssi - svolgimnto dgli srcizi ) Qusto srcizio richid di calcolar la potnza n-sima (n 45) di un numro complsso. Scriviamo z nlla forma sponnzial z ρ iθ dov ) ( ) ρ ( + θ π 6 dato ch sin θ cos
Problema 3: CAPACITA ELETTRICA E CONDENSATORI
Problma 3: CAPACITA ELETTRICA E CONDENSATORI Prmssa Il problma composto da qusiti di carattr torico da una succssiva part applicativa costituisc un validissimo smpio di quilibrio tra l divrs signz ch convrgono
LE FRAZIONI LE FRAZIONI. La frazione è un operatore che opera su una qualsiasi grandezza e che da come risultato una grandezza omogenea a quella data.
LE FRAZIONI La frazion è un oprator ch opra su una qualsiasi grandzza ch da com risultato una grandzza omogna a qulla data. AB (Il sgmnto AB è stato diviso i tr parti sono stat prs du) Una frazion è scritta
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Teorema (seconda condizione sufficiente per i campi conservativi piani): Sia F ( x, y)
Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
γ : y = 1 + 2t 1 + t 2 z = 1 + t t2
Politcnico di Milano Inggnria Industrial Analisi Gomtria Esrcizi sull curv. Si considri la curva x t + t : y 6 + 4t t t t R. z t t (a) Stabilir s la curva piana. (b) Stabilir s la curva smplic. (c) Stabilir
METODO DEGLI ELEMENTI FINITI
Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
Calore Specifico
6.08 - Calor Spcifico 6.08.a) Lgg Fondamntal dlla Trmologia Un modo pr far aumntar la Tmpratura di un Corpo è qullo di cdr ad sso dl Calor, pr smpio mttndolo in Contatto Trmico con un Corpo a Tmpratura
Soluzione. Un punto generico ha coordinate ( x, y) Per cui. Le coordinate del centro sono allora
Sssion suppltiva LS_ORD 7 Soluzion di D Rosa Nicola Soluzion Un punto gnrico ha coordinat, pr cui si ha: PO PA Pr cui PO PA [ ] L coordinat dl cntro sono allora O,, è R. C, d il raggio, visto ch la circonfrnza
ESERCIZI SULLA CONVEZIONE
Giorgia Mrli matr. 97 Lzion dl 4//0 ora 0:0-:0 ESECIZI SULLA CONVEZIONE Esrcizio n Considriamo un tubo d acciaio analizziamo lo scambio trmico complto, ossia qullo ch avvin sia all intrno sia all strno
PROCESSI DI CONSOLIDAZIONE
PROCESSI DI CONSOLIDAZIONE L applicazion di un carico su un trrno comporta l insorgr di sovrapprssion dll acqua intrstizial, la cui ntità varia da punto a punto all intrno dl volum individuato dal bulbo
1 Derivate parziali 1. 2 Regole di derivazione 5. 3 Derivabilità e continuità 7. 4 Differenziabilità 7. 5 Derivate seconde e teorema di Schwarz 8
UNIVR Facoltà di Economia Sd di Vicnza Corso di Matmatica Drivat dll funzioni di più variabili Indic Drivat parziali Rgol di drivazion 5 3 Drivabilità continuità 7 4 Diffrnziabilità 7 5 Drivat scond torma
ANALISI STRUTTURALE sistema STRUTTURA STRUTTURA. I modelli meccanici possono suddividersi in: MODELLI CONTINUI. STRUTTURA = modello meccanico
AZIONI ANALISI STRUTTURALE sistma STRUTTURA STATO I modlli mccanici possono suddividrsi in: MODELLI CONTINUI Forz Coazioni STRUTTURA = modllo mccanico IDEALIZZAZIONE DELLA STRUTTURA Posizion Vlocità Acclrazion
Modi dominanti. L evoluzione libera del sistema lineare. x(k + 1) = Ax(k) a partire dalla condizione iniziale x(0) = x 0 è:
Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
Funzioni lineari e affini. Funzioni lineari e affini /2
Funzioni linari aini In du variabili l unzioni linari sono dl tipo a b l unzioni aini sono dl tipo a b c Il graico di una unzion linar è un piano passant pr l origin il graico di una unzion ain è un piano.
Linee accoppiate. Corso di Componenti e Circuiti a Microonde. Ing. Francesco Catalfamo. 3 Ottobre 2006
orso di omponnti ircuiti a Microond Ing. Francsco atalamo 3 Ottobr 006 Indic Ond supriciali modi di ordin suprior Lin in microstriscia accoppiat Ond supriciali Un onda supricial è un modo guidato ch si
Prof. Fernando D Angelo. classe 5DS. a.s. 2007/2008. Nelle pagine seguenti troverete una simulazione di seconda prova su cui lavoreremo dopo le
Pro. Frnando D Anglo. class 5DS. a.s. 007/008. Nll pagin sgunti trovrt una simulazion di sconda prova su cui lavorrmo dopo l vacanz di Pasqua. Pr mrcoldì 6/03/08 guardat il problma 4 i qusiti 1 8 9-10.
Fisica Generale VI Scheda n. 1 esercizi di riepilogo dei contenuti di base necessari. 1.) Dimostrare le seguenti identità vettoriali:
Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
di disequazioni lineari
Capitolo Disquazioni Esrcizi sistmi di disquazioni linari Toria p. 68 L disquazioni l loro soluzioni Pr ciascuna dll sgunti disquazioni, invnta un problma ch possa ssr risolto con la disquazion stssa.
POTENZE NECESSARIE E DISPONIBILI
POTENZE NECESSARIE E DISPONIBILI In qusto capitolo ci proponiamo di dtrminar l curv dll potnz ncssari pr l vari condizioni di volo. Tali curv dipndranno da divrsi fattori com il pso dl vlivolo, la quota,
Misurazione del valore medio di una tensione tramite l uso di un voltmetro numerico
Misurazion dl valor mdio di una tnsion tramit l uso di un voltmtro numrico La zion si conduc slzionando la funzion dc dllo strumnto collgando i trminali dllo strumnto al gnrator sotto zion: tnndo conto
Tecniche per la ricerca delle primitive delle funzioni continue
Capitolo 4 Tcnich pr la ricrca dll primitiv dll funzioni continu Nl paragrafo.7 abbiamo dato la dfinizion di primitiva di una funzion f avnt pr dominio un intrvallo I; abbiamo visto ch s F 0 è una primitiva
1. Dati i tensori: { L = 3ex e y + 2e y e z + 3e z e x
1 Univrsità di Pavia Facoltà di Inggnria Corso di Laura in Inggnria Edil/Architttura Corrzion prova scritta Esam di Mccanica Razional 30 gnnaio 01 1. Dati i tnsori: { L = 3x y + y z + 3 z x M = x x y y
Teoria dell integrazione secondo Riemann per funzioni. reali di una variabile reale.
Capitolo 2 Toria dll intgrazion scondo Rimann pr funzioni rali di una variabil ral Esistono vari tori dll intgrazion; tutt hanno com comun antnato il mtodo di saustion utilizzato dai Grci pr calcolar l
ANALISI 2 ESERCITAZIONE DEL 06/12/2010 PUNTI CRITICI
ANALISI ESERCITAZIONE DEL 06//00 PUNTI CRITICI Un punto critico è un punto in cui la funzion è diffrnziabil il piano tangnt al grafico è orizzontal Riconosciamo qusti punti prché il gradint è il vttor
PROGRAMMA DI RIPASSO ESTIVO
ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}.
![Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}.](/thumbs/52/29110632.jpg "Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}.")
Soluzioni Capitolo [.] A B = {,,,, 7, 8}, A B = {, 7}, A\B = {,, }, B\A = {8}. [.] I) [, 0] V) VI) V [, 0] (, 0) V IX) [, 00) X) ( [, ],(, 00) (, 00) (, 0 + ) (, 0 ], ), (, 0 + ) [.] B\A = {} {b = n +,
( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA
![( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA](/thumbs/69/60720045.jpg "( ) ( ) ( ) [ ] 2 ( ) 18 9) DERIVATA DI UNA FUNZIONE COMPOSTA")
8 9 DERIVATA DI UNA FUNZIONE COMPOSTA La drivata di una funion composta ( funion di funion si ottin (dim all pagin 0 : a drivando la funion principal ( qulla ch si applica pr ultima risptto al suo argomnto
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE PROPRIETA GEOMETRICHE DELL ELLISSOIDE Al fin di stbilir un gomtri sull llissoid di rotzion è ncssrio non solo dfinir l quzioni dll curv idon d individur
Equation Chapter 1 Section 1 Vibrazioni torsionali di una trasmissione nautica Esercizio da portare in forma scritta all esame
Equation Chaptr Sction Vibrazioni torsionali di una trasission nautica Esrcizio da portar in fora scritta all sa In Figura è ostrato lo scha di un otor arino connsso all diant un riduttor ad ingranaggi
EQUAZIONI DIFFERENZIALI. Saper integrare equazioni differenziali del primo ordine lineari e a variabili separabili.
EQUAZIONI DIFFERENZIALI OBIETTIVI MINIMI Sapr riconoscr classificar l quazioni diffrnziali. Sapr intgrar quazioni diffrnziali dl primo ordin linari a variabili sparabili. Sapr intgrar quazioni diffrnziali
1 Il concetto di funzione 1. 2 Funzione composta 4. 3 Funzione inversa 6. 4 Restrizione e prolungamento di una funzione 8
UNIVR Facoltà di Economia Sd di Vicnza Corso di Matmatica 1 Funzioni Indic 1 Il conctto di funzion 1 Funzion composta 4 3 Funzion invrsa 6 4 Rstrizion prolungamnto di una funzion 8 5 Soluzioni dgli srcizi
CONOSCENZE. 1. La derivata di una funzione y = f (x)
ESAME D STATO ESEMP D QUEST D MATEMATCA PER LA TERZA PROVA CONOSCENZE. La drivata di una funzion y f (), in un punto intrno al suo dominio, : il it, s sist d è finito, dl rapporto incrmntal pr h, f ( h)
Lemma 2. Se U V é un sottospazio vettoriale di V allora 0 U.
APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
Ottimizzazione economica degli scambiatori di recupero.
Facoltà di Inggnria Univrsità dgli tudi di Bologna Dipartimnto di Inggnria Industrial Marco Gntilini Ottimizzazion conomica dgli scambiatori di rcupro Quadrni dl Dipartimnto MARCO GENTILINI OTTIMIZZAZIONE
Distribuzione gaussiana
Appunti di Misur Elttric Distribuion gaussiana Funion dnsità di probabilità di Gauss... Calcolo dlla distribuion cumulativa pr una variabil di Gauss... Funion dnsità di probabilità congiunta...6 Funion
Corso di Laurea in Economia Matematica per le applicazioni economiche e finanziarie. Esercizi 4
Corso di Laura in Economia Matmatica pr l applicazioni conomich finanziari Esrcizi 4 Vrificar s l sgunti funzioni, nll intrvallo chiuso indicato, soddisfano l ipotsi dl torma di Roll, in caso affrmativo,
INTRODUZIONE ALLO STUDIO DELLE MACCHINE ELETTRICHE ROTANTI
Gnralità INTRODUZIONE ALLO STUDIO DELLE MACCHINE ELETTRICHE ROTANTI Una acchina lttrica rotant è un convrtitor di nrgia ccanica in lttrica (gnrator) o, vicvrsa, di nrgia lttrica in ccanica (otor). Il fnono
Fisica Generale L-B - Prof. M. Villa. CdL in Ing. Elettronica e dell Automazione. I Parziale 25 Maggio Compito A
Fisica Gnral L-B - Prof. M. Villa CdL in Ing. Elttronica dll Automazion I Parzial 5 Maggio 006 Compito A In una rgion di spazio è prsnt un potnzial lttrostatico dato da V (x, y, z) = α(x y ) con α costant
Lezione 2. Richiami di aerodinamica compressibile. 2.1 Gas ideale. 2.2 Velocità del suono. 2.3 Grandezze totali
Lzion 2 Richiami di arodinamica comprssibil In qusto corso si considrano acquisit alcun nozioni di bas di trmodinamica di gas arodinamica comprssibil quali i conctti di gas idal nrgia intrna ntalpia ntropia
CLASSIFICAZIONE DEI PRODOTTI DA COSTRUZIONE
ALLEGATO A CLASSIFICAZIONE DEI PRODOTTI DA COSTRUZIONE Quando la condizion di uso final di un prodotto da costruzion è tal da contribuir alla gnrazion alla propagazion dl fuoco dl fumo all intrno dl local
Esercizi sullo studio di funzione
Esrcizi sullo studio di funzion Prima part Pr potr dscrivr una curva, data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: 1) Dtrminar l insim di sistnza dlla f () ) Dtrminar
Spettro roto-vibrazionale di HCl (H 35 Cl, H 37 Cl )
Spttro roto-vibrazional di HCl (H 5 Cl, H 7 Cl ) SCOPO: Misurar l nrgi dll transizioni vibro-rotazionali dll acido cloridrico gassoso utilizzar qust nrgi pr calcolar alcuni paramtri molcolari spttroscopici.
Alla temperatura di 300K è ragionevole ritenere che tutto il drogante sia attivato, cioè che ad ogni atomo accettore corrisponda una lacuna, per cui
1 1. Una ftta di silicio è drogata con una concntrazion N A = 10 16 atm/cm 3 di atomi accttori, si valuti la concntrazion di portatori maggioritari minoritari alla tmpratura T = 300K. Alla tmpratura di
R k = I k +Q k. Q k = D k-1 - D k
1 AMMORTAMENTO AMMORTAMENTO Dbito inizial D 0 si volv (al tasso fisso t) D k = D k-1 (1+t) R k [D k dbito (rsiduo) al tmpo k, R k pagamnto al tmpo k ] Condizioni [D n =0 : stinzion dl dbito in n priodi
2. Richiami di calcolo delle probabilità
. Richiai di calcolo dll probabilità L analisi sposta, consistnt nll ipotizzar la crisi in fas plastica, coporta, indubbiant, vantaggi risptto al todo lastico-linar, a non può considrarsi pinant accttabil
Esercizio 1. Cov(X,Y)=E(X,Y)- E(X)E(Y).
Esrcizi di conomtria: sri 4 Esrcizio Siano, Z variabili casuali distribuit scondo la lgg multinomial di paramtri n, p, p, p p p.. Calcolar la Covarianza tra l variabili d. Soluzion Dat du variabili dinit
Unità didattica: Grafici deducibili
Unità didattica: Grafici dducibili Dstinatari: Allivi di una quarta lico scintifico PNI tal ud è insrita nllo studio dll funzioni rali di variabil ral. Programmi ministriali dl PNI: Dal Tma n 3 funzioni
Coordinamento tra le protezioni della rete MT del Distributore e la protezione generale. degli Utenti MT.
Coordinamnto tra l protzioni dlla rt MT dl Distributor la protzion gnral 1. PREMESSA. dgli Utnti MT. ll rti di distribuzion a mdia tnsion (MT), l unico organo di manovra automatico è l intrruttor di lina
0 < a < 1 a > 1. In entrambi i casi la funzione y = a x si può studiare per punti e constatare che essa presenta i seguenti andamenti y.
INTRODUZIONE Ossrviamo, in primo luogo, ch l funzioni sponnziali sono dlla forma a con a costant positiva divrsa da (il caso a è banal pr cui non sarà oggtto dl nostro studio). Si possono allora vrificar
[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]
![[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]](/thumbs/70/62246785.jpg "[ ] ( ) ( ) ( e ) jωn. [ ] [ [ n. [ n] = T [ ] [ ] [ ] [ ]")
Sistmi Linari Tmpo Invarianti (LTI) a Tmpo Discrto Dfiniamo il sistma tramit una trasformaion T []. La proprità di linarità implica ch [ α 1x1[ n] + α2x2[ n ] α1t x1[ n] + α2t x La proprità di tmpo invariana
COMUNE DI MONTERIGGIONI DOCUMENTO UNICO DI VALUTAZIONE RICOGNITIVA DEI RISCHI INTERFERENTI STANDARD PARTE II SEZIONE IDENTIFICATIVA DEI RISCHI SPECIFICI DELL AMBIENTE E MISURE DI PREVENZIONE E PROTEZIONE
Nozioni di base sulle coniche (ellisse (x^2/a^2)+(y^2/b^2)=1, iperbole(x^2/a^2)-(y^2/b^2)=1, parabola e circonferenza):
Nozioni di bas sull conich (lliss (x^2/a^2)+(y^2/b^2)=1, iprbol(x^2/a^2)-(y^2/b^2)=1, parabola circonfrnza): Dlta =0, significa un solo punto di intrszion tra fascio di rtt conica Dlta >=0, significa 2
Istogrammi ad intervalli
Istogrammi ad intrvalli Abbiamo visto com costruir un istogramma pr rapprsntar un insim di misur dlla stssa granda isica. S la snsibilità dllo strumnto di misura è alta, è probabil ch tra gli N valori
IV-3 Derivate delle funzioni di più variabili
DERIVATE PARZIALI IV-3 Drivat dll funzioni di più variabili Indic Drivat parziali Rgol di drivazion 5 3 Drivabilità continuità 7 4 Diffrnziabilità 7 5 Drivat scond torma di Schwarz 8 6 Soluzioni dgli srcizi
Alberi di copertura minimi
Albri di coprtura minimi Albro di coprtura (spanning tr) Dato un grafo G=(V, E, w) non orintato, connsso psato, un albro di coprtura di G è un sottografo X=(V, T) tal ch X è un albro (quindi connsso) T
ESERCIZI SULLA DEMODULAZIONE INCOERENTE
Esrcitazioni dl corso di trasmissioni numrich - Lzion 4 6 Fbbraio 8 ESERCIZI SULLA DEMODULAZIONE INCOERENE I du sgnali passa basso di figura sono utilizzati pr la trasmission di simboli binari quiprobabili
TIPI TIPI DI DI DECADIMENTO RADIOATTIVO --ALFA
TIPI TIPI DI DI DECDIMENTO RDIOTTIVO --LF LF Dcadimnto alfa: il nuclo instabil mtt una particlla alfa (), ch è composta da du protoni du nutroni (un nuclo di 4 H), quindi una particlla carica positivamnt.
Studio di funzione. R.Argiolas
Studio di unzion R.Argiolas Introduzion Prsntiamo lo studio dl graico di alcun unzioni svolt durant l srcitazioni dl corso di analisi matmatica I assgnat nll prov scritt. Ringrazio anticipatamnt tutti
Calcoliamo innanzitutto la velocità media di spostamento dei portatori di carica (e - ): ogni portatore è sottoposto ad una forza:
6 Trasporto di carica in un zzo solido In un solido, gli lttroni di valnza, ch sono libri di uovrsi (fig. 1) vngono acclrati in una dirzion s il solido è irso in un capo lttrico E dirtto co in fig.2. nl
Appunti sulle disequazioni frazionarie
ppunti sull disquazioni frazionari Sono utili l sgunti dfinizioni Una disquazion fratta o frazionaria è una disquazion nlla qual l incognita compar in qualch suo dnominator. Una disquazion razional è una
FORMAZIONE TELEMATICA
9 Trimstral Anno IV Numro 46 Focus - Via dll Industri, 8/ - 35 Ponzano Vnto (TV. Spdizion in abbonamnto postal D.L. 353/3 (conv. in L. 7//4 N 46 art., comma DCB TV FORMAZIONE TELEMATICA snza sps di viaggio
GRANDEZZE OPERATIVE DELLE MACCHINE OPERANTI CON FLUIDI INCOMPRIMIBILI. v 1. + v 2 2. + gz ( 2. + z
CAPITOLO 5 GRANDEZZE OPERATIVE DELLE MACCHINE OPERANTI CON FLUIDI INCOMPRIMIBILI 5.1) Prvalnza salto motor. S considriamo un gnrico impianto idraulico in cui sia insrita una macchina oprant in rgim stazionario
Esercizi sugli studi di funzione
Esrcizi sugli studi di funzion Studiar l andamnto tracciar il grafico dll sgunti funzioni di : (a) ; (b) 4 3 + ; (c) cos sin ; (d) 3 ; () log 3 ; (f) arctg + ; (g) ( + ) log ; (h) sin ; (i) tg ; (j) +
INTEGRALI DOPPI Esercizi svolti
INTEGRLI OPPI Esrcizi svolti. Calcolar i sgunti intgrali doppi: a b c d f g h i j k y d dy, {, y :, y }; d dy, {, y :, y }; + y + y d dy, {, y :, y }; y d dy, {, y :, y }; y d dy, {, y :, y + }; + y d
CURVE DI PROBABILITÀ PLUVIOMETRICA Le curve di probabilità pluviometrica esprimono la relazione fra le altezze di precipitazione h e la loro durata
CURVE DI PROBABILITÀ PLUVIOMETRICA L curv di probabilità pluviomtrica sprimono la rlazion fra l altzz di prcipitazion h la loro durata t, pr un assgnato valor dl priodo di ritorno T. Tal rlazion vin spsso
ANALISI STRUTTURALE AD ELEMENTI FINITI CON APPROCCIO AGLI SPOSTAMENTI
ANAISI SRUURAE AD EEMENI FINII CON APPROCCIO AGI SPOSAMENI Abbiamo già avuto occasion di vdr ch con l tcnich ad lmnti finiti il procsso di discrtizzazion passa attravrso l'individuazion di un st discrto
Antenne e Telerilevamento. Esonero I ESONERO ( )
I ESONERO (28.6.21) ESERCIZIO 1 (15 punti) Si considri un sistma ricvnt oprant alla frqunza di 13 GHz, composto da un antnna a parabola a polarizzazion linar con un rapporto fuoco-diamtro f/d=.3, illuminata
METODO DI NEWTON Esempio di non convergenza
METODO DI NEWTON S F(x) è C 2 si sa ch (x R k ) F(x+h) = F(x) + F(x) t h + 1/2 h t H(x)h +o( h 3 ) d una stima possibil dl punto di minimo è data da x# = x - H(x) -1 F(x) dov H(x) è la matric hssiana in
Esame di Dispositivi Optoelettronici 29 Gennaio 2007
Esam di Dispositivi Optolttronici 9 Gnnaio 007 Domanda di toria : a: Introdurr il conctto di momnto rticolar di un lttron in un potnzial priodico d il suo lgam con la forza agnt sul portator. b: Discutr
Il transistor bipolare a giunzione (bjt( bjt) Dispositivi elettronici. npn bjt (bipolar junction transistor) pnp bjt (bipolar junction transistor)
Sommario Dispositivi lttronici l transistor bipolar a giunzion (bjt( bjt) l transistor bipolar a giunzion (bjt) com è fatto un bjt principi di funzionamnto (giunzion a bas corta) fftto transistor (
Capitolo 1. L insieme dei numeri complessi Introduzione ai numeri complessi
Capitolo 1 L insim di numri complssi 11 Introduzion ai numri complssi Dfinizion 111 Sia assgnata una coppia ordinata (a, b) di numri rali Si dfinisc numro complsso l sprssion z = a + ιb I numri a b sono
FORMA CHIUSA PER L OTTIMIZZAZIONE DELL ARMATURA IN STRUTTURE IN CALCESTRUZZO SOGGETTE A STATI PIANI DI TENSIONE
FORMA CHIUSA PER L OTTIMIZZAZIONE DELL ARMATURA IN STRUTTURE IN CALCESTRUZZO SOGGETTE A STATI PIANI DI TENSIONE Gabril Brtagnoli 1, Giordano Luca 1, Giuspp Mancini 1 1 Dipartimnto di Inggnria Struttural
CONDIZIONI DI FUNZIONAMENTO
CONDIZIONI DI FUNZIONAMENTO Anch il todolit più sofisticato, di pr sé, non garantisc la corrtta misura dgli angoli. Affinché un todolit possa assolvr al suo compito di misurar corrttamnt gli angoli, è
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2012
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 0 Il candidato risolva uno di du problmi di 0 qusiti in cui si articola il qustionario. PRBLEMA Dlla funzion f, dfinita pr 0, si sa ch è dotata
0.06 100 + (100 100)/4 (100 + 2 100)/3
A. Prtti Svolgimnto di tmi d sam di MDEF A.A. 5/ PROVA CONCLUSIVA DI MATEMATICA pr l DECISIONI ECONOMICO-FINANZIARIE Vicnza, 5// ESERCIZIO. Trovar una prima approssimazion dl tasso di rndimnto a scadnza
Franco Ferraris Marco Parvis Generalità sulle Misure di Grandezze Fisiche. Testi consigliati
Gnralità sull Misur di Grandzz Fisich - Misurazioni dirtt 1 Tsti consigliati Norma UNI 4546 - Misur Misurazioni; trmini dfinizioni fondamntali - Milano - 1984 Norma UNI-I 9 - Guida all sprssion dll incrtzza
REGRESSIONE LOGISTICA
0//04 METODI E TECNICHE DELLA RICERCA IN PSICOLOGIA CLINICA E LABORATORIO AA 04/05 PROF. V.P. SENESE Sconda Univrsità di Napoli (SUN) Facoltà di Psicologia Dipartimnto di Psicologia METODI E TECNICHE DELLA
Le città vengono modificate anche all interno degli spazi già costruiti
La città ch cra il progtto snsibil L città vngono modificat anch all intrno dgli spazi già costruiti pnso sia molto più intrssant quando si usa il trmin nuovo far rifrimnto a qualcosa di divrso, cioè alla
Teoria microscopica della conduzione elettrica. Indice
Toria microscopica dlla conduzion lttrica Indic 1. Un modllo microscopico dlla conduzion lttrica 1.1 Modllo classico dlla conduzion 1. Intrprtazion classica di v m di 1.3 Difficoltà dll intrprtazion classica.
Ing. Gestionale Ing. Informatica Ing. Meccanica Ing. Tessile. Cognome Nome Matricola
Ing Gstional Ing Informatica Ing Mccanica Ing Tssil Cognom Nom Matricola Univrsità dgli Studi di Brgamo Scondo Compitino di Matmatica II ) Si considri la matric 2 3 3 2 Si calcolino gli autovalori gli
Esercizio 3. Determinare la dimensione, la codimensione, una base, equazioni cartesiane, equazioni parametriche ed un complemento per U R 3, dove
Sapinza Univrsità di Roma Corso di laura in Inggnria Enrgtica Gomtria - A.A. 2015-2016 Foglio n.10 Somma intrszion di sottospazi vttoriali prof. Cigliola Esrcizio 1. Sono dati i vttori v 1 = ( 1, 0, 0),