INTRODUZIONE ALLA RELATIVITÀ SPECIALE: Dalla seconda legge di Newton a E = mc 2. 8 marzo 2017
|
|
|
- Paolina Donati
- 6 anni fa
- Visualizzazioni
Transcript
1 INTRODUZIONE ALLA RELATIVITÀ SPECIALE: Dalla seconda legge di Newton a E = mc 2 8 marzo 2017
2 Piano della presentazione Trasformazioni di Lorentz Red Shift Relatività e leggi di Newton Galileo Seconda Legge di Newton Energia relativistica E = mc 2 quadri-velocità e quadri-impulso Conservazione del 4-impulso Fissione Centrale nucleare
3 Trasformazioni di Lorentz t = γ(t vx c 2 ) { x 0 = γ(x 0 βx) } x { = γ(x vt) x = γ(x βx 0 ) } y = y z = z γ = 1 1 =: 1 v 2 1 β 2 c 2 Per v c 1, β 0, γ 1 e riotteniamo le usuali trasformazioni di Galileo!!
4 Red Shift Consideriamo una sorgente luminosa, a riposo in S che emette luce di lunghezza d onda λ e frequenza ν (in S). Vogliamo calcolare la lunghezza d onda λ e la frequenza ν che vede un osservatore S che si muove verso S con velocità v
5 Red Shift Consideriamo una sorgente luminosa, a riposo in S che emette luce di lunghezza d onda λ e frequenza ν (in S). Vogliamo calcolare la lunghezza d onda λ e la frequenza ν che vede un osservatore S che si muove verso S con velocità v
6 Se T è il tempo (misurato in S ) che intercorre tra l emmissione di due fronti d onda, nello stesso tempo la sorgente si è mossa verso S di un tratto vt di modo che la distanza tra due massimi sarà: λ = ct vt. Ricordando che λ ν = c otteniamo ν = c (c v)t
7 Se T è il tempo (misurato in S ) che intercorre tra l emmissione di due fronti d onda, nello stesso tempo la sorgente si è mossa verso S di un tratto vt di modo che la distanza tra due massimi sarà: λ = ct vt. Ricordando che λ ν = c otteniamo ν = c (c v)t
8 Se T è il tempo (misurato in S ) che intercorre tra l emmissione di due fronti d onda, nello stesso tempo la sorgente si è mossa verso S di un tratto vt di modo che la distanza tra due massimi sarà: λ = ct vt. Ricordando che λ ν = c otteniamo ν = c (c v)t
9 Se T è il tempo (misurato in S ) che intercorre tra l emmissione di due fronti d onda, nello stesso tempo la sorgente si è mossa verso S di un tratto vt di modo che la distanza tra due massimi sarà: λ = ct vt. Ricordando che λ ν = c otteniamo ν = c (c v)t
10 Ma T = γt ν = ν = ν oss. = 1 (v 2 /c 2 ) 1 (v/c) 1+(v/c) 1 (v/c) ν ν da cui: 1+(v/c) 1 (v/c) ν sorgente Notiamo che in questo caso: la sorgente si avvicina, ν oss > ν sorgente ; nel caso opposto: la sorgente si allontana, 1 (v/c) ν oss. = ν sorgente e ν oss < ν sorgente. 1+(v/c)
11 Ma T = γt ν = ν = ν oss. = 1 (v 2 /c 2 ) 1 (v/c) 1+(v/c) 1 (v/c) ν ν da cui: 1+(v/c) 1 (v/c) ν sorgente Notiamo che in questo caso: la sorgente si avvicina, ν oss > ν sorgente ; nel caso opposto: la sorgente si allontana, 1 (v/c) ν oss. = ν sorgente e ν oss < ν sorgente. 1+(v/c)
12 Ma T = γt ν = ν = ν oss. = 1 (v 2 /c 2 ) 1 (v/c) 1+(v/c) 1 (v/c) ν ν da cui: 1+(v/c) 1 (v/c) ν sorgente Notiamo che in questo caso: la sorgente si avvicina, ν oss > ν sorgente ; nel caso opposto: la sorgente si allontana, 1 (v/c) ν oss. = ν sorgente e ν oss < ν sorgente. 1+(v/c)
13 Ma T = γt ν = ν = ν oss. = 1 (v 2 /c 2 ) 1 (v/c) 1+(v/c) 1 (v/c) ν ν da cui: 1+(v/c) 1 (v/c) ν sorgente Notiamo che in questo caso: la sorgente si avvicina, ν oss > ν sorgente ; nel caso opposto: la sorgente si allontana, 1 (v/c) ν oss. = ν sorgente e ν oss < ν sorgente. 1+(v/c)
14 Redshift delle galassie La luce emessa dalle galassie contiene una distribuzione continua di lunghezze d onda perché la galassia contiene milioni di stelle che emettono in tutte le frequenze. All interno di questo spettro continuo si possono individuare delle linee strette in corrispondenza della radiazione assorbita da gas più freddo all interno della galassia. In particolare una nube di atomi di calcio ionizzato produce un forte assorbimento intorno a 394nm per una galassia a riposo rispetto alla terra. Nel caso della galassia Hydra, a 200 anni luce dalla terra, questo assorbimento si trova a 475nm. A che velocità si muove rispetto alla terra?
15 Siccome λ oss > λ sorgente e λν = c, Hydra si sta allontanando. In questo caso ν oss. = λ oss. = 1 (v/c) 1 + (v/c) ν sorgente da cui 1 + (v/c) 1 (v/c) λ sorgente v c v c = λ2 oss. λ 2 sorgente λ 2 oss. + λ 2 sorgente ossia = = dunque Hydra si sta allontanando da noi a una velocità v = 0.185c = m/s
16 Relatività e leggi di Newton Le trasformazioni di Lorentz mettono in crisi la conservazione dell impulso. Consideriamo il seguente urto anelastico:
17 Nel centro di massa (S) abbiamo: prima dell urto p 1 = mvu x ; p 2 = mvu x e quindi p prima tot = p 1 + p 2 = 0; la conservazione dell impulso implica che dopo l urto la velocità nel sistema S sia 0: = p prima tot = 0 p dopo tot e quindi, nel centro di massa le due masse si uniscono e restano ferme!
18 Analizziamo lo stesso urto in un riferimento che si muova da sinistra a destra con velocità v, avremo:
19 Galileo v 1 = 0, e v 2 = ( v v)u x = 2vu x di modo che prima dell urto p prima tot = 2mvu x, mentre dopo l urto: V = vu xequindi p dopo tot = 2mvu x dunque la legge della conservazione degli urti è verificata in meccanica Newtoniana. Facciamo la stessa analisi ma stavolta usiamo le trasformazioni di Lorentz nel passaggio da S a S :
20 Lorentz Dovremo usare le leggi di composizione delle velocità: u x = u y = u z = u x v 1 ( u x ) v c 2 u y γ [ 1 ( u x )] v c 2 u z γ [ 1 ( u x )] v c 2 Dove u x e v sono i moduli della velocità del corpo e del sistema di riferimento rispettivamente.
21 avremo: v 1 = v 2 = V = v 1 v 1 ( v 1 v c 2 ) = v 2 v 1 ( v 2 v c 2 ) = V v 1 ( Vv c 2 ) = v v 1 ( v 1 v c 2 ) = 0 v v 2v ( ) = 1 ( v)v 1 + c v ( (0)v c 2 ) = v ( v 2 c 2 )
22 dunque in S avremo: p prima tot = mv 1 + mv 2 = m(0) + m 2v 1 + ( v 2 c 2 ) = 2mv 1 + ( v 2 c 2 ) p dopo tot = 2mV = 2mv ossia l impulso non è conservato!!!
23 Impulso relativitico Affinché lo sia dobbiamo porre p = γmu = mu 1 (u 2 /c 2 ) dove m è la massa a riposo, ossia la massa misurata nel riferimento solidale alla particella, e u è la velocità della particella rispetto al riferimento S in cui si vuole analizzare il moto.
24 Verifichiamo in S: p prima tot = γ 1 mv 1 + γ 2 mv 2 = = p dopo tot = γmv = 0 1 mv v 1 2 c mv + m( v) = 0 1 v 2 c 1 ( v)2 2 c 2 1 mv 2 1 v 2 2 c 2 OK
25 Nel riferimento S : p prima tot = γ 1 mv 1 + γ 2 mv 2 1 = m(0) + ( 1 1 c 2 = 2mv 1 v 2 c 2 p dopo tot = γmv = 2mv 1 v 2 c 2 NON SI TROVA!!! 2v ( ) 1+ v 2 c 2 ) m 2v 1 + ( v 2 c 2 )
26 Seconda Legge di Newton (relativistica) F = dp dt = d dt (γmu) nel limite di piccole velocità: u c riotteniamo l usuale 2 a legge di Newton! Ma l accelerazione di una particella soggetta a una forza costante (diretta lungo u) è datat da: (1 u2 ) 3/2 a = F m c 2 e quindi per u c tende a zero: non possibile accelerare una particella a una velocità maggiore o uguale a c!!
27 Esempi Un elettrone si muove a una velocità v = 0.8c, calcolare il suo impulso classicamente e relativisticamente: (massa dell elettrone m = kg p class. = mu = (0.8) = kgm/s p rel. = γmu = (0.8) = kgm/s Quindi nel caso relativistico si ha un 70% in più!!
28 Energia relativistica La modifica della espressione dell impulso implica una modifica della forma relativistica dell energia cinetica. Infatti (assumendo tutto diretto lungo x): x2 x2 dp W = Fdx = x 1 x 1 dt dx se la particella è accelerata da 0 a u, x2 dv u = m dt dx = m vdv = 1 2 mu2 x 1 0
29 Ma relativisticamente W = dp dt W = W = x2 x 1 Fdx = x2 x 1 dp dt dx = d mu dt 1 (u 2 /c 2 ) = m du dt [1 (u 2 /c 2 )] 3/2 ossia, se la particella è accelerata da 0 a u, x2 ( x 1 m du dt udt = m [1 (u 2 /c 2 3/2 )] mc 2 1 (u 2 /c 2 ) ) u 0 = u 0 udu [1 (u 2 /c 2 )] 3/2 mc 2 1 (u 2 /c 2 ) mc2
30 Energia cinetica relativistica Ricordando che il teorema lavoro-energia stabilisce che il lavoro fatto da una forza su una particella è uguale alla variazione di energia cinetica della particella concludiamo che l energia cinetica relativistica della particella che si muove a velocità u è: K = mc 2 1 (u 2 /c 2 ) mc2
31 Energia cinetica relativistica Nel caso u c, ricordando che (1 x 2 ) 1/ x abbiamo ( K mc u 2 ) 2 c mc 2 = 1 2 mu2 che è la vecchia espressione dell energia cinetica.
32 Energia relativistica Notiamo che l energia cinetica si può scrivere: K = γmc 2 mc 2, il secondo pezzo non dipende in alcun modo dalla velocità, per questo si chiama energia a riposo della particella. La somma dell energia cinetica e dell energia a riposo è quello che chiamiamo energia totale della particella: E = K + mc 2 = γmc 2 Equazione di Einstein sull equivalenza tra massa ed energia.
33 Invariante relativistico Da E = γmc 2 e p = γmu otteniamo (mc 2 ) 2 = E 2 p 2 c 2 e, siccome m e c sono invarianti per trasformazioni di Lorentz anche E 2 p 2 c 2 deve essere invariante
34 Massa a riposo ed energia a riposo Quando si dice l elettrone ha massa (a riposo) 0.5MeV in realtà si pensa all energia a riposo: m e c 2 = kg( m/s) 2 = J = J J ev = ev = 0.511MeV quindi ( ) MeV m e = c 2 = ev J ( m/s) 2 = Kg
35 Un elettrone viaggia a velocità u = 0.8c, calcolare energia totale ed energia cinetica: E tot = γmc 2 = MeV = 0.852MeV ; K = E mc 2 = = 0.341MeV
36 Supponiamo ora di avere un protone ( m p c 2 = 938MeV ) con la stessa energia cinetica, a che velocità si muoverà? Quanto vale la sua energia? E il suo impulso? K = γm p c 2 m p c 2 quindi 1 1 u 2 /c 2 = K m p c = = u = c = 0.027c E tot = γm p c 2 = = MeV ( p = γm p u = MeV ) c c ( ) MeV = c
37 quadri-velocità e quadri-impulso Nella 3-geometria di Galileo definiamo velocità il vettore tangente alla traiettoria della particella. Nella 4-geometria definiamo la quadri-velocità come il vettore tangente alla linea di universo, e lungo c nel riferimento solidale alla particella
38 In questo modo: U 0 = γc, p 0 = mu 0 U 1 = γv p 1 = mu 1 e E/c = p 0 = γmc c mv 2 cioè energia a riposo più energia cinetica Galileiana
39 Conservazione del 4-impulso In un urto il 4-impulso totale è conservato p µ (p 0, p) (E, p) con E = γmc 2, p = γmu, e (mc 2 ) 2 = E 2 p 2 c 2 : Pµ tot,prima = Pµ tot,dopo P tot,prima 0 = P tot,dopo 0 = E tot,prima = E tot,dopo P tot,prima = P tot,dopo
40 Torniamo all analisi dell urto e chiediamoci quanto vale la massa a riposo della particella che si forma dopo l urto?: La conservazione della componente 0 del 4-impulso richiede (nel centro di massa dove, dopo l urto, le particelle sono ferme) E tot,prima = E tot,dopo ossia γ 1 m 1 c 2 + γ 2 m 2 c 2 = Mc 2 da cui, poiché γ 1 = γ 2 =: γ, m 1 = m 2 = m M = 2m γ(2m) = 1 v 2 c 2
41 Nel riferimento S : p prima tot = γ 1 mv 1 + γ 2 mv 2 1 = m(0) + ( 1 1 c 2 = 2mv 1 v 2 c 2 2v ( ) 1+ v 2 c 2 ) m 2v 1 + p dopo tot = γmv = γ(γ(2m))( v) = 2γ 2 mv = 2mv 1 v 2 c 2 SI TROVA!!! ( v 2 c 2 )
42 Fissione Consideriamo un nucleo radioattivo (a riposo) che decade in più (3) particelle di massa m i e velocità u i. La conservazione della energia relativistica totale implica Mc 2 = i γ i m i c 2 = γ 1 m 1 c 2 + γ 2 m 2 c 2 + γ 3 m 3 c 2 Siccome γ > 1, M > m 1 + m 2 + m 3 e la perdita di massa M (m 1 + m 2 + m 3 ) appare come energia di moto dei prodotti di disintegrazione : Q = [M (m 1 + m 2 + m 3 )]c 2 = mc 2
43 Centrale nucleare In una centrale nucleare un nucleo di uranio decade in rubidio +cesio secondo la seguente reazione: U Rb Cs n, quanto vale l energia di disintegrazione? M U = u; M Rb = u; M Cs = u; M n = 1.009u m = (89.915u ) = 0.177u = Kg = Kg quindi l energia prodotta sarà Q = mc 2 = 0.177(931.5 MeV c 2 ) = MeV
44 Quindi, se teniamo conto che in 1Kg di uranio ci sono N = nuclei, otteniamo che 1Kg di uranio può fornire circa E = NQ = = MeV = ( KWh/MeV ) = KWh
Da Maxwell a Einstein
 Da Maxwell a Einstein Le equazioni di Maxwell forniscono una spiegazione completa dei fenomeni elettromagnetici e ottici: La luce è un onda elettromagnetica e tutte le onde elettromagnetiche si propagano
Da Maxwell a Einstein Le equazioni di Maxwell forniscono una spiegazione completa dei fenomeni elettromagnetici e ottici: La luce è un onda elettromagnetica e tutte le onde elettromagnetiche si propagano
p e c = ev Å
 Corso di Introduzione alla Fisica Quantistica (f) Soluzioni Esercizi: Giugno 006 * Quale la lunghezza d onda di de Broglie di un elettrone che ha energia cinetica E 1 = KeV e massa a riposo m 0 = 9.11
Corso di Introduzione alla Fisica Quantistica (f) Soluzioni Esercizi: Giugno 006 * Quale la lunghezza d onda di de Broglie di un elettrone che ha energia cinetica E 1 = KeV e massa a riposo m 0 = 9.11
Dinamica relativistica
 Dinamica relativistica 111 impulso relativistico Utilizzando semplici problemi d urto, si può far vedere che la conservazione della quantità di moto classica non vale per velocità relativistiche. Es. urto
Dinamica relativistica 111 impulso relativistico Utilizzando semplici problemi d urto, si può far vedere che la conservazione della quantità di moto classica non vale per velocità relativistiche. Es. urto
La relatività ristretta. Lezioni d'autore
 La relatività ristretta Lezioni d'autore Superquark-Albert Einstein Relatività (prima parte) VIDEO Superquark-Albert Einstein Relatività (seconda parte) VIDEO Materia e antimateria (a cura dell'agenzia
La relatività ristretta Lezioni d'autore Superquark-Albert Einstein Relatività (prima parte) VIDEO Superquark-Albert Einstein Relatività (seconda parte) VIDEO Materia e antimateria (a cura dell'agenzia
L energia assorbita dall atomo durante l urto iniziale è la stessa del fotone che sarebbe emesso nel passaggio inverso, e quindi vale: m
 QUESITI 1 Quesito Nell esperimento di Rutherford, una sottile lamina d oro fu bombardata con particelle alfa (positive) emesse da una sorgente radioattiva. Secondo il modello atomico di Thompson le particelle
QUESITI 1 Quesito Nell esperimento di Rutherford, una sottile lamina d oro fu bombardata con particelle alfa (positive) emesse da una sorgente radioattiva. Secondo il modello atomico di Thompson le particelle
FAM A+B C. Considera la disintegrazione di una particella A in due particelle B e C: A B +C.
 Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI
 ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI Di Riccardo Messina L espressione dell equivalenza massaenergia che è qui riportata non
ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI Di Riccardo Messina L espressione dell equivalenza massaenergia che è qui riportata non
Relatività Ristretta
 1. L invarianza della velocità della luce 2. L esperimento di Michelson Morley 3. Gli assiomi della teoria della relatività ristretta 4. Relatività della simultaneità 5. La contrazione delle lunghezze
1. L invarianza della velocità della luce 2. L esperimento di Michelson Morley 3. Gli assiomi della teoria della relatività ristretta 4. Relatività della simultaneità 5. La contrazione delle lunghezze
FISICA. CdS Scienze Biologiche. Stefania Spagnolo. Dip. di Matematica e Fisica Ennio De Giorgi
 FISICA CdS Scienze Biologiche Stefania Spagnolo Dip. di Matematica e Fisica Ennio De Giorgi http://www.dmf.unisalento.it/~spagnolo stefania.spagnolo@le.infn.it (please, usate oggetto/subject: CdSBiologia)
FISICA CdS Scienze Biologiche Stefania Spagnolo Dip. di Matematica e Fisica Ennio De Giorgi http://www.dmf.unisalento.it/~spagnolo stefania.spagnolo@le.infn.it (please, usate oggetto/subject: CdSBiologia)
Trasformazioni di Lorentz
 Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
QUANTITA DI MOTO Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
Onde elettromagnetiche ed altre storie
 Onde elettromagnetiche ed altre storie Onde elettromagnetiche Un onda elettromagnetica è una oscillazione del campo elettromagnetico che si propaga nello spazio. Le onde elettromagnetiche si propagano
Onde elettromagnetiche ed altre storie Onde elettromagnetiche Un onda elettromagnetica è una oscillazione del campo elettromagnetico che si propaga nello spazio. Le onde elettromagnetiche si propagano
APPUNTI ASTROFISICA Processi radiativi
 APPUNTI ASTROFISICA Processi radiativi Claudio Chiuderi June 20, 2007 1 1 Processi radiativi Descriveremo brevemente le caratteristiche dei processi radiativi che non coinvolgono l emissione di righe da
APPUNTI ASTROFISICA Processi radiativi Claudio Chiuderi June 20, 2007 1 1 Processi radiativi Descriveremo brevemente le caratteristiche dei processi radiativi che non coinvolgono l emissione di righe da
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni
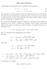 sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
APPUNTI SULLA RELATIVITA' RISTRETTA. X = X ' V t
 APPUNTI SULLA RELATIVITA' RISTRETTA TRASFORMAZIONI DI LORENTZ X è la posizione del punto P misurata dal sistema O e X' è la posizione del punto P misurata dal sistema O'. Le equazioni di trasformazione
APPUNTI SULLA RELATIVITA' RISTRETTA TRASFORMAZIONI DI LORENTZ X è la posizione del punto P misurata dal sistema O e X' è la posizione del punto P misurata dal sistema O'. Le equazioni di trasformazione
Raccolta di esercizi di fisica moderna
 Raccolta di esercizi di fisica moderna M. Quaglia IIS Avogadro Torino M. Quaglia (IIS Avogadro Torino) Raccolta di esercizi di fisica moderna Torino, 20/11/2014 1 / 30 Prova AIF e Sillabo http://www.aif.it/archivioa/aif_seconda_prova_di_fisica.pdf
Raccolta di esercizi di fisica moderna M. Quaglia IIS Avogadro Torino M. Quaglia (IIS Avogadro Torino) Raccolta di esercizi di fisica moderna Torino, 20/11/2014 1 / 30 Prova AIF e Sillabo http://www.aif.it/archivioa/aif_seconda_prova_di_fisica.pdf
Principio di Conservazione dell Energia
 Principio di Conservazione dell Energia Giuseppe Augello 6 dicembre 2016 Giuseppe Augello 1 Che cos e l Energia? Le forme dell Energia Il Principio di Conservazione dell Energia Stabilisce che esiste una
Principio di Conservazione dell Energia Giuseppe Augello 6 dicembre 2016 Giuseppe Augello 1 Che cos e l Energia? Le forme dell Energia Il Principio di Conservazione dell Energia Stabilisce che esiste una
Esercizi aprile Sommario Conservazione dell energia e urti a due corpi.
 Esercizi 2.04.8 3 aprile 208 Sommario Conservazione dell energia e urti a due corpi. Conservazione dell energia. Esercizio Il motore di un ascensore solleva con velocità costante la cabina contenente quattro
Esercizi 2.04.8 3 aprile 208 Sommario Conservazione dell energia e urti a due corpi. Conservazione dell energia. Esercizio Il motore di un ascensore solleva con velocità costante la cabina contenente quattro
5.4 Larghezza naturale di una riga
 5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
5.4 Larghezza naturale di una riga Un modello classico più soddisfacente del processo di emissione è il seguente. Si considera una carica elettrica puntiforme in moto armonico di pulsazione ω 0 ; la carica,
La meccanica relativistica
 La meccanica relativistica Una introduzione per le secondarie Feb 2015 / TFA Outline Il principio di relatività galileiano 1 Il principio di relatività galileiano 2 3 La dinamica classica Il principio
La meccanica relativistica Una introduzione per le secondarie Feb 2015 / TFA Outline Il principio di relatività galileiano 1 Il principio di relatività galileiano 2 3 La dinamica classica Il principio
Il cannone elettronico. Velocità = distanza / tempo
 Il cannone elettronico Velocità = distanza / tempo v = 2E m Vale solo per piccole v Velocità limite = c!! c 3 10 8 m/s Ma allora è tutta fatica sprecata? No, quello che conta è la Quantità di moto P =
Il cannone elettronico Velocità = distanza / tempo v = 2E m Vale solo per piccole v Velocità limite = c!! c 3 10 8 m/s Ma allora è tutta fatica sprecata? No, quello che conta è la Quantità di moto P =
Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ
 Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ 4.1 Grandezze fondamentali e derivate Come abbiamo già osservato la scelta di un Sistema di unità di misura è largamente arbitraria e dettata in gran parte da
Capitolo 4: CAMBIAMENTO DI SISTEMA DI UNITÀ 4.1 Grandezze fondamentali e derivate Come abbiamo già osservato la scelta di un Sistema di unità di misura è largamente arbitraria e dettata in gran parte da
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/02/2019
 Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
Soluzione prova scritta Fisica Generale I Ing. Elettronica e Telecomunicazioni 01/0/019 Esercizio 1 1) Sull uomo agiscono la forza di gravità, la reazione della scala e le sue forze muscolari, mentre sulla
produzione di particelle in laboratorio
 produzione di particelle in laboratorio In un urto tra due particelle, può essere prodotta una particella pesante a spese dell energia cinetica dello stato iniziale In questo modo possono essere prodotte
produzione di particelle in laboratorio In un urto tra due particelle, può essere prodotta una particella pesante a spese dell energia cinetica dello stato iniziale In questo modo possono essere prodotte
Docente: Alessandro Melchiorri
 Astronomia Lezione 26/11/2012 Docente: Alessandro Melchiorri e.mail:alessandro.melchiorri@roma1.infn.it Sito web per slides lezioni: oberon.roma1.infn.it:/alessandro/astro2012/ Le lezioni astronomia012_*.pdf
Astronomia Lezione 26/11/2012 Docente: Alessandro Melchiorri e.mail:alessandro.melchiorri@roma1.infn.it Sito web per slides lezioni: oberon.roma1.infn.it:/alessandro/astro2012/ Le lezioni astronomia012_*.pdf
Relativita speciale. A. Palano. Testo di riferimento: P.J. Nolan, Complementi di Fisica, fisica moderna, Zanichelli
 Relativita speciale A. Palano Testo di riferimento: P.J. Nolan, Complementi di Fisica, fisica moderna, Zanichelli Sistemi di riferimento in moto relativo. Moti relativi S: Assoluto, S : relativo, Moto
Relativita speciale A. Palano Testo di riferimento: P.J. Nolan, Complementi di Fisica, fisica moderna, Zanichelli Sistemi di riferimento in moto relativo. Moti relativi S: Assoluto, S : relativo, Moto
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 25 6.04.2018 Campo elettrico di una carica accelerata Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 25 6.04.2018 Campo elettrico di una carica accelerata Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica
Theory Italiano (Italy)
 Q3-1 Large Hadron Collider (10 punti) Prima di iniziare questo problema, leggi le istruzioni generali nella busta a parte. In questo problema è discussa la fisica dell acceleratore di particelle del CERN
Q3-1 Large Hadron Collider (10 punti) Prima di iniziare questo problema, leggi le istruzioni generali nella busta a parte. In questo problema è discussa la fisica dell acceleratore di particelle del CERN
Sistemi di più particelle
 Sistemi di più particelle Finora abbiamo considerato il modo di una singola particella. Che cosa succede in sistemi di molte particelle, o in un sistema non puntiforme? Scomponendo il sistema in N particelle
Sistemi di più particelle Finora abbiamo considerato il modo di una singola particella. Che cosa succede in sistemi di molte particelle, o in un sistema non puntiforme? Scomponendo il sistema in N particelle
Schema dell intervento didattico
 Massa ed energia Schema dell intervento didattico Crisi della cinematica classica Il valore della velocità della luce come velocità limite Espressione della energia cinetica in funzione della velocità
Massa ed energia Schema dell intervento didattico Crisi della cinematica classica Il valore della velocità della luce come velocità limite Espressione della energia cinetica in funzione della velocità
Dinamica relativistica Cenni di relatività generale Corso Mathesis Roma 2016 Prof. Sergio Savarino
 Dinamica relativistica Cenni di relatività generale Corso Mathesis Roma 2016 Prof. Sergio Savarino Dinamica relativistica Quantità di moto relativistica: Massa relativistica: (1+z) 3 =1+3z+3z 2 +z 3 se
Dinamica relativistica Cenni di relatività generale Corso Mathesis Roma 2016 Prof. Sergio Savarino Dinamica relativistica Quantità di moto relativistica: Massa relativistica: (1+z) 3 =1+3z+3z 2 +z 3 se
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Meccanica quantistica Mathesis 2016 Prof. S. Savarino
 Meccanica quantistica Mathesis 2016 Prof. S. Savarino Quanti Corpo nero: è un oggetto che assorbe tutta la radiazione senza rifletterla. Come una corda legata agli estremi può produrre onde stazionarie
Meccanica quantistica Mathesis 2016 Prof. S. Savarino Quanti Corpo nero: è un oggetto che assorbe tutta la radiazione senza rifletterla. Come una corda legata agli estremi può produrre onde stazionarie
(d) mostrare che l energia meccanica si conserva; (e) utilizzando la conservazione dell energia calcolare l altezza massima dal suolo;
 1 Esercizio Un sasso di massa m.5 Kg viene lanciato dalla cima di una torre alta h 2 m con velocità iniziale di modulo v 12 m/s, ad un angolo ϕ 6 o rispetto all orizzontale. La torre si trova in prossimità
1 Esercizio Un sasso di massa m.5 Kg viene lanciato dalla cima di una torre alta h 2 m con velocità iniziale di modulo v 12 m/s, ad un angolo ϕ 6 o rispetto all orizzontale. La torre si trova in prossimità
dilatazione dei tempi
 dilatazione dei tempi un orologio segna il tempo in base al tempo impiegato da un raggio di luce per andare avanti e indietro dalla sorgente luminosa al ricevitore l orologio (verde) segna un tempo quando
dilatazione dei tempi un orologio segna il tempo in base al tempo impiegato da un raggio di luce per andare avanti e indietro dalla sorgente luminosa al ricevitore l orologio (verde) segna un tempo quando
TEORIA DELLA RELATIVITA RISTRETTA
 TEORIA DELLA RELATIVITA RISTRETTA EVOLUZIONE DELLE TEORIE FISICHE Meccanica Classica Principio di Relatività Galileiano Meccanica Newtoniana Gravitazione (Newton) Costante Universale G = 6,67*10^-11Nm^2/Kg^2
TEORIA DELLA RELATIVITA RISTRETTA EVOLUZIONE DELLE TEORIE FISICHE Meccanica Classica Principio di Relatività Galileiano Meccanica Newtoniana Gravitazione (Newton) Costante Universale G = 6,67*10^-11Nm^2/Kg^2
Modelli atomici Modello atomico di Rutheford Per t s d u i diare la t s rutt ttura t a omica Ruth th f or (
 Modello atomico di Rutheford Per studiare la struttura tt atomica Rutherford (1871-1937) 1937) nel 1910 bombardòb una lamina d oro con particelle a (cioè atomi di elio) Rutherford suppose che gli atomi
Modello atomico di Rutheford Per studiare la struttura tt atomica Rutherford (1871-1937) 1937) nel 1910 bombardòb una lamina d oro con particelle a (cioè atomi di elio) Rutherford suppose che gli atomi
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 8. Generalizziamo, considerando due particelle interagenti.
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Appunti di Relatività Ristretta
 Appunti di Relatività Ristretta (per il corso di Elementi di Fisica Nucleare e Subnucleare 2007/08) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di Relatività Ristretta (per il corso di Elementi di Fisica Nucleare e Subnucleare 2007/08) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
ELENCO ANALITICO DEGLI ARGOMENTI
 PROGRAMMA PER ESAMI DI IDONEITÀ ALLA CLASSE II FISICA dipartimento e contiene gli argomenti essenziali per l accesso al II anno di corso. INTRODUZIONE ALLA FISICA: GRANDEZZE E MISURE Metodo scientifico,
PROGRAMMA PER ESAMI DI IDONEITÀ ALLA CLASSE II FISICA dipartimento e contiene gli argomenti essenziali per l accesso al II anno di corso. INTRODUZIONE ALLA FISICA: GRANDEZZE E MISURE Metodo scientifico,
Radioattività. 1. Massa dei nuclei. 2. Decadimenti nucleari. 3. Legge del decadimento XVI - 0. A. Contin - Fisica Generale Avanzata
 Radioattività 1. Massa dei nuclei 2. Decadimenti nucleari 3. Legge del decadimento XVI - 0 Nucleoni Protoni e neutroni sono chiamati, indifferentemente, nucleoni. Il numero di protoni (e quindi di elettroni
Radioattività 1. Massa dei nuclei 2. Decadimenti nucleari 3. Legge del decadimento XVI - 0 Nucleoni Protoni e neutroni sono chiamati, indifferentemente, nucleoni. Il numero di protoni (e quindi di elettroni
19. Le trasformazioni di coordinate spazio-temporali nella teoria della relatività ristretta
 19. Le trasformazioni di coordinate spazio-temporali nella teoria della relatività ristretta 1 Le trasformazioni di Galileo Consideriamo per semplicità un moto unidimensionale. Come abbiamo più volte sottolineato,
19. Le trasformazioni di coordinate spazio-temporali nella teoria della relatività ristretta 1 Le trasformazioni di Galileo Consideriamo per semplicità un moto unidimensionale. Come abbiamo più volte sottolineato,
1. La velocità limite
 1. La velocità limite Abbiamo più volte accennato al fatto che la luce rappresenta la velocità limite per la propagazione delle interazioni. Sulla base di questo abbiamo, per esempio, proceduto a classificare
1. La velocità limite Abbiamo più volte accennato al fatto che la luce rappresenta la velocità limite per la propagazione delle interazioni. Sulla base di questo abbiamo, per esempio, proceduto a classificare
UNIVERSITA DEGLI STUDI DI GENOVA SCUOLA POLITECNICA FISICA GENERALE I
 FISICA GENERALE I - Sede di Spezia Prova A del 11/01/2016 ME 1 Un ragno di massa m R = 5.0 g usa il proprio filo come una liana (lunghezza L =10 cm). Partendo da fermo con il filo inclinato di un angolo
FISICA GENERALE I - Sede di Spezia Prova A del 11/01/2016 ME 1 Un ragno di massa m R = 5.0 g usa il proprio filo come una liana (lunghezza L =10 cm). Partendo da fermo con il filo inclinato di un angolo
Relatività. June 5, Trasformazioni di Galileo e di Lorentz
 Relatività June 5, 2016 1 Trasformazioni di Lorentz 1.1 Trasformazioni di Galileo e di Lorentz a Si scriva la matrice Λ (y) che descrive un boost di Lorentz lungo l asse y. b Si scrivano le matrici G (x)
Relatività June 5, 2016 1 Trasformazioni di Lorentz 1.1 Trasformazioni di Galileo e di Lorentz a Si scriva la matrice Λ (y) che descrive un boost di Lorentz lungo l asse y. b Si scrivano le matrici G (x)
Nome Cognome Numero di matricola Coordinata posizione
 Nome Cognome Numero di matricola Coordinata posizione Terzo compito di Fisica Generale + Esercitazioni, a.a. 07-08 4 Settembre 08 ===================================================================== Premesse
Nome Cognome Numero di matricola Coordinata posizione Terzo compito di Fisica Generale + Esercitazioni, a.a. 07-08 4 Settembre 08 ===================================================================== Premesse
n(z) = n(0) e m gz/k B T ; (1)
 Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Corso di Introduzione alla Fisica Quantistica (f) Prova scritta 4 Luglio 008 - (tre ore a disposizione) [sufficienza con punti 8 circa di cui almeno 4 dagli esercizi nn. 3 e/o 4] [i bonus possono essere
Le trasformazioni di Lorentz
 Le trasformazioni di Lorentz NASA, STS-41B 1 TRASFORMAZIONI DI GALILEO Il principio di relatività è stato enunciato per la prima volta da Galileo Galilei nel libro Dialogo sopra i due massimi sistemi del
Le trasformazioni di Lorentz NASA, STS-41B 1 TRASFORMAZIONI DI GALILEO Il principio di relatività è stato enunciato per la prima volta da Galileo Galilei nel libro Dialogo sopra i due massimi sistemi del
Forze conservative. Conservazione dell energia. Sistemi a molti corpi 1 / 37
 Forze conservative Il nome forze conservative deriva dal fatto che le forze che appartengono a questa categoria sono tali da conservare l energia. Una forza è conservativa se il lavoro da essa compiuto
Forze conservative Il nome forze conservative deriva dal fatto che le forze che appartengono a questa categoria sono tali da conservare l energia. Una forza è conservativa se il lavoro da essa compiuto
FAM. T 1) α ν. (e α ν T 1) 2. (con l ipotesi ν > 0) si ottiene
 Serie 42: Soluzioni FAM C. Ferrari Esercizio 1 Corpo nero 1. Abbiamo: Sole λ max = 500nm - spettro visibile (giallo); Sirio B λ max = 290nm - ultravioletto; corpo umano λ max = 9300nm - infrarosso. 2.
Serie 42: Soluzioni FAM C. Ferrari Esercizio 1 Corpo nero 1. Abbiamo: Sole λ max = 500nm - spettro visibile (giallo); Sirio B λ max = 290nm - ultravioletto; corpo umano λ max = 9300nm - infrarosso. 2.
FISICA. Questi problemi si risolvono utilizzando la seconda legge di Newton F = m a che può scriversi, utilizzando le intensità. F = ma.
 Serie 9: Soluzioni FISICA I liceo Esercizio 1 Seconda legge di Newton Questi problemi si risolvono utilizzando la seconda legge di Newton F = m a che può scriversi, utilizzando le intensità Ricorda che
Serie 9: Soluzioni FISICA I liceo Esercizio 1 Seconda legge di Newton Questi problemi si risolvono utilizzando la seconda legge di Newton F = m a che può scriversi, utilizzando le intensità Ricorda che
Il linguaggio della relatività: le geometrie non euclidee
 Il linguaggio della relatività: le geometrie non euclidee Luca Lussardi Università Cattolica del Sacro Cuore Einstein 1916-2016 Università degli Studi di Brescia 6 Aprile 2016 Non sono certo che la geometria
Il linguaggio della relatività: le geometrie non euclidee Luca Lussardi Università Cattolica del Sacro Cuore Einstein 1916-2016 Università degli Studi di Brescia 6 Aprile 2016 Non sono certo che la geometria
ATOMI E PARTICELLE SUBATOMICHE
 ATOMI E PARTICELLE SUBATOMICHE ELETTRICITÀ DELL ATOMO ESISTONO DUE TIPI DI CARICHE ELETTRICHE, DENOMINATE CONVENZIONALMENTE NEGATIVA E POSITIVA CARICHE DI SEGNO UGUALE SI RESPINGONO, MENTRE CARICHE DI
ATOMI E PARTICELLE SUBATOMICHE ELETTRICITÀ DELL ATOMO ESISTONO DUE TIPI DI CARICHE ELETTRICHE, DENOMINATE CONVENZIONALMENTE NEGATIVA E POSITIVA CARICHE DI SEGNO UGUALE SI RESPINGONO, MENTRE CARICHE DI
Capitolo 12. Moto oscillatorio
 Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
Moto oscillatorio INTRODUZIONE Quando la forza che agisce su un corpo è proporzionale al suo spostamento dalla posizione di equilibrio ne risulta un particolare tipo di moto. Se la forza agisce sempre
4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi stato fondamentale stati eccitati
 4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi Accanto allo spettro continuo che i corpi emettono in ragione del loro stato termico, si osservano spettri discreti che sono caratteristici
4. Lo spettro discreto: emissione e assorbimento di luce da parte di atomi Accanto allo spettro continuo che i corpi emettono in ragione del loro stato termico, si osservano spettri discreti che sono caratteristici
Quantità di moto. p=m v
 Quantità di moto Come l'energia, ha una legge di conservazione che semplifica lo studio dei problemi Ha più moto un treno che si muove a 20 Km/h o una lepre alla stessa velocità? Ha piu' moto una lepre
Quantità di moto Come l'energia, ha una legge di conservazione che semplifica lo studio dei problemi Ha più moto un treno che si muove a 20 Km/h o una lepre alla stessa velocità? Ha piu' moto una lepre
La Teoria della Relatività Ristretta. Prof. Michele Barcellona
 La Teoria della Relatività Ristretta Prof. Michele Barcellona I Postulati della Teoria della Relatività ristretta Per risolvere le contraddizioni tra Meccanica ed Elettromagnetismo Einstein propose una
La Teoria della Relatività Ristretta Prof. Michele Barcellona I Postulati della Teoria della Relatività ristretta Per risolvere le contraddizioni tra Meccanica ed Elettromagnetismo Einstein propose una
Emissione α. La sua carica elettrica è pari a +2e La sua massa a riposo è circa 7x10-27 kg.
 Reazioni nucleari Un nucleo instabile può raggiungere una nuova condizione di stabilità attraverso una serie di decadimenti con emissione di particelle α, β, γ o di frammenti nucleari (fissione). Emissione
Reazioni nucleari Un nucleo instabile può raggiungere una nuova condizione di stabilità attraverso una serie di decadimenti con emissione di particelle α, β, γ o di frammenti nucleari (fissione). Emissione
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
23 maggio /17-FIS-5G-2-3-U QUESTIONARIO
 Secondo il modello formulato da Thomson l atomo B Gran parte delle particelle viene deviata dal foglio d oro C Le particelle alfa sono attratte dalla lamina d oro D Le particelle alfa non riescono ad attraversare
Secondo il modello formulato da Thomson l atomo B Gran parte delle particelle viene deviata dal foglio d oro C Le particelle alfa sono attratte dalla lamina d oro D Le particelle alfa non riescono ad attraversare
FISICA delle APPARECCHIATURE per RADIOTERAPIA
 Anno Accademico 2012-2013 Corso di Laurea in Tecniche Sanitarie di Radiologia Medica per Immagini e Radioterapia FISICA delle APPARECCHIATURE per RADIOTERAPIA Marta Ruspa 20.01.13 M. Ruspa 1 ONDE ELETTROMAGNETICHE
Anno Accademico 2012-2013 Corso di Laurea in Tecniche Sanitarie di Radiologia Medica per Immagini e Radioterapia FISICA delle APPARECCHIATURE per RADIOTERAPIA Marta Ruspa 20.01.13 M. Ruspa 1 ONDE ELETTROMAGNETICHE
Lezione XVI Impulso, forze impulsive e urti
 Lezione XVI Impulso, forze impulsive e urti 1 Impulso di una forza Sempre nell ambito della dinamica del punto materiale, dimostriamo il semplice teorema dell impulso, che discende immediatamente dalla
Lezione XVI Impulso, forze impulsive e urti 1 Impulso di una forza Sempre nell ambito della dinamica del punto materiale, dimostriamo il semplice teorema dell impulso, che discende immediatamente dalla
Se prendiamo in considerazione una sfera rotante su se stessa con velocità periferica C p
 Effetti giroscopici su una sfera rotante, teoria dell effetto Magnus, massa longitudinale e massa trasversale, Abbiamo visto che la presenza di materia può essere rilevata ( e dunque la materia esiste)
Effetti giroscopici su una sfera rotante, teoria dell effetto Magnus, massa longitudinale e massa trasversale, Abbiamo visto che la presenza di materia può essere rilevata ( e dunque la materia esiste)
Energia-quantita' di moto
 Energia-quantita' di moto quadri-vettore quantita' di moto E/c p=mu=m γ(c, v x, v y, v z ) cp = E = m c2 = Energia cinetica + Energia a riposo px Invariante: (P0)2 - P 2 = (m c)2 E R =m c 2 xxx Energia
Energia-quantita' di moto quadri-vettore quantita' di moto E/c p=mu=m γ(c, v x, v y, v z ) cp = E = m c2 = Energia cinetica + Energia a riposo px Invariante: (P0)2 - P 2 = (m c)2 E R =m c 2 xxx Energia
Concorso per l ammissione al Dottorato in Fisica AA XXVI ciclo (D.R. 552) Prova A
 Concorso per l ammissione al Dottorato in Fisica AA 2010-2011 - XXVI ciclo (D.R. 552) Prova A Si svolga a scelta uno dei tre temi (in non più di 3 facciate) e si risolvano due dei cinque esercizi proposti
Concorso per l ammissione al Dottorato in Fisica AA 2010-2011 - XXVI ciclo (D.R. 552) Prova A Si svolga a scelta uno dei tre temi (in non più di 3 facciate) e si risolvano due dei cinque esercizi proposti
FISICA. MECCANICA: Principio conservazione quantità di moto. Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica
 FISICA MECCANICA: Principio conservazione quantità di moto Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LA QUANTITA DI MOTO QUANTITA DI MOTO Consideriamo un corpo di massa m che si
FISICA MECCANICA: Principio conservazione quantità di moto Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica LA QUANTITA DI MOTO QUANTITA DI MOTO Consideriamo un corpo di massa m che si
Le leggi della meccanica
 Le leggi della meccanica ed il punto materiale Flavio DINAMICA DEL CORPO RIGIDO 1 Il I principio Il moto naturale di un punto materiale è rettilineo e uniforme quindi non circolare (le sfere celesti di
Le leggi della meccanica ed il punto materiale Flavio DINAMICA DEL CORPO RIGIDO 1 Il I principio Il moto naturale di un punto materiale è rettilineo e uniforme quindi non circolare (le sfere celesti di
La quantità di moto. Il masso ha più quantità di moto della persona in fuga.
 La quantità di moto Il masso ha più quantità di moto della persona in fuga. La quantità di moto La quantità di moto: esprime l inerzia nel movimento, cioè la difficoltà di fermare un oggetto in movimento
La quantità di moto Il masso ha più quantità di moto della persona in fuga. La quantità di moto La quantità di moto: esprime l inerzia nel movimento, cioè la difficoltà di fermare un oggetto in movimento
Fisica Moderna Torino, 31/01/2013. Dott. Morrone Davide Scienze M.F.N. - Unito
 Fisica Moderna Torino, 31/01/2013 Dott. Morrone Davide Scienze M.F.N. - Unito Diffrazione 1 FENDITURA 2 FENDITURE RETICOLO = N fenditure regolarmente spaziate Le curve dei massimi si stringono e diventano
Fisica Moderna Torino, 31/01/2013 Dott. Morrone Davide Scienze M.F.N. - Unito Diffrazione 1 FENDITURA 2 FENDITURE RETICOLO = N fenditure regolarmente spaziate Le curve dei massimi si stringono e diventano
Il moto ed i sistemi di riferimento
 Consideriamo il moto di un punto materiale riferito ad un sistema cartesiano S... che chiameremo fisso o assoluto e ad un sistema S che chiameremo mobile o relativo Il sistema S si può muovere perché si
Consideriamo il moto di un punto materiale riferito ad un sistema cartesiano S... che chiameremo fisso o assoluto e ad un sistema S che chiameremo mobile o relativo Il sistema S si può muovere perché si
LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA
 LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA I PROBLEMI DEL MODELLO PLANETARIO F Secondo Rutherford l elettrone si muoverebbe sulla sua orbita in equilibrio tra la forza elettrica di attrazione del
LE ONDE E I FONDAMENTI DELLA TEORIA QUANTISTICA I PROBLEMI DEL MODELLO PLANETARIO F Secondo Rutherford l elettrone si muoverebbe sulla sua orbita in equilibrio tra la forza elettrica di attrazione del
Quantità di moto e urti
 INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 14 15 OTTOBRE 2008 Quantità di moto e urti 1 Il lavoro La quantità di moto di una particella di massa m che si muove con velocità
INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu LEZIONE DEL 14 15 OTTOBRE 2008 Quantità di moto e urti 1 Il lavoro La quantità di moto di una particella di massa m che si muove con velocità
Meccanica dei sistemi di punti materiali
 Meccanica dei sistemi di punti materiali Centro di massa Conservazione della quantità di moto Teorema del momento angolare Conservazione del momento angolare Teoremi di König Urti Antonio Pierro @antonio_pierro_
Meccanica dei sistemi di punti materiali Centro di massa Conservazione della quantità di moto Teorema del momento angolare Conservazione del momento angolare Teoremi di König Urti Antonio Pierro @antonio_pierro_
Campi generati da cariche in movimento
 Campi generati da cariche in movimento (discussione qualitativa) Campo elettrico in diversi sistemi di riferimento inerziali Campo generato da una carica in moto rettilineo unif. Campo di una carica accelerata
Campi generati da cariche in movimento (discussione qualitativa) Campo elettrico in diversi sistemi di riferimento inerziali Campo generato da una carica in moto rettilineo unif. Campo di una carica accelerata
Cinematica in due o più dimensioni
 Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
Cinematica in due o più dimensioni Le grandezze cinematiche fondamentali: posizione, velocità, accelerazione, sono dei vettori nello spazio a due o tre dimensioni, dotati di modulo, direzione, verso. In
Carlo Cosmelli. La visione del mondo della Relatività e della Meccanica Quantistica
 La visione del mondo della Relatività e della Meccanica Quantistica Settimana 3 E= mc 2 e la Teoria della Relatività Generale Lezione 3.1 Carlo Cosmelli 1 c è veramente la velocità massima? Cosa fanno
La visione del mondo della Relatività e della Meccanica Quantistica Settimana 3 E= mc 2 e la Teoria della Relatività Generale Lezione 3.1 Carlo Cosmelli 1 c è veramente la velocità massima? Cosa fanno
Onde, Radiazione e Relativita
 Onde, Radiazione e Relativita XII Massa ed energia, forza e accelerazione 17/03/2009 E.Menichetti 1 Massa, impulso ed energia - I Relazione fra impulso, massa a riposo, en. cinetica: 2 2 4 2 2 E = m c
Onde, Radiazione e Relativita XII Massa ed energia, forza e accelerazione 17/03/2009 E.Menichetti 1 Massa, impulso ed energia - I Relazione fra impulso, massa a riposo, en. cinetica: 2 2 4 2 2 E = m c
I principi della dinamica come si insegnano e (soprattutto) cosa ci insegnano. mercoledì 4 febbraio 2015
 I principi della dinamica come si insegnano e (soprattutto) cosa ci insegnano 1 Perché sono così importanti i tre principi della dinamica? 2 e prima di tutto, cosa dicono i principi della dinamica? 3 Il
I principi della dinamica come si insegnano e (soprattutto) cosa ci insegnano 1 Perché sono così importanti i tre principi della dinamica? 2 e prima di tutto, cosa dicono i principi della dinamica? 3 Il
Poichési conserva l energia meccanica, il lavoro compiuto dal motore è pari alla energia potenziale accumulata all equilibrio:
 Meccanica 24 Aprile 2018 Problema 1 (1 punto) Un blocco di mass M=90 kg è attaccato tramite una molla di costante elastiìca K= 2 10 3 N/m, massa trascurabile e lunghezza a riposo nulla, a una fune inestensibile
Meccanica 24 Aprile 2018 Problema 1 (1 punto) Un blocco di mass M=90 kg è attaccato tramite una molla di costante elastiìca K= 2 10 3 N/m, massa trascurabile e lunghezza a riposo nulla, a una fune inestensibile
Unità didattica 10. Decima unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
 Unità didattica 10 Radioattività... 2 L atomo... 3 Emissione di raggi x... 4 Decadimenti nucleari. 6 Il decadimento alfa.... 7 Il decadimento beta... 8 Il decadimento gamma...... 9 Interazione dei fotoni
Unità didattica 10 Radioattività... 2 L atomo... 3 Emissione di raggi x... 4 Decadimenti nucleari. 6 Il decadimento alfa.... 7 Il decadimento beta... 8 Il decadimento gamma...... 9 Interazione dei fotoni
Meccanica del punto materiale
 Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Equazioni di Maxwell. (legge di Gauss per il campo elettrico) (legge di Gauss per il campo magnetico) C (legge di Faraday)
 Equazioni di Maxwell Φ S ( r E ) = Q ε 0 (legge di Gauss per il campo elettrico) Φ S ( r B ) = 0 (legge di Gauss per il campo magnetico) C l ( r Φ B ) = µ 0 ε S ( E r ) 0 + µ (legge di Ampère - Maxwell)
Equazioni di Maxwell Φ S ( r E ) = Q ε 0 (legge di Gauss per il campo elettrico) Φ S ( r B ) = 0 (legge di Gauss per il campo magnetico) C l ( r Φ B ) = µ 0 ε S ( E r ) 0 + µ (legge di Ampère - Maxwell)
SCUOLA GALILEIANA - CLASSE DI SCIENZE NATURALI PROVA DI AMMISSIONE A.A.: SOLUZIONE DELLA PROVA SCRITTA DI FISICA
 SCUOLA GALILEIANA - CLASSE DI SCIENZE NATURALI PROBLEMA 1. PROVA DI AMMISSIONE A.A.:2007-2008 SOLUZIONE DELLA PROVA SCRITTA DI FISICA a) da g = GM segue: M = gr2 R 2 G b) La forza centripeta che fa descrivere
SCUOLA GALILEIANA - CLASSE DI SCIENZE NATURALI PROBLEMA 1. PROVA DI AMMISSIONE A.A.:2007-2008 SOLUZIONE DELLA PROVA SCRITTA DI FISICA a) da g = GM segue: M = gr2 R 2 G b) La forza centripeta che fa descrivere
Un modello di studio. Gli urti tra palline
 QUANTITA DI MOTO Un modello di studio Gli urti tra palline Newton osservò che la velocità e la massa hanno un ruolo importante nel moto Quantità di Moto La quantità di moto di un corpo è il prodotto della
QUANTITA DI MOTO Un modello di studio Gli urti tra palline Newton osservò che la velocità e la massa hanno un ruolo importante nel moto Quantità di Moto La quantità di moto di un corpo è il prodotto della
Radiazioni ionizzanti
 Dipartimento di Fisica a.a. 2004/2005 Fisica Medica 2 Radiazioni ionizzanti 11/3/2005 Struttura atomica Atomo Nucleo Protone 10 10 m 10 14 m 10 15 m ev MeV GeV 3 3,0 0,3 0 0 0 Atomo Dimensioni lineari
Dipartimento di Fisica a.a. 2004/2005 Fisica Medica 2 Radiazioni ionizzanti 11/3/2005 Struttura atomica Atomo Nucleo Protone 10 10 m 10 14 m 10 15 m ev MeV GeV 3 3,0 0,3 0 0 0 Atomo Dimensioni lineari
Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli
 Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli Trasformazioni tra Sistemi di Riferimento Quantita di interesse in un esperimento: sezioni d urto, distribuzioni angolari, polarizzazioni. Confrontabili
Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli Trasformazioni tra Sistemi di Riferimento Quantita di interesse in un esperimento: sezioni d urto, distribuzioni angolari, polarizzazioni. Confrontabili
Il Nucleo. Dimensioni del nucleo dell'ordine di 10. m Il raggio nucleare R = R 0 -15
 Il Nucleo Nucleo e' costituito da nucleoni (protoni e neutroni). Mentre i neutroni liberi sono abbastanza instabili tendono a decadere in un protone ed un elettrone (t 1/2 circa 900 s), i protoni sono
Il Nucleo Nucleo e' costituito da nucleoni (protoni e neutroni). Mentre i neutroni liberi sono abbastanza instabili tendono a decadere in un protone ed un elettrone (t 1/2 circa 900 s), i protoni sono
Lezione n. 13. Radiazione elettromagnetica Il modello di Bohr Lo spettro dell atomo. di idrogeno. Antonino Polimeno 1
 Chimica Fisica Biotecnologie sanitarie Lezione n. 13 Radiazione elettromagnetica Il modello di Bohr Lo spettro dell atomo di idrogeno Antonino Polimeno 1 Radiazione elettromagnetica (1) - Rappresentazione
Chimica Fisica Biotecnologie sanitarie Lezione n. 13 Radiazione elettromagnetica Il modello di Bohr Lo spettro dell atomo di idrogeno Antonino Polimeno 1 Radiazione elettromagnetica (1) - Rappresentazione
Corso di laurea in Comunicazioni Digitali Compito di Fisica 26 Febbraio 2003
 Corso di laurea in Comunicazioni Digitali Compito di Fisica 26 Febbraio 2003 Nome: Matricola: Posizione: A 1) Nel piano cartesiano sono date due cariche puntiformi Q A = - 0.1 µc posta nel punto A(-1,0)
Corso di laurea in Comunicazioni Digitali Compito di Fisica 26 Febbraio 2003 Nome: Matricola: Posizione: A 1) Nel piano cartesiano sono date due cariche puntiformi Q A = - 0.1 µc posta nel punto A(-1,0)
Il semiconduttore è irradiato con fotoni a λ=620 nm, che vengono assorbiti in un processo a due particelle (elettroni e fotoni).
 Fotogenerazione -1 Si consideri un semiconduttore con banda di valenza (BV) e banda di conduzione (BC) date da E v =-A k 2 E c =E g +B k 2 Con A =10-19 ev m 2, B=5, Eg=1 ev. Il semiconduttore è irradiato
Fotogenerazione -1 Si consideri un semiconduttore con banda di valenza (BV) e banda di conduzione (BC) date da E v =-A k 2 E c =E g +B k 2 Con A =10-19 ev m 2, B=5, Eg=1 ev. Il semiconduttore è irradiato
V = qvb R. CICLOTRONE - Lawrence, 1932! B
 CICLOTRONE - Lawrence, 1932! B Ciclotrone nei Laboratori Nazionali INFN di Legnaro (PD) Ciclotrone: gli ioni accelerati effettuano traiettorie con raggio crescente => il campo magnetico occupa tutto lo
CICLOTRONE - Lawrence, 1932! B Ciclotrone nei Laboratori Nazionali INFN di Legnaro (PD) Ciclotrone: gli ioni accelerati effettuano traiettorie con raggio crescente => il campo magnetico occupa tutto lo
Fisica 1 Anno Accademico 2011/2012
 Matteo Luca Ruggiero DISAT@Politecnico di Torino Anno Accademico 2011/2012 (7 Maggio - 11 Maggio 2012) Sintesi Abbiamo introdotto riformulato il teorema dell energia cinetica in presenza di forze non conservative,
Matteo Luca Ruggiero DISAT@Politecnico di Torino Anno Accademico 2011/2012 (7 Maggio - 11 Maggio 2012) Sintesi Abbiamo introdotto riformulato il teorema dell energia cinetica in presenza di forze non conservative,
Capire la Fisica Livello intermedio.
 Capire la Fisica Livello intermedio. Quest opera è stata rilasciata con licenza Creative Commons ttribuzione - Non commerciale - Condividi allo stesso modo 3.0 Italia. Per leggere una copia della licenza
Capire la Fisica Livello intermedio. Quest opera è stata rilasciata con licenza Creative Commons ttribuzione - Non commerciale - Condividi allo stesso modo 3.0 Italia. Per leggere una copia della licenza
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni (Parte I):
 Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
Esame di Fisica per Ingegneria Elettronica e delle Telecomunicazioni Parte I: 06-07-06 Problema. Un punto si muove nel piano xy con equazioni xt = t 4t, yt = t 3t +. si calcolino le leggi orarie per le
La relatività generale. Lezioni d'autore
 La relatività generale Lezioni d'autore Il GPS (RaiScienze) VIDEO Einstein e la teoria della relativita (History Channel) VIDEO Einstein: dimostrazione della teoria generale della gravità (History Channel))
La relatività generale Lezioni d'autore Il GPS (RaiScienze) VIDEO Einstein e la teoria della relativita (History Channel) VIDEO Einstein: dimostrazione della teoria generale della gravità (History Channel))
IMPULSO E QUANTITÀ DI MOTO STA DLER DOCUMENTI T R AT T I O ISPIRATI DA L WEB
 IMPULSO E QUANTITÀ DI MOTO DI LUIGI BOSCAINO BIBLIOGRAFIA: I PROBLEMI DELLA FISICA - CUTNELL, JOHNSON, YOUNG, STA DLER DOCUMENTI T R AT T I O ISPIRATI DA L WEB L IMPULSO Il grafico a destra rappresenta
IMPULSO E QUANTITÀ DI MOTO DI LUIGI BOSCAINO BIBLIOGRAFIA: I PROBLEMI DELLA FISICA - CUTNELL, JOHNSON, YOUNG, STA DLER DOCUMENTI T R AT T I O ISPIRATI DA L WEB L IMPULSO Il grafico a destra rappresenta
25 gennaio 2013 Primo-Levi I pianeti del Sistema solare - introduzione
 25 gennaio 2013 Primo-Levi I pianeti del Sistema solare - introduzione Bedogni Roberto INAF Osservatorio Astronomico di Bologna http://www.bo.astro.it/~bedogni/primolevi/ email: roberto.bedogni@oabo.inaf.it
25 gennaio 2013 Primo-Levi I pianeti del Sistema solare - introduzione Bedogni Roberto INAF Osservatorio Astronomico di Bologna http://www.bo.astro.it/~bedogni/primolevi/ email: roberto.bedogni@oabo.inaf.it
Appunti di Relatività Ristretta
 Appunti di Relatività Ristretta Corso di Fisica 2 Prof. G. Carboni A.A. 2014-2015 1 Introduzione Postulati della relativita ristretta (Einstein, 1905) 1. Le leggi dell elettrodinamica, in particolare la
Appunti di Relatività Ristretta Corso di Fisica 2 Prof. G. Carboni A.A. 2014-2015 1 Introduzione Postulati della relativita ristretta (Einstein, 1905) 1. Le leggi dell elettrodinamica, in particolare la
