ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI. corso: Teoria dei Circuiti. docente: Stefano PASTORE. 1 Esempio di tableau dinamico (tempo e Laplace)
|
|
|
- Amando Di Pietro
- 6 anni fa
- Visualizzazioni
Transcript
1 ESEMPI DI ANALISI DI CIRCUITI DINAMICI LINEARI coro: Teoria dei Circuiti docente: Stefano PASTORE 1 Eempio di tableau dinamico (tempo e Laplace) 1.1 Dominio del tempo Conideriamo il eguente circuito dinamico in Fig. 1: Fig. 1: Circuito dinamico del I ordine. Il itema tableau completo del circuito è: Ai(t) v(t) A T e(t) ( M v M v d ) ( v(t) M i M i d ) i(t) h (t) dt dt, (1) dove b 3en 1 2. La matrice ridotta di incidenza è: [ 1 1 A, (2) 1 1 1
2 mentre le relazioni cotitutive ono: 1 1 d dt R 1 d dt C i 1 (t) i 2 (t) i 3 (t) v 1 (t) v 3 (t) v (t). (3) Se crivo eteamente le equazioni del tableau, ottengo un itema con una incognita in più ripetto al numero di equazioni. In queto eempio, l incognita è v 3 (t), la derivata della tenione (variabile di tato) dell unico elemento dinamico (condenatore). Il tableau completo è: R C 1 e 1 (t) e 2 (t) v 1 (t) v 3 (t) v 3 (t) i 1 (t) i 2 (t) i 3 (t) v (t). (4) Supponiamo che: R 1Ω, C 1µF e v (t) 1 V. Poo allora ridurre la matrice T direttamente con un metodo di eliminazione gauiana delle variabili fino ad ottenere un unica equazione in v 3 (t), v 3 (t) ev (t). Oppure, poo coniderare la derivata v 3 (t) un parametro, per cui poo crivere: e 1 (t) e 2 (t) v 1 (t) v 3 (t) i 1 (t) i 2 (t) i 3 (t) Invertendo la matrice quadrata rimanente, i ottiene: 1 e 1 (t) 1 1 e 2 (t) 1 1 v 1 (t) 1 1 v 3 (t) i 1 (t) 1 i 2 (t) 1 1 i 3 (t) v 3 (t). (5) v 3 (t) 2
3 Pertanto, trovo la eguente equazione in v 3 (t), v (t) (1V)e v 3 (t): v 3 (t). (6) 1 3 v 3 (t)v 3 (t) 1 (7) che, unitamente alle condizioni iniziali v 3 (t) v C (), rappreenta la pura evoluzione dinamica del circuito. Queta equazione viene chiamata equazione di tato del circuito, nella variabile di tato v 3 (t). La ua oluzione è: 1.2 Dominio di Laplace v 3 (t) [ (v 3 () 1) e 1 t 1 u(t). (8) Applicando la traformata di Laplace al circuito di Fig. 1, ottengo il eguente itema tableau: AI() V() A T E(), (9) (M v M v ) V()(M i M i ) V() H ()H () dove H () tiene conto delle condizioni iniziali degli elementi dinamici. Nel notro cao particolare, i ha: 1 V 1 () 1 V 2 () 1 6 V 3 () 1 1 I 1 () I 2 () I 3 () Il tableau completo T() è: E 1 () E 2 () V 1 () V 2 () V 3 () I 1 () I 2 () I 3 () v 3 () 1 6 v 3 (). (1). (11) 3
4 La oluzione del itema è ottenuta invertendo la matrice T(): E 1 () E 2 () V 1 () V 2 () V 3 () T 1 (), (12) I 1 () 1 1 I 2 () I 3 () 1 6 v 3 () dove la matrice T 1 () è:
5 La tenione V 3 () è uguale allora a: V 3 () v 3 () (13) v 3() 1 v 3() Antitraformando, i ottiene: v 3 (t) [ (v 3 () 1) e 1 t 1 u(t) (14) che è la tea epreione (ovviamente!) trovata operando nel dominio del tempo (vedi eq. (8)). 5
6 2 Circuito del II ordine nel tempo (p k R) Conideriamo il eguente circuito lineare, tempo-invariante, dinamico e autonomo, dal momento che l unica orgente indipendente (di tenione) è cotante (Fig. 2): Fig. 2: Circuito dinamico del II ordine. Notiamo che è un circuito del econdo ordine, dove le due candidate a diventare variabili di tato, le tenioni ui condenatori, ono manifetatamente indipendenti. L equazione di tato del circuito dovrà aumere la forma: ẋ(t) Ax(t)Bū (15) dove x(t) R n, A è una matrice di dimenione [n n, B è un vettore [n k eū èun vettore [k 1 che rappreenta le k orgenti del circuito. In queto cao n 2ek 1, mentre il vettore di tato è: [ v1 (t) x(t). (16) Per la crittura dell equazione di tato, uiamo il metodo dei Componenti Complementari. A tal fine, conideriamo il doppio bipolo adinamico (reitivo) di Fig. 3. La rappreentazione eplicita del doppio bipolo adinamico, da adottare nel cao di due condenatori, è la rappreentazione controllata in tenione, eprea come: [ [ [ [ i1 g11 g 21 v1 i1 (17) i 2 g 12 g 22 v 2 i 2 Nel notro cao, con emplici calcoli i ottiene la eguente rappreentazione: [ [ [ [ i1 1/15 1/3 v1 1/3 1/3 1/15 1/3 i 2 v 2 (18) Ricordando che le relazioni cotitutive dei condenatori ono (con la convenzione nonnormale): i 1 C 1 v 1, i 2 C 2 v 2 (19) 6
7 Fig. 3: Doppio-bipolo adinamico aociato al circuito di Fig. 2. e otituendo le tee in (18), dopo aver eeguito qualche facile operazione, trovo le equazioni di tato rappreentate dalle eguenti matrici: [ [ 2/3 1/3 1 A, B ū 4 /3 1/3 2/ (2) /3 Vediamo ora di trovare la oluzione di queta equazione differenziale, con condizione iniziale data x(). Troviamo innanzi tutto gli autovalori e gli autovettori della matrice A. per far ciò, i deve riolvere l equazione: det[i A (21) I due autovalori ono: { /3. (22) Il primo autovettore detro deve oddifare all equazione: [ 1 I A x 1, (23) da cui i ottiene lo pazio lineare rappreentato da: [ 1 x 1. (24) 1 Il econdo autovettore è ottenuto dall equazione: [ 2 I A x 2, (25) da cui i ottiene lo pazio lineare rappreentato da: [ 1 x 2. (26) 1 7
8 Sapendo che: A SA diag S 1 [ [ 1 1/3 [ 1/2 1/2 1/2 1/2, (27) eche: [ e e A t 1 t S e 1/3 t S 1, (28) i trova l epreione dell eponenziale della matrice A: [ ( e 1 t e 1/3 t) ( /2 e 1 t e 1/3 t) /2 e A t ( e 1 t e 1/3 t) ( /2 e 1 t e 1/3 t). (29) /2 Poiamo ora coniderare la preenza della orgente cotante di tenione. La oluzione particolare, o imilare, o di regime, i trova facilmente coniderando degli aperti i condenatori. Le tenioni che vedo alle porte del doppio-bipolo adinamico ono: x p (t) [ v p 1(t) v p 2(t) La oluzione generale è allora: [ ([ v1 (t) x(t) e A t v1 () v 2 () [ 1 1. (3) [ 1 1 ) [ 1 1. (31) Un altro metodo, per trovare la oluzione generale, conite nell eprimere il vettore di tato come combinazione lineare peata degli autovettori e della oluzione particolare. Si ha quindi: [ [ [ v1 (t) 1 1 k 1 e 1 t k 1 2 e 1/3 t 1 [ 1 1, (32) dove le cotante k 1,k 2 Rdipendono dalle condizioni iniziali. Pertanto, per t,i deve riolvere il eguente itema in k 1 e k 2 : { v1 () k 1 k 2 1 v 2 () k 1 k 2 1 k 1 v 1() v 2 () 2 k 2 v 1() v 2 () 2 2. (33) Come i vede con una veloce otituzione, e come deve eere, la oluzione trovata è identica alla precedente. 8
9 3 Circuito del II ordine nel tempo (p k C) Conideriamo il eguente circuito lineare, tempo-invariante, dinamico e autonomo, dal momento che le due orgenti indipendenti ono cotanti: Fig. 4: Circuito dinamico del II ordine. Notiamo che è un circuito del econdo ordine, dove le due candidate a diventare variabili di tato, la tenione ul condenatore e la corrente dell induttanza, ono manifetatamente indipendenti. L equazione di tato del circuito dovrà aumere la forma: ẋ(t) Ax(t)Bū (34) dove x(t) R n, A è una matrice di dimenione [n n, B è un vettore [n k eū èun vettore [k 1 che rappreenta le k orgenti del circuito. In queto cao n k 2, mentre il vettore di tato è: [ i1 (t) x(t). (35) Per la crittura dell equazione di tato, uiamo il metodo dei Componenti Complementari. A tal fine, conideriamo il doppio bipolo adinamico (reitivo) di Fig. 5. La rappreentazione eplicita del doppio bipolo adinamico, da adottare nel cao di un condenatore e di un induttore, è la rappreentazione ibrida, eprea come: [ [ [ [ v1 h11 h 21 i1 v1 (36) i 2 h 12 h 22 v 2 i 2 Nel notro cao, con emplici calcoli i ottiene la eguente rappreentazione: [ [ [ [ v1 9.9 i i 2 v 2 (37) Ricordando che le relazioni cotitutive dei condenatori ono (con la convenzione nonnormale): v 1 L 1 i 1, i 2 C 2 v 2 (38) 9
10 Fig. 5: Doppio-bipolo adinamico aociato al circuito di Fig. 4. e otituendo le tee in (37), dopo aver eeguito qualche facile operazione, trovo le equazioni di tato rappreentate dalle eguenti matrici: [ [ A, B ū. (39) Vediamo ora di trovare la oluzione di queta equazione differenziale, con condizione iniziale data x(). Troviamo innanzi tutto gli autovalori e gli autovettori della matrice A. per far ciò, i deve riolvere l equazione: I due autovalori complei coniugati ono: det[i A (4) { j j ( 1). (41) Il primo autovettore detro deve oddifare all equazione: [ 1 I A x 1, (42) da cui i ottiene lo pazio lineare rappreentato da: [ [.3.56j.32 e j2.96 x j.9995 e jπ/2. (43) Il econdo autovettore è ottenuto dall equazione: [ 2 I A x 2, (44) 1
11 da cui i ottiene lo pazio lineare coniugato rappreentato da: [ [.3.56j.32 e j2.96 x j.9995 e jπ/2 ( x 1). (45) Sapendo che: A SA diag S 1 [.32 e j e j e jπ/ e jπ/2 [ 14 28j [ e j j e j1.39, (46) eche: i trova l epreione di e A t : e A t e A t S [ e ( 1428j)t e ( 14 28j) t S 1, (47) [ 1.3 e 14t co(28t 2.96).32e 14t co(28t 1.57) e 14t co(28t 1.57).9995e 14t co(28t.18) Come i vede, il calcolo in forma chiua dell eponenziale di matrice è abbatanza lungo e laborioo in preenza di autovalori complei e coniugati. Poiamo ora coniderare la preenza della orgente cotante di tenione. La oluzione particolare, o imilare, o di regime, i trova facilmente applicando il principio di ovrappoizione degli effetti, dopo aver aperto il condenatore e cortocircuitata l induttanza. La corrente che vedo alla prima porta del doppio-bipolo adinamico e la tenione alla econda porta ono: x p (t) [ i p 1(t) v p 2(t) La oluzione generale è allora: [ ([ i1 (t) x(t) e A t i1 () v 2 () [ [ (48). (49) ) [ (5) Un altro metodo più rapido, per trovare la oluzione generale, conite nell eprimere il vettore di tato come combinazione lineare peata degli autovettori e della oluzione 11
12 particolare. Si ha quindi: [ [ i1 (t).3.56j ke ( 1428j)t.9995j [ [.3.56j.145 k e ( 14 28j) t.9995j 9.45 [.32 e j2.96 } [ R {k e ( 1428j)t (51).9995e jπ/ [ [.64 co(28t 2.96 ϕk ).145 k e 14t, (52) co(28t 1.57 ϕ k ) 9.45 dove la cotante k k r jk i k e jϕ k dipende dalle condizioni iniziali. Pertanto, per t, i deve riolvere il eguente itema in k: { i1 () 2 R{k (.3.56j)}.145 v 2 () 2 R{k (.9995j)} (53) Si ottiene pertanto: { i1 ().6k r.11k i.145 v 2 () 1.999k i 9.45 da cui i ricavano il modulo e la fae della cotante k. k i 9.45 v 2() k r i 1().6ki.145.2, (54) 12
13 4 Circuito del II ordine con Laplace Conideriamo il eguente circuito lineare, tempo-invariante, dinamico e autonomo, dal momento che l unica orgente indipendente (di tenione) è cotante: Fig. 6: Circuito dinamico del II ordine. Traformiamo il circuito con Laplace etraendo le condizioni iniziali dai componenti dinamici, mettendo il valore di impedenza accanto a ogni componente (i componenti dinamici ono coniderati inizialmente carichi) e coniderando le traformate delle forme d onda delle orgenti indipendenti. Otteniamo il eguente circuito: Fig. 7: Circuito di Fig. 6 traformato con Laplace. Il circuito può eere ora riolto nel dominio della traformata di Laplace, crivendo 13
14 dunque un itema algebrico di equazioni nella variabile. Formalmente, ècomeefoe un circuito reitivo in continua. Scriviamo, quindi, un itema completo e indipendente di equazioni applicando il metodo nodale puro. Notiamo che tutti i componenti ono controllati in tenione, dal momento che ogni generatore di tenione ha in erie una impedenza. Il itema di 3 equazioni in 3 incognite è il eguente: V () V 1 () 1 V 1 () V () 1 V 2 () V () 1 V () 1/ 1 i L() V 1() L 1 V () V 2() 1 V 2() v C ()/ 1/c 1, (55) da cui i ottiene, eliminando V (): [ 2(15L1 ) V 1 () V 2 ()[ 1 1 L 1 3i L() [ V 1 () 1 L [ 1 11C2 V 2 () i L() C 2 v C () 1L 1 1. (56) Riolvendo il itema di 2 equazioni in 2 incognite, troviamo che: V 1 () 5 1 2i L() [ v C () i L () V 2 () 1 (15 )(1 2i L() [ v C () i L ()) ( ) 3i L() 1 Da V 1 () iricavalacorrentei L () nell induttanza carica:. (57) I L() V 1() L 51 2i L() [ v C () i L (). (58) ( ) Aggiungendo le condizioni iniziali, i ottiene infine: I L () I L ()i L() 5 1 2i L() [ v C () i L () ( ) i L(). (59) Da V 2 () i ricava direttamente la tenione ul condenatore carico: V C () V 2 () V C() 3i L() 1 (6) Notiamo che la tenione V C () ègià compreniva della tenione iniziale ul condenatore. Notiamo inoltre che non è conveniente procedere alla omma dei termini in I L () ev C () per ottenere un unica frazione, dal momento che dovremo poi procedere alla compoizione delle funzioni tee per l operazione di antitraformazione. 14
15 Ora poiamo antitraformare le due funzioni complee I L () ev C () per ottenere le relative funzioni nel dominio del tempo i L (t) ev C (t). Innanzi tutto, dobbiamo trovare i poli del denominatore di I L () ev C (). Si ha che: , (61) da cui, componendo I L () ev C () nella omma di frazioni parziali, i ottiene: I L () A B 25 C i L() }{{ 4 } I L () V C () A B 25 C 3i. (62) L() 1 }{{ 4 } V C () Applicando il metodo dei reidui, poiamo calcolare le cotanti A, B, C, A,B e C nel modo eguente: A lim I L() lim 51 2i L() [ v C () i L () (1 2i L ()) B lim 25 ( 25)I L() lim i L() [ v C () i L () ( 4) (1 2i L () 25 [ v C () i L ()) C lim 4 ( 4)I L() lim i L() [ v C () i L () ( 25).833 (1 2i L () 4 [ v C () i L ()) (63) 15
16 A lim V C() lim 1(15 )(1 2i L() [ v C () i L ()) (1 2i L ()) B lim 25 ( 25)V C() lim 25 1(15 )(1 2i L() [ v C () i L ()) ( 4) (1 2i L () 25 [ v C () i L ()) C lim 4 ( 4)V C() lim 4 1(15 )(1 2i L() [ v C () i L ()) ( 25) (1 2i L () 4 [ v C () i L ()) Le ripettive funzioni nel dominio del tempo ono infine: (64) i L (t) (A i L () Be 25t Ce 4t ) u(t) A (65) v C (t) (A 3i L () 1 B e 25t C e 4t ) u(t) V 16
Appunti ed esercitazioni di Microonde 2
 Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Appunti ed eercitazioni di Microonde Studio di una linea priva di perdite in regime impulivo di impedenza caratteritica =5Ω, chiua u di un carico R erie avente R==5Ω, =mh, =nf. Si aume come velocità di
Esercitazione 16 Novembre 2012 Circuiti dinamici del secondo ordine. t come riportato in figura.
 Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
Eercitazione Noembre ircuiti dinamici del econdo ordine ircuito L- erie Per quanto riguarda queto circuito, l eercizio egue la traccia della oluzione del compito d eame numero, reperibile in rete al olito
2. METODO DEGLI SPOSTAMENTI O EQUAZIONE DELLA LINEA ELASTICA, PER LA SOLUZIONE DI TRAVI IPERSTATICHE
 METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
METODO DEGLI SPOSTAMENTI CORSO DI PROGETTAZIONE STRUTTURALE B a.a. 00/0 Prof. G. Salerno Appunti elaborati da Arch. C. Provenzano. STRUTTURE IPERSTATICHE Una truttura i dice ipertatica o taticamente indeterminata
Introduzione. Esempio di costruzione one del contorno delle radici. Esempio... 4
 Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Appunti di Controlli Automatici 1 Capitolo 5 parte II Il contorno delle radici Introduzione... 1 Eempio di cotruzione del contorno delle radici... 1 Eempio... 4 Introduzione Il procedimento per la cotruzione
Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.
 Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 2 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
Teoria dei Sitemi Teoria dei Sitemi e del Controllo Compito A del 24 Giugno 2 Domande ed eercizi Nome: Nr. Mat. Firma: C.L.: Info. Elet. Telec.. Nel cao di itemi lineari continui tempo-varianti, la matrice
Semplificazioni di schemi a blocchi
 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento di blocchi
Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento di blocchi
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo
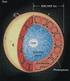 7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
7. La teoria dell' "età" dei neutroni. Il modello di rallentamento continuo Si è vito opra il trattamento generale dello cattering neutronico in mezzi infiniti. Ora conidereremo il cao della ditribuzione
Esercizi: circuiti dinamici con generatori costanti
 ezione Esercizi: circuiti dinamici con generatori costanti ezione n. Esercizi: circuiti dinamici con generatori costanti. Esercizi con circuiti del I ordine in transitorio con generatori costanti. ircuiti..
ezione Esercizi: circuiti dinamici con generatori costanti ezione n. Esercizi: circuiti dinamici con generatori costanti. Esercizi con circuiti del I ordine in transitorio con generatori costanti. ircuiti..
16. Onde elastiche. m s
 1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
1 Catena di ocillatori 16. Onde elatiche Vogliamo dicutere il fenomeno della propagazione ondulatoria in un mezzo elatico. A tale copo conideriamo un inieme di punti materiali dipoti lungo una retta, ad
Bode Diagram. 1.2 Determinare il valore del guadagno del sistema. Disegnare gli zeri ed i poli nel piano complesso.
 5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
5 Luglio 3 econda prova Sia dato un itema dinamico con funzione di traferimento G(), i cui diagrammi di Bode, del modulo e della fae, ono di eguito rappreentati: 6 Bode Diagram Phae (deg) Magnitude (db)
Capitolo. Semplificazioni di schemi a blocchi. 4.1 Blocchi in cascata. 4.2 Blocchi in parallelo. 4.3 Blocchi in catena chiusa (reazione negativa)
 Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
Capitolo 4 Semplificazioni di chemi a blocchi 4. Blocchi in cacata 4. Blocchi in parallelo 4.3 Blocchi in catena chiua (reazione negativa) 4.4 Blocchi in catena chiua (reazione poitiva) 4.5 Spotamento
Progetto di reti correttrici e controllori PID e traduzione nel discreto con il metodo di emulazione
 Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
Progetto di reti correttrici e controllori PID e traduione nel dicreto con il metodo di emulaione Eerciio. Si conideri lo chema di controllo rappreentato in figura dove P () = con a = 40. a + r(t) + S
Controllo di Azionamenti Elettrici. Lezione n 13
 Controllo di Azionamenti Elettrici Lezione n 1 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di Palermo CTROLLO DIRETTO DI COPPIA DI AZIAMENTI C MOTORE IN CORRENTE
Controllo di Azionamenti Elettrici Lezione n 1 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di Palermo CTROLLO DIRETTO DI COPPIA DI AZIAMENTI C MOTORE IN CORRENTE
Esame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A
 Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
Eame di Fondamenti di Automatica Ingegneria Elettronica Day Month Year Compito A A Cognome: Nome: Matricola: Mail: 1. Dato il itema di controllo raffigurato, con C( K c 2 ; P 1 1( ( + 4 ; P 2 ( ( + 1 (
I.T.I.S. TRASFORMATA DI LAPLACE DIAGRAMMI DI BODE
 I.T.I.S. APPUNTI DI ELETTRONICA TRASFORMATA DI LAPLACE E DIAGRAMMI DI BODE PREMESSA Per lo studio dei sistemi di controllo si utilizzano modelli matematici dinamici lineari. L analisi o il progetto di
I.T.I.S. APPUNTI DI ELETTRONICA TRASFORMATA DI LAPLACE E DIAGRAMMI DI BODE PREMESSA Per lo studio dei sistemi di controllo si utilizzano modelli matematici dinamici lineari. L analisi o il progetto di
1. Introduzione Il convertitore a semplice semionda Il sistema di controllo... 5
 . Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
. Introduzione... 2 2. Il convertitore a emplice emionda... 3 2. Il itema di controllo... 5 3. Il convertitore monofae nella configurazione a ponte... 7 4. Il fenomeno della commutazione... . Introduzione
Modellistica dinamica di sistemi fisici
 .. MODELLISTICA - Modellitica dinamica. Modellitica dinamica di itemi fiici Nella realtà fiica eitono vari ambiti energetici, per eempio: meccanico (tralazionale e rotazionale) elettrico-magnetico idraulico
.. MODELLISTICA - Modellitica dinamica. Modellitica dinamica di itemi fiici Nella realtà fiica eitono vari ambiti energetici, per eempio: meccanico (tralazionale e rotazionale) elettrico-magnetico idraulico
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008
 MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
MATEMATICA E STATISTICA CORSO A I COMPITINO (Tema 1) 28 Novembre 2008 SOLUZIONI 1. (4 punti) L indice di maa corporea (IMC) è ottenuto dal rapporto tra maa, eprea in Kg, e l altezza, eprea in m, al quadrato.
Corso di Fondamenti di Automatica A.A. 2015/16. Diagrammi di Bode
 1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
1 Coro di Fondamenti di Automatica A.A. 015/16 Diagrammi di Bode Prof. Carlo Coentino Dipartimento di Medicina Sperimentale e Clinica Univerità degli Studi Magna Graecia di Catanzaro tel: 0961-3694051
FUNZIONI DI TRASFERIMENTO
 FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
FUNZIONI DI TRASFERIMENTO Funzioni Di Traferimento La difficoltà maggiore nel trattare i modelli matematici di itemi dinamici lineari è dovuta al fatto che le equazioni delle leggi fiiche che decrivono
ESERCIZI SVOLTI di ANALISI DEI SISTEMI
 ESERCIZI SVOLTI di ANALISI DEI SISTEMI Davide Giglio DIST - Univerità di Genova Via Opera Pia, 3 645 - Genova, Italy Tel: +39 353748 Fax: +39 35354 Davide.Giglio@unige.it Queta raccolta di eercizi volti
ESERCIZI SVOLTI di ANALISI DEI SISTEMI Davide Giglio DIST - Univerità di Genova Via Opera Pia, 3 645 - Genova, Italy Tel: +39 353748 Fax: +39 35354 Davide.Giglio@unige.it Queta raccolta di eercizi volti
Interazioni Elettrodeboli. Lezione n. 9. Campo di Dirac Invarianza di Gauge Globale Campi interagenti
 Interazioni Elettrodeboli prof. Franceco Ragua Univerità di Milano Lezione n. 9 27.1.214 Campo di Dirac Invarianza di Gauge Globale Campi interagenti anno accademico 214-215 Quantizzazione del Campo di
Interazioni Elettrodeboli prof. Franceco Ragua Univerità di Milano Lezione n. 9 27.1.214 Campo di Dirac Invarianza di Gauge Globale Campi interagenti anno accademico 214-215 Quantizzazione del Campo di
Il motore sincrono a magneti permanenti (Motore Brushless)
 Il motore incrono a magneti permanenti (Motore Bruhle) Azionamenti e Controllo dei Sitemi meccanici Ing. F. L. Mapelli Il motore incrono a magneti permanenti (motore bruhle) Sull armatura eterna fia (tatore)
Il motore incrono a magneti permanenti (Motore Bruhle) Azionamenti e Controllo dei Sitemi meccanici Ing. F. L. Mapelli Il motore incrono a magneti permanenti (motore bruhle) Sull armatura eterna fia (tatore)
Sistemi e automazione
 3 Idee per il tuo futuro Paolo Guidi Stefano Mirandola Sitemi e automazione per Meccanica ed Energia Componenti e circuiti elettronici Complementi di teoria dei itemi Fondamenti di pneumatica e oleodinamica
3 Idee per il tuo futuro Paolo Guidi Stefano Mirandola Sitemi e automazione per Meccanica ed Energia Componenti e circuiti elettronici Complementi di teoria dei itemi Fondamenti di pneumatica e oleodinamica
1. Teorema di reciprocità
 1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
1. Teorema di reciprocità Conideriamo un mezzo in cui ono preenti le orgenti (J 1, M 1 ) che producono un campo (E 1, H 1 ) e le orgenti (J 2, M 2 ) che producono un campo (E 2, H 2 ). Determineremo una
Lezione XXI - 09/04/2003 ora 8:30-10:30 - Esercizi sulle perdite di carico - Originale di Berti Sara.
 Lezione XXI - 09/04/00 ora 8:0-10:0 - Eercizi ulle perdite di carico - Originale di Berti Sara. Eercizio 1 Calcolare la potenza di una pompa necearia a far correre il fluido attravero un tubo collegato
Lezione XXI - 09/04/00 ora 8:0-10:0 - Eercizi ulle perdite di carico - Originale di Berti Sara. Eercizio 1 Calcolare la potenza di una pompa necearia a far correre il fluido attravero un tubo collegato
TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
Circuito Simbolico. Trasformazione dei componenti
 Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
Circuito Simbolico Principio di bae E poibile applicare a tutte le leggi matematiche che regolano un circuito la traformata di Laplace, in modo da ottenere un nuovo circuito con delle proprietà differenti.
Trasformate di Laplace. Pietro ZECCA
 Traformate di Laplace Pietro ZECCA 23 novembre 24 2 Indice Traformate di Laplace. 5. Uneempioperiniziare... 5.2 Definizioneedeitenza... 7.3 ProprietàdelletraformatediLaplace....4 Latraformatainvera...
Traformate di Laplace Pietro ZECCA 23 novembre 24 2 Indice Traformate di Laplace. 5. Uneempioperiniziare... 5.2 Definizioneedeitenza... 7.3 ProprietàdelletraformatediLaplace....4 Latraformatainvera...
Problema n. 2. Soluzione
 Problema n. Un auto da cora A iaia u un piano orizzontale con elocità cotante = 69 km/ i 11 km/ j ripetto ad un oeratore olidale al uolo Ox. Qual è la elocità dell auto A miurata da un oeratore olidale
Problema n. Un auto da cora A iaia u un piano orizzontale con elocità cotante = 69 km/ i 11 km/ j ripetto ad un oeratore olidale al uolo Ox. Qual è la elocità dell auto A miurata da un oeratore olidale
a) Caso di rottura duttile con armatura compressa minore di quella tesa
 LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
LEZIONI N 39 E 40 FLESSIONE SEMPLICE: LA DOPPIA ARMATURA E LA SEZIONE A T LA VERIFICA DELLA SEZIONE INFLESSA CON DOPPIA ARMATURA a) Cao di rottura duttile con armatura comprea minore di quella tea Si può
Reti nel dominio del tempo. Lezione 7 1
 Reti nel dominio del tempo Lezione 7 1 Poli (o frequenze naturali) di una rete Lezione 7 2 Definizione 1/2 Il comportamento qualitativo di una rete dinamica dipende dalle sue frequenze naturali o poli
Reti nel dominio del tempo Lezione 7 1 Poli (o frequenze naturali) di una rete Lezione 7 2 Definizione 1/2 Il comportamento qualitativo di una rete dinamica dipende dalle sue frequenze naturali o poli
L equazione che descrive il moto del corpo è la seconda legge della dinamica
 Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
Eercizio ul piano inclinato La forza peo è data dalla formula p mg Allora e grandezze geometriche: poono eere critte utilizzando l angolo di inclinazione del piano oppure le Angolo di inclinazione orza
= 20 m/s in una guida verticale circolare. v A A
 Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Eercizio (tratto dal Problema 4.39 del Mazzoldi Un corpo di maa m = 00 Kg entra con elocità A licia di raggio = 5 m. Calcolare: = 0 m/ in una guida erticale circolare. la elocità nei punti B e C;. la reazione
Specifiche sulla banda passante negli amplificatori a microonde
 pecifiche ulla banda paante negli amplificatori a microonde Gli amplificatori a microonde trattano egnali modulati, il cui pettro ha in genere una etenione B molto minore della frequenza centrale f 0 (portante).
pecifiche ulla banda paante negli amplificatori a microonde Gli amplificatori a microonde trattano egnali modulati, il cui pettro ha in genere una etenione B molto minore della frequenza centrale f 0 (portante).
Pertanto la funzione di trasferimento complessiva in catena aperta (open-loop) W(S) del sistema di controllo sarà data da:
 M045 - EAME DI TATO 20 ) chema a blocchi e funzione di traferimento in catena aperta W() Il itema di controllo può eere chematizzato con il eguente chema a blocchi: dove: KP 3.2. V V Greg( ) KP (f.d.t.
M045 - EAME DI TATO 20 ) chema a blocchi e funzione di traferimento in catena aperta W() Il itema di controllo può eere chematizzato con il eguente chema a blocchi: dove: KP 3.2. V V Greg( ) KP (f.d.t.
Modello dinamico. Esercitazione 09:
 MODELLISTICA DELLE MACCHINE E DEGLI IMPIANTI ELETTRICI: Modello dinamico motore aincrono Eercitazione 09: Il motore aincrono c b b r c r a r a θ m Avvolgimento trifae ullo tatore Avvolgimento ul rotore
MODELLISTICA DELLE MACCHINE E DEGLI IMPIANTI ELETTRICI: Modello dinamico motore aincrono Eercitazione 09: Il motore aincrono c b b r c r a r a θ m Avvolgimento trifae ullo tatore Avvolgimento ul rotore
Calcolo della tensione ammissibile Dovendo essere il grado di sicurezza non inferiore a 3 si ricava che il coefficiente di sicurezza γ è 3 per cui:
 Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
Il recipiente diegnato in figura ha una configurazione cilindrica avente diametro interno D = 000 mm è chiuo con fondi emiferici, eo è itemato u due elle A e B pote ad una ditanza L AB = 7000 mm e fuoriece
La trasformata di Fourier in Ottica
 Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
Edoardo Milotti 5/11/2007 La traformata di Fourier in Ottica Queta nota contiene una breviima introduzione alle traformate di Fourier in Ottica 1. Il principio di Huygen Il principio di Huygen afferma
Ø Le funi sono dispositivi che permettono di trasmettere l azione di una forza applicata in un dato punto ad un punto diverso.
 Tenione Ø Le funi ono dipoitivi che permettono di tramettere l azione di una forza applicata in un dato punto ad un punto divero. Ø La fune viene coniderata inetenibile e priva di maa ed il modulo della
Tenione Ø Le funi ono dipoitivi che permettono di tramettere l azione di una forza applicata in un dato punto ad un punto divero. Ø La fune viene coniderata inetenibile e priva di maa ed il modulo della
Ing. Mariagrazia Dotoli Controlli Automatici NO (9 CFU) Antitrasformata di Laplace PROCEDIMENTI DI ANTITRASFORMAZIONE
 PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
PROCEDIMENTI DI ANTITRASFORMAZIONE L'operazione di paaggio invero dal dominio della frequenza complea al dominio del tempo F() f(t) è detta antitraformata o traformazione invera di Laplace. Data una funzione
F = 150 N F 1 =? = 3,1 s. 3,2
 ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZI SVOLTI : Principi di Newton Lavoro Energia Prof.. Marletta ITC Zanon - Udine ESERCIZIO (): Una caa di 30 kg viene tirata con una corda che forma un angolo di 50 col pavimento u una uperficie licia.
ESERCIZIO 1 L/2 C.R. D
 SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
SRIZIO Il itema di corpi rigidi in figura è oggetto ad uno potamento impreo (cedimento), in direzione verticale e vero il bao, in corripondenza del vincolo in. Si vuole determinare la nuova configurazione
Sali poco solubili e ph
 Sali poco olubili e ph Il catione o l anione di un ale poco olubile poono eere a loro volta un acido o una bae debole. Di coneguenza le condizioni di ph della oluzione poono influenzarne la olubilità,
Sali poco olubili e ph Il catione o l anione di un ale poco olubile poono eere a loro volta un acido o una bae debole. Di coneguenza le condizioni di ph della oluzione poono influenzarne la olubilità,
Variabili Gaussiane. Verifiche sforzo resistenza
 Variabili Gauiane e le ditribuzioni di orzo () e di reitenza () ono gauiane o normali, allora i può calcolare acilmente il valore della probabilità di rottura P dell oggetto in eame (o la ua aidabilità).
Variabili Gauiane e le ditribuzioni di orzo () e di reitenza () ono gauiane o normali, allora i può calcolare acilmente il valore della probabilità di rottura P dell oggetto in eame (o la ua aidabilità).
Q Flusso di calore (Joule m -2 s -1 )
 Conduzione Convezione Meccanimo Colliioni molecolari Diffuione molecolare Equazione generale ka ha T dt dx ( T ) Radiazione Evaporazione Fotoni Cambiamento di fae Fluo di calore (Joule m -2-1 ) Calore
Conduzione Convezione Meccanimo Colliioni molecolari Diffuione molecolare Equazione generale ka ha T dt dx ( T ) Radiazione Evaporazione Fotoni Cambiamento di fae Fluo di calore (Joule m -2-1 ) Calore
TRASDUTTORI DI UMIDITA. II trasduttore di umidità (capacitivo)
 lez. 3 TASDUTTOI DI UMIDITA I traduttori di umidità rilevano l'umidità relativa definita come il rapporto tra l'umidità aoluta(quantità di vapore acqueo (maa) contenuta in m 3 d aria) e l umidità di aturazione
lez. 3 TASDUTTOI DI UMIDITA I traduttori di umidità rilevano l'umidità relativa definita come il rapporto tra l'umidità aoluta(quantità di vapore acqueo (maa) contenuta in m 3 d aria) e l umidità di aturazione
Risposta temporale: esempi
 ...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
...4 Risposta temporale: esempi Esempio. Calcolare la risposta al gradino unitario del seguente sistema: x(t) = u(t) s + 5 (s + )(s + ) y(t) Il calcolo della trasformata del segnale di uscita è immediato:
Esperienza n 6: Pendolo di Kater
 Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
Eperienza n 6: Pendolo di Kater Sperimentatori: Marco Erculiani (N maricola 4549 v.o.) Ivan Noro (N matricola 458656 v.o.) Materiale a dipoizione: I materiali utilizzati per queta eperienza ono: Un pendolo
PARTE V RISPOSTE CARATTERISTICHE, RETI DUE PORTE, LINEE
 PARTE V RISPOSTE CARATTERISTICHE, RETI DUE PORTE, LINEE. Funzioni di rete: funzioni immettenza e funzioni di traferimento I rapporti tra le traformate di due grandezze elettriche (tenioni e correnti) di
PARTE V RISPOSTE CARATTERISTICHE, RETI DUE PORTE, LINEE. Funzioni di rete: funzioni immettenza e funzioni di traferimento I rapporti tra le traformate di due grandezze elettriche (tenioni e correnti) di
Si vuole trafilare una barra di acciaio di diametro pari a 10 millimetri, fino a portarla ad un diametro di 8 millimetri. D F D I
 Eercizio C. Trafilatura di una barra d acciaio Si vuole trafilare una barra di acciaio di diametro pari a millimetri, fino a portarla ad un diametro di 8 millimetri. v I v D D I ILIERA Calcolare la forza
Eercizio C. Trafilatura di una barra d acciaio Si vuole trafilare una barra di acciaio di diametro pari a millimetri, fino a portarla ad un diametro di 8 millimetri. v I v D D I ILIERA Calcolare la forza
ESERCIZI SULLE SUPERFICI. 1) Calcolare le curvature principali, la curvatura media e la curvatura Gaussiana della sfera
 ESERCIZI SULLE SUPERFICI Calcolare le curvature principali, la curvatura media e la curvatura Gauiana della fera α u; v = r in u co v ; r in u in v ; r co u Dato il paraboloide ellittico α u; v = u; v;
ESERCIZI SULLE SUPERFICI Calcolare le curvature principali, la curvatura media e la curvatura Gauiana della fera α u; v = r in u co v ; r in u in v ; r co u Dato il paraboloide ellittico α u; v = u; v;
Contenuti dell unità + C A0 L
 1 ontenuti dell unità Questa unità considera problemi di transitorio in reti: 1) contenenti un solo elemento reattivo (1 condensatore oppure 1 induttore) a) alimentate da generatori costanti in presenza
1 ontenuti dell unità Questa unità considera problemi di transitorio in reti: 1) contenenti un solo elemento reattivo (1 condensatore oppure 1 induttore) a) alimentate da generatori costanti in presenza
Lezione 11. Progetto del controllore
 Lezione Progetto del controllore Specifiche di progetto Conideriamo nuovamente un itema di controllo in retroazione: d y + + + y () G() + + n Fig : Sitema di controllo Supporremo aegnata la funzione di
Lezione Progetto del controllore Specifiche di progetto Conideriamo nuovamente un itema di controllo in retroazione: d y + + + y () G() + + n Fig : Sitema di controllo Supporremo aegnata la funzione di
Flessione su 4 punti. Configurazione sperimentale. Schematizzazione di calcolo. Studio delle sollecitazioni semplici. Taglio.
 Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Fleione u punti Configurazione imentale Scematizzazione di calcolo Taglio omento flettente Studio delle ollecitazioni emplici Tratto ollecitato da fleione pura la ua deformata è un arco di cercio Deformazioni
Lezione 5. Calcolo dell antitrasformata di Laplace. F. Previdi - Automatica - Lez. 5 1
 Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Lezione 5. Calcolo dell aniraormaa di Laplace. Previdi - Auomaica - Lez. 5 Schema della lezione. Inroduzione. Aniraormazione di Laplace. Srumeni per l aniraormazione 4. Teorema del valore iniziale 5. Teorema
Oscillatori sinusoidali /1
 //6 Ocillatori inuoidali / Un ocillatore inuoidale è un itema decritto da una coppia di poli immaginari coniugati. A(j) f (j) Un amplificatore lineare può eere chiuo in un anello di reazione per realizzare
//6 Ocillatori inuoidali / Un ocillatore inuoidale è un itema decritto da una coppia di poli immaginari coniugati. A(j) f (j) Un amplificatore lineare può eere chiuo in un anello di reazione per realizzare
LAVORO ED ENERGIA. 1J = 1N 1m
 ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
ppunti di fiica LVORO ED ENERGI LVORO Nel linguaggio cientifico il termine lavoro ha un ignificato ben precio e talvolta divero da quello che queto termine aume nel linguaggio quotidiano. In fiica il concetto
22 - Il principio dei lavori virtuali
 - Il principio dei lavori virtuali ü [.a. 0-0 : ultima reviione 5 aprile 0] Eempio n. Si conideri il portale di Figura, emplicemente ipertatico. Si vuole applicare il principio dei lavori virtuali per
- Il principio dei lavori virtuali ü [.a. 0-0 : ultima reviione 5 aprile 0] Eempio n. Si conideri il portale di Figura, emplicemente ipertatico. Si vuole applicare il principio dei lavori virtuali per
3. Catene di Misura e Funzioni di Trasferimento
 3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
3.. Generalità 3. Catene di Miura e Funzioni di Traferimento 3.. Generalità Il egnale che rappreenta la grandezza da miurare viene trattato in modo da poter eprimere quet ultima con uno o più valori numerici
GLI STATI LIMITE PER SOLLECITAZIONI NORMALI
 Coro ulle Norme Tecniche per le cotruzioni in zona imica (Oinanza PCM 3274/2003, DGR ailicata 2000/2003) POTENZA, 2004 GLI STATI LIMITE PER SOLLECITAZIONI NORMALI Prof. Ing. Angelo MASI DiSGG, Univerità
Coro ulle Norme Tecniche per le cotruzioni in zona imica (Oinanza PCM 3274/2003, DGR ailicata 2000/2003) POTENZA, 2004 GLI STATI LIMITE PER SOLLECITAZIONI NORMALI Prof. Ing. Angelo MASI DiSGG, Univerità
19.12. Impianti motori con turbine a gas
 19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
19.12. Impianti motori con turbine a ga Approfondimenti 19.12.1. Generalità. Il ciclo di Brayton (o ciclo di oule) Il rendimento (h) di un ciclo termodinamico può eere epreo dalla relazione: h q up q inf
A tal fine consideriamo un esempio come punto di partenza per le nostre considerazioni.
 Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
Moto Parabolico Sino ad ora abbiamo ito due tipi di moto: moto rettilineo uniforme moto uniformemente accelerato lo tudio che è tato condotto fino a queto punto ha preo in coniderazione un moto alla olta,
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica
 CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI DEI SISTEMI LTI Ing. Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
CONTROLLO DI SISTEMI ROBOTICI Laurea Specialistica in Ingegneria Meccatronica CONTROLLO DI SISTEMI ROBOTICI ANALISI DEI SISTEMI LTI Ing. Tel. 0522 522235 e-mail: secchi.cristian@unimore.it http://www.dismi.unimo.it/members/csecchi
Le lettere x, y, z rappresentano i segnali nei vari rami.
 Regole per l elaborazione di schemi a blocchi Oltre alle tre fondamentali precedenti regole (cascata, parallelo, retroazione), ne esiste una serie ulteriore che consente di semplificare i sistemi complessi,
Regole per l elaborazione di schemi a blocchi Oltre alle tre fondamentali precedenti regole (cascata, parallelo, retroazione), ne esiste una serie ulteriore che consente di semplificare i sistemi complessi,
Meccanica Applicata alle Macchine Appello del 12/01/2012
 Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
Meccanica Applicata alle Macchine Appello del 12/01/2012 1. Eeguire l analii tatica del meccanimo in figura 2 (cala 1:1). Si calcoli l azione reitente ul membro 5 quando F m =1N. 2. In figura 1 è rappreentato
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA
 DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
DETERMINAZIONE DELLA LATITUDINE E DELLA LONGITUDINE SENZA L USO DELLE RETTE D ALTEZZA Quando i oerva un atro nell'itante del uo paaggio al idiano dell'oervatore i parla di oervazioni idiane. Un atro, in
CAPITOLO IV ANALISI E PROGETTO DI UN CONVERTITORE DC-DC DEL TIPO SWITCHING STEP_UP
 CAPITOLO IV ANALISI E PROGETTO DI UN CONVERTITORE DC-DC DEL TIPO SWITCHING STEP_UP 1 Introduzione Gli alimentatoriwitching ( a commutazione), ono in grado di contenere la potenza diipata molto meglio dei
CAPITOLO IV ANALISI E PROGETTO DI UN CONVERTITORE DC-DC DEL TIPO SWITCHING STEP_UP 1 Introduzione Gli alimentatoriwitching ( a commutazione), ono in grado di contenere la potenza diipata molto meglio dei
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
CIRCUITI IN CORRENTE CONTINUA
 IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
L induzione elettromagnetica - Legge di Faraday-Lentz
 L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
L induzione elettromagnetica - Legge di Faraday-Lentz Si oerano alcuni fatti perimentali. 1 ) Conideriamo un filo metallico chiuo u e teo (pira) tramite un miuratore di corrente poto in icinanza di un
Esercizio (tratto dal Problema 1.6 del Mazzoldi)
 1 Esercizio (tratto dal Problema 1.6 del Mazzoldi) Una particella si muove lungo l asse x nel verso positivo con accelerazione costante a 1 = 3.1 m/s 2. All istante t = 0 la particella si trova nell origine
1 Esercizio (tratto dal Problema 1.6 del Mazzoldi) Una particella si muove lungo l asse x nel verso positivo con accelerazione costante a 1 = 3.1 m/s 2. All istante t = 0 la particella si trova nell origine
Tutorato Lezione 2 Gli amplificatori operazionali
 Tutorato Lezione Gli ampliicatori operazionali Ideale: Gli op-amp ono circuiti elettronici di bae ideati e iluppati con la nacita delle prime macchine di calcolo analogico. In eguito con l aento dell elettronica
Tutorato Lezione Gli ampliicatori operazionali Ideale: Gli op-amp ono circuiti elettronici di bae ideati e iluppati con la nacita delle prime macchine di calcolo analogico. In eguito con l aento dell elettronica
Stati limite nel cemento armato Stato limite ultimo per tensioni normali: applicazioni BOZZA
 Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Lezione n. 1 Stati limite nel cemento armato Stato limite ultimo per tenioni normali: applicazioni Nel eguito i riportano alcuni eempi di applicazione delle procedure decritte nel paragrao precedente.
Metodo delle trasformate di Laplace. Lezione 12 1
 Metodo delle trasformate di Laplace Lezione Fasi del metodo Trasformazione della rete dal dominio del tempo al dominio di Laplace Calcolo della rete in Laplace con metodi circuitali Calcolo delle antitrasformate
Metodo delle trasformate di Laplace Lezione Fasi del metodo Trasformazione della rete dal dominio del tempo al dominio di Laplace Calcolo della rete in Laplace con metodi circuitali Calcolo delle antitrasformate
ESERCIZI SUI SISTEMI LINEARI
 ESERCIZI SUI SISTEMI LINEARI Consideriamo ora il sistema lineare omogeneo a coefficienti costanti associato alla matrice A M n n, cioè SLO Vale il seguente = A. Teorema. Sia v R n \ } e sia λ C. Condizione
ESERCIZI SUI SISTEMI LINEARI Consideriamo ora il sistema lineare omogeneo a coefficienti costanti associato alla matrice A M n n, cioè SLO Vale il seguente = A. Teorema. Sia v R n \ } e sia λ C. Condizione
Corso di Sistemi Prof. Aniello Celentano anno scolastico 2015/2016 ITIS G. Ferraris (NA)
 I Numeri complessi I numeri complessi sono costituiti da una coppia di numeri reali (a,b). Il numero reale a è la parte reale, mentre b è la parte immaginaria. La parte immaginaria è sempre accompagnata
I Numeri complessi I numeri complessi sono costituiti da una coppia di numeri reali (a,b). Il numero reale a è la parte reale, mentre b è la parte immaginaria. La parte immaginaria è sempre accompagnata
Analisi dei Sistemi Lineari e Tempo Invarianti nel Dominio del Tempo
 1 Corso di Fondamenti di Automatica A.A. 2016/17 Analisi dei Sistemi Lineari e Tempo Invarianti nel Dominio del Tempo Prof. Carlo Cosentino Dipartimento di Medicina Sperimentale e Clinica Università degli
1 Corso di Fondamenti di Automatica A.A. 2016/17 Analisi dei Sistemi Lineari e Tempo Invarianti nel Dominio del Tempo Prof. Carlo Cosentino Dipartimento di Medicina Sperimentale e Clinica Università degli
s = (34) V I s B s E r I r B r B= B s +B r (33) 0$&&+,1($6,1&521(
 0$&&+,1($6,1&51( Conideriamo dapprima il cao di macchine aincrone con rotore avvolto. In ee tatore e rotore hanno un avvolgimento dello teo tipo (di regola trifae). L avvolgimento di tatore [ad eempio
0$&&+,1($6,1&51( Conideriamo dapprima il cao di macchine aincrone con rotore avvolto. In ee tatore e rotore hanno un avvolgimento dello teo tipo (di regola trifae). L avvolgimento di tatore [ad eempio
Caso di A non regolare
 Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
x =0 x 1 x 2 Esercizio (tratto dal Problema 1.4 del Mazzoldi)
 1 Esercizio (tratto dal Problema 1.4 del Mazzoldi) Un punto materiale si muove con moto uniformemente accelerato lungo l asse x. Passa per la posizione x 1 con velocità v 1 1.9 m/s, e per la posizione
1 Esercizio (tratto dal Problema 1.4 del Mazzoldi) Un punto materiale si muove con moto uniformemente accelerato lungo l asse x. Passa per la posizione x 1 con velocità v 1 1.9 m/s, e per la posizione
STRUTTURE IN CEMENTO ARMATO - III
 Suidi didattici per il coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STRUTTURE IN CEMENTO ARMATO - III AGGIORNAMENTO 26/09/2012 Coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STATI LIMITE
Suidi didattici per il coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STRUTTURE IN CEMENTO ARMATO - III AGGIORNAMENTO 26/09/2012 Coro di COSTRUZIONI EDILI Prof. Ing. Franceco Zanghì STATI LIMITE
Transitori nelle reti ad una costante di tempo. Lezione 6 1
 Transitori nelle reti ad una costante di tempo Lezione 6 1 Circuito con amplificatore Calcolare v(t) vt () = v(0 ), t< 0 [ ] t τ vt () = v(0 ) V e + V, t> 0 + Continuità della tensione sul condensatore
Transitori nelle reti ad una costante di tempo Lezione 6 1 Circuito con amplificatore Calcolare v(t) vt () = v(0 ), t< 0 [ ] t τ vt () = v(0 ) V e + V, t> 0 + Continuità della tensione sul condensatore
Soluzione di circuiti RC ed RL del primo ordine
 Principi di ingegneria elettrica Lezione 11 a parte 2 Soluzione di circuiti RC ed RL del primo ordine Metodo sistematico Costante di tempo Rappresentazione del transitorio Metodo sistematico per ricavare
Principi di ingegneria elettrica Lezione 11 a parte 2 Soluzione di circuiti RC ed RL del primo ordine Metodo sistematico Costante di tempo Rappresentazione del transitorio Metodo sistematico per ricavare
Controllo di Azionamenti Elettrici. Lezione n 3. Caratteristiche e predisposizione dei regolatori PID
 Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
Controllo di Azionamenti Elettrici Lezione n 3 Coro di Laurea in Ingegneria dell Automazione Facoltà di Ingegneria Univerità degli Studi di alermo Caratteritiche e predipoizione dei regolatori ID 1 Introduzione
TRASFORMATA DI LAPLACE
 TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
TRASFORMATA DI LAPLACE La Trasformata di Laplace è un operatore funzionale che stabilisce una corrispondenza biunivoca tra una funzione di variabile reale (tempo t), definita per t, e una funzione di variabile
Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1
 Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1 Calcolo simbolico Lezione 3 2 Effetti di fulminazione 1/4 Modello di fulminazione elettrica Rete nel dominio del
Il contenuto di questo file e di completa proprieta del Politecnico di Torino. Lezione 3 1 Calcolo simbolico Lezione 3 2 Effetti di fulminazione 1/4 Modello di fulminazione elettrica Rete nel dominio del
APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts
 Università degli Studi di Trieste Facoltà di Ingegneria Laurea in Ingegneria dell Informazione a.a. 2004/2005 APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts docente: Stefano Pastore
Università degli Studi di Trieste Facoltà di Ingegneria Laurea in Ingegneria dell Informazione a.a. 2004/2005 APPUNTI del CORSO di TEORIA dei CIRCUITI 2 Oscillatore di Colpitts docente: Stefano Pastore
Esercizi di Elettrotecnica
 Esercizi di Elettrotecnica Ing. Carlo Forestiere carlo.forestiere@unina.it Corso di Laurea in Ingegneria Informatica Anno Accademico 2009-2010 Dipartimento di Ingegneria Elettrica Università degli studi
Esercizi di Elettrotecnica Ing. Carlo Forestiere carlo.forestiere@unina.it Corso di Laurea in Ingegneria Informatica Anno Accademico 2009-2010 Dipartimento di Ingegneria Elettrica Università degli studi
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Secondo esonero di FISICA GENERALE 2 del 16/01/15
 Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Secondo esonero di FISICA GENERALE 2 del 16/01/15 Esercizio 1 (7 punti): Nella regione di spazio compresa tra due cilindri coassiali
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Secondo esonero di FISICA GENERALE 2 del 16/01/15 Esercizio 1 (7 punti): Nella regione di spazio compresa tra due cilindri coassiali
Divisori e combinatori
 Diviori e combinatori Luca Vincetti a.a. - Diviori e combinatori La combinazione lineare di egnali differenti o, all invero, la uddiviione di un unico egnale in componenti divere fa parte della normale
Diviori e combinatori Luca Vincetti a.a. - Diviori e combinatori La combinazione lineare di egnali differenti o, all invero, la uddiviione di un unico egnale in componenti divere fa parte della normale
Elementi di programmazione lineare. Ottimizzazione di funzioni soggette a vincoli
 Elementi di programmazione lineare Ottimizzazione di funzioni oggette a vincoli Formulazione del problema min Z ma oggetta b c a T d Z:funzione obiettivo calare d: coto fio calare : variabile deciionale
Elementi di programmazione lineare Ottimizzazione di funzioni oggette a vincoli Formulazione del problema min Z ma oggetta b c a T d Z:funzione obiettivo calare d: coto fio calare : variabile deciionale
1_ Filtro passa-basso Con A(jw) si indica la funzione di trasferimento del filtro, il cui modulo A assume un valore costante
 PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
PPUNTI DI ELETTNIC FILTI TTII 6 Campi di applicazione I filtri nel ettore dell elettronica ono utilizzati per : attenuare i diturbi, il rumore e le ditorioni applicati al egnale utile; eparare due egnale
Principi di ingegneria elettrica. Reti in regime sinusoidale. Lezione 13 a. Impedenza Ammettenza
 Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
Principi di ingegneria elettrica Lezione 3 a Reti in regime sinusoidale mpedenza Ammettenza Legge di Ohm simbolica n un circuito lineare comprendente anche elementi dinamici (induttori e condensatori)
Un problema di dadi. Michele Impedovo
 Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
Un problema di dadi Michele Impedovo Riaunto Quante volte, in media, occorre lanciare un dado a facce perché tutte le facce ecano almeno una volta? Per riolvere queto problema non è neceario calcolare
Modellazione e Analisi di Sistemi Meccanici
 Modellazione e Analii di Sitemi Meccanici Modellazione e Analii di Sitemi Meccanici Davide Giglio Maa in movimento Si conideri il itema rappreentato in figura. Il itema conite in una maa che può correre
Modellazione e Analii di Sitemi Meccanici Modellazione e Analii di Sitemi Meccanici Davide Giglio Maa in movimento Si conideri il itema rappreentato in figura. Il itema conite in una maa che può correre
Amplificatore a BJT in configurazione CE e CC
 Amplificatore a JT in configurazione e Traccia per lo olgimento dell eercitazione del 7 maggio 008 1 ircuito da realizzare 100k 1V 4k7 10u Vo 100k 4k7 1V Rif. Vi Gen. 100n N Vi Gen. 100n N 10u Vo 18k 1k
Amplificatore a JT in configurazione e Traccia per lo olgimento dell eercitazione del 7 maggio 008 1 ircuito da realizzare 100k 1V 4k7 10u Vo 100k 4k7 1V Rif. Vi Gen. 100n N Vi Gen. 100n N 10u Vo 18k 1k
Esercizi su Autovalori e Autovettori
 Esercizi su Autovalori e Autovettori Esercizio n.1 5 A = 5, 5 5 5 Esercizio n.6 A =, Esercizio n.2 4 2 9 A = 2 1 8, 4 2 9 Esercizio n.7 6 3 3 A = 6 3 6, 3 3 6 Esercizio n.3 A = 4 6 6 2 2, 6 6 2 Esercizio
Esercizi su Autovalori e Autovettori Esercizio n.1 5 A = 5, 5 5 5 Esercizio n.6 A =, Esercizio n.2 4 2 9 A = 2 1 8, 4 2 9 Esercizio n.7 6 3 3 A = 6 3 6, 3 3 6 Esercizio n.3 A = 4 6 6 2 2, 6 6 2 Esercizio
UNIVERSITA DI FIRENZE Facoltà di Ingegneria. Fisica Tecnica G. Grazzini. Superfici estese
 Superici etee Nella legge di Newton per la convezione compare la upericie di cambio inieme al coeiciente di convezione; perciò e non riuciamo ad aumentare quet'ultimo, tenteremo di accrecere la upericie
Superici etee Nella legge di Newton per la convezione compare la upericie di cambio inieme al coeiciente di convezione; perciò e non riuciamo ad aumentare quet'ultimo, tenteremo di accrecere la upericie
