Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 26. Docente: Laura Palagi
|
|
|
- Flaviana Zamboni
- 6 anni fa
- Visualizzazioni
Transcript
1 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 26 Docente: Laura Palagi
2 Modello di distribuzione Cardillo Raffaele Di Paola Catherine Trano Marco Salvatore
3 MODELLO DI DISTRIBUZIONE Il nostro problema è un particolare problema di trasporto in cui si hanno un certo numero di impianti (origini) ciascuno dei quali ha una quantità fissata di merce disponibile e un certo numero di clienti (destinazioni) i quali richiedono quantitativi precisi di merce. La domanda dei clienti viene soddisfatta dai centri di distribuzione che vengo riforniti dagli impianti. Quindi conoscendo il costo unitario del trasporto della merce da ciascun impianto origine a ciascun centro di distribuzione e da quest ultimo al cliente è necessario pianificare i trasporti, cioè la quantità di merce che deve essere trasportata in modo da soddisfare l ordine dei clienti minimizzando il costo complessivo derivante dai trasporti.
4 Modello di distribuzione IMPIANTI DI DISTRIBUZIONE F i i = 1,,n CENTRI DI DISTRIBUZIONE D j j = 1,,m CLIENTI C h h = 1,,p
5 c ij = costi unitari di trasporto ( euro/tonnellate ) dall i-esimo impianto di produzione al j-esimo centro di distribuzione w jh = costi unitari di trasporto ( euro/tonnellate ) dal j-esimo centro di distribuzione all h-esimo cliente z i = costo produzione relativo all i-esimo impianto P i = capacità produttiva massima mensile dell i-esimo impianto R h = richiesta mensile che deve essere soddisfatta esattamente per l h-esimo cliente
6 FORMULAZIONE VARIABILI DI DECISIONE: x ij = quantità trasportate (tonnellate) dall i-esimo impianto di produzione al j-esimo centro di distribuzione y jh = quantità trasportate (tonnellate) dal j-esimo centro di distribuzione all h-esimo cliente
7 FUNZIONE OBIETTIVO La funzione obiettivo da minimizzare è data dalla somma dei seguenti costi: m COSTO PRODUZIONE COSTO TRASPORTO (DAGLI IMPIANTI AI CENTRI DI DISTRIBUZIONE) n m i=1 j=1 c ij x ij COSTO TRASPORTO ( DAI CENTRI DI DISTRIBUZIONE AI CLIENTI) m j=1 p Z i x ij per i = 1,, n j=1 h=1 w jh y jh
8 Dunque la forma compatta della funzione obiettivo risulterà: n m i=1 j=1 c ij x ij + VINCOLI VINCOLO CAPACITA PRODUTTIVA IMPIANTI m j=1 x ij Pi per i = 1,.., n
9 VINCOLO DI DOMANDA MENSILE DEI CLIENTI m j=1 y jh = Rh per h = 1,, p VINCOLO DI DISTRIBUZIONE p n y jh h=1 i=1 x ij per j = 1,, m VINCOLO DI NON NEGATIVITA x ij 0 per i=1,,n j=1,,m y jh 0 per j=1,,m h=1,,p
10 ESEMPIO NUMERICO Costo unitario di distribuzione dall impianto al centro di distribuzione D1 D2 D3 CAPACITA PRODUTTIVA COSTO PRODUZIONE F1 3,2 2,2 4, ,5 F ,9 1, Costo unitario di distribuzione dal centro di distribuzione al cliente C1 C2 C3 C4 C5 C6 C7 C8 C9 D1 0,3 2,1 3,1 4,4 6, D2 5,2 5,4 4,5 6,0 2,7 4,7 3,4 3,3 2,7 D ,4 3,3 2,4 2,1 2,5 richiesta
11 Nel foglio DATI di excel esprimiamo l impossibilità di collegamento tra alcuni impianti/centri di distribuzione e tra alcuni centri di distribuzione/clienti con un valore del costo di distribuzione molto elevato (999999) rispetto agli altri in modo tale che, siccome stiamo minimizzando i costi, siamo certi che il solver attribuirà alla variabile corrispondente un valore nullo. COSTI DISTRIBUZIONE1 CD1 CD2 CD3 IMPIANTO 1 3,2 2,2 4,2 IMPIANTO ,9 1,2 COSTI DISTRIBUZIONE2 CLIENTE 1 CLIENTE2 CLIENTE3 CLIENTE4 CLIENTE5 CLIENTE6 CLIENTE7 CLIENTE8 CLIENTE9 CD1 0,3 2,1 3,1 4, CD2 5,2 5,4 4,5 6 2,7 4,7 3,4 3,3 2,7 CD ,4 3,3 2,4 2,1 2,5
12 VARIABILI DI DECISIONE D1 D2 D3 F1 X 11 X 12 X 13 F2 X 21 X 22 X 23 Quantita di contatori elettrici distribuiti dall impianto al centro di distribuzione Quantita di contatori elettrici distribuiti dal centro di distribuzione al cliente C1 C2 C3 C4 C5 C6 C7 C8 C9 D1 y 11 y 12 y 13 y 14 y 15 y 16 y 17 y 18 y 19 D2 y 21 y 22 y 23 y 24 y 25 y 26 y 27 y 28 y 29 D3 y 31 y 32 y 33 y 34 y 35 y 36 y 37 y 38 y 39
13 FUNZIONE OBIETTIVO La funzione obiettivo da minimizzare è data dalla somma dei seguenti costi: COSTO PRODUZIONE COSTO TRASPORTO (DAGLI IMPIANTI AI CENTRI DI DISTRIBUZIONE) 2 3 i=1 j=1 c ij x ij COSTO TRASPORTO ( DAI CENTRI DI DISTRIBUZIONE AI CLIENTI) 3 3 j=1 9 Z i x ij per i = 1,2 j=1 h=1 w jh y jh
14 Dunque la forma compatta della funzione obiettivo risulterà: i=1 j=1 c ij x ij + VINCOLI VINCOLO CAPACITA PRODUTTIVA IMPIANTI 3 j=1 x ij Pi per i = 1,2
15 VINCOLO DI DOMANDA MENSILE DEI CLIENTI 3 j=1 y jh = Rh per h = 1,, 9 VINCOLO DI DISTRIBUZIONE 9 2 y jh x ij 0 h=1 i=1 per j = 1,2,3 VINCOLO DI NON NEGATIVITA x ij 0 per i=1,2 j=1,2,3 y jh 0 per j=1,2,3 h=1,,9
16 Soluzione ottima intera trovata dal risolutore Essendo la matrice dei vincoli del nostro problema di distribuzione TOTALMENTE UNIMODULARE ci aspettiamo che la nostra soluzione ottima abbia valori interi infatti andando a risolvere il problema con il risolutore di excel otteniamo : VARIABILI X CD1 CD2 CD3 IMPIANTO IMPIANTO VARIABILI Y CLIENTE1 CLIENTE2 CLIENTE3 CLIENTE4 CLIENTE5 CLIENTE6 CLIENTE7 CLIENTE8 CLIENTE9 CD CD CD
17 Risultati ottenuti dal solutore RAPPORTO VALORI Cella obiettivo (Min) Cella Nome Valore originale Valore finale $C$49 MIN Qui riportiamo soltanto le variabili non nulle del rapporto valori: Celle variabili Cella Nome Valore originale Valore finale Intere $C$4 IMPIANTO1 CD Continue $D$4 IMPIANTO1 CD Continue $E$5 IMPIANTO2 CD Continue $C$10 CD1 CLIENTE Continue $D$10 CD1 CLIENTE Continue $E$10 CD1 CLIENTE Continue $F$10 CD1 CLIENTE Continue $G$11 CD2 CLIENTE Continue $I$11 CD2 CLIENTE Continue $K$11 CD2 CLIENTE Continue $H$12 CD3 CLIENTE Continue $I$12 CD3 CLIENTE Continue $J$12 CD3 CLIENTE Continue
18 Lo stato di un vincolo può essere vincolante o non vincolante. Si intende che il vincolo è rispettivamente attivo (ovvero soddisfatto all uguaglianza) o non attivo (ovvero soddisfatto con la disuguaglianza stretta) nella soluzione ottima determinata dal solutore. La tolleranza è la differenza(slack) tra la risorsa disponibile e la risorsa utilizzata. Vincoli Cella Nome Valore della cella Formula Stato Tolleranza $C$17 IMPIANTO 1 CAPACITA' PRODUTTIVA $C$17<=$E$17 Non vincolante 40 $C$18 IMPIANTO 2 CAPACITA' PRODUTTIVA $C$18<=$E$18 Vincolante 0 $C$22 CLIENTE 1 DOMANDA 6300 $C$22=$E$22 Vincolante 0 $C$23 CLIENTE 2 DOMANDA 4880 $C$23=$E$23 Vincolante 0 $C$24 CLIENTE 3 DOMANDA 2130 $C$24=$E$24 Vincolante 0 $C$25 CLIENTE 4 DOMANDA 1210 $C$25=$E$25 Vincolante 0 $C$26 CLIENTE 5 DOMANDA 6120 $C$26=$E$26 Vincolante 0 $C$27 CLIENTE 6 DOMANDA 4830 $C$27=$E$27 Vincolante 0 $C$28 CLIENTE 7 DOMANDA 2750 $C$28=$E$28 Vincolante 0 $C$29 CLIENTE 8 DOMANDA 8580 $C$29=$E$29 Vincolante 0 $C$30 CLIENTE 9 DOMANDA 4460 $C$30=$E$30 Vincolante 0 $C$36 CD1 DISTRIBUZIONE 0 $C$36<=$E$36 Vincolante 0 $C$37 CD2 DISTRIBUZIONE 0 $C$37<=$E$37 Vincolante 0 $C$38 CD3 DISTRIBUZIONE 0 $C$38<=$E$38 Vincolante 0
19 RAPPORTO SENSIBILITA Come possiamo vedere dalle prime righe del rapporto di sensibilità : Se il valore della variabile è nullo significa che non è vantaggioso distribuirla Il costo ridotto indica quanto minore dovrebbe essere il costo unitario relativo a quella variabile affinchè sia inserita nella soluzione ottima ad un valore non nullo Le colonne incremento consentito o decremento consentito corrispondono alla variazione in aumento o diminuzione del costo c ij per cui la soluzione rimane ottima Ad esempio se consideriamo la prima riga relativa alla variabile x 11 il coefficiente obiettivo può essere incrementato al più di 0,4 o decrementato al più di 4,3. Questo significa che se il coefficiente obiettivo c 11 della funzione obiettivo varia nell intervallo [ 9,4 ; 14,1 ] la soluzione ottima rimane invariata. Se invece consideriamo la riga relativa alla variabile x 13,il cui valore finale è nullo, il valore 1, del costo ridotto indica di quanto dovremmo diminuire il coefficiente obiettivo affinchè la variabile assuma un valore non nullo nella soluzione ottima. Celle variabili Finale Ridotto Obiettivo Consentito Consentito Cella Nome Valore Costo Coefficiente Incremento Decremento $C$4 IMPIANTO1 CD ,7 0,4 4,3 $D$4 IMPIANTO1 CD ,7 1, ,4 $E$4 IMPIANTO1 CD3 0 1, ,7 1E+30 1, $C$5 IMPIANTO2 CD , E ,8
20 Per quanto riguarda i vincoli del rapporto sensibilità possiamo notare che se il vincolo è non vincolante, come nella prima riga, il prezzo ombra è pari a 0 perché è inutile acquisire ulteriori quantità per una risorsa non completamente utilizzata; ciò viene rappresentato con 1E +30 nella colonna incremento consentito. Il decremento consentito è però limitato ossia ha un valore di 40 perché un eccessiva riduzione della risorsa può portare il vincolo ad essere vincolante. Se invece il vincolo è vincolante il prezzo ombra ha un valore non nullo. Nel nostro caso, siccome stiamo minimizzando, ogni unità aggiunta fino ad un massimo di 1860 (incremento consentito) produce una diminuzione del valore della funzione obiettivo pari a 2, per unità mentre ogni unità sottratta fino a un massimo di 40 (decremento consentito) produce un aumento del valore della funzione obiettivo di 2, per unità. Vincoli Finale Ombreggiatura Vincolo Consentito Consentito Cella Nome Valore Prezzo a destra Incremento Decremento $C$17 IMPIANTO 1 CAPACITA' PRODUTTIVA E $C$18 IMPIANTO 2 CAPACITA' PRODUTTIVA ,
21 SOLUZIONE ALTERNATIVA Come suggeritoci dal rapporto di sensibilità se volessimo diminuire il valore della funzione obiettivo e quindi del costo relativo alla distribuzione dei contatori elettrici aumentiamo la capacità produttiva dell IMPIANTO 2 fino ad un massimo di Cella obiettivo (Min) Cella Nome Valore originale Valore finale $C$49 MIN Cella obiettivo (Min) Cella Nome Valore originale Valore finale $C$49 MIN Possiamo notare che il valore della funzione obiettivo è diminuito precisamente di 2, *1860 = 4650
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 21. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 21 Docente: Laura Palagi Laboratorio di Ricerca Operativa Homework n 21 MODELLO DI MISCELAZIONE E
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 21 Docente: Laura Palagi Laboratorio di Ricerca Operativa Homework n 21 MODELLO DI MISCELAZIONE E
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 28. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 28 Docente: Laura Palagi Laboratorio di Ricerca Operativa Homework n 28 Prof.ssa Ing. Laura Palagi
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 28 Docente: Laura Palagi Laboratorio di Ricerca Operativa Homework n 28 Prof.ssa Ing. Laura Palagi
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 10. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 10 Docente: Laura Palagi Smaltimento dei rifiuti solidi urbani HOMEWORK N 10 Francesco Cambiotti
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 10 Docente: Laura Palagi Smaltimento dei rifiuti solidi urbani HOMEWORK N 10 Francesco Cambiotti
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 19. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 19 Docente: Laura Palagi Gruppo 19: Valentina Rabagliati Luca Quaresima Andrea Martullo Istanza del
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 19 Docente: Laura Palagi Gruppo 19: Valentina Rabagliati Luca Quaresima Andrea Martullo Istanza del
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 4. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 4 Docente: Laura Palagi Homework in Ricerca Operativa GRUPPO 4: Isabelle Pietroletti Matteo Marangio
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 4 Docente: Laura Palagi Homework in Ricerca Operativa GRUPPO 4: Isabelle Pietroletti Matteo Marangio
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 6. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 6 Docente: Laura Palagi PIANIFICAZIONE DELLA PRODUZIONE 2 Si distingue in: PRODUCTION PLANNING: Tentativo
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 6 Docente: Laura Palagi PIANIFICAZIONE DELLA PRODUZIONE 2 Si distingue in: PRODUCTION PLANNING: Tentativo
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 24. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 24 Docente: Laura Palagi Problema di Revenue management aereo in sistema Hub and Spoke Una compagnia
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 24 Docente: Laura Palagi Problema di Revenue management aereo in sistema Hub and Spoke Una compagnia
Vediamo come risolvere un problema di PL con Excel. Riprendiamo un esercizio già visto.
 Esempio di risoluzione di un problema di PL con Excel Vediamo come risolvere un problema di PL con Excel. Riprendiamo un esercizio già visto. Un azienda vinicola desidera produrre due tipi di vino: uno
Esempio di risoluzione di un problema di PL con Excel Vediamo come risolvere un problema di PL con Excel. Riprendiamo un esercizio già visto. Un azienda vinicola desidera produrre due tipi di vino: uno
Flusso a Costo Minimo
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Universita degli Studi di Siena
 Universita degli Studi di Siena Facolta di Ingegneria Dispense del corso di Sistemi di Supporto alle Decisioni I L algoritmo per la risoluzione di problemi di programmazione dinamica Chiara Mocenni Corso
Universita degli Studi di Siena Facolta di Ingegneria Dispense del corso di Sistemi di Supporto alle Decisioni I L algoritmo per la risoluzione di problemi di programmazione dinamica Chiara Mocenni Corso
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 13. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 13 Docente: Laura Palagi A.A. 2012/2013 Laboratorio di Ricerca Operativa BGER Leonardo Mastrantoni
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 13 Docente: Laura Palagi A.A. 2012/2013 Laboratorio di Ricerca Operativa BGER Leonardo Mastrantoni
Esercitazione n o 3 per il corso di Ricerca Operativa
 Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
Ricerca Operativa A.A. 2007/ Analisi di sensitività
 Ricerca Operativa A.A. 7/8. Analisi di sensitività Luigi De Giovanni - Ricerca Operativa -. Analisi di sensitività. Analisi di Sensitività: motivazioni I parametri (A, b e c) di un problema di programmazione
Ricerca Operativa A.A. 7/8. Analisi di sensitività Luigi De Giovanni - Ricerca Operativa -. Analisi di sensitività. Analisi di Sensitività: motivazioni I parametri (A, b e c) di un problema di programmazione
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 33. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 33 Docente: Laura Palagi Homework in Ricerca Operativa gruppo n 33 Turni del Personale Martina Conti
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 33 Docente: Laura Palagi Homework in Ricerca Operativa gruppo n 33 Turni del Personale Martina Conti
Introduzione alla RO - Parte II
 Introduzione alla RO - Parte II Andrea Scozzari a.a. 2013-2014 March 7, 2014 Andrea Scozzari (a.a. 2013-2014) Introduzione alla RO - Parte II March 7, 2014 1 / 18 Problema della pianificazione del personale:
Introduzione alla RO - Parte II Andrea Scozzari a.a. 2013-2014 March 7, 2014 Andrea Scozzari (a.a. 2013-2014) Introduzione alla RO - Parte II March 7, 2014 1 / 18 Problema della pianificazione del personale:
Management Sanitario. Modulo di Ricerca Operativa
 Management Sanitario per il corso di Laurea Magistrale SCIENZE RIABILITATIVE DELLE PROFESSIONI SANITARIE Modulo di Ricerca Operativa Prof. Laura Palagi http://www.dis.uniroma1.it/ palagi Dipartimento di
Management Sanitario per il corso di Laurea Magistrale SCIENZE RIABILITATIVE DELLE PROFESSIONI SANITARIE Modulo di Ricerca Operativa Prof. Laura Palagi http://www.dis.uniroma1.it/ palagi Dipartimento di
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 11. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 11 Docente: Laura Palagi Alina Volovei Ilaria Noce Lea Mariella Pianificazione degli approvvigionamenti
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 11 Docente: Laura Palagi Alina Volovei Ilaria Noce Lea Mariella Pianificazione degli approvvigionamenti
Problemi di Flusso: Il modello del Trasporto
 Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Problemi di Flusso: Il modello del rasporto Andrea Scozzari a.a. 2014-2015 April 27, 2015 Andrea Scozzari (a.a. 2014-2015) Problemi di Flusso: Il modello del rasporto April 27, 2015 1 / 25 Problemi su
Introduzione al Metodo del Simplesso. 1 Soluzioni di base e problemi in forma standard
 Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
Problemi di flusso a costo minimo
 p. 1/7 Problemi di flusso a costo minimo È data una rete (grafo orientato e connesso) G = (V,A). (i,j) A c ij, costo di trasporto unitario lungo l arco (i, j). i V b i interi e tali che i V b i = 0. p.
p. 1/7 Problemi di flusso a costo minimo È data una rete (grafo orientato e connesso) G = (V,A). (i,j) A c ij, costo di trasporto unitario lungo l arco (i, j). i V b i interi e tali che i V b i = 0. p.
Esercitazione n o 6 per il corso di Ricerca Operativa
 Esercitazione n o 6 per il corso di Ricerca Operativa Il problema è stato tratto dal libro C. Mannino, L.Palagi, M. Roma. Complementi ed esercizi di Ricerca Operativa, Edizioni Ingegneria 2000, 1998, ISBN:
Esercitazione n o 6 per il corso di Ricerca Operativa Il problema è stato tratto dal libro C. Mannino, L.Palagi, M. Roma. Complementi ed esercizi di Ricerca Operativa, Edizioni Ingegneria 2000, 1998, ISBN:
1 Riduzione per righe e matrici equivalenti per righe.
 Geometria Lingotto. LeLing2: Sistemi lineari omogenei. Ārgomenti svolti: Riduzione per righe e matrici equivalenti per righe. Forma echelon e sistemi gia risolti. Il metodo di Gauss-Jordan e la forma echelon.
Geometria Lingotto. LeLing2: Sistemi lineari omogenei. Ārgomenti svolti: Riduzione per righe e matrici equivalenti per righe. Forma echelon e sistemi gia risolti. Il metodo di Gauss-Jordan e la forma echelon.
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Teoria della Programmazione Lineare Intera
 Teoria della Programmazione Lineare Intera Laura Galli Dipartimento di Informatica Largo B. Pontecorvo, 567 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 7 Ottobre 0 Ricerca Operativa Laurea
Teoria della Programmazione Lineare Intera Laura Galli Dipartimento di Informatica Largo B. Pontecorvo, 567 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 7 Ottobre 0 Ricerca Operativa Laurea
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a Homework n 18. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 18 Docente: Laura Palagi Il gioco più bello del mondo dopo il calcio Il Fantacalcio è il gioco più
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 18 Docente: Laura Palagi Il gioco più bello del mondo dopo il calcio Il Fantacalcio è il gioco più
Programmazione Lineare Intera: Piani di Taglio
 Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
x 1 x 2 x 3 x 5 La base iniziale è B 0 = I e risulta x B 0 = , x N 0 = Iterazione 0. Calcolo dei costi ridotti. γ 0 = c N 0 (N 0 ) T c B 0 =
 56 IL METODO DEL SIMPLESSO 7.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
56 IL METODO DEL SIMPLESSO 7.4 IL METODO DEL SIMPLESSO In questo paragrafo sono riportati alcuni esercizi risolti sul metodo del simplesso. Alcuni sono risolti utilizzando la procedura di pivot per determinare,
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
problemi di assegnazione
 problemi di assegnazione I problemi di assegnazione fanno parte dei problemi lineari. I problemi di assegnazione (o problemi di assegnamento) sono quei problemi di ricerca operativa in cui bisogna assegnare
problemi di assegnazione I problemi di assegnazione fanno parte dei problemi lineari. I problemi di assegnazione (o problemi di assegnamento) sono quei problemi di ricerca operativa in cui bisogna assegnare
Esercizi svolti di Programmazione Lineare. a cura di Laura Scrimali Dipartimento di Matematica e Informatica Università di Catania
 Esercizi svolti di Programmazione Lineare a cura di Laura Scrimali Dipartimento di Matematica e Informatica Università di Catania Formulazione matematica e risoluzione grafica Esercizio Una pasticceria
Esercizi svolti di Programmazione Lineare a cura di Laura Scrimali Dipartimento di Matematica e Informatica Università di Catania Formulazione matematica e risoluzione grafica Esercizio Una pasticceria
Metodo di Gauss-Jordan 1
 Metodo di Gauss-Jordan 1 Nota Bene: Questo materiale non debe essere considerato come sostituto delle lezioni. Ārgomenti svolti: Riduzione per righe e matrici equivalenti per righe. Forma echelon e sistemi
Metodo di Gauss-Jordan 1 Nota Bene: Questo materiale non debe essere considerato come sostituto delle lezioni. Ārgomenti svolti: Riduzione per righe e matrici equivalenti per righe. Forma echelon e sistemi
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 9. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 9 Docente: Laura Palagi LA DIETA A COSTO MINIMO AL MCDONALD S Realizzata da: Erasmo Percoco Simone
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 9 Docente: Laura Palagi LA DIETA A COSTO MINIMO AL MCDONALD S Realizzata da: Erasmo Percoco Simone
N.B.: Gli esercizi di OFFICE vanno risolti prima dell esercizio sulla PL
 EIPE - I appello a.a. 2014-2015, 4-5-6 maggio 2015 Cognome:... Nome:... Matricola:... Office (I es.) x/10:... Office (II es.) x/10:... Office (III es.) x/10:... Bonus tempo: b b B B N.B.: Gli esercizi
EIPE - I appello a.a. 2014-2015, 4-5-6 maggio 2015 Cognome:... Nome:... Matricola:... Office (I es.) x/10:... Office (II es.) x/10:... Office (III es.) x/10:... Bonus tempo: b b B B N.B.: Gli esercizi
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 1. Docente: Laura Palagi
 Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 1 Docente: Laura Palagi Homework n. o 1 Problema di Revenue management aereo in sistema Hub and Spoke
Laboratorio di Ricerca Operativa Cad Ingegneria Gestionale (BGER3 - I semestre) a.a. 2012-13 Homework n 1 Docente: Laura Palagi Homework n. o 1 Problema di Revenue management aereo in sistema Hub and Spoke
Figura 1: 1) Si scriva la formulazione del problema come problema di PLI (con un numero minimo di vincoli) e la matrice dei vincoli.
 ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
ESERCIZIO 1 Sia dato il grafo orientato in Figura 1. Si consideri il problema di flusso a 1 2 4 Figura 1: costo minimo su tale grafo con b 1 = 4 b 2 = 2 b = b 4 = e c 12 = 2 c 1 = 4 c 14 = 1 c 2 = 1 c
COMPITO DI RICERCA OPERATIVA APPELLO DEL 08/01/04
 COMPITO DI RICERCA OPERATIVA APPELLO DEL 08/01/04 Esercizio 1 Si risolva con il metodo branch-and-bound il seguente problema di PLI max x 1 + x 4x 1 + x + x = 0 x 1 + x + x 4 = x 1, x, x, x 4 0 x 1, x,
COMPITO DI RICERCA OPERATIVA APPELLO DEL 08/01/04 Esercizio 1 Si risolva con il metodo branch-and-bound il seguente problema di PLI max x 1 + x 4x 1 + x + x = 0 x 1 + x + x 4 = x 1, x, x, x 4 0 x 1, x,
1 se k = r i. 0 altrimenti. = E ij (c)
 Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Gara Matematica. Dipartimento di Matematica Ulisse Dini. Viale Morgagni 67/a Firenze. Soluzioni edizione 2011
 Gara Matematica Dipartimento di Matematica Ulisse Dini Viale Morgagni 67/a - 50134 Firenze Soluzioni edizione 011 Esercizio 1. Determinare tutti gli interi positivi non nulli n che sono uguali alla somma
Gara Matematica Dipartimento di Matematica Ulisse Dini Viale Morgagni 67/a - 50134 Firenze Soluzioni edizione 011 Esercizio 1. Determinare tutti gli interi positivi non nulli n che sono uguali alla somma
Il metodo del simplesso
 Capitolo 5 Il metodo del simplesso 5. La forma standard Esercizio 5.. Porre il problema di Programmazione Lineare: in forma standard. min x +x + x + x x +x 5 x 4 x, x Si trasformano i vincoli di disuguaglianza
Capitolo 5 Il metodo del simplesso 5. La forma standard Esercizio 5.. Porre il problema di Programmazione Lineare: in forma standard. min x +x + x + x x +x 5 x 4 x, x Si trasformano i vincoli di disuguaglianza
Il modello duale. Capitolo settimo. Introduzione
 Capitolo settimo Il modello duale Introduzione Il modello duale e la teoria della dualità assumono una grande importanza nella teoria della programmazione matematica. In questo testo i modelli primale
Capitolo settimo Il modello duale Introduzione Il modello duale e la teoria della dualità assumono una grande importanza nella teoria della programmazione matematica. In questo testo i modelli primale
Lezioni di Ricerca Operativa 2 Dott. F. Carrabs
 Lezioni di Ricerca Operativa Dott. F. Carrabs.. 009/00 Lezione 6: - mmissibilità di un vincolo - Vincoli alternativi - Vincoli alternativi a gruppi - Rappresentazione di funzioni non lineari: Costi fissi
Lezioni di Ricerca Operativa Dott. F. Carrabs.. 009/00 Lezione 6: - mmissibilità di un vincolo - Vincoli alternativi - Vincoli alternativi a gruppi - Rappresentazione di funzioni non lineari: Costi fissi
Sistemi sovradeterminati
 Sistemi sovradeterminati Sia A una matrice m n ove m > n sia b R m trovare una soluzione del sistema sovradeterminato Ax = b significa cercare di esprimere un vettore di R m come combinazione lineare di
Sistemi sovradeterminati Sia A una matrice m n ove m > n sia b R m trovare una soluzione del sistema sovradeterminato Ax = b significa cercare di esprimere un vettore di R m come combinazione lineare di
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Un esempio di applicazione della programmazione lineare intera: il Sudoku
 Un esempio di applicazione della programmazione lineare intera: il Sudoku Corso di Ricerca Operativa per il Corso di Laurea Magistrale in Ingegneria della Sicurezza: Trasporti e Sistemi Territoriali AA
Un esempio di applicazione della programmazione lineare intera: il Sudoku Corso di Ricerca Operativa per il Corso di Laurea Magistrale in Ingegneria della Sicurezza: Trasporti e Sistemi Territoriali AA
Anno 4 Matrice inversa
 Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
AMPL: Esempi. F. Rinaldi. Corso di Laurea Matematica. Dipartimento di Matematica Università di Padova. Esempi di Modellazione in AMPL
 Dipartimento di Matematica Università di Padova Corso di Laurea Matematica Outline Esempi di Modellazione in AMPL Esempio 2 Problema della Dieta In questo problema é data una lista di cibi, a ciascuno
Dipartimento di Matematica Università di Padova Corso di Laurea Matematica Outline Esempi di Modellazione in AMPL Esempio 2 Problema della Dieta In questo problema é data una lista di cibi, a ciascuno
La dualità nella Programmazione Lineare
 Capitolo 3 La dualità nella Programmazione Lineare 3.1 Teoria della dualità Esercizio 3.1.1 Scrivere il problema duale del seguente problema di Programmazione Lineare: min x 1 x 2 + x 3 2x 1 +3x 2 3 x
Capitolo 3 La dualità nella Programmazione Lineare 3.1 Teoria della dualità Esercizio 3.1.1 Scrivere il problema duale del seguente problema di Programmazione Lineare: min x 1 x 2 + x 3 2x 1 +3x 2 3 x
3.6 Metodi basati sui piani di taglio
 3.6 Metodi basati sui piani di taglio Problema generale di Programmazione Lineare Intera (PLI) con A matrice m n e b vettore n 1 razionali min{ c t x : x X = {x Z n + : Ax b} } Sappiamo che esiste una
3.6 Metodi basati sui piani di taglio Problema generale di Programmazione Lineare Intera (PLI) con A matrice m n e b vettore n 1 razionali min{ c t x : x X = {x Z n + : Ax b} } Sappiamo che esiste una
TEORIA della DUALITÀ. Una piccola introduzione. Ricerca Operativa. Prof. R. Tadei. Politecnico di Torino. Teoria della Dualità / 1.
 Prof. R. adei EORIA della DUALIÀ Una piccola introduzione R. adei 1 R. adei 2 EORIA DELLA DUALIA' Il concetto di dualità fu introdotto nel 1947 da Von Neumann, anche se il teorema della dualità fu formulato
Prof. R. adei EORIA della DUALIÀ Una piccola introduzione R. adei 1 R. adei 2 EORIA DELLA DUALIA' Il concetto di dualità fu introdotto nel 1947 da Von Neumann, anche se il teorema della dualità fu formulato
ESERCITAZIONE CON EXCEL SULLE MATRICI
 ESERCITAZIONE CON EXCEL SULLE MATRICI PROBLEMA 1 commutativa. 2 1 0 e 1 2 4 B = 3 1 2, verificare che la loro somma è Per poter risolvere il problema proposto, è necessario predisporre le matrici sul foglio
ESERCITAZIONE CON EXCEL SULLE MATRICI PROBLEMA 1 commutativa. 2 1 0 e 1 2 4 B = 3 1 2, verificare che la loro somma è Per poter risolvere il problema proposto, è necessario predisporre le matrici sul foglio
3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI
 3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI ESISTENZA DI UN PUNTO DI OTTIMO VINCOLATO Il problema di ottimizzazione vincolata introdotto nel paragrafo precedente può essere formulato nel modo seguente:
3.3 FORMULAZIONE DEL MODELLO E CONDIZIONI DI ESISTENZA DI UN PUNTO DI OTTIMO VINCOLATO Il problema di ottimizzazione vincolata introdotto nel paragrafo precedente può essere formulato nel modo seguente:
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
1. seleziona una qualsiasi cella della tabella dati da analizzare 2. dal menu dati clicca su rapporto tabella pivot
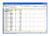 1. seleziona una qualsiasi cella della tabella dati da analizzare 2. dal menu dati clicca su rapporto tabella pivot si apre la finestra per la creazione guidata della tabella pivot come prima cosa viene
1. seleziona una qualsiasi cella della tabella dati da analizzare 2. dal menu dati clicca su rapporto tabella pivot si apre la finestra per la creazione guidata della tabella pivot come prima cosa viene
Def. 1. Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni:
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Esercizi di ottimizzazione vincolata
 Esercizi di ottimizzazione vincolata A. Agnetis, P. Detti Esercizi svolti 1 Dato il seguente problema di ottimizzazione vincolata max x 1 + x 2 x 1 4x 2 3 x 1 + x 2 2 0 x 1 0 studiare l esistenza di punti
Esercizi di ottimizzazione vincolata A. Agnetis, P. Detti Esercizi svolti 1 Dato il seguente problema di ottimizzazione vincolata max x 1 + x 2 x 1 4x 2 3 x 1 + x 2 2 0 x 1 0 studiare l esistenza di punti
Analisi delle corrispondenze
 Analisi delle corrispondenze Obiettivo: analisi delle relazioni tra le modalità di due (o più) caratteri qualitativi Individuazione della struttura dell associazione interna a una tabella di contingenza
Analisi delle corrispondenze Obiettivo: analisi delle relazioni tra le modalità di due (o più) caratteri qualitativi Individuazione della struttura dell associazione interna a una tabella di contingenza
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Algebra di Boole: minimizzazione di funzioni booleane
 Corso di Calcolatori Elettronici I A.A. 200-20 Algebra di Boole: minimizzazione di funzioni booleane Lezione 8 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Forme Ridotte p Vantaggi
Corso di Calcolatori Elettronici I A.A. 200-20 Algebra di Boole: minimizzazione di funzioni booleane Lezione 8 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Forme Ridotte p Vantaggi
Excel come foglio di calcolo. Altri Grafici con Excel Istogrammi, grafici a torta
 Excel come foglio di calcolo Altri Grafici con Excel Istogrammi, grafici a torta Funzioni di Excel per elaborazioni di dati presenti nel foglio Excel prevede una serie di funzioni predeterminate, raggruppate
Excel come foglio di calcolo Altri Grafici con Excel Istogrammi, grafici a torta Funzioni di Excel per elaborazioni di dati presenti nel foglio Excel prevede una serie di funzioni predeterminate, raggruppate
ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Un grafico utilizza i valori contenuti in un foglio di lavoro per creare una rappresentazione grafica delle relazioni esistenti tra loro;
 EXCEL Modulo 3 I Grafici Grafici Un grafico utilizza i valori contenuti in un foglio di lavoro per creare una rappresentazione grafica delle relazioni esistenti tra loro; Quando si crea un grafico ogni
EXCEL Modulo 3 I Grafici Grafici Un grafico utilizza i valori contenuti in un foglio di lavoro per creare una rappresentazione grafica delle relazioni esistenti tra loro; Quando si crea un grafico ogni
12. Dopo aver cliccato su INVIO, trascina il valore ottenuto nella cella a tutte le altre celle. Otterrai una tabella del tipo:
 Introduzione al concetto di limite con Excel Esercizio 1 Si consideri la funzione f x = x2 5x + 6 e se ne studi il comportamento per valori di x prossimi a 3. Analisi dell esercizio Bisogna predisporre
Introduzione al concetto di limite con Excel Esercizio 1 Si consideri la funzione f x = x2 5x + 6 e se ne studi il comportamento per valori di x prossimi a 3. Analisi dell esercizio Bisogna predisporre
Grafi e Funzioni di Costo ESERCIZI
 Grafi e Funzioni di Costo ESERCIZI Esercizio1 Si determini la matrice di incidenza archi-percorsi ed i costi di percorso per la rete di trasporto rappresentata in figura. 1 4 2 3 5 Ramo Costo Ramo Costo
Grafi e Funzioni di Costo ESERCIZI Esercizio1 Si determini la matrice di incidenza archi-percorsi ed i costi di percorso per la rete di trasporto rappresentata in figura. 1 4 2 3 5 Ramo Costo Ramo Costo
2. ALGORITMO DEL SIMPLESSO
 . ALGORITMO DEL SIMPLESSO R. Tadei Una piccola introduzione R. Tadei SIMPLESSO L obiettivo del capitolo è quello di fornire un algoritmo, l algoritmo del simplesso, che risolve qualsiasi problema di programmazione
. ALGORITMO DEL SIMPLESSO R. Tadei Una piccola introduzione R. Tadei SIMPLESSO L obiettivo del capitolo è quello di fornire un algoritmo, l algoritmo del simplesso, che risolve qualsiasi problema di programmazione
Corso di Matematica II Anno Accademico Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori
 Esercizio 1 Corso di Matematica II Anno Accademico 29 21. Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori May 7, 21 Commenti e correzioni sono benvenuti. Mi scuso se ci fosse qualche
Esercizio 1 Corso di Matematica II Anno Accademico 29 21. Esercizi di Algebra Lineare. Calcolo di autovalori ed autovettori May 7, 21 Commenti e correzioni sono benvenuti. Mi scuso se ci fosse qualche
Soluzione dei Problemi di Programmazione Lineare
 Soluzione dei Problemi di Programmazione Lineare Consideriamo un problema di Programmazione Lineare (PL) con m vincoli ed n variabili in Forma Standard dove: ma 0 c A b ( ) 0 ( 2) R è il vettore n delle
Soluzione dei Problemi di Programmazione Lineare Consideriamo un problema di Programmazione Lineare (PL) con m vincoli ed n variabili in Forma Standard dove: ma 0 c A b ( ) 0 ( 2) R è il vettore n delle
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
2.6 Calcolo degli equilibri di Nash
 92 2 Giochi non Cooperativi Per queste estensioni di giochi non finiti si possono provare risultati analoghi a quelli visti per i giochi finiti. Rimandiamo alla bibliografia per uno studio più approfondito
92 2 Giochi non Cooperativi Per queste estensioni di giochi non finiti si possono provare risultati analoghi a quelli visti per i giochi finiti. Rimandiamo alla bibliografia per uno studio più approfondito
Esercizi di PLI. a cura di A. Agnetis. Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory:
 Esercizi di PLI a cura di A. Agnetis Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory: max z = 40x + 24x 2 + 5x + 8x 4 8x + 6x 2 + 5x + 4x 4 22 x i 0 x i intero Si tratta di un
Esercizi di PLI a cura di A. Agnetis Risolvere il seguente problema di PLI con l algoritmo dei piani di Gomory: max z = 40x + 24x 2 + 5x + 8x 4 8x + 6x 2 + 5x + 4x 4 22 x i 0 x i intero Si tratta di un
Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto
 Il Metodo degli Elementi Finiti Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto Dalle dispense del prof. Dario Amodio e dalle lezioni del prof. Giovanni Santucci Per ottenere la
Il Metodo degli Elementi Finiti Assemblaggio degli Elementi: Soluzione del Problema Strutturale Discreto Dalle dispense del prof. Dario Amodio e dalle lezioni del prof. Giovanni Santucci Per ottenere la
Distribuzioni secondo due caratteri. Rappresentazioni e prime sintesi
 Distribuzioni secondo due caratteri Rappresentazioni e prime sintesi Rappresentazioni delle distribuzioni doppie Quando per ogni unità del collettivo rileviamo due caratteri otteniamo una Esempio. Ad alcuni
Distribuzioni secondo due caratteri Rappresentazioni e prime sintesi Rappresentazioni delle distribuzioni doppie Quando per ogni unità del collettivo rileviamo due caratteri otteniamo una Esempio. Ad alcuni
Motivazione: Come si fa? Matrici simmetriche. Fattorizzazioni di matrici speciali
 Motivazione: Fattorizzazioni di matrici speciali Diminuire la complessità computazionale = evitare operazioni inutili = risparmiare tempo di calcolo Diminuire l occupazione di memoria Come si fa? Si tiene
Motivazione: Fattorizzazioni di matrici speciali Diminuire la complessità computazionale = evitare operazioni inutili = risparmiare tempo di calcolo Diminuire l occupazione di memoria Come si fa? Si tiene
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
RICERCA OPERATIVA GRUPPO A prova scritta del 22 marzo 2007
 RICERCA OPERATIVA GRUPPO A prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
RICERCA OPERATIVA GRUPPO A prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
5.4.5 Struttura dell algoritmo ed esempi
 CAPITOLO 5. IL METODO DEL SIMPLESSO 6 5.4.5 Struttura dell algoritmo ed esempi Come abbiamo già ampiamente osservato, la fase II del metodo del simplesso, a partire da una soluzione di base ammissibile,
CAPITOLO 5. IL METODO DEL SIMPLESSO 6 5.4.5 Struttura dell algoritmo ed esempi Come abbiamo già ampiamente osservato, la fase II del metodo del simplesso, a partire da una soluzione di base ammissibile,
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
INFORMATICA 09-Foglio di calcolo-base
 INFORMATICA 09-Foglio di calcolo-base Marco Trapani trapani.marco@gmail.com trapani.marco@gmail.com 1 Storia Il foglio di calcolo nasce nel 1978 VISICALC Killer Application Sviluppo su sistemi di tutti
INFORMATICA 09-Foglio di calcolo-base Marco Trapani trapani.marco@gmail.com trapani.marco@gmail.com 1 Storia Il foglio di calcolo nasce nel 1978 VISICALC Killer Application Sviluppo su sistemi di tutti
Capitolo 11 Test chi-quadro
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
( ) le colonne della matrice dei coefficienti, con. , risulta A 3 = A 1 + 4A 2 + 4A 5, A 4 = A 1 + A 2,
 1 Elementi di Analisi Matematica e Ricerca Operativa prova del 6 luglio 2016 1) Discutere il seguente problema di Programmazione Lineare: Trovare il massimo di p x 1, x 2, x 3, x 4 # x 2 + 4 x 3 + x 4
1 Elementi di Analisi Matematica e Ricerca Operativa prova del 6 luglio 2016 1) Discutere il seguente problema di Programmazione Lineare: Trovare il massimo di p x 1, x 2, x 3, x 4 # x 2 + 4 x 3 + x 4
Modelli di programmazione lineare. Il metodo grafico è basato su linearità della funzione obiettivo linearità dei vincoli
 Ricerca Operativa 2. Modelli di Programmazione Lineare Modelli di programmazione lineare Il metodo grafico è basato su linearità della funzione obiettivo linearità dei vincoli Sotto queste ipotesi (come
Ricerca Operativa 2. Modelli di Programmazione Lineare Modelli di programmazione lineare Il metodo grafico è basato su linearità della funzione obiettivo linearità dei vincoli Sotto queste ipotesi (come
Marco Canu Excel Advanced: Note Operative Tabelle Pivot Excel 2013 Sella & Mosca Agg. 06/05/2017
 Indice Premessa... 2 Per generare una Tabella Pivot... 2 Esempio pratico... 5 Modifichiamo l esempio... 6 I Menu della Tabella Pivot... 9 Per realizzare un grafico Pivot... 10 Esposizione Tabella Pivot
Indice Premessa... 2 Per generare una Tabella Pivot... 2 Esempio pratico... 5 Modifichiamo l esempio... 6 I Menu della Tabella Pivot... 9 Per realizzare un grafico Pivot... 10 Esposizione Tabella Pivot
1 Definizione di sistema lineare omogeneo.
 Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
1 Il metodo dei tagli di Gomory
 Il metodo dei tagli di Gomory Esercizio Sia dato il problema min(x x ) x + x (P 0 ) x + x x, x 0, interi. Calcolare la soluzione ottima applicando il metodo dei tagli di Gomory. Risoluzione Per applicare
Il metodo dei tagli di Gomory Esercizio Sia dato il problema min(x x ) x + x (P 0 ) x + x x, x 0, interi. Calcolare la soluzione ottima applicando il metodo dei tagli di Gomory. Risoluzione Per applicare
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa 1 Seconda prova intermedia 17 giugno 2013
 A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia 7 giugno 0 Nome: Cognome: Matricola: Orale /06/0 ore aula N Orale 0/07/0 ore aula N
A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia 7 giugno 0 Nome: Cognome: Matricola: Orale /06/0 ore aula N Orale 0/07/0 ore aula N
Risoluzione di problemi ingegneristici con Excel
 Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Appendice A: un esempio di scelta del mix ottimo di produzione in presenza di vincoli 19
 14 18-12-07 19:04 Pagina 411 Le decisioni di breve termine fra alternative diverse 411 i minori costi differenziali, almeno nella misura in cui la dimensione di costo è la più importante. Sebbene i costi
14 18-12-07 19:04 Pagina 411 Le decisioni di breve termine fra alternative diverse 411 i minori costi differenziali, almeno nella misura in cui la dimensione di costo è la più importante. Sebbene i costi
Esercizi sulla Programmazione Lineare. min. cx Ax b x 0
 Soluzioni 4.-4. Fondamenti di Ricerca Operativa Prof. E. Amaldi Esercizi sulla Programmazione Lineare 4. Risoluzione grafica e forma standard. Si consideri il problema min x cx Ax b x dove x = (x, x )
Soluzioni 4.-4. Fondamenti di Ricerca Operativa Prof. E. Amaldi Esercizi sulla Programmazione Lineare 4. Risoluzione grafica e forma standard. Si consideri il problema min x cx Ax b x dove x = (x, x )
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Foglio Elettronico Lezione 1
 - Introduzione - Celle e riferimenti - Formule - Approfondimenti - Funzioni logiche Sommario Introduzione - Foglio elettronico o foglio di calcolo - Cos'è? Strumento per raccogliere dati organizzati in
- Introduzione - Celle e riferimenti - Formule - Approfondimenti - Funzioni logiche Sommario Introduzione - Foglio elettronico o foglio di calcolo - Cos'è? Strumento per raccogliere dati organizzati in
1 Combinazioni lineari.
 Geometria Lingotto LeLing5: Spazi Vettoriali Ārgomenti svolti: Combinazioni lineari Sistemi lineari e combinazioni lineari Definizione di spazio vettoriale Ēsercizi consigliati: Geoling 6, Geoling 7 Combinazioni
Geometria Lingotto LeLing5: Spazi Vettoriali Ārgomenti svolti: Combinazioni lineari Sistemi lineari e combinazioni lineari Definizione di spazio vettoriale Ēsercizi consigliati: Geoling 6, Geoling 7 Combinazioni
MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI. Anna TORRE
 MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI Anna TORRE Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100, Pavia, Italy. E-mail: anna.torre@unipv.it 1 SOLUZIONI:
MATEMATICA PER LO STUDIO DELLE INTERAZIONI STRATEGICHE: TEORIA DEI GIOCHI Anna TORRE Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100, Pavia, Italy. E-mail: anna.torre@unipv.it 1 SOLUZIONI:
Esercitazione 4. Dott.ssa Sabrina Pedrini
 Esercitazione 4 Dott.ssa Sabrina Pedrini Esercizio 1 Le funzioni seguenti sono caratterizzate da rendimenti di scala crescenti, costanti o decrescenti? Che cosa accade al prodotto marginale di ciascun
Esercitazione 4 Dott.ssa Sabrina Pedrini Esercizio 1 Le funzioni seguenti sono caratterizzate da rendimenti di scala crescenti, costanti o decrescenti? Che cosa accade al prodotto marginale di ciascun
Modelli di Ottimizzazione: definizione formale
 Modelli di Ottimizzazione: definizione formale Insieme delle possibili alternative Un criterio di ottimizzazione Soluzione ammissibile (Feasible) x appartiene ad un insieme F f: F funzione obiettivo finito
Modelli di Ottimizzazione: definizione formale Insieme delle possibili alternative Un criterio di ottimizzazione Soluzione ammissibile (Feasible) x appartiene ad un insieme F f: F funzione obiettivo finito
5. L elasticità dei costi totali rispetto alla quantità, in termini semplificati si scrive come = AC
 Capitolo 8 Le curve di costo Soluzioni delle Domande di ripasso 1. La curva del costo totale di lungo periodo mostra il costo totale minimo per ogni livello di output, tenendo fissi i prezzi degli input.
Capitolo 8 Le curve di costo Soluzioni delle Domande di ripasso 1. La curva del costo totale di lungo periodo mostra il costo totale minimo per ogni livello di output, tenendo fissi i prezzi degli input.
Integrazioni al corso di Economia Politica (anno accademico ) Marianna Belloc
 Integrazioni al corso di Economia Politica (anno accademico 2013-2014) Marianna Belloc 1 L elasticità Come è già noto, la funzione di domanda di mercato indica la quantità che il mercato è disposto ad
Integrazioni al corso di Economia Politica (anno accademico 2013-2014) Marianna Belloc 1 L elasticità Come è già noto, la funzione di domanda di mercato indica la quantità che il mercato è disposto ad
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
