Capitolo 5 - I sistemi lineari
|
|
|
- Timoteo Durante
- 6 anni fa
- Visualizzazioni
Transcript
1 Appuni di Teoria dei segnali Capiolo 5 - I sisemi lineari Definizioni principali... Esempio: moliplicaore...3 Esempio: sommaore...3 Esempio: derivaore...4 Esempio: inegraore...5 Esempio: sommaoria discrea...6 Esempio: riardo...7 Funzione risposa all impulso...8 Definizione...8 Imporanza della risposa all impulso...8 Sabilià (BIBO) di un sisema lineare empo-invariane... Premessa... Caso coninuo... Caso discreo... Esempio: riardo... 4 Esempio: inegraore... 5 Sisemi causali... 5 Definizione... 5 Caso coninuo... 5 Caso discreo... 6 Sisemi FIR causali... 7 Funzione risposa in frequenza... 8 Caso coninuo... 8 Caso discreo... 9 Esempio: sisema in reroazione... 9 Esempio: sisema passa-basso... Realizzabilià di un sisema lineare empo-invariane... 3 Esempio... 4 Esempio: filro passa-basso perfeo... 6 Esercizio... 8 Esercizio... 3 Filro di Hilber... 3 Definizione... 3 Risposa all impulso... 3 Trasformaa di Hilber Effeo del filro nel dominio della frequenza Segnale analiico Inviluppo complesso... 39
2 Appuni di Teoria dei Segnali - Capiolo 5 DEFINIZIONI PRINCIPALI Un sisema può essere viso come un qualcosa che, dao un ingresso x() coninuo o x(nt) discreo, opera su di esso una rasformazione e genera una uscia y() coninua o y(nt) discrea. Schemaicamene, possiamo indicare un sisema nel modo seguene: x() x(nt) T C T D y() y(nt) dove evidenemene [ ] D[ ] y( ) = T x( ) C y( nt) = T x( nt) caso coninuo caso discreo Def. Un sisema si dice lineare quando possiamo applicare ad esso il principio di sovrapposizione degli effei, ossia le proprieà di addiivià e di omogeneià. Vediamo cosa significa queso nel caso coninuo. Supponiamo di applicare due segnali in ingresso x() e g() e supponiamo che le rispeive rispose siano y() e z(); supponiamo adesso di applicare un nuovo ingresso che sia combinazione lineare degli alri due, ossia ax( ) + bg( ). Allora il sisema si dice lineare se la risposa a queso segnale è ay( ) + bz( ) ossia una combinazione lineare, con gli sessi coefficieni, delle corrispondeni rispose. Ovviamene lo sesso accade nel caso discreo. Def. Un sisema si dice inveribile quando possiamo ricavare l ingresso conoscendo solo la corrispondene uscia. Def. Un sisema si dice causale o anche non-anicipaivo quando il valore dell uscia ad un cero isane dipende SOLO dai valori dell ingresso relaivi all inervallo ]-,[. Def. Un sisema si dice sabile di ipo BIBO quando, applicando in ingresso un segnale limiao, noi oeniamo una uscia anch essa limiaa Def. Un sisema si dice empo-invariane quando, dai l ingresso x() e la corrispondene uscia y(), in corrispondenza di un nuovo ingresso x(- ) si oiene una uscia y(- ) In praica, quindi, diremo che un sisema è empo-invariane se, raslando nel empo a nosro piacimeno l ingresso x(), oeniamo sempre la sessa uscia, anch essa però raslaa come l ingresso.
3 I sisemi lineari Esempio: moliplicaore Consideriamo il sisema raffigurao qui di seguio: x() * y() Si raa del cosiddeo sisema moliplicaore: infai, dao il generico ingresso x(), l uscia y() è il prodoo di x() per un alra funzione g(). In queso caso, supponiamo ad esempio che g( ) = A cos πf + ϕ, per cui si ha, in generale, che ques alra funzione sia ( ) g() ( π ϕ) y( ) = x( ) A cos f + Vogliamo vedere se queso sisema è lineare e empo-invariane. Per farlo, dobbiamo ovviamene applicare le rispeive definizioni: consideriamo perciò due ingressi x () e x (): le rispeive rispose saranno y ( ) = x ( ) A cos πf + ϕ ( ) ( π ϕ) y ( ) = x ( ) A cos f + Adesso applichiamo in ingresso il segnale x( ) = ax ( ) + bx ( ) e valuiamo la risposa del sisema: y( ) = x( ) A cos πf + ϕ = ax ( ) + bx ( ) A cos πf + ϕ ( ) [ ] ( ) Da qui si deduce evidenemene che y( ) = ay ( ) + by ( ), ossia che il sisema è lineare. Passiamo a vedere se è anche empo-invariane o meno. Dao sempre l ingresso x () e la risposa y (), vediamo quale è la risposa al segnale x()=x (- ): ( π ϕ) ( π ϕ) y( ) = x( ) A cos f + = x ( ) A cos f + Da qui si noa che y( ) y( ), il che ci dice che il sisema non è empo-invariane. Esempio: sommaore Consideriamo adesso il sisema x() + y() g() 3
4 Appuni di Teoria dei Segnali - Capiolo 5 che prende il nome di sommaore in quano, dao il generico ingresso x(), l uscia y() è la somma di x() per un alra funzione g(). Supponiamo anche quesa vola che sia g( ) = A cos( πf + ϕ ), per cui si ha, in generale, che y( ) = x( ) + A cos πf + ϕ ( ) Vediamo anche qui se il sisema è lineare e empo-invariane. Cominciamo dalla linearià e consideriamo perciò due ingressi x () e x (): le rispeive rispose saranno ( π ϕ) ( π ϕ) y ( ) = x ( ) + A cos f + y ( ) = x ( ) + A cos f + Applicando in ingresso il segnale x( ) = ax ( ) + bx ( ), la risposa del sisema è ( π ϕ) [ ] ( π ϕ) y( ) = x( ) + A cos f + = ax ( ) + bx ( ) + A cos f + e da qui si deduce evidenemene che y( ) ay ( ) + by ( ), cioè che il sisema, quesa vola, NON è lineare. Passiamo a vedere se è empo-invariane o meno. Dao sempre l ingresso x () e la risposa y (), vediamo quale è la risposa al segnale x()=x (- ): ( π ϕ) ( π ϕ) y( ) = x( ) + A cos f + = x ( ) + A cos f + Si noa ancora una vola che y( ) y( ), per cui il sisema non è nemmeno empo-invariane. Esempio: derivaore Consideriamo adesso il sisema seguene: x() d/d y() Si raa quesa vola del cosiddeo derivaore, in quano l uscia è la derivaa rispeo al empo dx( ) dell ingresso: quindi y( ) =. d Verifichiamo ancora una vola linearià e empo-invarianza. Consideriamo due ingressi x () e x (): le rispeive rispose saranno d y d x ( ) = ( ) y d ( ) = d x ( ) Adesso applichiamo in ingresso il segnale x( ) = ax ( ) + bx ( ). La risposa del sisema è d y d x d ( ) = ( ) = ( ) + ( ) d [ ax bx ] 4
5 I sisemi lineari ed è evidene che y( ) = ay ( ) + by ( ). Quindi, il derivaore è un sisema lineare. Vediamo se è anche empo-invariane o meno. Considerao sempre l ingresso x () e la risposa y (), vediamo quale è la risposa al segnale x()=x (- ): d y d x d ( ) = ( ) = ( ) d [ x ] Perché il sisema sia empo-invariane, deve accadere che y( ) = y ( ), dove y() è quella calcolaa prima. Effeivamene queso accade, in quano, in base alla relazione generale che dx( ) caraerizza il sisema, ossia y( ) =, si ha che d y ( ) = dx ( ) d Quindi, il derivaore è un esempio di sisema lineare empo-invariane. Esempio: inegraore Consideriamo adesso il cosiddeo inegraore: x() x( τ) y() La relazione ra ingresso ed uscia è cioè y( ) = x( τ) Verifichiamo sempre una vola linearià e empo-invarianza. Consideriamo due ingressi x () e x (): le rispeive rispose saranno y ( ) = x ( τ) y ( ) = x ( τ) Adesso applichiamo in ingresso il segnale x( ) = ax ( ) + bx ( ). La risposa del sisema è [ ] y( ) = x( τ) = ax ( τ) + bx ( τ) 5
6 Appuni di Teoria dei Segnali - Capiolo 5 Sfruando la proprieà di linearià degli inegrali, è chiaro che y( ) = ay ( ) + by ( ), per cui l inegraore è un sisema lineare. Vediamo se è anche empo-invariane o meno. Considerao sempre l ingresso x () e la risposa y (), dobbiamo verificare se la risposa al segnale x()=x (- ) è Vediamo allora quano vale ale risposa: y( ) = y ( ) = x ( τ) y( ) = x( τ) = x ( τ ) Operando il cambio di variabile s=τ-, abbiamo che y( ) = x ( s) ds e il secondo membro non è alro che y (- ). Quindi, dopo il derivaore, abbiamo oenuo che anche l inegraore è un sisema lineare empo-invariane. Esempio: sommaoria discrea Fino ad ora abbiamo esaminao solo esempi di sisemi empo-coninui, ossia di sisemi in cui ad ingressi coninui corrispondono uscie coninue. Vediamo ora un esempio di sisema empodiscreo e precisamene il seguene: x(nt) N k= x( kt) y(nt) per il quale cioè il legame ingresso-uscia è N y( nt) = x( kt) k= Vediamo se queso sisema (che è, ovviamene, l analogo dell inegraore nel caso discreo) è lineare e empo-invariane. Conrolliamo per prima la linearià: dai due ingressi x (nt) e x (nt), le rispeive rispose saranno y ( nt) = x ( kt) k= y ( nt) = x ( kt) N N k= 6
7 I sisemi lineari Adesso applichiamo in ingresso il segnale x( nt) = ax ( nt) + bx ( nt). La risposa del sisema è N [ ] y( nt) = x( kt) = ax ( kt) + bx ( kt) k= N k= Sfruando la proprieà di linearià dell operaore sommaoria, è chiaro che y( nt) = ay ( nt) + by ( nt), per cui la sommaoria è un sisema (discreo) lineare. Vediamo se è anche empo-invariane o meno. Considerao sempre l ingresso x (nt) e la corrispondene risposa y (nt), dobbiamo verificare se la risposa al segnale x( nt) = x ( nt n T) Vediamo allora quano vale ale risposa: N n y( nt) = y ( nt n T) = x ( kt) N k= è y( nt) = x( kt) = x ( kt n T) k= N k= Operando il cambio di variabile i=k-n, abbiamo che N n i= y( nt) = x ( it) e il secondo membro non è alro che y (- ). Quindi, così come l inegraore nel caso coninuo, anche la sommaoria è un sisema (discreo) lineare empo-invariane. Esempio: riardo L ulimo esempio (ovviamene per adesso) che consideriamo è il sisema cosiddeo riardo, ossia un sisema che, sia nel caso coninuo sia in quello discreo, opera semplicemene una raslazione del empo dell ingresso. Possiamo schemaizzare ale sisema, nei due casi, nel modo seguene: x() R C y()=x(-t) x(nt) R D y(nt)=x((n-n )T) E facile verificare come anche quesi due sisemi siano lineari e empo-invariani. 7
8 Appuni di Teoria dei Segnali - Capiolo 5 Funzione risposa all impulso DEFINIZIONE Quando abbiamo inrodoo il conceo di sisema, abbiamo deo che si raa di un qualcosa che, dao un ingresso x() coninuo (o x(nt) discreo), opera su di esso una rasformazione e genera una uscia y() coninua (o y(nt) discrea). Viso in queso modo, possiamo caraerizzare il sisema mediane la relazione y( ) = T x( ) caso coninuo C [ ] D[ ] y( nt) = T x( nt) caso discreo Vogliamo adesso inrodurre una nuova funzione che consena di caraerizzare ancora meglio i sisemi LINEARI TEMPO-INVARIANTI, in quano consene di legare direamene ingresso ed uscia e consene anche di dedurre alcune imporani proprieà sul sisema sesso. Def. Si definisce risposa all impulso di un sisema (lineare empo-invariane) l uscia prodoa dal sisema sesso quando in ingresso viene applicao l impulso uniario La risposa all impulso si indica generalmene con h() nel caso coninuo e con h(nt) in quello discreo: in base a come l abbiamo definia, essa soddisfa la relazione [ δ ] D[ δ ] h( ) = T ( ) C h( nt) = T ( nt) caso coninuo caso discreo E ovvio anche che, il sisema è empo-invariane, vale anche la relazione [ δ ] D[ δ ] h( ) = T ( ) C h( nt n T) = T ( nt n T) caso coninuo caso discreo IMPORTANZA DELLA RISPOSTA ALL IMPULSO Esaminiamo adesso solo il caso coninuo, riservando per dopo quello discreo (che comunque è formalmene idenico). L imporanza fondamenale della funzione h() sa nel fao per cui essa soddisfa la seguene: relazione y( ) = x( ) * h( ) Quesa relazione dice che, noa la risposa in frequenza del nosro sisema e noo un qualsiasi ingresso x() ad esso applicao, possiamo conoscere (dal puno di visa analiico) la risposa y() a ale ingresso semplicemene effeuando la convoluzione ra x() e h(). 8
9 I sisemi lineari Vediamo allora di dimosrare quella relazione. Per farlo, ci ricordiamo di una proprieà della funzione δ() secondo la quale x( ) = x( ) * δ ( ). Usando quesa proprieà possiamo scrivere che [ ] C[ ] y( ) = T x( ) = T x( ) * δ( ) Espliciando l espressione di quel prodoo di convoluzione, abbiamo che C y( ) = TC x( τ) δ( τ) Noi siamo supponendo che il sisema sia LINEARE, il che significa che è lineare la rasformazione T C : queso ci consene di passarla soo il segno di inegrale, oenendo [ ] y( ) = TC x( τ) δ( τ) Per definizione di inegrale, la quanià x(τ) è una cosane, in quano τ si suppone fissao: daa sempre la linearià di T C, possiamo irar fuori ale cosane e scrivere che [ ] y( ) = x( τ) TC δ( τ) Abbiamo inolre viso prima che h( ) = TC [ δ ( )], per cui y( ) = x( τ) h( τ) = x( ) * h( ) e queso era quello che volevamo rovare. Vediamo adesso cosa accade quando il sisema considerao è discreo. In queso caso, la risposa all impulso h(nt) è la risposa del sisema all impulso uniario discreo, ossia il segnale δ( nt) n = = T n Facciamo vedere che y( nt) = x( nt) * h( nt) La dimosrazione è analoga a prima: si pare dal ricordare la proprieà secondo cui x( nt) = Tx( mt) δ( nt mt) = x( nt) * δ( nt) m= 9
10 Appuni di Teoria dei Segnali - Capiolo 5 In base a ale proprieà, abbiamo che y( nt) = TD [ x( nt) ] = TC [ x( nt) * δ( nt) ] = TC Tx( mt) δ( nt mt) m= Daa la linearià del sisema (e quindi di T D ) abbiamo poi che [ δ ] C[ δ ] y( nt) = TT x( mt) ( nt mt) = Tx( mt) T ( nt mt) m= Ma abbiamo deo che h( nt n T) = TD [ δ ( nt n T) ] C m=, per cui concludiamo che y( nt) = Tx( mt) h( nt mt) = x( nt) * h( nt) m= N.B. Le due dimosrazioni meono in evidenza come le due relazioni dimosrare valgano SOLO per i sisemi lineari empo-invariani Sabilià (BIBO) di un sisema lineare empo- invariane PREMESSA Abbiamo in precedenza già dao la definizione di sisema sabile di ipo BIBO: un sisema è ale quando, in corrispondenza di un ingresso limiao, si oiene una uscia anch essa limiaa. Vogliamo adesso vedere quali vincoli vengono imposi alla risposa impulsiva dal fao che il sisema è sabile. Ovviamene, ci riferiamo a sisemi lineari empo-invariani, sia coninui sia discrei, in quano solo per essi vale il conceo di risposa all impulso e solo per essi valgono inolre le relazioni y( ) = x( ) * h( ) caso coninuo y( nt) = x( nt) * h( nt) caso discreo CASO CONTINUO Cominciamo dal caso coninuo. Inendiamo dimosrare il seguene risulao: Teorema - Un sisema coninuo (lineare empo-invariane) è sabile SE E SOLO SE la risposa all impulso h() è una funzione assoluamene inegrabile
11 I sisemi lineari Deo in alri ermini, condizione necessaria e sufficiene affinché un sisema sia sabile è che valga la relazione < h( ) d < (dove nauralmene la scriura > è superflua in quano la funzione inegranda è ceramene posiiva). Dimosrazione Per dimosrare queso risulao, dobbiamo dimosrare evidenemene due implicazioni. Dimosriamo per prima quella secondo cui, nell ipoesi di h() assoluamene inegrabile, il sisema risula sabile. Le ipoesi sono dunque le segueni: il sisema è lineare empo-invariane; h() è assoluamene inegrabile; l ingresso x() applicao al sisema è limiao. Dobbiamo dimosrare che anche y(), risposa del sisema, è limiaa. Il puno di parenza è la relazione y( ) = x( ) * h( ) = x( τ) h( τ) Passando ai moduli, abbiamo che y( ) = x( τ) h( τ) In base ad una noa proprieà degli inegrali, possiamo passare il modulo all inerno dell inegrale e scrivere che y( ) x( τ) h( τ) x( τ) h( τ) Ora, dire che l ingresso x(τ) è limiao significa dire che x( τ) M τ, per cui abbiamo che y( ) M h( τ) = M h( τ) Essendo M un numero reale posiivo e avendo supposo che h() è assoluamene inegrabile, ossia che è evidene che anche y() è limiaa, ossia che h( ) d = N y( ) MN = M' Passiamo adesso alla implicazione inversa: nell ipoesi che il sisema sia sabile, dobbiamo far vedere che la risposa all impulso è assoluamene inegrabile.
12 Appuni di Teoria dei Segnali - Capiolo 5 Supporre il sisema sabile significa dire che, dao un qualsiasi ingresso limiao, la risposa a ale ingresso è anch essa limiaa. Consideriamo allora come ingresso limiao il seguene segnale: [ h τ ] x( τ) = sgn ( ) Si raa cioè del segnale che, in ogni isane τ, fornisce il segno (cioè + o -) del segnale h(τ) all isane -τ. La risposa a ale segnale sarà [ ] y( ) = x( ) * h( ) = x( τ) h( τ) = sgn h( τ) h( τ) Valuiamo in paricolare quesa risposa per = : [ ] y( ) = sgn h( τ) h( τ) La funzione inegranda è cosiuia dal prodoo della funzione h( τ ) per il suo segno: ale prodoo è evidenemene uguale al modulo della funzione sessa, per cui y( ) = h( τ) Ora supponiamo per assurdo che la esi non sia vera, ossia che, nonosane il sisema sia sabile, la funzione h() non sia assoluamene inegrabile: ciò significa che il valore dell ulimo inegrale ricavao non è finio, ossia che non è finio nemmeno il valore di y( ). Ma y( ) è il valore della risposa, valuaa all isane, all ingresso x(): dao che siamo supponendo che il sisema sia sabile e che x() sia un ingresso limiao, y( ) NON può essere infinio, per cui la esi deve essere necessariamene vera. CASO DISCRETO Il eorema appena dimosrao per il caso coninuo, vale anche per quello discreo: Teorema - Un sisema discreo (lineare empo-invariane) è sabile SE E SOLO SE la risposa all impulso h(nt) è una funzione assoluamene sommabile Deo in alri ermini, condizione necessaria e sufficiene affinché un sisema discreo sia sabile è che valga la relazione n= h( nt) < Dimosrazione Dimosriamo anche queso risulao, parendo dalla seconda implicazione: supponiamo cioè che il sisema sia lineare empo-invariane, che h(nt) sia assoluamene sommabile e che l ingresso x(nt) applicao al sisema sia limiao e facciamo vedere che anche y(nt), risposa del sisema, è limiaa.
13 I sisemi lineari Si pare anche qui dalla relazione Passando ai moduli si ha che y( nt) = x( nt) * h( nt) = Tx( mt) h( nt mt) m= y( nt) = Tx( mt) h( nt mt) Tx( mt) h( nt mt) T x( mt) h( nt mt) m= m= m= Ora, dire che l ingresso x(nt) è limiao significa dire che x( nt) M n, per cui abbiamo che y( nt) M T h( nt mt) m= Essendo M un numero reale posiivo e avendo supposo che h(nt) è assoluamene sommabile, è chiaro che anche y(nt) risula limiaa, ossia y( nt) M'. Passiamo adesso alla implicazione inversa: nell ipoesi che il sisema sia sabile, dobbiamo far vedere che la risposa all impulso è assoluamene inegrabile. Supporre il sisema sabile significa dire che, dao un qualsiasi ingresso limiao, la risposa a ale ingresso è anch essa limiaa. Consideriamo allora come ingresso limiao il seguene segnale: La risposa a ale segnale sarà [ ] x( nt) = sgn h( nt) [ ] y( nt) = x( nt) * h( nt) = Tx( mt) h( nt mt) = T sgn h( mt) h( nt mt) m= Valuiamo in paricolare quesa risposa per n=: [ ] m= y( ) = T sgn h( mt) h( mt) m= La funzione all inerno della sommaoria è cosiuia dal prodoo di una funzione per il suo segno, per cui è pari ancora una vola al modulo della funzione sessa: quindi y( ) = T h( mt) m= A queso puno, in modo analogo a quano fao nel caso coninuo, supponiamo per assurdo che la esi non sia vera, ossia che, nonosane il sisema sia sabile, la funzione h(nt) non sia assoluamene sommabile: ciò significa che il valore di quella sommaoria non è finio, ossia che non è finio nemmeno il valore di y(). Ma y() è il valore della risposa, valuaa all isane =, all ingresso x(nt): dao che siamo supponendo che il sisema sia sabile e che x(nt) sia un ingresso limiao, y() NON può essere infinio, per cui la esi deve essere necessariamene vera. 3
14 Appuni di Teoria dei Segnali - Capiolo 5 ESEMPIO: RITARDO Esaminiamo adesso alcuni esempi di sisemi sabili e alri di sisemi non sabili. Il primo che consideriamo è il sisema coninuo che abbiamo denominao riardo puro : x() R C y()=x(-t) Queso sisema (che sappiamo essere lineare empo-invariane) riceve dunque in ingresso il segnale x() e fornisce in uscia lo sesso segnale, ma raslao di una quanià T (>). Vediamo quano vale la risposa impulsiva di queso segnale, cioè la risposa fornia dal sisema quando in ingresso c è l impulso uniario: è ovvio che h( ) = x( T) = δ( T) Vediamo allora se h() è assoluamene inegrabile, al fine di sabilire se il sisema è sabile o meno: h( ) d = δ( T) d In base ad una noa proprieà della funzione δ(), si ha che δ( T) d = il che ci dice che, effeivamene, il nosro sisema è sabile. E inuiivo immaginare come anche il riardo nel caso discreo sia un sisema sabile: in queso caso, il sisema è x(nt) R D y(nt)=x((n-n )T) La sua risposa impulsiva è h( nt) = x( nt n T) = δ( nt n T) e, in base ad una proprieà della funzione impulso nel caso discreo, si ha che m= h( nt) = δ( nt nt) = m= 4
15 I sisemi lineari ESEMPIO: INTEGRATORE Un alro sisema lineare empo-invariane esaminao in precedenza è l inegraore: x() x( τ) y() La relazione ra ingresso ed uscia è y( ) = x( τ). Valuiamo anche qui la risposa impulsiva: per definizione, abbiamo inano che h( ) = δ ( τ ) d τ La funzione inegranda è l impulso uniario applicao in τ=; allora, in base alle proprieà della funzione δ(), quell inegrale vale quando < menre vale quando : h( ) = < Si noa dunque che h() risula essere il gradino uniario u(), che è evidenemene una funzione NON assoluamene inegrabile. Di conseguenza, l inegraore NON è un sisema sabile: se noi applichiamo un ingresso limiao, è possibile che l uscia non sia limiaa. Sisemi causali DEFINIZIONE La definizione di sisema causale è saa già daa: un sisema coninuo è causale quando, dao l ingresso x(), il valore della risposa all isane dipende SOLO dai valori di x() compresi nell inervallo di empo ]-,] (analoga definizione per i sisemi discrei). Al pari di quano fao per la sabilià, vediamo anche qui quali vincoli la causalià impone sulla risposa impulsiva. Ovviamene, supponiamo che i sisemi considerai siano lineari empo-invariani. CASO CONTINUO Cominciamo dal caso coninuo, per cui pariamo dalla relazione generale y( ) = x( ) * h( ) = x( τ) h( τ) 5
16 Appuni di Teoria dei Segnali - Capiolo 5 Per definizione di causalià, y() non può dipendere dai valori di x() successivi all isane, per cui l esremo superiore di inegrazione non può che essere : y( ) = x( ) * h( ) = x( τ) h( τ) Quindi, la causalià impone che valga la relazione x( τ) h( τ) = x( τ) h( τ) Quando accade queso?. L inegrale a primo membro può essere spezzao in due pezzi nel modo seguene: x( τ) h( τ) + x( τ) h( τ) = x( τ) h( τ) Da qui si ricava evidenemene che x( τ ) h( τ ) d τ = ossia che quesa è la condizione cui deve soddisfare h(τ) quando il sisema è causale. Ora, quell inegrale risula ceramene nullo quando h( τ) = τ >, ossia, anche, quando ossia anche, ponendo α=-τ, quando h( τ) = - τ < h( α) = α < Quindi, abbiamo rovao che un sisema è ceramene causale se la sua funzione di risposa all impulso è nulla negli isani precedeni allo zero. CASO DISCRETO Il discorso è analogo nel caso discreo. La relazione generale è y( nt) = x( nt) * h( nt) = Tx( mt) h( nt mt) m= Il sisema è causale se l esremo superiore della sommaoria divena n, ossia se accade che Tx( mt) h( nt mt) = m= n 6
17 I sisemi lineari ossia se h (nt mt) = m > n +, ossia, infine, ponendo k=n-m, se h( kt) = k < In base a quesa relazione, ci sono alcune imporani definizioni circa i sisemi discrei: quando esise solo un numero finio di valori di k per i quali h(kt), il sisema (discreo) si dice di ipo FIR ; quando, invece, esisono infinii valori di k per cui h(kt), il sisema si dice di ipo IIR. Sisemi FIR causali Consideriamo in paricolare un sisema discreo (lineare empo-invariane), di ipo FIR che sia anche causale. Dire che il sisema è causale significa dire che h( kt) = k < Dire, poi, che è di ipo FIR significa dire che quei pochi valori di k per i quali h(kt) sono ui posiivi. In base alla causalià, possiamo dunque scrivere che Sviluppiamo quesa sommaoria: y( nt) = x( nt) * h( nt) = Tx( mt) h( nt mt) m= y( nt) =... + Tx 444 ( T ) h( 444 nt+ 3 T) + Tx 44 ( T) h( 444 nt+ 3 T) + Tx 4 ( ) h 4 ( nt 3 ) + Tx 44 ( T) h ( nt 44 3 T) + Tx 4 ( T 4 ) h ( nt T) +... m= m= m= m= m= Essendo il sisema di ipo FIR, supponiamo che il numero di valori (posiivi) di k per i quali h(kt) sia L e, in paricolare, supponiamo che h( T) = α h( T) = α h( T) = α... h( L) = α Sulla base di ciò, è ovvio che y(nt) sarà la somma di un numero finio di ermini, che sono quelli in cui la funzione h non risula nulla: quindi L ( T) h T + ( ) y( nt) = Tx ( 4 nt ) h 44 ( 3 T) + Tx ( n ) ( )... Tx ( n L) T h( LT) m= n m= n m= n L 7
18 Appuni di Teoria dei Segnali - Capiolo 5 Funzione risposa in frequenza CASO CONTINUO Consideriamo un sisema lineare empo-invariane generico: x() x(nt) T C T D y() y(nt) In paricolare, per il momeno esaminiamo il caso coninuo, riservando per dopo quello discreo. Applichiamo in ingresso al nosro sisema il segnale esponenziale x( ) = e jπf. Valuiamo la risposa del sisema: jπf ( ) y( ) = x( ) * h( ) = x( τ) h( τ) = h( τ) x( τ) = h( τ) e τ Il ermine esponenziale può essere scisso in due ermini, per cui si ha che [ ] y h e j f e j f d e j f ( ) = ( τ) π π τ τ = π h( τ) e j π f τ Il ermini porao fuori dall inegrale non è alro che il nosro ingresso x(); l inegrale rimaso, invece, non è che la rasformaa di Fourier della funzione risposa all impulso h(), calcolaa nella specifica frequenza f : indicandola allora con H(f ), possiamo dunque concludere che y( ) x( ) H( f ) = Quesa relazione ci dice che, dao un generico sisema lineare empo-invariane, i segnali esponenziali non vengono da esso modificai, salvo la presenza di un faore moliplicaivo H(f ). Alla funzione H(f) si dà il nome di risposa in frequenza o funzione di rasferimeno del sisema. Vediamo nel deaglio come si può definire quesa funzione. Per farlo, consideriamo la relazione y( ) = x( ) * h( ). Se rasformiamo ambo i membri secondo Fourier, ricordando che la rasformaa di un prodoo di convoluzione è pari al prodoo delle rasformae, abbiamo evidenemene che Y( f ) = X( f ) H( f ),da cui Y( f ) H( f ) = X( f ) 8
19 I sisemi lineari Quindi, la risposa in frequenza di un sisema è la rasformaa di Fourier della funzione risposa all impulso e può essere ricavaa come rapporo ra la rasformaa dell uscia e la rasformaa dell ingresso. Ovviamene, si raa di una caraerisica del sisema, indipendene cioè dall ingresso. CASO DISCRETO Esaminiamo adesso il caso discreo. Come ingresso al nosro sisema (lineare empo-invariane), applichiamo il segnale esponenziale x( nt) = e jπf nt. La risposa del sisema è jπf ( n m) T y( nt) = x( nt) * h( nt) = Tx( mt) h( nt mt) = Th( mt) x( nt mt) = Th( mt) e = m= m= j f nt j f mt j f nt j f mt = Th( mt) e e = e Th( mt) e = x( nt) Th( mt) e m= m= m= π π π π jπfmt Abbiamo rovao che y(nt) è il prodoo di x(nt) per un faore cosane (quella sommaoria non presena ermini variabili, per cui è un numero). A ale faore cosane, come vedremo meglio nel seguio, si dà il nome di rasformaa di Fourier, discrea, del segnale h(), calcolaa ovviamene per f=f. Anche in queso caso, dunque, abbiamo rovao che = y( nt) x( nt) H( f ) m= ESEMPIO: SISTEMA IN RETROAZIONE Consideriamo il sisema schemaizzao nella figura seguene: α x() + * y() y(-t) T Vediamo inano quale effeo ha il sisema sull ingresso x(): la prima cosa è la moliplicazione di x() per una cosane α; si produce così il segnale y( ) = α x( ). Queso segnale, che già cosiuirebbe l uscia, viene prelevao e subisce un riardo, ossia una raslazione di una quanià T; si produce perciò il segnale y( T). Queso segnale viene sommao nuovamene all ingresso, per cui si produce il segnale y( T) + x( ). Infine, c è un ulima moliplicazione per α, per cui l uscia del sisema si può esprimere nella forma y( ) = αy( T) + αx( ) 9
20 Appuni di Teoria dei Segnali - Capiolo 5 Uno schema di queso ipo prende il nome di sisema in reroazione in quano l uscia viene riporaa in ingresso e quindi, si porebbe dire, conribuisce a modificare se sessa. Di queso sisema, nell ipoesi che sia lineare empo-invariane, ci ineressano la risposa all impulso h() e la risposa in frequenza H(f). Ovviamene, ci baserà deerminare una delle due funzioni e poi ricavare l alra rasformando o anirasformando secondo Fourier. Per prima cosa, esprimiamo in modo per noi più conveniene la y(): infai, in base alla espressione y( ) = αy( T) + α x( ) prima rovaa, è chiaro che per cui possiamo scrivere che [ ] y( T) = αy( T) + αx( T) y( ) = α αy( T) + αx( T) + αx( ) = α y( T) + α x( T) + αx( ) Facendo lo sesso discorso per y(-t) abbiamo che e quindi [ ] y( T) = αy( 3T) + αx( T) 3 3 y( ) = α αy( 3T) + αx( T) + α x( T) + αx( ) = α y( 3T) + α x( T) + α x( T) + αx( ) Procedendo in modo ricorsivo, per N ermini abbiamo che ( ) n+ n+ y( ) = α y ( N + ) T + αx( ) + α x( nt) Il ermine αx() può anche essere inglobao nella sommaoria, per cui abbiamo che ( ) N n= n+ n+ y( ) = α y ( N + ) T + α x( nt) A queso puno, facciamo l ipoesi che il segnale y() sia ad energia finia: quesa ipoesi implica, almeno a livello inuiivo, che il valore dell uscia, per, enda ad annullarsi, ossia N n= y( ) e che quindi il sisema risuli sabile. In paricolare, se y( ), possiamo esprimere la nosra uscia mediane l espressione N n y( ) = α α x( nt) n=
21 I sisemi lineari A parire da quesa espressione, siamo in grado di valuare la risposa impulsiva, ossia la risposa h() quando in ingresso è applicao l impulso uniario δ(): N n h( ) = α α δ( nt) n= Mediane una operazione di rasformazione secondo Fourier, possiamo anche oenere la risposa in frequenza: N N N n n n j fnt H( f ) = Fourier ( nt) Fourier[ ( nt) ] e n = = π αα δ αα δ αα = = n= n= = α N n= π ( αe ) j ft n Nel caso in cui α <, quella sommaoria non è alro che la serie geomerica di ragione cui concludiamo che = H(f ) α j αe πft α j ft e π, per A queso sesso risulao noi possiamo arrivare in modo molo più rigoroso: menre prima, per arrivare all espressione di h(), abbiamo ragionao esclusivamene nel dominio del empo, possiamo provare a ragionare nel dominio della frequenza. Infai, a parire dalla relazione y( ) = αy( T) + αx( ) operando una rasformazione di Fourier di enrambi i membri, abbiamo che j ft Y( f ) = Y( f ) e π α + αx( f ) da cui si ricava che jπft ( α ) e Y( f ) = αx( f ) La risposa in frequenza è definia come rapporo ra Y(f) e X(f), per cui oeniamo nuovamene Y( f ) H( f ) = = X( f ) e j π α ft α Per oenere h() dobbiamo anirasformare H(f): h() = Fourier αe jπft α = αfourier αe jπft = αfourier jπft [( αe ) ] =...
22 Appuni di Teoria dei Segnali - Capiolo 5 ESEMPIO: SISTEMA PASSA-BASSO Consideriamo il sisema seguene: x() + h () y() * α Vogliamo la risposa all impulso h() e quella in frequenza H(f) del nosro sisema, nell ipoesi, ovviamene, che esso sia lineare empo-invariane. Per prima cosa esaminiamo quale azione esercia il nosro sisema sul segnale in ingresso: la prima azione è quella eserciaa dal soosisema, la cui risposa all impulso è saa indicaa con h (). All uscia di queso soosisema, noi oeniamo il segnale y( ) = x( ) * h ( ). Traandosi di uno schema in reroazione, queso segnale passa per il moliplicaore e divena αy( ). Successivamene, esso viene sommao all ingresso, in modo da oenere il segnale αy( ) + x( ) ed enra nuovamene nel soosisema, in modo che il segnale in uscia sia infine [ ] y( ) = y( ) + x( ) * h ( ) α Per rovare h() e H(f), ci conviene evidenemene lavorare nel dominio della frequenza, ossia rovare H(f) e poi anirasformare per oenere h(). Allora, rasformando secondo Fourier ambo i membri di quella relazione abbiamo che [[ α ] ] [ α ] [ α ( ) * ( )] [ ( ) * ( )] α ( ) ( ) ( ) ( ) Y( f ) = Fourier y( ) + x( ) * h ( ) = Fourier y( ) * h ( ) + x( ) * h ( ) = = Fourier y h + Fourier x h = Y f H f + X f H f Da qui si oiene che e quindi anche che X f H f Y( f ) = ( ) ( ) αh ( f ) Y( f ) H ( f ) H( f ) = = X( f ) αh ( f ) Quindi, se è noa la risposa in frequenza del soosisema, siamo in grado di conoscere H(f) e, anirasformando, anche h(). Per esempio, supponiamo che H (f) sia la funzione seguene:
23 I sisemi lineari H (f) A -f +f f Analiicamene, la possiamo esprimere nel modo seguene: H ( A f f ) = [-f,+f ] alrimeni Di conseguenza, la risposa in frequenza del nosro sisema è e si raa perciò di un alro reangolo: A H( f ) = f < f αa A αa H(f) -f +f f Da un puno di visa praico, l effeo del sisema è dunque quello di lasciar passare, dao l ingresso, solo le frequenze comprese ra -f e +f e di azzerare ue le alre. Ecco perché queso sisema prende il nome di sisema passa-basso. Noa H(f), possiamo calcolarci h() anirasformando: h ( A ) = Fourier A rec f A = f A f sinc( f ) α α REALIZZABILITÀ DI UN SISTEMA LINEARE TEMPO-INVARIANTE Sulla base di queso esempio possiamo dare due definizioni ineressani: quando la funzione risposa all impulso h() è una funzione reale, si dice che il sisema è idealmene realizzabile ; 3
24 Appuni di Teoria dei Segnali - Capiolo 5 quando, invece, h() risula reale e anche CAUSALE, allora si dice che il sisema è fisicamene realizzabile. Nell esempio di prima, h() è una funzione sinc per cui è senz alro reale. Tuavia, essendo il sinc una funzione periodica, h() non è una funzione causale, per cui il nosro sisema è solo idealmene realizzabile. ESEMPIO Consideriamo il sisema rappresenao in figura: x() y() y( τ) z() T Abbiamo dunque un sisema cosiuio da due disini blocchi: in ingresso al primo blocco c è l ingresso x() del sisema complessivo; in uscia dal primo blocco c è il segnale y() che va in ingresso al secondo blocco (che è un inegraore) e l uscia z() di queso secondo blocco è anche l uscia del sisema complessivo. Di ques ulimo vogliamo conoscere la risposa in frequenza H(f). Abbiamo due modi di procedere: il primo modo è quello di lavorare nel dominio del empo, cioè di rovare quano vale la risposa impulsiva h() e poi di rasformarla secondo Fourier; il secondo modo è invece quello di lavorare nel dominio della frequenza, uilizzando la linearià della rasformaa di Fourier. Vediamo enrambi i meodi a cominciare dal primo. Per prima cosa, vediamo come è faa l uscia z() del nosro sisema: l ingresso x() viene subisce, nel primo blocco, un riardo e viene poi sorao da se sesso per dare y(), per cui abbiamo che y( ) = x( ) x( T). Successivamene, y() passa semplicemene per l inegraore, per cui possiamo concludere che l uscia del nosro sisema, in corrispondenza del generico ingresso x(), vale [ ] z( ) = x( τ) x( τ T) La risposa impulsiva è, per definizione, la risposa del sisema quando in ingresso viene applicao all impulso: ponendo allora x()=δ() e z()=h(), abbiamo che [ ] h( ) = δ ( τ ) δ ( τ T) d τ 4
25 I sisemi lineari Queso inegrale può essere risolo per via grafica; infai, la funzione inegranda può essere inerpreaa come il seguene segnale: δ( ) T Calcolarne l inegrale ra - e significa considerarne il segnale inegrao ossia, in alre parole, il segnale che, derivao, dà quei due impulsi. E facile allora verificare che ale segnale derivao è il seguene: T Infai esso vale per < e >T; in = passa repeninamene da a, da cui l impulso uniario del segnale derivao; poi si maniene cosane, per cui il segnale derivao è zero; infine in =T riorna bruscamene a zero, da cui l impulso uniario negaivo del segnale derivao. Il nosro h() è dunque l ulimo segnale disegnao, ossia un reangolo di alezza e base T, raslao di +T/: T h( ) = rec T Se quesa è la risposa all impulso, la sua rasformaa è la risposa in frequenza: T π H( f ) = Fourier rec = Tsinc( ft) e = Tsinc( ft) e T j f T jπft L alra srada per arrivare a queso risulao era lavorare in frequenza e considerare le funzioni di risposa in frequenza dei singoli blocchi di cui si compone il nosro sisema: infai, se l uscia y() del primo blocco in corrispondenza del generico ingresso x() è daa da y( ) = x( ) x( T), la sua rasformaa è Y( f ) = X( f ) X( f ) e j π ft 5
26 Appuni di Teoria dei Segnali - Capiolo 5 Quesa uscia y() passa araverso l inegraore: nel dominio della frequenza, queso equivale a moliplicare Y(f) per il ermine /jπf, per cui Z( f ) = X( f ) X( f ) e jπf jπft Infine, applicando la definizione di risposa in frequenza abbiamo che j Z f e H( f ) = ( ) X( f ) = jπf Quesa può essere opporunamene manipolaa: jπft jπft jπft jπft jπft jπft jπft jπft e e e e e e Te H( f ) = e = = sin( πft) = sin( πft) = jπf πf j πf Tπf = Te jπft sinc( ft) πft ESEMPIO: FILTRO PASSA-BASSO PERFETTO Consideriamo il seguene sisema lineare empo-invariane: x() H(f) y() -B +B f Queso sisema prende il nome di filro passa-basso perfeo in quano ha l effeo di lasciar passare il segnale in ingresso inalerao, ma solo enro un inervallo di frequenza presabilio, che in queso caso è [-B,+B]. Supponiamo allora di applicare in ingresso il segnale esponenziale A α x( ) = Ae 6
27 I sisemi lineari Ci poniamo il problema di deerminare il valore della banda B della risposa in frequenza affinché il segnale in uscia y() abbia il 9% dell energia del segnale in ingresso x(). Il primo passo è ovviamene quello di deerminare quano vale l energia del segnale in ingresso: applicando semplicemene la definizione di energia abbiamo che E x( ) d X = Sosiuendo l espressione di x() e considerando che esso è nullo per <, abbiamo che [ ] A E X = Ae α d = Ae α d = ( α) e α d = e α = e = α α α α α Quindi, a noi serve deerminare il valore B ale che l energia del segnale in uscia sia pari a.9/α. Per calcolare l energia del segnale in uscia dobbiamo conoscerne l espressione, in modo da poer applicare anche lì la formula E y( ) d Y = Tuavia, dao che conosciamo l ingresso x() e conosciamo la funzione di risposa in frequenza H(f), è più conveniene calcolare Y(f) e poi applicare la formula E Y( f ) df Y = Ricordando che Y(f) può essere espressa mediane la relazione Y( f ) = H( f ) X( f ), è ovvio che ci serve X(f). Applicando semplicemene la definizione di rasformaa di Fourier, abbiamo i segueni passaggi: [ ] [ ] α α α jπf α jπf ( α+ jπf ) X( f ) = Fourier Ae = AFourier e = A e e d = A e e d = A e d = ( α+ jπf ) A ( α+ jπf ) [ ] d [ e ] A = A D e = = ( α + jπf ) ( α + jπf ) jπf + α A queso puno, possiamo calcolarci l energia del segnale y(): abbiamo deo che la formula da applicare è E Y = X( f ) H( f ) df Sosiuendo l espressione di X(f) e considerando che la funzione di H(f), che è un reangolo, è solo quella di limiare gli esremi di inegrazione, abbiamo che 7
28 Appuni di Teoria dei Segnali - Capiolo 5 E Y + B A A = H( f ) df = df = A df = A j f + j f + π α π α jπf + α π + α B + B B + B B ( f) df A queso puno, per comodià poniamo w=πf: oeniamo E Y = A + πb πb Quello è un inegrale immediao e dà w + α dw = A + πb πb w α + w dw E Y = A + πb α α α A arcg w = arcg arcg πb πb πb Imponendo adesso che E X =.9/α, si rova il valore richieso di B. ESERCIZIO Consideriamo il sisema seguene: + i() R + x() - C y() - Abbiamo dunque un semplice circuio in cui in ingresso c è una ensione x() e, come uscia y(), viene consideraa la ensione ai capi del condensaore. Vogliamo conoscere la funzione di risposa all impulso h(). In primo luogo, osserviamo che parlare di risposa all impulso presuppone che il sisema sia lineare empo-invariane: queso è effeivamene vero in quano nel circuio compaiono un resisore ed un condensaore enrambi lineari e empo-invariani. Il problema della deerminazione di h() può essere facilmene risolo servendosi proprio della rasformaa di Fourier, ossia, in definiiva, rovando la risposa in frequenza H(f) e poi anirasformandola. La prima cosa da fare è individuare quale legame inercorre, nel dominio del empo, ra ingresso x() e uscia y(). Lo possiamo fare semplicemene applicando la legge di Kirchoff delle ensioni e le relazioni di lao di resisore e condensaore. In base alla LKT (applicaa in senso aniorario) abbiamo che x( ) y( ) V ( ) = R 8
29 I sisemi lineari In base alla relazione di lao del resisore, abbiamo che x( ) y( ) Ri( ) = da cui, espliciando la correne, si ha che i( ) = x( ) y( ) R Adesso, la relazione di lao del condensaore dice che i C dv C dy C ( ) ( ) ( ) = = d d per cui, eguagliando i secondi membri delle due espressioni rovae per i(), oeniamo x ( ) y ( ) = C dy( ) R d Espliciando la x() si oiene quindi x RC dy ( ) ( ) = + y( ) d Quesa è una equazione differenziale nella incognia y(). Allora, se poniamo x()=δ() e la risolviamo, roviamo proprio la h(). Tuavia, nonosane la risoluzione dell equazione non sia complicaa, possiamo fare molo più in frea lavorando nel dominio della frequenza: infai, se rasformiamo secondo Fourier ambo i membri di quella equazione (usando il eorema di derivazione nel empo) oeniamo che X( f ) = RC( jπf ) Y( f ) + Y( f ) da cui Y( f ) H( f ) = = X( f ) + jπrcf Noa la risposa in frequenza, dobbiamo anirasformarla per oenere h(). Come si anirasforma quella funzione? Ci basa ricordare di un risulao rovao in precedenza e precisamene che Fourier e a [ ] = a + jπf Se, al denominaore a secondo membro meiamo in evidenza a, oeniamo Fourier e a [ ] = a πf + j a e quindi anche che 9
30 Appuni di Teoria dei Segnali - Capiolo 5 Fourier ae a [ ] = πf + j a Allora, ponendo a =, oeniamo RC RC Fourier e = RC + jrc π f ossia che l anirasformaa di H ( f ) = + jπrcf h( ) = è la funzione RC e RC che era ciò che andavamo cercando. Adesso poniamoci un alro problema: noa h() (ossia noe le caraerisiche del nosro sisema), vogliamo la risposa del sisema all ingresso T x( ) = rec T T Il problema è di immediaa risoluzione in quano sappiamo che vale la relazione y( ) = x( ) * h( ), per cui y( ) = x( τ) h( τ) La funzione x() è un semplice reangolo, il quale ha dunque il solo effeo di resringere l inervallo di inegrazione: quindi T T y h d RC e RC d RC e RC T e RC d e RC T D e RC d e RC T ( τ ) τ τ e RC ( ) = ( ) = = =... = = τ τ τ τ τ 3
31 I sisemi lineari ESERCIZIO Consideriamo adesso ques alro circuio: R + i() + C x() y() - R C - L ingresso è la ensione x() e l uscia y() è la ensione ai capi di C e/o di R. Troviamo anche in queso caso la funzione di risposa all impulso h(). Il meodo è lo sesso del caso precedene: applicando la LKT alla maglia di sinisra e le relazioni di lao di resisore e condensaore oeniamo che i( ) = x( ) y( ) + C d R d [ x( ) y( ) ] In modo analogo, per la maglia di desra oeniamo Eguagliando le due relazioni oeniamo y( ) i C dy ( ( ) ) = + R d da cui x( ) y( ) C d y( ) [ x y ] C dy ( ( ) ( ) ) + = + R d R d x( ) C dx ( ) y( ) C dy ( ) C dy ( ) y( ) + = R d R d d R Trasformando secondo Fourier oeniamo R + C j f X f ( C C ) j f R R Y f = ( π ) ( ) π ( ) e quindi Y( f ) H( f ) = = X( f ) + C ( jπf ) R + + ( C + C ) jπf R R 3
32 Appuni di Teoria dei Segnali - Capiolo 5 Filro di Hilber DEFINIZIONE Sappiamo che un qualsiasi sisema lineare empo-invariane può essere caraerizzao in modo esremamene compleo mediane la sua funzione di risposa all impulso h(), o, equivalenemene, dalla sua funzione di rasferimeno (che è la rasformaa di Fourier della funzione di risposa all impulso). Consideriamo allora una paricolare sisema avene la seguene funzione di rasferimeno: j f > H ( H f ) = f = j f < Un sisema avene quesa funzione di rasferimeno prende il nome di filro di Hilber e ci appresiamo a sudiarne le caraerisiche. La prima cosa che osserviamo è che la funzione H H (f) presena una disconinuià nel puno f=: per convenzione si pone = il valore della funzione in f=, ma è bene ricordare che si raa di una disconinuià e che, di conseguenza, alcuni dei risulai che ci appresiamo a ricavare vanno presi un po' con le pinze. RISPOSTA ALL IMPULSO Ricaviamo la funzione di risposa all impulso h() del nosro sisema: sappiamo che [ H ] h ( ) = Fourier H ( f ) H per cui la prima cosa da fare è esprimere in modo per noi più comodo la H H (f). E facile verificare che essa si può esprimere in due alri modi, del uo equivaleni ra loro: H ( f ) = j sgn( f ) = e π H j sgn( f ) In paricolare, prendiamo la prima espressione, che dobbiamo adesso anirasformare. Per effeuare quesa anirasformaa, uilizziamo due risulai precedenemene ricavai: il primo è la rasformaa di Fourier del segnale sgn(), che sappiamo essere [ ] Fourier sgn( ) = jπf 3
33 I sisemi lineari L alro è la proprieà di dualià, secondo la quale s( ) S(f ) S() s( f ) Nel nosro caso, l applicazione della proprieà di dualià ci pora a dire che sgn( ) jπ jπf sgn( f ) Ricordando inolre che la funzione sgn è una funzione dispari, abbiamo che f jπ sgn( ) Infine, porando il ermine j al secondo membro, possiamo concludere che π jsgn( f ) Dao, allora, che H ( f ) = H j sgn( f ), deduciamo che h ( H ) = π Quesa funzione h H () presena due caraerisiche imporani: essa è REALE ma non è causale, per cui sappiamo di poer affermare che queso sisema è solo IDEALMENTE REALIZZABILE, menre non è possibile oenerlo nella praica. Da un puno di visa grafico, la funzione h H () ha il seguene andameno: 33
34 Appuni di Teoria dei Segnali - Capiolo 5 TRASFORMATA DI HILBERT Consideriamo adesso un generico segnale empo-coninuo s() e facciamo su di esso due ipoesi fondamenali:. la prima è che sia ad energia finia, il che significa che { } E = S s ( ) d R. la seconda è che sia ad area nulla (o anche a media nulla), ossia, in definiiva, che S(f = ) = dove S(f) è la rasformaa di Fourier di s() (rasformaa che sicuramene esise daa l ipoesi di prima). Adesso supponiamo che queso segnale venga poso in ingresso al filro di Hilber. Vogliamo valuare quano vale la risposa y(). In base alla noa relazione y( ) = s( ) * h ( ), abbiamo che H y( ) = s( τ) π ( τ ) Il segnale y() così calcolao prende il nome di rasformaa di Hilber del segnale s(). In verià, è bene ricordare che il ermine rasformaa è un po' improprio: infai, menre con le rasformae classiche (Fourier e Laplace) il dominio di arrivo è diverso da quello di parenza, in queso caso si raa sempre dello sesso dominio, quello del empo. Ad ogni modo, viene usaa quesa espressione e il simbolo che si usa soliamene è $s(). EFFETTO DEL FILTRO NEL DOMINIO DELLA FREQUENZA Adesso facciamo lo sesso discorso di prima, cioè la deerminazione della risposa del sisema, ma nel dominio della frequenza: la relazione da uilizzare è in queso caso Y( f ) = S(f ) H H ( f ). Per capire quale effeo abbia il filro, ossia la funzione H H (f), sul segnale in ingresso, ossia S(f), valuiamo quano valgono modulo e fase di H H (f): sapendo che j f > H ( H f ) = f = j f < è subio chiaro che H ( H f ) = f 34
35 I sisemi lineari Queso ci consene di dire subio che il filro non ha alcun effeo sul modulo di S(f), ossia lo lascia inalerao. y Passiamo alla fase: ricordando che la fase del generico numero complesso z=x+jy è z = arcg, z noi abbiamo che ( ) H ( f ) arcg f > H = arcg ( + ) f < e quindi H H ( f ) = π π f > f < Da qui si deduce che l effeo del filro è quello di lasciare inalerao il modulo del segnale in ingresso e di effeuare, di ale segnale, una roazione di 9 in anicipo per le frequenze negaive e in riardo per quelle posiive. Se volessimo diagrammare l andameno grafico della funzione H ( f ), avremmo quano segue: H ( H f ) H SEGNALE ANALITICO Consideriamo un generico segnale empo-coninuo s(): facciamo, come unica ipoesi, quella per cui esso sia rasformabile secondo Fourier e indichiamo con S(f) la sua rasformaa. Meiamo queso segnale in ingresso ad un sisema lineare empo-invariane che abbia come funzione di rasferimeno il gradino uniario: H A (f) f 35
36 Appuni di Teoria dei Segnali - Capiolo 5 Indicaa con y() l uscia del sisema, supponendo che anch essa sia rasformabile secondo Fourier e che Y(f) sia la sua rasformaa, sappiamo che vale la relazione Y( f ) = S(f ) H A ( f ). Daa la sruura di H A (f), si capisce subio che il segnale in uscia di queso sisema non è alro che il segnale in ingresso, privao però delle componeni di frequenza negaiva, che vengono ue azzerae. Il segnale y() così oenuo prende il nome di segnale analiico del segnale s(). In generale, si dirà analiico un qualsiasi segnale empo-coninuo che presena spero nullo per f<. Tano per fare un esempio, se lo spero del segnale fosse S(f) f C f lo spero del suo segnale analiico sarebbe il seguene: S+(f) f C f Una osservazione imporane è la seguene: perché un qualsiasi segnale y() possa essere analiico, è necessario che sia un segnale complesso. Infai, se y() fosse reale, varrebbe la cosiddea proprieà di simmeria hermiiana del suo spero, secondo la quale * S( f ) = S ( f) [ S f ] = [ S f ] [ S f ] = [ S f ] Re ( ) Re ( ) Im ( ) Im ( ) e queso evidenemene non consene che la pare negaiva dello spero sia nulla menre quella posiiva no. Adesso, vediamo di calcolare quano vale la funzione di risposa all impulso h A () del nosro sisema. Sappiamo bene che h ( ) = Fourier H ( f ) A [ A ] Per effeuare quesa anirasformaa, uilizziamo re risulai precedenemene ricavai: il primo è la rasformaa di Fourier del segnale u(), che sappiamo essere 36
37 I sisemi lineari Fourier[ u( ) ] = + δ( f ) jπf L alro è la proprieà di dualià, secondo la quale s( ) S(f ) S() s( f ) Nel nosro caso, l applicazione della proprieà di dualià ci pora a dire che u( ) + δ( f ) jπf + δ( ) u( f ) jπ Il erzo risulao che sfruiamo è la proprieà di scala, secondo la quale Applicandolo in queso caso, abbiamo che s( ) S(f ) ( ) s( ) S f + δ( ) u( f ) jπ + δ( ) u( f ) jπ Ricordando inolre che l impulso di Dirac è una funzione pari, concludiamo che Dao che H A (f)=u(f), possiamo scrivere che + δ( ) u( f ) jπ ha ( ) = + δ( ) jπ Quesa è evidenemene una funzione complessa, il che significa che il nosro sisema non è idealmene realizzabile né ano meno fisicamene realizzabile. Volendo rappresenare graficamene quesa funzione, possiamo diagrammare la sua pare reale, che è semplicemene un impulso di area ½ posizionao nell origine, e il coefficiene della pare immaginaria, che ha un andameno del ipo seguene: 37
38 Appuni di Teoria dei Segnali - Capiolo 5 [ h A ] Im ( ) A queso puno, così come abbiamo fao prima per il filro di Hilber, ricaviamo l espressione analiica dell uscia del sisema nel dominio del empo, cioè del segnale analiico di s(): sappiamo inano che Sosiuendo l espressione di h A (), oeniamo y( ) = s( ) * h A ( ) = s( τ) h A ( τ) y( ) = s( ) * h A ( ) = s( τ) δ( τ) d j π( τ) τ Scomponendo in due l inegrale abbiamo y( ) = s( τ) δ( τ) s( τ) jπ( τ) Il primo inegrale, in base alla proprieà di seaccio della funzione impulso di Dirac, vale proprio s(), per cui y( ) = s( ) s( τ) jπ( τ) Il secondo inegrale, invece, se poriamo fuori il ermine /j, è proprio la rasformaa di Hilber del segnale s(), per cui possiamo concludere che il segnale analiico di s() ha l espressione j y ( ) = s ( ) + s $( ) Di solio, il segnale analiico viene indicao con il simbolo s + (). E evidene, dalla sua espressione, che è possibile ricavare da esso il segnale di parenza s(), che è infai pari al doppio della sua pare reale: quindi 38
39 I sisemi lineari + [ ] s( ) = Re s ( ) Quesa relazione indica una corrispondenza biunivoca ra s() ed il suo segnale analiico, per cui ques ulimo può cosiuire una rappresenazione alernaiva di s(). INVILUPPO COMPLESSO Sia dao il generico segnale s() che supponiamo essere rasformabile secondo Fourier. Abbiamo + j appena definio il segnale analiico di s() come s ( ) = s( ) + s $( ), dicendo che si raa di s() salvo per il fao che le componeni negaive del suo spero sono ue nulle. A parire dal segnale analiico di un cero segnale s(), è possibile definire un uleriore segnale, sempre legao a s(): si raa del segnale definio mediane la relazione ~ s( ) s + ( ) e j f = π e che prende il nome di inviluppo complesso del segnale di parenza s(). Per capire di cosa si raa, conviene come al solio riferirsi al dominio della frequenza: infai, è evidene, applicando la proprieà di raslazione in frequenza, che la rasformaa di Fourier di queso segnale è ~ + S( f ) = S ( f + f ), ossia, a meno del faore, è lo spero del segnale analiico raslao, verso sinisra, di f. Tano per fare un esempio, supponiamo che il nosro segnale di parenza abbia il seguene spero: S(f) Allora, lo spero del suo segnale analiico è S+(f) f C f f C f menre quello dell inviluppo complesso, a meno del faore è 39
ESERCIZI di TEORIA dei SEGNALI. La Correlazione
 ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
SISTEMI LINEARI TEMPO INVARIANTI
 SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale x(, deo ingresso, generando
SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale x(, deo ingresso, generando
Teoria dei Segnali. La Convoluzione (esercizi) parte prima
 Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
Equazioni Differenziali (5)
 Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
Equazioni Differenziali (5) Daa un equazione differenziale lineare omogenea y n + a n 1 ()y n 1 + a 0 ()y = 0, (1) se i coefficieni a i non dipendono da, abbiamo viso che le soluzioni si possono deerminare
SISTEMI LINEARI TEMPO INVARIANTI. Fondamenti Segnali e Trasmissione
 SISTEMI LINEARI TEMPO INVARIANTI Fondameni Segnali e Trasmissione Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale (), deo ingresso, generando il segnale y(),
SISTEMI LINEARI TEMPO INVARIANTI Fondameni Segnali e Trasmissione Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale (), deo ingresso, generando il segnale y(),
SISTEMI LINEARI TEMPO INVARIANTI
 SISTEMI LINEARI TEMPO INVARIANTI Fondameni di Segnali e Trasmissione Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale, deo ingresso, generando il segnale,
SISTEMI LINEARI TEMPO INVARIANTI Fondameni di Segnali e Trasmissione Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale, deo ingresso, generando il segnale,
Sistemi Lineari e Tempo-Invarianti (SLI) Risposta impulsiva e al gradino
 Sisemi Lineari e Tempo-Invariani (SLI) Risposa impulsiva e al gradino by hp://www.oasiech.i Con sisema SLI si inende un sisema lineare e empo invariane, rispeo alla seguene figura: Lineare: si ha quando
Sisemi Lineari e Tempo-Invariani (SLI) Risposa impulsiva e al gradino by hp://www.oasiech.i Con sisema SLI si inende un sisema lineare e empo invariane, rispeo alla seguene figura: Lineare: si ha quando
Esercizio 1 [punti 4] Si tracci il grafico dei segnali a. x 1 (t) = x( t + 2), t R, b. x 2 (t) = x( t 1), t R, sapendo che x(t) =
![Esercizio 1 [punti 4] Si tracci il grafico dei segnali a. x 1 (t) = x( t + 2), t R, b. x 2 (t) = x( t 1), t R, sapendo che x(t) = Esercizio 1 [punti 4] Si tracci il grafico dei segnali a. x 1 (t) = x( t + 2), t R, b. x 2 (t) = x( t 1), t R, sapendo che x(t) =](/thumbs/59/43423096.jpg) Esercizio [puni 4] Prova scria di SEGNALI E SISTEMI 5 seembre 2003 Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 2002-2003) Teso e Soluzione (redaa da L. Finesso) Si racci il grafico dei segnali a. x
Esercizio [puni 4] Prova scria di SEGNALI E SISTEMI 5 seembre 2003 Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 2002-2003) Teso e Soluzione (redaa da L. Finesso) Si racci il grafico dei segnali a. x
SISTEMI LINEARI TEMPO INVARIANTI
 SISTEMI LINEARI TEMPO INVARIANTI SISTEMI LINEARI TEMPO INVARIANTI Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale x(), deo ingresso, generando il segnale
SISTEMI LINEARI TEMPO INVARIANTI SISTEMI LINEARI TEMPO INVARIANTI Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale x(), deo ingresso, generando il segnale
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondameni di elecomunicazioni - SEGNALI E SPERI Prof. Mario Barbera [pare ] Sruura della lezione Proprieà dei segnali Valore medio, valore efficace, poenza, energia rasformaa di Fourier e speri
Corso di Fondameni di elecomunicazioni - SEGNALI E SPERI Prof. Mario Barbera [pare ] Sruura della lezione Proprieà dei segnali Valore medio, valore efficace, poenza, energia rasformaa di Fourier e speri
Teoria dei Segnali. La Convoluzione (esercizi) parte seconda
 Teoria dei Segnali La Convoluzione (esercizi) pare seconda 1 Esercizio n.8 Calcolare la convoluzione ra i due segnali : e x() = rec ( ) rec ( 2 ) y() = rec 2 ( ) Conviene inizialmene disegnare i due segnali
Teoria dei Segnali La Convoluzione (esercizi) pare seconda 1 Esercizio n.8 Calcolare la convoluzione ra i due segnali : e x() = rec ( ) rec ( 2 ) y() = rec 2 ( ) Conviene inizialmene disegnare i due segnali
Regime di capitalizzazione: una famiglia di funzioni fattore di montante che dipende da uno o più parametri.
 5. Teoria generale Regimi finanziari Nel capiolo precedene abbiamo inrodoo alcuni parameri in grado di descrivere ualsiasi ipo di regime. Ciò ci permee di definire in generale i regimi finanziari. Regime
5. Teoria generale Regimi finanziari Nel capiolo precedene abbiamo inrodoo alcuni parameri in grado di descrivere ualsiasi ipo di regime. Ciò ci permee di definire in generale i regimi finanziari. Regime
RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI
 RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Inroduzione Se il segnale d ingresso di un sisema Lineare Tempo-Invariane LTI e un esponenziale
RISPOSTA IN FREQUENZA DEI SISTEMI LINEARI TEMPO INVARIANTI 1 Fondameni di segnali Fondameni e rasmissione TLC Inroduzione Se il segnale d ingresso di un sisema Lineare Tempo-Invariane LTI e un esponenziale
Circuiti dinamici. Circuiti del primo ordine. (versione del ) Circuiti del primo ordine
 ircuii dinamici ircuii del primo ordine www.die.ing.unibo.i/pers/masri/didaica.hm (versione del 4-5- ircuii del primo ordine ircuii del primo ordine: circuii il cui sao è definio da una sola variabile
ircuii dinamici ircuii del primo ordine www.die.ing.unibo.i/pers/masri/didaica.hm (versione del 4-5- ircuii del primo ordine ircuii del primo ordine: circuii il cui sao è definio da una sola variabile
Esercizi di Teoria dei Segnali. La Trasformata di Fourier
 Esercizi di Teoria dei Segnali La Trasformaa di Fourier 1 Esercizio 1 Calcolare la rasformaa di Fourier del segnale di fig. 1.1. x() A B - T/ T/ fig.1.1 Per calcolare la rasformaa di queso segnalesi può
Esercizi di Teoria dei Segnali La Trasformaa di Fourier 1 Esercizio 1 Calcolare la rasformaa di Fourier del segnale di fig. 1.1. x() A B - T/ T/ fig.1.1 Per calcolare la rasformaa di queso segnalesi può
Calcolo di integrali - svolgimento degli esercizi
 Calcolo di inegrali - svolgimeno degli esercizi Calcoliamo una primiiva di cos(e 5. Inegriamo due vole per pari, scegliendo e 5 d come faore differenziale e cos( come faore finio. Si ha cos(e 5 d e5 5
Calcolo di inegrali - svolgimeno degli esercizi Calcoliamo una primiiva di cos(e 5. Inegriamo due vole per pari, scegliendo e 5 d come faore differenziale e cos( come faore finio. Si ha cos(e 5 d e5 5
TRASFORMATE DI LAPLACE
 CONTROLLI AUTOMATICI Ingegneria della Gesione Indusriale e della Inegrazione di Impresa hp://www.auomazione.ingre.unimore.i/pages/corsi/conrolliauomaicigesionale.hm Trasformae di Laplace Gli esempi visi
CONTROLLI AUTOMATICI Ingegneria della Gesione Indusriale e della Inegrazione di Impresa hp://www.auomazione.ingre.unimore.i/pages/corsi/conrolliauomaicigesionale.hm Trasformae di Laplace Gli esempi visi
Teoria dei segnali. Unità 2 Sistemi lineari. Sistemi lineari: definizioni e concetti di base. Concetti avanzati Politecnico di Torino 1
 Sisemi lineari: deinizioni e concei di base Teoria dei segnali Unià 2 Sisemi lineari Sisemi lineari Deinizioni e concei di base Concei avanzai 2 25 Poliecnico di Torino Sisemi lineari: deinizioni e concei
Sisemi lineari: deinizioni e concei di base Teoria dei segnali Unià 2 Sisemi lineari Sisemi lineari Deinizioni e concei di base Concei avanzai 2 25 Poliecnico di Torino Sisemi lineari: deinizioni e concei
Tratto dal Corso di Telecomunicazioni Vol. I Ettore Panella Giuseppe Spalierno Edizioni Cupido. lim. 1 t 1 T
 rao dal Corso di elecomunicazioni Vol. I ore Panella Giuseppe Spalierno dizioni Cupido 4. nergia e Poenza Dao un segnale di ampiezza s() si definisce energia oale il valore del seguene inegrale: + / /
rao dal Corso di elecomunicazioni Vol. I ore Panella Giuseppe Spalierno dizioni Cupido 4. nergia e Poenza Dao un segnale di ampiezza s() si definisce energia oale il valore del seguene inegrale: + / /
Ci domandiamo allora se e sempre possibile rappresentare una funzione in questo modo.
 1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
1. Serie di Fourier I problemi al bordo associai ad equazioni differenziali si sanno risolvere con il meodo di separazione delle variabili solano se il dao iniziale si rappresena nella forma fx = a cosx
Geometria analitica del piano pag 7 Adolfo Scimone. Rette in posizioni particolari rispetto al sistema di riferimento
 Geomeria analiica del piano pag 7 Adolfo Scimone Ree in posizioni paricolari rispeo al sisema di riferimeno L'equazione affine di una rea a + + c = 0 può assumere forme paricolari in relazione alla posizione
Geomeria analiica del piano pag 7 Adolfo Scimone Ree in posizioni paricolari rispeo al sisema di riferimeno L'equazione affine di una rea a + + c = 0 può assumere forme paricolari in relazione alla posizione
0.0.1 Esercizio Q1, tema d esame del 10 settembre 2009, prof. Dario d Amore Testo R 3
 1 0.0.1 Esercizio Q1, ema d esame del 10 seembre 2009, prof. Dario d more 0.0.1.1 Teso E1 Il circuio di figura opera in regime sazionario. Sapendo che R 1 = 2 kω, = 4 kω, = 2 kω, = 2 kω E=12 V, =3 m Deerminare,
1 0.0.1 Esercizio Q1, ema d esame del 10 seembre 2009, prof. Dario d more 0.0.1.1 Teso E1 Il circuio di figura opera in regime sazionario. Sapendo che R 1 = 2 kω, = 4 kω, = 2 kω, = 2 kω E=12 V, =3 m Deerminare,
Capitolo 1 - Introduzione ai segnali
 Appuni di eoria dei egnali Capiolo - Inroduzione ai segnali egnali coninui... Definizioni inroduive... Esempio: segnale esponenziale...3 Esempio: coseno...3 Osservazione: poenza di un segnale periodico...5
Appuni di eoria dei egnali Capiolo - Inroduzione ai segnali egnali coninui... Definizioni inroduive... Esempio: segnale esponenziale...3 Esempio: coseno...3 Osservazione: poenza di un segnale periodico...5
Volume FISICA. Elementi di teoria ed applicazioni. Fisica 1
 Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Interruttore ideale. + v(t) i(t) t = t 0. i(t) = 0 v(t) = 0. i(t) v(t) v(t) = 0 i(t) = 0. Per t > t 0. interruttore di chiusura
 Inerruore ideale inerruore di chiusura { i() = 0 v() = 0 inerruore di aperura { v() = 0 i() = 0 per < 0 per > 0 per < 0 per > 0 v() i() = 0 v() i() = 0 Esempio: inerruore ideale di aperura Per < 0, i()
Inerruore ideale inerruore di chiusura { i() = 0 v() = 0 inerruore di aperura { v() = 0 i() = 0 per < 0 per > 0 per < 0 per > 0 v() i() = 0 v() i() = 0 Esempio: inerruore ideale di aperura Per < 0, i()
intervalli di tempo. Esempio di sistema oscillante: Fig. 1 Massa m che può traslare in una sola direzione x, legata ad una molla di rigidezza k.
 Sudio delle vibrazioni raa ogni oscillazione di una grandezza inorno ad una posizione di equilibrio. La forma piu semplice di oscillazione e il moo armonico che puo i essere descrio da un veore roane Ae
Sudio delle vibrazioni raa ogni oscillazione di una grandezza inorno ad una posizione di equilibrio. La forma piu semplice di oscillazione e il moo armonico che puo i essere descrio da un veore roane Ae
UNITA 3. LE EQUAZIONI GONIOMETRICHE.
 UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
UNITA. LE EQUAZIONI GONIOMETRICHE.. Generalià sulle equazioni goniomeriche.. Equazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Alri ipi di equazioni goniomeriche elemenari.. Le funzioni
27 DERIVATE DI ORDINI SUCCESSIVI
 27 DERIVATE DI ORDINI SUCCESSIVI Definizione Sia f derivabile sull inervallo I. Se esise la derivaa della funzione x f (x) in x, allora (f ) (x) si dice la derivaa seconda di f in x, e si denoa con f (x)
27 DERIVATE DI ORDINI SUCCESSIVI Definizione Sia f derivabile sull inervallo I. Se esise la derivaa della funzione x f (x) in x, allora (f ) (x) si dice la derivaa seconda di f in x, e si denoa con f (x)
Soluzione. Le componenti del gradiente sono le derivate parziali della funzione: cos y 0 (x 0, y 0 ) domf =R 2. sin y 0 (x x 0 ) + e x 0
 Gradiene e piano angene Definizione 1 Sia f : A R 2 R, f derivabile in (x 0, y 0 ) A). Definiamo il veore gradiene di f in (x 0, y 0 ): f(x 0, y 0 ) = (f x (x 0, y 0 ), f y (x 0, y 0 )). Definiamo il piano
Gradiene e piano angene Definizione 1 Sia f : A R 2 R, f derivabile in (x 0, y 0 ) A). Definiamo il veore gradiene di f in (x 0, y 0 ): f(x 0, y 0 ) = (f x (x 0, y 0 ), f y (x 0, y 0 )). Definiamo il piano
Esercizi aggiuntivi Unità A1
 Esercizi aggiunivi Unià A Esercizi svoli Esercizio A Concei inroduivi Daa la grandezza impulsiva periodica la cui forma d onda è rappresenaa nella figura A., calcolarne il valore medio nel periodo, il
Esercizi aggiunivi Unià A Esercizi svoli Esercizio A Concei inroduivi Daa la grandezza impulsiva periodica la cui forma d onda è rappresenaa nella figura A., calcolarne il valore medio nel periodo, il
Outline. La trasformata di Laplace. (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi
 Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
Ouline La rasformaa di Laplace La rasformaa di Laplace (Meodi Maemaici e Calcolo per Ingegneria) Enrico Berolazzi DIMS Universià di reno anno accademico 28/29 (aggiornaa al 2/9/28) 2 Proprieà della rasformaa
Soluzione degli esercizi del Capitolo 3
 Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Ricordando dal Paragrafo A.6 dell Appendice A che è facile oenere ẋ () d d ( (e A e A x + Ae (e A A x + ( A e A( ) x + Ax () + Bu () d ( e
Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Ricordando dal Paragrafo A.6 dell Appendice A che è facile oenere ẋ () d d ( (e A e A x + Ae (e A A x + ( A e A( ) x + Ax () + Bu () d ( e
Laboratorio di Fisica I: laurea in Ottica e Optometria
 Laboraorio di Fisica I: laurea in Oica e Opomeria Misura del empo caraerisico di carica e scarica di un condensaore araverso una resisenza Descrizione Si vuole cosruire un circuio in serie collegando generaore
Laboraorio di Fisica I: laurea in Oica e Opomeria Misura del empo caraerisico di carica e scarica di un condensaore araverso una resisenza Descrizione Si vuole cosruire un circuio in serie collegando generaore
Il modello di crescita deriva dalla logica del tasso di interesse semplice
 Eserciazione 7: Approfondimeni sui modelli di crescia. Crescia arimeica, geomerica, esponenziale. Calcolo del asso di crescia e del empo di raddoppio. Viviana Amai 03/06/2009 Modelli di crescia Nella prima
Eserciazione 7: Approfondimeni sui modelli di crescia. Crescia arimeica, geomerica, esponenziale. Calcolo del asso di crescia e del empo di raddoppio. Viviana Amai 03/06/2009 Modelli di crescia Nella prima
CM89sett.tex COMPLEMENTI DI MATEMATICA a.a Laurea magistrale in Ingegneria Elettrotecnica
 1 CM89se.ex COMPLEMENTI DI MATEMATICA a.a. 28-29 Laurea magisrale in Ingegneria Eleroecnica Nona seimana 24.11.28 - lunedì (2 ore) Commeno della prova parziale (vd. file CM8IcoA-B-C-D.pdf). Definizione
1 CM89se.ex COMPLEMENTI DI MATEMATICA a.a. 28-29 Laurea magisrale in Ingegneria Eleroecnica Nona seimana 24.11.28 - lunedì (2 ore) Commeno della prova parziale (vd. file CM8IcoA-B-C-D.pdf). Definizione
Nome: Nr. Mat. Firma:
 Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Fondameni di Conrolli Auomaici Prova Parziale 8 Aprile 2 - A.A. 2/ Nome: Nr. Ma. Firma: a) Deerminare la rasformaa di Laplace X i (s) dei segueni segnali emporali x i (): x () = 4 + 2 e +5 cos(3 6), x
Raggiungibilità e controllabilità (2 )
 eoria dei sisemi - Capiolo 8 Raggiungibilià e conrollabilià ( ) Sisemi empo-coninui lineari empo-invariani... Inroduzione... Deerminazione del soospazio di raggiungibilià e crierio di Kalman... La conrollabilià...6
eoria dei sisemi - Capiolo 8 Raggiungibilià e conrollabilià ( ) Sisemi empo-coninui lineari empo-invariani... Inroduzione... Deerminazione del soospazio di raggiungibilià e crierio di Kalman... La conrollabilià...6
APPUNTI INTEGRATIVI Provvisori circa: Risposta in Frequenza: Introduzione ai Filtri Passivi e Attivi. Filtri del I ordine
 APPUNTI INTEGATIVI Provvisori circa: isposa in Frequenza: Inroduzione ai Filri Passivi e Aivi Filri del I ordine. Passa-Basso Consideriamo la funzione di ree: Trasferimeno in ensione ai capi di un condensaore
APPUNTI INTEGATIVI Provvisori circa: isposa in Frequenza: Inroduzione ai Filri Passivi e Aivi Filri del I ordine. Passa-Basso Consideriamo la funzione di ree: Trasferimeno in ensione ai capi di un condensaore
Processo di Arrivi di Poisson
 CALCOLO DELLE PROBABILITA Processo di Arrivi di Poisson Per arrivo riferimeno. si inende un qualsiasi eveno casuale che si realizza in un deerminao sisema di Un processo di arrivi è un flusso di eveni
CALCOLO DELLE PROBABILITA Processo di Arrivi di Poisson Per arrivo riferimeno. si inende un qualsiasi eveno casuale che si realizza in un deerminao sisema di Un processo di arrivi è un flusso di eveni
25.2. Osservazione. Siccome F(x, y, z) = 0 è un equazione e non un identità, una superficie non contiene tutti gli 3 punti dello spazio.
 . Cono e cilindro.. Definiione. Diremo superficie il luogo geomerico dei puni dello spaio le cui coordinae soddisfano un equaione del ipo F che viene dea equaione caresiana della superficie. Se F è un
. Cono e cilindro.. Definiione. Diremo superficie il luogo geomerico dei puni dello spaio le cui coordinae soddisfano un equaione del ipo F che viene dea equaione caresiana della superficie. Se F è un
Soluzioni di reti elettriche lineari PAS Introduzione
 Soluzioni di rei eleriche lineari PAS Inroduzione Domanda: Cosa sono le rei eleriche lineari in regime Periodico Alernao Sinusoidali PAS? Risposa: Sono rei lineari in cui i generaori hanno dipendenza dal
Soluzioni di rei eleriche lineari PAS Inroduzione Domanda: Cosa sono le rei eleriche lineari in regime Periodico Alernao Sinusoidali PAS? Risposa: Sono rei lineari in cui i generaori hanno dipendenza dal
, proporzionale alla RH%, si fa riferimento allo schema di figura 3 composto dai seguenti blocchi:
 Esame di Sao di Isiuo Tecnico Indusriale A.S. 007/008 Indirizzo: ELETTRONICA E TELECOMUNICAZIONI Tema di: ELETTRONICA Si deve rilevare l umidià relaiva RH% presene in un ambiene, nell inervallo 0 90%,
Esame di Sao di Isiuo Tecnico Indusriale A.S. 007/008 Indirizzo: ELETTRONICA E TELECOMUNICAZIONI Tema di: ELETTRONICA Si deve rilevare l umidià relaiva RH% presene in un ambiene, nell inervallo 0 90%,
( x) Soluzione. Si consideri la figura sottostante, che rappresenta la questione geometrica:
 Sessione sraordinaria LS_ORD 7 Soluzione Si consideri la figura soosane, ce rappresena la quesione geomerica: Il riangolo APB, essendo inscrio in una semicirconferenza è reangolo, per cui AP r sin, PB
Sessione sraordinaria LS_ORD 7 Soluzione Si consideri la figura soosane, ce rappresena la quesione geomerica: Il riangolo APB, essendo inscrio in una semicirconferenza è reangolo, per cui AP r sin, PB
La risposta di un sistema lineare viscoso a un grado di libertà sollecitato da carichi periodici. Prof. Adolfo Santini - Dinamica delle Strutture 1
 La risposa di un sisema lineare viscoso a un grado di liberà solleciao da carichi periodici Prof. Adolfo Sanini - Dinamica delle Sruure 1 Inroduzione 1/ Un carico p() si dice periodico quando assume indefiniamene
La risposa di un sisema lineare viscoso a un grado di liberà solleciao da carichi periodici Prof. Adolfo Sanini - Dinamica delle Sruure 1 Inroduzione 1/ Un carico p() si dice periodico quando assume indefiniamene
PIL NOMINALE, PIL REALE E DEFLATORE
 PIL NOMINALE, PIL REALE E DEFLATORE Il PIL nominale (o a prezzi correni) Come sappiamo il PIL è il valore di ui i beni e servizi finali prodoi in un cero periodo all inerno del paese. Se per calcolare
PIL NOMINALE, PIL REALE E DEFLATORE Il PIL nominale (o a prezzi correni) Come sappiamo il PIL è il valore di ui i beni e servizi finali prodoi in un cero periodo all inerno del paese. Se per calcolare
Anno 4 Equazioni goniometriche lineari e omogenee
 Anno 4 Equazioni goniomeriche lineari e omogenee Inroduzione In quesa lezione descriveremo le equazioni goniomeriche lineari e omogenee. Esamineremo le definizioni e illusreremo i meodi risoluivi per ogni
Anno 4 Equazioni goniomeriche lineari e omogenee Inroduzione In quesa lezione descriveremo le equazioni goniomeriche lineari e omogenee. Esamineremo le definizioni e illusreremo i meodi risoluivi per ogni
Verifica di Matematica Classe V
 Liceo Scienifico Pariario R. Bruni Padova, loc. Pone di Brena, 6/3/17 Verifica di Maemaica Classe V Soluzione Problemi. Risolvi uno dei due problemi: 1. Facciamo il pieno. Il serbaoio del carburane di
Liceo Scienifico Pariario R. Bruni Padova, loc. Pone di Brena, 6/3/17 Verifica di Maemaica Classe V Soluzione Problemi. Risolvi uno dei due problemi: 1. Facciamo il pieno. Il serbaoio del carburane di
Filtri. RIASSUNTO: Sviluppo in serie di Fourier Esempi:
 Filri RIASSUNTO: Sviluppo in serie di Fourier Esempi: Onda quadra Onda riangolare Segnali non peridiodici Trasformaa di Fourier Filri lineari sazionari: funzione di rasferimeno T() Definizione: il decibel
Filri RIASSUNTO: Sviluppo in serie di Fourier Esempi: Onda quadra Onda riangolare Segnali non peridiodici Trasformaa di Fourier Filri lineari sazionari: funzione di rasferimeno T() Definizione: il decibel
Soluzione degli esercizi del Capitolo 1
 Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Il valore più opporuno ū di u è quello per cui, in condizioni nominali, la variabile conrollaa assume il valore desiderao; perciò si rova
Soluzione degli esercizi del Capiolo Soluzione dell Esercizio. Il valore più opporuno ū di u è quello per cui, in condizioni nominali, la variabile conrollaa assume il valore desiderao; perciò si rova
Approccio Classico: Metodi di Scomposizione
 Approccio Classico: Meodi di Scomposizione Il Modello di Scomposizione Il modello maemaico ipoizzao nel meodo classico di scomposizione è: y =f(s, T, E ) dove y è il dao riferio al periodo S è la componene
Approccio Classico: Meodi di Scomposizione Il Modello di Scomposizione Il modello maemaico ipoizzao nel meodo classico di scomposizione è: y =f(s, T, E ) dove y è il dao riferio al periodo S è la componene
UNITA 4. LE DISEQUAZIONI GONIOMETRICHE.
 UNITA. LE DISEQUAZIONI GONIOMETRICHE.. Generalià sulle disequazioni goniomeriche.. Disequazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Disequazioni riconducibili a disequazioni goniomeriche
UNITA. LE DISEQUAZIONI GONIOMETRICHE.. Generalià sulle disequazioni goniomeriche.. Disequazioni goniomeriche elemenari con seno, coseno, angene e coangene.. Disequazioni riconducibili a disequazioni goniomeriche
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI
 DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine segnale si indica una funzione, generalmene del empo, che rappresena la legge di variazione di una grandezza fisica: (acusica, elerica, oica, ) ad
DEFINIZIONE E CLASSIFICAZIONE DEI SEGNALI Con il ermine segnale si indica una funzione, generalmene del empo, che rappresena la legge di variazione di una grandezza fisica: (acusica, elerica, oica, ) ad
1 Catene di Markov a stati continui
 Caene di Markov a sai coninui In queso caso abbiamo ancora una successione di variabili casuali X 0, X, X,... ma lo spazio degli sai è un insieme più che numerabile. Nel seguio supporremo che lo spazio
Caene di Markov a sai coninui In queso caso abbiamo ancora una successione di variabili casuali X 0, X, X,... ma lo spazio degli sai è un insieme più che numerabile. Nel seguio supporremo che lo spazio
Proprietà razionali per il prezzo
 Proprieà razionali per il prezzo delle opzioni call 8/09/0 Corso di Finanza quaniaiva L aricolo di Rober Meronpubblicao nel 973, heoryofraionalopionpricing idenifica una serie di proprieà che devono valere
Proprieà razionali per il prezzo delle opzioni call 8/09/0 Corso di Finanza quaniaiva L aricolo di Rober Meronpubblicao nel 973, heoryofraionalopionpricing idenifica una serie di proprieà che devono valere
9.4.4 Filtro adattato 9.4. FILTRAGGIO DI SEGNALI E PROCESSI 235
 9.4. FILRAGGIO DI SEGNALI E PROCESSI 35 Rispose ) Calcoliamo la media emporale: P x = ; / / x () d = /4 /4 () d = 4 = ) Sappiamo che P y = Py (f) df, in cui Py (f) = Y (f), ed a sua vola Y (f) = X (f)
9.4. FILRAGGIO DI SEGNALI E PROCESSI 35 Rispose ) Calcoliamo la media emporale: P x = ; / / x () d = /4 /4 () d = 4 = ) Sappiamo che P y = Py (f) df, in cui Py (f) = Y (f), ed a sua vola Y (f) = X (f)
sedimentazione Approfondimenti matematici
 sedimenazione Approfondimeni maemaici considerazioni sulla velocià L espressione p A F = R (1) che fornisce la relazione sulle forze ageni nel processo della sedimenazine, indica che all inizio il moo
sedimenazione Approfondimeni maemaici considerazioni sulla velocià L espressione p A F = R (1) che fornisce la relazione sulle forze ageni nel processo della sedimenazine, indica che all inizio il moo
Osservabilità (1 parte)
 eoria dei sisemi - Capiolo 9 sservabilià ( pare) Inroduzione al problema della osservabilià: osservazione e ricosruzione. Sai indisinguibili e sai non osservabili...3 Soospazi di osservabilià e non osservabilià
eoria dei sisemi - Capiolo 9 sservabilià ( pare) Inroduzione al problema della osservabilià: osservazione e ricosruzione. Sai indisinguibili e sai non osservabili...3 Soospazi di osservabilià e non osservabilià
PROVA SCRITTA DI AUTOMATICA I (Prof. Bittanti, BIO A-K) 25 Settembre 2006 Cognome Nome Matricola. y=x 2 =i L
 .9.8.7.6.5.4.3.. - 3 4 5 6 7 8 9 PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) 5 Seembre 6 Cognome Nome Maricola............ Verificare che il fascicolo sia cosiuio da 9 pagine. La chiarezza e precisione
.9.8.7.6.5.4.3.. - 3 4 5 6 7 8 9 PROVA SCRITTA DI AUTOMATICA I (Prof. Biani, BIO A-K) 5 Seembre 6 Cognome Nome Maricola............ Verificare che il fascicolo sia cosiuio da 9 pagine. La chiarezza e precisione
ESERCIZI SUL CALCOLO DI LIMITI CON GLI SVILUPPI DI TAYLOR
 ESERCIZI SUL CALCOLO DI LIMITI CON GLI SVILUPPI DI TAYLOR a cura di Michele Scaglia SVILUPPI DI MACLAURIN DELLE PRINCIPALI FUNZIONI Ricordiamo nella abella che segue gli sviluppi di Taylor per x 0 delle
ESERCIZI SUL CALCOLO DI LIMITI CON GLI SVILUPPI DI TAYLOR a cura di Michele Scaglia SVILUPPI DI MACLAURIN DELLE PRINCIPALI FUNZIONI Ricordiamo nella abella che segue gli sviluppi di Taylor per x 0 delle
L impedenza. RIASSUNTO Richiamo: algebra dei numeri complessi I FASORI Derivate e integrali Esempio: circuito RC. Il concetto di impedenza :
 L impedena RASSUNTO Richiamo: algebra dei numeri complessi FASOR Derivae e inegrali Esempio: circuio RC Transiene Soluione saionaria l conceo di impedena : Resisena: Z R R nduana: Z L ω L Capacia : Z C
L impedena RASSUNTO Richiamo: algebra dei numeri complessi FASOR Derivae e inegrali Esempio: circuio RC Transiene Soluione saionaria l conceo di impedena : Resisena: Z R R nduana: Z L ω L Capacia : Z C
GENERATORE DI ONDE QUADRE REALIZZATO CON AMPLIFICATORE OPERAZIONALE A SINGOLA ALIMENTAZIONE
 LASSE : A E.T.A. 007-008 ALUNNO: Bovino Silvano GENERATORE DI ONDE QUADRE REALIZZATO ON AMPLIFIATORE OPERAZIONALE A SINGA ALIMENTAZIONE SOPO:onfrono ra la frequenza eorica e quella sperimenale del segnale
LASSE : A E.T.A. 007-008 ALUNNO: Bovino Silvano GENERATORE DI ONDE QUADRE REALIZZATO ON AMPLIFIATORE OPERAZIONALE A SINGA ALIMENTAZIONE SOPO:onfrono ra la frequenza eorica e quella sperimenale del segnale
Modelli ARMA, regressione spuria e cointegrazione Amedeo Argentiero
 Modelli ARMA, regressione spuria e coinegrazione Amedeo Argeniero amedeo.argeniero@unipg.i Definizione modello ARMA Un modello ARMA(p, q) (AuoRegressive Moving Average of order p and q) ha la seguene sruura:
Modelli ARMA, regressione spuria e coinegrazione Amedeo Argeniero amedeo.argeniero@unipg.i Definizione modello ARMA Un modello ARMA(p, q) (AuoRegressive Moving Average of order p and q) ha la seguene sruura:
Minimi Quadrati Ricorsivi
 Minimi Quadrai Ricorsivi Minimi Quadrai Ricorsivi Fino ad ora abbiamo sudiao due diversi meodi per l idenificazione dei modelli: - Minimi quadrai, uilizzao per l idenificazione dei modelli ARX, in cui
Minimi Quadrai Ricorsivi Minimi Quadrai Ricorsivi Fino ad ora abbiamo sudiao due diversi meodi per l idenificazione dei modelli: - Minimi quadrai, uilizzao per l idenificazione dei modelli ARX, in cui
SOLUZIONE ESERCIZI: CONCORRENZA PERFETTA E OLIGOPOLIO. ECONOMIA INDUSTRIALE Università degli Studi di Milano-Bicocca. Christian Garavaglia
 SOLUZIONE ESERCIZI: CONCORRENZA PERFETTA E OLIGOPOLIO ECONOMIA INDUSTRIALE Universià degli Sudi di Milano-Bicocca Chrisian Garavaglia Soluzione 4 a) Indicando con θˆ la sima di θ, il profio aeso dell impresa
SOLUZIONE ESERCIZI: CONCORRENZA PERFETTA E OLIGOPOLIO ECONOMIA INDUSTRIALE Universià degli Sudi di Milano-Bicocca Chrisian Garavaglia Soluzione 4 a) Indicando con θˆ la sima di θ, il profio aeso dell impresa
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1- soluzioni - Leggi finanziarie, rendite ed ammortamenti
 Esercizi di Maemaica Finanziaria - Corso Par Time scheda - soluzioni - Leggi finanziarie, rendie ed ammorameni. Le soluzioni sono: (a) M 3 = 00 ( + 3) = 5, M 8 = 5 ( + 5) = 43.75. (b) Va risola l equazione
Esercizi di Maemaica Finanziaria - Corso Par Time scheda - soluzioni - Leggi finanziarie, rendie ed ammorameni. Le soluzioni sono: (a) M 3 = 00 ( + 3) = 5, M 8 = 5 ( + 5) = 43.75. (b) Va risola l equazione
10 ESERCITAZIONE. Esercizi svolti: Capitolo 15 Curva di Phillips Esercizio 2. Capitolo 16 Disinflazione, disoccupazione e crescita Esercizio 3
 10 SRCITAZION sercizi svoli: Capiolo 15 Curva di Phillips sercizio 2 Capiolo 16 Disinflazione, disoccupazione e crescia sercizio 3 1 CAPITOLO 15 CURVA DI PHILLIPS Curva di Phillips Relazione che lega inflazione
10 SRCITAZION sercizi svoli: Capiolo 15 Curva di Phillips sercizio 2 Capiolo 16 Disinflazione, disoccupazione e crescia sercizio 3 1 CAPITOLO 15 CURVA DI PHILLIPS Curva di Phillips Relazione che lega inflazione
Diodi a giunzione p/n.
 iodi a giunzione p/n. 1 iodi a giunzione p/n. anodo caodo Fig. 1 - Simbolo e versi posiivi convenzionali per i diodi. diodi sono disposiivi eleronici a 2 erminali caraerizzai dalla proprieà di poer condurre
iodi a giunzione p/n. 1 iodi a giunzione p/n. anodo caodo Fig. 1 - Simbolo e versi posiivi convenzionali per i diodi. diodi sono disposiivi eleronici a 2 erminali caraerizzai dalla proprieà di poer condurre
Perturbazioni Dipendenti dal tempo
 Perurbazioni dipendeni dal empo in Meccanica Quanisica, Perurbazioni Periodiche, Transizioni di Dipolo Elerico, Dipolo Magneico, Quadripolo Elerico e relaive Regole di Selezione Di Giorgio Busoni Perurbazioni
Perurbazioni dipendeni dal empo in Meccanica Quanisica, Perurbazioni Periodiche, Transizioni di Dipolo Elerico, Dipolo Magneico, Quadripolo Elerico e relaive Regole di Selezione Di Giorgio Busoni Perurbazioni
ALIMENTATORI SWITCHING
 ALIMENAORI SWIHING osiuiscono l alra caegoria dei converiori / impiegai per le applicazioni di piccola po_ enza ( 10 100 Wa ) e, più in paricolare, per l alimenazione di carichi passivi prevalenemene resisivi,
ALIMENAORI SWIHING osiuiscono l alra caegoria dei converiori / impiegai per le applicazioni di piccola po_ enza ( 10 100 Wa ) e, più in paricolare, per l alimenazione di carichi passivi prevalenemene resisivi,
del materiale sul carico critico
 se compresse: ffei della non linearià RIF: LC III pag 39 del maeriale sul carico criico Il carico criico per unià di superficie corrispondene alla perdia di unicià della risposa in caso di comporameno
se compresse: ffei della non linearià RIF: LC III pag 39 del maeriale sul carico criico Il carico criico per unià di superficie corrispondene alla perdia di unicià della risposa in caso di comporameno
CAMPO ROTANTE DI GALILEO FERRARIS.doc pag. 1 di 5
 CAPO ROANE DI GALILEO FERRARIS. È noo che un solenoide percorso da correne elerica dà origine nel suo inerno a un campo magneico che ha come direzione quella del suo asse come mosrao in fig.. Se esso e
CAPO ROANE DI GALILEO FERRARIS. È noo che un solenoide percorso da correne elerica dà origine nel suo inerno a un campo magneico che ha come direzione quella del suo asse come mosrao in fig.. Se esso e
TIPI DI REGOLATORI. Esistono diversi tipi di regolatori che ora analizzeremo.
 TIPI DI REGOLATORI Esisono diversi ipi di regolaori che ora analizzeremo 1REGOLATORI ON-OFF Abbiamo deo che i regolaori sono quei sisemi che cercano di manenere l uscia cosane On-Off sa per indicare che
TIPI DI REGOLATORI Esisono diversi ipi di regolaori che ora analizzeremo 1REGOLATORI ON-OFF Abbiamo deo che i regolaori sono quei sisemi che cercano di manenere l uscia cosane On-Off sa per indicare che
Esempi di progetto di alimentatori
 Alimenaori 1 Esempi di progeo di alimenaori Progeo di alimenaore senza circuio di correzione del faore di poenza (PFC) Valore del condensaore Correne di picco Scela diodi Correne RMS Progeo di alimenaore
Alimenaori 1 Esempi di progeo di alimenaori Progeo di alimenaore senza circuio di correzione del faore di poenza (PFC) Valore del condensaore Correne di picco Scela diodi Correne RMS Progeo di alimenaore
Note applicative sul timer 555
 Noe applicaive sul imer 555. Premessa Il imer 555 è un circuio inegrao che coniene al suo inerno elemeni analogici (come BJT e comparaori) ed elemeni digiali in logica sequenziale (flip flop SR) allo scopo
Noe applicaive sul imer 555. Premessa Il imer 555 è un circuio inegrao che coniene al suo inerno elemeni analogici (come BJT e comparaori) ed elemeni digiali in logica sequenziale (flip flop SR) allo scopo
Lezione n.7. Variabili di stato
 Lezione n.7 Variabili di sao 1. Variabili di sao 2. Funzione impulsiva di Dirac 3. Generaori impulsivi per variabili di sao disconinue 3.1 ondizioni iniziali e generaori impulsivi In quesa lezione inrodurremo
Lezione n.7 Variabili di sao 1. Variabili di sao 2. Funzione impulsiva di Dirac 3. Generaori impulsivi per variabili di sao disconinue 3.1 ondizioni iniziali e generaori impulsivi In quesa lezione inrodurremo
P8 CIRCUITI SEQUENZIALI ELEMENTARI
 P8 CICUITI EUENZIALI ELEMENTAI P8. - Tracciare lo schema a blocchi di un sisema sequenziale secondo il modello di Moore. Nel modello di Moore di un sisema sequenziale, si suppone che lo sao successivo
P8 CICUITI EUENZIALI ELEMENTAI P8. - Tracciare lo schema a blocchi di un sisema sequenziale secondo il modello di Moore. Nel modello di Moore di un sisema sequenziale, si suppone che lo sao successivo
( ) I METODI DI INTEGRAZIONE. f x da integrare nella somma di più. x,..., f n x che si sappiano già integrare. Ne segue che:
 I METODI DI INTEGRAZIONE In queso paragrafo verranno illusrai i vari meodi di inegrazione che, pur non cosiuendo un procedimeno generale per effeuare l'inegrazione indefinia, permeono senz'alro di calcolare
I METODI DI INTEGRAZIONE In queso paragrafo verranno illusrai i vari meodi di inegrazione che, pur non cosiuendo un procedimeno generale per effeuare l'inegrazione indefinia, permeono senz'alro di calcolare
velocità angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un intervallo di tempo)
 V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
V A = AMPIEZZA = lunghezza di V A ALTERNATA Proiezione di V X ISTANTE = velocià angolare o pulsazione (gradi /s oppure rad/s) (angolo percorso da V in un inervallo di empo) DEVE ESSERE COSTANTE Angolo
Capitolo 2 Sistemi lineari tempo-invarianti: analisi nel dominio del tempo
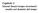 Capiolo 2 Sisemi lineari empo-invariani: analisi nel dominio del empo 1. Inroduzione In queso capiolo ci occuperemo dell analisi nel dominio del empo dei sisemi dinamici lineari empo-invariani. Vale a
Capiolo 2 Sisemi lineari empo-invariani: analisi nel dominio del empo 1. Inroduzione In queso capiolo ci occuperemo dell analisi nel dominio del empo dei sisemi dinamici lineari empo-invariani. Vale a
Elettronica delle Telecomunicazioni Esercizi cap. 3: Anelli ad aggancio di fase
 3. Effeo della variazioni di parameri del PLL - A Un PLL uilizza come demodulaore di fase un moliplicaore analogico, e il livello dei segnali sinusoidale di ingresso (Vi) e locale (Vo) è ale da manenere
3. Effeo della variazioni di parameri del PLL - A Un PLL uilizza come demodulaore di fase un moliplicaore analogico, e il livello dei segnali sinusoidale di ingresso (Vi) e locale (Vo) è ale da manenere
Esercizi di Analisi Matematica Equazioni differenziali
 Esercizi di Analisi Maemaica Equazioni differenziali Tommaso Isola 8 gennaio 00 Indice Generalià. Equazioni del primo ordine inegrabili 3. Teoria............................................ 3. Equazioni
Esercizi di Analisi Maemaica Equazioni differenziali Tommaso Isola 8 gennaio 00 Indice Generalià. Equazioni del primo ordine inegrabili 3. Teoria............................................ 3. Equazioni
CONVERTITORI CC / CC
 CONETITOI CC / CC I converiori CC/CC sono dei circuii che, ricevendo in ingresso una ensione coninua, presenano in uscia una ensione ancora coninua ( in realà un valore medio ) ma di valore diverso rispeo
CONETITOI CC / CC I converiori CC/CC sono dei circuii che, ricevendo in ingresso una ensione coninua, presenano in uscia una ensione ancora coninua ( in realà un valore medio ) ma di valore diverso rispeo
Osservatore asintotico dello stato
 Osservaore asinoico dello sao Si consideri il sisema: x () = Ax () + Bu () y () = Cx () () Problema: Deerminare un disposiivo in grado di inseguire asinoicamene lo sao di un processo assegnao con modalià
Osservaore asinoico dello sao Si consideri il sisema: x () = Ax () + Bu () y () = Cx () () Problema: Deerminare un disposiivo in grado di inseguire asinoicamene lo sao di un processo assegnao con modalià
Esercizi 5. Sistemi lineari
 Esercizi 5 10\04\017 Sisemi lineari David Barbao Esercizio 1 (Appello 014-015 ese 3). Dao il sisema lineare: x 1 + x + 3x 3 + 4x 4 = 0 x + x 3 + 3x 4 = 0 x 1 x x 3 x 4 = 0 (1) sia T lo spazio delle soluzioni
Esercizi 5 10\04\017 Sisemi lineari David Barbao Esercizio 1 (Appello 014-015 ese 3). Dao il sisema lineare: x 1 + x + 3x 3 + 4x 4 = 0 x + x 3 + 3x 4 = 0 x 1 x x 3 x 4 = 0 (1) sia T lo spazio delle soluzioni
RISPOSTA NEL DOMINIO DEL TEMPO
 RISPOSTA NEL DOMINIO DEL TEMPO Nel dominio del empo le variabili sono esaminae secondo la loro evoluzione emporale. Normalmene si esamina la risposa del sisema a un segnale di prova canonico, cioè si sollecia
RISPOSTA NEL DOMINIO DEL TEMPO Nel dominio del empo le variabili sono esaminae secondo la loro evoluzione emporale. Normalmene si esamina la risposa del sisema a un segnale di prova canonico, cioè si sollecia
Fisica Generale Modulo di Fisica II A.A Ingegneria Meccanica Edile - Informatica Esercitazione 4 CIRCUITI ELETTRICI
 Fisica Generale Modulo di Fisica II A.A. 6-7 Ingegneria Meccanica Edile - Informaica Eserciazione IUITI ELETTII b. Nel circuio della figura si ha 5, e 3 3 e nella resisenza passa una correne di A.Il volaggio
Fisica Generale Modulo di Fisica II A.A. 6-7 Ingegneria Meccanica Edile - Informaica Eserciazione IUITI ELETTII b. Nel circuio della figura si ha 5, e 3 3 e nella resisenza passa una correne di A.Il volaggio
Capitolo 3 - Parte III Circuiti combinatori: alee
 Appuni di Eleronica Digiale Capiolo 3 - Pare III Circuii combinaori: alee Inroduzione... Alee funzionali saiche...5 Alee funzionali dinamiche...6 Alee saiche logiche...8 Alee dinamiche logiche... 4 Esempio...
Appuni di Eleronica Digiale Capiolo 3 - Pare III Circuii combinaori: alee Inroduzione... Alee funzionali saiche...5 Alee funzionali dinamiche...6 Alee saiche logiche...8 Alee dinamiche logiche... 4 Esempio...
Il Debito Pubblico. In questa lezione: Studiamo il vincolo di bilancio del governo.
 Il Debio Pubblico In quesa lezione: Sudiamo il vincolo di bilancio del governo. Esaminiamo i faori che influenzano il debio pubblico nel lungo periodo. Sudiamo la sabilià del debio pubblico. 327 Il disavanzo
Il Debio Pubblico In quesa lezione: Sudiamo il vincolo di bilancio del governo. Esaminiamo i faori che influenzano il debio pubblico nel lungo periodo. Sudiamo la sabilià del debio pubblico. 327 Il disavanzo
Capitolo 8 Il regime periodico e il regime alternativo sinusoidale
 Capiolo 8 Il regime periodico e il regime alernaivo sinusoidale Capiolo 8 Il regime periodico e il regime alernaivo sinusoidale 8.1 Definizioni 8.1.1 Periodo, frequenza, pulsazione Una grandezza si dice
Capiolo 8 Il regime periodico e il regime alernaivo sinusoidale Capiolo 8 Il regime periodico e il regime alernaivo sinusoidale 8.1 Definizioni 8.1.1 Periodo, frequenza, pulsazione Una grandezza si dice
Il Value at Risk secondo l approccio parametrico: un esempio semplificato
 Universià degli Sudi di Napoli Federico II Caedra di Economia delle Aziende di Assicurazione Il Value a Risk secondo l approccio paramerico: un esempio semplificao Domenico Curcio, Ph. D. Value a Risk
Universià degli Sudi di Napoli Federico II Caedra di Economia delle Aziende di Assicurazione Il Value a Risk secondo l approccio paramerico: un esempio semplificao Domenico Curcio, Ph. D. Value a Risk
g Y g M p g Y g g + g M p dove p è il tasso di crescita dei prezzi, ovvero il tasso di inflazione. Poiché g è costante, g
 APPENDICI 465 g Y g g + g M p dove p è il asso di crescia dei prezzi, ovvero il asso di inflazione. Poiché g è cosane, g g è uguale a zero. Quindi: g Y g M p Il asso di crescia della produzione è approssimaivamene
APPENDICI 465 g Y g g + g M p dove p è il asso di crescia dei prezzi, ovvero il asso di inflazione. Poiché g è cosane, g g è uguale a zero. Quindi: g Y g M p Il asso di crescia della produzione è approssimaivamene
CALENDARIO BOREALE 2 AMERICHE 2015 PROBLEMA 1
 www.maefilia.i Indirizzi: LI2, EA2 SCIENTIFICO; LI3 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE 2 AMERICHE 21 PROBLEMA 1 Sai seguendo un corso, nell'amio dell'orienameno universiario,
www.maefilia.i Indirizzi: LI2, EA2 SCIENTIFICO; LI3 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE 2 AMERICHE 21 PROBLEMA 1 Sai seguendo un corso, nell'amio dell'orienameno universiario,
P suolo in P; 2. la distanza d, dall uscita dello
 acolà di Ingegneria Prova Generale di isica I 1.07.004 Compio A Esercizio n.1 Uno sciaore di massa m = 60 Kg pare da fermo da un alezza h = 8 m rispeo al suolo lungo uno scivolo inclinao di un angolo α
acolà di Ingegneria Prova Generale di isica I 1.07.004 Compio A Esercizio n.1 Uno sciaore di massa m = 60 Kg pare da fermo da un alezza h = 8 m rispeo al suolo lungo uno scivolo inclinao di un angolo α
SESSIONE SUPPLETIVA PROBLEMA 2
 www.maefilia.i SESSIONE SUPPLETIVA - 26 PROBLEMA 2 Fissao k R, la funzione g k :R R è così definia: g k = e kx2. Si indica con Γ k il suo grafico, in un riferimeno caresiano Oxy. ) Descrivi, a seconda
www.maefilia.i SESSIONE SUPPLETIVA - 26 PROBLEMA 2 Fissao k R, la funzione g k :R R è così definia: g k = e kx2. Si indica con Γ k il suo grafico, in un riferimeno caresiano Oxy. ) Descrivi, a seconda
Alcuni strumenti per misure di portata e velocità
 Capiolo 8 lcuni srumeni per misure di poraa e velocià 8. Meodi sperimenali per misure di velocià lcune delle principali ecniche che si uilizzano in fluidodinamica per misure di velocià (o poraa) sono riassune
Capiolo 8 lcuni srumeni per misure di poraa e velocià 8. Meodi sperimenali per misure di velocià lcune delle principali ecniche che si uilizzano in fluidodinamica per misure di velocià (o poraa) sono riassune
Corso di Laurea in Ingegneria Informatica (Laurea on Line) Prima prova Intermedia
 Milano, 0/0/00 Corso di Laurea in Ingegneria Inormaica (Laurea on Line) Corso di Fondameni di elecomunicazioni Prima prova Inermedia Carissimi sudeni, scopo di quesa prima prova inermedia è quello di veriicare
Milano, 0/0/00 Corso di Laurea in Ingegneria Inormaica (Laurea on Line) Corso di Fondameni di elecomunicazioni Prima prova Inermedia Carissimi sudeni, scopo di quesa prima prova inermedia è quello di veriicare
Esercizi Scheda N Fisica II. Esercizi con soluzione svolta
 Poliecnico di Torino etem Esercizi Scheda N. 0 45 Fisica II Esercizi con soluzione svola Esercizio 0. Si consideri il circuio V R T R T V I V 0 Vols R 5 Ω R 0 Ω µf sapendo che per 0 T on T off 5 µs T off
Poliecnico di Torino etem Esercizi Scheda N. 0 45 Fisica II Esercizi con soluzione svola Esercizio 0. Si consideri il circuio V R T R T V I V 0 Vols R 5 Ω R 0 Ω µf sapendo che per 0 T on T off 5 µs T off
Vantaggio temporale. Problemi sul moto rettilineo uniforme. Risoluzione
 Creao il 25/2/2 19.35. elaborao il 14/5/26 alle ore 18.3.26 Problemi sul moo reilineo uniforme anaggio emporale m s (m) Un moociclisa passa dall origine del sisema di riferimeno ( m) al empo s ad una velocià
Creao il 25/2/2 19.35. elaborao il 14/5/26 alle ore 18.3.26 Problemi sul moo reilineo uniforme anaggio emporale m s (m) Un moociclisa passa dall origine del sisema di riferimeno ( m) al empo s ad una velocià
UNIVERSITÀ DEGLI STUDI DELLA CALABRIA CORSI DI LAUREA IN INGEGNERIA. - Seconda prova scritta di ANALISI MATEMATICA 1 - APPELLO DEL 9 settembre 2013
 UNIVERSITÀ DEGLI STUDI DELLA CALABRIA CORSI DI LAUREA IN INGEGNERIA - Seconda prova scria di ANALISI MATEMATICA - APPELLO DEL 9 seembre 0 COGNOME... NOME... MATRICOLA... IMPORTANTE Al ermine della prova
UNIVERSITÀ DEGLI STUDI DELLA CALABRIA CORSI DI LAUREA IN INGEGNERIA - Seconda prova scria di ANALISI MATEMATICA - APPELLO DEL 9 seembre 0 COGNOME... NOME... MATRICOLA... IMPORTANTE Al ermine della prova
Il concetto di punto materiale
 Il conceo di puno maeriale Puno maeriale = corpo privo di dimensioni, o le cui dimensioni sono rascurabili rispeo a quelle della regione di spazio in cui può muoversi e degli alri oggei con cui può ineragire
Il conceo di puno maeriale Puno maeriale = corpo privo di dimensioni, o le cui dimensioni sono rascurabili rispeo a quelle della regione di spazio in cui può muoversi e degli alri oggei con cui può ineragire
