Propagazione nelle fibre ottiche
|
|
|
- Casimiro Toscano
- 8 anni fa
- Visualizzazioni
Transcript
1 Propagazione nelle fibre ottiche Appunti dal Corso di Complementi di Campi Elettromagnetici Fac. di Ingegneria, Università di Pavia, a.a La teoria delle guide dielettriche può essere usata per trattare le fibre ottiche a salto d indice. La Fig. 1 rappresenta un a fibra circolare di questo tipo, costituita da un nucleo di indice di rifrazione n 1 e raggio a e da un mantello indice di rifrazione n 2 (< n 1 ) e di raggio molto maggiore. Le comuni fibre sono realizzate in un vetro a base di Silice, il cui indice di rifrazione viene aggiustato al valore desiderato mediante drogaggio. Dentro la fibra si possono propagare uno o più modi guidati, che si attenuano radialmente all interno del mantello. Le dimensioni del mantello sono tali da poter assumere che il campo alla sua periferia sia praticamente nullo. Grazie a questo fatto la dimensione finita del mantello ha influenza trascurabile sulla propagazione dei modi, che possono essere studiati come in una guida dielettrica circolare di raggio a e indice di rifrazione n 1 circondata da un mezzo illimitato, di indice di rifrazione n 2. Si distinguono fibre multimodo e fibre monomodo in cui, alla lunghezza d onda di lavoro (λ 0 = 2π/k 0 ), si possono propagare diversi modi o un solo modo, rispettivamente. Nelle fibre multimodo il diametro del nucleo è normalizzato a 50 µm, in quelle monomodo è di pochi micron. L indice di rifrazione del mantello è solo leggermente minore di quello del nucleo (ordine di qualche per cento nelle fibre multimodo, e di qualche per mille in quelle monomodo), così che la costante di fase dei modi guidati è compresa in uno stretto intervallo (k 0 n 2 < β < k 0 n 1 ), ed è prossima a quella delle onde piane uniformi, sia nel materiale che costituisce il nucleo, sia in quello che costituisce il mantello. I. APPROSSIMAZIONI CONSEGUENTI ALLA PROSSIMITÀ DEGLI INDICI DI RIFRAZIONE A causa della prossimità degli indici di rifrazione si ha = n2 1 n 2 2 2n mantello n 2 n 1 2a nucleo Fig. 1. Fibra ottica circolare a salto d indice.
2 2 Pertanto nelle equazioni caratteristiche dei modi guidati si può porre 0, ottenendo così le seguenti equazioni semplificate J m (ua) uj m (ua) = K m (va) vk m (va) + mu2 + v 2 au 2 v 2 modi EH mn (e modi TM n, nel caso m = 0) (1) J m (ua) uj m (ua) = K m (va) vk m (va) mu2 + v 2 au 2 v 2 modi HE mn (e modi TE n, nel caso m = 0) (2) Se m = 0 (modi TE o TM), le equazioni caratteristiche semplificate divengono identiche. Pertanto, nei limiti dell approssimazioni fatta, i modi TE n e TM n hanno la stessa costante di fase alla stessa frequenza (modi quasi-degeneri). Utilizzando due identità che intercorrono fra le funzioni di Bessel e le loro derivate 1, le equazioni caratteristiche si riscrivono nella seguente più semplice forma: J m+1 (ua) uj m (ua) + K m+1(va) vk m (va) = 0 modi EH mn (3) J m 1 (ua) uj m (ua) K m 1(va) vk m (va) = 0 modi HE mn (4) Poiché le due equazioni sono diverse, i modi EH e HE con uguali indici non sono degeneri, nemmeno approssimativamente. Una quasi-degenerazione si ha invece fra i modi EH m 1,n e HE m+1,n, con m = 2, 3,.... Infatti le equazioni caratteristiche dei due tipi di modo sono J m (ua) uj m 1 (ua) + K m(va) vk m 1 (va) = 0 modi EH m 1,n (m = 2, 3,...) (5) J m (ua) uj m+1 (ua) K m(va) vk m+1 (va) = 0 modi HE m+1,n (m = 0, 1,...) (6) e tali equazioni sono identiche, come si mostra facilmente utilizzando le formule ricorrenti (v. nota 1) J m+1 (ua) = 2m ua J m(ua) J m 1 (ua) K m+1 (ua) = 2m ua K m(ua) + K m 1 (ua) (7) Un altra proprietà dei modi, nel caso 0, consiste nel fatto che entrambe le componenti longitudinali, E z e H z, sono trascurabili rispetto a quelle trasversali. Pertanto tutti modi sono quasi-tem 2. 1 Valgono le seguenti identità ( ) J mjm(x) m(x) = ± J m±1(x) x K m(x) = ± mkm(x) x K m±1(x) Quelle con il segno superiore vengono utilizzate per trasformare la (1), quelle con il segno inferiore per trasformare la (2), rispettivamente. Uguagliando le espressioni con i due segni si ottengono le formule ricorrenti utilizzate per scrivere le (7). 2 Per le espressioni delle varie componenti del campo si veda, per esempio, i Par e del testo: P. Bassi, G. Bellanca, G. Tartarini, Propagazione ottica libera e guidata, CLUEB, Si richiama l attenzione sul fatto che, in tale testo, i simboli u e w corrispondono ai nostri ua e va.
3 3 II. MODI LP E ben noto che una combinazione lineare di modi degeneri è ancora un modo, che si propaga con la stessa costante di fase dei modi originari. Si può quindi pensare di combinare i modi quasi-degeneri EH m 1,n e HE m+1,n (con m > 0), ottenendo, approssimativamente, un nuovo modo. Questa possibilità è interessante perché, combinando opportunamente i modi delle coppie suddette, è possibile ottenere onde polarizzate linearmente, in direzione ortogonali 3. Le onde risultanti dalla combinazione sono i cosiddetti modi LP (linearly polarized), più precisamente pseudo-modi, dato che la degenerazione è imperfetta. Il modo ottenuto combinando i modi EH m 1,n e HE m+1,n viene indicato con la sigla LP mn. I modi HE 1n (fra questi, il modo dominante HE 11 della guida dielettrica a sezione circolare) non sono degeneri con altri modi (EH 1,n non esiste!). Ciascuno di essi, però, esiste sotto due forme degeneri, come del resto tutti gli altri modi asimmetrici. Si può mostrare che, anche in questo caso, combinando opportunamente tali modi, si ottiene una nuova coppia di modi degeneri, polarizzati linearmente in direzioni ortogonali. Tali modi vengono indicati con la sigla LP 0n. La forma dei campi trasversali dei modi LP mn è molto semplice. Considerando quelli polarizzati nella direzione ŷ si ha E T = ŷe 0 e jβz cos mϕ J m (ur) J m (ua) K m (vr) K m (va) per r a per r > a m = 0, 1, 2,... (8) H T = ẑ E T η 0 /n 1 (9) dove E 0 rappresenta l intensità del campo elettrico alla periferia del nucleo, e dove β è la n-esima soluzione dell equazione caratteristica (6), che è in cui J m (ua) uj m+1 (ua) K m(va) vk m+1 (va) = 0 equazione caratteristica dei modi LP mn (10) u = k0n β 2 v = β 2 k0n Le componenti longitudinali del campo sono trascurabili, poiché, come si è detto, nell approssimazione 0 i modi sono quasi TEM. Si noti che, la relazione esistente fra H t ed E t è proprio quella tipica le onde TEM (η/n 1 η/n 2 è l impedenza caratteristica del mezzo). I diagrammi di dispersione possono essere ottenuti in forma normalizzata introducendo le quantità w = k 0 a n 2 1 n 2 2 = a u 2 + v 2 b = β2 k0n k0(n n 2 2) = Infatti, come si verifica immediatamente, si ha v2 u 2 + v 2 (0 < b < 1) ua = w 1 b va = w b 3 Per i dettagli si veda P. Bassi et al, op. cit.
4 b w Fig. 2. Diagramma di dispersione normalizzato per i primi venti modi della fibra circolare a salto d indice. cosicchè, introducendo queste espressioni nella (10), l equazione caratteristica viene trasformata in una relazione fra b e w, in cui non figurano più né il raggio del nucleo, né gl indici di rifrazione. Risolvendo tale equazione per vari valori di m si di ottengono i diagrammi di dispersione normalizzati riportati nella Fig. 2. Si osserva che β = k0n v 2 = k0n bw2 a 2 = k 0 n b n2 1 n 2 2 k 0 n 2 (1 + b ) dato che n 1 /n 2 1 e 1. Pertanto, considerata una certa frequenza e calcolato il corrispondente valore di w, si legge sul diagramma il valore di b corrispondente al modo che interessa; tale valore, introdotto nell ultima delle precedenti espressioni, permette di ricavare la costante di fase del modo alla frequenza considerata. Si dimostra che i modi LP sono ortogonali, nel senso che considerando i campi E e E di due modi distinti, risulta sempre π π 0 E T E T r dϕ dr = 0 (11) III. POTENZA E FATTORE DI CONFINAMENTO DEI MODI LP Le espressioni (8) e (9) permettono di determinare il vettore di Poynting (S = ẑ E T 2 /2(η 0 /n 1 )) nel nucleo e nel mantello. Pertanto, si possono determinare le potenze trasmessa da un modo, attraverso il nucleo e attraverso il mantello. Considerando i flussi attraverso un piano trasversale alla fibra si ottiene
5 5 P nucleo = n 1 E 0 2 2π 2η 0 Jm(ua) 2 0 P mant = n 1 2η 0 E 0 2 K 2 m(va) 2π Inoltre, l espressione della potenza trasmessa dal modo è 0 a cos 2 mϕ dϕ 0 rj 2 m(ur) dr (12) cos 2 mϕ dϕ a rkm(vr) 2 dr (13) P = P nucleo + P mant Calcolando gli integrali (che sono noti come integrali indefiniti) si perviene alle seguenti espressioni: dove δ m0 è il simbolo di Kronecker e P mant P P = n 1 E 0 2 η 0 κ m π(1 b) 2(2 δ m0 )b (14) = (1 κ m )b (15) κ m = K 2 m(w b) K 2 m 1(w b) K 2 m+1(w b) Poiché b è funzione di w, il rapporto P mant /P e funzione delle sola variabile w. Tale rapporto prende il nome di fattore di confinamento. Esso vale 1 alla frequenza di taglio, decresce rapidamente al crescere della frequenza e tende a zero per w. Dunque, al crescere della frequenza il flusso di energia tende a concentrarsi sempre più nel nucleo. Per il modo fondamentale LP 01, tale rapporto scende al di sotto del 25% per valori di w maggiori di 2 rad. La potenza trasmessa nelle fibre multimodo è pari alla somma delle potenze trasmesse dai singoli modi, come se ciascuno di essi si propagasse in assenza di tutti gli altri. Come nelle guide metalliche, questo risultato è conseguenza dell ortogonalità dei modi (Equazione 11). IV. CENNI SULL ATTENUAZIONE NELLE FIBRE OTTICHE Nelle fibre ottiche reali i modi si attenuano a causa di tre principali meccanismi: perdite dielettriche; diffusione all esterno della fibra; confinamento insufficiente. Di seguito ci si limita a spiegare sinteticamente la natura di tali effetti. Come si vedrà l attenuazione varia con la lunghezza d onda d impiego. Nelle moderne fibre in silice il minimo d attenuazione si trova attorno a 1.55µm ed è dell ordine di 0.2db/km. Questo basso valore ha reso possibile l impiego delle fibre nei collegamenti a grande distanza. Perdite dielettriche - Alle frequenze ottiche le perdite dielettriche sono dovute all assorbimento atomico e molecolare. Come è ben noto, questi effetti sono collegati alle vibrazioni degli strutture elettroniche negli atomi e alle vibrazioni d insieme delle molecole. Tali vibrazioni sono particolarmente intense in corrispondenza delle frequenze di risonanza (frequenze di transizione fra livelli energetici). Nella silice tali risonanze sono collocate nell ultravioletto (risonanze elettroniche) e nell infrarosso
6 6 (risonanze molecolari). Il loro effetto, tuttavia, si risente anche all interno della banda d utilizzo delle fibre (lunghezze d onda dell ordine di 1µm). Risonanze derivanti dalla presenza di particolari impurezze (in particolare l ione OH), danno luogo a picchi d assorbimento indesiderati all interno della banda d interesse. Però i moderni processi di fabbricazione hanno ridotto l effetto delle impurezze, permettendo così di diminuire drasticamente l attenuazione per assorbimento. Perdite per diffusione - Le inevitabili disuniformità del materiale sono sensibili su scale di lunghezza dell ordine del micron. Per quanto riguarda le caratteristiche macroscopiche del materiale (in particolare l indice di rifrazione), tali disuniformità sono ininfluenti se la lunghezza d onda è molto maggiore del micron 4 mentre fanno sentire i loro effetti alle lunghezze d onda d utilizzo delle fibre. Infatti, quando le fluttuazioni d indice di rifrazione sono sensibili sulla scala della lunghezza d onda, diventa importante l effetto di diffusione (di Rayleigh), per cui parte dell energia trasmessa da un onda che si propaga in una ben determinata direzione viene irradiata nelle altre direzioni. Nel caso delle fibre, tale fenomeno può essere visto come un effetto dell accoppiamento fra modi guidati e modi radianti, causato dalle fluttuazioni dell indice di rifrazione. Un effetto simile è provocato dalle imperfezioni geometriche della fibra, dovute al processo di fabbricazione, che possono essere viste come perturbazioni che determinano l accoppiamento fra modi guidati e modi radianti. Perdite per confinamento insufficiente - Il fattore di confinamento si avvicina a 1 per i modi con frequenza di taglio prossima a quella di lavoro. Ne consegue che, nelle fibre multimodo, il campo non è del tutto trascurabile sulla periferia del mantello. Si ha quindi un accoppiamento con il mondo esterno e più precisamente com il rivestimento della fibra, che introduce perdite aggiuntive. V. DISPERSIONE E ben noto che la dispersione limita l utilizzo dei mezzi trasmissivi, poiché provoca la distorsione dei segnali. Nel caso delle fibre si hanno tre diversi tipi di dispersione: intermodale, cromatica, di polarizzazione. I tre effetti vengono brevemente discussi nel seguito. Dispersione intermodale - Quest effetto è presente nelle fibre multimodo ed è causato dalla diversa velocità di propagazione dei modi. Pensando ad un segnale ottico modulato ad impulsi (come quelli usati nel PCM) ogni impulso viene simultaneamente trasmesso da più modi e, quindi, giunge all uscita con ritardi diversi. Il segnale in uscita è quindi costituito dalla sovrapposizione di impulsi di varia ampiezza, sfalsati nel tempo. L effetto complessivo è quello di un allargamento dell impulso, che può provocare interferenza inter-simbolica, se l allargamento supera il tempo di ripetizione degli impulsi. L allargamento degli impulso può essere stimato facendo ricorso ad un modello a raggi. Tale modello può essere usato grazie al fatto che le dimensioni del nucleo delle fibre multimodo sono molto maggiori della lunghezza d onda, permettendo così di utilizzare l approssimazione dell ottica geometrica. La Fig. 3 rappresenta il raggi emessi da una sorgente puntiforme posta sull asse di una fibra a salto d indice. L insieme dei raggi che rimangono intrappolati nel nucleo (a causa del fenomeno della riflessione totale) serve a determinare il campo prodotto dalla sorgente, che -rigorosamente- è rappresentato da una combinazione dei modi guidati. L impulso che per primo raggiunge la sezione trasversale aa 4 Per esempio, se la lunghezza d onda è maggiore di 1 mm, i parametri macroscopici che caratterizzano il materiale possono essere ottenuti mediando su volumetti fisicamente infinitesimi di dimensioni sufficientemente grandi (per esempio 50µm) da spianare le fluttuazioni dell indice di rifrazione, facendolo apparire costante.
7 7 P! L Q n 2 n 1 a S R d a Fig. 3. Raggi in una fibra multimodo a salto d indice. posta alla distanza d dalla sorgente è quello che viaggia lungo il raggio diretto secondo l asse (congiungente i punti P e S); quello che arriva per ultimo è quello che percorre il cammino ottico più lungo (PQRS), attraverso il raggio che incide sulla periferia del nucleo secondo l angolo limite θ L = arcsin n 2 n 1 Nella sezione aa l insieme degli impulsi sfalsati occupa l intervallo di tempo Si ha τ = PQRS c/n 1 d c/n 1 d = PQRS sin θ L ossia PQRS = d sin θ L = n 1 n 2 d Sostituendo nell espressione di τ e osservando che (n 1 n 2 )/n 2 si ottiene: τ n 1 d (16) c La larghezza di banda del sistema trasmissivo è B = 1/τ. Pertanto si ottiene il prodotto bandadistanza Bd = c n 1 Per esempio, nel caso di una fibra con n 1 = 1.5 e = 1% si ha Bd =20 MHz km. Questo risultato mostra che le fibre multimodo non sono adatte a realizzare collegamenti a largha banda su grandi distanze. Banda più larghe vengono ottenute nelle fibre a variazione graduale dell indice di rifrazione (graded index). In queste fibre l indice di rifrazione decresce gradualmente dal centro verso la periferia, così che i raggi non hanno più la forma di spezzate (come nella figura) ma sono curvi con andamento ondulato. I raggi che partono in direzione prossima all asse si discostano dall asse meno degli altri, così che, lungo questi raggi, la distanza geometrica fra la sorgente e la sezione d arrivo è minore che nei raggi
8 8 più inclinati. D altro canto, i raggi più vicini all asse attraversano una zona in cui l indice di rifrazione è più alto cosicché, se il profilo dell indice è studiato opportunamente, il cammino ottico 5 tende a compensarsi fra i vari raggi. Alla compensazione dei cammini ottici corrisponde una compensazione nei tempi di propagazione, che risultano pressocché uguali lungo i vari raggi. Ne consegue che la distorsione intermodale risulta molto minore di quella che si ha nelle fibre a salto d indice. Ovviamente, il problema della dispersione intermodale è radicalmente rimosso nelle fibre monomodo. Dispersione cromatica - La dispersione cromatica dipende da due effetti concomitanti, la dispersività del modo e la dispersività del materiale. Quest ultima è determinata dal fatto che la costante dielettrica (e quindi l indice di rifrazione) varia con la frequenza. La distorsione provocata dalla dispersività su un segnale modulato a larga banda dipende dal fatto che la velocità di gruppo non è costante all interno della banda. La dispersione è caratterizzata dalla quantità D = d2 β dω 2 che corrisponde alla derivata del ritardo di gruppo per unità di lunghezza 6. Calcoli dettagliati evidenziano il fatto che, nei modi fortemente confinati, la dispersione di una fibra non differisce troppo da quella dovuta al solo effetto del materiale, cioè a quella che si avrebbe se la trasmissione avvenisse mediante onde piane uniformi nel mezzo che costituisce il nucleo. In questo caso la distorsione sarebbe D mat = d2 (k 0 n 1 ) dω 2 da cui, dopo alcuni passaggi si ottiene D mat = λ3 0 2πc 2 d 2 n 1 dλ 2 0 Nelle fibre in silice si trova che la dispersione è nulla intorno a λ 0 = 1.3µm, valore diverso da quello per cui è minima l attenuazione (1.55µm). Questa differenza può essere colmata considerando fibre a doppio rivestimento, che utilizzano materiali con diverse caratteristiche di dispersione, opportunamente scelti in modo da compensare reciprocamente gli effetti dispersivi alla lunghezza d onda desiderata. Dispersione di polarizzazione - Questo effetto diventa significativo in assenza dei due precedenti. Esso è dovuto a tutte le cause che rendono asimmetrica la fibra (discostamento dalla geometria circolare dovuto alla lavorazione, curve, asimmetrie dell indice di rifrazione dovute a tensioni meccaniche, etc.). Si tratta di effetti molto piccoli che, tuttavia sono sufficienti a far venir meno l esatta degenerazione che si ha fra le due polarizzazioni ortogonali dello stesso modo. Per esempio il modo LP 01 che si propaga nelle fibre monomodo si suddivide in due modi, polarizzati secondo x e y, che si propagano con velocità leggermente diverse. Ne consegue che, anche nelle fibre monomodo, si ha un effetto simile a quello discusso per la distorsione intermodale, ma molto meno accentuato. 5 Si ricorda che in un mezzo a indice di rifrazione variabile il cammino ottico fra due punti posti sullo stesso raggio è dato dall integrale dell indice di rifrazione fra i due punti, lungo il raggio. 6 Il ritardo di gruppo per unità di lunghezza è l inverso della velocità di gruppo, cioé dβ/dω.
Propagazione in fibra ottica
 Propagazione in fibra ottica Struttura delle fibre ottiche In questa sezione si affronteranno: Modi in fibra ottica Dispersione multimodale Confronto multimodo-singolo modo. I modi in fibra ottica Il campo
Propagazione in fibra ottica Struttura delle fibre ottiche In questa sezione si affronteranno: Modi in fibra ottica Dispersione multimodale Confronto multimodo-singolo modo. I modi in fibra ottica Il campo
Guide d onda. Cerchiamo soluzioni caratterizzate da una propagazione lungo z
 GUIDE D ONDA Guide d onda Cerchiamo soluzioni caratterizzate da una propagazione lungo z Onde progressive e regressive Sostituendo nell equazione d onda ( essendo Valido anche per le onde regressive Equazione
GUIDE D ONDA Guide d onda Cerchiamo soluzioni caratterizzate da una propagazione lungo z Onde progressive e regressive Sostituendo nell equazione d onda ( essendo Valido anche per le onde regressive Equazione
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
INTRODUZIONE: PERDITE IN FIBRA OTTICA
 INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Introduzione alle fibre ottiche
 Introduzione alle fibre ottiche Struttura delle fibre ottiche Una fibra ottica è sostanzialmente un cilindro (solitamente in vetro) con una parte centrale, detta core, con un indice di rifrazione superiore
Introduzione alle fibre ottiche Struttura delle fibre ottiche Una fibra ottica è sostanzialmente un cilindro (solitamente in vetro) con una parte centrale, detta core, con un indice di rifrazione superiore
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici. a Corrente Alternata. Sergio Benenti 7 settembre 2013
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
4 La Polarizzazione della Luce
 4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
RISONANZA. Introduzione. Risonanza Serie.
 RISONANZA Introduzione. Sia data una rete elettrica passiva, con elementi resistivi e reattivi, alimentata con un generatore di tensione sinusoidale a frequenza variabile. La tensione di alimentazione
RISONANZA Introduzione. Sia data una rete elettrica passiva, con elementi resistivi e reattivi, alimentata con un generatore di tensione sinusoidale a frequenza variabile. La tensione di alimentazione
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Induzione magnetica. Corrente indotta. Corrente indotta. Esempio. Definizione di flusso magnetico INDUZIONE MAGNETICA E ONDE ELETTROMAGNETICHE
 Induzione magnetica INDUZIONE MAGNETICA E ONDE ELETTROMAGNETICHE Che cos è l induzione magnetica? Si parla di induzione magnetica quando si misura una intensità di corrente diversa da zero che attraversa
Induzione magnetica INDUZIONE MAGNETICA E ONDE ELETTROMAGNETICHE Che cos è l induzione magnetica? Si parla di induzione magnetica quando si misura una intensità di corrente diversa da zero che attraversa
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
(2) t B = 0 (3) E t In presenza di materia, le stesse equazioni possono essere scritte E = B
 Equazioni di Maxwell nei mezzi e indice di rifrazione I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E ϱ ɛ 0 () E B (2) B 0 (3) E B µ 0 j + µ 0 ɛ 0
Equazioni di Maxwell nei mezzi e indice di rifrazione I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E ϱ ɛ 0 () E B (2) B 0 (3) E B µ 0 j + µ 0 ɛ 0
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
I.P.S.I.A. Di BOCCHIGLIERO. ---- Fotoemettitori e Fotorivelatori ---- Materia: Telecomunicazioni. prof. Ing. Zumpano Luigi. Filippelli Maria Fortunata
 I..S.I.A. Di BOCCHIGLIERO a.s. 2010/2011 -classe III- Materia: Telecomunicazioni ---- Fotoemettitori e Fotorivelatori ---- alunna Filippelli Maria Fortunata prof. Ing. Zumpano Luigi Fotoemettitori e fotorivelatori
I..S.I.A. Di BOCCHIGLIERO a.s. 2010/2011 -classe III- Materia: Telecomunicazioni ---- Fotoemettitori e Fotorivelatori ---- alunna Filippelli Maria Fortunata prof. Ing. Zumpano Luigi Fotoemettitori e fotorivelatori
Il Campionameto dei segnali e la loro rappresentazione. 1 e prende il nome frequenza di
 Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
 1 Le equazioni di Maxwell e le relazioni costitutive 1 1.1 Introduzione... 1 1.2 Richiami sugli operatori differenziali...... 4 1.2.1 Il gradiente di uno scalare... 4 1.2.2 La divergenza di un vettore...
1 Le equazioni di Maxwell e le relazioni costitutive 1 1.1 Introduzione... 1 1.2 Richiami sugli operatori differenziali...... 4 1.2.1 Il gradiente di uno scalare... 4 1.2.2 La divergenza di un vettore...
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Interferenza e diffrazione
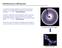 Interferenza e diffrazione La radiazione elettromagnetica proveniente da diverse sorgenti si sovrappongono in ogni punto combinando l intensita INTERFERENZA Quando la radiazione elettromagnetica passa
Interferenza e diffrazione La radiazione elettromagnetica proveniente da diverse sorgenti si sovrappongono in ogni punto combinando l intensita INTERFERENZA Quando la radiazione elettromagnetica passa
Spettrofotometria. Le onde luminose consistono in campi magnetici e campi elettrici oscillanti, fra loro perpendicolari.
 Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
 FIBRE OTTICHE 1 2 3 4 5 6 7 Le fibre ottiche monomodali sono caratterizzate da un diametro Dcr del core (nucleo) compreso tra 4 e 10 μm (micrometri o micron) e da un diametro Dcl del cladding (mantello)
FIBRE OTTICHE 1 2 3 4 5 6 7 Le fibre ottiche monomodali sono caratterizzate da un diametro Dcr del core (nucleo) compreso tra 4 e 10 μm (micrometri o micron) e da un diametro Dcl del cladding (mantello)
DETERMINAZIONE DI V S30 ReMi software
 DETERMINAZIONE DI V S30 ReMi software Il calcolo di questo parametro dinamico può essere effettuato attraverso le classiche prove sismiche in foro del tipo DOWN-HOLE oppure con metodi innovativi indiretti.
DETERMINAZIONE DI V S30 ReMi software Il calcolo di questo parametro dinamico può essere effettuato attraverso le classiche prove sismiche in foro del tipo DOWN-HOLE oppure con metodi innovativi indiretti.
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
T13 FIBRE OTTICHE. T13.1 Elencare i principali vantaggi delle fibre ottiche come mezzo trasmissivo, in confronto con le linee di trasmissione in rame.
 T13 FIBRE OTTICHE T13.1 Elencare i principali vantaggi delle fibre ottiche come mezzo trasmissivo, in confronto con le linee di trasmissione in rame. T13. Perché le fibre ottiche possono essere considerate
T13 FIBRE OTTICHE T13.1 Elencare i principali vantaggi delle fibre ottiche come mezzo trasmissivo, in confronto con le linee di trasmissione in rame. T13. Perché le fibre ottiche possono essere considerate
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
La propagazione della luce in una fibra ottica
 La propagazione della luce in una fibra ottica La rifrazione della luce Consideriamo due mezzi trasparenti alla luce, separati da una superficie piana. Il primo mezzo ha indice di rifrazione n, il secondo
La propagazione della luce in una fibra ottica La rifrazione della luce Consideriamo due mezzi trasparenti alla luce, separati da una superficie piana. Il primo mezzo ha indice di rifrazione n, il secondo
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
illuminazione artificiale
 illuminazione artificiale Illuminazione artificiale degli interni Il progetto di illuminazione degli interni deve essere studiato e calcolato in funzione della destinazione d uso e dei compiti visivi del
illuminazione artificiale Illuminazione artificiale degli interni Il progetto di illuminazione degli interni deve essere studiato e calcolato in funzione della destinazione d uso e dei compiti visivi del
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Dispensa sulle funzioni trigonometriche
 Sapienza Universita di Roma Dipartimento di Scienze di Base e Applicate per l Ingegneria Sezione di Matematica Dispensa sulle funzioni trigonometriche Paola Loreti e Cristina Pocci A. A. 00-0 Dispensa
Sapienza Universita di Roma Dipartimento di Scienze di Base e Applicate per l Ingegneria Sezione di Matematica Dispensa sulle funzioni trigonometriche Paola Loreti e Cristina Pocci A. A. 00-0 Dispensa
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
TEORIA MODALE IN UNA GUIDA CIRCOLARE
 3 TEORIA MODALE IN UNA GUIDA CIRCOLARE Per studiare la propagazione in fibra ottica dal punto di vista della teoria elettromagnetica bisogna partire dalle equazioni di Maxwell, in questo capitolo si discute
3 TEORIA MODALE IN UNA GUIDA CIRCOLARE Per studiare la propagazione in fibra ottica dal punto di vista della teoria elettromagnetica bisogna partire dalle equazioni di Maxwell, in questo capitolo si discute
I SISTEMI TRIFASI B B A N B B
 I SISTEMI TRIFSI ITRODUZIOE Un sistema polifase consiste in due o più tensioni identiche, fra le quali esiste uno sfasamento fisso, che alimentano, attraverso delle linee di collegamento, dei carichi.
I SISTEMI TRIFSI ITRODUZIOE Un sistema polifase consiste in due o più tensioni identiche, fra le quali esiste uno sfasamento fisso, che alimentano, attraverso delle linee di collegamento, dei carichi.
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15
 Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15 Esercizio 1 (9 punti): Una distribuzione di carica è costituita da un guscio sferico
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15 Esercizio 1 (9 punti): Una distribuzione di carica è costituita da un guscio sferico
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Regole della mano destra.
 Regole della mano destra. Macchina in continua con una spira e collettore. Macchina in continua con due spire e collettore. Macchina in continua: schematizzazione di indotto. Macchina in continua. Schematizzazione
Regole della mano destra. Macchina in continua con una spira e collettore. Macchina in continua con due spire e collettore. Macchina in continua: schematizzazione di indotto. Macchina in continua. Schematizzazione
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
RETI DI TELECOMUNICAZIONE SISTEMI M/G/1 e M/D/1 Sistemi M/G/1 Nei sistemi M/G/1: i clienti arrivano secondo un processo di Poisson con parametro λ i tempi di servizio hanno una distribuzione generale della
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Economia Applicata ai sistemi produttivi. 06.05.05 Lezione II Maria Luisa Venuta 1
 Economia Applicata ai sistemi produttivi 06.05.05 Lezione II Maria Luisa Venuta 1 Schema della lezione di oggi Argomento della lezione: il comportamento del consumatore. Gli economisti assumono che il
Economia Applicata ai sistemi produttivi 06.05.05 Lezione II Maria Luisa Venuta 1 Schema della lezione di oggi Argomento della lezione: il comportamento del consumatore. Gli economisti assumono che il
Onde elettromagnetiche
 Onde elettromagnetiche Alla metà del XIX secolo Maxwell prevede teoricamente le onde e.m. Sono scoperte sperimentalmente da Hertz Danno la possibilità di comunicare a distanza (radio, televisione, telecomandi
Onde elettromagnetiche Alla metà del XIX secolo Maxwell prevede teoricamente le onde e.m. Sono scoperte sperimentalmente da Hertz Danno la possibilità di comunicare a distanza (radio, televisione, telecomandi
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Corso di Fondamenti di Telecomunicazioni 5 - EGALI DIGITALI E A IMPULI I BADA BAE Prof. Mario Barbera [parte ] Codifica La fase di codifica prevede che venga fatta una associazione tra il livello del segnale
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Reti in fibra ottica. Cosa c è nella lezione. In questa lezione si parlerà di: Caratterizzazione analitica. Cause fisiche della dispersione.
 Reti in fibra ottica Cosa c è nella lezione In questa lezione si parlerà di: Caratterizzazione analitica Cause fisiche della dispersione. 2/41 Generalità La dispersione cromatica può limitare drasticamente
Reti in fibra ottica Cosa c è nella lezione In questa lezione si parlerà di: Caratterizzazione analitica Cause fisiche della dispersione. 2/41 Generalità La dispersione cromatica può limitare drasticamente
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
POLARIZZAZIONE ORIZZONTALE O VERTICALE?
 A.R.I. Sezione di Parma Conversazioni del 1 Venerdì del Mese POLARIZZAZIONE ORIZZONTALE O VERTICALE? Venerdi, 7 dicembre, ore 21:15 - Carlo, I4VIL Oscillatore e risuonatore di Hertz ( http://www.sparkmuseum.com
A.R.I. Sezione di Parma Conversazioni del 1 Venerdì del Mese POLARIZZAZIONE ORIZZONTALE O VERTICALE? Venerdi, 7 dicembre, ore 21:15 - Carlo, I4VIL Oscillatore e risuonatore di Hertz ( http://www.sparkmuseum.com
La trasformata Zeta. Marco Marcon
 La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ
 LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
LA MASSIMIZZAZIONE DEL PROFITTO ATTRAVERSO LA FISSAZIONE DEL PREZZO IN FUNZIONE DELLE QUANTITÀ In questa Appendice mostreremo come trovare la tariffa in due parti che massimizza i profitti di Clearvoice,
Sistemi di Telecomunicazione
 Sistemi di Telecomunicazione Parte 6: Sistemi Ottici Parte 6.1: Propagazione in Fibra Ottica Universita Politecnica delle Marche A.A. 2013-2014 A.A. 2013-2014 Sistemi di Telecomunicazione 1/42 Trasmissione
Sistemi di Telecomunicazione Parte 6: Sistemi Ottici Parte 6.1: Propagazione in Fibra Ottica Universita Politecnica delle Marche A.A. 2013-2014 A.A. 2013-2014 Sistemi di Telecomunicazione 1/42 Trasmissione
I PRINCIPI DEL RISCALDAMENTO A MICROONDE
 I PRINCIPI DEL RISCALDAMENTO A MICROONDE Prof. Paolo ARCIONI Dipartimento di Elettronica Università di Pavia UNIVERSITA DEGLI STUDI DI MODENA E REGGIO EMILIA DIPARTIMENTO DI INGEGNERIA DEI MATERIALI E
I PRINCIPI DEL RISCALDAMENTO A MICROONDE Prof. Paolo ARCIONI Dipartimento di Elettronica Università di Pavia UNIVERSITA DEGLI STUDI DI MODENA E REGGIO EMILIA DIPARTIMENTO DI INGEGNERIA DEI MATERIALI E
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
GRANDEZZE ALTERNATE SINUSOIDALI
 GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Circuiti amplificatori
 Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Circuiti amplificatori G. Traversi Strumentazione e Misure Elettroniche Corso Integrato di Elettrotecnica e Strumentazione e Misure Elettroniche 1 Amplificatori 2 Amplificatori Se A V è negativo, l amplificatore
Visione d insieme DOMANDE E RISPOSTE SULL UNITÀ
 Visione d insieme DOMANDE E RISPOSTE SULL UNITÀ Che cos è la corrente elettrica? Nei conduttori metallici la corrente è un flusso di elettroni. L intensità della corrente è il rapporto tra la quantità
Visione d insieme DOMANDE E RISPOSTE SULL UNITÀ Che cos è la corrente elettrica? Nei conduttori metallici la corrente è un flusso di elettroni. L intensità della corrente è il rapporto tra la quantità
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Campione sciolto in un solvente (deuterato) e. posto in un tubo. di vetro a pareti sottili di diametro di 5 mm e lungo circa 20 cm
 posto in un tubo Campione sciolto in un solvente (deuterato) e di vetro a pareti sottili di diametro di 5 mm e lungo circa 20 cm o spettrometro NMR è formato da alcuni mponenti fondamentali: un magnete,
posto in un tubo Campione sciolto in un solvente (deuterato) e di vetro a pareti sottili di diametro di 5 mm e lungo circa 20 cm o spettrometro NMR è formato da alcuni mponenti fondamentali: un magnete,
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
MODELLIZZAZIONE DI UNA LINEA ELETTRICA
 MODEIZZAZIONE DI UNA INEA EETTRICA Appunti a cura dell Ing. Emanuela Pazzola Tutore del corso di Elettrotecnica per meccanici, chimici e biomedici A.A. 005/006 Facoltà d Ingegneria dell Università degli
MODEIZZAZIONE DI UNA INEA EETTRICA Appunti a cura dell Ing. Emanuela Pazzola Tutore del corso di Elettrotecnica per meccanici, chimici e biomedici A.A. 005/006 Facoltà d Ingegneria dell Università degli
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
a t Esercizio (tratto dal problema 5.10 del Mazzoldi)
 1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Ottica fisiologica (2): sistemi ottici
 Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Indice. 1 La disoccupazione ---------------------------------------------------------------------------------------- 3. 2 di 6
 INEGNAMENO DI EONOMIA OLIIA LEZIONE VIII IL EORE DELL OUAZIONE ROF. ALDO VAOLA Economia olitica Indice 1 La disoccupazione ----------------------------------------------------------------------------------------
INEGNAMENO DI EONOMIA OLIIA LEZIONE VIII IL EORE DELL OUAZIONE ROF. ALDO VAOLA Economia olitica Indice 1 La disoccupazione ----------------------------------------------------------------------------------------
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
FIBRA OTTICA. A cura di Alessandro Leonardi Dipartimento di Ingegneria Informatica e delle Telecomunicazioni Università degli studi di Catania
 FIBRA OTTICA A cura di Alessandro Leonardi Dipartimento di Ingegneria Informatica e delle Telecomunicazioni Università degli studi di Catania Fibra ottica Minuscolo e flessibile filo di vetro costituito
FIBRA OTTICA A cura di Alessandro Leonardi Dipartimento di Ingegneria Informatica e delle Telecomunicazioni Università degli studi di Catania Fibra ottica Minuscolo e flessibile filo di vetro costituito
Istituto d Istruzione Secondaria Superiore M.BARTOLO. A cura del Prof S. Giannitto
 Istituto d Istruzione Secondaria Superiore M.BATOLO PACHINO (S) APPUNTI DI SISTEMI AUTOMATICI 3 ANNO MODELLIZZAZIONE A cura del Prof S. Giannitto MODELLI MATEMATICI di SISTEMI ELEMENTAI LINEAI, L, C ivediamo
Istituto d Istruzione Secondaria Superiore M.BATOLO PACHINO (S) APPUNTI DI SISTEMI AUTOMATICI 3 ANNO MODELLIZZAZIONE A cura del Prof S. Giannitto MODELLI MATEMATICI di SISTEMI ELEMENTAI LINEAI, L, C ivediamo
