Enrico Borghi RELATIVIZZAZIONE DELL EQUAZIONE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN CORPO CONTINUO
|
|
|
- Carla Di Mauro
- 6 anni fa
- Visualizzazioni
Transcript
1 Enrio Borghi RELATIVIZZAZIONE DELL EQUAZIONE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN CORPO CONTINUO Ci proponiamo di relativizzare l equazione fondamentale della Meania newtoniana per un orpo ontinuo espressa dall eq. (C24 dell Appendie C he qui risriviamo (ρ mu + (ρ m U U + f ( ( ρm U k + ( ρm U k U l kl + f k ; k,l,2,3 x l x l Teniamo onto del fatto he, trattandosi di una desrizione euleriana di materia in movimento (v. Appendie C, le quantità ρ m ρ m (R,t (densità di massa, U U (R,t (ampo di veloità, (R,t (tensore degli sforzi e f f (R,t (densità di forza di volume sono misurate all istante t nel punto R on riferimento a un sistema di oordinate S dal quale la materia in movimento viene osservata. Si ha quindi per definizione: ρ m dm d dove dm è una porzione di materia e d è un volumetto infinitesimo riferito a S. Per un sistema di oordinate solidale on la porzione di materia dm in movimento si può srivere: ρ m dm d e dalla Teoria della Relatività speiale si ha d d ; m m (2 (3
2 E. Borghi - Relativizzazione della Meania newtoniana (orpi ontinui periò e infine ρ m d d m ρ m ρ m Ora osserviamo he la ( si può srivere osì: ρ m ( U + + ρ m ( U U dm d + f Tenendo onto della (4 e della (A5 dell Appendie A dello studio Relativizzazione dell equazione fondamentale della Meania newtoniana per una partiella he qui risriviamo U α U x U y U z ; U α e passando alla notazione indiiale si ottiene U (ρ k U m U x U y U z (4 ; α,,2,3 (5 + x l ( ρm U k U l + kl f k ; k,l,2,3 (6 dove kl è la versione relativistia di kl e f k f k è la parte spaziale della densità di forza relativistia espressa da (v. eq. (7 dello studio sopramenzionato f α f U f x f y f z f U f ; f α x f y f z ; α,,2,3 (7 Riprendiamo ora in onsiderazione l equazione di onservazione della massa, (v. Appendie C, eq. (C9 he, ome riordiamo dall Appendie C, non è impliita nella (C24 e quindi neppure nella (6. Si ha ρ m + (ρ m U (8 2
3 E. Borghi - Relativizzazione della Meania newtoniana (orpi ontinui Dal punto di vista relativistio non è la sola massa di un sistema fisio he si onserva, ma è la somma della massa e dell energia. Oorre periò tener presente l equazione di onservazione dell energia espressa dalla (E4 dell Appendie E e risrivere la (8 nel modo seguente ( ρ m + w m + ( ρ m U + S m f U dove si noti he la (E4 è stata divisa per per rendere omogenei gli addendi entro iasuna oppia di parentesi tonde. Infatti: [S m / ] [w m / ] Riordando la (4 si può srivere: ρ m energia volume veloità M densità di massa 2 L3 potenza MLT superfiie veloità2 L 3 densità di quantità di moto + w m + ρ m U + S m f U Moltiplihiamo per : ρ m + w m + ρ m U + S m f U Si ha osì infine, tenendo onto della (5 e della (7: U (ρ U m + w m + ( ρ x l m U U l + Sl m f ; l,2,3 (9 dove w m e S m sono rispettivamente le versioni relativistihe di w m e S m (v., ad esempio, Landau-Lifsits, Teoria dei ampi, par. 35. Ora onsideriamo l insieme delle quattro equazioni ostituito dalla (9 e dalle tre (6 nelle quali aggiungiamo all argomento della derivata temporale la quantità S k m/,k,2,3, trasurabile per valori di U/ osihé le (6 diventano: U (ρ k U m + Sk m + x (ρ l m U k U l + kl f k ( Notiamo l analogia on la densità di quantità di moto elettromagnetia espressa da S e / dove S e è il vettore di Poynting. 3
4 E. Borghi - Relativizzazione della Meania newtoniana (orpi ontinui Introduiamo il seguente 4-tensore simmetrio di seondo ordine E αβ ρ m U α U β ; E ρ m U U ( ovvero U U U U U U 2 U U 3 U U U U U U 2 U U 3 E αβ ρ m ρ m U 2 U U 2 U U 2 U 2 U 2 U 3 U 3 U U 3 U U 3 U 2 U 3 U 3 U U 2 U 3 U U 2 U 3 U U U U 2 U U 3 U 2 U U 2 U 2 U 2 U 3 U 3 U U 3 U 2 U 3 U 3 (2 osihé la (9 e la ( possono essere sritte rispettivamente osì: ( E + w x m + x l ( E k + Sk m x ( E l + Sl m f + x l ( E kl + kl f k ; k,l,2,3 (3 Introduiamo anhe il 4-tensore simmetrio di seondo ordine T, detto tensore energiasforzo meanio, osì definito w m S m / S2 m / S3 m / T αβ S m/ 2 3 S 2 m/ S 3 m/ (4 osihé le (3 diventano ( E αβ + T αβ x β f α Introduendo il tensore energetio ; α,β,,2,3 ; (E + T f si ha infine T αβ (E αβ + T αβ ; T αβ T βα ; [T] energia volume L MT 2 (5 T αβ x β fα ; T f (6 Questa equazione rappresenta la versione relativizzata dell equazione fondamentale della Meania newtoniana per un orpo ontinuo. 4
5 E. Borghi - Relativizzazione della Meania newtoniana (orpi ontinui Essa esprime on la sua omponente temporale T β x β la legge di onservazione della massa-energia della distribuzione di materia e on le sue omponenti spaziali T kβ x β fk ; k,2,3 l equazione del moto di tale materia. Se manano gli sforzi interni, ome quando si è in presenza di materia disaggregata, si ha U U U U U U 2 U U 3 w m U U U U U U 2 U U 3 T αβ E αβ + T αβ ρ m + U 2 U U 2 U U 2 U 2 U 2 U 3 U 3 U U 3 U U 3 U 2 U 3 U 3 Ora osserviamo he periò ρ m U U ρ m ρ m ρ m U U k ρ m U k U ρ m ρ m U k U l ρ m U k T αβ E αβ + T αβ ρ m U U 2 U 3 U l f U k ρ m U k ρ m Uk ρ m U k U l ρ m Uk U l U U 2 U 3 U U U U 2 U U 3 w m + U 2 U U 2 U 2 U 2 U 3 U 3 U U 3 U 2 U 3 U 3 Se U/ si ha ρ m ρ m (v. eq. (4 e w m w m 2 ρ m U 2 e sono trasurabili tutte le omponenti di E αβ rispetto a E periò T αβ ρ m + 2 ρ m U 2 5
6 E. Borghi - Relativizzazione della Meania newtoniana (orpi ontinui e quindi ( T αβ ρ m + U 2 2 Poihé U 2 / è trasurabile rispetto a si ottiene infine T αβ ρ m (7 6
7 APPENDICI C, D, E dello studio Reinterpretare l Elettromagnetismo per spiegare la Meania quantistia
8 E. Borghi - Appendie C Appendie C Rihiamiamo aluni onetti fondamentali utilizzati nella desrizione fenomenologia di un orpo ontinuo (Meania newtoniana dei orpi ontinui. Innanzitutto un orpo oupa una erta porzione di spazio tridimensionale, ioè un sottoinsieme di R 3, esprimibile mediante l integrale d Ciasun punto R di si sposta nel tempo seguendo una erta traiettoria. Questa può essere desritta in due modi diversi. Si può far riferimento a una equazione del tipo: R R(R,t (C he fornise, per ogni istante t, la posizione raggiunta dal punto he in t ha la posizione R. La (C è la versione ontinua della ollezione di equazioni he desrivono il moto di un insieme disreto di punti R (i R (i (t ; i,2,3,... intendendo on iò he quest ultima può essere trasformata nella (C faendo assumere all indie i una ontinuità di valori orrispondenti a quelli he può assumere R. Questo può essere onsiderato la etihetta identifiativa di un punto di, osì ome l indie i è l etihetta identifiativa di una partiella. La desrizione dei punti fornita dalla (C è detta lagrangiana o materiale. Si può d altra parte introdurre una espressione del tipo R R (R,t (C2 la quale fornise la etihetta identifiativa R del punto he si trova a transitare in R all istante t. La (C2 può essere riavata per inversione della (C, se è diverso da zero il determinante della matrie jaobiana della trasformazione. Questa desrizione è detta euleriana o spaziale. L insieme dei vettori R ostituise un ampo (vettoriale di etihette identifiative. Esempi. Nella desrizione euleriana si può introdurre un ampo salare di densità di massa ρ m ρ m (R,t he fornise la densità di massa ρ m del punto he si trova a transitare in R al tempo t; oppure un ampo vettoriale di veloità U U (R,t he fornise la veloità U del punto he si trova a transitare in R al tempo t, e. Nella desrizione lagrangiana si ha invee rispettivamente ρ m ρ m (R,t 8
9 E. Borghi - Appendie C U U(R,t Queste espressioni indiano ome variano nel tempo rispettivamente la densità di massa e la veloità del punto he in t si trovava in R. La selta dell una o dell altra desrizione dipende dal fenomeno he si sta studiando. Ad esempio la desrizione spaziale è utilizzabile on vantaggio quando si studiano ampi di pressioni o veloità, nei quali di solito lo sviluppo matematio non viene spinto fino al alolo delle posizioni iniziali delle partielle. La desrizione lagrangiana mette invee in evidenza le posizioni iniziali. La veloità di variazione nel tempo di una proprietà fisia P di un ontinuo è detta derivata onvettiva o derivata materiale di quella proprietà rispetto al tempo. La derivata onvettiva si intende eseguita lungo la traiettoria di iasun punto del ontinuo e può essere immaginata ome la variazione nel tempo misurata da un osservatore he si muova solidalmente ol punto. Nel aso di desrizione lagrangiana, in ui è P P(R,t, si ha dp(r,t P(R,t + P R k R k Ma R k / periò dp(r,t P(R,t e quindi la derivata materiale oinide on la ordinaria derivata parziale. Nel aso di desrizione euleriana si ha P P ( R(t,t periò (C3 ovvero dp (R,t P (R,t dp P + P R k R k P (R,t + (P U P + U ( P + P R k Uk (R,t (C4 (C5 dove si noti he dp/ si ridue all ordinaria derivata parziale se U, oppure se P (ioè se la proprietà P non varia nello spazio, oppure se il prodotto salare di U e P è nullo (ioè se P varia in direzione perpendiolare a U. Esempi. Consideriamo un lago esposto al sole e in esso un bagnante dotato di un termometro e fermo in un punto. Il bagnante osserverà, nell aro di una giornata, una variazione della temperatura dell aqua del lago dovuta al variare delle ondizioni di insolazione (v. eq. (C5 on U e on la proprietà fisia P espressa dalla temperatura dell aqua. Supponiamo ora he in un tratto di riva del lago sia presente una sorgente he rende la temperatura dell aqua diversa da quella dell aqua in prossimità della riva opposta. Se il bagnante nuota dall una all altra riva portando on sé il termometro osserverà una variazione temporale di temperatura dovuta a due ause (v. eq. (C5: una, indipendente dal 9
10 E. Borghi - Appendie C moto del bagnante, dovuta alla variazione delle ondizioni di insolazione del lago durante la (lunga nuotata, e un altra dipendente dal modulo, dalla direzione e dal verso della veloità U on ui il bagnante nuota rispetto al modulo, direzione e verso del gradiente di temperatura dell aqua dovuto alla presenza della sorgente. Se la proprietà P è la densità di massa ρ m, si avrà, nella desrizione lagrangiana e in quella euleriana dρ m (R,t ρ m(r,t dρ m (R,t ρ m (R,t + U (R,t ( ρ m Se la proprietà P è il ampo di veloità U dei punti del orpo, si avrà nella desrizione lagrangiana e in quella euleriana du (R,t du(r,t U (R,t U(R,t + (U U (R,t * * * Consideriamo ora una proprietà fisia di un ontinuo espressa da un integrale di volume. Nella desrizione euleriana si ha P n (t (t e n (R,td ; [e n ] [proprietà] volume (C6 dove e n è il ampo della densità volumia della proprietà (n india un ordine di tensorialità qualsiasi e (t è la porzione di spazio oupata dal ontinuo all istante t. Ci proponiamo di alolare la derivata materiale della P n : dp n d e n (R,td Per fare iò erheremo innanzitutto l espressione della P n nella desrizione lagrangiana. A questo fine osserviamo he la desrizione lagrangiana della densità della proprietà si ottiene effettuando la sostituzione osihé R R(R,t e n (R,t l n (R,t ; d Jd J(R,tdR dr 2 dr 3 (C7 essendo J il determinante jaobiano della trasformazione da R a R, determinante he viene simboliamente indiato osì: ( R, R 2, R 3 J J R, R2, (R, R 2, R 3 R3 (R, R2, R3
11 E. Borghi - Appendie C e he ha le seguenti espressioni equivalenti: J R R R R 2 R R 3 J R R R R 2 R R R R R 2 R R R R 2 R R R 2 R R 2 R 2 R 2 R R 2 R 2 R 2 R 2 R R 2 R R 2 R i R j R k ε ijk R R 2 ijk R R 2 ε R i R j R k (C8 Per ottenere la (C7 onsideriamo (v. figura un punto R R, R2, R3 e ostruiamo un volumetto avente la forma di un parallelepipedo infinitesimo d on un vertie in R e spigoli ostituiti da segmenti generati ome spostamenti infinitesimi paralleli agli assi oordinati da R l a R l + dr l,l,2,3. Si ha osì d dr dr2 dr3 Nella desrizione euleriana si ha in orrispondenza un volumetto d avente un vertie in R e spigoli ostituiti da tre segmenti generati da spostamenti infinitesimi non più paralleli agli assi oordinati ma diretti da R a R + dr (m (on m,2,3 essendo dr (m dr (m,dr (m2,dr (m3 (nella figura viene indiato solamente lo spostamento dr ( dr (,dr (2,dR (3 ed essendo R l (R, R 2, R 3 + dr (l R l (R + dr, R 2, R 3 R l (R, R 2, R 3 + dr (2l R l (R, R 2 + dr 2, R 3 R l (R, R 2, R 3 + dr (3l R l (R, R 2, R 3 + dr 3
12 E. Borghi - Appendie C osihé dr (ml R l (, R m + dr m, R l (R, R 2, R 3 Rl R m dr m (C9 dove il soprassegno sugli indii ripetuti sta a indiare he non è sottintesa l operazione di somma. Ora è noto he il volume d è espresso da d dr ( dr ( dr (2 dr (3 dr (2 dr (3 dr (2 dr (22 dr (23 dr (3 dr (32 dr (33 osihé tenendo onto della (C9 si può srivere (a b ε. : (ab ε ijk a i b j k ovvero d R R dr R R 2 dr 2 R dr 3 R 2 R dr R 2 R 2 dr 2 R 2 dr 3 R dr R 2 dr 2 dr 3 ε ijk R i R R i R j R k d ε ijk R R 2 d he, tenuto onto della (C8, oinide on la (C7. dr R j R 2 Ritorniamo alla (C6 ed effettuiamo in essa le sostituzioni (C7 osihé P n (t l n (R,tJd R k dr 2 dr 3 (C Abbiamo osì ottenuto l espressione della proprietà fisia del ontinuo nella desrizione lagrangiana. In questa desrizione il alolo della derivata materiale della P n (t è faile: Ma ( dj d εijk dp n d ( ln J d R ( R 2 ijk R d R i R j R k +ε R i R 2 R j ( dln J + l n R k dj d ijk R +ε R i R 2 R j ( d (C Consideriamo la derivata materiale nel primo termine a membro destro e osserviamo he l argomento della derivata è una funzione di R,t periò (v. eq. (C3 R k d R R i R R i R R i U (R,t R i U R l R r R l R r R i 2
13 E. Borghi - Appendie C Per semplifiare la srittura poniamo U R l R l R r U R r osihé Segue d R R i U R r R r R i ε ijk ( d R R 2 R i R j R k ( U ε ijk R r R 2 R r R i R j R k { ε ijk U R R 2 R R i R j R k ; r,2,3 + U R 2 R 2 R 2 R i R j + R k + U R 2 R i R j } Ora osserviamo he il seondo termine entro parentesi graffe è simmetrio rispetto agli indii i e j, mentre il terzo termine è simmetrio rispetto a i e k osihé il prodotto ontratto del tensore di Levi-Civita, he è antisimmetrio rispetto a tutte le oppie dei suoi indii, on iasuno di questi termini dà zero e quindi rimane: ε ijk ( d R R 2 R i R j R k Con ragionamenti simili si ottiene: ( ijk R d R 2 ε R i R j e quindi la (C diviene periò ijk U R R 2 ε R R i R j R k R k U2 R R 2 J ; εijk R2 R i R j U R R 2 εijk R R i R j R k ( d R k dj ( U R + U2 R + U3 J Uk J ( UJ 2 Rk dp n A questo punto, operando la trasformazione { } dln + l n( U Jd R R (R,t e tenendo presente la (C7 ritorniamo alla desrizione euleriana: dp n U3 J R k U R J (C2 { den (R,t + e n (R,t ( U (R,t } d (C3 Abbiamo osì ottenuto quello he i eravamo proposti di alolare, ioè l espressione della derivata materiale di P n, proprietà fisia di un ontinuo espressa da un integrale di volume. 3
14 E. Borghi - Appendie C Tenendo presente la definizione di derivata materiale per una grandezza euleriana (v. eq. (C5 si può risrivere la (C3 nel modo seguente: Esempi. dp n { } en + U ( e n + e n ( U d (C4 In meania newtoniana la massa m di un orpo avente densità volumia ρ m e ontenuto in un volume m ρ m d (C5 si onserva nel tempo, nel senso he può variare solo se vi è passaggio di materia in entrata o usita attraverso la superfiie di. Si ha quindi dm d ρ m d Dalla (C3, essendo e n ρ m e P n m, si ottiene ( dρm + ρ m ( U d mentre dalla (C4, essendo U ( ρ m + ρ m ( U (ρ m U, si riava ( ρm + (ρ m U d (C6 (C7 equivalente alla (C6. Dalle (C6 e (C7 si riavano le versioni puntuali delle equazioni di onservazione: dρ m + ρ m ( U (C8 ρ m + (ρ m U (C9 Riordando il teorema di Gauss si può srivere la seonda delle (C7 nel modo seguente: ρ m d + ρ m U nd (C2 Essa mostra he la massa di un orpo ontinuo dotato di volume può mutare solo se vi è flusso di massa in ingresso o in usita attraverso la superfiie di. Se ρ m U è il vettore densità volumia di quantità di moto, allora l equazione fondamentale della meania newtoniana per un orpo ontinuo avente volume e superfiie è: d ρ m U d nd + f d (C2 4
15 E. Borghi - Appendie C dove è il tensore degli sforzi meanii e f è una densità di forza di volume. Se assumiamo e n ρ m U ; P n ρ m U d otteniamo dalla (C4 dp n d { ρm U ρ m U d periò la (C2 può essere risritta in questo modo ( ρm U + U ( (ρ m U } + ρ m U( U d + U ( (ρ m U + ρ m U( U d nd + f d (C22 Tenendo presente he U ( (ρ m U + ρ m U( U (ρ m U U si ottiene infine ( ρm U + (ρ m U U d nd + f d (C23 Le (C2, (C22 e (C23 sono espressioni equivalenti della legge fondamentale della Meania newtoniana per un orpo ontinuo. Appliando il Teorema di Gauss all integrale di superfiie e supponendo n rivolta verso l interno di si ottiene la seguente versione puntuale della (C23: ρ m U + (ρ m U U + f (C24 * * * Riprendiamo in onsiderazione la (C3 e supponiamo he e n rappresenti non una densità riferita al volume ome si è supposto finora (v. eq. (C6, ma una densità riferita alla massa he indihiamo on e n (m : [e n (m ] [proprietà] (C25 massa Ne segue he si può srivere periò la (C3 diviene dp n [ρ m e n (m ] massa [proprietà] volume massa { dρ m e (m n { dρ m e(m n { (dρm + ρ m e (m n ( U } d + ρ de n (m m + ρ m ( U e n (m 5 [e n ] (C26 + ρ m e (m n ( U } d } de n (m + ρ m d
16 E. Borghi - Appendie C Se vale la (C8 ne segue he dp n de n (m ρ m d (C27 Le (C3, (C4 e (C27 sono modi diversi di formulare la derivata materiale di una proprietà fisia di un ontinuo espressa da un integrale di volume. Esempio. L integrando a membro sinistro della (C2 può essere onsiderato ome il prodotto di ρ m e della densità di massa di quantità di moto espressa da U quantità di moto massa densità di massa di q. di m. (C28 e quindi per il membro sinistro della (C2 vale la (C27, osihé d d(densità di massa di q. di m. du ρ m U d ρ m d ρ m d periò la (C2 diviene du ρ m d nd + f d (C29 he è un altro modo di esprimere la legge fondamentale della Meania newtoniana per un orpo ontinuo. Appliando il Teorema di Gauss e supponendo n rivolta verso l interno di si ottiene du ρ m d ( + f d la ui versione puntuale è ρ m du + f (C3 6
17 E. Borghi - Appendie D Appendie D Determiniamo l espressione della densità dell energia potenziale di deformazione elastia w D di un orpo avente volume, superfiie e normale n (int rivolta verso l interno (l indiazione int verrà talvolta omessa per semplifiare la srittura in stato di tensione elastia desritta dal tensore degli sforzi. Assumiamo le seguenti definizioni e onvenzioni (n ( n (n (n n f densità di forza di volume agente entro (D forza di superfiie agente su ; (n è positiva se è una forza di pressione e quindi n è diretta verso l interno di definizione del tensore degli sforzi (D2 kl lk simmetria del tensore degli sforzi (D3 s vettore spostamento (D4 e ( s + s definizione del tensore della deformazione 2 (D5 : e ; ij ijkl e kl legge di Hooke (D6 ρ m U + f equazione newtoniana della meania (v. eq. (C3 (D7 f equazione dell equilibrio del orpo elastio (D8 e teniamo presente he la teoria lassia della deformazione, alla quale i stiamo riferendo, prende in onsiderazione pioli spostamenti e pioli gradienti dello spostamento. In queste ipotesi la differenza fra la desrizione lagrangiana e la desrizione euleriana (v. Appendie C tende ad annullarsi osihé in luogo dei tensori lagrangiano ed euleriano di deformazione si onsidera un unio tensore di deformazione e (v. eq. (D5, e la derivata materiale (V. Appendie C tende a diventare indistinguibile dalla derivata parziale ordinaria periò la (C3 viene espressa dalla (D7. In entrambe le Appendii D ed E si farà impliitamente riferimento a queste assunzioni. Ciò posto, indihiamo on ds uno spostamento infinitesimo di un generio punto di he assumiamo in ondizioni di equilibrio. Lo spostamento è molto lento e il orpo rimane in equilibrio. Il lavoro ompiuto dalle forze f agenti in e dalle forze (n agenti sulla superfiie, è espresso da dw D f dsd + Ma il orpo è in equilibrio, periò, per la (D8 dw D ( ds d + 7 (n dsd (n dsd
18 E. Borghi - Appendie D Ma e quindi o anhe periò (a,b ds da ui Ma b ( a + a : ( b ı k b k ( l ı l a mn ı m ı n + a mn ı m ı n : ( r ı r b s ı s dw D b n ( m a mn + a mn ( m b n m (a mn b n b ( a + a : ( b (a b ( a b + a : ( b (a b ( ds ( ds : (ds ( dsd : ( dsd + (n dsd ds 2 ( ds + ds + 2 ( ds ds de + ( ds ds 2 (D9 dove si è tenuto onto della (D5, periò dw D ( dsd : ded 2 : ( ds ds d + (n dsd Il terzo integrale a membro destro è nullo perhé è il prodotto salare del tensore simmetrio per il tensore antisimmetrio ds ds periò dw D ( dsd : de d + (n dsd Applihiamo il teorema di Gauss al primo termine a membro destro. Poihé la normale n è rivolta verso l interno segue dw D ds nd (n dsd : ded + : de d + (n dsd (n dsd e infine ovvero, in termini di densità dw D : ded Questa espressione differenziale è esatta se dw D : de ij de ij ij e kl kl e ij (D 8
19 Ma per un orpo elastio vale la legge di Hooke (v. eq. (D6 osihé E. Borghi - Appendie D ij e kl ijkl ; kl e ij klij periò la (D è verifiata se ijkl klij (D Questa ondizione di simmetria esiste per un orpo isotropo. Assumeremo he il orpo he stiamo onsiderando lo sia, periò è possibile definire una energia potenziale elastia he aloliamo nel modo seguente (v. eq. (D6 dw D ijkl e kl de ij Sambiamo gli indii ij on gli indii kl e teniamo onto della (D e sommiamo a membro a membro dw D klij e ij de kl ijkl e ij de kl 2dw D ijkl (e kl de ij + e ij de kl ijkl d(e kl e ij d( ijkl e kl e ij ovvero, per la (D6 e quindi 2dw D d( : e w D 2 : e (D2 Questa è l espressione della densità di energia potenziale elastia he i eravamo proposti di determinare. 9
20 E. Borghi - Appendie E Appendie E È data una distribuzione di materia dotata di densità di massa ρ m in un ampo di veloità U. Consideriamo la porzione di materia ontenuta in un volume irondato da una superfiie ; la normale n alla superfiie è rivolta verso l interno e quindi n n (int. In è presente un ampo di forze di volume aventi densità f; la materia è in uno stato di deformazione elastia desritta dal ampo tensoriale e dovuta a uno stato di tensione elastia desritta dal ampo tensoriale. Indihiamo on w m la densità volumia di energia meania presente in espressa dalla somma delle densità volumihe di energia inetia e di energia potenziale di deformazione elastia w D della materia: Dalla Appendie D (v. eq. (D2 riaviamo w m 2 ρ mu 2 + w D w D 2 : e e quindi la densità volumia di energia meania totale w m è espressa da w m 2 ρ mu 2 2 : e della quale ora i interessa determinare la derivata rispetto al tempo. A questo fine ominiamo ol onsiderare la d w m d d 2 ρ mu 2 d 2 d : e d Poniamo e quindi P n dp n d 2 ρ mu 2 d 2 ρ mu 2 d Ma 2 U2 dt dm densità massia dell energia inetia T 2 m U 2 osihé dp n d Tenendo presente la (C27 possiamo srivere ρ m dt dm d dp n e quindi d dt d d ρ m d ρ m dm 2 U2 d ρ m ( 2 U Ud ρ m U du d d w m d ρ m U du d d : ed 2 2
21 E. Borghi - Appendie E Questa equazione, per quanto si è detto sulla teoria lassia della deformazione all inizio dell Appendie D, può essere onsiderata valida sia nella desrizione euleriana sia nella desrizione lagrangiana, periò da ui w m d ρ m U U d 2 : e d w m ρ m U U : e 2 Ora osserviamo he si ha (legge di Hooke, eq. (D6: (E ( : e 2 2 ( : e : e 2 : e Ma in un orpo isotropo vale la (D periò ovvero e quindi ( : e 2 : e + e ( : e : 2 e ( : 2 : e + e ( : e : 2 e kl ijkl eij ij ekl klij e ( : e e : e ( : e : e ( : e : 2 + e ( : e : 2 dove si è tenuto onto della (D6. Segue, per la (D5 e ( : e : : e Ora osserviamo he : de : ( s + s 2 : ( s 2 + s ( 2 : s + ( s 2 : ( s 2 : ( 2 sk kl l ( 2 s k kl l Ma è simmetrio (v. eq. (D3 dell Appendie D e quindi Segue ( : e 2 ( s 2 : ( 2 s k lk l : e ( 2 : s + 2 : ( 2 2 : ( s s ( : s : ( U
22 E. Borghi - Appendie E Inserendo nella (E e riordando la (D7, ioè ρ m U + f, possiamo srivere w m U ( + f : ( U ( U ( + : ( U + f U Tenendo presente l eq. (D9 dell Appendie D segue (a,b U w m ( U + f U (E2 dove f U è la densità volumia di potenza sviluppata dalle forze di volume. Poniamo S m U ; S k m kl U l ; [S m ] potenza superfiie (E3 Il vettore S m rappresenta la densità volumia di flusso di potenza assoiata allo stato di tensione elastia. Segue w m S m + f U (E4 he è l espressione he i eravamo proposti di determinare. 22
Enrico Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE
 Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Lagrangiana del campo elettromagnetico. Il campo elettromagnetico nel vuoto è descritto dalle equazioni di Maxwell (in unità MKSA)
 Lagrangiana del ampo elettromagnetio Il ampo elettromagnetio nel vuoto è desritto dalle equazioni di Maxwell (in unità MKSA) B = 0 () E = B (2) E = ϱ (3) ɛ 0 B = µ 0 j + µ 0 ɛ 0 E L equazione di ontinuità
Lagrangiana del ampo elettromagnetio Il ampo elettromagnetio nel vuoto è desritto dalle equazioni di Maxwell (in unità MKSA) B = 0 () E = B (2) E = ϱ (3) ɛ 0 B = µ 0 j + µ 0 ɛ 0 E L equazione di ontinuità
Enrico Borghi LE VARIABILI DINAMICHE DEL CAMPO DI MAXWELL
 Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO DI MAXWELL E. Borghi - Le variabili dinamihe del ampo di Maxwell Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo di Maxwell
Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO DI MAXWELL E. Borghi - Le variabili dinamihe del ampo di Maxwell Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo di Maxwell
1 La Lagrangiana di una particella in una campo di forze potenziale
 Introduzione alle equazioni di Eulero-Lagrange e ai potenziali generalizzati G.Falqui, Dipartimento di Matematia e Appliazioni, Università di Milano Bioa. Corso di Sistemi Dinamii e Meania Classia, a.a.
Introduzione alle equazioni di Eulero-Lagrange e ai potenziali generalizzati G.Falqui, Dipartimento di Matematia e Appliazioni, Università di Milano Bioa. Corso di Sistemi Dinamii e Meania Classia, a.a.
APPUNTI SULLA RELATIVITA RISTRETTA (2/2) a) Quantità di moto e massa relativistica. b) Seconda legge di Newton ed energia
 APPUNTI SULLA RELATIVITA RISTRETTA (2/2) 1. Dinamia relativistia a) Quantità di moto e massa relativistia b) Seonda legge di Newton ed energia ) L equivalenza fra massa ed energia d) Unità di misura per
APPUNTI SULLA RELATIVITA RISTRETTA (2/2) 1. Dinamia relativistia a) Quantità di moto e massa relativistia b) Seonda legge di Newton ed energia ) L equivalenza fra massa ed energia d) Unità di misura per
Spin. La hamiltoniana classica di una particella di massa m e carica q in presenza di un potenziale elettromagnetico (Φ, A) si scrive.
 Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Espansione dell Universo e redshift
 Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
Gli approcci alla programmazione dinamica: alcuni esempi
 Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Gli approi alla programmazione dinamia: aluni esempi Franeso Menonin February, 2002 Ottimizzazione dinamia Il problema he qui si onsidera è quello di un soggetto he intende massimizzare (o minimizzare)
Enrico Borghi PARADOSSO DEI GEMELLI
 Enrio Borghi PARADOSSO DEI GEMELLI Premessa. In questo studio le definizioni di: - punto-evento; - linea di universo; - tempo proprio; - metria pseudoeulidea oltre he la legge relativistia di omposizione
Enrio Borghi PARADOSSO DEI GEMELLI Premessa. In questo studio le definizioni di: - punto-evento; - linea di universo; - tempo proprio; - metria pseudoeulidea oltre he la legge relativistia di omposizione
Enrico Borghi DESCRIZIONI CLASSICHE DEI FENOMENI ELETTROMAGNETICI
 Enrico Borghi DESCRIZIONI CLASSICHE DEI FENOMENI ELETTROMAGNETICI La materia ordinaria contiene, fra altre, particelle di due tipi, elettroni e protoni, che interagiscono scambiando fra loro particelle
Enrico Borghi DESCRIZIONI CLASSICHE DEI FENOMENI ELETTROMAGNETICI La materia ordinaria contiene, fra altre, particelle di due tipi, elettroni e protoni, che interagiscono scambiando fra loro particelle
FACOLTÀ DI INGEGNERIA. ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meccanica PROF. A. PRÁSTARO 21/01/2013
 FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
FACOLTÀ DI INGEGNERIA ESAME DI MECCANICA RAZIONALE Corso di Laurea in Ingegneria Meania PROF A PRÁSTARO /0/03 Fig Diso D, ruotante, on rihiamo elastio radiale in un piano vertiale π, e portatore di aria
TEORIE RELATIVISTICHE. Dispensa N. 2 CINEMATICA E DINAMICA RELATIVISTICHE
 TEORIE RELATIVISTICHE Dispensa N. CINEMATICA E DINAMICA RELATIVISTICHE . CINEMATICA RELATIVISTICA. Trasformazione delle veloità In questo paragrafo useremo le trasformazioni di Lorentz per mettere in relazione
TEORIE RELATIVISTICHE Dispensa N. CINEMATICA E DINAMICA RELATIVISTICHE . CINEMATICA RELATIVISTICA. Trasformazione delle veloità In questo paragrafo useremo le trasformazioni di Lorentz per mettere in relazione
ESERCIZI ELEMENTARI DI FLUIDODINAMICA
 ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ESERCIZI ELEMENTRI I FLUIOINMIC RICHIMI INTROUTTII Il fluido viene onsiderato ome un ontinuo, ossia vengono identifiate alune grandezze
ISTITUZIONI I INGEGNERI EROSPZILE ESERCIZI ELEMENTRI I FLUIOINMIC ESERCIZI ELEMENTRI I FLUIOINMIC RICHIMI INTROUTTII Il fluido viene onsiderato ome un ontinuo, ossia vengono identifiate alune grandezze
Derivata materiale (Lagrangiana) e locale (Euleriana)
 ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
ispense di Meccanica dei Fluidi 0 0 det 0 = [ (0 ) + ( ( ) ) + (0 0 ) ] = 0. Pertanto, v e µ sono indipendenti tra loro e costituiscono una nuova base. Con essi è possibile descrivere altre grandezze,
Esercizi sulle reti elettriche in corrente continua
 serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
serizi sulle reti elettrihe in orrente ontinua serizio 1: eterminare la P erogata generatore, e la P R assorita resistore R del iruito in figura 4 Ω Ω Ω 15 Ω 5 Ω Ω R Ω 10 Ω Soluzione: P = 150 W P R =.08
Relatività ristretta. Capitolo Equazioni di Maxwell
 Amadori-Lussardi Introduzione alla teoria della relatività Capitolo Relatività ristretta Fra l Ottoento ed il Noveento la meania lassia entrò in una grave risi he portò ad una ritia profonda dei suoi fondamenti.
Amadori-Lussardi Introduzione alla teoria della relatività Capitolo Relatività ristretta Fra l Ottoento ed il Noveento la meania lassia entrò in una grave risi he portò ad una ritia profonda dei suoi fondamenti.
L invarianza della velocità della luce. Dai postulati della teoria della relatività alle equazioni di Lorentz. (2) R
 L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Proprietà delle operazioni sui numeri naturali
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Moto vario elastico: fenomeno del colpo d ariete
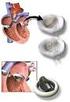 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Origine fisica di equazioni alle derivate parziali
 Origine fisica di equazioni alle derivate parziali Equazione del calore Dato un corpo nello spazio, rappresentato con un sottoinsieme A di 3, indichiamo con u(, y, z, t) la temperatura del corpo nel punto(,
Origine fisica di equazioni alle derivate parziali Equazione del calore Dato un corpo nello spazio, rappresentato con un sottoinsieme A di 3, indichiamo con u(, y, z, t) la temperatura del corpo nel punto(,
CHIMICA FISICA I. Le leggi dei gas
 A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
A.A. 2014-2015 Corso di Laurea in CHIMICA INDUSTRIALE CHIMICA FISICA I Le leggi dei gas Lezioni di Chimia Fisia I A.A. 2014-2015 Leggi dei gas - Pagina 1 Un sistema ostituito da un gas puro si omporta
Proprietà delle operazioni sui numeri naturali. Introduzione geometrica alle proprietà delle operazioni = 11 = 8 + 3
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
ANGOLI ORIENTA ORIENT TI A
 ANGOLI OIENTATI DEFINIZIONE CLASSICA DI ANGOLO L angolo è la porzione di piano ontenuta tra due semirette on la stessa origine. A - L origine omune O è detta vertie. a - Le due semirette OA a e OB b sono
ANGOLI OIENTATI DEFINIZIONE CLASSICA DI ANGOLO L angolo è la porzione di piano ontenuta tra due semirette on la stessa origine. A - L origine omune O è detta vertie. a - Le due semirette OA a e OB b sono
Lezione 5: Richiami di termomeccanica dei mezzi continui
 Lezione 5: Richiami di termomeccanica dei mezzi continui Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
Lezione 5: Richiami di termomeccanica dei mezzi continui Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO
 NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO G. Martinelli Abstrat Questi appunti ostituisono un sommario delle prinipali formule relative alla trattazione del orpo nero. 1 Le Equazioni di Maxwell Le
NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO G. Martinelli Abstrat Questi appunti ostituisono un sommario delle prinipali formule relative alla trattazione del orpo nero. 1 Le Equazioni di Maxwell Le
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
1 Integrale multiplo di una funzione limitata su di un rettangolo
 INTEGLE DELLE FUNZIONI DI PIÙ VIBILI INTEGLE MULTIPLO DI UN FUNZIONE LIMITT SU DI UN ETTNGOLO Integrale delle funzioni di più variabili Indie Integrale multiplo di una funzione limitata su di un rettangolo
INTEGLE DELLE FUNZIONI DI PIÙ VIBILI INTEGLE MULTIPLO DI UN FUNZIONE LIMITT SU DI UN ETTNGOLO Integrale delle funzioni di più variabili Indie Integrale multiplo di una funzione limitata su di un rettangolo
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Meccanica del punto materiale
 Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Meccanica del punto materiale Princìpi della dinamica. Forze. Momento angolare. Antonio Pierro @antonio_pierro_ (https://twitter.com/antonio_pierro_) Per consigli, suggerimenti, eventuali errori o altro
Università degli Studi di Teramo Facoltà di Scienze Politiche
 Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
Applicazione del principio di conservazione dell energia a sistemi aventi un gran numero di particelle.
 PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
PRIMO PRINCIPIO DLLA RMODINAMICA In una trasformazione adiabatia: In una trasformazione isoora: L In una trasformazione generia: L (7) (Primo riniio della termodinamia) Aliazione del riniio di onservazione
CAMPO ELETTRICO. F r e = q E r. Newton ;
 1 CAMPO ELETTRICO Si definisce campo elettrico (o elettrostatico) una qualunque regione dello spazio nella quale si manifestano azioni su cariche elettriche. 1. DESCRIZIONE DEL CAMPO Per descrivere un
1 CAMPO ELETTRICO Si definisce campo elettrico (o elettrostatico) una qualunque regione dello spazio nella quale si manifestano azioni su cariche elettriche. 1. DESCRIZIONE DEL CAMPO Per descrivere un
AIMETA. Studio di lastre forate mediante il Metodo delle Celle
 AIMEA XII Convegno Italiano di Meania Computazionale Bresia, -5 novembre 000 Studio di lastre forate mediante il Metodo delle Celle Franesa COSMI Dipartimento di Energetia, Università di rieste, via A.
AIMEA XII Convegno Italiano di Meania Computazionale Bresia, -5 novembre 000 Studio di lastre forate mediante il Metodo delle Celle Franesa COSMI Dipartimento di Energetia, Università di rieste, via A.
Equazione d onda per il campo elettromagnetico
 Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
Il TEOREMA DI TRASPORTO DI REYNOLDS
 CAPITOLO 4. Il TEOREMA DI TRASPORTO DI REYNOLDS 4.1 Il Teorema di Trasporto di Reynolds Le leggi di conservazione della Massa, della Quantità di Moto (Momentum) e dell Energia costituiscono le relazioni
CAPITOLO 4. Il TEOREMA DI TRASPORTO DI REYNOLDS 4.1 Il Teorema di Trasporto di Reynolds Le leggi di conservazione della Massa, della Quantità di Moto (Momentum) e dell Energia costituiscono le relazioni
FUNZIONI CONTINUE. funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si dice continua in un punto c D se risulta.
 FUNZIONI CONTINUE funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si die ontinua in un punto D se risulta Analizza bene la definizione: lim x f ( x) = f ( ) Il punto deve
FUNZIONI CONTINUE funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si die ontinua in un punto D se risulta Analizza bene la definizione: lim x f ( x) = f ( ) Il punto deve
Esercitazioni di Elettrotecnica
 Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Principi di Fisica - Relatività Speciale; grafici spazio-temporali Carlo Cosmelli 2013
 Prinipi di Fisia - Relatività Speiale; grafii spazio-temporali Carlo Cosmelli 0 Definizione dei simboli utilizzati - S(,): Sistema di riferimento inerziale on origine in, e assi (, ); = veloità della lue
Prinipi di Fisia - Relatività Speiale; grafii spazio-temporali Carlo Cosmelli 0 Definizione dei simboli utilizzati - S(,): Sistema di riferimento inerziale on origine in, e assi (, ); = veloità della lue
Cinematica. Velocità. Riferimento Euleriano e Lagrangiano. Accelerazione. Elementi caratteristici del moto. Tipi di movimento
 Cinematica Velocità Riferimento Euleriano e Lagrangiano Accelerazione Elementi caratteristici del moto Tipi di movimento Testo di riferimento Citrini-Noseda par. 3.1 par. 3.2 par 3.3 fino a linee di fumo
Cinematica Velocità Riferimento Euleriano e Lagrangiano Accelerazione Elementi caratteristici del moto Tipi di movimento Testo di riferimento Citrini-Noseda par. 3.1 par. 3.2 par 3.3 fino a linee di fumo
Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici. Dinamica delle Strutture Aerospaziali
 Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici Franco Mastroddi http://www.diaa.uniroma1.it/docenti/f.mastroddi dal Dinamica delle Strutture Aerospaziali Anno Accademico
Dalla meccanica del continuo alle Equazioni di Lagrange g per i solidi elastici Franco Mastroddi http://www.diaa.uniroma1.it/docenti/f.mastroddi dal Dinamica delle Strutture Aerospaziali Anno Accademico
GEOMETRIA ANALITICA 8 LE CONICHE
 GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
Elettricità e Magnetismo. M. Cobal, Università di Udine
 Elettricità e Magnetismo M. Cobal, Università di Udine Forza di Coulomb Principio di Sovrapposizione Lineare Campo Ele8rico Linee di campo Flusso, teorema di Gauss e applicazioni Condu8ori Energia potenziale
Elettricità e Magnetismo M. Cobal, Università di Udine Forza di Coulomb Principio di Sovrapposizione Lineare Campo Ele8rico Linee di campo Flusso, teorema di Gauss e applicazioni Condu8ori Energia potenziale
29. Mezzi elastici RELAZIONE SFORZO-DEFORMAZIONE
 29. Mezzi elastici I mezzi continui solidi sono caratterizzati da piccole deformazioni, che consentono di stabilire una relazione lineare tra sforzo e deformazione nota come legge di Hook. Linearizzando
29. Mezzi elastici I mezzi continui solidi sono caratterizzati da piccole deformazioni, che consentono di stabilire una relazione lineare tra sforzo e deformazione nota come legge di Hook. Linearizzando
Le onde elettromagnetiche
 Le onde elettromagnetihe orgente di onde elettromagnetihe è un sistema di arihe aelerate he produono un ampo elettrio (x,y,z,t) e un ampo magnetio B(x,y,z,t) I due ampi (x,y,z,t) e B(x,y,z,t) sono strettamente
Le onde elettromagnetihe orgente di onde elettromagnetihe è un sistema di arihe aelerate he produono un ampo elettrio (x,y,z,t) e un ampo magnetio B(x,y,z,t) I due ampi (x,y,z,t) e B(x,y,z,t) sono strettamente
Corso di Laurea: INGEGNERIA INFORMATICA (classe 09) Insegnamento: n Lezione: Titolo: V M. Fig. 5.1 Schematizzazione di una macchina a fluido
 Corso di Laurea: INGEGNERIA INFORMATICA (lasse 09) Le equazioni del moto dei fluidi L equazione di onservazione dell energia in forma termodinamia V M Ω Ω Fig. 5. Shematizzazione di una mahina a fluido
Corso di Laurea: INGEGNERIA INFORMATICA (lasse 09) Le equazioni del moto dei fluidi L equazione di onservazione dell energia in forma termodinamia V M Ω Ω Fig. 5. Shematizzazione di una mahina a fluido
Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto
 Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto Claudio Tamagnini Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di
Lezione 4: Principi di Conservazione Conservazione della quantità di moto e del momento della quantità di moto Claudio Tamagnini Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di
La figura che segue mostra il corpo in questione e la posizione della cavità interna: + +
 ESECIZI 2 UN C SFEIC DI AGGI =10 cm è UNIFMEMENTE CAIC CN DENSITA DI CAICA ρ=10 6 C/m 3 IN TUTT IL VLUME, TANNE IN UNA CAVITA INTENA SFEICA DI AGGI r 1 =/2. IL CENT DELLA CAVITA SI TVA A DISTANZA d=r 1
ESECIZI 2 UN C SFEIC DI AGGI =10 cm è UNIFMEMENTE CAIC CN DENSITA DI CAICA ρ=10 6 C/m 3 IN TUTT IL VLUME, TANNE IN UNA CAVITA INTENA SFEICA DI AGGI r 1 =/2. IL CENT DELLA CAVITA SI TVA A DISTANZA d=r 1
Lezione 3: Principi di Conservazione Conservazione della massa per un continuo poroso
 Lezione 3: Principi di Conservazione per un continuo poroso Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
Lezione 3: Principi di Conservazione per un continuo poroso Dipartimento di Ingegneria Civile e Ambientale Università degli Studi di Perugia Dottorato Internazionale Congiunto Firenze Braunschweig Firenze,
Momento angolare L. P. Maggio Prodotto vettoriale
 Momento angolare L. P. Maggio 2007 1. Prodotto vettoriale 1.1. Definizione Il prodotto vettoriale di due vettori tridimensionali a e b è un vettore c così definito: a) Il modulo di c è pari all area del
Momento angolare L. P. Maggio 2007 1. Prodotto vettoriale 1.1. Definizione Il prodotto vettoriale di due vettori tridimensionali a e b è un vettore c così definito: a) Il modulo di c è pari all area del
B B B'' A'' x x LEZIONE III L OROLOGIO A LUCE
 EZIONE III OROOGIO A UCE Nella preedente lezione abbiamo visto he le trasformazioni di orentz, he disendono direttamente dal Prinipio di Relatività, impliano nuovi effetti noti ome ontrazione delle lunghezze
EZIONE III OROOGIO A UCE Nella preedente lezione abbiamo visto he le trasformazioni di orentz, he disendono direttamente dal Prinipio di Relatività, impliano nuovi effetti noti ome ontrazione delle lunghezze
L elettromagnetismo nella ricerca per l energia da fusione nucleare di plasma d idrogeno
 L elettromagnetismo nella riera per l energia da fusione nuleare di plasma d idrogeno Roberto Cesario esario@frasati.enea.it Assoiazione EURATOM-ENEA sulla Fusione Centro Rierhe ENEA Frasati Sommario della
L elettromagnetismo nella riera per l energia da fusione nuleare di plasma d idrogeno Roberto Cesario esario@frasati.enea.it Assoiazione EURATOM-ENEA sulla Fusione Centro Rierhe ENEA Frasati Sommario della
IL TORNANTE RETTIFILO CONTROCURVA RETTIFILO
 IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
IL TORNANTE il tornante è quella partiolare urva, esterna ai rettifili, he onsente un inversione della direzione dell asse, onsentendo di prendere quota all interno di una fasia di terreno relativamente
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE.
 PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
G. Griva. 9529P - Macchine e Azionamenti Elettrici
 G. Griva 959 - Mahine e Azionamenti Elettrii rova di Esonero del 7 giugno 000. on proposta di soluzione 1 NTODUONE Questa proposta di soluzione è rivolta agli studenti he, avendo seguito il tutorato del
G. Griva 959 - Mahine e Azionamenti Elettrii rova di Esonero del 7 giugno 000. on proposta di soluzione 1 NTODUONE Questa proposta di soluzione è rivolta agli studenti he, avendo seguito il tutorato del
PROFILI DI CORRENTE IN MOTO PERMANENTE
 PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
Dipolo Elettrico: due cariche (puntiformi) +q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo
 Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
RICERCA OPERATIVA (a.a. 2015/16) Nome: Cognome: Matricola:
 o Appello //6 RICERCA OPERATIVA (a.a. /6) Nome: Cognome: Matriola: ) Si rappresenti il ono finitamente generato C = ono,, R ome ono poliedrio, giustifiando algebriamente le risposta fornita. Per derivare
o Appello //6 RICERCA OPERATIVA (a.a. /6) Nome: Cognome: Matriola: ) Si rappresenti il ono finitamente generato C = ono,, R ome ono poliedrio, giustifiando algebriamente le risposta fornita. Per derivare
Algoritmo di best-fit (o fitting) sinusoidale a 3 parametri ( ) ( )
 Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
Algoritmo di best-it (o itting) sinusoidale a 3 parametri Supponiamo di disporre della versione digitalizzata di un segnale sinusoidale di ampiezza di pio A, requenza nota, ase assoluta ϕ e on omponente
Superfici. V. Tibullo, rev.1, 04/04/2006.
 uperfici. Tibullo, rev.1, 04/04/2006. 1 Integrali di superficie Consideriamo una superficie nello spazio tridimensionale R 3. Il concetto di superficie è noto dalla geometria elementare e non se ne darà
uperfici. Tibullo, rev.1, 04/04/2006. 1 Integrali di superficie Consideriamo una superficie nello spazio tridimensionale R 3. Il concetto di superficie è noto dalla geometria elementare e non se ne darà
Anna Pandolfi Analisi Strutturale e Termica 4.1
 Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
Statica e Cinematica Ammissibili Deformazioni e sforzi sono detti virtuali (non necessariamente veri) quando sono rispettosi di determinate condizioni. Corpo in equilibrio nella configurazione deformata
Figura 1. Entrambi gli osservatori O e O' osservano che le onde sull'acqua si propagano verso l'esterno dall'origine O.
 Onde nei mezzi materiali e onde luminose. Supponiamo di avere due sistemi di oordinate, O e O', he hanno un veloità relativa V. Supponiamo inoltre he vi sia una massa d'aqua, stazionaria rispetto al sistema
Onde nei mezzi materiali e onde luminose. Supponiamo di avere due sistemi di oordinate, O e O', he hanno un veloità relativa V. Supponiamo inoltre he vi sia una massa d'aqua, stazionaria rispetto al sistema
ESPONENZIALI E LOGARITMI. chiameremo logaritmica (e si legge il logaritmo in base a di c è uguale a b ).
 ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
ESPONENZIALI E LOGARITMI Data una espressione del tipo a b = c, che chiameremo notazione esponenziale (e dove a>0), stabiliamo di scriverla anche in un modo diverso: log a c = b che chiameremo logaritmica
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
Problema (tratto dal 7.42 del Mazzoldi 2)
 Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
Interazione radiazione materia Equazioni del LASER. Simone Cialdi
 Interazione radiazione materia Equazioni del LASER Simone Cialdi Outline Proessi fondamentali Emissione ed assorbimento stimolati (teoria perturbativa al primo ordine) Emissione spontanea (modello di Einstein)
Interazione radiazione materia Equazioni del LASER Simone Cialdi Outline Proessi fondamentali Emissione ed assorbimento stimolati (teoria perturbativa al primo ordine) Emissione spontanea (modello di Einstein)
Gas ideale: velocità delle particelle e pressione (1)
 Gas ideale: velocità delle particelle e pressione (1) In un gas ideale le particelle sono considerate puntiformi e risentono di forze solo durante gli urti (perfettamente elastici) con le pareti del recipiente.
Gas ideale: velocità delle particelle e pressione (1) In un gas ideale le particelle sono considerate puntiformi e risentono di forze solo durante gli urti (perfettamente elastici) con le pareti del recipiente.
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Test di autovalutazione
 Test di autovalutazione 0 0 0 0 0 0 0 0 0 0 n Il mio punteggio, in entesimi, è Nel numero, il valore della ifra è: a d 0 00 b e 00 0 a,0 b,0, d, e, a 0, b 0, d, e, Il numero deimale 0,, espresso ome frazione
Test di autovalutazione 0 0 0 0 0 0 0 0 0 0 n Il mio punteggio, in entesimi, è Nel numero, il valore della ifra è: a d 0 00 b e 00 0 a,0 b,0, d, e, a 0, b 0, d, e, Il numero deimale 0,, espresso ome frazione
Modelli di assegnazione (cenni)
 Corso di Trasporti e Ambiente http://www.uniroma.it/didattia/ta_ ing. Antonio Comi novembre Modelli di assegnazione (enni) Struttura del sistema di modelli per la simulazione dei sistemi di trasporto OFFERTA
Corso di Trasporti e Ambiente http://www.uniroma.it/didattia/ta_ ing. Antonio Comi novembre Modelli di assegnazione (enni) Struttura del sistema di modelli per la simulazione dei sistemi di trasporto OFFERTA
Robotica industriale. Richiami di statica del corpo rigido. Prof. Paolo Rocco
 Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
Robotica industriale Richiami di statica del corpo rigido Prof. Paolo Rocco (paolo.rocco@polimi.it) Sistemi di forze P 1 P 2 F 1 F 2 F 3 F n Consideriamo un sistema di forze agenti su un corpo rigido.
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Elettromagnetismo e Relatività dr.ing. Alberto Sacchi Sviluppo Progetti Avanzati srl- R&D Dept.
 Elettromagnetismo e Relatività dr.ing. Alberto Sahi Sviluppo Progetti Avanzati srl- R&D Dept. ing.sahi@alie.it SNTES (ABSTRACT) Analisi ritia dell esperimento di Feynman volto ad illustrare la orrelazione
Elettromagnetismo e Relatività dr.ing. Alberto Sahi Sviluppo Progetti Avanzati srl- R&D Dept. ing.sahi@alie.it SNTES (ABSTRACT) Analisi ritia dell esperimento di Feynman volto ad illustrare la orrelazione
Università del Sannio
 Università del Sannio Corso di Fisica 1 Lezione 6 Dinamica del punto materiale II Prof.ssa Stefania Petracca 1 Lavoro, energia cinetica, energie potenziali Le equazioni della dinamica permettono di determinare
Università del Sannio Corso di Fisica 1 Lezione 6 Dinamica del punto materiale II Prof.ssa Stefania Petracca 1 Lavoro, energia cinetica, energie potenziali Le equazioni della dinamica permettono di determinare
Derivata di una funzione
 Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
Derivata di una funzione Derivabilità e derivata in un punto Sia y = f x una funzione reale di variabile reale di dominio D(f), e sia D(f). Si die he la funzione è derivabile in se esiste ed è finito il
e del guadagno percentuale in conto capitale, dato da e v
 Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
Corso di Idraulica ed Idrologia Forestale
 Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 5: Cinematica dei fluidi Anno Accademico 2008-2009
Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 5: Cinematica dei fluidi Anno Accademico 2008-2009
Meccanica. 5. Moti Relativi. Domenico Galli. Dipartimento di Fisica e Astronomia
 Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
Meccanica 5. Moti Relativi http://campus.cib.unibo.it/2423/ Domenico Galli Dipartimento di Fisica e Astronomia 22 febbraio 2017 Traccia 1. Cambiamento del Sistema di Riferimento 2. Trasformazione del Vettore
Vd Vd Vd Re = Per definire il REGIME di moto si individua il: Numero indice di Reynolds (adimensionale)
 CINEMATICA Esperienza di Osborne Reynolds (1842-1912) Per basse velocità: moto per filetti viscoso laminare Al crescere velocità: moto di transizione V d V d Per elevate velocità: moto turbolento V d CINEMATICA
CINEMATICA Esperienza di Osborne Reynolds (1842-1912) Per basse velocità: moto per filetti viscoso laminare Al crescere velocità: moto di transizione V d V d Per elevate velocità: moto turbolento V d CINEMATICA
Analisi di segnali campionati
 Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Geometria delle masse
 Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
= E qz = 0. 1 d 3 = N
 Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
Prova scritta d esame di Elettromagnetismo 7 ebbraio 212 Proff.. Lacava,. Ricci, D. Trevese Elettromagnetismo 1 o 12 crediti: esercizi 1, 2, 4 tempo 3 h; Elettromagnetismo 5 crediti: esercizi 3, 4 tempo
TEORIE DI CAMPO MEDIO
 EORIE DI CAMPO MEDIO A ausa della impossibilità di trovare sempre una soluzione analitia esatta per gran parte dei modelli disussi nel apitolo MODELLI è neessario riorrere a metodi approssimati per la
EORIE DI CAMPO MEDIO A ausa della impossibilità di trovare sempre una soluzione analitia esatta per gran parte dei modelli disussi nel apitolo MODELLI è neessario riorrere a metodi approssimati per la
Nome Cognome: RICERCA OPERATIVA (a.a. 2010/11) 6 o Appello 2/9/ Corso di Laurea: L Sp Matricola:
 o Appello /9/ RICERCA OPERATIVA (a.a. /) Nome Cognome: Corso di Laurea: L- Sp Matriola: ) Si individui un albero dei ammini minimi di radie sul grafo in figura 8-7 utilizzando l algoritmo più appropriato
o Appello /9/ RICERCA OPERATIVA (a.a. /) Nome Cognome: Corso di Laurea: L- Sp Matriola: ) Si individui un albero dei ammini minimi di radie sul grafo in figura 8-7 utilizzando l algoritmo più appropriato
proiezione della Terra su un cilindro che, per non far torto a nessun paese, conserva le aree). Indubbiamente tutte
 CATE NAUTICHE Sono sempre stato attratto dalla artografia: ogni arta ha la propria aratteristia he dipende dall uso he uno deve farne (per esempio la arta dell ONU o proiezione di Gall-Peters è un partiolare
CATE NAUTICHE Sono sempre stato attratto dalla artografia: ogni arta ha la propria aratteristia he dipende dall uso he uno deve farne (per esempio la arta dell ONU o proiezione di Gall-Peters è un partiolare
Analisi dei segnali campionati
 Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio s( onsiste nel prenderne solo i valori
Analisi dei segnali ampionati - 1 Analisi dei segnali ampionati 1 - Il teorema del ampionamento Campionamento ideale Il ampionamento (sampling) di un segnale analogio s( onsiste nel prenderne solo i valori
Laboratorio di didattica Della matematica
 Didattia della matematia a.a. 004/00 Laboratorio di didattia Della matematia (La probabilita elementare ome strumento per un diverso approio ai numeri razionali) ANITA GARIBALDI Classe 9 Il onetto di frazione,
Didattia della matematia a.a. 004/00 Laboratorio di didattia Della matematia (La probabilita elementare ome strumento per un diverso approio ai numeri razionali) ANITA GARIBALDI Classe 9 Il onetto di frazione,
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014
 MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 9 palline olorate: 2 rosse, 4 verdi e 3 gialle. Si fanno 3 estrazioni on rimessa. a) Calola la probabilità
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 9 palline olorate: 2 rosse, 4 verdi e 3 gialle. Si fanno 3 estrazioni on rimessa. a) Calola la probabilità
Fili, finiti e infiniti, uniformemente carichi
 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca, Aprile 003 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca DIIMA - Università degli Studi di Salerno 84084 Fisciano (SA).
Fili, finiti e infiniti, uniformemente carichi Roberto De Luca, Aprile 003 Fili, finiti e infiniti, uniformemente carichi Roberto De Luca DIIMA - Università degli Studi di Salerno 84084 Fisciano (SA).
Lavoro ed energia. Lavoro di una forza Teorema dell energia cinetica Forze conservative Conservazione dell energia
 Lavoro ed energia Lavoro di una forza Teorema dell energia cinetica Forze conservative Conservazione dell energia Lavoro di una forza Consideriamo una forza F applicata ad un punto materiale P che si sposti
Lavoro ed energia Lavoro di una forza Teorema dell energia cinetica Forze conservative Conservazione dell energia Lavoro di una forza Consideriamo una forza F applicata ad un punto materiale P che si sposti
FFT (FAST FOURIER TRANSFORM ALGORITHM) ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER. Slide 1
 FFT (FAST FOURIER TRANSFORM ALGORITHM ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER Slide Introduzione / Gli algoritmi noti ome Fast Fourier Transorm hanno rivoluzionato l'analisi di segnali
FFT (FAST FOURIER TRANSFORM ALGORITHM ALGORITMI VELOCI per la TRASFORMATA DISCRETA DI FOURIER Slide Introduzione / Gli algoritmi noti ome Fast Fourier Transorm hanno rivoluzionato l'analisi di segnali
Proprietà globali delle funzioni continue
 Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
Proprietà globali delle funzioni ontinue Tramite i limiti, abbiamo studiato il omportamento di una funzione nell intorno di un punto (proprietà loali). Ora i oupiamo di funzioni ontinue su tutto un intervallo,
L offerta della singola impresa: le curve di costo
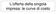 L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO
 APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Potenziale elettrostatico
 Doppio strato piano Potenziale elettrostatico Consideriamo il lavoro compiuto dalla forza elettrica quando una particella di prova di carica q viene spostata in un campo elettrico E. Possiamo definire
Doppio strato piano Potenziale elettrostatico Consideriamo il lavoro compiuto dalla forza elettrica quando una particella di prova di carica q viene spostata in un campo elettrico E. Possiamo definire
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
Elementi di Teoria dei Sistemi. Definizione di sistema dinamico. Cosa significa Dinamico? Sistema dinamico a tempo continuo
 Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Pag. 1. Esercizi sui Diagrammi di Flusso. Stampa di alcuni numeri interi
 Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
Università degli studi di Parma Dipartimento di Ingegneria dell Informazione Informatia a.a. 202/ Stampa di aluni numeri interi Informatia Faoltà di Mediina Veterinaria a.a. 202/ prof. Stefano Cagnoni
