Appunti per l Orale di Statistica
|
|
|
- Agostino Antonucci
- 6 anni fa
- Visualizzazioni
Transcript
1 Apputi per l Orale di Statistica Matteo Giaello 6 ottobre
2 Idice 1 Media e variaza campioaria Media campioaria Variaza campioaria Legge dei gradi umeri Distribuzioi campioarie Itervalli di cofideza Itervalli di cofideza per la media Itervalli di cofideza per la variaza Teoria della stima putuale Defiizioi Errore quadratico medio Stimatori o distorti Proprietà asitotiche degli stimatori Diseguagliaza di Fréchet-Cramer-Rao Verifica di ipotesi Defiizioi Lemma di Neyuma-Pearso
3 1 Media e variaza campioaria 1.1 Media campioaria Defiiamo campioe casuale lugo u isieme di variabili aleatorie i.i.d. estratte da ua popolazioe di desità f. La media µ = EX 1 uguale per tutte le X i del campioe prede il ome di media della popolazioe e la comue variaza σ 2 è detta variaza della popolazioe. Si chiama media campioaria di u campioe casuale X 1... X la quatità: X X e si idica co X. La media campioaria dipede dal campioe è perciò ua variabile aleatoria. Valore atteso e variazaq della media campioaria possoo essere facilmete calcolate tramite le proprietà di valore atteso e variaza: EX = E X j E X j = V arx = V ar 1.2 Variaza campioaria X j = V arx 1 2 = µ = σ2 Dato u campioe casuale X 1... X si defiisce variaza campioaria la quatità: S 2 = 1 1 X j X 2 per dimostrare la o distorsioe di questo stimatore dobbiamo iazitutto dimostrare le segueti espressioi: X j X 2 = = µ X j µ 2 X µ 2 1 Dimostrazioe 1 E X j X 2 = 1σ 2 2 X j X 2 = [X j µ X µ] 2 3
4 = = [X j µ 2 + X µ 2 2X j µx µ] X j µ 2 + X µ 2 2X j µ = X µ X j µ 2 + X µ 2 2X j µ 2 = X j µ 2 X µ 2 Dimostrazioe 2 E X j X 2 = E X j µ 2 EX µ 2 EX j µ 2 V arx = σ 2 σ 2 Da queste due formule ricaviamo che ES 2 = σ 2 codizioe ecessaria e sufficete per la o distorsioe dello stimatore. 1.3 Legge dei gradi umeri Sia X 1, X 2,... ua successioe di variabili aleatorie i.i.d. co media µ e variaza σ 2 fiite e sia X la media campioaria, allora per ogi ɛ > 0: lim P X µ > ɛ = 0 Dalla diseguagliaza di Chebychev che afferma: 1.4 Distribuzioi campioarie P X EX > ɛ V arx ɛ 2 La prima desità che itroduciamo è la desità Γα, β questa desità è utile i quato permette di ricavare altre desità favose da essa. La sua fuzioe di desità ha la forma seguete: fx, α, β = 1/βα x Γα e β x α 1 1 0,+ x Metre la sua fuzioe geeratrice dei mometi è: Mt = Ee tx = 1 1 βt α t < 1/β 4
5 Nel caso i cui α = 1 abbiamo che la desità Gamma diveta u espoeziale di parametro beta ξβ. Nel caso ivece i qui sia α = 2 la desità che troviamo è ua χ2. Se X N0, 1 allora X 2 χ 2 1 ; se prediamo u campioe casuale X 1,..., X N0, 1 allora X2 j χ2 Vediamo ora alcue proprietà che portao alle affermazioi appea fatte 1. Se X Γα, β, c > 0 e Y = cx allora Y Γα, cβ; 2. Se X,Y soo v.a. idipedeti co X Γα, β e Y Γc, β allora X + Y Γα + c, β e viceversa. Dimostrazioe 1. M Y t = Ee tcx = M X ct = 1 1 βct α t < 1 cβ 2. M X+Y t = Ee tx+y = Ee tx e ty = Ee tx Ee ty = M X tm Y t = 1 1 βt α 1 1 βct c = 1 1 βct α + c 5
6 2 Itervalli di cofideza 2.1 Itervalli di cofideza per la media Abbiamo visto prima come el caso di u campioe casuale X 1,..., X estratto da ua popolazioe di desità gaussiaa di parametri µ, σ si possa stimare la media co la media campioaria X e la variaza co la variaza campioaria S 2. Questo tipo di stima però o ha molto seso i quato sappiamo che: P µ,σ 2X = c = 0 Ovvero è ulla la probabilità che X assuma il vero valore di µ. Partiamo dal caso i cui solo la media µ è icogita metre la variaza è ota e pari ad u valore fissato; oi possiamo allora stabilire ua regioe di probabilità i cui possiamo stabilire co ua certa precisioe la probabilità che il vero valore di µ sia i quella regioe. P µ,σ 2 ɛ < X µ σ/ < ɛ = γ Dove γ è la cofideza co la quale siamo certi che il parametro stimato cada ell itervallo. Svolgedo i calcoli sopra per isolare µ troviamo che gli estremi dell itevallo di cofideza soo: σ σ µ X z 1+γ ; X + z 1+γ 2 2 Nel caso i cui la media o sia ota si può utilizzare la variaza campioaria per stimare u IC per la media i questo caso le formule divetao: P µ,σ 2 ɛ < X µ S/ < ɛ = γ Questa volta la quatità X µ/s è ua t-studet co -1 gradi di libertà t 1 perciò l iotervallo di cofideza diveta: µ X t γ σ ; X + t γ σ Itervalli di cofideza per la variaza Nel caso i cui vogliamo trovare u itervallo di cofideza per la variaza quado la media è icogita, partiamo dalla quatità aleatoria S 2 1/σ 2 χ 2 1 fissato u certo valore γ dobbiamo fissare gli estremi dell itervallo che come prima: P µ,σ 2 a < S2 1 σ 2 < b = γ 6
7 Essedo la distribuzioe χ 2 ua distribuzioe asimmetrica possiamo ritrovarci i tre casi specifici: 1. σ 2 S 2 1 χ 2 1 γ ; + 2. σ 2 0 ; S γ χ S σ χ γ 2 ; S2 1 χ γ 2 Nel caso di media ota i ragioameti appea fatti soo acora validi ma stimiamo σ 2 co la quatità: S0 2 = X j µ 2 7
8 3 Teoria della stima putuale 3.1 Defiizioi Sia X ua va co fuzioe di ripartizioe F e desità di probabilità f o completamete specificata, ovvero co u parametro θ m-dimesioalea valori i Θ sottoisieme di R m. Defiiamo la statistica T come ua variabile aleatoria fuzioe del campioe T = gx 1,..., X. La distribuzioe di ua statistica T è detta distribuzioe o legge campioaria. Ua statistica T o dipede mai dal parametro icogito metre la distribuzioe campioaria i geerale dipederà da θ. Ua fuzioe κ : Θ R è detta caratteristica della popolazioe. Siao X 1,..., X fx, θ, θ Θ e κθ ua caratteristica della popolazioe. Uo stimatore di κθ basato sul campioe X 1,..., X è ua statistica T = gx 1,..., X usata per stimare κθ. Il valore assuto dallo stimatore è detta stima di κθ Errore quadratico medio Potremmo trovarci, i u problema di stima, ella situazioe di dover decidere fra stimatori diversi della stessa caratteristica κθ. Utilizzeremo come criterio di scelta la media della prossimità di T a κθ che esprimiamo i termii di E θ [T κθ 2 ]. Se T è stimatore di κθ tale che E θ [T κθ 2 ] < θ Θ, allora E θ [T κθ 2 ] è detto errore quadratico medio di T rispetto a κθ. Il MSE di uo stimatore T esiste solo se T ha media e variaza fiite, o, equivaletemete, se e solo se ha mometo secodo fiito. Osservazioe: Per calcolare l errore quadratico medio è utile decomporlo el seguete modo: E θ [T κθ 2 ] = V ar θ T + [E θ T κθ] 2 i cui la quatità [E θ T κθ] è detta distorsioe di bias. Tra tutti gli stimatori di κθ ci piacerebbe scegliere quello co MSE miore. Questa cosa equivale a miimizzare cotemporaeamete variaza e distorsioe; ma questo è impossibile per ogi θ perciò ci accotetiamo di utilizzare la sottoclasse di stimatori che hao distorsioe ulla; questa classe è detta di stimatori o distorti o corretti. L erroe quadratico medio di uo stimatore o distorto coicide co la sua variaza. 3.2 Stimatori o distorti Ua statistica T che ammette media per ogi θ i Θ è detta stiamtore o distorto della caratteristica κθ se E θ T = κθ θ Θ Se X 1,..., X iid fx, θ, θ Θ ed E θ X 1 esiste qualuque sia θ allora E θ X = E θ X 1, θ e quidi: La media campioaria X è stimatore o distorto della media teorica. La variaza campioaria S 2 è stimatore o distorto della variaza teorica. 8
9 3.3 Proprietà asitotiche degli stimatori Defiizioe 3.1. Sia X 1,..., X ua successioe di variabili aleatorie i.i.d. co comue fuzioe di desità fx, θ, θ Θ e sia T uo stimatore di κθ che è fuzioe delle prime osservazioi. La successioe {T } è asitoticamete o distorta per κθ se lim E θt = κθ θ Θ Defiizioe 3.2. Sia X 1,..., X ua successioe di variabili aleatorie i.i.d. co comue fuzioe di desità fx, θ, θ Θ e sia T uo stimatore di κθ che è fuzioe delle prime osservazioi. La successioe {T } è cosistete i media quadratica per κθ se lim E[T κθ 2 ] = 0 θ Θ Defiizioe 3.3. Sia X 1,..., X ua successioe di variabili aleatorie i.i.d. co comue fuzioe di desità fx, θ, θ Θ e sia T ua statistica fuzioe soltato delle prime osservazioi. La successioe {T } è asitoticamete gaussiaa co media asitotica µ θ e variaza asitotica σθ 2 se lim P T µ θ z σ θ 3.4 Diseguagliaza di Fréchet-Cramer-Rao = Φz, z R Abbiamo visto ei capitoli precedeti come per uo stimatore o distorto ridurre il MSE sigifichi ridurre la variaza dello stimatore. Ora ci chiediamo qual è la miima variaza che lo stimatore può avere e quale sia lo stimatore co tale variaza. Siao X 1,..., X variabile aleatorie iid co comue desità fx, θ, θ Θ e sia T = gx 1,..., X uo stimatore o distorto della caratteristica κθ a variaza fiita. Assumiamo che le segueti codizioi di regolarità siao soddisfatte: 1. Θ è u itervallo aperto i R; 2. S = {x : fx, θ > 0 è idipedete da θ; 3. θ fx, θ è derivabile su Θ, x S; 4. E θ θ logfx 1, θ = 0 θ Θ; 5. 0 < E θ [ θ logfx 1, θ 2 ] < θ Θ; 6. κ : Θ R è derivabile su Θ e: k θ = E θ T θ logl θx 1,..., X θ Θ 9
10 Allora Dove è ota come iformazioe di Fisher. V ar θ T κ θ 2 Iθ [ 2 ] Iθ = E θ θ logfx 1, θ θ Θ 3 Dimostrazioe Per maggiore semplicità itroduciamo le variabili aleatorie Y 1,..., Y defiite da Y j = θ logfx j, θ, j = 1,..., Y 1,..., Y soo variabili aleatorie iid a media ulla e variaza fiita Iθ θ. Ifatti E θ Y j = = E θ θ logfx j, θ = 0 [per l ipotesi 4] e [ 2 ] V ar θ Y j = E θ Yj 2 = E θ θ logfx j, θ = Iθ 0, [per l ipotesi 5] Ioltre θ logl θx 1,..., X = θ log fx j, θ = da cui ricaviamo che e E θ θ logl θx 1,..., X = V ar θ θ logl θx 1,..., X = θ logfx j, θ = Y j E θ Y j 4 V ar θ Y j = Iθ 5 Dall ipotesi 6 e dall equazioe 4 ricaviamo che κ θ = E θ T θ logl θx 1,..., X = Cov T, θ logl θx 1,..., X cosicché κ θ 2 = [ Cov T, ] 2 θ logl θx 1,..., X da cui per le proprietà della covariaza V ar θ T V ar θ θ logl θx 1,..., X = V ar θ T Iθ [per l equazioe 5] 10
11 4 Verifica di ipotesi 4.1 Defiizioi U ipotesi statistica è u asserzioe o ua cogettura sulla fdr F. Se F, e quidi la corrispodete desità f, è ota a meo di u parametro θ = θ 1,..., θ m Θ R m, l ipotesi statistica è u asserzioe su θ. U ipotesi è semplice se specifica completamete la f.d.r. F della popolazioe; è composta se o è semplice. I questo capitolo ci occuperemo di ipotesi che riguardao solo il parametro icogito. Nei problemi che affroteremo soo preseti due ipotesi chiamate H 0 e H 1 ua è detta ipotesi ulla metre l altra è detta ipotesi alterativa. Il vero valore che il parametro θ assume i atura è compatibile solo o co H 0 o co H 1 ma o co etrambi. Dobbiamo ora stabilire ua regola che ci permetta di decidere tra le due ipotesi. Decidiamo di partizioare l isieme R di tutte le realizzazioi campioarie X 1,..., X i due regioi G e G c ed effettuiamo il campioameto; se x 1,..., x G rifiutiamo H 0 se ivece x 1,..., x G c allora accettiamo H 0. La G è detta regioe di rifiuto o regioe critica metre G c è detta regioe di accettazioe. Può capitare di predere delle decisioi sbagliate; gli errori che si possoo commettere soo di due tipi: Errore di I tipo o prima specie: quado rifiutiamo H 0 ma H 0 è vera. Errore di II tipo o secoda specie: quado accettiamo H 0 ma H 0 è falsa. Questi due errori o possoo essere calcolati co precisioe ma possiamo calcolare la loro probabilità. Sia αθ la probabilità di errore del I tipo e sia βθ la probabilità di errore di II tipo allora: αθ = P θ Rifiutare H 0 = P θ x 1,..., x G, θ Θ 0 6 βθ = P θ Accettare H 0 = P θ x 1,..., x G c, θ Θ Lemma di Neyuma-Pearso U buo test è tale per cui α e β soo trascurabili; ma i realtà esiste u trade-off cosicchè è impossibile miimizzare etrambi. Perciò si procede a fissare u valore per l errore che si ritiee più grave quello di I tipo e poi si miimizza il secodo. U test creato secodo questo criterio è detto test uiformemete più potete. Nel caso di ipotesi etrambi semplice il test creato è specificato dal Lemma di Neyma-Pearso. Sia X 1,..., X u campioe casuale co verosimigliaza L θ x 1,..., x e suppoiamo di voler verificare H 0 : θ = θ 0 cotro H 1 : θ = θ 1. Sia G la regioe critica defiita da: { } L θ0 x 1,..., x G = x 1,..., x : L θ1 x 1,..., x δ 11
12 Allora G è la regioe critica che geera massima poteza fra tutte le regioi critiche di ampiezza miore o uguale all ampiezza di G. Dimostrazioe Dobbiamo dimostrare che per qualuque regioe critica F di ampiezza al più pari a quella di G cioè tale che P θ0 F P θ0 G vale P θ1 F P θ1 G. Osserviamo che possiamo rappresetare F e G come: allora Ioltre F = F G F G c, G = F G F c G P θi F P θi G se solo se P θi F G c P θi F c G per i = 0, 1. 8 da cui otteiamo che: L θ0 x 1,..., x δl θ1 x 1,..., x L θ1 x 1,..., x < L θ0 x 1,..., x /δ Ifatti P θ1 B = L θ1 x 1,..., x dx 1... dx = 1 B δ Pertato x 1,..., x G x 1,..., x G c P θ0 A δp θ1 A A G 9 P θ1 B δp θ0 B B G c 10 P θ1 F G c P θ0 F G c /δ [per la 10] P θ0 F c G/δ [per la 8 co i = 0] δp θ1 F G c /δ [per la 9] B = P θ1 F G c L θ0 x 1,..., x dx 1... dx = P θ 0 B δ 12
1 Famiglia delle densità gamma
 olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
olitecico di Milao, Statistica INF, TEL [A-LZ], Epifai I., AA 7/8 Famiglia delle desità gamma Le espressioi delle desità espoeziale di parametro θ e χ date da (E(β)) (χ ) /θe x/β (, ) (x), β > (/) / x
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Soluzioni quarta esercitazione
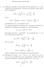 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
4. L ipotesi è falsa e la rifiuto bene. H 0 ) p = 0.5. Facciamo dunque n lanci. Otteniamo k teste ed n k croci:
 7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
7 Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla I base ai dati che ho a disposizioe devo decidere
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
Esercizi 2 Pietro Caputo 14 dicembre se ξ n > log n
 Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Esercizi 2 Pietro Caputo 4 dicembre 2006 Esercizio. Siao Y, per =, 2,..., variabili aleatorie co distribuzioe biomiale di parametri e p := λ, per qualche λ > 0. Dimostrare che Y coverge i distribuzioe
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Sommario. Facoltà di Economia. Campionamento e inferenza statistica
 Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Appunti di Probabilità e Statistica. a.a. 2014/2015 C.d.L. Informatica Bioinformatica I. Oliva. 1 Statistica Inferenziale.
 Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
Politecnico di Milano Appunti delle lezioni del corso di Statistica (2L) per gli allievi INF e TEL, AA 2007/2008. Intervalli di confidenza
 Politecico di Milao Apputi delle lezioi del corso di Statistica L per gli allievi INF e TEL, AA 007/008 Itervalli di cofideza Ileia Epifai 5 maggio 010 Il coteuto di queste dispese è protetto dalle leggi
Politecico di Milao Apputi delle lezioi del corso di Statistica L per gli allievi INF e TEL, AA 007/008 Itervalli di cofideza Ileia Epifai 5 maggio 010 Il coteuto di queste dispese è protetto dalle leggi
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Sommario. Corso di Statistica Facoltà di Economia. Test o verifica delle ipotesi. Lezione n 25. Francesco Mola. Obiettivi della verifica delle ipotesi
 orso Statistica Facoltà coomia Lezioe 5 a.a. - Fracesco Mola z Sommario Test o verifica delle ipotesi fodameti dei test costruzioe dei test rrori e probabilità errori oteza dei test a.a. - statistica-fracesco
orso Statistica Facoltà coomia Lezioe 5 a.a. - Fracesco Mola z Sommario Test o verifica delle ipotesi fodameti dei test costruzioe dei test rrori e probabilità errori oteza dei test a.a. - statistica-fracesco
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
0.1 Il teorema limite centrale
 0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
0. Il teorema limite cetrale 0. Il teorema limite cetrale Teorema 0.. Teorema limite cetrale). Sia X i ) i N ua successioe di variabili aleatorie i.i.d. che ammettoo mometo secodo fiito, co media µ e co
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
6. Intervalli di confidenza
 6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
6. Itervalli di cofideza La media campioaria e la variaza campioaria ci offroo ua stima dei parametri media e variaza del campioe statistico i esame. Abbiamo però bisogo di sapere quato ci si possa fidare
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Copyright Michele Tartara
 File distribuito co liceza Creative Commos BY-NC-SA.5 IT Copyright 008 - Michele Tartara Parte 1. Ifereza parametrica Alcue formule e proprietà utili: Fuzioe di ripartizioe: F X = P X x Desità: f X x =
File distribuito co liceza Creative Commos BY-NC-SA.5 IT Copyright 008 - Michele Tartara Parte 1. Ifereza parametrica Alcue formule e proprietà utili: Fuzioe di ripartizioe: F X = P X x Desità: f X x =
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Elementi di Probabilità e Statistica - 052AA - A.A
 Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
Elemeti di Probabilità e Statistica - 05AA - AA 05-06 Prova scritta - 9 settembre 06 Problema pt Su uo spazio probabilizzato Ω, F, P, suppoiamo di avere ua successioe Z di va discrete idipedeti, tali che
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Università degli Studi di Salerno Pietro Coretto. Corso di Statistica FORMULARIO
 Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
Versioe: 16 ottobre 2017 (h17:25) Uiversità degli Studi di Salero Pietro Coretto Corso di Statistica FORMULARIO Valori osservati per statistiche di posizioe, variabilità e correlazioe Nota: per ua distribuzioe
1 Esponenziale e logaritmo.
 Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Espoeziale e logaritmo.. Risultati prelimiari. Lemma a b = a b Lemma Disuguagliaza di Beroulli per ogi α e per ogi ln a k b k. k=0 + α + α Teorema Disuguagliaza delle medie Per ogi ln, per ogi upla {a
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Primo appello di Calcolo delle probabilità Laurea Triennale in Matematica 22/01/2018
 Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
Primo appello di Calcolo delle probabilità Laurea Trieale i Matematica 22/0/20 COGNOME e NOME... N. MATRICOLA... Esercizio. Siao X e Y due variabili aleatorie idipedeti, co le segueti distribuzioi: X Uif(0,
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
INFERENZA o STATISTICA INFERENTE
 INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
LEGGE DEI GRANDI NUMERI
 LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
LEGGE DEI GRANDI NUMERI E. DI NARDO 1. Legge empirica del caso e il teorema di Beroulli I diverse occasioi, abbiamo mezioato che la ozioe ituitiva di probabilità si basa sulla seguete assuzioe: se i sperimetazioi
Example 2 Una variabile o un vettore aleatorio X è degenere in c se P (X = c) = 1. Dato che la funzione di ripartizione di questa variabile è
 La covergeze i legge per variabili o vettori aleatori è solitamete formulata i termii di fuzioi di ripartizioe. Ricordiamo che la fuzioe di ripartizioe di ua variabile aleatoria X è ua fuzioe di variabile
La covergeze i legge per variabili o vettori aleatori è solitamete formulata i termii di fuzioi di ripartizioe. Ricordiamo che la fuzioe di ripartizioe di ua variabile aleatoria X è ua fuzioe di variabile
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI
 DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Dispense Inferenza PRELIMINARY DRAFT
 Dispese Ifereza PRELIMINARY DRAFT Cristia Mollica & Ja Marti Rossi 1 Esercizio 3 - Prova scritta del 1-0-018 Esercizio 3. Ua baca vuole stimare la proporzioe π di persoe che accetterebbe di sottoscrivere
Dispese Ifereza PRELIMINARY DRAFT Cristia Mollica & Ja Marti Rossi 1 Esercizio 3 - Prova scritta del 1-0-018 Esercizio 3. Ua baca vuole stimare la proporzioe π di persoe che accetterebbe di sottoscrivere
Statistica. variabili aleatorie indipendenti e tali che F X1
 Statistica µ Defiizioi: Ø X variabili aleatorie idipedeti e tali che F X = = F X si dicoo capioe co µ e icogiti Per deteriare i paraetri icogiti si fa ifereza statistica capioi e ϑ paraetro icogito: Ua
Statistica µ Defiizioi: Ø X variabili aleatorie idipedeti e tali che F X = = F X si dicoo capioe co µ e icogiti Per deteriare i paraetri icogiti si fa ifereza statistica capioi e ϑ paraetro icogito: Ua
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
DISTRIBUZIONE NORMALE MULTIVARIATA
 Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Distribuzioe ormale uivariata DISTRIBUZIONE NORMALE MULTIVARIATA ANALISI MULTIVARIATA A.A. 00/ CORSO DI LAUREA IN STATISTICA Carla Rampichii Desità Normale μ, σ Normale stadardizzata: μ=0, σ= Distribuzioe
Università di Napoli Federico II, DISES, A.a , CLEC, Corso di Statistica (L-Z) Lezione 22 La verifica delle ipotesi. Corso di Statistica (L-Z)
 Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Esercizi di econometria: serie 2
 Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi di ecoometria: serie Esercizio Per quali delle segueti uzioi di desità cogiuta le variabili casuali ed soo idipedeti?......3.4.5..5 (a) (b) 3 4....3.6.9..4...5..5 3.. 3.8..4.6 (c) (d) Nel caso
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 2007/2008
 UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
UNIVERSITÀ DEGLI STUDI DI LECCE APPUNTI PER IL SEMINARIO DI ELEMENTI DI TEORIA DELLA PROBABILITÀ A.A. 007/008 Questi apputi soo stati cocepiti come u aiuto didattico per gli studeti della Facoltá di Ecoomia.
