Ing. Guido Bellagamba Allegretti. Quaderno 1

Transcript

1 Ing. Guido Bellagamba Allegretti Quaderno 1 onsolidazione edimenti proa edometria proe in sito: SPT CPT Cedimenti ammissibili Cario limite delle fondazioni Fattori di siurezza

2 INDICE 1. CONSOLIDAMENTO Determinazione del oeffiiente di onsolidazione C Taylor Casagrande Metodo dipendente dalla permeabilità CEDIMENTI PROVA EDOMETRICA Correzione di Shmertmann CALCOLO DEL CEDIMENTO EDOMETRICO Metodo operatio PROVE PENETROMETRICHE PROVA SPT: Standard Penetration Test (PROVA PENETROMETRICA DINAMICA) PROVA CPT: Cone Penetration Test (PROVA PENETROMETRICA STATICA) CEDIMENTI DI FONDAZIONI SU SABBIE METODO DI BURLAND E BURBIDGE METODO DI SCHMERTMANN Metodo operatio ESEMPI APPLICATIVI Esempio 1 (Burland e Burbidge) Esempio (Shmertmann) Esempio 3 (Shmertmann) COMPLESSO FONDAZIONE-SOVRASTRUTTURA Cedimenti ammissibili CARICO LIMITE DELLE FONDAZIONI DIRETTE Tipi di rottura del terreno Rottura generale (formula trinomia del ario limite di Terzaghi ) Generalizzazione di Brinh Hansen (1970) Condizioni non drenate (terreni oesii) Considerazioni sull euazione di Brinh Hansen Punzonamento Fattore di siurezza F s Esempi appliatii Esempio Esempio Esempio Esempio Esempio Esempio Esempio

3 9. Appendie I La formula trinomia Appendie II Altre espressioni dei oeffiienti della formula trinomia

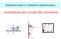
4 1. CONSOLIDAMENTO È il fenomeno on ui, appliando un ario ad un terreno, uesto si trasferise al suo sheletro passando per l aua. Più il terreno è permeabile e minore è il ruolo gioato dall aua. Quando inee si ha a he fare on basse permeabilità (k<10-8 m/s) il ario, appena appliato, agise sull aua in toto. Solo a seguito dell allontanamento di uest ultima (moto filtrazioni ondizioni drenate), entra in gioo lo sheletro del terreno. Quindi inizialmente rese on lo sforzo totale anhe la pressione neutra (per effetto del ario appliato). Con la filtrazione, a ario ostante, diminuise la pressione nutra e rese la tensione effiae. Il proesso di onsolidazione ha termine uando la pressione neutra è tornata in ondizioni idrostatihe e le tensioni effiai sono pari alle totali. Un modello he spiega bene il fenomeno è ostituito da un reipiente pieno di aua, superiormente hiuso da un pistone (dotato di alola per fare usire aua), on una molla interna (a ontrasto fra fondo reipiente e pistone superiore) Questo fenomeno, molto eloe on terreni aenti eleata permeabilità e lento per basse permeabilità, è aompagnato da edimenti douti in prima istanza all allontanamento dell aua e al moimento relatio dei grani ed in seonda analisi a fenomeni deformatii differiti nel tempo dello sheletro del terreno (effetti isosi legati anhe alla rottura dei grani). Ridurre al minimo uesti edimenti e uindi apirne l eoluzione, ha la onseguenza di portare in siurezza la ostruzione delle strutture. Va da sé he il problema è più sentito per bassi alori di permeabilità, doe la risoluzione sta nella riduzione del perorso del moto di filtrazione. In ia analitia le ipotesi assunte per risolere il problema della onsolidazione sono: 1) terreno ontinuo, inomprimibile, omogeneo e saturo; ) aua inomprimibile; 3) deformazioni infinitesime; 4) alidità legge di Dary. Risultato della trattazione analitia è l euazione della onsolidazione monodimensionale di Terzaghi da ui è riaabile il edimento ρ(t) durante il proesso di onsolidazione: 4

5 Doe: m H = m 0 H [ σ u( z, t) ] dz = m ρ ( t) ρ 0 u( z, t) dz e = σ è i oeffiiente di omprimibilità ( ε = m σ ) 1+ e σ è l inremento di tensioni totali per effetto del ario ostante u ( z, t ) = f ( σ, T ) pressione interstiziale dell aua in fase transitoria, on C t T = (H H spessore strato onsolidato) Normalizzando l euazione del edimento, si ottiene il rapporto U ( t) = ρ ( t) (sempre ρ minore dell unità), detto grado di onsolidazione (doe ρ è il edimento a tempo infinito, uindi a fine onsolidazione). Questa è una ura adimensionale, alida per ogni tipo di terreno, on andamento tipo uello riportato nella figura a seguire: Diagramma del grado di onsolidazione nel tempo doe : U=0.3 T V = = T 50 U=0.8 T V = = T 90 Con uesta ura, noto il edimento totale ρ, si può stimare in uanto tempo T si arà il edimento ρ(t). Unio problema he rimane è la determinazione di C (oeffiiente di onsolidazione). Due sono i modi più diffusi: Taylor e Casagrande. 5

6 1.1 Determinazione del oeffiiente di onsolidazione C Entrambi i metodi (Taylor e Casagrande) si basano sulle risultanze sperimentali della proa edometria, he errà trattata al paragrafo 3. Comunue sono sottostime di uelli reali in sito (e uindi a faore di siurezza) perhé la filtrazione è più eloe in sito he nel proino (size effet) Taylor Dalla proa edometria si riaa il diagramma ρ ( t) t (analogo a uello dimensionale della figura preedente). Si ossera he fino al 60% della onsolidazione, tale relazione è pressohé lineare. Se si onsidera un punto ualsiasi della retta di interpolazione (del tratto iniziale) e lo si maggiora del 15% (uindi si onsidera l asissa di un punto della retta e la si maggiora di 1.15 olte) si indiidua una seonda retta, passante per uesto punto e l origine. Doe uesta seonda retta intersea la ura sperimentale si troa un edimento pari al 90% di ρ, definito al tempo t 90. on aluni passaggi matematii si ottiene: ρ U = 90 H = 0.9 T = C = ρ t90 H T = t Casagrande Dalla proa edometria si riaa il diagramma seguire, doe: AB: onsolidazione primaria per flusso transitorio; CD: onsolidazione seondaria per effetti transitori. ρ ( t) logt, ome riportato nella figura a 6

7 Per onsolidazione si onsidera la sola legata a edimenti elasto-plastii, he troa uindi termine nel punto B. Poi si mette in relazione il tempo t per ottenere ρ 50, ioè t 50 uindi: ρ U = 50 H = 0.5 T = C = ρ t50 H T = t Metodo dipendente dalla permeabilità Si determina il oeffiiente di permeabilità K del terreno e poi: K ρ C = doe m = m H σ w. CEDIMENTI Con edimento di una fondazione superfiiale si intende l abbassamento del piano di posa a ausa di deformazioni del terreno sottostante. Cause di iò possono essere: arihi trasmessi al terreno, osillazioni della falda, ibrazioni di ualsiasi natura. Lo studio dei edimenti sia assoluti he differenziali dee poter giungere a garantire la ompatibilità dei medesimi on la statia e la funzionalità della sorastruttura. Quando aiene un edimento si indiiduano tre momenti: 1 edimento immediato: è di interesse pratio per i terreni di media ed eleata plastiità, doe possono silupparsi sensibili deformazioni di taglio per effetto di plastiizzazioni loali e deformazioni isose in ondizioni non drenate; edimento primario o di onsolidazione: rappresenta uasi sempre l aliuota predominante e he uindi influenza le onsiderazioni progettuali; 3 edimento seondario o isoso: può essere signifiatio per terreni organii o in aso in ui il edimento primario aenga molto rapidamente (ed esempio per effetto di dreni ertiali). 7

8 La differente permeabilità he distingue i terreni a grana fine da uelli a grana grossa, fa sì he uesti ultimi si omportino ome sistemi drenati, in ui l appliazione di arihi ha effetto sulle pressioni interstiziali per brei lassi temporali. L euilibrio originale uindi, in ui il ario si trasferise interamente allo sheletro solido del terreno (ariazioni di tensioni totali ed effiai oinidono, essendo la pressione dell aua anora on distribuzione idrostatia) si ristabilise agilmente, in tal modo il moto di filtrazione transitorio può ritenersi trasurabile. Perde dunue di signifiato la distinzione fra edimento immediato e edimento primario, he di seguito erranno hiamati ol solo termine di edimento iniziale (douto a deformazioni di natura elasto-plastia), a ui farà seguito il seondario (deformazioni isose). A seguire si onsiderano aluni metodi sperimentali per definire i edimenti, assieme alle relatie trattazioni analitihe. 3. PROVA EDOMETRICA È una proa he riprodue in laboratorio le ondizioni di onsolidazione monodimensionale. Consiste nell appliare ad un proino onfinato lateralmente e ontrastato alle estremità da due pietre porose, una seuenza di arihi in modo he le deformazioni ed il flusso d aua aengano nella sola direzione ertiale. Il proino, durante la proa, è immerso in aua per simulare in fase disario il rigonfiamento. La diffioltà a preleare ampioni in sabbia, fa sì he tale proa risulti più diffusa per le argille. Le argille, aendo bassi alori di permeabilità, saranno soggette a steps di ario 8

9 lenti nel tempo (4h) per garantire l espulsione dell aua e dunue il ripristino delle ondizioni idrostatihe nel ampione. Di interesse è la onsolidazione primaria: la seondaria è rileante solo in asi partiolari ome terreni a omponente organia o simili. Posto ε = H H 0 il diagramma iene in genere, riportato in sala semilogaritmia (ε, log σ ), per una più immediata lettura, ome si ede nei due esempi di seguito riportati, relatii al medesimo terreno: Il diagramma mantiene ualitatiamente lo stesso andamento se al posto della deformazione relatia ε si onsidera l indie dei uoti e:unia differenza è he l asse è riolto erso l alto (all aumentare del ario, la deformazione rese e l indie dei uoti diminuise). Nel diagramma sono distinguibili alune parti: AB: riompressione, doe: ε rapporto di riompressione RR = logσ Cr = 1+ e 0 indie di riompressione C r e = ; logσ BC: ompressione, deformazioni sia elastihe (modeste) sia plastihe, doe: ε rapporto di ompressione CR = logσ C = 1+ e 0 9

10 indie di ompressione C e = ; logσ CD: sario o rigonfiamento, reupero della sola deformazione elastia, doe: ε rapporto di rigonfiamento SR = logσ Cs = 1+ e 0 indie di rigonfiamento C s e = ; logσ DC : riompressione; CF: ompressione. Dal diagramma ε σ si riaano: oeffiiente di ompressibilità m ε = σ modulo edometrio M = 1 m σ = ε indie di ompressibilità a e = σ Un terreno NC si omporterà seondo la ura ABC (doe σ p rappresenta le ondizioni litostatihe in loo, azzerate a seguito del prelieo del proino); un terreno OC inee arà andamento seondo la DC F. Contrariamente alle fasi di ompressione, durante le riompressioni le deformazioni sono modeste. Il alore di σ p in B, pressione di preonsolidazione, è la massima tensione a ui è stato sottoposto il terreno (Casagrande), determinabile ome segue: 1) nel punto di massima uratura si traiano orizzontale, tangente e loro bisettrie; ) l intersezione della bisettrie on il prolungamento del tratto di ompressine fornise σ p erato. 10

11 Noto σ p per ia sperimentale e alolato in ia analitia il alore di tensione effiae σ 0 si può definire il grado di soraonsolidazione OCR (Oer Consolidation Ratio): σ p OCR = σ 0 = 1 NC = > 1 OC Doe σ rappresenta il ario litostatio in sito. 0 L OCR (insieme a K 0 ) desrie in termini uantitatii la storia tensionale di un deposito. 3.1 Correzione di Shmertmann Shmertmann ha proposto una orrezione dei risultati delle proe edometrihe in modo da aere una stima più affidabile dei parametri geotenii in sito. 1) definizione di C r (indie di riompressione) on un ilo di ario-sario; ) dal punto A=( σ,e 0 0 ), he rappresenta le ondizioni in sito, si traia retta on pendenza C r ; 3) si traia la retta dal punto C (appartenente alla retta del punto 1) e per ui σ = σ ), al punto D (orrispondente all indie dei uoti 0.4e 0 punto di 0 p onergenza sperimentale delle ure edometrihe); 4) si diagramma e in funzione delle tensioni σ, sia la sperimentale he la riostruita 5) si onsidera σ p uando il diagramma al punto 4) è simmetrio rispetto a σ p stesso. Con uesta orrezione in genere si ha un inremento di σ p dell ordine del 15±5%. 11

12 4. CALCOLO DEL CEDIMENTO EDOMETRICO Questo metodo di alolo dei edimenti, aleole per argille, si applia al aso di ario esteso su terreno omogeneo (per ipotesi di monodimensionalità). Operatiamente uindi si determina la tensione effiae σ 0 nello strato di terreno (se lo spessore è eleato si suddiide il medesimo in più strati) e la si onfronta on la tensione di preonsolidazione σ p. Nel aso di terreni preonsolidati (OCR>1), si arà σ p σ H = H 0 RR log + CR log σ σ σ p Sempre per i terreno preonsolidati, nel aso in ui il ario trasmesso non sia suffiiente a superare la tensione di preonsolidazione, ioè σ + σ < σ, uindi le deformazioni aengono nel tratto di riompressione: 0 p H σ 0 + σ = H 0 RR log σ 0 Nel aso di terreni normalonsolidati (OCR=1), si arà σ = σ e le deformazioni 0 p aerranno nel solo tratto di ompressione: σ 0 + σ H = H 0 CR log. σ Metodo operatio 1) suddiisione del terreno in strati; 1

13 ) alolo delle tensioni effiai litostatihe in mezzeria agli strati; 3) alutazione degli inrementi di tensione a seguito dell appliazione del ario, nei ari strati, ipotizzando la resita lineare dell impronta di ario on la profondità; 4) determinazione on proedura sperimentale dei parametri edometria e della tensione di preonsolidazione; 5) alolo delle deformazioni dei singoli strati; 6) definizione del edimento ome sommatoria delle deformazioni elementari dei ari strati. 5. PROVE PENETROMETRICHE Le proe penetrometrihe possono essere fatte sia in ia statia he dinamia. Le proe anno spinte fino a profondità doe risulta anora signifiatio il ontributo delle tensioni trasmesse dai arihi. 5.1 PROVA SPT: Standard Penetration Test (PROVA PENETROMETRICA DINAMICA) Questa proa onsente di determinare la resistenza di un terreno a seguito della penetrazione dinamia dal fondo foro di un sondaggio di un ampionatore. Si fa adere un maglio da 63.5 kg, da un altezza di 760 mm su una batteria di aste all estremo inferiore della uale è posto il ampionatore (diametro esterno di 51 mm, interno di 35 mm ed altezza di 457 mm). Il numero di olpi per ottenere una penetrazione di 300 mm (dopo la penetrazione uasi-statia per graità e dopo i 150 mm di infissione dinamia di posizionamento) è il dato assunto ome resistenza alla penetrazione, indiato on N SPT. Vantaggi della proa sono: - eonomiità e diffusione; - ersatilità on ogni tipo di terreno; - permette il prelieo di ampioni. Lo santaggio prealente è inee il fatto he l appliazione dinamia dei arihi non simula la realtà in opera, doe i arihi possono ritenersi statii, uindi le unihe orrelazioni on i parametri geotenii he si possono fare sono di natura empiria. Se durante la proa, 100 olpi non bastano per aere la penetrazione di 300 mm, la proa iene interrotta. 13

14 La freuenza di battitura (30 olpi/min) non dee essere eessia per permettere il ristabilirsi di ondizioni di euilibrio fra due battiture suessie. Nel aso di sabbie fini e sabbie limose sotto falda, ualora N SPT > 15, il alore misurato errà orretto seondo le indiazioni di Terzaghi-Pek, per depurarlo dai possibili effetti delle sorapressioni neutre generatesi durante l infissione: N CORRETTO = (N-15) Altra orrezione he si può impiegare è nel aso di terreni ghiaiosi o sabbioso ghiaiosi: N SPT * = 1.5 N 5. PROVA CPT: Cone Penetration Test (PROVA PENETROMETRICA STATICA) Consiste nell infiggere a pressione enl terreno una punta onia, misurando on ontinuità lo sforzo neessario alla penetrazione di punta ( ) e l adesione tereno-aiaio in un maniotto posto sulla punta ( s ). Qualora la punta sia dotata di un settore poroso, la misura risulta integrata on alori di pressione. SPT CPT Questa proa sere per: - ostruire stratigrafie (e uindi definire i terreni attraersati); - misurare l angolo di attrito e la ompressibilità drenati di terreni granulari; - definire la resistenza a taglio non drenata di terreni oesii; 14

15 - liello di falda e grado di onsolidazione. Il tipo di dati forniti dalla proa sono: Resistenza alla punta = Q x A (Q ario assiale sul ono; A area di base del ono); Attrito laterale f s = Q s x A s (Q s forza di attrito per infiggere il ono; A area laterale del maniotto); Spinta totale Q t (forza per spingere aste e punta); Resistenza per attrito totale Q st = Q t + Q ; Frition Ratio R f = 100 x f s / (%). Il maniotti ha superfiie laterale di 1.5x10 4 mm. L infissione della punta aiene on una eloità di 0 mm/s. Esempi di diagrammi della proa in esame sono riportati a seguire. 15

16 6. CEDIMENTI DI FONDAZIONI SU SABBIE Non potendo preleare ampioni indisturbati, uando si ha a he fare on materiali granulari si farà uso delle proe in sito, on partiolare attenzione alle proe penetrometrihe sia dinamihe he statihe (di ui sopra). 6.1 METODO DI BURLAND E BURBIDGE Sia w il edimento esprimibile on la relazione: w Z I = I doe: C 0.7 Z I = B : zona di influenza del ario he si estende fino ad una profondità doe il edimento è pari a 5% del edimento superfiiale; 1.7 I C = : indie di ompressibilità (anhe definibile ome ariazione di indie di uoti su 1.4 N ariazione di tensioni effiai); :ario uniforme trasmesso da una fondazione uadrata. Espliitando i termini, si ottiene il edimento w (in mm) di una sabbia normalonsolidata: w = B Se la fondazione si troa ad una profondità da p.. oe è presente una tensione litostatia σ, l euazione dienta, nella sua forma generalizzata: 0 w = σ I I C 0.7 C 0 B ( σ 0 ) B 0.7 I C Doe il primo termine si riferise al tratto di riompressione aratteristio di un omportamento elastio del terreno (finhé non raggiunge lo stato tensionale pari a uello litostatio in sito), mentre il seondo termine si riferise alla ura di ario (per arihi appliati superiori a uelli litostatii a parità di profondità). Se il terreno è soraonsolidato, l euazione sopra si mantiene alida, on l unio aorgimento he al posto di σ 0 si troerà σ p, tensione di preonsolidazione (si riordi il diagramma semilogaritmio delle proe edometrihe). L espressione è una forma generalizzazione del problema: se infatti si onsidera una sabbia NC (per ui non esiste una tensione di preonsolidazione σ p ) ioè σ 0 = σ p =0 e l euazione si riporta al primo aso. 16

17 Nel tratto di riompressione l indie di ompressibilità è onsiderato pari ad 1/3 di uello del tratto di ompressione. Di fatto, il σ 0 del primo termine, è anhe esso un delta di tensioni: stato tensionale ad inizio proa (sario). σ 0-0, doe lo 0 è lo Il alore di N impiegato nella definizione di I C è la media dei alori di N SPT riaati on proe SPT per una profondità pari alla zona di influenza: i Z N i N =. i Appliando il metodo seondo le indiazioni su esposte, il risultato ottenuto è il alore del edimento iniziale, inteso ome somma dell immediato e del primario (legato alla onsolidazione), nel aso speifio di fondazione uadrata e on spessore dello strato di appoggio omprimibile H maggiore della zona in influenza. Appliando tre fattori orrettii si ottiene la generalizzazione del metodo di Burland e Burbidge: f s ) fattore di forma della fondazione: 1.5 L se > 1 f = B s > 1 B L B uesto fattore ha oma massimo alore 1.56 nel aso di fondazioni nastriformi; f H ) fattore di altezza dello strato omprimibile: 0.7 H H se H < Z I = B f H = ( ) < 1; Z Z I f t ) fattore per effetti differiti nel tempo (per t>3 ann): f t t = ( 1+ R3 + R log ) ; 3 doe R 3 = 0.3 e R = 0. per arihi statii R 3 = 0.7 e R = 0.8 per arihi ilii (NOTA: il logaritmo è in base 10). I Con tali fattori, uindi l espressione generalizzata del edimento diiene: 0.7 IC 0.7 w = f s f H ft σ 0 B + ( σ 0) B I C 3 i 17

18 Quello troato appliando la formula sopra riportata rappresenta un alore medio di edimento. Per riportarsi al alore massimo di edimento he i si può attendere, si dee moltipliare tale alore per METODO DI SCHMERTMANN È un metodo di alolo dei edimenti in asse ad una fondazione in terreni non oesii on l impiego dei risultati derianti dalle proe CPT. L espressione generia del edimento assume la forma: Doe: = ( σ 0 s = C 1 C H I z z E 0 ) = pressione effiae netta, uindi sorappressione rispetto al ario litostatio douta alla fondazione ( σ ); σ 0 0 = tensione ertiale effiae agente alla uota di imposta della fondazione; C 1 e C sono due oeffiienti he tengono onto rispettiamente dell approfondimento relatio della fondazione rispetto al p.. e del tempo t (espresso in anni), seondo le seguenti relazioni: C C 1 σ 0 = t = log( )

19 I z è il oeffiiente di influenza. Esso aria on la geometria della fondazione (L/B), on la pressione appliata ( ) e on l approfondimento relatio della fondazione (e uindi on la tensione ertiale effiae agente σ ), seondo il diagramma preedente. 0 Il modulo di deformazione E deria dalle proe CPT e per esso si può assumere: E =.5 per fondazioni uadrate o irolari E = 3.5 per fondazioni nastriformi. Aluni autori formalizzano il legame fra E e on la relazione: 6..1 Metodo operatio L =.5 + ( 1) B E 1) alolo dei alori di C 1 (on σ 0 al piano di imposta della fondazione = x D), C (predefinendo la ita dell opera, assumibile ome 30 anni) e = - σ 0. ) Definizione della profondità della zona di influenza, in base alla tipologia di fondazione (rapporto L/B). Nei asi intermedi a uelli grafiati, si opera per interpolazione; 3) Suddiisione della zona di influenza in strati, in funzione della regolarità del diagramma deriante dalla proa CPT. In tali strati si onsidereranno ostanti i alori di I zi ed E i ; 4) Definizione del alore I zmax e della profondità a ui si troa dal piano di imposta della fondazione; 5) Definizione dei due punti di origine e fine della bilatera e determinazione dell euazione delle rette passanti per tali punti; 6) Calolo del alore di I zi a metà di ogni strato (nota la profondità, on le rette del punto 5 si troa il alore erato); 7) Visto he ogni strato è stato definito per omogeneità di, si estrae dal diagramma della CPT il alore di ostante nello strato definito; 8) Si alola il modulo di Young E in base ai dati di progetto; 9) Dalla tabella predisposta si può uindi riaare il edimento atteso. 6.3 ESEMPI APPLICATIVI Si riportano a seguire aluni esempi di alolo dei edimenti seondo i due metodi riportati nei paragrafi 6.1 e 6.. i primi due studiano la stessa fondazione nei due metodi di alolo. I dati di uesti due problemi sono: 19

20 fondazione uadrata di lato B=.5 m piano di imposta della fondazione a m da p.. terreno: sabbia medio fine on ρ = 1900 kg/m 3 ario trasmesso dalla fondazione = 00 kpa Esempio 1 (Burland e Burbidge) 0

21 1

22

23 6.3. Esempio (Shmertmann) 3

24 4

25 5

26 6.3.3 Esempio 3 (Shmertmann) 6

27 7

28 7. COMPLESSO FONDAZIONE-SOVRASTRUTTURA Due sono le domande da porsi: 1) uali saranno i edimenti preedibili? Diersi sono i diersi tipi di approio (empirio-probabilistio o approssimato), tutti aratterizzati da noteole empirismo e generale sorastima delle distorsioni. Le onlusioni he però si possono trarre sono: - in terreni inoerenti i edimenti assoluti sono ontenuti, mentre sono rileanti i edimenti relatii (ieersa per i terreni oerenti). Questo a ausa della ridotta ompressibilità e della spiata eterogeneità dei terreni a grana grossa. - A parità di edimento, la rotazione relatia aumenta passando da fondazioni ontinue a fondazioni isolate e da terreni a grana fine a terreni a grana grossa. - Fra fondazioni dirette e fondazioni su pali, iò he ambia è l entità dei edimenti, più ridotta per ueste ultime. ) Questi edimenti saranno aettabili? Diersi autori hanno proposto alori di riferimento ammissibili per edimenti relatii ed assoluti. L eterogeneità di tali limiti è legata alla soggettiità del danno aettabile. In generale si onsiderano i alori più restrittii laddoe deono prealere riteri di estetia e funzionali (edifii nuoi, pregiati destinati a iile abitazione o uso pubblio), mentre alori più eleati sono aettabili per edifii industriali. 7.1 Cedimenti ammissibili La definizione del danno subito da una struttura a seguito di un edimento non è un operazione unioa in uanto deria da molteplii fattori legati alla struttura, alla sua destinazione ed a onsiderazioni eonomihe. Non neessariamente il danno è unioamente inteso in termini di omparsa di repe e fessure, ma in una sua aezione più ampia, bisogna onsiderare anhe le modifihe dell assetto d insieme in relazione alla destinazione e funzionalità della struttura e delle sue parti. La definizione dunue dei alori di soglia dei edimenti da prendere in riferimento per eitare danni strutturali può aenire solo per ia empiria, sulla base di molteplii osserazioni su asi reali. 8

29 In uest ottia è neessario definire i parametri di distribuzione dei edimenti nello spazio he erranno presi in onsiderazione per ueste alutazioni empirihe. Rotazione relatia β: rotazione subita da una retta ongiungente due punti di riferimento, una olta sorporata la rotazione rigida ω della struttura. La distorsione angolare α è definita ome: s s L B A B α = +. AB s L s BC L inflessione relatia india il massimo edimento riferito alla ongiungente di due punti di riferimento a distanza L ed il rapporto /L è indiato ome rapporto di inflessione. Aluni esempi di edimenti ammissibili sono di seguito riportati. Strutture a telaio in.a. β rotazione relatia Tamponature 1/300 1/500 Strutture portanti - telaio 1/150 1/00 Skempton-M Donald Poshin-Tokar 9

30 Per le strutture in muratura non armata, Burland-Wroth hanno proposto per il rapporto di inflessione i seguenti alori limite prima di raggiungere la fessurazione: 10 L 4 10 L 4 4 L per = 1 H L per = 5 H Definiti i alori di soglia, il problema è poi di definire i edimenti differenziali. Benhé sia relatiamente attendibile la preisione di un edimento totale di una struttura, altrettanto non può dirsi per i edimenti differenziali, dipendendo uesti ultimi da fattori ome la rigidezza della struttura ed eterogeneità del terreno. Per definire uindi i edimenti differenziali, la strada aettata è uella di impiegare orrelazioni fra i edimenti relatii ed il edimento massimo osserato. Per uanto riguarda i alori limite del edimento S, Grant et al. hanno proposto: S max (mm) terreni sabbiosi Terreni oesii formula on β = 1/ 500 formula on β = 1/ 500 Plinti Platee β max β max β max β max 70 In aggiunta a ueste orrelazioni si può dire: terzaghi-pek, per fondazioni su sabbie, hanno posto il edimento differenziale in termini del 75% di uello totale, on un minimo a 5 mm; Skempton e Ma Donald, per strutture ordinari fondate su sabbia, pongono il massimo edimento tollerabile in termini di 40 mm per fondazioni isolate e mm per platee, on un edimento differenziale massimo di 5 mm. Nel aso di terreni di natura argillosa, il edimento differenziale massimo sale a 40 mm on edimenti massimi di 65 e mm rispettiamente per plinti e platee. Altri autori hanno fornito alutazioni su strutture esistenti. I parametri da uesti riportati deono sempre essere presi ome ordine di grandezza dei fenomeni in studio. Quando i edimenti preisti superano uelli ammissibili si può interenire in diersi modi: 1) ambiare tipo di fondazione (magari on l impiego di pali); ) modifiare la struttura (più o meno rigida. La preisione di un piano seminterrato è in grado di ompensare ira 4 piani fuori terra); 30

31 3) modifiare le fondazioni (più rigide laddoe siano presenti edimenti differenziali); 4) migliorare le proprietà dei terreni (impiego di rileati di preario, oppure ostruire su rileati strutturali, addensamento meanio on rullatura, drenaggi ertiali,.). 8. CARICO LIMITE DELLE FONDAZIONI DIRETTE Immaginiamo di appliare ad una fondazione un ario ertiale Q e di far resere gradualmente uesto ario, osserando al ontempo il edimento ertiale w della fondazione. Il edimento rese dapprima ol ario seondo una legge lineare e poi on un gradiente resente fino a raggiungere una fase finale doe a pioli inrementi di ario si hanno eleate deformazioni. La ura ario-edimento tende ad un asintoto (parallelo all asse del edimento) il ui alore di ario è indiato ome ario limite Q lim del omplesso terreno-opera di fondazione. La apaità limite uindi rappresenta la pressione he, appliata alla fondazione, prooa la rottura del terreno. 8.1 Tipi di rottura del terreno Due sono fondamentalmente i tipo di rottura del terreno: 1) rottura generale: aratterizzato dalla formazione di una superfiie di sorrimento. Il terreno sottostante la fondazione rifluise lateralmente e erso l alto. Il terreno irostante la fondazione uindi subise un solleamento e si può osserare l emersione della superfiie di sorrimento. A uesto meanismo orrisponde un omportamento della fondazione di tipo plastio o fragile, aompagnato da una rotazione della fondazione. 31

32 ) punzonamento: aratterizzato dall assenza di una superfiie di sorrimento definita. Il terreno sottostante la fondazione si omprime (diminuzione della porosità). Il terreno irostante la fondazione si abbassa, attenuandosi on l allontanamento dalla fondazione stessa. A uesto meanismo orrisponde un omportamento della fondazione di tipo plastio on inrudimento (i edimenti resono ol ario, senza raggiungere un alore preiso di ario limite), doe si indiiduano piano di taglio subertiali, aompagnati da affondamento della struttura senza solleamento del terreno. Fra i due meanismi di ui sopra è la rottura loale, intermedia nelle manifestazione e nell interpretazione. La ompressibilità del terreno al di sotto della fondazione ha importanza rileante, ma allo stesso tempo si erifia anhe la formazione di superfii di sorrimento he terminano all interno della massa di terreno, senza ioè emergere in superfiie (ome per la rottura generale). 3

33 I meanismi di rottura dipendono da diersi fattori, uali: - aratteristihe del terreno (tipologia ed addensamento e uindi densità relatia D R ); - profondità del piano di posa della fondazione (o approfondimento relatio D/B). La rottura generale aiene in terreni addensati e per fondazioni superfiiali mentre la rottura per punzonamento in terreni poo densi e fondazioni profonde. La figura a seguire mostra he nel aso di un terreno sabbioso ad eleata densità relatia, una fondazione superfiiale arria al ollasso seondo una rottura generale; la stessa fondazione arria a ollasso per punzonamento se posta su sabbia siolta (diminuzione di D R ). inoltre una fondazione su sabbia densa arria a rottura seguendo il meanismo di rottura generale se posta in superfiie o a profondità relatie D/B modeste, mentre il punzonamento si erifia on eleati alori di profondità del piano di posa. Rotture per punzonamento sono inoltre possibili uando, al di sotto dello strato di sabbia densa, si troa un terreno più ompressibile (sabbia siolta o argilla tenera) 33

34 8.1.1 Rottura generale (formula trinomia del ario limite di Terzaghi ) Si erifia in terreni poo deformabili (sabbie addensate, argille onsistenti), doe le ondizioni non drenate permettono deformazioni senza ariazioni di olume. Il medesimo fenomeno può aenire on ariazione di olume, in tal aso però il fenomeno predominante non è la ompressione, bensì lo sorrimento (deformazione da taglio). Nei terreni sabbiosi si assume he realizzi la rottura generale uando l indie di rigidezza I r (definito nel paragrafo ) risulta superiore ai alori ritii del medesimo indie. Definito il tipo di rottura, si alola la apaità portante del terreno ome di seguito desritto. Si onsideri una fondazione su terreno omogeneo, on forma in pianta di strisia indefinita (B<L/5), in modo da trattare il problema in ondizioni di deformazioni piane. Il piano di posa della fondazione e la superfiie del terreno siano orizzontali ed i arihi ertiali e entrati. Il terreno fra piano di posa e p.. iene onsiderato solo ome ario ( 1 xd). Il terreno sottostante è aratterizzato da oesione e da angolo di attrito φ. La omplessità del problema, insieme al numero di ariabili in gioo, ha permesso di definire il omportamento dei terreni solo relatiamente a asi semplii. L assunzione dell appliazione del prinipio di Sorapposizione degli effetti, ha uindi permesso la definizione della formula trinomia di Terzaghi per il alolo della apaità portante di un terreno. In ondizioni ordinarie non sarebbe appliabile tale prinipio però, dato he non 34

35 è definibile una relazione ompleta, ma solo parziale e isto he il risultato è autelatio, lo si ritiene un proedimento aettabile. Di primo ahito, si può indiiduare la dipendenza della apaità limite a tre fattori: uno relatio al ontributo delle forze di attrito, doute al peso proprio del terreno interno alla superfiie di sorrimento: N 1 D = N ; uno he esprime il on tributo della oesione lungo la superfiie di sorrimento: N ; uno he definise l effetto stabilizzante del soraario agente ai lati della fondazione (ad esempio douto all approfondimento del piano di fondazione rispetto al p..): N B. Il ario limite unitario assume dunue la forma: lim B = N 1 D + N + N 1 e sono le masse olumihe rispettiamente del terreno al di sopra ed al di sotto del piano di imposta della fondazione; D è la profondità del piano di imposta della fondazione dal p..; è la oesione del terreno al di sotto del piano di posa della fondazione; B è il lato minore della fondazione. I alori dei oeffiienti di ario limito o fattori di apaità portante N, N e N assumono le seguenti espressioni: ϕ π N = tan (45 + ) e N = ( N 1) ot gϕ N = ( N + 1) tanϕ tan ϕ Per omodità si riporta a seguire una tabella dei suddetti oeffiienti in funzione dell angolo di attrito φ del terreno sottostante la fondazione (Vesi 1975): 35

36 Generalizzazione di Brinh Hansen (1970) Le limitazioni imposte nell ipotesi iniziali di Terzaghi, possono essere rimosse appliando opportuni fattori orrettii he tengono onto di: - forma della fondazione: s; - inlinazione ed eentriità del ario: i; - inlinazione del piano di posa della fondazione: b; - inlinazione del piano ampagna: g; - profondità del piano di imposta: d. L espressione diiene uindi: g b i d s N g b i d s N g b i s N B + + = lim 1 A seguire si fornisono relazioni per poter determinare i singoli fattori orrettii: FATTORI DI FORMA Per estendere l euazione a fondazioni rettangolari B x L (giahé sono stati risolti solamente asi di fondazioni irolari o nastriformi), si appliano i seguenti fattori:

37 37 ϕ ϕ ϕ ϕ sen sen L B s s s sen sen L B s + + = = + + = INCLINAZIONE ED ECCENTRICITÀ DEL CARICO Seondo Vesi (1970) le espressioni empirihe dei fattori di inlinazione del ario, onsiderando la somposizione nelle omponenti orizzontale H e ertiale N, sono: L B L B m N i i i g L B N H i g L B N H i m m + + = = + = + = + 1 tan 1 ot 1 ot 1 1) ( ϕ ϕ ϕ Questi fattori erranno appliati alla erifia del ario ertiale. Per il ario orizzontale inee si imposterà una erifia a sorrimento doe ϕ tan lim + = N H. Per l eentriità e della risultante dei arihi si dee, seondo Meyerhof (1953), adottare un alore di B orrispondente all area effettia euialente, ale a dire la minima superfiie ridotta rispetto alla uale la risultante risulta entrata. Per fondazioni uadrate o rettangolari, B diiene: e B B R =

38 Va da se he se l eentriità è lungo la diagonale dell impronta di fondazione, la riduzione dorà farsi su ambo i lati B ed L. INCLINAZIONE PIANO DI POSA Questo aso è tipio di arihi trasmessi aenti rileante omponente orizzontale, ome ad esempio muri di sostegno. Nel aso in ui α sia l angolo rispetto all orizzontale di ui il piano di posa è inlinato: b b b = (1 α tanϕ) = b = b 1 b N tanϕ Questi oeffiienti engono appliati nella formula per erifiare il ario limite inteso normale al piano di posa (inlinato) INCLINAZIONE DEL PIANO CAMPAGNA Questo aso è tipio di fondazioni su pendii aentuati. Sia dunue ω l angolo rispetto all orizzontale di inlinazione del pendio: g g g = (1 tanω) = g = g 1 g N tanϕ Gli ultimi due oeffiienti orrettii sono alidi nella limitazione ε < π/4, ω < π/4 e ω < φ. PROFONDITÀ DEL PIANO DI POSA In ondizioni normali, il piano di posa è più basso rispetto al piano ampagna, ol duplie effetto di un ario stabilizzante al ontorno douto a 1 X D, oltre ad aere a disposizione anhe la resistenza a taglio mobilitabile lungo la parte di superfiie di 38

39 sorrimento tra piano di posa e piano ampagna, per l altezza D (in genere trasurata, onsiderando il terreno sopra il piano posa solo ome soraario). Se D D B d = 1+ tanϕ (1 senϕ) B 1 D Se D > B d = 1+ tanϕ (1 senϕ) tan ( ) B d = d 1 d N tanϕ Condizioni non drenate (terreni oesii) Nel aso di fondazioni su terreni oesii saturi, ad eezione dei terreni soraonsolidato on omportamento dilatante, le ondizioni ritihe nei onfronti della rottura si erifiano immediatamente dopo l appliazione del ario. In uesti asi si effettua l analisi in ondizioni non drenate, in termini di tensioni totali (essendo diffiile alutare nel tempo l andamento delle pressioni neutre), doe: = u (oesione non drenata) e φ=0. L euazione della apaità portante assume uindi la forma: lim = u N s d i b g + Doe è il soraario totale ai bordi della fondazione (= x D); N = + π = 5.14 s d d i b g = B L B = se D B L 1 B = tan ( ) se D>B L m H =1 doe B L N α = 1 π + ω = 1 π + u + B m = L 1 + B L 39

40 Da notare è he il aso di piano ampagna inlinato di ω rispetto all orizzontale, presuppone l aggiunta nell euazione del termine s B = L. 1 B N s doe N = senω e Una prima alutazione del alore di u (oesione non drenata) è fornita dalla seguente relazione di Koutsoftas e Ladd (1985): σ u 0 = ( 0. ± 0.03) OCR 0.8 Doe σ 0 è la tensione ertiale effiae preesistente al ario, ad una profondità di B/ al di sotto del piano di posa ed OCR è il rapporto di soraonsolidazione Considerazioni sull euazione di Brinh Hansen - il termine legato alla oesione è predominante per i terreni oesii; - il termine legato al ario è predominante nei terreni inoerenti; - per fondazioni on B<3-4 m il termine legato a B può essere trasurato; - il termine di profondità xn è predominante in terreni inoerenti. Anhe una piola profondità D produe un sensibile aumento di ult ; - i oeffiienti N resono rapidamente all aumentare di φ, la ui determinazione dee essere molto aurata; - in presenza di falda si dee usare il peso speifio effiae = ( tot w ) e uindi la apaità portante diminuise; - l euazione trinomia può essere impiegato per rotture loali in sabbie eseguendo una riduzione dell angolo di attrito del terreno (Terzaghi ϕ = artg (0.67 tanϕ) ; Vesi, per densità relatie minori di 0.67% ϕ [ ] ϕ = R artg D R 0.75 D tan ); - l angolo di attrito a orrelato ol rapporto L/B: se L/B il alore di φ è uello trassiale (φ tr ); se inee L/B> si adotta un angolo d attrito φ ps = 1.5 x φ tr 17 ; - Nei terreni aratterizzati da eleata ompressibilità (sabbie siolte e dense) la erifia relatia ai edimenti risulta già autelatia, rendendo pratiamente superflua la erifia della apaità portante; - Nessuno getterebbe una fondazione superfiiale su un terreno granulare; - Se una fondazione dee essere gettata su un terreno siolto (D R <0.5), preedentemente dorà essere ompattato aumentandone la densità; 40

41 - Quando si progetta la larghezza di una fondazione soggetta ad un dato ario è neessario usare un proedimento iteratio in uanto i fattori di forma, profondità ed inlinazione dipendono da B; - La formula di Terzaghi, ha alidità appliatia nel aso di fondazioni soggette a ario ertiale on profondità relatie limitate (D/B 1) Punzonamento Questo meanismo rihiede una ariazione di olume del terreno in ondizioni drenate (è uindi tipio di sabbie poo addensate e argille poo onsistenti). Per lo studio di uesto meanismo Vesi ha impiegato un metodo approssimato, assimilando il terreno ad un mezzo elastio-perfettamente plastio, doe il fenomeno è retto da un indie di rigidezza I r : I r G = + σ tgϕ Doe s è la tensione normale media, posta pari alla tensione effettia litostatia alla profondità z=d+b/ (D profondità piano fondazione da p.. e B lato della fondazione). G è il modulo di elastiità trasersale del terreno he, per un mezzo elastio è: E G = (1 + ν ) Con E Modulo di Young e ν Modulo di Poisson. In ondizioni non drenate (in termini totali) ν = 0.5, uindi G = E u /3 (on E u modulo non drenato) mentre in ondizioni drenate (in termini effettii) il alore di G disende dai dati a disposizione. L espressione del ario limite uindi riala uella della formula trinomia, però on ulteriori oeffiienti orrettii (ψ, ψ e ψ ), detti di punzonamento (dipendenti da φ, I r e B/L): lim B = ψ N 1 D + ψ N + ψ N La rottura per punzonamento si erifia uando i oeffiienti di punzonamento sono inferiori all unità, ioè uando l indie di rigidezza I r risulta inferiore ad un alor ritio definito ome segue: 41

42 I r, rit 1 B π ϕ = exp ( ) tg( ) L 4 La tabella a fiano dell espressione, riporta i alori dell indie di rigidezza ritio nei asi in ui B/L=0 (fondazione nastriforme) e B/L=1 (fondazione uadrata), per ari angoli di attrito. A seguire si riportano poi le espressioni dei oeffiienti di punzonamento, nonhé i loro alori diagrammati nei asi in ui B/L=0 (fondazione nastriforme) e B/L=1 (fondazione uadrata): tipo terreno Terreno on attrito e oesione Puramente oesio ψ ψ B 3.07senϕ lg(i r ) exp ( ) tgϕ + 1 L 1+ senϕ ψ ψ 1 N tgϕ B lg I L r ψ ψ 1 8. Fattore di siurezza F s Il fattore di siurezza è un parametro he permette di alutare le ondizioni di laori di una erta opera o struttura in relazione alle ondizioni ritihe he si possono erifiare. Esprime dunue il margine on ui una erta opera può laorare, soggetta a dati 4

43 arihi, rispetto a ondizioni ritihe. È dato dal rapporto fra azioni resistenti ed azioni agenti; dee uindi essere sempre maggiore di 1. In ondizioni ordinarie, per ondizioni limite di rottura il fattore di siurezza è espresso ome rapporto di forze o tensioni, mentre, per ondizioni limite di eserizio il rapporto è fra deformazioni. Nel aso di rottura del terreno, il fattore di siurezza adottato dee essere appliato al ario limite per definire il alore ammissibile amm da porre a onfronto on i arihi trasmessi dalla sorastruttura. I fattori di siurezza generalmente aettati sono riportati nella tabella a seguire. Con maggiore rigore si dorebbe appliare il fattore di siurezza alla sola parte eedente al ario 0 preesistente alla uota del piano di posa della fondazione, ioè: = 0. F lim 0 amm + s 8.3 Esempi appliatii Si riportano aluni asi di appliazione della formula trinomia in dierse ondizioni, Esempio 1 Il terreno sia sabbioso on φ=35, =0 e =0 kn/m 3. 43

44 Determinare le dimensioni minime di un plinto uadrato he erifia un fattore di siurezza pari a 3 nei onfronti della rottura del terreno di fondazione, nel aso in ui uesta sia soggetta ad un ario di 300 tonnellate. 44

45 8.3. Esempio Sia data una fondazione nastriforme aente B=3 m he trasmette al terreno un ario ertiale entrato N di 1800 kn. Ai fianhi della fondazione sia presente un soraario distribuito pari a 0 kpa. Il terreno sia sabbioso on φ=36, =0 e =0 kn/m 3. Determinare il ario limite ed il fattore di siurezza per la data fondazione. 45

46 8.3.3 Esempio 3 Il terreno presenta le medesime aratteristihe dell esempio 1. Ai arihi trasmessi dalla fondazione si aggiunge un momento M=540 knm/m. La fondazione è anora nastriforme. Il terreno ha un fronte di sao, ome si trattasse della fondazione di un muro di sostegno. 46

47 47

48 8.3.4 Esempio 4 Sia data una fondazione rettangolare B= m e L=3 m su ui agise un ario entrato e ertiale N pari a 1000 kn, oltre ad un soraario ai lati della fondazione pari a 0 kpa. Il terreno sia sabbioso on φ=36, =0 e =0 kn/m 3. Determinare il ario limite ed il fattore di siurezza per la data fondazione. 48

49 8.3.5 Esempio 5 All esempio 4 si aggiungano ome arihi esterni una omponente orizzontale H x =150 kn ed un momento M x =300 knm. Determinare il ario limite ed il fattore di siurezza per la data fondazione e erifiarne la stabilità a slittamento. 49

50 8.3.6 Esempio 6 In figura è riportato lo shema di una fondazione rettangolare posta a m di profondità rispetto al piano ampagna. Il terreno è ostituito da sabbia aente φ =33 e = 0 kn/m 3. Determinare la apaità portante della fondazione e erifiarne la stabilità. L euazione trinomia perde il termine relatio alla oesione, troandoi nel aso di un terreno inoerente. N 5000 σ = = = 1000kN / m = s A,5 N = 35,19 N F S = 6,09 I 1 + sen s I sen = 1 + 0,1 1 1 I I lim = N B s + = 731,157 kn / m = lim S = B = 1,4 = s L N s = 731,157 =,731 >,5 VERIFICATO ,19,5 1, ,09 1,4 = 149, ,91 = 50

51 8.3.7 Esempio 7 Considerando la medesima fondazione dell esempio preedente: determinarne la apaità portante e erifiarne la stabilità sapendo he, oltre al ario N agise un momento M xx =1000 knm. Al aso preedente si deono appliare i oeffiienti riduttii della geometria della fondazione per effetto del momento. B e = s N N F R S S lim = B M N I 1+ sen = s I sen = 1+ 0,1 1 = 35,19 = N A I = = 6, = = 1190,5 kn / m,1 1 I = N lim = = S = B e =,5 0,4 =,1 m = 0, m B s 417, 1190,5 + I N s B L = = 1, ,19,1 1, ,09 1,356 = 417, kn / m =,03 <,5 NON VERIFICATO 51

52 9. Appendie I La formula trinomia Formula trinomia di Terzaghi: lim B = N 1 D + N + N 1 e sono le masse olumihe rispettiamente del terreno al di sopra ed al di sotto del piano di imposta della fondazione; D è la profondità del piano di imposta della fondazione dal p..; è la oesione del terreno al di sotto del piano di posa della fondazione; B è il lato minore della fondazione. I alori dei oeffiienti di ario limito o fattori di apaità portante N, N e N sono: ϕ π N = tan (45 + ) e N = ( N 1) ot gϕ N = ( N + 1) tanϕ tan ϕ Tabella dei oeffiienti in funzione dell angolo di attrito φ del terreno (Vesi 1975): Generalizzazione di Brinh Hansen (1970) forma della fondazione: s; inlinazione ed eentriità del ario: i; inlinazione del piano di posa della fondazione: b; inlinazione del piano ampagna: g; profondità del piano di imposta: d. lim 1 = B N s i b g + N s d i b g N s d i b g FATTORI DI FORMA Per estendere l euazione a fondazioni rettangolari B x L: s s s = = s B L 1+ senϕ 1 senϕ B 1+ senϕ = L 1 senϕ INCLINAZIONE ED ECCENTRICITÀ DEL CARICO ( m+ 1) i H = 1 N B L g + ot ϕ H i = 1 N B L g + ot ϕ 1 i i = i N tanϕ + B m = L 1+ B L m PROFONDITÀ DEL PIANO DI POSA Se D D B d = 1+ tanϕ (1 senϕ) B Se D > B 1 D d = 1+ tanϕ (1 senϕ) tan ( ) B 1 d d = d N tanϕ 5

53 INCLINAZIONE DEL PIANO CAMPAGNA Sia dunue ω l angolo rispetto all orizzontale di inlinazione del pendio: g = (1 tanω) g g = g = g 1 g N tanϕ INCLINAZIONE PIANO DI POSA Nel aso in ui α sia l angolo rispetto all orizzontale di ui il piano di posa è inlinato: b = (1 α tanϕ) b b = b = b 1 b N tanϕ 53

54 10. Appendie II Altre espressioni dei oeffiienti della formula trinomia 54