COGNOME e NOME: FIRMA: MATRICOLA:
|
|
|
- Agnella Evangelina Cara
- 8 anni fa
- Visualizzazioni
Transcript
1 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale log x x x + ) è l insieme a) ], + [ b) ], + [ \ } c) [, + [ \ } d) [, [ ], + [. ) Il derivato D E dell insieme E = a), 5} b) 5} c), 5} d) 0, 5 }. ) n n +n n + ) n n+ : n N+ } ], + [ è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione f f x) ) è uguale a [f a) f x) ) f x) + f f x) )] [f x)] + f f x) ) } fx)f x) b) f f x) ) f x) + f f x) ) f x) } [f c) f x) ) fx) + f f x) )] fx) [f x)] + f f x) ) } fx)f x) d) f f x) ) fx) [f x)] + f f x) ) [ [f x)] + f f x) ) ]} f x). 4) Il massimo assoluto della funzione ) x x+ 5x nell intervallo ], ] a) non esiste b) è un numero maggiore di c) è uguale a ) 5 d) viene preso in un punto dell intervallo [, 0]. 5) Il limite lim x + a) è uguale a b) è uguale a + c) è uguale a 5 d) è uguale a 5. + sen sen x)) 5 arctg x x +
2 6) Data la serie ) x n + n x+, x R, è vero che a) la *) diverge a + per ogni x 0 b) la *) diverge a + solo se x > c) la *) converge se x ]0, ] d) la *) diverge a per ogni x < 0. 7) Sia f : R R una funzione limitata. L affermazione: sup x ],0[ fx) < sup x ]0,+ [ fx) equivale all affermazione [ ] a) β R : x ], 0[ : fx) < β e x ]0, + [ : fx) > β [ ] b) β R : fx) < β x ], 0[ e x ]0, + [ : fx) > β c) β R : [ fx) < β x ], 0[ e fx) > β x ]0, + [ ] d) β, γ R : [ β < γ, fx) < β x ], 0[ e fx) > γ x ]0, + [ ]. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? a) f è convessa nell intervallo ], π [ b) f ha minimo assoluto e x x se x 0 cos x se x > 0. c) nel punto x 0 = 0 esiste la derivata terza f 0) d) il grafico di f ha un asintoto obliquo. 9) L integrale [ a) 0 x x dx è uguale a 5x + 6 ) ] 4 log x 5x log x x [ + b) [ log x 5x log x log x ] log x 5x + 6 log x x c) F ) F ) + F 0), essendo F x) = log x 5x log d) F ) F 0), essendo F x) = log x 5x log x x ) 4. ) 4 ] 0 [ log x 5x log x log x ] 0 4 x x ) 0) Sia a n } una successione limitata inferiormente. La condizione La successione a n } è crescente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia convergente. ) L integrale indefinito x sen 7x dx è uguale a a) x4 x 4 sen 7x 7 cos 7x + c b) 7x [x cos 7x sen 7x] + 4 x cos 7x dx + c [ x cos 7x 7 sen 7x] 6 49 c) x 7 x sen 7x dx + c d) 7 4 x4 cos 7x x sen 7x x cos 7x dx + c.
3 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito B) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale a) ], 5] b) ]5, + [ c) [5, + [ d) ] +, + [ \ 5}. ) Il derivato D E dell insieme E = a), 5} b) 5} c), 5} d),, 5}. log x 5 x 6x + 6) è l insieme ) n n +n n + ) n n+ : n N+ } ], + [ è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione f fx)) è uguale a [ ]} a) [f fx))] f x) + f fx)) f fx)) [f x)] + f fx)) f x) } b) [f fx))] [f x)] + f fx)) [f fx)) f x) + f fx)) f x)] [ ] } c) [f fx))] + f fx)) f fx)) [f x)] + f fx)) f fx)) f x) } d) f fx)) [f x)] + f fx)) f x). 4) Il massimo assoluto della funzione ) x x+ 5x nell intervallo [ 6, ] a) viene preso nel punto 5 b) viene preso nel punto c) è un numero minore di d) è uguale a. + sen sen )) 5 x 5) Il limite lim x + arctg x x + a) è uguale a 0 b) è uguale a + c) è uguale a 5 d) è uguale a 5.
4 6) Data la serie ) x n + n x+ a) la *) converge se x ], [ b) la *) non è regolare per x =, x [, ], è vero che c) la *) diverge se e solo se x ], 0] d) la *) diverge se e solo se x [, 0]. 7) Sia f : R R una funzione limitata. L affermazione: inf x ],0[ fx) > inf x ]0,+ [ fx) equivale all affermazione [ ] a) β R : fx) β x ], 0[ e x ]0, + [ : fx) < β [ ] b) β R : x ], 0[ : fx) > β e x ]0, + [ : fx) < β [ ] c) β R : fx) > β x ], 0[ e x ]0, + [ : fx) = β d) β, γ R : [ β > γ, fx) β x ], 0[ e fx) γ x ]0, + [ ]. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? a) f è convessa solo nell intervallo ], π [ b) f ha un unico zero nell intervallo], 0[ c) f è uniformemente continua in ]0, π] e x x se x 0 cos x se x > 0. d) esiste la retta tangente al grafico di f nel punto 0, ). 9) L integrale [ a) 0 x x dx è uguale a 5x + 6 ) ] log x 5x log x x [ ) ] b) log x 5x log x x [ + [ log x 5x + 6 log x x log x 5x log x x c) F ) + F ) F 0), essendo F x) = log x 5x log d) F ) F 0), essendo F x) = log x 5x log x x ). ) ] 0 ) ] 0 x x ) 0) Sia a n } una successione limitata superiormente. La condizione La successione a n } è crescente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia convergente. ) L integrale indefinito x sen 9x dx è uguale a a) x4 x 4 sen 9x 9 b) x 9 c) x 9 cos 9x + 7 cos 9x + 7 d) x4 4 sen 9x x 4 6 cos 9x dx + c. cos 9x + c [ x sen 9x ] 9 x sen 9x dx + c [ x sen 9x x sen 9x dx ] + c
5 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito C) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale a) [, + [ b) ], + [ \ } c) [, + [ \ } d) ], ] [, + [. ) Il derivato D E dell insieme E = a), } b) } c), 5} d),, 5}. log x+ x x + ) è l insieme ) n n +n n + ) n n+ : n N+ } ], [ è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione f fx ) ) è uguale a a) x [f fx )) [ f x ) ] + f fx ) ) ] f x ) + f fx ) ) } f x ) b) x f fx )) [ f x ) ] + f fx ) ) [ xf x ) + f x ) ]} [ c) x f fx )) [ f x ) ] + f fx ) ) ] f x ) + f fx ) ) } f x ) [ d) x f fx )) [ f x ) ] + f fx ) ) ] f x ) + f fx ) ) } f x ). 4) Il massimo assoluto della funzione ) x x+ 5x nell intervallo ] 6, ] a) viene preso nel punto 5 b) viene preso nel punto c) è uguale a d) non esiste. 5) Il limite lim x + a) è uguale a b) è uguale a + c) è uguale a 5 d) è uguale a 5. + sen sen x)) 5 arctg x x +
6 6) Data la serie ) x n + n x+ a) la *) diverge se x, x 0, è vero che b) la *) diverge se x 0} ], + [ c) la *) converge solo se x ]0, [ d) la *) converge solo se x [0, [. 7) Siano f, g : R R due funzioni limitate. L affermazione: sup x R fx) < sup x R gx) equivale all affermazione a) β R : x R : fx) < β < gx) ] [ ] b) β R : x R : fx) < β e x R : gx) > β [ ] c) β R : fx) β x R e x R : gx) > β d) β, γ R : [ β < γ, x R : fx) < β e gx) > γ x R ]. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? a) f è integrabile secondo Riemann in [, π] e x x se x 0 cos x se x > 0. b) f ha massimo assoluto nell intervallo ], + [ c) esiste la derivata seconda f 0) d) esiste a < 0 tale che f [a,π] è iniettiva. 9) L integrale [ a) 0 x x dx è uguale a 9x + 0 ) ] 8 log x 9x log x 5 x 4 [ b) [ log x 9x log x 5 7 log x 4 ] log x 9x log x 5 x 4 c) F ) F ) + F 0), essendo F x) = log x 9x + 0 log d) F ) F 0), essendo F x) = log x 9x log x 5 x 4) 8. ) 8 ] 0 [ log x 9x log x 5 7 log x 4 ] 0 8 x 5 x 4) 0) Sia a n } una successione limitata inferiormente. La condizione La successione a n } è strettamente crescente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia convergente. ) L integrale indefinito x sen 9x dx è uguale a a) x sen 9x x4 cos 9x x 7 sen 9x dx + c [ ] b) x 9 x cos 9x + sen 9x + 7 x sen 9x dx + c [ c) x 9 cos 9x + 7 x sen 9x x sen 9x dx ] + c d) x4 cos 9x 4 sen 9x x 9.
7 Tutti i quesiti dei compiti D, E e F del 6 febbraio 05 si trovano in uno dei compiti A, B e C
8 Anno Accademico Corsi di Analisi Matematica I A.Villani, R. Cirmi e F.Faraci) Prova d Esame del giorno 6 febbraio 05 Seconda prova scritta - COMPITO A Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Si possono consegnare al massimo due fogli a quadri in bella copia in entrambi devono essere apposti nome e cognome a stampatello e la firma del candidato. Alla fine della prova il presente foglio deve essere riconsegnato debitamente compilato. Rispondere ai seguenti quesiti. Il requisito minimo per superare la prova, con la conferma del voto della prima prova scritta quale voto finale dell esame, è di rispondere in maniera corretta ad un quesito di tipo D e ad uno di tipo T. Le ulteriori risposte corrette, se valutate positivamente, comportano un incremento del voto finale dell esame fino ad un massimo di quattro punti. Tempo disponibile: 90 minuti. Quesiti di tipo D definizioni ) ) Sia f : A R A R, A ). Un punto x 0 A si dice di punto di minimo relativo o locale per la funzione f se... completare la definizione). ) Sia a n } una successione di numeri reali. Si dice che la serie + diverge negativamente se... completare la definizione). ) Sia f : A R A R, A ) Si dice che f è dotata di primitive in A se... completare la definizione). a n Quesiti di tipo T teoremi ) ) Dimostrare che ogni successione convergente é limitata. É vero il viceversa? Giustificare la risposta. ) Enunciare e dimostrare il teorema di derivazione della funzione composta. ) Dimostrare la formula fondamentale del calcolo degli integrali definiti. Quesiti di tipo E esercizi ) ) Studiare la funzione e tracciarne il grafico. fx) = x + ) log x ) Calcolare e x + e x + e x dx. + 8 ) Studiare, al variare del parametro reale x > 0, il carattere della serie + x n n n.
9 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 0 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale x +9x 4 + log 4 x x + 9x 4) è l insieme a) ], ] [5, + [ b) ], 5[ ], + [ ] [ c) ], 5] 9+ 4, d) ], 5] [, [. ) Il derivato D E dell insieme E = a) } b), } c),, } d), }. } ) n n n +n+ : n N+ ], [ è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione f e fx)) è uguale a a) f e fx)) [ e fx) f x) ] + f e fx)) ] e [[f fx) x)] + f x) b) e fx) [f x)] [ f e fx)) + f e fx))] + f e fx)) e fx) f x) c) f e fx)) e fx) f x) [ d) e fx) f x) f e fx)) + [f x)] ] + f e fx)) e f x) f x). 4) In quali dei seguenti intervalli la funzione )x 4 6x +8x+ ha massimo assoluto: a) ) e ) b) ), ) e ) c) ), ) e 4) d) ), ) e 4). 5) Il limite lim x + a) è uguale a b) è uguale a + c) è uguale a 5 d) è uguale a 5. ) ], 0] ) ], 0] ) [, 0[ 4) ], 0]? + sen sen x)) 5 log x+ x
10 6) Data la serie ) x n + n x+, x R, è vero che a) la *) diverge a + per ogni x < 0 b) la *) converge se x [, ] c) la *) converge se x ], ] d) la *) non è regolare se x <. A 7) Sia f : R R una funzione limitata. L affermazione: sup x ],0] fx) < sup x [0,+ [ fx) equivale all affermazione a) fx) < f0) x ], 0[ e x ]0, + [ : fx) > f0) [ ] b) β R : fx) < β x ], 0] e x [0, + [ : fx) β c) β R : [ fx) < β x ], 0] e fx) > β x [0, + [ ] [ ] d) β, γ R : β < γ, fx) < β x ], 0] e x [0, + [ : fx) γ. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? a) f è convessa nell intervallo ] π, +, [ b) f ha minimo assoluto cos x se x 0 e x x se x > 0. c) nel punto x 0 = 0 esiste la derivata terza f 0) d) il grafico di f non ha asintoti. 9) L integrale a) 0 x x dx è uguale a x + 6 [ ] logx x + 6) + arctg x [ logx 5x + 6) + arctg x b) log 4 c) F ) + F ) F 0), essendo F x) = logx x + 6) d) F ) F 0), essendo F x) = logx x + 6). ] 0 0) Sia f : R R una funzione derivabile in R. La condizione f x) > 0 x R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia strettamente crescente in R. ) L integrale indefinito e 4x [ a) tt 5) t +t 5 ]t= dt e x +5 [ ] z b) 4 z + dz z +5 z=e [ x c) t t 5) t +t 5 ]t= dt e x +5 [ ] d) z 4 z+ z+5 dz e x + e x +5 z=e x. dx è uguale a
11 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 0 febbraio 05 Prima prova scritta compito B) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale a) ], 5 ] ] [ + 7 4, 5 b) ], 5 ] [, 5 [ c) ], 5 [ ], 5 [ d) ], ] ] 5, + [. ) Il derivato D E dell insieme E = a), } b),, } c), } d) }. 5 x + x 9 + log 6 x x + x 9) } ) n n n +n+ : n N+ ], + [ è l insieme è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione e ffx)) è uguale a a) e ffx)) f fx))f x) b) e [f [ ] } ffx)) x)] [f fx)] + f fx)) + f fx))f x) [ ] } c) e f ffx)) x) [f fx)] + f x)f fx)) + f fx))f x) } d) e [f ffx)) x)] [f fx) + f fx))] + f fx))f fx)). 4) In quali dei seguenti intervalli la funzione )x 4 6x +8x+ ha minimo assoluto: a) ) e 4) b) solo 4) c) ) e 4) d) ), ) e 4). 5) Il limite lim x + a) è uguale a 0 b) è uguale a c) è uguale a 5 d) è uguale a +. ) ], 0] ) ], 0] ) [, 0[ 4) [, 0]? )) 5 + sen sen log x x log x x+log x
12 6) Data la serie ) x n + n x+, x ], ], è vero che a) esistono valori di x per cui la *) non è regolare b) la *) converge se e solo se x [0, ] c) la *) converge se e solo se x ], ] d) la *) converge se e solo se x [, ]. B 7) Sia f : R R una funzione limitata. L affermazione: inf x ],0] fx) > inf x [0,+ [ fx) equivale all affermazione [ ] a) β R : fx) > β x ], 0] e x [0, + [ : fx) β [ ] b) β R : fx) β x ], 0] e x [0, + [ : fx) < f0) c) β, γ R : β > γ, fx) β x ], 0] e fx) γ x [0, + [ ] [ ] d) β, γ R : β > γ, fx) β x ], 0] e x [0, + [ : fx) γ. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? a) f è convessa solo nell intervallo ] π, +, [ b) f ha un unico zero nell intervallo [0, + [ cos x se x 0 e x x se x > 0. c) esiste la retta tangente al grafico di f nel punto 0, ) d) f è uniformemente continua nell intervallo ] π, π[. 9) L integrale a) log 48 b) log 7 log ) c) F ) F 5 0 x 5 x dx è uguale a 5x ) + F 0), essendo F x) = logx 5x + 9) + arctg x 5 d) F ) F 0), essendo F x) = logx 5x + 9). 0) Sia f : R R una funzione derivabile in R. La condizione f x) 0 x R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia crescente in R. ) L integrale indefinito e 4x [ a) t 5 t 5) +t ]t= dt e x +5 [ ] b) z z + z+5 dz z=e [ x c) t t 5) 4 t 5) +t ]t= dt e x +5 [ ] z d) z + z+5 dz z=e x. e 4x + e x +5 dx è uguale a
13 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 0 febbraio 05 Prima prova scritta compito C) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale a) ], [ ]5, + [ b) ], 5] [, + [ c) ], ] [5, + [ ] d), 9 4 [ [5, + [. ) Il derivato D E dell insieme E = a) } b), } c),, } d), }. x 9x 4 + log x+5 x 9x 4) } ) n n n +n+ : n N+ ], + [ è l insieme è l insieme ) Sia f : R R una funzione derivabile due volte. La derivata seconda della funzione ffe x )) è uguale a } a) e f x fe x )) [f e x )] + f fe x ))f e x ) + f fe x ))f e x ) b) e x f e x ) f fe x ))f e x ) e x + f fe x ))} + f fe x ))f e x ) e x } c) e f x fe x )) [f e x )] + f fe x ))f e x ) e x + f fe x ))f e x ) d) f fe x ))f e x ) e x. 4) In quali dei seguenti intervalli la funzione )x 4 6x +8x+ ha massimo assoluto: a) ) e ) b) ), ) e ) c) ) e ) d) ), ) e 4). 5) Il limite lim x + a) è uguale a 0 b) è uguale a + c) è uguale a 5 d) è uguale a 5. ) ], 5[ ) ], 0[ ) [, 0[ 4) [, 0[? + sen sen x ) ) 5 arctg x x
14 6) Data la serie ) x n + n x+ a) la *) non è regolare per x = b) la *) diverge a + se x, x R, è vero che c) la *) diverge a + se x ], ] ], + [ d) la *) converge per ogni x [, ]. C 7) Siano f, g : R R due funzioni limitate. L affermazione: inf x R fx) > inf x R gx) equivale all affermazione [ ] a) β R : fx) > β x R e x [0, + [ : gx) < β [ ] b) β R : fx) β x R e x R : gx) β c) β, γ R : β > γ, fx) β x R e gx) γ x R ] [ ] d) β, γ R : β > γ, fx) β x R e x R : gx) γ. 8) Sia f : R R definita come segue: fx) = Quali delle seguenti affermazioni è falsa? cos x se x 0 e x x se x > 0. a) esiste a < 0 tale che la restrizione f [a,+ [ è iniettiva b) f ha un unico zero nell intervallo [0, + [ c) f è derivabile due volte in tutto R d) f è integrabile secondo Riemann in [ π, ]. 9) L integrale a) 0 x x dx è uguale a x + 5 [ logx x + 5) + arctg x ] [ logx x + 5) + arctg x b) log ) 4 c) log ) 4 + arctg 5 d) F ) F ) + F 0), essendo F x) = logx x + 5). ] 0 0) Sia f : R R una funzione continua in R. La condizione La funzione f è derivabile in R e risulta f x) 0 x R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia crescente in R. ) L integrale indefinito e 5x [ a) tt 5) 4 t 5) +t ]t= dt e x +5 [ ] b) z 4 5 z + z+5 dz z=e [ x c) t 5) 5 t 5) +t ]t= dt e x +5 [ ] d) z dz z+ z+5 e x + e x +5 z=e x. dx è uguale a
15 Tutti i quesiti dei compiti D, E e F del 0 febbraio 05 si trovano in uno dei compiti A, B e C
16 Anno Accademico Corsi di Analisi Matematica I A.Villani, R. Cirmi e F.Faraci) Prova d Esame del giorno 0 febbraio 05 Seconda prova scritta - COMPITO A Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Si possono consegnare al massimo due fogli a quadri in bella copia in entrambi devono essere apposti nome e cognome a stampatello e la firma del candidato. Alla fine della prova il presente foglio deve essere riconsegnato debitamente compilato. Rispondere ai seguenti quesiti. Il requisito minimo per superare la prova, con la conferma del voto della prima prova scritta quale voto finale dell esame, è di rispondere in maniera corretta ad un quesito di tipo D e ad uno di tipo T. Le ulteriori risposte corrette, se valutate positivamente, comportano un incremento del voto finale dell esame fino ad un massimo di quattro punti. Tempo disponibile: 90 minuti. Quesiti di tipo D definizioni ) ) Sia f : A R A R, A ). Si dice che f non è limitata inferiormente in A se... completare la definizione). ) Sia a n } una successione di numeri reali. Si dice che a n } converge a se... completare la definizione). ) Siano f : a, b) R e x 0 a, b) Si dice che f A R, A ) Si dice che f è derivabile in x 0 se... completare la definizione) e si chiama derivata di f in x 0... completare la definizione). Quesiti di tipo T teoremi ) ) Enunciare e dimostrare il criterio del confronto per le serie numeriche. ) Enunciare e dimostrare il corollario al Teorema di Lagrange sulle funzioni costanti in un intervallo. ) Enunciare e dimostrare il teorema sull integrabilità secondo Riemann delle funzioni continue. Quesiti di tipo E esercizi ) ) Studiare la funzione e tracciarne il grafico. fx) = x + x e x ) Determinare F x) primitiva in ], + [ della funzione fx) = log x ) x + ) e tale che F ) = 0. ) Studiare, al variare del parametro reale x, il carattere della serie + n n + ) x n. n
17 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 marzo 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale 4 log 4 x x + 9x ) log 4 x ] [ a)], 5] 9+ 4, b) ], 5[ ], + [ c) ], ] [5, + [ d) ], 5] [, [. ) Il derivato D E dell insieme E = a) [, ] ) b) ], [ \ R \ Q) ], ] c) E, } d) ], [ ], ]. ) La derivata della funzione arcsen x è uguale a: x x a) x x + ) 4 x b) c) d) +x x 4 x x +x x 4 x +x x 4 x 4 x + x ) x x 4 x + x ) x +x x 4 x 4 x + x ). ) ], [ \ R \ Q) ], ] } è l insieme 4) La restrizione della funzione 4x 6x 9x + all insieme [0, ] Q a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. 5) Il limite lim x a) è uguale a b) è uguale a 5 c) è uguale a 0 d) è uguale a +. + tg tg x x)) 5 5x è l insieme
18 6) La serie a) converge e la sua somma è un numero minore di zero b) converge e la sua somma è un numero maggiore di 9 c) non è regolare d) non verifica nessuna delle precedenti condizioni. A 7) Sia f : R R una funzione limitata. L affermazione: sup x ],0] fx) > sup x [0,+ [ fx) equivale all affermazione a) a n } n N, b n } n N : a n 0 n N, b n 0 n N e lim n fa n ) > lim n fb n ) b) a n } n N, b n } n N : a n 0 n N, b n 0 n N e lim n fa n ) > sup n N fb n ) c) β R, a n } n N : a n 0 n N e lim n fa n ) β > fb) b 0 d) β R, a n } n N : a n 0 n N e lim n fa n ) > β fb) b 0. 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = a) f è convessa nell intervallo ], +, [ b) f ha minimo assoluto x e se x < 0 x +x se x 0. c) nel punto x 0 = 0 esiste la derivata seconda f 0) d) il grafico di f ha un asintoto orizzontale. 9) L integrale π π 6 a) + 5 b) 5 c) + 5 d) 5. sen x +cos x) dx è uguale a 0) Sia f : R R. La condizione lim x 0 f x) f0) x = l R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia derivabile nel punto x 0 = 0. ) Data la funzione f : R R definita ponendo fx) = è vera? a) l integrale π π fx) d x è uguale a zero cos x se x 0 sen x se x > 0 b) una primitiva di f in R è la funzione G così definita: Gx) = c) la funzione f non ha primitive in R d) una primitiva di f in R è la funzione H così definita: Hx) =, quali delle seguenti affermazioni sen x x se x 0 cos x x se x > 0 sen x x se x 0 cos x x se x > 0.
19 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 marzo 05 Prima prova scritta compito B) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale 6 log 6 x x + x 7) log 6 x a) ], 5 ] [, 5 [ b) ], 5 [ ], 5 [ c) ], 5 ] ] + 7 4, 5 d) ], ] ] 5, + [. [ ) Il derivato D E dell insieme E = a) ], [ ], ] b) [, ] c) E, } d) ], ] \, }. ) La derivata della funzione arccos x è uguale a: x a) x x 4 x + ) x 4 x b) +x x 4 c) x +x x 4 d) x +x x 4 x x x + ) 4 x x x 4 x + ) x x x 4 x + ) x. ) ) ], [ \ R \ Q) ], ] \ Q è l insieme 4) La restrizione della funzione 4x 6x 9x + all insieme [, ] R \ Q) a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. + arctg arctg 7 5) Il limite lim x ) x + tg x + a) è uguale a + b) è uguale a 0 c) è uguale a d) è uguale a 7. è l insieme
20 6) La serie a) converge assolutamente b) converge, ma non converge assolutamente c) non è regolare d) non verifica nessuna delle precedenti condizioni. B 7) Sia f : R R una funzione limitata. L affermazione: inf x ],0] fx) < inf x [0,+ [ fx) equivale all affermazione a) a n } n N, b n } n N : a n 0 n N, b n 0 n N e lim n fa n ) < inf n N fb n ) b) a n } n N, b n } n N : a n 0 n N, b n 0 n N e lim n fa n ) < lim n fb n ) c) β R, a n } n N : a n 0 n N e lim n fa n ) < β fb) b 0 d) β R, a n } n N : a n 0 n N e lim n fa n ) β < fb) b 0. 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = a) f è convessa solo nell intervallo [0, +, [ b) f ha un unico zero in R x e se x < 0 x +x se x 0. c) esiste la retta tangente al grafico di f nel punto 0, 0) d) f è uniformemente continua in ] e, e [. 9) L integrale π π 6 a) 6 b) 6 + c) 6 + d). sen x cos x) dx è uguale a fx ) f0) 0) Sia f : R R. La condizione lim x 0 x = l R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia derivabile nel punto x 0 = 0. ) Data la funzione f : R R definita ponendo fx) = è vera? cos x se x 0 sen x se x > 0 a) l integrale π π fx) d x è uguale a un numero minore di 7 b) una primitiva di f in R è la funzione G così definita: Gx) = c) la funzione f non ha primitive in R d) una primitiva di f in R è la funzione H così definita: Hx) =, quali delle seguenti affermazioni sen x x + se x 0 cos x x se x > 0 sen x x se x 0 cos x x se x > 0.
21 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 marzo 05 Prima prova scritta compito C) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale 8 log x+5 x 9x ) log x+5 a) ], 5] [, + [ b) ], [ ]5, + [ ] c), 9 4 [ [5, + [ d) ], ] [5, + [. ) Il derivato D E dell insieme E = ], [ ], ] \ Q) è l insieme a) ], [ b) [, ] c) E, } d) ], [ ], ]. ) La derivata della funzione arctg x + è uguale a: x a) x x +x + b) x x +x + c) x x +x + x x + x ) x ) x + x ) x x x + x d) x +x + x x + ) + x. 4) La restrizione della funzione 4x 6x 9x + all insieme [, ] Q a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. + arcsen arcsen x x) 5) Il limite lim x + sen x a) è uguale a + b) è uguale a 0 c) è uguale a d) è uguale a. è l insieme
22 6) La serie a) converge assolutamente b) converge, ma non converge assolutamente c) non è regolare d) non verifica nessuna delle precedenti condizioni. C 7) Siano f, g : R R due funzioni limitate. L affermazione: sup x R fx) > sup x R gx) equivale all affermazione a) a n } n N, b n } n N : lim n fa n ) > lim n gb n ) b) a n } n N, b n } n N : lim n fa n ) > sup n N gb n ) c) β R, a n } n N : lim n fa n ) β > gb) b R d) β R, a n } n N : lim n fa n ) > β gb) b R. 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = x e se x < 0 x +x se x 0. a) esiste a < 0 tale che la restrizione f ],a] è iniettiva b) il grafico di f non ha asintoti obliqui c) f è derivabile in tutto R d) f è integrabile secondo Riemann in [ e, ]. 9) L integrale π π 4 a) + b) c) d) 4 6. cos x sen x) dx è uguale a fx ) f0) 0) Sia f : R R. La condizione lim x 0 x = l R a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la funzione f sia derivabile nel punto x 0 = 0. ) Data la funzione f : R R definita ponendo fx) = è vera? cos x se x 0 sen x + x se x > 0 a) l integrale π π π fx) d x è uguale a un numero maggiore di b) una primitiva di f in R è la funzione G così definita: Gx) = c) la funzione f non ha primitive in R d) una primitiva di f in R è la funzione H così definita: Hx) =, quali delle seguenti affermazioni sen x x + se x 0 cos x + x + se x > 0 sen x x se x 0 cos x + x se x > 0.
23 Tutti i quesiti dei compiti D, E e F del 6 marzo 05 si trovano in uno dei compiti A, B e C
24 Anno Accademico Corsi di Analisi Matematica I A.Villani, R. Cirmi e F.Faraci) Prova d Esame del giorno 6 marzo 05 Seconda prova scritta Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Si possono consegnare al massimo due fogli a quadri in bella copia in entrambi devono essere apposti nome e cognome a stampatello e la firma del candidato. Alla fine della prova il presente foglio deve essere riconsegnato debitamente compilato. Rispondere ai seguenti quesiti. Il requisito minimo per superare la prova, con la conferma del voto della prima prova scritta quale voto finale dell esame, è di rispondere in maniera corretta ad un quesito di tipo D e ad uno di tipo T. Le ulteriori risposte corrette, se valutate positivamente, comportano un incremento del voto finale dell esame fino ad un massimo di quattro punti. Tempo disponibile: 90 minuti. Quesiti di tipo D definizioni ) ) Sia f : A R A R, A ). Si dice che f è limitata in A se... completare la definizione). ) Sia a n } una successione di numeri reali. Si dice che a n } diverge positivamente se... completare la definizione). ) Sia f : A R A R, A ). Si dice che f è invertibile o iniettiva) in A se... completare la definizione). Quesiti di tipo T teoremi ) ) Dimostrare che ogni successione monotona è regolare. ) Enunciare e dimostrare il teorema di Rolle. ) Enunciare e dimostrare il teorema fondamentale del calcolo integrale. Quesiti di tipo E esercizi ) ) Studiare la funzione e tracciarne il grafico. fx) = x x x logx + ) ) Determinare F x) primitiva in ]0, + [ della funzione e tale che F ) = 0. fx) = arctanx + ) x ) Studiare, al variare del parametro reale x, il carattere della serie + n + ) x n + n.
25 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 7 aprile 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale [ ] a) 7, + 7 [ ] b) 0, + 7 [, ] [ ] c) 7, + 7 [, ] [ ] d) 7,. ) Il derivato D E dell insieme E = a) e } [, + [ b), e } c) e } d) e, e }. ) La derivata della funzione arcsen x x è uguale a: x a) x x x + ) 4 x b) c) d) x 4 +x x x 4 +x x x 4 +x x x 4 +x x 4 x + x ) x x 4 x + x ) x 4 x + x ). x x x + x + è l insieme ) n } + n) n : n N + [, + [ è l insieme 4) La restrizione della funzione x + x 6x + all insieme [0, ] Q a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. 5 arcsen x x 5) Il limite lim x + sen x a) è uguale a log 5 b) è uguale a log 5 c) è uguale a 0 d) è uguale a +.
26 6) Quali delle seguenti serie sono convergenti: n + 5 ) n n +, ) ) e + n+, ) a) ) e ) b) ), ) e 4) c) ) e 4) d) ) e 4). n 7) La successione n + n} a) è crescente n N + b) è decrescente, ma non è strettamente decrescente c) è decrescente e divergente d) è decrescente e convergente. n + log 5 n, 4) ) n + log 5 n? A 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = a) f è convessa nell intervallo [, 0] b) f non ha massimo assoluto c) f è derivabile in R d) il grafico di f ha asintoti orizzontali. 9) L integrale a) b) + 8 c) 0 d) x x dx è uguale a x + 6) x e se x < 0 x se x 0. +x 0) Sia a n } una successione limitata inferiormente. La condizione La successione a n } è convergente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia limitata superiormente. ) Data la funzione f : R R definita ponendo fx) = è vera? a) l integrale definito π π fx) d x è uguale a zero cos x se x 0 sen x se x > 0 b) l integrale indefinito fx) d x è uguale a Gx) + c, essendo Gx) = c) l integrale definito π π fx) d x è uguale a π d) l integrale indefinito fx) d x è uguale a Hx) + c, essendo Hx) =, quali delle seguenti affermazioni sen x x se x 0 cos x x se x > 0 sen x x se x 0 cos x x se x > 0.
27 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 7 aprile 05 Prima prova scritta compito B) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale [ ] a), + 7 [ ] 7, + 7 b) ], ] [ ] c) 0, + 7 d) [, ] [ ] 7, + 7. ) Il derivato D E dell insieme E = a) e, } b) e, e } c) e } d) ], ] e }. ) La derivata della funzione arccos x x è uguale a: a) x x + x ) x 4 x b) x x 4 +x x + x ) 4 x x c) x x + x ) 4 +x x 4 x d) x x 4 +x x x 4 x + x ). + x x x + x + è l insieme ) n } + n) n : n N + ], [ è l insieme 4) La restrizione della funzione x + x 6x + all insieme [0, ] R \ Q) a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. arctg 7 x 5) Il limite lim x + tg x + a) è uguale a log b) è uguale a 7 log c) è uguale a + d) è uguale a 0.
28 6) Quali delle seguenti serie sono convergenti: n n + π n+ ) n, ) + 4 n, ) a) ) e ) b) ), ) e ) c) ), ) e 4) d) ) e 4). n 7) La successione n + n} n N + a) è crescente ed il suo minimo è uguale a n + logn + ), 4) arctg n +? b) è decrescente ed il suo estremo superiore è uguale a 0 c) è decrescente ed il suo estremo inferiore è uguale a d) non è monotòna. B 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = a) f è convessa solo nell intervallo [, 0] b) f ha un unico zero in R c) il grafico di f ha punti angolosi d) f è uniformemente continua in ], [. 9) L integrale a) b) 9 c) d) x 5 x dx è uguale a 5x + 9) x e se x < 0 x se x 0. +x 0) Sia a n } una successione crescente. La condizione Esiste una sottosuccessione a kn } convergente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia convergente. ) Data la funzione f : R R definita ponendo fx) = è vera? a) l integrale definito π π fx) d x è un numero positivo cos x se x 0 sen x se x > 0 b) l integrale indefinito fx) d x è uguale a Gx) + c, essendo Gx) = c) l integrale definito π π fx) d x è uguale a π d) l integrale indefinito fx) d x è uguale a Hx) + c, essendo Hx) =, quali delle seguenti affermazioni sen x x + se x 0 cos x x se x > 0 sen x x se x 0 cos x x se x > 0.
29 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 7 aprile 05 Prima prova scritta compito C) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale a) ], [ [ 7, + 7 ] b) [, + 7 ] c) [, ] [ 7, + 7 ] d) [ 0, + 7 ]. ) Il derivato D E dell insieme E = a) e, e } b) 0, e, e } c) 0, e } d) [ 0, + [. ) La derivata della funzione arcsen x x) è uguale a: x x+ a) x x x +x x ) x b) x x +x x x + x c) d) x x x +x x x x+ x x x 4 +x x x x + x ) + 4x x x+ + è l insieme ) n } + n) n : n N + ] 0, + [ è l insieme. 4) La restrizione della funzione x + x 6x + all insieme [, 0] Q a) ha minimo e massimo assoluti) b) ha minimo ma non ha massimo c) ha massimo ma non ha minimo d) non ha né massimo né minimo. tg x x 5) Il limite lim x 5 5x a) è uguale a + b) è uguale a 0 c) è uguale a log log 5 d) è uguale a log log 5.
30 6) Quali delle seguenti serie sono convergenti: n + 5 ) n n +, ) ) π n+, ) a) ) e ) b) ), ) e 4) c) ) e 4) d) ) e 4). n 7) La successione n + n} a) è divergente a + n N b) è decrescente e convergente a c) è limitata inferiormente d) non è regolare. n n 0, 4) ) n arctg? n C 8) Sia f : R R definita come segue: Quali delle seguenti affermazioni è falsa? fx) = x e se x < 0 x se x 0. +x a) esiste a > 0 tale che la restrizione f [a,+ [ è iniettiva b) il grafico di f non ha asintoti obliqui c) f non ha punti di massimo locale d) f è integrabile secondo Riemann in [, ]. 9) L integrale a) 0 b) 5 c) d) x x dx è uguale a x + 5) 0) Sia a n } una successione crescente. La condizione Esiste una sottosuccessione a kn } convergente a) è necessaria e sufficiente b) è necessaria ma non sufficiente c) è sufficiente ma non necessaria d) non è né necessaria né sufficiente affinché la successione a n } sia limitata. ) Data la funzione f : R R definita ponendo fx) = è vera? a) l integrale definito π π fx) d x è uguale a zero cos x se x 0 sen x + x se x > 0 b) l integrale indefinito fx) d x è uguale a Gx) + c, essendo Gx) = c) l integrale definito 0 π fx) d x è un numero positivo d) l integrale indefinito fx) d x è uguale a Hx) + c, essendo Hx) =, quali delle seguenti affermazioni sen x x + se x 0 cos x + x + se x > 0 sen x x se x 0 cos x + x + se x > 0.
31 Tutti i quesiti dei compiti D, E e F del 7 aprile 05 si trovano in uno dei compiti A, B e C
32 Anno Accademico Corsi di Analisi Matematica I A.Villani, R. Cirmi e F.Faraci) Prova d Esame del giorno 7 aprile 05 Seconda prova scritta - COMPITO A Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Si possono consegnare al massimo due fogli a quadri in bella copia in entrambi devono essere apposti nome e cognome a stampatello e la firma del candidato. Alla fine della prova il presente foglio deve essere riconsegnato debitamente compilato. Rispondere ai seguenti quesiti. Il requisito minimo per superare la prova, con la conferma del voto della prima prova scritta quale voto finale dell esame, è di rispondere in maniera corretta ad un quesito di tipo D e ad uno di tipo T. Le ulteriori risposte corrette, se valutate positivamente, comportano un incremento del voto finale dell esame fino ad un massimo di quattro punti. Tempo disponibile: 90 minuti. Quesiti di tipo D definizioni ) ) Sia f : A R A R, A ). Si dice che la la funzione f ha un minimo assoluto in A se... completare la definizione). ) Sia a n } una successione di numeri reali. Si dice che la successione a n } é convergente se... completare la definizione). Si dice che la serie + é convergente se... completare la definizione). ) Sia f : A R A R, A ) Si dice che f è decrescente in A se... completare la definizione). a n Quesiti di tipo T teoremi ) ) Enunciare e dimostrare il Teorema di esistenza degli zeri. ) Siano f, g : a, b) R due funzioni derivabili in un punto x 0 a, b). Allora la funzione prodotto fg... completare l enunciato del teorema e svolgerne la dimostrazione). ) Svolgere lo studio completo della serie geometrica. Quesiti di tipo E esercizi ) ) Studiare la funzione e tracciarne il grafico. fx) = xe x ) Calcolare logx + ) x + ) dx. ) Studiare, al variare del parametro reale x, il carattere della serie + nx n + + ) n+.
33 Anno Accademico Corsi di Analisi Matematica I A.Villani, R. Cirmi e F.Faraci) Prova d Esame del giorno 7 aprile 05 Seconda prova scritta - COMPITO B Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Si possono consegnare al massimo due fogli a quadri in bella copia in entrambi devono essere apposti nome e cognome a stampatello e la firma del candidato. Alla fine della prova il presente foglio deve essere riconsegnato debitamente compilato. Rispondere ai seguenti quesiti. Il requisito minimo per superare la prova, con la conferma del voto della prima prova scritta quale voto finale dell esame, è di rispondere in maniera corretta ad un quesito di tipo D e ad uno di tipo T. Le ulteriori risposte corrette, se valutate positivamente, comportano un incremento del voto finale dell esame fino ad un massimo di quattro punti. Tempo disponibile: 90 minuti. Quesiti di tipo D definizioni ) ) Sia f : A R A R, A ). Si dice che la la funzione f ha un massimo assoluto in A se... completare la definizione). ) Sia a n } una successione di numeri reali. Si dice che la successione a n } diverge positivamente se... completare la definizione). Si dice che la serie + diverge positivamente a n se... completare la definizione). ) Sia f : A R A R, A ) Si dice che f è crescente in A se... completare la definizione). Quesiti di tipo T teoremi ) ) Dimostrare il Teorema di Bolzano-Weirstrass sui punti di accumulazione di un insieme.. ) Siano a n } e b n } due successioni convergenti. Allora la successione prodotto a n b n }... completare l enunciato del teorema e svolgerne la dimostrazione). ) Dimostrare che la serie armonica é divergente. Quesiti di tipo E esercizi ) ) Studiare la funzione e tracciarne il grafico. fx) = xe x ) Calcolare logx + ) x + ) dx. ) Studiare, al variare del parametro reale x, il carattere della serie + nx n 4 + ) n+.
34 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 giugno 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti, libri e calcolatori non è consentito comunicare con i colleghi ogni mezzo di comunicazione elettronico deve essere tenuto spento. Verrà escluso dalla prova lo studente che, ad una verifica, fosse sprovvisto di un documento di riconoscimento. Durante la prova non è possibile uscire dall aula prima di avere consegnato definitivamente il compito. Rispondere ai seguenti quesiti. Il punteggio viene attribuito nel modo seguente: punti 0 se vi sono almeno cinque risposte corrette punti per ciascuna risposta esatta in aggiunta alle prime cinque punti - per ciascuna risposta errata punti 0 per ogni risposta non data. Tempo disponibile: 90 minuti. ) Il dominio della funzione reale di variabile reale log a)], [ ], + [ b) ], [ [, [ [, + [ c) ], [ ], [ ], + [ d) ], [. x x + x è l insieme ) Dati gli insiemi A = x R : x 4x + > 0}, B = x R : x + > 0} e C = x R : x + < 4}, quali delle seguenti affermazioni è falsa? a) C \ B A b) B C) \ A è un intervallo chiuso c) B C non ha il minimo d) A C = R. ) La derivata seconda della funzione arctg x è uguale a: a) x 4 x 6 x ) x b) x 4 +6x ) x ) x ) c) x 4 x 6 x ) x ) x d) 5x 4 9x +6 x ) x ) 4) La funzione. ) x x 6x+5 è strettamente crescente a) nell intervallo [, ] b) in ciascuno degli intervalli ], ] e [, + [ c) nell intervallo [, ] d) nell intervallo ], [ ma non nell intervallo [, ]. arcsen x x 5) Il limite lim x + sen x a) è uguale a log b) è uguale a log log c) è uguale a 0 d) è uguale a +.
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
FACOLTÀ DI INGEGNERIA ESAME DI ANALISI MATEMATICA A A.A. 2008/2009 - Ing. Biomedica, Elettrica, Elettronica, Informatica - L Z
 FACOLTÀ DI INGEGNERIA ESAME DI ANALISI MATEMATICA A A.A. 2008/2009 - Ing. Biomedica, Elettrica, Elettronica, Informatica - L Z L esame è costituito da una prova scritta (o, in alternativa, da due prove
FACOLTÀ DI INGEGNERIA ESAME DI ANALISI MATEMATICA A A.A. 2008/2009 - Ing. Biomedica, Elettrica, Elettronica, Informatica - L Z L esame è costituito da una prova scritta (o, in alternativa, da due prove
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA I - 11 Febbraio 2011, ore 8.30
 Esame di ANALISI MATEMATICA I - 11 Febbraio 2011, ore 830 A ESERCIZIO 1 (8 punti) Data la funzione = 1 + sin x 2 2 x (a) determinare lo sviluppo di MacLaurin al terzo ordine della funzione ; (b) determinare
Esame di ANALISI MATEMATICA I - 11 Febbraio 2011, ore 830 A ESERCIZIO 1 (8 punti) Data la funzione = 1 + sin x 2 2 x (a) determinare lo sviluppo di MacLaurin al terzo ordine della funzione ; (b) determinare
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Analisi I - IngBM - 2014-15 COMPITO A 21 Febbraio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE... +... =...
 Analisi I - IngBM - 2014-15 COMPITO A 21 Febbraio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioni Gli
Analisi I - IngBM - 2014-15 COMPITO A 21 Febbraio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioni Gli
Prove d'esame a.a. 20082009
 Prove d'esame aa 008009 Andrea Corli settembre 0 Sono qui raccolti i testi delle prove d'esame assegnati nell'aa 00809, relativi al Corso di Analisi Matematica I (trimestrale, 6 crediti), Laurea in Ingegneria
Prove d'esame aa 008009 Andrea Corli settembre 0 Sono qui raccolti i testi delle prove d'esame assegnati nell'aa 00809, relativi al Corso di Analisi Matematica I (trimestrale, 6 crediti), Laurea in Ingegneria
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica
 Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica Nome... N. Matricola... Ancona, 29 marzo 2014 1. (7 punti) Studiare la funzione determinandone: f(x) = e x x il dominio;
Corso di Laurea in Ingegneria Edile Anno Accademico 2013/2014 Analisi Matematica Nome... N. Matricola... Ancona, 29 marzo 2014 1. (7 punti) Studiare la funzione determinandone: f(x) = e x x il dominio;
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Analisi Matematica I Palagachev
 Analisi Matematica I Palagachev Numeri complessi Risolvere nel campo complesso C la seguente equazione: ) 3 z i = i z + 2 Risolvere nel campo complesso C la seguente equazione: z 2 + 2iz = 2 3 Risolvere
Analisi Matematica I Palagachev Numeri complessi Risolvere nel campo complesso C la seguente equazione: ) 3 z i = i z + 2 Risolvere nel campo complesso C la seguente equazione: z 2 + 2iz = 2 3 Risolvere
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
Esame di Analisi Matematica prova scritta del 23 settembre 2013
 Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
3. Quale affermazione è falsa?
 1. Quale affermazione è falsa? Se la funzione f) è continua e monotona crescente su R e se f) = 1 e f4) =, allora ha un unico zero nell intervallo, 4) f) non si annulla mai in R f ) > nell intervallo,
1. Quale affermazione è falsa? Se la funzione f) è continua e monotona crescente su R e se f) = 1 e f4) =, allora ha un unico zero nell intervallo, 4) f) non si annulla mai in R f ) > nell intervallo,
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
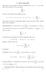 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Soluzione del tema d esame di matematica, A.S. 2005/2006
 Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Diario del corso di Analisi Matematica 1 (a.a. 2015/16)
 Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
PROGRAMMA CONSUNTIVO
 PROGRAMMA CONSUNTIVO a.s. 2014/2015 MATERIA MATEMATICA CLASSE DOCENTE 5^ SEZIONE D DI LEO CLELIA Liceo Scientifico delle Scienze Applicate ORE DI LEZIONE 4 **************** OBIETTIVI saper definire e classificare
PROGRAMMA CONSUNTIVO a.s. 2014/2015 MATERIA MATEMATICA CLASSE DOCENTE 5^ SEZIONE D DI LEO CLELIA Liceo Scientifico delle Scienze Applicate ORE DI LEZIONE 4 **************** OBIETTIVI saper definire e classificare
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
PIANO DI LAVORO DEL PROFESSORE
 ISTITUTO DI ISTRUZIONE SUPERIORE STATALE IRIS VERSARI - Cesano Maderno (MB) PIANO DI LAVORO DEL PROFESSORE Indirizzo: LICEO SCIENTIFICO MATERIA: MATEMATICA ANNO SCOLASTICO: 2014-2015 PROF: MASSIMO BANFI
ISTITUTO DI ISTRUZIONE SUPERIORE STATALE IRIS VERSARI - Cesano Maderno (MB) PIANO DI LAVORO DEL PROFESSORE Indirizzo: LICEO SCIENTIFICO MATERIA: MATEMATICA ANNO SCOLASTICO: 2014-2015 PROF: MASSIMO BANFI
Ingegneria Elettronica, Informatica e delle Telecomunicazioni Prova scritta di ANALISI B - 06/04/2006
 Ingegneria Elettronica, Informatica e delle Telecomunicazioni Prova scritta di ANALISI B - 06/04/2006 CORSO DI STUDI IN INGEGNERIA... NOME E COGNOME:... NUMERO DI MATRICOLA:... (scrivere nome e cognome
Ingegneria Elettronica, Informatica e delle Telecomunicazioni Prova scritta di ANALISI B - 06/04/2006 CORSO DI STUDI IN INGEGNERIA... NOME E COGNOME:... NUMERO DI MATRICOLA:... (scrivere nome e cognome
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
x ( 3) + Inoltre (essendo il grado del numeratore maggiore del grado del denominatore, d ancora dallo studio del segno),
 6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
Grafico qualitativo di una funzione reale di variabile reale
 Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Esercizi sugli integrali impropri
 Esercizi sugli integrali impropri Esercizio. Studiare 2 x4 dx. Svolgimento: è un integrale improprio, in quanto f(x) =, x (, 2] ha una singolarità in : x4 lim x + x4 = +. Osserviamo che f è positiva, quindi
Esercizi sugli integrali impropri Esercizio. Studiare 2 x4 dx. Svolgimento: è un integrale improprio, in quanto f(x) =, x (, 2] ha una singolarità in : x4 lim x + x4 = +. Osserviamo che f è positiva, quindi
LA FUNZIONE INTEGRALE
 LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 2012/2013 12 febbraio 2013
 Tempo massimo 2 ore. Consegnare solamente la bella copia. Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 212/213 12 febbraio 213 1. Disegnare il grafico della funzione: [1
Tempo massimo 2 ore. Consegnare solamente la bella copia. Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 212/213 12 febbraio 213 1. Disegnare il grafico della funzione: [1
POLITECNICO di BARI - A.A. 2012/2013 Corso di Laurea in INGEGNERIA Informatica e dell Automazione
 POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Numeri Complessi. 4. Ricordando che, se z è un numero complesso, zz è un numero reale, mettere sotto la forma. z 2 + 2z + 2 = 0. z 2 + 2z + 6 = 0.
 Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
FUNZIONI ELEMENTARI Esercizi risolti
 FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Studio grafico-analitico delle funzioni reali a variabile reale
 Studio grafico-analitico delle funzioni reali a variabile reale Sequenza dei passi Classificazione In pratica Classifica il tipo di funzione: Funzione razionale: intera / fratta Funzione irrazionale: intera
Studio grafico-analitico delle funzioni reali a variabile reale Sequenza dei passi Classificazione In pratica Classifica il tipo di funzione: Funzione razionale: intera / fratta Funzione irrazionale: intera
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
MATEMATICA GENERALE - (A-D) Prova d esame del 7 febbraio 2012 - FILA A
 MATEMATICA GENERALE - (A-D) Prova d esame del 7 febbraio 2012 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando
MATEMATICA GENERALE - (A-D) Prova d esame del 7 febbraio 2012 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Corso di Matematica per CTF Appello 15/12/2010
 Appello 15/12/2010 Svolgere i seguenti esercizi: 1) Calcolare entrambi i limiti: a) lim(1 x) 1 e x 1 ; x 0 x log 2 x b) lim x 1 1 cos(x 1). 2) Data la funzione: f(x) = x log x determinarne dominio, eventuali
Appello 15/12/2010 Svolgere i seguenti esercizi: 1) Calcolare entrambi i limiti: a) lim(1 x) 1 e x 1 ; x 0 x log 2 x b) lim x 1 1 cos(x 1). 2) Data la funzione: f(x) = x log x determinarne dominio, eventuali
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Liceo scientifico Albert Einstein. Anno scolastico 2009-2010. Classe V H. Lavoro svolto dalla prof.ssa Irene Galbiati. Materia: MATEMATICA
 Liceo scientifico Albert Einstein Anno scolastico 2009-2010 Classe V H Lavoro svolto dalla prof.ssa Irene Galbiati Materia: MATEMATICA PROGRAMMA DI MATEMATICA CLASSE V H Contenuti Ripasso dei prerequisiti
Liceo scientifico Albert Einstein Anno scolastico 2009-2010 Classe V H Lavoro svolto dalla prof.ssa Irene Galbiati Materia: MATEMATICA PROGRAMMA DI MATEMATICA CLASSE V H Contenuti Ripasso dei prerequisiti
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni +2 CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni +2 CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
Matematica Generale II (5 Cfu) Economia e amministrazione delle imprese (A-Lh)
 Matematica Generale II (5 Cfu) Economia e amministrazione delle imprese (A-Lh) A.A. 2014-2015 Docente Vanda Tulli e-mail: vanda.tulli@unimib.it tel: 0264483164 Edificio U7, quarto piano, stanza 4018 Esercitatore
Matematica Generale II (5 Cfu) Economia e amministrazione delle imprese (A-Lh) A.A. 2014-2015 Docente Vanda Tulli e-mail: vanda.tulli@unimib.it tel: 0264483164 Edificio U7, quarto piano, stanza 4018 Esercitatore
MODALITA E DATE DEGLI ESAMI
 A.A. 2015/16 CORSO DI ANALISI MATEMATICA 1 PER I CORSI DI LAUREA IN MATEMATICA E FISICA I semestre, 12 crediti Teoria: 9 crediti, tenuti da me Esercitazioni: 3 crediti, tenuti dal Dott. Bruno Scardamaglia
A.A. 2015/16 CORSO DI ANALISI MATEMATICA 1 PER I CORSI DI LAUREA IN MATEMATICA E FISICA I semestre, 12 crediti Teoria: 9 crediti, tenuti da me Esercitazioni: 3 crediti, tenuti dal Dott. Bruno Scardamaglia
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
NOME:... MATRICOLA:... Scienza dei Media e della Comunicazione, A.A. 2007/2008 Analisi Matematica 1, Esame scritto del 08.02.2008. x 1.
 NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Durata della prova: 3h. 2 +y 4. tan y sin y lim = 1. (x 4 +y 2 )y 3
 Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Marco Tolotti - Corso di Esercitazioni di Matematica 12 Cfu - A.A. 2010/2011 1
 Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
Marco Tolotti - Corso di Esercitazioni di Matematica 1 Cfu - A.A. 010/011 1 Esercitazione 1: 4/09/010 1. Determinare il dominio delle seguenti funzioni: log a) f() = 5 ( 1). b) g() = log 3 (3 6) log 13.
Attenzione: i programmi sono cambiati negli anni. Non tutti gli esercizi nella presente raccolta riguardano argomenti trattati.
 Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-4 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-4 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Funzioni e loro invertibilità
 Funzioni e loro invertibilità Una proposta didattica di Ettore Limoli Definizione di funzione Sono dati due insiemi non vuoti A (dominio) e B (codominio) Diremo che y=f(x) è una funzione, definita in A
Funzioni e loro invertibilità Una proposta didattica di Ettore Limoli Definizione di funzione Sono dati due insiemi non vuoti A (dominio) e B (codominio) Diremo che y=f(x) è una funzione, definita in A
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Funzioni. Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi:
 Funzioni Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi: da un rilevamento empirico da una formula (legge) ESEMPI: 1. la temperatura
Funzioni Il concetto di funzione nasce da quello di corrispondenza fra grandezze. Tale corrispondenza può essere data in svariati modi: da un rilevamento empirico da una formula (legge) ESEMPI: 1. la temperatura
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
Trigonometria: breve riepilogo.
 Corso di laurea in Matematica Corso di Analisi Matematica - Dott.ssa Sandra Lucente Trigonometria: breve riepilogo. Definizioni iniziali Saper misurare un angolo in gradi sessagesimali, saper svolgere
Corso di laurea in Matematica Corso di Analisi Matematica - Dott.ssa Sandra Lucente Trigonometria: breve riepilogo. Definizioni iniziali Saper misurare un angolo in gradi sessagesimali, saper svolgere
LE FUNZIONI E LE LORO PROPRIETÀ
 LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
