MATRICI E OPERAZIONI
|
|
|
- Aniello Stefani
- 5 anni fa
- Visualizzazioni
Transcript
1 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni e proprietà Determinanti Esercizio Scrivere per esteso le seguenti matrici: A (a ij con a ij 2i + 3j per i,2,3 e j,2,3,4; 2 B (b ij con b ij siniπ + cos jπ + ij 0 con i,2,3 e j,2,3,4; 3 H ( i+j con i,j,2,3,4 La matrice H è detta matrice di Hilbert (qui scritta per l ordine 4 ed estendibile per l ordine n qualsiasi ed è utilizzata per testare vari algoritmi numerici Esercizio 2 Senza scrivere tutta la matrice, scrivere la diagonale principale di: (4i j 2 con i,j,2,3; 2 ( sin( iπ 4 cos(iπ 4 con i,j,2,3,4 Esercizio 3 Siano date le matrici ( A 0, B ( 2, C ( Calcolare: i 2A B; ii 3A + 2B 4C; iii 2A + B + 2C 2B; iv 3B + 2(2A C (A + B + C; v 2(A B + C 3( 2B + 3C + (4C A + 3B 2 Risolvere, se possibile, le equazioni matriciali: i 3X + 2(A X + B + 2(C + 2X 0; ii 4A + 2(B + 2X 3(C + X + 2A 0; iii 4(A + B + X + 4( A B + X 4(A B + X 0 Esercizio 4 Sia A una matrice 7 e B una matrice 7 Il prodotto AB è una matrice: (i 49, (ii 7 7, (iii, (iv 7 Esercizio 5 Sia A 2 e sia B ( Calcolare AB 3 Esercizio 6 Sia A ( e B ( Calcolare AB BA
2 MATRICI E SISTEMI - Matrici e operazioni 2 Esercizio 7 Siano date le matrici: A ( 0, B 2 0 2, C 0 0 Calcolare, quando possibile: i AC; ii (BCA; iii B + CA; iv BA; v B(A T ; vi 3A T + BC Esercizio 8 Siano date le matrici: A (, B 2 ( 0 0 0, C Calcolare: i A T, B T, C T ; ii P AB, Q B T A T, P T ; iii V BC, W C T B T, V T, W T Esercizio 9 Dire quali delle seguenti matrici sono simmetriche: ( L, M 5 6 7, N 4, R ( , S , T Esercizio 0 Date le matrici: A ( 6 2, P 2 6 ( x, 0 determinare x R tale che la matrice D P T AP sia diagonale Esercizio Mostrare che: se Y è un vettore colonna con entrate reali, allora Y T Y 0 se e solo se Y 0; 2 dati una matrice quadrata reale A e un vettore colonna reale Z, allora A T AZ 0 se e solo se AZ 0; 3 date una matrice quadrata reale A e una matrice reale X, allora A T AX 0 se e solo se AX 0 Esercizio 2 Date due matrici A e B che soddisfano le uguaglianze AB 0 e BA 0, dire, giustificando la risposta, se sono vere le seguenti affermazioni: (i AB BA; (ii A o B sono la matrice nulla
3 MATRICI E SISTEMI - Matrici e operazioni 3 Esercizio 3 Siano A e B due matrici quadrate che commutano (cioè tali che AB BA Mostrare che: A T e B T commutano; 2 A p e B q commutano per ogni p,q N; 3 (AB m A m B m per ogni m N; 4 i polinomi 3A 2 5A + 6I e 2B + 3I commutano; 5 ogni polinomio matriciale in A commuta con ogni polinomio matriciale in B Esercizio 4 Verificare che le seguenti coppie di matrici sono una l inversa dell altra: ( ( A, A ; B 2 0, B ; C 2, C ; /5 0 0 D 0 0, D ; /2 3 /3 /3 0 T 0, T 2 0 / /2 Calcolare anche l inversa delle seguenti matrici: 5A, B C, 2C B T 2 Esercizio 5 Una matrice quadrata A si dice idempotente se A 2 A Stabilire se esistono valori del parametro reale k tali che la matrice k k A 0 0 k 0 0 sia idempotente 2 Date due matrici quadrate A e B di ordine n, verificare che se AB A e BA B allora A è idempotente Esercizio 6 Una matrice quadrata A è nilpotente se esiste p N tale che A p 0; il più piccolo intero p per cui ciò avviene viene detto indice di nilpotenza Stabilire se la matrice 3 A è nilpotente e, in caso positivo, calcolarne l indice di nilpotenza
4 MATRICI E SISTEMI - Matrici e operazioni 4 Esercizio 7 Considerate le matrici: A 0, E 0 0, mostrare che: E 3 0; 2 A I + E e A I E + E 2 Esercizio 8 Mostrare che l inversa della matrice ( cos θ sin θ R sinθ cos θ è data da R R T Esercizio 9 Determinare una matrice X tale che dove A 3X + (A + B 2 2AB, ( 2 3 e B ( 2 3 Esercizio 20 Dimostrare che, data una matrice quadrata A, si ha che: A 2 I (I + A(I A 0 E vero che date due matrici quadrate A e B si ha che A 2 B 2 (A + B(A B 0? Esercizio 2 Calcolare i determinanti delle seguenti matrici: ( A,B,C a 0,D dove a è un parametro reale Esercizio 22 Data la matrice si ha che: (i det(a 0; A , (ii det(a 4; (iii det(a ; (iv il determinante di A non si può calcolare
5 MATRICI E SISTEMI - Matrici e operazioni 5 SVOLGIMENTI Svolgimento Esercizio Si ha a , a , a , a , a , a , 2 Si ha a , a , a , a , a , a A b sin π + cos π , b 2 sinπ + cos 2π , b 2 sin 2π + cos π , b 22 sin2π + cos 2π , b 3 sin 3π + cos π , b 32 sin3π + cos 2π , b 3 sin π + cos 3π , b 4 sin π + cos 4π , b 23 sin 2π + cos 3π , b 24 sin 2π + cos 4π , b 33 sin 3π + cos 3π , b 34 sin 3π + cos 4π , 3 Risulta H B /2 /3 /4 /2 /3 /4 /5 /3 /4 /5 /6 /4 /5 /6 /7 Svolgimento Esercizio 2 Gli elementi della diagonale principale di una matrice quadrata A (a ij sono gli elementi a ii Se a ij 4i j 2 con i,j,2,3, allora allora a ii 4i i 2 a 4 3, a , a Se a ij sin iπ 4 cos jπ 4 con i,j,2,3,4, allora a ii sin iπ 4 cos iπ 4 a sin π 4 cos π 4 2, a 22 sin π 2 cos π 2 0, a 33 sin 3π 4 cos 3π 4 2, a 44 sin π cos π 0
6 MATRICI E SISTEMI - Matrici e operazioni 6 Svolgimento Esercizio 3 Utilizziamo l algebra delle matrici per semplificare le espressioni, quando possibile: risulta ( ( ( ( ( i 2A B 2, ( ( ( ( ii 3A + 2B 4C +, ( ( iii 2A + B + 2C 2B 2A B + 2C, iv 3B + 2(2A C (A + B + C 3B + 4A 2C A B C 2B + 3A 3C ( ( 7, 7 ( 3 0 v 2(A B + C 3( 2B + 3C + (4C A + 3B ( A 2B + 2C + 6B 9C + 4C A + 3B A + 7B 3C ( ( ( 3 0 ( Utilizziamo l algebra delle matrici per isolare l incognita X, quando possibile: i si ha risulta 3X + 2(A X + B + 2(C + 2X 0 X 2 5 3X + 2A 2X + B + 2C + 4X 0 ( 0 5 ( X 2A B 2C X (2A + B + 2C 5 ( (
7 MATRICI E SISTEMI - Matrici e operazioni 7 ii si ha 4A + 2(B + 2X 3(C + X + 2A 0 4A + 2B + 4X 3C 3X 6A 0 4X 2A 2B + 3C risulta X 2 ( 0 2 ( ( ( iii si ha 4(A + B + X + 4( A B + X 4(A B + X 0 (A + B + X + ( A B + X (A B + X 0 A + B + X A B + X A + B X 0 B + X A 0 risulta X ( 0 ( ( Svolgimento Esercizio 4 Le dimensioni della matrice prodotto, quando esiste, si ottengono con la regola (m n(n p m p, quindi AB è di tipo Svolgimento Esercizio 5 Risulta 2 ( Svolgimento Esercizio 6 Si ha ( ( ( + ( + ( + ( + ( ( ( ( + ( + ( + ( + ( AB BA AB ( ( 2 2, 2 2 ( Svolgimento Esercizio 7 i Risulta ( 0 0 AC 0 ( 0
8 MATRICI E SISTEMI - Matrici e operazioni 8 ii Si ha iii Risulta BC (BCA B + CA ( ( iv Il prodotto BA non esiste, in quanto B è di tipo 3 3 ed A è di tipo 2 3 v Si ha A T 0 B ( A T vi Risulta A T + BC Svolgimento Esercizio 8 i Si ha A T (, B T 2 (com era prevedibile, perché C è simmetrica ii Risulta 0 0, C T C 3 4 ( ( ( P AB, ( 2 Q B T A T 0 2, 2 0 2
9 MATRICI E SISTEMI - Matrici e operazioni 9 P T (AB T B T A T Q iii Risulta ( ( V BC , W C T B T CB T , V T (BC T C T B T W e W T ( V T T V Svolgimento Esercizio 9 L, N e T sono simmetriche (a ij a ji per ogni i,j, mentre non sono simmetriche M (ad esempio a 3 a 3, R (a 2 a 2 ed S (a 4 a 4 Svolgimento Esercizio 0 Calcoliamo D P T AP Si ha ( ( ( ( ( ( x 0 6 6x x + 2 D x x 2 2x + 6 6x + 2 6x 2 + 4x + 6 Dunque D è diagonale (cioè a ij 0 se i j se e solo se 6x + 2 0, ossia x 2/6 Svolgimento Esercizio Sia Allora Y Y T Y ( y y n y y n y y n y y 2 n Y T Y 0 se e solo se y y2 n 0, il che, essendo gli y i reali, equivale a y y 2 y n 0, cioè Y 0 2 Se Z 0, non c è nulla da dimostrare Supponiamo allora Z 0 In questo caso, la relazione A T AZ 0 equivale a Z T A T AZ 0 (ottenuta moltiplicando ambo i membri per Z T 0, ossia a (AZ T AZ 0 Ma AZ è un vettore colonna reale (AZ T AZ 0 significa AZ 0, per quanto provato al punto precedente 3 Se A è di tipo m m, perché il prodotto A T AX abbia senso, X deve essere di tipo m n Indichiamo con X,,X n le colonne di X (ciascuna di tipo m, in modo che x x n X ( X X 2 X n x m x mn Osserviamo ora che, se a a m M a m a mm
10 MATRICI E SISTEMI - Matrici e operazioni 0 è una qualsiasi matrice di tipo m m, le colonne del prodotto a a m x x n MX a m a mm x m x mn a x + a m x m a x n + a m x mn a m x + a mm x m a x + a m x m sono cioè a a m MX a m a mm a a m MX n a m a mm Allora, prendendo M A T A, risulta x x m x n x mn MX ( MX MX 2 MX n A T AX ( A T AX A T AX n a x + a m x m a m x + a mm x m a x n + a m x mn a x + a m x m A T AX 0 se e solo se A T AX A T AX n 0 Ma le X j sono colonne reali, per quanto dimostrato al punto precedente, A T AX A T AX n 0 significa AX AX n 0 Ciò equivale ad AX 0, in quanto (prendendo questa volta M A si ha AX ( AX AX n, Svolgimento Esercizio 2 La (i è vera solo se le matrici A e B sono quadrate e della stessa taglia Altrimenti, nelle uguaglianze AB 0 e BA 0, le matrici nulle hanno taglie diverse e quindi sono diverse La (ii invece è falsa, perché prendendo ad esempio si ottiene AB BA 0 A ( , B Svolgimento Esercizio 3 Se BA AB, risulta ( A T B T (BA T (AB T B T A T 2 Se p 0 oppure q 0, allora una tra A p e B q è la matrice identica risulta A p B q B q A p banalmente Se p,q, allora A p B q A p ABB q A p BAB q A p 2 ABAB q A p 2 BAAB q A p 2 BA 2 B q BA p B q
11 MATRICI E SISTEMI - Matrici e operazioni e procedendo nello stesso modo si può cambiare posto a tutti i fattori B ad uno ad uno, fino ad ottenere A p B q B q A p 3 Se m, allora risulta (AB m A m B m banalmente Per m 2, potremmo ragionare in modo simile al punto (2, esplicitando la potenza (AB m, ma conviene procedere per induzione: supponiamo (AB m A m B m e deduciamo (AB m A m B m Si ha (AB m (AB m AB A m B m AB A m AB m B A m B m dove si è usata l uguaglianza B m A AB m dimostrata al punto (2 4 Applicando ripetutamente la distributività della somma rispetto al prodotto, si ottiene e (3A 2 5A + 6I(2B + 3I (3A 2 5A + 6I2B + (3A 2 5A + 6I3I 6A 2 B 0AB + 2B + 9A 2 5A + 8I (2B + 3I(3A 2 5A + 6I 2B(3A 2 5A + 6I + 3I(3A 2 5A + 6I 6BA 2 0BA + 2B + 9A 2 5A + 8I Poiché A 2 B BA 2 per quanto dimostrato al punto (2, i secondi membri risultano uguali e quindi lo stesso vale per i primi 5 Si ragiona come al punto (4: si ottiene ( n [( m m n ] a i A i b j B j a i A i b j B j i0 j0 j0 i0 m j0 i0 n a i b j A i B j e ( m n b j B j a i A i j0 i0 n m m m b j B j a i A i b j a i B j A i, i0 j0 j0 j0 dove a i b j b j a i perché il prodotto di numeri reale è commutativo e A i B j B j A i per quanto dimostrato al punto (2 Svolgimento Esercizio 4 Per verificare che due matrici sono l una l inversa dell altra è sufficiente controllare che il loro prodotto (in un ordine qualsiasi dia la matrice identica ; ad esempio A A 2 ( ( Lasciamo al lettore il calcolo degli altri prodotti ( ( 5 3( ( 5 5( ( 0 0 L inversa di 5A è 5 A 5 A 2 (in generale: (λa λ A per ogni λ 0 e A invertibile L inversa di B C è (B C B C (l inversa del prodotto di matrici invertibili è il prodotto delle inverse in ordine inverso, poiché B B 2 e C C 2, risulta infatti, AB I implica det Adet B entrambe A e B risultano invertibili, per cui da AB I segue A B moltiplicando ambo i membri a destra per B
12 MATRICI E SISTEMI - Matrici e operazioni 2 (B C B 2 C 2 L inversa di 2C B2 T è ( 2C B2 T ( 2 B T 2 C ( A T per ogni A invertibile, poiché B 2 BT C 2 2 ( B T 2 C (in generale: 2 B e C C 2, risulta ( 2C B T 2 Svolgimento Esercizio 5 Si ha k k k k + k + k 2 k k A k k, k 0 0 k 0 0 k k 2 k 2 quindi A è idempotente se e solo se + k + k 2 k k k k k k 0 0, k k 2 k 2 k 0 0 ossia che è soddisfatto per k 0 + k + k 2 k 0, k 2 0 ( A T 2 Scrivendo l uguaglianza AB A come A AB e moltiplicando a destra per A si ottiene A 2 ABA Sostituendo ora BA B prima e AB A poi, si conclude A 2 ABA AB A Svolgimento Esercizio 6 Si ha A e A 3 A 2 A Dunque A ha indice di nilpotenza p 3 Svolgimento Esercizio 7 Si ha E E 3 E 2 E
13 MATRICI E SISTEMI - Matrici e operazioni 3 2 Si ha I + E A ( I E + E 2 A ( I E + E 2 (I + E I E + E 2 + ( I E + E 2 E I E + E 2 + E E 2 + E 3 I + E 3 I Ciò prova che A I E + E 2, in quanto due matrici sono l una l inversa dell altra se e solo se il loro prodotto (in un ordine qualsiasi è la matrice identica (v nota allo svolgimento dell Esercizio 4 Svolgimento Esercizio 8 Si ha R T ( cos θ sinθ sin θ cos θ R T R ( ( ( cos θ sinθ cos θ sin θ cos 2 θ + sin 2 θ 0 sin θ cos θ sinθ cos θ 0 cos 2 θ + sin 2 θ ( 0 0 Ciò prova che R R T, in quanto due matrici sono l una l inversa dell altra se e solo se il loro prodotto (in un ordine qualsiasi è la matrice identica (v nota allo svolgimento dell Esercizio 4 Svolgimento Esercizio 9 L equazione 3X + (A + B 2 2AB equivale a 3X 2AB (A + B 2 (attenzione a non svolgere il quadrato (A + B 2 con l usuale formula valida nel campo dei numeri reali: si ha (A + B 2 A 2 + BA + AB + B 2, che è diverso da A 2 + 2AB + B 2 a meno che A e B commutino, ossia ( ( 2 2 3X ( ( [( ( ( ] 2 ( ( e pertanto X 3 ( ( 4 8 4/3 8/ /3 Svolgimento Esercizio 20 Distribuendo il prodotto rispetto alla somma, si ha (I + A (I A (I + A I (I + A A I + A A A 2 I A 2
14 MATRICI E SISTEMI - Matrici e operazioni 4 (I + A (I A 0 equivale a I A 2 0, cioè I A 2 Procedendo come sopra, si ottiene (A + B(A B (A + BA (A + BB A 2 + BA AB B 2 risulta (A + B(A B 0 se e solo se A 2 + BA AB B 2, che non equivale ad A 2 B 2, a meno che A e B commutino La risposta è dunque negativa Svolgimento Esercizio 2 Si ha deta 2 a a 22 a 2 a 2 2 Calcoliamo il determinante di B sviluppando rispetto alla prima riga (che contiene uno 0: 0 detb 2 2 ( + a 2 + ( +2 a ( +3 a ( 2 (2 2 3 Calcoliamo il determinante di C sviluppando rispetto alla terza colonna (che contiene uno 0: 2 det C a ( +3 a 3 a ( 2+3 a ( 3+3 a 23 a a a + 2(2 + a 3 + 2a Iniziamo il calcolo del determinante di D sviluppando rispetto alla quarta colonna (che contiene due elementi nulli: 2 det D ( +4 2 a ( 3+4 a A questo punto potremmo procedere sviluppando direttamente i due determinanti 3 3 ottenuti D altra parte, un determinante non cambia operando trasformazioni elementari del primo tipo (cioè sommando ad una riga o colonna un multiplo non nullo di un altra, quindi semplifichiamo il loro calcolo facendo comparire un maggior numero di zeri: si ha R 3 R 3 2R (
15 MATRICI E SISTEMI - Matrici e operazioni 5 e R 2 R 2 R Dunque det D 2(3 + 2( R 3 R 3 2R ( Svolgimento Esercizio 22 Ovviamente l affermazione (iv è falsa, perché il determinante di una matrice esiste se e solo se la matrice è quadrata In questo caso, la matrice A è triangolare superiore e perciò, siccome il determinante di una matrice triangolare (superiore o inferiore è il prodotto degli elementi della sua diagonale, risulta deta a a 22 a 33 a 44 ( (2 ( ( 2 4
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
MATRICI. 1. Esercizi
 MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
RIDUZIONE E RANGO , C = 2 5 1
 MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 19 Ottobre
 Esercizi Di Geometria (BAER Canale Da consegnare Lunedi 9 Ottobre SETTIMANA 3 (2 8 Ottobre Moltiplicazione di matrici Gli esercizi sono presi dal libro Intorduction to Linear Algebra di Serge Lang Esercizio
Esercizi Di Geometria (BAER Canale Da consegnare Lunedi 9 Ottobre SETTIMANA 3 (2 8 Ottobre Moltiplicazione di matrici Gli esercizi sono presi dal libro Intorduction to Linear Algebra di Serge Lang Esercizio
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R.
 1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Esercizi di Geometria 1 - Foglio 1
 Esercizi di Geometria 1 - Foglio 1 Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso 22 dicembre 2017 Esercizio 1. Sia V uno spazio vettoriale sul
Esercizi di Geometria 1 - Foglio 1 Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso 22 dicembre 2017 Esercizio 1. Sia V uno spazio vettoriale sul
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
ALGEBRA DELLE MATRICI
 ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
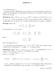 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
0.1 Soluzioni Foglio di esercizi 1: Matrici
 0.1 Soluzioni Foglio di esercizi 1: Matrici Esercizio 1 (dal Test di Autovalutazione 3/11/2015 M.Manaresi) Siano 1 1 1 1 A 2 2 0, B 1, 1 0 X M 3 (R) Si stabilisca per quali valori del parametro reale k
0.1 Soluzioni Foglio di esercizi 1: Matrici Esercizio 1 (dal Test di Autovalutazione 3/11/2015 M.Manaresi) Siano 1 1 1 1 A 2 2 0, B 1, 1 0 X M 3 (R) Si stabilisca per quali valori del parametro reale k
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Matematica II
 Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
1 Spazi vettoriali. Sottospazi.
 CORSO DI ALGEBRA LINEARE. A.A. 004-005. Esercitazione del 10 Gennaio 005. (Prof. Mauro Saita, e-mail: maurosaita@tiscalinet.it) 1 Spazi vettoriali. Sottospazi. Esercizio 1.1 Siano v 1 = (, 5, 1, 3), v
CORSO DI ALGEBRA LINEARE. A.A. 004-005. Esercitazione del 10 Gennaio 005. (Prof. Mauro Saita, e-mail: maurosaita@tiscalinet.it) 1 Spazi vettoriali. Sottospazi. Esercizio 1.1 Siano v 1 = (, 5, 1, 3), v
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE
 ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Geometria per Fisica e Astrofisica
 Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij
![a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij](/thumbs/102/154682810.jpg) Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
I determinanti. a11 a A = 12 a 21 a 22
 I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
Sommario lezioni di geometria
 Sommario lezioni di geometria C. Franchetti November 12, 2006 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 ) indica
Sommario lezioni di geometria C. Franchetti November 12, 2006 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 ) indica
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi e matrici - Risposte pagina 1 di 17 4
 Sistemi e matrici - isposte pagina di 7 4 Premessa: Uso dei simboli [, ] e [ ± ]. Questi simboli di uso corrente possono significare la congiunzione logica e o la congiunzione logica o a seconda delle
Sistemi e matrici - isposte pagina di 7 4 Premessa: Uso dei simboli [, ] e [ ± ]. Questi simboli di uso corrente possono significare la congiunzione logica e o la congiunzione logica o a seconda delle
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
4 0 = 4 2 = 4 4 = 4 6 = 0.
 Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Matematica II
 Matematica II 231111 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Matematica II 231111 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
ESERCIZI DI MATEMATICA DISCRETA ANNO 2006/2007
 ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Corso di Studi in Fisica. Geometria e Algebra Lineare II Prova scritta del 6 luglio 2009
 Corso di Studi in Fisica Geometria e Algebra Lineare II Prova scritta del 6 luglio 009 Esercizio 1. Si considerino le matrici 3 1 1 3 1 1 A = 0 4 0, B = 3 1 3 1 1 3 0 a. (4 punti) Dimostrare che A e B
Corso di Studi in Fisica Geometria e Algebra Lineare II Prova scritta del 6 luglio 009 Esercizio 1. Si considerino le matrici 3 1 1 3 1 1 A = 0 4 0, B = 3 1 3 1 1 3 0 a. (4 punti) Dimostrare che A e B
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI. Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte.
 Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
