O4 - LO SPETTRO OTTICO
|
|
|
- Cristina Fusco
- 9 anni fa
- Visualizzazioni
Transcript
1 O4 - LO SPETTRO OTTICO Non parliamo di fantasmi, lenzuoli e catene. In fisica, uno spettro è una successione di radiazioni, della stessa natura, di lunghezza d onda compresa fra un minimo ed un massimo. Ci limitiamo per ora a richiamare quanto già accennato all inizio del primo articolo della serie (O1) e ad illustrare alcune esperienze; un approfondimento teorico si trova più avanti, alla pag. 32 e nella bibliografia citata all inizio (vedi anche il manuale Problemi tecnici della microscopia, Cap. 1.1). Sappiamo già che, per i suoni, una differenza di frequenza (o di lunghezza d onda), procura al nostro orecchio sensazioni di diversa altezza : si parla di suoni gravi ed acuti. Il nostro orecchio ( medio, cioè per una persona giovane e sana senza difetti particolari) è sensibile a suoni con frequenza compresa fra circa 20 Hz e Hz. Questo intervallo di frequenze rappresenta lo spettro acustico, cioè l intera gamma dei suoni udibili. Le vibrazioni di frequenza inferiore a 20 Hz si chiamano infrasuoni ; quelle di frequenza superiore a o Hz sono dette ultrasuoni. Sembra che taluni animali di gran mole siano sensibili agli infrasuoni, mentre quelli piccoli possono percepire ultrasuoni ad elevata frequenza. Un suono, o per meglio dire un rumore, che contiene tutte le frequenze dello spettro acustico, si chiama rumore bianco, per analogia con ciò che si fa per lo spettro ottico. Per le radiazioni elettromagnetiche, abbiamo già chiarito che l occhio medio percepisce onde di lunghezza d onda λ21 compresa fra circa 0,4 μ e 0,75 μ; questo è lo spettro ottico e quelle sono le radiazioni ottiche. Ricordiamo che 1 μ = 0,001 mm. Ebbene, una sorgente che emettesse tutte le lunghezze d onda comprese nello spettro ottico ci darebbe la sensazione di bianco : il nostro occhio non sarebbe in grado di distinguere tutte le lunghezze d onda presenti e ci fornirebbe una sensazione globale. Ma, se noi offriamo all occhio una radiazione monocromatica, formata da onde della stessa lunghezza, che sensazione ci dà il nostro occhio? Dalla tavola a pag. 36, fig. 63, e dalla striscia colorata a destra di essa, risulta che, partendo dall alto (λ = 0,4 μ), e supponendo di variare la λ fino a 0,75 μ, il nostro occhio ci fa percepire dei colori molto vivi, che corrispondono a quelli dell iride (= arcobaleno). Sono questi i colori puri o colori spettrali. Ma i colori dei corpi che vediamo ogni giorno sono misti, cioè creati da un miscuglio assai vario di differenti lunghezze d onda o di intere porzioni ( bande ) dello spettro ottico. In maggioranza, le sorgenti abituali (sole, cielo, lampadine ad incandescenza ed alogene fiamme, ecc.) sono bianche, ma non ideali, nel senso che non emettono con la stessa intensità per tutto lo spettro. Se prevale la regione a forte lunghezza d onda (giallo-rosso), il bianco avrà una dominante giallognola, come il sole al tramonto o una lampadina ad incandescenza; se prevale la regione a minor lunghezza d onda (blu-viola), il bianco avrà una dominante azzurrognola, come il cielo sereno, e così via. Per descrivere la composizione della radiazione emessa da una qualunque sorgente non basta quindi scrivere di quali lunghezze d onda essa è composta, ma occorre dire anche per ogni valore di λ quale è l intensità della sorgente; ciò si rappresenta bene con una curva di emissione spettrale, cioè un diagramma cartesiano in cui si mette in ascissa il valore di λ (all interno dello spettro ottico o di regioni simili) ed in ordinata il valore di intensità. Si veda la fig. 64 o 68, più avanti. Volendo descrivere una certa sorgente, magari seguita da qualche filtro selettivo, sarebbe dunque utile ricavarne la curva di emissione; ciò richiede però uno strumento speciale (spettrometro). Noi dobbiamo limitarci ad una valutazione qualitativa; ecco come. Nelle figure degli articoli precedenti, per es. la 15, 17, 19, 21 e soprattutto nella 37, in O2, si sarà notata la riproduzione in bianco e nero, proprio per escludere temporaneamente il problema dei colori. Ora dobbiamo occuparcene. Consideriamo per es. la fig. 37 in O2, e riprendiamo un altra foto dello stesso dispositivo, ma a colori (fig. 56); il fascio emergente dalla faccia 1 del prisma P (fascio R - FD), che già in bianco e nero appariva leggermente allargato a ventaglio, appare ora suddiviso in fasci minori, di 21 Per la regione ottica e per quelle contigue, in luogo della frequenza, che raggiunge valori elevatissimi, si indica di solito la lunghezza d onda indicata, come si è già detto, colla lettera greca lambda (λ). 27
2 diverso colore. Fig. 56 Un prisma retto, utilizzato per deviare un fascio parallelo (I diventa R). Poiché l angolo di deviazione dipende anche dalla lunghezza d onda e quindi dal colore, ecco che la luce bianca del fascio I viene dispersa e nel fascio risultante (FD) si vedono i colori dell iride, dal viola (il più deviato) al rosso (il meno deviato). Ecco uno spettro. Questa disposizione è già stata utilizzata varie volte, per es. nella figura 19 (in O2): la lente a fessure (Lf, a sinistra) produce cinque fasci paralleli; di questi, due da una parte e due dall altra vengono intercettati da due squadrette di cartoncino nero (C); il fascio centrale rimanente (I) incide sulla faccia ipotenusa del prisma P ed emerge da una faccia cateto (1); il fascio dr proviene da due riflessioni interne; quello pr da una prima riflessione esterna sulla faccia 3. Non avevamo detto, all inizio dell articolo O2, che la deviazione di un fascio di luce nella rifrazione dipende, fra l altro, dalla lunghezza d onda (λ) della radiazione utilizzata? Il fatto è che, variando la lunghezza d onda λ, varia anche l indice di rifrazione n e quindi anche la deviazione del fascio rifratto22. Se sul prisma incidesse radiazione monocromatica ( di un solo colore, in greco; per noi di una sola lunghezza d onda), avremmo un solo fascio rifratto. Ma la luce bianca, abbiamo detto, è composta da tutte le lunghezze d onda comprese fra due estremi, cioè da tutto lo spettro ottico. Ne consegue che nel fascio disperso FD avremo tanti fasci diversamente deviati quante sono le lunghezze d onda comprese nel fascio incidente. Qualcosa di simile avviene durante la formazione dell arcobaleno ed i colori di quest ultimo sono ancora quelli della fig. 58 B, più sotto, semplicemente meno saturi a causa della diffusione, ecc. Per meglio separare i vari colori all interno dello spettro prodotto dal prisma, occorrerebbe uno strumento apposito, lo spettroscopio. Un tale strumento però, oltre al prisma, richiede un sistema ottico complesso ed una montatura meccanica non realizzabili con mezzi casalinghi. Consigliamo perciò di perfezionare il dispositivo di fig. 56 sfruttando un proiettore da diapositive. Fig. 57 Il telaietto a fessura (T), da porre nel proiettore da diapositive, in luogo della diapositi-va normale, con la fessura verticale. Mettere a fuoco l obbiettivo del proiettore per avere un im-magine nitida della fessura. Dopo aver comple-tato il dispositivo della figura seguente, si potrà migliorare la saturazione dei colori ritoccando la messa a fuoco. Occorre prima costruire un telaietto speciale: ci si procuri un normale telaietto da diapositive in plastica, senza vetri ; lo si separi nelle due metà; all interno di una di esse, invece della pellicola, si incollino due pezzetti di cartoncino nero (C) di dimensioni tali da occupare l intera finestra del telaietto, salvo una fessura, parallela al lato corto della finestra, al centro della 22 È questa la dispersione dell indice. 28
3 finestra stessa, larga 3-4 mm. Si prenda ora una normale lametta da barba (L in figura) e la si spezzi in due per il lungo (1/2 L). S incollino le due metà della lametta, con la parte affilata verso il centro, sui due cartoncini già incollati, in modo da restringere la fenditura dei cartoncini a circa 1 mm (F)23. Si curi il parallelismo dei due bordi. La ragione di sostituire i bordi del cartoncino col filo di una lametta sta nella necessità di avere bordi netti, senza le sfilacciature delle fibre del cartone. Si richiudano infine le due metà del telaietto. Con altri due pezzetti di cartoncino, è bene accorciare la fessura fino a 4-6 mm di lunghezza. Si ponga ora il telaietto a fessura nel proiettore, con la fessura verticale; si accenda e si focalizzi l immagine della fessura (If) su uno schermo bianco, come in fig. 58 A. Fig. 58 A e B Il proiettore Pr proietta su uno schermo un immagine del telaietto a fessura (If). Una parte del fascio emergente dall obbiettivo (Ob) viene però intercettata dal prisma P, portato alla giusta altezza poggiandolo su uno scatolino (Sc). Sullo schermo si formerà quindi un immagine dispersa della fessura (Sp), sotto forma di piccolo spettro. Sotto, si vede un immagine più dettagliata dello spettro. I colori non hanno né la fedeltà né la brillantezza dei colori reali: nessun sistema fotografico può riprodurre fedelmente ciò che l occhio vede e, per giunta, l illuminazione artificiale dell ambiente ha creato un fondo giallastro. La realizzazione pratica di questo semplice dispositivo fornirà immagini assai più gradevoli di quanto la foto possa fare. Si osservi che i colori associati a minore lunghezza d onda (blu e viola) sono più deviati degli altri poiché ad essi corrisponde un maggior indice di rifrazione. Interponendo lungo il fascio un filtro colorato, si potrà valutare qualitativamente l effetto del filtro in base alla diminuita luminosità di una regione o l altra dello spettro. In mancanza di uno spettrometro Con qualche ritocco, sarà possibile proiettare un immagine come quella di fig. 58 B, ma più brillante: una serie di infinite immagini della fessura, corrispondenti a tutti i valori di lunghezza d onda presenti nella luce bianca della lampadina del proiettore. Poiché l immagine della fenditura non è infinitamente sottile, come già s intuisce dall immagine If di fig. 58 A, le immagini corrispondenti ai vari colori si sovrappongono in parte ed i colori non saranno così puri come dovrebbero. Ridurre la larghezza della fenditura nel telaietto renderebbe più definiti i colori, ma la brillanza dell immagine diminuirebbe. Si cerchi il miglior compromesso. Pensiamo ora ad eseguire l operazione inversa: rimescolare tutti i colori dello spettro per riottenere la luce bianca di partenza. Un primo sistema consiste nell uso di specchietti (fig. 59): si ritaglino col diamante (o rotellina ) tagliavetro, reperibile in ferramenta, da 5 a 10 quadratini di circa 2 2 cm, partendo da uno specchietto da toilette. Si incollino con silicone o plastilina i 5-10 specchietti su una base in cartone o compensato, in modo da tenerli verticali, affiancati come in fig. 59. Conviene mettere la serie degli specchietti almeno a mezzo metro dal proiettore, in modo che il fascio disperso (FD in fig. 56) abbia una larghezza di qualche centimetro. Se si dispone, ad es., di sette 23 Occorrerà accorciare le due mezze lamette per farle entrare nel telaietto: dovrebbe andar bene un pezzo lungo circa 24 mm, ottenuto spezzando la mezza lametta con un paio di pinze. 29
4 specchietti24, si divide per sette la larghezza dello spettro e quella dovrà essere la larghezza utile di ogni singolo specchio. Per facilitare il lavoro, abbiamo supposto di disporre di specchietti di circa 2 2 cm; per evitare che gli specchietti perdano qualche porzione dello spettro, basta disporre gli specchietti in maniera embricata, come si vede dal dettaglio a destra della fig. 59 e lasciare scoperta quella porzione dello specchietto che corrisponde alla larghezza dello spettro divisa per sette. Fatto questo, si orientino gli specchietti (il silicone impiega alcune ore ad indurire; la plastilina non ha limiti) in modo che i sette fasci riflessi convergano verso un unico punto, e lì si metterà un pezzo di cartone bianco verticale (Sc in figura). Fig. 59 Dispositivo per la ricomposizione della luce bianca partendo da un fascio disperso prodotto dal prisma P. Schema visto dall alto. Anche in questo caso, sarà bene ritoccare la messa a fuoco del proiettore per ottimizzare la saturazione dei colori. Tutto il dispositivo andrà poggiato su una tavoletta di legno; un blocchetto, di legno o di polistirolo espanso, permetterà di portare alla giusta altezza gli specchietti. Inutile dire che sullo schermo Sc non si vedrà una macchia puntiforme ma rettangolare, piuttosto grande; infatti, i sette specchietti intercettano sette porzioni rettangolari del fascio disperso prodotto dal prisma, e tali fasci rimangono dispersi dopo la riflessione (gli specchietti sono piani); e non importa che i sette fasci vengano poi riflessi fino a sovrapporsi in Sc. L operazione di allineare i sette specchietti è naturalmente delicatissima, poiché i sette fasci riflessi debbono terminare nello stesso punto dello schermo Sc, sia in direzione verticale che orizzontale. In luogo dei sette specchietti piani, si può far convergere il fascio disperso prodotto dal prisma usando un unico specchio concavo posto in luogo degli specchietti. Si cerchi in una profumeria uno specchio da toilette da ingrandire (i commessi lo chiamano a lente, dimostrando di non saper distinguere fra lente e specchio). Tali specchi si usano per radersi la barba o per il trucco, e forniscono un immagine (virtuale) leggermente ingrandita. Provando e riprovando, si dovrebbe trovare una posizione ed un orientamento dello specchio concavo in grado di dare buoni risultati. Per evitare però di dover mettere lo specchio troppo lontano dal prisma, occorre uno specchietto molto ricurvo, che avrà in genere un diametro minore e forse insufficiente. Se questo non è reperibile, conviene ricorrere ad uno specchietto concavo del tipo che si usava una volta nei microscopi privi d illuminatore incorporato. Un altro modo di ricomporre la luce bianca partendo da un fascio disperso è quello di usare una lente convergente. Va bene una lente d ingrandimento del tipo già usato (vedi l articolo O3, fig. 41, 50, 51). La spiegazione e lo schema di principio del dispositivo sono illustrati più sotto (pag. 39, fig. 67). Vediamo concretamente come si può fare. Si torni alla disposizione di fig. 58 A; lungo il percorso del fascio disperso, fra il prisma P e lo schermo, si interponga una lente d ingrandimento di qualche centimetro di diametro. Le distanze prisma-lente e lente-schermo andranno trovate per tentativi, poiché dipendono dalla focale della lente. Anche la focalizzazione del proiettore andrà ritoccata. La lente dovrà trovarsi col centro alla stessa altezza dell asse dell obbiettivo del proiettore; per far ciò potrebbe bastare il blocchetto di legno che si è già usato in altri dispositivi per sostenerla col manico verticale. Così è stato fatto nella disposizione di fig Si è scelto il numero sette poiché, fin dai tempi di I. Newton, che per primo eseguì la scomposizione della luce bianca a mezzo di un prisma, si sono considerati sette i colori dello spettro: rosso, arancio, giallo, verde, azzurro, indaco, violetto. In realtà i colori spettrali sono infiniti, poiché, fra i due estremi dello spettro ottico, infiniti sono i valori possibili di lunghezza d onda. Che poi il nostro occhio riesca a distinguerli tutti, è un altro paio di maniche 30
5 Fig. 60 La lente d ingrandimento L intercetta il fascio prodotto dal proiettore Pr e disperso dal prisma P ; poiché tale fascio è divergente, la lente lo fa convergere in una figura ristretta (If) sullo schermo posto a distanza adeguata. Un cartoncino orizzontale (Sp), leggermente inclinato, mostra come il fascio, appena emerso dalla lente, sia già più ristretto ma non completamente ricomposto: in esso i colori si distinguono ancora. La macchia If che compare sullo schermo dovrebbe essere bianca, ma non perfettamente; infatti, la sorgente del sistema è la fessura ricavata nel telaietto a fessura e, fra essa e lo schermo, si trova l obbiettivo del proiettore (Ob) e soprattutto la lente L che non è corretta e pertanto è affetta da numerose aberrazioni (vedi O5). Per migliorare le cose, si orienti la lente L, sempre rimanendo verticale il suo piano, ruotandola attorno ad un asse verticale e spostandola orizzontalmente in modo che il fascio attraversi una regione più o meno periferica di essa. Nella fig. 61 si osserva qualche dettaglio in più. Fig. 61 Stesso dispositivo della figura precedente. Per reggere la lente L nella giusta posizione e consentire i suoi spostamenti come descritti nel testo, si è usato lo stesso blocchetto di legno che si vede nella fig. 50 (in O3). Nel blocchetto si è praticato un foro dello stesso diametro del manico della lente; la vite, visibile a destra del blocchetto, serve a fissare tale manico. A parte le inevitabili imperfezioni, la macchia If, almeno al centro, dovrebbe essere quasi bianca. Ecco la ricomposizione della luce bianca. 31
6 LUCE BIANCA SCOMPOSIZIONE e RICOMPOSIZIONE dello SPETTRO OTTICO La luce 25 è una radiazione elettro-magnetica, vale a dire una forma d energia che si irradia nello spazio propagandosi (in un mezzo omogeneo) in linea retta; le linee di propagazione si chiamano raggi. In particolare, si tratta di una variazione periodica di due campi (uno elettrico ed uno magnetico) collegati fra loro. Non deve stupire questa natura complessa della luce; infatti, qualunque sia la sorgente che si considera (lampade, fiamme, corpi celesti, ecc.), la luce è sempre emessa dagli elettroni contenuti negli atomi. Un elettrone può essere disturbato dal suo stato normale, di riposo, quando viene eccitato, cioè quando assorbe una quantità opportuna di energia. Poco importa se quest energia proviene da reazioni chimiche ( chemioluminescenza, come quella delle lucciole ed altri animali e piante luminosi), o dal calore (fiamme, corpi incandescenti, corpi celesti) o da altre radiazioni (fluorescenza, vedi l articolo O 10). Sta di fatto che, in tempi brevissimi, l elettrone ritorna al suo stato di riposo e riemette l energia che aveva assorbito. La quantità d energia emessa dipende dallo stato d eccitazione che l elettrone aveva raggiunto e dallo stato di riposo a cui l elettrone ritorna. Per ogni dato tipo di atomi, cioè per ogni elemento chimico, vi sono numerosi di questi salti energetici possibili dell elettrone e ad ogni salto corrisponde una diversa radiazione che trasporta una diversa quantità di energia. Ora, si pensi che ogni elettrone ruotante attorno ad un nucleo atomico non è altro che una carica elettrica che si sposta nello spazio secondo un orbita periodica, percorsa all infinito, sempre uguale a sé stessa. La fisica insegna che una carica crea attorno a sé un campo elettrico, cioè una porzione di spazio in cui essa può esercitare su altre cariche una forza di attrazione o repulsione. Poiché la carica dell elettrone si può spostare nello spazio (avvicinandosi od allontanandosi al nucleo dell atomo, semplificando molto), essa può cedere od acquistare energia; quando la cede, lo fa sotto forma di onda. Si ha così un campo elettrico oscillante. Allo stesso modo si produce un campo magnetico oscillante: un elettrone rappresenta una carica in movimento e cioè una elementare corrente elettrica. Ebbene, qualunque corrente elettrica produce un campo magnetico; basta pensare alle elettrocalamite dei campanelli e dei motori elettrici. Così l elettrone produce simultaneamente un campo elettrico ed uno magnetico; poiché l elettrone si comporta anche come un onda, così pure i campi da esso prodotti oscillano; e poiché la causa è unica, i due campi oscillano in perfetto sincronismo. Per ogni grandezza oscillante, come i nostri campi elettrico e magnetico, si può dire che qualcosa, per es. l intensità dei campi, varia continuamente di valore, da un minimo ad un massimo e viceversa, con andamento periodico. In altre parole, ad intervalli di tempo regolari, il campo riassume (periodicamente) lo stesso valore, che sia il massimo, il minimo, o qualunque altro valore intermedio. Si chiama periodo (T) questo intervallo costante di tempo dopo il quale il campo oscillante riassume lo stesso valore 26. E si chiama frequenza il numero di volte, ogni secondo, in cui il campo ritorna allo stesso valore, cioè il numero di periodi contenuti in un secondo. L unità di misura della frequenza è l Hertz 27, simboleggiato con Hz. Un Hertz ( 1 Hz ) è la frequenza di un oscillazione che ripete una volta ogni secondo il ciclo completo delle sue variazioni. Ma quest oscillazione del campo si propaga nello spazio e quindi, se supponiamo di metterci in un dato punto dello spazio, vedremo l oscillazione che passa: il campo in quel punto varierà periodicamente nel tempo. Possiamo visualizzare questo fenomeno osservando uno specchio d acqua tranquilla e creandovi un disturbo, alterandone lo stato di riposo. Basta gettarvi un oggetto qualunque: una certa massa d acqua è bruscamente spostata, potremmo dire eccitata, e, nel tornare allo stato di 25 Meglio dire radiazione ottica per indicare che si tratta di un agente fisico; il termine luce si riferisce ad una sensazione, ad una rappresentazione psichica (vedi il manuale Problemi tecnici della microscopia, Cap. 1.1). 26 variando nello stesso senso e dopo aver traversato l intero ciclo periodico di variazione 27 tratto dal nome di Heinrich Rudolf HERTZ ( ), fisico tedesco, scopritore delle onde elettromagnetiche (1887). 32
7 riposo, restituisce l energia assorbita producendo un onda 28. Se vicino al punto di caduta, vale a dire alla sorgente delle onde, si trova un qualunque oggetto galleggiante, si osserva che quest oggetto oscilla, sale e scende periodicamente; si osserva anche che l onda, l oscillazione della superficie del liquido, si propaga dalla sorgente in tutte le direzioni colla stessa velocità: le onde sono, infatti, circolari. Se ora fissiamo l attenzione sul corpo galleggiante, vedremo l onda che passa e si propaga, ma il corpo oscilla rimanendo fermo nella stessa posizione media: ciò che si propaga è l oscillazione, non l acqua. Se guardiamo la fig. 62, vediamo un piano P che può rappresentare la superficie dell acqua; il piano V è il piano in cui si verificano le oscillazioni della superficie dell acqua; D è la direzione di propagazione dell onda; E è lo spostamento della superficie, rispetto alla posizione di riposo, in un dato istante; Eo è il valor massimo dello spostamento, detto ampiezza dell onda. Il piano V della figura può rappresentare un diagramma cartesiano; se l asse D (ascisse) rappresenta il tempo che passa, allora la curva rappresenta il movimento della superficie in un dato punto dello spazio; se D invece rappresenta lo spazio, cioè le distanze crescenti dalla sorgente, la curva rappresenta, in un dato istante, la posizione della superficie dell acqua lungo una direzione di propagazione. Fig Schema di un oscillazione non smorzata con andamento sinusoidale. Spiegazione nel testo. Dalla fig. 62, supponendo che l onda si propaghi nella direzione D, è chiaro che due creste dell onda, due punti equivalenti (in questo caso, di massimo spostamento verso l alto) sono distanti della lunghezza λ, in cui il simbolo λ 29 indica la lunghezza d onda. Il tempo impiegato dall onda a percorrere la lunghezza λ è il periodo sopra definito. Indicando con T il periodo (un tempo), con ν la frequenza 30 (il numero di periodi che stanno in un secondo), con λ la lunghezza d onda (una lunghezza), con V la velocità di propagazione dell onda, cioè lo spazio percorso nell unità di tempo, si può intuire che: ν = 1 / T = V / λ (1) λ = V / ν = V T (2) V = λ ν (3) Dalla (2) e dalla (3) si vede che frequenza (ν) e lunghezza d onda (λ) sono inversamente proporzionali: al crescere dell una decresce l altra. Si suppone che, per un dato tipo di onda ed un dato materiale 31, la velocità V sia costante: V = cost. Esaminiamo ora un altro tipo di onde, quelle acustiche, i suoni. Si tratta ancora di onde che consistono nello spostamento di materia (i suoni si propagano nei gas, nei liquidi o nei solidi, ma non nel vuoto) ma, invece dell altezza della superficie dell acqua, ciò che varia, che oscilla, è la pressione del mezzo. Per rendersene conto, basta collegare un altoparlante ad un generatore di segnali acustici, tramite un amplificatore 32 : sfiorando colle dita la membrana dell altoparlante, si sentirà una rapida successione di urti; se il volume è sufficiente, si potrà far vibrare un foglio di carta posto in prossimità dell altoparlante. Perciò l aria circostante viene compressa e decompressa periodicamente. Ciò che si propaga intorno non è una corrente d aria, ma una successione d onde di pressione. Così la fig. 62 può rappresentare la variazione della pressione nel tempo, in un dato punto dello spazio, oppure la distribuzione della pressione nello spazio (lungo la direzione di 28 In verità, quest onda consiste in uno spostamento di materia (acqua), non nella variazione di un campo elettromagnetico come nel caso delle onde elettromagnetiche, ma il paragone calza ugualmente. 29 λ è la lettera l minuscola dell alfabeto greco o lambda. 30 ν è la lettera n minuscola dell alfabeto greco o nu. 31 Il materiale in cui si propaga un onda è detto mezzo. 32 La frequenza sia fra 10 e 200 Hz, l ampiezza sufficiente a far vibrare di qualche decimo di mm il cono dell altoparlante. 33
8 propagazione) in un dato istante. Ma c è una differenza: le onde sulla superficie dell acqua sono trasversali, cioè la superficie dell acqua si sposta su e giù mentre l onda si propaga orizzontalmente; invece, nel caso delle onde sonore, l aria (o comunque il mezzo ) oscilla avanti e indietro, cioè lungo la stessa direzione di propagazione. Si dice che le onde sonore sono longitudinali. Per il resto, si applicano ai suoni gli stessi concetti di periodo, frequenza, lunghezza d onda e velocità di propagazione. La frequenza ν dei suoni udibili (che un orecchio sano mediamente percepisce) va da 20 a Hz circa; la velocità di propagazione (V) nell aria in condizioni normali di temperatura e pressione è di circa 340 m al secondo; la lunghezza d onda va da 17 m (20 Hz) a 2,3 cm (a Hz). Ma ora dobbiamo porci un problema: variando la frequenza di un suono, cosa succede? Ovviamente varia la λ (formula (2)), ma ciò ci fa percepire il suono più acuto, più alto (maggior frequenza) oppure più grave, più basso (minor frequenza); dunque la frequenza determina l altezza dei suoni; un parametro fisico ( ν ) influisce su una percezione (altezza dei suoni). E torniamo alle onde elettromagnetiche, quelle in cui oscillano insieme un campo elettrico ed uno magnetico. Si tratta di onde trasversali, come dimostrano certe osservazioni 33, di lunghezza d onda e di frequenza assai variabili. Poiché frequenza e lunghezza d onda variano entro limiti assai ampi (in teoria, da 0 all infinito), occorre dividere le onde elettromagnetiche in tante gamme o bande 34 con proprietà ed interesse pratico assai diversi. La tavola alla pagina seguente illustra l intero spettro delle radiazioni elettro-magnetiche. Per spettro s intende una successione di onde dello stesso tipo, con frequenza variabile da un minimo ad un massimo. Si noti che, nella tavola, le colonne che indicano la frequenza, la lunghezza d onda, ecc. sono disegnate in scala logaritmica, e cioè ognuna delle caselle di altezza costante non corrisponde ad intervalli unitari (1, 2, 3, 4, ecc.) ma a potenze di 10 (es = 10 ; 102 = 100 ; 103 = ; 10 4 = ; 105 = ; 106 = , ecc.). In altre parole, una data casella indica valori di frequenza o lunghezza d onda pari a quelli delle caselle contigue moltiplicati o divisi per 10. Per le frequenze, come si fa per altre grandezze, si usano i multipli: Kilo (K) pari a (10 3 ); per es. 1 KHz = Hz. Mega (M) pari a un milione (10 6 ). 1 Mz = Hz. Giga (G) pari ad un miliardo (10 9 ). Tera (T) pari a miliardi (10 12 ). Per le lunghezze si sono usati i sottomultipli: milli (m) pari ad un millesimo = 0,001 = 1 / 10 3 = 10-3 ; es.: 1 mm = 0,001 m. micro (μ) pari ad un milionesimo = 1 / 10 6 = 10-6 nano (n) pari ad un miliardesimo = 10-9 pico (p) pari al millesimo di miliardesimo = Applicati al metro ( m ), questi sottomultipli portano a: millimetro = mm (millesimo di m = m = 10-3 m) micromètro o micron = μm o μ (millesimo di mm = milionesimo di metro = 10-6 m) nanomètro = nm = milionesimo di mm ( = miliardesimo di m = 10-9 m) picomètro = pm = miliardesimo di mm = m Per frequenze molto basse, al di sotto di 10 KHz, non si parla normalmente di onde, poiché la loro trasmissione è molto debole; si tratta di campi elettromagnetici generati da correnti alternate a frequenza acustica, come le correnti usate negli impianti acustici, nelle reti di distribuzione dell energia elettrica, in molte macchine elettriche, ecc. Per frequenze maggiori (10 o più KHz, fino a MHz) si può parlare di radio-onde nel senso che tali onde sono utilizzabili per trasmissioni di qualche genere. La loro lunghezza d onda è relativamente grande, sempre superiore ad 1 mm. Nelle bande radio, le onde a lunghezza d onda minore (micro-onde) hanno applicazioni anche in medicina, nella tecnologia radar, ecc.; esse sono facilmente concentrabili in fasci stretti, e ciò permette la 33 i fenomeni di polarizzazione, la diffusione della luce nei gas, ecc. 34 Per banda s intende una porzione più o meno larga dello spettro, in cui l intensità della radiazione può variare in funzione della lunghezza d onda. 34
9 direttività dei sistemi di rilevamento radar o il riscaldamento localizzato di organi nella Marconi-terapia. In cucina, i forni a micro-onde sfruttano analoghe radiazioni per riscaldare e per cuocere cibi e bevande. Al di sotto di 1 mm 35 si parla di infrarosso (IR). Queste onde possono ancora essere usate come mezzi di trasmissione (sistemi antifurto, telecomandi, ecc.), ma il loro effetto è essenzialmente termico, nel senso che provocano il riscaldamento del corpo su cui cadono 36. Non hanno apprezzabili effetti chimici. Possono traversare alcuni corpi opachi alla luce, come del resto fanno anche le radio-onde 37. A questo punto, le lunghezze d onda divengono assai piccole: la banda IR si prolunga al di sotto del millesimo di mm e precisamente fino a circa 0,0008 mm = 0,8 μm = 800 nm. Al di sotto di 0,8 o 0,75 μ e fino a 0,4 μ, le radiazioni elettro-magnetiche producono un effetto percepibile da parte dell occhio umano sano; si parla di radiazioni ottiche (il termine visibili è improprio poiché una radiazione o uno spettro non sono di per sé visibili o luminosi : essi producono solo un effetto ottico, cioè una reazione fisiologica nell occhio umano). Quindi lo spettro ottico, la banda di radiazioni elettro-magnetiche capaci di darci la sensazione di luce, comprende onde elettromagnetiche con lunghezza d onda compresa fra circa 0,4 e 0,75 μ. All interno di questo particolare spettro, molto ristretto in confronto all intero spettro elettromagnetico, il nostro occhio ci mostra le differenze di lunghezza d onda come differenze di colore; ricordiamo che, nello spettro delle onde elastiche, il nostro orecchio ci fa percepire le differenze di lunghezza d onda come differenze di altezza dei suoni. Con le lunghezze d onda maggiori, il nostro occhio ci dà la sensazione di rosso; da 0,65 a 0,6 μ circa si passa all arancio ed al giallo; fra 0,6 e 0,5 μ si passa dal verde al blu; fino al limite inferiore di circa 0,4 μ si passa al viola sempre più scuro. Di sotto a 0,4 μ il nostro occhio mediamente non viene più stimolato. Le onde di lunghezza d onda ancora minore (dette ultraviolette o UV, poiché si trovano al di là del viola nello spettro generale), hanno essenzialmente effetti chimici e biologici, possono suscitare una fluorescenza visibile (articolo O 10) ed impressionano le emulsioni fotografiche. Sono prodotte da lampade speciali (in misura minima dalle normali lampade ad incandescenza), dal sole e da altri corpi celesti, ecc. Per lunghezze d onda inferiori a circa 10 nm si parla di raggi X (o Röntgen, dal nome dello scopritore), ben noti per le loro applicazioni nella diagnosi medica, con forti effetti chimici e biologici. Vi sono anche radiazioni più corte, come i raggi γ ( gamma, lettera g minuscola dell alfabeto greco), che vengono prodotti da salti energetici del nucleo atomico. Queste radiazioni sono molto penetranti; per esse, come per i raggi X, i tessuti molli degli organismi sono trasparenti. Si formano nel decadimento dei nuclei radioattivi, in certi corpi celesti, ecc. 35 I limiti fra una banda e l altra non sono universalmente condivisi; riferendosi alle sorgenti disponibili, alle tecniche di manipolazione e di rivelazione, molti autori indicano limiti diversi. 36 In realtà, qualunque radiazione elettro-magnetica, quando è assorbita da un corpo, viene più o meno trasformata in calore. 37 L infrarosso è emesso da tutti i corpi caldi (con temperatura superiore allo zero assoluto). Un animale omeotermo (35-40 C) emette su una lunghezza d onda intorno a 10 μm. 35
10 Fig
11 A questo punto, è chiara la posizione e l estensione dello spettro ottico nel generale spettro delle onde elettromagnetiche: una frazione molto piccola. All interno dello spettro ottico supponiamo ora di isolare un fascio di radiazione dotata di una lunghezza d onda unica, vale a dire monocromatica (dal greco: Di un solo colore ); in realtà, qualunque sorgente reale produce radiazioni comprese in uno spettro, per quanto ristretto; ma con opportuni accorgimenti si ottiene una radiazione che si può considerare monocromatica sotto molti aspetti. Ebbene, variando la lunghezza d onda entro i limiti dello spettro ottico, il nostro occhio ci dà una sensazione di vario colore, secondo l ordine sopra riassunto, e tali colori si possono chiamare puri. Ma il nostro occhio, nonostante le sue elevate prestazioni, è un cattivo giudice della composizione spettrale di una radiazione ottica. Chiariamoci: in un diagramma cartesiano come quello di fig. 64, si possono indicare in ascissa le lunghezze d onda ed in ordinata le intensità di un fascio ottico per ogni valore di λ. In tale diagramma, una radiazione monocromatica sarebbe indicata da un segmento verticale (curva 1 in fig. 64), di altezza proporzionale all intensità. La curva 2 rappresenta l emissione di una lampadina ad incandescenza, che ha un massimo di emissione nell infrarosso. Si vede bene che tale sorgente emette con tutti i colori dello spettro ottico, in misura maggiore o minore; eppure essa ci appare bianca, o almeno giallognola. Ciò avviene con altre sorgenti artificiali, con le fiamme, il sole ed in genere le stelle, ecc. Dunque la sensazione di bianco è falsa, poiché ci nasconde i singoli colori puri, come sopra definiti. Ma c è di più: vi sono coppie di colori più o meno puri che, mescolati assieme, producono la sensazione di bianco: per es. rosso e verde-azzurro, oppure viola e giallo: sono i cosiddetti colori complementari. Ancora una volta, l occhio non c indica la composizione spettrale di una radiazione composta e le nostre sensazioni sono ingannevoli. Del resto, molti sistemi di riproduzione dei colori (stampa tipografica in tricromìa, fotografia a colori, televisione a colori) ottengono la riproduzione di quasi tutti i colori, compreso il bianco, con fedeltà accettabile, utilizzando tre colori fondamentali e mescolandoli in rapporto opportuno. Le deficienze di questi sistemi, e le differenze fra l uno e l altro, stanno soprattutto nella difficoltà di definire e riprodurre i colori fondamentali secondo una curva spettrale standardizzata. La riproduzione di tutti i colori e del bianco mediante la somma ponderata di tre colori fondamentali si chiama sintesi additiva. Fig. 64 Distribuzione spettrale di una lampada ad incandescenza (2) e di un laser ad He Ne (1). La curva (3) dà la sensibilità spettrale dell occhio medio in visione diurna (fotopica); con scarsa illuminazione, la risposta dell occhio è spostata verso le minori lunghezze d onda, e si chiama scotopica. Se dunque noi disponiamo della radiazione di una sorgente bianca (sole, fiamme, lampade ad incandescenza, ecc.), noi possiamo decomporla nei suoi colori puri con un opportuno strumento: lo spettroscopio. Più semplicemente, si può fare ciò, con qualche limitazione, usando un fascio ristretto proveniente da una sorgente lontana (per es. un fascio di sole attraverso una fessura nelle imposte) e decomponendolo con un prisma in vetro. Ne abbiamo parlato sopra, e qui entriamo in qualche dettaglio. Si veda la fig. 65: il raggio incidente (I) attraversa una prima volta la faccia di sinistra del prisma, da aria a vetro, poi emerge dalla faccia destra, da vetro ad aria. Tutte le volte che un fascio di radiazione attraversa la superficie di separazione fra due materiali ( mezzi ) diversi e trasparenti, avviene la rifrazione ed il fascio 38 viene deviato. Questa deviazione avviene secondo leggi note e dipende da una proprietà dei mezzi trasparenti, detta indice di rifrazione (n); questo n è pari a poco più di 1,00 per l aria ed i gas leggeri, è 1,5 / 1,6 per i normali vetri, è 1,33 per l acqua, ecc. Tutte cose che abbiamo già detto nei precedenti articoli. 38 Tranne il caso che il fascio incida perpendicolarmente sulla superficie. 37
12 Fig Deviazione operata da un prisma Fig Dispersione di un fascio di luce bianca Si può dimostrare che, emergendo dal prisma di fig. 65, il raggio incidente è stato deviato due volte dalla stessa parte e la deviazione totale è indicata con δ 39. Questo schema è però rigoroso solo se il fascio incidente è formato da onde della stessa lunghezza d onda (monocromatico). Con una radiazione mista, in particolare bianca, vale a dire che si estende per tutto lo spettro ottico, l angolo δ non è unico, ma dipende dalla lunghezza d onda: fra valore massimo e minimo di δ vi è un angolo di dispersione (Δ δ in fig. 66); in alte parole, il fascio emergente è disperso, cioè allargato a ventaglio e, proiettandolo su uno schermo, si osserva la normale serie dei colori dell arcobaleno: rosso (il meno deviato), arancio, giallo, verde, blu viola. Prima del rosso, vi sarà normalmente una regione non visibile occupata dalla radiazione infrarossa, rivelabile con opportuna fotocellula 40. Oltre il viola vi sarà un fascio ultravioletto, anch esso non visibile ma rivelabile con una lastra fotografica, con un corpo fluorescente 41, ecc. Indicazioni pratiche su come osservare lo spettro ottico sono già state date. Per rivelare le componenti UV ed IR di solito presenti in una sorgente bianca si può anche utilizzare il fascio diretto di una lampada interponendo un opportuno filtro, trasparente solo per la banda desiderata. Per l ultravioletto prossimo si può usare il vetro all ossido di cobalto (per es. il vetro Schott UG 1); per l infrarosso va bene il filtro in gelatina Kodak Wratten n 97. Nel fascio che ha traversato tali filtri, l occhio non percepisce più la radiazione della sorgente bianca, poiché lo spettro ottico è stato assorbito dal filtro. Solo con i sensori citati sopra si può dimostrare la presenza di radiazione non ottica, UV od IR (a volte chiamata impropriamente luce nera ) 42. Una volta ottenuta la decomposizione della radiazione bianca nei suoi colori elementari (colori spettrali puri), si può anche eseguire il passaggio inverso, ricomponendo la luce bianca per sovrapposizione di tutti i colori puri dello spettro. Il metodo più classico è quello del disco di Newton : un disco diviso in settori circolari, di solito sette, colorati secondo le varie parti dello spettro della luce bianca. Ruotando il disco con sufficiente velocità, la persistenza delle immagini retiniche fa sì che l impressione data da uno dei settori permanga per un tempo sufficiente (mediamente 1 / 30 di secondo) perché si sommino le impressioni date dai settori di tutti gli altri colori. Il mescolamento dei colori puri avviene dunque nella rètina e l occhio ha l impressione che il disco rotante sia bianco. In pratica, poiché i colori a stampa non possono avere la purezza dei colori dello spettro, il bianco così ottenuto sarà piuttosto sporco. Più fedele è il bianco ottenuto concentrando l intero spettro (ottenuto per dispersione da un prisma) per mezzo di una lente convergente, come nella fig. 67 : da sinistra proviene un fascio collimato di luce bianca (I); il prisma P lo disperde e forma uno spettro nel piano di L ; qui si 39 La lettera δ (delta minuscola) è la d dell alfabeto greco. 40 Meglio usare una fotocellula al silicio collegata ad un microamperometro, ma va bene anche una fotoresistenza (LDR) collegata ad un ohmmetro. Con queste fotocellule è in genere possibile rivelare anche la componente UV dello spettro, benché la loro sensibilità sia massima nell IR. 41 Può bastare un cartoncino grigio, non sbiancato, colorato con un pennarello evidenziatore giallo o verde. Vedi l articolo O È bene eseguire questa prova con una lampada a fascio concentrato, un faretto, una lampada da microscopìa, ecc. 38
13 trova una lente convergente di sufficiente potenza che fa convergere in F i singoli fasci corrispondenti agli infiniti colori puri dello spettro 43. In questo caso, sono le stesse radiazioni costituenti lo spettro a sovrapporsi in F ; se il bianco ricomposto in F non è identico a quello del fascio incidente I, ciò può dipendere da un imperfetta trasparenza dei vetri, dalle aberrazioni cromatiche della lente L 44 e simili. Come realizzare questo dispositivo con mezzi semplici è già stato detto (fig. 60 e 61). Fig Ricomposizione della luce bianca da un fascio disperso A questo punto, con una disposizione come quella di fig. 67, è possibile creare i colori di sottrazione : si intende con ciò il colore misto che si ottiene sottraendo dalla luce bianca una qualche regione dello spettro ottico. Nel piano S, a ridosso della lente L, si trova l intero spettro, cioè il fascio bianco I disperso dal prisma P ; se interponiamo in S un qualunque corpo opaco O (largo circa 1/5 o 1 / 10 dell intero spettro), il fascio bianco di sintesi proiettato in F sarà privato della banda spettrale obliterata da O, quindi non sarà più bianco ma colorato; il suo colore per altro non potrà mai essere un colore spettrale puro, bensì un colore misto, pari ad un bianco privato di qualche sua porzione. Sono interessanti a questo proposito i colori di sottrazione usati in alcuni sistemi di riproduzione delle immagini a colori: si possono ottenere (quasi) tutti i colori mescolando opportunamente tre colori di sottrazione fondamentali: il Cyan, il Magenta, il Giallo di sottrazione. Ognuno di questi è derivato da un fascio bianco, privato di uno dei tre colori fondamentali per la sintesi additiva sopra citati: il Cyan deriva da un bianco privato della banda rossa ( bianco meno rosso, quindi una somma di giallo-verde-blu-viola); il Magenta è un bianco privato della regione verde ( bianco meno verde, quindi una somma di rosso-arancio-blu-viola) ed il Giallo di sottrazione è un bianco privato del blu-viola ( meno viola, quindi una somma di rosso-giallo-verde). Si noti che è facile definire un colore puro come porzione dello spettro di larghezza infinitesimale; basta indicare la lunghezza d onda λ. Più difficile è definire un colore fondamentale, di addizione o di sottrazione, poiché si tratta di bande al cui interno va definita una curva come quella di fig. 64, che indica l energia contenuta in un fascio per ogni valore di lunghezza d onda. Per es., dire che il Cyan è un colore misto ottenuto da un bianco meno rosso è del tutto generico: bisogna indicare la larghezza di questa banda del rosso e, all interno di questa, come varia l intensità in funzione di λ. In fig. 68 sono indicate tre curve che possono tutte corrispondere al Cyan, ma con diversa tonalità e diversa saturazione. 43 Si noti che F non è il fuoco della lente; è solo l immagine coniugata della sorgente virtuale da cui provengono i fasci dispersi, e che si trova molto vicino al prisma. 44 a causa delle quali i fasci monocromatici dello spettro non vengono fatti convergere esattamente nello stesso punto. 39
14 Fig Curve spettrali tutte corrispondenti al colore di sottrazione Cyan Molti dei concetti sopra esposti (cfr. anche la fig. 67) possono essere illustrati disponendo di un proiettore da diapositive e di pochi componenti ottici disposti secondo lo schema di quella figura e delle figure 60 e 61. Nel proiettore Pr si inserisce una diapositiva contenente una fenditura di circa 1 7 mm; davanti all obbiettivo (a 2 o 3 cm) si pone un prisma retto o equilatero (vedi O2). Alla distanza di almeno 50 cm si avrà su uno schermo bianco il dispiegarsi dello spettro ottico. Si dovrà focheggiare l obbiettivo del proiettore fino ad ottenere la maggior saturazione dei colori. È bene oscurare l ambiente. Spostando il prisma lateralmente rispetto al proiettore, si può far sì che una parte del fascio passi di lato al prisma e formi sullo schermo anche un immagine bianca, non dispersa, della fenditura (tornare alla fig.58 A, If). Come si è detto sopra, una fotocellula collegata ad un tester, posta oltre la regione rossa dello spettro, rivelerà l IR; una cellula foto-voltaica al Selenio non si presta bene, poiché ha il massimo di sensibilità nel giallo; più adatta è una cellula fotovoltaica al Silicio o una fotoresistenza (LDR) 45, che hanno il massimo di sensibilità nell arancio-rosso, ma rivelano la presenza di radiazione anche oltre il rosso estremo. Con gli stessi sensori si può rivelare l IR prodotto da un faretto IR o da una lampada ad incandescenza seguita da un filtro IR (per es. il Kodak 97). Se si cerca di rivelare la porzione di spettro UV oltre il limite (violetto) dello spettro ottico si dovrà fare i conti con la scarsa emissione UV delle lampade ad incandescenza, ma si può avere una risposta con un buon tester riparando la cellula dalla luce diffusa Per avere la ricomposizione della luce bianca (fig. 67), ad una trentina di cm dal prisma va disposta la lente d ingrandimento L leggermente disassata ed inclinata46, in modo che l immagine che si forma in F sia il più possibile bianca. A questo punto, subito dopo la lente si disponga un cartoncino largo pochi mm (O in fig. 67), e spostandolo per tutta la lunghezza dello spettro si ha in F un fascio concentrato dotato di un colore di sottrazione, che varia al variare della posizione del cartoncino (è facile ottenere la serie Cyan - Magenta - Giallo di sottrazione). Se in O si pone un cartoncino con due fessure, si avrà in F la sovrapposizione di due bande spettrali e, spostando opportunamente le fessure, le bande possono corrispondere a coppie di colori complementari (verde/blu e rosso; viola e giallo/arancio, per es.) e l immagine in F sarà ancora bianca. Con un cartoncino a tre fessure si possono isolare tre fasci: rosso - verde - e blu/viola (colori fondamentali, di addizione); il fascio concentrato in F sarà di nuovo bianco (o quasi). La larghezza e la distanza delle tre strisce di cartoncino diventeranno sempre più critiche ed il colore risultante in F sarà difficilmente un bianco puro. Ottenere i colori di sottrazione con una sola strisciolina di cartone è facile; ottenere i colori complementari con due o tre diverse fenditure diventa assai più delicato. 45 Le cellule foto-voltaiche vanno collegate al tester disposto per la misura di tensioni (fondo scala 1 V cc o anche meno); per le foto-resistenze (LDR = Light Dependent Resistor), il tester deve essere disposto per la misura di resistenze elevate. 46 Intendiamo che, rispetto alla linea di congiunzione prisma-spettro, la lente dovrà essere leggermente decentrata ed inclinata. 40
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
LA MATERIA MATERIA. COMPOSIZIONE (struttura) Atomi che la compongono
 LA MATERIA 1 MATERIA PROPRIETÀ (caratteristiche) COMPOSIZIONE (struttura) FENOMENI (trasformazioni) Stati di aggregazione Solido Liquido Aeriforme Atomi che la compongono CHIMICI Dopo la trasformazione
LA MATERIA 1 MATERIA PROPRIETÀ (caratteristiche) COMPOSIZIONE (struttura) FENOMENI (trasformazioni) Stati di aggregazione Solido Liquido Aeriforme Atomi che la compongono CHIMICI Dopo la trasformazione
L osservazione in luce bianca è, per così dire, l osservazione del Sole al naturale ovviamente dopo averne attenuato la fortissima emissione di luce.
 L osservazione in luce bianca è, per così dire, l osservazione del Sole al naturale ovviamente dopo averne attenuato la fortissima emissione di luce. Questa attenuazione si ottiene mediante l uso di un
L osservazione in luce bianca è, per così dire, l osservazione del Sole al naturale ovviamente dopo averne attenuato la fortissima emissione di luce. Questa attenuazione si ottiene mediante l uso di un
Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
 Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE
 I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
Spettrofotometria. Le onde luminose consistono in campi magnetici e campi elettrici oscillanti, fra loro perpendicolari.
 Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
All interno dei colori primari e secondari, abbiamo tre coppie di colori detti COMPLEMENTARI.
 Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
www.andreatorinesi.it
 La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto
 Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto rimanda indietro arriva ai nostri occhi. Dipende da: SI PROPAGA
Noi vediamo gli oggetti, perché la luce emessa dalla sorgente arriva all oggetto e si diffonde in tutte le direzioni poi la luce che l oggetto rimanda indietro arriva ai nostri occhi. Dipende da: SI PROPAGA
1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini 1.1 Caratteristiche ottiche dei materiali oftalmici
 1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini Esaminiamo in questo capitolo le principali caratteristiche dei vari materiali utilizzati nel campo dell'ottica oftalmica,
1 Caratteristiche dei materiali utilizzati in ottica oftalmica di Alessandro Farini Esaminiamo in questo capitolo le principali caratteristiche dei vari materiali utilizzati nel campo dell'ottica oftalmica,
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA
 EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
CONOSCERE LA LUCE. Propagazione nello spazio di un onda elettromagnetica.
 FOTODIDATTICA CONOSCERE LA LUCE Le caratteristiche fisiche, l analisi dei fenomeni luminosi, la temperatura di colore. Iniziamo in questo fascicolo una nuova serie di articoli che riteniamo possano essere
FOTODIDATTICA CONOSCERE LA LUCE Le caratteristiche fisiche, l analisi dei fenomeni luminosi, la temperatura di colore. Iniziamo in questo fascicolo una nuova serie di articoli che riteniamo possano essere
1. LE GRANDEZZE FISICHE
 1. LE GRANDEZZE FISICHE La fisica (dal greco physis, natura ) è una scienza che ha come scopo guardare, descrivere e tentare di comprendere il mondo che ci circonda. La fisica si propone di descrivere
1. LE GRANDEZZE FISICHE La fisica (dal greco physis, natura ) è una scienza che ha come scopo guardare, descrivere e tentare di comprendere il mondo che ci circonda. La fisica si propone di descrivere
LA TERMOGRAFIA SPETTRO ONDE ELETTROMAGNETICHE
 SPETTRO ONDE ELETTROMAGNETICHE La radiazione elettromagnetica è un mezzo di trasmissione dell energia sotto forma di onde aventi entrambe le componenti elettriche e magnetiche. La sequenza ordinata delle
SPETTRO ONDE ELETTROMAGNETICHE La radiazione elettromagnetica è un mezzo di trasmissione dell energia sotto forma di onde aventi entrambe le componenti elettriche e magnetiche. La sequenza ordinata delle
OTTICA TORNA ALL'INDICE
 OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
28/05/2009. La luce e le sue illusioni ottiche
 La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Radiazione elettromagnetica
 Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose.
 Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose. 2.1 Spettro di emissione Lo spettro di emissione di
Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose. 2.1 Spettro di emissione Lo spettro di emissione di
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni?
 La natura della luce Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni? Se si potesse fotografare un fotone in un certo istante vedremmo una deformazione
La natura della luce Einstein ci dice che la luce è costituita da unità elementari chiamate fotoni. Cosa sono questi fotoni? Se si potesse fotografare un fotone in un certo istante vedremmo una deformazione
Costruirsi un cannocchiale galileiano
 Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
Costruirsi un cannocchiale galileiano I. INFORMAZIONI PRELIMINARI - IL PRINCIPIO OTTICO Un cannocchiale galileiano impiega due sole lenti. La lente obbiettiva è convergente (piano-convessa), la lente oculare
Traduzioni & Corsi di Lingue Udine. Via Cussignacco 27/4. P. IVA: 02159420302 tel/fax: 0432-229621 scuola@jmi.it
 APPUNTI PRIMO INCONTRO Sono passati quasi duecento anni dall invenzione dei primi strumenti in grado di registrare immagini ma si può dire che la fotocamera è costituita dagli stessi elementi basilari
APPUNTI PRIMO INCONTRO Sono passati quasi duecento anni dall invenzione dei primi strumenti in grado di registrare immagini ma si può dire che la fotocamera è costituita dagli stessi elementi basilari
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it
 LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
4 La Polarizzazione della Luce
 4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
4 La Polarizzazione della Luce Per comprendere il fenomeno della polarizzazione è necessario tenere conto del fatto che il campo elettromagnetico, la cui variazione nel tempo e nello spazio provoca le
Onde elettromagnetiche
 Onde elettromagnetiche Alla metà del XIX secolo Maxwell prevede teoricamente le onde e.m. Sono scoperte sperimentalmente da Hertz Danno la possibilità di comunicare a distanza (radio, televisione, telecomandi
Onde elettromagnetiche Alla metà del XIX secolo Maxwell prevede teoricamente le onde e.m. Sono scoperte sperimentalmente da Hertz Danno la possibilità di comunicare a distanza (radio, televisione, telecomandi
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Dai colori alle stelle: un excursus tra Fisica e Ottica
 Dai colori alle stelle: un excursus tra Fisica e Ottica Martina Giordani Facoltà di Scienze matematiche, fisiche e naturali Corso di Laurea in Ottica e Optometria Federica Ricci Facoltà di Scienze matematiche,
Dai colori alle stelle: un excursus tra Fisica e Ottica Martina Giordani Facoltà di Scienze matematiche, fisiche e naturali Corso di Laurea in Ottica e Optometria Federica Ricci Facoltà di Scienze matematiche,
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini
 SSIS indirizzo Fisico - Informatico - Matematico 2 anno - a.a.. 2006/2007 Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini LA LUCE La luce è un onda elettromagnetica Il principio
SSIS indirizzo Fisico - Informatico - Matematico 2 anno - a.a.. 2006/2007 Corso di Laboratorio di Fisica prof. Mauro Casalboni dott. Giovanni Casini LA LUCE La luce è un onda elettromagnetica Il principio
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
INTRODUZIONE: PERDITE IN FIBRA OTTICA
 INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
INTRODUZIONE: PERDITE IN FIBRA OTTICA Il nucleo (o core ) di una fibra ottica è costituito da vetro ad elevatissima purezza, dal momento che la luce deve attraversare migliaia di metri di vetro del nucleo.
Genova 15 01 14 TIPOLOGIE DI LAMPADE
 Genova 15 01 14 TIPOLOGIE DI LAMPADE Le lampade a vapori di mercurio sono sicuramente le sorgenti di radiazione UV più utilizzate nella disinfezione delle acque destinate al consumo umano in quanto offrono
Genova 15 01 14 TIPOLOGIE DI LAMPADE Le lampade a vapori di mercurio sono sicuramente le sorgenti di radiazione UV più utilizzate nella disinfezione delle acque destinate al consumo umano in quanto offrono
Il campionamento. La digitalizzazione. Teoria e pratica. La rappresentazione digitale delle immagini. La rappresentazione digitale delle immagini
 ACQUISIZIONE ED ELABORAZIONE DELLE IMMAGINI Teoria e pratica La digitalizzazione La digitalizzazione di oggetti legati a fenomeni di tipo analogico, avviene attraverso due parametri fondamentali: Il numero
ACQUISIZIONE ED ELABORAZIONE DELLE IMMAGINI Teoria e pratica La digitalizzazione La digitalizzazione di oggetti legati a fenomeni di tipo analogico, avviene attraverso due parametri fondamentali: Il numero
LA CORRENTE ELETTRICA
 L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
Misura delle proprietà di trasmissione e assorbimento della luce da parte dei materiali mediante spettrofotometro
 Misura delle proprietà di trasmissione e assorbimento della luce da parte dei materiali mediante spettrofotometro Apparato sperimentale: Spettrofotometro digitale SPID HR (U21830) con software di acquisizione,
Misura delle proprietà di trasmissione e assorbimento della luce da parte dei materiali mediante spettrofotometro Apparato sperimentale: Spettrofotometro digitale SPID HR (U21830) con software di acquisizione,
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) Prof. Gianluca Todisco
 Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) 1 LA LUCE NELLA STORIA Nell antica Grecia c era chi (i pitagorici) pensavano che ci fossero dei fili sottili che partono dagli
Che cos è la luce? (Luce, colori, visioni.quale sarà mai il loro segreto?) 1 LA LUCE NELLA STORIA Nell antica Grecia c era chi (i pitagorici) pensavano che ci fossero dei fili sottili che partono dagli
La candela accesa. Descrizione generale. Obiettivi. Sequenza didattica e metodo di lavoro. Esperimenti sulla crescita delle piante
 Esperimenti sulla crescita delle piante unità didattica 1 La candela accesa Durata 60 minuti Materiali per ciascun gruppo - 1 candela - 1 vaso di vetro - 1 cronometro - 1 cannuccia - fiammiferi - 1 pezzo
Esperimenti sulla crescita delle piante unità didattica 1 La candela accesa Durata 60 minuti Materiali per ciascun gruppo - 1 candela - 1 vaso di vetro - 1 cronometro - 1 cannuccia - fiammiferi - 1 pezzo
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione
 Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione 1. L elettrone ha una massa di 9.1 10-31 kg ed una carica elettrica di -1.6 10-19 C. Ricordando che la forza gravitazionale
Esercizi su elettrostatica, magnetismo, circuiti elettrici, interferenza e diffrazione 1. L elettrone ha una massa di 9.1 10-31 kg ed una carica elettrica di -1.6 10-19 C. Ricordando che la forza gravitazionale
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
In anticipo sul futuro. La tecnica termografica come strumento di verifica e diagnosi di malfunzionamenti
 La tecnica termografica come strumento di verifica e diagnosi di malfunzionamenti La tecnica termografica genesi e definizioni Termografia: definizioni e principio di misura Dal greco: Scrittura del calore
La tecnica termografica come strumento di verifica e diagnosi di malfunzionamenti La tecnica termografica genesi e definizioni Termografia: definizioni e principio di misura Dal greco: Scrittura del calore
PROGRAMMA OPERATIVO NAZIONALE
 PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
Ottica fisiologica (2): sistemi ottici
 Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
FONDAMENTI DI ILLUMINOTECNICA
 Prof. Ceccarelli Antonio ITIS G. Marconi Forlì Articolazione: Elettrotecnica Disciplina: Tecnologie e progettazione di sistemi elettrici ed elettronici A.S. 2012/13 FONDAMENTI DI ILLUMINOTECNICA CHE COSA
Prof. Ceccarelli Antonio ITIS G. Marconi Forlì Articolazione: Elettrotecnica Disciplina: Tecnologie e progettazione di sistemi elettrici ed elettronici A.S. 2012/13 FONDAMENTI DI ILLUMINOTECNICA CHE COSA
Con il termine elettrosmogsi designa il presunto inquinamento derivante dalla formazione di campi elettromagnetici (CEM) dovuti a radiazioni
 ELETTROSMOG Con il termine elettrosmogsi designa il presunto inquinamento derivante dalla formazione di campi elettromagnetici (CEM) dovuti a radiazioni elettromagnetiche non ionizzanti, quali quelle prodotte
ELETTROSMOG Con il termine elettrosmogsi designa il presunto inquinamento derivante dalla formazione di campi elettromagnetici (CEM) dovuti a radiazioni elettromagnetiche non ionizzanti, quali quelle prodotte
Appunti sul galleggiamento
 Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
Informatica per la comunicazione" - lezione 7 -
 Informatica per la comunicazione - lezione 7 - Campionamento La codifica dei suoni si basa sulla codifica delle onde che li producono, a sua volta basata su una procedura chiamata campionamento.! Il campionamento
Informatica per la comunicazione - lezione 7 - Campionamento La codifica dei suoni si basa sulla codifica delle onde che li producono, a sua volta basata su una procedura chiamata campionamento.! Il campionamento
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Come costruire una distribuzione di frequenze per caratteri quantitativi continui
 Come costruire una distribuzione di frequenze per caratteri quantitativi continui Consideriamo i dati contenuti nel primo foglio di lavoro (quello denominato dati) del file esempio2.xls. I dati si riferiscono
Come costruire una distribuzione di frequenze per caratteri quantitativi continui Consideriamo i dati contenuti nel primo foglio di lavoro (quello denominato dati) del file esempio2.xls. I dati si riferiscono
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
La lente singola rimane ancora in uso nelle macchine più economiche e, entro certi limiti, dà dei risultati accettabili.
 O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
 IL TRASFORMATORE Prof. S. Giannitto Il trasformatore è una macchina in grado di operare solo in corrente alternata, perché sfrutta i principi dell'elettromagnetismo legati ai flussi variabili. Il trasformatore
IL TRASFORMATORE Prof. S. Giannitto Il trasformatore è una macchina in grado di operare solo in corrente alternata, perché sfrutta i principi dell'elettromagnetismo legati ai flussi variabili. Il trasformatore
Queste note non vogliono essere esaustive, ma solo servire come linee guida per le lezioni
 Alessandro Farini: note per le lezioni di ottica del sistema visivo Queste note non vogliono essere esaustive, ma solo servire come linee guida per le lezioni 1 Lo spettro elettromagnetico La radiazione
Alessandro Farini: note per le lezioni di ottica del sistema visivo Queste note non vogliono essere esaustive, ma solo servire come linee guida per le lezioni 1 Lo spettro elettromagnetico La radiazione
L analisi della luce degli astri: fotometria e spettrometria
 Università del Salento Progetto Lauree Scientifiche Attività formativa Modulo 1 L analisi della luce degli astri: fotometria e spettrometria Vincenzo Orofino Gruppo di Astrofisica LA LUCE Natura della
Università del Salento Progetto Lauree Scientifiche Attività formativa Modulo 1 L analisi della luce degli astri: fotometria e spettrometria Vincenzo Orofino Gruppo di Astrofisica LA LUCE Natura della
L'impulso di una forza che varia nel tempo
 Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
I CIRCUITI ELETTRICI. Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi.
 I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Dispositivo di conversione di energia elettrica per aerogeneratori composto da componenti commerciali.
 Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
VERIFICA DELLA LEGGE DI MALUS E MISURA DELLA CONCENTRAZIONE DI UNA SOLUZIONE CON DUE POLAROIDI
 VERIFICA DELLA LEGGE DI MALUS E MISURA DELLA CONCENTRAZIONE DI UNA SOLUZIONE CON DUE POLAROIDI A) VERIFICA DELLA LEGGE DI MALUS L intensità luminosa trasmessa da un sistema costituito da due polaroidi
VERIFICA DELLA LEGGE DI MALUS E MISURA DELLA CONCENTRAZIONE DI UNA SOLUZIONE CON DUE POLAROIDI A) VERIFICA DELLA LEGGE DI MALUS L intensità luminosa trasmessa da un sistema costituito da due polaroidi
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
 Capitolo 1 Radiazione elettromagnetica e occhio In questo capitolo prendiamo in considerazione alcune grandezze fondamentali riguardanti l illuminazione e alcuni concetti legati alla visione umana che
Capitolo 1 Radiazione elettromagnetica e occhio In questo capitolo prendiamo in considerazione alcune grandezze fondamentali riguardanti l illuminazione e alcuni concetti legati alla visione umana che
Il colore. IGEA 2006-07 7 febbraio 2007
 Il colore IGEA 2006-07 7 febbraio 2007 La luce Radiazione elettromagnetica 380 740 nanometri (790 480 THz) Percezione della luce /1 Organi sensoriali: Bastoncelli Molto sensibili (anche a un solo fotone:
Il colore IGEA 2006-07 7 febbraio 2007 La luce Radiazione elettromagnetica 380 740 nanometri (790 480 THz) Percezione della luce /1 Organi sensoriali: Bastoncelli Molto sensibili (anche a un solo fotone:
REALIZZAZIONE E STUDIO DI UN OSCILLATORE A DENTI DI SEGA
 REALIZZAZIONE E STUDIO DI UN OSCILLATORE A DENTI DI SEGA ATTENZIONE: PERICOLO! In questa esperienza si impiegano alte tensioni. E fatto obbligo di fare controllare i collegamenti al tecnico prima di accendere.
REALIZZAZIONE E STUDIO DI UN OSCILLATORE A DENTI DI SEGA ATTENZIONE: PERICOLO! In questa esperienza si impiegano alte tensioni. E fatto obbligo di fare controllare i collegamenti al tecnico prima di accendere.
Giorgio Maria Di Nunzio
 Università degli Studi di Padova Dipartimento di Scienze Storiche, Geografiche e dell Antichità Fondamenti di Informatica A.A. 2012/2013 Giorgio Maria Di Nunzio Immagini Digitali Ä Dispense aggiuntive
Università degli Studi di Padova Dipartimento di Scienze Storiche, Geografiche e dell Antichità Fondamenti di Informatica A.A. 2012/2013 Giorgio Maria Di Nunzio Immagini Digitali Ä Dispense aggiuntive
CORRENTE E TENSIONE ELETTRICA LA CORRENTE ELETTRICA
 CORRENTE E TENSIONE ELETTRICA La conoscenza delle grandezze elettriche fondamentali (corrente e tensione) è indispensabile per definire lo stato di un circuito elettrico. LA CORRENTE ELETTRICA DEFINIZIONE:
CORRENTE E TENSIONE ELETTRICA La conoscenza delle grandezze elettriche fondamentali (corrente e tensione) è indispensabile per definire lo stato di un circuito elettrico. LA CORRENTE ELETTRICA DEFINIZIONE:
Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale...
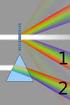 IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
1 Giochi d ombra [Punti 10] 2 Riscaldatore elettrico [Punti 10] AIF Olimpiadi di Fisica 2015 Gara di 2 Livello 13 Febbraio 2015
![1 Giochi d ombra [Punti 10] 2 Riscaldatore elettrico [Punti 10] AIF Olimpiadi di Fisica 2015 Gara di 2 Livello 13 Febbraio 2015 1 Giochi d ombra [Punti 10] 2 Riscaldatore elettrico [Punti 10] AIF Olimpiadi di Fisica 2015 Gara di 2 Livello 13 Febbraio 2015](/thumbs/24/2276739.jpg) 1 Giochi d ombra [Punti 10] Una sorgente di luce rettangolare, di lati b e c con b > c, è fissata al soffitto di una stanza di altezza L = 3.00 m. Uno schermo opaco quadrato di lato a = 10cm, disposto
1 Giochi d ombra [Punti 10] Una sorgente di luce rettangolare, di lati b e c con b > c, è fissata al soffitto di una stanza di altezza L = 3.00 m. Uno schermo opaco quadrato di lato a = 10cm, disposto
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi.
 IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
Lunghezza ocale. Donato Di Bello
 F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Relazione di Fisica. IV E a.s. 2011/2012. Badioli Federico, Ciprianetti Sofia, Pasqualini Roberto.
 Relazione di Fisica IV E a.s. 2011/2012 Badioli Federico, Ciprianetti Sofia, Pasqualini Roberto. Scopo: Misurare la lunghezza d onda (λ) di un laser HeNe attraverso un reticolo di diffrazione. Materiale
Relazione di Fisica IV E a.s. 2011/2012 Badioli Federico, Ciprianetti Sofia, Pasqualini Roberto. Scopo: Misurare la lunghezza d onda (λ) di un laser HeNe attraverso un reticolo di diffrazione. Materiale
Interferenza e diffrazione
 Interferenza e diffrazione La radiazione elettromagnetica proveniente da diverse sorgenti si sovrappongono in ogni punto combinando l intensita INTERFERENZA Quando la radiazione elettromagnetica passa
Interferenza e diffrazione La radiazione elettromagnetica proveniente da diverse sorgenti si sovrappongono in ogni punto combinando l intensita INTERFERENZA Quando la radiazione elettromagnetica passa
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
GRANDEZZE ALTERNATE SINUSOIDALI
 GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
quale agisce una forza e viceversa. situazioni. applicate a due corpi che interagiscono. Determinare la forza centripeta di un
 CLASSE Seconda DISCIPLINA Fisica ORE SETTIMANALI 3 TIPO DI PROVA PER GIUDIZIO SOSPESO Test a risposta multipla MODULO U.D Conoscenze Abilità Competenze Enunciato del primo principio della Calcolare l accelerazione
CLASSE Seconda DISCIPLINA Fisica ORE SETTIMANALI 3 TIPO DI PROVA PER GIUDIZIO SOSPESO Test a risposta multipla MODULO U.D Conoscenze Abilità Competenze Enunciato del primo principio della Calcolare l accelerazione
ONDE ELETTROMAGNETICHE
 ONDE ELETTROMAGNETICHE ONDE ELETTROMAGNETICHE Sono parte integrante dell ambiente in cui viviamo e lavoriamo Di origine artificiale (per esempio le onde radio, radar e nelle telecomunicazioni) Di origine
ONDE ELETTROMAGNETICHE ONDE ELETTROMAGNETICHE Sono parte integrante dell ambiente in cui viviamo e lavoriamo Di origine artificiale (per esempio le onde radio, radar e nelle telecomunicazioni) Di origine
PRINCIPI DI TRASDUZIONE
 PRINCIPI DI TRASDUZIONE Passiva Trasduzione resistiva Trasduzione capacitiva Trasduzione induttiva Attiva Trasduzione fotovoltaica Trasduzione piezoelettrica Trasduzione elettromagnetica Trasduzione fotoconduttiva
PRINCIPI DI TRASDUZIONE Passiva Trasduzione resistiva Trasduzione capacitiva Trasduzione induttiva Attiva Trasduzione fotovoltaica Trasduzione piezoelettrica Trasduzione elettromagnetica Trasduzione fotoconduttiva
TX Figura 1: collegamento tra due antenne nello spazio libero.
 Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
Collegamenti Supponiamo di avere due antenne, una trasmittente X e una ricevente X e consideriamo il collegamento tra queste due antenne distanti X X Figura : collegamento tra due antenne nello spazio
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Classificazione dei Sensori. (raccolta di lucidi)
 Classificazione dei Sensori (raccolta di lucidi) 1 Le grandezze fisiche da rilevare nei processi industriali possono essere di varia natura; generalmente queste quantità sono difficili da trasmettere e
Classificazione dei Sensori (raccolta di lucidi) 1 Le grandezze fisiche da rilevare nei processi industriali possono essere di varia natura; generalmente queste quantità sono difficili da trasmettere e
