UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
|
|
|
- Veronica Olivieri
- 8 anni fa
- Visualizzazioni
Transcript
1 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze geometriche parte 2 a Tolleranze geometriche generali Docente: Gianmaria Concheri gianmaria.concheri@unipd.it Tel Tolleranze geometriche di posizione (in senso lato) La tolleranza di posizione limita gli scostamenti della reciproca posizione di due o più elementi, dei quali uno è quello prescelto come elemento di riferimento per la prescrizione della tolleranza. L elemento di riferimento a sua volta può essere soggetto a tolleranza di forma. Se vi è necessità si può adottare più di un elemento di riferimento.
2 Elementi di riferimento Di preferenza gli elementi di riferimento sono: una superficie relativamente grande; due superfici anche relativamente modeste ma dislocate distanti l'una dall'altra; un asse abbastanza lungo; due assi anche corti ma situati distanti l'uno dall'altro; un asse corto ed una superficie ortogonale all'asse stesso. Elementi di riferimento Elementi geometrici integrali: indicazione sul contorno, su un estensione del contorno o su una linea di richiamo
3 Elementi geometrici derivati: indicazione sull estensione della linea di misura Quando come elemento di riferimento si sceglie un asse geometrico, questi non è fisicamente rilevabile e pertanto quale elemento di riferimento può venire adottata la corrispondente superficie cilindrica Elementi di riferimento Se l elemento di riferimento è definito su di una parte limitata di un elemento geometrico, tale parte deve essere individuata e quotata. Errate indicazioni dei riferimenti ERRORI di indentificazione di elementi derivati
4 Elementi di riferimento Elemento di riferimento stabilito da un singolo elemento geometrico: Elemento di riferimento comune stabilito da due elementi geometrici: Sistema di elementi di riferimento (due o più elementi geometrici in ordine di priorità): Orientamento nella UNI :1986 Tolleranze di orientamento
5 Tolleranza geometrica di parallelismo PARALLELISMO (una linea retta riferita a una linea retta di riferimento) La zona di tolleranza è definita da un cilindro di diametro t = 0,3 mm, parallelo al riferimento, se il segno Ø precede il valore di tolleranza. L asse estratto sarà contenuto all interno di un volume cilindrico di diametro 0,03mm parallelo alla linea retta di riferimento A Tolleranza geometrica di parallelismo PARALLELISMO (linea retta rispetto a sistema di riferimenti) Esempio: tolleranza di parallelismo dell asse di un foro riferito a un sistema di riferimenti e i relativi intervalli di tolleranza. In entrambi i casi l intervallo di tolleranza è limitato da due piani paralleli. I piani sono paralleli ai riferimenti e in diverse direzioni specificate. La direzione risulta dal posizionamento della linea di misura sul disegno.
6 Tolleranza geometrica di parallelismo PARALLELISMO (linea retta rispetto a superficie di riferimento) La zona di tolleranza proiettata in un piano è limitata da due piani paralleli distanti t e paralleli alla superficie di riferimento. Tolleranza geometrica di parallelismo PARALLELISMO (linea retta riferita a un sistema di riferimento) LE =Line Element La tolleranza si riferisce a linee singole e non all intero piano. L intervallo di tolleranza è limitato da due linee rette parallele distanziate di t = 0,02 mm, orientate parallelamente al piano di riferimento A e al riferimento B. Nell esempio ogni linea estratta (reale) sarà contenuta tra due linee rette parallele distanziate di 0,02 mm, che sono orientate parallelamente rispetto il piano di riferimento A e al riferimento B.
7 Tolleranza geometrica di parallelismo PARALLELISMO (superficie rispetto a retta di riferimento) La zona di tolleranza proiettata in un piano è limitata da due piani paralleli distanti t e paralleli alla retta di riferimento. Tolleranza geometrica di parallelismo PARALLELISMO (superficie rispetto a superficie di riferimento) La zona di tolleranza proiettata in un piano è limitata da due piani paralleli distanti t e paralleli alla superficie di riferimento.
8 Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (linea retta rispetto a retta di riferimento) La zona di tolleranza proiettata in un piano è limitata da due piani paralleli distanti t e perpendicolari alla retta di riferimento. Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (linea retta rispetto a un sistema di riferimento) L asse estratto di un cilindro sarà contenuto tra due piani paralleli distanziati di 0,1mm i quali sono perpendicolari al piano di riferimento A e nella direzione specificata rispetto al piano di riferimento B.
9 Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (linea retta rispetto a un sistema di riferimento) La zona di tolleranza è limitata da due coppie di piani paralleli. Entrambe le coppie sono perpendicolari al piano A. Una coppia è parallela al piano B mentre la seconda è perpendicolare al piano B. Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (linea retta rispetto a superficie di riferimento) ESEMPIO: La zona di tolleranza è limitata da un cilindro di diametro t e perpendicolare alla superficie di riferimento.
10 Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (superficie rispetto a retta di riferimento) La zona è limitata da due piani paralleli distanti t e perpendicolari alla retta di riferimento. Tolleranza geometrica di perpendicolarità PERPENDICOLARITA (superficie rispetto a superficie di riferimento) La zona è limitata da due piani paralleli distanti t e perpendicolari alla superficie di riferimento.
11 Dimensioni teoricamente esatte Dimensioni che determinano la posizione o l orientazione teoricamente esatta degli elementi geometrici posti in tolleranza rispetto agli elementi di riferimento: Tolleranza geometrica di inclinazione INCLINAZIONE (linea rispetto a retta di riferimento) ESEMPIO: La zona di tolleranza proiettata è limitata da due rette parallele distanti t e inclinate rispetto alla retta di riferimento dell angolo prescritto. Altri casi: linea rispetto a superficie di riferimento superficie rispetto a retta di riferimento superficie rispetto a superficie di riferimento
12 LOCALIZZAZIONE (un punto) Tolleranze geometriche La zona di tolleranza è limitata da un cerchio di diametro t il cui centro è nella posizione teorica esatta del punto considerato. Tolleranze geometriche LOCALIZZAZIONE (una linea) ESEMPIO: La zona di tolleranza è limitata da un parallelepipedo di sezione t 1 x t 2 il cui asse è nella posizione teorica esatta della linea considerata, se la tolleranza è prescritta in due direzioni perpendicolari tra di loro.
13 Tolleranze geometriche LOCALIZZAZIONE (una superficie piana o un piano mediano) La zona di tolleranza è limitata da due piani paralleli distanti t e disposti simmetricamente rispetto alla posizione teorica esatta della superficie considerata. CONCENTRICITA (un punto) Tolleranze geometriche La zona di tolleranza è limitata da un cerchio di diametro t il cui centro coincide con il punto di riferimento
14 COASSIALITA (un asse) Tolleranze geometriche La zona di tolleranza è limitata da un cilindro di diametro t il cui asse coincide con l asse di riferimento Tolleranze geometriche SIMMETRIA (una linea o un asse) ESEMPIO: La zona di tolleranza è limitata da un parallelepipedo di sezione t 1 x t 2 il cui asse coincide con l asse di riferimento, se la tolleranza è prescritta in due direzioni perpendicolari tra di loro.
15 OSCILLAZIONE (circolare radiale) Tolleranze geometriche ESEMPIO: La zona di tolleranza è limitata in ogni piano di misura perpendicolare all asse, da due cerchi concentrici e distanti t il cui centro coincide con l asse di riferimento. Tolleranze geometriche OSCILLAZIONE CIRCOLARE ASSIALE ESEMPIO: La zona di tolleranza è limitata per ogni posizione radiale, da due cerchi distanti t giacenti sul cilindro di misura avente per asse l asse di riferimento. Altri casi: circolare in tutte le direzioni circolare in una direzione specificata superficie rispetto a superficie di riferimento
16 OSCILLAZIONE TOTALE RADIALE Tolleranze geometriche ESEMPIO: La zona di tolleranza è limitata per ogni posizione radiale, da due cerchi distanti t giacenti sul cilindro di misura avente per asse l asse di riferimento. Altro caso: totale assiale Tolleranze geometriche Tipo Riferimento Caratteristiche Simbolo 2D/3D Forma zona Valori tipici Applicabilità Riferimento Quote riquadrate L M L M Rettilineità elemento 2D IT No n/a No Rettilineità asse o piano mediano 3D Funzione Si n/a No Forma No Planarità 3D IT/2 No n/a No Circolarità 2D IT/2 No n/a No Cilindricità 3D IT/2 No n/a No Parallelismo 3D IT Solo assi Solo assi No Orientamento Si Perpendicolarità 3D IT Solo assi Solo assi No Inclinazione 3D IT Solo assi Solo assi Si (angoli) Circolare 2D IT/2 No No No Oscillazione Si Totale 3D IT/2 No No No Si/No Profilo di linea 2D Funzione No Solo assi Si Profili Si Profilo di superficie 3D Funzione No Solo assi Si Localizzazione 3D Funzione Si Solo assi Si Posizione Si Concentricità 3D IT No No No Simmetria 3D Funzione No No No
17 Tolleranze geometriche generali: premessa Tolleranze geometriche generali UNI EN :1993 Le tolleranze geometriche per elementi isolati: rettilineità planarità, circolarità, cilindricità. Le tolleranze geometriche per elementi associati: parallelismo perpendicolarità, simmetria, coassialità oscillazione Sono fornite tre classi per le tolleranze geometriche generali, (designate attraverso le lettere maiuscole H, K, L)
18 Tolleranze Geometriche Generali UNI EN :1993 La norma specifica le tolleranze geometriche generali per le caratteristiche prive di indicazioni di tolleranze geometriche specifiche. Essa prevede tre gradi di precisione di tolleranze geometriche ed ha lo scopo di: 1. semplificare le indicazioni sui disegni riguardanti le tolleranze geometriche e di 2. indirizzare i progettisti alla scelta della classe di tolleranza ottenibile con macchine o tecnologie correnti Una prescrizione di tolleranza più ampia non arreca alcun vantaggio al costruttore Tolleranze Geometriche Generali UNI EN :1993 Quando la funzione dell elemento ammette una tolleranza uguale o più ampia delle tolleranze geometriche generali, la stessa tolleranza non va indicata accanto alla quota, ma è sufficiente indicarla sul disegno. Questo tipo di tolleranza permette la completa applicazione del concetto di tolleranze geometriche generali. Fa eccezione alla regola il caso in cui la funzione dell elemento ammetta una tolleranza più ampia della tolleranza generale, che permetta di realizzare un economia nella produzione. In questo caso particolare la tolleranza più ampia deve essere indicata singolarmente vicino alla relativa caratteristica (per esempio, la tolleranza di circolarità di un grande anello di piccolo spessore).
19 Tolleranze Geometriche Generali UNI EN :1993 Tolleranze generali secondo ISO mh Tolleranze Geometriche Generali UNI EN :1993 Il superamento della tolleranza generale non dovrebbe dare origine allo scarto della produzione se la sua funzionalità non è compromessa
20 Rettilineità e Planarità Le tolleranze di planarità e di rettilineità sono specificate nella tabella seguente. Quando una tolleranza è scelta tra quelle in tabella, deve essere riferita: 1 - per la rettilineità, alla lunghezza della linea corrispondente; 2 - per la planarità, alla più grande dimensione laterale della superficie o del diametro nel caso di superficie circolare. Classe di tollera n. Fino a 10 Oltre 10 fino a 30 Oltre 30 fino a 100 Oltre 100 fino a 300 Oltre 300 fino 1000 Oltre 1000 fino 3000 H 0,02 0,05 0,1 0,2 0,3 0,4 K 0,05 0,1 0,2 0,4 0,6 0,8 L 0,1 0,2 0,4 0,8 1,2 1,6 Rappresentazione dell errore di planarità in funzioni delle dimensioni nominali del pezzo Fino a 10mm Simmetria Le tolleranze generali di simmetria si applicano quando: 1 - almeno due elementi del pezzo hanno un piano mediano di complanarità; 2 - gli assi di due elementi del pezzo sono coassiali tra loro; Classe di tolleranza <=100mm >100mm <=300mm >300mm <=1000mm >1000mm <=3000mm H 0,5 K 0,6 0,8 1 L 0,6 1 1,5 2 La zona di tolleranza di simmetria limita lo scostamento di planarità del piano mediano, e nello stesso tempo non deve essere inferiore alla tolleranza di rettilineità (quindi limita anche la rettilineità dell asse).
21 Simmetria Deve essere preso come riferimento l elemento maggiore; se gli elementi hanno lunghezza nominale uguale può essere preso come riferimento uno qualsiasi. NOTA: l indicazione del riferimento come riportata in figura NON è conforme alla nuova ISO 1101:2004 poiché non identifica il riferimento mediante lettera. Oscillazione Circolare Le tolleranze generali di oscillazione circolare (radiale, assiale e di superfici qualunque di rivoluzione) sono indicate nella tabella. Per le tolleranze generali di oscillazione circolare, le superfici portanti (sedi dei cuscinetti) devono essere prese come riferimento solo se esse sono state disegnate come tali; negli altri casi deve essere preso in considerazione l elemento più lungo; se gli elementi hanno lunghezza nominale uguale, può essere preso come riferimento uno qualsiasi. Classe di tolleranza Tolleranza di oscillazione radiale H K L 0,1 0,2 0,5 Tolleranze generali di oscillazione radiale (valori in mm).
22 Perpendicolarità Classe di tolleranza <=100 >100 <=300 >300 <=1000 >1000 <=3000 H 0,2 0,3 0,4 0,5 K 0,4 0,6 0,8 1 L 0,6 1 1,5 2 Tolleranze generali di perpendicolarità (valori in mm). Deve essere preso come riferimento il maggiore dei due lati formanti l angolo retto ma, se i lati hanno lunghezza nominale uguale, può essere preso come riferimento uno qualsiasi. La zona di tolleranza limita anche lo scostamento di rettilineità o di planarità e l oscillazione assiale degli elementi in tolleranza. Perciò la tolleranza generale di perpendicolarità non deve essere più piccola della tolleranza generale di planarità e quella di oscillazione assiale. Coassialità e Concentricità Lo scostamento di concentricità, in casi estremi, può essere grande quanto il valore della tolleranza di oscillazione radiale, dal momento che lo scostamento di oscillazione radiale può considerarsi come l effetto congiunto dello scostamento di concentricità e quello di circolarità. Analogamente lo scostamento di coassialità può essere grande quanto il valore della tolleranza di oscillazione radiale totale, dal momento che lo scostamento di oscillazione radiale totale può considerarsi come l effetto congiunto dello scostamento di coassialità e quello di cilindricità.
23 Parallelismo La tolleranza di parallelismo è uguale, in valore numerico, alla tolleranza dimensionale o alla tolleranza di planarità, assumendo il valore più grande. Circolarità La tolleranza generale di circolarità è uguale, in valore numerico, alla tolleranza sul diametro, ma in nessun caso deve essere più grande del corrispondente valore della tolleranza di oscillazione circolare radiale Quindi i valori numerici delle tolleranze di oscillazione radiale sono stati presi come limiti superiori delle tolleranze generali di circolarità
24 Circolarità La tolleranza sul diametro e la forma della deviazione dalla circolarità definiscono se la deviazione dalla circolarità può occupare tutta o una porzione della zona di tolleranza. Nel caso di una forma ellittica, la deviazione può solamente occupare metà del valore numerico della zona di tolleranza, altrimenti la dimensione locale potrebbe uscire dalla zona di tolleranza. Cilindricità Lo scostamento di cilindricità comprende i tre seguenti scostamenti: scostamento di circolarità, scostamento di rettilineità dell asse, scostamento di parallelismo delle generatrici opposte. Ciascuno di questi scostamenti è limitato da proprie tolleranze specifiche o da una tolleranza generale.
25 Oscillazione totale Classe di tolleranza Tolleranza di oscillazione circolare mm H K L 0,1 0,2 0,5 L oscillazione radiale totale consiste in tre componenti: scostamento di oscillazione radiale, scostamento di rettilineità dell asse e di parallelismo. L oscillazione assiale totale consiste in due componenti: scostamento di oscillazione assiale e scostamento dalla planarità. Esempi Indicazione sul disegno Tolleranze secondo ISO 8015 Tolleranze generali ISO 2768-mL Interpretazione Lo scostamento del diametro è indicato direttamente nel disegno tecnico; perciò le tolleranze generali si applicano solamente alla lunghezza del cilindro e alla forma dello stesso. La tolleranza generale sulla lunghezza del cilindro è 0,6 mm (scostamento di ±0,3 mm) La tolleranza generale di circolarità è uguale alla tolleranza del diametro. Per le tolleranza di forma 3D e orientamento si veda in precedenza.
26 Esempi Indicazione sul disegno Tolleranze secondo ISO 8015 Tolleranze generali ISO 2768-cK Interpretazione Tolleranze generali in accordo con l applicazione della ISO 2768-cK. La tabella fornisce uno scostamento per il diametro di ± 0,8 mm (tolleranza generale 1,6 mm) ma la tolleranza di oscillazione permessa è di soli 0,2 mm, perciò viene applicato quest ultimo valore al diametro La tolleranza generale sulla lunghezza del cilindro è di 1,6 mm (scostamento di ±0,8 mm). La tolleranza generale di circolarità è pari a quella di oscillazione (0,2 mm). La tolleranza generale di rettilineità della generatrice del cilindro è di 0,2 mm.
Principi generali di normativa per il Disegno Tecnico e introduzione alle Proiezioni Ortogonali
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10 Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Docente: Gianmaria
Corso di Disegno di Macchine + Abilità Informatiche. Test di autovalutazione 14 marzo 2012 / A
 Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
Test di autovalutazione 14 marzo 2012 / A 1) Quali, tra le seguenti coppie, è composta da forme duali? a. Il piano punteggiato e la stella di piani; b. la retta punteggiata e lo spazio punteggiato; c.
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico
 La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico 1 La quotatura è ottenuta con i seguenti elementi La linea
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
 6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
6 Generalità Quando un pezzo presenta fori o cavità, il disegno può risultare di difficile comprensione a causa della presenza di numerose linee tratteggiate. 7 Generalità Sezionando ( tagliando ) con
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08 Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
RUOTE DENTATE. Introduzione
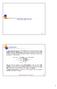 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
Minicorso Regole di Disegno Meccanico
 Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
Unificazione nel disegno. Enti di unificazione
 Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
Unificazione nel disegno Norme per l esecuzione e la lettura dei disegni finalizzate ad una interpretazione univoca conforme alla volontà del progettista. Enti di unificazione ISO: International standard
INDICAZIONE DELLA FINITURA SUPERFICIALE E DELLE TOLLERANZE DI LAVORAZIONE DAL PROGETTO AL PRODOTTO
 INDICAZIONE DELLA FINITURA SUPERFICIALE E DELLE TOLLERANZE DI LAVORAZIONE DAL PROGETTO AL PRODOTTO Il progetto, dalla parola latina proiectus, è un insieme di operazioni che hanno lo scopo di realizzare
INDICAZIONE DELLA FINITURA SUPERFICIALE E DELLE TOLLERANZE DI LAVORAZIONE DAL PROGETTO AL PRODOTTO Il progetto, dalla parola latina proiectus, è un insieme di operazioni che hanno lo scopo di realizzare
di sfere a contatto radiale 262
 Cuscinetti a due corone di sfere Cuscinetti a due corone di sfere a contatto radiale 262 Definizione ed attitudini 262 Serie 262 Tolleranze e giochi 262 Elementi di calcolo 263 Suffissi 263 Caratteristiche
Cuscinetti a due corone di sfere Cuscinetti a due corone di sfere a contatto radiale 262 Definizione ed attitudini 262 Serie 262 Tolleranze e giochi 262 Elementi di calcolo 263 Suffissi 263 Caratteristiche
Rappresentazione delle saldature
 TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
TIPI DI GIUNTI SALDATI (UNI 1307-2a parte) Si definisce giunto saldato la zona in cui avviene il collegamento dei pezzi mediante saldatura. Le superfici minori dei pezzi, vicine e interessate alla saldatura,
r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI
 r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI 1. Proiezioni Assonometriche e ortogonali 2. Teoria delle proiezioni ortogonali Pag. 1 Pag. 2. 3. SCHEDE OPERATIVE SULLE PROIEZIONI
r.berardi NOTE E SCHEDE OPERATIVE PER APPRENDERE LE PROIEZIONI ORTOGONALI 1. Proiezioni Assonometriche e ortogonali 2. Teoria delle proiezioni ortogonali Pag. 1 Pag. 2. 3. SCHEDE OPERATIVE SULLE PROIEZIONI
QUOTATURA. Introduzione
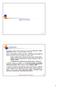 QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
QUOTATURA 182 Introduzione Per quotatura si intende l insieme delle norme che permettono l indicazione esplicita delle dimensioni(lineari ed angolari) dell oggetto rappresentato. Poiché a ciascun disegno
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni
 Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere informazioni Il DISEGNO TECNICO è un linguaggio convenzionale che ha la funzione di trasferire e diffondere
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
RUGOSITÀ. Introduzione
 RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
RUGOSITÀ 299 Introduzione Le superfici degli oggetti reali sono di solito affette da irregolarità microgeometriche. Tali irregolarità possono essere casuali (tipico nei pezzi prodotti per fusione), ovvero
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
Università degli Studi della Calabria. Collegamenti smontabili non filettati
 Collegamenti smontabili non filettati Collegamenti albero-mozzo ELEMENTI ESIGENZE Anelli Scanalati Chiavette Linguette Spine elastici a Impedimento alla rotazione si si si si Impedimento alla traslazione
Collegamenti smontabili non filettati Collegamenti albero-mozzo ELEMENTI ESIGENZE Anelli Scanalati Chiavette Linguette Spine elastici a Impedimento alla rotazione si si si si Impedimento alla traslazione
Eurocodici Strutturali
 Eurocodici Strutturali 5 Capitolo Strutture in acciaio Rappresentazione saldature Unificazione viti/bulloni Indicazioni pratiche collegamenti bullonati Rappresentazione bullonature Caratteristiche dimensionali
Eurocodici Strutturali 5 Capitolo Strutture in acciaio Rappresentazione saldature Unificazione viti/bulloni Indicazioni pratiche collegamenti bullonati Rappresentazione bullonature Caratteristiche dimensionali
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Fig. 2. Proiezioni ortogonali di un parallelepipedo su piani esterni alla figura
 3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
Introduzione al 3D con Autocad
 2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Ruote Dentate. Ing. Alessandro Carandina A.A. 2014/2015. Disegno Tecnico Industriale per Ingegneria Meccanica
 Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
Ruote Dentate Ing. Alessandro Carandina A.A. 2014/2015 Disegno Tecnico Industriale per Ingegneria Meccanica Introduzione TRASMISSIONE DEL MOTO DA UN ASSE AD UN ALTRO 2 CINGHIA SINCRONA Assi paralleli Alberi
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI
 DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
Rapporto di taratura di strumenti per pesare
 Rapporto di taratura di strumenti per pesare Cliente esempio Indirizzo CAP 15121 Località Alessandria (AL) Relazione n 114 del 12/01/2013 Data di emissione relazione: 12/01/2013 Data di esecuzione prove:
Rapporto di taratura di strumenti per pesare Cliente esempio Indirizzo CAP 15121 Località Alessandria (AL) Relazione n 114 del 12/01/2013 Data di emissione relazione: 12/01/2013 Data di esecuzione prove:
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
IMPOSTAZIONE DELLE TAVOLE GRAFICHE
 IMPOSTAZIONE DELLE TAVOLE GRAFICHE Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
IMPOSTAZIONE DELLE TAVOLE GRAFICHE Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
COLLEGAMENTI ALBERO-MOZZO
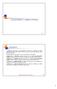 COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
COLLEGAMENTI ALBERO-MOZZO 342 Introduzione I collegamenti albero-mozzo sono collegamenti smontabili che consentono di rendere solidali, rispetto alla rotazione attorno ad un asse comune, una parte piena
ALLEGATO II Dispositivi di attacco
 ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
ALLEGATO II Dispositivi di attacco. : il testo compreso fra i precedenti simboli si riferisce all aggiornamento di Maggio 2011 Nel presente allegato sono riportate le possibili conformazioni dei dispositivi
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
 Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Proiezioni Ortogonali Scopo del Disegno e del Disegno Tecnico Disegno: Rappresentare su un piano bidimensionale (ad esempio un foglio di carta) un oggetto nella realtà tridimensionale. Non è richiesta
Progettazione funzionale di sistemi meccanici e meccatronici.
 Progettazione funzionale di sistemi meccanici e meccatronici. Progetto d anno: Laser 2dof A.A. 2010/2011 Progettazione Funzionale di Sistemi Meccanici e Meccatronici Taglio laser a due gradi di libertà
Progettazione funzionale di sistemi meccanici e meccatronici. Progetto d anno: Laser 2dof A.A. 2010/2011 Progettazione Funzionale di Sistemi Meccanici e Meccatronici Taglio laser a due gradi di libertà
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato
 ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato Nella presente esercitazione si redige il programma CNC per la fresatura del pezzo illustrato nelle Figure 1 e 2. Figura
ESERCITAZIONE Scrittura di un programma CNC per la fresatura di un componente dato Nella presente esercitazione si redige il programma CNC per la fresatura del pezzo illustrato nelle Figure 1 e 2. Figura
Lo Stato Superficiale dei Pezzi Meccanici
 Lo Stato Superficiale dei Pezzi Meccanici Superfici Reali e Nominali Ing. Alessandro Carandina Disegno Tecnico Industriale per Ingegneria Meccanica Disegno tecnico Informazioni qualitative (i vari tipi
Lo Stato Superficiale dei Pezzi Meccanici Superfici Reali e Nominali Ing. Alessandro Carandina Disegno Tecnico Industriale per Ingegneria Meccanica Disegno tecnico Informazioni qualitative (i vari tipi
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Gli oggetti 3D di base
 Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
Guida a croce LM Tipo CSR
 Guida a croce LM Tipo CSR Rotaia LM Tenuta frontale Frontale di ricircolo Sfere Lamierino di trattenuta delle sfere Nipplo ingrassatore Carrello LM Tenuta laterale Rotaia LM Figura 1: Struttura della guida
Guida a croce LM Tipo CSR Rotaia LM Tenuta frontale Frontale di ricircolo Sfere Lamierino di trattenuta delle sfere Nipplo ingrassatore Carrello LM Tenuta laterale Rotaia LM Figura 1: Struttura della guida
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
Corso di. Dott.ssa Donatella Cocca
 Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Università degli Studi della Calabria. Ruote dentate
 Trasmissione di moto rotatorio mediante ruote di frizione (ad assi paralleli od anche sghembi) Accoppiamento ruota/dentiera Coppia di ruote dentate fra loro ingrananti: la distanza fra i denti lungo la
Trasmissione di moto rotatorio mediante ruote di frizione (ad assi paralleli od anche sghembi) Accoppiamento ruota/dentiera Coppia di ruote dentate fra loro ingrananti: la distanza fra i denti lungo la
REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE
 30.11.2011 Gazzetta ufficiale dell Unione europea L 317/17 REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE del 29 novembre 2011 recante modifica del regolamento (CE) n. 1222/2009 del Parlamento europeo
30.11.2011 Gazzetta ufficiale dell Unione europea L 317/17 REGOLAMENTO (UE) N. 1235/2011 DELLA COMMISSIONE del 29 novembre 2011 recante modifica del regolamento (CE) n. 1222/2009 del Parlamento europeo
MISURE DIMENSIONALI MISURE DIMENSIONALI: - Sistemi a contatto. - Sistemi senza contatto.
 MISURE DIMENSIONALI Modello: tubo cilindrico misurato con forcelle del calibro caratterizzate da superfici piane e parallele fra loro. MISURE DIMENSIONALI: D Diametro del tubo misurato con calibro. Ripetendo
MISURE DIMENSIONALI Modello: tubo cilindrico misurato con forcelle del calibro caratterizzate da superfici piane e parallele fra loro. MISURE DIMENSIONALI: D Diametro del tubo misurato con calibro. Ripetendo
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
www.rodacciai.it PROVA DI TRAZIONE L 0 = 5.65 S 0 PROVE MECCANICHE
 PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
PROVA DI TRAZIONE La prova, eseguita a temperatura ambiente o più raramente a temperature superiori o inferiori, consiste nel sottoporre una provetta a rottura per mezzo di uno sforzo di trazione generato
Guida alla segnaletica di sicurezza (prima parte)
 Guida alla segnaletica di sicurezza (prima parte) Pubblicato il: 16/06/2004 Aggiornato al: 16/06/2004 di Gianfranco Ceresini L utilizzo della segnaletica di sicurezza può sembrare a prima vista un elemento
Guida alla segnaletica di sicurezza (prima parte) Pubblicato il: 16/06/2004 Aggiornato al: 16/06/2004 di Gianfranco Ceresini L utilizzo della segnaletica di sicurezza può sembrare a prima vista un elemento
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15
 Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15 Esercizio 1 (9 punti): Una distribuzione di carica è costituita da un guscio sferico
Università del Salento Corso di Laurea Triennale in Ingegneria Industriale Appello di FISICA GENERALE 2 del 27/01/15 Esercizio 1 (9 punti): Una distribuzione di carica è costituita da un guscio sferico
IL SISTEMA CARTOGRAFICO NAZIONALE
 IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Università degli Studi di Verona Corsi di Laurea in Matematica Applicata, Informatica e Informatica Multimediale. Test di autovalutazione (matematica)
 Università degli Studi di Verona Corsi di Laurea in Matematica Applicata, Informatica e Informatica Multimediale Test di autovalutazione (matematica) 1. Eseguendo la divisione con resto di 3437 per 225
Università degli Studi di Verona Corsi di Laurea in Matematica Applicata, Informatica e Informatica Multimediale Test di autovalutazione (matematica) 1. Eseguendo la divisione con resto di 3437 per 225
QUOTATURA DISEGNO TECNICO
 QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
QUOTATURA DISEGNO TECNICO La quotatura costituisce il complesso delle informazioni in un disegno che precisano le dimensioni di un oggetto o di un componente meccanico. La quotatura deve quindi definire
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Schede tecniche - Ingranaggi di precisione
 Schede tecniche Ingranaggi di precisione Ingranaggi a denti dritti ed elicoidali Formula Formula Descrizione Simbolo Unità Ingranaggi a denti diritti Ingranaggi elicoidali Modulo reale m n Modulo apparente
Schede tecniche Ingranaggi di precisione Ingranaggi a denti dritti ed elicoidali Formula Formula Descrizione Simbolo Unità Ingranaggi a denti diritti Ingranaggi elicoidali Modulo reale m n Modulo apparente
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
11. Criteri di analisi e di verifica
 11. Criteri di analisi e di verifica Il progetto dell edificio esistente riflette naturalmente lo stato delle conoscenze al tempo della costruzione e può contenere difetti di impostazione e di realizzazione,
11. Criteri di analisi e di verifica Il progetto dell edificio esistente riflette naturalmente lo stato delle conoscenze al tempo della costruzione e può contenere difetti di impostazione e di realizzazione,
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Trasportatori a nastro
 Trasportatori a nastro Realizzano un trasporto di tipo continuo, in orizzontale o in pendenza, di materiali alla rinfusa e di carichi concentrati leggeri. incastellatura di sostegno Trasporti interni 1
Trasportatori a nastro Realizzano un trasporto di tipo continuo, in orizzontale o in pendenza, di materiali alla rinfusa e di carichi concentrati leggeri. incastellatura di sostegno Trasporti interni 1
Prodotti Siderurgici. 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate
 Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
Prodotti Siderurgici 12. SISTEMI DI GIUNZIONE Unioni saldate, unioni bullonate Premessa Il presente documento vuole fornire indicazioni semplici e concrete per i collegamenti nelle costruzioni metalliche,
Norme. Norme. Università degli Studi di Brescia DIMI
 - UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
- UNI Disegno Tecnico 1 Normazione e unificazione Norma: Regola che fissa le condizioni di esecuzione di un oggetto o di elaborazione di un prodotto di cui si vogliano UNIFICARE l impiego od assicurarne
Modulo della PGQ 13 Revisione: 13 Direzione Centrale Ricerca & Sviluppo e Direzione Laboratori Pagina 1 di 5
 Direzione Centrale Ricerca & Sviluppo e Direzione Laboratori Pagina 1 di 5 PREMESSA Il laboratorio metrologico della Direzione Centrale Ricerca & Sviluppo del CTG, di seguito denominato CENTRO, è accreditato
Direzione Centrale Ricerca & Sviluppo e Direzione Laboratori Pagina 1 di 5 PREMESSA Il laboratorio metrologico della Direzione Centrale Ricerca & Sviluppo del CTG, di seguito denominato CENTRO, è accreditato
Soluzione Punto 1 Si calcoli in funzione di x la differenza d(x) fra il volume del cono avente altezza AP e base il
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 74 PROBLEMA Considerata una sfera di diametro AB, lungo, per un punto P di tale diametro si conduca il piano α perpendicolare ad esso
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 74 PROBLEMA Considerata una sfera di diametro AB, lungo, per un punto P di tale diametro si conduca il piano α perpendicolare ad esso
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
La Qualità il Controllo ed il Collaudo della macchina utensile. Dr. Giacomo Gelmi
 La Qualità il Controllo ed il Collaudo della macchina utensile Dr. Giacomo Gelmi Che cosa è una macchina utensile? E uno spazio fisico in cui si collocano, sostenuti da adeguate strutture ed in posizioni
La Qualità il Controllo ed il Collaudo della macchina utensile Dr. Giacomo Gelmi Che cosa è una macchina utensile? E uno spazio fisico in cui si collocano, sostenuti da adeguate strutture ed in posizioni
Il ciclo di lavorazione
 INTRODUZIONE AI CICLI DI LAVORAZIONE Rif. Bibliografico: Giusti-Santochi TECNOLOGIA MECCANICA e studi di fabbricazione Capitolo 9 1 Il ciclo di lavorazione DEFINIZIONE: Si dice CICLO DI LAVORAZIONE tutto
INTRODUZIONE AI CICLI DI LAVORAZIONE Rif. Bibliografico: Giusti-Santochi TECNOLOGIA MECCANICA e studi di fabbricazione Capitolo 9 1 Il ciclo di lavorazione DEFINIZIONE: Si dice CICLO DI LAVORAZIONE tutto
LAVORI SPECIALI. (Articolo 148 D.Lgs 81/08)
 146 LAVORI SPECIALI (Articolo 148 D.Lgs 81/08) Prima di procedere alla esecuzione di lavori su lucernari, tetti, coperture e simili, fermo restando l obbligo di predisporre misure di protezione collettiva,
146 LAVORI SPECIALI (Articolo 148 D.Lgs 81/08) Prima di procedere alla esecuzione di lavori su lucernari, tetti, coperture e simili, fermo restando l obbligo di predisporre misure di protezione collettiva,
RESISTENZA DEI MATERIALI TEST
 RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
RESISTENZA DEI MATERIALI TEST 1. Nello studio della resistenza dei materiali, i corpi: a) sono tali per cui esiste sempre una proporzionalità diretta tra sollecitazione e deformazione b) sono considerati
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Proiezioni Grafica 3d
 Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
LA PROGRAMMAZIONE N10 G0 X5 Y5
 LA PROGRAMMAZIONE Un programma per una Macchina Utensile CNC è costituito da una sequenza logica di informazioni geometriche, tecnologiche ed ausiliarie (fasi di lavoro). Le informazioni geometriche riguardano
LA PROGRAMMAZIONE Un programma per una Macchina Utensile CNC è costituito da una sequenza logica di informazioni geometriche, tecnologiche ed ausiliarie (fasi di lavoro). Le informazioni geometriche riguardano
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
REGOLA 1 IL RETTANGOLO DI GIOCO
 REGOLA 1 IL RETTANGOLO DI GIOCO Superficie del rettangolo di gioco Le gare devono essere giocate su superfici piane, lisce e prive di asperità, preferibilmente fatte di legno o di materiale sintetico,
REGOLA 1 IL RETTANGOLO DI GIOCO Superficie del rettangolo di gioco Le gare devono essere giocate su superfici piane, lisce e prive di asperità, preferibilmente fatte di legno o di materiale sintetico,
TAVOLA 1 ORGANIZZAZIONE DELLO SPAZIO. Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore.
 TAVOLA 1 ORGANIZZAZIONE DELLO SPAZIO Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
TAVOLA 1 ORGANIZZAZIONE DELLO SPAZIO Esercizio di divisione dello spazio, costruzioni grafiche elementari, scritturazioni e uso del colore. IL E I SUOI FORMATI Formati e disposizioni degli elementi grafici
Metodologia di monitoraggio Impianti fotovoltaici
 Metodologia di monitoraggio Impianti fotovoltaici Per effettuare il monitoraggio degli impianti fotovoltaici è stato scelto il metodo di acquisizione dati proposto dal Dott. Ing. F. Spertino, Dott. Ing.
Metodologia di monitoraggio Impianti fotovoltaici Per effettuare il monitoraggio degli impianti fotovoltaici è stato scelto il metodo di acquisizione dati proposto dal Dott. Ing. F. Spertino, Dott. Ing.
3DEverywhere S.r.l. sito web: http://www.3deverywhere.com
 3DE Modeling Analyzer 3DE Modeling Analyzer permette di effettuare un'analisi accurata dei modelli ottenuti con 3DE Modeling Professional. 3DE Modeling Analyzer consente: il caricamento di singole viste
3DE Modeling Analyzer 3DE Modeling Analyzer permette di effettuare un'analisi accurata dei modelli ottenuti con 3DE Modeling Professional. 3DE Modeling Analyzer consente: il caricamento di singole viste
MOMENTI DI INERZIA. m i. i=1
 MOMENTI DI INEZIA Massa Ad ogni punto materiale si associa uno scalare positivo m che rappresenta la quantità di materia di cui è costituito il punto. m, la massa, è costante nel tempo. Dato un sistema
MOMENTI DI INEZIA Massa Ad ogni punto materiale si associa uno scalare positivo m che rappresenta la quantità di materia di cui è costituito il punto. m, la massa, è costante nel tempo. Dato un sistema
RAPPORTO DI PROVA Venezia,. Foglio n. 1 di 7. Protocollo: Luogo e Data della prova: Richiedente: Materiale testato:
 Foglio n. 1 di 7 Protocollo: Luogo e Data della prova: Mestre, Richiedente: Materiale testato: Prova eseguita: Conducibilità termica Riferimento Normativo: UNI EN 12667 DESCRIZIONE DEL CAMPIONE SOTTOPOSTO
Foglio n. 1 di 7 Protocollo: Luogo e Data della prova: Mestre, Richiedente: Materiale testato: Prova eseguita: Conducibilità termica Riferimento Normativo: UNI EN 12667 DESCRIZIONE DEL CAMPIONE SOTTOPOSTO
TABELLE DI TOLLERANZE ISO PER ALBERI
 dimensione ALBERO in mm TABELLE DI TOLLERANZE ISO PER ALBERI s6 r6 n6 m6 j6 h5 h6 h8 h9 h11 g5 g6 f7 f8 e8 d11 da > 1 +20 +16 +10 +8 +4 0 0 0 0 0-2 -2-6 -6-14 -20 a 3 +14 +10 +4 +2-2 -4-6 -14-25 -60-6
dimensione ALBERO in mm TABELLE DI TOLLERANZE ISO PER ALBERI s6 r6 n6 m6 j6 h5 h6 h8 h9 h11 g5 g6 f7 f8 e8 d11 da > 1 +20 +16 +10 +8 +4 0 0 0 0 0-2 -2-6 -6-14 -20 a 3 +14 +10 +4 +2-2 -4-6 -14-25 -60-6
Guida Compilazione Piani di Studio on-line
 Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
Sezioni e Norme di rappresentazione
 Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
Knowledge ided Engineering Manufacturing and Related Technologies DISEGNO TECNICO INDUSTRILE Sezioni e Norme di rappresentazione Ing. Daniele Regazzoni Dipartimento di Ingegneria 1... nella lezione precedente
SOLUZIONI D = (-1,+ ).
 SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Richiami sulle derivate parziali e definizione di gradiente di una funzione, sulle derivate direzionali. Regola della catena per funzioni composte.
 PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
f : A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che si può invertire.
 Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
