Equazioni differenziali ordinarie del primo ordine
|
|
|
- Timoteo Pace
- 5 anni fa
- Visualizzazioni
Transcript
1 Equazini differenziali rdinarie del rim rdine DEFINIZIONE Dicesi equazine differenziale rdinaria del rim rdine una equazine nella quale figura cme incgnita una funzine stabilisca un legame fra la variabile, la funzine e la derivata La frma generale dell equazine differenziale del rim rdine è la seguente : dve F è una funzine delle variabili, F,, 0 [], della sla variabile e che di questa funzine. ensate indiendenti tra lr e definite in un insieme aert A R. Nell equazine [] ssn nn cmarire la, la entrambe, ma la deve essere semre resente. Se l equazine [] è rislta risett alla variabile, assume il seguente asett: f, [] e diciam che l equazine differenziale del rim rdine è scritta in frma nrmale in frma cannica. Ogni funzine che sstituita, assieme alla sua derivata rima, nella data equazine differenziale trasfrma l equazine in una identità F,, 0 raresenta una sluzine un integrale dell equazine differenziale [] ed il su grafic si chiama curva integrale. Rislvere integrare l equazine differenziale [] significa trvare tutte le sue sluzini. L equazine differenziale f, ssiede infinite sluzini esresse dalla frmula, C sluzini C che, di slit, sn cntenente una cstante arbitraria C. Csì una famiglia di, è chiamata sluzine generale integrale generale dell equazine differenziale []. Attribuend alla cstante C valri articlari tteniam le sluzini articlari integrali articlari dell equazine differenziale [].
2 Terema di Cauch Sia f, una funzine di due variabili, definita in un cert insieme aert D R del ian ed ivi cntinua assieme alla derivata arziale risett ad ( f ). Stt queste itesi, se, è un unt qualsiasi dell insieme D, l equazine differenziale f una ed una sla sluzine, ammette definita in un rtun intrn I ] a, b[ ] h, h[ del unt sddisfacente la cndizine: 0 [] I numeri ed sn detti valri iniziali er la sluzine detta cndizine iniziale er questa sluzine. Il rblema di determinare la sluzine rblema di Cauch. e la cndizine [] è sddisfacente la cndizine iniziale [] dicesi OSSERVAZIONE Abbiam vist che le sluzini dell equazine differenziale f, si ssn esrimere mediante una famiglia di funzini, c diendenti da un arametr reale C. Abbiam dett anche che la funzine, c è l integrale generale dell equazine differenziale []. Fissat il unt D R,, se esistn un intrn ed una funzine : ] a, b[ R derivabile, tali che: a b ], [, D ( cndizine iniziale ) I ] a, b[ ] h, h[ del unt f, ] a, b[ direm che la funzine è una sluzine ( lcale ) del rblema di Cauch :, f Nella ratica, er trvare una sluzine lcale del rblema di Cauch si rcede cme segue : ) si calcla l integrale generale, c dell equazine differenziale [] ) si determina C in md che si abbia, C. Suniam di trvare er C il valre C ) la sluzine lcale del rblema di Cauch è:, L intrn C I ] a, b[ ] h, h[ nn è, in generale, un dat del rblema, ma una incgnita che viene trvata a sterire, ciè d avere rislt l equazine differenziale.
3 Quand, invece, è ssibile fissare a riri ( ciè rima della risluzine dell equazine differenziale ) l intervall I ] a, b[ ] h, h[, si dice che il rblema di Cauch è rislubile glbalmente in I ] a, b[ ] h, h[. La sluzine Interretazine gemetrica del terema di Cauch sddisfacente la cndizine [], la cui cndizine è garantita dal terema di Cauch, raresenta gemetricamente una curva integrale assante er il unt P,. << Per gni unt P TEOREMA, di D assa una ed una sla curva integrale dell equazine [] >> Dal terema enunciat segue che l equazine differenziale [] ammette infinite curve integrali, tali che er gni dat unt di D, ne assi una sla. Si sservi che il terema di Cauch garantisce l esistenza e l unicità della sluzine, C sltant in un cnveniente intrn I del unt iniziale. Si dimstra che la curva integrale assante, ad esemi, er il unt P, si rlunga fin ad incntrare la frntiera dell insieme D, il quale è, ertant attraversat da curve integrali che nn si incntran, in quant er gni unt di D ne assa una sltant. DEFINIZIONE: Si chiama integrale generale sluzine generale dell equazine differenziale f, una funzine, C una cstante arbitraria C, sddisfacente le seguenti cndizini : [4] della variabile e di ) verifica l equazine differenziale, qualunque sia il valre numeric attribuit alla cstante C ) se P, è un qualunque unt dell insieme D, è ssibile ( in un sl md ) determinare, C un valre C er cui risulti : A vlte, uò caitare che l integrale generale dell equazine [] sia calclat stt frma imlicita mediante una relazine del ti:,, C 0 DEFINIZIONE: Si chiama integrale articlare sluzine articlare dell equazine differenziale [], gni funzine generale C, C [5] dedtta dalla sluzine,, sstituend in quest ultima funzine il generic valre della cstante C cl valre articlare ttenut C in crrisndenza ad un refissat unt iniziale P, di D.
4 Integrali singlari di frntiera er l equazine differenziale f, Nelle itesi del terema di Cauch, cmunque si fissi un unt P, dell insieme aert D, e quindi intern a D, esiste un ed un sl integrale dell equazine differenziale [] sddisfacente la cndizine iniziale []. Suniam di scegliere il unt P, sulla frntiera di D e di cercare ancra un integrale dell equazine [] sddisfacente alla []. In quest cas il terema di Cauch nn è iù alicabile in quant ess è valid sl er unti interni del dmini della funzine f,. Tuttavia, susta ƒ cntinua in D e sulla frntiera di D, uò darsi che esistan ugualmente una iù curve integrali sddisfacenti alla cndizine []. Si ssn resentare due casi: Prim cas La curva integrale assante er il unt P funzine, ha unti interni a D, La, C raresenta un integrale articlare dell equazine differenziale [], in quant ess si ttiene dall integrale generale, c er un valre articlare di C Secnd cas : La curva integrale giace interamente sulla frntiera dell insieme D. In quest cas l integrale trvat raresenta un integrale singlare dell equazine differenziale [] in quant ess nn trà mai essere ricavat dall integrale generale mediante la sstituzine della cstante C cn un su valre articlare ( e nemmen er C ). DEFINIZIONE : Si chiama integrale singlare integrale di frntiera dell equazine differenziale [] gni eventuale integrale la cui crrisndente curva integrale risulta tracciata interamente sulla frntiera dell insieme D. Un integrale singlare è un integrale articlare che nn uò essere dedtt dall integrale generale attribuend alla cstante C un valre articlare. Cncludend ssiam affermare che l integrale singlare di una equazine differenziale del rim rdine f una funzine, è il cui grafic cincide cn la frntiera del dmini della funzine f, cn una sua arte. 4
5 Equazini differenziali a variabili searate Una equazine differenziale del rim rdine si dice a variabili searate, in un cert insieme D, quand uò essere scritta nella seguente frma: dbd0 A [6] ciè quand il cefficiente del differenziale d è una funzine della sla ed il cefficiente del differenziale d è una funzine della sla. La [6] uò essere scritta anche nella seguente maniera: A0 B [7] L integrale generale dell equazine differenziale a variabili searate si ttiene integrand d amb i membri della [6]. Otteniam: d B A C [8] d d d d C C <<Rislvere il seguente rblema di Cauch: d d 0 >> d d ln ln C ln C C ( se C R allra anche h C aartiene ad R ). 0 h e C e he Abbiam csì rislt il rblema di Cauch rst ttenend il seguente integrale articlare : e che teva essere ricavat anche utilizzand i seguenti integrali definiti: d 0 d ln ln ln e Equazini differenziali a variabili searabili Sess avrem a che fare cn equazini differenziali del rim rdine in cui le variabili nn sn inizialmente searate ma l ssn essere mediante semlici erazini algebriche. Una equazine del rim rdine si dice a variabili searabili quand uò essere scritta nella seguente frma cannica : MdB Nd0 A [9] ciè quand i cefficienti dei differenziali d e d sn entrambi i rdtti di una funzine della sla er una funzine della sla, nn escludend che il cefficiente del differenziale d ssa essere funzine della sla e quell del differenziale d ssa essere funzine della sla. Nell equazine trvata nn cmare il valre asslut nell argment del lgaritm in quant la è maggire di 5
6 Una equazine differenziale del rim rdine a variabili searabili uò resentarsi anche nella seguente frma: MB N 0 A [0] in una delle due seguenti frme : A B ure A B [] L equazine [9] diventa una equazine differenziale a variabili searate se dividiam amb i membri er il rdtt M B M né, ricrdand che la divisine è lecita in un insieme D dve né B si annullan. D la divisine tteniam: A B N d M Pi si rcede cme nel cas recedente delle equazini a variabili searate. d0 [] Se abbiam B 0 ure M 0 allra le equazini, ssn essere sia integrali articlari che integrali singlari. Si dvrà decidere cas er cas. Sarann integrali articlari se tali equazini trann essere dedtte dall integrale generale assegnand alla cstante C valri articlari ( al limite anche il valre infinit ). d d0 Searand le variabili ssiam scrivere l equazine rsta nella frma: d d 0 ln d d d ln ln ln C ln ln C ln C Ce (integrale generale) è un integrale articlare er l equazine rsta in quant ess uò essere dedtt dall integrale generale quand alla cstante C attribuiam il valre zer. C 0 0 d d d d d d C C C In quest cas l integrale generale nn uò essere esress in frma eslicita 6
7 << Rislvere la seguente equazine differenziale a variabili searabili : d d 0 >> d d d d ln ln ln C ln ln C C C Ma C è una cstante reale relativa e quindi è lecit rre : C h h è l integrale generale dell equazine differenziale rsta. Questa equazine differenziale nn ammette integrale singlare in quant il dmini dell equazine è R, ciè l inter ian, la cui frntiera è la retta imrria, ciè l insieme dei unt imrri del ian. << Rislvere il seguente rblema di Cauch d d 0 >> equazine : h h La curva integrale assante er il unt P. Si uò rcedere anche nella seguente maniera :, ha d d ln ln ln ln ln ln Integrale generale, integrale articlare, integrale singlare Le equazini differenziali a variabili searabili ssn essere semre ricndtte alla seguente frma cannica nrmale: A B la seguente sluzine : [] [] ed ammettn cme integrale generale B d A d D avere calclat l integrale generale bisgna rislvere l equazine essa ammette sluzini. Se è una di queste, ciè se sluzine dell equazine rsta in quant risulta B K B 0 e vedere se 0 allra l equazine è una 0 ed anche 0 A 0, 0 0 Bisgna i stabilire sl se raresenta un integrale articlare un integrale singlare. ln ln ln K K K nend C K tteniam l integrale generale: essere ricavat dall integrale generale er C 0 C B 0 integrale articlare in uò Essend > ed > l argment di ciascun lgaritm è sicuramente sitiv e quindi nn ccrre il valre asslut 7
8 cme abbiam vist in recedenza il su integrale generale è C [] ure h [] se niam C kh h k B 0 0 che si ttiene dall integrale generale [] er C dall integrale generale [] er k 0. Si tratta ertant di un integrale articlare. Le sluzini dell equazine d d C sin C B 0 sn e nn rientran, nemmen cme cas limite, nella famiglia delle sinusidi sra scritta. Questa vlta siam in resenza di due integrali singlari Il dmini dell equazine differenziale rsta si ttiene rislvend la seguente inequazine : 0 er Il dmini richiest è la arte di ian interna alla striscia individuata dalle rette, rette che raresentan la frntiera del dmini. CONCLUSIONE Nei rimi due esemi le sluzini dell equazine 0 articlari, nel terz esemi le sluzini dell equazine 0 B dann lug ad integrali B raresentan integrali singlari ed esrimn la frntiera dell insieme di esistenza (dmini) dell equazine differenziale rsta. 8
9 Equazine lineare del rim rdine mgenea E una equazine differenziale ricnducibile alla seguente frma cannica: a 0 [4] Si tratta di una equazine mgenea a variabili searabili che saiam integrare. d d ln h a, d a d, d a d k ln h, ln ln a d, h a d e he a d a d he [5] è l integrale generale dell equazine differenziale [4]. h a d 0 he d = he d d ln h e ln h 0 si ttiene er h 0 e quindi raresenta un integrale articlare. Equazine lineare del rim rdine cmleta Una equazine differenziale si dice lineare del rim rdine cmleta quand è ricnducibile alla [6] seguente frma cannica: a f dve a ed f sn funzini cntinue in un rtun intervall refissat. La funzine è l incgnita dell equazine differenziale. L integrale generale differenziale [6] è dat dalla smma dell integrale generale mgenea assciata e di un integrale articlare Siccme il calcl dell integrale articlare dell equazine dell equazine dell equazine differenziale cmleta. nn semre è agevle è referibile utilizzare, er integrare l equazine differenziale [6] il metd della variazine della cstante arbitraria ( metd di Lagrange) il metd dirett dett anche metd della smiglianza metd di Cauch metd della frma del termine nt. [4] Cnsideriam l equazine mgenea assciata: a 0 il cui integrale generale è: a d h e [5] 9
10 Vediam adess, se er cas, l integrale generale dell equazine differenziale [6] ha cme integrale generale una funzine frmalmente identica alla funzine [5] che è l integrale generale dell equazine mgenea assciata. Il tentativ ha esit sitiv se sstituiam la cstante arbitraria h cn la funzine determinare, vediam ciè se la funzine a d e A [7] da ( h st er cmdità A e a d ) uò essere cnsiderata l integrale generale dell equazine differenziale [6]. La funzine [7] è l integrale generale dell equazine differenziale [6] se essa, assieme alla sua derivata rima, verifica l equazine [6]. Ricrdand che: A a A ssiam scrivere: A A A a A Sstituend nella [6] tteniam: Aa A a A f Semlificand tteniam: A f, [ d f A d Integrand amb i membri tteniam : f d A f A d Sstituend nella [7] tteniam: d d ] d a d a d e e f d C [8] d d f A La funzine della frmula [8] è l integrale generale dell equazine differenziale [6]. Quindi er calclare l integrale generale dell equazine differenziale [6] basta alicare la frmula [8]. Tuttavia, nel cas di risluzine di una equazine differenziale lineare del rim rdine cmleta, è cnsigliabile nn alicare direttamente la frmula trvata (anche quand un la riuscisse a ricrdare) ma effettuare tutti i calcli fin alla determinazine dell integrale generale richiest. 4 4 Le equazini lineari del rim rdine nn ammettn integrali singlari e l integrale generale riassume in sé tutti gli integrali dell equazine 0
11 Osservazine: Trvat l integrale generale a d h e h A dell equazine mgenea assciata ved se ss trvare un integrale articlare dell equazine cmleta avente la seguente struttura: rim rdine cmleta ssiam rcedere in due mdi:. Per calclare l integrale generale dell equazine lineare del (0) Se la funzine è riva della cstante additiva, allra è un integrale articlare dell equazine differenziale cmleta. Per calclare l integrale generale dell equazine differenziale cmleta a f la seguente frmula:. bisgna alicare () Se la funzine C, cntiene la cstante additiva, allra l integrale generale dell equazine differenziale cmleta basta alicare la seguente frmula:, C A Prblema di Cauch er le equazini lineari del rim rdine Sia un unt di un intervall dve a e f sn cntinue. Per gni numer reale è ssibile scegliere in maniera univca la cstante C in md da sddisfare la cndizine iniziale. Ciò equivale a rislvere il seguente sistema, dett rblema di Cauch: a f si Sintesi: Per rislvere l equazine lineare cmleta del rim rdine a f rcede cme segue: 0) Si calcla l integrale generale he a d dell equazine mgenea assciata a 0 che è un equazine differenziale a variabili searabili 0) Si sstituisce nell integrale generale he a d e si determina in md che la nuva funzine la cstante h cn la funzine incgnita a d generale dell equazine lineare cmleta del rim rdine a f 0) Si calcla la derivata rima della funzine a f i valri di e di e sia l integrale a d e e sstituiam nell equazine, imnend che l uguaglianza trvata sia una identità.
12 04) Quest ci cnsente di determinare in maniera univca il valre della funzine. Osservazine: Per la risluzine dell equazine lineare cmleta del rim rdine a f è iù cnveniente alicare il metd della variazine della cstante arbitraria a f Scriv l equazine mgenea assciata: 0 d d d d d d ln ln lnc ln lnc C 5 C Sstituend nell equazine rsta tteniam: 4 5 d C 4 d 4 d C, 4 Se nella risluzine dell integrale d 4 d C 5 d C tralasci la cstante C, tteng un 5 5 integrale articlare dell equazine differenziale rsta L integrale generale generale. di tale equazine è dat dalla smma dell integrale dell equazine mgenea assciata e di un integrale articlare dell equazine differenziale cmleta.. Nel nstr abbiam: C 5 5 che è l stess risultat ttenut in recedenza. Osservazine: Se la funzine è riva della cstante additiva, allra è un integrale articlare dell equazine differenziale cmleta. Per calclare l integrale generale dell equazine differenziale cmleta a f la seguente frmula:. Se la funzine C, allra l integrale generale seguente frmula:, C A bisgna alicare cntiene la cstante additiva, dell equazine differenziale cmleta basta alicare la
13 Equazine lineare del secnd rdine mgenea a cefficienti cstanti E una equazine ricnducibile alla seguente frma: Ae B e se radici realieedistinte a b c 0 cs sin A e B e A B e se A q B q e se qi 9 cn a, b, c cstanti numeriche reali. Per trvare l integrale generale dell equazine 9 basta trvare due integrali articlari linearmente indiendenti. La natura dell equazine rsta ci suggerisce la ricerca tra le funzini del ti e cn cstante reale. Infatti, funzini di quest ti hann derivate rime e secnde che assmiglian alla funzine di artenza e che, quindi, mltilicate er rtuni numeri a, b, c ssn dare una funzine identicamente nulla. Pertant se vlte abbiam: Sstituend nell equazine differenziale 9 tteniam: L equazine in e a e b e c e e è una sluzine dell equazine [9], derivand due e 0 ciè: e a b c 0 e 0 R 0 0 a b c csì ttenuta dicesi equazine caratteristica dell equazine differenziale lineare del secnd rdine mgenea. Le radici, dell equazine 0 ssn essere reali e distinte, reali e cincidenti, cmlesse e cniugate a secnda che il discriminante b 4 ac sia risettivamente sitiv, null, negativ. Si ssn resentare tre casi: PRIMO CASO: Le radici, dell equazine [0] sn reali e distinte. L equazine 9 ha cme integrali articlari le funzini: e e che sn fra lr linearmente indiendenti. L integrale generale dell equazine differenziale Determinare la funzine 9 è: c e c e cstituisce il csiddett rblema di Cauch. che sddisfa l equazine differenziale e le cndizini iniziali
14 0 Se le cndizini iniziali sn 0 0, 0 articlare (I.P.) si ricava imnend le seguenti cndizini: c c c c 5 c c alle cndizini iniziali 0, 0 5 è: e e c e c e 5 allra la crrisndente sluzine c e c e c e c e L integrale articlare assciat SECONDO CASO: Le radici, dell equazine [0] sn reali e cincidenti. b ( a ) e, e L integrale generale della [9] è: c e c e c c e c c e TERZO CASO: Le radici q i e q i sn cmlesse e cniugate. e quindi l' integrale generale dell'equazine mgenea [] è: C e q C e q C q C q e [] cs sin cs sin In quant due integrali articlari fra lr linearmente indiendenti ci vengn frniti dalle due seguenti funzini: e cs q e sinq i i cs sin e C C Equazine lineare del secnd rdine cmleta a cefficienti cstanti E una equazine ricnducibile alla seguente frma: a b c f 4 cn a, b, c cstanti numeriche reali. Per itesi sn nte le tre cstanti a, b,c e la funzine <<L integrale generale integrale generale dell equazine cmleta>>. f. dell equazine cmleta si ttiene aggiungend all dell equazine mgenea assciata un integrale articlare 4
15 L integrale articlare l ssiam calclare: 0) alicand il metd di Lagrange della variazine delle cstanti arbitrarie 0) ure tenend resente la articlare struttura della funzine f (metd di Cauch della frma del termine nt dei cefficienti indeterminati). Metd di Lagrange Per alicare quest metd dbbiam cnscere l integrale generale della crrisndente equazine mgenea. Il metd di Lagrange è alicabile sia se a,b,c sn cstanti sia se sn delle funzini della. Nella ratica erò quest metd è cnveniente sl quand l equazine mgenea assciata è a cefficienti cstanti, in quant in quest cas saiam calclare l integrale generale. Trvati gli integrali articlari ed dell equazine mgenea assciata ssiam scrivere il su integrale generale nella seguente maniera: c c 5 Pi cercherem di trvare un integrale articlare dell equazine [4] avente la seguente struttura: dve [5] e sn due funzini delle da determinare imnend che la funzine sluzine dell equazine differenziale [4] ed ed sia sn due integrali articlari linearmente indiendenti dell equazine mgenea assciata a b c 0. Rislvend il sistema : e e. 0 f ci trviam rima le funzini e, successivamente, attravers altre due integrazini, determiniam le funzini L integrale generale dell equazine differenziale [4] risulta uguale a: tg 0 0 i c cs c sin cs sin sin cs 5 ed c c 0 debbn essere linearmente indiendenti, ciè tali che:, e c c 0 5
16 Il sistema da rislvere è: W cs sin cs cs sin sin sin cs 0 sin tg cs W W sin W W cs 0 tg cs 0 sin sin tg sin cs sin cs W W sin sin cs d d cs d sinlntg k sin cs d sin d sin d cs k cs 4 dve k e k sn due cstanti arbitrarie. sin ln tg sin cs cs 4 = sin lntg sin c c sin cs cs cs 4 cs 4 lntg c csc sin Dimstrazine: Ni dbbiam determinare due funzini e che debbn verificare l equazine [4]. Quest ci dà una relazine tra le due funzini incgnite e. Ma, in generale, er determinare due quantità incgnite ni dbbiam avere due relazini. La secnda relazine la ssiam intrdurre arbitrariamente. Derivand l uguaglianza [5] tteniam: Può essere mlt cnveniente di imrre cme secnda relazine tra che l esressine della e la cndizine sia frmalmente identica all esressine dell integrale articlare, ciè alla [5]. Quest biettiv ci imne di rre: 0 [A] [B] Adess ci calcliam la derivata secnda della funzine Allra: : Sstituend,, nella [4] tteniam: a b c f a b c a b c a f 6
17 Le esressini resenti all intern delle arentesi rtnde sn nulle in quant le funzini sn sluzini dell equazine mgenea a b c Pertant, erché la funzine 0. ed sddisfi l equazine [4] deve essere verificata la cndizine: f Per determinare le funzini e quindi bisgna rislvere il sistema: [C] dbbiam tenere resente le cndizini [A] e [C] e 0 f Se il determinante (dett Wrnskian) del sistema di equazini [6] è divers da zer, allra ssiam determinare in maniera univca le funzini integrazini, ci cnsentn di individuare le funzini W W W 0 (Wrnskian ) W W W d Se vengn date le cndizini iniziali abbiam: W W d e e. 0 f W W W W d [6] che, cn due successive W W W d 0 f W W d d W W L integrale generale dell equazine differenziale [4] risulta uguale a: Osservazine: Se, quand integriam le funzini e, ni intrduciam le crrisndenti cstanti arbitrarie, allra tteniam direttamente l integrale generale dell equazine differenziale [4], che uò essere scritt nella seguente maniera: W W d h W W d k Cme è facile intuire, il metd aena esst er la determinazine di un integrale articlare ha il grave incnveniente di ridursi alle integrazini: d, d che, sess, resentan ntevli difficltà. Per tale ragine esrrem, in seguit, un metd mediante il quale tali integrazini si ssn evitare. Tale metd uò essere alicat quand il termine nt f dell equazine differenziale assume frme articlari. 7
18 Osservazine: Se in e Equazini Differenziali è l integrale generale rsta. Infatti: incrriam le cstanti k e k, allra dell equazine differenziale sin lntg k sin k c c sin cs cs cs 4 cs lntg k cs k sin 4 è una funzine identica a quella trvata recedentemente se niam c k e c k Metd di Cauch della frma del termine nt dei cefficienti indeterminati Serve er calclare un integrale articlare dell equazine differenziale [4] k k f b b b P Pk k k = linmi di grad k a b c k Qk se 0 0 ( c 0) Q se 0 0 ( c 0) Qk se 0 ( b c 0) k k 0 Q A A A k k cn A, A,, Ak, Ak da determinare alicand il rincii di identità dei linmi. <<Se il termine nt f dell equazine differenziale lineare cmleta del secnd rdine è un linmi, allra un su integrale articlare ci viene dat da un linmi Qk avente l stess grad k (se c 0) da un linmi di grad k (se c 0 ) da un linmi avente grad k (se b dve Qk c 0) >> r r k k Q A A A cn r 0 r r k k raresenta un linmi di grad k, ciè un linmi avente l stess grad di f, r raresenta l rdine di mltelicità della radice zer dell equazine caratteristica a b c 0. c 0 r 0 c 0 r b c 0 r Sstituend nell equazine [4] le esressini di,, ed alicand il rincii di identità dei linmi ci ricaviam i valri delle cstanti A k e quindi dell integrale articlare 0 0 f k r, Q A A [ r 0, k ], A c c e 0 8
19 A A A, A A A Se le cndizini iniziali sn: 0, 0, A A c c e tteniam: c c e c e c c c c e c c f h e cn h, R nti Ae se ( ) A e se A e se Un integrale articlare dell equazine differenziale [4] assume la frma: k A e cn k assegnat ed A da determinare. In articlare risulta: a) k 0 se nn è radice dell equazine caratteristica assciata b) k se è radice semlice dell equazine caratteristica assciata c) k se è radice dia dell equazine caratteristica assciata e 4 P a b c 0 = equazine caratteristica 4 0 Ae Ae 4Ae 8Ae Ae e Ae c e c e 4Ae e A c e c e e f P e cn k k Qk e se Qk e se Q e se P linmi di grad k e Q k k k alicand il rincii di identità dei linmi. cas k linmi di grad k i cui cefficienti vann calclati Q A A A k k k nn è radice dell equazine caratteristica assciata k A A e 9
20 Mi calcl la derivata rima e la derivata secnda della funzine, sstituisc le esressini trvate nell equazine differenziale [4], alic il rincii di identità dei linmi er calclare i valri delle cstanti A A. L integrale articlare è csì calclat. k cas è radice avente mltelicità r (ciè ure ) dell equazine caratteristica assciata e A A e r k k L equazine caratteristica dell equazine differenziale mgenea assciata è: 0 0 L equazine caratteristica dell mgenea assciata ammette la radice dia. Il su integrale generale è: C e C e Piché risulta un integrale articlare dell equazine differenziale rsta avrà la seguente struttura: B C e B B C C e B C e B C e B e B B C C e B B C C e B 6B C 6B 4C C e Sstituend nell equazine differenziale rsta tteniam: B B C B C C e B B C C e B C e e B B C B C C B B C C B C 6B C Alicand il rincii di identità dei linmi tteniam: B 0 6 e 6 C Pertant l integrale generale dell equazine differenziale rsta è: f cs k q sin k cn qk,, valri dati cs sin A k B k se, ik C e C e e 6 Acs k Bsin k se, i k A cs k B sin k se, i k A cs k B sin k, ik Prcedend cme rima ci calcliam i valri di A e di B e quindi ssiam disrre di un integrale articlare dell equazine differenziale [4]. 0
21 4 5sin 4 0, i c cs c sin e Piché risulta i i ssiam individuare un integrale articlare avente la frma: Asin B cs sin A B cs Sstituend nell equazine data tteniam: 4Acs 4Bsin 4Acs 4Bsin 8Asin 8Bcs Acs Bsin 5sin 8A 9B 5 9 A 8B 0 8 A 9 9 B cs sin c c e 9 9 cs sin cs sin f P cs k ure f Q sin k ure cs M cs k N sin k se, i k M cs k N sin k se, i k, ik k 0 equazine caratteristica cn P linmi di grad r, grad uguale al maggire dei gradi dei linmi 4 sin 0 i k 4 s Q linmi di grad s. P ed Q. R linmi di rim grad C cs C sin cs sin cn M A B, M k N k f P k Q sin k M ed N sn linmi di N C D linmi di rim grad. Essend: ki i un integrale articlare dell equazine differenziale rsta avrà la seguente struttura: cs M k N sin k ciè: cs A B C D sin 4 cs 4 sin A B cs C D sin Acs A B sin C sin A B cs A C B A D C A D C B Sstituend e semlificand tteniam: C A D cs A C B sin sin
22 Questa uguaglianza è una identità se risultan uguali i cefficienti di cs e di sin Quest si verifica se: C 0 A D 0 A C B 0 A, B 0, C 0, D sin cs C cs C sin sin cs 4sin In questa equazine differenziale abbiam: 0, k, i numeri i sn radici dell equazine caratteristica assciata 0 4 cs 4 cs A B C D sin A C B A D C A D C B sin Sstituend nell equazine data tteniam : cs C A D A C B sin sin C 0, A D 0, A, C B 0 A, B C 0, D sin cs c cs c sin sin cs c cs c sin f e cs k q sin k f e cs k sin e Acs k Bsin k se, ki e A csk B sink se, ki f e q k Essend A e B due cstanti da determinarsi. f e P cs k Qsin k f e P cs k sin M ed e M cs k N sin k se, ki e M csk N sink se, ki N sn linmi di grad uguale al maggire dei gradi dei linmi cs e M k N sin k cs e M k N sin k se f e Q k P ed Q. se i numeri k i nn sn radici dell equazine caratteristica assciata f è la smma di iù termini f f se i numeri k i sn radici dell equazine caratteristica assciata,, dei tii sra cnsiderati, allra l integrale articlare ci viene dat dalla smma degli integrali articlari crrisndenti a ciascun termine di f.
23 e e 4 [] e 4 e 6 4 e [G] 4 0,,, è radice avente mltelicità ( r ) dell equazine caratteristica., C e C e A b e, A B e A B e Ae A B e A B e Sstituend queste esressini nell equazine [G] tteniam: Ae A B e A B e 4 A B e A B e A b e e A B 0 4A A Be e 4 A A 4 B 4 Un integrale articlare della [] è: e 4 e e 4 c e c e e e 4 L integrale generale della [] è: Generalizzand il rblema ssiam affermare che la ricerca di un integrale articlare di una equazine lineare nn mgenea (a cefficienti cstanti variabili) uò, in mlti casi, essere facilitata dalla seguente sservazine. Se il secnd membr f dell equazine differenziale lineare è cstituit dalla smma di iù funzini, vale a dire f f f f cnsideran le seguenti equazini: Se a b c f a b c f a b c f, si è un integrale articlare della rima equazine, della secnda, terza, allra rsta. della è un integrale articlare dell equazine differenziale lineare Vlend, ssiam alicare quest rcediment nei seguenti casi: f cs k qsin n P e f P h e k 6 Vedere esemi recedente
24 f cs k q sin n Sintesi er le equazini differenziali del secnd rdine: a b c a a b c f = equazine caratteristica assciata ) a b c m q ) a b m q ) a m q ), ) ure ) f he f linmi in ), A B C A B C A B C A B C A B C 4 a b c h e Ae A e A e f m q e ) ure ) a b c m q e A B C e A B Ce A B C 4 A B Ce A B C f cs k q sin k a b c cs k q sin k ) ki ure ki ) ki ure ki Acs k B sin k A cs k B sink cs a b c e cs k q sin k f e k q sin k ) ki ure ki ) ki ure ki cs e P k R sink cs e P k R sink 4
25 dve R P ed Equazini Differenziali R sn linmi di grad uguale al maggire dei gradi dei linmi P ed Tabella rieilgativa f m q A B C m q m q he he he m q e m q e m q e anntazini a b c f a b f A B C A B C a f A B C A B C 4 Ae A e A e A B C e A B C e A B C e c 0 bc 0 a b c f, a b c f a b c f, cs k qsink Acs k B sin k ki, ki k qsink cs A k Bsink cs sin cs e P k Q k cs sin cs e P k Q k cs, ki e M k N sin k, ki e M k N sin k, ki M ed N sn linmi di grad uguale al maggire dei gradi dei linmi P ed Q. 5
26 a b c 0 0, radici dell equazine caratteristica a b c Ae B e se radici realieedistinte Ae B e A B e se cs sin A q B q e se qi a b c f 0, a b c k k f b b b P k k k Qk se 0 0( c 0) Q se 0 0 ( c 0) Qk se 0 ( b c 0) k k P = linmi di grad k k Q A A A linmi di grad k i cui k k cefficienti vann calclati alicand il rincii di identità dei linmi. f h e cn h, R nti Cn A cstante da determinare. Ae se ( ) A e se A e se f P e k k Qk e se Qk e se Q e se 6
27 cn P linmi di grad k e Q k k linmi di grad k i cui cefficienti vann calclati Q A A A k k alicand il rincii di identità dei linmi. f cs k q sin k cn qk,, valri dati e cn A e B due cstanti da determinare. k k Acs k Bsin k se, i k A cs k B sin k se, i k f P cs k ure f Q sin k ure cs f P k Q sin k r M cs k N sin k se, i k M cs k N sin k se, i k cn P linmi di grad r, Q linmi di grad s. grad uguale al maggire dei gradi dei linmi determinare. P ed M ed N sn linmi di Q ed i cui cefficienti sn da f e cs k q sin k f e cs k sin f e q k e Acs k Bsin k se, ki e A csk B sink se, ki cn A e B due cstanti da determinare. f e P cs k Qsin k f e P cs k sin f e Q k e M cs k N sin k se, ki e M csk N sink se, ki M ed N sn linmi di grad uguale al maggire dei gradi dei linmi ed i cui cefficienti sn da determinare. P ed Q 7
28 N.B. Una equazine di secnd grad uò avere: (0) due radici reali e distinte ure () due radici reali e cincidenti ure () due radici cmlesse e cniugate. 0 a b c d a b c d 0,, radici dell equazine caratteristica Ae B e C e se Ae B e C e Ae B C e se R radici reali e distinte Ae B e C e A B C e se R Ae B cs q C sin q e se R, qi Una equazine algebrica di terz grad uò avere una radice reale e due cmlesse e cniugate, ure tre radici reali. Le radici reali ssn essere tra lr distinte cincidenti. k k f b b b P k k k k k k P = linmi di grad k k Qk se d 0 Q se d 0 c 0 ( 0) Q sec d 0b 0 ( 0) Qk seb c d 0a 0( 0) Q A A A linmi di grad k i cui k k cefficienti vann calclati alicand il rincii di identità dei linmi. f h e cn h, R nti Cn A cstante da determinare. ( ) Ae se A e se A e se A e se 8
29 f P e cn k P linmi di grad k e Q k k k k Q e se k Q e se Q e se Qk e se k k alicand il rincii di identità dei linmi. f cs k q sin k linmi di grad k i cui cefficienti vann calclati Q A A A cn qk,, valri dati e cn A e B due cstanti da determinare. k k Acs k Bsin k se, i k A cs k B sin k se, i k f P cs k ure f Q sin k ure cs f P k Q sin k r M cs k N sin k se, i k M cs k N sin k se, i k cn P linmi di grad r, Q linmi di grad s. grad uguale al maggire dei gradi dei linmi determinare. P ed M ed N sn linmi di Q ed i cui cefficienti sn da f e cs k q sin k f e cs k sin f e q k e Acs k Bsin k se, ki e A csk B sink se, ki Essend A e B due cstanti da determinarsi. f e P cs k Qsin k f e P cs k sin f e Q k e M cs k N sin k se, ki e M csk N sink se, ki 9
30 M ed N sn linmi di grad uguale al maggire dei gradi dei linmi ed i cui cefficienti sn da determinare. P ed Q 0 4 a b c d e 4 a b c d e 0,,, 4 radici dell equazine caratteristica 4 Ae B e C e D e se 4 R 4 A B e C e D e se 4 R A B e C D e se 4 R Ae B C D e se 4 R A B C D e se 4 R Ae B e C csq D sinqe se R,4 iq A B e C csq D sinqe se R,4 iq m Acs n B sin n e C cs q D sin q e se, m in,4 q i Una equazine algebrica di quart grad uò avere (0) 4 radici reali (0) radici reali e due radici cmlesse e cniugate (0) quattr radici cmlesse a due a due cniugate. Nn uò avere un numer disari di radici reali un numer disari di radici cmlesse. Infatti, una equazine algebrica, se ammette una radice cmlessa ammette anche la sua cniugata. k k f b b b P k k k k k Q se d e c 4 a b c d e 0 Qk se e 0 Q se e 0 d 0 ( 0) 0 0 ( 0) Q sec d e 0b 0( 0) 4 Qk seb c d e 0 a 0( 4 0) k k P = linmi di grad k k Q A A A linmi di grad k i cui k k cefficienti vann calclati alicand il rincii di identità dei linmi. 0
31 f h e cn h, R nti cn A cstante da determinare. f P e cn k P linmi di grad k e Q k Ae se A e se 4 4 ( ) A e se k k k Q e se A e se 4 4 A e se 4 Q e se k 4 Q e se 4 4 Q e se 4 4 Qk e se 4 k k alicand il rincii di identità dei linmi. k linmi di grad k i cui cefficienti vann calclati Q A A A k k f cs k q sin k cn qk,, valri dati e cn A e B due cstanti da determinare. Acs k Bsin k se, i k,4 i k A cs k B sin k se, i k,4 i k f P cs k ure f Q sin k ure cs f P k Q sin k r cn P linmi di grad r, M cs k N sin k se, i k,4 i k M cs k N sin k se, i k,4 i k Q linmi di grad s. grad uguale al maggire dei gradi dei linmi determinare. P ed M ed N sn linmi di Q ed i cui cefficienti sn da f e cs k q sin k f e cs k sin f e q k e Acs k B sin k se, ki,4 ki e A csk B sink se, ki,4 ki Essend A e B due cstanti da determinarsi.
32 f e P cs k Qsin k f e P cs k sin M ed f e Q k e M cs k N sin k se, ki,4 ki e M csk N sink se, ki,4 ki N sn linmi di grad uguale al maggire dei gradi dei linmi ed i cui cefficienti sn da determinare. Equazini differenziali rdinarie P ed Q Definizine: Si chiama equazine differenziale (rdinaria) di rdine n una equazine del ti: n F,,,,, 0 [] dve F è una funzine assegnata che lega la variabile indiendente cn la funzine incgnita n e le sue derivate successive,,, fin all rdine n. Ordine di una equazine differenziale è il massim rdine di derivazine che aare nell equazine stessa. Una equazine differenziale di rdine n si dice ridtta a frma nrmale quand è rislta risett alla derivata di rdine massim, ciè quand la [] è equivalente ad una equazine del ti: n n f,,,,, [] dve ƒ è una funzine assegnata delle ( n ) variabili,,,,, n. Particlarmente imrtanti sn le equazini differenziali lineari di rdine n, ciè le equazini differenziali del ti: n n n n a a a a f [] Il nme lineare è dvut al fatt che in essa la e le sue derivate successive hann esnente un (ciè sn termini di rim grad) e nn sn mltilicate tra lr. Se risulta f 0 l equazine differenziale si dice mgenea, in cas cntrari si dice cmleta. Una equazine differenziale lineare di rdine n mgenea ha la seguente frma: Una funzine a a a a [4] n n n n n 0, definita e cntinua nell intervall I n e tale che risulti I : F,,,, 0 n R, derivabile n vlte in tale intervall, si dice integrale sluzine dell equazine differenziale []. Pertant integrare l equazine differenziale [] significa determinare una funzine stessa. Ogni sluzine che, [5] I, verifica l equazine di una equazine differenziale di rdine n cntiene n cstanti
33 arbitrarie. Queste cstanti sn cmletamente ed univcamente determinate quand, accant all equazine [], assegniam n cndizini. Le cndizini da imrre ssn essere di natura diversa, e dann lug a rblemi diversi, i iù ntevli dei quali sn: a) rblema dei valri iniziali ( di Cauch) se è assegnat l stat iniziale del sistema, ciè se, in crrisndenza di un determinat valre della variabile indiendente, cnsciam i valri della e delle sue rime ( n ) derivate. b) rblemi ai limiti, nei quali le cndizini rescritte riguardan almen due valri distinti della variabile indiendente. Prblemi ai valri iniziali Assegnare l stat iniziale della iù generale funzine che verifica l equazine [] significa che sn da cnsiderarsi nti i valri: che la funzine incgnita n,,, [6] n e le sue rime ( n ) derivate assumn in crrisndenza del valre iniziale della variabile indiendente. Un rblema ai valri iniziali cnsiste nella ricerca di una sluzine della [] che verifichi le cndizini [6]. Integrale generale Si dice integrale generale dell equazine [] una funzine che diende dalla variabile indiendente e da n arametri c, c,, tale che: ) la,,,, (cstanti di integrazine) c c c c n [7],,,, n c c c n e le sue derivate successive fin all rdine n verifichin la [] I ed indiendentemente dai valri attribuiti alle n cstanti c, c,, ) le n cstanti c, c,, c n sian linearmente indiendenti Quest significa quand in crrisndenza di gni refissat stat iniziale del sistema individuat dai valri n,,,, il sistema di n equazini:, c, c,, cn, c, c,, cn..., c, c,, cn n n c n [8]
34 nelle n incgnite c, c,, è rislubile, ciè ammette una sla sluzine. c n Integrali articlari Integrale articlare dell equazine differenziale [] è un qualsiasi integrale che si uò ttenere dall integrale generale [7] er una articlare scelta delle cstanti d integrazine c, c,,. c n Integrale singlare Integrale singlare di un equazine differenziale è un integrale dell equazine differenziale rsta che nn è deducibile assegnand valri articlari alle cstanti arbitrarie dell integrale generale [7]. Quindi l Integrale singlare è una funzine che nn diende da alcuna cstante e nn uò essere ricavat dall integrale generale er articlari valri numerici delle cstanti c, c,,, ma che è sluzine dell equazine differenziale cnsiderata. c n Da ciò si deduce che l Integrale singlare di una equazine differenziale nn esaurisce la ttalità delle curve integrali. 8 Equazini differenziali lineari di rdine n 7 Se dell equazine differenziale lineare mgenea a a a a n n n n n 0 cnsciam n integrali articlari,,, fra lr linearmente indiendenti (ciè a Wrnskian divers da zer), allra l integrale generale della [4] è la funzine: c c c [9] n n c, c,, cstanti arbitrarie fra lr linearmente indiendenti. Si sservi che gni integrale c n dell equazine lineare è esrimibile cme cmbinazine lineare di n integrali articlari. Ciè le equazini lineari nn ammettn integrali singlari. n 7 Tale è il cas, ad esemi, dell eventuale invilu eventuale lug gemetric dei unti multili delle curve integrali [7] al variare dei arametri c, c,, c n ( quand, naturalmente, tale invilu lug nn sia una curva limite della famiglia di curve integrali. 8 I diagrammi delle sluzini di una equazine differenziale si dicn curve integrali 4
35 Wrnskian Equazini Differenziali W di n funzini,,, è il determinante frmat dalle n funzini e dalle lr derivate fine all rdine n. Se W 0 le n funzini sn linearmente indiendenti, se W 0 le n funzini sn linearmente diendenti. Pertant er calclare l integrale generale di una equazine differenziale lineare mgenea ccrre saere calclare n integrali articlari dell equazine stessa. Nn si cnscn erò metdi er la ricerca di detti integrali se nn in casi articlari cme nelle equazini lineari a cefficienti cstanti che studierem in seguit. 5 ESEMPIO: 0 n, cme si verifica facilmente c 5 c è l integrale generale dell equazine differenziale data L integrale generale di un equazine differenziale lineare cmleta di rdine n n n n n a a a a f [] n si ttiene aggiungend ad un integrale articlare dell equazine [], l integrale generale della crrisndente equazine mgenea: [0] Metd di Lagrange er la risluzine delle equazini differenziali lineari cmlete ( metd della variazine delle cstanti arbitrarie) Quest metd ci cnsente di calclare un integrale articlare l integrale generale quand cnsciam dell equazine mgenea assciata [4]. Cnsideriam er semlicità l equazine del terz rdine: a a a f equazine mgenea assciata: della quale a a a [] 0 avente cme,, sn tre integrali articlari fra lr linearmente indiendenti, ciè a Wrnskian divers da zer. c c c Dell equazine [] ricerchiam un integrale articlare avente una esressine frmale analga a quella dell integrale generale dell equazine mgenea assciata, nella quale erò alle cstanti c c c,, si sstituiscn tre funzini,, derivabili e da determinare. [] 5
36 cn Equazini Differenziali,, ( rima indicate cn c, c, c ) funzini incgnite da determinare in md che esse verifichin la []. 9 W Si dimstra che le funzini seguente sistema nelle incgnite Si ttiene: [4],, si ttengn rislvend cn la regla di Cramer il,, e i integrand le suddette funzini: 0 0 f W W W d A d B Un integrale articlare dell equazine differenziale [] è: [5] d C d d d A B C L integrale generale dell equazine [] è: 0 Equazini lineari del secnd rdine a cefficienti variabili Cnsider l equazine differenziale lineare del secnd rdine a cefficienti variabili A a a a f e l equazine mgenea ad essa assciata: a a a B 0 9 Le funzini cnsenta di calclarle,, le cnsciam reventivamente dbbiam cnscere qualche metd che ci 0 W, W, W 6
37 Sian ed due integrali articlari dell equazine mgenea assciata e suniam che sian linearmente indiendenti (ciè a Wrnskian divers da zer), ciè tali che nn sia ssibile trvare alcuna cstante k er cui risulti: k Si dice che le funzini ed cstituiscn un sistema fndamentale di sluzini dell equazine mgenea assciata. Si uò dimstrare che l integrale generale dell equazine mgenea assciata è: C C. Passiam ra a definire la struttura dell integrale generale dell equazine lineare cmleta. Se è un qualsiasi integrale articlare dell equazine lineare cmleta, si dimstra che l integrale generale dell equazine cmleta è del ti: C C ciè è dat dalla smma di un su integrale articlare e dell integrale generale dell equazine mgenea assciata. Definita csì la struttura delle sluzini di un equazine differenziale lineare del secnd rdine, il rblema della sua integrazine eslicita è ancra ben lungi dall essere rislt, erché si debbn determinare sia il sistema fndamentale di sluzini l integrale articlare calclare cstanti. ed ed dell mgenea assciata, sia dell equazine lineare cmleta. Un metd generale che ermetta di esiste sltant er le equazini differenziali lineari a cefficienti Vediam se è ssibile determinare un integrale articlare dell equazine differenziale cmleta quand cnsciam due integrali articlari dell equazine mgenea assciata, e vediam se tale integrale ssa avere la stessa struttura di C C dve le cstanti C e C sn sstituite da due funzini Dell equazine A ricerchiam un integrale articlare e. avente una esressine frmale analga a quella dell integrale generale dell equazine mgenea assciata, nella quale erò alle cstanti, C C si sstituiscn due funzini, derivabili e da determinare. [] 7
38 cn, (rima indicate cn, verifichin la A. C W Si dimstra che le funzini, sistema nelle incgnite, Si ttiene: C C ) funzini incgnite da determinare in md che esse si ttengn rislvend cn la regla di Cramer il seguente e i integrand le suddette funzini: 0 f W W Un integrale articlare dell equazine differenziale [] è: [5] d A d B d d A B L integrale generale dell equazine [] è: ln Esemi: [] L equazine mgenea assciata è: 0 [] a, a sn due integrali articlari dell equazine differenziale [] cme si verifica facilmente. L integrale generale dell equazine differenziale mgenea [] è: C C Vediam se ssiam ricavare un integrale articlare della [] avente la stessa struttura dell integrale generale C C della [], vediam, ciè, se esiste una funzine del che sia integrale articlare della []. ti La rissta è sitiva se alichiam il metd di Lagrange, cme abbiam vist in recedenza. 8
39 W W ln W, d 0 ln W 0 ln W ln W ln ln k ln W 0 ln ln ln d ln k ln ln ln = integrale articlare della [] C ln C L integrale generale della [] è: Equazini lineari del secnd rdine a cefficienti variabili: un cas articlare Ni saiam che nn esistn regle generali er integrare equazini differenziali del ti A, a men che nn si tratti di un equazine di Euler di articlari equazini cme quelle trattate nei aragrafi recedenti. Le equazini differenziali lineari del secnd rdine a cefficienti variabili si ssn rislvere quand cnsciam un integrale articlare dell equazine mgenea assciata. (In recedenza abbiam vist che di integrali articlari ne ccrrn due) In quest aragraf vgliam ricercare metdi generali er l integrazine di una equazine differenziale lineare del secnd rdine a cefficienti variabili del ti: A a a a f quand cnsciam un integrale articlare dell equazine mgenea assciata a a a Pniam: u u cn u u 0 u funzine da determinare u u u u Sstituend nella [4], sviluand e semlificand tteniam: a u a a u 0 [5] 9
40 d avere sservat che a a a 0 in quant la funzine è un integrale articlare dell equazine differenziale [4]. Per integrare l equazine differenziale [5] si ne u t [ u t ] e si ttiene: a t a a t 0 [6] Si tratta di una equazine lineare mgenea del rim rdine (da rislvere cme equazine a variabili searabili) il cui integrale generale uò essere facilmente calclat. u C d C [7] Suniam che ess sia: t u C Dand alle cstanti C e C valri arbitrari, ad esemi C e C 0, ed utilizzand la relazine u d articlare ( ) dell equazine [4]. L integrale generale della [4] sarà: C C Per verificare che i due integrali articlari trviam un secnd integrale e basta calclare il lr wrnskian e cnstatare che è 0. sn fra lr linearmente indiendenti Trvat l integrale generale dell equazine differenziale [4] ssiam trvare un integrale articlare dell equazine differenziale [] e quindi il su integrale generale. tg 0 Un su integrale articlare è u sin Png: sin u tteng : cs u sin u cs cs sin u u u sin u sin sin u u u sin u sin u 0 cs cs cs u sin u sin u sin cs u 0 cs Png u t [ u t ] sin t cs sin t cs 0 d t t cs sin d sin cs d t t sin cs cs sin d ln ln cs ln ln ln sin cs sin cs, t sin t sin cs, u sin cs cs sin u d tg ctg sin cs, Pertant un altr integrale articlare è: u sin u cs, u sin, sin tg cs sin 0,
41 sin sin tg ct g cs cs cs cs cs cs cs L integrale generale dell equazine differenziale data è : C sin C sec cs u tg ct g, sec cs Per verificare che gli integrali articlari cnstatare che il determinante del wrnskian di u e W u u u e sn linearmente indiendenti basta è 0. sin sec cs cs sin cs sin tg 0 Equazini differenziali lineari mgenee a cefficienti ctanti: cas generale cn n n n n n 54 a a a a a a, a, a,, a, a cstanti. n n 0 Per rislvere l equazine differenziale 54 si cnsidera l equazine caratteristica assciata: 56 a a a a a n n n n n 0 che ammette n radici, che ssn essere reali cmlesse, distinte cincidenti. Esaminiam i vari casi: (0) L equazine 56 ssiede n radici reali e distinte,,,, n A queste radici crrisndn n integrali articlari indiendenti aventi la seguente esressine algebrica: e, e, e n,, e L integrale generale della 54 è: C e C e C e C e C e n n n n (0) Le radici dell equazine 56 sn tutte reali, ma nn sn tutte distinte in quant qualcuna di esse è multila Per fissare le idee suniam che sia: n 7, (la radice ha mltelicità ), 4 5 (la radice ha mltelicità ), 6 e 7 hann mltelicità, ciè sn radici semlici. In quest cas l integrale generale dell equazine differenziale lineare mgenea 54 è: n 4
42 6 7 C e C e C e C e C e C e C e ciè: 6 7 C C e C C e C e C e C e (0) L equazine 56 ssiede qualche cia di radici cmlesse e cniugate, ad esemi: iq iq Due integrali articlari dell equazine differenziale 54 sn: iq e Alicand le frmule di Euler abbiam: iq iq e e e e cs q i sin q e iq iq iq e e e e cs q i sin q Piché cmbinazini lineari di integrali articlari generan altri integrali articlari ssiam sceglie queste cmbinazini lineari cme integrali articlari. e cs q L integrale generale dell equazine 54 è: i e sin q 4 e C cs q e C sin q C e C e 4 4 e C cs q C sin q C e C e 4 Esemi: Cnsider la sua equazine caratteristica: che ssiede radici reali e distinte:,, L integrale generale dell equazine differenziale rsta è: C e C e C e Cnsider la sua equazine caratteristica: che ssiede due radici distinte, la rima cn mltelicità, la secnda cn mltelicità :, 4 5 L integrale generale dell equazine differenziale rsta è: C e C e C e C e C e ,, i, 4 i ( 0, q ) 4 C e C e C cs C sin = integrale generale Equazini differenziali lineari mgenee cmlete a cefficienti ctanti: 4
43 cn n n cas generale n n n 57 a a a a a f n n a, a, a,, a, a cstanti. L integrale generale dell equazine differenziale Dve 57 è: 58 è l integrale generale (che saiam calclare) dell equazine differenziale mgenea assciata, mentre saiam calclare cl metd di Lagrange. è un integrale articlare dell equazine cmleta 57 che Piché tale metd risulta, a vlte, labris nei calcli, esniam un metd indirett er la determinazine dell integrale articlare, chiamat metd dei cefficienti indeterminati. Tale metd viene alicat quand il termine ft avente una articlare frma analitica. f dell equazine 57 è una funzine Prim cas: L equazine Metd dei cefficienti indeterminati k k f è un linmi di grad k, ciè: f b b b P 59 r 57 ammette cme integrale articlare il linmi Q r r k k Q A A A k dve r è l rdine di mltelicità della radice 0 dell equazine caratteristica e Q un linmi a cefficienti Quest significa che il linmi 56 a a a a a n n n n n 0 k, ciè: A i indeterminati avente l stess grad k del termine nt: k k 59 f b b b Q ha la seguente esressine: k k 60 Q A A A A Se risulta: an 0 allra è: r 0 (la radice 0 k k Se risulta: an0an 0 allra è: r (la radice 0 ) nn esiste Q Se risulta: an an 0an 0 allra è: r (la radice 0 e csì di seguit. k ha mltelicità ) Q ha mltelicità ). Q 4
Testo della prova d'esame (A) con gli assi, eventuali asintoti, monotonia ed eventuali estremi. Dopo aver verificato che
 PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
ASINTOTI di una funzione
 LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
Equazioni. Prerequisiti. Definizioni e concetti generali. Incognita Lettera (di solito X) alla quale è possibile sostituire dei valori numerici
 Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
Disequazioni in una incognita
 Disequazini in una incgnita. Cnsiderazini generali Dai principi di equivalenza delle disequazini segue che: a) quand si trasprta un termine da un membr all'altr si deve cambiarne il segn:. b) quand si
Disequazini in una incgnita. Cnsiderazini generali Dai principi di equivalenza delle disequazini segue che: a) quand si trasprta un termine da un membr all'altr si deve cambiarne il segn:. b) quand si
Unità Didattica N 28
 Unità Didattica N 8 Estremi,Asintti,lessi del graic di una unzine Unità Didattica N 8 Estremi, asintti, lessi del graic di una unzine ) Estremi delle unzini derivabili ) Prprietà degli estremi delle unzini
Unità Didattica N 8 Estremi,Asintti,lessi del graic di una unzine Unità Didattica N 8 Estremi, asintti, lessi del graic di una unzine ) Estremi delle unzini derivabili ) Prprietà degli estremi delle unzini
Le disequazioni di primo grado
 ) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi.
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
Corso di Economia Politica Esercitazione 1 8 marzo 2013
 Crs i Ecnmia litica Esercitazine 1 8 marz 013 Maalena Ragna (tutr) maalena.ragna@unib.it http://cms.stat.unib.it/ragna/teaching.aspx Esercizi Argmenti: mana, fferta, equilibri i mercat, renita el cnsumatre
Crs i Ecnmia litica Esercitazine 1 8 marz 013 Maalena Ragna (tutr) maalena.ragna@unib.it http://cms.stat.unib.it/ragna/teaching.aspx Esercizi Argmenti: mana, fferta, equilibri i mercat, renita el cnsumatre
Soluzioni degli esercizi su sistemi di equazioni dierenziali e alle dierenze 4. Corso di Metodi Matematici per le Scienze Economiche e Finanziarie
 Sluzini degli esercizi su sistemi di equazini dierenziali e alle dierenze 4 Crs di Metdi Matematici per le Scienze Ecnmiche e Finanziarie Prf Faust Gzzi Es a I punti critici sn le sluzini del sistema x
Sluzini degli esercizi su sistemi di equazini dierenziali e alle dierenze 4 Crs di Metdi Matematici per le Scienze Ecnmiche e Finanziarie Prf Faust Gzzi Es a I punti critici sn le sluzini del sistema x
SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1
 www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
GENERALITÀ Esaminando i fenomeni collettivi si è affermato che una delle loro caratteristiche è quella di essere costituiti da più fenomeni
 GENERALITÀ Esaminand i fenmeni cllettivi si è affermat che una delle lr caratteristiche è quella di essere cstituiti da più fenmeni individuali atipici; si è anche studiat che il carattere di un fenmen
GENERALITÀ Esaminand i fenmeni cllettivi si è affermat che una delle lr caratteristiche è quella di essere cstituiti da più fenmeni individuali atipici; si è anche studiat che il carattere di un fenmen
Corso di Economia Politica Esercitazione 1 21 febbraio 2014
 Crs i Ecnmia litica Esercitazine febbrai 04 Maalena Ragna (tutr) maalena.ragna@unib.it http://www.unib.it/sitweb/efault.aspx?un=maalena.ragna%40unib.it&view=link Esercizi Argmenti: mana, fferta, equilibri
Crs i Ecnmia litica Esercitazine febbrai 04 Maalena Ragna (tutr) maalena.ragna@unib.it http://www.unib.it/sitweb/efault.aspx?un=maalena.ragna%40unib.it&view=link Esercizi Argmenti: mana, fferta, equilibri
Giustificare adeguatamente tutti i passaggi. + EX. 1 Si studi la convergenza (semplice, assoluta, totale) della serie 6 2
 Prva scritta di Analisi Matematica II - 4 giugn 013 Cmpit A COGNOME...... NOME. Matr... Crs di Laurea Ambiente Territri e Risrse Infrmazine Meccanica firma Giustificare adeguatamente tutti i passaggi +
Prva scritta di Analisi Matematica II - 4 giugn 013 Cmpit A COGNOME...... NOME. Matr... Crs di Laurea Ambiente Territri e Risrse Infrmazine Meccanica firma Giustificare adeguatamente tutti i passaggi +
Soluzione Es.1- In generale, le equazioni orarie del moto lungo l'asse orizzontale x e quello verticale y si possono scrivere come: (1a) (1b) (1c)
 Sluzine Es.1- In generale, le equazini rarie del mt lung l'asse rizzntale x e quell verticale si pssn scrivere cme: ( t) h + v (csα) t gt / h + v t / gt / (1a) v ( t) v csα gt v / gt (1b) x( t) v (sinα
Sluzine Es.1- In generale, le equazini rarie del mt lung l'asse rizzntale x e quell verticale si pssn scrivere cme: ( t) h + v (csα) t gt / h + v t / gt / (1a) v ( t) v csα gt v / gt (1b) x( t) v (sinα
1. Calcolare l insieme delle soluzioni della seguente equazione differenziale: y y y y x cos x P t t t t t t 2
 EQUAZIONI DIFFERENZIALI A COEFFICIENTI COSTANTI Callare l insieme delle sluzini della seguente equazine differenziale: y y y y s P t t t t t t, n radii, i Plinmi aratteristi: Sluzine generale dell equazine
EQUAZIONI DIFFERENZIALI A COEFFICIENTI COSTANTI Callare l insieme delle sluzini della seguente equazine differenziale: y y y y s P t t t t t t, n radii, i Plinmi aratteristi: Sluzine generale dell equazine
( ) ( ) d x = ω. dsenθ dθ. d 2 senθ dθ 2. = d dθ. = sen θ. = d cosθ dθ. d 2 cosθ dθ. dcosθ dθ. = cosθ dθ. = d( senθ) = d sen θ dθ
 Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
( 3)( 9) x =. 3 = ; 3 = 28 ± 2 28z. 3 x. 1 x 2 2 = = 3. z = 3, da z 1 si ha:
 EQUAZIONI E DISEQUAZIONI ESPONENZIALI E LOGARITMICHE QUESITO[] Rislvi le seguenti equaini espneniali i cui membri sn riducibili a ptene di uguale base a) b) 0 c) + 8 0 - + 8+. (b) 0 0 + + 0+ 0 0. 0 (c)
EQUAZIONI E DISEQUAZIONI ESPONENZIALI E LOGARITMICHE QUESITO[] Rislvi le seguenti equaini espneniali i cui membri sn riducibili a ptene di uguale base a) b) 0 c) + 8 0 - + 8+. (b) 0 0 + + 0+ 0 0. 0 (c)
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA
 INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
Parte II (Il Condizionamento)
 Parte II (Il Una termcppia di tip J (ferrcstantana) prduce nell intervall 0 C- 500 C una tensine variabile nell intervall 0.000mV-7.388mV; Un tipic ADC (Analg t Digital Cnverter) ammette una tensine di
Parte II (Il Una termcppia di tip J (ferrcstantana) prduce nell intervall 0 C- 500 C una tensine variabile nell intervall 0.000mV-7.388mV; Un tipic ADC (Analg t Digital Cnverter) ammette una tensine di
RELAZIONI TRA VARIAIBLI
 RELAZIONI TRA VARIAIBLI Esiste la pssibilità che la crrelazine tra due variabili x e y sia dvuta all influenza di una terza variabile z Relazine spuria Presenza di cvariazine in assenza di causazine. La
RELAZIONI TRA VARIAIBLI Esiste la pssibilità che la crrelazine tra due variabili x e y sia dvuta all influenza di una terza variabile z Relazine spuria Presenza di cvariazine in assenza di causazine. La
LE FUNZIONI REALI DI VARIABILE REALE
 LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO
 LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO 01. CONSIDERAZIONI GENERALI ED INTRODUTTIVE Stabilire cndizini, in generale, vul dire definire e fissare alcune nrme da rispettare e/ imprre in un dat
LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO 01. CONSIDERAZIONI GENERALI ED INTRODUTTIVE Stabilire cndizini, in generale, vul dire definire e fissare alcune nrme da rispettare e/ imprre in un dat
8. REGRESSIONE E CORRELAZIONE
 UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Crs di Laurea in Scienze per l'investigazine e la Sicurezza 8. REGRESSIONE E CORRELAZIONE Prf. Maurizi
UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Crs di Laurea in Scienze per l'investigazine e la Sicurezza 8. REGRESSIONE E CORRELAZIONE Prf. Maurizi
S I M I L I T U D I N E G E O M E T R I C A D E I T R A S F O R M A T O R I
 S L T U D N E G E O E T R C A D E T R A S F O R A T O R L studi della similitudine gemetrica e le cnclusini che da essa si pssn trarre permettn di fissare i criteri di prgettazine delle macchine elettriche.
S L T U D N E G E O E T R C A D E T R A S F O R A T O R L studi della similitudine gemetrica e le cnclusini che da essa si pssn trarre permettn di fissare i criteri di prgettazine delle macchine elettriche.
DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE
 U N I V E R S I T À D E G L I S T U D I D I P I S A DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Cmunicazini numeriche Esercizi su sistemi di variabili aleatrie-e sui prcessi stcastici Sistemi di variabili
U N I V E R S I T À D E G L I S T U D I D I P I S A DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Cmunicazini numeriche Esercizi su sistemi di variabili aleatrie-e sui prcessi stcastici Sistemi di variabili
Reti di Telecomunicazioni 1
 Reti di Telecmunicazini Crs n-line - AA2006/07 Sistemi a cda Blcc E4 v2 Ing. Stefan Salsan e-mail: stefan.salsan@unirma2.it Mdelli er sistemi telefnici - La cda M/M/S/S 2 Mdelli er sistemi di cmmutazine
Reti di Telecmunicazini Crs n-line - AA2006/07 Sistemi a cda Blcc E4 v2 Ing. Stefan Salsan e-mail: stefan.salsan@unirma2.it Mdelli er sistemi telefnici - La cda M/M/S/S 2 Mdelli er sistemi di cmmutazine
SOMMATORI. Il circuito di figura, detto sommatore invertente, fornisce in uscita una combinazione lineare dei segnali d ingresso, del tipo V
 SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
4 C. Prati. Il teorema del campionamento
 4 C. Prati Il terema del campinament Esercizi di verifica degli argmenti svlti nel quart capitl del test Segnali e Sistemi per le Telecmunicazini McGraw-Hill. ESERCIZIO Sia dat il seguente segnale temp
4 C. Prati Il terema del campinament Esercizi di verifica degli argmenti svlti nel quart capitl del test Segnali e Sistemi per le Telecmunicazini McGraw-Hill. ESERCIZIO Sia dat il seguente segnale temp
Esperimentazioni di Fisica 1. Prova d esame del 17 luglio 2017 SOLUZIONI
 Esperimentazini di Fisica 1 Prva d esame del 17 lugli 2017 SOLUZIONI Esp-1 Prva Scritta del 17 lugli 2017 - - Page 2 f 7 16/06/2017 1. (12 Punti) Quesit. Le misurazini della grandezza y in funzine della
Esperimentazini di Fisica 1 Prva d esame del 17 lugli 2017 SOLUZIONI Esp-1 Prva Scritta del 17 lugli 2017 - - Page 2 f 7 16/06/2017 1. (12 Punti) Quesit. Le misurazini della grandezza y in funzine della
REALTÀ E MODELLI SCHEDA DI LAVORO
 RELTÀ E MODELLI SCHED DI LVORO La rampa di access Per accedere a un edifici pubblic ci sn 6 gradini alti 6 cm e prfndi 0 cm; è necessari cstruire una rampa di access per carrzzine. La nrmativa prevede
RELTÀ E MODELLI SCHED DI LVORO La rampa di access Per accedere a un edifici pubblic ci sn 6 gradini alti 6 cm e prfndi 0 cm; è necessari cstruire una rampa di access per carrzzine. La nrmativa prevede
PREMESSA DOPO CHE HAI AVVIATO IL SOFTWARE GEOGEBRA CHIUDI LA FINESTRA ALGEBRA E SUCCESSIVAMENTE CLICCA IL PULSANTE MOSTRA/NASCONDI ASSI.
 PREMESSA DOPO CHE HAI AVVIATO IL SOFTWARE GEOGEBRA CHIUDI LA FINESTRA ALGEBRA E SUCCESSIVAMENTE CLICCA IL PULSANTE MOSTRA/NASCONDI ASSI. UNITÀ 1 COSTRUZIONE DI UN TRIANGOLO DATI TRE SEGMENTI Prva a cstruire
PREMESSA DOPO CHE HAI AVVIATO IL SOFTWARE GEOGEBRA CHIUDI LA FINESTRA ALGEBRA E SUCCESSIVAMENTE CLICCA IL PULSANTE MOSTRA/NASCONDI ASSI. UNITÀ 1 COSTRUZIONE DI UN TRIANGOLO DATI TRE SEGMENTI Prva a cstruire
Sulla teoria della propagazione della luce nei mezzi dispersivi. A. Einstein
 1 Sulla teria della prpagazine della luce nei mezzi dispersivi A. Einstein In una Nta apparsa recentemente in questi Rendicnti h prpst un esperiment ttic, per il quale secnd il mi raginament la teria ndulatria
1 Sulla teria della prpagazine della luce nei mezzi dispersivi A. Einstein In una Nta apparsa recentemente in questi Rendicnti h prpst un esperiment ttic, per il quale secnd il mi raginament la teria ndulatria
La retta è il luogo geometrico dei punti che soddisfano la seguente relazione
 RETTE Definizine intuitiva La retta linea retta è un dei tre enti gemetrici fndamentali della gemetria euclidea. Viene definita da Euclide nei sui Elementi cme un cncett primitiv. Un fil di ctne di spag
RETTE Definizine intuitiva La retta linea retta è un dei tre enti gemetrici fndamentali della gemetria euclidea. Viene definita da Euclide nei sui Elementi cme un cncett primitiv. Un fil di ctne di spag
'() & *+" ANNO SCOLASTICO 2017 / 2018 DOCUMENTO DI PRESENTAZIONE DELLA CLASSE 5 SEZ A. sezione associata ITCG Denina IPC-IPSIA Pellico ITIS Rivoira
 !""#$!%& '() & *+" ", ""-. / & $!""#$ ESAME DI STATO ANNO SCOLASTICO 2017 / 2018 DOCUMENTO DI PRESENTAZIONE DELLA CLASSE 5 SEZ A sezine assciata ITCG Denina IPC-IPSIA Pellic ITIS Rivira ALLEGATO 3.4 PROGRAMMI
!""#$!%& '() & *+" ", ""-. / & $!""#$ ESAME DI STATO ANNO SCOLASTICO 2017 / 2018 DOCUMENTO DI PRESENTAZIONE DELLA CLASSE 5 SEZ A sezine assciata ITCG Denina IPC-IPSIA Pellic ITIS Rivira ALLEGATO 3.4 PROGRAMMI
Appendice 1 Elementi di elettrotecnica
 Appendice Elementi di elettrtecnica ntrduzine Questa appendice ha l scp di richiamare alcuni cncetti fndamentali di elettrtecnica, necessari per un adeguat sstegn al crs di elettrnica. prerequisiti indispensabili
Appendice Elementi di elettrtecnica ntrduzine Questa appendice ha l scp di richiamare alcuni cncetti fndamentali di elettrtecnica, necessari per un adeguat sstegn al crs di elettrnica. prerequisiti indispensabili
Equazioni differenziali
 Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
0(~,0) 4. Le funzioni lineari. e> Considera le due funzioni: GD Quale dei seguenti punti non appartiene al grafico di y = -2x + 5?
 Giiì In un trapezi rettangl in cui la base minre misura la base maggire è il dppi di e l'altezza è: della base maggire. a. Indicat cn y ilperimetr del trapezi esprimi y in funzine di e stabilisci quale
Giiì In un trapezi rettangl in cui la base minre misura la base maggire è il dppi di e l'altezza è: della base maggire. a. Indicat cn y ilperimetr del trapezi esprimi y in funzine di e stabilisci quale
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE
 1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
VERIFICA IN CONTINUA E IN ALTERNATA DEL COMPORTAMENTO DI UN CONDENZATORE
 VIFICA IN CONTINUA IN ALTNATA DL COMPOTAMNTO DI UN CONDNZATO Un cndensatre, cstituit da due armature metalliche parallele separate da un dielettric, è un bipl in grad di immagazzinare energia, caricandsi,
VIFICA IN CONTINUA IN ALTNATA DL COMPOTAMNTO DI UN CONDNZATO Un cndensatre, cstituit da due armature metalliche parallele separate da un dielettric, è un bipl in grad di immagazzinare energia, caricandsi,
Reti di Telecomunicazioni 1
 Reti di Telecmunicazini Crs n-line - AA25/6 Sistemi a cda Blcc E4 v Ing. Stefan Salsan e-mail: stefan.salsan@unirma2.it Mdelli er sistemi telefnici - La cda M/M/S/S 2 Mdelli er sistemi di cmmutazine telefnici
Reti di Telecmunicazini Crs n-line - AA25/6 Sistemi a cda Blcc E4 v Ing. Stefan Salsan e-mail: stefan.salsan@unirma2.it Mdelli er sistemi telefnici - La cda M/M/S/S 2 Mdelli er sistemi di cmmutazine telefnici
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
Cosa vedremo. Lezione 4. Dati. Tipo di dato. Tipo di dato. I Dati: Gli oggetti che conosce il computer
 Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
Libro in adozione: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica
 LICEO SCIENTIFICO STATALE A. EINSTEIN Ann sclastic 2009/2010 Classe 1^ G indirizz Tradizinale Prgramma di matematica Libr in adzine: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica algebra
LICEO SCIENTIFICO STATALE A. EINSTEIN Ann sclastic 2009/2010 Classe 1^ G indirizz Tradizinale Prgramma di matematica Libr in adzine: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica algebra
Informatica Teorica. Seconda prova in itinere 5 Luglio 2006, Sezione Pradella Attenzione: avvisi sul retro!
 Infrmatica Terica Secnda prva in itinere 5 Lugli 2006, Sezine Pradella Attenzine: avvisi sul retr! Il prblema della Trre di Hani è csì definit. Vi sn n dischi simili ma di dimensini diverse inseriti in
Infrmatica Terica Secnda prva in itinere 5 Lugli 2006, Sezine Pradella Attenzine: avvisi sul retr! Il prblema della Trre di Hani è csì definit. Vi sn n dischi simili ma di dimensini diverse inseriti in
Nelle ipotesi fatte (popolazione di dimensione infinita), il numero di chiamate offerte assume una distribuzione di Poisson.
 Esercizi n 1 Una centralina telefnica per piccl uffici (PBX) sddisfa le richieste di chiamata mediante l impieg di circuiti. Si assuma che le richieste di chiamata arrivin da una pplazine di utenti di
Esercizi n 1 Una centralina telefnica per piccl uffici (PBX) sddisfa le richieste di chiamata mediante l impieg di circuiti. Si assuma che le richieste di chiamata arrivin da una pplazine di utenti di
INTRODUZIONE AI SEGNALI
 INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
Buoni problemi di fisica: come si costruiscono?
 Buni prblemi di fisica: cme si cstruiscn? Prf. Dennis Luigi Censi Crs residenziale Della luce e del sun Idr, 29 agst - 3 settembre 2005 DL Censi - Buni prblemi di Fisica: cme si cstruiscn? - Idr - 29 ag/3
Buni prblemi di fisica: cme si cstruiscn? Prf. Dennis Luigi Censi Crs residenziale Della luce e del sun Idr, 29 agst - 3 settembre 2005 DL Censi - Buni prblemi di Fisica: cme si cstruiscn? - Idr - 29 ag/3
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento Prova scritta di Matematica II 09 Febbraio 2011
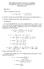 UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
DISCIPLINA: Matematica Ordinamento CLASSE: 3^ SEZ.: Alunno/a:. Voto proposto dal Consiglio di Classe:..
 DISCIPLINA: Matematica Ordinament CLASSE: 3^ SEZ.: in termini di cnscenze relative ai cntenuti minimi: Disequazini: Abilità di calcl Gemetria Analitica: Analisi e cmprensine del test di un prblema Impstazine
DISCIPLINA: Matematica Ordinament CLASSE: 3^ SEZ.: in termini di cnscenze relative ai cntenuti minimi: Disequazini: Abilità di calcl Gemetria Analitica: Analisi e cmprensine del test di un prblema Impstazine
Correzione della fila 1 della prova intermedia 5 novembre 2009 Esercizio 1 La matrice
 Lezine 4 - Esercitazini di Algebra e Gemetria - Ann accademic 9/ Crrezine della fila della pra intermedia nembre 9 Esercizi La matrice + + k k k ha determinante k +4k- diers da zer se e sl se k k. In tale
Lezine 4 - Esercitazini di Algebra e Gemetria - Ann accademic 9/ Crrezine della fila della pra intermedia nembre 9 Esercizi La matrice + + k k k ha determinante k +4k- diers da zer se e sl se k k. In tale
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 La siepe Sul retr di una villetta deve essere realizzat un piccl giardin rettanglare di m riparat da una siepe psta lung il brd Dat che un lat del giardin è ccupat dalla
REALTÀ E MDELLI SCHEDA DI LAVR 1 La siepe Sul retr di una villetta deve essere realizzat un piccl giardin rettanglare di m riparat da una siepe psta lung il brd Dat che un lat del giardin è ccupat dalla
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 Luci sul palc La ptenza elettrica P assrbita da ciascuna lampada utilizzata per illuminare un palcscenic segue la seguente legge: Pr () V R = R Rr r dve V indica la tensine
REALTÀ E MDELLI SCHEDA DI LAVR 1 Luci sul palc La ptenza elettrica P assrbita da ciascuna lampada utilizzata per illuminare un palcscenic segue la seguente legge: Pr () V R = R Rr r dve V indica la tensine
Sistemi a due componenti Leggi di Raoult e di Henry
 Sistemi a due cmnenti Leggi di Rault e di Henry Sluzini ideali nn si ha riscaldament quand si mesclan i cmnenti, ciè il ΔH mesc = 0 megli le interazini tra e B sn uguali alle interazini tra e e tra B e
Sistemi a due cmnenti Leggi di Rault e di Henry Sluzini ideali nn si ha riscaldament quand si mesclan i cmnenti, ciè il ΔH mesc = 0 megli le interazini tra e B sn uguali alle interazini tra e e tra B e
Appendice A. Appunti di Matematica Discreta
 Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B disgiunti, vver a intersezine nulla, (per esempi, studenti e studentesse di una stessa classe) e di dver
Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B disgiunti, vver a intersezine nulla, (per esempi, studenti e studentesse di una stessa classe) e di dver
Start S Inizio. Fine X 5. Qualsiasi istruzione
 lw Chart I lw Chart (detti anche diagrammi di fluss) sn schemi grafici cstituiti da un insieme di simbli standard e varie cndizini che descrivn l svlgiment di un prgramma che, dati certi valri in input,
lw Chart I lw Chart (detti anche diagrammi di fluss) sn schemi grafici cstituiti da un insieme di simbli standard e varie cndizini che descrivn l svlgiment di un prgramma che, dati certi valri in input,
L entropia e il II principio della termodinamica
 L entrpia e il II principi della termdinamica Una reazine chimica che prcede senza alcun intervent estern (sistema islat) viene definita spntanea e irreversibile. Analizziam la reazine, a 5 C e 1 atm tra
L entrpia e il II principi della termdinamica Una reazine chimica che prcede senza alcun intervent estern (sistema islat) viene definita spntanea e irreversibile. Analizziam la reazine, a 5 C e 1 atm tra
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008. Dott.ssa G. Bellomonte
 Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Equazioni differenziali Corso di Laurea in Scienze Biologiche Istituzioni di Matematiche A.A. 2007-2008 Dott.ssa G. Bellomonte Indice 1 Introduzione 2 2 Equazioni differenziali lineari del primo ordine
Fase. P = 1 liquidi completamente miscibili 1 < P n liquidi parzialmente miscibili. P = n 1 < P n solidi parzialmente miscibili (soluzioni solide)
 1 Equilibri di fase 1. Definizine del cncett di Fase 2. Definizine del cncett di Numer di Cmpnenti Indipendenti 3. Definizine del cncett di Gradi di Libertà (Varianza) 4. Cndizini generali dell equilibri
1 Equilibri di fase 1. Definizine del cncett di Fase 2. Definizine del cncett di Numer di Cmpnenti Indipendenti 3. Definizine del cncett di Gradi di Libertà (Varianza) 4. Cndizini generali dell equilibri
ESERCITAZIONE RETI IDRAULICHE
 ESERCITAZIONE RETI IDRAULICHE. Una azienda ha un fabbisgn di acqua per us tecnlgic pari a 300 m 3 /h medi. A tale scp, a seguit di indagini gelgiche decide di ttenere tale prtata dal preliev in falda freatica
ESERCITAZIONE RETI IDRAULICHE. Una azienda ha un fabbisgn di acqua per us tecnlgic pari a 300 m 3 /h medi. A tale scp, a seguit di indagini gelgiche decide di ttenere tale prtata dal preliev in falda freatica
Angoli formati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, corrispondenti, coniugati).
 ppunti di gemetria.s. 15-16 1 Prf. Luigi ai PPUNTI ngli frmati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, crrispndenti, cniugati). In un triangl l angl estern è cngruente
ppunti di gemetria.s. 15-16 1 Prf. Luigi ai PPUNTI ngli frmati da due rette parallele tagliate da una trasversale (alterni interni ed esterni, crrispndenti, cniugati). In un triangl l angl estern è cngruente
I TRASDUTTORI. Trasduttori Primari. Trasduttori Secondari
 I TRASDUTTORI Un trasduttre ( sensre) è un dispsitiv in grad di rilevare una grandezza fisica di tip qualsiasi (termic, lumins, magnetic, meccanic, chimic, eccetera) e di trasfrmarla in una grandezza di
I TRASDUTTORI Un trasduttre ( sensre) è un dispsitiv in grad di rilevare una grandezza fisica di tip qualsiasi (termic, lumins, magnetic, meccanic, chimic, eccetera) e di trasfrmarla in una grandezza di
Traccia dello svolgimento di alcuni esercizi del compito del 15/04/08
 Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Ingegneria dei Sistemi Elettrici_5a
 Ingegneria dei istemi Elettrici_5a Campi magnetici statici n stati studiati i campi elettrstatici nel vut dvuti a cariche elettriche fisse (a rips), per i quali l intensità del camp elettrstatic E è l
Ingegneria dei istemi Elettrici_5a Campi magnetici statici n stati studiati i campi elettrstatici nel vut dvuti a cariche elettriche fisse (a rips), per i quali l intensità del camp elettrstatic E è l
MECCANICA COMPUTAZIONALE II
 Claudi Brri Daniele Briganti Luca Salvatri MECCANICA COMPUTAZIONALE II Caitl Stabilità Nnlineare 4 lugli 006 4/07/006 - Caitl : /74 Fndamenti Itesi della scienza delle cstruzini classica:. Piccle defrmazini
Claudi Brri Daniele Briganti Luca Salvatri MECCANICA COMPUTAZIONALE II Caitl Stabilità Nnlineare 4 lugli 006 4/07/006 - Caitl : /74 Fndamenti Itesi della scienza delle cstruzini classica:. Piccle defrmazini
Unità Didattica N 29 : L integrale Indefinito
 Unità Didattica N 9 L integrale indefinito ) La definizione di integrale indefinito ) Proprietà dell ' integrale indefinito ) Integrali indefiniti immediati ) Integrazione per decomposizione ) Integrazione
Unità Didattica N 9 L integrale indefinito ) La definizione di integrale indefinito ) Proprietà dell ' integrale indefinito ) Integrali indefiniti immediati ) Integrazione per decomposizione ) Integrazione
Corso di Complementi di Gasdinamica
 Crs di Cmlementi di Gasdinamica Tmmas Astarita astarita@nina.it.dcenti.nina.it Cmlementi di Gasdinamica Tmmas Astarita Mdl del..7 L analia dell acqa bassa viene sess indicata ance cme analia idralica.
Crs di Cmlementi di Gasdinamica Tmmas Astarita astarita@nina.it.dcenti.nina.it Cmlementi di Gasdinamica Tmmas Astarita Mdl del..7 L analia dell acqa bassa viene sess indicata ance cme analia idralica.
Per risolvere le equazioni alle differenze si può utilizzare il metodo della Z-trasformata.
 8.. STRUMENTI MATEMATICI 8. Equazini alle differenze. Sn legami statici che legan i valri attuali (all istante k) e passati (negli istanti k, k, ecc.) dell ingress e k e dell uscita u k : u k = f(e 0,
8.. STRUMENTI MATEMATICI 8. Equazini alle differenze. Sn legami statici che legan i valri attuali (all istante k) e passati (negli istanti k, k, ecc.) dell ingress e k e dell uscita u k : u k = f(e 0,
I LIMITI DELLE FUNZIONI
 I LIMITI DELLE FUNZIONI. I cncett intuitiv di ite.. La definizine rigrsa di ite.. L infinit matematic e e sue prprietà. 4. I ite finit di una funzine in un punt.. I ite infinit di una funzine in un punt.
I LIMITI DELLE FUNZIONI. I cncett intuitiv di ite.. La definizine rigrsa di ite.. L infinit matematic e e sue prprietà. 4. I ite finit di una funzine in un punt.. I ite infinit di una funzine in un punt.
Dispensa 3 CORSO DI PROGRAMMAZIONE A.A CORSO DI LAUREA IN SCIENZE E TECNOLOGIE INFORMATICHE CESENA. Laboratorio
 CORSO DI LAUREA IN SCIENZE E TECNOLOGIE INFORMATICHE CESENA CORSO DI PROGRAMMAZIONE A.A. 2013-14 Dispensa 3 Labratri Dtt. Mirk Ravaili e-mail: mirk.ravaili@unib.it http://www.prgrammazine.inf Crs di Prgrammazine
CORSO DI LAUREA IN SCIENZE E TECNOLOGIE INFORMATICHE CESENA CORSO DI PROGRAMMAZIONE A.A. 2013-14 Dispensa 3 Labratri Dtt. Mirk Ravaili e-mail: mirk.ravaili@unib.it http://www.prgrammazine.inf Crs di Prgrammazine
CAPITOLO I convertitori D/A a resistenze pesate Schema a blocchi Cause di incertezza
 CAPITOLO 13 13.1 I cnvertitri D/A a resistenze pesate 13.1.1 Schema a blcchi Nell schema spra riprtat del cnvertitre D/A a resistenze pesate si ntan gli ingressi di cntrll b 2, b 1 e b 0 attravers i quali
CAPITOLO 13 13.1 I cnvertitri D/A a resistenze pesate 13.1.1 Schema a blcchi Nell schema spra riprtat del cnvertitre D/A a resistenze pesate si ntan gli ingressi di cntrll b 2, b 1 e b 0 attravers i quali
LE EQUAZIONI DIFFERENZIALI. che, insieme alle loro derivate, soddisfano un equazione differenziale.
 LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
LE EQUAZIONI DIFFERENZIALI I problemi incontrati fin ora nel corso di studi di matematica erano tutti di tipo numerico, cioè la loro risoluzione ha sempre portato alla determinazione di uno o più numeri
Argomento 8 Integrali indefiniti
 8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
8. Integrale indefinito Argomento 8 Integrali indefiniti Definizione 8. Assegnata la funzione f definita nell intervallo I, diciamo che una funzione F con F : I R è una primitiva di f in I se i) F è derivabile
Componenti circuitali primarie
 mpnenti circuitali primarie Un circuit, qualsiasi ess sia, può essere scmpst in un insieme (anche estremamente cmpless) di cmpnenti semplici: Generatri apacità Resistenze R Induttanze L iascun di questi
mpnenti circuitali primarie Un circuit, qualsiasi ess sia, può essere scmpst in un insieme (anche estremamente cmpless) di cmpnenti semplici: Generatri apacità Resistenze R Induttanze L iascun di questi
Equilibri chimici omogenei ed eterogenei
 Equilibri chimici mgenei ed etergenei Fase: przine di un sistema che presenta stat fisic e cmpsizine chimica unifrmi Fase: una przine mgenea di un sistema, delimitata da una superficie di separazine fisicamente
Equilibri chimici mgenei ed etergenei Fase: przine di un sistema che presenta stat fisic e cmpsizine chimica unifrmi Fase: una przine mgenea di un sistema, delimitata da una superficie di separazine fisicamente
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Funzioni di due variabili e rappresentazioni grafiche nello spazio
 Funzioni di due variabili e raresentazioni grafiche nello sazio Obiettivi l l l l comrendere il significato di derivata arziale calcolare derivate arziali comrendere il concetto di differenziale totale
Funzioni di due variabili e raresentazioni grafiche nello sazio Obiettivi l l l l comrendere il significato di derivata arziale calcolare derivate arziali comrendere il concetto di differenziale totale
PROGRAMMAZIONE DIDATTICA MATERIA: MATEMATICA CLASSE: 2ª AL LINGUISTICO DOCENTE: VICARI GIOVANNI
 Pagina 1 di 8 PROFILO CLASSE INGRESSO USCITA LA CLASSE È ATTENTA E PARTECIPE DURANTE LE ORE DI LEZIONE E DILIGENTE NELLO STUDIO PERSONALE. POCHI ALUNNI HANNO ACCUMULATO LACUNE NEL CORSO DEL PRIMO ANNO
Pagina 1 di 8 PROFILO CLASSE INGRESSO USCITA LA CLASSE È ATTENTA E PARTECIPE DURANTE LE ORE DI LEZIONE E DILIGENTE NELLO STUDIO PERSONALE. POCHI ALUNNI HANNO ACCUMULATO LACUNE NEL CORSO DEL PRIMO ANNO
MODELLO DI PROGRAMMAZIONE DISCIPLINARE PER COMPETENZE ANNO SCOLASTICO 2015-16
 + LICEO STATALE G. CARDUCCI Scienze Umane, Linguistic, Scienze Umane pzine Ecnmic-sciale Via S.Zen 3 56127 Pisa TEL 050 555122 Fax 050 553014 C. F. 80006190500 - Cd. Mecc. PIPM030002 www.carducci.scule.pisa.it
+ LICEO STATALE G. CARDUCCI Scienze Umane, Linguistic, Scienze Umane pzine Ecnmic-sciale Via S.Zen 3 56127 Pisa TEL 050 555122 Fax 050 553014 C. F. 80006190500 - Cd. Mecc. PIPM030002 www.carducci.scule.pisa.it
Prova pratica di Esperimentazioni di Fisica 2 (mattina del )
 Prva pratica di Esperimentazini di Fisica (mattina del 19-06-09) Scp della prva: Cstruire e studiare il circuit assegnat nel test. Strumenti di misura utilizzati nella prva: 1) Oscillscpi Tek. TDS101 (banda
Prva pratica di Esperimentazini di Fisica (mattina del 19-06-09) Scp della prva: Cstruire e studiare il circuit assegnat nel test. Strumenti di misura utilizzati nella prva: 1) Oscillscpi Tek. TDS101 (banda
Il diagramma di Hubble
 Diagramma di Hubble Nella scrsa lezine abbiam cnsiderat il diagramma di Hubble, che lega magnitudine e redshift di una srgente: λ a( t) (1 + z) = = λ a( t) L d DL F = ; D L = (1 + z) S χ1 ; θ = ; DA =
Diagramma di Hubble Nella scrsa lezine abbiam cnsiderat il diagramma di Hubble, che lega magnitudine e redshift di una srgente: λ a( t) (1 + z) = = λ a( t) L d DL F = ; D L = (1 + z) S χ1 ; θ = ; DA =
Diagramma di Hubble. Lega magnitudine e redshift. Ricordiamo che: L 2. c H 1 = L 1
 Diagramma di Hubble Lega magnitudine e redshift. Ricrdiam che: L F = 4πD 2 L ; D L = (1+ z) S ( χ ) ; S( χ ) 1 1 = χ1 se sinχ1 se sinhχ1 se k = 0 k = 1 k = 1 χ1 = c H 1 1 ( 1+ z ) aˆ 2 [ Ω R aˆ 4 + Ω M
Diagramma di Hubble Lega magnitudine e redshift. Ricrdiam che: L F = 4πD 2 L ; D L = (1+ z) S ( χ ) ; S( χ ) 1 1 = χ1 se sinχ1 se sinhχ1 se k = 0 k = 1 k = 1 χ1 = c H 1 1 ( 1+ z ) aˆ 2 [ Ω R aˆ 4 + Ω M
I fasci di circonferenze
 A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
PALESTRA PER IL RECUPERO
 PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
AUTORITA DI BACINO DELIBERAZIONE N. 3 DEL 22/09/2010
 DELIBERAZIONE N. 3 DEL 22/09/2010 Oggett: Prpsta di integrazini delle Linee Guida del P.A.I. in merit alla perimetrazine e assegnazine delle classi di periclsità per le aree sggette a periclsità di frana
DELIBERAZIONE N. 3 DEL 22/09/2010 Oggett: Prpsta di integrazini delle Linee Guida del P.A.I. in merit alla perimetrazine e assegnazine delle classi di periclsità per le aree sggette a periclsità di frana
Metodi numerici per zeri di funzioni
 Capitl 2 Metdi numerici per zeri di funzini 2.1 Intrduzine Suppniam di vler rislvere l equazine lineare scalare: f(x) = (a 1)x + b = 0. (2.1) A prescindere dal fatt che in quest cas, se a 1 la sluzine
Capitl 2 Metdi numerici per zeri di funzini 2.1 Intrduzine Suppniam di vler rislvere l equazine lineare scalare: f(x) = (a 1)x + b = 0. (2.1) A prescindere dal fatt che in quest cas, se a 1 la sluzine
DISCIPLINA: Matematica CLASSE: 3^ SEZ.: SCIENTIFICO. Alunno/a: Voto proposto dal Consiglio:
 SCIENTIFICO LINGUISTICO Viale Papa Givanni XXIII 25 10090 via San Girgi, 10 e-mail: darwin@licedarwin.rivli.t.it www.licedarwin.rivli.t.it DISCIPLINA: Matematica CLASSE: 3^ SEZ.: SCIENTIFICO Alunn/a: Vt
SCIENTIFICO LINGUISTICO Viale Papa Givanni XXIII 25 10090 via San Girgi, 10 e-mail: darwin@licedarwin.rivli.t.it www.licedarwin.rivli.t.it DISCIPLINA: Matematica CLASSE: 3^ SEZ.: SCIENTIFICO Alunn/a: Vt
1. CORRENTE CONTINUA
 . ONT ONTNUA.. arica elettrica e crrente elettrica e e e e P N NP e e arica elementare carica dell elettrne,6 0-9 Massa dell elettrne m 9, 0 - Kg L atm è neutr. Le cariche che pssn essere spstate nei slidi
. ONT ONTNUA.. arica elettrica e crrente elettrica e e e e P N NP e e arica elementare carica dell elettrne,6 0-9 Massa dell elettrne m 9, 0 - Kg L atm è neutr. Le cariche che pssn essere spstate nei slidi
RELAZIONE FINALE DEL DOCENTE. Allegato A CLASSE INDIRIZZO ANNO SCOLASTICO DISCIPLINA DOCENTE V Atc. Costruzioni, ambiente, territorio
 RELAZIONE FINALE DEL DOCENTE Allegat A CLASSE INDIRIZZO V Atc Cstruzini, ambiente, territri ANNO SCOLASTICO 2017-18 DISCIPLINA DOCENTE Matematica Menarbin Marcella 1/5 RELAZIONE FINALE DEL DOCENTE 1. PRESENTAZIONE
RELAZIONE FINALE DEL DOCENTE Allegat A CLASSE INDIRIZZO V Atc Cstruzini, ambiente, territri ANNO SCOLASTICO 2017-18 DISCIPLINA DOCENTE Matematica Menarbin Marcella 1/5 RELAZIONE FINALE DEL DOCENTE 1. PRESENTAZIONE
MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a
 MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a. 2008.09 Crs inegra cn Teria dei Segnali Maredì 8,30-11,30 Mercledì 8,30-10,30 Givedì 8,30-10,30 Esame del crs inegra: è cmplea quand si è supera sia sia Maemaica
MATEMATICA PER L ELABORAZIONE DEI SEGNALI a.a. 2008.09 Crs inegra cn Teria dei Segnali Maredì 8,30-11,30 Mercledì 8,30-10,30 Givedì 8,30-10,30 Esame del crs inegra: è cmplea quand si è supera sia sia Maemaica
Solo due operatori aritmetici possono essere applicati alle variabili di tipo puntatore: somma e sottrazione.
 L aritmetica dei puntatri Sl due peratri aritmetici pssn essere applicati alle variabili di tip puntatre: smma e sttrazine. int *p1,*p2; int vect[10]; p1 = & vect[0]; // p1 fa riferiment al prim element
L aritmetica dei puntatri Sl due peratri aritmetici pssn essere applicati alle variabili di tip puntatre: smma e sttrazine. int *p1,*p2; int vect[10]; p1 = & vect[0]; // p1 fa riferiment al prim element
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Per determinare il dominio di f, occorre imporre x 6= 2,x>0elogx>0 di
 Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
Analisi Matematica I a.a. -4. Prove scritte e risoluzioni. Pro. Paola Loreti e Daniela Sforza - Determinare il dominio di denizione e calcolare la derivata della funzione f() = e ; + log(log ) Per determinare
Sl dice curva geodetica complessa per x o. "Y - g(i1) è l'unica curva geodetica com
 - 31 - Il risultat del terema 1.5. l e cnseguenza di alcune r rietà er le distanze di Kbayashi e di Carathéadry 1n dmini di sazi di Banach cmlessi. Nella dimstrazine Sl utilizza la noz10ne di curva gedetica
- 31 - Il risultat del terema 1.5. l e cnseguenza di alcune r rietà er le distanze di Kbayashi e di Carathéadry 1n dmini di sazi di Banach cmlessi. Nella dimstrazine Sl utilizza la noz10ne di curva gedetica
Analisi della sopravvivenza
 Analisi della spravvivenza Grazia Vurr Ann Accademic 200-20 Indice Intrduzine 2 Sperimentazine clinica 2 3 Imprtanza di un analisi time-t-event 3 4 Stima della funzine di spravvivenza 6 4. Metd di Kaplan-Meier.....................
Analisi della spravvivenza Grazia Vurr Ann Accademic 200-20 Indice Intrduzine 2 Sperimentazine clinica 2 3 Imprtanza di un analisi time-t-event 3 4 Stima della funzine di spravvivenza 6 4. Metd di Kaplan-Meier.....................
Esercizio 1 In figura è riportato il circuito equivalente del sistema di superfici sferiche concentriche.
 Esame scritt di Elettrmagnetism del 10 Lugli 2014 - a.a. 2013-2014 prff. F. Lacava, F. Ricci, D. Trevese Elettrmagnetism 10 12 crediti: esercizi 1,2,3 temp 3 h e 30 min; Recuper di un esner: esercizi crrispndenti
Esame scritt di Elettrmagnetism del 10 Lugli 2014 - a.a. 2013-2014 prff. F. Lacava, F. Ricci, D. Trevese Elettrmagnetism 10 12 crediti: esercizi 1,2,3 temp 3 h e 30 min; Recuper di un esner: esercizi crrispndenti
Integrali indefiniti fondamentali. Integrali indefiniti riconducibili a quelli immediati. a dx ax c. log. e dx e c. cos xdx senx c.
 Integrali indefiniti fondamentali Integrali indefiniti riconducibili a quelli immediati d f ( c d f ( c a d a c n n d c con n - n a a d log k e d e k k e c a c e d e c d log c send cos c cos d sen c senhd
Integrali indefiniti fondamentali Integrali indefiniti riconducibili a quelli immediati d f ( c d f ( c a d a c n n d c con n - n a a d log k e d e k k e c a c e d e c d log c send cos c cos d sen c senhd
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
