DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34
|
|
|
- Linda Lazzari
- 5 anni fa
- Visualizzazioni
Transcript
1 DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34
2 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione considera la probabilità per conteggi con variabili di tipo binario.
3 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione considera la probabilità per conteggi con variabili di tipo binario. Una variabile binaria è una variabile che misura solo due possibili esiti, usualmente indicati con 1e 0 chiamati successo e insuccesso.
4 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione considera la probabilità per conteggi con variabili di tipo binario. Una variabile binaria è una variabile che misura solo due possibili esiti, usualmente indicati con 1e 0 chiamati successo e insuccesso. Una variabile con distribuzione binomiale conta il numero di successi in n prove indipendenti.
5 Distribuzione Binomiale 3 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si sa che la probabilità che un seme germogli è pari a P(G) = 0.8, mentre la probabilità che non germogli è P(N) = 0.2.
6 Distribuzione Binomiale 3 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si sa che la probabilità che un seme germogli è pari a P(G) = 0.8, mentre la probabilità che non germogli è P(N) = 0.2. Assumiamo che le prove condotte siano indipendenti, ossia lo stesso seme non viene ripiantato due volte, e che la germogliazione di uno dei semi non influenzi quella degli altri.
7 Distribuzione Binomiale 3 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si sa che la probabilità che un seme germogli è pari a P(G) = 0.8, mentre la probabilità che non germogli è P(N) = 0.2. Assumiamo che le prove condotte siano indipendenti, ossia lo stesso seme non viene ripiantato due volte, e che la germogliazione di uno dei semi non influenzi quella degli altri. Possiamo allora aspettarci 8 possibili esiti per l esperimento con le seguenti probabilità.
8 Distribuzione Binomiale 4 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino.
9 Distribuzione Binomiale 4 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si definisca ora la variabile casuale discreta che conta il numero di germogliazioni.
10 Distribuzione Binomiale 4 / 34 Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si definisca ora la variabile casuale discreta che conta il numero di germogliazioni. Allora possiamo scrivere la seguente tabella di distribuzione della probabilità
11 Distribuzione Binomiale Si consideri un esperimento in cui si osservano le germogliazioni di tre semi di pino. Si definisca ora la variabile casuale discreta che conta il numero di germogliazioni. Allora possiamo scrivere la seguente tabella di distribuzione della probabilità Per costruire la distribuzione sopra abbiamo utilizzato la regola del prodotto di probabilità indipendenti per cui P(N G G) = P(N)P(G)P(G) = Abbiamo anche utilizzato la regola della somma per cui P(GNN NGN NNG) = P(GNN) + P(NGN) + P(NNG). 4 / 34
12 Distribuzione Binomiale 5 / 34 Esiste una regola generale per il calcolo delle probabilità binomiali per ogni possibile numerosità n.
13 Distribuzione Binomiale 5 / 34 Esiste una regola generale per il calcolo delle probabilità binomiali per ogni possibile numerosità n. Se si indica la probabilità di successo con p, allora in n prove indipendenti, la probabilità di ottenere esattamente x successi è pari a P(x) = ( ) n p x (1 p) (n x) n! = x x!(n x)! px (1 p) (n x), x = 0,1,2,3,...,n
14 Distribuzione Binomiale 5 / 34 Esiste una regola generale per il calcolo delle probabilità binomiali per ogni possibile numerosità n. Se si indica la probabilità di successo con p, allora in n prove indipendenti, la probabilità di ottenere esattamente x successi è pari a P(x) = ( ) n p x (1 p) (n x) n! = x x!(n x)! px (1 p) (n x), x = 0,1,2,3,...,n e diremo che X Binom(n,p)
15 Distribuzione Binomiale 5 / 34 Esiste una regola generale per il calcolo delle probabilità binomiali per ogni possibile numerosità n. Se si indica la probabilità di successo con p, allora in n prove indipendenti, la probabilità di ottenere esattamente x successi è pari a P(x) = ( ) n p x (1 p) (n x) n! = x x!(n x)! px (1 p) (n x), x = 0,1,2,3,...,n e diremo che X Binom(n,p) ossia X ha distribuzione binomiale con parametri n e p.
16 Distribuzione Binomiale: esercizio 1 6 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8.
17 Distribuzione Binomiale: esercizio 1 6 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è la probabilità che germoglieranno esattamente 7 semi?
18 Distribuzione Binomiale: esercizio 1 6 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è la probabilità che germoglieranno esattamente 7 semi? b) Qual è la probabilità che germoglieranno più di 6 semi?
19 Distribuzione Binomiale: esercizio 1 6 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è la probabilità che germoglieranno esattamente 7 semi? b) Qual è la probabilità che germoglieranno più di 6 semi? Per risolvere l esercizio applichiamo la formula della probabilità binomiale.
20 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8)
21 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi?
22 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? P(X = 7) =
23 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) = 7
24 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) =
25 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1!
26 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1! b) Qual è la probabilità che germoglieranno più di 6 semi?
27 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1! b) Qual è la probabilità che germoglieranno più di 6 semi? P(X > 6) =
28 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1! b) Qual è la probabilità che germoglieranno più di 6 semi? P(X > 6) = P(X = 7)+P(X = 8) =
29 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1! b) Qual è la probabilità che germoglieranno più di 6 semi? ( ) 8 P(X > 6) = P(X = 7)+P(X = 8) = (1 0.8) (8 8) = 8
30 Distribuzione Binomiale: esercizio 1 7 / 34 n = 8 p = 0.8 X Binom(n = 8,p = 0.8) a) Qual è la probabilità che germoglieranno esattamente 7 semi? ( ) 8 P(X = 7) = (1 0.8) (8 7) 8! = 7 7!(8 7)! 0.87 (0.2) (1) = = 8 1! b) Qual è la probabilità che germoglieranno più di 6 semi? ( ) 8 P(X > 6) = P(X = 7)+P(X = 8) = (1 0.8) (8 8) = ! 8!0! 0.88 (0.2) (0) =
31 Distribuzione Binomiale: esercizio 2 8 / 34 Il 5% delle componenti prodotte in una fabbrica di orologi sono difettose. Se selezioniamo casualmente 10 pezzi: a) Qual è la probabilità che esattamente 2 siano difettosi?
32 Distribuzione Binomiale: esercizio 2 8 / 34 Il 5% delle componenti prodotte in una fabbrica di orologi sono difettose. Se selezioniamo casualmente 10 pezzi: a) Qual è la probabilità che esattamente 2 siano difettosi? b) Qual è la probabilità che meno di 2 siano difettosi?
33 Distribuzione Binomiale: esercizio 2 8 / 34 Il 5% delle componenti prodotte in una fabbrica di orologi sono difettose. Se selezioniamo casualmente 10 pezzi: a) Qual è la probabilità che esattamente 2 siano difettosi? b) Qual è la probabilità che meno di 2 siano difettosi? b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi?
34 Distribuzione Binomiale: esercizio 2 Il 5% delle componenti prodotte in una fabbrica di orologi sono difettose. Se selezioniamo casualmente 10 pezzi: a) Qual è la probabilità che esattamente 2 siano difettosi? b) Qual è la probabilità che meno di 2 siano difettosi? b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi? Per risolvere l esercizio applichiamo la formula della probabilità binomiale. Sia X = {numero delle componenti difettose} allora X Binom(n = 10,p = 0.05) dove abbiamo considerato successo il selezionare un pezzo difettoso. 8 / 34
35 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi?
36 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) =
37 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( ) (1 0.05) (10 2) = 2
38 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8)
39 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi?
40 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) =
41 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) = P(X = 0) + P(X = 1) =
42 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) = P(X = 0) + P(X = 1) = ( 10 0 ) (0.95) (10) + ( 10 1 ) (0.95) (10 1) = = 10! 0!(10)! (0.95)(10) + 10! 1!(9)! 0.05(0.95)(9) = b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi?
43 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) = P(X = 0) + P(X = 1) = ( 10 0 ) (0.95) (10) + ( 10 1 ) (0.95) (10 1) = = 10! 0!(10)! (0.95)(10) + 10! 1!(9)! 0.05(0.95)(9) = b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi? P(1 < X < 4)
44 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) = P(X = 0) + P(X = 1) = ( 10 0 ) (0.95) (10) + ( 10 1 ) (0.95) (10 1) = = 10! 0!(10)! (0.95)(10) + 10! 1!(9)! 0.05(0.95)(9) = b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi? P(1 < X < 4) = P(X = 2) + P(X = 3) =
45 Distribuzione Binomiale: esercizio 2 9 / 34 a) Qual è la probabilità che esattamente 2 siano difettosi? P(X = 2) = ( 10 2 ) (1 0.05) (10 2) = 10! 2!(10 2)! (0.95) (8) b) Qual è la probabilità che meno di 2 siano difettosi? P(X < 2) = P(X = 0) + P(X = 1) = ( 10 0 ) (0.95) (10) + ( 10 1 ) (0.95) (10 1) = = 10! 0!(10)! (0.95)(10) + 10! 1!(9)! 0.05(0.95)(9) = b) Qual è la probabilità che più di 1 e meno di 4 siano difettosi? P(1 < X < 4) = P(X = 2) + P(X = 3) = ( ) (0.95) (10 3) = 3 = ! 4!(7)! (0.95) (7)
46 Forma della distribuzione Binomiale 10 / 34 La forma della distribuzione binomiale dipende dai valori dei parametri p ed n
47 Sintesi della distribuzione Binomiale 11 / 34 Per una distribuzione binomiale con probabilità di successo p in ognuna delle n prove indipendenti allora µ = E(X) = np
48 Sintesi della distribuzione Binomiale 11 / 34 Per una distribuzione binomiale con probabilità di successo p in ognuna delle n prove indipendenti allora µ = E(X) = np σ 2 = E(X µ) 2 = np(1 p)
49 Sintesi della distribuzione Binomiale 11 / 34 Per una distribuzione binomiale con probabilità di successo p in ognuna delle n prove indipendenti allora µ = E(X) = np σ 2 = E(X µ) 2 = np(1 p) σ = np(1 p)
50 Distribuzione Binomiale: esercizio 1 12 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8.
51 Distribuzione Binomiale: esercizio 1 12 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è il valor medio della variabile che conta il numero di semi germogliati?
52 Distribuzione Binomiale: esercizio 1 12 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è il valor medio della variabile che conta il numero di semi germogliati? µ = np = = 6.4
53 Distribuzione Binomiale: esercizio 1 12 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è il valor medio della variabile che conta il numero di semi germogliati? µ = np = = 6.4 b) Qual è la varianza della variabile che conta il numero di semi germogliati?
54 Distribuzione Binomiale: esercizio 1 12 / 34 Riconsideriamo il problema della germogliazione dei semi, stavolta prendiamo 8 semi. In altre parola stavolta abbiamo n = 8 prove e probabilità p ancora 0.8. a) Qual è il valor medio della variabile che conta il numero di semi germogliati? µ = np = = 6.4 b) Qual è la varianza della variabile che conta il numero di semi germogliati? σ 2 = np(1 p) = = 1.28
55 Approssimazione della distribuzione Binomiale con la Normale 13 / 34 La forma della distribuzione binomial è approssimativamente Normale se n è grande.
56 Approssimazione della distribuzione Binomiale con la Normale La forma della distribuzione binomial è approssimativamente Normale se n è grande. La normale è una buona approssimazione della binomiale se np(1 p) > 7 13 / 34
57 Approssimazione della distribuzione Binomiale con la Normale 13 / 34 La forma della distribuzione binomial è approssimativamente Normale se n è grande. La normale è una buona approssimazione della binomiale se np(1 p) > 7 Se X Binom(n,p) e si ha np(1 p) > 7 allora possiamo considerare la standardizzazione della normale: Z = X µ σ = X np np(1 p)
58 Approssimazione della distribuzione Binomiale con la Normale 13 / 34 La forma della distribuzione binomial è approssimativamente Normale se n è grande. La normale è una buona approssimazione della binomiale se np(1 p) > 7 Se X Binom(n,p) e si ha np(1 p) > 7 allora possiamo considerare la standardizzazione della normale: In questo caso allora P(a < X < b) = P Z = X µ σ = X np np(1 p) ( ) a np < Z < b np np(1 p) np(1 p)
59 Approssimazione normale Binomiale: esercizio 14 / 34 Supponiamo che un seme di abete piantato in una certa area abbia una probabilità dello 0.7 di sopravvivere oltre il primo anno. Calcolare la probabilità che su 200 semi piantati:
60 Approssimazione normale Binomiale: esercizio 14 / 34 Supponiamo che un seme di abete piantato in una certa area abbia una probabilità dello 0.7 di sopravvivere oltre il primo anno. Calcolare la probabilità che su 200 semi piantati: a) più di 150 siano sopravvissuti;
61 Approssimazione normale Binomiale: esercizio 14 / 34 Supponiamo che un seme di abete piantato in una certa area abbia una probabilità dello 0.7 di sopravvivere oltre il primo anno. Calcolare la probabilità che su 200 semi piantati: a) più di 150 siano sopravvissuti; b) siano sopravvissuti tra i 150 e i 155 semi.
62 Approssimazione normale Binomiale: esercizio 14 / 34 Supponiamo che un seme di abete piantato in una certa area abbia una probabilità dello 0.7 di sopravvivere oltre il primo anno. Calcolare la probabilità che su 200 semi piantati: a) più di 150 siano sopravvissuti; b) siano sopravvissuti tra i 150 e i 155 semi. La distribuzione di probabilità è di tipo binomiale in quanto l evento di interesse è binario, sopravvivenza o meno, e si hanno un numero di 200 prove indipendenti tra loro. Sia indicato il successo con la sopravvivenza, allora la variabile casuale X che misura il numero di semi sopravvissuti ha distribuzione: X Binom(200, 0.7)
63 Approssimazione normale Binomiale: esercizio 15 / 34 X Binom(200, 0.7) applicare la formula della binomiale sarebbe lungo, ma osserviamo che np(1 p) = = 42 >> 7 possiamo quindi applicare l approssimazione con la distribuzione Normale. Calcoliamo le probabilità che: a) più di 150 semi siano sopravvissuti;
64 Approssimazione normale Binomiale: esercizio 15 / 34 X Binom(200, 0.7) applicare la formula della binomiale sarebbe lungo, ma osserviamo che np(1 p) = = 42 >> 7 possiamo quindi applicare l approssimazione con la distribuzione Normale. Calcoliamo le probabilità che: a) più di 150 semi siano sopravvissuti; P(X > 150) =
65 Approssimazione normale Binomiale: esercizio 15 / 34 X Binom(200, 0.7) applicare la formula della binomiale sarebbe lungo, ma osserviamo che np(1 p) = = 42 >> 7 possiamo quindi applicare l approssimazione con la distribuzione Normale. Calcoliamo le probabilità che: a) più di 150 semi siano sopravvissuti; P(X > 150) = P ( ) X > = (1 0.7) (1 0.7)
66 Approssimazione normale Binomiale: esercizio 15 / 34 X Binom(200, 0.7) applicare la formula della binomiale sarebbe lungo, ma osserviamo che np(1 p) = = 42 >> 7 possiamo quindi applicare l approssimazione con la distribuzione Normale. Calcoliamo le probabilità che: a) più di 150 semi siano sopravvissuti; ( P Z > P(X > 150) = P ( ) X > = (1 0.7) (1 0.7) ) = P(Z > 1.54) = 1 P(Z < 1.54) =
67 Approssimazione normale Binomiale: esercizio 16 / 34 X Binom(200, 0.7) b) siano sopravvissuti tra i 150 e i 155 semi.
68 Approssimazione normale Binomiale: esercizio 16 / 34 X Binom(200, 0.7) b) siano sopravvissuti tra i 150 e i 155 semi. P(150 < X < 155) =
69 Approssimazione normale Binomiale: esercizio 16 / 34 X Binom(200, 0.7) b) siano sopravvissuti tra i 150 e i 155 semi. P(150 < X < 155) = P ( (1 0.7) < X (1 0.7) < (1 0.7) ) =
70 Approssimazione normale Binomiale: esercizio 16 / 34 X Binom(200, 0.7) b) siano sopravvissuti tra i 150 e i 155 semi. P(150 < X < 155) = P ( ( = P < Z < (1 0.7) < X (1 0.7) < (1 0.7) ) = ) = P(1.54 < Z < 2.31) = P(Z < 2.31) P(Z < 1.54) = 6.48
71 Approssimazione normale Binomiale: esercizio 16 / 34 X Binom(200, 0.7) b) siano sopravvissuti tra i 150 e i 155 semi. P(150 < X < 155) = P ( ( = P < Z < (1 0.7) < X (1 0.7) < (1 0.7) ) = ) = P(1.54 < Z < 2.31) = P(Z < 2.31) P(Z < 1.54) = 6.48 =
72 Distribuzioni campionarie 17 / 34 Gli strumenti della probabilità possono essere applicati per analizzare quanto è probabile che i risultati sul campione, o campionari, siano vicini ai valori della popolazione.
73 Distribuzioni campionarie 17 / 34 Gli strumenti della probabilità possono essere applicati per analizzare quanto è probabile che i risultati sul campione, o campionari, siano vicini ai valori della popolazione. I metodi inferenziali utilizzano statistiche calcolate sui dati campionari per elaborare decisioni e fare previsioni su una popolazione.
74 Distribuzioni campionarie 17 / 34 Gli strumenti della probabilità possono essere applicati per analizzare quanto è probabile che i risultati sul campione, o campionari, siano vicini ai valori della popolazione. I metodi inferenziali utilizzano statistiche calcolate sui dati campionari per elaborare decisioni e fare previsioni su una popolazione. Generalmente, considerata una popolazione, non conosciamo i valori dei parametri della sua distribuzione, tali valori sono stimati utilizzando dati campionari provenienti da indagini, studi osservazionali o esperimenti.
75 Distribuzioni campionarie 17 / 34 Gli strumenti della probabilità possono essere applicati per analizzare quanto è probabile che i risultati sul campione, o campionari, siano vicini ai valori della popolazione. I metodi inferenziali utilizzano statistiche calcolate sui dati campionari per elaborare decisioni e fare previsioni su una popolazione. Generalmente, considerata una popolazione, non conosciamo i valori dei parametri della sua distribuzione, tali valori sono stimati utilizzando dati campionari provenienti da indagini, studi osservazionali o esperimenti. Per questo motivo si introduce una particolare distribuzione di probabilità, chiamata distribuzione campionaria, che ci aiuta nel determinare quanto è probabile che una statistica campionaria cada vicino al parametro della popolazione.
76 Distribuzioni campionarie 18 / 34 Una distribuzione campionaria è una distribuzione di tutti i possibili valori di una statistica ottenuti da campioni della stessa ampiezza estratti dalla popolazione.
77 Distribuzioni campionarie 18 / 34 Una distribuzione campionaria è una distribuzione di tutti i possibili valori di una statistica ottenuti da campioni della stessa ampiezza estratti dalla popolazione. Specifica le probabilità per i possibili valori che la statistica può assumere.
78 Distribuzioni campionarie 19 / 34 Possiamo fare la distinzione tra tre tipi di distribuzione: Distribuzione della popolazione: la distribuzione da cui estraiamo il campione. I suoi parametri sono fissi ma generalmente incogniti. Il parametro della popolazione è ciò che vorremmo conoscere, su cui facciamo inferenza.
79 Distribuzioni campionarie 19 / 34 Possiamo fare la distinzione tra tre tipi di distribuzione: Distribuzione della popolazione: la distribuzione da cui estraiamo il campione. I suoi parametri sono fissi ma generalmente incogniti. Il parametro della popolazione è ciò che vorremmo conoscere, su cui facciamo inferenza. Distribuzione dei dati: la distribuzione dei dati campionari, ossia la distribuzione che effettivamente osserviamonella pratica. Tale distribuzione è descritta da statistiche campionarie. Poichè le statistiche varieranno da campione a campione, anche le distribuzioni dei dati cambieranno da un campione all altro.
80 Distribuzioni campionarie 19 / 34 Possiamo fare la distinzione tra tre tipi di distribuzione: Distribuzione della popolazione: la distribuzione da cui estraiamo il campione. I suoi parametri sono fissi ma generalmente incogniti. Il parametro della popolazione è ciò che vorremmo conoscere, su cui facciamo inferenza. Distribuzione dei dati: la distribuzione dei dati campionari, ossia la distribuzione che effettivamente osserviamonella pratica. Tale distribuzione è descritta da statistiche campionarie. Poichè le statistiche varieranno da campione a campione, anche le distribuzioni dei dati cambieranno da un campione all altro. Distribuzione campionaria: la distribuzione di una statistica campionaria. Fornisce la probabilità per tutti i possibili valori della statistica. Svela quanto una statistica campionaria cada vicino al parametro incognito corrispondente.
81 Distribuzione campionaria: proporzione campionaria 20 / 34 Molto spesso si è interessati a studiare la proporzione di oggetti con delle specifiche caratteristiche in una popolazione: la proporzione di semi che sopravvivono un anno dopo essere stati piantati;
82 Distribuzione campionaria: proporzione campionaria 20 / 34 Molto spesso si è interessati a studiare la proporzione di oggetti con delle specifiche caratteristiche in una popolazione: la proporzione di semi che sopravvivono un anno dopo essere stati piantati; la proporzione di una specie animale in un area protetta;
83 Distribuzione campionaria: proporzione campionaria 20 / 34 Molto spesso si è interessati a studiare la proporzione di oggetti con delle specifiche caratteristiche in una popolazione: la proporzione di semi che sopravvivono un anno dopo essere stati piantati; la proporzione di una specie animale in un area protetta; la proporzione di alberi infettati da un parassita in un area.
84 Distribuzione campionaria: proporzione campionaria 20 / 34 Molto spesso si è interessati a studiare la proporzione di oggetti con delle specifiche caratteristiche in una popolazione: la proporzione di semi che sopravvivono un anno dopo essere stati piantati; la proporzione di una specie animale in un area protetta; la proporzione di alberi infettati da un parassita in un area. La proporzione è associata ad una variabile casuale discreta binaria di tipo successo o insuccesso, in quanto la caratteristica studiata può presentarsi o meno.
85 Distribuzione campionaria: proporzione campionaria 20 / 34 Molto spesso si è interessati a studiare la proporzione di oggetti con delle specifiche caratteristiche in una popolazione: la proporzione di semi che sopravvivono un anno dopo essere stati piantati; la proporzione di una specie animale in un area protetta; la proporzione di alberi infettati da un parassita in un area. La proporzione è associata ad una variabile casuale discreta binaria di tipo successo o insuccesso, in quanto la caratteristica studiata può presentarsi o meno. Stiamo quindi descrivendo una variabile casuale binomiale e la popolazione segue una distribuzione binomiale con probabilità determinata dalla proporzione di successi osservati in n prove.
86 Distribuzione campionaria: proporzione campionaria 21 / 34 p = proporzione della popolazione che possiede una certa caratteristica
87 Distribuzione campionaria: proporzione campionaria 21 / 34 p = proporzione della popolazione che possiede una certa caratteristica Se selezioniamo un campione di n osservazioni da una popolazione binomiale con parametro p,e indichiamo con x i = 1 il successo e con x i = 0 l insuccesso, allora la media campionaria sarà la proporzione di successi:
88 Distribuzione campionaria: proporzione campionaria 21 / 34 p = proporzione della popolazione che possiede una certa caratteristica Se selezioniamo un campione di n osservazioni da una popolazione binomiale con parametro p,e indichiamo con x i = 1 il successo e con x i = 0 l insuccesso, allora la media campionaria sarà la proporzione di successi: x = ˆp = n i=1 x i n = numero di successi n
89 Distribuzione campionaria: proporzione campionaria 21 / 34 p = proporzione della popolazione che possiede una certa caratteristica Se selezioniamo un campione di n osservazioni da una popolazione binomiale con parametro p,e indichiamo con x i = 1 il successo e con x i = 0 l insuccesso, allora la media campionaria sarà la proporzione di successi: x = ˆp = n i=1 x i n = numero di successi n la proporzione campionaria fornisce una stima della proporzione reale.
90 Distribuzione campionaria: proporzione campionaria 21 / 34 p = proporzione della popolazione che possiede una certa caratteristica Se selezioniamo un campione di n osservazioni da una popolazione binomiale con parametro p,e indichiamo con x i = 1 il successo e con x i = 0 l insuccesso, allora la media campionaria sarà la proporzione di successi: x = ˆp = n i=1 x i n = numero di successi n la proporzione campionaria fornisce una stima della proporzione reale. 0 ˆp 1;
91 Distribuzione campionaria: proporzione campionaria 22 / 34 Indichiamo con ˆP = X numero di successi = n n la variabile casuale che considera le proporzioni di successo in n prove.
92 Distribuzione campionaria: proporzione campionaria 22 / 34 Indichiamo con ˆP = X numero di successi = n n la variabile casuale che considera le proporzioni di successo in n prove. Si ha che E( ˆP) = E ( ) ( ) X X = p σ 2ˆP n = var p(1 p) = n n
93 Distribuzione campionaria: proporzione campionaria 22 / 34 Indichiamo con ˆP = X numero di successi = n n la variabile casuale che considera le proporzioni di successo in n prove. Si ha che E( ˆP) = E ( ) ( ) X X = p σ 2ˆP n = var p(1 p) = n n Se n è sufficientemente grande (n 30), allora la distribuzione campionaria della proporzione è approssimativamente normale.
94 Distribuzione campionaria: proporzione campionaria 22 / 34 Indichiamo con ˆP = X numero di successi = n n la variabile casuale che considera le proporzioni di successo in n prove. Si ha che E( ˆP) = E ( ) ( ) X X = p σ 2ˆP n = var p(1 p) = n n Se n è sufficientemente grande (n 30), allora la distribuzione campionaria della proporzione è approssimativamente normale.
95 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07?
96 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04
97 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04 σ ˆP = p(1 p) n 0.04(0.96) =
98 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04 σ ˆP = p(1 p) n 0.04(0.96) = Costruiamo la variabile Z standardizzata sottraendo il valor medio e dividendo per la deviazione standard: P( ˆP > 0.07) =
99 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04 σ ˆP = p(1 p) n 0.04(0.96) = Costruiamo la variabile Z standardizzata sottraendo il valor medio e dividendo per la deviazione standard: P( ˆP > 0.07) = P ( Z > )
100 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04 σ ˆP = p(1 p) n 0.04(0.96) = Costruiamo la variabile Z standardizzata sottraendo il valor medio e dividendo per la deviazione standard: P( ˆP > 0.07) = P ( Z > ) P(Z > 1.03) 1 P(Z < 1.03)
101 Proporzione campionaria: esercizio 23 / 34 La proporzione, p, di pezzi difettosi in una produzione è Qual è la probabilità che, in un campione di 45 componenti estratte senza reimissione, la proporzione di pezzi difettosi sia maggiore di 0.07? n 30 e di conseguenza possiamo usare l approssimazione normale con E( ˆP) = p = 0.04 σ ˆP = p(1 p) n 0.04(0.96) = Costruiamo la variabile Z standardizzata sottraendo il valor medio e dividendo per la deviazione standard: P( ˆP > 0.07) = P ( Z > ) P(Z > 1.03) 1 P(Z < 1.03)
102 Distribuzione campionaria: media campionaria 24 / 34
103 Distribuzione campionaria: media campionaria 25 / 34 Calcoliamo le misure di sintesi per la popolazione sotto studio: µ = N x i i=1 N = = 21
104 Distribuzione campionaria: media campionaria 25 / 34 Calcoliamo le misure di sintesi per la popolazione sotto studio: µ = N x i i=1 N = = 21 σ = N i=1 (x i µ) 2 N = 2.236
105 Distribuzione campionaria: media campionaria 25 / 34 Calcoliamo le misure di sintesi per la popolazione sotto studio: µ = N x i i=1 N = = 21 σ = N i=1 (x i µ) 2 N = 2.236
106 Distribuzione campionaria: media campionaria 26 / 34 Adesso consideriamo tutti i possibili campioni con dimensione n = 2, e calcoliamo per ognuno la media campionaria. I possibili campioni sono 4 2 = 16, abbiamo un estrazione con reimissione e quindi sono disposizioni con ripetizione.
107 Distribuzione campionaria: media campionaria 27 / 34 Costruiamo la distribuzione di tutte le medie campionarie ottenute:
108 Distribuzione campionaria: media campionaria 28 / 34 Calcoliamo le misure di sintesi del campione: E( X) = 16 i=1 x i 16 = = 21 =
109 Distribuzione campionaria: media campionaria 28 / 34 Calcoliamo le misure di sintesi del campione: E( X) = 16 i=1 x i 16 = = 21 = µ
110 Distribuzione campionaria: media campionaria 28 / 34 Calcoliamo le misure di sintesi del campione: 16 x i E( X) = = = 21 = µ i= σ X = 16 ( x i µ) 2 (18 21) = 2 + (19 21) (24 21) 2 = 1.58 i=
111 Distribuzione campionaria: media campionaria 29 / 34 Confrontiamo le due distribuzioni, della popolazione e del campione.
Esercitazione 5 del corso di Statistica 2 Prof. Domenico Vistocco
Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Il campionamento e l inferenza. Il campionamento e l inferenza
Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Gli intervalli di confidenza. Intervallo di confidenza per la media (σ 2 nota) nel caso di popolazione Gaussiana
Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Modelli probabilistici variabili casuali
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
DISTRIBUZIONI DI CAMPIONAMENTO
DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
Distribuzioni campionarie. Antonello Maruotti
Distribuzioni campionarie Antonello Maruotti Outline 1 Introduzione 2 Concetti base Si riprendano le considerazioni fatte nella parte di statistica descrittiva. Si vuole studiare una popolazione con riferimento
LA MEDIA CAMPIONARIA 14-1
LA MEDIA CAMPIONARIA Prendiamo un urna e inseriamo 10 palline numerate da 0 a 9 (questa è la nostra popolazione ). La media dei 10 valori è 4.5 (questa è la media vera µ). La varianza dei 10 valori è 8.25
Università degli studi della Tuscia. Principi di Statistica dr. Luca Secondi A.A. 2014/2015. Esercitazione di riepilogo Variabili casuali
Università degli studi della Tuscia Principi di Statistica dr. Luca Secondi A.A. 014/015 Esercitazione di riepilogo Variabili casuali ESERCIZIO 1 Il peso delle compresse di un determinato medicinale si
APPUNTI DI STATISTICA INFERENZIALE. Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO
APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
Statistica Inferenziale
Statistica Inferenziale a) L Intervallo di Confidenza b) La distribuzione t di Student c) La differenza delle medie d) L intervallo di confidenza della differenza Prof Paolo Chiodini Dalla Popolazione
Elementi di base su modello binomiale e modello normale
Elementi di base su modello binomiale e modello normale (alcune note) Parte 1: il modello binomiale Di fondamentale importanza nell analisi della qualità sono i modelli. I due principali modelli statistico-probablistici
Capitolo 8. Intervalli di confidenza. Statistica. Levine, Krehbiel, Berenson. Casa editrice: Pearson. Insegnamento: Statistica
Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 8 Intervalli di confidenza Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 4
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 4 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Stimatore media campionaria Il tempo in minuti necessario a un certo impiegato dell anagrafe
LE DISTRIBUZIONI CAMPIONARIE
LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
Verifica delle ipotesi
Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Campionamento La statistica media campionaria e la sua distribuzione. Paola Giacomello Dip. Scienze Sociali ed Economiche Uniroma1
Campionamento La statistica media campionaria e la sua distribuzione 1 Definisco il problema da studiare: es. tempo di percorrenza tra abitazione e università Carattere: tempo ossia v.s. continua Popolazione:
Esercizio 1. Durante un inchiesta su 500 studenti frequentanti i corsi di Algebra (A), Fisica (F) e Statistica è stato rilevato che:
Esercizio 1 Durante un inchiesta su 500 studenti frequentanti i corsi di Algebra (A), Fisica (F) e Statistica è stato rilevato che: A 329 F 186 S 295 AS 217 AF 83 FS 63 AFS 53 Determinare la partizione
STATISTICA APPLICATA Prof.ssa Julia Mortera. INTRODUZIONE al STATISTICA
STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
Argomenti della lezione: Campionamento Stima Distribuzione campionaria Campione Popolazione Sottoinsieme degli elementi (o universo) dell '
Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Statistica Applicata all edilizia: alcune distribuzioni di probabilità
Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Statistica. Capitolo 10. Verifica di Ipotesi su una Singola Popolazione. Cap. 10-1
Statistica Capitolo 1 Verifica di Ipotesi su una Singola Popolazione Cap. 1-1 Obiettivi del Capitolo Dopo aver completato il capitolo, sarete in grado di: Formulare ipotesi nulla ed ipotesi alternativa
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
Parametri e statistiche Popolazione Parametri Valori fissi, spesso non noti Campione Statistiche o Stimatori Variabili casuali, le cui determinazioni dipendono dalle particolari osservazioni scelte Parametri
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Metodi statistici per le ricerche di mercato
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2017-2018 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
05. Errore campionario e numerosità campionaria
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Alcune v.a. discrete notevoli
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
La distribuzione t. Federico Plazzi. 7 Novembre 2015
La distribuzione t Federico Plazzi 7 Novembre 2015 Popolazione e campioni Popolazione e campioni Definizioni ed assunzioni di partenza Campione: l insieme di individui che abbiamo potuto osservare. Popolazione
Corso di Laurea: Diritto per le Imprese e le istituzioni a.a Statistica. Probabilità. Lezioni : 11, 12. Docente: Alessandra Durio
Corso di Laurea: Diritto per le Imprese e le istituzioni a.a. 2016-17 Statistica Probabilità Lezioni : 11, 12 Docente: Alessandra Durio 1 Contenuti 1. Variabili casuali notevoli DISCRETE (uniforme, di
1. Quali sono i possibili campioni di numerosità 2 senza reimmissione? X 1 e X 2 sono indipendenti?
Esercizio 1 Consideriamo una popolazione X, dove X = {3,5,7}. 1. Quali sono i possibili campioni di numerosità 2 senza reimmissione? X 1 e X 2 sono indipendenti? 2. Quali sono i possibili campioni di numerosità
Statistica. Lezione : 18, 19. Variabili casuali
Corsi di Laurea: a.a. 2017-18 Diritto per le Imprese e le istituzioni Scienze dell Amministrazione e Consulenza del Lavoro sienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
Statistica Corso Base Serale Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it Campionamento Esercizio 1. Da una ricerca si è osservato che il peso del prodotto A varia tra i e i 530 grammi. 1 Ipotizzando
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali. Esercitazione E
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Distribuzioni e inferenza statistica
Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Statistica. Lezione 4
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 4 a.a 2011-2012 Dott.ssa Daniela
Tecniche di sondaggio
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
un elemento scelto a caso dello spazio degli esiti di un fenomeno aleatorio;
TEST DI AUTOVALUTAZIONE - SETTIMANA 3 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Una variabile casuale
C.I. di Metodologia clinica
C.I. di Metodologia clinica Modulo 5. I metodi per la sintesi e la comunicazione delle informazioni sulla salute Quali errori influenzano le stime? L errore casuale I metodi per la produzione delle informazioni
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 7: Basi di statistica
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
STATISTICA: esercizi svolti sulle VARIABILI CASUALI
STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7?
![Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7?](/thumbs/94/122023687.jpg "Esercizi. 2. [Conteggio diretto] Due dadi vengono lanciati in successione. a) Qual è la probabilità che la somma dei due risultati faccia 7?")
1 E. Vitali Matematica (Scienze Naturali) Esercizi 1. [Conteggio diretto] Quattro ragazzi, A, B, C e D, dispongono di due biglietti per il teatro e decidono di tirare a sorte chi ne usufruirà. a) Qual
Tipi di variabili. Indici di tendenza centrale e di dispersione
Tipi di variabili. Indici di tendenza centrale e di dispersione L. Boni Variabile casuale In teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o random variable)
Probabilità: teoremi e distribuzioni
Probabilità: teoremi e distribuzioni OBIETTIVO DIDATTICO DELLA LEZIONE Illustrare le più importanti distribuzioni di probabilità che vengono utilizzate in statistica Distribuzioni di probabilità 1. La
6 - Distribuzione Binomiale
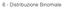6 - Distribuzione Binomiale Probabilita' (binomiale) o densita' di probabilita' (gaussiana) Binomiale, N=3, p=0.25 0.5 Gaussiana, µ=np=0.8, σ= Np(1-p)=0.8 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5
Teorema del Limite Centrale
Teorema del Limite Centrale Problema. Determinare come la media campionaria x e la deviazione standard campionaria s misurano la media µ e la deviazione standard σ della popolazione. È data una popolazione
Intervallo di confidenza
Intervallo di confidenza Esempio: siamo intressati al peso dei maschi in una certa regione. Vogliamo stimare il peso medio µ della popolazione. Siano x 1,...,x n i pesi di n individui scelti a caso. La
Richiami di inferenza statistica Strumenti quantitativi per la gestione
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Richiami di inferenza statistica. Strumenti quantitativi per la gestione. Emanuele Taufer
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
STATISTICA ESERCITAZIONE 9
STATISTICA ESERCITAZIONE 9 Dott. Giuseppe Pandolfo 19 Gennaio 2015 REGOLE DI CONTEGGIO Sequenze ordinate Sequenze non ordinate Estrazioni con ripetizione Estrazioni senza ripetizione Estrazioni con ripetizione
Esame di Statistica del 19 settembre 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova).
Esame di Statistica del 19 settembre 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione: si
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
UNIVERSITÀ di ROMA TOR VERGATA
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 205- P.Baldi Lista di esercizi 5, 8 febbraio 20. Esercizio Si fanno 25 estrazioni
ESERCITAZIONE N. 5 corso di statistica
ESERCITAZIONE N. 5corso di statistica p. 1/27 ESERCITAZIONE N. 5 corso di statistica Marco Picone Università Roma Tre ESERCITAZIONE N. 5corso di statistica p. 2/27 Introduzione Variabili aleatorie discrete
Università del Piemonte Orientale. Corso di laurea in medicina e chirurgia. Corso di Statistica Medica. Le distribuzioni teoriche di probabilità.
Università del Piemonte Orientale Corso di laurea in medicina e chirurgia Corso di Statistica Medica Le distribuzioni teoriche di probabilità. La distribuzione di probabilità binomiale Corso di laurea
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3 Sui PC a disposizione sono istallati diversi sistemi operativi. All accensione scegliere Windows. Immettere Nome utente b## (##
PROBABILITA E STATISTICA Docente: Bruno Gobbi
UNIVERSITA DEGLI STUDI DI VERONA PROBABILITA E STATISTICA Docente: Bruno Gobbi LE VARIABILI CASUALI DISCRETE VARIABILE CASUALE - DEFINIZIONE Si definisce Variabile Casuale una grandezza che, associata
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
I modelli probabilistici
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
SOLUZIONI ESERCITAZIONE NR. 8 Test statistici
SOLUZIONI ESERCITAZIONE NR. 8 Test statistici ESERCIZIO nr. 1 Un campione casuale di dieci pazienti di sesso maschile in cura per comportamenti aggressivi nell ambito del contesto familiare è stato classificato
UNIVERSITÀ di ROMA TOR VERGATA
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 2010-11 P.Baldi Lista di esercizi 3. Corso di Laurea in Biotecnologie Esercizio 1 Una v.a. X segue una legge N(2, ). Calcolare a1) P(X 1) a2) P(2
Campionamento e distribuzioni campionarie
Campionamento e distribuzioni campionarie Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona Inferenza statistica = processo che, partendo dalle informazioni contenute
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Università del Piemonte Orientale. Corso di laurea in biotecnologie. Corso di Statistica Medica. Le distribuzioni teoriche di probabilità.
Università del Piemonte Orientale Corso di laurea in biotecnologie Corso di Statistica Medica Le distribuzioni teoriche di probabilità. La distribuzione di probabilità binomiale Corso di laurea in biotecnologie
Esame di Statistica (10 o 12 CFU) CLEF 11 febbraio 2016
Esame di Statistica 0 o CFU) CLEF febbraio 06 Esercizio Si considerino i seguenti dati, relativi a 00 clienti di una banca a cui è stato concesso un prestito, classificati per età e per esito dell operazione
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La variabile Uniforme Continua Data una scheda telefonica da 5 euro di cui non si sa se sia
Esercitazione 4 del corso di Statistica (parte 2)
Esercitazione 4 del corso di Statistica (parte ) Dott.ssa Paola Costantini Febbraio Esercizio n. Il tempo di percorrenza del treno che collega la stazione di Roma Termini con l aeroporto di Fiumicino è
La casualità nello spazio o nel tempo: la distribuzione di Poisson
La casualità nello spazio o nel tempo: la distribuzione di Poisson Cosa potrebbero rappresentare questi punti? o Organismi o eventi presenti in una certa area Per esempio, ci interessa capire come avviene
INTERVALLI DI CONFIDENZA e TEST D IPOTESI 1 / 30
INTERVALLI DI CONFIDENZA e TEST D IPOTESI 1 / 30 Intervallo di confidenza: media 2 / 30 Supponiamo di considerare la media campionaria X e assumiamo che Intervallo di confidenza: media 2 / 30 Supponiamo
Esercizi di Probabilità e Statistica
Esercizi di Probabilità e Statistica parte 1 Massimo Guerriero Ettore Benedetti Indice Esercizi Presentazione dei dati Misure di sintesi numerica Probabilità Distribuzioni teoriche di probabilità Distribuzione
Approssimazione normale alla distribuzione binomiale
Approssimazione normale alla distribuzione binomiale P b (X r) costoso P b (X r) P(X r) per N grande Teorema: Se la variabile casuale X ha una distribuzione binomiale con parametri N e p, allora, per N
Variabili aleatorie. Variabili aleatorie
Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
Metodi statistici per le ricerche di mercato
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2016-2017 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Variabili aleatorie discrete. Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia
Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Probabilità e Statistica
Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
Cenni di statistica statistica
Cenni di statistica La statistica è una disciplina che ha come fine lo studio quantitativo e qualitativo di un particolare fenomeno in condizioni di incertezza o non determinismo, ovvero di non completa
UNIVERSITÀ DEGLI STUDI DI PERUGIA
SIGI, Statistica II, esercitazione n. 3 1 UNIVERSITÀ DEGLI STUDI DI PERUGIA FACOLTÀ DI ECONOMIA CORSO DI LAUREA S.I.G.I. STATISTICA II Esercitazione n. 3 Esercizio 1 Una v.c. X si dice v.c. esponenziale
FENOMENI CASUALI. fenomeni casuali
PROBABILITÀ 94 FENOMENI CASUALI La probabilità si occupa di fenomeni casuali fenomeni di cui, a priori, non si sa quale esito si verificherà. Esempio Lancio di una moneta Testa o Croce? 95 DEFINIZIONI
STATISTICA (2) ESERCITAZIONE 2. Dott.ssa Antonella Costanzo
STATISTICA (2) ESERCITAZIONE 2 5.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. La v.c. Normale: uso delle tavole E noto che un certo tipo di dati si distribuiscono secondo una gaussiana di media 10
esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno dei possibili esiti di un esperimento casuale;
Capitolo 15 Suggerimenti agli esercizi a cura di Elena Siletti Esercizio 15.1: Suggerimento Si ricordi che: esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno
Università del Piemonte Orientale Corsi di Laurea triennale di area tecnica. Corso di Statistica Medica. Le distribuzioni teoriche di probabilità
Università del Piemonte Orientale Corsi di Laurea triennale di area tecnica Corso di Statistica Medica Le distribuzioni teoriche di probabilità La distribuzione binomiale La distribuzione Normale (o di
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
STATISTICA ESERCITAZIONE
STATISTICA ESERCITAZIONE Dott. Giuseppe Pandolfo 1 Giugno 2015 Esercizio 1 Una fabbrica di scatole di cartone evade il 96% degli ordini entro un mese. Estraendo 300 campioni casuali di 300 consegne, in
lezione 4 AA Paolo Brunori
AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
ES.2.2. Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili. Una partizione finita di Ω è una sequenza di K eventi
ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
Esercizi di statistica
Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Intervallo di confidenza
Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Distribuzione normale
Distribuzione normale istogramma delle frequenze di un insieme di misure relative a una grandezza che varia con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
M 3 = ..p x.q n x. σ 3 = npq q p. npq npq = q p. npq.
Distribuzioni teoriche A. DISTRIBUZIONI DISCRETE - Distribuzione binomiale - Distribuzione multinomiale - Distribuzione di Poisson - Distribuzione ipergeometrica - Distribuzione uniforme B. DISTRIBUZIONI
Intervallo di confidenza
Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Intervallo di confidenza
Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
SOLUZIONI DEL 2 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
SOLUZIONI DEL 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA Esercizio 0.1 Una moneta non truccata viene lanciata 10 volte. Calcolare la probabilità che non esca mai testa. Quale risulta la probabilità
Statistica 1- parte II
Statistica 1- parte II Esercitazione 1 Dott.ssa Antonella Costanzo 11/02/2016 Esercizio 1. Modelli discreti di probabilità: le v.c. binomiale e geometrica (come caso particolare della v.c. binomiale negativa),
Distribuzioni campionarie
1 Inferenza Statistica Descrittiva Distribuzioni campionarie Statistica Inferenziale: affronta problemi di decisione in condizioni di incertezza basandosi sia su informazioni a priori sia sui dati campionari
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia. Corso di Statistica Medica. La distribuzione Normale (o di Gauss)
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in medicina e chirurgia - Corso di Statistica
NOZIONI DI CALCOLO DELLE PROBABILITÀ
NOZIONI DI CALCOLO DELLE PROBABILITÀ ESPERIMENTO CASUALE: un esperimento si dice casuale quando gli esiti (manifestazioni o eventi) non possono essere previsti con certezza. PROVA: le ripetizioni, o occasioni