A =, c d. d = ad cb. c d A =
|
|
|
- Rocco Scala
- 5 anni fa
- Visualizzazioni
Transcript
1 Geometria e Algebra (II), Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il determinante di una matrice quadrata di ordine n ad entrate reali e un numero reale, che puo essere definito in vari modi equivalenti; di seguito noi ne diamo una definizione ricorsiva: definiamo il determinante per le matrici di ordine 1 e, assumendo di avere definito il determinante per le matrici di ordine n 1, definiamo il determinante per le matrici di ordine n Denoteremo il determinante di una matrice A con det(a) (come abbiamo fatto nel caso n 2) o con A (piu spesso, quasi sempre); cosi, per il determinante della matrice [ ] a b A, c d alla notazione [ a b det(a) det c d preferiremo spesso la notazione A a c ] ad cb, b d ad cb 2 Sia n 0, 1, 2, 3, un intero positivo, e sia a 11 a 1n A a n1 a nn una matrice quadrata di ordine n ad elementi reali a ij R; il determinante di A e il numero reale a 11 a 1n A R a n1 a nn definito ricorsivamente come segue per n 1, il determinante della matrice A [a 11 ] e il suo unico elemento: A a 11 a 11 1
2 sia n > 1 Supponiamo che sia definito il determinante per ogni matrice quadrata di ordine n 1 Per ogni coppia (i, j), con i, j 1,, n, consideriamo il determinante della matrice di ordine n 1 ottenuta da A cancellando la riga i ma e la colonna j ma, lo chiamiamo minore complementare (i, j) mo di A e lo indichiamo con M ij : a 11 a 1j a 1n poniamo inoltre 1 M ij ε ij ( 1) i+j a i1 a ij a in a n1 a nj a nn ; { +1 se i + j pari, 1 se i + j dispari Diciamo determinate di A il numero reale ottenuto sommando i prodotti degli elementi di una colonna di A per i rispettivi complementi algebrici, pesati con i segni dati dagli ε Precisamente, poniamo A ε 1j a 1j M 1j + ε 2j a 2j M 2j + + ε nj a nj M nj ε 1j a 1j a 11 a 1j a 1n a 11 a 1j a 1n a 21 a 2j a 2n +ε 2j a 2j + a n1 a nj a nn a n1 a nj a nn a 11 a 1j a 1n + + ε nj a nj, a n1 a nj a nn 1 esplicitamente, i valori degli ε ij sono dati dalla matrice
3 dove j e un qualsiasi indice scelto fra 1, 2,, n Questa espressione viene detta sviluppo di Laplace del determinante di A secondo la colonna j ma La definizione di determinante e consistente, in quanto si dimostra che Teorema 1 Tutti gli sviluppi di Laplace del determinante di una matrice quadrata rispetto alle sue varie colonne danno lo stesso risultato 3 La definizione di determinante data ora e coerente con la definizione di determinante data nella lezione scorsa per le matrici quadrate di ordine 2 Infatti: lo sviluppo di Laplace secondo la prima colonna porge a 11 a 12 a 21 a 22 ε 11a 11 M 11 + ε 21 a 21 M 21 +a 11 a 22 a 21 a 12, e lo sviluppo di Laplace secondo la seconda colonna porge a 11 a 12 a 21 a 22 ε 12a 12 M 12 + ε 22 a 22 M 22 a 12 a 21 + a 22 a 11 I due sviluppi sono uguali per la proprieta commutativa dei numeri reali 4 Passiamo ora alle matrici quadrate del terzo ordine Consideriamo ad esempio la matrice Gli sviluppi del suo determinate sono: rispetto alla prima colonna: ( ) + 7( ) 2 4( 4) + 7( 3) 3; rispetto alla seconda colonna:
4 2( ) + 5( ) 8( ) 2( 2) + 5( 11) 8( 6) 3; rispetto alla terza colonna: ( ) 6( ) + 10( ) 3( 3) 6( 6) + 10( 3) 3 5 Il determinate della generica matrice quadrata del terzo ordine, a 1 b 1 c 1 a 2 b 2 c 2, a 3 b 3 c 3 sviluppato rispetto alla prima colonna, e a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 +a 1 b 2 c 2 b 3 c 3 a 2 b 1 c 1 b 3 c 3 + a 3 b 1 c 1 b 2 c 2 a 1 (b 2 c 3 b 3 c 2 ) a 2 (b 1 c 3 b 3 c 1 ) + a 3 (b 1 c 2 b 2 c 1 ) a 1 b 2 c 3 a 1 b 3 c 2 a 2 b 1 c 3 + a 2 b 3 c 1 + a 3 b 1 c 2 a 3 b 2 c 1 Abbiamo ottenuto un polinomio nelle nove variabili a i, b j, c k, osserviamo che: e omogeneo di terzo grado; e somma con segni di termini del tipo a i b j c k ; le terne di indici (i, j, k) variano fra tutte le permutazioni (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) della terna (1, 2, 3) Gli sviluppi rispetto alle altre colonne danno lo stesso polinomio, scritto in altro modo 6 Consideriamo ora, fra le matrici del terzo ordine, quelle a scala L unica matrice a scala di rango 0 e la matrice nulla, che ha determinante 0 Le matrici a scala di rango 1 sono del tipo a 1 b 1 c , dove la prima riga non e nulla; queste matrici hanno determinante 0 Le matrici a scala di rango 2 sono del tipo a 1 b 1 c 1 0 b 2 c 2,
5 dove la prima riga e la seconda riga sono non nulle, e il pivot della seconda riga e strettamente a destra del pivot della prima; queste matrici hanno determinante 0 Le matrici a scala di rango 3 sono del tipo a 1 b 1 c 1 0 b 2 c c 3 dove a 1, b 2, c 3 sono i pivot; il determinante e dato da a 1 b 1 c 1 0 b 2 c c 3 a 1b 2 c 3 0 Abbiamo dunque visto che, per una matrice a scala del terzo ordine si ha: se il rango della matrice e minore di 3, allora il suo determinante e 0, se il rango della matrice e 3, allora il suo determinante e uguale al prodotto dei suoi pivot, dunque diverso da 0 7 La generica matrice a scala di ordine n e del tipo d 1 0 d d 3, d n con le dovute condizioni sui pivot delle righe Sviluppando i determinanti sempre rispetto alla prima colonna si ha d 1 0 d d d n d 2 0 d 3 d 3 d 1 d 1 d 2 d 1 d 2 d n 0 0 d n 0 d n Dunque, se S e una matrice quadrata di ordine n, a scala con elementi diagonali d 1,, d n, allora S d 1 d 2 d n Osserviamo che: se r(s) < n, allora d n 0 e dunque S 0;, se r(s) n, allora d 1,, d n 0 e dunque S 0 5
6 8 Proprieta rispetto alle righe Una matrice quadrata di ordine n puo essere riguardata come una colonna di n righe, ciascuna con n componenti scalari r 2 Cosi, il determinante di una matrice quadrata di ordine n, che e appunto una funzione di una variabile matrice quadrata di ordine n, puo essere riguardato come una funzione di n variabili vettoriali in R n r 2 r 2 In quest ottica, le proprieta salienti del detrminante sono le seguenti se tre matrici A, B, C di ordine n sono in tutto uguali, tranne che nella riga i ma, e se la riga i ma di A e la somma della riga i ma di B con la riga i ma di C, allora A B + C ; in altri termini, s i + t i s i + t i ; se due matrici A, B di ordine n sono in tutto uguali, tranne che nella riga i ma, e se la riga i ma di A e il prodotto di uno scalare α per la riga i ma di B, allora A α B ; in altri termini, αr ị α r i ; se A e B sono matrici di ordine n che differiscono fra loro solo per uno 6
7 scambio di righe, allora A B ; in altri termini, s t t s ; se una matrice A ha due righe uguali, allora A 0; in altri termini, s s 0 Non dimostriamo queste proprieta 9 Siamo ora in grado di stabilire l effetto che le operazioni elementari sulle righe,, della generica matrice A quadrata di ordine n hanno sul determinante di A moltiplicare una riga di A per uno scalare α R ha per effetto moltiplicare il determinate di A per α; scambiare due righe di A ha per effetto cambiare segno al determinante di A; sommare ad una riga di A un multiplo scalare di un altra riga di A non ha alcun effetto sul determinante di A, lo lascia invariato Per semplicita di scrittura, verifichiamo che sommare alla seconda riga di A un multiplo scalare della prima riga di A non ha alcun effetto sul determinante di A : r 2 + α r 2 + α r 2 + α r 2 ; Dunque possiamo usare l algoritmo di Gauss per calcolare il determinante di una matrice numerica Ad esempio
8 10 Siamo ora nella posizione di stabilire e provare la relazione fra rango e determinante di una matrice quadrata Teorema 2 Una matrice A quadrata di ordine n ha rango massimo n se e solo se il suo determinante e diverso da 0: r(a) n A 0 Dim Applichiamo ad A l algoritmo di Gauss, ed otteniamo una matrice a scala S Le operazioni elementari lasciano invariato il rango di una matrice, dunque il rango di A e n se e solo se il rango di S e n Ora, il rango della una matrice a scala S e n se e solo se il deteriminante di S e diverso da 0 Applichiamo ad S le operazioni elementari inverse in ordine inverso, ed otteniamo A Le operazioni elementari lasciano invariato l annullarsi/non annullarsi del determinante, dunque il determinante di S e diverso da 0 se e solo se il determinate di A e diverso da 0 Riassumendo: r(a) n r(s) n S 0 A 0; dunque r(a) n A 0 11 Trasposizione, sviluppi per righe Nella prima parte del corso si e visto il rilevante teorema secondo il quale il rango per righe di una matrice e uguale al suo rango per colonne; in altri termini, il rango di una matrice e uguale al rango della matrice trasposta Un teorema analogo vale per il determinante Teorema 3 Il determinante di una matrice quadrata A e uguale al determinate della matrice trasposta A T : A A T Questo teorema e ovvio per le matrici di ordine 1, immediato per le matrici di ordine 2, dimostrabile direttamente per le matrici di ordine 3; nel caso generale, puo essere dimostrato riconducendosi al caso delle matrici a scala, ed usando il teorema sulla equivalenza degli sviluppi di Laplace per colonne; non diamo la dimostrazione Per questo teorema, il determinante di una matrice A quadrata di ordine n puo essere definito anche come il numero reale ottenuto sommando i prodotti degli elementi di una riga di A per i rispettivi complementi algebrici, pesati con i segni dati dagli ε Precisamente: A ε i1 a i1 M i1 + ε i2 a i2 M i2 + + ε in a in M in 8
9 dove i e un qualsiasi indice scelto fra 1, 2,, n Questa espressione viene detta sviluppo di Laplace del determinante di A secondo la riga i ma In definitiva, si ha che tutti gli sviluppi di Laplace del determinante di una matrice quadrata, rispetto alle varie righe ed alle varie colonne danno lo stesso risultato 12 Proprieta rispetto alle colonne Una matrice quadrata di ordine n puo essere riguardata come una riga di n colonne, ciascuna con n componenti scalari [c 1, c 2,, c n ] Cosi, il determinante di una matrice quadrata di ordine n, che e appunto una funzione di una variabile matrice quadrata di ordine n, puo essere riguardato come una funzione di n variabili vettoriali in R n [c 1, c 2,, c n ] c 1, c 2,, c n In quest ottica, le proprieta salienti del determinante sono le seguenti se tre matrici A, B, C di ordine n sono in tutto uguali, tranne che nella colonna j ma, e se la colonna j ma di A e la somma della colonna j ma di B con la colonna j ma di C, allora A B + C ; in altri termini, c 1,, f j + g j,, c n c 1,, f j,, c n + c 1,, g j,, c n ; se due matrici A, B di ordine n sono in tutto uguali, tranne che nella colonna j ma, e se la colonna j ma di A e il prodotto di uno scalare α per la colonna j ma di B, allora A α B ; in altri termini, c 1,, αc j,, c n α c 1,, c j,, c n ; se A e B sono matrici di ordine n che differiscono fra loro solo per uno scambio di colonne, allora A B ; in altri termini,, g,, f,, f,, g, ; se una matrice A ha due colonne uguali, allora A 0; in altri termini,, f,, f, 0 Queste proprieta del determinante rispetto alle colonne, per il teorema della sezione precedente, seguono dalle proprieta del determinante rispetto alle righe 13 Sistemi lineari 9
10 Teorema 4 Sia A una matrice quadrata di ordine n, e b R n il sistema lineare omogeneo Ax 0 ha solo la soluzione banale x 0 se e solo se A 0 il sistema lineare Ax b ha una ed una sola soluzione se e solo se A 0 Dim Dimostriamo la seconda parte dell enunciato; la prima e una sua conseguenza Consideriamo la matrice completa [A b] associata al sistema Ax b, applichiamo l algoritmo di Gauss, ed otteniamo una matrice a scala [S c], associata al sistema a scala Sx c Ora: il sistema Ax b ha una ed una sola soluzione se e solo se il sistema Sx c ha una ed una sola soluzione; il sistema Sx c ha una ed una sola soluzione se e solo se il determinante di S e diverso da 0; il determinante di S e diverso da zero se e solo se il determinante di A e diverso da 0 Dunque, il sistema Ax b ha una ed una sola soluzione se e solo se A 0 La regola di Cramer si estende dal caso n 2 al caso generale Teorema 5 Sia dato un sistema lineare di n equazioni nelle n incognite x 1,, x n, a 11 x a 1n x n b 1, in breve a 1 x a n x n b, a n1 x a nn x n b n dove a 1,, a n, b sono le colonne dei coefficienti e la colonna dei termini noti Sotto la condizione a 1, a 2,, a n 0, il sistema ha una ed una sola soluzione, data da x i a 1,, b,, a n, i 1, 2,, n a 1,, a i,, a n Dim Sia i un indice fissato fra 1, 2, n L uguaglianza fra vettori colonna n a j x j b j1 implica l uguaglianza fra le matrici ottenute dalla matrice dei coefficienti [a 1,, a i,, a n ] sostituendo alla colonna i ma da una parte la colonna n 1 a jx j e dall altra la colonna b : [ a 1,, ] n a j x j,, a n [a 1,, b,, a n ] j1 10
11 Questa uguaglianza fra matrici implica l uguaglianza fra i loro determinanti: n a 1,, a j x j,, a n a 1,, b,, a n j1 Applicando le proprieta dei determinanti, il primo membro puo essere riscritto n n a 1,, a j x j,, a n a 1,, a j x j,, a n j1 j1 n a 1,, a j,, a n x j j1 a 1,, a i,, a n x i ; l ultimo passaggio deriva dal fatto che per j i nella matrice [a 1,, a j,, a n ] la colonna i e la colonna j ma sono uguali, cosi a 1,, a j,, a n 0 Dunque si ha l equazione a 1,, a i,, a n x i a 1,, b,, a n dalla quale, essendo a 1,, a i,, a n 0, si ricava x i a 1,, b,, a n a 1,, a i,, a n 14 Interpolazione, determinante di Vandermonde Sia dato un fenomeno descritto da due variabili x e y, e siano date n osservazioni (x 1, y 1 ), (x 2, y 2 ), (x n, y n ) Supposto che la variabile y dipenda dalla variabile x, si cerca una funzione y f(x) che sia compatibile con le osservazioni, cioe tale che y 1 f(x 1 ), y 2 f(x 2 ), y n f(x n ) Un primo modo di affrontare il problema e cercare la funzione f fra le funzioni polinomiali di grado n 1 f(x) c 0 + c 1 x + +c 2 x c n 1 x n 1 Imponendo le condizioni di compatibilita con le osservazioni, si ottiene il sistema y 1 c 0 + c 1 x 1 + c 2 x c n 1 x1 n 1 y 2 c 0 + c 1 x 2 + c 2 x c n 1 x2 n 1 y n c 0 + c 1 x n + c 2 x 2 n + + c n 1 x n 1 n 11
12 di n equazioni lineari nelle n incognite c 0, c 1,, c n 1 Il determinante della matrice dei coefficienti e 1 x 1 x 2 1 x n x 2 x 2 2 x n x 3 x 2 3 x n 1 3 ; 1 x n x 2 n x n 1 n viene detto determinante di Vandermonde di ordine n Per n 2 abbiamo 1 x 1 1 x 2 Per n 3 abbiamo 1 x 1 x x 2 x x 3 x 2 3 In generale, si prova che x 2 x 1 1 x 1 x x 2 x 1 x 2 2 x x 3 x 1 x 2 3 x 2 1 (x 2 x 1 )(x 3 x 1 ) (x 2 x 1 )(x 3 x 1 ) 1 x 1 x x 2 x 1 (x 2 x 1 )(x 2 + x 1 ) 0 x 3 x 1 (x 3 x 1 )(x 3 + x 1 ) (x 2 x 1 )(x 3 x 1 )(x 3 x 2 ) 1 x 1 x 2 1 x n x 2 x 2 2 x n x 3 x 2 3 x n x n x 2 n x n 1 n n h>k 1 1 x 1 x x 2 + x x 3 + x 1 1 x 1 x x 2 + x x 3 x 2 (x h x k ) Per il teorema sui sistemi lineari e i determinanti, abbiamo dunque che Sotto le condizioni x h x k, h k, il polinomio cercato esiste ed e unico I coefficienti del polinomio possono essere ricavati con la regola di Cramer 12
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Matematica II,
 Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
1. Un sistema di m equazioni lineari in n incognite x 1,... x n aventi tutte termine noto nullo A =...
 Algebra/ Algebra Lineare, 230207 1 Un sistema di m equazioni lineari in n incognite x 1, x n aventi tutte termine noto nullo a i1 x 1 + a i2 x 2 + + a in x n = 0, i = 1,, m si dice omogeneo; ponendo x
Algebra/ Algebra Lineare, 230207 1 Un sistema di m equazioni lineari in n incognite x 1, x n aventi tutte termine noto nullo a i1 x 1 + a i2 x 2 + + a in x n = 0, i = 1,, m si dice omogeneo; ponendo x
Sistemi di equazioni lineari
 Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Matematica II,
 Matematica II 181111 1 Matrici a scala Data una riga R = [a 1 a 2 a n ] di numeri reali non tutti nulli il primo elemento non nullo di R si dice pivot di R Cosi il pivot di R compare come j mo elemento
Matematica II 181111 1 Matrici a scala Data una riga R = [a 1 a 2 a n ] di numeri reali non tutti nulli il primo elemento non nullo di R si dice pivot di R Cosi il pivot di R compare come j mo elemento
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Corso introduttivo pluridisciplinare Matrici e sistemi lineari
 Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
1 Risoluzione di sistemi lineari con l uso dei determinanti
 2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
2006 Trapani Dispensa di Geometria, 1 Risoluzione di sistemi lineari con l uso dei determinanti Sia A una matrice n n con det(a) 0 consideriamo il sistema lineare AX = b abbiamo n = numero di righe di
DETERMINANTE DI MATRICI QUADRATE
 DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Soluzioni del Foglio 2 I sistemi lineari
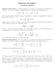 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Testi consigliati e contatti
 Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Esercizi di Algebra Lineare Determinanti
 Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
ESERCIZI DI ALGEBRA LINEARE. Vincenzo Di Gennaro
 ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
Istituzioni di Matematiche sesta parte
 Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 19 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 19 Capitolo
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
I determinanti. a11 a A = 12 a 21 a 22
 I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Appunti di Geometria - 2
 Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
ESERCIZI DI ALGEBRA LINEARE. Vincenzo Di Gennaro
 ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria che ho tenuto presso la
ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria che ho tenuto presso la
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
Lezione 8: Determinante e Inversa
 Lezione 8: Determinante e Inversa In questa lezione vogliamo descrivere due concetti fondamentali, il determinante, che è un numero associato ad ogni matrice quadrata, e l inversa di una matrice. L importanza
Lezione 8: Determinante e Inversa In questa lezione vogliamo descrivere due concetti fondamentali, il determinante, che è un numero associato ad ogni matrice quadrata, e l inversa di una matrice. L importanza
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
Matematica II,
 Matematica II, 171110 1 processo di triangolarizzazione, esempio I Consideriamo il sistema lineare di tre equazioni nelle incognite x, y, z 2x + 3y + 4z = 8 4x + 9y + 16z = 14 8x + 27y + 64z = 14 Primo
Matematica II, 171110 1 processo di triangolarizzazione, esempio I Consideriamo il sistema lineare di tre equazioni nelle incognite x, y, z 2x + 3y + 4z = 8 4x + 9y + 16z = 14 8x + 27y + 64z = 14 Primo
